A Deep Reinforcement Learning with Gumbel Distribution Approach for Contention Window Optimization in IEEE 802.11 Networks

1  Introduction

The exponential growth in connected devices continues to heighten collision risks in wireless networks, motivating extensive research on enhancing network performance. For instance, Ahamad et al. [1] propose dynamic power control schemes to mitigate interference in Device to Device (D2D)-enhanced 5G networks, thereby boosting network performance, while Sivaram et al. [2] integrated Dual Busy Tone Multiple Access (DBTMA) with Contention-aware Admission Control Protocol (CACP) to further enhanced the bandwidth utilization. Likewise, Binzagr et al. [3] propose energy-efficient resource allocation schemes that considerably improve system performance. In IEEE 802.11 (Wi-Fi) networks, reducing collisions is essential for throughput enhancement, and the Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) technique [4] dynamically adjusts the Contention Window (CW) to mitigate initial transmission collisions. Consequently, optimizing CW size is vital to sustaining robust Wi-Fi performance.

Early CW optimization methods have predominantly relied on non-learning-based strategies. For example, Adaptive Contention Window Control (ACWC) [5] employs a single backoff stage while preserving the standard IEEE 802.11 protocol, and Probability-based Opportunity Dynamic Adaptation (PODA) [6] extends the Binary Exponential Backoff (BEB) algorithm by adaptively modifying the CW minimum (CWminimum) prior to contention. Other approaches, such as Exponential Increase Exponential Decrease (EIED) [7] and Linear Increase Linear Decrease (LILD) [8], modify the CW size using fixed exponential or linear increments/decrements, simultaneously. Similarly, a contention method [9] increases CW upon collision and resets CW after successful transmissions. The Smart Exponential-Threshold-Linear backoff algorithm (SETL) [10] further refines the above methods by optimizing the CW Threshold (CWThreshold), surpassing EIED and LILD in packet transmission metrics. Nevertheless, these deterministic approaches [4–10] rely on predetermined adjustments demanded by dynamic network scenarios, underscoring the need for more flexible, learning-based solutions.

Machine Learning (ML) approaches have gained traction for addressing complex tasks, with Reinforcement Learning (RL) [11] emerging as a robust technique for selecting optimal CW values. Several studies [12–17] have employed Q-learning algorithms to dynamically adjust CW sizes, using observed transmission successes and collisions as feedback to optimize performance. However, the exhaustive exploration of state–action pairs in traditional Q-learning proves computationally demanding, prompting the transition to Deep Q-learning Networks (DQNs) [18], which utilizes Deep Neural Networks (DNNs) for efficient state–action mapping. As a branch of Deep Reinforcement Learning (DRL), DQN exemplifies how deep models enhance policy learning under high-dimensional and dynamic environments. DRL has also been utilized in secure networked systems, including data aggregation in edge-enabled IoT [19] and trust management in 5G vehicular infrastructures [20], demonstrating its flexibility in complex decision-making tasks. Similarly, in the context of IEEE 802.11 networks, DQN-based applications for CW adaptation include drone networks [21], centralized schemes like the Centralized Contention Window Optimization with the DQN model (CCOD-DQN) [22], and methods incorporating additional performance metrics [23,24]. More recently, integration of the SETL mechanism with the DQN framework [25,26] has been proposed for CWThreshold optimization in various network scenarios. Nonetheless, DQN-based methods [18–26] are still prone to overestimation bias, particularly under severe contention, undermining decision-making in dense Wi-Fi settings.

Grounded in Van Hasselt et al. [27], Double DQN (DDQN) reduces overestimation bias by decoupling action selection from value estimation, using an online network for action selection and a target network for stable Q-value updates. Asaf et al. [28] extend this concept to the DRL-based Contention Window Optimization (DCWO) method, a DDQN-based improvement of CCOD-DQN [22]. Yet, DCWO-DDQN continues to rely on the classic CSMA/CA process [4] and frequently expands CW to its maximum (CWmaximum) under heavy congestion, prolonging backoff periods and raising latency. To tackle these challenges, we propose SETL-DDQN, which incorporates a dynamic threshold-based CW adjustment mechanism [10] within the DDQN framework to design adaptively fine-tunes the CW in response to change network states, improving Q-value accuracy. However, the standard ε-greedy exploration used in DQN/DDQN models provides only limited coverage of the action space in stochastic wireless environments. As a result, agents converge more slowly and struggle to adapt when network load fluctuates, making it hard to discover globally optimal CW settings. To address this, we further propose SETL-DDQN(Gumbel), with an adoption of Gumbel mechanism that employs smooth, differentiable sampling of discrete actions via Gumbel-Softmax technique using its extreme value theory [29], which better captures stochastic and extreme behaviors in network contention, ensuring a more comprehensive exploration of the action space rather than uniform random action selection.

The Gumbel distribution has proven effective in many fields for modeling rare and extreme events. In transportation [30], it improves predictions of unpredictable pedestrian movements. In healthcare [31], it handles asymmetric and extreme medical data better than traditional models. For communication systems [32], it captures rare signal fades to boost reliability, supports smart node selection under constraints [33], and models delays in energy-harvesting systems [34]. These successes highlight Gumbel’s advantage in various scenarios, supporting its use in our SETL-DDQN(Gumbel) design. To the best of our knowledge, this is the first work to incorporate a Gumbel distribution method into DRL for CW optimization under IEEE 802.11 network scenarios. This unified design mitigates overestimation and selection bias while reinforcing the model’s adaptability in congested or uncertain network conditions, ultimately driving substantial improvements in overall network performance.

To summarize, this study presents three main contributions: (i) We propose SETL-DDQN, a threshold-based CW control scheme integrated DDQN model for decoupling action selection from value estimation to reduce the overestimation bias error. This approach enables scalable and adaptive CW optimization across diverse IEEE 802.11 topologies, reducing packet delays and stabilizing throughput. (ii) We further introduce SETL-DDQN(Gumbel), a Gumbel distribution integrated to SETL-DDQN that leverages an extreme value theory [29] to capture distributed stochastic action space exploration via Gumbel-Softmax technique, leading to more robust and high-impact CW decisions in dense scenarios. (iii) Comprehensive simulations in both static and time-varying IEEE 802.11 scenarios show that SETL-DDQN and SETL-DDQN(Gumbel) outperform existing methods—including the IEEE 802.11 standard [4], SETL [10], CCOD-DQN [22], SETL-DQN [25], SETL-DQN(MA) [26], and DCWO-DDQN [28]—by delivering higher throughput, lower collision rates, and superior adaptability to various network conditions.

2  Related Works

2.1 The Q-Learning for CW Optimization

Q-learning approaches have been widely investigated to optimize CW parameters and enhance throughput in IEEE 802.11 networks. Kim & Hwang [12] propose a Q-learning algorithm where Stations (STAs) select backoff values that maximize transmission success probability, while Zerguine et al. [13] employ Q-learning in Mobile Ad-hoc Networks (MANETs), adjusting CW based on the cumulative success transmissions and collisions. Kwon et al. [14] apply Q-learning in Wireless Body Area Networks (WBANs) by leveraging Acknowledgment (ACK) feedback for improved reliability. Pan et al. [15] jointly optimize CW and Transmission Opportunity (TxOP) to increase throughput, and Lee et al. [16] introduce a Frame Size Control (FSC) mechanism to address the throughput drop at high node densities. Zheng et al. [17] further refine the learning process via ε-greedy adjustments and learning rate tuning, enhancing Medium Access Control (MAC)-level performance under diverse traffic conditions.

2.2 The DQN-Based Approaches for Scalable CW Adaptation

To overcome Q-learning’s high computational overhead, DQNs have been implemented for CW adaptation in network with high STAs density and dynamic traffic scenarios. Subash & Nithya [21] leverage DQN in high-mobility, interference-prone aerial networks to reduce collisions by CW tuning, while Wydmański & Szott [22] propose the CCOD-DQN framework for centralized CW decisions under varying traffic patterns. Sheila de Cássia et al. [23] argument CCOD-DQN with average queue length as an additional observation, and Lei et al. [24] further develop DQN-CSMA/CA to better accommodate dynamic Wi-Fi usage. Ke & Astuti [25,26] integrate the SETL algorithm [10] with DQN for single- and multi-agent CWThreshold tuning, outperforming classical centralized solutions in throughput measures.

2.3 The DDQN Enhancements and Remaining Gaps

In dense Wi-Fi networks, DQN offers a scalable framework but struggles with Q-value overestimation under noisy conditions, resulting in overly aggressive CW settings that increase collisions and decrease throughput. Asaf et al. [28] introduced DCWO, a DDQN-based enhancement of CCOD-DQN [22] designed to mitigate this bias by decoupling action selection from value estimation. However, DCWO remains bound to the conventional CSMA/CA mechanism [4] and frequently adjusts the CW to its CWmaximum under heavy loads, which increases latency and extends backoff times. Its ε-greedy policy also constrains action diversity, slowing convergence and diminishing adaptability in dynamic environments.

In response, we present SETL-DDQN and SETL-DDQN(Gumbel) for CW optimization in dense Wi-Fi environments. SETL-DDQN integrates a threshold-based CW adjustment within the DDQN framework to enable rapid adaptation. Recognizing the non-linear and highly variable characteristic of wireless channels, we note that the standard ε-greedy exploration owing to its uniform sampling of non-greedy actions, which suffers from sample inefficiency and a lack of sensitivity to high-reward extremes, hindering the identification of optimal CW values. We thus adopt a distribution more suitable for non-linearity and extreme variations. Motivated by extreme value theory [29], the Gumbel distribution effectively captures heavy-tail behavior and asymmetrical load fluctuations via Gumbel-Softmax technique, accommodating abrupt shifts and outliers in packet transmission demand. This approach underscores the importance of selecting robust distributions that broaden policy searches and counter selection bias in volatile wireless environments.

Our decision to use the Gumbel distribution in DRL is supported by its proven success in various fields for modeling uncertainty and extreme events. Astuti et al. [30] applied a Gumbel-based Transformer network to capture sudden and discrete changes in pedestrian and cyclist trajectories. Daud et al. [31] introduced an extended Gumbel model to represent asymmetric and heavy-tailed distributions in biomedical data. Mehrnia & Coleri [32] used extreme value theory with Gumbel-related modeling to describe rare fading events in wireless systems. Strypsteen & Bertrand [33] incorporated Conditional Gumbel-Softmax for selecting features and nodes under constraints in sensor networks. Miridakis et al. [34] modeled the extreme Age of Information (AoI) in energy-harvesting systems using the Gumbel distribution to enable analytical characterizations. These studies demonstrate that the Gumbel distribution is a flexible and reliable tool for capturing irregular, high-impact behaviors. Based on this, our SETL-DDQN(Gumbel) incorporates Gumbel-Softmax sampling via extreme value theory to improve exploration under static and time-varying Wi-Fi network conditions.

3  Applying DRL to IEEE 802.11 Networks

3.1 The System Model

We consider an IEEE 802.11 network comprising a single Access Point (AP) and a set of N STAs, each employing a collision-avoidance backoff protocol for packet transmission. The collisions occur when two or more STAs transmit simultaneously, while successful delivery requires only one STA transmitting in a time slot. The goal of this work is to maximize throughput and minimize collisions via efficient CW management.

In this study, we employ a threshold-based CW approach [10], where a fixed CWThreshold=512 to distinguish between light and heavy traffic situations. Under light load (i.e., CW <CWThreshold), the CW doubles after a collision and halves upon a successful transmission, ensuring prompt medium access in low contention scenarios. Conversely, under heavy load (i.e., CW≥CWThreshold), the CW is adjusted by a minimum step (CWminimum) after collisions or successes to prevent excessive expansion and stabilize the channel. This dual-mode mechanism enables rapid adaptation to variable traffic levels, reducing collisions and maintaining higher throughput.

To further optimize CW adaptation, we develop our SETL-DDQN and SETL-DDQN(Gumbel) frameworks in a centralized, single-agent configuration at the AP. The AP collects collision and throughput metrics from the STAs (via management frames or feedback), aggregates these into a global CW configuration, and periodically broadcasts the updated CWThreshold settings through beacon frames. This centralized control ensures that all STAs operate with synchronized and adaptive backoff behavior. Since each STA observes only its local channel conditions, we model the network environment as a Partially Observable Markov Decision Process (POMDP) [35], which captures the limitations of partial observability and guides the agent’s adaptation strategy.

3.2 The Problem Formulation

To address the decision-making process within a partially observable wireless environment, we formulate our DRL-based CW optimization as a POMDP [35]. The framework is characterized by the tuple {S,A,T,Ω,O,γ,R}, where each element captures a distinct aspect of the learning process.

Here, S denotes the set of states describing the connected STAs and their respective transmission conditions—each state s∈S encodes information regarding network occupancy, contention levels, and ongoing transmissions at a given time.

The action set A comprises all possible adjustments of the CWThreshold, allowing the AP agent to manage both light and heavy traffic by selecting discrete threshold indices a∈{0,1,…,7}. The updated CWThreshold is calculated according to:

CWThreshold=27×(1+a),(1)

where CWThreshold could be resulted in from 128 up to 1024, depending on the network conditions and the number of STAs.

The transition probability T(st+1|st,a) describes how the network stochastically evolves from state st to st+1 once the agent executes to a new CWThreshold. In this process, collision rates, channel occupancy, and queue states may fluctuate.

The observable quantity Ω is defined by the instantaneous collision probability Pcol, indicating the likelihood of transmission failures at each timestep. We define:

Pcol=(Nt−Nr)Nt,(2)

where Nt denotes the total number of frames transmitted by the STAs, and Nr signifies the number of frames successfully received by the AP (e.g., confirmed via ACKs). As each STA manages its own transmissions, the AP aggregates Nt and infers Nr to derive a global collision profile.

Given the partial observability of the environment, O consists of historical collision records H(Pcol), allowing the agent to analyze both past and current Pcol values, thereby tracking network load fluctuation and the impact of prior actions on collision rates.

The discount coefficient γ∈[0,1] balances short-term versus long-term rewards, ensuring that the CW adaptation strategy considers both immediate throughput gains and sustained performance.

Finally, the reward function R∈[0, 1] is designed to maximize normalized saturation throughput, measured in successfully transmitted bits per second. After each action, the agent updates its policy based on the observed throughput to prioritize decisions that enhance the packet transmissions and reduce collisions.

As detailed above, Fig. 1 illustrates the uplink transmission process, where STAs transmit packets to the AP while the centralized agent dynamically adjusts the most appropriate CWThreshold to effectively manage contention in dynamic network conditions.

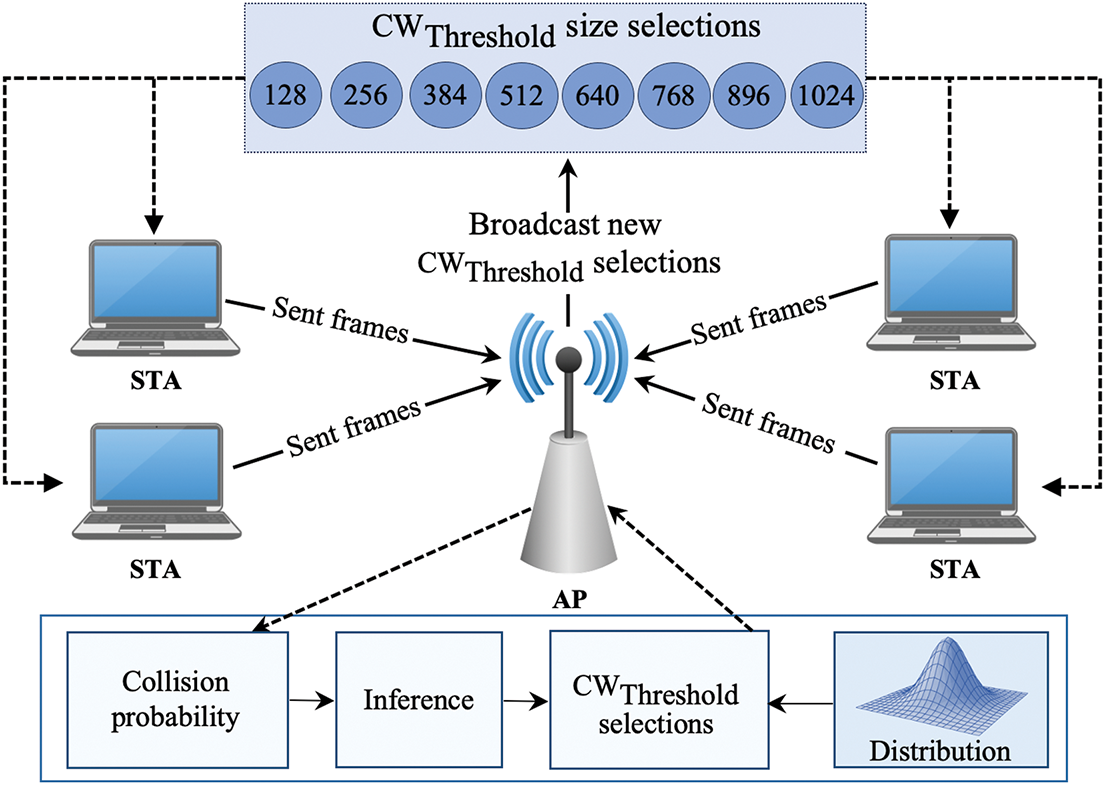
Figure 1: The proposed SETL-DDQN and additional Gumbel distribution frameworks manages STA-initiated data transmission via centralized CWThreshold selection, dynamically balancing backoff procedures and throughput to optimize performance in both static and time-varying network conditions

4  The Proposed SETL-DDQN and SETL-DDQN(Gumbel) Schemes

In our proposed schemes, the key contribution is to integrate DDQN with a dynamic CW adjustment mechanism, reducing overestimation bias and improving learning stability. We proposed two schemes—SETL-DDQN and SETL-DDQN(Gumbel)—to optimize the CWThreshold selection in IEEE 802.11 networks through advanced exploration strategies and robust value estimation.

4.1 The DDQN-Based CW Optimization

In the SETL-DDQN architecture, two neural networks are maintained—a primary (online) network with parameters θ and a secondary (target) network with parameters θ′. Both networks initially share identical weights. Let (st,at,rt+1,st+1) denote the agent’s state–action transitions, where st represents the partial channel state observed at time t and at is the discrete action that adjusts the CWThreshold (see Section 3). The immediate reward rt+1 indicates the normalized throughput gain after the adjustment, while st+1 captures the updated channel state.

(1) The DDQN Update Rule: To mitigate overestimation bias common to single network DQN, SETL-DDQN applies the following update:

YtDDQN=rt+1+γQ(st+1,argmaxa Q(st+1,a;θ);θ′),(3)

where Q(⋅;θ) is the online network. The term argmaxa Q(st+1,a;θ) selects the best action, while Q(⋅;θ′) denotes the target network to provide its evaluation. This separation reduces positive bias and stabilizes learning in heavy load scenarios.

(2) The Loss Function and Experience Replay: We minimize the following loss function to update the parameters θ:

ℒ(θ)=E(st,at,rt+1,st+1)∼D[(Q(st,at;θ)−YtDDQN)2],(4)

where D denotes the replay buffer storing past transitions. Sampling mini-batches from D improves data efficiency and helps the model converge. We also periodically synchronize θ→θ′ to reduce non-stationary updates.

(3) The ε-Greedy Exploration: In basic SETL-DDQN, we adopt an ε-greedy strategy to balance exploration and exploitation. At each step, a random value ξ∼𝒰(0,1) is drawn. If ξ<ε, the agent randomly selects an action from {0,…,7}; otherwise, it exploits the actions with the highest Q-value from the online network. Over time, ε linearly decreases to a small bound, guiding the agent toward exploitation.

The interaction between SETL mechanism and DDQN model is illustrated in Fig. 2. The agent begins by observing the network state st (e.g., collision rate and past performance). This state is processed by the SETL logic, which computes a dynamic CWThreshold value based on Eq. (1). Using this CWThreshold, SETL filters the full action space into a valid subset At, excluding actions outside the useful CW range for the current network condition. The online Q-network then evaluates only the filtered actions, and an action at is selected using an ε-greedy policy. The chosen at∈CWThreshold is applied to all STAs, influencing their backoff behavior. The environment responds with the next state st+1 and reward rt+1, reflecting throughput and collision outcomes. This transition (st,at,rt+1,st+1) is stored in the replay buffer. A mini-batch is then sampled to train the online network, using targets from the periodically updated target network. The Q-value difference is minimized via gradient descent to complete the learning step. This design reduces the action space to relevant CW ranges, improving learning efficiency while reducing the impact of discretization bias common in fixed-threshold approaches.

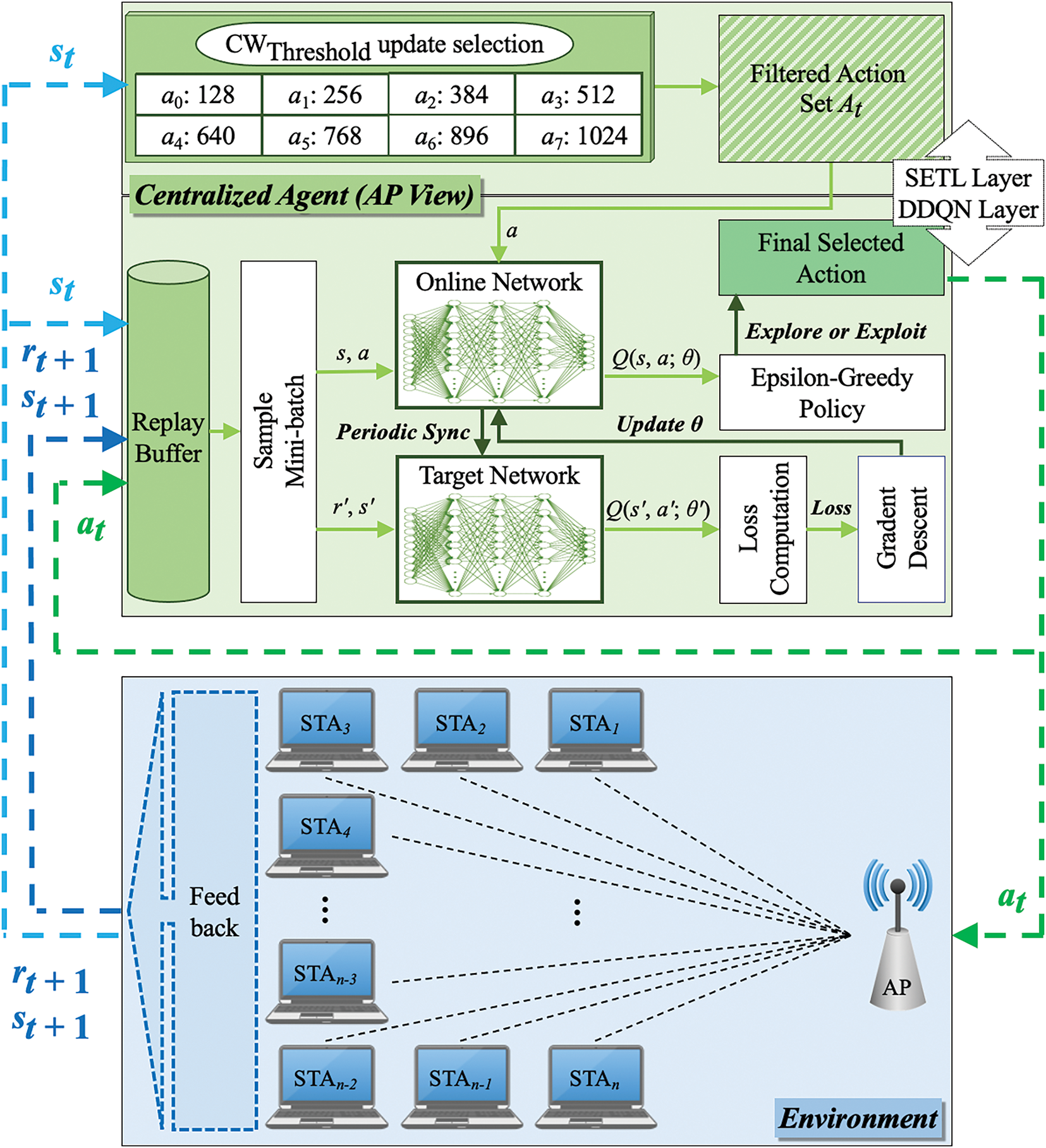
Figure 2: The SETL-DDQN framework is a centralized CW control architecture that integrates a SETL layer with a DDQN layer, enabling efficient and adaptive CWThreshold selection through filtered action spaces and optimal decision-making under varying network conditions with STA interaction

However, the ε-greedy exploration used in DQN/DDQN models may not sufficiently sample actions from the extreme tails of the reward distribution. Meanwhile, we address this limitation by integrating the Gumbel-enhanced exploration via extreme value theory [29].

4.2 The Gumbel-Enhanced Exploration via Extreme Value Theory

This study further proposes SETL-DDQN(Gumbel), which leverages extreme value theory by incorporating Gumbel noise for stochastic action sampling, increasing exploration diversity and refining CW optimization under different level of traffic loads.

(1) The Gumbel Noise Generation: To introduce stochasticity that targets extreme rewards, we generate Gumbel noise to capture extreme tail behaviors using inverse transform sampling. Specifically, we first sample U from a uniform distribution, where U∼𝒰(0,1). Then, computing the noise g as:

g=−ln⁡[−ln⁡(U+ε′)+ε′],(5)

where ln denotes the natural logarithm and ε′ is a small constant to ensure numerical stability. Here, the inner operation −ln⁡(U+ε′) transforms the uniform variable U into an exponential-like form, and the outer −ln⁡(⋅) converts this into Gumbel-distributed noise, thereby emphasizing extreme tail events.

(2) The Action Sampling Strategies: Once the noise g is generated, we introduce several sampling techniques based on Gumbel noise [36] to increase exploration diversity under different traffic conditions. Each method adds randomness to the Q-values in different ways, influencing the agent’s action selection policy during training. Let Q(s;θ)∈RK be the unnormalized Q-values from the online network, where K=8 is the possible discrete CW actions, and let g∼Gumbel(0,1)K is a vector of independent noise samples drawn via inverse transform sampling. The final action output is denoted by y∗, where ∗ specifies the variant name. The design and properties of each strategy are described as follows.

The Gumbel-Max Sampling (ymax). This method selects the action with the highest perturbed Q-value. It adds Gumbel noise to each Q-value and chooses the index with the maximum sum. The selected action is calculated as:

ymax=argmax(Q(s;θ)+g).(6)

This strategy is equal to the classical Gumbel trick, often used for sampling from categorical distributions, and supports non-uniform but deterministic exploration with ε-greedy fallback.

The Gumbel-Softmax Sampling (ysoft). To provide smoother exploration with adjustable sampling sharpness, the Gumbel-Softmax strategy transforms the noisy Q-values into a probability distribution through scaled softmax. It is given by:

ysoft=softmax(log⁡Q(s;θ)+gτ),(7)

where log⁡Q(s;θ) converts the Q-values to a log-space representation, and τ>0 controls the peakiness of the softmax distribution. As τ→0, ysoft approximates a one-hot vector, leaning to near-deterministic action selection. Higher values of τ result in more uniform exploration across actions. This method is beneficial for continuous training and differentiable approximations.

The Top-k Gumbel Sampling (ytop−k). To limit randomness while maintaining diversity, this strategy selects the top-k actions based on their perturbed Q-values and then chooses randomly among them. Let TopKk(⋅) return the indices of the top k values. The selected action is:

ytop−k= random(TopKk(Q(s;θ)+g)),(8)

This variant ensures that exploration focuses only on a limited set of high-value actions, reducing variance while still escaping local optimal.

The Boltzmann-Gumbel Sampling (yboltz). This strategy incorporates an adaptive exploration mechanism by scaling Gumbel noise based on temporal uncertainty. For each action a, a scale factor is computed using visitation statistics. Let t denote the global training step. The action is selected as:

yboltz=argmax(Q(s;θ)+log⁡(t+ε′)Na+ε′⋅g),(9)

This method promotes actions with low visitation frequency and gradually anneals exploration as learning progresses.

By sampling a from ymax, ysoft, ytop−k, and yboltz, the agent is guided toward diverse exploration behaviors that prioritize unconventional (tail) actions, which might deliver superior throughput gains in dense Wi-Fi scenarios.

(3) The Gumbel Distribution Cumulative Distribution Function (CDF): The heavy-tailed characteristic of the Gumbel distribution is mathematically captured by its Cumulative Distribution Function (CDF), expressed as:

F(x)=exp⁡(−exp⁡(−x−μβ)).(10)

where x is representing possible Q-value outcomes. In this expression, μ is the location parameter (indicating the distribution mode) and β>0 is the scale parameter controlling the spread. The inner exponential, exp⁡(−x−μβ), measures the deviation of x from μ, and the outer exponential transforms this into a probability.

The reason for adopting the Gumbel distribution lies in its foundation in extreme value theory [29], particularly its role in modeling the distribution of the maximum of independent and identically distributed (i.i.d.) variables. This property aligns well with our goal of prioritizing high-reward actions in dynamic and stochastic wireless environments. In such settings, where contention and Q-values change rapidly, exploring extreme outcomes is important. Compared to other distributions such as Fréchet and Weibull [37], the Gumbel distribution presents two critical advantages. First, it has full support over the real line (x∈(−∞,+∞)), allowing for unrestricted modeling of reward distributions. By contrast, Fréchet is restricted to x∈(xmin,+∞) and Weibull to x∈(−∞,xmax), which may limit their applicability in environments with both low and high Q-value variance. Second, the Gumbel distribution provides a moderately heavy-tailed distribution, enabling robust sampling of high-value actions without the excessive variance risk associated with the heavy tails of Fréchet.

4.3 The Overall Procedure

As outlined in Algorithm 1, the proposed SETL-DDQN and SETL-DDQN(Gumbel) frameworks proceed through three stages: Warmup, Training, and Evaluation. During Warmup Phase, the replay buffer D is filled with initial experiences (st,at,rt+1,st+1) samples, gathered as the agent observes the instantaneous collision probabilities in Eq. (2) and throughput—where the CWThreshold is dynamically updated according to Eq. (1)—using either an ε-greedy or one of the Gumbel-enhanced sampling strategies (ymax, ysoft, ytop−k, yboltz) based on Eqs. (6)–(9), each incorporating Gumbel noise as defined in Eq. (5). Once D reaches its predefined capacity, the Training Phase begins. Here, mini-batches are sampled to update the online network by minimizing the loss defined in Eq. (4). Simultaneously, the DDQN update rule in Eq. (3) decouples action selection from evaluation to mitigate overestimation bias, and the target network is synchronized periodically for stability. As training progresses, the exploration parameter ε is gradually decay, reducing random action selection. Meanwhile, SETL-DDQN(Gumbel) adds Gumbel noise before softmax sampling, guided by the distribution’s heavy-tailed characteristics (Eq. (10)). In the final Evaluation Phase, the learned policy is applied without further updates, resulting in reduced collision rates and improved throughput in dense IEEE 802.11 networks.

4.4 The Computational Complexity Analysis

The overall computational complexity of the proposed SETL-DDQN and SETL-DDQN(Gumbel) schemes is dominated by the forward pass through the neural network and subsequent action selection. For both schemes, a single forward pass over the Q-network requires 𝒪(H⋅K), where H is the total number of hidden layer parameters and K=8 is the number of discrete CW actions. Each Gumbel-based sampling strategy introduces only lightweight elementwise operations on the output Q-values—such as noise addition (Gumbel-Max), logarithmic scaling and softmax transformation (Gumbel-Softmax), top-k selection (Top-k Gumbel), or adaptive noise scaling based on visitation (Boltzmann-Gumbel)—each of which is 𝒪(K). Therefore, the added cost of Gumbel noise generation and sampling remains negligible compared to the core inference step.

5  Evaluation Results

5.1 The Implementation Details

We implement the DRL models using a feed-forward architecture with two hidden layers (128 neurons each) activated by ReLU, and a linear output layer mapping to eight discrete CWThreshold actions. A replay buffer of capacity 20,000 gathers past transitions, with 200 warmup steps collecting initial samples before training starts. Each iteration processes a mini-batch of 32, updating network weights under a fixed 0.001 learning rate, a 0.9 discount factor, and an Adam optimizer. For the baseline SETL-DDQN, a periodically synchronized target network mitigates overestimation bias, coupled with a gradually decaying ε-greedy policy and randomness. Conversely, SETL-DDQN(Gumbel) incorporates Gumbel noise with a tunable parameter and supports multiple sampling strategies—including Gumbel-Max, Gumbel-Softmax, Top-k, and Boltzmann—to accelerate stochastic exploration. We evaluate performance in two scenarios: (1) a static setting where the number of STAs ranges from 10 to 100 in increments of 10, and (2) a time-varying setting where STAs begin at 5 and increase by 5 every 30 s until reaching 100 at 600 s. Across all experiments, we adopt CWminimum of 16, a CWmaximum of 1024, and a CWThreshold set to 512 to distinguish light from heavy loads. We record collision rates, throughput, training loss, and potential overestimation trends. Tables 1 and 2 summarize the primary DRL model and CSMA/CA protocol parameters.

The System-Level Considerations. To ensure practical deployability, we design the agent to rely only on lightweight local metrics—namely, collision probability and instantaneous throughput—for decision-making. These statistics are efficiently derived from MAC-layer feedback (ACK/NACK signals and channel occupancy) and are updated periodically at the episode level (every 1–2 s), thus incurring minimal overhead from centralized control. To assess operational efficiency, we measure the forward inference time of the trained model on an Intel Core i9-14900K CPU, which averages 0.38 ms per decision. This latency is well below the typical CW adjustment interval within (~100 ms), ensuring that decision-making remains efficient relative to network conditions and does not slow down policy evaluation.

5.2 The DRL Model Comparison

Fig. 3 presents a comparison of three DRL-based CW adaptation models—DQN, attention-DQN, DDQN, and DDQN(Gumbel)—across four metrics that assess accuracy, stability, and robustness. The attention-DQN extends DQN by adding a Squeeze-and-Excitation (SE) module [38], which helps the agent focus on key traffic features and reduce irrelevant signals. Panel (a) displays training loss under a static STA scenario, highlighting long-term learning consistency in a fixed environment. Panel (b) presents training loss behavior under different traffic distributions, capturing the impact of changing traffic distributions on model stability. Panel (c) reports overestimation bias by comparing predicted and actual Q-values, and Panel (d) plots as the absolute difference between online and target Q-values. While Panels (a), (c), and (d) reflect stability under controlled training conditions, Panel (b) highlights how each model responds when the network load changes over time.

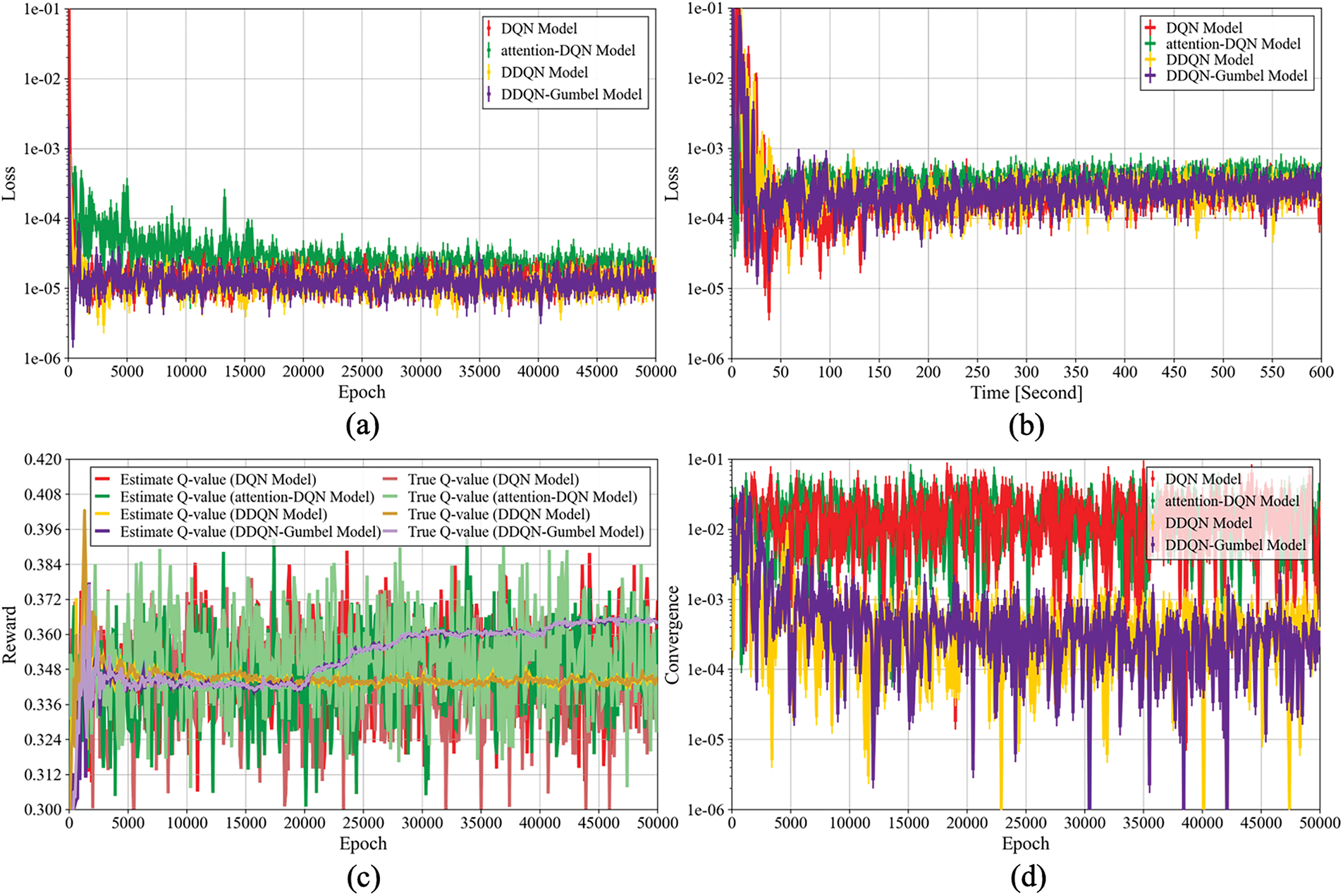
Figure 3: Comparison of DQN, attention-DQN, DDQN, and DDQN-Gumbel models, where (a) shows training loss over 50,000 epochs in a static setting, (b) illustrates training loss under time-varying STA distributions, (c) presents estimated versus actual Q-values to analyze overestimation bias, and (d) visualizes convergence trends across training epochs

Fig. 3a illustrates the training loss trajectories of DQN, attention-DQN, DDQN, and DDQN(Gumbel) over 50,000 epochs under a static STA setting. The DQN model shows fast early convergence, but its single-network design leads to noticeable fluctuations and instability in later stages due to overestimation errors. The attention-DQN model incorporates a SE mechanism to emphasize relevant features, which helps reduce initial noise but results in elevated and persistent variance throughout training, indicating limited gain in stability under static conditions. The DDQN model achieves a consistently smooth and low-loss profile across epochs. Its double-network structure effectively separates action evaluation and selection, mitigating overestimation and enabling stable learning. The DDQN(Gumbel) model maintains a similar stable trend with slightly higher variance in early epochs due to stochastic exploration. However, the noise injection does not destabilize training and may support broader policy discovery, especially during early learning.

Fig. 3b shows the training loss of DQN, attention-DQN, DDQN, and DDQN(Gumbel) models over 600 s as the number of STAs gradually increases from 5 to 100. All models exhibit rapid initial loss reduction under light traffic (0–100 s). As STA density rises, DQN begins to show growing instability, with frequent fluctuations due to its single-network design and limited adaptability to dynamic contention. The attention-DQN improves early-phase performance by emphasizing relevant traffic features through its SE module, but its loss remains noisy under high contention, indicating that attention alone cannot resolve DQN’s weak generalization. DDQN maintains low and steady loss throughout, benefiting from its dual-network architecture that reduces overestimation and stabilizes learning across traffic transitions. Notably, DDQN(Gumbel) adapts the best under increasing congestion. While its stochastic exploration introduces slight early variance, it quickly stabilizes and maintains a low loss level. The added Gumbel noise enables targeted exploration of high-reward CW actions, improving responsiveness without degrading training stability.

Fig. 3c quantifies overestimation bias as the gap between predicted (estimated) and actual Q-values over training epochs. Smaller gaps indicate better value estimation and more reliable policy updates. The DQN model shows clear overestimation throughout training, with a mean estimated Q-value of 0.3488 and a true value of 0.3424. The attention-DQN model slightly reduces variance and captures useful traffic features, but it reverses the bias direction with a mean estimate of 0.3469 and actual value of 0.3518, leading to mild underestimation in later stages. The DDQN model achieves the best alignment, with nearly identical estimated and actual values (0.3446 vs. 0.3448), thanks to its separate networks for action selection and evaluation, which effectively mitigate overestimation. The DDQN(Gumbel) model follows this trend closely, maintaining strong alignment (0.3516 vs. 0.3518) while gradually increasing its estimated values after epoch 20,000. This upward shift results from Gumbel-driven tail exploration, encouraging the agent to discover high-reward actions. Overall, both DDQN-based models outperform DQN in bias control, with DDQN(Gumbel) offering enhanced adaptability while maintaining estimation precision.

Fig. 3d depicts the convergence behavior of the DQN, attention-DQN, DDQN, and DDQN(Gumbel) models over 50,000 training epochs. The convergence metric, defined as the absolute difference between predicted and target Q-values, reflects the alignment and stability of updates. The DQN model exhibits persistent fluctuations around 1e−2. The attention-DQN shows similar improvement, as its feature reweighting slightly smooths early instability, but fails to resolve deeper Q-value misalignment. Compare to this, the DDQN model achieves improved consistency, with convergence values narrowing to the 1e−3 to 1e−4 range due to its use of separate networks for action selection and evaluation. Despite introducing Gumbel noise, the DDQN(Gumbel) model retains stable convergence similar to DDQN. These findings validate that incorporating Gumbel-based exploration into DDQN not only preserves training stability and convergence, but also improves robustness in dynamic traffic conditions. Given the promising results of DDQN(Gumbel), we evaluate various Gumbel-based exploration strategies to identify the most effective method for adaptive CW optimization under varying network loads.

5.3 The Action Exploration Stratgies Comparison

Fig. 4 compares the throughput performance of four Gumbel-based exploration strategies—Gumbel-Max, Gumbel-Softmax, Top-k Gumbel, and Boltzmann-Gumbel—under a time-varying setting where the number of STAs increases gradually from 5 to 100. Gumbel-Softmax consistently delivers the highest throughput (0.675–0.685), benefiting from smooth, tunable sampling that promotes tail actions without destabilizing policy transitions. Its ability to fine-tune exploration intensity allows stable adaptation as contention increases. Boltzmann-Gumbel performs second-best (0.645–0.670), adaptively prioritizing underexplored actions via noise scaling based on visitation frequency; however, this adaptability diminishes under saturated states where noise contribution flattens, slightly reducing performance during late-stage congestion. Gumbel-Max (0.615–0.645) aggressively samples extreme actions by selecting the max perturbed Q-value, but without smoothing, its policy becomes erratic as STAs grow, causing unstable CW decisions and more collisions. Top-k Gumbel shows the weakest performance (~0.63→~0.60), as its random sampling from a limited action subset suppresses exploration diversity and prevents precise CW tuning under heavy contention. These observations confirm that Gumbel-Softmax achieves the best trade-off between exploration focus and decision smoothness, making it the most reliable strategy under dynamic loads. Hence, it is adopted in SETL-DDQN(Gumbel) for all subsequent benchmarking and evaluations.

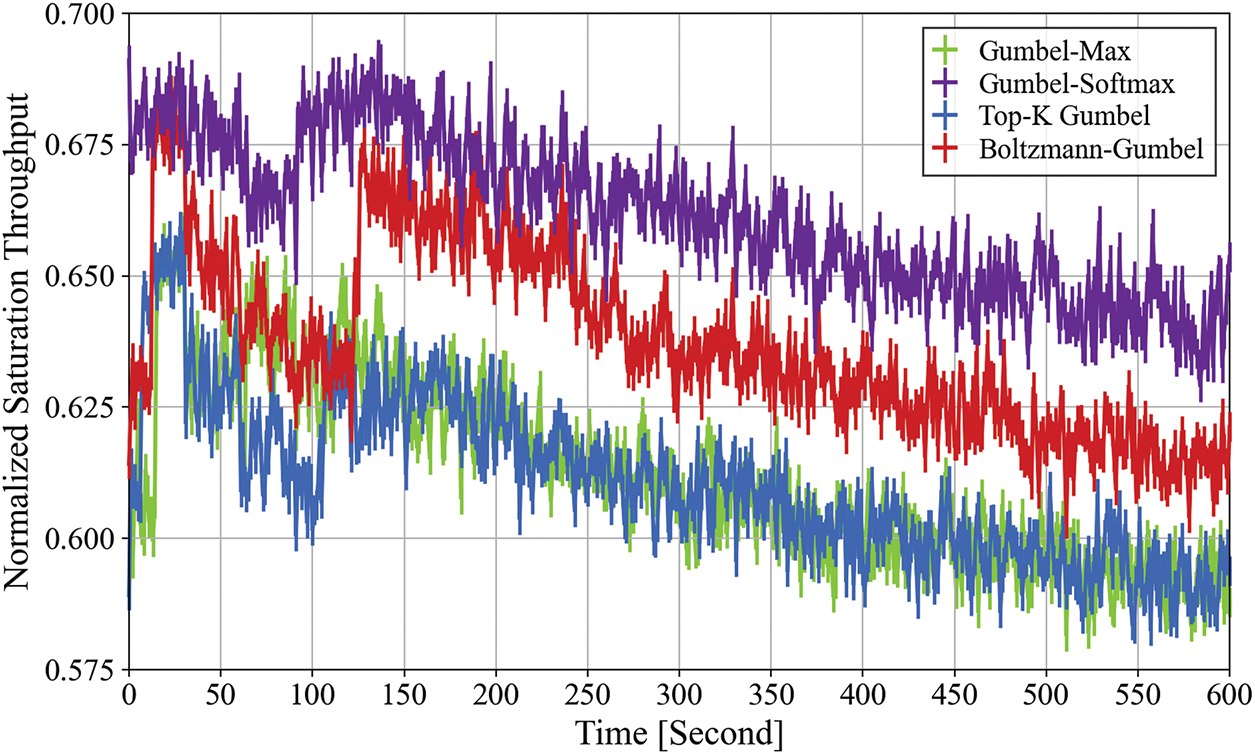
Figure 4: Normalized saturation throughput of four Gumbel-based exploration strategies under time-varying STA growth (5–100 over 600 s), highlighting adaptability and stability in time-varying scenario

5.4 The Performance Benchmarking

This study benchmarks our proposed SETL-DDQN and SETL-DDQN(Gumbel) methods against established CW adaptation approaches. The deterministic methods include standard CSMA/CA [4] and SETL [10], while DRL-based comparisons involve DQN-based models such as CCOD-DQN [22] and SETL-DQN [25], along with the DDQN-based DCWO-DDQN [28]. To broaden the evaluation, we also include SETL-DQN(MA) [26], a distributed multi-agent DRL approach for CW optimization. All benchmarks are evaluated under static and time-varying scenarios (see Table 2), providing a comprehensive assessment of collision rates (Figs. 5 and 6) and normalized saturation throughput (Figs. 7 and 8) across diverse network settings.

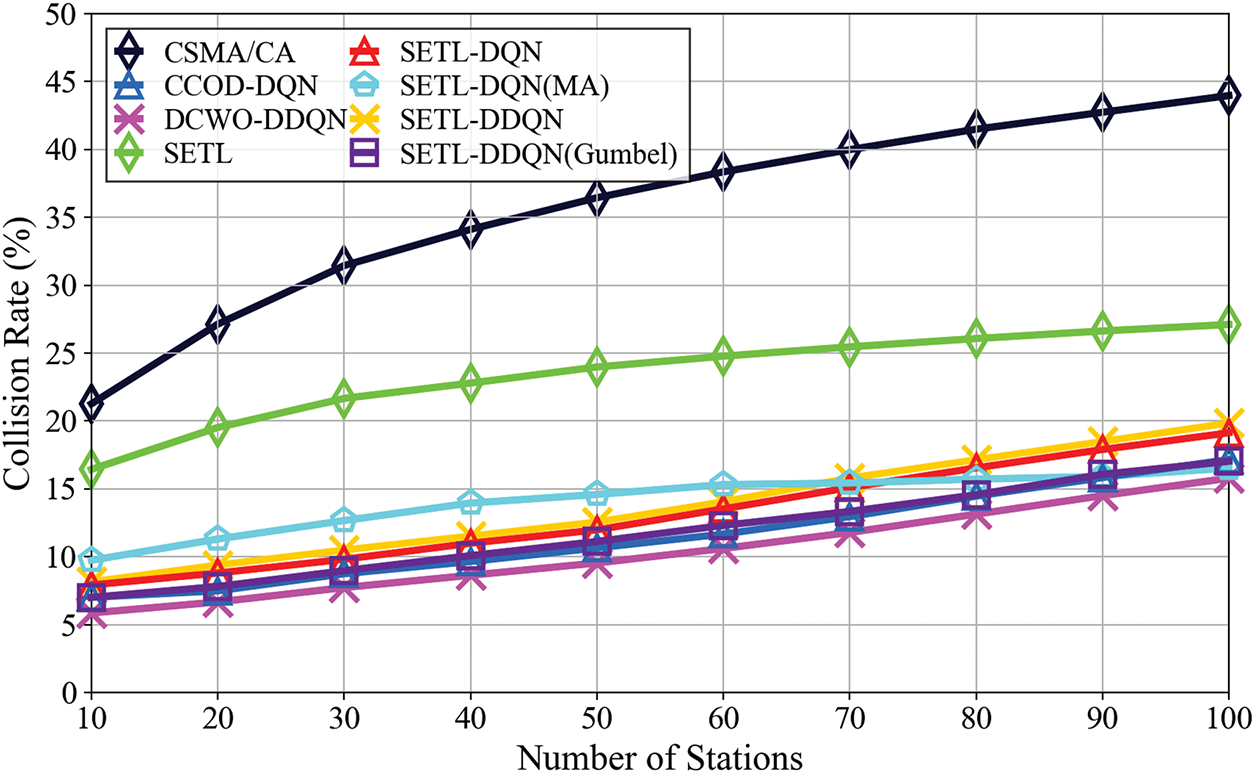
Figure 5: Collision rate convergence in static topology

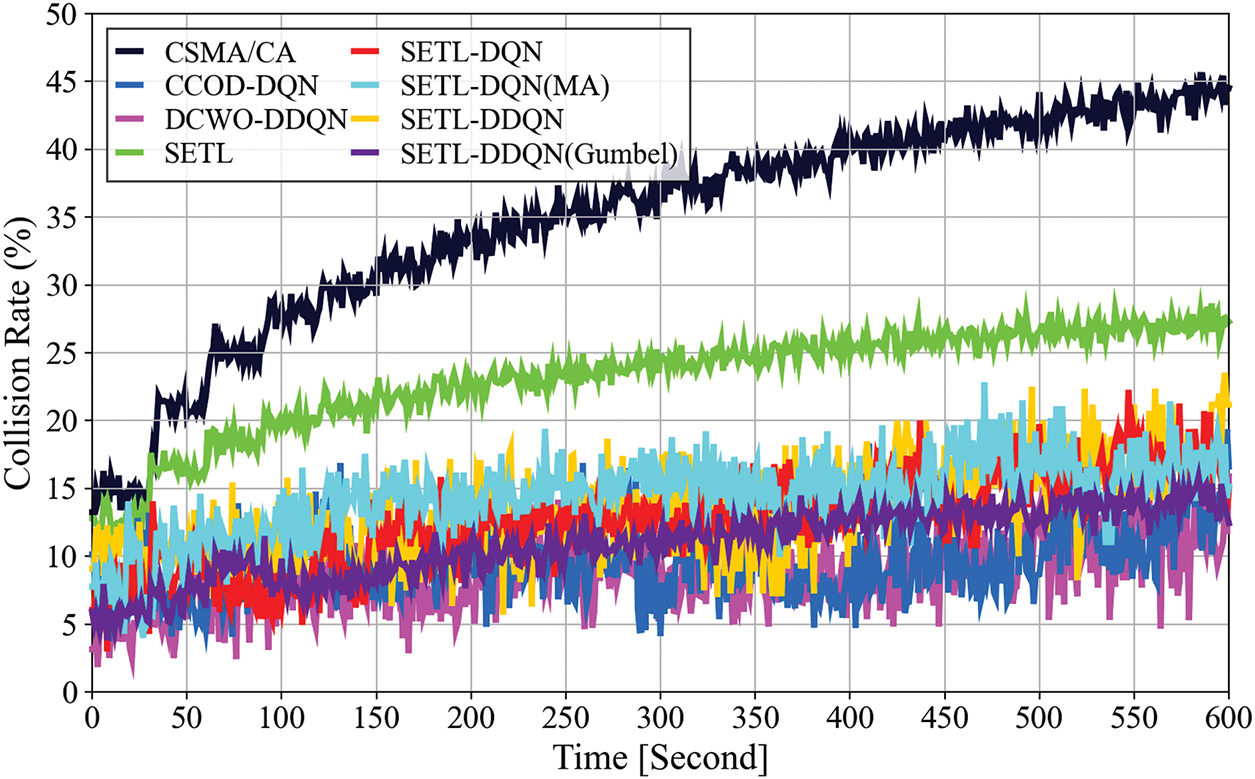
Figure 6: Experimental collision rate convergence in time-varying topology

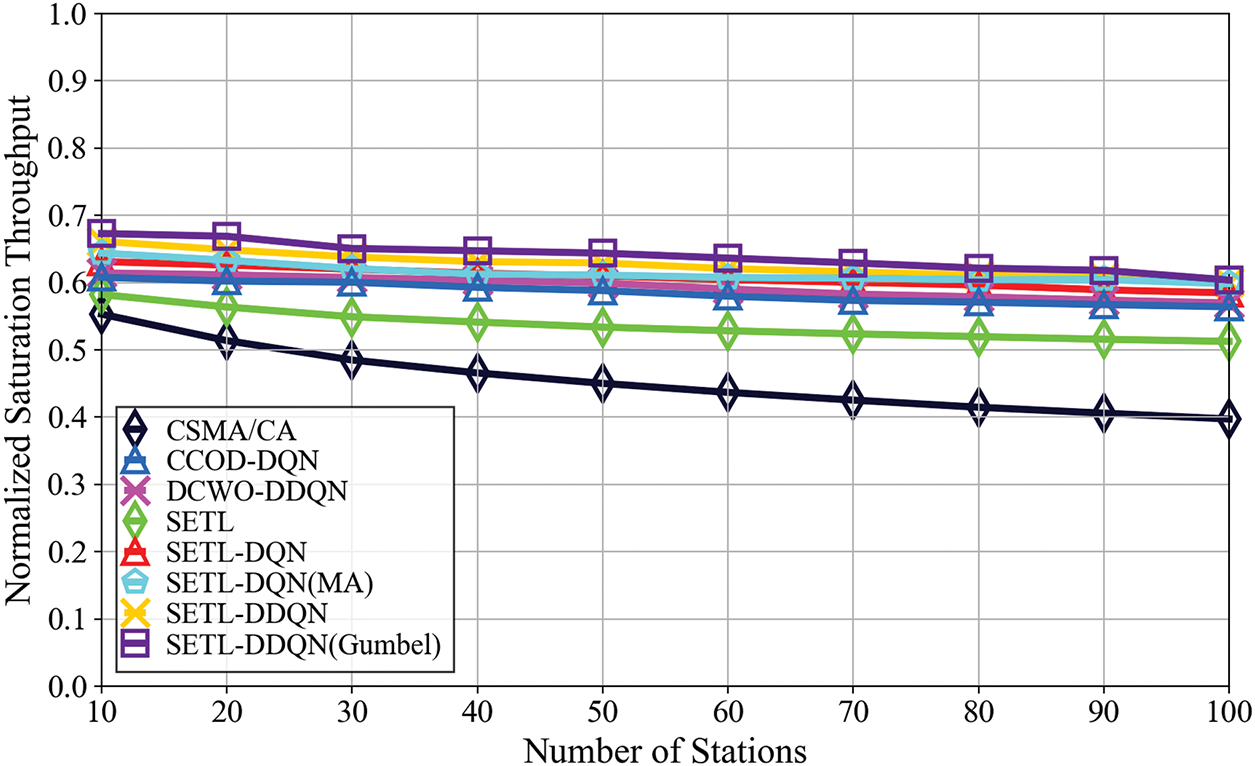
Figure 7: Normalized saturation throughput convergence for static topology

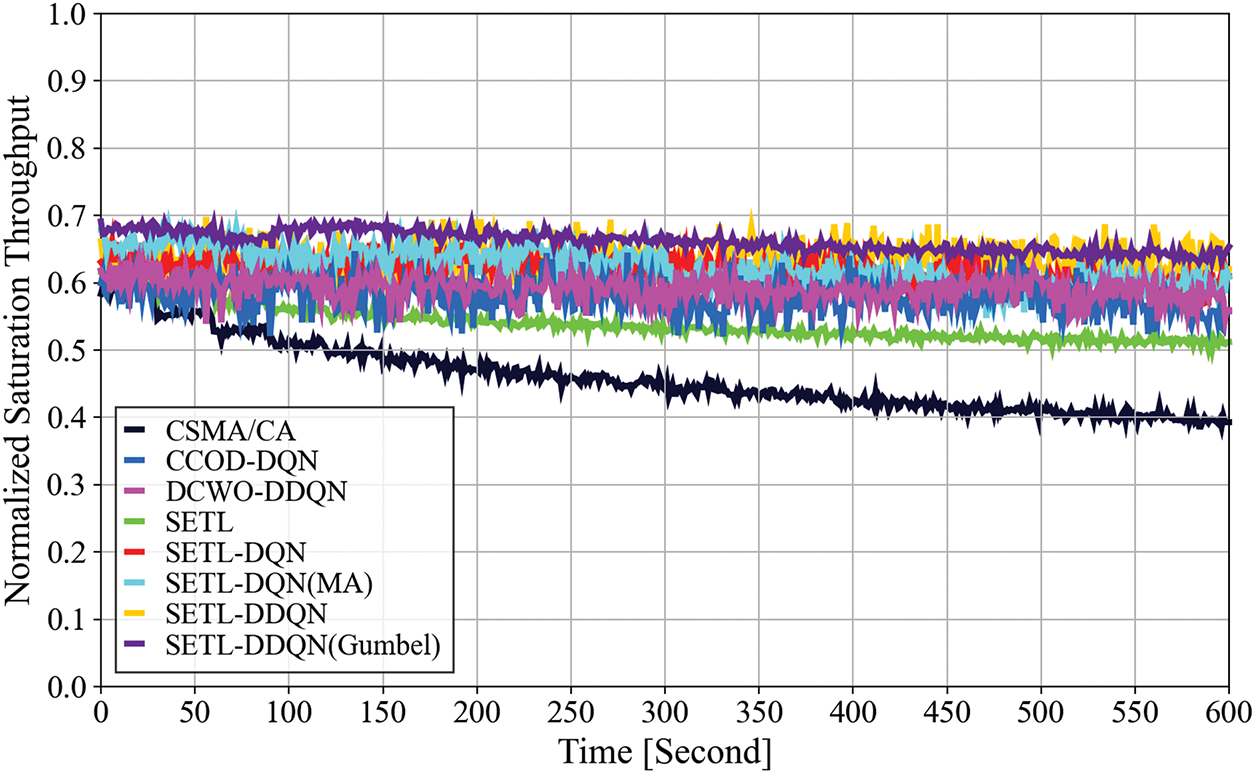
Figure 8: Experimental normalized saturation throughput convergence under time-varying topology

Fig. 5 compares collision rates under a static scenario (10–100 STAs) for deterministic and DRL-based CW adaptation methods. Legacy CSMA/CA shows the highest collision rates (21.26%–43.96%), reflecting its exponential backoff’s inability to balance collisions and idle periods in dense conditions. The SETL method reduces collisions to 16.43%–27.10% using threshold-based exponential and linear adjustments, though its performance degrades with increasing contention. In contrast, DRL methods like CCOD-DQN (7.00%–17.16%) and DCWO-DDQN (5.85%–15.78%) dynamically adjust CW values over extended training, significantly lowering collisions. SETL-DQN (7.91%–19.12%) and SETL-DDQN (8.15%–19.84%) further decrease collision rates by incorporating the SETL mechanism into DQN/DDQN frameworks. We also include SETL-DQN(MA), a fully cooperative multi-agent variant of SETL-DQN, which achieves collision rates of 9.74%–16.53% by enabling agents to coordinate CW decisions. Although its early-stage performance is favorable, its collision rate increases with STA density due to overhead from frequent coordination. Notably, our proposed SETL-DDQN(Gumbel) achieves collision rates between 7.00% and 17.02%, closely matching CCOD-DQN while leveraging Gumbel-driven exploration to enhance adaptability under fluctuating loads. Although DCWO-DDQN achieves the lowest collision rates overall, SETL-DDQN(Gumbel) remains competitive and performs robustly in moderate contention scenarios.

Fig. 6 depicts that in a time-varying scenario (0–600 s). The legacy CSMA/CA shows the widest collision range (13.23%–44.52%), reflecting its limited adaptability as STA counts increase. The SETL method, which employs a threshold-based CW adjustment, reduces collisions 12.81%–27.28% compared to basic BEB; however, its fixed CWThreshold can still lead to higher collisions during traffic network load spikes. On the other hand, DRL-based methods dynamically fine-tune CW values. CCOD-DQN and DCWO-DDQN achieve collision ranges of 10.13%–16.62% and 3.14%–15.88%, respectively, by aggressively expanding the CW under high traffic. SETL-DQN and SETL-DDQN, which integrate the SETL mechanism with DQN and DDQN, yield ranges of 6.03%–14.95% and 9.07%–21.18%, respectively. Yet, SETL-DDQN relies on standard ε-greedy exploration strategy, which suffers from uniform action sampling and insufficient tail sensitivity, limiting its adaptability under varying load conditions. SETL-DQN(MA), achieves a range of 7.76%–15.15%, improving low-density adaptability through agent coordination but showing diminishing gains under higher contention. Compared to SETL-DDQN, the proposed SETL-DDQN(Gumbel) employs a Gumbel-Softmax mechanism that biases exploration toward rare, high-reward CW adjustments, reducing collision ranges to 5.92%–12.44% and achieving a mean collision rate of 10.93% rather than 13.55%, which represents a 19.34% improvement overall.

Fig. 7 presents the normalized saturation throughput for varying network loads (10–100 STAs), where SETL-DDQN(Gumbel) delivers the highest throughput across light (10–40 STAs), medium (40–70 STAs), and heavy (70–100 STAs) conditions. In light loads, throughput of about 0.67–0.647 is sustained through rapid CWThreshold adaptation and stable Q-value estimates. In medium loads, Gumbel-Softmax sampling identifies high-reward actions to maintain throughput (about 0.643–0.636). Under heavy loads, the Gumbel distribution’s heavy-tailed characteristics, keeping throughput around 0.603 despite intense contention. This improvement is achieved because, unlike standard ε-greedy exploration that uniformly samples actions, the Gumbel approach actively targets the tail of the reward distribution, enabling the agent to fine-tune the CWThreshold more effectively under high contention. This leads to a significant throughput improvement, as SETL-DDQN(Gumbel) achieves highest mean throughput of 0.64, surpassing SETL-DDQN by 2.04%, SETL-DQN by 5.21%, SETL-DQN(MA) by 4.07%, DCWO-DDQN by 7.78%, CCOD-DDQN by 9.33%, SETL by 19.04%, and legacy CSMA/CA by 40.58%.

Fig. 8 illustrates normalized saturation throughput in a time-varying scenario. As in the static case, our SETL-DDQN(Gumbel) achieves the highest mean throughput (0.66), followed by SETL-DDQN (0.63), SETL-DQN(MA) (0.62), and SETL-DQN (0.62). These threshold-based methods with DQN/DDQN models benefit from adaptive CWThreshold updates and reliable Q-value estimation. By incorporating Gumbel-Softmax sampling, SETL-DDQN(Gumbel) more effectively identifies high-value actions. DCWO-DDQN and CCOD-DQN deliver mean throughputs of 0.59 and 0.58, respectively, while the deterministic SETL method reaches 0.54 and legacy CSMA/CA with BEB only 0.46. Overall, SETL-DDQN(Gumbel) achieves a 43.95% improvement over CSMA/CA, 22.76% over SETL, 14.01% over CCOD-DQN, 11.81% over DCWO-DDQN, 6.98% over SETL-DQN, and 4.72% over SETL-DDQN. Furthermore, SETL-DDQN yields substantial throughput gains, achieving 37.46% higher normalized throughput than legacy CSMA/CA, 17.23% higher than SETL, 8.87% higher than CCOD-DDQN, 6.77% higher than DCWO-DDQN, and 2.16% higher than SETL-DQN, and 1.35% higher than SETL-DQN(MA).

6  Conclusion

This paper proposes SETL-DDQN and SETL-DDQN(Gumbel) for Contention Window (CW) optimization in IEEE 802.11 Networks, which are designed to mitigate overestimation bias and adapt to varying traffic loads. Through the synergy of threshold-based backoff control (CWThreshold) and Double DQN (DDQN), the proposed frameworks effectively reduce collision rates and maintain robust throughput under dense contention. The novelty lies in Gumbel-distribution exploration, grounded in extreme value theory, which outperforms conventional ε-greedy approaches by widening the action search space for more effective collision avoidance and throughput gains. Our experiments demonstrate that both SETL-DDQN and SETL-DDQN(Gumbel) consistently surpass established benchmarks—including CSMA/CA, SETL, CCOD-DQN, SETL-DQN, SETL-DQN(MA), and DCWO-DDQN—by sustaining higher throughput and significantly reducing collision rates. Crucially, SETL-DDQN(Gumbel) achieves the most optimal action selection with a comprehensive convergence under dense contention, demonstrating enhanced learning stability, faster convergence rates, and improved adaptability across various traffic scenarios.

Acknowledgement: The authors would like to thank all individuals who contributed to this work. Their support and insights were valuable in shaping the results presented in this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yi-Hao Tu; software and data collection: Yi-Hao Tu; analysis and interpretation of results: Yi-Hao Tu; draft manuscript preparation: Yi-Hao Tu; manuscript review and editing: Yi-Hao Tu, Yi-Wei Ma; project supervision and funding acquisition: Yi-Wei Ma. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ahamad RZ, Javed AR, Mehmood S, Khan MZ, Noorwali A, Rizwan M. Interference mitigation in D2D communication underlying cellular networks: towards green energy. Comput Mater Contin. 2021;68(1):45–58. doi:10.32604/cmc.2021.016082. [Google Scholar] [CrossRef]

2. Sivaram M, Yuvaraj D, Mohammed AS, Manikandan V, Porkodi V, Yuvaraj N. Improved enhanced DBTMA with contention-aware admission control to improve the network performance in MANETs. Comput Mater Contin. 2019;60(2):435–54. doi:10.32604/cmc.2019.06295. [Google Scholar] [CrossRef]

3. Binzagr F, Prabuwono AS, Alaoui MK, Innab N. Energy efficient multi-carrier NOMA and power controlled resource allocation for B5G/6G networks. Wire Net. 2024;30(9):7347–59. doi:10.1007/s11276-023-03604-1. [Google Scholar] [CrossRef]

4. Crow BP, Widjaja I, Kim JG, Sakai PT. IEEE 802.11 wireless local area networks. IEEE Commun Mag. 1997;35(9):116–26. doi:10.1109/35.620533. [Google Scholar] [CrossRef]

5. Lee MW, Hwang G. Adaptive contention window control scheme in wireless ad hoc networks. IEEE Commun Letters. 2018;22(5):1062–5. doi:10.1109/LCOMM.2018.2813361. [Google Scholar] [CrossRef]

6. Liew JT, Hashim F, Sali A, Rasid MFA, Jamalipour A. Probability-based opportunity dynamic adaptation (PODA) of contention window for home M2M networks. J Net Comp App. 2019;144(5):1–12. doi:10.1016/j.jnca.2019.06.011. [Google Scholar] [CrossRef]

7. Song NO, Kwak BJ, Song J, Miller ME. Enhancement of IEEE 802.11 distributed coordination function with exponential increase exponential decrease backoff algorithm. In: Proceedings of the 57th IEEE Semiannual Vehicular Technology Conference; 2003 Apr 22–25; Jeju, Republic of Korea. [Google Scholar]

8. Bharghavan V, Demers A, Shenker S, Zhang L. MACAW: a media access protocol for wireless LANs. ACM SIGCOMM Comp Commun Rev. 1994;24(4):212–25. doi:10.1145/190809.190334. [Google Scholar] [CrossRef]

9. Chen WT. An effective medium contention method to improve the performance of IEEE 802.11. Wire Net. 2008;14(6):769–76. doi:10.1007/s11276-006-0012-7. [Google Scholar] [CrossRef]

10. Ke CH, Wei CC, Lin KW, Ding JW. A smart exponential-threshold-linear backoff mechanism for IEEE 802.11 WLANs. Inter J Commun Sys. 2011;24(8):1033–48. doi:10.1002/dac.1210. [Google Scholar] [CrossRef]

11. Shakya AK, Pillai G, Chakrabarty S. Reinforcement learning algorithms: a brief survey. Expert Sys App. 2023;231(7):120495. doi:10.1016/j.eswa.2023.120495. [Google Scholar] [CrossRef]

12. Kim TW, Hwang GH. Performance enhancement of CSMA/CA MAC protocol based on reinforcement learning. J Info Commun Conv Eng. 2021;19(1):1–7. doi:10.6109/jicce.2021.19.1.1. [Google Scholar] [CrossRef]

13. Zerguine N, Mostefai M, Aliouat Z, Slimani Y. Intelligent CW selection mechanism based on Q-learning (MISQ). Ingénierie Des Systèmes D’Inf. 2020;25(6):803–11. doi:10.18280/isi.250610. [Google Scholar] [CrossRef]

14. Kwon JH, Kim D, Kim EJ. Reinforcement learning-based contention window adjustment for wireless body area networks. In: Proceedings of the 4th International Conference on Big Data Analytics and Practices; 2023 Aug 25–27; Bangkok, Thailand. [Google Scholar]

15. Pan TT, Lai IS, Kao SJ, Chang FM. A Q-learning approach for adjusting CWS and TxOP in LAA for Wi-Fi and LAA coexisting networks. Inter J Wire Mobile Comp. 2023;25(2):147–59. doi:10.1504/IJWMC.2023.133061. [Google Scholar] [CrossRef]

16. Lee CK, Lee DH, Kim J, Lei X, Rhee SH. Q-learning-based collision avoidance for 802.11 stations with maximum requirements. KSII Trans Int Info Sys (TIIS). 2023;17(3):1035–48. doi:10.3837/tiis.2023.03.019. [Google Scholar] [CrossRef]

17. Zheng Z, Jiang S, Feng R, Ge L, Gu C. An adaptive backoff selection scheme based on Q-learning for CSMA/CA. Wire Net. 2023;29(4):1899–909. doi:10.1007/s11276-023-03257-0. [Google Scholar] [CrossRef]

18. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level control through deep reinforcement learning. Nature. 2015;518:529–33. doi:10.1038/nature14236. [Google Scholar] [PubMed] [CrossRef]

19. Wang X, Garg S, Lin H, Kaddoum G, Hu J, Hossain MS. A secure data aggregation strategy in edge computing and blockchain-empowered Internet of Things. IEEE Internet Things J. 2022;9(16):14237–46. doi:10.1109/JIOT.2020.3023588. [Google Scholar] [CrossRef]

20. Wang X, Garg S, Lin H, Kaddoum G, Hu J, Hassan MM. Heterogeneous blockchain and AI-driven hierarchical trust evaluation for 5G-enabled intelligent transportation systems. IEEE Trans Intel Transport Syst. 2023;24(2):2074–83. doi:10.1109/TITS.2021.3129417. [Google Scholar] [CrossRef]

21. Subash N, Nithya B. Dynamic adaptation of contention window boundaries using deep Q networks in UAV swarms. Inter J Comp App. 2024;46(3):167–74. doi:10.1080/1206212X.2023.2296720. [Google Scholar] [CrossRef]

22. Wydmański W, Szott S. Contention window optimization in IEEE 802.11 ax networks with deep reinforcement learning. In: Proceedings of the 2021 IEEE Wireless Communications and Networking Conference; 2021 Mar 29–Apr 1; Nanjing, China. [Google Scholar]

23. Sheila de Cássia SJ, Ouameur MA, de Figueiredo FAP. Reinforcement learning-based Wi-Fi contention window optimization. J Commun Info Sys. 2023;38(1):128–43. doi:10.14209/jcis.2023.15. [Google Scholar] [CrossRef]

24. Lei J, Tan D, Ma X, Wang Y. Reinforcement learning-based multi-parameter joint optimization in dense multi-hop wireless networks. Ad Hoc Net. 2024;154(11):103357. doi:10.1016/j.adhoc.2023.103357. [Google Scholar] [CrossRef]

25. Ke CH, Astuti L. Applying deep reinforcement learning to improve throughput and reduce collision rate in IEEE 802.11 networks. KSII Trans Int Info Syst. 2022;16(1):334–49. doi:10.3837/tiis.2022.01.019. [Google Scholar] [CrossRef]

26. Ke CH, Astuti L. Applying multi-agent deep reinforcement learning for contention window optimization to enhance wireless network performance. ICT Exp. 2023;9(5):776–82. doi:10.1016/j.icte.2022.07.009. [Google Scholar] [CrossRef]

27. Van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double Q-learning. In: Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence; 2016 Feb 12–17; Phoenix, AZ, USA. [Google Scholar]

28. Asaf K, Khan B, Kim GY. Wireless LAN performance enhancement using double deep Q-networks. Appl Sci. 2022;12(9):4145. doi:10.3390/app12094145. [Google Scholar] [CrossRef]

29. Chakraborty S, Chakravarty D. A discrete Gumbel distribution. arXiv:1410.7568. 2014. [Google Scholar]

30. Astuti L, Lin YC, Chiu CH, Chen WH. Predicting vulnerable road user behavior with Transformer-based Gumbel distribution networks. IEEE Trans Auto Sci Eng. 2025;22:8043–56. doi:10.1109/TASE.2024.3476382. [Google Scholar] [CrossRef]

31. Daud H, Suleiman AA, Ishaq AI, Alsadat N, Elgarhy M, Usman A, et al. A new extension of the Gumbel distribution with biomedical data analysis. J Radiat Res Appl Sci. 2024;17(4):101055. doi:10.1016/j.jrras.2024.101055. [Google Scholar] [CrossRef]

32. Mehrnia N, Coleri S. Wireless channel modeling based on extreme value theory for ultra-reliable communications. IEEE Trans Wire Commun. 2022;21(2):1064–76. doi:10.1109/TWC.2021.3101422. [Google Scholar] [CrossRef]

33. Strypsteen T, Bertrand A. Conditional Gumbel-Softmax for constrained feature selection with application to node selection in wireless sensor networks. arXiv:2406.01162. 2024. [Google Scholar]

34. Miridakis NI, Shi Z, Tsiftsis TA, Yang G. Extreme age of information for wireless-powered communication systems. IEEE Wire Commun Letters. 2022;11(4):826–30. doi:10.1109/LWC.2022.3146389. [Google Scholar] [CrossRef]

35. Lauri M, Hsu D, Pajarinen J. Partially observable markov decision processes in robotics: a survey. IEEE Trans Robot. 2022;39(1):21–40. doi:10.1109/TRO.2022.3200138. [Google Scholar] [CrossRef]

36. Xie SM, Ermon S. Reparameterizable subset sampling via continuous relaxations. arXiv:1901.10517. 2019. [Google Scholar]

37. Afify AZ, Yousof HM, Cordeiro GM, M. Ortega EM, Nofal ZM. The Weibull Fréchet distribution and its applications. J Appl Stat. 2016;43(14):2608–26. doi:10.1080/02664763.2016.1142945. [Google Scholar] [CrossRef]

38. Hu J, Shen L, Sun G. Squeeze-and-excitation networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 19–21; Salt Lake, UT, USA. [Google Scholar]