Investigation of TWIP/TRIP Effects in the CrCoNiFe System Using a High-Throughput CALPHAD Approach

1  Introduction

High-entropy alloys (HEAs) represent a compelling area of materials research due to their unique and tunable properties [1–3]. These multi-component systems are being actively developed for a wide range of applications, including aerospace engineering, biomedical devices, energy storage, and environmental technologies [4–8]. Comprising five or more principal elements, HEAs exhibit a broad spectrum of material behaviors. HEAs can be derived from alloy systems with fewer elements, usually ones that have shown superior properties. Among those alloys, the Cr-Co-Ni ternary system has demonstrated promising mechanical properties among the materials systems studied [9–11]. In general, alloys within this system that contain a high percentage of Cr tend to have high corrosion resistance and high-temperature strength, while alloys with a high percentage of Co tend to have superior wear resistance and high-temperature strength [12–14]. Alloys with a high percentage of Ni typically display excellent corrosion resistance and ductility, as well as high strength [15]. For example, the equiatomic CrCoNi alloy has a tensile strength of 1.4 GPa while maintaining a ductility of approximately 90% [16]. Furthermore, the Cr-Co-Ni system can be enhanced by introducing new elements, including Fe, Mn, Nb, Mo, Al, etc. [17–20]. For example, Cr-Co-Ni-based alloys have shown improvements in various properties such as strength, plasticity, oxidation resistance, and wear resistance [21,22]. Among these properties, the CrCoNi ternary system is particularly noteworthy for its high strength and ductility, even outperforming more complex quaternary or quinary systems derived from it. For instance, the tensile strength of the CrCoNi system is significantly higher than that of the well-studied Cantor alloy (CrCoNiFeMn), which is also based on this ternary system [23–25]. Ongoing experimental research targets the compositional variations in this system because even minimal changes yield substantial impacts on mechanical performance. TRIP (Transformation-Induced Plasticity) and TWIP (Twinning-Induced Plasticity) type alloys are known for their excellent mechanical properties, with TWIP alloys displaying higher ductility and TRIP alloys excelling in strength [26,27]. Although initially developed for steels, TWIP/TRIP mechanisms are now observed in other alloy systems, including HEAs, due to similar metastable FCC phase and comparable FCC to HCP deformation modes. A recent review highlights that coupling the TRIP effect with tailored alloying and processing strategies can effectively break the strength–ductility trade-off, positioning metastable HEAs as strong candidates for structural applications [28]. Recent research has been done showing that TWIP/TRIP effects can improve the properties of metastable HEAs [29,30]. These alloys are usually identified through the stacking fault energy (SFE) between FCC and HCP phases [31,32]. Typically, a TWIP alloy has an SFE between 20~40 mJ/m2, whereas a TRIP alloy has a lower SFE below 20 mJ/m2 [33]. These thresholds function as guidelines for selecting appropriate compositions for these deformation mechanisms, but slight differences may occur across different systems. While this study focuses on FCC-to-HCP transitions relevant to TWIP/TRIP, FCC-to-BCC transitions may also occur in certain HEAs, especially under deformation or thermal treatment. These pathways are worth exploring in future extensions of this framework.

The traditional experimental approach investigates new materials case by case. However, the vast compositional space of HEAs makes their design and optimization particularly challenging, as experimental approaches are often time-consuming and resource-intensive. Recent advances in computational material design have provided an alternative approach to HEA development [34–37]. Computational material design offers an alternative approach, using simulation and modeling techniques to design and discover new materials with specific properties and characteristics. Simulations of the behavior of materials can be used to predict the properties of a material. This approach allows for the predetermination of candidates for new alloys, resulting in greater efficiency in further experimentation.

To accelerate the discovery of TWIP/TRIP HEAs, computational approaches have become common tools alongside experiments to expedite the identification of TWIP/TRIP HEAs, especially in the Cr-Co-Ni system. CALPHAD (Computer Coupling of Phase Diagrams and Thermochemistry) represents a well-established technique for modeling intricate alloy systems. The CALPHAD method can be implemented through a variety of computational software, such as Thermo-Calc, Pandat, and FactSage. There are also open-source tools, including OpenCalphad and PyCalphad. A high-throughput CALPHAD (HT-CALPHAD) approach is developed where programming is combined with CALPHAD methods to perform computational modeling in large quantities on computer clusters, significantly increasing the efficiency of calculations and enabling applications to material studies that are otherwise impossible.

In this work, an HT-CALPHAD approach is used to discover TWIP/TRIP compositions within the Cr-Co-Ni and Cr-Co-Ni-Fe systems through the application of HT-CALPHAD. Our study seeks to tackle the problem of precise SFE modeling in HEAs, as traditional empirical models do not effectively apply. A multi-step computational pipeline is created to enhance mechanical performance by combining several screening criteria, including SFE, FCC phase stability, and the FCC-to-HCP transition temperature (T0) for alloy composition optimization.

2  Computational Methods

2.1 HT-CALPHAD Calculation

Among the CALPHAD implementations, Thermo-Calc software applies the methodology to forecast phase diagrams and thermodynamic properties across multi-element systems. Thermo-Calc (TC) is an implementation of the CALPHAD method that has been used for decades to calculate phase diagrams and thermodynamic properties based on databases containing data for a wide range of materials. It has been widely used in the material design of alloys containing more than three elements [38]. In this work, high-throughput calculations are carried out using TC-python. The Thermo-Calc software was first developed in the 1970s and is used to calculate phase diagrams and the thermodynamic properties of materials. It has many reliable databases for various calculations. The TC-python software kit is a recent development that is based on Python, allowing users to execute Thermo-Calc commands with python codes, resulting in better efficiency [39]. In this work, an in-house python code is developed for HT calculations. The python code takes manually defined compositions and temperatures as inputs and executes TC commands in Thermo-Calc. TC-Python alone performs the same tasks as Thermo-Calc. To calculate large numbers of compositions, an HT method is utilized based on previous research [40–42]. Parallel calculations are performed on CPU cores on a high-performance computing cluster. With this approach, over a hundred calculations can be processed simultaneously, and ~400,000 calculations can be done in a day. For the current work, thousands to hundreds of thousands of compositions are calculated depending on the complexity of the alloy systems, and all calculations can be finished in relatively short periods.

In order to determine the values of SFE, Gibbs energy calculations are performed using the HT-CALPHAD method. The Gibbs energy difference is related to the stacking-fault energy by:

γ=2ρΔGfcc→hcp+2σfcc/hcp(1)

ρ=43αfcc21NA(2)

Eq. (1) [43] is an empirical equation for SFE calculations, where γ is the SFE (mJ/m2), ρ is the molar surface density (mol/m2) of the (111) plane, ΔGfcc→hcp is the Gibbs energy difference between FCC and HCP phases at a given temperature, and σfcc/hcp is the interfacial energy. In this work, σfcc/hcp is set to a constant value (8 mJ/m2) based on the experimental value of CrCoNi equiatomic alloy. While a constant interfacial energy was assumed for simplicity, this is a known limitation. Interfacial energy varies with composition, crystal orientation, and temperature. Incorporating composition-dependent models—whether from ab initio simulations or machine learning approaches—could significantly improve the accuracy of SFE predictions in future studies. ρ can be determined from Eq. (2), where αfcc (3.5~3.6 Å) is the lattice parameter of the FCC phase, NA is Avogadro’s number [44]. Thermo-Calc has a built-in function to calculate Gibbs energy values, and with TC-python, Gibbs energy and ΔG calculations are performed for the Cr-Co-Ni ternary and the Cr-Co-Ni-Fe quaternary system. After the ΔGfcc→hcp results are obtained, SFE values can be determined with Eq. (1).

2.2 Multi-Step Calculation and Composition Screening

Even though ΔG is a critical value to determine SFE and TWIP/TRIP compositions, it alone cannot yield accurate predictions for alloy design since Eq. (1) is based mainly on empirical data of steels instead of HEAs. To improve the results, HT calculations are performed for other criteria as well, including the T0 temperature and FCC phase stability. FCC phase stability can be quantified by the calculation of FCC presence during cooling, which gives insights into the FCC to HCP transformations that induce TWIP/TRIP effects. Further calculations are done to find compositions with a T0 temperature, which is defined as the temperature where ΔGfcc→hcp is zero, since the transition between the two phases occurs when the Gibbs energy of one phase surpasses the other. The screening process follows a sequential filtering hierarchy rather than weighted scoring. To save computation cost and emphasize each criterion by priority, ΔG calculations are performed first. After ΔG results are obtained, only compositions showing FCC dominance are used as inputs for the FCC phase stability calculations. The same rule applies to the T0 calculations. After all the HT calculations are done, the results from these calculations are combined to screen through the alloy system to determine compositions with the greatest potential of TWIP/TRIP occurrence.

3  Results

3.1 Cr-Co-Ni Calculations

High-throughput calculations were performed for the Cr-Co-Ni system as an efficient method for determining SFE, serving as a foundation for more complex higher-order systems. The computational approach allowed for the rapid evaluation of numerous compositions, significantly reducing the need for costly experimental trials. The Gibbs energies of the FCC and HCP phases were systematically calculated across uniformly generated compositions in the ternary system with a 1 at% step size. These calculations enabled the identification of key regions where phase transformations are most likely to occur, contributing to a deeper understanding of the material behavior.

Fig. 1a,b illustrates the Gibbs energy values calculated using the HT method with Thermo-Calc. Each dataset includes about 5000 compositions, which provides a solid statistical foundation for phase stability assessment. The standard phases of pure Cr, Co, and Ni, which display BCC, HCP, and FCC structures, respectively, serve as reference points for the Gibbs energy values. The stability of these phases was assessed by determining the Gibbs energy difference ΔG (FCC-HCP) by subtracting GFCC from GHCP. These results highlight the thermodynamic diversity across the compositional space. Notably, the energy values exhibit a wide distribution—on the order of hundreds of J/mol—reflecting substantial variation in phase stability driven by compositional effects. This is expected in high-entropy systems where configurational complexity can significantly alter phase energies.

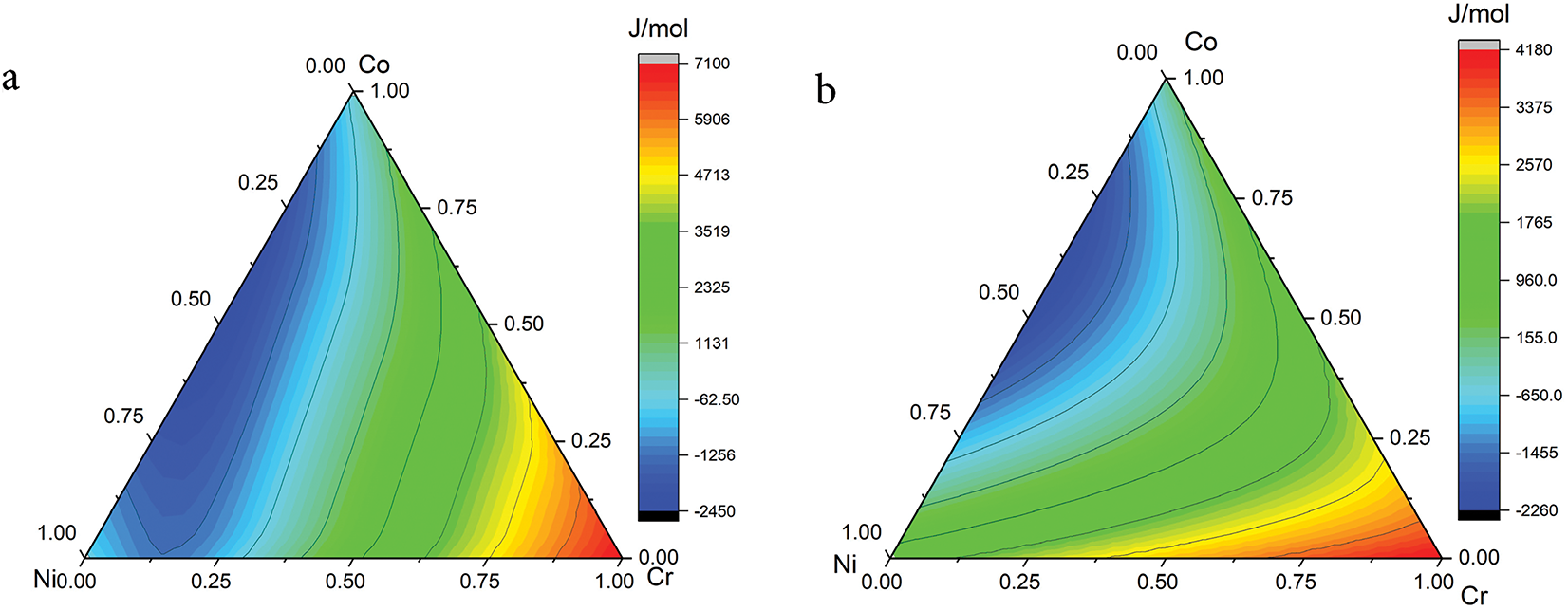
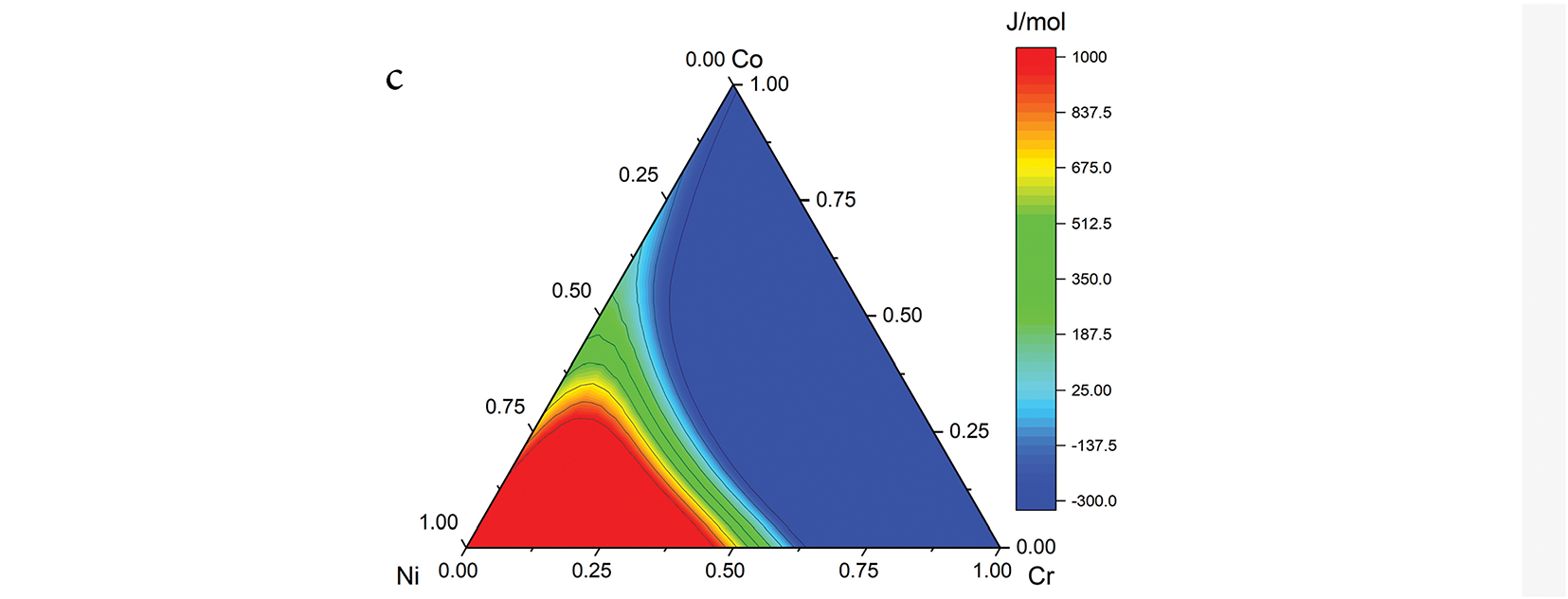
Figure 1: (a) Gibbs energy of the FCC phase (b) Gibbs energy of the HCP phase (c) Gibbs energy difference between the FCC and HCP phases, at 298 K. Compositions in at%

Fig. 2 displays the SFEFCC-HCP of Cr-Co-Ni system at 298 K. Based on the mathematical relation between ΔG and SFE in Eq. (1), extreme ΔGFCC-HCP values would result in SFE falling far beyond the established TWIP (0–20 mJ/m2) and TRIP (20–40 mJ/m2) ranges. Both GFCC and GHCP have shown an extensive distribution of values. Therefore, FCC and HCP each dominate the Ni- and Co-rich side, where the magnitude ΔGFCC-HCP is too high, as demonstrated in Fig. 1c. TWIP and TRIP effects would not occur in these regions.

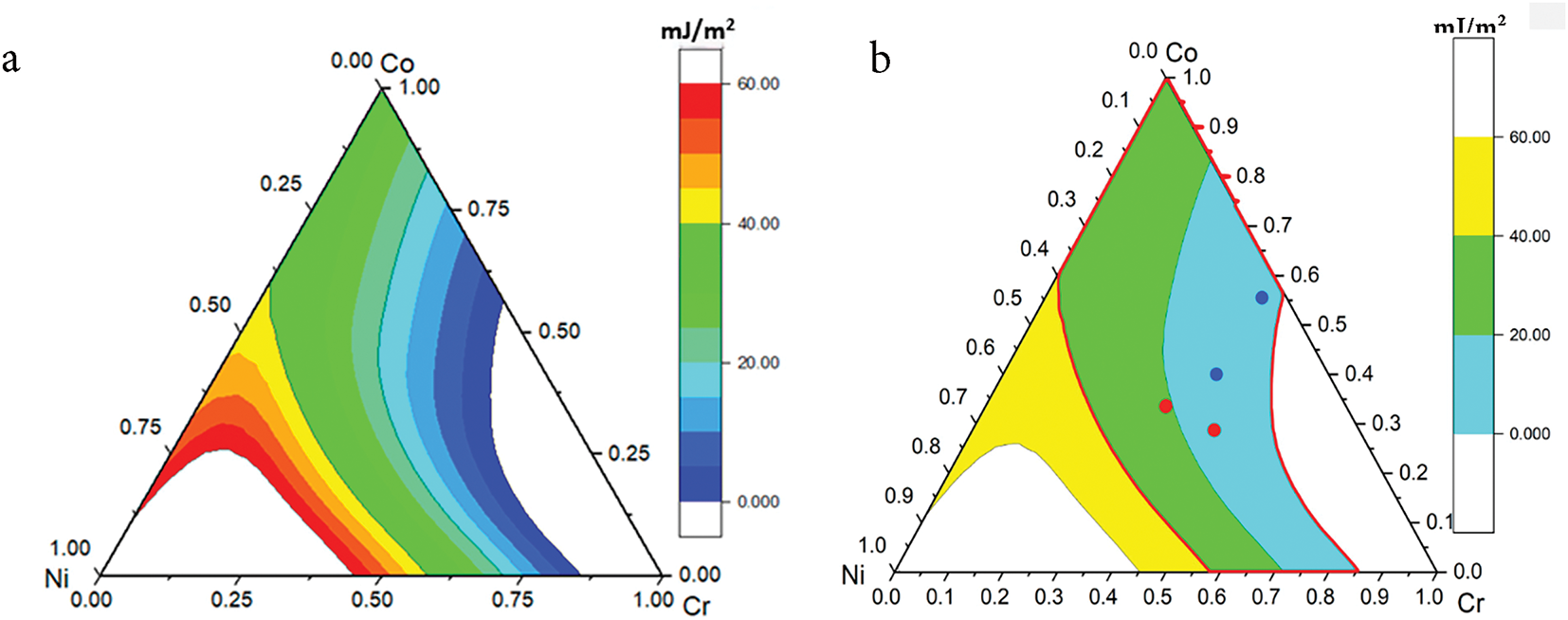
Figure 2: SFEFCC-HCP of Cr-Co-Ni system at 298 K, (a) results in 0–60 mJ/m2, (b) TWIP/TRIP criteria regions. Compositions in at%

ΔG values indicate that while some compositions exhibit strong FCC stability (large negative ΔG), others are more prone to HCP transformation (small ΔG). These differences are critical: regions with low ΔG magnitude correspond to compositions where phase metastability and thus TWIP/TRIP behavior are most likely. By contrast, the composition regions in the middle have more reasonable ΔGFCC-HCP values, and thus are more likely for TWIP/TRIP behaviors to occur there. ΔGFCC-HCP values are then used to determine SFE. Fig. 2 shows the SFE results for CrCoNi system. Compositions with SFE below ~20 mJ/m2 are likely candidates for deformation-induced ε-martensite (TRIP), while those with intermediate values (~20–40 mJ/m2) support mechanical twinning (TWIP). Higher SFE values typically promote dislocation glide over transformation mechanisms. This spread reflects the compositional sensitivity of SFE and motivates a thermodynamic filter. An arbitrary limit of SFE was applied, and compositions with SFE values outside this range are excluded for TWIP/TRIP consideration. Obviously, a smaller range of SFE would screen out more compositions and reduce the number of results to be further processed. However, a smaller range may also falsely exclude TWIP/TRIP compositions. A broad range of 0–60 mJ/m2 was used as an inclusive upper bound, allowing for the preservation of compositions that might be misclassified due to interfacial energy uncertainty.

The SFE map shows that SFE increases with Ni content, as expected based on ΔGFCC-HCP. According to the 0–20 mJ/m2 and 20~40 mJ/m2 SFE criteria, TRIP and TWIP occur through a wide range of compositions. Four compositions are marked on the current results. The points are Cr33.3-Co33.3-Ni33.3 (TWIP), Cr40-Co40-Ni20 (TWIP), Cr45-Co27.5-Ni27.5 (TRIP), Cr40-Co55-Ni5 (TRIP), respectively. Two red points correspond to the TWIP compositions, and two blue points are the TRIP compositions. Results show that the overall SFE of TWIP compositions is higher than that of TRIP compositions, but these reference points were not all located in TWIP/TRIP regions as indicated on the plot from calculation results.

The SFE values are used as a general standard for TWIP/TRIP materials. However, the SFE criteria are empirical and not strictly settled. Therefore, additional approaches are needed for further investigation. During the cooling process of TWIP/TRIP alloys, the metastable FCC phase can undergo a transformation to the HCP phase. This FCC-HCP transition plays a crucial role in determining the stability of the FCC phase and the likelihood of TRIP/TWIP deformation. To gain a more comprehensive understanding of the TWIP/TRIP behavior, it is necessary to investigate the FCC-HCP transition temperature. This investigation can provide valuable insights into the stability of the FCC phase and help establish additional criteria for identifying TWIP/TRIP compositions.

Fig. 3 displays the calculated phase diagrams of the Cr-Co-Ni system at 900 K and 1500 K, generated using Thermo-Calc, encompassing the melting temperature range of the system. The comparison indicates that the HCP phase becomes thermodynamically stable as the temperature decreases. For greater clarity, the FCC phase boundaries are plotted in Fig. 4 for 900 K and 1500 K. The comparative representation at these two temperatures reveals a contraction of the FCC region as temperature decreases, where the FCC phase may transform into the HCP structure. The referenced TWIP/TRIP compositions are also included in Fig. 4. All reference points fall between the FCC boundary lines at the two temperatures. Compared to the SFE results, the FCC boundary lines cover different compositions where TWIP/TRIP behaviors are likely to occur while overlapping in certain regions. Therefore, combining both criteria would result in a more accurate description of TWIP/TRIP compositions.

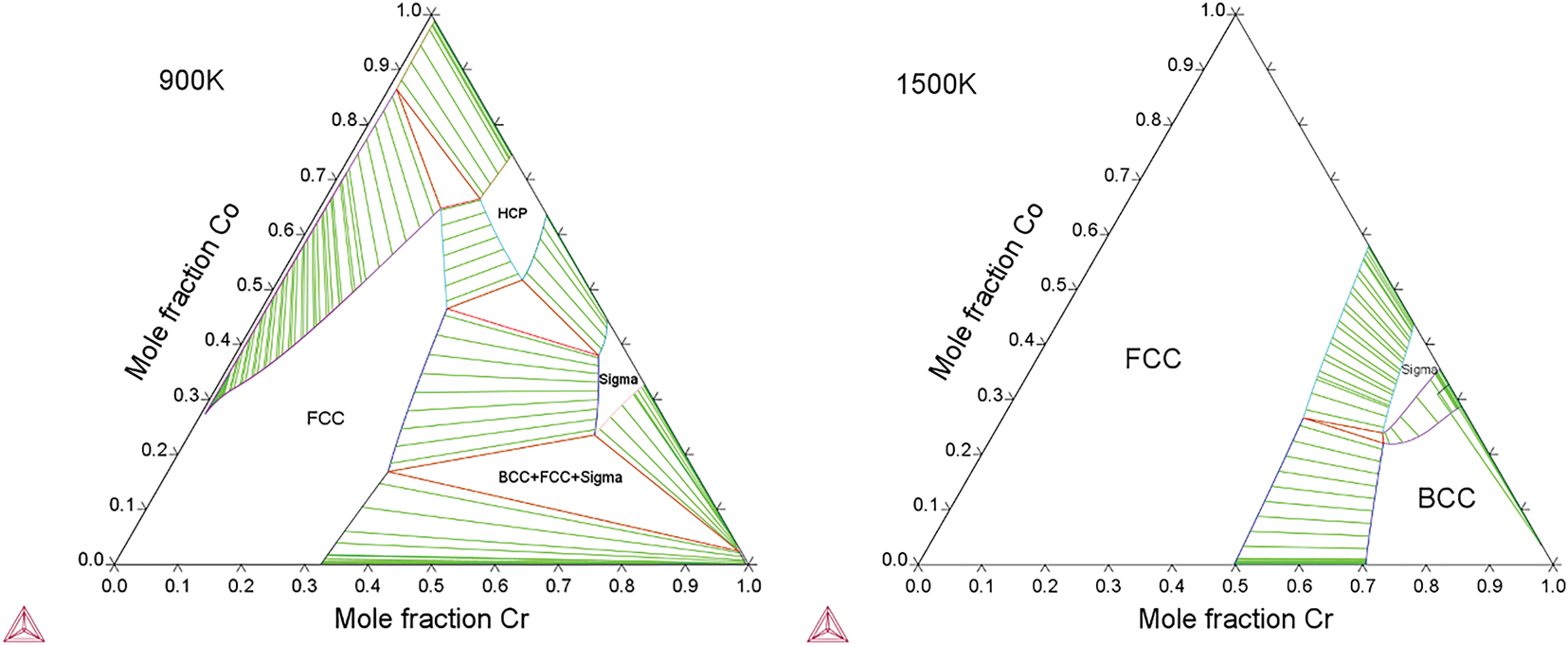
Figure 3: Calculated Cr-Co-Ni isothermal phase diagrams at 900 K and 1500 K

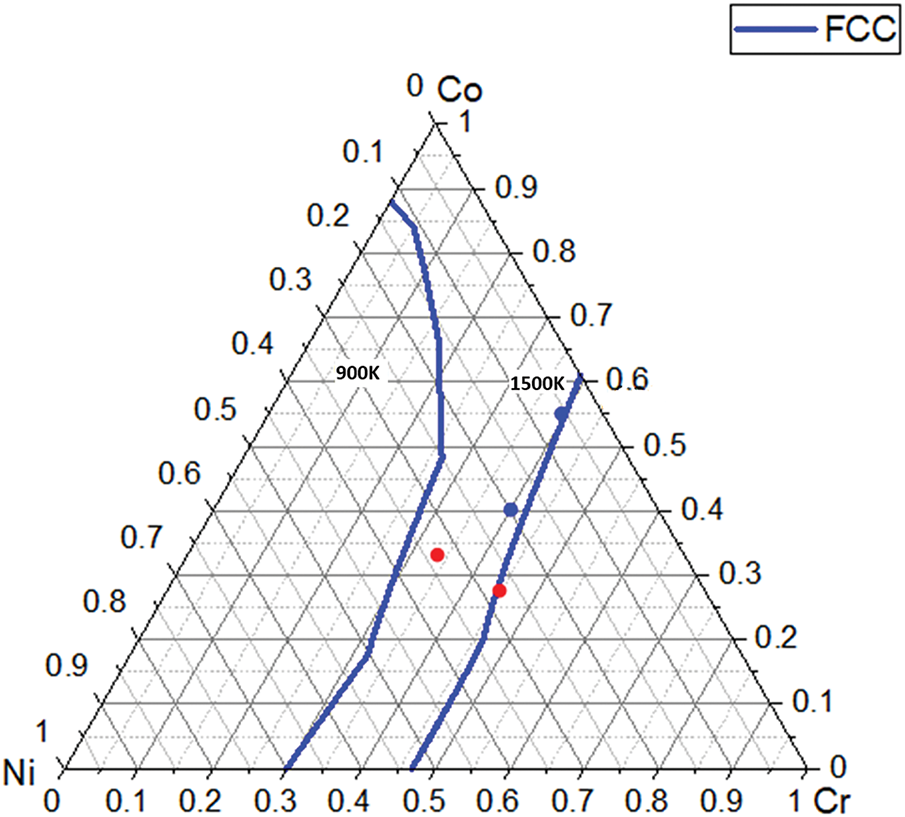
Figure 4: FCC phase boundary comparison at 900 K and 1500 K for CrCoNi compositions (at%)

To further improve the accuracy of TWIP/TRIP prediction and reduce the composition range, a third criterion called Temperature zero (T0) is added. T0 is defined as the temperature where ΔGFCC-HCP is zero, where FCC-HCP transitions are most probable. T0 was calculated using a similar approach to the Gibbs energy calculations but covers a large range of temperatures instead of fixed room temperature. The result is shown in Fig. 5, highlighting the regions where T0 is found.

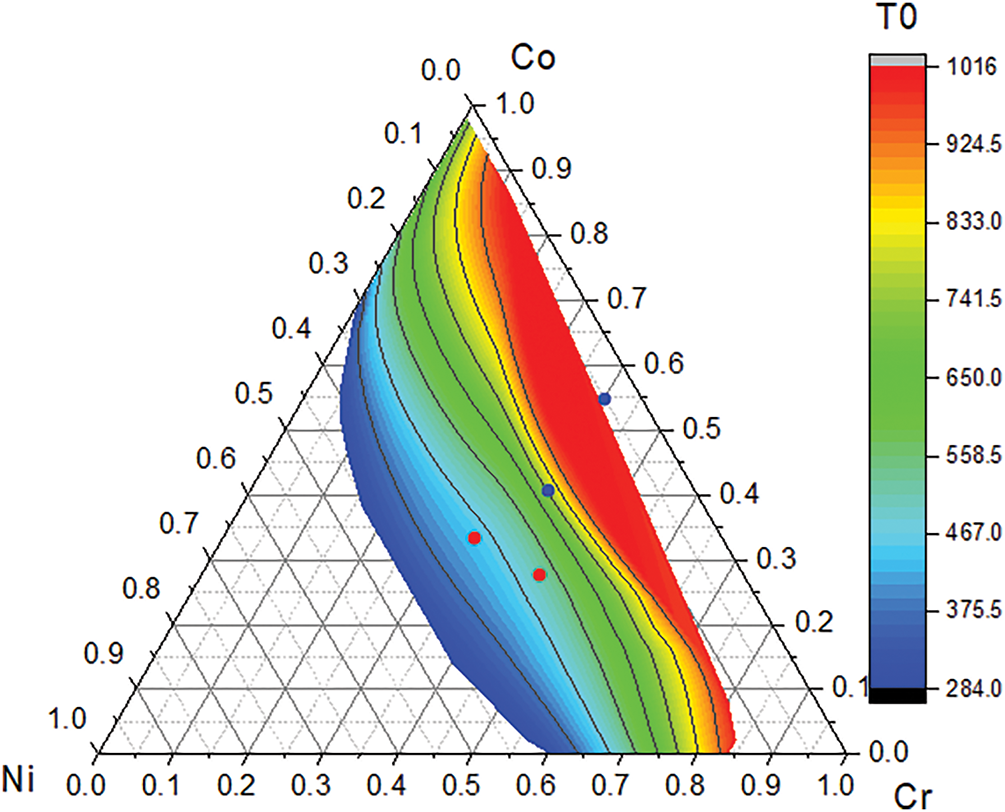
Figure 5: T0 temperature (K) of the CrCoNi compositions (at%)

The compositional dataset was progressively refined into a final collection of TWIP/TRIP candidates through the sequential application of stacking fault energy (SFE), FCC phase stability, and T0 criteria. Initially, approximately 5000 compositions were evaluated using Gibbs energy calculations. The first screening step, based on SFE, substantially reduced the candidate pool by eliminating compositions that did not meet TWIP/TRIP requirements, leaving around 1500 compositions. Subsequent phase stability screening, based on FCC phase boundaries, further narrowed the selection to approximately 800 compositions. In the final stage, T0 temperature calculations were used to retain compositions exhibiting the highest probability of FCC-to-HCP transformation, ultimately refining the dataset to approximately 300 candidates. This layered filtering process underscores the effectiveness of high-throughput CALPHAD modeling in identifying promising TWIP/TRIP alloy systems while significantly reducing the potential experimental workload. The final dataset could be made even more targeted by applying stricter filtering criteria, such as narrowing the acceptable SFE range from 0–60 mJ/m2 to 0–40 mJ/m2, or by restricting FCC stability to a narrower temperature interval. Fig. 6 overlays all screening criteria—SFE, FCC stability, and T0—onto the Cr-Co-Ni ternary composition space. As shown in Fig. 6, the final screening results exhibit strong agreement with experimentally reported TWIP/TRIP compositions, thereby validating the predictive capability and robustness of the high-throughput CALPHAD approach.

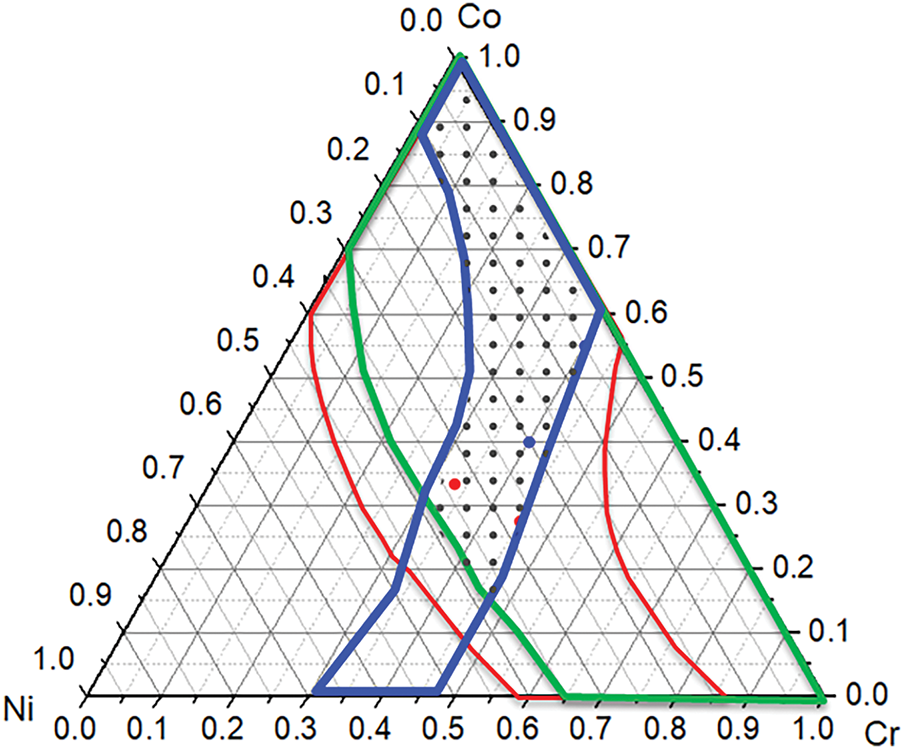
Figure 6: Combined results based on the criteria of SFE (green), FCC boundaries (blue), and T0 (red). Compositions in at%

3.2 Cr-Co-Ni-Fe Quaternary

The ternary computations establish a foundation for extending the approach to higher-order systems. In this study, Fe was added to the Cr-Co-Ni system to create a more complex case study. The Cr-Co-Ni-Fe quaternary system has been investigated in prior studies and has demonstrated potential for TWIP/TRIP alloy development. The principles for identifying TWIP/TRIP compositions in the Cr-Co-Ni-Fe system are consistent with those applied to the Cr-Co-Ni ternary system, but with a significantly larger design space encompassing over 160,000 initial compositions. Gibbs energies of the FCC and HCP phases were calculated using a high-throughput (HT) method. Stacking fault energy (SFE) values were then derived from the Gibbs energy difference (ΔGfcc→hcp). Unlike in the Cr-Co-Ni system, where calculations were performed separately for each composition, such an approach would be highly inefficient for the quaternary system due to the vastly increased number of candidates. Therefore, a multi-step computational strategy was adopted. ΔGfcc→hcp values were first computed for the entire composition set, and SFE values were subsequently obtained. Applying the TWIP/TRIP SFE criterion reduced the number of viable compositions to approximately 35,000. Further screening was conducted based on phase stability. In contrast to the ternary case, FCC phase boundaries in the quaternary system cannot be directly determined from a phase diagram and instead were evaluated using Gibbs energy calculations. For FCC to be the dominant phase, the condition GFCC < GHCP must be satisfied. The application of this FCC stability criterion reduced the candidate pool to around 8000 compositions. The final screening step, analogous to that employed for the ternary system, involved calculating the T0 temperature for the remaining compositions, ultimately yielding a final set of approximately 1500 compositions. Fig. 7 illustrates the evolution of SFE values during the screening process, showing the progressive reduction in the number of candidate compositions after each criterion was applied. This multi-stage high-throughput strategy effectively manages the complexity inherent in quaternary systems and enables the efficient identification of promising TWIP/TRIP alloys.

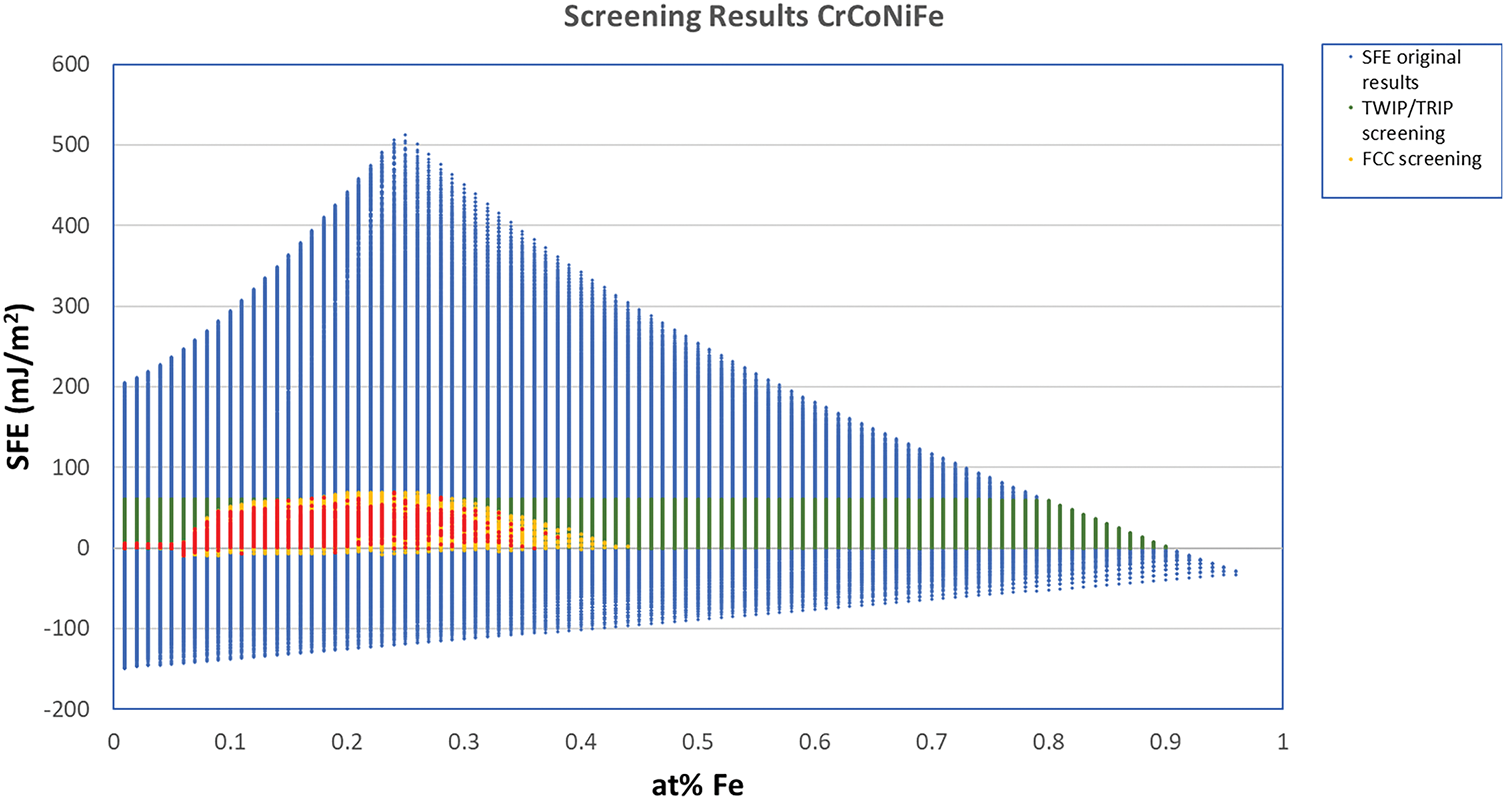
Figure 7: SFE of CrCoNiFe compositions from TWIP/TRIP screening with various criteria

To further enhance the accuracy of our predictions, a stricter application of the three screening criteria—SFE range, FCC phase stability, and T0—was employed to refine the dataset further. This additional filtering step significantly narrowed down the number of viable compositions, bringing the dataset from 1500 compositions to 214. Following this stricter screening, valence electron concentration (VEC) calculations were performed to validate the results. It has been established that VEC > 8 is indicative of a material existing predominantly in an FCC phase, making it a crucial factor in assessing TWIP/TRIP behavior. The VEC analysis ensured that the remaining compositions were not only within the expected SFE range but also structurally stable in an FCC phase, further strengthening the reliability of the predictions. The results of this refined selection process are illustrated in Fig. 8. During the calculations and screening procedures, some leniency was given to include more potential compositions. These matrices can be strengthened to reduce further the final number of TWIP/TRIP candidates (e.g., reduce the temperature range for FCC boundaries). The calculations consider all possible compositions in the alloy system, even if some compositions are not practical in real-life applications. For future experiments, compositions can be selected from the computational results based on both elemental preference and application focus.

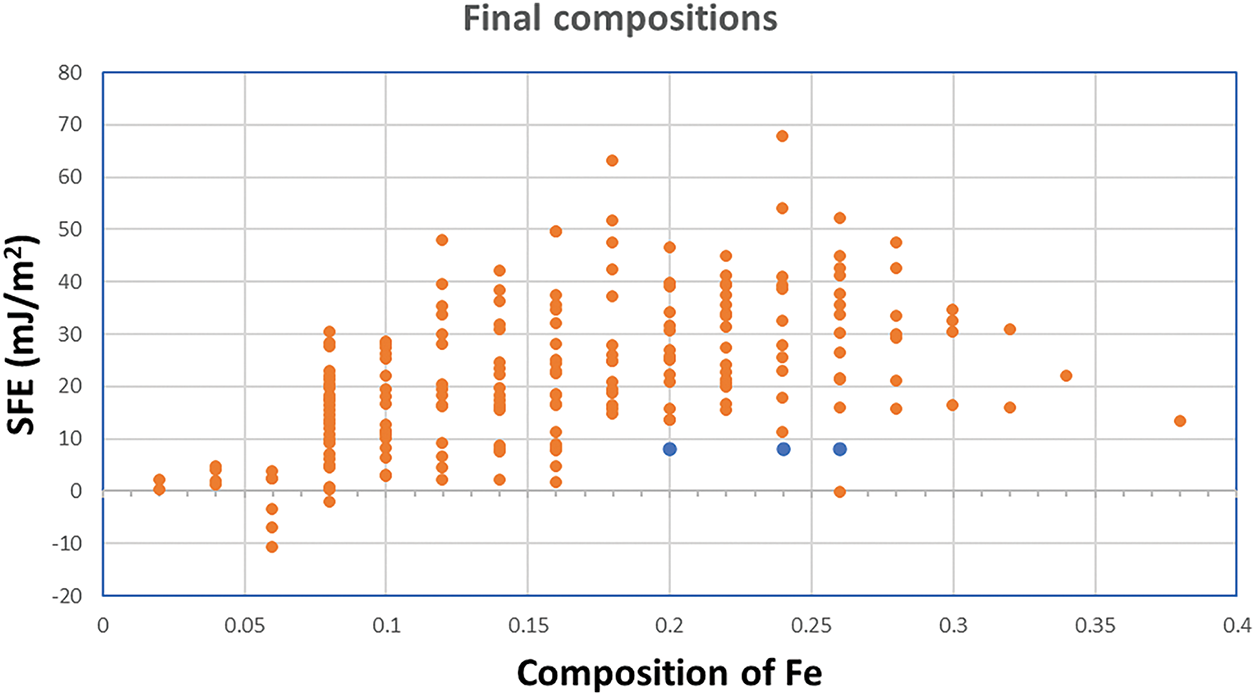
Figure 8: SFE of CrCoNiFe compositions after screening, with VEC measurement vs. composition of Fe (at%)

The calculations for the quaternary system are finished, with successful modification and implementation of the HT method. However, based on the results from ternary calculations, SFE results are not accurate due to the σfcc/hcp interfacial energy in Eq. (1). In the present work, σfcc/hcp has been assumed to be a constant value, where, as a matter of fact, it varies with composition.

Table 1 shows the SFE values from HT calculations and experimental observations of TWIP/TRIP behaviour. The calculation results apparently exceed the 20~40 mJ/m2 and 0~20 mJ/m2 thresholds for TWIP/TRIP alloys. On the other hand, the results are consistent with experimental data such that TWIP compositions have higher SFE values compared to TRIP compositions. This indicates the overall values are higher than expected while the trend is good. It has already been determined in ternary calculations that the interfacial energy can have a strong influence on SFE values. Although the SFE magnitudes deviate from experimental thresholds, the relative ranking of TWIP and TRIP behavior is preserved, supporting the use of this approach for qualitative prediction. Uncertainty in σfcc/hcp is likely the dominant contributor to error, and future refinement of its compositional dependence is critical.

4  Conclusion

The high-throughput calculations performed on the Cr-Co-Ni and Cr-Co-Ni-Fe systems established a method for the design of HEAs with TWIP/TRIP behavior. The method provides an efficient approach to determining TWIP and TRIP compositions through the calculations of SFE to select the compositions with the highest TWIP/TRIP potential. Results from the HT calculations for the Cr-Co-Ni system demonstrated the capability of the computational method. Combining SFE, phase boundaries, and T0 criteria allowed for a more comprehensive screening process. This multi-faceted approach reduced the initial pool of compositions to a refined selection of TWIP/TRIP candidates, increasing the accuracy and reliability of the results. The final screening results closely aligned with experimentally verified TWIP/TRIP compositions. However, the results for the quaternary system showed some discrepancy from the experiments. Despite the overall success, the study identified areas for improvement. The assumption of a constant interfacial energy (σfcc/hcp) in the SFE calculations led to higher-than-expected SFE values. Future work should focus on refining interfacial energy modeling, potentially through composition-dependent ab initio or machine learning approaches, and incorporating elastic and magnetic contributions to ΔG to improve SFE accuracy. Overall, this study demonstrates that even in the presence of systematic overestimation, multi-criteria thermodynamic filtering enables robust narrowing of TWIP/TRIP candidates in complex HEAs.

Acknowledgement: Not applicable.

Funding Statement: This work is supported by the U.S. Army Research Laboratory through their award # W911NF-22-2-0040. T. P. C. Klaver acknowledges support by the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 90254).

Author Contributions: Jize Zhang: conceptualization, methodology, computation, analysis, visualization, writing; T. P. C. Klaver: conceptualization, methodology, writing; Songge Yang: validation, writing, review, editing; Brajendra Mishra: supervisor, fund acquisition; Yu Zhong: conceptualization, review, supervisor, fund acquisition. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data not available due to restrictions imposed by the funding agency.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. George EP, Raabe D, Ritchie RO. High-entropy alloys. Nat Rev Mater. 2019;4(8):515–34. doi:10.1038/s41578-019-0121-4. [Google Scholar] [CrossRef]

2. Miracle DB, Senkov ON. A critical review of high entropy alloys and related concepts. Acta Mater. 2017;122:448–511. doi:10.1016/j.actamat.2016.08.081. [Google Scholar] [CrossRef]

3. Florea I, Florea RM, Bǎlţǎtescu O, Soare V, Chelariu R, Carcea I. High entropy alloys. J Optoelectron Adv Mater. 2013;15(7–8):761–7. [Google Scholar]

4. Woo W, Naeem M, Jeong J-S, Lee C-M, Harjo S, Kawasaki T, et al. Comparison of dislocation density, twin fault probability, and stacking fault energy between CrCoNi and CrCoNiFe medium entropy alloys deformed at 293 and 140 K. Mater Sci Eng A. 2020;781(4):139224. doi:10.1016/j.msea.2020.139224. [Google Scholar] [CrossRef]

5. Afolabi AE, Popoola API, Popoola OM. High entropy alloys: advance material for landing gear aerospace applications. In: Kharissova OV, Torres-Martínez LM, Kharisov BI, editors. Handbook of nanomaterials and nanocomposites for energy and environmental applications. Cham, Switzerland: Springer International Publishing; 2021. p. 2359–85. doi:10.1007/978-3-030-36268-3_179. [Google Scholar] [CrossRef]

6. Bai X. High-entropy alloys for advanced energy-related applications. Highlights Sci Eng Technol. 2022;17:245–54. [Google Scholar]

7. Ding Z, Li Y, Jiang H, Zhou Y, Wan H, Qiu J, et al. The integral role of high-entropy alloys in advancing solid-state hydrogen storage. Interdiscip Mater. 2025;4(1):75–108. doi:10.1002/idm2.12216. [Google Scholar] [CrossRef]

8. Trofimov E, Moghaddam AO, Zaitseva O, Fereidonnejad R, Naser M, Shaburova N, et al. Synthesis and characterization of intermetallic compounds with one medium- or high-entropy sublattice occupied by p-block elements. Mater Chem Phys. 2023;301:127596. doi:10.1016/j.matchemphys.2023.127596. [Google Scholar] [CrossRef]

9. Chang H, Zhang TW, Ma SG, Zhao D, Xiong RL, Wang T, et al. Novel Si-added CrCoNi medium entropy alloys achieving the breakthrough of strength-ductility trade-off. Mater Des. 2021;197(7):109202. doi:10.1016/j.matdes.2020.109202. [Google Scholar] [CrossRef]

10. Gludovatz B, Hohenwarter A, Thurston KVS, Bei H, Wu Z, George EP, et al. Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nat Commun. 2016;7(1):10602. doi:10.1038/ncomms10602. [Google Scholar] [PubMed] [CrossRef]

11. Bajpai S, MacDonald BE, Rupert TJ, Hahn H, Lavernia EJ, Apelian D. Recent progress in the CoCrNi alloy system. Materialia. 2022;24:101476. doi:10.1016/j.mtla.2022.101476. [Google Scholar] [CrossRef]

12. Ren Z, Eppell S, Collins S, Ernst F. Co–Cr–Mo alloys: improved wear resistance through low-temperature gas-phase nitro-carburization. Surf Coat Technol. 2019;378(3):124943. doi:10.1016/j.surfcoat.2019.124943. [Google Scholar] [CrossRef]

13. Koga GY, Birbilis N, Zepon G, Kiminami CS, Botta WJ, Kaufman M, et al. Corrosion resistant and tough multi-principal element Cr-Co-Ni alloys. J Alloys Compd. 2021;884(6):161107. doi:10.1016/j.jallcom.2021.161107. [Google Scholar] [CrossRef]

14. Cao BX, Kong HJ, Ding ZY, Wu SW, Luan JH, Jiao ZB, et al. A novel L12-strengthened multicomponent Co-rich high-entropy alloy with both high γ′-solvus temperature and superior high-temperature strength. Scr Mater. 2021;199(49):113826. doi:10.1016/j.scriptamat.2021.113826. [Google Scholar] [CrossRef]

15. Miao J, Guo T, Ren J, Zhang A, Su B, Meng J. Optimization of mechanical and tribological properties of FCC CrCoNi multi-principal element alloy with Mo addition. Vacuum. 2018;149:324–30. doi:10.1016/j.vacuum.2018.01.012. [Google Scholar] [CrossRef]

16. Ding J, Qin Y, Asta M, Ritchie RO. Tunable stacking fault energies by tailoring local chemical order in CrCoNi medium-entropy alloys. Proc Natl Acad Sci. 2018;115(36):8919–24. doi:10.1073/pnas.1808660115. [Google Scholar] [PubMed] [CrossRef]

17. Zhang YH, Zhuang Y, Hu A, Kai JJ, Liu CT. The origin of negative stacking fault energies and nano-twin formation in face-centered cubic high entropy alloys. Scr Mater. 2017;130:96–9. doi:10.1016/j.scriptamat.2016.11.014. [Google Scholar] [CrossRef]

18. Wu X, Li Z, Rao Z, Ikeda Y, Dutta B, Kormann F, et al. Role of magnetic ordering for the design of quinary TWIP-TRIP high entropy alloys. Phys Rev Mater. 2020;4(3):033601. doi:10.1103/physrevmaterials.4.033601. [Google Scholar] [CrossRef]

19. Liu Y, Zheng GP. The effects of chemical disorder and external loading conditions on the structural transformation between HCP and FCC phases in CrCoFeNi high-entropy alloys: a first-principles study. Philos Mag. 2020;100:22. doi:10.1080/14786435.2020.1798534. [Google Scholar] [CrossRef]

20. Kivy MB, Zaeem MA. Generalized stacking fault energies, ductilities, and twinnabilities of CoCrFeNi-based face-centered cubic high entropy alloys. Scr Mater. 2017;139(13):83–6. doi:10.1016/j.scriptamat.2017.06.014. [Google Scholar] [CrossRef]

21. Fang W, Chang R, Ji P, Zhang X, Liu B, Qu X, et al. Transformation induced plasticity effects of a non-equal molar Co-Cr-Fe-Ni high entropy alloy system. Metals. 2018;8(5):369. doi:10.3390/met8050369. [Google Scholar] [CrossRef]

22. Liu Y, Wang K, Xiao H, Chen G, Wang Z, Hu T, et al. Theoretical study of the mechanical properties of CrFeCoNiMox (0.1 ≤ x ≤ 0.3) alloys. RSC Adv. 2020;10(24):14080–8. doi:10.1039/d0ra00111b. [Google Scholar] [PubMed] [CrossRef]

23. Li L, Chen Z, Yuge K, Kishida K, Inui H, Heilmaier M, et al. Plastic deformation of single crystals of the equiatomic Cr-Fe-Co-Ni medium entropy alloy—a comparison with Cr-Mn-Fe-Co-Ni and Cr-Co-Ni alloys. Int J Plast. 2023;169:103732. doi:10.1016/j.ijplas.2023.103732. [Google Scholar] [CrossRef]

24. Yang S, Zhong Y. Ab Initio modeling of fcc Fe-Co-Cr-Ni high entropy alloys with full composition range. J Phase Equilibria Diffus. 2021;42(5):656–72. doi:10.1007/s11669-021-00905-w. [Google Scholar] [CrossRef]

25. Gao X, Lu Y, Liu J, Wang J, Wang T, Zhao Y. Extraordinary ductility and strain hardening of Cr26Mn20Fe20Co20Ni14 TWIP high-entropy alloy by cooperative planar slipping and twinning. Materialia. 2019;8:100485. doi:10.1016/j.mtla.2019.100485. [Google Scholar] [CrossRef]

26. Su J, Raabe D, Li Z. Hierarchical microstructure design to tune the mechanical behavior of an interstitial TRIP-TWIP high-entropy alloy. Acta Mater. 2019;163:40–54. doi:10.1016/j.actamat.2018.10.017. [Google Scholar] [CrossRef]

27. Shi CX, Du XH, Zhang JY, Duan GS, Yang MC, Zu RF, et al. Superb strength-ductility synergy in a medium-entropy CoCrNi alloy via reinforced TRIP effect. J Mater Res Technol. 2022;20(15):104–13. doi:10.1016/j.jmrt.2022.07.060. [Google Scholar] [CrossRef]

28. Mehranpour MS, Sohrabi MJ, Jalali A, Kalhor A, Heydarinia A, Aghdam MZ, et al. Coupling different strengthening mechanisms with transformation-induced plasticity (TRIP) effect in advanced high-entropy alloys: a comprehensive review. Mater Sci Eng A. 2025;926(5):147914. doi:10.1016/j.msea.2025.147914. [Google Scholar] [CrossRef]

29. Bahramyan M, Mousavian RT, Brabazon D. Study of the plastic deformation mechanism of TRIP-TWIP high entropy alloys at the atomic level. Int J Plast. 2020;1271:02649. doi:10.1016/j.ijplas.2019.102649. [Google Scholar] [CrossRef]

30. Kishore K, Chandan AK, Hung PT, Kumar S, Kawasaki M, Gubicza J. On the enhanced hardening ability and plasticity mechanisms in a novel Mn-added CoCrNi medium entropy alloy during high-pressure torsion. J Alloys Compd. 2022;904(201):163941. doi:10.1016/j.jallcom.2022.163941. [Google Scholar] [CrossRef]

31. Li R, Lu S, Kim D, Schönecker S, Zhao J, Kwon SK, et al. Stacking fault energy of face-centered cubic metals: thermodynamic and ab initio approaches. J Phys Condens Matter. 2016;28(39):395001. doi:10.1088/0953-8984/28/39/395001. [Google Scholar] [PubMed] [CrossRef]

32. Sanchez-Burgos I, Sanz E, Vega C, Espinosa JR. Fcc vs. hcp competition in colloidal hard-sphere nucleation: on their relative stability, interfacial free energy and nucleation rate. Phys Chem Chem Phys. 2021;23(35):19611–26. doi:10.1039/d1cp01784e. [Google Scholar] [PubMed] [CrossRef]

33. Bertoli G, Otani LB, Clarke AJ, Kiminami CS, Coury FG. Hall-petch and grain growth kinetics of the low stacking fault energy TRIP Cr40Co40Ni20 multi-principal element alloy. Appl Phys Lett. 2021;119(6):061903. doi:10.1063/5.0057888. [Google Scholar] [CrossRef]

34. Odetola PI, Babalola BJ, Afolabi AE, Anamu US, Olorundaisi E, Umba MC, et al. Exploring high entropy alloys: a review on thermodynamic design and computational modeling strategies for advanced materials applications. Heliyon. 2024;10(22):e39660. doi:10.1016/j.heliyon.2024.e39660. [Google Scholar] [PubMed] [CrossRef]

35. Peivaste I, Jossou E, Tiamiyu AA. Data-driven analysis and prediction of stable phases for high-entropy alloy design. Sci Rep. 2023;13(1):22556. doi:10.1038/s41598-023-50044-0. [Google Scholar] [PubMed] [CrossRef]

36. Anand A, Liu SJ, Singh CV. Recent advances in computational design of structural multi-principal element alloys. iScience. 2023;26(10):107751. doi:10.1016/j.isci.2023.107751. [Google Scholar] [PubMed] [CrossRef]

37. Gao T, Gao J, Yang S, Zhang L. Data-driven design of novel lightweight refractory high-entropy alloys with superb hardness and corrosion resistance. npj Comput Mater. 2024;10(1):256. doi:10.1038/s41524-024-01457-6. [Google Scholar] [CrossRef]

38. Wu X, Mayweg D, Ponge D, Li Z. Microstructure and deformation behavior of two TWIP/TRIP high entropy alloys upon grain refinement. Mater Sci Eng A. 2021;802:140661. doi:10.1016/j.msea.2020.140661. [Google Scholar] [CrossRef]

39. Zhang J, Wang R, Zhong Y. Identification of the eutectic points in the multicomponent systems with the high-throughput CALPHAD approach. J Phase Equilibria Diffus. 2022;43(6):844–57. doi:10.1007/s11669-022-01003-1. [Google Scholar] [CrossRef]

40. Klaver TPC, Simonovic D, Sluiter MHF. Brute force composition scanning with a CALPHAD database to find low temperature body centered cubic high entropy alloys. Entropy. 2018;20(12):911. doi:10.3390/e20120911. [Google Scholar] [PubMed] [CrossRef]

41. Yang S, Lu J, Xing F, Zhang L, Zhong Y. Revisit the VEC rule in high entropy alloys (HEAs) with high-throughput CALPHAD approach and its applications for material design—a case study with Al–Co–Cr-Fe–Ni system. Acta Mater. 2020;192:11–9. doi:10.1016/j.actamat.2020.03.039. [Google Scholar] [CrossRef]

42. Conway P, Klaver TPC, Steggo J, Ghassemali E. High entropy alloys towards industrial applications: high-throughput screening and experimental investigation. Mater Sci Eng A. 2021;830:142297. doi:10.1016/j.msea.2021.142297. [Google Scholar] [CrossRef]

43. Wang X, Xiong W. Stacking fault energy prediction for austenitic steels: thermodynamic modeling vs. machine learning. Sci Technol Adv Mater. 2020;21(1):626–34. doi:10.1080/14686996.2020.1808433. [Google Scholar] [PubMed] [CrossRef]

44. Aravindh SA, Kistanov AA, Alatalo M, Kömi J, Huttula M, Cao W. Incorporation of Si atoms into CrCoNiFe high-entropy alloy: a DFT study. J Phys Condens Matter. 2021;33(13):135703. doi:10.1088/1361-648x/abda78. [Google Scholar] [PubMed] [CrossRef]