An Adaptive and Parallel Metaheuristic Framework for Wrapper-Based Feature Selection Using Arctic Puffin Optimization

1  Introduction

1.1 Background

In the era of Industry 4.0, the unprecedented growth of data across different domains has introduced significant challenges in processing and deriving actionable insights from massive datasets. Among these challenges is the overwhelming presence of irrelevant and redundant input features within the raw dataset. Such extraneous features not only increase computational demands but also diminish the efficiency of machine learning models. A phenomenon known as “curse of dimensionality” often occurs when numerous input features prolong model training without proportionate improvements in model performance [1]. Furthermore, training machine learning models with redundant features often leads to overfitting, ultimately deteriorating predictive accuracy. To address these limitations, feature selection has become an indispensable step in modern machine learning pipelines. By identifying the most relevant features, it reduces computational complexity, accelerates model training, and enhances generalizability while maintaining or even improving predictive accuracy [1]. Feature selection is widely applied across domains such as telecommunication [2], manufacturing [3], healthcare [4] and energy [5].

Feature selection techniques are typically classified into three main categories based on their evaluation strategies: filter-based, wrapper-based, and embedded approaches [6–8]. Filter-based methods evaluate features using intrinsic statistical metrics, such as correlation measures and distance criteria, independently of any specific learning algorithm. While computationally efficient, the lack of direct interaction with classifiers can sometimes yield suboptimal predictive outcomes, as interactions between features and classifiers are not considered [6–8]. Wrapper-based methods explicitly integrate a classifier, such as k-nearest neighbors or support vector machines, into the feature evaluation process. Although this direct integration can substantially improve predictive accuracy by effectively capturing interactions between features and classifiers, it comes at the expense of higher computational complexity [6–8]. A typical wrapper-based feature selection framework comprises three key elements: the evaluation criterion for feature subsets, the classifier employed for subset evaluation, and the search algorithm used to explore the feature space [1]. Embedded approaches, meanwhile, integrate feature selection directly within the model training procedure, identifying relevant features as part of the learning algorithm itself. By leveraging intrinsic model-based feature importance metrics, embedded methods offer computational advantages and efficient feature selection [6–8]. However, despite the computational efficiency and integrated model evaluation provided by embedded methods, wrapper-based approaches are preferred in this study because they offer greater flexibility in employing diverse classifiers and directly optimize predictive performance, allowing more precise tailoring to specific datasets and application contexts.

From a computational perspective, feature selection is inherently a Nondeterministic Polynomial (NP) hard combinatorial optimization problem. Specifically, given a dataset containing a dataset containing |ℱTotal| input features, the potential number of feature subsets grows exponentially, reaching up to (2|ℱTotal|−1) combinations. While exhaustive search methods could feasibly evaluate all combinations for small-scale feature sets, they become computationally impractical for larger-scale problems, thus necessitating alternative optimization approaches [9]. Traditional wrapper-based methods, such as Sequential Forward Selection (SFS) [10] and sequential backward selection (SBS) [11], utilize greedy local search strategies that iteratively add or remove features. Although these local search strategies can effectively handle datasets with limited dimensionality, they often struggle to manage high-dimensional datasets, where feature interactions can be complex and nonlinear [12]. For example, the inclusion of a seemingly strong feature might degrade overall performance when combined with certain others, while apparently weaker features may contribute valuable predictive information when appropriately paired. To address these challenges, integrating global search algorithms into wrapper-based feature selection has become increasingly important. Unlike local search techniques, global search methods are better equipped to capture complex and nonlinear feature interactions, making them particularly suitable for large datasets with high-dimensional feature spaces.

1.2 Problem Statement

In recent years, the metaheuristic optimization community has increasingly embraced the No-Free-Lunch (NFL) theorem, which states that no single algorithm can perform optimally across all problem domains. This has led to a proliferation of newly proposed metaheuristic search algorithms (MSAs), each inspired by different natural, social, or physical metaphors. However, a common criticism of such developments lies in their limited validation scope: most new algorithms are tested solely on synthetic mathematical benchmarks, which often fail to reflect the complexity and unpredictability of real-world scenarios [13].

Consequently, while many MSAs exhibit strong theoretical potential, their practical effectiveness remains unverified in domains where robustness, scalability, and computational efficiency are essential. Feature selection represents one such real-world challenge. It involves high-dimensional, discrete decision spaces, intricate feature interactions, and direct implications on model interpretability, efficiency, and accuracy, making it an ideal testbed for evaluating the practical strength of emerging MSAs.

The recently proposed Arctic Puffin Optimization (APO) algorithm [14] exemplifies a novel MSA that warrants further investigation. Inspired by the adaptive survival behaviors of Arctic puffins, APO models aerial flight and underwater foraging to dynamically balance exploration and exploitation throughout the optimization process. This balance is governed by a behavioral transition coefficient, allowing APO to adjust its search strategy as optimization progresses. While APO has demonstrated competitive performance on continuous mathematical benchmarks, its effectiveness in solving complex real-world problems, particularly high-dimensional and discrete challenges such as feature selection, remains underexplored.

This gap in empirical validation is especially important given the computational complexity of feature selection. The exponential number of possible feature subsets and intricate interdependencies among features make it a computationally intensive and non-trivial problem. Without rigorous testing on such practical tasks, the true applicability and advantages of APO over existing algorithms cannot be firmly established.

1.3 Motivation

Motivated by these challenges, this study proposes a rigorous evaluation of the APO algorithm in the context of wrapper-based feature selection for classification tasks. Feature selection presents a particularly demanding problem due to its high dimensionality, discrete nature, and complex feature interdependencies, i.e., conditions under which robust and adaptive optimization techniques are crucial. APO, inspired by the survival strategies of Arctic puffins, dynamically balances exploration and exploitation through aerial flight and underwater foraging behaviors. This adaptive mechanism offers potential advantages over traditional MSAs, particularly in mitigating premature convergence and enhancing search diversity.

In addition to algorithmic robustness, practical implementation concerns also motivate this work. Wrapper-based feature selection frameworks are often hindered by high computational costs, as they require repeated classifier training and validation during the fitness evaluation phase. This overhead becomes particularly burdensome for large datasets or when using population-based metaheuristics like APO, which involve evaluating multiple candidate solutions per iteration. To address this critical bottleneck, we further enhance the APO-based framework by implementing a fully parallelized version using MATLAB’s Parallel Computing Toolbox. In the proposed design, both the metaheuristic search operations, including exploration and exploitation phases, and the fitness evaluations are executed concurrently. This concurrent execution architecture significantly reduces computation time, improves scalability, and enables practical deployment on large-scale feature selection tasks. By applying APO to real-world feature selection problems and enhancing its scalability through parallelization, this study not only demonstrates its practical effectiveness but also contributes empirical insights to the broader metaheuristic optimization community.

1.4 Contributions

Specifically, the main technical contributions of this paper are summarized as follows:

•   An advanced wrapper-based feature selection framework is proposed, explicitly leveraging the specialized exploration and exploitation operators of APO. This framework systematically identifies optimal feature subsets, thereby maximizing classification accuracy and minimizing computational complexity across diverse datasets.

•   A specialized conversion procedure is introduced to transform the continuous search outputs of APO into binary vectors suitable for discrete feature selection. This adaptation broadens the applicability of APO to binary optimization and provides a generalizable approach for binarizing continuous metaheuristics.

•   A fully parallelized implementation of the APO-based feature selection framework is developed using MATLAB’s Parallel Computing Toolbox. In this design, both the metaheuristic search operators and fitness evaluations are executed concurrently, substantially improving runtime efficiency and scalability, particularly for high-dimensional datasets.

•   To the best of the authors’ knowledge, this work presents the first comprehensive empirical evaluation of APO in the context of wrapper-based binary feature selection. Unlike previous studies that focused solely on continuous benchmark functions, this study addresses practical feature selection tasks characterized by complex interdependencies and large discrete search spaces.

•   Extensive experiments are conducted using 15 benchmark datasets from the University of California, Irvin (UCI) Machine Learning Repository, benchmarking APO against 14 recent and state-of-the-art metaheuristic algorithms. The results consistently demonstrate APO’s superior classification accuracy, feature compactness, and robust search behavior across diverse classification problems.

1.5 Paper Organization

The remainder of this paper is structured as follows: Section 2 provides a review of related work. Section 3 formulates wrapper-based feature selection as an optimization problem and presents the APO-based framework, including its binary conversion and parallel implementation. Section 4 presents experimental evaluations and comparative analyses. Finally, Section 5 concludes the paper and outlines future research directions.

2  Literature Review

2.1 General Overview of MSAs

MSAs constitute a powerful class of optimization techniques capable of navigating complex, high-dimensional, and multimodal search spaces to identify near-optimal solutions. Unlike classical optimization methods, which typically rely on gradient information or explicit mathematical properties, MSAs operate without such constraints [15]. This feature makes them especially suitable for diverse real-world problems characterized by nonlinearity, discontinuity, and uncertainty [16–20]. Fundamental to their effectiveness is the careful balance between two critical search behaviors: exploration, which broadly surveys the solution space to prevent premature convergence, and exploitation, which intensively refines solutions around promising regions.

The landscape of metaheuristics encompasses several distinct categories based on their underlying inspirations and operational mechanisms [15]. Evolutionary algorithms (EAs), for example, are inspired by biological evolution and utilize selection, crossover, mutation, and recombination to iteratively improve solutions. Genetic Algorithms (GA) and Differential Evolution (DE) represent classic examples of this approach. Human-based algorithms simulate cognitive and social behaviors, such as the Teaching-Learning-Based Optimization (TLBO) algorithm, which models the processes of knowledge transfer and social interaction. Physics-based algorithms draw on natural physical phenomena, with prominent examples including the Gravitational Search Algorithm (GSA) and Simulated Annealing (SA). Swarm intelligence algorithms mimic collective natural behaviors, exemplified by Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and the Grey Wolf Optimizer (GWO).

Recent developments in metaheuristic research have produced several innovative MSAs, each incorporating unique strategies to enhance search performance and overcome traditional limitations. The Dholes Hunting-based Optimization (DhoH) algorithm is a novel swarm-inspired approach inspired by the coordinated hunting strategies of Dholes [21]. It utilizes multi-local searches coordinated by clustering techniques and gradient approximation, making it effective for complex and multi-modal problems such as blockchain consensus optimization. The Artificial Rabbits Optimization (ARO) algorithm, inspired by rabbits’ survival strategies, employs detour foraging and random hiding behaviors. These adaptive strategies enhance exploration and exploitation capabilities, proving highly effective across diverse engineering optimization problems and practical scenarios, such as fault diagnosis in mechanical systems [22]. Additionally, the Improved Life Choice-based Optimization (ILCO) algorithm leverages decision-making processes inherent in human life choices to improve convergence speed and solution diversity. It has demonstrated superior effectiveness in complex task scheduling challenges within fog-cloud blockchain environments [23].

The Energy Valley Optimizer (EVO), inspired by advanced physical principles related to particle stability and decay, excels in global optimization and has achieved notable success across various benchmark tests and real-world engineering problems [24]. The Augmented Artificial Ecosystem Optimization (AAEO) enhances traditional ecosystem optimization approaches by integrating Levy-flight trajectories and Gaussian randomness to balance exploration and exploitation, significantly improving performance in hydrological modeling and prediction tasks [25]. The Salp Swarm Algorithm (SSA), inspired by the swarming behavior of salps during navigation and foraging, offers robust mechanisms for balancing exploration and exploitation [26]. Its chain-based leader-follower dynamic effectively improves convergence towards optimal solutions, proven through extensive evaluations in both single-objective and multi-objective optimization contexts, including demanding engineering design problems.

Despite these substantial theoretical and methodological advancements, metaheuristics continue to face challenges such as susceptibility to premature convergence, complexity in parameter tuning, and insufficient validation across extensive real-world scenarios. Addressing these limitations through rigorous empirical testing and innovative implementation strategies remains critical to unlocking the full potential of metaheuristics for diverse practical applications. To this end, increasing attention has been paid to their application in challenging discrete domains, particularly feature selection, where their ability to navigate large combinatorial search spaces can offer significant advantages. This motivates a focused discussion on how metaheuristics are currently being leveraged and evaluated in the context of feature selection.

2.2 Application of Metaheuristic in Feature Selection

Feature selection is a fundamental preprocessing step in machine learning, aimed at identifying the most relevant subset of features to reduce dimensionality, enhance model interpretability, and improve predictive performance. Among the many optimization approaches employed, MSAs have gained substantial traction due to their global search capabilities, flexibility, and robustness in navigating discrete, nonlinear, and high-dimensional search spaces. Consequently, their deployment in wrapper-based feature selection has become increasingly popular for maximizing classifier performance while reducing feature redundancy. Typically, wrapper-based feature selection frameworks consist of three primary components: representation, search strategy, and evaluation criterion. Representation often involves converting the optimization problem into binary or discrete forms suitable for subset selection. MSAs provide adaptive search strategies that balance exploration and exploitation, while classifiers such as K-Nearest Neighbors (KNN), Support Vector Machines (SVM), or Random Forests (RF) assess each subset’s predictive performance. Despite the breadth of MSAs proposed for feature selection, few studies have explored the integration of parallel computing frameworks, i.e., an underdeveloped yet crucial direction, particularly for high-dimensional, computationally intensive tasks.

Recent literature emphasizes significant advancements and emerging trends in the application of MSAs for feature selection. A comprehensive survey in [27] extensively analyzed the application of nature-inspired metaheuristic methods in feature selection. This survey highlighted various representation and search strategies employed by contemporary algorithms, emphasizing their simplicity, effectiveness in global search, and adaptability. The authors underscored important unresolved issues, including the need for robust mechanisms to avoid premature convergence and the importance of more comprehensive evaluations beyond benchmark datasets. Another systematic review conducted in [28] critically examined the effectiveness of metaheuristic optimization techniques specifically within disease diagnosis contexts. This review covered ten prominent algorithms, including the spider monkey algorithm, cuckoo search algorithm, grey wolf optimizer, and whale optimization, among others. The study detailed their practical applications in selecting and optimizing features for predicting various diseases such as heart disease, Alzheimer’s, diabetes, and COVID-19. It systematically evaluated algorithmic performance using comprehensive metrics such as accuracy, precision, sensitivity, specificity, and F1 score, highlighting critical insights for future application in healthcare domains.

Numerous recent studies have proposed innovative metaheuristic approaches for feature selection. Lee et al. [29] employed Genetic Algorithm (GA) and Harmony Search (HS) for feature selection in machine learning models aimed at diagnosing sarcopenia. Their approach demonstrated that HS combined with SVM classifier delivered superior accuracy and F1 score. Kwakye et al. [30] introduced Particle Swarm-guided Bald Eagle Search (PS-BES), a hybrid metaheuristic that incorporates an Attack-Retreat-Surrender strategy to enhance robustness and mitigate premature convergence in global optimization and feature selection tasks. Braik et al. [31] proposed a Binary Capuchin Search Algorithm (BCSA), integrating Levy flights and chaotic strategies to maintain population diversity, thereby enhancing search efficiency. Khafaga et al. [32] presented a wrapper-based approach combining Adaptive Squirrel Search Optimization Algorithm (ASSOA) with KNN, employing innovative relocation equations and movement strategies to improve search capabilities across multiple datasets. Additional studies explored integrating the Dipper Throated Optimization Algorithm with the Grey-Wolf Optimizer [33] and Sine Cosine Algorithm [34] to develop feature selection methods that improve classification accuracy and reduce model complexity.

Pan et al. [35] developed a Modified Teaching-Learning-Based Optimization with a Hierarchical Learning Scheme (MTLBO-HLS). Their approach featured a hierarchical structure allowing higher-tier solutions to guide lower tiers, combined with dynamic peer interactions to enhance overall search efficiency. Abdel-Salam et al. [36] introduced Adaptive Chaotic RIME (ACRIME), implementing chaotic initialization, adaptive modified mutualism phases, and mixed mutation strategies to mitigate local optima entrapment and enhance global search capabilities. In a separate study, Abdel-Salam et al. [37] proposed an Improved Genghis Khan Shark Optimizer (I-GKSO) for high-dimensional feature selection tasks. This approach incorporated solution modification strategies and Quasi-Opposite-Based Learning (QOBL) to refine solutions and enhance performance. Qu et al. [38] introduced Explicit and Size-Adaptive PSO (ESAPSO), which utilized an explicit particle representation and a size-adaptive expansion strategy based on feature importance, significantly reducing computational costs. Li et al. [39] proposed the Equilibrium Optimizer with Divided Population Based on Distance (DEO), employing adaptive Beta distribution parameters to dynamically balance exploration and exploitation.

Wang et al. [40] developed Probabilistic Sequence-based Ant Colony Optimization (SPACO), which utilized symmetric uncertainty and probabilistic sequencing to effectively select informative features. Gupta and Gupta [41] introduced Fitness and Historical Success Information-Assisted Binary Particle Swarm Optimization (FPSO), which dynamically adjusted acceleration coefficients using historical success information to facilitate transitions between exploration and exploitation. Wang et al. [42] developed Fast Multiobjective Feature Selection Method (FMABC-FS), utilizing improved Artificial Bee Colony algorithms, k-means clustering-based differential selection, and ladder-like sample strategies for efficient feature selection. Singh et al. [43] combined Bacterial Foraging Optimization and Emperor Penguin Optimization (BFOEPO) for glaucoma classification from fundus images, achieving superior classification accuracy. Wu et al. [44] enhanced Sparrow Search Algorithm with Quantum Computation and Multi-Strategy Enhancement (QMESSA), employing chaotic maps and quantum gate mutations to improve initial population diversity, convergence, and overall performance.

In summary, recent advances in metaheuristics have provided numerous MSAs demonstrating strong theoretical capabilities. Nevertheless, limitations such as insufficient validation on real-world problems, computational inefficiencies, and susceptibility to premature convergence remain prominent challenges. The present study addresses these gaps by adapting the recently proposed APO to the wrapper-based feature selection task. Furthermore, our fully parallelized implementation of APO significantly enhances computational efficiency, offering a scalable solution to high-dimensional search problems where existing algorithms often struggle with computational overhead. Through comprehensive empirical validation on real-world datasets, the proposed APO framework aims to robustly address these identified gaps, advancing both the theoretical foundations and practical effectiveness of metaheuristic optimization techniques in feature selection, including those found in recent developments such as DhoH, ILCO, and EVO, while uniquely incorporating a parallel implementation strategy to improve runtime performance and scalability. Unlike these recent MSAs, which have demonstrated promising results in continuous or application-specific domains, this study evaluates APO’s efficacy in discrete, high-dimensional wrapper-based feature selection tasks, further strengthening its relevance and competitiveness.

Despite considerable theoretical progress in metaheuristic-based feature selection, several challenges persist, i.e., most notably, limited empirical validation on real-world datasets, computational inefficiencies due to exhaustive fitness evaluations, and the risk of premature convergence in high-dimensional search spaces. This study addresses these challenges by adapting the recently proposed APO algorithm to wrapper-based feature selection tasks and introducing a fully parallelized implementation to improve runtime efficiency. This parallel design offers a scalable solution where many existing MSAs, including DhoH, ILCO, and EVO, often struggle with computational burden. Through comprehensive empirical validation on diverse UCI datasets, the proposed APO framework demonstrates strong classification accuracy, compact subset selection, and runtime scalability. While the aforementioned MSAs have shown promise in continuous or domain-specific optimization tasks, this study positions APO as a competitive alternative for discrete, high-dimensional wrapper-based feature selection problems, advancing the practical relevance of recent metaheuristic research.

3  Proposed Wrapper-Based Feature Selection Method

Fig. 1 illustrates the overall workflow of the proposed wrapper-based feature selection method utilizing parallelized APO as the global search algorithm. The key steps of the feature selection process and the search mechanism employed by parallelized APO are detailed in the following subsections.

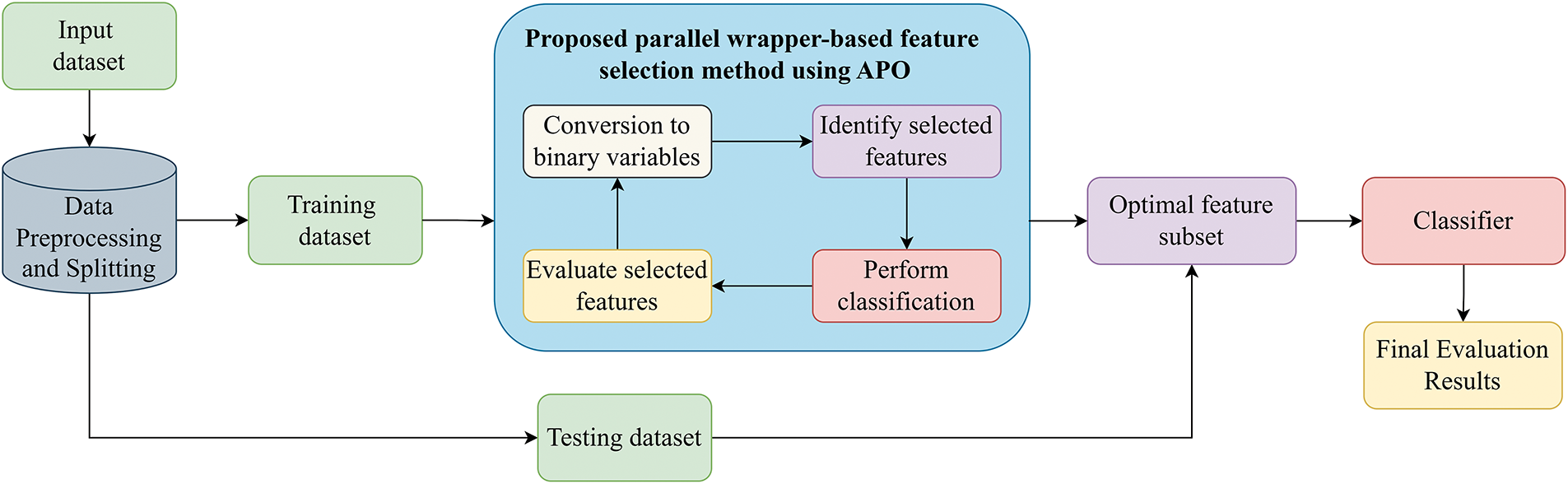
Figure 1: Overall workflow of the proposed parallel wrapper-based feature selection method using APO

3.1 Solution Encoding and Specialized Conversion Processes

Feature selection is inherently a discrete optimization problem, where each feature is either included (1) or excluded (0). However, APO operates in a continuous search space. To enable compatibility, a binarization scheme is used to map continuous positions to binary feature selection decisions. Specifically, the position of each n-th puffin is represented as a continuous solution vector Xn=[Xn,1,…,Xn,d,…,Xn,D], where D=|ℱTotal| is the total number of features. A threshold ρ is applied to convert each element into binary form:

Xn,dBin=I(Xn,d≥ρ)(1)

where I(⋅) is the indicator function, and Xn,dBin∈{0,1} indicates whether the d-th feature is selected. This produces a binary vector XnBin used during fitness evaluation.

Notably, this conversion from continuous to binary values is a well-established practice in wrapper-based feature selection using MSAs. The binarization process enables the MSA to clearly differentiate selected from non-selected features, streamlining the search for optimal subsets. While this transformation simplifies representation, it is purposefully designed to direct the optimization toward relevance and interpretability without compromising accuracy. Continuous values typically represent selection probabilities or weights, and once binarized, translate into decisive inclusion or exclusion. Attempting to recover original continuous values is neither standard nor necessary, as the binary outcome is the intended and sufficient solution for subset selection. Prior studies have consistently demonstrated the effectiveness of such binary representations in feature selection contexts, reinforcing the validity of this approach [45].

3.2 Fitness Function

In wrapper-based feature selection, the objective is to identify a feature subset that balances two criteria, i.e., minimizing classification error and reducing the number of selected features. This trade-off is quantified by the following fitness function [1]:

f(XnBin)=μ⋅γError+(1−μ)⋅|ℱSelect||ℱTotal|(2)

where γError denotes the classification error, |ℱSelect| is the number of selected features, |ℱSelect| is the total number of features, and μ∈[0,1] is the weight controlling the trade-off between accuracy and feature subset size.

In this study, a KNN classifier is used to evaluate each candidate solution XnBin. A lower fitness value of f(XnBin) indicates a superior solution with higher predictive accuracy and fewer features. This formulation encourages the selection of compact, relevant subsets that reduce redundancy while maintaining classification performance and improving interpretability.

3.3 Search Mechanisms of APO

This subsection outlines the search mechanisms of APO [14], which are inspired by the survival strategies of Arctic puffins both in the air and on the water. The algorithm’s operations are structured into three primary stages: population initialization, aerial flight stage focuses on exploration, and underwater foraging stage emphasizes exploitation. Each stage is detailed in the next subsections, along with the mechanisms employed to maintain a balance between exploration and exploitation during the optimization process.

3.3.1 Population Initialization

In APO, each individual in the population represents a candidate solution for the feature selection tasks. Specifically, the position of the n-th solution is defined as a continuous vector Xn=[Xn,1,…,Xn,d,…,Xn,D], where D is the total number of features and n=1,…,N indexes the population size. The initial positions are generated using a uniform distribution as follows:

Xn=XLB+r1(XUB−XLB)(3)

where r1∈[0,1]D is a vector of uniformly distributed random values, XUB and XLB are the upper and lower bounds of the search space, respectively.

Each initialized solution Xn is then binarized using the conversion scheme in Eq. (1), producing XnBin, which defines the selected feature subset. The fitness value for each solution is computed using Eq. (2), and the individual with the lowest fitness is designated as the current best solution XBest.

3.3.2 Exploration-Exploitation Balancing Mechanism

Following population initialization, APO proceeds with its iterative search process by dynamically alternating between exploration and exploitation phases. This switching behavior is governed by a behavioral control parameter B, which decreases over time to promote global exploration in the early stages and local refinement in later stages. The behavioral switching coefficient B is defined as:

B=2×log⁡(1r2)×(1−fesFESmax)(4)

where r2∈[0,1] is a uniformly distributed random number, fes denotes the number of fitness evaluations performed so far, and FESmax is the maximum number of fitness evaluations. As optimization progresses, the term (1−fes/FESmax) reduces B, thereby increasing the likelihood of shifting from exploration to exploitation.

An additional control parameter C∈[0,1] is introduced to determine the behavior mode at each iteration. The phase selection is governed by the following rule:

•   If B>C, the APO executes the exploration phase, promoting search diversity by investigating new regions of the solution space.

•   If B≤C, the APO enters the exploitation phase, refining candidate solutions around promising regions to accelerate convergence.

This adaptive mechanism ensures a dynamic balance between exploration and exploitation throughout the search process. The detailed search operators associated with each phase are presented in the subsequent subsections.

3.3.3 Exploration Phase

In the exploration phase, APO simulates global search behavior using two stochastic update strategies that promote diversity and improve the ability to escape local optima. These strategies are loosely inspired by the adaptive aerial movements of Arctic puffins when scanning large areas.

The first update mechanism models aerial displacement, where the current solution Xn is perturbed using a Lévy flight-based operator:

Un=Xn+(Xn−Xr)×Levy(D)+R(5)

where Xr is a randomly selected peer (r≠n), Levy(D) generates a step vector with long-tailed distribution, and R is a small stochastic perturbation computed as:

R=round(0.5×(0.05+r3))×α(6)

where r3∈[0,1] sampled from a uniform distribution and α∼N(0,1). This operator enhances global search by allowing occasional long-range moves while maintaining variation through Gaussian noise.

The second update mechanism, referred to as swooping displacement, adjusts the magnitude and direction of Un using a velocity scaling coefficient S:

S=round((r4−0.5)×π)(7)

Vn=Un×S(8)

where r4∈[0,1] is a uniformly distributed random number. The coefficient S introduces stochastic scaling that allows the algorithm to randomly amplify, attenuate, or reverse the direction of the displacement. This mechanism enhances the flexibility of the search, enabling both coarse and fine-grained exploration depending on the current landscape.

After these updates, the candidate positions Un and Vn are converted into binary solutions UnBin and VnBin, using Eq. (1). Their corresponding fitness values are evaluated using Eq. (2), and the best among XnBin, UnBin, and VnBin is selected as the updated position Xn for the next iteration.

3.3.4 Exploitation Phase

In the exploitation phase, APO intensifies local search through three mechanisms designed to refine candidate solutions. These mechanisms are loosely inspired by underwater behaviors observed in puffins: (a) gathering foraging, (b) intensified search, and (c) predator avoidance. Each serves a unique purpose in enhancing convergence speed, solution quality, and local search robustness.

The first operator, i.e., gathering foraging, simulates cooperative behavior where individuals converge based on peer observations. Three distinct solutions Xr1, Xr2 and Xr3, are randomly selected from the population (r1≠r2≠r3≠n), and a cooperative factor F guides the new displacement:

Wn={Xr1+F×(Xr2−Xr3), if rand<0.5Xr1+F×Levy(D)×(Xr2−Xr3), if rand≥0.5(9)

This dual-strategy approach balances incremental adjustments with larger stochastic shifts. If rand<0.5, a direct cooperative movement is applied. Otherwise, Lévy perturbation enhances search flexibility. This improves local refinement and expands neighborhood exploration.

The second operator, i.e., intensified search, mimics adaptive repositioning in response to diminishing rewards. After applying Eq. (9), the solution Wn is scaled using an adaptive factor f, yielding:

Yn=Wn×(1+f)(10)

f=0.1×(r5−1)×(FESmax−fes)FESmax(11)

where r5∈[0,1] is a uniformly distributed random number. This formulation gradually reduces search aggressiveness as the optimization progresses, allowing solutions to settle near promising regions.

The third operator, i.e., predator avoidance, introduces perturbations to escape local optima by mimicking evasive maneuvers. A random binary switch governs the strategy:

Zn={Xi+β×(Xr1−Xr2), if rand<0.5Xi+F×Levy(D)×(Xr1−Xr2), if rand≥0.5(12)

where β∈[0,1] is a uniformly distributed random number. The first strategy induces moderate exploration, while the second facilitates large jumps out of local traps. This operator enhances robustness, particularly in complex landscapes.

After applying these three operators, the resulting vectors Wn, Yn and Zn are binarized using Eq. (1) to yield WnBin, YnBin and ZnBin. Their fitness values are computed using Eq. (2), and the best-performing solution among XnBin, WnBin, YnBin, and ZnBin is retained as the updated Xn for the next iteration.

3.4 Parallel Wrapper-Based Feature Selection Framework Using APO

Feature selection is a high-dimensional combinatorial problem that becomes computationally intensive when wrapper-based methods are employed. The primary bottleneck arises from repeated fitness evaluations, which often involve training and validating machine learning classifiers. To address this challenge and enhance the scalability of the APO algorithm, this study proposes a fully parallelized wrapper-based feature selection framework. The parallel implementation is developed using MATLAB’s Parallel Computing Toolbox, and it supports concurrent computation of both search operator updates and fitness evaluations. This design allows the optimization process to efficiently handle large-scale datasets and high-dimensional feature spaces. It is important to note that while the core APO algorithm remains unchanged in terms of its original search operators, the novelty of this study lies in its full integration within a parallel computing framework, specifically tailored for computationally intensive wrapper-based feature selection tasks in real-world scenarios.

To facilitate a clear understanding of the execution pipeline, the overall workflow of the proposed parallelized APO-based feature selection technique is outlined in Algorithm 1. The process begins with loading the dataset and extracting its dimensionality, denoted as D=|ℱTotal|. Key algorithmic parameters are initialized, including the population size N, the fitness evaluation counter fes, and the weight parameter μ that governs the trade-off between classification accuracy and feature reduction. Each candidate solution vector Xn is randomly generated within the continuous search space. To evaluate the fitness of each candidate, a binarization process in Eq. (1) is applied to transform continuous vectors into binary feature masks. These binary vectors are then used for wrapper-based evaluation using a KNN classifier. Both binarization and evaluation are conducted in parallel across all puffins using MATLAB’s parfor loop, ensuring efficiency during the population initialization stage. Once the population has been evaluated, the best-performing solution is recorded as the global best solution XBest.

With the initial population established, the proposed parallelized APO algorithm enters its main iterative loop. At each iteration, the behavioral switching coefficient B is calculated using Eq. (4) to determine whether the search should focus on global exploration or local exploitation. During the exploration phase (triggered when B>C), each puffin updates its position via aerial flight and swooping predation operators, as introduced in Section 3.3.3. These operations generate two new candidates Un and Vn, which are independently binarized and evaluated in parallel. Among the original candidate Xn, and the new candidates Un and Vn, the best-performing one is retained for the next iteration. Alternatively, when B≤C, the population enters the exploitation phase. Here, each puffin generates three new candidate solutions using the gathering foraging, intensified search, and predator avoidance strategies (see Section 3.3.4), producing vectors Wn, Yn and Zn. These candidates are likewise binarized, evaluated using the KNN classifier, and compared to the current solution. The best-performing candidate replaces the existing puffin’s position. Both exploration and exploitation processes are fully parallelized to maximize efficiency.

After each iteration, the fitness evaluation counter is updated, and the global best solution XBest is refreshed if a superior candidate is found. This iterative process continues until the maximum number of fitness evaluations FESMax is reached. Upon termination, the binary version of the best-performing solution, XBin,Best, is returned as the final selected feature subset. The pseudocode for the entire parallel wrapper-based feature selection framework using APO is detailed in Algorithm 1. It reflects all aspects of the proposed implementation, including the parallel execution of both search and evaluation components. This fully parallelized design not only preserves the original structural benefits of APO but also overcomes one of the most significant limitations of wrapper-based methods, i.e., high computational cost. By leveraging parallelization at both the search and fitness evaluation stages, the proposed framework significantly reduces runtime and enhances scalability. These performance advantages are further validated in Section 4, where APO demonstrates superior runtime, convergence, and classification outcomes compared to other MSAs on various types of datasets.

4  Experimental Results and Analysis

This section presents a comprehensive evaluation of the proposed APO-based wrapper feature selection framework. The experiments are designed to assess multiple performance dimensions, including classification accuracy, feature subset compactness, runtime efficiency, convergence behavior, statistical significance, and classifier diversity. A total of 15 benchmark datasets with varying dimensionalities and class complexities are used to validate the framework’s generalizability. The analysis begins with a description of the experimental setup, followed by detailed performance evaluations and a final discussion highlighting the key findings and future research directions.

4.1 Experimental Setup

To evaluate the effectiveness of the proposed parallelized APO-based wrapper feature selection framework, a comprehensive comparative study was conducted against 14 recent and competitive MSAs. The baseline algorithms include the Aquila Optimizer (AO) [46], Bezier Search Differential Evolution (BeSD) [47], Cheetah Optimizer (CO) [48], Dwarf Mongoose Optimization Algorithm (DMOA) [49], Differential Squirrel Search Algorithm (DSSA) [50], Flow Direction Algorithm (FDA) [51], Opposition Death Mechanism Shuffled Frog and Moth Flame Optimization (ODSFMFO) [52], Osprey Optimization Algorithm (OOA) [53], Red-Tailed Hawk Algorithm (RTH) [54], Propagation Search Algorithm (PSA) [55], Chinese Pangolin Optimizer (CPO) [56], Dholes Hunting (DhoH) [21], Energy Valley Optimizer [24] and Improved Life-Choice-Based Optimization (ILCO) [23]. All algorithm-specific parameters were tuned according to their original publications to ensure reproducibility and fairness. For binarization of continuous solutions into feature selection vectors, a threshold value of ρ=0.5 was uniformly applied across all MSAs.

Fifteen widely used benchmark datasets from the UCI Machine Learning Repository were employed for empirical validation. These datasets were selected to cover a broad range of characteristics, including variation in the number of instances, feature dimensionality, and class distribution, as summarized in Table 1. For each dataset, 80% of the data was allocated for training and the remaining 20% for testing. A KNN classifier with k=5 was adopted uniformly across all feature selection frameworks to evaluate classification performance based on classification error.

To ensure a fair evaluation, all algorithms were executed under identical experimental conditions. The population size was fixed at N = 20, and the maximum number of fitness evaluations was capped at Max_Fes = 2000. Each algorithm was independently run 30 times on each dataset to account for stochastic variability and to allow for statistically meaningful comparisons.

All algorithms were implemented in MATLAB R2024a and executed on a workstation configured with an Intel® Core™ i9-14900HX CPU @ 2.20 GHz, 32 GB RAM, and running Windows 11 Pro (64-bit). The parallelized version of the proposed APO-based framework leveraged MATLAB’s built-in parallel computing toolbox, enabling concurrent execution of fitness evaluations and significantly improving runtime efficiency across all datasets.

4.2 Classification Accuracy Comparison

Table 2 summarizes the average classification accuracy achieved by the proposed parallelized APO-based wrapper feature selection method and 14 competing state-of-the-art MSAs across 15 benchmark datasets (DS1 to DS15). Each result is averaged over 30 independent runs to ensure statistical robustness. For each dataset, the best result is boldfaced, while the second-best result is italicized and underlined for each of comparison.

The results clearly show that the proposed APO-based wrapper method achieves the highest classification accuracy in 14 out of the 15 datasets (DS1 to DS8 and DS10 to DS15), outperforming all other compared MSAs. The only exception is DS9, where it secures the second-highest accuracy. Among the other methods, the wrapper-based feature selection using DMOA demonstrates strong performance, achieving the top accuracy in five datasets (DS2 to DS5 and DS12), and ranking second in DS1 and DS14. Likewise, ILCO performs competitively by obtaining the best accuracies in DS2, DS3, DS5, DS10, and DS12. Several other MSAs also deliver competitive results. For instance, AO, CO, and RTH each attain the highest classification accuracy in at least three datasets. CO performs well on DS1, DS5, DS9, and DS12, and ranks second-best in DS2, DS3, and DS11. AO achieves top accuracy in DS2, DS4, DS5, and DS10, and secures second place in DS15. RTH, meanwhile, leads in DS2, DS3, and DS5, and ranks second-best in DS13 and DS15.

In contrast, MSAs such as ODSFMFO, OOA, PSA, CPO, and EVO demonstrate more moderate performance across the datasets. These methods neither dominate in accuracy nor perform consistently poorly. For example, ODSFMFO ranks highest in DS3 to DS5, but also records the lowest accuracy in DS1 and DS11, and the second-lowest in DS9. Similarly, OOA performs best on DS4, DS5, and DS15, yet ranks second-lowest in DS3. PSA achieves top accuracy in DS3 and DS5, but falls significantly in DS6, where it ranks near the bottom. EVO shows a similar pattern, excelling in DS5 and DS12, but scoring poorly in DS3. CPO delivers the best performance in DS5, but performs poorly in DS2, DS11, and DS13, where it ranks second-lowest.

Finally, MSAs such as BeSD, CO, DSSA, FDA, and DhoH display consistently weak performance across most datasets. BeSD performs particularly poorly, recording the lowest accuracy in DS8, DS12, and DS13, and the second-worst in DS14. Although CO achieves competitive accuracy on a few datasets, it suffers from high performance variability, ranking lowest in DS6, DS7, and DS10, and second-worst in DS8 and DS15. Both DSSA and FDA exhibit similar patterns, with DSSA ranking last in DS1, DS2, and DS4, and FDA in DS3, DS9, and DS15. DhoH performs worst on DS14 and ranks second-worst on DS2, DS4, and DS13.

4.3 Feature Reduction Analysis

Beyond classification accuracy, the effectiveness of a feature selection method is also assessed based on the number of selected features. Reducing redundant and irrelevant features enhances model interpretability and computational efficiency. An optimal feature selection method aims to achieve a balance between minimizing the size of the selected feature subset and maintaining high classification accuracy.

To evaluate this trade-off, this study considers the average number of selected features required for classification using the KNN classifier as an additional performance metric. Table 3 presents the mean number of selected features for each MSA across the 15 datasets (DS1 to DS15), computed over 30 independent runs. The MSA achieving the smallest average feature subset for each dataset is highlighted in bold, while the second-smallest is italicized and underlined.

The results in Table 3 show that the proposed APO-based wrapper method consistently selects fewer features than most other MSAs. Specifically, APO identifies the smallest subset in seven datasets (DS1 to DS5, DS7, and DS10), and the second-smallest in four more (DS9, DS11, DS12, and DS15). DMOA follows closely, obtaining the smallest subset in DS5, DS9, DS10, and DS12, and the second-smallest in DS11 and DS15. BeSD also performs well in feature reduction, selecting the smallest subset in DS8, DS14, and DS15, and the second-smallest in DS13.

Although methods such as DSSA, OOA, RTH, and PSA do not frequently produce the smallest subsets, they consistently rank among the top performers in feature reduction. For example, RTH identifies the smallest subset in DS5 and DS13, and the second-smallest in DS7, DS9, DS10, DS11, and DS15. OOA finds the smallest subset in DS11 and ranks second in DS1, DS4, DS5, DS9, and DS15. Similarly, PSA selects the smallest subset in DS6 and ranks second in DS9, DS11, and DS15. DSSA is observed to obtain the second-smallest subset in DS3, DS6, DS8, DS14, and DS15.

Meanwhile, MSAs such as AO, FDA, DhoH, EVO, and ILCO exhibit moderate performance in terms of feature reduction. These methods generally do not achieve either the smallest or largest feature subset sizes across most datasets. For instance, FDA selects the smallest subset in DS5, ranks second-smallest in DS11 and DS15, and second-largest in DS9. AO identifies the smallest subsets in DS3 and DS10, the second-smallest in DS15, and the second-largest in DS9. DhoH, EVO, and ILCO tend to produce feature subsets of intermediate size. Notably, ILCO and DhoH achieve the second-smallest subsets in two datasets each, while EVO does so in only one.

In contrast, MSAs such as ODSFMFO, CO, and CPO exhibit consistently poor performance in minimizing the number of selected features. These methods frequently generate the largest or second-largest subsets, indicating limited capability in reducing model complexity. Among them, ODSFMFO performs worst, producing the largest subsets in ten datasets (DS1, DS2, DS3, DS6, DS8, DS9, DS10, DS11, DS12, and DS14), and the second-largest in DS7. CO also struggles in this aspect, yielding the second-largest subsets in DS6, DS8, DS11, DS13, and DS14. While CPO occasionally performs better by identifying the second-smallest subset in DS9 and DS15, it also produces the largest subsets in DS7, DS10, and DS13, further highlighting its instability in subset size minimization.

4.4 Runtime and Scalability Analysis

To complement the evaluation of classification accuracy and feature subset size, this section presents a comprehensive runtime and scalability analysis of the proposed parallelized APO-based wrapper feature selection method, benchmarked against 14 other state-of-the-art MSAs across 15 datasets. Runtime performance is a critical aspect of wrapper-based methods due to their intensive reliance on repeated classifier evaluations. Therefore, it is important to assess whether the parallel implementation of APO provides a favorable trade-off between classification performance and computational efficiency.

Table 4 reports the mean computational time (in seconds) for each MSA, averaged over 30 independent runs per dataset. As shown, the parallelized APO consistently demonstrates lower execution time across datasets of varying dimensionality and instance size. In small-to-moderate datasets such as DS1, DS2, and DS3, the APO-based method achieves execution times of 2.39, 1.99, and 1.94 s, respectively, i.e., outperforming other MSAs such as DSSA and CPO. For example, on DS1, APO’s runtime (2.39 s) is slightly higher than DSSA (2.13 s), but APO significantly outperforms DSSA in classification accuracy (1.000 vs. 0.977) and in selecting more compact feature subsets (3.00 vs. 7.67). This highlights APO’s superior balance of speed, accuracy, and feature reduction.

The advantages of APO become even more pronounced in high-dimensional datasets. In DS4, which contains 4000 features, APO completes execution in just 4.25 s, faster than most competitors, including FDA (20.03 s), AO (18.31 s), CPO (17.27 s), and CO (11.12 s). Even the few MSAs with comparable runtime, such as OOA (4.82 s) and RTH (5.02 s), do not match APO’s classification accuracy or subset compactness. A similar trend is observed in DS13, where APO achieves a near-best runtime (7.08 s), while maintaining the highest classification accuracy (0.962) and a competitive feature subset size (140.67). Although DSSA is marginally faster (6.93 s), its accuracy (0.920) and subset size (145.07) are inferior.

In large-instance datasets, such as DS8 (5000 samples) and DS14 (20,000 samples), APO continues to demonstrate strong scalability. Despite the increased number of evaluations required, APO completes execution in 8.98 and 79.89 s, respectively. These runtimes are substantially lower than those of several other MSAs, such as AO, BeSD, and CO, which exceed 100 s in DS14. This confirms the effectiveness of APO’s parallelization in mitigating computational cost while preserving performance.

To further validate the effectiveness of the parallelization strategy, a direct comparison was conducted between the parallelized and non-parallelized APO implementations. Table 5 summarizes three key metrics: classification accuracy, average feature subset size, and mean runtime, across all datasets. This comparative analysis offers a comprehensive perspective on the effectiveness (accuracy), compactness (feature subset size), and efficiency (runtime) of the two implementations.

Results show that the classification accuracy remains the same or slightly improves with parallelization. For example, the same accuracy is observed in DS1 to DS5 and DS10, while marginal improvements occur in DS6, DS11, DS13, and DS14, likely due to enhanced convergence from increased computational throughput. The feature subset size remains highly consistent across both versions, indicating that parallel execution does not affect the solution trajectory or stability.

The most significant improvement is in runtime. APO’s parallelized version achieves more than 30% reduction in runtime in several datasets (e.g., DS1–DS3, DS6, DS9–DS12), and remains efficient even in high-dimensional (DS4, DS13) and large-instance (DS8, DS14) datasets. These results highlight the scalability and practical applicability of the proposed approach.

4.5 Convergence and Stability Behavior

This section presents an in-depth analysis of the convergence behavior and selection stability of the proposed parallelized APO-based wrapper feature selection method. Two analyses are conducted: (a) convergence curves of APO and 14 other state-of-the-art MSAs on six representative datasets (DS2, DS4, DS8, DS12, DS13, and DS14), and (b) the variation in classification accuracy and the number of selected features of APO as a function of fitness evaluations. These datasets were strategically chosen to represent diverse characteristics in instance size, feature dimensionality, and class complexity. Specifically, DS2 and DS12 represent small-sample datasets with moderate feature counts; DS4 and DS13 are ultra-high-dimensional and high-dimensional, respectively; and DS8 and DS14 are large-sample datasets with thousands to tens of thousands of records.

Fig. 2 presents the convergence curves of APO and 14 other MSAs across the six representative datasets. Across all six datasets, the proposed parallelized APO consistently demonstrates superior convergence behavior, both in terms of speed and final fitness values. In DS2 and DS12, APO exhibits a steep fitness decline in the early stages, converging toward near-optimal solutions far earlier than most competitors. In DS2, although DMOA initially performs well, APO quickly surpasses it and stabilizes at a lower fitness level. Similarly, in DS12, APO outpaces most algorithms within the first 250 evaluations and maintains consistently low fitness values throughout, indicating strong early exploitation and reliable convergence under small-sample conditions, where overfitting risks are high.

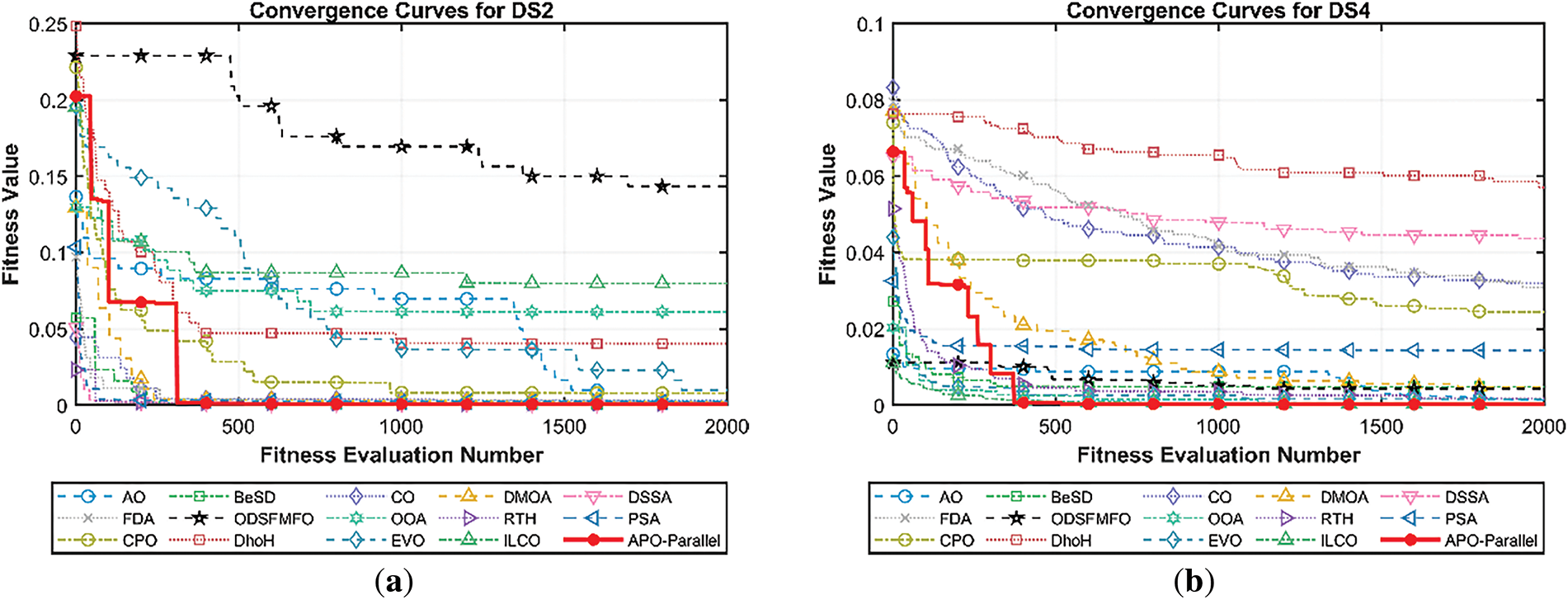
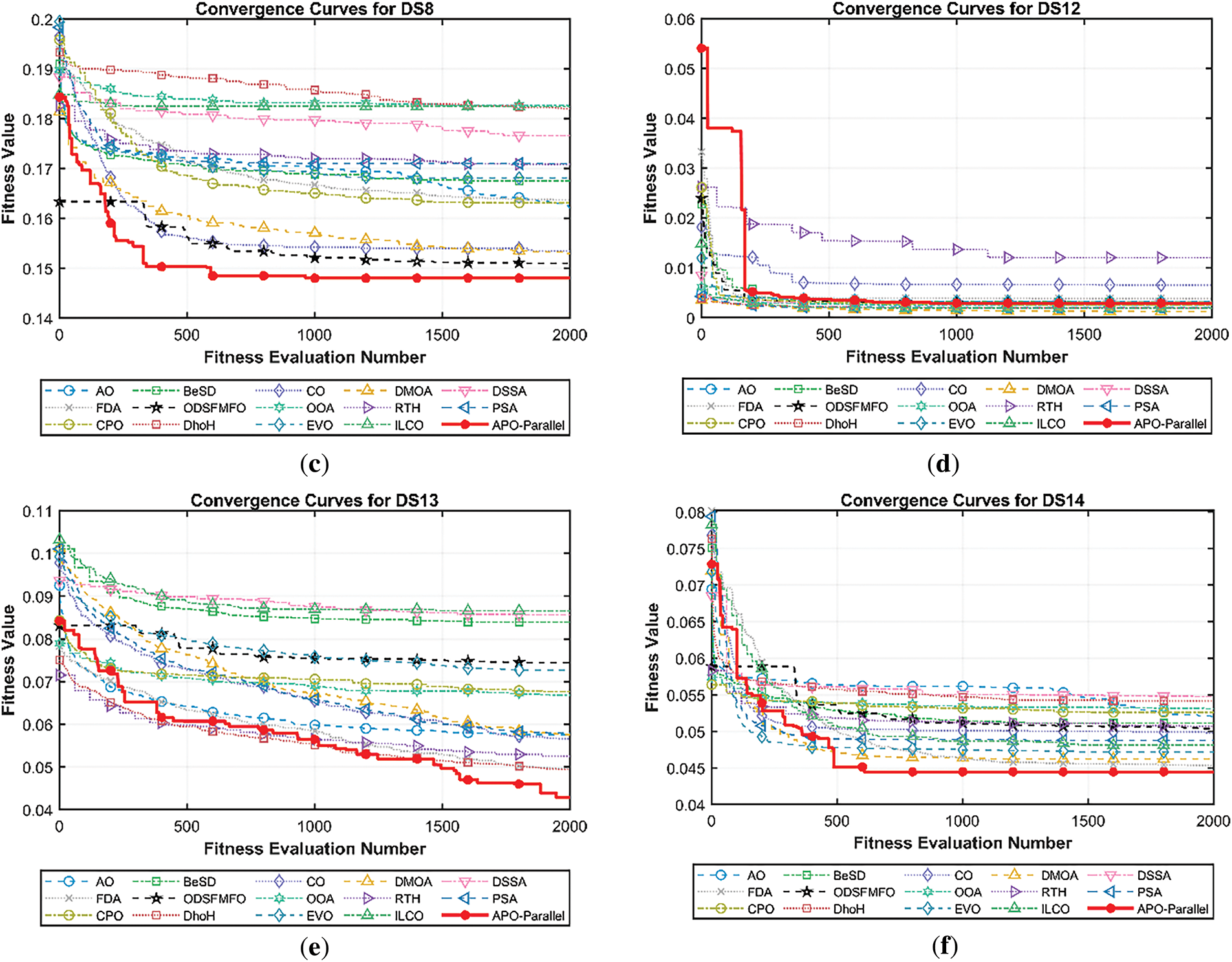
Figure 2: Convergence curves of parallelized APO and other MSAs over six representative datasets: (a) DS2, (b) DS4, (c) DS8, (d) DS12, (e) DS13, and (f) DS14

In high-dimensional datasets like DS4 and DS13, APO again outperforms the alternatives. In DS4, it shows a rapid and smooth decline in fitness, converging well before most MSAs. Algorithms such as DSSA, FDA, DhoH, CPO, PSA, and BeSD exhibit sluggish or unstable convergence, suggesting reduced robustness in high-dimensional search spaces. In DS13, while MSAs like DhoH, AO, FDA, and RTH perform relatively well at the initial stage, APO maintains a consistent and deeper descent in the subsequent stage, ultimately achieving the lowest fitness value. This highlights APO’s capacity to efficiently navigate the curse of dimensionality and eliminate irrelevant features.

For large-instance datasets like DS8 and DS14, APO continues to demonstrate efficient convergence. In DS8, despite the large number of evaluations, its convergence curve remains smooth and monotonic, demonstrating the parallel design’s ability to manage computational load. In DS14, APO exhibits a notably steeper and faster convergence than all other algorithms, including ILCO, DhoH, and EVO, which perform moderately but lag in speed and final solution quality.

Notably, MSAs such as DSSA, FDA, and BeSD often show flat or erratic convergence across these datasets, reflecting ineffective search dynamics. In contrast, algorithms like ILCO, EVO, and DhoH show more consistent convergence patterns but eventually settle at higher fitness values than APO. These findings highlight the effectiveness of the proposed APO framework in accelerating convergence and maintaining high search reliability across diverse problem landscapes.

In addition to convergence speed, the stability and robustness of the parallelized APO are evaluated by examining how classification accuracy and feature subset size evolve throughout the optimization. Fig. 3 presents these two metrics across the same six representative datasets. In all cases, classification accuracy exhibits smooth and generally monotonic improvement, indicating reliable convergence dynamics. Notably, in DS2, DS4, DS12, and DS14, near-optimal accuracy is reached early in the search, reflecting strong exploitation. Even in complex datasets like DS8 and DS13, the steady improvement without oscillations confirms APO’s capacity to maintain consistent learning behavior.

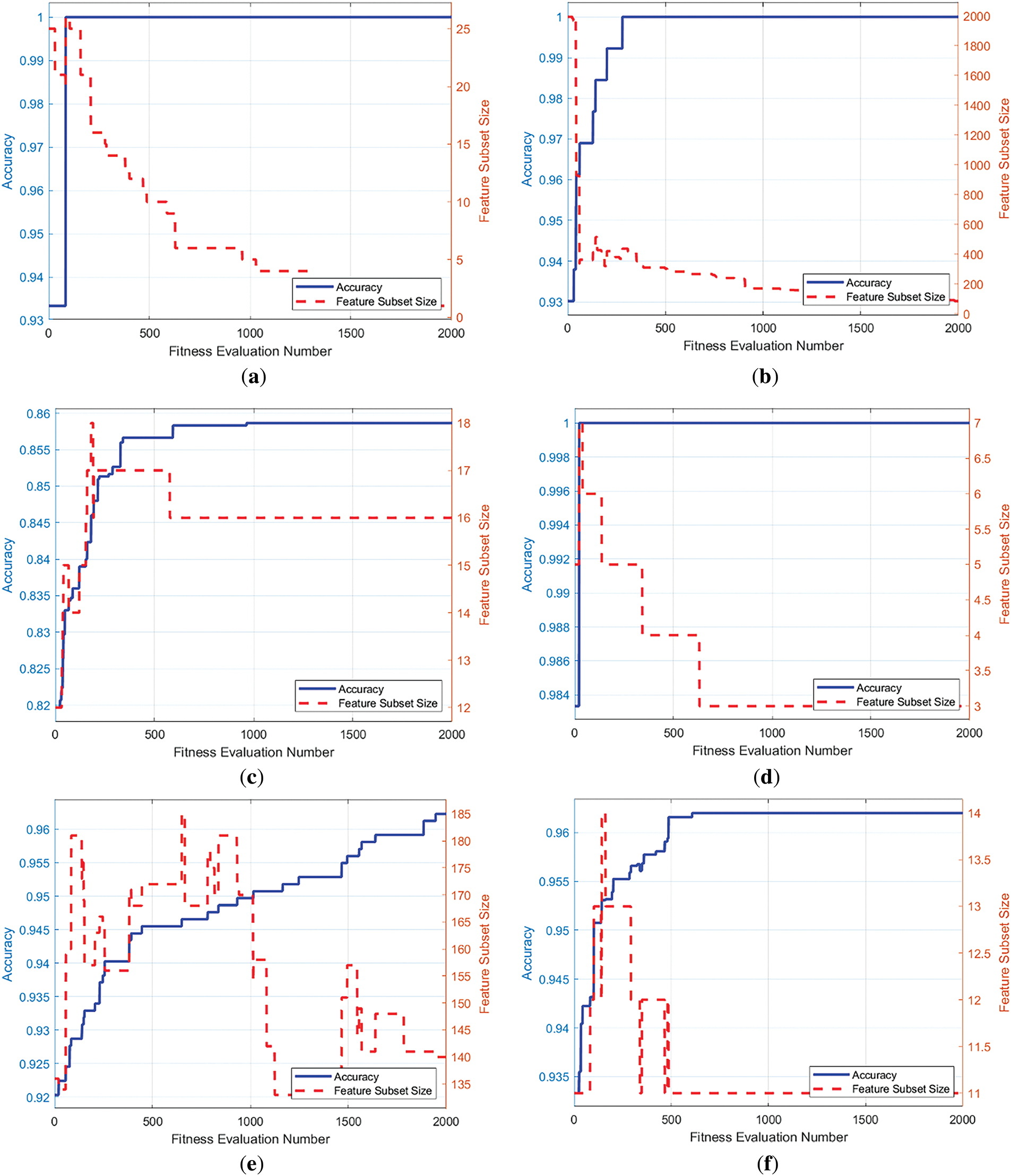
Figure 3: Variation of classification accuracy and number of selected features with respect to fitness evaluation number for parallelized APO on six representative datasets: (a) DS2, (b) DS4, (c) DS8, (d) DS12, (e) DS13, and (f) DS14

The evolution of feature subset size reveals further insights. In most datasets, the subset size declines rapidly during early stages and then stabilizes. This trend is most prominent in DS4 and DS13, where APO discards large numbers of irrelevant features early and converges to compact subsets, effectively handling high dimensionality without compromising predictive performance. In DS8 and DS14, APO explores larger subsets initially but consistently converges to minimal configurations, demonstrating a balanced trade-off between exploration and refinement. The final stages show simultaneous plateaus in accuracy and subset size, confirming the method’s convergence maturity.

Importantly, the coupled trajectories of accuracy and subset size suggest high intra-run stability. Minimal volatility in both metrics, even under stochastic search dynamics, demonstrates APO’s consistency in identifying robust feature subsets. Although Fig. 3 illustrates a representative run, the consistent patterns observed across multiple trials reinforce the algorithm’s reliability in producing repeatable and generalizable results. Altogether, this section validates the parallelized APO as not only fast and accurate but also stable and trustworthy for real-world feature selection tasks where both performance and consistency are critical.

4.6 Non-Parametric Statistical Testing

To evaluate the significance of performance differences among the wrapper-based feature selection methods developed using the parallelized APO and 14 other MSAs, three widely adopted non-parametric statistical tests are conducted, i.e., the Wilcoxon signed-rank test, the Friedman test, and associated post-hoc procedures. All tests are conducted at a significance level of α=0.05, corresponding to a 95% confidence interval. A p-value below this threshold indicates statistically significant differences, while a p-value greater than α=0.05 suggests the differences are not statistically significant.

The Wilcoxon signed-rank test is first employed to perform pairwise comparisons between the classification accuracies achieved by the parallelized APO-based method and each of the 14 competing MSAs across the 15 benchmark datasets. As summarized in Table 6, the test evaluates the sum of ranks R+ and R−, where R+ indicates the number of datasets in which APO outperforms a given competitor, and R− denotes the datasets in which it underperforms. The results show that the proposed APO-based method significantly outperforms all compared MSAs. Specifically, all p-values are below 0.05, indicating that the observed performance advantages of parallelized APO are statistically significant and unlikely to be due to random chance.

Next, the Friedman test is conducted to assess overall performance differences across all 15 MSAs based on their classification accuracy rankings across the 15 datasets. In this test, algorithms achieving higher accuracy receive lower average ranks. As shown in Table 7, the parallelized APO-based method achieves the lowest (best) average rank of 2.3000, followed by DMOA (5.8000), ILCO (6.8000), RTH (6.9000), OOA (6.9000), EVO (7.6667), AO (7.9333), and others. The Friedman test yields a chi-square statistic of 47.125 with an associated p-value of 0.000018, which is significantly below the 0.05 threshold. This confirms the presence of statistically meaningful differences among the 15 algorithms.

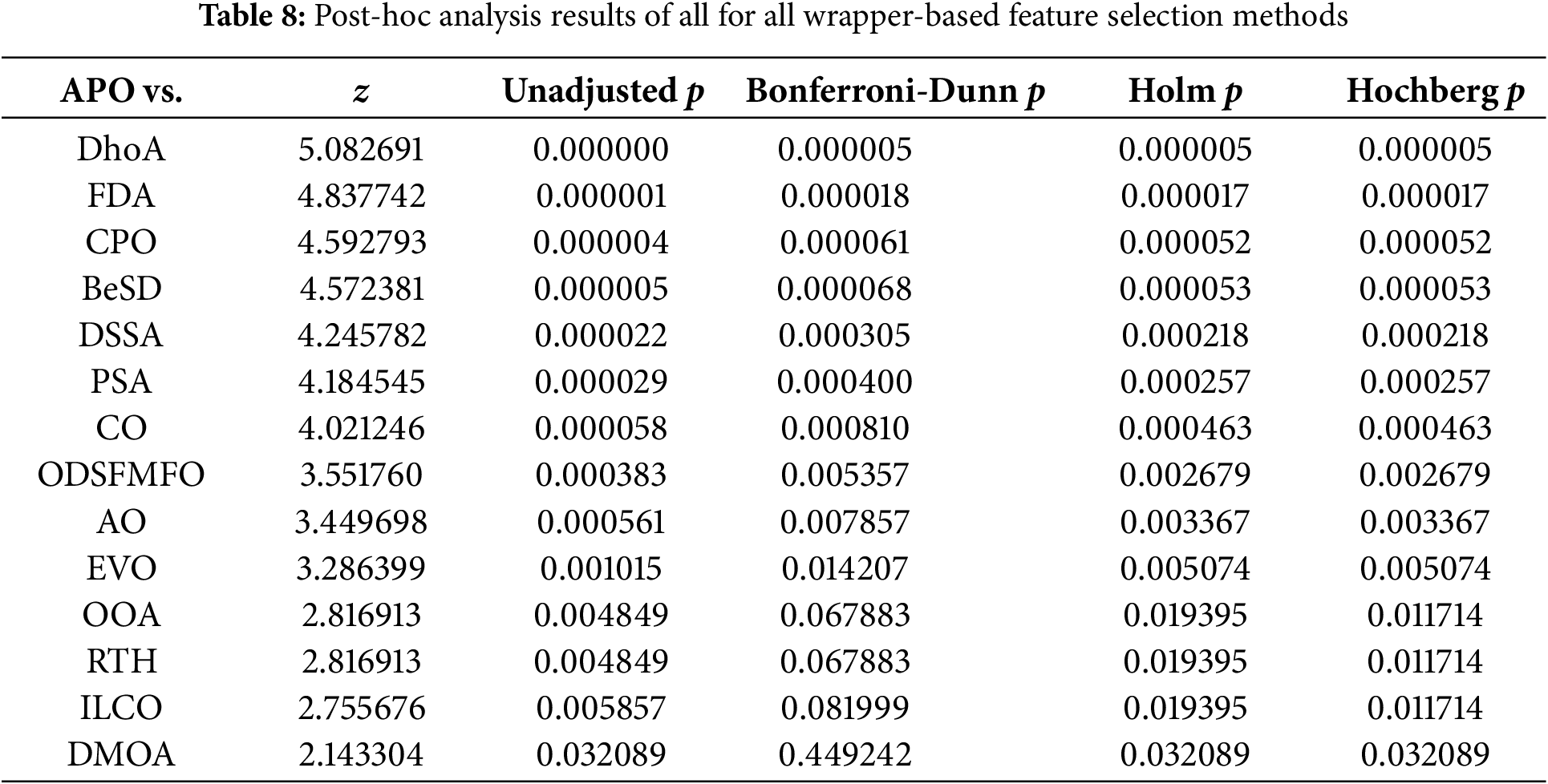
To further explore these differences, three post-hoc tests, namely Bonferroni-Dunn, Holm, and Hochberg procedures, are performed to identify which MSAs are statistically inferior to APO. The z-values, unadjusted p-values, and adjusted p-values from all three procedures are presented in Table 8. All three tests consistently show that APO significantly outperforms DhoH, FDA, CPO, BeSD, DSSA, PSA, CO, ODSFMFO, AO, and EVO, with adjusted p-values below 0.05 across all correction methods. Moreover, the Holm and Hochberg procedures also confirm statistically significant differences between APO and OOA, RTH, ILCO, and DMOA.

4.7 Impact of Classifier Diversity

To assess the generalizability of the APO-based wrapper feature selection framework, additional experiments were conducted using a variety of classification algorithms beyond the original KNN classifier. Specifically, Support Vector Machine (SVM), Random Forest (RF), Logistic Regression (LR), and Multilayer Perceptron (MLP) were incorporated into the experimental setup. This extension aimed to verify the stability and effectiveness of the selected feature subsets under diverse learning paradigms. The results, presented in Table 9, focus on six representative datasets that vary in size, dimensionality, and class complexity: DS2 (very small-scale), DS4 (ultra-high dimensional), DS8 (large-instance), DS12 (moderate), DS13 (high-dimensional), and DS14 (very large-scale). For each classifier-dataset pair, both classification accuracy and average number of selected features over 30 runs are reported to evaluate predictive performance and subset compactness.

In DS2, which contains only 27 samples and 56 features, APO achieves perfect classification accuracy (1.000) across all classifiers. This confirms the robustness of the selected feature subsets across different learning paradigms in a low-data regime. Moreover, the number of selected features remains highly consistent, ranging from 2.33 to 3.33, with KNN, LR, and MLP producing the most compact subsets (2.33 features), and SVM selecting slightly more (2.67).

In DS4, an extremely high-dimensional dataset with 4000 features, all classifiers again achieve accuracy of 1.000. However, the number of selected features differs significantly depending on the classifier. The RF classifier yields the most compact subset (42.33), followed by SVM (65.00) and KNN (86.33), while LR and MLP select notably larger subsets (137.00 and 115.33, respectively). These results suggest that APO’s feature selection mechanism is responsive to the inductive biases of the underlying classifiers, favoring fewer features for tree-based and margin-based models, while neural and linear models may require more redundant features for stability.

In DS8, a large-instance dataset with 5000 samples, classification accuracy varies slightly across classifiers. KNN and MLP attain the highest accuracies (0.859 and 0.857, respectively), while LR trails slightly at 0.835. The feature subset sizes remain relatively stable, with all classifiers selecting between 16.33 and 18.67 features. Notably, MLP achieves the second-best accuracy using the smallest feature subset (16.33), indicating APO’s ability to balance compactness and performance even under computationally intensive scenarios.

DS12 shows a similar pattern, i.e., perfect classification accuracy (1.000) across all classifiers, but varying subset sizes. KNN selects the smallest subset (3.33), followed by MLP (4.33), RF (4.67), LR (5.00), and SVM (6.00). This variation underscores the robustness of the selected features, which remain effective across different classification boundaries despite changes in subset size.

In DS13, a high-dimensional dataset with 256 features, KNN again achieves the highest accuracy (0.962), followed by SVM and MLP (0.954 each), RF (0.951), and LR (0.948). Although the feature subsets are relatively large across classifiers due to the complexity of the dataset, APO still reduces the dimensionality substantially. KNN selects the most compact subset (140.67), while MLP selects the largest (171.00). The correlation between smaller subset size and higher accuracy for KNN further demonstrates APO’s ability to achieve effective trade-offs between reduction and accuracy.

Finally, for DS14, a very large-scale dataset with 20,000 instances, all classifiers perform closely. KNN and RF achieve the highest accuracy (0.962), followed by SVM (0.957), LR (0.959), and MLP (0.959). Interestingly, all classifiers converge on nearly identical feature subset sizes (between 11.00 and 12.00), indicating a high level of consensus and stability in feature selection, regardless of the classification model.

The simulation results in Table 9 collectively demonstrate that the APO-based wrapper framework is classifier-agnostic in terms of classification accuracy and generates consistent feature subset sizes with minimal degradation in performance across diverse classifiers. APO reliably identifies core feature subsets that generalize well across varying learning paradigms, reinforcing its practical applicability in real-world machine learning deployments where model choices may vary.

4.8 Discussion

The comparative results presented in Table 2 clearly demonstrate that while MSAs such as AO, CO, DMOA, RTH, and ILCO generally achieve high classification accuracy on datasets with binary or low output class counts, their performance noticeably deteriorates on multiclass classification tasks involving higher output dimensionality. For instance, in DS2 (10 output classes), CO records the lowest accuracy (0.953), significantly trailing behind APO, AO, DMOA, RTH, and ILCO, which all achieve perfect accuracy (1.000). A similar trend is observed in DS12 (7 output classes), where AO and RTH show minor accuracy drops to 0.965 and 0.992, respectively, compared to the perfect scores attained by APO, ILCO, CO, and DMOA. The disparity becomes more pronounced in DS13 and DS14, two datasets characterized by 10 and 26 output classes, respectively. In these more complex scenarios, APO consistently exhibits superior classification performance, clearly outperforming all competing MSAs. These findings confirm the robustness and adaptability of APO in handling feature selection tasks for datasets with high output-class complexity, reinforcing its reliability in real-world applications compared to other state-of-the-art MSAs.

Beyond classification accuracy, an equally critical factor is the trade-off between maximizing predictive accuracy and minimizing the number of selected features. An analysis of Tables 2 and 3 reveals substantial variability in how the evaluated MSAs manage this balance. Algorithms such as BeSD, CO, CPO, ODSFMFO, DhoH, and EVO generally exhibit poor trade-offs, either yielding low classification accuracy with large feature subsets or showing inconsistent feature reduction capabilities. For example, BeSD and CO consistently fail to optimize both objectives, often selecting unnecessarily large subsets that undermine model interpretability and computational efficiency. Conversely, MSAs like AO, DSSA, OOA, PSA, FDA, and ILCO show moderate but inconsistent performance, where they may excel in either classification accuracy or feature compactness but rarely in both simultaneously. In contrast, APO consistently demonstrates superior ability to balance these two competing objectives. By effectively eliminating redundant and irrelevant features, APO reduces model complexity without compromising accuracy, thus improving both interpretability and runtime efficiency. As such, APO stands out as the most robust and practically viable method among the compared MSAs, offering significant advantages for real-world feature selection tasks.

This study initially employed the canonical APO model, enhanced only by a dedicated binarization mechanism, to demonstrate its baseline suitability for discrete feature selection problems. Building on this foundation, the current work further enhances the APO framework through the introduction of a parallelized implementation, enabling significantly reduced computational overhead without compromising solution quality. As detailed in Sections 4.4 and 4.5, the parallelized APO not only retains the high accuracy and compact feature subsets of the original version but also exhibits marked improvements in computational efficiency and inter-run stability, especially on high-dimensional datasets such as DS4 and DS13. Furthermore, results from Section 4.7 confirm that the features selected by APO generalize well across diverse classifiers (e.g., SVM, RF, LR, MLP), underscoring the robustness and versatility of the APO-based wrapper framework. Taken together, these extensions not only reinforce the effectiveness of APO but also elevate its practical deployment potential, especially in large-scale and time-sensitive applications where performance, efficiency, and consistency are critical.

5  Conclusion

This study explored the adaptation of the APO algorithm to the domain of wrapper-based feature selection. Recognizing that feature selection inherently requires navigating a binary decision space, the original continuous APO framework was extended through the integration of a dedicated binarization mechanism. This conversion strategy enables effective and consistent selection of optimal feature subsets, allowing APO to be successfully applied to discrete optimization problems typically encountered in real-world classification tasks. The native balance between exploration and exploitation in APO, governed by its dynamic behavioral transition coefficient inspired by puffin foraging strategies, remains central to its search capability and was preserved in this adaptation. In addition to the binary adaptation, a key technical advancement introduced in this work is the development of a parallelized implementation of the APO-based wrapper framework. By concurrently evaluating fitness functions and applying search operators across multiple processors, the parallel design significantly reduces execution time across all tested datasets. This computational gain is particularly pronounced in high-dimensional and large-instance datasets, where traditional wrapper methods often face scalability bottlenecks. Experimental results verify that this parallelization preserved classification accuracy and feature selection stability while delivering substantial runtime savings, thus making the method more viable for time-sensitive and resource-constrained deployments.

Empirical validation was conducted on fifteen benchmark datasets that varied widely in feature dimensionality, instance count, and class complexity. The proposed APO-based wrapper consistently outperformed fourteen recent and competitive metaheuristic search algorithms, demonstrating superior classification performance, effective feature subset reduction, and high solution stability. These advantages were further validated across multiple classifiers, including KNN, SVM, RF, LR, and MLP, underscoring the framework’s robustness to classifier choice and its general applicability in diverse machine learning scenarios. Collectively, these findings position the APO-based parallel wrapper framework as a powerful, scalable, and generalizable approach to feature selection. Its ability to deliver strong predictive accuracy, reduce model complexity, and lower computational costs establishes it as a compelling tool for modern data-driven applications in both academic and industrial settings.

Despite these promising results, several limitations merit acknowledgment. First, the binarization procedure used to convert continuous decision variables into discrete feature selection decisions, although standard and widely adopted in wrapper-based approaches, may not fully exploit nuanced interactions among continuous decision variables. While this does not significantly hinder the primary goal, i.e., identifying an optimal feature subset, it is worth exploring more sophisticated binarization strategies, such as fuzzy or probabilistic thresholding, to preserve more nuanced information in future studies. Additionally, the computational complexity and scalability of APO under extremely high-dimensional scenarios remain areas for further exploration, as efficiency in very large feature spaces is critical for practical deployment. Lastly, while this study focuses on APO, the proposed wrapper-based framework is adaptable and can be applied to other optimization algorithms. Future work could involve validating the framework’s effectiveness when integrated with alternative metaheuristic search strategies, or when applied to different machine learning tasks such as regression and multi-label classification.

Acknowledgement: The authors thank Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R120), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R120), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Wy-Liang Cheng, Wei Hong Lim, and Sew Sun Tiang; methodology, Wy-Liang Cheng, Wei Hong Lim, Kim Soon Chong, and Sew Sun Tiang; software, Wy-Liang Cheng, Yit Hong Choo, and El-Sayed M. El-kenawy; validation, Yit Hong Choo, El-Sayed M. El-kenaway and Amal H. Alharbi; formal analysis, Amal H. Alharbi and Marwa M. Eid; writing—original draft preparation, Wy-Liang Cheng, Wei Hong Lim, Kim Soon Chong, and Sew Sun Tiang; writing—review and editing, El-Sayed M. El-kenawy, Amal H. Alharbi and Marwa M. Eid; supervision, Wei Hong Lim; project administration, Wei Hong Lim and El-Sayed M. El-kenawy; funding acquisition, El-Sayed M. El-kenawy and Amal H. Alharbi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Akinola OO, Ezugwu AE, Agushaka JO, Zitar RA, Abualigah L. Multiclass feature selection with metaheuristic optimization algorithms: a review. Neural Comput Appl. 2022;34(22):19751–90. doi:10.1007/s00521-022-07705-4. [Google Scholar] [PubMed] [CrossRef]

2. Jdid B, Lim WH, Dayoub I, Hassan K, Juhari MRBM. Robust automatic modulation recognition through joint contribution of hand-crafted and contextual features. IEEE Access. 2021;9:104530–46. doi:10.1109/access.2021.3099222. [Google Scholar] [CrossRef]

3. Chow LS, Tang GS, Solihin MI, Gowdh NM, Ramli N, Rahmat K. Quantitative and qualitative analysis of 18 deep Convolutional Neural Network (CNN) models with transfer learning to diagnose COVID-19 on Chest X-Ray (CXR) images. SN Comput Sci. 2023;4(2):141. doi:10.1007/s42979-022-01545-8. [Google Scholar] [PubMed] [CrossRef]

4. Azeez II, Chow LS, Solihin MI, Ang CK. 3D brain tumour segmentation using UNet with quantitative analysis of the tumour features. J Phys Conf Ser. 2023;2622(1):012015. doi:10.1088/1742-6596/2622/1/012015. [Google Scholar] [CrossRef]

5. Alrifaey M, Lim WH, Ang CK, Natarajan E, Solihin MI, Juhari MRM, et al. Hybrid deep learning model for fault detection and classification of grid-connected photovoltaic system. IEEE Access. 2022;10:13852–69. doi:10.1109/access.2022.3140287. [Google Scholar] [CrossRef]

6. Guyon IM, Elisseeff A. An introduction to variable and feature selection. J Mach Learn Res. 2003;3:1157–82. [Google Scholar]

7. Dokeroglu T, Deniz A, Kiziloz HE. A comprehensive survey on recent metaheuristics for feature selection. Neurocomputing. 2022;494(13):269–96. doi:10.1016/j.neucom.2022.04.083. [Google Scholar] [CrossRef]

8. Maldonado J, Riff MC, Neveu B. A review of recent approaches on wrapper feature selection for intrusion detection. Expert Syst Appl. 2022;198(2):116822. doi:10.1016/j.eswa.2022.116822. [Google Scholar] [CrossRef]

9. Xue Y, Tang T, Pang W, Liu AX. Self-adaptive parameter and strategy based particle swarm optimization for large-scale feature selection problems with multiple classifiers. Appl Soft Comput. 2020;88(4):106031. doi:10.1016/j.asoc.2019.106031. [Google Scholar] [CrossRef]

10. Whitney AW. A direct method of nonparametric measurement selection. IEEE Trans Comput. 1971;100(9):1100–3. doi:10.1109/t-c.1971.223410. [Google Scholar] [CrossRef]

11. Marill T, Green D. On the effectiveness of receptors in recognition systems. IEEE Trans Inf Theory. 1963;9(1):11–7. doi:10.1109/tit.1963.1057810. [Google Scholar] [CrossRef]

12. Wei B, Zhang W, Xia X, Zhang Y, Yu F, Zhu Z. Efficient feature selection algorithm based on particle swarm optimization with learning memory. IEEE Access. 2019;7:166066–78. doi:10.1109/access.2019.2953298. [Google Scholar] [CrossRef]

13. Rajwar K, Deep K, Das S. An exhaustive review of the metaheuristic algorithms for search and optimization: taxonomy, applications, and open challenges. Artif Intell Rev. 2023;56(11):13187–257. doi:10.1007/s10462-023-10470-y. [Google Scholar] [PubMed] [CrossRef]

14. Wang WC, Tian WC, Xu DM, Zang HF. Arctic puffin optimization: a bio-inspired metaheuristic algorithm for solving engineering design optimization. Adv Eng Softw. 2024;195:103694. doi:10.1016/j.advengsoft.2024.103694. [Google Scholar] [CrossRef]

15. Lim WH, Isa NAM, Tiang SS, Tan TH, Natarajan E, Wong CH, et al. A self-adaptive topologically connected-based particle swarm optimization. IEEE Access. 2018;6:65347–66. doi:10.1109/access.2018.2878805. [Google Scholar] [CrossRef]

16. Machmudah A, Parman S, Abbasi A, Solihin MI, Manan TSA, Beddu S, et al. Cyclic path planning of hyper-redundant manipulator using whale optimization algorithm. Int J Adv Comput Sci Appl. 2021;12(8):677–86. doi:10.14569/ijacsa.2021.0120879. [Google Scholar] [CrossRef]

17. Solihin MI, Chuan CY, Astuti W. Optimization of fuzzy logic controller parameters using modern meta-heuristic algorithm for gantry crane system (GCS). Mater Today Proc. 2020;29(2):168–72. doi:10.1016/j.matpr.2020.05.641. [Google Scholar] [CrossRef]

18. Yao L, Damiran Z, Lim WH. A fuzzy logic based charging scheme for electric vechicle parking station. In: Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC); 2016 Jun 7–10; Florence, Italy. [Google Scholar]

19. Yao L, Lai CC, Lim WH. Home energy management system based on photovoltaic system. In: Proceedings of the 2015 IEEE International Conference on Data Science and Data Intensive Systems; 2015 Dec 11–13; Sydney, NSW, Australia. [Google Scholar]

20. Yao L, Shen JY, Lim WH. Real-time energy management optimization for smart household. In: Proceedings of the 2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData); 2016 Dec 15–18; Chengdu, China. [Google Scholar]

21. Nguyen BM, Nguyen T, Vu QH, Hung TH, Hai TH, Binh HTT, et al. Dholes hunting—a multi-local search algorithm using gradient approximation and its application for blockchain consensus problem. IEEE Access. 2024;12:93333–49. doi:10.1109/access.2024.3419172. [Google Scholar] [CrossRef]

22. Wang L, Cao Q, Zhang Z, Mirjalili S, Zhao W. Artificial rabbits optimization: a new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng Appl Artif Intell. 2022;114(4):105082. doi:10.1016/j.engappai.2022.105082. [Google Scholar] [CrossRef]

23. Nguyen BM, Nguyen T, Vu QH, Tran HH, Vo H, Son DB, et al. A novel nature-inspired algorithm for optimal task scheduling in fog-cloud blockchain system. IEEE Internet Things J. 2024;11(2):2043–57. doi:10.1109/jiot.2023.3292872. [Google Scholar] [CrossRef]

24. Azizi M, Aickelin U, Khorshidi HA, Baghalzadeh Shishehgarkhaneh M. Energy valley optimizer: a novel metaheuristic algorithm for global and engineering optimization. Sci Rep. 2023;13(1):226. doi:10.1038/s41598-022-27344-y. [Google Scholar] [PubMed] [CrossRef]

25. Nguyen VT, Deb Barma S, Van Lam T, Kisi O, Mahesha A. Groundwater level modeling using augmented artificial ecosystem optimization. J Hydrol. 2023;617(2):129034. doi:10.1016/j.jhydrol.2022.129034. [Google Scholar] [CrossRef]

26. Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM. Salp Swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw. 2017;114:163–91. doi:10.1016/j.advengsoft.2017.07.002. [Google Scholar] [CrossRef]

27. Nssibi M, Manita G, Korbaa O. Advances in nature-inspired metaheuristic optimization for feature selection problem: a comprehensive survey. Comput Sci Rev. 2023;49(2):100559. doi:10.1016/j.cosrev.2023.100559. [Google Scholar] [CrossRef]

28. Kaur S, Kumar Y, Koul A, Kumar Kamboj S. A systematic review on metaheuristic optimization techniques for feature selections in disease diagnosis: open issues and challenges. Arch Comput Methods Eng. 2023;30(3):1863–95. doi:10.1007/s11831-022-09853-1. [Google Scholar] [PubMed] [CrossRef]

29. Lee J, Yoon Y, Kim J, Kim YH. Metaheuristic-based feature selection methods for diagnosing sarcopenia with machine learning algorithms. Biomimetics. 2024;9(3):179. doi:10.3390/biomimetics9030179. [Google Scholar] [PubMed] [CrossRef]

30. Kwakye BD, Li Y, Mohamed HH, Baidoo E, Asenso TQ. Particle guided metaheuristic algorithm for global optimization and feature selection problems. Expert Syst Appl. 2024;248(3):123362. doi:10.1016/j.eswa.2024.123362. [Google Scholar] [CrossRef]

31. Braik M, Hammouri A, Alzoubi H, Sheta A. Feature selection based nature inspired capuchin search algorithm for solving classification problems. Expert Syst Appl. 2024;235(1):121128. doi:10.1016/j.eswa.2023.121128. [Google Scholar] [CrossRef]

32. Khafaga DS, El-kenawy ESM, Alrowais F, Kumar S, Ibrahim A, Abdelhamid AA. Novel optimized feature selection using metaheuristics applied to physical benchmark datasets. Comput Mater Contin. 2023;74(2):4027–41. doi:10.32604/cmc.2023.033039. [Google Scholar] [CrossRef]

33. Khafaga DS, El-kenawy ESM, Karim FK, Abotaleb M, Ibrahim A, Abdelhamid AA, et al. Hybrid dipper throated and grey wolf optimization for feature selection applied to life benchmark datasets. Comput Mater Contin. 2023;74(2):4531–45. doi:10.32604/cmc.2023.033042. [Google Scholar] [CrossRef]

34. Abdelhamid AA, El-Kenawy ESM, Ibrahim A, Eid MM, Khafaga DS, Alhussan AA, et al. Innovative feature selection method based on hybrid sine cosine and dipper throated optimization algorithms. IEEE Access. 2023;11:79750–76. doi:10.1109/access.2023.3298955. [Google Scholar] [CrossRef]

35. Pan L, Cheng WL, Lim WH, Sharma A, Jately V, Tiang SS, et al. A robust wrapper-based feature selection technique based on modified teaching learning based optimization with hierarchical learning scheme. Eng Sci Technol Int J. 2025;61(1):101935. doi:10.1016/j.jestch.2024.101935. [Google Scholar] [CrossRef]

36. Abdel-Salam M, Hu G, Çelik E, Gharehchopogh FS, El-Hasnony IM. Chaotic RIME optimization algorithm with adaptive mutualism for feature selection problems. Comput Biol Med. 2024;179:108803. doi:10.1016/j.compbiomed.2024.108803. [Google Scholar] [PubMed] [CrossRef]

37. Abdel-Salam M, Alzahrani AI, Alblehai F, Zitar RA, Abualigah L. An improved Genghis Khan optimizer based on enhanced solution quality strategy for global optimization and feature selection problems. Knowl-Based Syst. 2024;302:112347. doi:10.1016/j.knosys.2024.112347. [Google Scholar] [CrossRef]

38. Qu L, He W, Li J, Zhang H, Yang C, Xie B. Explicit and size-adaptive PSO-based feature selection for classification. Swarm Evol Comput. 2023;77:101249. doi:10.1016/j.swevo.2023.101249. [Google Scholar] [CrossRef]

39. Li Y, Wang W, Liu J, Zhou H. Equilibrium optimizer with divided population based on distance and its application in feature selection problems. Knowl Based Syst. 2022;256(99):109842. doi:10.1016/j.knosys.2022.109842. [Google Scholar] [CrossRef]

40. Wang Z, Gao S, Zhang Y, Guo L. Symmetric uncertainty-incorporated probabilistic sequence-based ant colony optimization for feature selection in classification. Knowl Based Syst. 2022;256(12):109874. doi:10.1016/j.knosys.2022.109874. [Google Scholar] [CrossRef]

41. Gupta S, Gupta S. Fitness and historical success information-assisted binary particle swarm optimization for feature selection. Knowl Based Syst. 2024;306:112699. doi:10.1016/j.knosys.2024.112699. [Google Scholar] [CrossRef]

42. Wang XH, Zhang Y, Sun XY, Wang YL, Du CH. Multi-objective feature selection based on artificial bee colony: an acceleration approach with variable sample size. Appl Soft Comput. 2020;88(4):106041. doi:10.1016/j.asoc.2019.106041. [Google Scholar] [CrossRef]

43. Singh LK, Khanna M, Garg H, Singh R. Emperor penguin optimization algorithm- and bacterial foraging optimization algorithm-based novel feature selection approach for glaucoma classification from fundus images. Soft Comput. 2024;28(3):2431–67. doi:10.1007/s00500-023-08449-6. [Google Scholar] [CrossRef]

44. Wu R, Huang H, Wei J, Ma C, Zhu Y, Chen Y, et al. An improved sparrow search algorithm based on quantum computations and multi-strategy enhancement. Expert Syst Appl. 2023;215(8):119421. doi:10.1016/j.eswa.2022.119421. [Google Scholar] [CrossRef]

45. Barrera-García J, Cisternas-Caneo F, Crawford B, Gómez Sánchez M, Soto R. Feature selection problem and metaheuristics: a systematic literature review about its formulation, evaluation and applications. Biomimetics. 2024;9(1):9. doi:10.3390/biomimetics9010009. [Google Scholar] [PubMed] [CrossRef]

46. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-qaness MAA, Gandomi AH. Aquila Optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng. 2021;157(11):107250. doi:10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]

47. Civicioglu P, Besdok E. Bezier search differential evolution algorithm for numerical function optimization: a comparative study with CRMLSP, MVO. WA SHADE and LSHADE Expert Syst Appl. 2021;165(2):113875. doi:10.1016/j.eswa.2020.113875. [Google Scholar] [CrossRef]

48. Akbari MA, Zare M, Azizipanah-abarghooee R, Mirjalili S, Deriche M. The cheetah optimizer: a nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci Rep. 2022;12(1):10953. doi:10.1038/s41598-022-14338-z. [Google Scholar] [PubMed] [CrossRef]

49. Agushaka JO, Ezugwu AE, Abualigah L. Dwarf mongoose optimization algorithm. Comput Methods Appl Mech Eng. 2022;391(10):114570. doi:10.1016/j.cma.2022.114570. [Google Scholar] [CrossRef]

50. Jena B, Naik MK, Wunnava A, Panda R. A differential squirrel search algorithm. In: Proceedings of the 3rd International Conference on Intelligent Computing and Advances in Communication (ICAC 2020); 2020 Nov 25–26; Bhubaneswar, India. [Google Scholar]

51. Karami H, Anaraki MV, Farzin S, Mirjalili S. Flow Direction Algorithm (FDAa novel optimization approach for solving optimization problems. Comput Ind Eng. 2021;156(4):107224. doi:10.1016/j.cie.2021.107224. [Google Scholar] [CrossRef]

52. Li Z, Zeng J, Chen Y, Ma G, Liu G. Death mechanism-based moth-flame optimization with improved flame generation mechanism for global optimization tasks. Expert Syst Appl. 2021;183(6):115436. doi:10.1016/j.eswa.2021.115436. [Google Scholar] [CrossRef]

53. Dehghani M, Trojovský P. Osprey optimization algorithm: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems. Front Mech Eng. 2023;8:1126450. doi:10.3389/fmech.2022.1126450. [Google Scholar] [CrossRef]

54. Ferahtia S, Houari A, Rezk H, Djerioui A, Machmoum M, Motahhir S, et al. Red-tailed hawk algorithm for numerical optimization and real-world problems. Sci Rep. 2023;13(1):12950. doi:10.1038/s41598-023-38778-3. [Google Scholar] [PubMed] [CrossRef]

55. Qais MH, Hasanien HM, Alghuwainem S, Loo KH. Propagation search algorithm: a physics-based optimizer for engineering applications. Mathematics. 2023;11(20):4224. doi:10.3390/math11204224. [Google Scholar] [CrossRef]

56. Guo Z, Liu G, Jiang F. Chinese Pangolin Optimizer: a novel bio-inspired metaheuristic for solving optimization problems. J Supercomput. 2025;81(4):517. doi:10.1007/s11227-025-07004-4. [Google Scholar] [CrossRef]