 Open Access
Open Access
ARTICLE
Differential Evolution with Improved Equilibrium Optimizer for Combined Heat and Power Economic Dispatch Problem
1 Xiangsihu College of Guangxi Minzu University, Nanning, 530006, China
2 Faculty of Information Science and Technology, National University of Malaysia (UKM), Bangi Selangor, 43600, Malaysia
3 College of Artificial Intelligence, Guangxi Minzu University, Nanning, 530006, China
4 Guangxi Key Laboratories of Hybrid Computation and IC Design Analysis, Nanning, 530006, China
* Corresponding Author: Qifang Luo. Email:
(This article belongs to the Special Issue: Advancements in Evolutionary Optimization Approaches: Theory and Applications)
Computers, Materials & Continua 2025, 85(1), 1235-1265. https://doi.org/10.32604/cmc.2025.066527
Received 10 April 2025; Accepted 24 June 2025; Issue published 29 August 2025
Abstract
The combined heat and power economic dispatch (CHPED) problem is a highly intricate energy dispatch challenge that aims to minimize fuel costs while adhering to various constraints. This paper presents a hybrid differential evolution (DE) algorithm combined with an improved equilibrium optimizer (DE-IEO) specifically for the CHPED problem. The DE-IEO incorporates three enhancement strategies: a chaotic mechanism for initializing the population, an improved equilibrium pool strategy, and a quasi-opposite based learning mechanism. These strategies enhance the individual utilization capabilities of the equilibrium optimizer, while differential evolution boosts local exploitation and escape capabilities. The IEO enhances global search to enrich the solution space, and DE focuses on local exploitation for more accurate solutions. The effectiveness of DE-IEO is demonstrated through comparative analysis with other metaheuristic optimization algorithms, including PSO, DE, ABC, GWO, WOA, SCA, and equilibrium optimizer (EO). Additionally, improved algorithms such as the enhanced chaotic gray wolf optimization (ACGWO), improved particle swarm with adaptive strategy (MPSO), and enhanced SCA with elite and dynamic opposite learning (EDOLSCA) were tested on the CEC2017 benchmark suite and four CHPED systems with 24, 84, 96, and 192 units, respectively. The results indicate that the proposed DE-IEO algorithm achieves satisfactory solutions for both the CEC2017 test functions and real-world CHPED optimization problems, offering a viable approach to complex optimization challenges.Keywords
The CHPED problem revolves around optimizing costs to achieve the lowest possible system expenses while adhering to various equations and inequality constraints. Statistics indicate that CHP systems can enhance fuel efficiency by up to 90%, reduce production costs by 10% to 40%, and lower environmental pollution by 13% to 18% [1,2]. These systems consist of three main components: power-only units (POUs), CHP units (CHPUs), and heat-only units (HOUs). The power output of each CHP unit is influenced by the heat produced by the system and vice versa, creating a bi-directional relationship [3] known as the feasibility operating region (FOR). Additionally, the valve point effect, power losses, and prohibited operation zones (POZs) contribute to the CHPED problem being a nonlinear, multi-constrained, non-convex optimization challenge. This complexity in bi-directional dependence and constraints significantly complicates the resolution of the CHPED problem.
Numerous researchers have employed a variety of methods to address CHPED issues, including numerical optimization techniques like quadratic programming [4], branch and bound algorithms [5], Bender decomposition [6], and Lagrangian relaxation [7]. These numerical methods can quickly yield exact solutions; however, they face challenges due to the non-convex nature of the problem. As a result, several metaheuristic algorithms have been introduced and are increasingly seen as effective alternatives for tackling CHPED problems, include CS [8], WOA [9,10], DE [11,12], PSO [13], and BCO [14]. These algorithms have been widely utilized in large-scale CHPED systems with over 50 units, owing to their excellent performance [15]. The bi-directional dependence of CHP units causes a significant rise in the number of local minima as the size of the CHPED problem increases, resulting in an exponential growth of candidate solutions. This cascading effect severely impacts the accuracy of solutions for large-scale CHPED. Additionally, the No Free Lunch Theorem (NFL) [16] indicates that no single optimization algorithm can effectively address all optimization problems. Therefore, we introduce a hybrid EO [17] combined with DE [18] to tackle large-scale CHPED problems.
The EO is a metaheuristic algorithm grounded in physical principles and applied in many engineering fields, including multi-objective optimization [19], fuel cells [20], power distribution systems [21], image segmentation [22], engineering design [23], discrete optimization [24], feature selection [25], and quantum optimization [26]. However, the concentration update process of EO primarily relies on equalization among candidate individuals, which limits its utilization of the search space and population data, making it prone to escape local optima—an unfavorable situation for addressing the CHPED. Therefore, we propose three strategies to enhance EO’s global search capabilities and help it avoid local minima. Additionally, EO is combined with DE to preserve EO’s strong global exploration abilities while enhancing its local exploration capabilities. The main contributions are summarized as follows.
(1) Three enhancement strategies are presented: the chaotic mechanism initialized population strategy, the improved equilibrium pool strategy, and the quasi-opposite based learning mechanism strategy, which are integrated into the EO to boost individual utilization capabilities, while DE enhances local exploitation and escape abilities.
(2) A hybrid DE-IEO algorithm is introduced, where the improved EO enhances global search to enrich the solution space, and DE focuses on local exploitation to find more accurate solutions.
(3) The DE-IEO algorithm is utilized to optimize the CEC2017 test suite and large-scale CHPED problems, with numerical experiment show achieved satisfactory results.
To date, numerous metaheuristic algorithms (MHAs) have been developed to address small-scale CHPED. For instance, Subbaraj et al. utilized an enhanced real-valued coded genetic algorithm (SARGA) to tackle a 4-unit CHPED problem, incorporating a parameter-free penalty strategy to manage different constraints and assess the solution’s validity [27]. Similarly, Mellal et al. employed an improved cuckoo search with a penalty function to solve small-scale CHPED problem involving 4 units [28].
As industrial technology advances, the medium-scale CHPED problem has arisen. Haghrah et al. proposed an enhancement to the basic genetic algorithm by utilizing Mühlenbein mutation instead of the standard mutation used in real-value coded genetic algorithms, addressing the CHPED problem while considering power loss effects. Additionally, hybrid algorithms are increasingly being applied to this issue [29]. Narang et al. integrated the civilization swarm algorithm with Powell’s pattern search method (CSO-PPS), where the civilization swarm algorithm conducts a global search and Powell’s method focuses on local search, successfully tackling the CHPED problem involving 48 units while accounting for valve-point effects, POZs, and power loss [30]. Beigvand et al. introduced TVAC-GSA-PSO, which combines an adaptive learning strategy with GSA and PSO to address the CHPED problem with 24 and 48 units, also considering the impacts of power loss and valve-point effects [31]. Zou et al. developed a genetic algorithm featuring innovative mutation and crossover operators (IGA-NCM) to optimize the CHPED problem with 48 units, employing a new approach to create the penalty function [32]. Chen et al. merged the biogeography algorithm with the PSO (BLPSO) to solve the medium-scale CHPED problem, utilizing repair techniques to manage constraints and direct particles toward feasible areas [33]. Lastly, Nasir et al. combined the firefly algorithm with a self-regulating PSO(FSRPSO), achieving satisfactory results for a medium-scale CHPED problem involving 48 units [34].
Regarding the large-scale CHPED problem, Meng et al. were the first to address it using a crisscross optimization algorithm for a scale of 192 units [35], significantly increasing the complexity of the issue. Liu et al. tackled problems with 84, 96, and 192 units by employing a differential evolution (DE) method enhanced with a mutation strategy and neighborhood and direction-induced strategies [36]. Ramachandran et al. combined an improved crow search algorithm (FRCSA) with ABC (FRSCA-ABC) using an adaptive ranking strategy, further enhancing it with three improvement techniques, which led to impressive results on large-scale CHPED challenges [37]. Additionally, Ramachandran et al. enhanced the GOA and the HHO by incorporating sine-cosine acceleration coefficients (SCAC) and an adaptive search mechanism (MGOA-IHHO), respectively, and successfully applied a hybrid of both to solve the CHPED problem with 84 units [38]. Therefore, creating hybrid algorithms that leverage the strengths of individual methods while minimizing weaknesses is an effective approach to addressing this problem [39].
The CHPED is to find the best combination of all unit production with minimum total production costs. For CHP units, their power and heat production must also meet the restrictions of the FOR as shown in Fig. 1, and solutions not in this restricted region are considered invalid, and the two types of output of CHP units are mutually constrained.
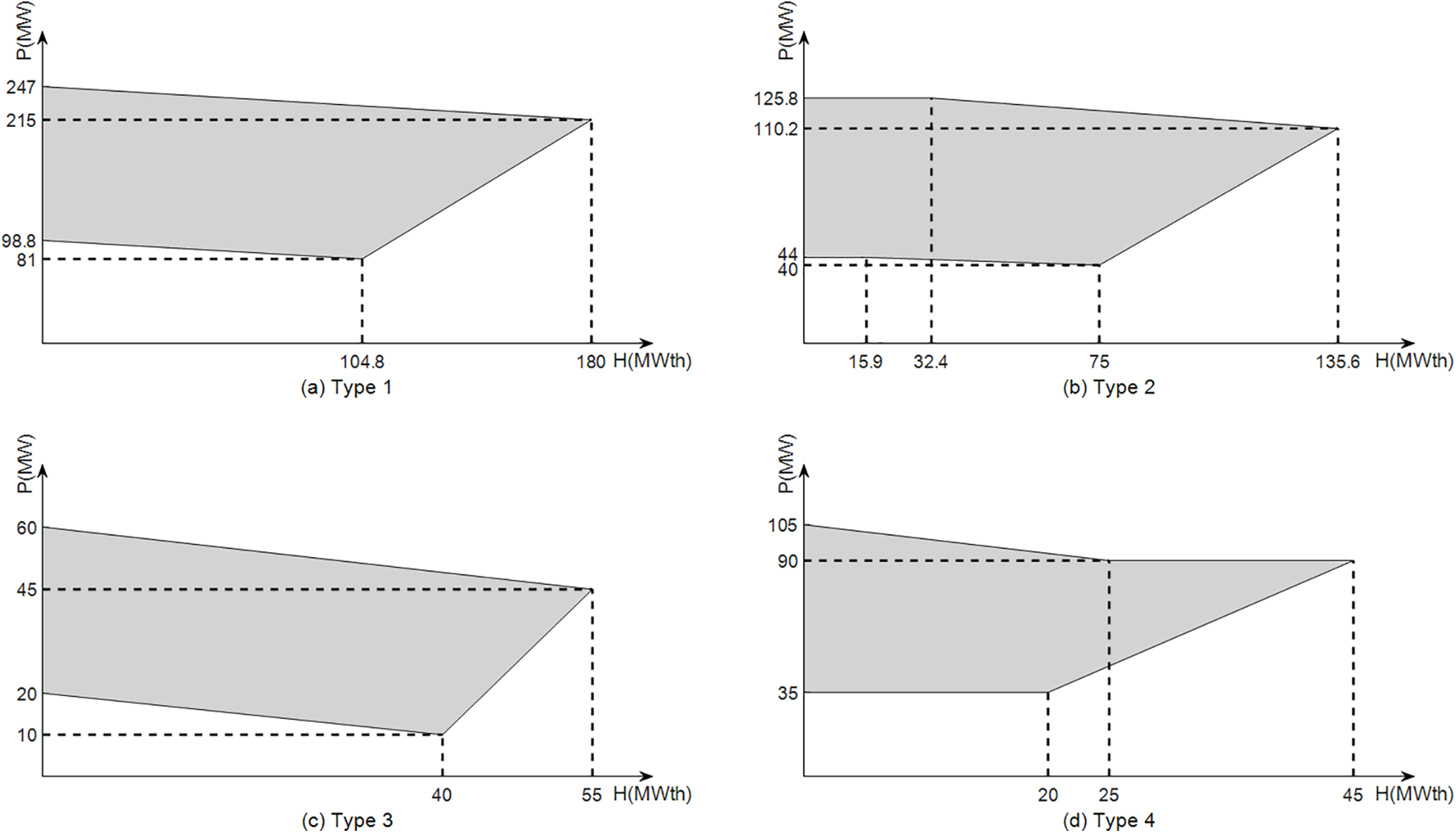
Figure 1: CHP unit feasible operating region
The objective function of the CHPED is the sum of the fuel costs of each unit, which is modeled:
where
The power-only unit with the valve-point effect is responsible for converting fuel into electricity only without considering the heat generation.
where
Fig. 2 shows the relationship between power generation and cost of the unit after considering the valve-point effect. It can see that the fuel cost of each unit with the valve-point effects is higher than that of the conventional unit for the same power generation.
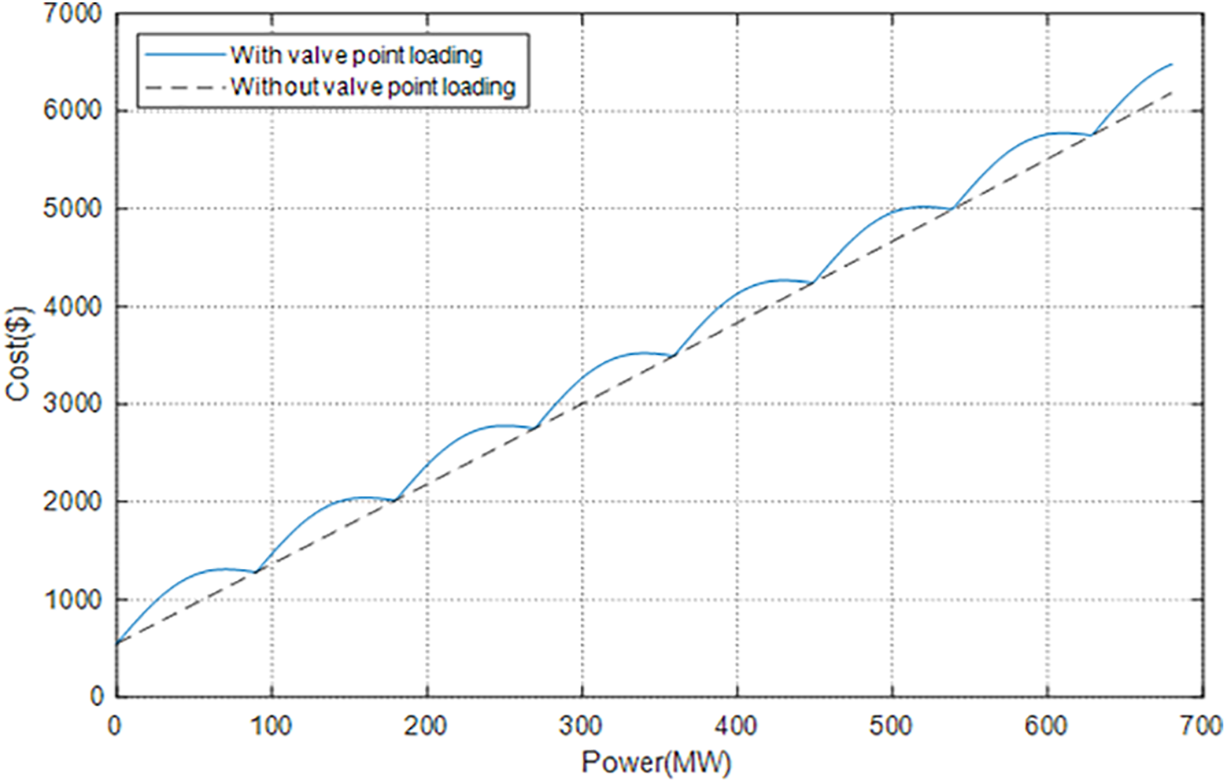
Figure 2: Value-point effects
The CHP unit converts fuel into electricity and available heat with a convex cost function consisting of a quadratic polynomial as follows.
where a, b, c, d, e and f are cost factor.
The heat-only unit generates only heat, and its cost function is also a convex function consisting of a quadratic polynomial, expressed as follows.
where a, b and c are cost factor.
(1) Power balance: the power production of the POU and CHPU must meet the power demand (
Here
(2) Heat balance: The heat generated by the CHPU and the HOU must meet the heat demand (
The prohibited operating zones (POZs) effect means that the power generation is suspended due to machine bearing vibration and other failures, so the POZs effect should be avoided in the actual power generation process.
where
4 Equilibrium Optimizer and Differential Evolution Algorithm
Equilibrium optimizer (EO) as a physics-based optimization algorithm is by Afshin Faramarzi et al. proposed in 2020 [17], and is widely used in complex function optimization, engineering optimization, intelligent control and other fields. The EO include four components, which are initialization, equilibrium pool (
The EO equilibrium pool consists of five candidate particles, of which the first four are the best particles in terms of fitness, and the fifth is generated by the average of the first four particles.
where
4.1.2 Concentration Update Mechanism
In the concentration update step, the update mechanism has two components, the exponent term that balances the exploration and exploitation phases and affects the concentration update rule, and the generation rate that controls the exploitation phase. It is defined:
where a1 is a constant value 2,
where a2 is a constant value 1.
The generation rate is defined:
where
In summary, the update mechanism of EO can be defined as
where V is a unit.
DE is proposed by Storn and Price [18] in 1997, it have two important parameters, namely mutation factor
In DE, each target vector
Among them,
In crossover operation,
where
The fitness values of
where
5 Proposed Hybrid DE-IEO Algorithm
Recently, many kinds of efficient hybrid metaheuristic optimization algorithms are proposed and successfully applied to solving complex optimization problems, such as, Broad sparse fine-grained image classification model [41], QDE [42], and so on.
This section proposed a hybrid DE-IEO algorithm, detailing the three improvement strategies and hybrid mechanisms utilized by the proposed algorithm. To overcome drawbacks of EO, three improvement strategies are integrated into EO, and the improved EO is hybrid with DE, as shown in Algorithm 1. The three improvement strategies are as follows.
(1) Initialized search agents using chaotic mechanism.
(2) Candidate particle selection mechanism for equilibrium pool.
(3) Quasi-opposite based learning (QOBL) mechanism for EO update mechanism.

5.1 Chaotic Mechanism Initialized Population Strategy
Random initialization is the primary step of all MHAs. However, the distribution of population individual generated using random initialization alone is likely to be inhomogeneous, leading to difficulties for EO to find the global optimal or a significant increase in the time to find the global optimal solution. In order to combat this drawback, this paper uses the chaotic system (CS) mechanism to initialize the algorithm instead of just random initialization. The common chaotic mappings are Logistic mapping, Cubic mapping, Tent mapping, etc., while Tent mapping has good distributivitiy and randomness. To make the generated chaotic sequence more uniform [43], the Tent mapping is used in this paper for the generation of random sequences with the following expression.
Here
Then the initialization of the proposed algorithm is shown below.
Here
5.2 Equilibrium Pool Improved Strategy
EO has a unique equilibrium pool mechanism to better balance exploration capability and exploitation capability, the selection strategy leads to a high concentration and similarity of the candidate particles, which is the fundamental reason for the weak information utilization among the candidates in the equilibrium pool, and the removal of
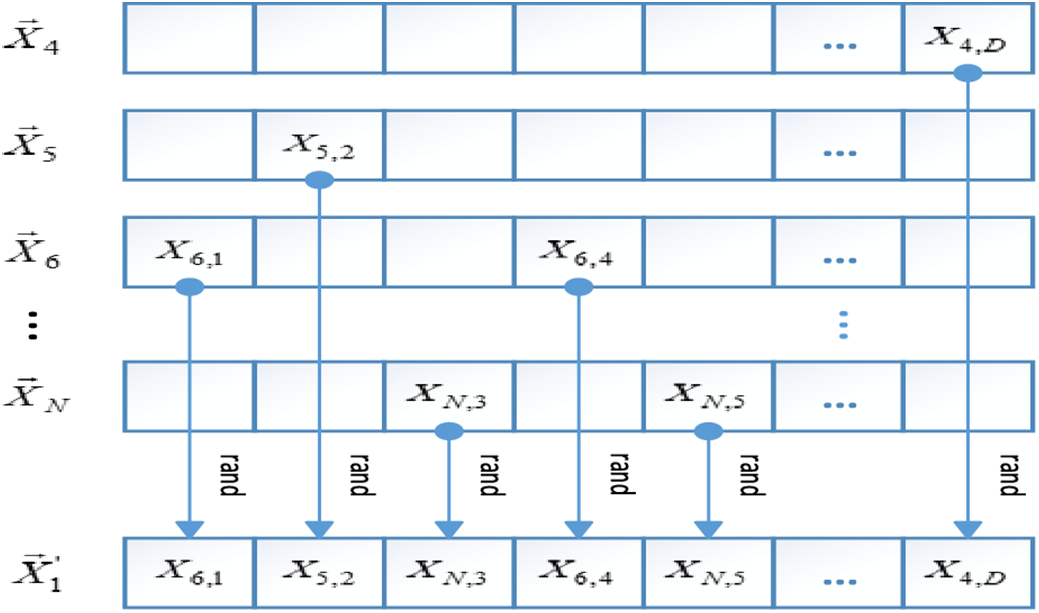
Figure 3: The equilibrium pool particle generation process
Similarly, the operation of Fig. 3 is performed again for
The EO uses random selection the best candidate particles, but this will lead to the same selection probability of
5.3 Quasi-Opposite Based Learning Mechanism Strategy
The QOBL [44] is an improvement on the OBL [45], it can be applied in MHAs, one is in population initialization to obtain better quality initial candidate solutions, and is applied in the update mechanism of MHAs. The QOBL is calculated:
Calculate the opposite of the original point.
Next, calculate the center the interval
Final calculation of the quasi-opposite point in Eq. (26).
6 Simulation Results and Discussions
To verify the superiority of DE-IEO, two parts of experiments, CEC2017 test suite [46] and CHPED problem are designed. The overall performance of DE-IEO is then analyzed in detail based on the experimental results.
6.1 Performance of DE-IEO on CEC2017
In the experiments, the performance of DE-IEO is using 29 CEC2017 benchmark functions (F2 is removed due to its instability in high-dimensional). We use the average value (AVG) and standard deviation (SD) to scientifically compare the optimization results, Friedman test [47,48] is used to rank the algorithms. The population size N and dimension D were set to 30, the experiment repeated 30 times.
The experiment compared algorithms include basic algorithms and improved algorithms. The classical algorithms include PSO, DE, ABC, GWO, WOA, SCA, and EO. Improved algorithms include improved ACGWO, improved MPSO, enhanced sine cosine algorithm with elite and dynamic opposite learning (EDOLSCA). The comparison results are shown in Table 1. Figs. 4–6 represent the convergence curves, where F1 is the unimodal function, F5, F6 are multimodal functions, F11, F13, F15, F17 and F19 are hybrid functions, and F20, F22, F26 and F30 are composition functions.
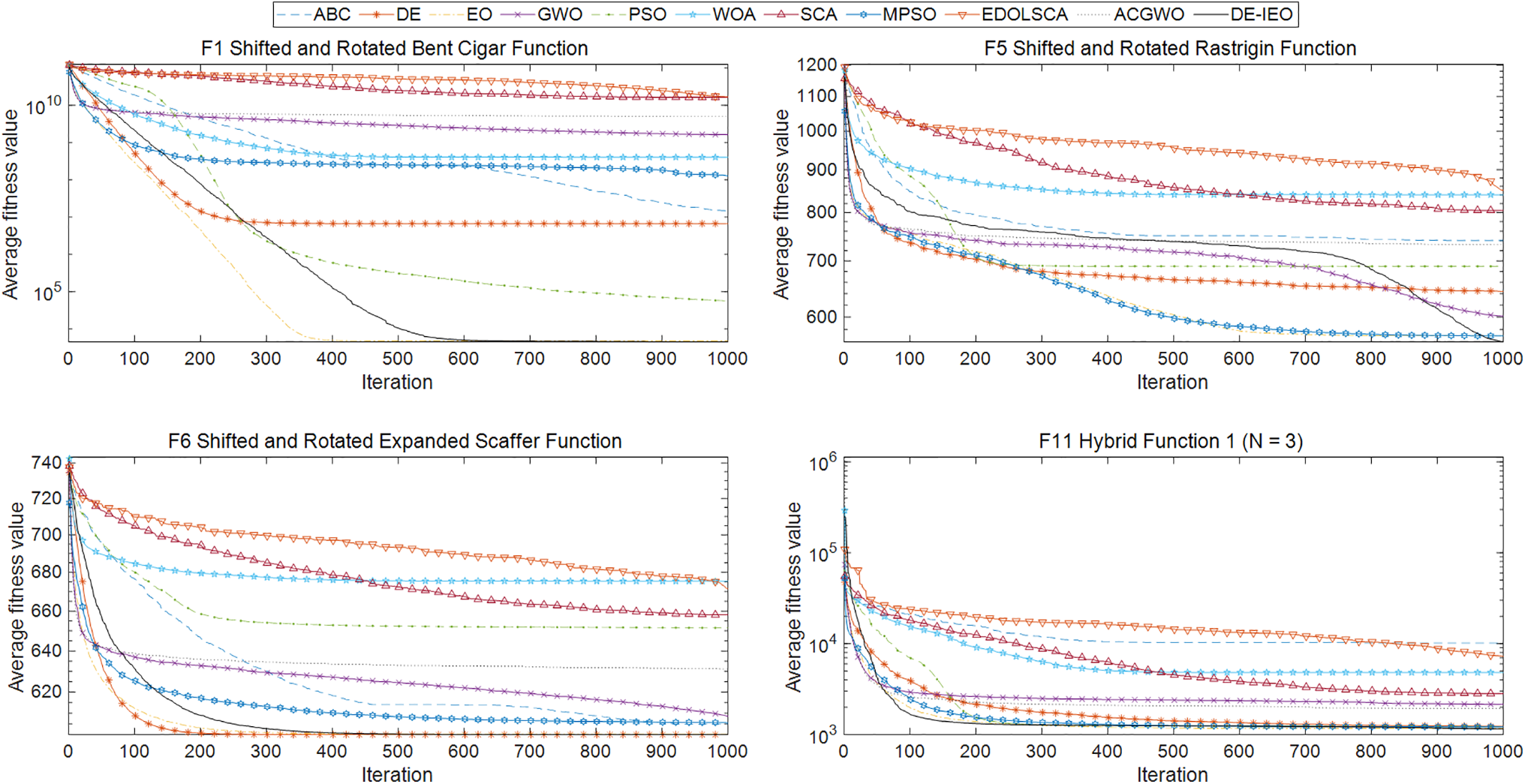
Figure 4: Eleven algorithms convergence curves of functions F1, F5, F6, F11
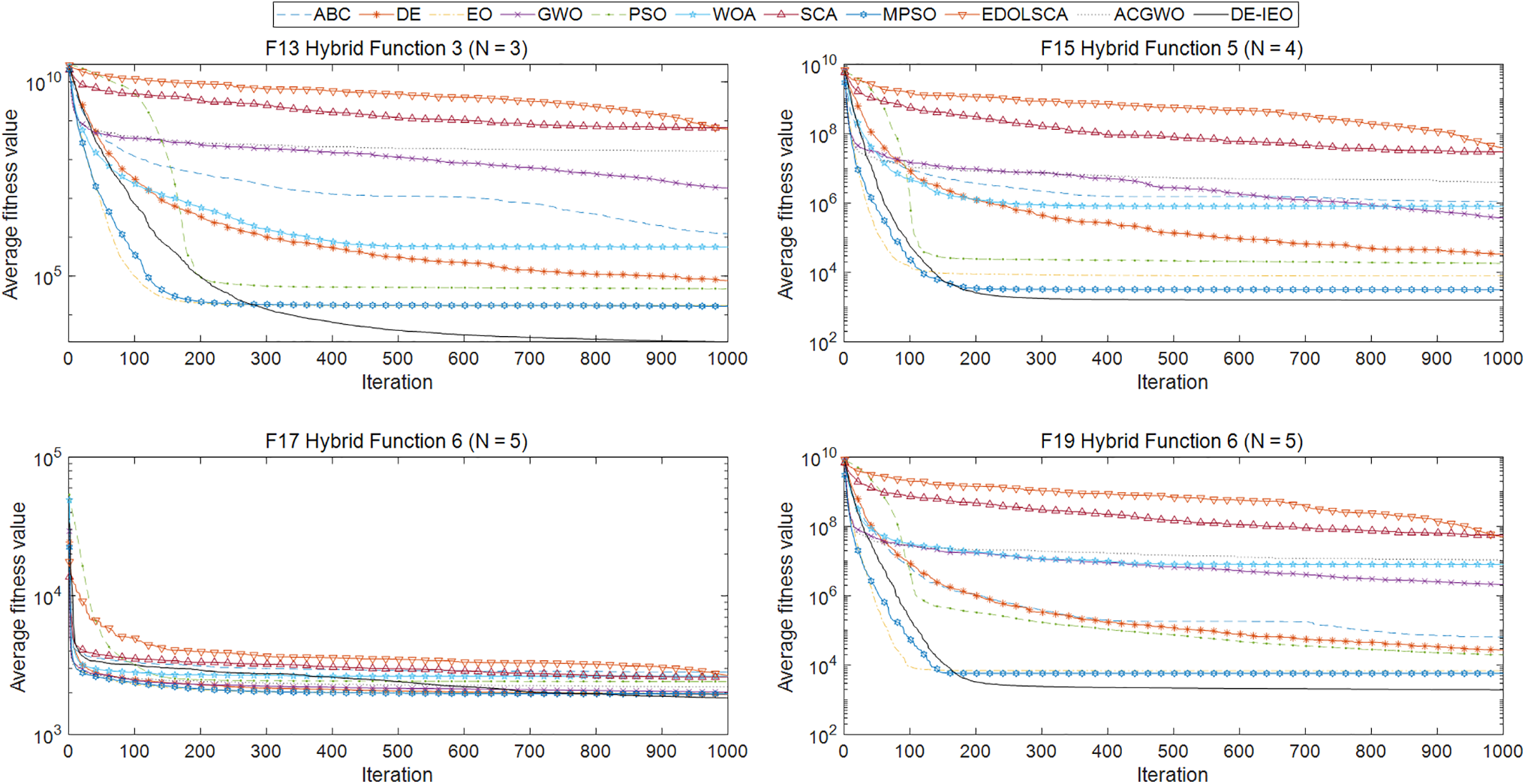
Figure 5: Eleven algorithms convergence curves of functions F13, F15, F17, F19
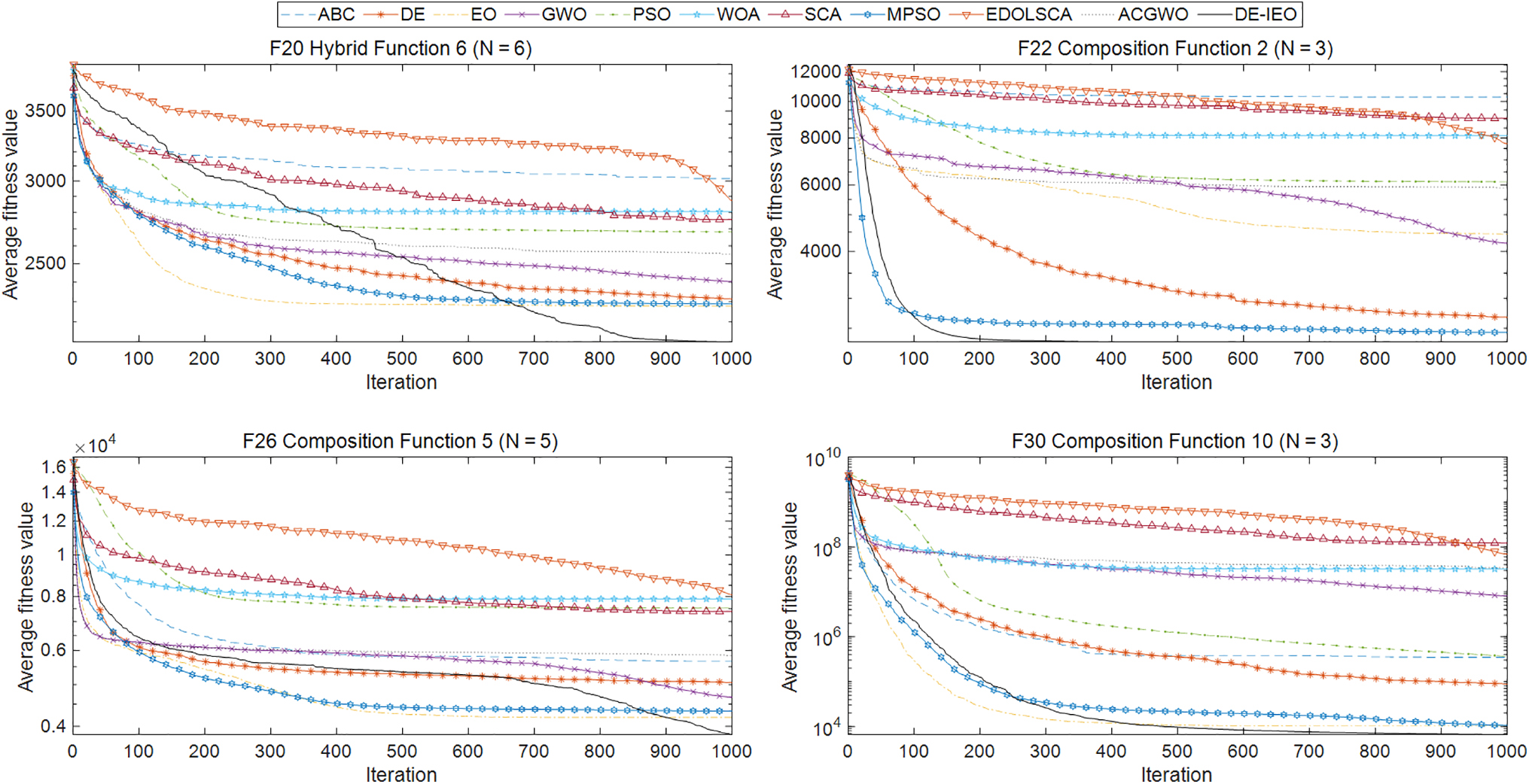
Figure 6: Each algorithms convergence curves of functions F20, F22, F26, F30
Figs. 7–9 show the boxplots of the algorithm for each function. It is important to know that the narrower the boxplot means that the algorithm is more concentrated in the data obtained in 30 runs, which means is more stable; the lower the median of the boxplots, the closer the algorithm is to the theoretical values. So it is clear from the boxplots that the stability and accuracy of DE-IEO is the best among most functions.
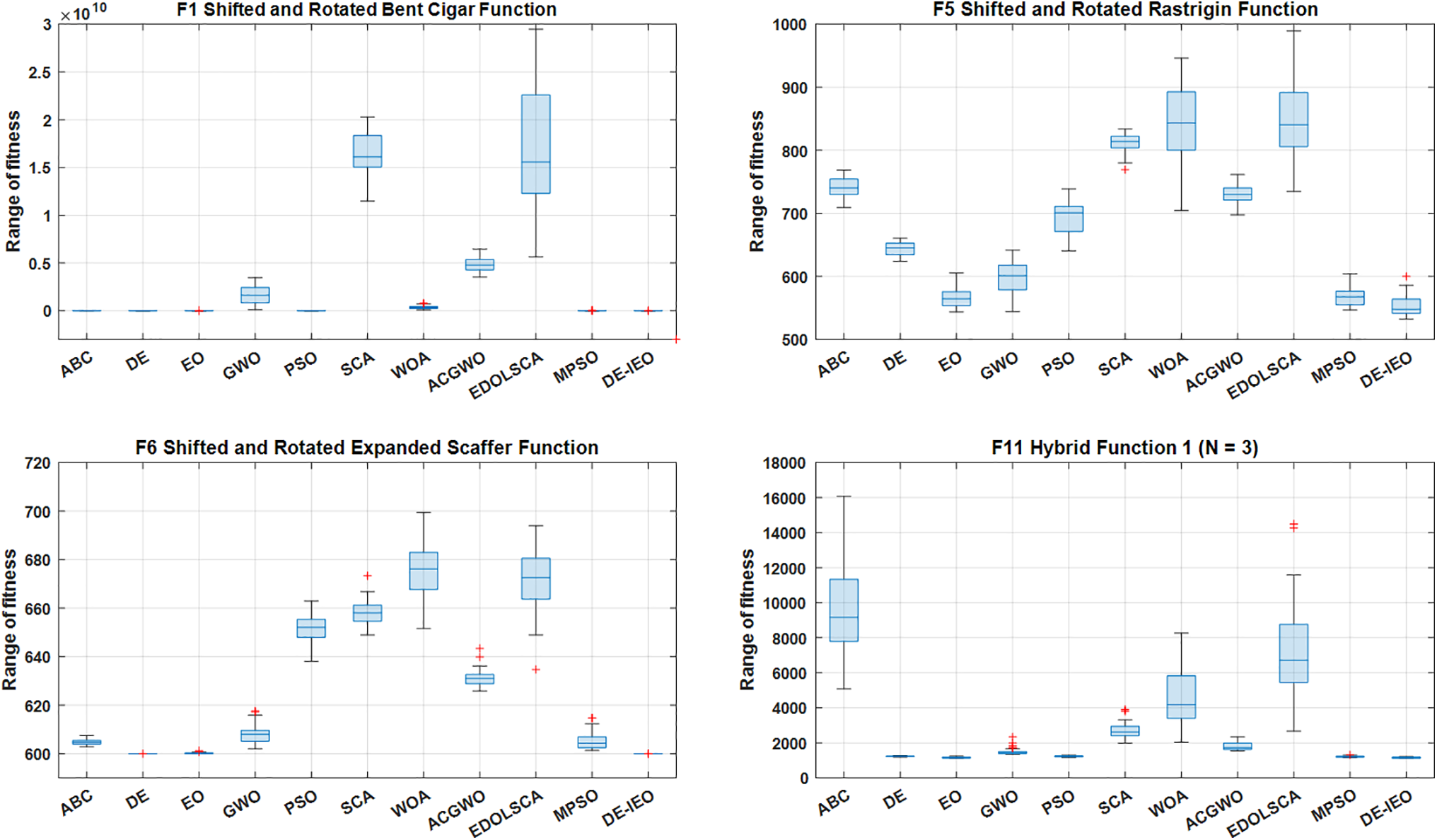
Figure 7: Boxplots obtained by each algorithm on F1, F5, F6, F11
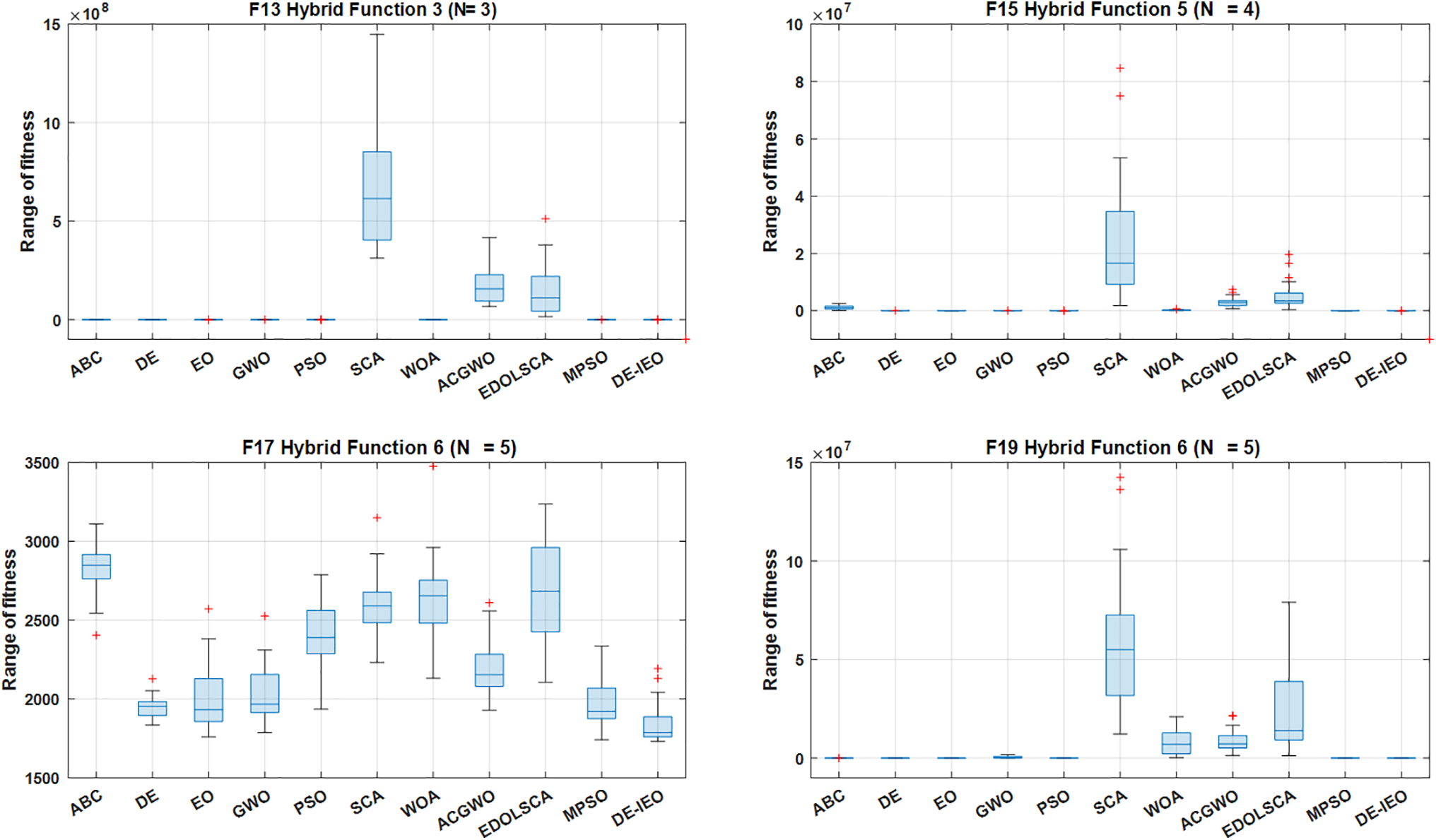
Figure 8: Boxplots obtained by each algorithm on F13, F15, F17, F19
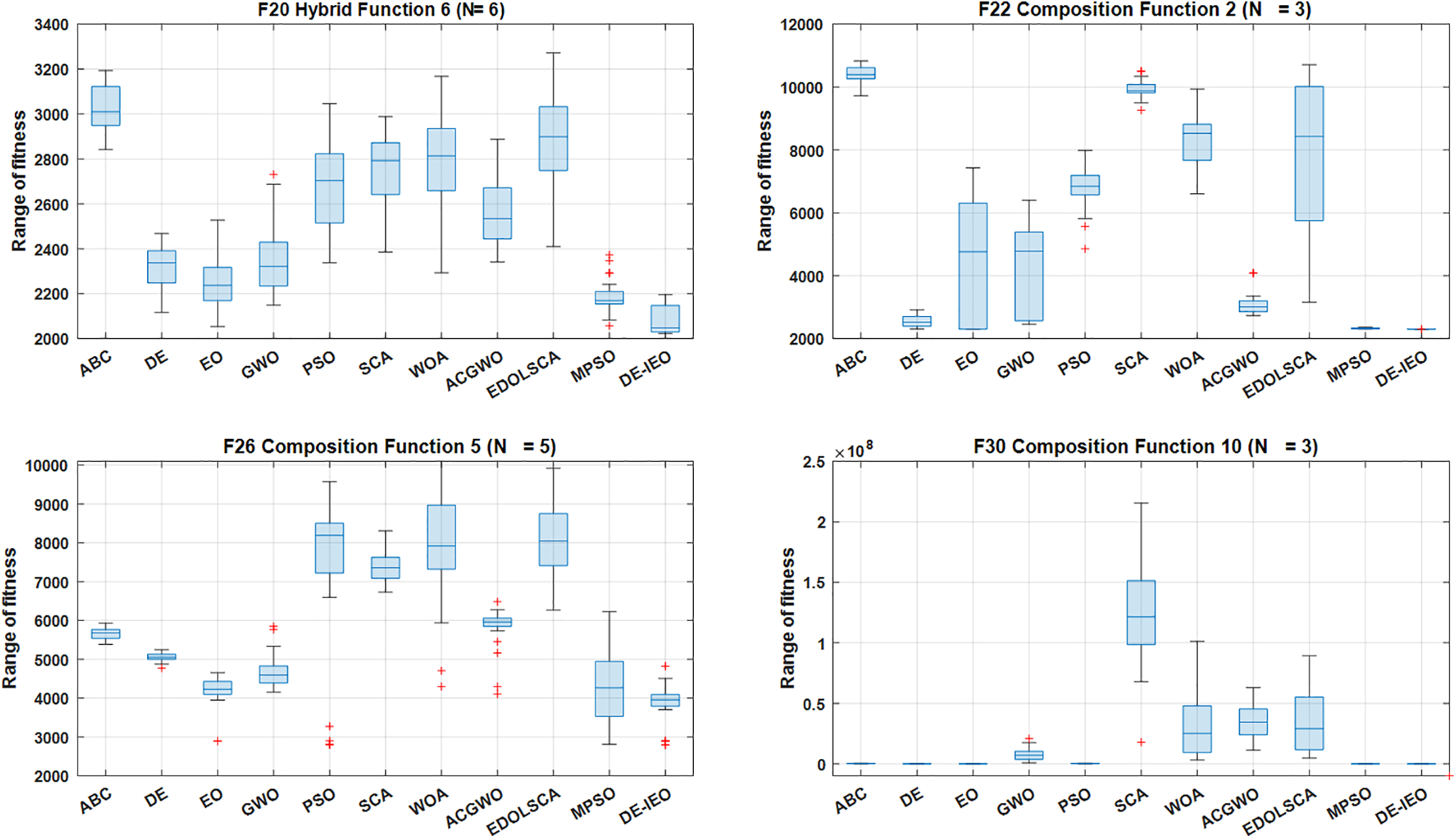
Figure 9: Boxplots obtained by each algorithm on F20, F22, F26, F30
6.2 Performance of DE-IEO for CHPED Problem
In this subsection, we first conduct a comprehensive performance test of DE-IEO using 4 cases in the CHPED problem, which contain one small and four large CHPED systems. Secondly, the obtained compared experimental results to verify the effectiveness of DE-IEO. The relevant data for large-scale CHPED systems above 84 units are obtained by scaling up to 24 units [15]. The 24-unit system is divided into two cases depending on whether POZs are considered or not. The penalty factor should be as large as possible, and is set to 1010 in [37]. To exclude the effect of rounding on the results, the error of
6.2.1 CHPED System 1 with 24 Units
This test system contains 24 units, of which 1–13 are POUs, 14–19 are CHP units, and 20–24 are HOUs, and the total demand for power is 2350 MW and the total demand for heat is 1250 MWth.
Case 1: POZs are not considered
Considering only the valve-point effects, the three types of costs obtained by DE-IEO are compared with other algorithms, including NDE [15], RCGA-IMM [29], CSO-PPS [30], TVAC-GSA-PSO [31], IGA-NCM [32], BLPSO [33] and OGSO [57]. Table 2 that IDE-EO obtained the best results among all the compared algorithms in terms of minimum and average cost, and the cost savings of DE-IEO compared with other algorithms can be visually found in Fig. 10. And overall IDE-EO is very competitive in this case compared to other algorithms.
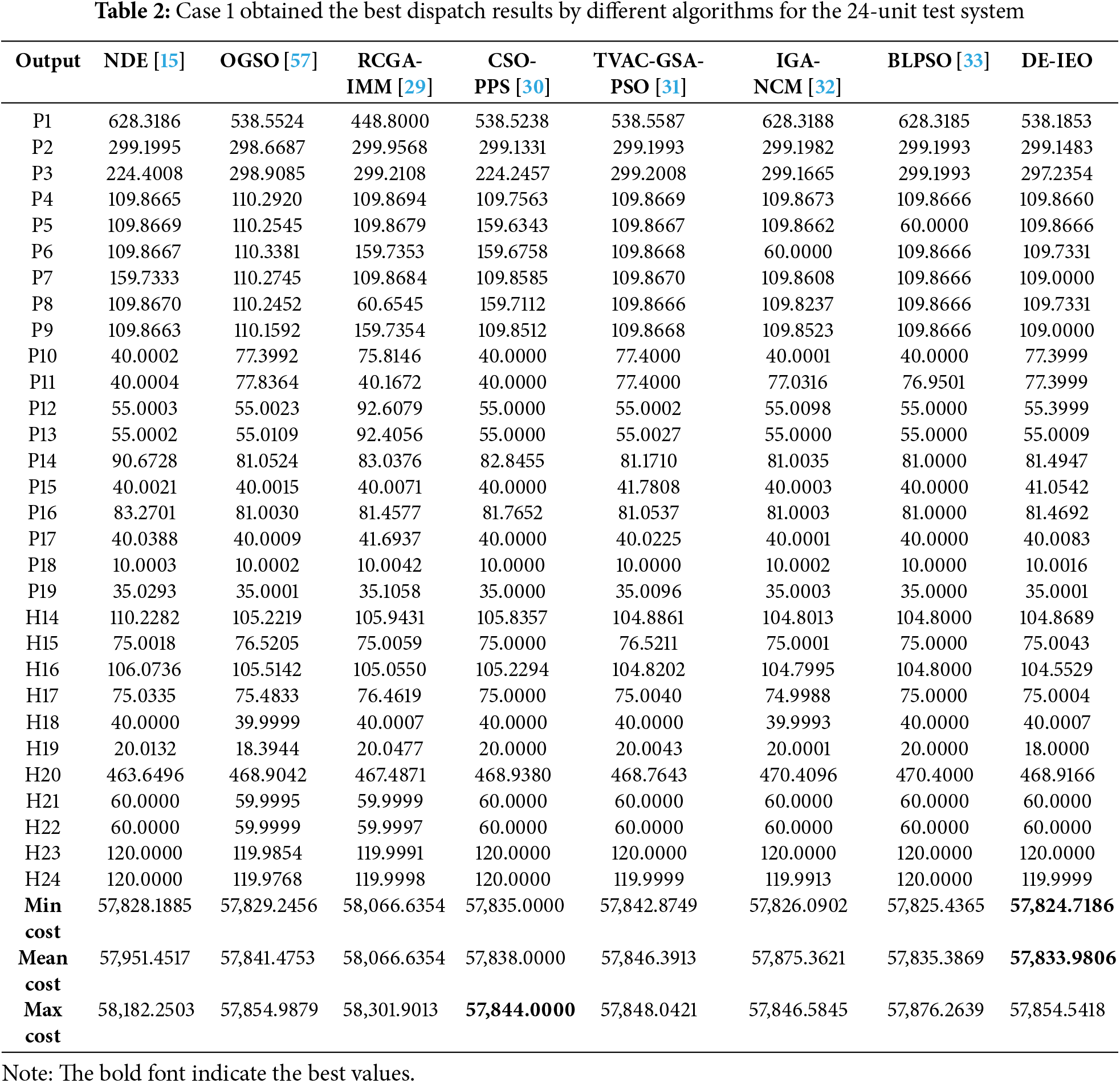
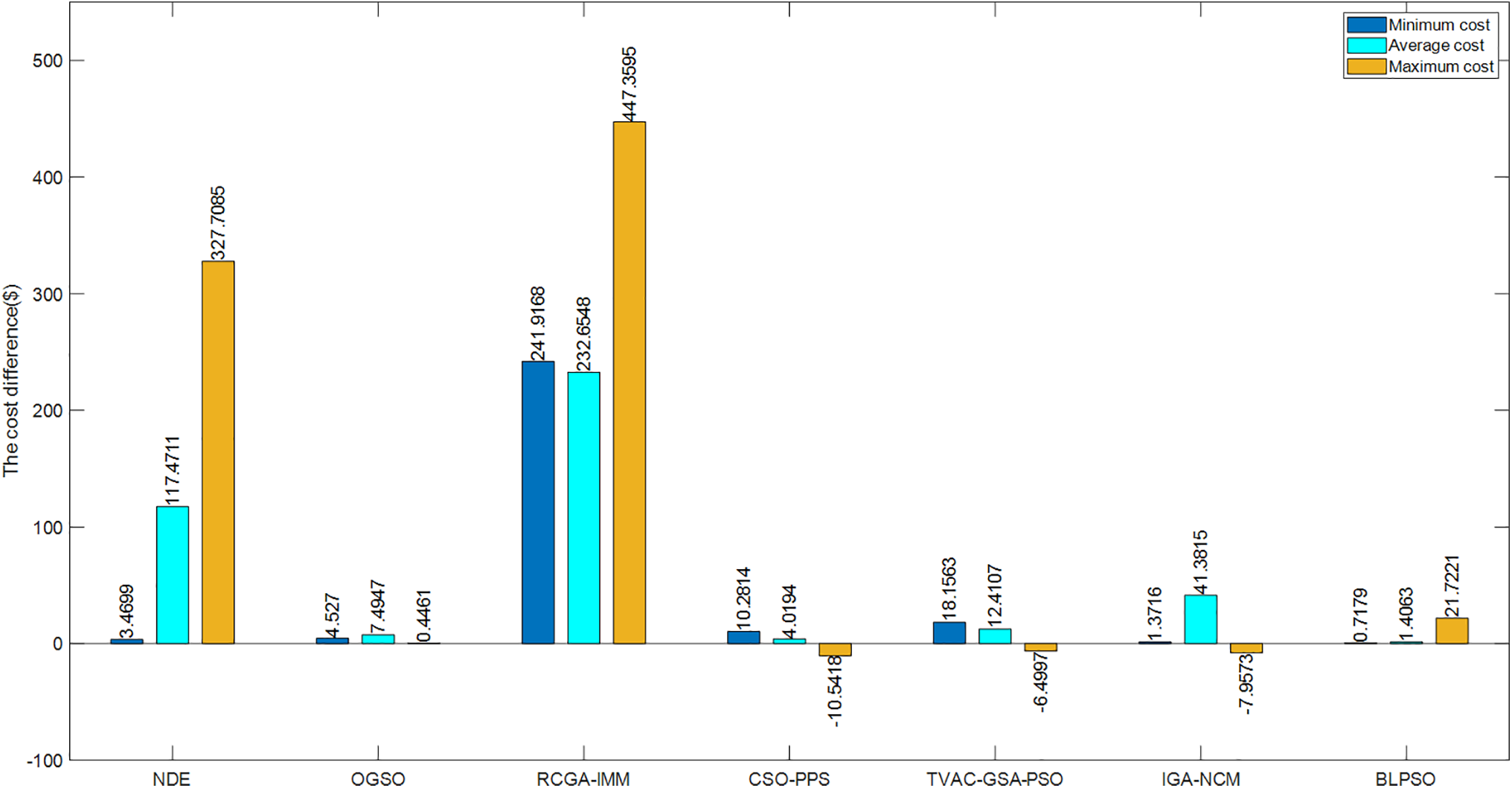
Figure 10: Cost savings of IDE-EO compared to other algorithms for case 1 of the 24-unit system
Case 2: Consider POZs
This case is based on case 1 and introduces the prohibited operating zones constraint. In Table 3, DE-IEO is compared with the results of some literature, such as NDE [15], CSO-PPS [30], IGA-NCM [32], BLPSO [33], OGSO [58] and HTS [59]. From Fig. 11, it can be found that some of the cost savings of DE-IEO compared to the other comparison algorithms are negative, which indicates that the results obtained by DE-IEO are inferior to these comparison algorithms in general. Although the results obtained by DE-IEO are not the best, they are better than half of the other algorithms in terms of minimum and average cost.
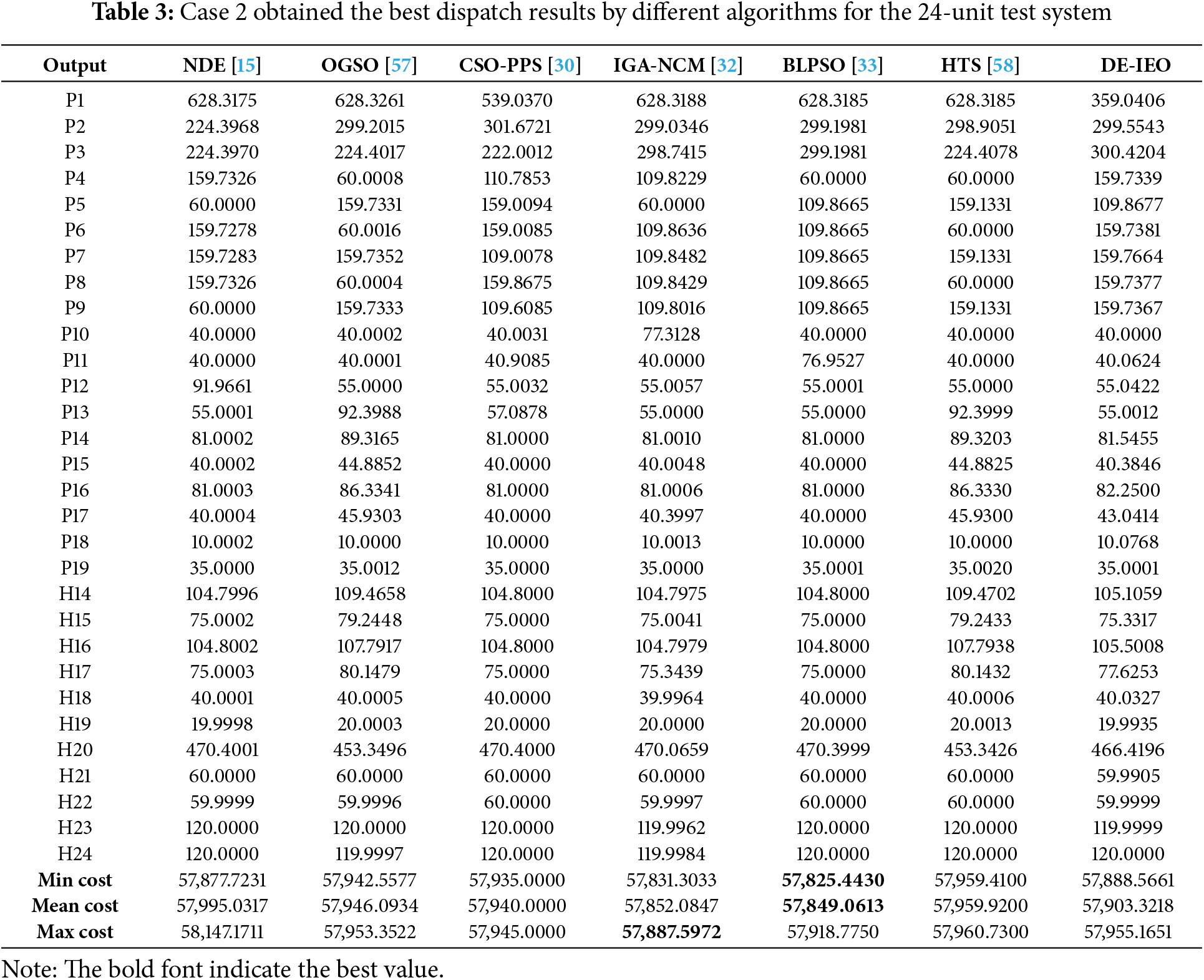
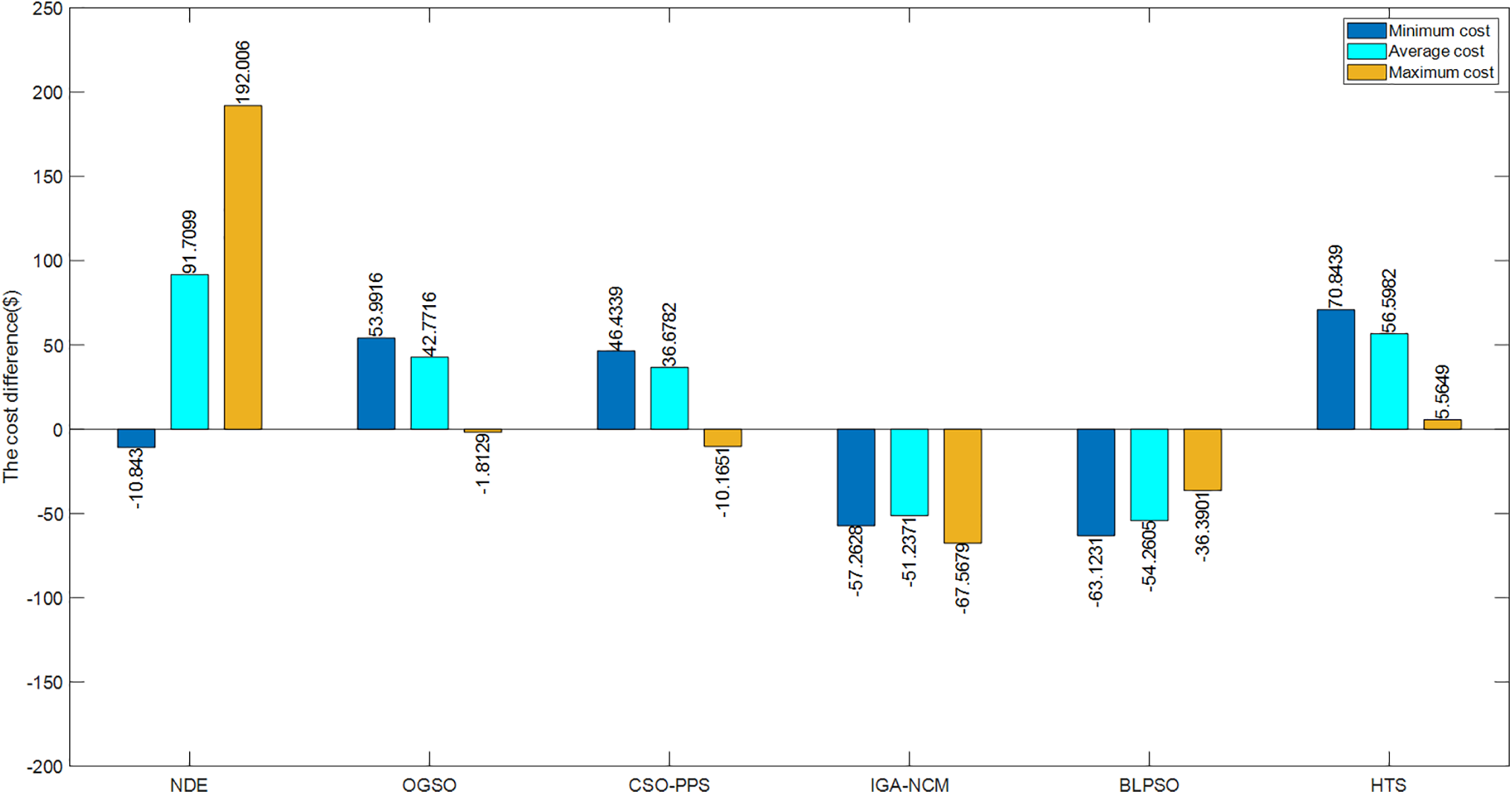
Figure 11: Cost savings of IDE-EO compared to other algorithms for case 2 of the 24-unit system
6.2.2 CHPED System 2 with 84 Units
This test contains 84 units, of which 1–40 are POUs, 41–64 are CHP units, and 65–84 are HOUs, and the total demand for power is 12,700 MW and the total demand for heat is 5000 MWth. Table 4 provides the compared results of DE-IEO, from which it can be seen that all three indexes are the best without violating the FOR constraint. Fig. 12 shows the position of the CHP unit results on FOR obtained by WOA at unit 84, and it can be seen that the solutions obtained by WOA are outside their regional range, which further proves that although WOA obtains the minimum cost, its solution is invalid; for MPHS, similar to WOA, Fig. 13 is showing that the solution it obtains is invalid. Fig. 14 depicts the cost savings of DE-IEO compared to other algorithms in terms of minimum cost, it can be seen DE-IEO is the best in terms of minimum cost.
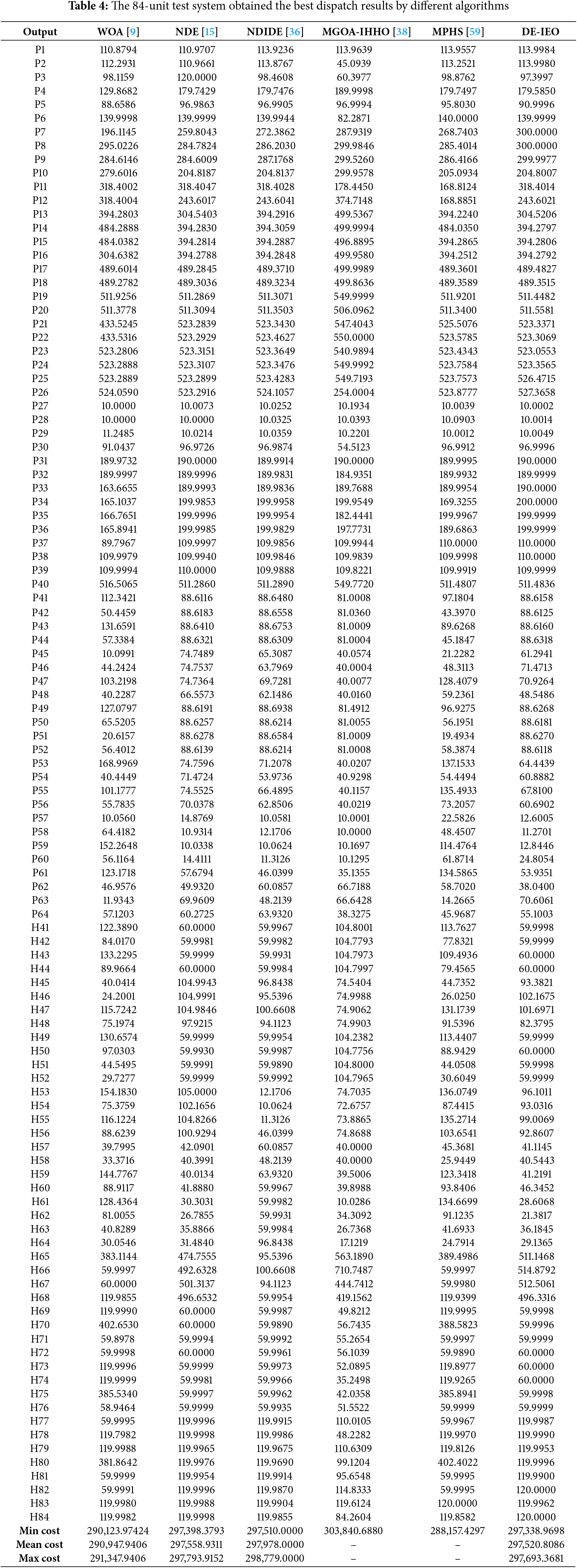
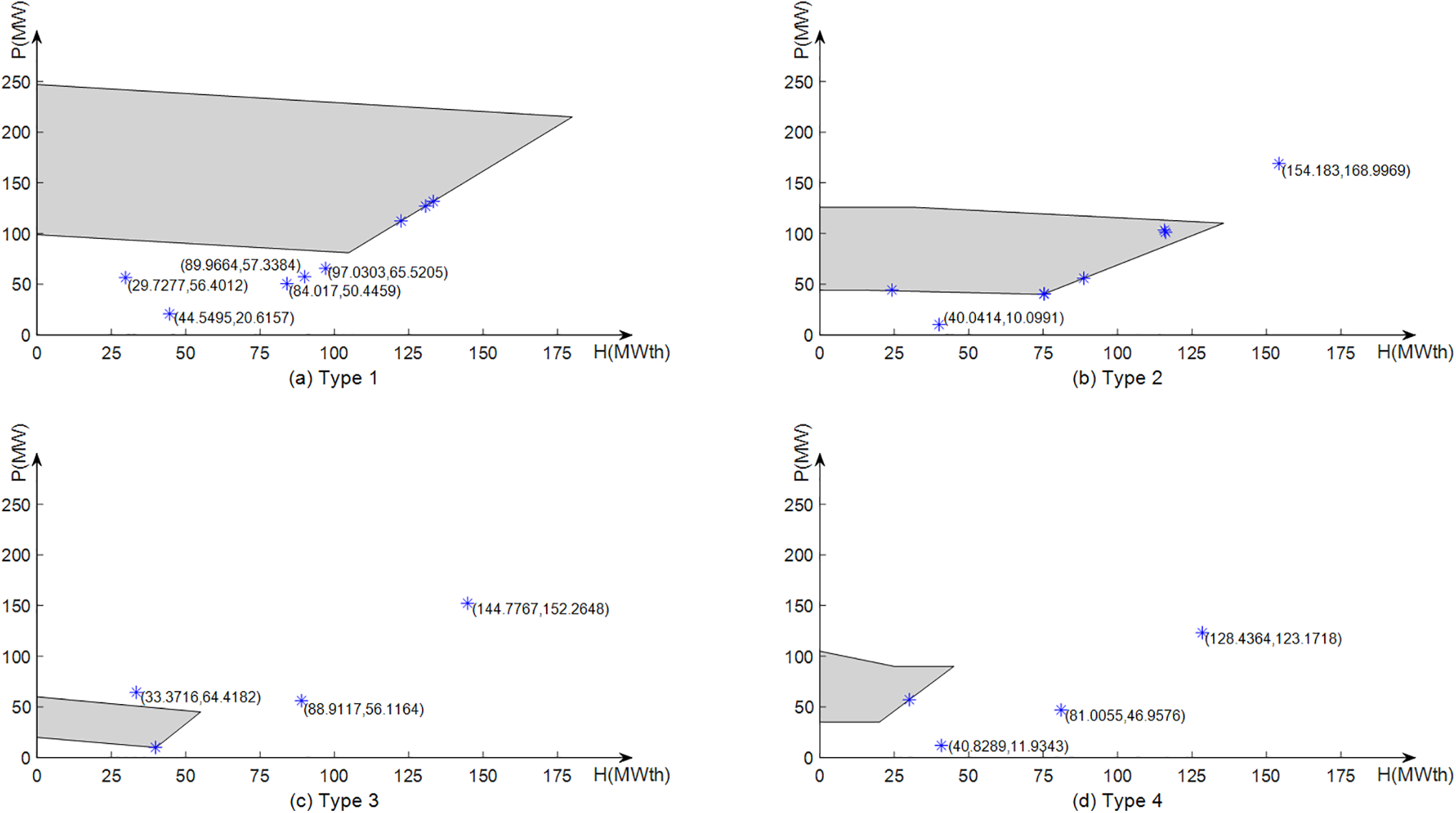
Figure 12: Location of WOA in the FOR of the 84-unit system
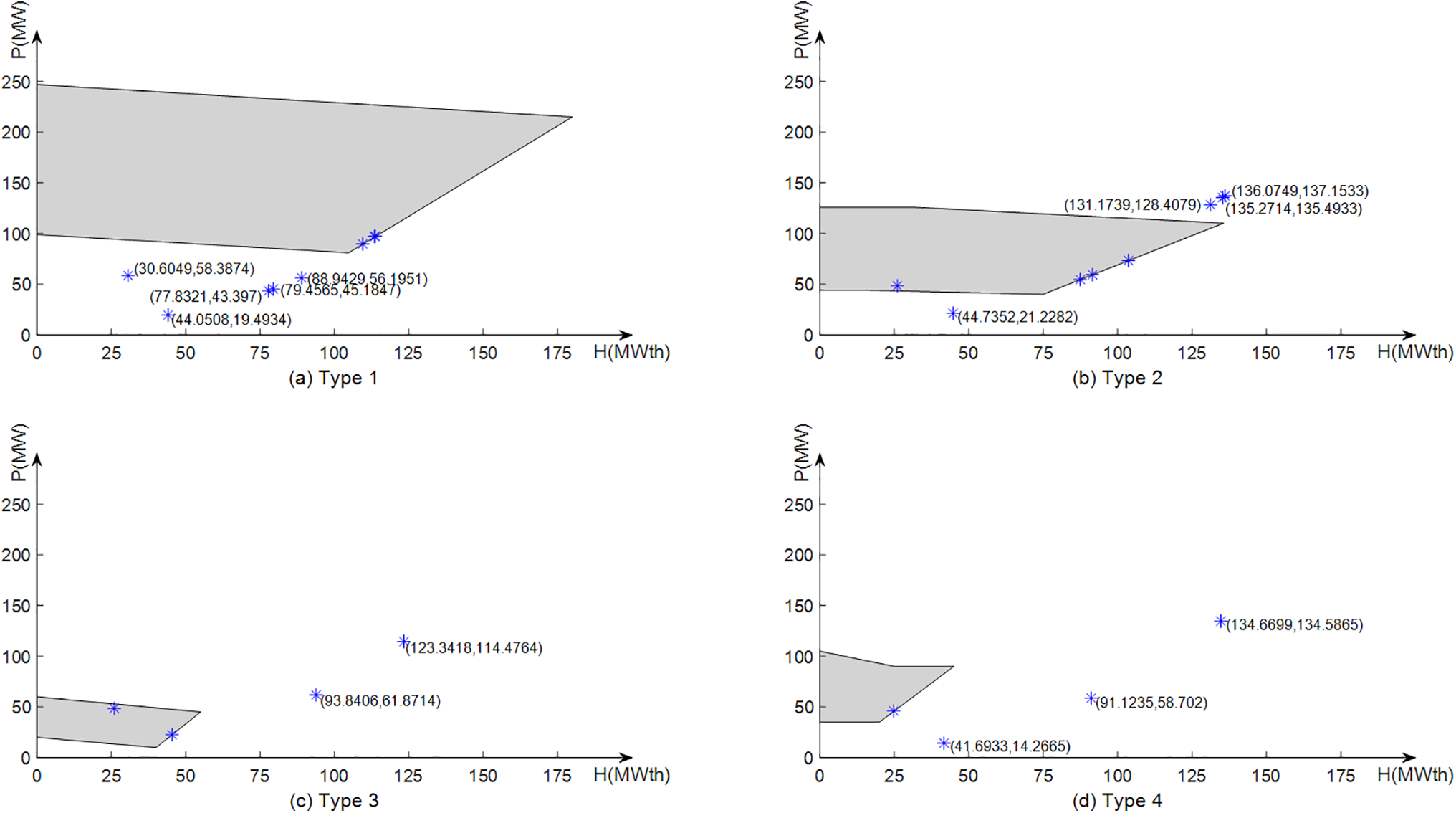
Figure 13: Location of MPHS in the FOR of the 84-unit system
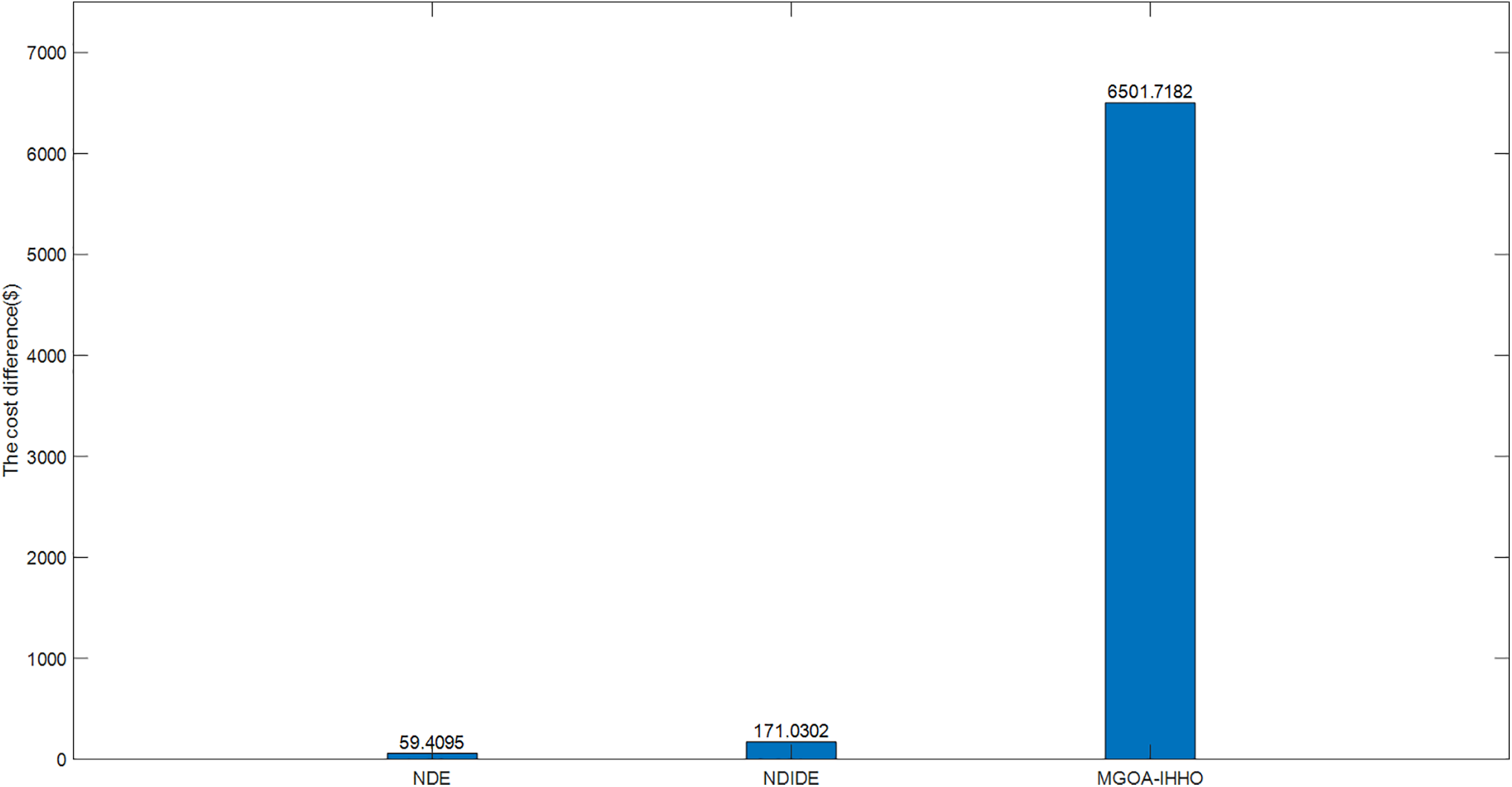
Figure 14: Minimum cost savings of IDE-EO compared to other algorithms in 84 unit system
6.2.3 CHPED System 3 with 96 Units
This test system contains 96 units, of which 1–52 are POUs, 53–76 are CHP units, and 77–96 are HOUs, and the total demand for power is 9400 MW and the total demand for heat is 5000 MWth.
Table 5 shows the results of comparing DE-IEO with other algorithms, which includes WOA, NDE, and NDIDE. Fig. 15 is DE-IEO obtains the minimum cost, which is the best among all the algorithms, and the maximum and average cost also get the best results. Compared with the small-scale CHPED system case with 24 units, DE-IEO is obviously more advantageous for the large-scale problem.
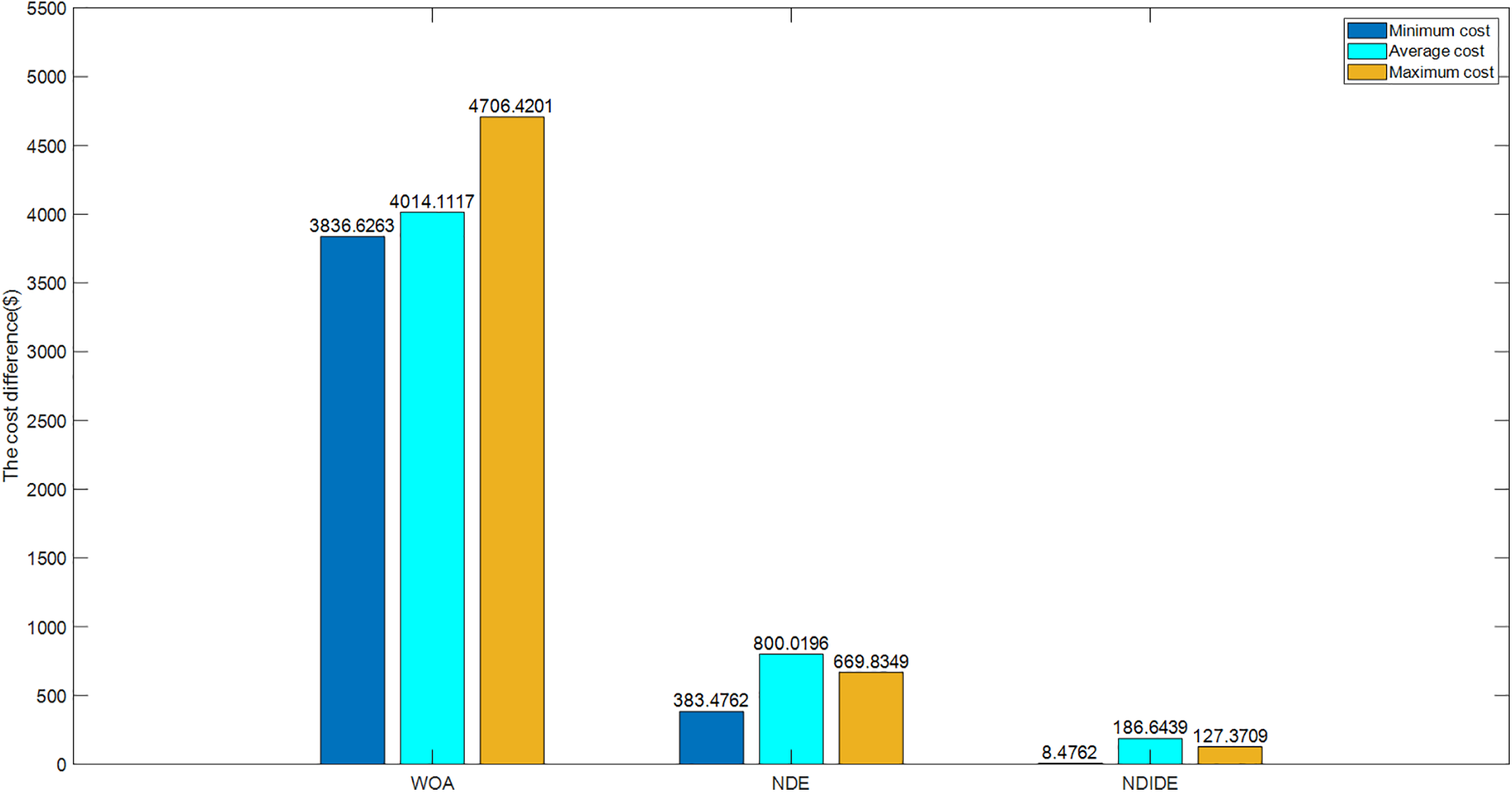
Figure 15: Cost savings of IDE-EO compared to other algorithms for the 96-unit system
6.2.4 CHPED System 4 with 192 Units
This section test systems contain 192 units, of which 1–104 are POUs, 105–152 are CHPUs, and 153–192 are HOUs, and the total demand for power is 18,800 MW and the total demand for heat is 10,000 MWth. Table 6 shows the comparison results, Fig. 16 shows that DE-IEO achieves the best results are superiority of DE-IEO on the large-scale systems.
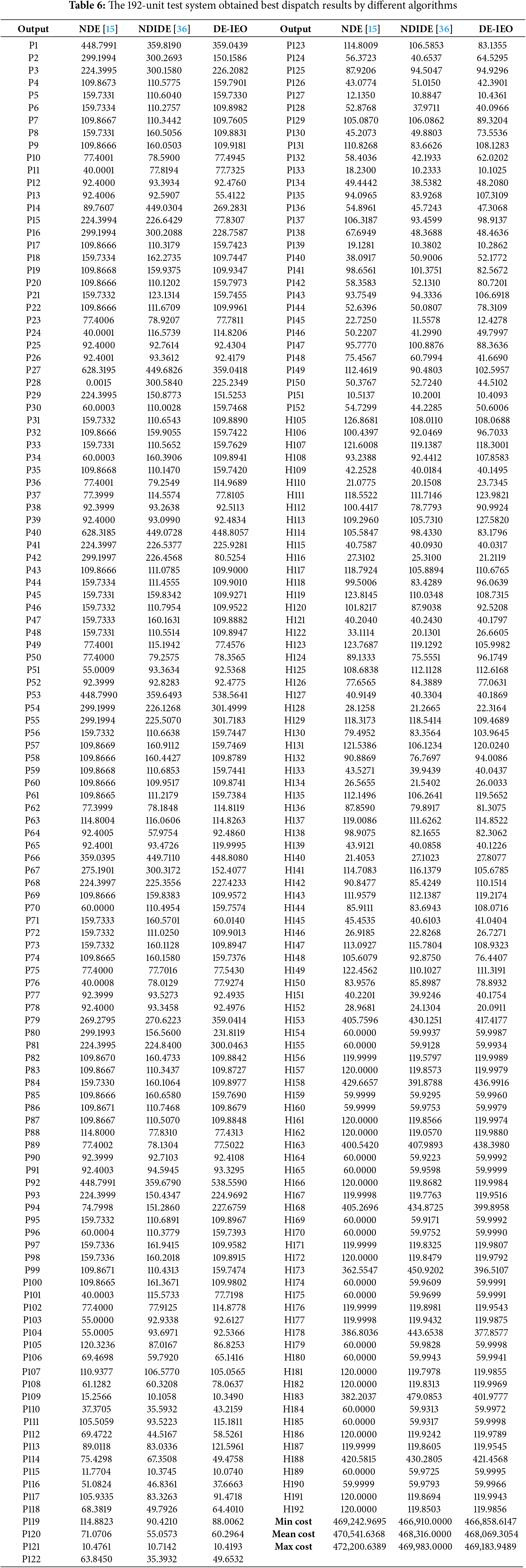
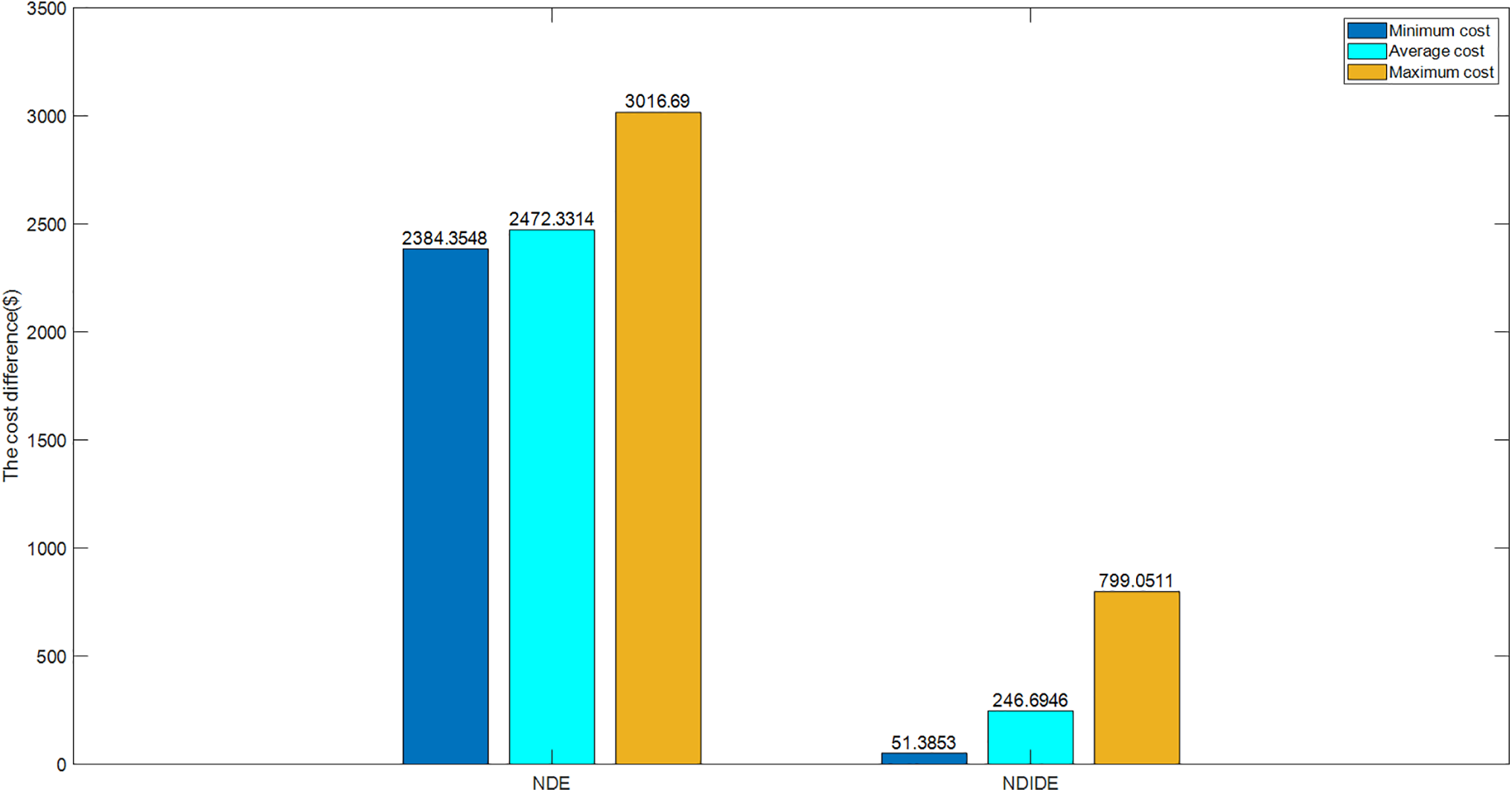
Figure 16: Cost savings of IDE-EO compared to other algorithms for the 24-unit system
The performance of DE-IEO are evaluated on the CEC2017 test suite and the CHPED. For the first part of the experiments, 29 standard test functions in the CEC2017 test suites are selected to benchmark the performance of DE-IEO in this paper. In Table 1, DE-IEO ranks first among all algorithms. Among the 29 test functions, DE-IEO achieves the optimal mean 18 times. Among the four types of functions, DE-IEO can reach the optimum, which shows that DE-IEO has more comprehensive performance, especially in multimodal and hybrid functions DE-IEO has more advantages, which is also more conducive to the solution of the CHPED problem to be discussed. Compared with EO and DE, the hybrid algorithm achieves optimality on more than half of the functions, which fully indicates that DE-IEO, which is made by combining EO and DE, is very successful. Specifically, from Figs. 4–6, the convergence speed of DE-IEO is not the fastest, but the final result achieved is the best. From the convergence curve, we can also find that EO tends to stop converging earlier than DE-IEO, which is the characteristic of falling into local optimum, while DE can keep converging slowly, so mixing the two can achieve a better convergence effect. It is evident from Figs. 7–9 that DE-IEO has narrower boxplots for most functions, indicating that it is more stable compared to other algorithms; it is also evident that DE-IEO has relatively lower boxplots, indicating that the results obtained are closer to the theoretical optimum. In addition, the mutation and crossover steps in DE can well help EO to jump out of local optimum and avoid premature maturity of the algorithm, while the selection steps in DE can ensure better individuals are inherited to the next generation, which can ensure the excellent performance of DE-IEO in test functions and real-world problems. Although DE-IEO performs well on the test function, it is not enough to prove that DE-IEO has excellent performance on real problems, because the constraints in real problems are much more complex than the test function, such as the CHPED problem. Based on this, a second part of experiments is also designed in this paper to demonstrate the excellent performance of DE-IEO in solving real-world problems.
For the second part of the experiment, 4 test cases of the CHPED problem are selected for analysis and discussion to demonstrate the superior performance of DE-IEO. Figs. 10–11 and Figs. 14–16 show that DE-IEO did not obtain the best results for all three metrics for the 24-unit system, but the best results were obtained for the 84-, 96-, and 192-unit CHPED systems. This indicates that DE-IEO has obvious advantages in solving large-scale CHPED problems.
The main contributions of this paper are outlined: (1) A novel hybrid DE-IEO algorithm is introduced. (2) The DE-IEO is utilized to optimize the CEC2017 test suite, with detailed experimental results confirming its validity while discarding any invalid outcomes. (3) The DE-IEO has been effectively employed to tackle large-scale CHPED problems, where it is compared against ten other high-performing algorithms. The results indicate that DE-IEO achieves superior outcomes on most of the tested functions. Additionally, DE-IEO is tested on six CHPED cases, including systems with 24, 84, 96, and 192 units, with numerous figures and tables demonstrating its significant advantages in large-scale CHPED scenarios. DE-IEO proves to be competitive in both test functions and practical applications. Future research will explore: (1) Integrating wind, tidal, and other power generation methods with the CHPED problem, while also addressing environmental pollution to create a multi-objective problem. (2) Investigating the multi-region CHPED problem as a potential research avenue. (3) Applying DE-IEO to other optimization challenges, such as microgrid energy management, image threshold segmentation, and data clustering.
Acknowledgement: This work was supported by the National Natural Science Foundation of China. Thanks.
Funding Statement: This work was supported by the Scientific Research Project of Xiangsihu College of Guangxi Minzu University, Grant No. 2024XJKY06, and the National Natural Science Foundation of China under Grant No. U21A20464.
Author Contributions: Yuanfei Wei: writing—draft; Panpan Song: Investigation, experiment; Qifang Luo: Algorithm design, writing—review; Yongquan Zhou: Supervision, writing—review and editing. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Ghorbani N. Combined heat and power economic dispatch using exchange market algorithm. Int J Electr Power Energy Syst. 2016;82(1):58–66. doi:10.1016/j.ijepes.2016.03.004. [Google Scholar] [CrossRef]
2. Davoodi E, Zare K, Babaei E. A GSO-based algorithm for combined heat and power dispatch problem with modified scrounger and ranger operators. Appl Therm Eng. 2017;120(4):36–48. doi:10.1016/j.applthermaleng.2017.03.114. [Google Scholar] [CrossRef]
3. Niknam T, Azizipanah-Abarghooee R, Roosta A, Amiri B. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch. Energy. 2012;42(1):530–45. doi:10.1016/j.energy.2012.02.041. [Google Scholar] [CrossRef]
4. Rooijers FJ, van Amerongen RAM. Static economic dispatch for co-generation systems. IEEE Trans Power Syst. 1994;9(3):1392–8. doi:10.1109/59.336125. [Google Scholar] [CrossRef]
5. Rong A, Lahdelma R. An efficient envelope-based Branch and Bound algorithm for non-convex combined heat and power production planning. Eur J Oper Res. 2007;183(1):412–31. doi:10.1016/j.ejor.2006.09.072. [Google Scholar] [CrossRef]
6. Abdolmohammadi HR, Kazemi A. A Benders decomposition approach for a combined heat and power economic dispatch. Energy Convers Manag. 2013;71(1):21–31. doi:10.1016/j.enconman.2013.03.013. [Google Scholar] [CrossRef]
7. Sashirekha A, Pasupuleti J, Moin NH, Tan CS. Combined heat and power (CHP) economic dispatch solved using Lagrangian relaxation with surrogate subgradient multiplier updates. Int J Electr Power Energy Syst. 2013;44(1):421–30. doi:10.1016/j.ijepes.2012.07.038. [Google Scholar] [CrossRef]
8. Mehdinejad M, Mohammadi-Ivatloo B, Dadashzadeh-Bonab R. Energy production cost minimization in a combined heat and power generation systems using cuckoo optimization algorithm. Energy Effic. 2017;10(1):81–96. doi:10.1007/s12053-016-9439-6. [Google Scholar] [CrossRef]
9. Nazari-Heris M, Mehdinejad M, Mohammadi-Ivatloo B, Babamalek-Gharehpetian G. Combined heat and power economic dispatch problem solution by implementation of whale optimization method. Neural Comput Appl. 2019;31(2):421–36. doi:10.1007/s00521-017-3074-9. [Google Scholar] [CrossRef]
10. Paul C, Roy PK, Mukherjee V. Optimal solution of combined heat and power dispatch problem using whale optimization algorithm. Int J Appl Metaheuristic Comput (IJAMC). 2022;13(1):1–26. doi:10.4018/ijamc.290532. [Google Scholar] [CrossRef]
11. Zou D, Gong D. Differential evolution based on migrating variables for the combined heat and power dynamic economic dispatch. Energy. 2022;238(1):121664. doi:10.1016/j.energy.2021.121664. [Google Scholar] [CrossRef]
12. Yang Q, Liu P, Zhang J, Dong N. Combined heat and power economic dispatch using an adaptive cuckoo search with differential evolution mutation. Appl Energy. 2022;307(1):118057. doi:10.1016/j.apenergy.2021.118057. [Google Scholar] [CrossRef]
13. Mohammadi-Ivatloo B, Moradi-Dalvand M, Rabiee A. Combined heat and power economic dispatch problem solution using particle swarm optimization with time varying acceleration coefficients. Electr Power Syst Res. 2013;95(3):9–18. doi:10.1016/j.epsr.2012.08.005. [Google Scholar] [CrossRef]
14. Basu M. Bee colony optimization for combined heat and power economic dispatch. Expert Syst Appl. 2011;38(11):13527–31. doi:10.1016/j.eswa.2011.03.067. [Google Scholar] [CrossRef]
15. Liu D, Hu Z, Su Q, Liu M. A niching differential evolution algorithm for the large-scale combined heat and power economic dispatch problem. Appl Soft Comput. 2021;113(9):108017. doi:10.1016/j.asoc.2021.108017. [Google Scholar] [CrossRef]
16. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]
17. Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: a novel optimization algorithm. Knowl Based Syst. 2020;191:105190. doi:10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]
18. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]
19. Abdel-Basset M, Mohamed R, Mirjalili S, Chakrabortty RK, Ryan MJ. MOEO-EED: a multi-objective equilibrium optimizer with exploration-exploitation dominance strategy. Knowl Based Syst. 2021;214(6):106717. doi:10.1016/j.knosys.2020.106717. [Google Scholar] [CrossRef]
20. Wang J, Yang B, Li D, Zeng C, Chen Y, Guo Z, et al. Photovoltaic cell parameter estimation based on improved equilibrium optimizer algorithm. Energy Convers Manag. 2021;236(3):114051. doi:10.1016/j.enconman.2021.114051. [Google Scholar] [CrossRef]
21. Ali Shaik M, Mareddy PL, Visali N. Enhancement of voltage profile in the distribution system by reconfiguring with DG placement using equilibrium optimizer. Alex Eng J. 2022;61(5):4081–93. doi:10.1016/j.aej.2021.09.063. [Google Scholar] [CrossRef]
22. Houssein EH, Helmy BE, Oliva D, Jangir P, Premkumar M, Elngar AA, et al. An efficient multi-thresholding based COVID-19 CT images segmentation approach using an improved equilibrium optimizer. Biomed Signal Process Control. 2022;73(4):103401. doi:10.1016/j.bspc.2021.103401. [Google Scholar] [CrossRef]
23. Liu J, Li W, Li Y. LWMEO: an efficient equilibrium optimizer for complex functions and engineering design problems. Expert Syst Appl. 2022;198(9):116828. doi:10.1016/j.eswa.2022.116828. [Google Scholar] [CrossRef]
24. Faramarzi A, Mirjalili S, Heidarinejad M. Binary equilibrium optimizer: theory and application in building optimal control problems. Energy Build. 2022;277:112503. doi:10.1016/j.enbuild.2022.112503. [Google Scholar] [CrossRef]
25. Guha R, Ghosh KK, Bera SK, Sarkar R, Mirjalili S. Discrete equilibrium optimizer combined with simulated annealing for feature selection. J Comput Sci. 2023;67(1):101942. doi:10.1016/j.jocs.2023.101942. [Google Scholar] [CrossRef]
26. Zhong C, Li G, Meng Z, Li H, He W. A self-adaptive quantum equilibrium optimizer with artificial bee colony for feature selection. Comput Biol Med. 2023;153(10):106520. doi:10.1016/j.compbiomed.2022.106520. [Google Scholar] [PubMed] [CrossRef]
27. Subbaraj P, Rengaraj R, Salivahanan S. Enhancement of combined heat and power economic dispatch using self adaptive real-coded genetic algorithm. Appl Energy. 2009;86(6):915–21. doi:10.1016/j.apenergy.2008.10.002. [Google Scholar] [CrossRef]
28. Mellal MA, Williams EJ. Cuckoo optimization algorithm with penalty function for combined heat and power economic dispatch problem. Energy. 2015;93(1):1711–8. doi:10.1016/j.energy.2015.10.006. [Google Scholar] [CrossRef]
29. Haghrah A, Nazari-Heris M, Mohammadi-ivatloo B. Solving combined heat and power economic dispatch problem using real coded genetic algorithm with improved Mühlenbein mutation. Appl Therm Eng. 2016;99(10):465–75. doi:10.1016/j.applthermaleng.2015.12.136. [Google Scholar] [CrossRef]
30. Narang N, Sharma E, Dhillon JS. Combined heat and power economic dispatch using integrated civilized swarm optimization and Powell’s pattern search method. Appl Soft Comput. 2017;52:190–202. doi:10.1016/j.asoc.2016.12.046. [Google Scholar] [CrossRef]
31. Beigvand SD, Abdi H, La Scala M. Hybrid gravitational search algorithm-particle swarm optimization with time varying acceleration coefficients for large scale CHPED problem. Energy. 2017;126:841–53. doi:10.1016/j.energy.2017.03.054. [Google Scholar] [CrossRef]
32. Zou D, Li S, Kong X, Ouyang H, Li Z. Solving the combined heat and power economic dispatch problems by an improved genetic algorithm and a new constraint handling strategy. Appl Energy. 2019;237(10):646–70. doi:10.1016/j.apenergy.2019.01.056. [Google Scholar] [CrossRef]
33. Chen X, Li K, Xu B, Yang Z. Biogeography-based learning particle swarm optimization for combined heat and power economic dispatch problem. Knowl Based Syst. 2020;208(1):106463. doi:10.1016/j.knosys.2020.106463. [Google Scholar] [CrossRef]
34. Nasir M, Sadollah A, Aydilek İ.B, Lashkar Ara A, Ali Nabavi-Niaki S. A combination of FA and SRPSO algorithm for combined heat and power economic dispatch. Appl Soft Comput. 2021;102(5):107088. doi:10.1016/j.asoc.2021.107088. [Google Scholar] [CrossRef]
35. Meng A, Mei P, Yin H, Peng X, Guo Z. Crisscross optimization algorithm for solving combined heat and power economic dispatch problem. Energy Convers Manag. 2015;105(3):1303–17. doi:10.1016/j.enconman.2015.09.003. [Google Scholar] [CrossRef]
36. Liu D, Hu Z, Su Q. Neighborhood-based differential evolution algorithm with direction induced strategy for the large-scale combined heat and power economic dispatch problem. Inf Sci. 2022;613(3):469–93. doi:10.1016/j.ins.2022.09.025. [Google Scholar] [CrossRef]
37. Ramachandran M, Mirjalili S, Malli Ramalingam M, Charles Gnanakkan CAR, Parvathysankar DS, Sundaram A. A ranking-based fuzzy adaptive hybrid crow search algorithm for combined heat and power economic dispatch. Expert Syst Appl. 2022;197(3):116625. doi:10.1016/j.eswa.2022.116625. [Google Scholar] [CrossRef]
38. Ramachandran M, Mirjalili S, Nazari-Heris M, Parvathysankar DS, Sundaram A, Charles Gnanakkan CAR. A hybrid grasshopper optimization algorithm and Harris Hawks optimizer for combined heat and power economic dispatch problem. Eng Appl Artif Intell. 2022;111:104753. doi:10.1016/j.engappai.2022.104753. [Google Scholar] [CrossRef]
39. Thymianis M, Tzanetos A. Is integration of mechanisms a way to enhance a nature-inspired algorithm? Nat Comput. 2024;23(3):567–87. doi:10.1007/s11047-022-09920-3. [Google Scholar] [CrossRef]
40. Victoire TAA, Jeyakumar AE. Reserve constrained dynamic dispatch of units with valve-point effects. IEEE Trans Power Syst. 2005;20(3):1273–82. doi:10.1109/TPWRS.2005.851958. [Google Scholar] [CrossRef]
41. Zheng J, Liang P, Zhao H, Deng W. A broad sparse fine-grained image classification model based on dictionary selection strategy. IEEE Trans Reliab. 2024;73(1):576–88. doi:10.1109/tr.2023.3309278. [Google Scholar] [CrossRef]
42. Deng W, Wang J, Guo A, Zhao H. Quantum differential evolutionary algorithm with quantum-adaptive mutation strategy and population state evaluation framework for high-dimensional problems. Inf Sci. 2024;676(6):120787. doi:10.1016/j.ins.2024.120787. [Google Scholar] [CrossRef]
43. Li M, Yang S, Zhang M. Power supply system scheduling and clean energy application based on adaptive chaotic particle swarm optimization. Alex Eng J. 2022;61(3):2074–87. doi:10.1016/j.aej.2021.08.008. [Google Scholar] [CrossRef]
44. Rahnamayan S, Tizhoosh HR, Salama MMA. Quasi-oppositional differential evolution. In: 2007 IEEE Congress on Evolutionary Computation; 2007 Sep 25–28; Singapore. p. 2229–36. doi:10.1109/CEC.2007.4424748. [Google Scholar] [CrossRef]
45. Tizhoosh HR. Opposition-based learning: a new scheme for machine intelligence. In: International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06); 2005 Nov 28–30; Vienna, Austria. p. 695–701. doi:10.1109/CIMCA.2005.1631345. [Google Scholar] [CrossRef]
46. Awad NH, Ali MZ, Liang JJ, Qu BY, Suganthan PN. Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective bound constrained real-parameter numerical optimization. Technical report. Singapore: Nanyang Technological University; 2016 [Internet]. [cited 2025 Jun 23]. Available from: https://www.researchgate.net/publication/317228117. [Google Scholar]
47. Demšar J. Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res. 2006;7:1–30. [Google Scholar]
48. García S, Fernández A, Luengo J, Herrera F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: experimental analysis of power. Inf Sci. 2010;180(10):2044–64. doi:10.1016/j.ins.2009.12.010. [Google Scholar] [CrossRef]
49. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95—International Conference on Neural Networks; 1995 Nov 27–Dec 1; Perth, WA, Australia. p. 1942–8. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]
50. Karaboga D. An idea based on honey bee swarm for numerical optimization. Technical report-tr06, Erciyes university, engineering faculty, computer engineering department, 2005 [Internet]. [cited 2025 Jun 23]. Available from: http://www.lia.deis.unibo.it/Courses/SistInt/articoli/bee-colony1.pdf. [Google Scholar]
51. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]
52. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]
53. Mirjalili S. SCA: a Sine Cosine Algorithm for solving optimization problems. Knowl Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]
54. He M, Hong L, Yang ZY, Yang TB, Zeng J. Bioactive assay and hyphenated chromatography detection for complex supercritical CO2 extract from Chaihu Shugan San using an experimental design approach. Microchem J. 2018;142:394–402. doi:10.1016/j.microc.2018.07.016. [Google Scholar] [CrossRef]
55. Liu H, Zhang XW, Tu LP. A modified particle swarm optimization using adaptive strategy. Expert Syst Appl. 2020;152(3):113353. doi:10.1016/j.eswa.2020.113353. [Google Scholar] [CrossRef]
56. Zhang L, Hu T, Yang Z, Yang D, Zhang J. Elite and dynamic opposite learning enhanced sine cosine algorithm for application to plat-fin heat exchangers design problem. Neural Comput Appl. 2023;35(17):12401–14. doi:10.1007/s00521-021-05963-2. [Google Scholar] [CrossRef]
57. Basu M. Combined heat and power economic dispatch using opposition-based group search optimization. Int J Electr Power Energy Syst. 2015;73(3):819–29. doi:10.1016/j.ijepes.2015.06.023. [Google Scholar] [CrossRef]
58. Pattanaik JK, Basu M, Dash DP. Heat transfer search algorithm for combined heat and power economic dispatch. Iran J Sci Technol Trans Electr Eng. 2020;44(2):963–78. doi:10.1007/s40998-019-00280-w. [Google Scholar] [CrossRef]
59. Nazari-Heris M, Mohammadi-Ivatloo B, Asadi S, Geem ZW. Large-scale combined heat and power economic dispatch using a novel multi-player harmony search method. Appl Therm Eng. 2019;154:493–504. doi:10.1016/j.applthermaleng.2019.03.095. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF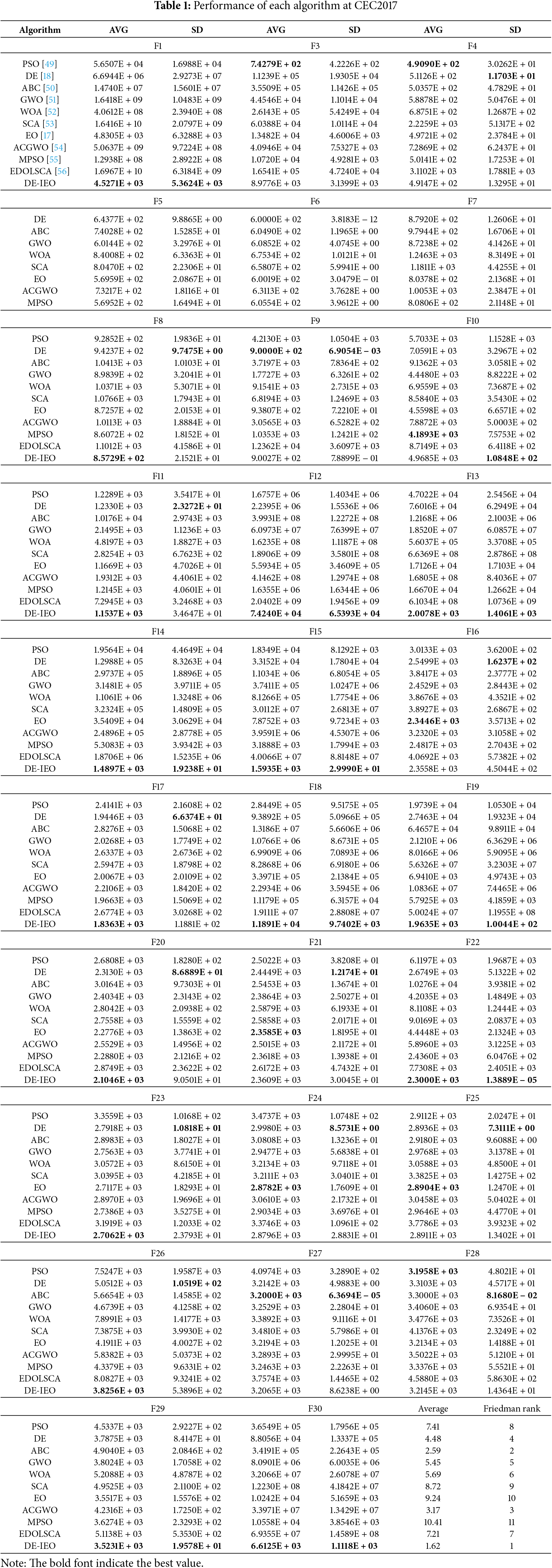
 Downloads
Downloads
 Citation Tools
Citation Tools