 Open Access
Open Access
REVIEW
A Review of Artificial Intelligence-Enhanced Fuzzy Multi-Criteria Decision-Making Approaches for Sustainable Transportation Planning
1 College of Science and Engineering, Hamad bin Khalifa University, Doha, 34110, Qatar
2 Department of Industrial Engineering, Yildiz Technical University, Istanbul, 34349, Türkiye
3 Department of Industrial Engineering, Karadeniz Technical University, Trabzon, 61080, Türkiye
* Corresponding Author: Nezir Aydin. Email:
(This article belongs to the Special Issue: Fuzzy Logic: Next-Generation Algorithms and Applications)
Computers, Materials & Continua 2025, 85(2), 2625-2650. https://doi.org/10.32604/cmc.2025.067290
Received 29 April 2025; Accepted 25 August 2025; Issue published 23 September 2025
Abstract
Transportation systems are rapidly transforming in response to urbanization, sustainability challenges, and advances in digital technologies. This review synthesizes the intersection of artificial intelligence (AI), fuzzy logic, and multi-criteria decision-making (MCDM) in transportation research. A comprehensive literature search was conducted in the Scopus database, utilizing carefully selected AI, fuzzy, and MCDM keywords. Studies were rigorously screened according to explicit inclusion and exclusion criteria, resulting in 73 eligible publications spanning 2006–2025. The review protocol included transparent data extraction on methodological approaches, application domains, and geographic distribution. Key findings highlight the prevalence of hybrid fuzzy AHP and TOPSIS methods, the widespread integration of machine learning for prediction and optimization, and a predominant focus on logistics and infrastructure planning within the transportation sector. Geographic analysis underscores a marked concentration of research activity in Asia, while other regions remain underrepresented, signaling the need for broader international collaboration. The review also addresses persistent challenges such as methodological complexity, data limitations, and model interpretability. Future research directions are proposed, including the integration of reinforcement learning, real-time analytics, and big data-driven adaptive solutions. This study offers a comprehensive synthesis and critical perspective, serving as a valuable reference for researchers, practitioners, and policymakers seeking to enhance the efficiency, resilience, and sustainability of transportation systems through intelligent decision-making frameworks.Keywords
Recent natural disasters, rapid population growth, and environmental problems arising from urbanization have brought the need for sustainable and efficient transportation systems back to the agenda [1]. Transportation planning plays a strategic role not only in meeting current societal needs but also in coping with future mobility challenges [2]. Optimizing resources, reducing environmental impact, and increasing accessibility and equity in different regions are also critical aspects of the necessity of efficient transportation systems [3]. Consequently, traditional transportation systems may be inadequate for the challenges of modern transportation systems, such as complexity, uncertainty, and dynamic nature [4,5]. These systems can be affected by many criteria such as traffic flow, energy consumption, and passenger reliability [6]. Therefore, there is an increasing need for more adaptive, intelligent, and data-driven approaches in decision-making processes and transportation planning [7,8].
In recent years, AI techniques have become a valuable tool for solving complex problems that transportation systems face [9]. Methods such as Machine Learning (ML), Deep Learning (DL), and Evolutionary Algorithms have shown significant success in traffic forecasting, route optimization, public transport management, and Electric Vehicle (EV) applications [10]. In integrating these techniques with fuzzy logic, the need for AI inference capabilities in decision-making processes under uncertainty comes to the fore. The combination of AI and fuzzy logic offers a vital opportunity to develop sustainable and efficient solutions in transportation planning, where uncertainties dominate [11]. The combination of these two approaches makes it possible to develop intelligent systems that can work with big data, adapt to changing conditions, and respond flexibly to complex situations [12]. Thus, more robust and effective decisions can be made in areas such as traffic management, infrastructure planning, and reducing environmental impacts [12]. For example, the integration of fuzzy logic with AI-based predictive models has successfully improved urban traffic signal optimization, significantly reducing congestion and emissions in dense urban areas. Therefore, it is inevitable that more systematic, flexible, and analytical methods will be used to solve transportation problems. Especially in developing intelligent transportation systems (ITS), approaches such as Fuzzy logic and MCDM methods provide great convenience to decision makers.
MCDM methods are preferred for solving problems where decisions need to be made within the scope of various criteria [13]. It has been observed that various criteria, such as cost, time, safety, environmental impact, and user satisfaction, are encountered in solving problems in transportation systems [14]. Since it is possible to handle many criteria systematically with MCDM methods, it can be said that MCDM methods have an essential place in the studies in this field.
The effectiveness of MCDM methods is limited by the fact that they are based on the unclear and uncertain opinions of decision makers. Uncertainty, ambiguity, and subjective judgments are inevitable when dealing with real-life problems. Fuzzy logic is integrated into the traditional MCDM methods to manage such uncertainties effectively. Fuzzy logic aims to model uncertainty with linguistic expressions that may vary according to the type of fuzzy logic [15]. Fuzzy logic has been successfully applied to model user preferences, expert opinions, and risk factors, especially in transportation systems [16].
The combination of fuzzy logic and MCDM methods provides flexibility in the decision-making process, while at the same time providing more realistic results with modeling closer to human thinking. It is possible to handle real-life applications more accurately. In the literature, it has been observed that more comprehensive solutions to problems such as transportation infrastructure selection [17], route optimization [18], and vehicle selection [19] have been proposed with this integration. Within the scope of this study, the applications of MCDM, fuzzy logic, and AI-based methods in ITS are systematically examined, and the basic approaches, methods used, and application areas of the existing literature are analyzed. The aim is to reveal the role of decision support systems in transportation and to provide a basis for new research in this field. The review includes studies published between 2006 and 2025, specifically addressing diverse transportation problems such as route optimization, vehicle selection, infrastructure planning, risk assessment, and logistics management.
This review follows a systematic protocol to ensure transparency and reproducibility. Studies were identified through a structured Scopus search using combinations of keywords related to AI, fuzzy logic, and MCDM. Only peer-reviewed English-language articles in the transportation domain were included. Two independent reviewers screened titles and abstracts, resolved disagreements by discussion, and extracted relevant data from eligible studies. Detailed criteria and procedures are reported in Section 2.
The remainder of the manuscript is structured as follows: Section 2 outlines the review protocol and the detailed screening process; Section 3 presents a comprehensive analysis of the studies, examining temporal trends, geographic distributions, methodological approaches, and transportation application areas; Section 4 identifies key research themes and conceptual trends through keyword analysis; and finally, Section 5 discusses critical findings, methodological considerations, and future research directions.
This chapter describes the methodology used for the literature analysis, which is the study’s main objective and first phase. This study aims to systematically examine the application of MCDM, fuzzy logic, and AI-based methods in ITS. The SCOPUS database was used to access relevant studies on the subject. The Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) methodology was used to conduct a more systematic literature review [20]. The methodology consists of five main steps: defining criteria, identifying sources, selecting literature, collecting data, and selecting data elements [21]. This methodology was adopted to reduce bias in the literature search and to develop more systematic methods [22].
In this article, the applications of MCDM, fuzzy logic and AI techniques in ITS are searched through SCOPUS using the keywords “(“artificial intelligence” OR “AI” OR “machine learning” OR “deep learning” OR “ML” OR “DL” OR “ Hybrid AI” OR “Big data” OR “Data mining” OR “Natural Language Processing” OR “Computer vision” OR “Pattern recognition” OR “Supervised Learning” OR “Unsupervised Learning” OR “Artificial Neural Networks” OR “ANN”OR “Genetic Algorithms” OR “GA” OR “Automated decision making” OR “Artificial neural networks” OR “Evolutionary Algorithms”) AND (fuzzy OR “Fuzzy Logic AI”) AND (“multi-criteria” OR “mcdm” OR “mcda” OR “madm” OR “Multi-Objective Decision Making” OR “Multi-Criteria Decision Analysis” OR ahp OR topsis OR vikor OR codas OR waspas OR edas OR bwm OR aras OR saw OR swara OR fucom OR anp OR electre OR promethee OR moora OR multimoora OR copras OR dematel OR critic OR cocoso OR mabac OR “entropy method” OR “Analytic Hierarchy Process” OR “Technique for Order of Preference by Similarity to Ideal Solution” OR “Vise Kriterijumska Optimizacija I Kompromisno Resenje” OR “entropy method” OR “Combinative Distance-Based Assessment” OR “Weighted Aggregated Sum Product Assessment” OR “Evaluation Based on Distance from Average Solution” OR “Best-Worst Method” OR “Additive Ratio Assessment” OR “Simple Additive Weighting” OR “Step-wise Weight Assessment Ratio Analysis” OR “Full Consistency Method” OR “Analytic Network Process” OR “Elimination et Choice Translating Reality” OR “Preference Ranking Organization Method for Enrichment Evaluations” OR “Multi-Objective Optimization on the Basis of Ratio Analysis” OR “Complex Proportional Assessment” OR “Decision-Making Trial and Evaluation Laboratory” OR “Criteria Importance Through Intercriteria Correlation”) AND (transportation OR transport)”. As a result of the search, a total of 192 studies were found. Following this search, some studies were eliminated as unnecessary, and 148 were found. The full text of some studies could not be accessed, some were not in English, and the content of some was not suitable for the subject of our research.
Specifically, studies were first identified through keyword-based searches, followed by screening titles and abstracts independently by two reviewers to ensure adherence to predefined inclusion and exclusion criteria. Any disagreements were resolved through discussion or consultation with a third reviewer. A full-text review was then conducted to confirm the final selection, ensuring methodological relevance and quality. With the elimination of these studies, a final total of 73 studies was found. Additionally, a qualitative methodological assessment was conducted, evaluating three critical dimensions: (1) sample validity, considering the representativeness and appropriateness of data samples used; (2) algorithm validation, examining whether the methods were validated through empirical data, sensitivity analysis, or comparative analyses; and (3) results reporting, assessing the clarity, completeness, and reproducibility of findings. Although no formal quantitative scale was applied, this assessment provided insights into the overall methodological rigor and potential biases within the reviewed studies, highlighting areas for future methodological improvement. A detailed flowchart illustrating each step of the screening and selection process is given in Fig. 1.
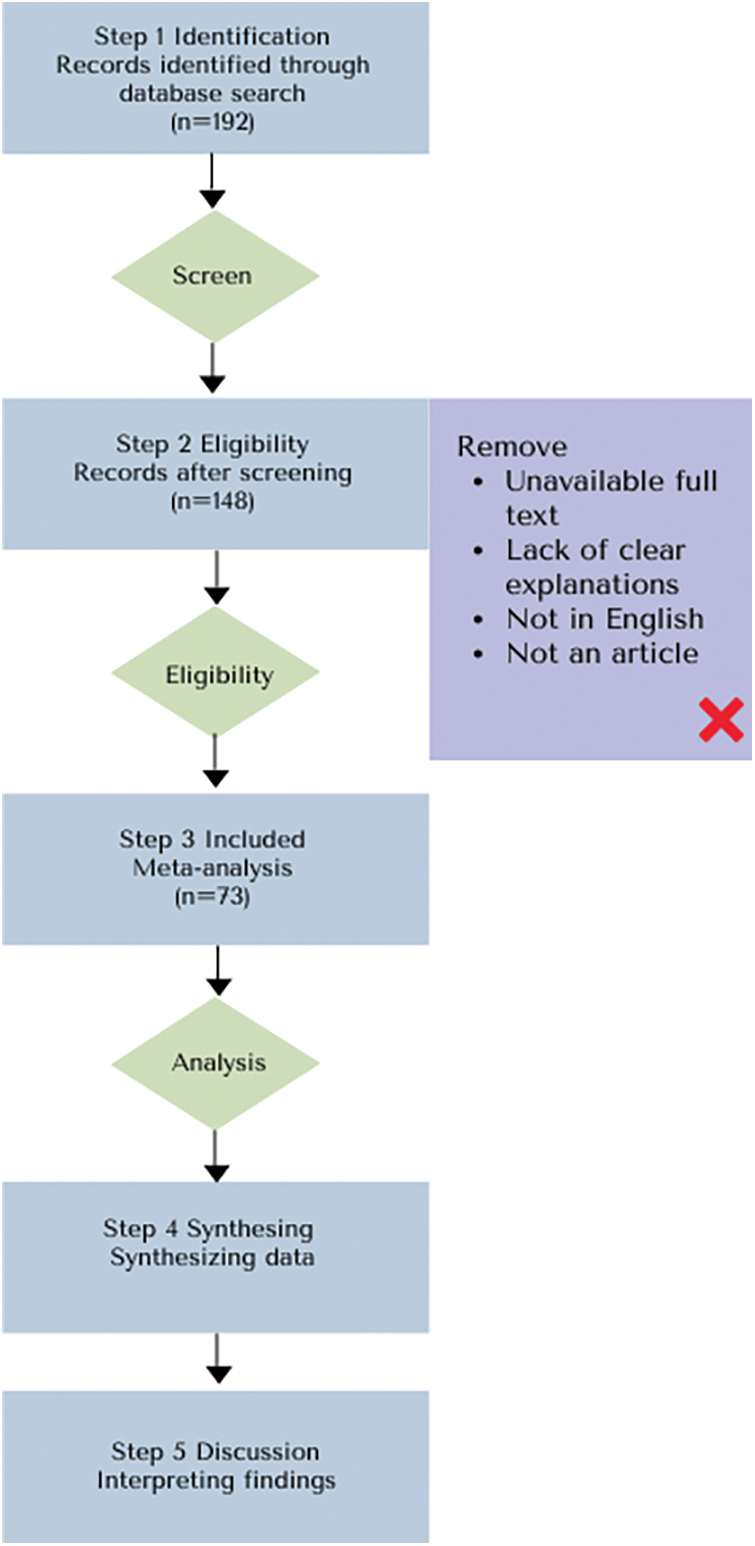
Figure 1: The systematic review flow diagram
Finally, an in-depth analysis of the 73 studies was conducted, and graphical representations are provided in the following sections.
The articles obtained from a systematic and detailed literature search were analyzed in detail. The problems the studies focused on, the MCDM techniques used, the AI techniques, the transportation applications, and the country/region where the application was performed are presented in Table 1. The review focuses on publications from 2006 onward, as earlier studies were scarce and generally limited to theoretical applications without significant practical integration of AI and fuzzy logic with MCDM methods in transportation. This period marks the beginning of increased academic interest and more robust practical applications, making it a meaningful starting point for comprehensive analysis. Then, summary diagrams were created based on the characteristics of the studies. Thanks to the diagrams created, the studies in Table 1 were handled statistically and visually.
Bibliometric co-occurrence network analyses offer a comprehensive view of the evolving methodological and thematic structure within the reviewed literature.
As visualized in Fig. 2, the method co-occurrence network illustrates how key decision-making techniques such as AHP, TOPSIS, and various fuzzy logic methods frequently interact and cluster together, while the emergence of AI techniques (e.g., machine learning) in recent years is also highlighted by their increasing prominence and network connections. The temporal color scale in Fig. 2 further allows readers to observe the chronological development of methodological trends.
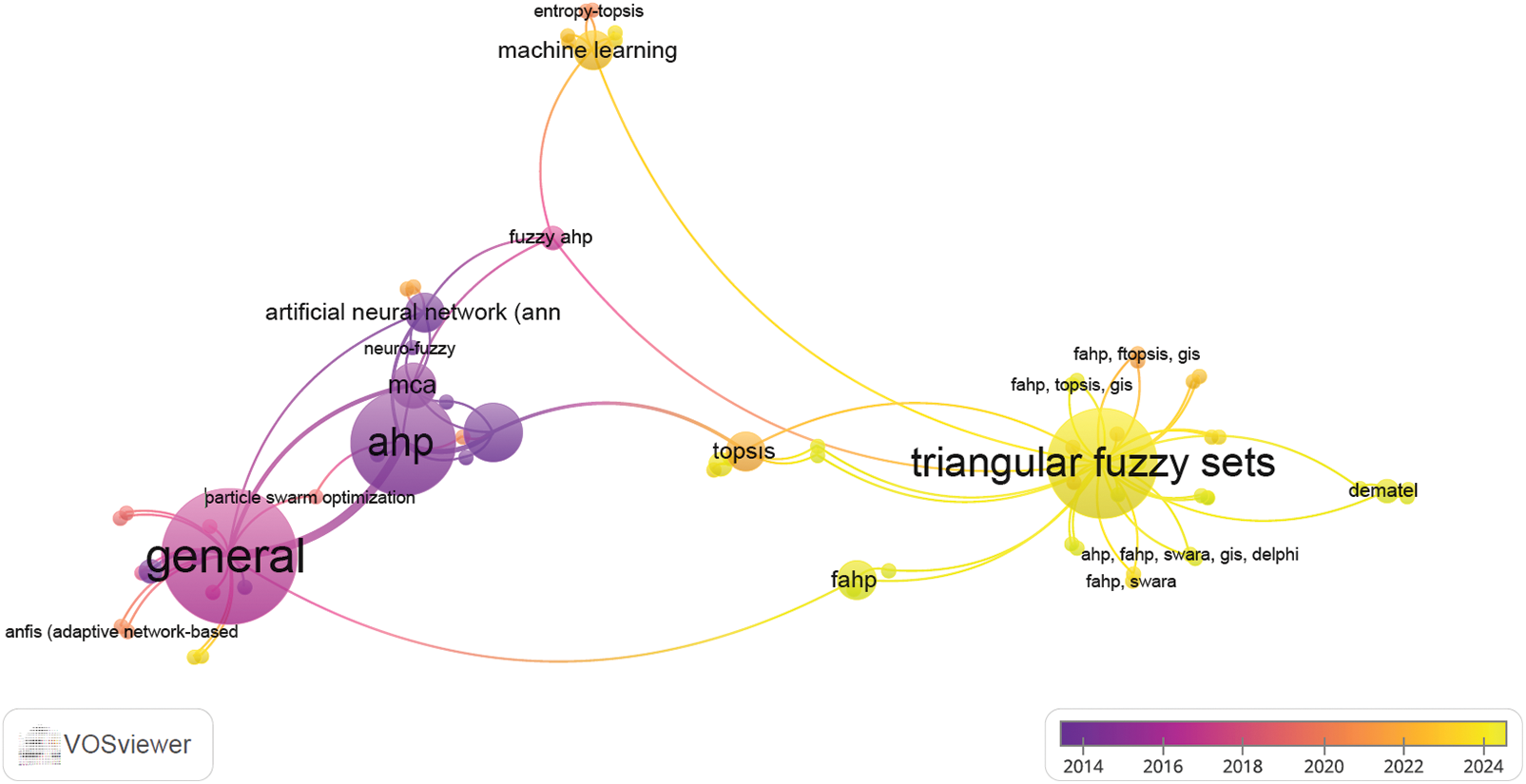
Figure 2: Method co-occurrence network
In parallel, Fig. 3 displays the keyword co-occurrence network, mapping the conceptual landscape and research directions in the field. This visualization highlights the strong interconnections between foundational topics such as transportation, decision making, and artificial intelligence, while also capturing the recent emergence of new research areas like COVID-19, sustainability, and big data analytics. The color gradient in Fig. 3 similarly reflects the time dimension, enabling an analysis of how thematic priorities have shifted over the years. Together, Figs. 2 and 3 provide a dynamic, data-driven perspective on both the methodological backbone and conceptual evolution of AI-fuzzy MCDM research in transportation.
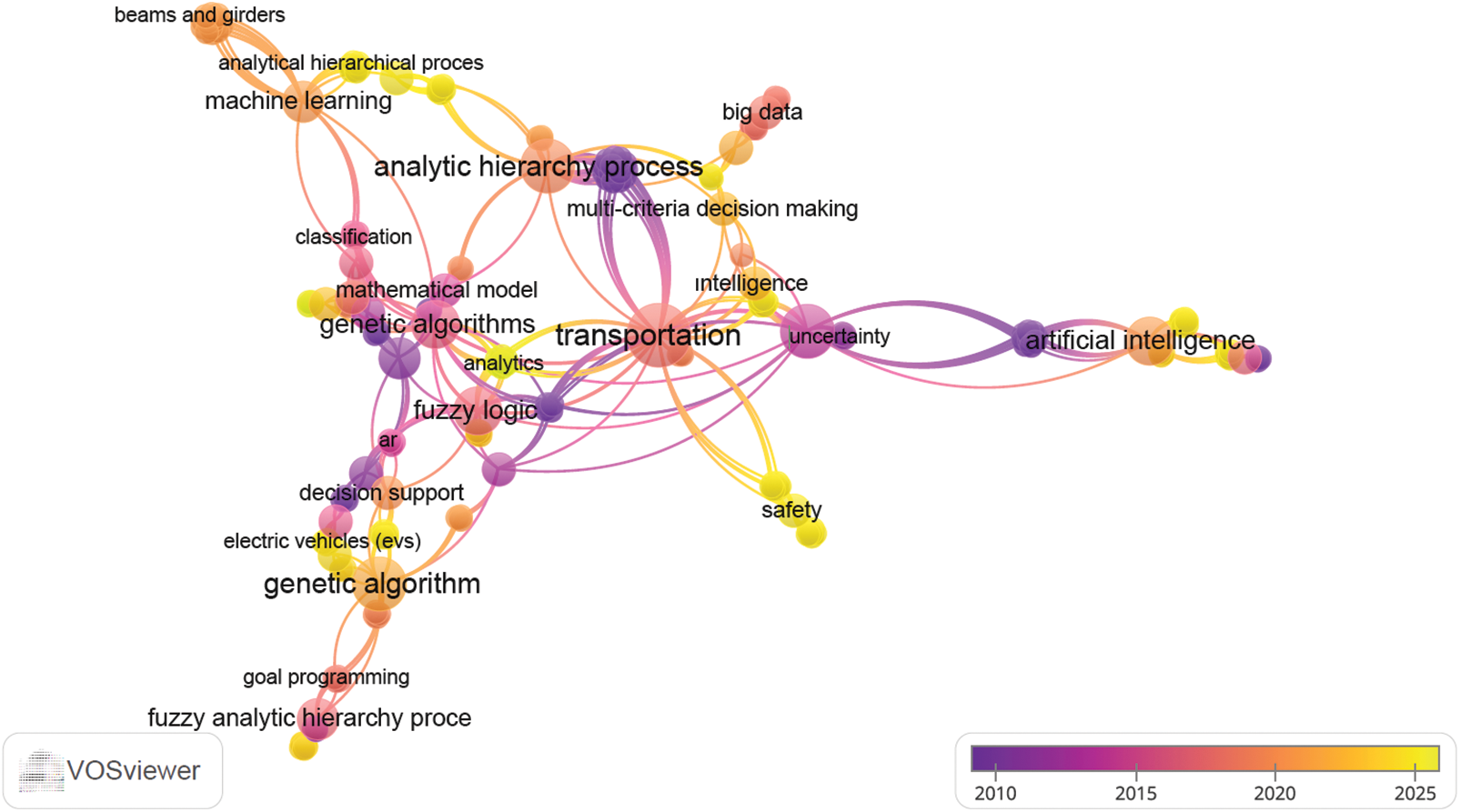
Figure 3: Keyword co-occurrence network
3.1 Temporal Distribution of Studies
Fig. 4 presents the temporal distribution of research studies, highlighting notable trends and patterns in the application of AI-enhanced fuzzy logic within the field of transportation. The literature review reveals a growing interest and evolving focus in this domain over the years.
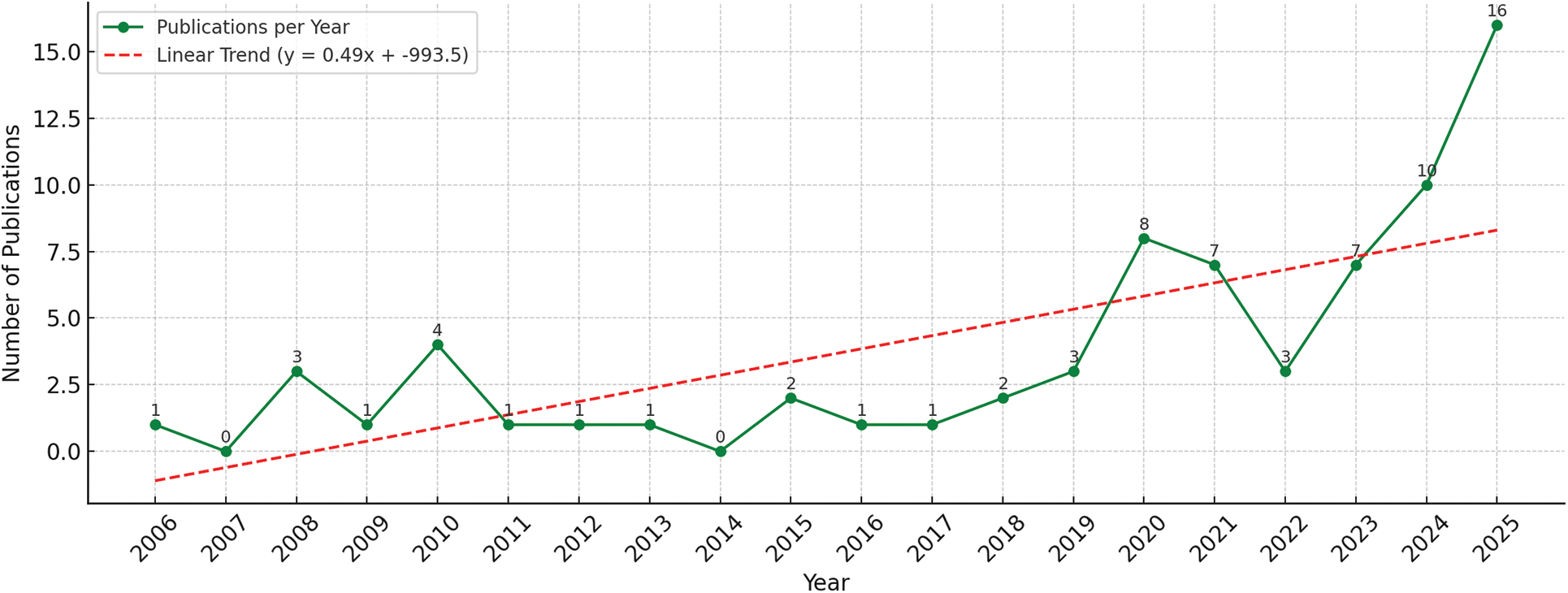
Figure 4: Publication trend for AI-enhanced fuzzy MCDM in transportation
Early applications of fuzzy MCDM in transportation date back to around 2006–2010, with only 1–4 papers per year and a mix of case-specific studies. We see a slight uptick around 2010, possibly due to early interest in fuzzy AHP for transport project selection. The period 2011–2015 remained relatively quiet (often 0–2 publications annually), indicating that combining AI with fuzzy MCDM was still a nascent concept in transport research at that time. A moderate rise is evident in 2016–2018 (3–5 publications per year). This corresponds with the growing adoption of AI techniques in transport and the wider use of fuzzy MCDM in sustainability and smart city studies. Notably, from 2019 onward, the growth accelerates: 2019 saw about eight papers, and 2020–2021 continued with around 7–10 studies each. The most significant surge occurs in 2022–2024, where the annual count jumps into double digits. 2023 included roughly 10 publications, and 2024 peaked at 15+ publications. This sharp increase reflects a convergence of trends: the maturation of AI (especially data analytics and ML in transport) and the continued relevance of fuzzy decision-making for complex, uncertain planning problems. By 2024, the topic has gained traction, with many new hybrid methodologies proposed in a single year. The slight drop in 2025 (only a couple of studies as of early 2025) is likely because the year had not fully progressed, or publications were still in press at the time of review.
A time-series regression was conducted to statistically validate the observed increase in annual publication counts. The linear regression model (y = 0.49x − 993.54; R2 = 0.51) confirms a significant upward trend over the 2006–2025 period. As shown in Fig. 2, this suggests that, on average, the number of publications in this domain grows by approximately 0.5 each year. The R2 value indicates that about half of the variation in publication counts can be attributed to this temporal trend.
Overall, the publication trend demonstrates an exponential growth in interest over the last five years. This suggests that AI-enhanced fuzzy MCDM is an emerging research frontier, aligning with the rise of smart transportation systems, big data, and the need for decision tools that handle uncertainty. We can expect this trend to continue or even further accelerate, as more researchers recognize the value of combining machine intelligence with human-like fuzzy reasoning for tackling multi-criteria transportation decisions. The timeline also implies earlier works focused on simpler fuzzy MCDM without AI, whereas recent works increasingly integrate AI for improved decision support capabilities.
3.2 Geographic Distribution of Studies
This subsection explores the geographical spread of AI-enhanced fuzzy MCDM studies within the transportation domain, highlighting regional research intensity and disparities across countries. The global distribution of reviewed studies is visualized in Fig. 5 through a choropleth world map, where the names and study count of countries with three or more publications are explicitly labeled.
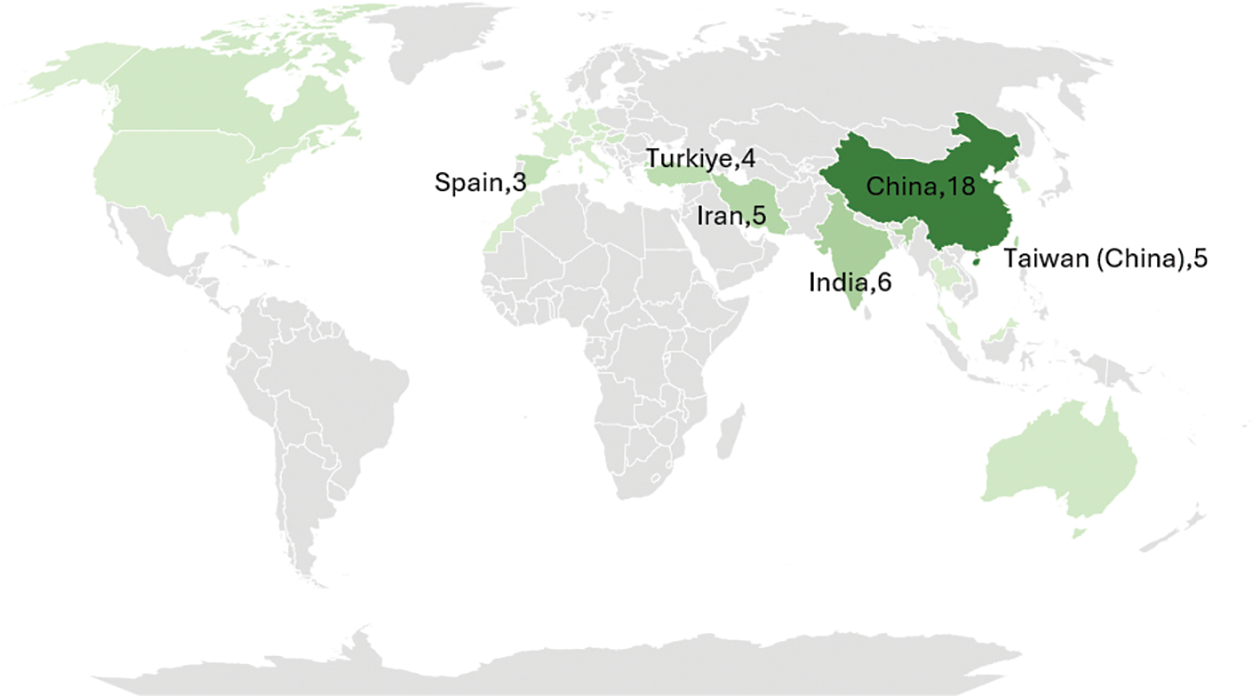
Figure 5: Geographic distribution of reviewed studies
The choropleth world map illustrates the geographical distribution of reviewed studies focusing on AI-enhanced fuzzy MCDM applications in transportation. A significant concentration was observed in Asia; China stands out as the most prolific contributor with 18 studies, while Taiwan (China) from East Asia has five studies. India also plays a prominent role with six studies, highlighting its growing research output in ITS and sustainable mobility. These countries’ dominance is likely driven by their rapid urbanization, growing transportation infrastructure, and national-level interest in digital transformation and smart city development. Turkiye (4) and Iran (5) represent significant contributions from the Middle East, indicating regional engagement with fuzzy decision-making approaches in infrastructure and logistics planning. The map reveals a regional imbalance, as most studies are clustered in a few countries, while large portions of Africa, South/North America, and parts of Europe remain underrepresented. It should be noted that the observed low representation of studies from Africa and South America could partially result from database limitations (SCOPUS) and the English-language inclusion criterion, potentially underrepresenting research published in other languages or local journals. This suggests an opportunity for broader international collaboration and knowledge dissemination, particularly in developing and emerging economies where transport optimization and sustainability could yield substantial societal benefits.
3.3 AI Techniques Used in Transportation Studies
This subsection presents the types and frequencies of AI techniques utilized in transportation studies employing fuzzy MCDM approaches. The distribution of AI techniques, with a particular emphasis on ML and DL, is depicted in Fig. 6.

Figure 6: AI techniques used in the reviewed studies
ML approaches (including classical algorithms like SVM, Random Forests (RF), etc.) are the most prevalent AI techniques integrated with fuzzy MCDM, appearing in 17 instances. DL methods (primarily Artificial Neural Networks (ANN)) were noted 10 times. It is important to distinguish between ML, encompassing classical predictive algorithms (e.g., support vector machines, random forests), and DL, referring specifically to neural network-based methods characterized by multiple processing layers and advanced representation learning capabilities. Evolutionary algorithms are also common: Genetic Algorithms (GA) were used 6 times, often to optimize or calibrate decision models, and other heuristic algorithms (e.g., Particle Swarm Optimization—PSO) collectively appeared 5 times. Notably, reinforcement learning was virtually absent, indicating a gap in current research. These AI techniques are typically leveraged to handle large data or complex optimization sub-tasks—for example, ANN models are used for predicting traffic outcomes or demand, feeding results into a fuzzy decision framework, while GA/PSO optimize network designs or parameter weights. In summary, data-driven AI (ML/DL) dominates usage, whereas search heuristics (GA/others) play a secondary but important role in enhancing fuzzy decision models.
3.4 MCDM Methodologies in Reviewed Studies
This subsection examines the frequency and functional roles of fuzzy MCDM methods employed in transportation studies. Fig. 7 shows the frequency of methodologies.
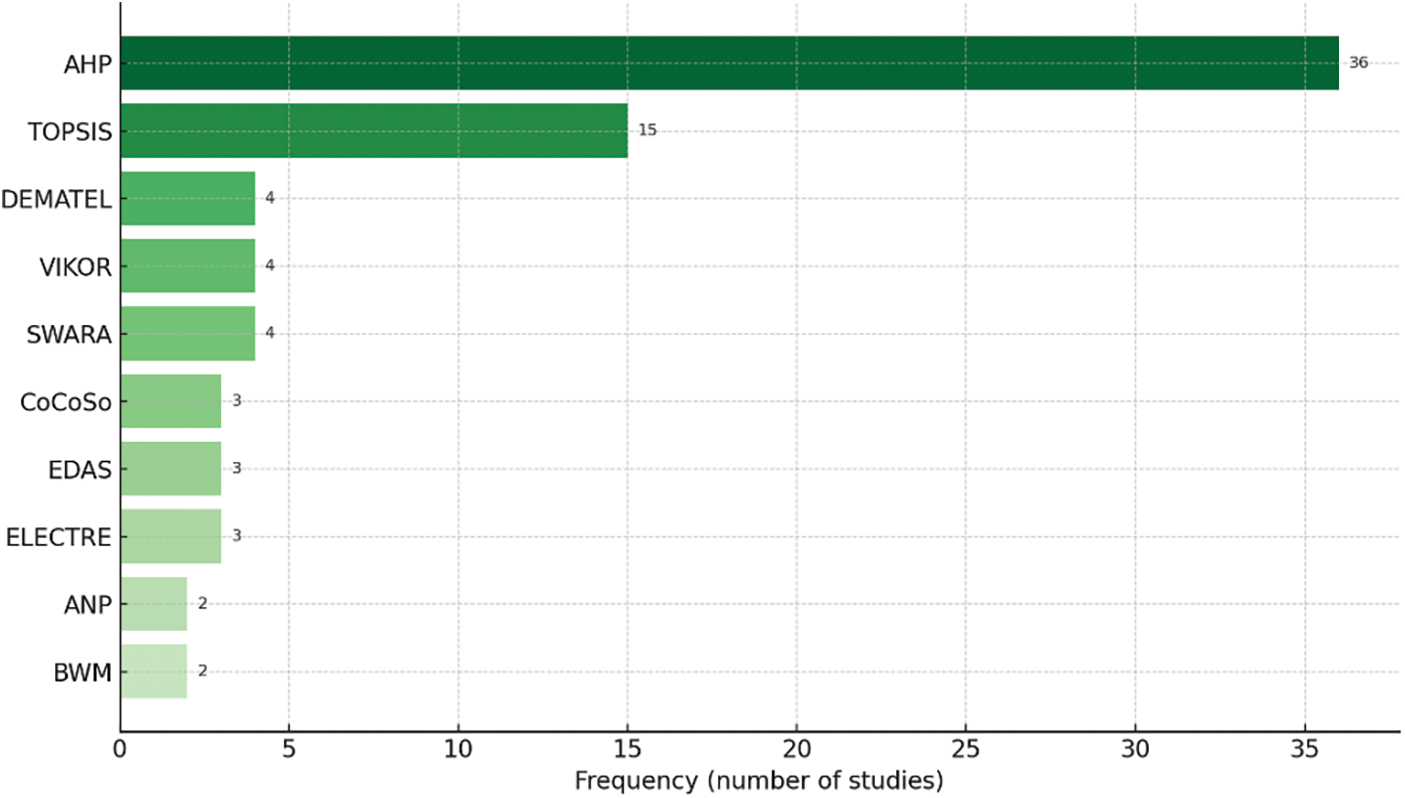
Figure 7: Frequency of fuzzy MCDM methods applied in reviewed studies
The overwhelming majority of studies employ Fuzzy AHP, reflecting its popularity for structuring criteria and deriving weights under uncertainty. Fuzzy AHP appears in 36 reviewed works, often as the weighting step in a hybrid approach [88]. Fuzzy TOPSIS is the second most common (15 studies), frequently used to rank transport alternatives (such as route options or project priorities) based on their distance to an ideal solution [88]. A few studies use Fuzzy VIKOR (4 instances) to identify compromise solutions balancing group utility and individual regret [89], and Fuzzy DEMATEL (4 cases) to analyze cause–and–effect relationships among criteria in a complex transport system [89]. Other methods like Fuzzy SWARA (4) and Fuzzy BWM (2) serve as alternative criteria-weighting techniques, and newer methods (CoCoSo, EDAS, etc., each in 3 cases) have begun to appear. The dominance of Fuzzy AHP and TOPSIS indicates that hierarchical weighting + alternative ranking is a common framework. Many studies use Fuzzy AHP to determine criteria weights, followed by Fuzzy TOPSIS (or VIKOR) for final ranking. Less commonly, fuzzy network or causal methods (ANP, DEMATEL) are used to capture interdependencies or feedback among factors (e.g., evaluating interrelated risks or policy criteria). The field is heavily oriented toward fuzzy extensions of classical MCDM (AHP, TOPSIS, VIKOR), with emerging interest in more complex fuzzy methods.
The methodological landscape is summarized in Table 2, which outlines each fuzzy MCDM method’s typical purpose in transportation contexts. The frequent pairing of Fuzzy AHP for weighting and Fuzzy TOPSIS or VIKOR for ranking suggests a preferred hybrid structure for modeling transportation decision problems.

As shown in Fig. 5 and Table 2, AHP and TOPSIS form the backbone of many studies, reflecting their ease of use and interpretability in transport decision contexts. Although Fuzzy AHP and Fuzzy TOPSIS are widely utilized, each method has distinct advantages and limitations. Fuzzy AHP is highly effective in structuring decision problems hierarchically and facilitating pairwise comparisons, making it suitable for capturing expert judgment under uncertainty [90]. However, it may become cumbersome with numerous criteria due to the quadratic growth of comparisons [91]. On the other hand, Fuzzy TOPSIS efficiently ranks alternatives based on their proximity to ideal solutions, providing intuitive results easily interpretable by decision-makers [92]. Nonetheless, TOPSIS assumes equal importance of criteria unless explicitly weighted, making it dependent on prior weight determination (often using AHP). The hybridization of these two methods, combining hierarchical criteria weighting from AHP with alternative ranking by TOPSIS, leverages the strengths of both approaches, offering robust and comprehensible results in transportation planning scenarios.
VIKOR, though less frequent, is valued for reaching compromise decisions (practical in public policy settings), and fuzzy DEMATEL/ANP addresses criteria interdependency (important in complex system analyses). Simpler fuzzy weighting techniques like BWM and SWARA are emerging as alternatives to AHP for criteria weight determination.
3.5 Co-Occurrence of AI Techniques and Fuzzy MCDM Methodologies
The integration patterns between specific AI techniques and fuzzy MCDM methods are explored to identify prevalent hybrid approaches in transportation studies. The distribution of these combinations is visualized in Fig. 8, where the number of studies using each pairing is indicated within the heatmap cells.
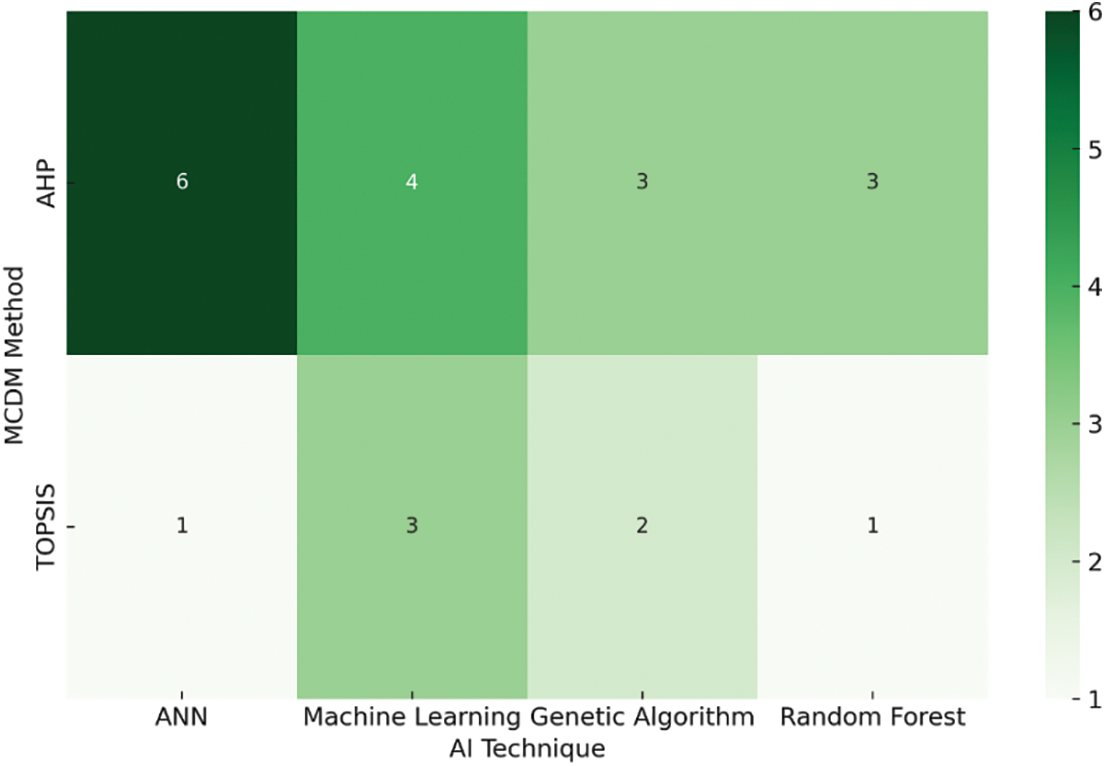
Figure 8: Heatmap of co-occurrence between specific AI techniques and fuzzy MCDM methods
We observe clear patterns of methodological pairing in the literature. Fuzzy AHP, in particular, co-occurs frequently with several AI techniques, notably neural network models. ANNs + Fuzzy AHP appeared in 6 studies [14,25,49,27,56,54], making it the single most common pairing: these studies typically use an ANN to predict or simulate something (e.g., travel demand, emission levels) and then apply fuzzy AHP to weight criteria or scenarios based on those predictions. Fuzzy AHP was also combined with generic ML approaches in 4 studies (where “ML” refers broadly to applying learned models or data mining before decision-making). Additionally, 3 studies [77,67,84] paired GA with Fuzzy AHP—usually to optimize the AHP weight calculations or to search for the best alternative by evolving solutions—and similarly 3 cases combined RF or other ML classifiers with Fuzzy AHP (for example, using a RF to cluster or classify inputs that feed into an AHP-based decision). By contrast, Fuzzy TOPSIS was less frequently augmented by AI. A couple of studies each combined Fuzzy TOPSIS with ML (3) [87,43,72] or GA (2) [84,85]. One example is using a GA to fine-tune the performance ratings of alternatives before applying Fuzzy TOPSIS for final ranking [84]. Only 1–2 instances involved ANN or other specific algorithms with Fuzzy TOPSIS. Fuzzy VIKOR and other methods show very few co-occurrences with AI (only one case of Fuzzy VIKOR paired with an ML approach was noted). This suggests that the “AI + fuzzy MCDM” synergy is most pronounced for the AHP-based frameworks. Likely, this is because AHP is often used for criteria weighting, such as a step that can benefit from AI inputs (like clustering of criteria or learning criteria importance from data). Meanwhile, TOPSIS and VIKOR are terminal ranking methods where AI’s role might be more limited (unless used to preprocess alternative performance scores). In practical terms, the most common integrated workflows are: ANN + Fuzzy AHP/TOPSIS (for hybrid prediction–evaluation systems) and GA/optimization + Fuzzy AHP/TOPSIS (for searching optimal solutions in multi-criteria space). The dominance of ANN with Fuzzy AHP points to the popularity of combining predictive analytics with expert-driven decision weighting. The relative rarity of reinforcement learning or advanced DL models (beyond ANN) in combination with fuzzy MCDM indicates potential for exploration. For example, using deep reinforcement learning to generate alternatives or using NLP (like BERT) to derive criteria from text and then fuzzy MCDM to evaluate them, which only one identified study did for analyzing customer feedback in airlines.
3.6 Transportation Application Areas
The reviewed studies address a variety of transportation domains. As illustrated in Fig. 9, the most frequently explored areas include freight/logistics and road traffic systems.
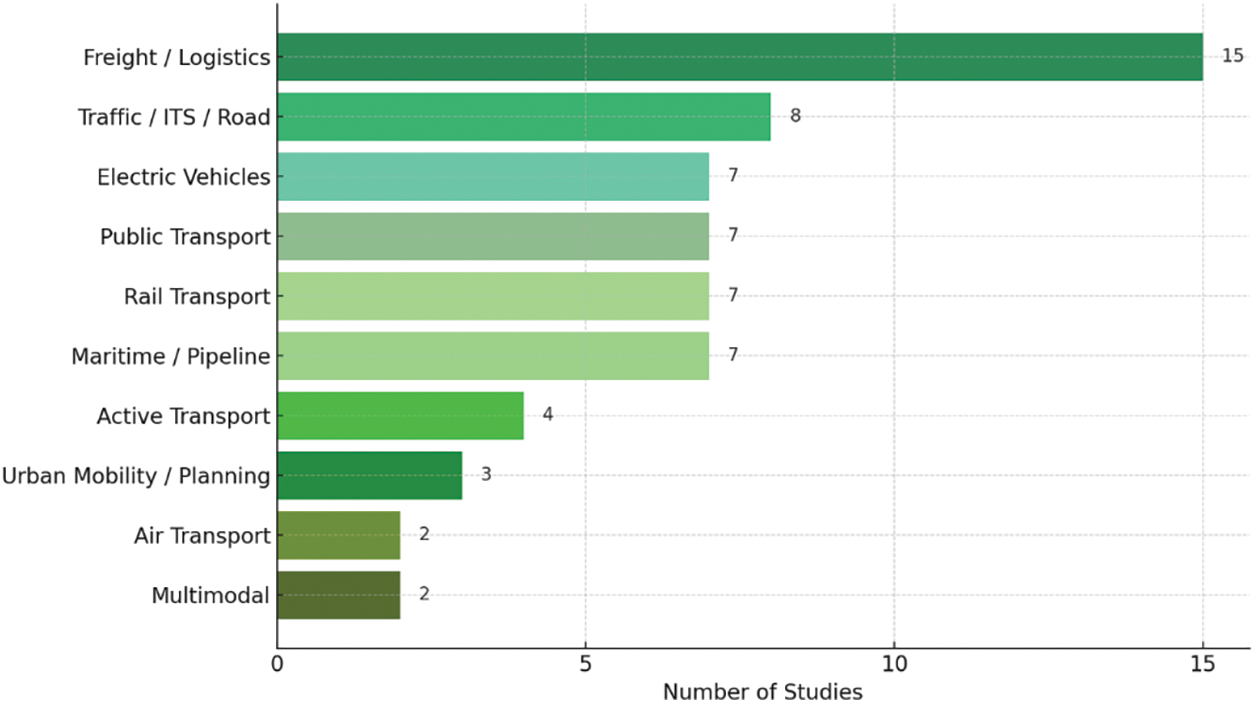
Figure 9: Distribution of transportation application areas addressed by the reviewed studies
The reviewed literature spans a broad range of transportation planning domains. The most frequent application is freight and logistics (15 studies), including problems like vehicle routing, distribution network design, and supply chain facility location. This indicates a strong interest in using AI-fuzzy MCDM to optimize logistics operations (e.g., selecting optimal routes or warehouse sites under multiple criteria such as cost, time, and risk). A comparative analysis revealed that fuzzy TOPSIS frequently outperformed other methods in scenarios prioritizing ease of interpretability and computational efficiency, whereas fuzzy AHP was preferred for its robust handling of expert judgment and criteria weighting. About 8 studies focus on road traffic management (urban traffic congestion, signal control, or highway safety), showing the relevance of fuzzy MCDM for operational decisions in ITS and safety evaluations.
Several works (≈7 each) target public transport planning (e.g., evaluating transit service quality or transit route selection), EV infrastructure and policy (such as siting EV charging stations or assessing EV adoption initiatives), rail transport (including rail network planning and rail safety assessment), and even maritime/pipeline transportation (for example, port logistics decisions or pipeline routing problems). This diversity illustrates that AI-enhanced fuzzy decision models are being applied across virtually all transport modes—from transit systems to emerging modes like EVs. A smaller subset of studies addresses active transport and micromobility (bike networks, e-scooter programs) and air transportation (airport efficiency, airline service evaluation), each with a few instances. Additionally, a few papers deal with multimodal transport or high-level urban mobility planning, employing fuzzy MCDM to prioritize policies for sustainable mobility and accessibility.
In summary, logistics and freight decisions have seen the greatest uptake of these hybrid methods. Meanwhile, strategic planning areas (public transit, EV infrastructure, etc.) are also well-represented, demonstrating fuzzy MCDM’s flexibility to handle infrastructure investment decisions and operational management in transportation. The relatively few studies in air transport and micromobility suggest that these are niche applications or emerging opportunities for future research.
3.7 Decision Criteria Used in Transportation Studies
Decision criteria play a central role in shaping the quality and robustness of MCDM processes. In AI-enhanced fuzzy MCDM applications in transportation, selecting and weighting these criteria help address uncertainty and complexity systematically. Commonly used criteria reflect both operational concerns and broader strategic considerations. The most frequently used criteria across the reviewed studies provide insights into what factors are prioritized in transportation decision-making under uncertainty. Fig. 8 illustrates the most commonly used decision criteria, focusing on those that appeared in at least 10 studies. The high frequency of these criteria underscores their critical importance in shaping transportation planning and optimization efforts in the reviewed literature.
The chart given in Fig. 10 displays the most frequently used evaluation criteria in transport-related studies. Time and cost stand out as the most dominant criteria, reflecting the critical importance of minimizing travel time and operational expenses in transportation planning and decision-making. These are followed closely by accessibility and infrastructure, which indicate the significance of user-centered design and the availability of transportation facilities. Further, safety and environment are frequently emphasized, underlining the growing global focus on secure and sustainable transportation systems. The appearance of efficiency also reflects the field’s aim to optimize both resource usage and performance outcomes. This distribution of criteria suggests a balanced concern in the literature between operational performance, user satisfaction, and environmental responsibility.
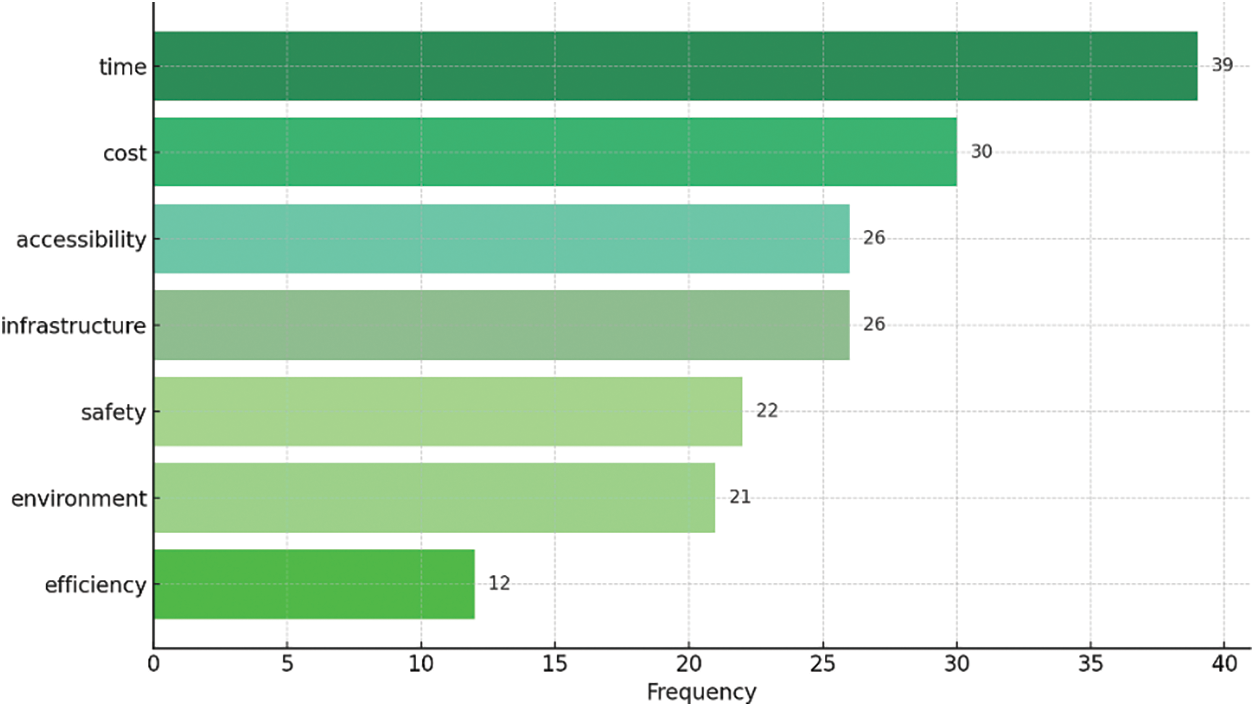
Figure 10: Top recurring decision criteria in reviewed studies
4 Key Research Themes and Conceptual Trends
This section explores the major conceptual and thematic directions in the reviewed body of literature, providing a high-level synthesis of the recurring research topics, methodological orientations, and emerging areas of interest. To illustrate these thematic patterns, word clouds were generated from three sources within the studies: abstracts, author-provided keywords, and key findings. Fig. 11 presents two-word clouds side by side: one generated from the abstracts and the other from the author-provided keywords of the reviewed studies. Common filler words such as “the,” “used,” “and,” etc., were excluded to improve clarity and relevance.
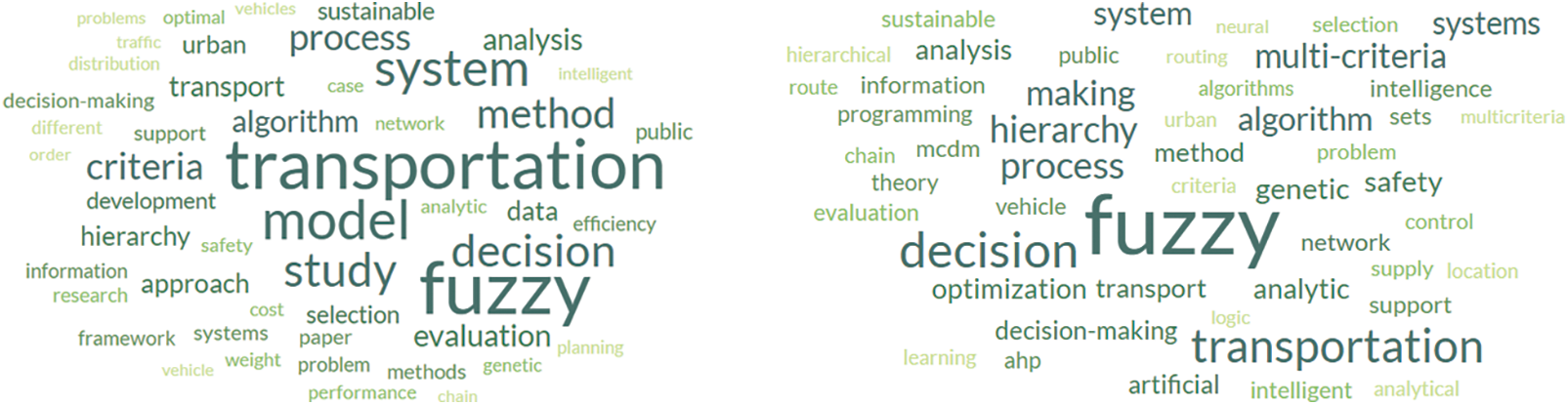
Figure 11: Word clouds for the abstract and keywords
As visualized in Fig. 11, the left panel (abstracts) highlights frequently discussed concepts such as transportation, fuzzy, model, system, and criteria, indicating a strong emphasis on modeling and evaluation processes in fuzzy-based transport research. Similarly, the right panel (keywords) reinforces the prevalence of terms like fuzzy, decision, transportation, and multi-criteria, confirming the widespread integration of fuzzy decision-making frameworks in transportation studies.
Fig. 12 visualizes the most frequently occurring terms in the key findings sections of the studies. The word cloud generated from the reviewed studies highlights the core focus areas in the intersection of fuzzy logic, AI, and transportation research.
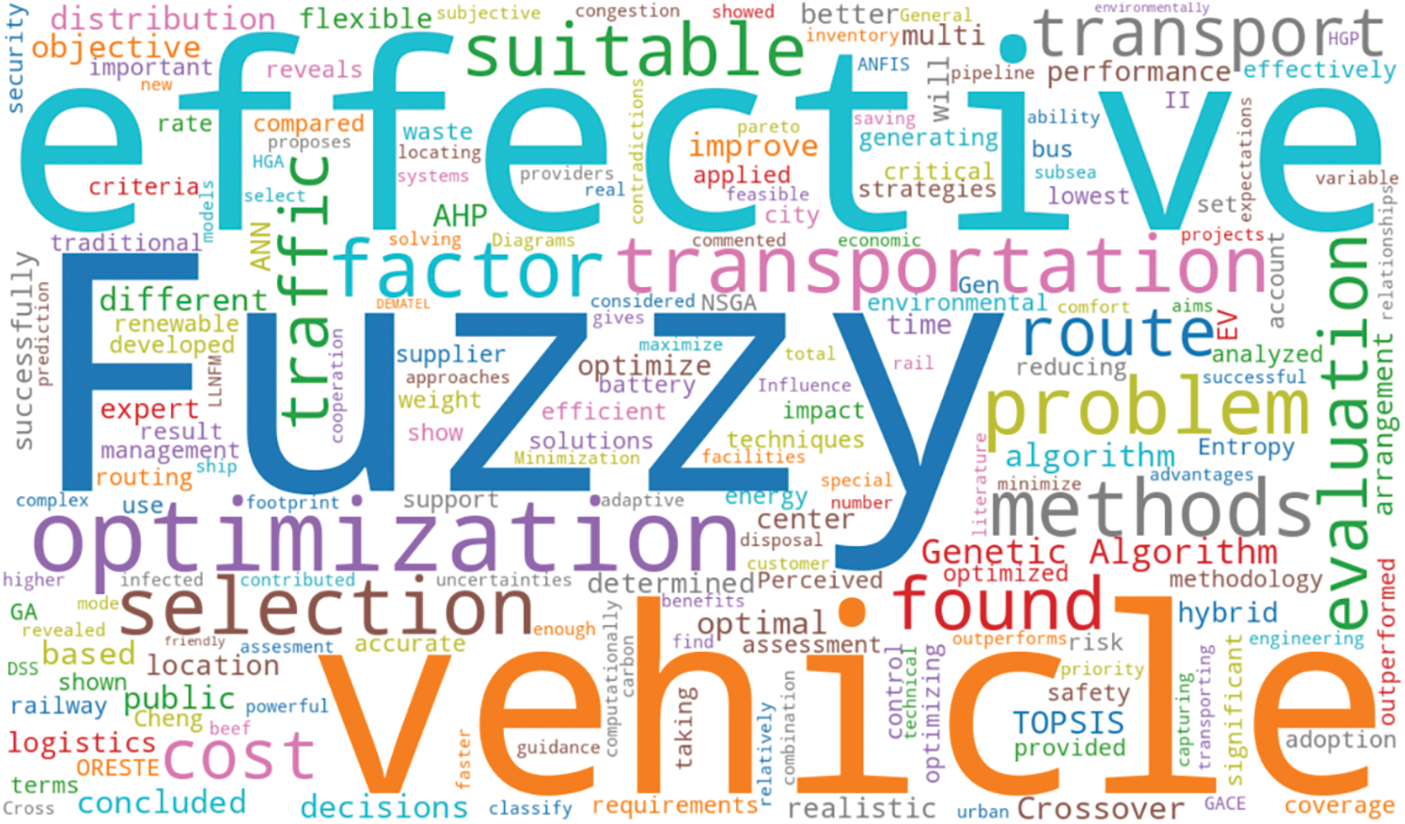
Figure 12: Word cloud for key findings
Key terms such as “fuzzy,” “optimization,” “vehicle,” and “evaluation” demonstrate the central role of intelligent and flexible decision-making frameworks in solving complex transportation challenges. These studies commonly apply fuzzy-based approaches to enhance optimization processes, particularly in vehicle routing, evaluation of alternatives, and performance assessments under uncertainty. Additionally, frequently occurring words like “traffic,” “transportation,” “selection,” and “effective” suggest a practical orientation toward improving real-world systems, especially in urban mobility and public transportation planning. The prominence of “environmental,” “cost,” “public,” “logistics,” and “sustainability” further indicates a multidimensional research agenda that balances operational efficiency with ecological and social concerns. Overall, the word cloud underscores a comprehensive effort in the literature to develop robust, sustainable, and intelligent solutions for transportation systems by integrating fuzzy MCDM and AI techniques.
In addition to frequency-based analysis, a temporal examination of key terms revealed significant thematic shifts over the review period. Earlier research (2006–2015) predominantly focused on traditional optimization and route selection methodologies. However, recent years have seen the emergence of advanced themes such as large language models (e.g., BERT), connected and autonomous vehicles (CAVs), and sentiment analysis, reflecting growing interest in incorporating sophisticated AI capabilities into transportation systems. This indicates a transition toward real-time adaptive analytics and predictive decision-making models, aligning with broader technological advancements in AI.
Today, due to the dense population in cities, it is critical that transportation systems are efficient and user-oriented. In addition, due to the increasing effects of climate change and environmental sensitivity, it is necessary to produce sustainable solutions to transportation problems. In this context, the integration of AI, fuzzy logic, and MCDM methods stands out as a powerful tool for solving complex, uncertain, and multidimensional problems encountered in transportation planning.
The review highlighted critical methodological gaps and geographic disparities. Future research should prioritize targeted research questions, such as: “How can real-time fuzzy reinforcement learning systems optimize dynamic traffic management in high-density urban areas?” or “What hybrid methodologies combining deep learning and fuzzy logic best address electric vehicle infrastructure planning under uncertainty?” Additionally, methodological recommendations include developing standardized validation protocols for fuzzy AI hybrid models, increasing transparency in algorithmic decision-making processes, and fostering international research collaborations, particularly involving underrepresented regions.
The review provides a comprehensive synthesis of how AI-enhanced fuzzy MCDM models are applied to transportation challenges. Beyond confirming the dominance of fuzzy AHP and TOPSIS, this study uncovers methodological gaps, such as limited exploration of reinforcement learning and underrepresentation in certain geographic regions. The results emphasize the potential of hybrid AI-fuzzy approaches for complex, real-world decision-making and highlight actionable directions for future research, including the adoption of more diverse AI techniques and broader international collaboration.
As a result, this study reveals how AI and fuzzy logic-based MCDM methods are applied in transportation planning and provides a guiding resource for researchers who want to work in this field. Furthermore, developing recommendations in light of current trends and methodological preferences offers new research pathways that will contribute to making transportation systems more intelligent, flexible, and sustainable.
This review identified critical insights and current methodological gaps. However, limitations exist, notably potential biases from language and database restrictions, and variability in study methodological rigor. Future research should address these gaps explicitly, focusing on enhancing real-time adaptive analytics through the hybridization of fuzzy MCDM with reinforcement learning and big data techniques. Specific areas such as improved model transparency, cross-region collaboration, and standardized evaluation frameworks represent actionable priorities to advance intelligent transportation decision-making.
Recent studies, such as the application of deep reinforcement learning for adaptive traffic signal control [93–95] and big data analytics in predicting transportation demand patterns [96–98] demonstrate practical advancements in this direction. Integrating these sophisticated AI techniques with fuzzy MCDM could significantly enhance the responsiveness and adaptability of transport planning systems, offering robust solutions to complex real-time transportation challenges.
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Nezir Aydin, Ertugrul Ayyildiz; data collection: Melike Cari, Betul Kara; analysis and interpretation of results: Nezir Aydin, Ertugrul Ayyildiz, Melike Cari; draft manuscript preparation: Melike Cari, Betul Kara, Ertugrul Ayyildiz. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available within the article. The authors confirm that the data supporting the findings of this study are available within the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
List of Abbreviations
| Abbreviations | Definition |
| ABSA | Aspect-based Sentiment Analysis |
| AHP | Analytical Hierarchy Process |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| ANFIS | Adaptive Neural Fuzzy Inference System |
| ANFSMC | Adaptive Neural-Fuzzy Sliding Mode Control |
| ANP | Analytic Network Process |
| BERT | Bi-directional Encoder Representations from Transformers |
| BWM | Best Worst Method |
| CART | Classification & Regression Tree |
| CE | Cross Entropy |
| CoCoSo | Combined Compromise Solution |
| CODAS | Combinative Distance-based Assessment |
| CRITIC | Criteria Importance Through Intercriteria Correlation |
| DSS | Decision Support System |
| DL | Deep Learning |
| DEMATEL | The Decision-Making Trial and Evaluation Laboratory |
| EDAS | Evaluation based on Distance from Average Solution |
| ELECTRE | Elimination and Choice Translating Reality English |
| EWM | Entropy weight method |
| EV | Electric Vehicle |
| FANN | Feedforward Artificial Neural Networks |
| GA | Genetic Algorithm |
| GeoGAM | Geospatial Generalized Additive Model |
| GWO | Gray Wolf Optimizer |
| GWR | Geographically Weighted Regression |
| ICA | Imperialist Competitive Algorithm |
| ITS | Intelligent Transportation Systems |
| LTE-R | Long-term Evolution for Railway |
| MCA | Multicriteria Analysis Algorithm |
| MCDM | Multi-Criteria Decision Making |
| MHNSGA | Multi-Strategy Hybrid Nondominated Sorting Genetic Algorithm |
| ML | Machine Learning |
| MODM | Multi-Objective Decision Making |
| NLP | Natural Language Processing |
| ORESTE | Organisation, Rangement et Synthèse de Données Relationnelles |
| PID | Proportional–Integral–Derivative |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| PSO | Particle Swarm Optimization |
| PWD | Person with Disabilities |
| RBF-NNSMC | RBF Neural Network Sliding Mode Control |
| RF | Random Forest |
| RT | Regression Tree |
| SAW | Simple Additive Weighting |
| SOM | Self-Organizing Maps |
| SVM | Support Vector Machine |
| SWARA | Step-Wise Weight Assessment Ratio Analysis |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| UAV | Unmanned Aerial Vehicle |
| VIKOR | VlseKriterijumska Optimizacija I Kompromisno Resenje |
| WASPAS | Weighted Aggregated Sum Product Assessment |
| WP | Weighting Product |
References
1. Zhang X, Lu Y, Wang J, Qi Y. Enhancing highway transportation safety resilience during emergencies: a network-based analysis and assessment. PLoS One. 2024;19(7):e0307233. doi:10.1371/journal.pone.0307233. [Google Scholar] [PubMed] [CrossRef]
2. Liu H, Lu C, Hao X, Zhao H. Optimal performance selection of sustainable mobility service projects based on IFSS-Prospect theory-VIKOR: a case study of electric vehicle sharing program. PLoS One. 2024;19(11):e0309512. doi:10.1371/journal.pone.0309512. [Google Scholar] [PubMed] [CrossRef]
3. Al-Quran A, Jamil N, Tehrim ST, Riaz M. Cubic bipolar fuzzy VIKOR and ELECTRE-II algorithms for efficient freight transportation in Industry 4.0. AIMS Math. 2023;8(10):24484–514. doi:10.3934/math.20231249. [Google Scholar] [CrossRef]
4. Wey WM, Huang JY. Urban sustainable transportation planning strategies for livable City’s quality of life. Habitat Int. 2018;82(6):9–27. doi:10.1016/j.habitatint.2018.10.002. [Google Scholar] [CrossRef]
5. Batty M, Marshall S. Thinking organic, acting civic: the paradox of planning for Cities in Evolution. Landsc Urban Plan. 2017;166:4–14. doi:10.1016/j.landurbplan.2016.06.002. [Google Scholar] [CrossRef]
6. Erdoğan M, Kaya İ. A systematic approach to evaluate risks and failures of public transport systems with a real case study for bus rapid system in Istanbul. Sustain Cities Soc. 2020;53(1):101951. doi:10.1016/j.scs.2019.101951. [Google Scholar] [CrossRef]
7. He L, Liu S, Shen ZM. Smart urban transport and logistics: a business analytics perspective. Prod Oper Manag. 2022;31(10):3771–87. doi:10.1111/poms.13775. [Google Scholar] [CrossRef]
8. Ben Rabia MA, Bellabdaoui A. Collaborative intuitionistic fuzzy-AHP to evaluate simulation-based analytics for freight transport. Expert Syst Appl. 2023;225(1):120116. doi:10.1016/j.eswa.2023.120116. [Google Scholar] [CrossRef]
9. Chen CH, Tsao YC, Chen CH, Lin TH, Vu TL. Development of a comprehensive safety evaluation mechanism for the highway bus industry. Transp Res Rec J Transp Res Board. 2025;2679(4):67–80. doi:10.1177/03611981241287538. [Google Scholar] [CrossRef]
10. Afandizadeh S, Abdolahi S, Mirzahossein H. Deep learning algorithms for traffic forecasting: a comprehensive review and comparison with classical ones. J Adv Transp. 2024;2024(1):9981657. doi:10.1155/2024/9981657. [Google Scholar] [CrossRef]
11. Kaczorek M, Jacyna M. Fuzzy logic as a decision-making support tool in planning transport development. AoT. 2022;1(61):51–70. doi:10.5604/01.3001.0015.8154. [Google Scholar] [CrossRef]
12. Saxena RR. Artificial intelligence in traffic systems. arXiv:2412.12046. 2024. [Google Scholar]
13. Saaty RW. The analytic hierarchy process—what it is and how it is used. Math Model. 1987;9(3–5):161–76. doi:10.1016/0270-0255(87)90473-8. [Google Scholar] [CrossRef]
14. Qu L, Chen Y. A hybrid MCDM method for route selection of multimodal transportation network. In: Advances in neural networks-ISNN 2008. Berlin/Heidelberg, Germany: Springer; 2008. p. 374–83. doi:10.1007/978-3-540-87732-5_42. [Google Scholar] [CrossRef]
15. Zadeh LA. Fuzzy sets. Inf Control. 1965;8(3):338–53. doi:10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
16. Chen SJ, Hwang CL. Fuzzy multiple attribute decision making. 1992 [cited 2025 Apr 11]. Available from: http://link.springer.com/10.1007/978-3-642-46768-4. [Google Scholar]
17. Bottero M, Ferretti V, Pomarico S. Assessing the sustainability of alternative transport infrastructures. Int J Anal Hierarchy Process. 2012;4(1). doi:10.13033/ijahp.v4i1.101. [Google Scholar] [CrossRef]
18. Wichapa N, Khokhajaikiat P. Using the hybrid fuzzy goal programming model and hybrid genetic algorithm to solve a multi-objective location routing problem for infectious waste disposal. J Ind Eng Manag. 2017;10(5):853. doi:10.3926/jiem.2353. [Google Scholar] [CrossRef]
19. Galińska B. Intelligent decision making in transport. evaluation of transportation modes (types of vehicles) based on multiple criteria methodology. In: Integration as solution for advanced smart urban transport systems. Cham, Switzerland: Springer International Publishing; 2018. p. 161–72. doi:10.1007/978-3-319-99477-2_15. [Google Scholar] [CrossRef]
20. Moher D, Liberati A, Tetzlaff J, Altman DG. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Int J Surg. 2010;8(5):336–41. doi:10.1016/j.ijsu.2010.02.007. [Google Scholar] [PubMed] [CrossRef]
21. Santi RP, Putra H. A systematic literature review of business intelligence technology, contribution and application for higher education. In: 2018 International Conference on Information Technology Systems and Innovation (ICITSI); 2018 Oct 22–26; Bandung, Indonesia: IEEE. p. 404–9. doi:10.1109/ICITSI.2018.8696019. [Google Scholar] [CrossRef]
22. Satria D, Sensuse DI, Noprisson H. A systematic literature review of the improved agile software development. In: International Conference on Information Technology Systems and Innovation (ICITSI); 2017 Oct 23–24; Bandung, Indonesia: IEEE. p. 94–9. doi:10.1109/ICITSI.2017.8267925. [Google Scholar] [CrossRef]
23. Lin JJ. Multi-objective decision making for vehicle routing problem with fuzzy due time. In: 2006 IEEE International Conference on Systems, Man and Cybernetics; 2006 Oct 8–11; Taipei, Taiwan: IEEE. p. 2903–8. doi:10.1109/ICSMC.2006.385315. [Google Scholar] [CrossRef]
24. Iglesias A, Del Castillo MD, Santos M, Serrano JI, Oliva I. A comparison between possibility and probability in multiple criteria decision making. In: Computational intelligence in decision and control. Madrid, Spain: WORLD SCIENTIFIC; 2008. p. 307–12. doi:10.1142/9789812799470_0050. [Google Scholar] [CrossRef]
25. Qu L, Chen Y, Mu X. A transport mode selection method for multimodal transportation based on an adaptive ANN system. In: 2008 Fourth International Conference on Natural Computation; 2008 Oct 18–20; Jinan, China: IEEE. p. 436–40. doi:10.1109/ICNC.2008.165. [Google Scholar] [CrossRef]
26. Arslan T. A hybrid model of fuzzy and AHP for handling public assessments on transportation projects. Transportation. 2009;36(1):97–112. doi:10.1007/s11116-008-9181-9. [Google Scholar] [CrossRef]
27. Kayikci Y. A conceptual model for intermodal freight logistics centre location decisions. Procedia Soc Behav Sci. 2010;2(3):6297–311. doi:10.1016/j.sbspro.2010.04.039. [Google Scholar] [CrossRef]
28. Chakraborty M, Ray A. Parametric approach and genetic algorithm for multi objective linear programming with imprecise parameters. OPSEARCH. 2010;47(1):73–92. doi:10.1007/s12597-010-0005-2. [Google Scholar] [CrossRef]
29. Bi Y, Li W. Research on distribution center location model of maximum coverage based on collaborative inventory of supply chain. In: ICLEM 2010. Chengdu, China: American Society of Civil Engineers; 2010. p. 2600–5. doi:10.1061/41139(387)363. [Google Scholar] [CrossRef]
30. Meng L. Fuzzy theory and AHP applied to urban rail transit operation opinion. In: 2010 International Conference on Artificial Intelligence and Education (ICAIE); 2010 Oct 29–30; Hangzhou, China: IEEE. p. 651–5. doi:10.1109/ICAIE.2010.5641083. [Google Scholar] [CrossRef]
31. Wang R, Sun X, Li Y. Evaluation on system risk of capsule object piped hydraulic transportation based on fuzzy analytic hierarchy process. In: Artificial intelligence and computational intelligence. Berlin/Heidelberg, Germany: Springer; 2011. p. 571–9. doi:10.1007/978-3-642-23881-9_74. [Google Scholar] [CrossRef]
32. Wibowo S, Deng H. Intelligent decision support for effectively evaluating and selecting ships under uncertainty in marine transportation. Expert Syst Appl. 2012;39(8):6911–20. doi:10.1016/j.eswa.2012.01.003. [Google Scholar] [CrossRef]
33. Pahlavani P, Delavar MR. Multi-criteria route planning based on a driver’s preferences in multi-criteria route selection. Transp Res Part C Emerg Technol. 2014;40(3):14–35. doi:10.1016/j.trc.2014.01.001. [Google Scholar] [CrossRef]
34. Xu Y, Zhao X, Wang L, Liu X, Zhang Q. Optimal control of automatic train operation based on multi-scale dynamic programming. In: Proceedings of the 33rd Chinese Control Conference; 2014 Jul 28–30; Nanjing, China: IEEE. p. 3429–33. [Google Scholar]
35. Balogun AL, Matori AN, Hamid-Mosaku AI. A fuzzy multi-criteria decision support system for evaluating subsea oil pipeline routing criteria in East Malaysia. Environ Earth Sci. 2015;74(6):4875–84. doi:10.1007/s12665-015-4499-z. [Google Scholar] [CrossRef]
36. Lopez-Garcia P, Osaba E, Onieva E, Masegosa AD, Perallos A. Short-term traffic congestion forecasting using hybrid metaheuristics and rule-based methods: a comparative study. In: Advances in artificial intelligence. Cham, Switzerland: Springer International Publishing; 2016. p. 290–9. doi:10.1007/978-3-319-44636-3_27. [Google Scholar] [CrossRef]
37. Mladenovic MN, Mangaroska K, Abbas MM. Decision support system for planning traffic operations assets. J Infrastruct Syst. 2017;23(3):05017001. doi:10.1061/(asce)is.1943-555x.0000358. [Google Scholar] [CrossRef]
38. Yazdani M, Zarate P, Coulibaly A, Zavadskas EK. A group decision making support system in logistics and supply chain management. Expert Syst Appl. 2017;88(1):376–92. doi:10.1016/j.eswa.2017.07.014. [Google Scholar] [CrossRef]
39. Wichapa N, Khokhajaikiat P. Solving a multi-objective location routing problem for infectious waste disposal using hybrid goal programming and hybrid genetic algorithm. Int J Ind Eng Comput. 2018;9(1):75–98. doi:10.5267/j.ijiec.2017.4.003. [Google Scholar] [CrossRef]
40. Singh A, Kumari S, Malekpoor H, Mishra N. Big data cloud computing framework for low carbon supplier selection in the beef supply chain. J Clean Prod. 2018;202(3):139–49. doi:10.1016/j.jclepro.2018.07.236. [Google Scholar] [CrossRef]
41. Sun D, Jia Y, Wu J, Chen Z, Zhao L. Application of fuzzy theory in the optimization algorithm of the indicator weight for railway passenger transport safety evaluation. Intell Decis Technol. 2019;12(4):483–90. doi:10.3233/idt-180351. [Google Scholar] [CrossRef]
42. Ma D, Hu L, Liu K. Safety evaluation of high speed railway LTE-R communication system based on AHP and fuzzy comprehensive evaluation. In: 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS); 2019 Jan 12–13; Changsha, China: IEEE. p. 211–4. doi:10.1109/icitbs.2019.00057. [Google Scholar] [CrossRef]
43. Vachan BR, Mishra S. A user monitoring road traffic information collection using SUMO and scheme for road surveillance with deep mind analytics and human behavior tracking. In: 2019 IEEE 4th International Conference on Cloud Computing and Big Data Analysis (ICCCBDA); 2019 Apr 12–15; Chengdu, China: IEEE. p. 274–8. doi:10.1109/ICCCBDA.2019.8725761. [Google Scholar] [CrossRef]
44. Karimi B, Niknamfar AH, Hassan Gavyar B, Barzegar M, Mohtashami A. Multi-objective multi-facility green manufacturing closed-loop supply chain under uncertain environment. Assem Autom. 2019;39(1):58–76. doi:10.1108/aa-09-2018-0138. [Google Scholar] [CrossRef]
45. Liu G, Wang Q, Huang G, Tu L, Wu G. Research on the most throwing position of UAV based on mathematical modeling. In: 2019 International Conference on Artificial Intelligence and Advanced Manufacturing (AIAM); 2019 Oct 16–18; Dublin, Ireland: IEEE. p. 134–7. doi:10.1109/AIAM48774.2019.00034. [Google Scholar] [CrossRef]
46. Pamungkas J, Wiijaya CW. Optimization the waste management based on genetic algorithm multiobjective. In: 2019 IEEE 10th International Conference on Software Engineering and Service Science (ICSESS); 2019 Oct 18–20; Beijing, China: IEEE. p. 1–4. doi:10.1109/ICSESS47205.2019.9040812. [Google Scholar] [CrossRef]
47. Lai CM, Chiu CC, Liu WC, Yeh WC. A novel nondominated sorting simplified swarm optimization for multi-stage capacitated facility location problems with multiple quantitative and qualitative objectives. Appl Soft Comput. 2019;84:105684. doi:10.1016/j.asoc.2019.105684. [Google Scholar] [CrossRef]
48. Jing Y, Guo SY, Wang X, Chen FQ. Research on coordinated development of a railway freight collection and distribution system based on an “entropy-TOPSIS coupling development degree model” integrated with machine learning. J Adv Transp. 2020;2020(13):8885808. doi:10.1155/2020/8885808. [Google Scholar] [CrossRef]
49. Sun Y, Wang L, Xu J, Lin G. An intelligent coupling 3-grade fuzzy comprehensive evaluation approach with AHP for selection of levitation controller of maglev trains. IEEE Access. 2020;8:99509–18. doi:10.1109/ACCESS.2020.2991300. [Google Scholar] [CrossRef]
50. Wang X, Gou X, Xu Z. Assessment of traffic congestion with ORESTE method under double hierarchy hesitant fuzzy linguistic environment. Appl Soft Comput. 2020;86(12):105864. doi:10.1016/j.asoc.2019.105864. [Google Scholar] [CrossRef]
51. Mehlawat MK, Gupta P, Khaitan A, Pedrycz W. A hybrid intelligent approach to integrated fuzzy multiple depot capacitated green vehicle routing problem with split delivery and vehicle selection. IEEE Trans Fuzzy Syst. 2020;28(6):1155–66. doi:10.1109/TFUZZ.2019.2946110. [Google Scholar] [CrossRef]
52. Nasanjargal K, Lu J. Application of analytic hierarchy process-fuzzy comprehensive evaluation in public transport of ulaanbaatar city, Mongolia. In: Proceedings of the 2020 5th International Conference on Machine Learning Technologies. Beijing China: ACM; 2020. p. 93–102. doi:10.1145/3409073.3409075. [Google Scholar] [CrossRef]
53. Huang CY, Lin YC, Lu YF, Wang LC, Kuo YT, Cheng JC, et al. An ANFIS based derivations of inference rules for users’ adoptions of autonomous vehicles. In: 2020 International Conference on Fuzzy Theory and Its Applications (iFUZZY); 2020 Nov 4–7; Hsinchu, Taiwan: IEEE. p. 1–5. doi:10.1109/ifuzzy50310.2020.9297811. [Google Scholar] [CrossRef]
54. Singh A, Das A, Bera UK, Lee GM. Prediction of transportation costs using trapezoidal neutrosophic fuzzy analytic hierarchy process and artificial neural networks. IEEE Access. 2021;9:103497–512. doi:10.1109/ACCESS.2021.3098657. [Google Scholar] [CrossRef]
55. Krishankumar R, Pamucar D, Deveci M, Ravichandran KS. Prioritization of zero-carbon measures for sustainable urban mobility using integrated double hierarchy decision framework and EDAS approach. Sci Total Environ. 2021;797(1):149068. doi:10.1016/j.scitotenv.2021.149068. [Google Scholar] [PubMed] [CrossRef]
56. Song Y, Thatcher D, Li Q, McHugh T, Wu P. Developing sustainable road infrastructure performance indicators using a model-driven fuzzy spatial multi-criteria decision making method. Renew Sustain Energy Rev. 2021;138(12):110538. doi:10.1016/j.rser.2020.110538. [Google Scholar] [CrossRef]
57. Yilmaz MK, Kusakci AO, Aksoy M, Hacioglu U. The evaluation of operational efficiencies of Turkish airports: an integrated spherical fuzzy AHP/DEA approach. Appl Soft Comput. 2022;119:108620. doi:10.1016/j.asoc.2022.108620. [Google Scholar] [CrossRef]
58. Maiti A, Vinayaga-Sureshkanth N, Jadliwala M, Wijewickrama R, Griffin G. Impact of E-scooters on pedestrian safety: a field study using pedestrian crowd-sensing. In: 2022 IEEE International Conference on Pervasive Computing and Communications Workshops and Other Affiliated Events (PerCom Workshops); 2022 Mar 21–25; Pisa, Italy: IEEE. p. 799–805. doi:10.1109/PerComWorkshops53856.2022.9767450. [Google Scholar] [CrossRef]
59. Nodari C, Crispino M, Toraldo E. From traditional to electrified urban road networks: the integration of fuzzy analytic hierarchy process and GIS as a tool to define a feasibility index—an Italian case study. World Electr Veh J. 2022;13(7):116. doi:10.3390/wevj13070116. [Google Scholar] [CrossRef]
60. Alver Y, Katanalp BY. Evaluating the pedestrian gap acceptance in semicontrolled midblock crosswalks with an integrated AHP-FL approach. J Transp Eng Part A Syst. 2022;148(9):04022066. doi:10.1061/jtepbs.0000720. [Google Scholar] [CrossRef]
61. Nasrollahi M, Ghadikolaei AS, Ghasemi R, Sheykhizadeh M, Abdi M. Identification and prioritization of connected vehicle technologies for sustainable development in Iran. Technol Soc. 2022;68:101829. doi:10.1016/j.techsoc.2021.101829. [Google Scholar] [CrossRef]
62. Deveci M, Pamucar D, Gokasar I, Delen D, Martínez L. A fuzzy Einstein-based decision support system for public transportation management at times of pandemic. Knowl Based Syst. 2022;252(1):109414. doi:10.1016/j.knosys.2022.109414. [Google Scholar] [CrossRef]
63. Torkayesh AE, Yazdani M, Ribeiro-Soriano D. Analysis of industry 4.0 implementation in mobility sector: an integrated approach based on QFD, BWM, and stratified combined compromise solution under fuzzy environment. J Ind Inf Integr. 2022;30(3):100406. doi:10.1016/j.jii.2022.100406. [Google Scholar] [CrossRef]
64. Hezam IM, Mishra AR, Rani P, Alshamrani A. Assessing the barriers of digitally sustainable transportation system for persons with disabilities using Fermatean fuzzy double normalization-based multiple aggregation method. Appl Soft Comput. 2023;133(3):109910. doi:10.1016/j.asoc.2022.109910. [Google Scholar] [CrossRef]
65. Nourbakhshrezaei A, Jadidi M, Sohn G. Improving cyclists’ safety using intelligent situational awareness system. Sustainability. 2023;15(4):2866. doi:10.3390/su15042866. [Google Scholar] [CrossRef]
66. Deveci M, Pamucar D, Gokasar I, Tavana M. Spacecraft tracking control and synchronization: an assessment of conventional, unconventional, and combined methods. Adv Space Res. 2023;71(9):3534–51. doi:10.1016/j.asr.2022.07.056. [Google Scholar] [CrossRef]
67. Zavareh A, Fallahiarezoudar E, Ahmadipourroudposht M. Development of an optimized maintenance scheduling for emergency rescue railway wagons using a genetic algorithm: a case study of Iran railways company. Int J Qual Reliab Manag. 2023;40(6):1540–63. doi:10.1108/ijqrm-04-2022-0129. [Google Scholar] [CrossRef]
68. Peng S, Liu Q, Hu J. Green distribution route optimization of medical relief supplies based on improved NSGA-II algorithm under dual-uncertainty. Sustainability. 2023;15(15):11939. doi:10.3390/su151511939. [Google Scholar] [CrossRef]
69. Zöller MA, Huber MF. Benchmark and survey of automated machine learning frameworks. J Artif Intell Res. 2021;70:409–72. doi:10.1613/jair.1.11854. [Google Scholar] [CrossRef]
70. Sarkar A, Moslem S, Esztergár-Kiss D, Akram M, Jin L, Senapati T. A hybrid approach based on dual hesitant q-rung orthopair fuzzy Frank power partitioned Heronian mean aggregation operators for estimating sustainable urban transport solutions. Eng Appl Artif Intell. 2023;124(3):106505. doi:10.1016/j.engappai.2023.106505. [Google Scholar] [CrossRef]
71. Jeevaraj S, Gokasar I, Deveci M, Delen D, Zaidan BB, Wen X, et al. Adoption of energy consumption in urban mobility considering digital carbon footprint: a two-phase interval-valued Fermatean fuzzy dominance methodology. Eng Appl Artif Intell. 2023;126(4):106836. doi:10.1016/j.engappai.2023.106836. [Google Scholar] [CrossRef]
72. Lakhan A, Mohammed MA, Abdulkareem KH, Jaber MM, Kadry S, Nedoma J, et al. Fuzzy decision based energy-evolutionary system for sustainable transport in ubiquitous fog network. Hum Centric Comput Inf Sci. 2023;13:34. [Google Scholar]
73. Wang S, Wang J, Wang X. Risk analysis of human evacuation aboard passenger ships based on fuzzy DEMATEL-ISM-BN. Ocean Eng. 2024;313(6):119520. doi:10.1016/j.oceaneng.2024.119520. [Google Scholar] [CrossRef]
74. Nilashi M, Ali Abumalloh R, Ahmadi H, Alrizq M, Abosaq H, Alghamdi A, et al. Using DEMATEL, clustering, and fuzzy logic for supply chain evaluation of electric vehicles: a SCOR model. AIMS Environ Sci. 2024;11(2):129–56. doi:10.3934/environsci.2024008. [Google Scholar] [CrossRef]
75. Sinha P, Roychowdhury S, Tanaji BA. Customer feedback analysis using aspect based sentiment analysis and fuzzy analytic hierarchy process. In: 2024 IEEE 9th International Conference for Convergence in Technology (I2CT); 2024 Apr 5–7; Pune, India: IEEE. p. 1–6. doi:10.1109/I2CT61223.2024.10544032. [Google Scholar] [CrossRef]
76. Yang YC, Hsieh YH. The critical success factors of smart port digitalization development in the post-COVID-19 era. Case Stud Transp Policy. 2024;17(5):101231. doi:10.1016/j.cstp.2024.101231. [Google Scholar] [CrossRef]
77. Choi M, Van Fan Y, Lee D, Kim S, Lee S. Location and capacity optimization of EV charging stations using genetic algorithms and fuzzy analytic hierarchy process. Clean Technol Environ Policy. 2025;27(4):1785–98. doi:10.1007/s10098-024-02986-w. [Google Scholar] [CrossRef]
78. Hussain MT, Ur Rehman F, Rashid T. An algorithmic approach to minimize road accidents in the highway system using Hamiltonian fuzzy influence graphs. Neural Comput Appl. 2025;37(6):5019–38. doi:10.1007/s00521-024-10874-z. [Google Scholar] [CrossRef]
79. Hassannayebi E, Hashemi H, Basirati M, Saidi S, Ebrahimi A. Data-driven multi-criteria assessment framework for analyzing the reliability of bus services. Transp Res Rec J Transp Res Board. 2024;2678(4):415–39. doi:10.1177/03611981231185140. [Google Scholar] [CrossRef]
80. Rani P, Mishra AR, Deveci M, Gokasar I, Yemlihalioglu E, Brito-Parada PR. Evaluation of micromobility risk management alternatives using interval-valued q-rung orthopair fuzzy interaction operators-based WISP method. Appl Soft Comput. 2024;156(1):111496. doi:10.1016/j.asoc.2024.111496. [Google Scholar] [CrossRef]
81. Elomiya A, Křupka J, Jovčić S, Simic V, Švadlenka L, Pamucar D. A hybrid suitability mapping model integrating GIS, machine learning, and multi-criteria decision analytics for optimizing service quality of electric vehicle charging stations. Sustain Cities Soc. 2024;106(4):105397. doi:10.1016/j.scs.2024.105397. [Google Scholar] [CrossRef]
82. Guan X, Yu F, Xu H, Li C, Guan Y. Flood risk assessment of urban metro system using random forest algorithm and triangular fuzzy number based analytical hierarchy process approach. Sustain Cities Soc. 2024;109(3):105546. doi:10.1016/j.scs.2024.105546. [Google Scholar] [CrossRef]
83. Moslem S, Tezel BT, Ovgu Kinay A, Pilla F. A hybrid approach based on magnitude-based fuzzy analytic hierarchy process for estimating sustainable urban transport solutions. Eng Appl Artif Intell. 2024;137(4):109112. doi:10.1016/j.engappai.2024.109112. [Google Scholar] [CrossRef]
84. Elomiya A, Křupka J, Simic V, Švadlenka L, Průša P, Jovčić S. An advanced spatial decision model for strategic placement of off-site hydrogen refueling stations in urban areas. eTransportation. 2024;22(11):100375. doi:10.1016/j.etran.2024.100375. [Google Scholar] [CrossRef]
85. Nozari H, Abdi H, Szmelter-Jarosz A, Motevalli SH. Design of dual-channel supply chain network based on the Internet of Things under uncertainty. Math Comput Appl. 2024;29(6):118. doi:10.3390/mca29060118. [Google Scholar] [CrossRef]
86. Pinki, Kumar R, Vimal S, Alghamdi NS, Dhiman G, Pasupathi S, et al. Artificial intelligence-enabled smart city management using multi-objective optimization strategies. Expert Syst. 2025;42(1):e13574. doi:10.1111/exsy.13574. [Google Scholar] [CrossRef]
87. Tripathi SK, Kant R, Shankar R. Investigating the electric vehicle adoption initiatives for achieving sustainable development goals. Sustain Futur. 2025;9:100469. doi:10.1016/j.sftr.2025.100469. [Google Scholar] [CrossRef]
88. Torfi F, Farahani RZ, Rezapour S. Fuzzy AHP to determine the relative weights of evaluation criteria and Fuzzy TOPSIS to rank the alternatives. Appl Soft Comput. 2010;10(2):520–8. doi:10.1016/j.asoc.2009.08.021. [Google Scholar] [CrossRef]
89. Kim Y, Chung ES. Fuzzy VIKOR approach for assessing the vulnerability of the water supply to climate change and variability in South Korea. Appl Math Model. 2013;37(22):9419–30. doi:10.1016/j.apm.2013.04.040. [Google Scholar] [CrossRef]
90. Ayyildiz E, Taskin Gumus A. Pythagorean fuzzy AHP based risk assessment methodology for hazardous material transportation: an application in Istanbul. Environ Sci Pollut Res Int. 2021;28(27):35798–810. doi:10.1007/s11356-021-13223-y. [Google Scholar] [PubMed] [CrossRef]
91. Bouraima MB, Gore A, Ayyildiz E, Yalcin S, Badi I, Kiptum CK, et al. Assessing of causes of accidents based on a novel integrated interval-valued Fermatean fuzzy methodology: towards a sustainable construction site. Neural Comput Appl. 2023;35(29):21725–50. doi:10.1007/s00521-023-08948-5. [Google Scholar] [CrossRef]
92. Seker S, Aydin N. Hydrogen production facility location selection for Black Sea using entropy based TOPSIS under IVPF environment. Int J Hydrog Energy. 2020;45(32):15855–68. doi:10.1016/j.ijhydene.2019.12.183. [Google Scholar] [CrossRef]
93. Yau KA, Qadir J, Khoo HL, Ling MH, Komisarczuk P. A survey on reinforcement learning models and algorithms for traffic signal control. ACM Comput Surv. 2018;50(3):1–38. doi:10.1145/3068287. [Google Scholar] [CrossRef]
94. Wei H, Zheng G, Gayah V, Li Z. Recent advances in reinforcement learning for traffic signal control: a survey of models and evaluation. SIGKDD Explor Newsl. 2021;22(2):12–8. doi:10.1145/3447556.3447565. [Google Scholar] [CrossRef]
95. Chu T, Wang J, Codecà L, Li Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans Intell Transp Syst. 2020;21(3):1086–95. doi:10.1109/TITS.2019.2901791. [Google Scholar] [CrossRef]
96. Graells-Garrido E, Peña-Araya V, Bravo L. Adoption-driven data science for transportation planning: methodology, case study, and lessons learned. Sustainability. 2020;12(15):6001. doi:10.3390/su12156001. [Google Scholar] [CrossRef]
97. Yang M, Luo W, Ashoori M, Mahmoudi J, Xiong C, Lu J, et al. Big-data driven framework to estimate vehicle volume based on mobile device location data. Transp Res Rec J Transp Res Board. 2024;2678(2):352–65. doi:10.1177/03611981231174240. [Google Scholar] [CrossRef]
98. Murugaiyan S, Nagappan K, Savaridassan P, Maranco M. Leveraging big data to drive smarter and sustainable transportation policies. In: Urban mobility and challenges of intelligent transportation systems; 2025. p. 327–48. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools