A New Quadrilateral Finite Element Formulation for the Free Vibration Analysis of CNT-Reinforced Plates with Cutouts

1  Introduction

In recent years, carbon nanotube-reinforced composite (CNTRC) structures have received increasing attention due to the exceptional mechanical, thermal, and vibrational properties imparted by carbon nanotubes (CNTs) embedded within polymer matrices [1–4]. Numerical and experimental results in the literature consistently indicate that a low volume fraction of CNT reinforcements contributes notably to the mechanical enhancement of nanocomposite plates [5,6]. As a result, CNT-based composites are now being considered for critical applications in aerospace, mechanical, and civil engineering, where lightweight and high-performance materials are essential. Extensive research has been devoted to plates containing geometric discontinuities, including cutouts, which serve practical purposes such as weight reduction and access provision [7–9]. However, it is now well established that these discontinuities significantly affect changes in the global dynamic characteristics and the local stress distribution [10,11]. The mechanical impact of cutouts manifests in elevated stress zones and reduced local rigidity, leading to abrupt deformation gradients, which are more severe in CNT-reinforced composites due to their anisotropy and functional gradation of constituents [12–15]. Various cutout shapes, such as circular, elliptical, and polygonal openings, influence nanocomposites’ vibrational and stability behavior and functionally graded plates, and have been extensively investigated [16–19]. A common framework adopted in earlier studies involves the application of classical or first-order shear deformation plate theories, integrated with Ritz-based solutions using polynomial or Chebyshev expansions [20–22]. Although these approaches offer fundamental insights, their predictive accuracy tends to degrade in regions exhibiting steep strain gradients near cutouts and under different boundary conditions. Moreover, conventional low-order finite elements frequently encounter numerical artifacts, including shear locking and sensitivity to mesh refinement near cutout regions [23–25]. Several advanced theories have emerged to address these challenges: higher-order deformation kinematics, nonlocal and gradient-enhanced elasticity, and NURBS-based isogeometric approaches [26–29]. Nonetheless, the practical application of these techniques remains constrained by their intensive computational requirements and complex formulation procedures [30–32]. In addition, several of these approaches are unsuited for capturing the interaction between perforation shape, material gradation patterns, and mechanical modeling strategy. Recent research has increasingly turned toward the detailed analysis of advanced composite structures, with particular attention given to functionally graded carbon nanotube-reinforced composites and porous materials featuring intricate cutouts. Several analytical models have been proposed to explore their vibration and damping behaviors; many utilize higher-order shear deformation theory, various energy-based approaches, and the Rayleigh–Ritz method. These models have proven effective in capturing the dynamic response of CNT-reinforced plates embedded with viscoelastic layers. In parallel, bending behavior in FG-CNTRC panels has been assessed using shell elements derived from Kirchhoff–Love theory, integrating correction factors to reflect the efficiency of carbon nanotube reinforcement. Porous solids with irregular cutout shapes have been examined on a structural complexity front using three-dimensional elasticity formulations and hybrid Q4-T4 finite element meshes [33–37]. These studies highlight the impact of porosity distribution and cutout geometry on the system’s natural frequencies. Experimental investigations have also contributed to the field. Notably, tests conducted on honeycomb sandwich beams under clamped-free boundary conditions have offered valuable insights into vibrational behavior, particularly with core structure and fundamental damping mechanisms. In light of these challenges, a new quadrilateral finite element is presented to investigate the free vibration behavior of CNTRC plates with cutouts. The formulation is founded in first-order shear deformation theory (FSDT) and incorporates refined membrane and shear components interpolations to enhance numerical accuracy. This enrichment allows for accurately modeling strain gradients near the cutout region and effectively avoids shear locking without requiring refined meshes or higher interpolation functions. The formulation accommodates both uniform and functionally graded CNT distributions using rule-of-mixtures micromechanical-based models. The performance of the proposed IQ4 element is assessed through a series of benchmark problems involving CNTRC plates both with and without cutouts, and the obtained results are compared against established reference solutions. The effects of cutout shape, size, CNT volume fraction, distribution patterns, boundary conditions, and plate geometry on the vibrational response are systematically investigated. The developed approach is well-positioned for integration into the structural optimization of lightweight, cutout-bearing components exposed to vibratory environments.

2  Problem Formulation

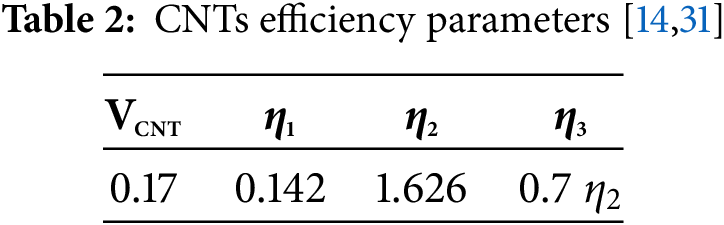
2.1 Mechanical Properties of CNTs Reinforced Plates

A functionally graded carbon nanotube-reinforced composite (FG-CNTRC) plate with a central rectangular cutout and a uniform thickness h is considered, as illustrated in Fig. 1. The Cartesian coordinate system (x, y, z) is defined such that the plane z = 0 coincides with the mid-surface of the plate. The rectangular cutout located at the center of the plate has side lengths c and d, representing its dimensions in the x- and y-directions, respectively. In Fig. 2, the FG-CNTRC plate is modeled as a two-phase nanocomposite of aligned carbon nanotubes (CNTs) embedded in an isotropic polymer matrix. CNTs are continuously distributed through the thickness according to one of four patterns: UD (uniform distribution), FG-O (mid-plane concentration), FG-X (symmetric surface concentration), and FG-V (graded from top to bottom). These gradation schemes define the CNT volume fraction as a function of the thickness z-coordinate, designed to optimize the mechanical performance of the nanocomposite plate.

Figure 1: Geometrical configuration of a FG-CNTRC plate with a central rectangular cutout

Figure 2: CNTs through the z-direction distribution patterns: (a) FG-UD; (b) FG-O; (c) FG-X; (d) FG-V; (e) z-thickness distribution patterns of CNT volume fraction VCNTs(z) for FG-CNTRC plates with VCNTs∗=0.17

The volume fraction of CNTs VCNTs(z) according to each distribution pattern, it is defined as follows [38,39]:

VCNTs(z)={VCNTs∗for FG-UDVCNTs∗(2−4|z|h)for FG-OVCNTs∗(4|z|h)for FG-XVCNTs∗(1+2zh)for FG-A(1)

here, VCNTs∗ represents the intended amount of CNT reinforcement within the matrix material related to the distribution through the z-coordinate. The effective elastic properties, including Young’s modulus E(z), shear modulus G(z), and mass density ρ(z), are estimated using the rule of mixtures, as described [40,41]:

{E11(z)=η1VCNTs(z)E11CNTs+Vm(z)Emη2E22(z)=VCNTs(z)E22CNTs+Vm(z)Emη3G12(z)=VCNTs(z)G12CNTs+Vm(z)Gmρ(z)=VCNTs(z)ρCNTs+Vm(z)ρm(2)

For convenience, the volume fraction of the polymer matrix is assumed to be:

Vm(z)=1−VCNTs(z)(3)

here, E11CNTs, E22CNTs and G12CNTs denote the longitudinal and transverse Young’s moduli and the shear modulus of the carbon nanotubes, respectively. While Em and Gm represent the corresponding elastic properties of the polymer matrix. The coefficients η1, η2 and η3 are the efficiency parameters introduced to account for the scale-dependent behavior of CNTs. In the present study, Poisson’s ratio ν (z) of the CNTs and the matrix constituents is expressed as follows:

υ(z)=VCNTs(z)υCNTs+Vm(z)υm(4)

2.2 Basic Formulation

In this investigation, the first-order shear deformation theory is employed. The corresponding kinematic assumptions are introduced through the displacement field, which is expressed as:

{u(x,y,z,t)=u0(x,y,t)−zβx(x,y,t)v(x,y,z,t)=v0(x,y,t)−zβy(x,y,t)w(x,y,z,t)=w0(x,y,t)(5)

here, u0 and v0 represent the in-plane displacements, while w0 denotes the transverse displacement at a point on the mid-plane of the CNTRC plate. The rotations of the normal to the mid-surface, due to transverse shear deformation, are represented by βx and βy about the y- and x-axes, respectively. The strain components associated with the displacement field defined in Eq. (5) are given as follows:

{εxεyγxy}={εxmεymγxym}+z{χxχyχxy}(6)

{γxzγyz}={γxzsγyzs}

where

{εxmεymγxym}={u0,xv0,yu0,y+v0,x},{χxχyχxy}=−{βx,xβy,yβx,y+βy,x},{γxzsγyzs}={w0,x−βxv0,y−βy}(7)

The constitutive relations for the CNTRC plate are formulated based on the linear elasticity theory for orthotropic materials. These relations define the stress-strain behavior in terms of the effective material properties, which vary through the thickness according to the presented CNTs distribution patterns as:

{σxσyτxyτxzτyz}=[Q11Q12000Q12Q2200000Q6600000Q4400000Q55]{εxεyγxyγxzγyz}(8)

The stiffness coefficients Qij, associated with the CNT reinforced nanocomposite material, are defined in terms of the effective elastic constants as follows:

Q11=E11(z)1−υ21υ12;Q22=E22(z)1−υ21υ12;Q12=υ21E11(z)1−υ21υ12;Q66=G12(z);Q44=ksG13(z);Q55=ksG23(z)(9)

here, ks denotes the shear correction factor, which is taken as 5/6.

2.3 Variational Formulation

The governing equations of the CNTRC nanocomposite plate are derived using Hamilton’s variational principle, which accounts for the balance of strain energy and kinetic energy as follows:

∫t1t2δ(ΠP−ΠK)dt=0(10)

In this expression, δΠP denotes the variation of the strain energy of the CNT reinforced nanocomposite plate, while δΠK represents the variation of kinetic energy. The strain energy variation is given by:

δΠP=∫V(σxδεx+σyδεy+τxzδγxz+τyzδγyz+τxyδγxy)dV=∫−a/2+a/2∫−b/2+b/2(Nxδεxm+Nyδεym+Nxyδγxym+Mxδχx+Myδχy+Mxyδχxy+Sxzδγxzs+Syzδγyzs)dxdy(11)

The stress resultants, including the membrane forces N, bending moments M, and transverse shear forces S, are obtained by integrating the corresponding stress components through the thickness of the CNT reinforced nanocomposite plate:

{NijMij}=∫−h/2+h/2σij{1z}dz;(ij=x,y,xy)andSij=∫−h/2+h/2τijdz;(j=xz,yz)(12)

By substituting Eqs. (8) and (9) into Eq. (11), the final expressions for the stress resultants are obtained in the following form:

{NijMijSij}=[AijBij0BijDij000ASij]{εijmχijγijs}(13)

The detailed expressions for the stiffness coefficients are given as follows:

[Aij]=[A11A120A12A22000A66];[Bij]=[B11B120B12B22000B66];[Dij]=[D11D120D12D22000D66];[ASij]=[As4400As55](14)

where

{AijBijDij}=∫−h/2+h/2Qij{1zz2}dz(ij=11,12,22,66)and{As44As55}=ks∫−h/2+h/2{Q44Q55}dz(15)

The variation of kinetic energy for the CNT-reinforced nanocomposite plate is expressed as follows:

δΠK=∫Vρ(z)(u˙δu˙+v˙δv˙+w˙δw˙)dV=∫−a/2+a/2∫−b/2+b/2[I0u˙0δu˙0+I0v˙0δv˙0+I0w˙0δw˙0−I1(u˙0δβx˙+βx˙δu˙0)−I1(v˙0δβy˙+βy˙δv˙0)+I2(βx˙δβx˙+βy˙δβy˙)]dxdy(16)

here, ρ(z) denotes the mass density varying through the thickness, (I0,I1 and I2) represent the mass inertia terms, defined as follows:

{I0I1I2}=∫−h/2h/2ρ(z){1zz2}dz(17)

By substituting Eqs. (11) and (16) into Eq. (10), and expressing the δΠP and δΠK variations in explicit form, followed by the application of integration by parts and setting the virtual displacements δu0, δv0, δw0, δβx and δβy, the weak variational form of the governing equations for the CNT-reinforced plate is derived as follows:

∫ds(⟨δεm⟩[A]{εm}+⟨δεm⟩[B]{χ}+⟨δχ⟩[B]{εm}+⟨δχ⟩[D]{χ}+⟨δγs⟩[As]{γs}+⟨δu0⟩I0{u¨0}+⟨δv0⟩I0{v¨0}+⟨δw0⟩I0{w¨0}−⟨δu0⟩I1{β¨x}−⟨δβx⟩I1{u¨0}−⟨δv0⟩I1{β¨y}−⟨δβy⟩I1{v¨0}+⟨δβx⟩I2{β¨x}+⟨δβy⟩I2{β¨y})ds=0(18)

Consequently, the weak form presented in Eq. (18) can be discretized and reformulated into the standard matrix form of the governing equations:

(Km+Kmb+Kbm+Kb+Ks){di}+(Mu0+Mv0+Mw0−Mu0βx−Mβxu0−Mv0βy−Kβyv0+Mβx+Mβy){d¨i}=0(19)

2.4 New Improved IQ4 Finite Element Formulation

A new finite element model is proposed for FG-CNTRC plates based on the FSDT assumptions. The formulation enhances the classical Q4 membrane part by incorporating side-based average projection to accurately evaluate membrane–bending coupling, which is essential for graded composite materials. To avoid shear locking, the shear strain projection method is employed. This combination leads to an improved and advanced element formulation with enhanced accuracy and convergence performance.

2.4.1 IQ4 Finite Element Stiffness Matrix

The fundamental idea is to replace the normal strain components εx and εy by their averaged values over the element domain. Unlike the standard Q4 element, which ignores edge orientations, the proposed B-type method incorporates side-based projections for the element geometry. This modification effectively avoids locking under near-incompressible conditions and improves membrane strain accuracy, particularly for distorted or refined meshes. The position vector of any point M located on the mid-surface of the element can be interpolated from the nodal coordinates using the standard bilinear isoparametric shape functions, which depend explicitly on the natural coordinates ξ and η, as follows:

Ni=1,2,3,4(ξi,ηi)=14(1+ξiξ)(1+ηiη)ξi∈[−1,+1]andηi∈[−1,+1](20)

The derivatives with respect to the physical coordinates (x, y) are obtained through the Jacobian matrix transformation.

∂Ni∂x=J−1∂Ni∂ξ;∂Ni∂y=J−1∂Ni∂η(21)

where

J=[∂x∂ξ∂x∂η∂y∂ξ∂y∂η]=∑i=14{xiyi}⟨∂Ni∂ξ;∂Ni∂η⟩(22)

The average strains over the element are computed using numerical integration based on a 2 × 2 Gauss quadrature scheme.

ε~x=14∑i=14εx(ξi,ηi),ε~y=14∑i=14εy(ξi,ηi)(23)

The modified matrix is explicitly expressed as follows:

B~m={B~xB~yBxy}(24)

where the modified components are explicitly defined as:

B~x=14∑i=14Bxm(ξi,ηi),B~y=14∑i=14Bym(ξi,ηi)(25)

with the initial components given by:

{BxmBymBxy}=[J]−1[∂ξ][Ni00Ni⋯NiNi]and[∂ξ]=[(),ξ0(),ξ00(),η0(),η](26)

The final expression of the modified B~m matrix corresponding to the membrane part is given by:

B~m=[14∑j=14(J11−1Ni,ξ|j+J12−1Ni,η|j)0000014∑j=14(J21−1Ni,ξ|j+J22−1Ni,η|j)000⋯(J21−1Ni,ξ+J22−1Ni,η)(J11−1Ni,ξ+J12−1Ni,η)000]i=1,2,3,4(27)

Finally, the membrane stiffness contribution is expressed as:

[Km]=∫−1+1∫−1+1[B~m]T[Aij][B~m]|J|∂ξ∂η(28)

The variation of the strain energy associated with the bending deformation of the CNTRC plate is expressed as:

δKb=∫ds⟨δχ⟩[Dij]{χ}ds(29)

with

χ={−βx,x−βy,y−(βx,y+βy,x)}=[Bb]{βxβy}(30)

The rotations of the normal to the mid-surface are interpolated using a bilinear shape function of the Q4 element, and are given by:

{βxβy}=∑i=14⟨Ni⟩{βxiβyi}(31)

where the differential operator matrix [Bb] associated with the bending stiffness part is defined as:

[Bb]=[000(J11−1Ni,ξ+J12−1Ni,η)0⋯0000(J21−1Ni,ξ+J22−1Ni,η)⋯000(J21−1Ni,ξ+J22−1Ni,η)(J11−1Ni,ξ+J12−1Ni,η)⋯]i=1,2,3,4(32)

Finally, the bending stiffness contribution is expressed as:

[Kb]=∫−1+1∫−1+1[Bb]T[Dij][Bb]|J|∂ξ∂η(33)

In the present formulation, membrane–bending coupling is evaluated through an enhanced membrane strain–displacement matrix B~m, specifically developed to reflect the interaction neglected in classical models. This coupling is important for accurately representing asymmetric through-thickness CNT distribution patterns:

[Kmb]=[Kbm]=∫−1+1∫−1+1[B~m]T[Bij][Bb]|J|∂ξ∂η(34)

This study adopts the discrete shear projection technique to avoid shear locking without introducing spurious modes or sensitivity to mesh distortion [42–45]. Refining the shear strain field within the Q4γ element achieves accurate shear deformation across various thicknesses without additional variables or reduced integration. The resulting formulation remains efficient and stable for both thick and thin plates. The variation of the shear strain energy is given by:

δKs=∫ds⟨δγs⟩[As]{γs}ds(35)

with

{γxzsγyzs}={w0,x−βxw0,y−βy}(36)

and in isosparametric coordinates:

{γξzsγηzs}={w0,ξ−βξw0,η−βη}=[Bξ]{de}(37)

In matrix form:

[Bξ]=[00Ni,ξξiNi,ξ0⋯00Ni,η0ηiNi,η⋯]i=1,2,3,4(38)

Eq. (37) defines the transverse shear deformation along each side of the plate element in terms of the nodal displacement parameters:

∫−11[γξz−(∂w0∂ξ−φξ)]dξ=0

∫−11[γηz−(∂w0∂η−φη)]dη=0(39)

The transverse shear strain components γ are then interpolated over the element using the projected side values as:

γ=∑i=14Niγ(ξ,η)γjk(40)

where Niγ are the interpolation functions associated with the element sides, and γjk are the corresponding constant shear strains projected along each side. The transverse shear strain field is interpolated from side-based constant values using appropriate shape functions as:

{γξij=12(1−η)γξ12+12(1+η)γξ34γηij=12(1−ξ)γξ13+12(1+ξ)γξ24(41)

The Bξ matrix corresponding to the shear strain–displacement relation is defined as:

[Bξ]=[00Ni,ξξiNi,ξJ11−1ξiNi,ξJ12−1⋯00Ni,ηηiNi,ηJ21−1ηiNi,ηJ22−1⋯]i=1,2,3,4(42)

and

[Bs]=[J]−1[Bξ](43)

The shear stiffness contribution is expressed as:

[Ks]=∫−1+1∫−1+1[Bs]T[[As]][Bs]|J|∂ξ∂η(44)

Finally, the element stiffness matrix for the IQ4 element, which includes membrane, bending, membrane–bending coupling, and transverse shear effects, is expressed as:

[Ke]=[Km]+[Kmb]+[Kbm]+[Kb]+[Ks](45)

2.4.2 IQ4 Finite Element Mass Matrix

The IQ4 mass matrix is derived from the virtual variation of kinetic energy. This formulation considers translational and rotational inertial effects, including the coupling terms arising from asymmetric mass distribution through the plate thickness. Based on the weak form of the kinetic energy of the CNT-reinforced nanocomposite plate, the mass matrix may be expressed by:

δΠK=∫ds(I0(⟨δu0⟩{u¨0}+⟨δv0⟩{v¨0}+⟨δw0⟩{w¨0})−I1(⟨δu0⟩{β¨x}+⟨δβx⟩{u¨0}⟨δv0⟩I1{β¨y}+⟨δβy⟩I1{v¨0})+I2(⟨δβx⟩{β¨x}+⟨δβy⟩{β¨y}))ds(46)

The bilinear isoparametric shape functions Ni(ξ,η) are employed to interpolate the translational and rotational degrees of freedom within the element domain:

{dT}=[Ni000Ni000Ni]{u0v0w0}i=1,2,3,4(47)

and,

{dR}=[Ni00Ni]{βxβy}i=1,2,3,4(48)

where {dT} and {dR} are the translational and rotational d.o.f, respectively. Accordingly, the final expression of the computed element mass matrix is given by:

[Me]=∫ds(NTTI0NTT−NTTI1NRT−NRTI1NTT+NRTI2NRT)ds(49)

where

[Me]=[MTMRTMRTMR](50)

By assembling the contributions from all elements, the global stiffness matrix Kg and the global mass matrix Mg are obtained as:

[K]g=∑e=1n[Ke]and[M]g=∑e=1n[Me](51)

After rewriting Eq. (19), the free vibration eigenvalue analysis is obtained in the form:

([K]g−ω2[M]g){d}=0(52)

In Eq. (52), ω denotes the system’s natural frequencies. All element matrices are integrated using a 2 × 2 Gauss quadrature scheme, ensuring sufficient numerical accuracy for evaluating stiffness and mass contributions.

3  Numerical Simulation and Discussion

This section provides a series of computational examples to assess the accuracy and robustness of the formulated IQ4 model in predicting the free vibration behavior of FG-CNTRC nanocomposite plates. Both comparative and parametric studies are carried out, drawing on reference solutions available in the literature for validation purposes. The FG-CNTRC plates analyzed in this study feature various CNT distributions embedded within a polymer matrix. Detailed information on the material properties and volume fractions is presented in Tables 1–3. The boundary conditions applied in each case are summarized in Table 4. A systematic investigation evaluates the effects of CNT distribution patterns, material gradation, and geometric parameters, including central cutouts. Both intact plates and those with cutouts are examined, allowing for a clear assessment of the cutout size and shape influence the dynamic response. To ensure consistency and facilitate comparison, the natural frequencies are reported in normalized form [14,31]:

ω¯=ω(a2h)ρmDm;Dm=Emh212(1−νm2)(53)

The first example provides a convergence study to assess the performance of the proposed IQ4 finite element in the free vibration analysis of CNT-reinforced plates. Fig. 3 presents results for FG-UD and FG-X distribution patterns, respectively, with comparisons made against the classical Q4 element using selective reduced integration. Across both patterns, the IQ4 element demonstrates faster and more stable convergence, achieving accurate fundamental frequencies with fewer mesh divisions. In contrast, the Q4 element shows slower convergence and higher sensitivity to mesh refinement. These results confirm the improved numerical robustness and efficiency of the IQ4 formulation, making it particularly suitable for analyzing nanocomposite plates with advanced material gradations. The next section investigates the vibrational behavior of FG-CNTRC plates with central cutouts through a comparative analysis against benchmark solutions reported by Mirzaei and Kiani [31] and Mirzaei [14]. The IQ4 finite element model demonstrates excellent agreement with the reference Ritz-based results across various CNT distribution configurations. For clarity, the results are presented separately: Tables 5–8 correspond to simply supported plates, whereas Tables 9–12 report the case of fully clamped plates. Notably, the IQ4 element effectively captures both in-plane and transverse shear effects induced by material gradation, while maintaining reduced computational cost compared to the high-order Ritz and Ritz–Chebyshev approaches. As consistently observed, the FG-X distribution exhibits the highest natural frequencies due to the concentration of CNTs near the plate surfaces, thereby enhancing bending stiffness.

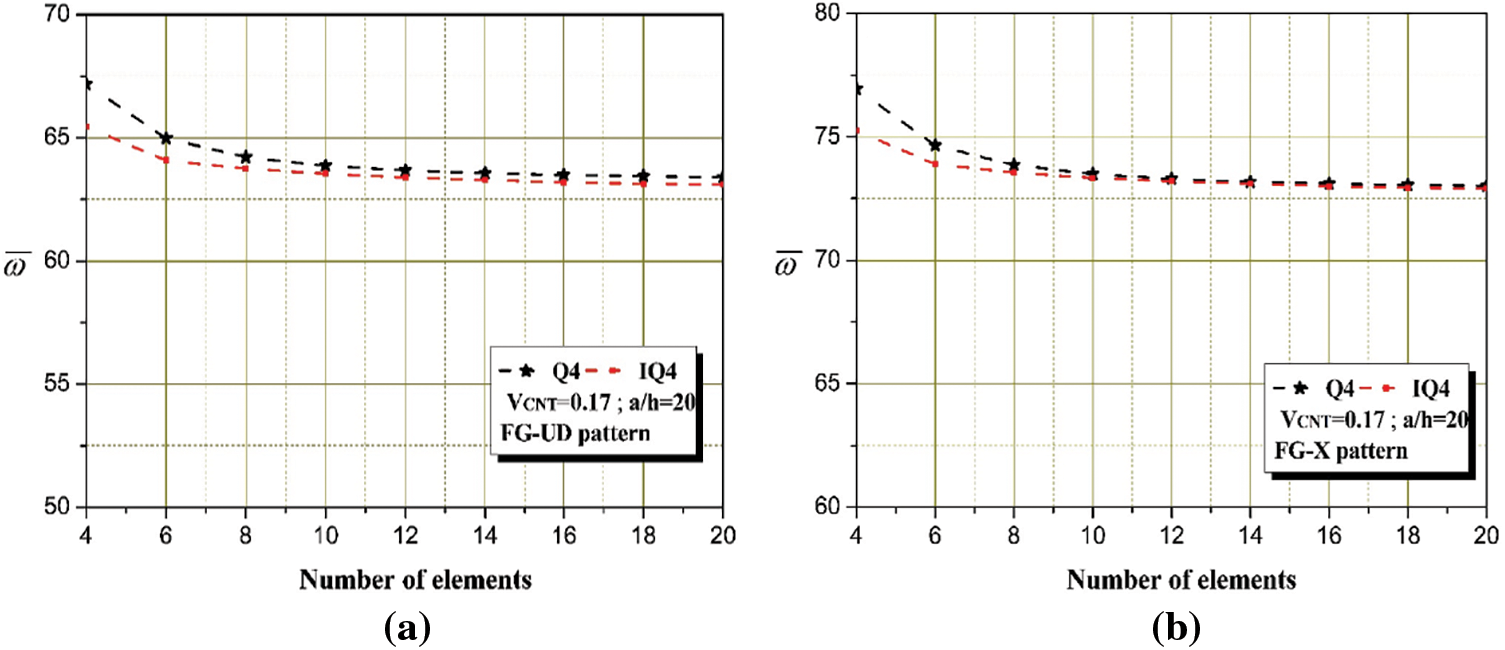
Figure 3: Convergence comparison of fundamental frequency using classical Q4 and improved IQ4 elements for CNT-reinforced plates with different CNTs distribution patterns: (a) FG-UD pattern; (b) FG-X

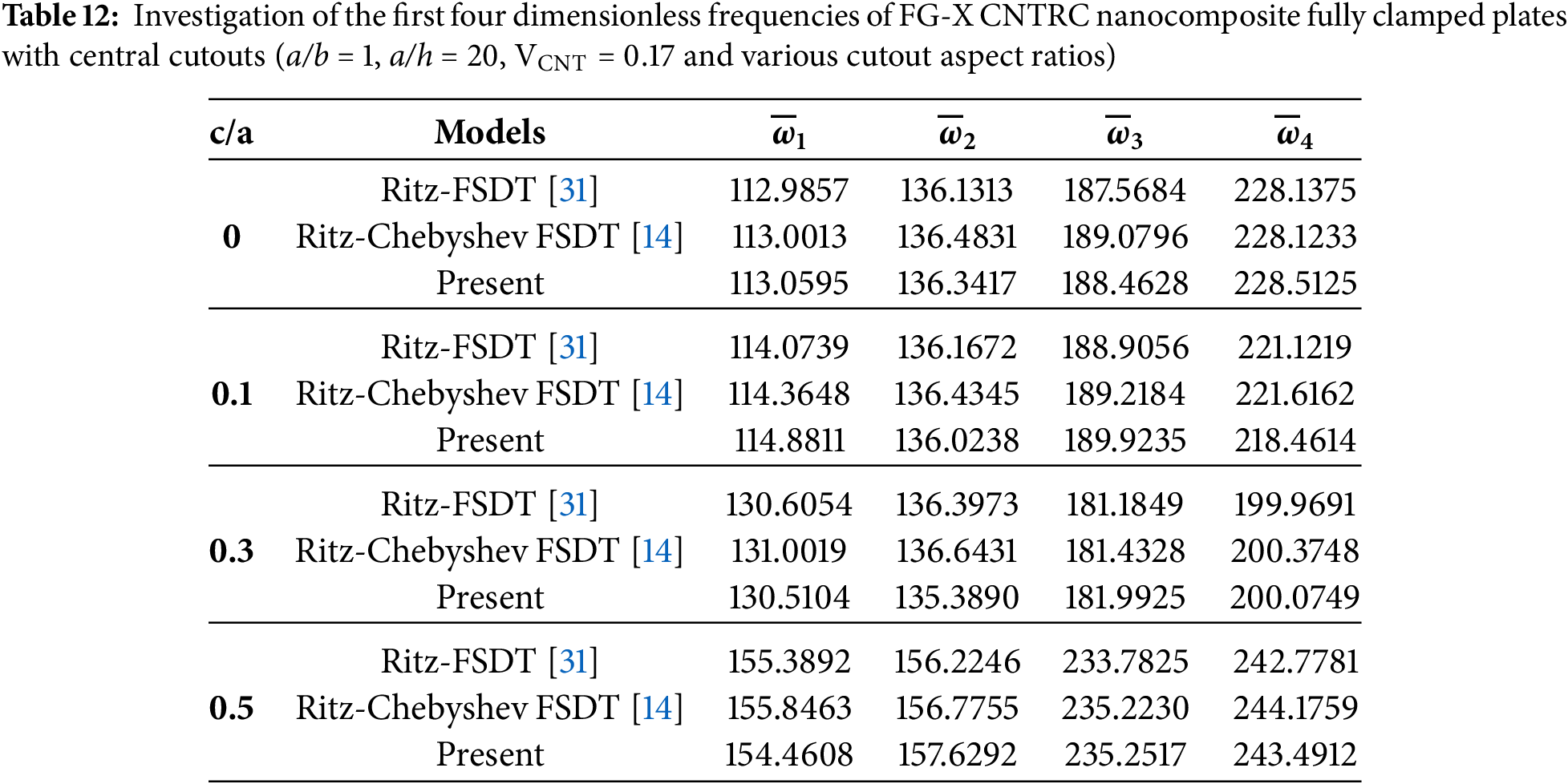
Conversely, with CNTs concentrated near the mid-plane, the FG-O pattern results in the lowest stiffness and frequencies. The FG-UD and FG-V distributions yield intermediate values, with FG-UD demonstrating higher stiffness attributed to its uniform reinforcement profile. This uniformity ensures that the reinforcing CNTs contribute consistently across the entire thickness, enhancing the stiffness. By contrast, while still effective, the FG-V distribution concentrates CNTs toward the surfaces, improving bending resistance locally but not providing the same balanced contribution throughout the plate. As a result, FG-UD exhibits slightly higher natural frequencies than FG-V, since its uniform stiffness distribution increases the global structural resistance to deformation. In contrast, FG-V shows a more mode-dependent sensitivity to bending and shear interactions. These trends are in close accordance with the reference data presented in Mirzaei and Kiani [31] and Mirzaei [14]. For plates with clamped–free (CFCF) boundary conditions on both sides, as presented in Tables 13–16, the proposed IQ4 model yields results that are in close agreement with the reference solutions. The frequency ordering FG-X > FG-UD > FG-V > FG-O is consistently maintained. Minor discrepancies are attributed to shear deformation treatments in thick plate configurations. Nonetheless, the IQ4 model achieves comparable accuracy with significantly reduced computational effort, confirming its suitability for large-scale parametric studies and practical engineering applications.

The influence of cutout geometry on the dynamic response is examined with particular attention to aspect ratio variations. As the longitudinal cutout ratio c/a increases, a marked reduction in effective stiffness is observed, particularly for the FG-O and FG-V distributions. This results in a corresponding decrease in natural frequencies. The sensitivity of the third mode to asymmetrical CNT gradation is also notable, indicating the role of in-plane stiffness in higher-order dynamic behavior. Further analysis of the effect of cutout dimensions is presented in Table 17, where variations in c/a and d/b are considered independently. It is observed that increases in c/a lead to a more significant frequency reduction than equivalent variations in d/b, for all CNT distribution patterns. This highlights the dominant influence of longitudinal stiffness reduction, particularly in distributions where axial reinforcement is less effective. The trend remains consistent across all FG configurations, reaffirming the enhanced stiffness contribution of outer-surface reinforcement (FG-X) and the reduced rigidity of mid-plane-oriented distributions (FG-O).

Fig. 4 illustrates the mesh and geometric configuration of square FG-CNTRC plates with central cutouts for varying cutout aspect ratios c/a, ranging from 0 (no cutout) to 0.5. As the cutout size increases, the effective cross-sectional area is reduced, thereby decreasing the global stiffness of the plate. This geometric simplification is crucial for systematically investigating the influence of cutout geometry on vibrational characteristics under simply supported boundary conditions. The mesh remains consistent across configurations to ensure convergence and maintain numerical stability in the frequency evaluation. Fig. 5 presents the variation of the first dimensionless natural frequencies as a function of both longitudinal (c/a) and transversal (d/b) cutout aspect ratios for four distinct CNT distribution patterns: FG-UD, FG-O, FG-X, and FG-A. Across all configurations, a progressive decrease in natural frequencies is observed as the cutout ratio increases, confirming that removing material significantly lowers the plate’s bending stiffness. However, the longitudinal aspect ratio (c/a) effect is consistently more pronounced than the transversal one (d/b). This trend is particularly evident for FG-O and FG-V patterns, where reinforcement is concentrated near the mid-plane or distributed asymmetrically, reducing their effectiveness in resisting in-plane and flexural deformation. The FG-X configuration demonstrates the highest frequency values throughout the parametric range, which is attributable to the CNT reinforcement being concentrated near the plate surfaces, substantially enhancing the flexural rigidity. In contrast, FG-O consistently exhibits the lowest frequencies, as its central reinforcement minimizes bending resistance.

Figure 4: Finite element mesh and geometric configurations of simply supported square FG-CNTRC plates with central cutouts for various cutout aspect ratios: (a) FG-UD; (b) FG-O; (c) FG-X; (d) FG-V

Figure 5: Variation of the first dimensionless natural frequency with respect to longitudinal (c/a) and transversal (d/b) cutout aspect ratios for different CNT distribution patterns: (a) FG-UD; (b) FG-O; (c) FG-X; (d) FG-A

4  Conclusion

In the present study, the free vibration characteristics of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) plates with central cutouts have been thoroughly investigated by developing an improved finite element formulation. A novel IQ4γ element, based on the first-order shear deformation theory (FSDT), was implemented by incorporating an enhanced membrane formulation and a discrete shear projection technique. This improved formulation effectively eliminates shear locking and captures the membrane–bending coupling behavior, thereby extending the applicability of conventional FSDT-based plate elements to complex nanocomposite configurations. The accuracy and reliability of the proposed model were verified through systematic comparisons with benchmark results available in the literature. Subsequent parametric studies assessed the influence of CNT distribution profiles, cutout aspect ratios, and boundary conditions. The principal findings can be summarized as follows:

–   The proposed IQ4 element demonstrated excellent performance in predicting natural frequencies of FG-CNTRC plates, particularly in capturing shear deformation and coupling effects, with reduced computational cost.

–   Among the CNT distribution patterns, the FG-X configuration consistently yielded the highest natural frequencies due to the surface-concentrated reinforcement. At the same time, the FG-O layout resulted in the lowest frequencies due to mid-plane CNT concentration.

–   The increase in longitudinal cutout aspect ratio (c/a) had a more significant effect on frequency reduction than the transverse ratio (d/b), especially in FG-O and FG-V configurations, highlighting the importance of axial stiffness in dynamic response.

–   Larger cutout sizes were generally associated with decreased stiffness and reduced frequency values, with the FG-X layout exhibiting the most robust performance under increasing geometric discontinuities.

–   The effect of boundary conditions was observed, where fully clamped plates exhibited higher frequencies than simply supported ones, due to enhanced edge constraints and stiffness.

–   The study confirms that optimal CNT distribution, particularly surface-focused patterns like FG-X, combined with controlled cutout geometry, can significantly improve nanocomposite plates’ dynamic performance in advanced engineering applications.

The developed computational model provides an accurate and efficient tool for the vibrational analysis of FG-CNTRC plates with geometric discontinuities. This study’s findings are a useful reference for future investigations involving different cutout shapes, locations, and composite configurations, contributing to the structural optimization of high-performance materials in aerospace, mechanical, and civil engineering domains.

Acknowledgement: The authors thank all collaborators for contributing to this research.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Boudjema Bendaho and Zakaria Belabed; methodology, Zakaria Belabed; software, Abdelhak Mesbah; validation, Boudjema Bendaho, Abdelhak Mesbah, and Zakaria Belabed; formal analysis, Zakaria Belabed; investigation, Boudjema Bendaho; resources, Abdelhak Mesbah; data curation, Boudjema Bendaho; writing—original draft preparation, Boudjema Bendaho; writing—review and editing, Zakaria Belabed; visualization, Abdelhak Mesbah; supervision, Zakaria Belabed; project administration, Zakaria Belabed. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The corresponding author can provide the datasets generated or analyzed during this study, upon a reasonable request.

Ethics Approval: The present work is purely computational/theoretical and did not require approval from an ethics committee, as no human or animal subjects were involved.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kalhori A, Bayat MJ, Asemi K. Buckling analysis of stiffened functionally graded multilayer graphene platelet reinforced composite plate with circular cutout embedded on elastic support subjected to in-plane normal and shear loads. Results Eng. 2023;20(6348):101563. doi:10.1016/j.rineng.2023.101563. [Google Scholar] [CrossRef]

2. Singh D, Kiran R, Vaish R. Vibration and buckling analysis of agglomerated CNT composite plates via isogeometric analysis using non-polynomial shear deformation theory. Eur J Mech A. 2023;98(1):104892. doi:10.1016/j.euromechsol.2022.104892. [Google Scholar] [CrossRef]

3. Kalgutkar AP, Banerjee S. Dynamic instability analysis of perforated stiffened laminated composite panels subjected to non-uniform in-plane edge load under hygrothermal condition. Thin Walled Struct. 2022;181(2):109961. doi:10.1016/j.tws.2022.109961. [Google Scholar] [CrossRef]

4. Taibi N, Belabed Z, Boucham B, Benguediab M, Tounsi A, Khedher KM. On the thermomechanical behavior of laminated composite plates using different micromechanical-based models for coefficients of thermal expansion (CTE). J Appl Comput Mech. 2024;10(2):224–44. doi:10.22055/jacm.2023.44257.4191. [Google Scholar] [CrossRef]

5. Guerine MHE, Belabed Z, Tounsi A, Mohamed SM, Althobaiti S, Selim MM. On the free vibration behavior of carbon nanotube reinforced nanocomposite shells: a novel integral higher order shear theory approach. Struct Eng Mech. 2024;91(1):1. doi:10.12989/sem.2024.91.1.001. [Google Scholar] [CrossRef]

6. Ratankumar SV, Koteswara Rao L, Kiran Kumar M. Design of multi-valued logic circuit using carbon nano tube field transistors. Comput Mater Contin. 2022;73(3):5283–98. doi:10.32604/cmc.2022.027975. [Google Scholar] [CrossRef]

7. Wang Y, Liu B, Zhu J, Zhou W, Jiang L, Pan C, et al. Thermal vibration of stiffened FGM plates with cutouts using Nitsche-based isogeometric approach. Thin Walled Struct. 2025;210(8):113026. doi:10.1016/j.tws.2025.113026. [Google Scholar] [CrossRef]

8. Zeinali M, Rahimi G, Hosseini S. Buckling load optimization of sandwich plates with trapezoidal corrugated core and elliptical cutout using vibration correlation techniques and artificial neural network; experimental and numerical analysis. Thin Walled Struct. 2024;200(2):111957. doi:10.1016/j.tws.2024.111957. [Google Scholar] [CrossRef]

9. Yu W, Guo R, Zhao Y, Chen M. Isogeometric flutter analysis of a heated laminated plate with and without cutout. Thin Walled Struct. 2025;206:112652. doi:10.1016/j.tws.2024.112652. [Google Scholar] [CrossRef]

10. Dewangan HC, Panda SK, Sharma N. A review of linear and nonlinear structural responses of laminated flat/curved panels with and without cutout under thermo-mechanical loading. Compos Struct. 2023;303:116340. doi:10.1016/j.compstruct.2022.116340. [Google Scholar] [CrossRef]

11. Fan F, Cai X, Sahmani S, Safaei B. Isogeometric thermal postbuckling analysis of porous FGM quasi-3D nanoplates having cutouts with different shapes based upon surface stress elasticity. Compos Struct. 2021;262(6):113604. doi:10.1016/j.compstruct.2021.113604. [Google Scholar] [CrossRef]

12. Jana K, Pal S, Haldar S. Modal analysis of power law functionally graded material plates with rectangular cutouts. Mech Based Des Struct Mach. 2024;52(5):2411–39. doi:10.1080/15397734.2023.2180033. [Google Scholar] [CrossRef]

13. Geng X, Zhao L, Zhou W. Finite-element buckling analysis of functionally graded GPL-reinforced composite plates with a circular hole. Mech Based Des Struct Mach. 2021;49(7):1028–44. doi:10.1080/15397734.2019.1707688. [Google Scholar] [CrossRef]

14. Mirzaei M. Vibrations of FG-CNT reinforced composite cylindrical panels with cutout. Mech Based Des Struct Mach. 2022;50(1):79–99. doi:10.1080/15397734.2019.1705165. [Google Scholar] [CrossRef]

15. Tran TT, Huong HTT. The nonlinear free vibration analysis-based an enhanced finite element procedure of tri-functionally graded sandwich plates with a square central cutout. Mech Based Des Struct Mach. 2025;53(5):3736–58. doi:10.1080/15397734.2024.2435567. [Google Scholar] [CrossRef]

16. Prusty JK, Papazafeiropoulos G, Sahu DP, Mohanty SC. Free vibration analysis of sandwich shells with cutouts: an experimental and numerical study with artificial neural network modelling. Mech Adv Mater Struct. 2024;1–13. doi:10.1080/15376494.2024.2414412. [Google Scholar] [CrossRef]

17. Ghadiri Rad MH, Hosseini SM. Application of the CUF-EFG method for buckling analysis of the multilayer GPLs–CNTs-reinforced FG plates with cutout. Mech Adv Mater Struct. 2024;31(3):533–49. doi:10.1080/15376494.2022.2116664. [Google Scholar] [CrossRef]

18. Singh D, Gupta A. Effect of circular and elliptical cutouts on the free vibration analysis of sandwich FGM plate under the elastic foundations. Mech Based Des Struct Mach. 2025;53(3):2363–89. doi:10.1080/15397734.2024.2408604. [Google Scholar] [CrossRef]

19. Shi S, Qi Y, Zhang C, Meng Q, Liu Y, Jin G, et al. In-plane vibration analysis of square plate with multiple cutouts. Shock Vib. 2021;2021(1):5540123. doi:10.1155/2021/5540123. [Google Scholar] [CrossRef]

20. Zheng J, Zhang C, Khan A, Sebaey TA, Farouk N. On the asymmetric thermal stability of FGM annular plates reinforced with graphene nanoplatelets. Eng Comput. 2022;38(5):4569–81. doi:10.1007/s00366-021-01463-y. [Google Scholar] [CrossRef]

21. Lee SY. Dynamic stability and nonlinear transient behaviors of CNT-reinforced fiber/polymer composite cylindrical panels with delamination around a cutout. Nonlinear Dyn. 2020;99(4):2551–69. doi:10.1007/s11071-020-05477-x. [Google Scholar] [CrossRef]

22. Chen SX, Sahmani S, Safaei B. Size-dependent nonlinear bending behavior of porous FGM quasi-3D microplates with a central cutout based on nonlocal strain gradient isogeometric finite element modelling. Eng Comput. 2021;37(2):1657–78. doi:10.1007/s00366-021-01303-z. [Google Scholar] [CrossRef]

23. Zeighami V, Jafari M. Stress analysis of perforated composite plates reinforced with carbon nanotubes with different distributions. Emergent Mater. 2021;4(6):1711–23. doi:10.1007/s42247-021-00191-9. [Google Scholar] [CrossRef]

24. Shojaee T, Mohammadi B, Pourhosseinshahi M, Zeydabadi I. Buckling and post-buckling analysis of composite laminates with cutout under compressional loading based on the first-order shear deformation theory. Acta Mech. 2023;234(5):2145–65. doi:10.1007/s00707-023-03486-6. [Google Scholar] [CrossRef]

25. Kumar R, Kumar R, Tiwari S, Hirwani CK. Finite element modelling and dynamic behavior analysis of sandwich panel with cutout. In: Polymer composites: from computational to experimental aspects. Singapore: Springer Nature; 2024. p. 287–311. doi:10.1007/978-981-97-0888-8_14. [Google Scholar] [CrossRef]

26. Ansari R, Hassani R, Hasrati E, Rouhi H. Geometrically nonlinear vibrations of FG-GPLRC cylindrical panels with cutout based on HSDT and mixed formulation: a novel variational approach. Acta Mech. 2021;232(9):3417–39. doi:10.1007/s00707-021-03000-w. [Google Scholar] [CrossRef]

27. Fazilati J, Khalafi V. Panel flutter analysis of perforated plate repaired by VSCL bonded patch using the multi-patch IGA approach. Thin Walled Struct. 2021;169(1):108465. doi:10.1016/j.tws.2021.108465. [Google Scholar] [CrossRef]

28. Chand Dewangan H, Kumar Panda S, Kumar Hirwani C. Numerical deflection and stress prediction of cutout borne damaged composite flat/curved panel structure. Structures. 2021;31:660–70. doi:10.1016/j.istruc.2021.02.016. [Google Scholar] [CrossRef]

29. Mohamed NA, Shanab RA, Eltaher MA, Abdelrahman AA. Vibration response of viscoelastic nanobeams including cutouts under moving load. Results Eng. 2023;20(5):101407. doi:10.1016/j.rineng.2023.101407. [Google Scholar] [CrossRef]

30. Li Q, Huang W, Sanchez J, Wang P, Ding Q, Wang J. Free vibration analysis of rectangular plate with cutouts under elastic boundary conditions in independent coordinate coupling method. Comput Model Eng Sci. 2023;134(3):2093–121. doi:10.32604/cmes.2022.021340. [Google Scholar] [CrossRef]

31. Mirzaei M, Kiani Y. Free vibration of functionally graded carbon-nanotube-reinforced composite plates with cutout. Beilstein J Nanotechnol. 2016;7:511–23. doi:10.3762/bjnano.7.45. [Google Scholar] [PubMed] [CrossRef]

32. Al-Wesabi FN, Alsolai H, Mustafa Hilal A, Ahmed Hamza M, Al Duhayyim M, Negm N. Piezoresistive prediction of CNTs-embedded cement composites via machine learning approaches. Comput Mater Contin. 2022;71(1):1503–19. doi:10.32604/cmc.2022.020485. [Google Scholar] [CrossRef]

33. Wang S, Li S, Zhai Z, Guo A, Qu P. Vibration characteristics of composite damping plate with randomly oriented carbon nanotube reinforced stiffeners. Int J Mech Mater Des. 2024;20(3):525–43. doi:10.1007/s10999-023-09689-y. [Google Scholar] [CrossRef]

34. Zghal S, Dammak F. Functionally graded materials: analysis and applications to FGM, FG-CNTRC and FG Porous structures. Philadelphia, PA, USA: CRC Press; 2024. doi:10.1201/9781003483786. [Google Scholar] [CrossRef]

35. Zghal S, Nasri R. Experimental investigation for forced vibration of honeycomb sandwich beams. In: Advances in acoustics and vibration. Berlin/Heidelberg, Germany: Springer; 2016. p. 223–33. doi:10.1007/978-3-319-41459-1_22. [Google Scholar] [CrossRef]

36. Zghal S, Frikha A. Static behavior of carbon nanotubes reinforced functionally graded nanocomposite cylindrical panels. In: Design and modeling of mechanical systems—III. Berlin/Heidelberg, Germany: Springer; 2017. p. 199–207. doi:10.1007/978-3-319-66697-6_20. [Google Scholar] [CrossRef]

37. Hadrich A, Zghal S, Koubaa S, Bouaziz Z. Free vibration of functionally graded porous perforated solid structures with complex shaped holes. Int J Solids Struct. 2025;319(3):113449. doi:10.1016/j.ijsolstr.2025.113449. [Google Scholar] [CrossRef]

38. Tornabene F, Viscoti M, Dimitri R. Free vibration analysis of laminated anisotropic doubly-curved shell structures reinforced with three-phase polymer/CNT/fiber material. Eng Anal Bound Elem. 2024;164:105762. doi:10.1016/j.enganabound.2024.105762. [Google Scholar] [CrossRef]

39. Wang S, Zheng C, Li S, Guo A, Qu P, Hu Y. Free vibration of functionally graded carbon nanotube-reinforced composite damping structure based on the higher-order shear deformation theory. Polym Compos. 2023;44(2):873–85. doi:10.1002/pc.27138. [Google Scholar] [CrossRef]

40. Masoodi AR, Ghandehari MA, Tornabene F, Dimitri R. Natural frequency response of FG-CNT coupled curved beams in thermal conditions. Appl Sci. 2024;14(2):687. doi:10.3390/app14020687. [Google Scholar] [CrossRef]

41. Seyfi A, Teimouri A, Dimitri R, Tornabene F. Dispersion of elastic waves in functionally graded CNTs-reinforced composite beams. Appl Sci. 2022;12(8):3852. doi:10.3390/app12083852. [Google Scholar] [CrossRef]

42. Akhila G, Natarajan S, Lian H, Katili I. Locking-free polygonal plate element based on the discrete shear projection method. Comput Struct. 2025;309:107661. doi:10.1016/j.compstruc.2025.107661. [Google Scholar] [CrossRef]

43. Makarim Katili A, Bletzinger KU, Katili I. An enrichment of Q4γ plate finite element using incomplete quadratic functions, an assumed energy orthogonality of Bergan’s free formulation, and mixed transverse shear strains. Comput Struct. 2025;307:107619. doi:10.1016/j.compstruc.2024.107619. [Google Scholar] [CrossRef]

44. Belabed Z. A new application of quadrilateral finite element model incorporating the discrete shear projection technique for free vibration response of CNT reinforced plates. Int J Solids Struct. 2025;309(23):113204. doi:10.1016/j.ijsolstr.2024.113204. [Google Scholar] [CrossRef]

45. Batoz JL, Katili I, Widyatmoko S, Antaluca E. An efficient shear and bending-locking-free quadrilateral plate element using a modified Hellinger-Reissner functional and the Bergan free formulation. Int J Numer Meth Eng. 2024;125(12):e7451. doi:10.1002/nme.7451. [Google Scholar] [CrossRef]