Generated Preserved Adversarial Federated Learning for Enhanced Image Analysis (GPAF)

1  Introduction

Recent advances in artificial intelligence (AI) have significantly improved healthcare quality and increased life expectancy. Deep learning models show particular promise in addressing complex healthcare challenges [1]. These models, however, require access to large-scale, high-quality datasets to achieve robust performance. Therefore, Limited datasets constrained the development of effective AI applications in healthcare field. To address this limitation, federated learning (FL) enables multiple medical institutions to train a global model collaboratively while preserving strict privacy guarantees. Specifically, each medical site shares only its local model parameters with a central server. This decentralized paradigm provides a viable alternative to traditional centralized learning [2]. Therefore, FL has gained wide adoption in critical medical applications, such as brain tumor detection [3] and COVID-19 diagnosis [4]. However, one key challenge in FL is data heterogeneity. Clients collect their private data using different equipment, scanners, and imaging protocols [5]. As a result, shifts in feature distributions arise across clients, causing a domain shift issue. Consequently, models trained under these conditions fail to learn robust domain-invariant representations and may not capture domain characteristics beyond their local datasets. A common aggregation method in federated learning (FL), such as FedAvg [6], computes the global model by averaging local model updates. While this approach has demonstrated its effectiveness in use cases, it does not account for differences in data distributions. This can lead to increased divergence among client models in the parameter space. As a result, the global model may become biased toward dominant local distributions, thereby hindering the overall performance of the FL system. To tackle this issue, a significant effort has been made in domain adaptation (DA) [7], which aims to reduce the distribution shifts between source and target domains. However, this approach faces two key limitations: First it requires access to a labeled target dataset, which is often impractical in privacy-sensitive domains like healthcare. Secondly, it must be retrained for each new unseen target domain, leading to computational and time-consuming burdens. Therefore, Domain generalization (DG) methods [8] have been proposed to align feature distributions across multiple source domains. This is achieved by training a model that can generalize effectively to unseen domains, without requiring access to the target domain during training. However, most existing methods rely on simultaneous access to diverse datasets to learn domain-invariant features, which is not feasible in a federated learning setting due to privacy constraints and communication overhead. To address this, significant efforts have been directed toward federated domain generalization (FedDG). These methods aim to enhance model robustness on unseen data distributions while adhering to the core principles of federated learning (FL). For example, a disease diagnosis model trained collaboratively by multiple hospitals should perform accurately when applied to new hospitals, even when their data distributions shift. This requires the model to learn domain-invariant representations across clients in a decentralized manner. One common approach involves clients sharing data-related information to learn a global data distribution [9]. However, these methods contradict the core privacy principles of the FL paradigm and introduces significant communication overhead. Similarly, adversarial learning approaches [10] align the local feature distributions of multiple participants through the optimization of a domain loss on the server. These methods necessitate that clients upload their local feature representations and then receive domain loss gradients for local optimization. Such frequent exchanges of local features, gradients, and data information expose the FL training process to privacy vulnerabilities [11]. For instance, this information is susceptible to exploitation in model inversion attacks [12]. Furthermore, a key limitation of these methods is their reliance on strict synchronous updates, which forces clients to wait for server-side domain loss gradients to perform local optimization. In practice, this design can lead to significant delays due to client unavailability and computational heterogeneity, leading to the rise of stragglers. The subsequent use of stale or outdated features from these clients negatively impacts adversarial optimization, which consequently reduces the scalability and robustness of real-world FL systems. To solve these challenges, we propose a preserved adversarial framework (GPAF) that learns domain-invariant features by aligning both marginal and conditional distributions across clients. GPAF tackles two key challenges: (1) mitigating domain and label shifts in federated settings, and (2) ensuring robust model generalization without compromising privacy or requiring synchronous coordination. Notably, GPAF introduces no additional communication overhead or coordination requirements. Clients perform domain alignment locally and communicate only their model parameters to the server, which preserves the classic FedAvg structure. In this way, GPAF enables scalable and stable training in asynchronous FL environments.

Moreover, existing approaches primarily align marginal feature distributions across clients to learn domain-invariant representations. These methods often assume the conditional distribution, P(Y∣X), remains consistent across different domains in a federated learning (FL) setting. Similarly, much of the research in domain adaptation (DA) adopts the label shift assumption, which holds that P(Y∣X) is consistent while the marginal distribution, P(X), differs. However, this foundational assumption is typically violated in practice, especially in fields like medicine where healthcare institutions serve distinct populations influenced by local demographics, healthcare practices, and resource availability. This means that data on each node is collected in a non-IID manner, with both the prevalence of labels, P(Y), and the conditional relationship between features and labels, P(Y∣X), varying across clients. Consequently, models trained under these assumptions often fail to generalize when both domain and label shifts are present. For instance, during the COVID-19 pandemic, changes in patient age distribution and treatment protocols were shown to alter clinical outcomes [13], thereby violating the label shift assumption. As a result, FL models trained under these assumptions often fail to generalize when both domain and label shifts are present. Data-free knowledge distillation [14] employs a global server-side generator to synthesize pseudo features. However, they merely perform simple model aggregation at the server, which ignores features shifts across clients. This motivate us to leverage a global generator to model conditional distribution at server. We further enhance the generator with a consistency loss, which encourages the generator to converge toward a consensus representation, and a diversity loss to mitigate mode collapse, thus improving the robustness of the global model. On the other hand, aggregating local models neglects the diverse data distributions across clients, which can potentially harm the FL performance.

Motivated by these observations, we propose GPAF, a novel approach that aligns conditional distribution across clients to encourage the learning of robust, domain-invariant features. Our method integrates adversarial alignment during local training to enforce conditional alignment. At the server, the global generator models a global conditional Q(Y∣X). On the client side, adversarial learning is employed to reduce discrepancies between local and global representations, thereby aligning the conditional distributions across all clients. GPAF ensures that clients perform conditional alignment using only their own data through local adversarial training. GPAF uses this generator as a reference for aligning client representations. In this work, we highlight the following main contributions:

•   We propose GPAF, a novel federated learning framework that addresses both domain and label shifts by aligning marginal and conditional distribution.

•   GPAF aligns each client’s local conditional feature distribution with a global distribution through local adversarial learning, eliminating the need for a target dataset on the cloud.

•   We introduce a new global model F, initialized with global parameters, to guide the generator in learning consistent features. We further enhance the generator with a consistency loss and a diversity loss to mitigate mode collapse and improve overall generator performance.

•   GPAF performs domain alignment locally, guided by the server’s global knowledge, to ensure privacy and communication efficiency, thus enhancing DG approaches that require synchronous coordination between client feature extractors and server-side domain losses.

•   Through extensive experiments on two medical benchmarks, we show that GPAF outperforms several state-of-the-art (SOTA) federated learning methods, such as FedAvg, MOON, and FedDG.

The paper is organized into the following sections. In Section 1, the limitations of existing approaches in handling domain shift are outlined. Section 2 reviews related works and highlights their limitations. In Section 3, we present our proposed method, GPAF, a privacy-preserving federated learning framework that addresses both domain and label shifts. We describe the training of a global generator at the server and adversarial learning with variational autoencoders (VAEs) to align local and global distributions on the client side. In Section 4, we validate our method using 2 medical benchmark datasets under domain shift and non-IID settings. Finally, in Section 5, we discuss future directions for advancing federated learning in healthcare field through robust domain generalization strategies.

2  Related Works

A primary obstacle in federated learning (FL) is the performance degradation that results from data heterogeneity. There is a large body of existing work on regularization techniques to mitigate statistical heterogeneity and client drift [15,16]. However, these methods often fail to generalize to new domains due to domain shift. To address this, Federated Domain Generalization (FedDG) has emerged, integrating domain generalization (DG) principles into FL. A key approach to achieving this goal is representation learning, which has shown great success in DG. This approach captures common structures across various source domains. Consequently, representation learning can be extended to compel clients to learn domain-invariant features within a federated learning setting. For instance, Wu and Gong [17] proposed the COPA framework that encourages learning domain-invariant feature representation through a local feature extractor with hybrid batch-instance normalization. While the server aggregates the feature extractors, it also broadcasts an ensemble of domain-specific classifiers to all clients. This practice, however, can raise privacy concerns and increase communication overhead. Liu et al. [9] proposed FedDG, a method that leverages frequency domain transformation to preserve privacy. In this approach, clients share the amplitude spectrum and retain the phase spectrum locally to protect semantic content. The server then aggregates the shared amplitudes into a distribution bank, which clients use during local training to synthesize style-transferred data. A key limitation of this approach is that the frozen amplitude information may still leak distribution-specific characteristics, thereby posing a privacy risk as adversaries could potentially infer sensitive information. Chen et al. [18] proposed CCST, a framework that mitigates distributions discrepancies across clients. Clients extract style representations using a transformation technique (e.g., AdaIN) and send them to the server, which aggregates them into a global style bank. This bank is then redistributed to clients for local data augmentation. Each client augments their data with diverse styles to reduce client-specific biases. While this strategy enhances generalization, it introduces privacy concerns and increased communication costs, especially when multiple style representations are shared per client.

Recent works have extended Domain-Adversarial Neural Networks (DANN) to the federated learning setting to extract domain-invariant features across clients. DANN introduces a domain discriminator to identify the origin of the feature representations [19]. In FedAKA [20], a two-phase adversarial framework is employed to enhance domain generalization in FL. In the first phase, a global discriminator is trained at the server using both clients’ local features and target features. The discriminator objective is to learn to distinguish between features originating from a specific client or those from the target domain. In the second phase, the server transmits the gradients of the domain loss to each client. A gradient reversal layer is then applied to adversarially update local encoders, a process that encourages the extraction of domain-invariant features. Additionally, FedAKA reduces distributions discrepancies between sources and target domains by minimizing the (MMD) loss.

In federated fault diagnosis, recent methods adopt adversarial learning to handle domain shifts. These approaches jointly optimize a domain loss at server to encourage domain-invariant features [21]. Another federated transfer learning for machinery fault diagnosis uses synthetic priors to align class-wise distributions via MMD in a privacy-preserving manner [22]. However, these approaches compromise privacy by sharing client-specific information with the server, which exposes clients to potential attacks and leads to significant communication overhead. Moreover, several methods also depend on a centralized target dataset for domain alignment, contradicting the privacy-preserving goals of FL. Additionally, adversarial methods with GRL require strict synchronization between clients and the server to prevent gradient staleness, which is difficult to guarantee under communication constraints. Another line of work aims to improve privacy and employ data-free generative models to transfer knowledge in FL. For instance, FedDF [23] uses a server-side generator to synthesize data for ensemble distillation, enabling the fusion of knowledge from multiple client models into a single student model. Similarly, FedGen [14] leverages a lightweight generator to aggregate knowledge across clients and to regularize local training. However, FedGen synthesized features for local training regularization, but it fails to address domain-invariant representation learning within a federated domain generalization context. In contrast, our approach introduces a mechanism to align the conditional distributions across clients, implements a customized local adversarial alignment, and incorporates a global model F at the server to evaluate the semantic consistency of generated representations.

3  Method

3.1 Problem Statement

We propose Generated Preserved Adversarial Federated Learning (GPAF) to address the limitations of existing FL methods under both domain shift and label shift. We consider a standard FL scenario with K clients, where each client iε{1,…,K} is associated with a private dataset Di. A data sample from client i is denoted as (xji,yjj) where xji∈X is the input and yjj∈Y is its corresponding label. A feature extractor g:X→Z maps the input space X to a latent representation Z. Our goal is to train a model over these K sources domains that learn a domain invariant representation z and remain robust and generalizable across all participants.

Prior studies commonly assume that the conditional distribution P(Y∣X) remains consistent across domains. However, in real-world federated learning, this assumption is often violated due to clients’ heterogeneous conditional distributions and imbalanced label distributions.

Existing methods that align distributions at the input level, such as style harmonization [24] or data augmentation [25], primarily focus on the marginal distribution P(X). This approach, however, has key drawbacks: First, it poses potential risks to client privacy due to the necessity of indirectly exchanging data statistics. Second, it imposes substantial computational overhead. Finally, it does not ensure semantic consistency across domains, which may hinder the generalization of learned representations. To overcome these limitations, motivated by recent advances in representation learning [26], we propose GPAF, a data-free approach that aligns conditional feature distributions P(Z∣Y) across clients in the latent space. Hence, our method mitigates discrepancies among local models while preserving data privacy. Therefore, our main objective is to ensure that for each class y, the conditional feature distributions are aligned across all clients:

∀i;j=1…K,Pi(Z|Y=y)=Pj(Z|Y=y)(1)

where Pi(Z|Y=y) denotes the conditional feature distribution of client i.

Many Domain Generalization (DG) approaches aim to learn domain-invariant representations, z. To achieve this, these approaches ensure that the marginal distribution, Pi(z), and/or the conditional distributions, Pi(z|y), are consistent across domains. Conceptually, Eq. (1) illustrates that although samples from the same class may vary considerably across domains, a shared latent space can still be learned in which their representations remain consistent across clients. Direct alignment cannot be enforced in federated scenarios, as privacy requirements prohibit sharing client data and communication resources are limited. To address this, GPAF leverages a global generator at the server to model a reference distribution Q(z|y). Additionally, an adversarial alignment strategy aligns local feature distributions with global features, thus encouraging the learning of robust and domain-invariant representations. Our framework comprises two phases: A generative preserved adversarial learning and local adversarial alignment, as illustrated in Fig. 1 and detailed in Algorithm 1. During the local adversarial alignment, each client trains a VAE-based architecture with a classifier and then applies an adversarial alignment against samples generated from the global distribution, to learn robust latent representations. In generative preserved adversarial learning, a generator is trained on the server side to produce global representations z∗∼Gw(z|y) that are semantically meaningful and consistent. This entire setup enables both conditional alignment and representation diversity while preserving client privacy.

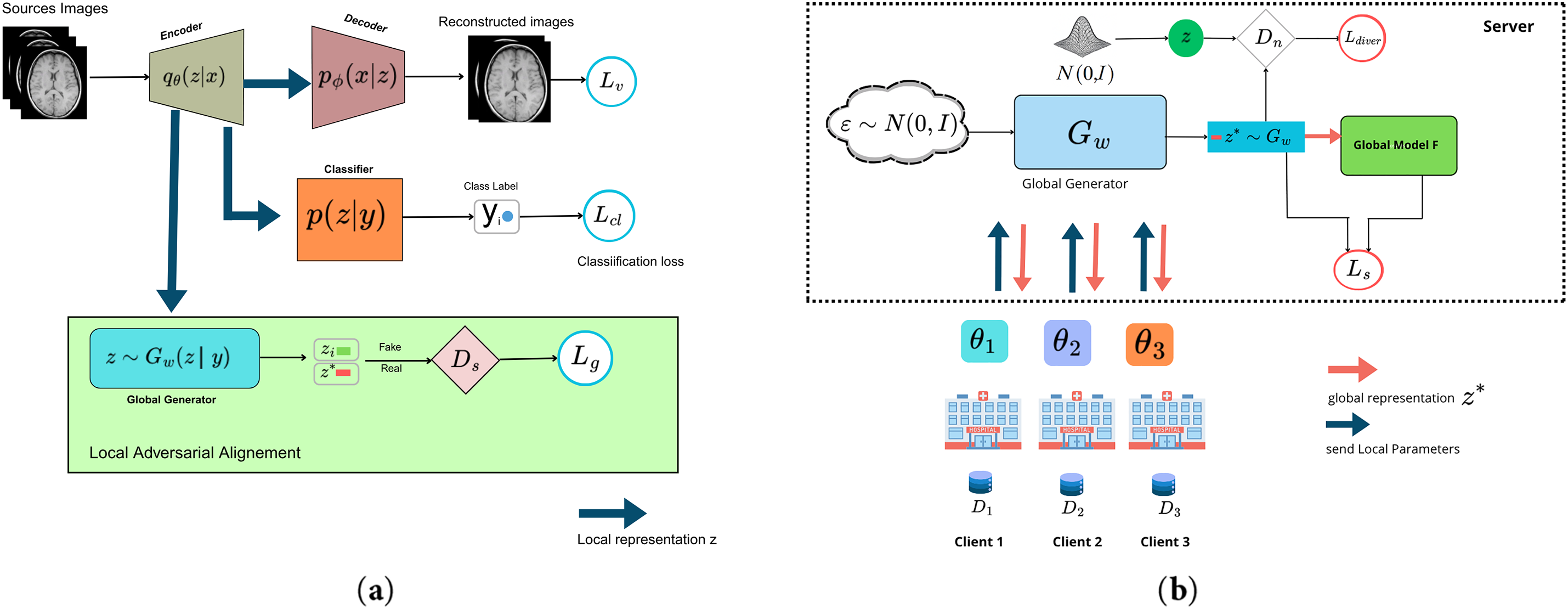
Figure 1: Overview of our federated domain generalization framework (GPAF). (a) Local adversarial alignment: each client encodes local data samples into latent representations encoder. The classifier predicts labels from latent features, and a decoder reconstructs input images. To align conditional distributions P(z|y) across clients, we sample global representations z∗∼Gw(z|y) from a class-conditional generator shared by all clients. An adversarial discriminator Ds encourages the encoder to generate features indistinguishable from z∗, minimizing Lg. (b) Generative preserved adversarial learning at server: the server the generator Gw optimized loss to generate global representation z∗. These samples are fed into a global model F, and supervised using a Ls loss. A discriminator Dn enforces class diversity in the generated features via the loss Ldiver

3.2 Generative Preserved Adversarial Learning

To model global latent representations, we aim to learn a conditional distribution Q(z|y) at the server, where z denotes the latent feature vector and y the target label. Variational Autoencoders (VAEs) [27] provide a principle approach for learning robust latent representation. A VAE models a joint distribution p(x,z)=p(z)p(x|z), where p(z) is a prior distribution over the latent space. To enable backpropagation through Gaussian latent variables, we apply the reparameterization trick: z=μ(x)+σ2(x)+ε, where ε∼N(0,1). The decoder reconstructs the true distribution pθ(x|z) from the latent representation z:p(x|z)=μ(z)+σ(z) and the encoder approximates the posterior q∅(z|x). The VAE is trained to minimize the following empirical loss:

LVAE(x,θ,ϕ)=−KL(q∅(z|x)||pθ(z))+1L∑l=1Llog⁡pθ(x|z)(2)

VAEs are trained to minimize an objective Eq. (2) that includes a Kullback-Leibler (KL) divergence term, which regularizes the posterior q∅(z|x) toward the prior p(z) and a reconstruction term, which ensures accurate reconstruction of the input data. However, the implementation of VAEs models on the server side directly in a federated learning setting presents significant challenges. These models can be complex and computationally expensive to train. Furthermore, some approaches still require clients to transmit sensitive feature information, which could potentially compromise FL’s privacy-preserving design. To address this issue, we leverage a data-free knowledge distillation generator which aligns the ensemble clients’ predictions with the ground-truth labels: p^(y|x)≈1K∑k=1Klog⁡p(y|x;θk), where θkC denotes the parameters of the local classifier at client k. Concretely, the server trains a global generator Gw(z|y) parametrized by w, to generate global features representation z∼Gw(z|y). During global training, we feed the generator with label vectors y that are sampled from a Dirichlet distribution. Hence the latent representations z are generated via the reparameterization trick: z=μ(y)+σ(y)⋅ε where ε ∼N(0,I) to solve the following objective:

LKD=Ez∼Gw(z|y)[ℓ(σ(1K∑k=1Kg(z;θkC)),y)](3)

here, ℓ denotes the cross-entropy loss and σ is the SoftMax function. The loss compares the ensemble prediction, which results from averaging the logits of all local classifiers, to the ground truth label y. LKD encourages the global generator to produce semantically meaningful representations that remain consistent with the collective knowledge of all clients. Meanwhile, we introduce a new global classifier model F as shown in Fig. 1 in server that maps the latent representations z to predict the correct label. Hence, we minimize a new consistence loss LGM Eq. (4), which aligns the generator output with the current F prediction. Specifically, the objective function is defined as:

LGM=Ez∼Gw(z|y)[ℓ(σ(1K∑k=1Kg(z;θkc));(z))](4)

LGM encourages the generator to optimize its output toward regions where the ensemble consensus is strongest in the latent space. As a result, the generated representations are correctly classified by the global model F, which mitigates early-stage representation drift. The overall loss is given by:

Ls=λLKD+(1−λ)LGM(5)

where λ balances the contributions of the two terms. The generator minimizes Ls to produce semantically meaningful representations while maintaining robustness and alignment across all clients.

Moreover, generative models often suffer from mode collapse, where the generator learns to produce samples from only a few regions of the data distribution, thereby failing to capture its complete diversity [28]. In order to mitigate this issue, prior studies [29,30] have proposed adding a discriminator to an autoencoder to enforce a match between the learned posterior and the prior, p(z). Following this principle, we incorporate a discriminator Dn, trained to differentiate between samples from the global conditional distribution Q(z|y), and those from the prior p(y). This adversarial setup is optimized using a minimax objective [31]:

Ldiver=minDmaxGEz∼p(z)[log⁡(Dn((z))]+Ey∼p(y)Ez∼Q(z|y)[log⁡(1−Dn(z))](6)

The global training aims to minimize a global loss J, as defined in Eq. (7):

minwJ=λ1Ls+λ2Ldiver(7)

where λ1 and λ2 are hyperparameters tuned during evaluation. The global generator acts as a proxy for the collective knowledge of all clients, resulting in potential privacy enhancement. Once the training completes, the server updates the global model parameters through aggregation using the standard FedAvg optimization. Specially, the aggregated parameters are computed as:

θC=1k∑i=1KθiCand θE=1k∑i=1KθiE(8)

where θC and θE denote the global classifier and encoder classifier parameters, respectively. The server then sends the updated global model and the lightweight optimized generator Gt.

3.3 Local Adversarial Alignment

On the client side, we establish the training as a classification imaging task. Each client’s local model consists of four components: an encoder Es, a decoder Us, a discriminator Ds and a classifier Cs. Our solution adheres to the same security principles as the traditional FL. We only share model parameters to the server with a communication-efficient strategy. The primary goal of the local model is to learn robust feature representations through the local encoder Es. The encoder maps input images xi∈RC×H×W to latent vector zi∈Rd and estimates the posterior distribution q(z|x). The decoder Us then reconstructs the input image from local features zi, i.e., Us(zi)=x^i, thus modeling the true distribution p(x|z). The VAE can be formulated by the following objective:

Lv=−KL(qθ(z|x),p(z))+‖x−x^‖22(9)

where the KL term acts as a regularizer to ensure the learned latent representations remain close to the prior distribution p(z), while the second term measures how well the reconstructed image x^ approximates the true input x from the generated local representation zi. The goal of the classifier Cs is to predict label y^ from zi, by minimizing the classification loss, which can be formulated by the following cross-entropy as follow:

Lcl=∑j=1Nk∑i=1C1{yj=i}log⁡efj,i∑m=1Cefj,m(10)

where efj,i is the i-th output of the final layer of the classifier Cs on client k for the j-th sample, C is the number of classes, and Nk is the number of training samples on client k.

From the objective in Eq. (1), our approach aims to align the conditional feature distributions P(z|y) across clients to achieve a form of domain-invariant representation learning. However, estimating P(z|y) directly is computationally challenging, as it involves integration over the input space x. Inspired by the class-conditional alignment bounds of Smith et al. [32], which show that minimizing the KL divergence between the posterior P(z|x) and a reference distributions Q(z∣y) serves as an upper bound on the KL divergence between Pi(z|y) and distribution reference. We formalize this insight with the following proposition:

Proposition 1: Let qi(x|y) be the posterior of client i, and let Q(z|y) be the global conditional distribution at server, then we have:

Epi(x,y)[KL(qi(x|y)||Q(z|y)]≥Ey∼pi(y)[KL(pi(z|y)||Q(z|y))](11)

Given the bound established in Eq. (11), we effectively minimize the KL divergence KL(pi(z|y)|Q(z|y)) for all labels y. Therefore, this alignment encourages pi(z∣y) to converge toward the global Q(z|y), i.e., pi(z∣y)≈Q(z|y). As a result, this also implies that the conditional distributions across different clients are aligned:

pi(z∣y)≈Q(z∣y)≈pj(z∣y)(12)

To avoid the computational intractability of directly minimizing the KL divergence between local and global conditional distributions KL(pi(z|y)|Q(z|y)) in Eq. (11). We adopt an adversarial objective that is equivalent to the minimization of the Jensen–Shannon divergence (JSD). Hence, we propose a client-side adversarial learning. Each client trains a discriminator Ds, which distinguishes between samples from the global distribution Q(z|y) and those generated by local encoder q(z|x). The encoder Es is trained to confuse the discriminator, thus encouraging its output to be indistinguishable Q(z|y). The adversarial loss is given by:

Lg=minEmaxDEz*∼Q(z|y)[log⁡(Ds((z*))]+Ez∼q(z|x)[log⁡(1−Ds(z))](13)

Crucially, the adversarial loss in Eq. (13) is computed entirely on the client side and does not require gradient exchange or synchronization with the server. As a result, GPAF is both communication-efficient and robust to asynchronous setting. Hence, the total local training is optimized by the following loss:

LTotal=Lv+Lcl+λ1Lg(14)

where λ1 is a hyperparameter tuned during validation and model parameters are optimized as follows:

θ^Es=arg⁡{minθEsLcl+Lg},θ^Ds=arg⁡{maxθDsLg},θ^Cs=arg⁡{minθCsLcl}(15)

This optimization is performed during local training, after which the updated encoder and classifier parameters θ^Es, θ^Cs are transmitted to the server for global aggregation as defined in Eq. (8). The complete training procedure is summarized in Algorithm 1.

4  Experiment

4.1 Implementation Detail

To evaluate our method, we conducted experiments on two medical imaging datasets. For binary classification, we used BreastMnist [33], which contains 780 grayscale breast ultrasound images resized to 28 × 28 pixels and categorized into benign, and malignant. Following the Medmnist-C benchmark [34], we design two scenarios. In Scenario 1, we simulated domain shift and partitioned the training set into three clients representing different imaging conditions: Client 0, as the original domain of the dataset, represents a High-end equipment. Client 1 emulates mid-range equipment typically used in resource-constrained settings with a subtle change in brightness between 0.2% and 15%, lower resolution and contrast between 0.6 and 1.4. Client 2 simulates a degraded condition, mimicking challenging real-world scenarios, with increased brightness (+0.3), added gaussian noise (0.12) noise and contrast varying between 0.5 to 1.5. As shown in Fig. 2, these perturbations yield distinct pixel intensity distributions. In scenario 2, we used PathMnist dataset to simulate a realistic case of domain shift. The training set includes 100,000 hematoxylin & eosin-stained histological images from one clinical center and the test set includes 7180 images from another center. Assigning the training set to Client 0 and the test set to Client 1 introduces both domain and label shift, since Client 0 contains more samples per class. Each client’s data was further split into validation and training. We compared GPAF with three FL baselines: FedAvg, MOON, FedDG, as well as the centralized learning. On the server, a global generator Gt is a Multilayer Perceptron (MLP) with a layer normalization and a leaky ReLU activation, while the global discriminator Dt is a three-layer MLP with a sigmoid output layer. Server training optimizes Eq. (7) using Adam optimizer with a learning rate of 0.001. The adversarial and KL weights are set to λadv(s)=0.3 and λkl(s)=0.4, with batch size of 13 and 32. Labels yj are sampled from a Dirichlet distribution controlled by alpha α. The server ran for 15 epochs per round. On the client side, the encoder is a Convolutional Neural Networks (CNN) with two conv layers (64 and 128 filters, kernels 4 × 4, stride 2), the decoder uses transposed convolutions to reconstruct images from z and the classifier is an MLP, all optimized with Adam with a learning rate 0.00013914064388085564. During evaluation, we tuned the VAE and the adversarial losses lambda, respectively: λvae=1, and λadv=0.3. We set the dimensionality of the latent space z = 64 for both local and global training. We already test over different values {32, 64, 128}. This choice was guided by the fact that both PathMNIST and BreastMNIST share the same image resolution (28 × 28). The selected value of 64 offered the best trade-off between representation capacity and training stability. We use Flower framework [35] and for fair comparison we use the same hyperparameters for all FL methods. Each client trains for 30 local epochs and with 10 global iterations for BreastMnist, while for PathMnist we set the local epochs to 3 and global rounds to 300 iterations.

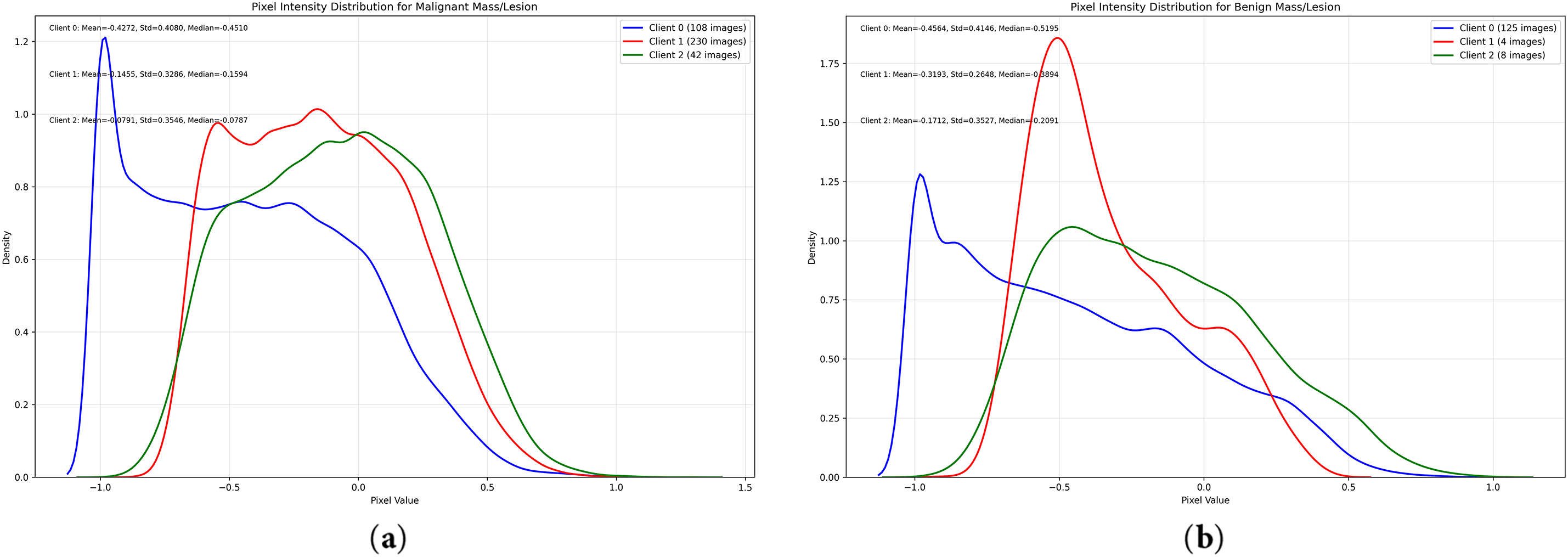
Figure 2: Profile intensities across the three clients in both classes (a) and (b) with BreastMnist dataset

4.2 Results

Table 1 presents the performance of GPAF and baseline algorithms on the BreastMnist dataset under both domain and label shift, using the Dirichlet distribution with varying alpha α. GPAF achieves the highest accuracy among all the FL methods. Our algorithm outpaces FedAvg by 8.5% when (α = 0.5) and 17% when (α = 0.1), and MOON by 10% when (α = 0.5) and by 13% when (α = 0.1). While GPAF experiences a slight accuracy drop under sever label shift (α = 0.1), it still outperforms MOON, which shows no improvement when features distributions are highly skewed. MOON learns global representation based on all clients’ average parameters without any additional information about the features’ characteristics, which limits its performance under severe domain shift. In contrast, GPAF leverages a global distribution Q(z|y) to guide each client’s local encoder toward a shared, domain-invariant latent representation through local adversarial. We also compared GPAF to a state-of-the-art centralized learning model based on the SWIM architecture. The centralized approach achieved a slightly higher accuracy (85.44%) compared to GPAF (84.62%). However, centralized approaches assume access to large, diverse, and well-labeled datasets from one domain across multiples clients, which are rarely available. Consequently, models trained on data from one site often generalize poorly to other medical sites. GPAF effectively mitigates the domain shift issue between clients without introducing additional privacy risks. To provide a more precise measurement of discrepancies in feature representation distributions, we use an t-SNE visualization as shown in Fig. 3. In subfigure (a), GPAF’s local features for the same classes form tight clusters across clients and align closely with the global features. This demonstrates an effective conditional distribution alignment of local features with a shared global distribution as their reference. The higher validation accuracies demonstrate the effective of this method. In contrast, subfigure (b) shows that MOON’s local features are scattered across distinct clusters, with global representations positioned distant from local ones. This misalignment results in poor domain generalization and reduce classification performances. Consequently, under severe domain shifts, these global representations represent the average of heterogenous clients’ parameters and lack other feature domain information. Furthermore, Fig. 4 presents a t-distributed Stochastic Neighbor Embedding (t-SNE) visualization of the conditional feature distributions across clients at iteration 8 for GPAF and FedAvg on the PathMNIST dataset. GPAF achieves superior alignment of clients’ features compared to FedAvg, which suggests that the proposed adversarial alignment effectively reduces domain discrepancies. The improved feature alignment is also reflected in classification performance: GPAF achieves an accuracy of 85%, outperforming FedAvg at 81% in the same iteration. These findings highlight that integrating a global generator with local adversarial learning enhances both representation consistency and predictive performance under domain-shifted healthcare data.

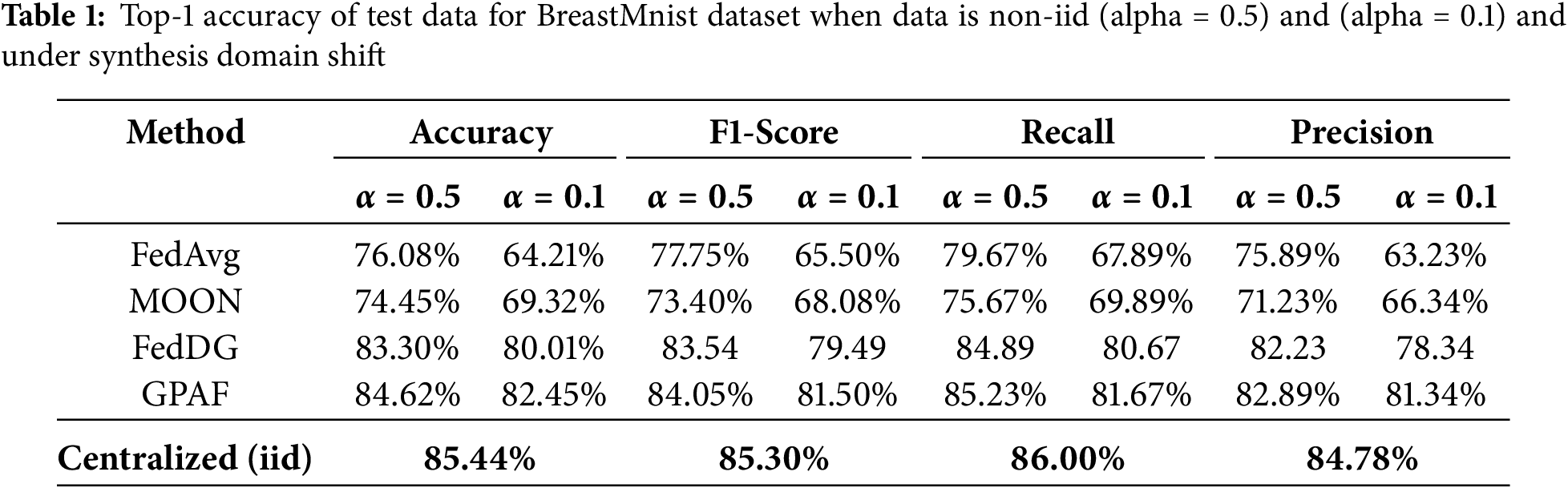
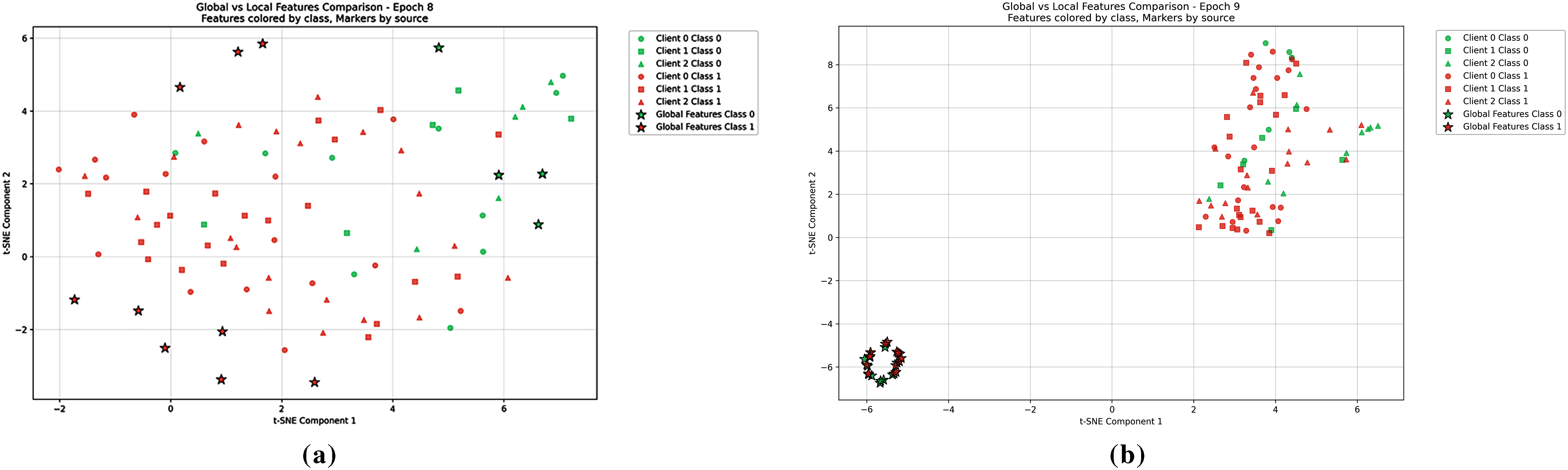
Figure 3: t-SNE visualization shows the local features of different clients of method GPAF (a) and MOON (b)

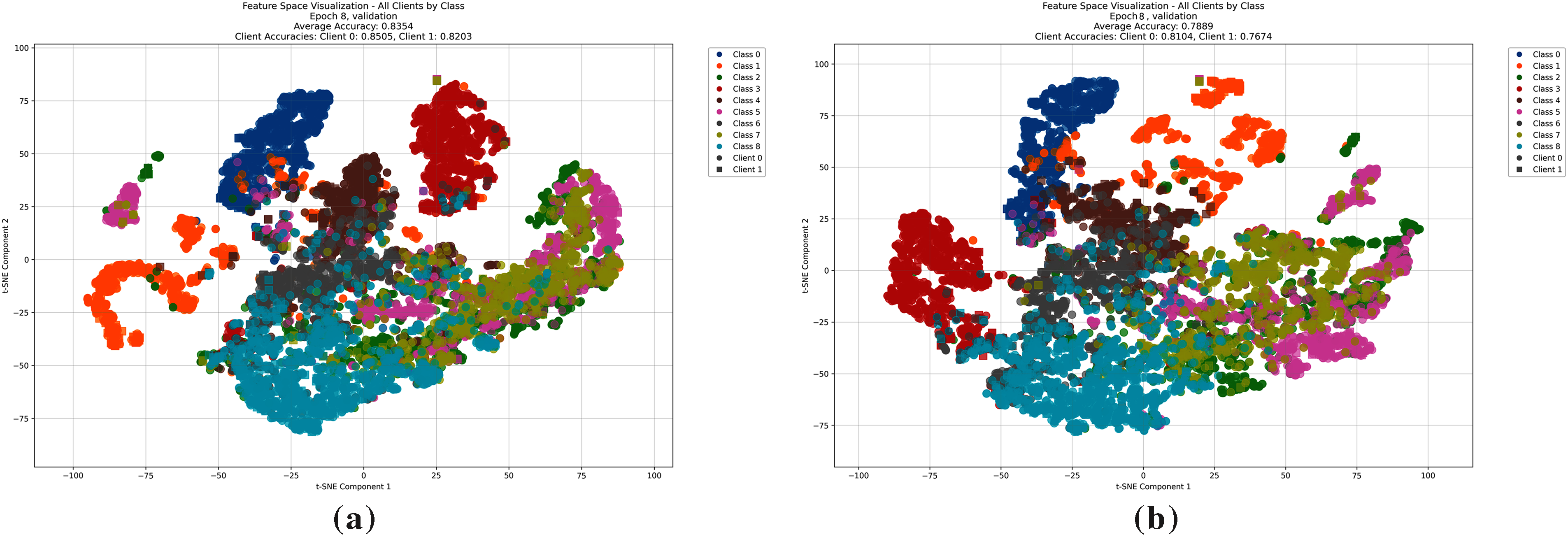
Figure 4: A t-SNE visualization of the conditional distribution across clients in iteration 8 between GPAF (a) and FedAvg (b) in PathMnist dataset

Fig. 5a shows the average validation accuracy across clients during local training phase. We recorded the accuracy only when it surpassed the previous best to monitor convergence. Although FedAvg performs well during early local epochs, GPAF surpasses it by the second global round and achieves its best accuracy at epoch 12. Fig. 5b presents the training loss curves per client. GPAF initially exhibits a significant loss variation in the early iterations, primarily because the global generator has not yet incorporated knowledge from the clients. As a result, the model experiences instability during the initial iterations. In contrast, FedAvg shows a more stable start with a lower initial loss, but it struggles to converge effectively due to the discrepancies in features distributions across clients. In later iterations, however, GPAF outperforms FedAvg and converges more rapidly. This indicates that GPAF’s global generator and local adversarial help align clients’ local features and encourage client to learn more domain invariant representations under domain shift.

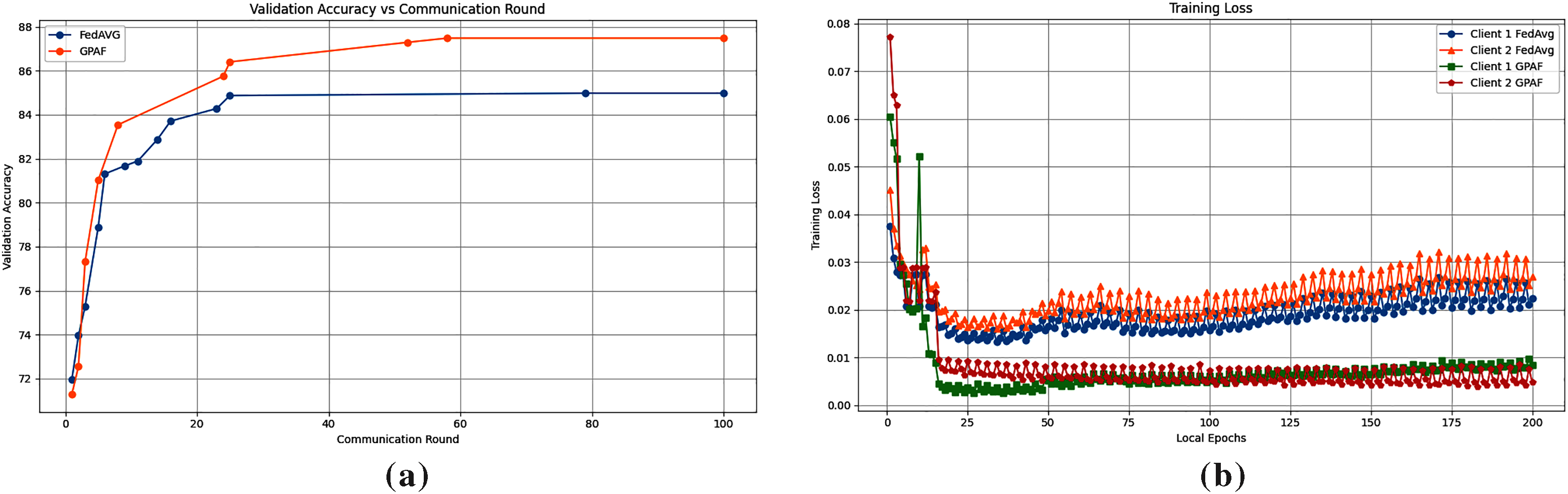
Figure 5: Comparing FedAvg to GPAF in (a) we report best average during communication rounds accuracy in valid set and (b) we report the training loss of clients in local epochs

5  Conclusion

Existing (FDG) methods face privacy risks from client data exposure, incur high communication costs, and often depend on centralized target datasets. We propose GPAF, a communication-efficient framework designed to address both domain and label shift challenges in healthcare field. Clients learn domain-invariant features locally without sharing any other information than client parameters. We believe that enhancing privacy in domain generalization is a promising direction. This opens a compelling path for future research toward privacy-aware domain generalization in real-world FL. Consequently, we aim to evaluate robust aggregation methods [36,37] within DG-FL methods for strengthening privacy. Further, we aim to extend GPAF to asynchronous federated learning, where client-server interactions do not require strict synchronization to handle domain shift. Unlike existing FDG methods that rely on client-server coordination to learn domain invariant features across clients or shared client data. However, because domain alignment is performed locally, resource-constrained clients may face computational bottlenecks. This trade-off highlights an important direction for future research. We further believe that improving efficiency on the client side supports robust, scalable deployment in real-world healthcare systems.

Acknowledgement: The authors acknowledge the support of Smart Communication Research Team of Mohammedia School of Engineers. We also thank the reviewers for their valuable feedback.

Funding Statement: No funding.

Author Contributions: Sanaa Lakrouni: Writing—original draft Software, Methodology, Formal analysis. Slimane Bah: Writing—review & editing, Supervision. Marouane Sebgui: Supervision, writing—review. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available at https://github.com/MedMNIST/MedMNIST (accessed on 25 August 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Rieke N, Hancox J, Li W, Milletarì F, Roth HR, Albarqouni S, et al. The future of digital health with federated learning. npj Digit Med. 2020;3(1):119. doi:10.1038/s41746-020-00323-1. [Google Scholar] [PubMed] [CrossRef]

2. Yan R, Qu L, Wei Q, Huang SC, Shen L, Rubin DL, et al. Label-efficient self-supervised federated learning for tackling data heterogeneity in medical imaging. IEEE Trans Med Imaging. 2023;42(7):1932–43. doi:10.1109/TMI.2022.3233574. [Google Scholar] [PubMed] [CrossRef]

3. Sheller MJ, Edwards B, Reina GA, Martin J, Pati S, Kotrotsou A, et al. Federated learning in medicine: facilitating multi-institutional collaborations without sharing patient data. Sci Rep. 2020;10(1):12598. doi:10.1038/s41598-020-69250-1. [Google Scholar] [PubMed] [CrossRef]

4. Dayan I, Roth HR, Zhong A, Harouni A, Gentili A, Abidin AZ, et al. Federated learning for predicting clinical outcomes in patients with COVID-19. Nat Med. 2021;27(10):1735–43. doi:10.1038/s41591-021-01506-3. [Google Scholar] [PubMed] [CrossRef]

5. Li L, Xie N, Yuan S. A federated learning framework for breast cancer histopathological image classification. Electronics. 2022;11(22):3767. doi:10.3390/electronics11223767. [Google Scholar] [CrossRef]

6. McMahan HB, Moore E, Ramage D, Hampson S, Arcas BA. Communication-efficient learning of deep networks from decentralized data. arXiv:1602.05629. 2016. doi:10.48550/ARXIV.1602.05629. [Google Scholar] [CrossRef]

7. Guan H, Liu M. Domain adaptation for medical image analysis: a survey. arXiv:2102.09508. 2021. doi:10.48550/ARXIV.2102.09508. [Google Scholar] [CrossRef]

8. Zhou K, Liu Z, Qiao Y, Xiang T, Loy CC. Domain generalization: a survey. IEEE Trans Pattern Anal Mach Intell. 2023;45(4):4396–415. doi:10.1109/TPAMI.2022.3195549. [Google Scholar] [PubMed] [CrossRef]

9. Liu Q, Chen C, Qin J, Dou Q, Heng PA. FedDG: federated domain generalization on medical image segmentation via episodic learning in continuous frequency space. arXiv:2103.06030. 2021. doi:10.48550/ARXIV.2103.06030. [Google Scholar] [CrossRef]

10. Peng X, Huang Z, Zhu Y, Saenko K. Federated adversarial domain adaptation. arXiv:1911.02054. 2019. doi:10.48550/ARXIV.1911.02054. [Google Scholar] [CrossRef]

11. Hitaj B, Ateniese G, Perez-Cruz F. Deep models under the GAN: information leakage from collaborative deep learning. arXiv:1702.07464. 2017. doi:10.48550/ARXIV.1702.0746. [Google Scholar] [CrossRef]

12. Fredrikson M, Jha S, Ristenpart T. Model inversion attacks that exploit confidence information and basic countermeasures. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security; 2015 Oct 12–16; Denver, CO, USA. doi:10.1145/2810103.2813677. [Google Scholar] [CrossRef]

13. Garg S, Erickson N, Sharpnack J, Smola A, Balakrishnan S, Lipton ZC. RLSbench: domain adaptation under relaxed label shift. arXiv:2302.03020. 2023. doi:10.48550/ARXIV.2302.03020. [Google Scholar] [CrossRef]

14. Zhu Z, Hong J, Zhou J. Data-free knowledge distillation for heterogeneous federated learning. arXiv:2105.10056. 2021. doi:10.48550/ARXIV.2105.10056. [Google Scholar] [CrossRef]

15. Karimireddy SP, Kale S, Mohri M, Reddi SJ, Stich SU, Suresh AT. SCAFFOLD: stochastic controlled averaging for federated learning. arXiv:1910.06378. 2019. doi:10.48550/ARXIV.1910.06378. [Google Scholar] [CrossRef]

16. Li T, Sahu AK, Zaheer M, Sanjabi M, Talwalkar A, Smith V. Federated optimization in heterogeneous networks. arXiv:1812.06127. 2018. doi:10.48550/ARXIV.1812.06127. [Google Scholar] [CrossRef]

17. Wu G, Gong S. Collaborative optimization and aggregation for decentralized domain generalization and adaptation. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV); 2021 Oct 10–17; Montreal, QC, Canada. doi:10.1109/ICCV48922.2021.00642. [Google Scholar] [CrossRef]

18. Chen J, Jiang M, Dou Q, Chen Q. Federated domain generalization for image recognition via cross-client style transfer. arXiv:2210.00912. 2022. doi:10.48550/ARXIV.2210.00912. [Google Scholar] [CrossRef]

19. Ganin Y, Ustinova E, Ajakan H, Germain P, Larochelle H, Laviolette F, et al. Domain-adversarial training of neural networks. arXiv:1505.07818. 2015. doi:10.48550/ARXIV.1505.07818. [Google Scholar] [CrossRef]

20. Sun Y, Chong N, Ochiai H. Feature distribution matching for federated domain generalization. arXiv:2203.11635. 2022. doi:10.48550/ARXIV.2203.11635. [Google Scholar] [CrossRef]

21. Zhang W, Li X. Federated transfer learning for intelligent fault diagnostics using deep adversarial networks with data privacy. IEEE/ASME Trans Mechatron. 2022;27(1):430–9. doi:10.1109/TMECH.2021.3065522. [Google Scholar] [CrossRef]

22. Zhang W, Li X. Data privacy preserving federated transfer learning in machinery fault diagnostics using prior distributions. Struct Health Monit. 2022;21(4):1329–44. doi:10.1177/14759217211029201. [Google Scholar] [CrossRef]

23. Lin T, Kong L, Stich SU, Jaggi M. Ensemble distillation for robust model fusion in federated learning. arXiv:2006.07242. 2020. doi:10.48550/ARXIV.2006.07242. [Google Scholar] [CrossRef]

24. Jiang M, Wang Z, Dou Q. HarmoFL: harmonizing local and global drifts in federated learning on heterogeneous medical images. Proc AAAI Conf Artif Intell. 2022;36(1):1087–95. doi:10.1609/aaai.v36i1.19993. [Google Scholar] [CrossRef]

25. Volpi R, Namkoong H, Sener O, Duchi JC, Murino V, Savarese S. Generalizing to unseen domains via adversarial data augmentation. In: Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018); 2018 Dec 2–8; Montreal, QC, Canada. [Google Scholar]

26. Zhuang F, Cheng X, Luo P, Pan SJ, He Q. Supervised representation learning: transfer learning with deep autoencoders. In: Proceedings of the 24th International Joint Conference on Artificial Intelligence (IJCAI 2015); 2015 Jul 25–31; Buenos Aires, Argentina. [Google Scholar]

27. Kingma DP, Welling M. Auto-encoding variational bayes. arXiv:1312.6114. 2013. doi:10.48550/ARXIV.1312.6114. [Google Scholar] [CrossRef]

28. Mao Q, Lee HY, Tseng HY, Ma S, Yang MH. Mode seeking generative adversarial networks for diverse image synthesis. arXiv:1903.05628. 2019. doi:10.48550/ARXIV.1903.05628. [Google Scholar] [CrossRef]

29. Srivastava A, Valkov L, Russell C, Gutmann MU, Sutton C. VEEGAN: reducing mode collapse in GANs using implicit variational learning. arXiv:1705.07761. 2017. doi:10.48550/ARXIV.1705.07761. [Google Scholar] [CrossRef]

30. Makhzani A, Shlens J, Jaitly N, Goodfellow I, Frey B. Adversarial autoencoders. arXiv:1511.05644. 2015. doi:10.48550/ARXIV.1511.05644. [Google Scholar] [CrossRef]

31. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. arXiv:1406.2661. 2014. doi:10.48550/ARXIV.1406.2661. [Google Scholar] [CrossRef]

32. Nguyen AT, Torr P, Lim SN. FedSR: a simple and effective domain generalization method for federated learning. In: Proceedings of the Neural Information Processing Systems 35 (NeurIPS 2022); 2022 Nov 28–Dec 9; New Orleans, LA, USA. [Google Scholar]

33. Al-Dhabyani W, Gomaa M, Khaled H, Fahmy A. Dataset of breast ultrasound images. Data Brief. 2020;28(5):104863. doi:10.1016/j.dib.2019.104863. [Google Scholar] [PubMed] [CrossRef]

34. Di Salvo F, Doerrich S, Ledig C. MedMNIST-C: comprehensive benchmark and improved classifier robustness by simulating realistic image corruptions. arXiv:2406.17536. 2024. doi:10.48550/ARXIV.2406.17536. [Google Scholar] [CrossRef]

35. Beutel DJ, Topal T, Mathur A, Qiu X, Fernandez-Marques J, Gao Y, et al. Flower: a friendly federated learning research framework. arXiv:2007.14390. 2020. doi:10.48550/ARXIV.2007.14390. [Google Scholar] [CrossRef]

36. Pillutla K, Kakade SM, Harchaoui Z. Robust aggregation for federated learning. IEEE Trans Signal Process. 2022;70:1142–54. doi:10.1109/TSP.2022.3153135. [Google Scholar] [CrossRef]

37. Nabavirazavi S, Taheri R, Shojafar M, Iyengar SS. Impact of aggregation function randomization against model poisoning in federated learning. In: 2023 IEEE 22nd International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom); 2023 Nov 1–3; Exeter, UK. doi:10.1109/TrustCom60117.2023.00043. [Google Scholar] [CrossRef]