 Open Access
Open Access
ARTICLE
Day-Ahead Electricity Price Forecasting Using the XGBoost Algorithm: An Application to the Turkish Electricity Market
Department of Industrial Engineering, Faculty of Engineering, Ondokuz Mayis University, Samsun, 55139, Türkiye
* Corresponding Author: Ahad Beykent. Email:
(This article belongs to the Special Issue: Advancements and Challenges in Artificial Intelligence, Data Analysis and Big Data)
Computers, Materials & Continua 2026, 86(1), 1-16. https://doi.org/10.32604/cmc.2025.068440
Received 29 May 2025; Accepted 15 September 2025; Issue published 10 November 2025
Abstract
Accurate short-term electricity price forecasts are essential for market participants to optimize bidding strategies, hedge risk and plan generation schedules. By leveraging advanced data analytics and machine learning methods, accurate and reliable price forecasts can be achieved. This study forecasts day-ahead prices in Türkiye’s electricity market using eXtreme Gradient Boosting (XGBoost). We benchmark XGBoost against four alternatives—Support Vector Machines (SVM), Long Short-Term Memory (LSTM), Random Forest (RF), and Gradient Boosting (GBM)—using 8760 hourly observations from 2023 provided by Energy Exchange Istanbul (EXIST). All models were trained on an identical chronological 80/20 train–test split, with hyperparameters tuned via 5-fold cross-validation on the training set. XGBoost achieved the best performance (Mean Absolute Error (MAE) = 144.8 TRY/MWh, Root Mean Square Error (RMSE) = 201.8 TRY/MWh, coefficient of determination (R2) = 0.923) while training in 94 s. To enhance interpretability and identify key drivers, we employed Shapley Additive Explanations (SHAP), which highlighted a strong association between higher prices and increased natural-gas-based generation. The results provide a clear performance benchmark and practical guidance for selecting forecasting approaches in day-ahead electricity markets.Keywords
Electricity price forecasting is a critical component of competitive power markets. Accurate forecasts allow generators, retailers, and consumers to optimize bidding strategies, hedge against price volatility, and support grid stability. In the Turkish electricity market, rapid demand growth and the increasing penetration of renewable energy have amplified price fluctuations and uncertainty. For example, the average day-ahead market price surged from approximately 300 TL/MWh in early 2021 to peaks exceeding 1500 TL/MWh in 2022, driven by supply-demand imbalances and external shocks (Energy Exchange Istanbul, 2022). Historically, short-term electricity price forecasting has relied on traditional statistical methods such as autoregressive integrated moving average (ARIMA) and other time-series models. These approaches are effective for capturing linear patterns, seasonality, and trends but often fall short in modeling the highly nonlinear and stochastic dynamics of electricity markets [1,2]. To address these limitations, researchers have increasingly adopted machine learning (ML) and artificial intelligence (AI) techniques, which offer greater flexibility in capturing complex relationships in price formation [3].
In recent years, artificial intelligence and machine learning-based approaches have been increasingly employed in energy market analysis. These methods offer higher forecasting accuracy due to their ability to extract complex patterns from large datasets. In particular, tree-based ensemble learning algorithms are favored for their ability to capture nonlinear relationships in data. Support Vector Machines (SVM), Random Forest (RF), Long Short-Term Memory (LSTM), Gradient Boosting Machines (GBM), and Extreme Gradient Boosting (XGBoost) have gained prominence in electricity price forecasting due to their capabilities in modeling nonlinear and complex temporal dependencies. SVM effectively captures non-linear relationships using kernel functions [4], while Random Forest (RF) leverages ensemble learning by combining many decision trees to model nonlinear relationships and excels at high-dimensional problems particularly when the number of predictors is large relative to observations [5]. LSTM networks, equipped with explicit memory cells and gating mechanisms, efficiently manage information flow to capture long-term sequential dependencies and mitigate the vanishing gradient issue [6]. Gradient Boosting Machines (GBM) and especially XGBoost as introduced by Chen and Guestrin [7] are efficient, regularized, scalable tree-boosting systems widely adopted in forecasting.
Despite significant advances in electricity price forecasting methods, gaps persist in the literature due to insufficient benchmarking across diverse models and techniques using consistent datasets and evaluation metrics, particularly within unique market contexts like Turkey’s electricity market. Many studies often focus on single or hybrid models without comprehensive comparative analyses against alternative methods. To address these issues, this study provides a rigorous comparative analysis of five forecasting models SVM, LSTM, RF, GBM and XGBoost using hourly Turkish day-ahead price data from 2023. Additionally, SHAP (Shapley Additive Explanations) analysis is employed to enhance model interpretability by identifying the importance of input variables.
The remainder of this paper is organized as follows: Section 2 reviews the relevant literature on electricity price forecasting, as well as prior studies on the Turkish electricity market. Section 3 describes the data, methodology, and forecasting models employed in the study, including details on hyperparameter optimization and performance evaluation metrics. Section 4 presents the experimental results and comparative analysis of the forecasting models, including graphical and SHAP-based interpretations. Finally, Section 5 concludes the study by summarizing key findings and offering recommendations for future research.
Electricity price forecasting has become an increasingly strategic area of research in energy markets due to rising volatility, market liberalization, and technological transformation. Among energy commodities, oil, natural gas, and electricity markets are among the most extensively studied in terms of price prediction. In electricity markets, the inability to store the product necessitates a real-time balance between supply and demand. These markets, characterized by dynamic and instant consumption, often experience price fluctuations, which emphasizes the importance of reliable and accurate forecasting models [1]. Factors such as increasing competition, infrastructure limitations, smart grid integration, and the increasing utilization of renewable energy sources have further intensified the need for effective load and price forecasting for system planning and operation [8]. Electricity price forecasts are generally classified into short-, medium-, and long-term categories depending on the planning horizon [9]. Electricity trading is conducted through Day-Ahead and Intra-Day Markets, in which both statistical and AI-based forecasting methods are employed [10]. Short-term forecasts are typically grouped into three methodological categories: time-series statistical models, machine learning techniques, and hybrid approaches [9].
Among traditional statistical models, ARIMA, GARCH, and ARMAX are widely used. Nogales et al. [11], using hourly data from the Spanish and Californian markets, showed that the transfer function model produced more accurate results than dynamic regression. Jakaša et al. [12] applied ARIMA models to EPEX data and obtained satisfactory results with proper parameterization. González et al. [13] demonstrated that the Hilbertian ARMAX model outperformed the seasonal ARMAX model in terms of forecasting accuracy.
In reviewing prior works, we observe an evolution in forecasting strategies: early studies often relied on linear models (ARIMA variants), whereas more recent works increasingly employ machine learning and hybrid techniques to capture non-linear dynamics. Techniques such as Support Vector Machines (SVM), Random Forest (RF), Gradient Boosting, and Long Short-Term Memory (LSTM) networks have demonstrated success in modeling high-dimensional and complex relationships. Sansom et al. [14] showed that SVM outperformed ANN in forecasting using data from the Australian National Electricity Market. Mei et al. [15] emphasized the stable performance of RF under varying conditions, outperforming ANN and ARMA in real-time forecasts. Foruzan et al. [16] highlighted that while ANN captures nonlinear patterns effectively, SVM performs better in high-dimensional contexts. Zhang et al. [17] reported that DRNN provided more realistic forecasts than SVM in the New England electricity market. Albahli et al. [18], using IESO data from Ontario, Canada, demonstrated that XGBoost outperformed SVM and RF in both price prediction and cost reduction. Bitirgen and Filik [19], in their study on New York ISO data, concluded that XGBoost achieved lower error rates and shorter computation times than ARIMA. O’Leary et al. [20], using data from the Irish electricity market, compared RF, SVM, LSTM, CNN, K-NN, and CapsNet models. While CapsNet performed well, they found K-NN to be more effective due to training time and compatibility issues. Wang et al. [21] showed that RF adapted well to market fluctuations caused by renewables in Gansu Province, providing high prediction accuracy. Poggi et al. [22] compared AR, ARIMA, LSTM, SARMA, and XGBoost using German electricity market data and found that XGBoost delivered the highest forecasting accuracy. Silva et al. [23] compared DNN, LSTM, CNN, Gradient Boosting, and MLR under exceptional conditions such as COVID-19 and found CNN to yield the most accurate results. Tightiz et al. [24] improved XGBoost forecasts on ISO New England data through error correction and Bayesian optimization. Conejo et al. [25] applied a Wavelet-ARIMA approach on Spanish hourly data across seasons, and Carpio et al. [26] found it outperformed ARIMA in the Singapore market. Shafie-khah et al. [27] proposed a hybrid WT-ARIMA-RBFN model for the Spanish electricity market, demonstrating higher accuracy and reliability than single models. Cerjan et al. [28] improved short-term forecasts using a hybrid system combining MLP and calendar-based similar-day analysis on EEX data. Saini et al. [29] suggested a hybrid model based on LR and SVM. Tang et al. [30] developed a hybrid forecasting model using Lasso, RF, Gradient Boosting, SVM, BP Neural Networks, and LSTM for the Australian market. Zhou et al. [31] applied LSTM and SMBO-based hyperparameter optimization on EMD-decomposed data. Bhatia et al. [32] analyzed the effects of renewables and combined RF and XGBoost via bagging to achieve high accuracy and efficiency. Manfre Jaimes et al. [33] conducted multi-day forecasts using LSTM and XGBoost for the Alberta electricity market to support more profitable bidding strategies. A summary of the applied forecasting techniques is provided in Table 1.
2.1 Studies on the Turkish Electricity Market
In the Turkish electricity market, both statistical and AI-based models have been utilized for day-ahead price forecasting. Adalı [38] applied regression and neural networks, while Biricik et al. [39] developed ANN-based short-term models using calendar, load, and weather data. Ugurlu et al. [40] reported successful results with GRU architecture, and Ertaylan et al. [41] emphasized the positive impact of data diversity on prediction accuracy. Demirezen and Çetin [42] found that RF outperformed SVM in day-ahead price forecasting. Boru İpek [43] demonstrated satisfactory results using ANN, CNN, XGBoost, CatBoost, and AdaBoost models in the energy sector. Arslan and Ertuğrul [44] reported the superior performance of neural networks, while Karatekin and Başaran [45] highlighted the advantages of XGBoost in terms of both accuracy and speed. Arifoglu and Kandemir [46] identified LSTM as the most effective model on average. Yorat et al. [47] showed that XGBoost produced better results than MLR and ARIMA in terms of error rates. Table 2 summarizes key studies conducted in recent years.

In conclusion, a wide range of methodologies including traditional statistical approaches, machine learning, and deep learning has been effectively applied to day-ahead price forecasting in the Turkish electricity market. This study highlights that forecasting outcomes vary considerably across different markets. For instance, while XGBoost demonstrated superior performance over SVM and RF in the Ontario market, in another case a deep learning model achieved promising results but was constrained by substantial training challenges. These observations indicate that the selection of an appropriate forecasting method must be informed by both the characteristics of the underlying data and the operational constraints of the application environment. Building on this premise, our study provides a comparative analysis within Turkish market, with particular emphasis on practical considerations such as computational efficiency and model interpretability. By positioning our work within the broader literature, we identify an emerging trend: although advanced ensemble and deep learning approaches are increasingly favored, their relative advantages remain dependent on market-specific conditions. This represents a critical gap that our research seeks to address in the Turkish market.
Beyond price-forecasting models, recent research has expanded to broader energy-management strategies that underscore the value of accurate forecasts. For example, Sui et al. [48] develop a day-ahead energy management system (EMS) for pelagic islanded microgrid groups that explicitly handles non-integer-hour inter-island energy transfers via electric vessels by coordinating “mirror” and original unit commitments within a 1-h schedule. Tan et al. [49] propose a robust day-ahead dispatch model for integrated electricity–heat networks that derives a linear district-heating network under a variable-flow/constant-temperature (VF–CT) strategy and embeds price-based integrated demand response using demand–price elasticity and thermal-sensation vote; formulated as a two-stage robust optimization, it co-optimizes prices and generation to hedge wind, ambient-temperature, and demand-response uncertainties. Sui et al. [50] present an optimal scheduling strategy for integrated electric–hydrogen systems that models continuous hydrogen-vessel transit and berthing times and exploits controllable grid components (e.g., UPFCs/switching) and overlying-ice effects; cast as a MILP and solved via decomposition, it reduces total energy-transfer costs by ≈12.9% in IEEE-RTS79/Jiangsu case studies. Finally, Xu et al. [51] introduce a VMD-based multi-attention feature-fusion model (V-MAF) that couples SE-TCN and SE-GRU with multi-head attention to capture multi-scale price/load patterns; on Singapore data it achieves RMSE = 1.3168 and reduces errors by 11–59% relative to XGBoost, ATT-CNN-LSTM, BiGRU, and VMD-Transformer.
In light of the above literature, our study contributes to the field in three significant ways: first, it demonstrates the applicability of XGBoost in a highly volatile market such as the Turkish electricity market; second, it presents a comparative analysis of various forecasting methods, highlighting their respective advantages and limitations; and third, it enhances the interpretability of model outputs through SHAP-based variable importance analysis. The findings indicate that such models can be effectively utilized in the decision-making processes of energy market stakeholders.
This study aims to forecast the hourly day-ahead market clearing price (MCP) in the Turkish electricity market. To this end, a comparative analysis was conducted using several machine learning models. No artificial intelligence (AI) tools were used in the preparation of data or analysis of this study; all work was conducted by the authors.
Dataset Description: The study utilizes hourly data from 2023, comprising 8760 observations of the Turkish day-ahead market clearing price (in TRY) and related features. Key input variables include total electricity demand, generation by source (natural gas, coal, hydro, wind, etc.), weather factors (e.g., hourly temperature), and calendar indicators (weekday/weekend and holiday flags). All price and generation data were obtained from Energy Exchange Istanbul (EXIST), and weather data (temperature) were sourced from the Turkish State Meteorological Service, ensuring real-world relevance.
During the data preprocessing phase, missing values were completed using appropriate imputation methods. In addition, categorical variables such as weekday/weekend, month, and hour were encoded and formatted to be suitable for model input.
3.1 Applied Forecasting Models
The following forecasting algorithms were implemented and their performances were compared:
LSTM (Long Short-Term Memory): A deep learning architecture capable of learning long-term dependencies in time series data. It was developed to overcome the vanishing gradient problem observed in classical RNNs. LSTM cells regulate information flow through input, forget, and output gates, enabling the network to retain critical past information over extended periods and learn complex sequential patterns.
SVM (Support Vector Machines): Support Vector Machines are supervised learning algorithms used for both classification and regression tasks. In the context of regression referred to as Support Vector Regression (SVR) the model aims to determine an optimal hyperplane that fits the data within an epsilon-insensitive margin, minimizing prediction error while maintaining model simplicity. SVM’s capability to handle non-linear relationships is enabled through the use of kernel functions, which map input data into higher-dimensional feature spaces. In this study, the Radial Basis Function (RBF) kernel was employed and yielded the most accurate results.
Random Forest (RF): An ensemble learning method that constructs multiple decision trees using random subsets of data and features. The final prediction is obtained by averaging the outputs of individual trees. This structure reduces overfitting and yields stable results in high-dimensional datasets.
Gradient Boosting (GBM): This technique sequentially builds weak learners (typically decision trees) to reduce prediction errors. Each subsequent model is trained to correct the errors of its predecessor. Key hyperparameters, such as the learning rate and maximum depth, greatly influence the model’s performance.
XGBoost (Extreme Gradient Boosting): XGBoost is an optimized, regularized implementation of gradient-boosted decision trees noted for speed, scalability, and strong predictive accuracy. It parallelizes split-finding, handles missing values via sparsity-aware default directions, and applies both L1 and L2 regularization (along with shrinkage and subsampling) to control overfitting [7].
3.2 Performance Evaluation Metrics
To objectively assess the performance of the forecasting models, the following error metrics were employed:
MAE (Mean Absolute Error): The average of the absolute differences between actual and predicted values. A lower MAE indicates that the model has a lower average prediction error.
MSE (Mean Squared Error): The average of the squared differences between actual and predicted values. This metric penalizes larger errors more heavily, making it sensitive to outliers.
RMSE (Root Mean Squared Error): The square root of the MSE. It shares the same unit as the predicted variable, making it easier to interpret.
R2 (Coefficient of Determination): Indicates the proportion of variance in the dependent variable that is explained by the model. A value closer to 1 implies a higher explanatory power.
3.3 Hyperparameter Optimization
The predictive performance of the XGBoost model largely depends on the effective tuning of its hyperparameters. Therefore, in this study, the RandomizedSearchCV method was employed for hyperparameter optimization. This method evaluates randomly selected combinations within the predefined ranges shown in Table 3.

To ensure a robust evaluation of model performance, 5-fold cross-validation was conducted. We observed that the model’s performance was relatively stable for small changes in hyperparameters around the optimal values. For instance, altering XGBoost’s learning rate by ±0.02 or maximum tree depth by ±1 from the chosen settings changed the RMSE by less than 1%. This indicates the model is not unduly sensitive to minor tuning differences, lending confidence that our chosen parameters are robust. The hyperparameter combination that achieved the highest overall performance across the validation folds was selected for the final model.
To improve the interpretability of the XGBoost model’s predictions, the SHapley Additive exPlanations (SHAP) method was employed. SHAP is based on Shapley values from cooperative game theory and quantitatively determines the contribution of each input variable to the model’s output. It also provides a visual representation of these contributions.
This approach allows for a clear understanding of which variables influence the model and to what extent they affect the predictions. As a result, the model not only achieves high forecasting accuracy but also ensures transparency and interpretability in the decision-making process.
4 Implementation and Forecasting Results
This section presents the experimental findings obtained from the implementation of the theoretical approaches and machine learning models previously detailed in the methodology, aimed at forecasting day-ahead electricity prices in the Turkish electricity market. The dataset used in the implementation consists of 8760 hourly observations (one year of data) from the Turkish electricity market. Of this, 80% was allocated for model training and the remaining 20% (1752 entries) for testing. A rolling forecasting origin was utilized for model evaluation: starting with an initial training period (the first 80% of data, January–September 2023), models were retrained at regular intervals (monthly) as new data became available, and day-ahead forecasts were generated for the next period. This walk-forward approach ensured that each test prediction was truly out-of-sample. Notably, the dedicated test set (the final 20% of data, October–December 2023) remained completely unseen during model training and tuning, providing a strict out-of-sample evaluation. The implementation was carried out in the Python Jupyter Notebook environment, utilizing core libraries such as pandas, numpy, matplotlib.pyplot, sklearn.metrics, and time throughout the modeling process. A comparative summary of the models’ performances is presented in Table 4.
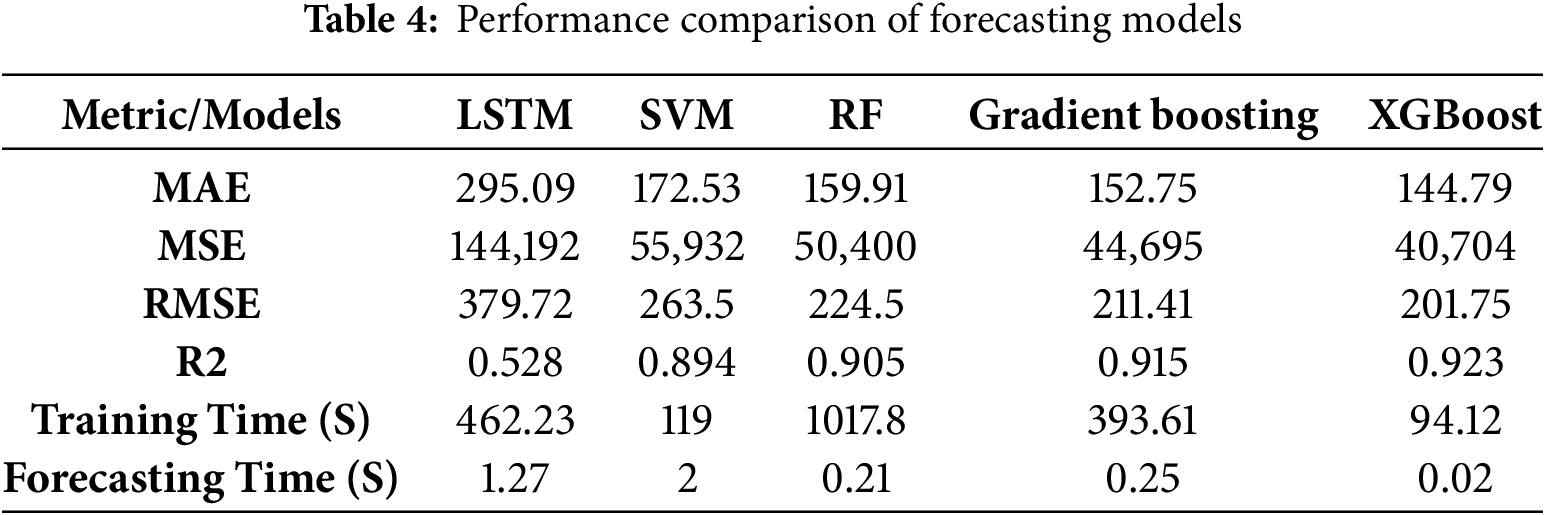
An examination of Table 4 reveals that five models were evaluated based on MAE, MSE, RMSE, R2, training time, and prediction time. Among these, the XGBoost model achieved the best overall performance, with MAE (144.79), MSE (40,704), RMSE (201.75), and R2 (0.923). The Gradient Boosting model also performed well (MAE: 152.75; RMSE: 211.41; R2: 0.915), although it fell slightly behind XGBoost. The Random Forest model yielded satisfactory results (MAE: 159.91; RMSE: 224.5) but required significantly longer training time, making it less favorable for real-time applications. The LSTM model showed moderate success, outperforming traditional methods with MAE (295.09), RMSE (379.72), and R2 (0.528), though its high MSE (144,192) suggests considerable deviation in its forecasts. While the SVM model achieved a relatively high R2 (0.894), its RMSE (263.5) and MSE (55,932) indicate susceptibility to higher errors in certain scenarios (Note: All error metrics are in Turkish Lira. For international context, the average exchange rate in late 2023 was approximately 1 EUR ≈ 25 TL. Thus, for example, XGBoost’s MAE of 144.79 TL corresponds to about 5.79 EUR).
To determine if the performance differences are statistically significant, we conducted a Diebold-Mariano (DM) test comparing XGBoost with the second-best model (Gradient Boosting) using their one-day-ahead forecast error series. The DM test yielded a statistic of 2.11 with a p-value of 0.035, indicating that XGBoost’s error improvements are statistically significant at the 5% level. In other words, the probability that XGBoost’s better performance is due to random chance is only ~3.5%. This confirms that XGBoost’s advantage is robust.
LSTM predictions in Fig. 1a are relatively accurate during stable periods but deviate significantly at the extremes. As shown in Fig. 1b, SVM is successful in capturing high-price episodes, although prediction errors increase during sudden changes. Fig. 1c shows that Random Forest can generally follow market trends but exhibits unexpected deviations during periods of high volatility. In Fig. 1d, the Gradient Boosting model demonstrates strong trend-tracking ability, although it sometimes reacts with a delay at peak points.

Figure 1: Actual vs. forecasted electricity prices using the compared models
The forecast performance of the XGBoost model is detailed in Fig. 1e, which confirms its ability to capture both overall trends and sudden shifts in electricity prices. The model’s low MAE and RMSE reinforce its consistency and reliability.
All experiments were run on a standard PC with an Intel Core i7-9700 CPU (3.0 GHz) and 16 GB RAM; no GPU acceleration was used. In terms of computational cost, the results in Table 4 show that the deep learning model (LSTM) required substantially longer training time (~462 s). XGBoost achieved its superior accuracy with a relatively low training time (≈94 s), highlighting its computational efficiency. The Random Forest model, although accurate, took the longest to train (~1018 s), making it less practical for real-time use. These hardware and timing details illustrate the trade-off between accuracy and speed: XGBoost and Random Forest provided high accuracy, but XGBoost did so with far less computation.
4.1 Graphical Comparative Analysis
Fig. 2 provides a visual comparative analysis of the models’ performance across MAE, MSE, RMSE, R2, training time, and prediction time. The intensity of colors in the figure reflects the models’ relative success across metrics, clearly demonstrating that XGBoost outperforms all others. Although Gradient Boosting and Random Forest are competitive in terms of accuracy, they lack XGBoost’s efficiency in computation time. LSTM and SVM may be preferred in specific use cases, but ARIMA fails to deliver satisfactory performance either in terms of accuracy or interpretability.

Figure 2: Comparison matrix of the models based on performance metrics
To enhance the interpretability and reliability of the most successful model, SHAP analysis was conducted for XGBoost. As shown in Fig. 3 (Beeswarm plot), the most influential variable on electricity price forecasting is the volume of electricity generated from natural gas. The plot highlights both the positive and negative directional impacts of variables, aiding in understanding the model’s decision-making processes.

Figure 3: Beeswarm plot of the SHAP method for the XGBoost model
Fig. 4 presents the SHAP bar plot, ranking the features by their average absolute impact on the output. Natural gas-based electricity generation stands out as the most influential factor, followed by the monthly maximum market clearing price (max_ptf), hour of the day, imported coal-based electricity generation, and average temperature. These insights can guide market actors and regulators in understanding and potentially intervening in price formation mechanisms.

Figure 4: SHAP bar plot for the XGBoost model
Fig. 5 displays a SHAP dependence plot, indicating a nonlinear, threshold-based relationship between natural gas-based electricity generation and price forecasts. Notably, when production exceeds 5000 MWh, the SHAP effect becomes strongly positive, underscoring the fragility of the supply-demand equilibrium. This insight can be valuable in shaping strategic energy policies and cost-efficient production planning.
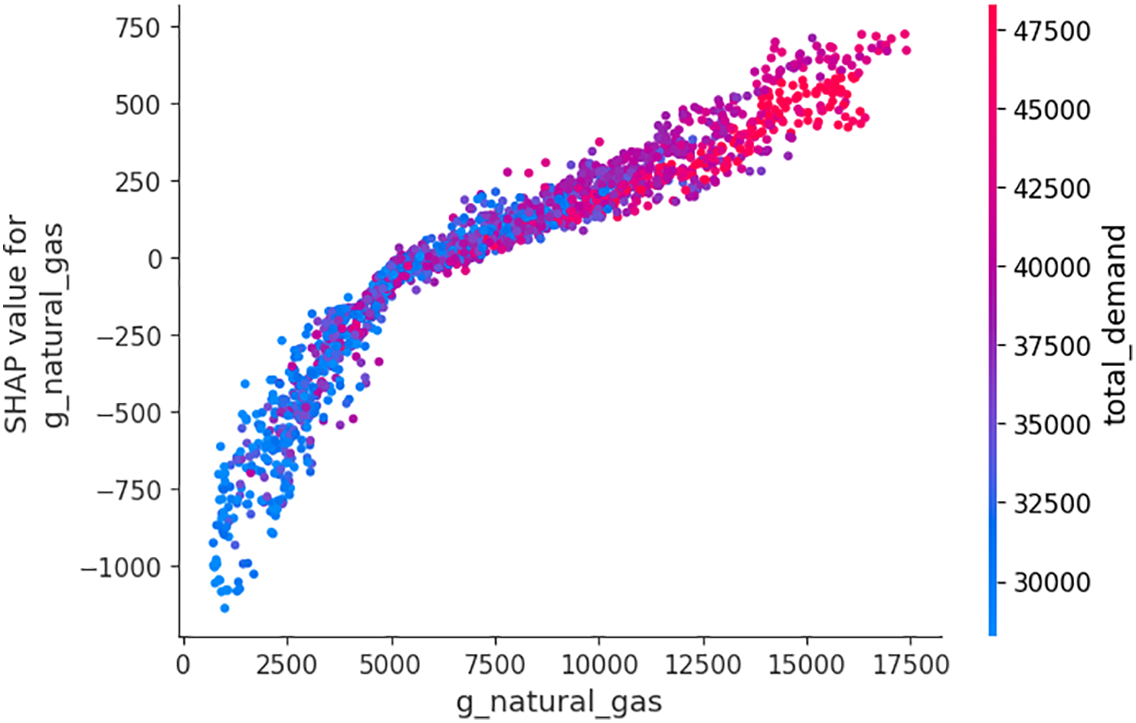
Figure 5: Dependence plot of natural gas-based electricity generation in the XGBoost model using the SHAP method
In conclusion, the application of various models for day-ahead electricity price forecasting in the Turkish market revealed that XGBoost stands out with its high accuracy, fast computation time, and strong interpretability. These findings provide actionable insights and strategic decision support for stakeholders in the energy sector. It is important to acknowledge the limitations of this study. First, the analysis was conducted on a single year of data from one market (Turkey); while this provided interesting insights, the models’ performance and the SHAP interpretations might differ under other market conditions or with more extensive datasets. Second, although we included several exogenous features (e.g., temperature, generation by source), other factors such as public holidays or fuel prices were not incorporated and could be explored in future research.
This study demonstrated that among various forecasting methods, the XGBoost algorithm achieved the highest accuracy in predicting day-ahead electricity prices in the Turkish market, with the lowest RMSE of approximately 201.8 TL (≈8 EUR) and an R2 of 0.923. Compared with alternative models such as SVM and LSTM, XGBoost proved more effective in capturing complex nonlinear dynamics, while the SHAP analysis provided valuable interpretability by identifying natural gas generation, maximum market clearing price (max_ptf), hour of the day, imported coal generation, and average temperature as the most influential drivers of price fluctuations.
The results imply that ensemble learning methods like XGBoost can effectively address the challenges of volatile electricity markets by offering both predictive accuracy and transparency. For practitioners, the speed and reliability of the model suggest that it could be deployed in real-time pricing and operational planning systems, supporting risk management and more informed decision-making. At the academic level, this work contributes to the energy forecasting literature by illustrating the dual benefit of accuracy and interpretability, which is increasingly valued in modern power system analytics. Although our case involves only dozens of input variables, XGBoost scales well to high-dimensional data. Even with thousands of predictors, its tree-splitting tends to ignore irrelevant variables and focus on the most informative ones an implicit form of feature selection. Training is also parallelizable. We therefore expect strong performance to carry over to larger problems, albeit with longer training times and higher memory use.
Certain limitations should be acknowledged. The analysis was restricted to a single-year dataset from one market, which constrains the generalizability of the findings. The study also followed a deterministic forecasting framework without incorporating probabilistic measures such as confidence intervals, which would be valuable for risk-sensitive applications. Future research should therefore expand to multi-year and multi-market datasets, integrate additional exogenous variables such as holidays, fuel prices, and macroeconomic indicators, and test hybrid or probabilistic models to improve robustness. Extending the use of SHAP or similar tools for example, through interactive dashboards could further support transparent decision-making and bridge forecasting research with practical applications.
Acknowledgement: The authors acknowledge that the language of this manuscript was polished using an artificial intelligence (AI) tool.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Yağmur Yılan: Data curation, Software, Visualization, Writing—original draft. Ahad Beykent: Conceptualization, Methodology, Writing—review & editing, Supervision. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are openly available in [EPİAŞ] at [https://www.epias.com.tr] (accessed on 14 September 2025).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Weron R. Electricity price forecasting: a review of the state-of-the-art with a look into the future. Int J Forecast. 2014;30(4):1030–81. doi:10.1016/j.ijforecast.2014.08.008. [Google Scholar] [CrossRef]
2. Singh N, Mohanty SR. A review of price forecasting problem and techniques in deregulated electricity markets. J Power Energy Eng. 2015;3(9):1–19. doi:10.4236/jpee.2015.39001. [Google Scholar] [CrossRef]
3. Jędrzejewski A, Lago J, Marcjasz G, Weron R. Electricity price forecasting: the dawn of machine learning. IEEE Power Energy Mag. 2022;20(3):24–31. doi:10.1109/MPE.2022.3150809. [Google Scholar] [CrossRef]
4. Papadimitriou T, Gogas P, Stathakis E. Forecasting energy markets using support vector machines. Energy Econ. 2014;44:135–42. doi:10.1016/j.eneco.2014.03.017. [Google Scholar] [CrossRef]
5. Dudek G. A comprehensive study of random forest for short-term load forecasting. Energies. 2022;15(20):7547. doi:10.3390/en15207547. [Google Scholar] [CrossRef]
6. Kılıç DK, Nielsen P, Thibbotuwawa A. Intraday electricity price forecasting via LSTM and trading strategy for the power market: a case study of the West Denmark DK1 grid region. Energies. 2024;17(12):2909. doi:10.3390/en17122909. [Google Scholar] [CrossRef]
7. Chen T, Guestrin C. Xgboost: a scalable tree boosting system. In: Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining; 2016 Aug 13–17; San Francisco, CA, USA. p. 785–94. doi:10.1145/2939672.2939785. [Google Scholar] [CrossRef]
8. Nowotarski J, Weron R. Recent advances in electricity price forecasting: a review of probabilistic forecasting. Renew Sustain Energy Rev. 2018;81:1548–68. doi:10.1016/j.rser.2017.05.234. [Google Scholar] [CrossRef]
9. Cerjan M, Krželj I, Vidak M, Delimar M. A literature review with statistical analysis of electricity price forecasting methods. Eurocon. 2013;2013:756–63. doi:10.1109/EUROCON.2013.6625068. [Google Scholar] [CrossRef]
10. Wolff G, Feuerriegel S. Short-term dynamics of day-ahead and intraday electricity prices. Int J Energy Sector Manage. 2017;11(4):557–73. doi:10.1108/IJESM-05-2016-0009. [Google Scholar] [CrossRef]
11. Nogales FJ, Contreras J, Conejo AJ, Espínola R. Forecasting next-day electricity prices by time series models. IEEE Trans Power Syst. 2002;17(2):342–8. doi:10.1109/TPWRS.2002.1007902. [Google Scholar] [CrossRef]
12. Jakaša T, Andročec I, Sprčić P. Electricity price forecasting—ARIMA model approach. In: 2011 8th International Conference on the European Energy Market (EEM); 2011 May 25–27; Zagreb, Croatia: IEEE. p. 222–5. doi:10.1109/EEM.2011.5953012. [Google Scholar] [CrossRef]
13. González JP, Roque AMSMS, Pérez EA. Forecasting functional time series with a new hilbertian ARMAX model: application to electricity price forecasting. IEEE Trans Power Syst. 2018;33(1):545–56. doi:10.1109/TPWRS.2017.2700287. [Google Scholar] [CrossRef]
14. Sansom D, Downs T, Saha T. Evaluation of support vector machine based forecasting tool in electricity price forecasting for Australian national electricity market participants. J Electr Electron Eng Aust. 2003;22(3):227–33. doi:10.3316/informit.494183070923146. [Google Scholar] [CrossRef]
15. Mei J, He D, Harley R, Habetler T, Qu G. A random forest method for real-time price forecasting in New York electricity market. In: 2014 IEEE PES General Meeting| Conference & Exposition; 2014 Jul 27–31; National Harbor, MD, USA: IEEE. p. 1–5. doi:10.1109/PESGM.2014.6939932. [Google Scholar] [CrossRef]
16. Foruzan E, Scott SD, Lin J. A comparative study of different machine learning methods for electricity prices forecasting of an electricity market. In: 2015 North American Power Symposium (NAPS); 2015 Oct 4–6; Charlotte, NC, USA: IEEE. p. 1–6. doi:10.1109/NAPS.2015.7335095. [Google Scholar] [CrossRef]
17. Zhang C, Li R, Shi H, Li F. Deep learning for day-ahead electricity price forecasting. IET Smart Grid. 2020;3(4):462–9. doi:10.1049/iet-stg.2019.0258. [Google Scholar] [CrossRef]
18. Albahli S, Shiraz M, Ayub N. Electricity price forecasting for cloud computing using an enhanced machine learning model. IEEE Access. 2020;8:200971–81. doi:10.1109/ACCESS.2020.3035328. [Google Scholar] [CrossRef]
19. Bitirgen K, Filik ÜB. Electricity price forecasting based on xgboost and arima algorithms. BSEU J Eng Res Technol. 2020;1(1):7–13. [Google Scholar]
20. O’Leary C, Lynch C, Bain R, Smith G, Grimes D. A comparison of deep learning vs traditional machine learning for electricity price forecasting. In: 4th International Conference on Information and Computer Technologies (ICICT); 2021 Mar 11–14; Kahului, HI, USA. p. 6–12. doi:10.1109/ICICT52872.2021.00009. [Google Scholar] [CrossRef]
21. Wang P, Xu K, Ding Z, Du Y, Liu W, Sun B, et al. An online electricity market price forecasting method via random forest. IEEE Trans Ind Appl. 2022;58(6):7013–21. doi:10.1109/TIA.2022.3198393. [Google Scholar] [CrossRef]
22. Poggi A, Di Persio L, Ehrhardt M. Electricity price forecasting via statistical and deep learning approaches: the german case. AppliedMath. 2023;3(2):316–42. doi:10.3390/appliedmath3020018. [Google Scholar] [CrossRef]
23. Silva AR, Fidalgo JN, Andrade JR, IEEE, editors. Easing predictors selection in electricity price forecasting with deep learning techniques. In: 19th International Conference on the European Energy Market (EEM); 2023 Jun 6–8; Lappeenranta, Finland. doi:10.1109/EEM58374.2023.10161909. [Google Scholar] [CrossRef]
24. Tightiz L, Yoo J, Al-Shibli WK. Strategic enhancements in electricity price forecasting: the role of XGBoost and error correction features. Results Eng. 2025;26:105609. doi:10.1016/j.rineng.2025.105609. [Google Scholar] [CrossRef]
25. Conejo AJ, Plazas MA, Espinola R, Molina AB. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans Power Syst. 2005;20(2):1035–42. doi:10.1109/TPWRS.2005.846054. [Google Scholar] [CrossRef]
26. Carpio KJE, Go AML, Roncal CKM. Forecasting day-ahead electricity prices of Singapore through ARIMA and wavelet-ARIMA. DLSU Bus Econ Rev. 2012;22(1):97–118. [Google Scholar]
27. Shafie-khah M, Moghaddam MP, Sheikh-El-Eslami MK. Price forecasting of day-ahead electricity markets using a hybrid forecast method. Energy Conv Manage. 2011;52(5):2165–9. doi:10.1016/j.enconman.2010.10.047. [Google Scholar] [CrossRef]
28. Cerjan M, Matijaš M, Delimar M. Dynamic hybrid model for short-term electricity price forecasting. Energies. 2014;7(5):3304–18. doi:10.3390/en7053304. [Google Scholar] [CrossRef]
29. Saini D, Saxena A, Bansal R. Electricity price forecasting by linear regression and SVM. In: 2016 International Conference on Recent Advances and Innovations in Engineering (ICRAIE); 2016 Dec 23–25; Jaipur, India: IEEE. p. 1–7. doi:10.1109/ICRAIE.2016.7939509. [Google Scholar] [CrossRef]
30. Tang Y, Zou B, Zhang L. A novel combined electricity price forecasting method based on data driven. In: 2019 IEEE 3rd International Electrical and Energy Conference (CIEEC); 2019 May 8–10; Seogwipo, Republic of Korea: IEEE. p. 1–7. doi:10.1109/CIEEC47146.2019.CIEEC-2019299. [Google Scholar] [CrossRef]
31. Zhou S, Zhou L, Mao M, Tai H-M, Wan Y. An optimized heterogeneous structure LSTM network for electricity price forecasting. IEEE Access. 2019;7:108161–73. doi:10.1109/ACCESS.2019.2932999. [Google Scholar] [CrossRef]
32. Bhatia K, Mittal R, Varanasi J, Tripathi M. An ensemble approach for electricity price forecasting in markets with renewable energy resources. Utilities Policy. 2021;70:101185. doi:10.1016/j.jup.2021.101185. [Google Scholar] [CrossRef]
33. Manfre Jaimes D, Zamudio López M, Zareipour H, Quashie M. A hybrid model for multi-day-ahead electricity price forecasting considering price spikes. Forecasting. 2023;5(3):499–521. doi:10.3390/forecast5030028. [Google Scholar] [CrossRef]
34. Contreras J, Espinola R, Nogales FJ, Conejo AJ. ARIMA models to predict next-day electricity prices. IEEE Trans Power Syst. 2003;18(3):1014–20. doi:10.1109/TPWRS.2002.804943. [Google Scholar] [CrossRef]
35. Chang Z, Zhang Y, Chen W. Effective adam-optimized LSTM neural network for electricity price forecasting. In: 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS); 2018 Nov 23–25; Beijing, China: IEEE. p. 245–8. [Google Scholar]
36. Miletić M, Pavić I, Pandžić H, Capuder T. Day-ahead electricity price forecasting using LSTM networks. In: 2022 7th International Conference on Smart and Sustainable Technologies (SpliTech); 2022 Jul 5–8; Split / Bol, Croatia: IEEE. p. 1–6. doi:10.23919/SpliTech55088.2022.9854351. [Google Scholar] [CrossRef]
37. Plakas K, Karampinis I, Alefragis P, Birbas A, Birbas M, Papalexopoulos A. A predictive fuzzy logic model for forecasting electricity day-ahead market prices for scheduling industrial applications. Energies. 2023;16(10):4085. doi:10.3390/en16104085. [Google Scholar] [CrossRef]
38. Adalı E. Hourly and Daily Electricity Price Forecasting in the Day-Ahead Market [Master thesis]. Istanbul, Türkiye: Istanbul Technical University; 2015. Available from: http://hdl.handle.net/11527/17977. [Google Scholar]
39. Biricik G, Bozkurt Ö, Taysi ZC. Analysis of features used in short-term electricity price forecasting for deregulated markets. In: 23nd Signal Processing and Communications Applications Conference (SIU); 2015 May 16–19; Malatya, Türkiye: Inonu Univ; 2015. doi:10.1109/SIU.2015.7129895. [Google Scholar] [CrossRef]
40. Ugurlu U, Oksuz I, Tas O. Electricity price forecasting using recurrent neural networks. Energies. 2018;11(5):1255. doi:10.3390/en11051255. [Google Scholar] [CrossRef]
41. Ertaylan A, Aktaş Ö, Doğan Y. Market clearing price prediction with artificial neural networks. Dokuz Eylul Univ Fac Eng J Sci Eng. 2021;23(67):93–105. doi:10.21205/deufmd.2021236708. [Google Scholar] [CrossRef]
42. Demirezen S, Çetin M. Forecasting of market clearing price with random forest regression and support vector regression. J Quant Sci. 2021;3(1):1–15. doi:10.51541/nicel.832164. [Google Scholar] [CrossRef]
43. Boru İpek A. Prediction of market-clearing price using neural networks based methods and boosting algorithms. Int Adv Res Eng J. 2021;5(2):240–6. doi:10.35860/iarej.824168. [Google Scholar] [CrossRef]
44. Arslan B, Ertuğrul İ. Forecasting and analysis in Turkish electricity market with multiple regression, arima and artificial neural network methods. J Manage Econ Res. 2022;20(1):331–53. doi:10.11611/yead.988146. [Google Scholar] [CrossRef]
45. Karatekin C, Başaran T. Forecasting the day ahead electricity energy price by using data analysis methods. J Instit Sci Technol. 2022;12(4):2075–84. doi:10.21597/jist.1082880. [Google Scholar] [CrossRef]
46. Arifoglu A, Kandemir T. Electricity price forecasting in turkish day-ahead market via deep learning techniques. J Mehmet Akif Ersoy Univ Econ Adm Sci Fac. 2022;9(2):1433–58. doi:10.30798/makuiibf.1097686. [Google Scholar] [CrossRef]
47. Yorat E, Zor K, Özbek NS, Sarıbulut L. Day-ahead electricity price forecasting using artificial intelligence-based algorithms. In: 2023 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT); 2023 Nov 20–21; Sakheer, Bahrain: IEEE. p. 121–6. doi:10.1109/3ICT60104.2023.10391547. [Google Scholar] [CrossRef]
48. Sui Q, Wei F, Wu C, Lin X, Li Z. Day-ahead energy management for pelagic island microgrid groups considering non-integer-hour energy transmission. IEEE Trans Smart Grid. 2020;11(6):5249–59. doi:10.1109/TSG.2020.2994236. [Google Scholar] [CrossRef]
49. Tan H, Yan W, Ren Z, Wang Q, Mohamed MA. A robust dispatch model for integrated electricity and heat networks considering price-based integrated demand response. Energy. 2022;239:121875. doi:10.1016/j.energy.2021.121875. [Google Scholar] [CrossRef]
50. Sui Q, Zhang J, Li J, Li Z, Su C, Liu C. Optimal scheduling for renewable power grid and vessel-based hydrogen chain integrated systems considering flexible energy transfer. Appl Energy. 2024;367:123401. doi:10.1016/j.apenergy.2024.123401. [Google Scholar] [CrossRef]
51. Xu Y, Huang X, Gao Z, Mohamed MA, Jin T. A novel electricity price forecasting approach based on multi-attention feature fusion model optimized by variational mode decomposition. Measurement. 2025;253:117596. doi:10.1016/j.measurement.2025.117596. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2026 The Author(s). Published by Tech Science Press.
Copyright © 2026 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF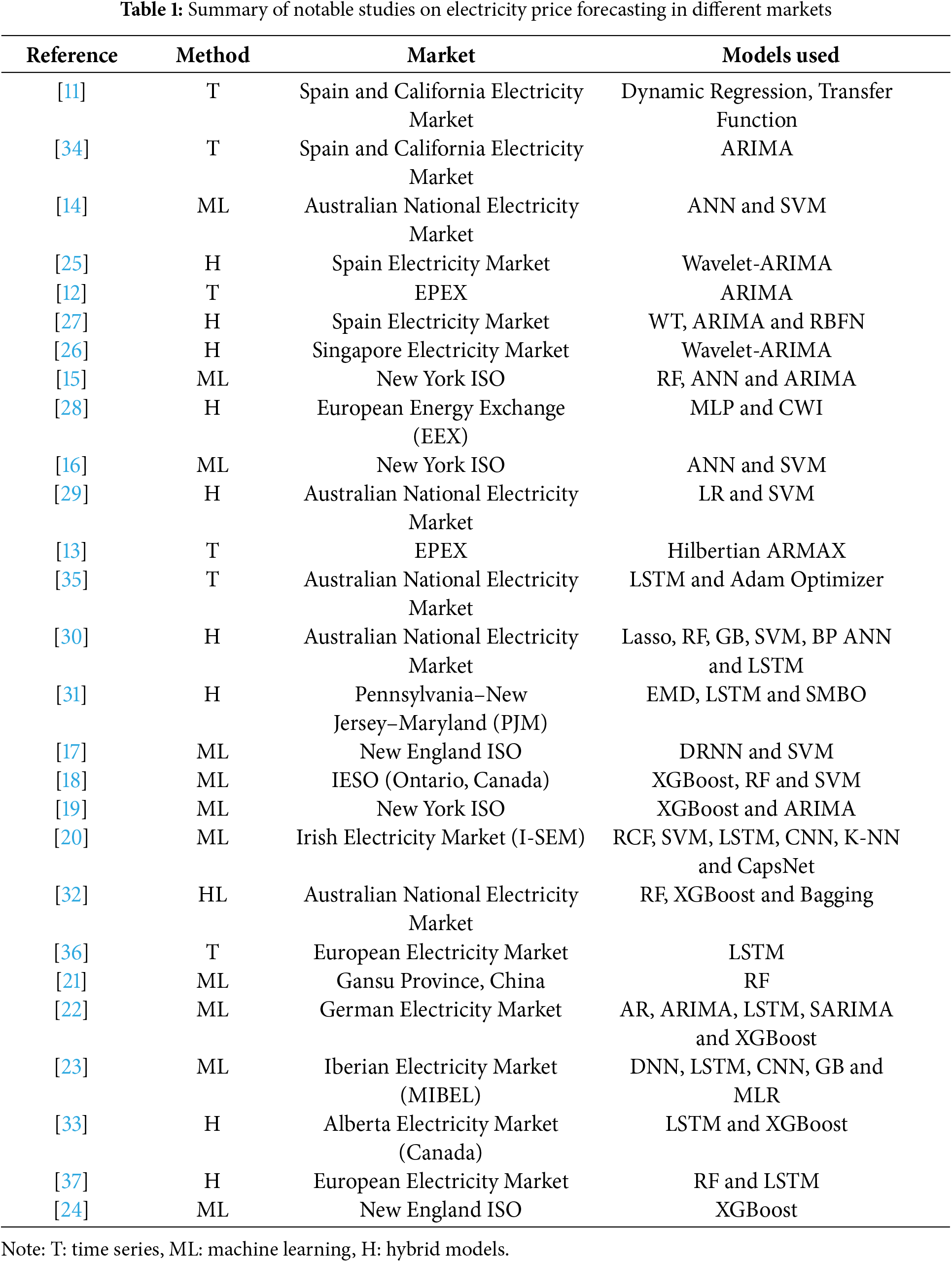
 Downloads
Downloads
 Citation Tools
Citation Tools