UGEA-LMD: A Continuous-Time Dynamic Graph Representation Enhancement Framework for Lateral Movement Detection

1  Introduction

As enterprise networks grow more complex, attack methods have become increasingly stealthy and sophisticated. Advanced Persistent Threat (APTs) attackers often use lateral movement (LM) to gradually extend their control after the initial intrusion to achieve penetration and persistent control of critical systems [1]. For instance, in the 2023 supply chain attack on the MOVEit file transfer software, attackers exploited LM techniques to infiltrate energy, healthcare, and government networks worldwide, resulting in the exposure of sensitive data belonging to over 8 million users [2]. Lateral movement is highly stealthy and typically involves multi-stage sequential operations, making accurate detection of anomalous links essential for halting persistent APTs infiltration and minimizing potential damage.

Early lateral movement detection techniques relied on rule-based matching and statistical anomaly detection [3–5]. Although such methods can quickly identify known attacks using predefined rules or thresholds, they heavily depend on expert knowledge, struggle to adapt to novel attack tactics, and exhibit high false alarm rates in complex networks. Subsequently, machine learning techniques [6–9] were introduced for anomaly detection by extracting statistical features from logs and network traffic and then applying classification or clustering algorithms. While these methods reduce reliance on prior knowledge, their dependence on handcrafted features limits their ability to capture fine-grained temporal and topological evolution among nodes.

In recent years, the rapid development of deep learning, particularly graph neural networks (GNNs) [10–13], has yielded new methods for detecting lateral movement. GNN-based approaches improve detection performance by leveraging network topology and spatio-temporal dependencies to model complex lateral interaction paths. For example, GraphSAGE [14] generates local node representations through neighbor sampling and aggregation; GAT [15] employs an attention mechanism to weigh neighbor importance; Anomal-E [16] represents the network as a dynamic line graph and applies the graph convolutional network for attack detection. These methods have shown initial success in extracting complex spatio-temporal features from network interactions, providing a foundation for more intelligent detection systems.

Despite these advances, GNN-based LM detection faces two major challenges in practical deployments. (1) Sample scarcity. To alleviate the limited data, researchers often employ graph data augmentation. However, most existing augmentation techniques perform heuristic perturbations at the topology level [17], such as random edge deletion, node attribute masking, or subgraph sampling. These operations can disrupt the causality of real attack paths and introduce noise that exacerbates model overfitting. For dynamic graphs, frameworks like MeTA [18] incorporate multi-level memory enhancement to capture structural and temporal features, but their rules are tightly coupled to specific model modules, resulting in high implementation complexity and poor adaptability. (2) Cold-start. New nodes lack neighbor or history information before their first interaction, making it difficult for models to learn meaningful representations [19]. Most existing methods rely on static graphs or discrete-time dynamic graphs (DTDGs). Static graphs only consider overall topology and ignore temporal evolution, leaving new nodes “isolated” until incorporated into the global graph. DTDGs divide interactions into fixed time-window snapshots, which break the causal ordering of events across windows and impede learning representations that balance fine-grained temporal information with long-term dependencies. Both approaches fail to provide complete context for cold-start nodes, hindering timely threat recognition.

To address these issues, we propose UGEA-LMD, an uncertainty-driven graph embedding-enhanced framework for LM detection. Inspired by the ConUMIP [20] approach, UGEA-LMD uses a continuous-time graph encoder [21] to encode each interaction event incrementally, fusing network topology and temporal context so that a new node's first interaction yields a preliminary representation with spatio-temporal dependencies. Next, the joint distribution of node embeddings across feature dimensions is modeled via a Gaussian copula, enabling adaptive sampling to generate augmented representations that preserve spatio-temporal semantics while introducing diversity, thereby expanding the sparse sample space. Original and augmented embeddings are then aligned through contrastive learning to mitigate noise bias and preserve semantic consistency. Finally, edge prediction on these augmented embeddings enables accurate LM detection. Unlike static-graph perturbation or module-specific enhancement, UGEA-LMD's data augmentation module operates independently of the underlying GNN architecture. This independence preserves the temporal integrity of augmented samples and significantly improves recognition of scarce samples and cold-start nodes. Our main contributions to this work are as follows:

•   Embedding-space uncertainty-based data augmentation: We introduce Gaussian copula modeling and adaptive sampling in the graph embedding space to generate diverse augmented samples, effectively broadening the representation of scarce samples and mitigating overfitting.

•   Continuous-time dynamic graph inductive learning: By leveraging the incremental update feature of CTDG, we adopt an inductive learning setting to validate model generalization and robustness for unseen nodes without historical context.

•   Large-scale real log evaluation: Experiments on two highly imbalanced authentication log datasets show that UGEA-LMD consistently outperforms state-of-the-art methods, achieving significant gains in key metrics such as AUC and accuracy.

The remainder of this paper is organized as follows. Section 2 reviews related works. Section 3 describes our methodology. Section 4 presents the experimental setup and evaluation metrics. Section 5 provides comparative analysis and ablation studies. Section 6 concludes the paper.

2  Related Works

2.1 Traditional Lateral Movement Detection

Early LM detection relied primarily on expert-crafted rule engines and statistical anomaly analysis. These methods rapidly identify known attack patterns using predefined policies or thresholds but suffer from three main limitations: reliance on a priori knowledge, poor adaptability to novel attack techniques, and high false alarm rates in large-scale networks. To overcome these issues, researchers have proposed several enhancements. For example, Bowman [6] constructs an authentication graph from log data and trains a logistic regression link predictor using random walk sampling and embedding. Although this approach achieves high true positive rates and low false positive rates on simulated datasets, it cannot handle cold-start scenarios; the absence of historical interaction logs renders embeddings ineffective, preventing the detection of lateral movement involving new nodes. The Hopper system [5] achieves high detection rates and low false positives by building a logon activity graph from logs, applying a path inference algorithm to identify suspicious logon paths, and combining predefined rules with an anomaly scoring algorithm. However, its performance depends heavily on network topology accuracy and parameter settings, which may undermine effectiveness in practice. Smiliotopoulos et al. [7] convert Sysmon logs into a turnkey dataset and apply supervised machine learning to detect lateral movement, yielding high F1 and AUC scores on Windows platforms; nonetheless, this Windows-specific method does not generalize to other operating systems.

2.2 Lateral Movement Detection Based on Graph Neural Networks

Graph neural networks (GNNs) have recently achieved significant success in domains such as fraud detection [22,23], cybersecurity [24], and social networking [25,26]. Researchers have leveraged GNN for LM detection by constructing interaction graphs that represent hosts, users, and authentication events to facilitate anomaly detection. For example, Liu et al. [10] introduced the Latte system, which models hosts, accounts, and their authentication behaviors as a static knowledge graph and applies graph embedding combined with rule matching to detect lateral movement. However, it does not account for network dynamics and depends on the Windows system log structure, limiting its cross-platform applicability.

To capture the temporal evolution of attack paths, dynamic graph representations have been adopted to model and analyze complex interactions and structural changes. Dynamic graphs are typically categorized into discrete-time dynamic graphs (DTDG) and continuous-time dynamic graphs (CTDG) [27]. DTDG represents evolution as a sequence of static graph snapshots sampled at regular intervals. For instance, King et al.'s Euler system [11] generates per-interval snapshots, encodes evolving topology using GNNs, and uses sequence models (e.g., recurrent neural networks) to capture correlations among snapshots for temporal link prediction. Nevertheless, the coarse granularity of DTDG segmentation leads to loss of fine-grained event information. Zhou et al. [12] proposed LMDetect, which constructs authentication logs as heterogeneous authentication multigraphs and employs multiscale attention encoders to capture both local and global dependencies, coupled with a time-aware subgraph classification module. Although it significantly outperforms traditional approaches, its performance is susceptible to hyperparameter settings. In contrast, CTDG modeling dynamically updates node embeddings at each event timestamp, preserving causal and temporal dependencies without relying on discrete windows. For example, Jbeil [13] incorporates a dataset-specific threat sample enhancement module during preprocessing, employs a Temporal Graph Network (TGN) to compute node embeddings, and performs link prediction via a temporal memory mechanism. While this approach fully exploits fine-grained temporal information, its enhancement module lacks generalizability.

Despite these advances, existing methods remain limited. Traditional and GNN-based approaches often rely on fixed static graph topologies, hindering timely embedding updates for newly emerged entities and thereby degrading detection performance. Furthermore, real-world attack samples are incredibly scarce. Current methods either adopt dataset-specific augmentation strategies, which restrict generalization, or apply heuristic perturbations that disrupt the causal continuity of attack paths, thereby increasing the risk of overfitting.

3  Methodology

3.1 Overview of the Framework

Fig. 1 presents the UGEA-LMD framework, comprising four primary modules:

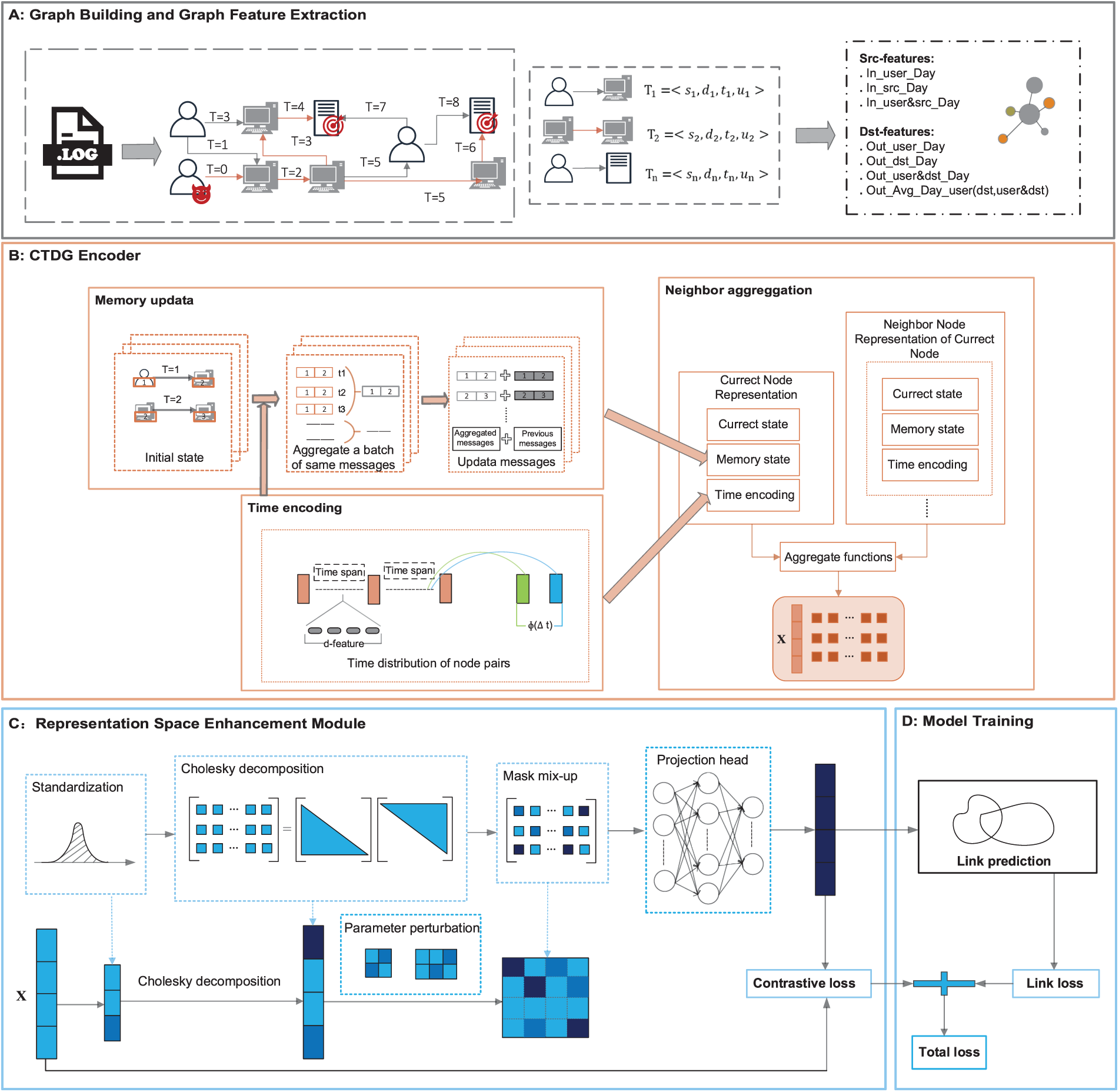
Figure 1: Overview of the UGEA-LMD framework

Authentication Graph Construction (Fig. 1A): This module transforms raw authentication logs into an incrementally constructed CTDG, denoted as G. Entities—specifically users, hosts, and servers—are extracted from each log entry and represented as timestamped edges. These edges are loaded into G in chronological order, yielding an authentication graph that evolves with incoming events. Simultaneously, each node's basic structural, temporal, and statistical features are precomputed and incorporated into its initial embedding to improve the encoder's efficacy.

Continuous-Time Graph Encoding (Fig. 1B): Upon receiving the event stream from graph G, this module uses a continuous-time graph encoder to update edge states. For each event e involving source node i and target node j, the encoder aggregates their historical states from event-level neighborhoods, integrates temporal encodings, and applies an attention mechanism to update node embeddings xi and xj. This process captures both network topology and temporal context in a unified manner.

Representation-Space Sample Enhancement (Fig. 1C): After computing node embeddings, this module leverages a Gaussian copula—a statistical technique that couples multivariate margins into a joint distribution. Each embedding dimension is mapped into a standard normal space, where inter-dimensional dependencies are modeled. Adaptive sampling is then performed in this space, followed by an inverse transform back to the original embedding space, producing an augmented representation ZA that preserves spatio-temporal semantics while introducing diversity. Finally, contrastive learning aligns original and augmented embeddings, ensuring that the generated samples enrich scarce data without deviating from true semantics.

Model Training (Fig. 1D): A two-layer multilayer perceptron (MLP) serves as the link prediction head, projecting concatenated node-pair embeddings into an edge existence probability y^. Prediction error is measured via binary cross-entropy loss. The total loss is a weighted sum of the prediction loss LP and the contrastive loss LC. End-to-end training under this joint objective enables robust detection, particularly in low-frequency event and cold-start scenarios.

3.2 Authentication Graph Construction

In lateral movement detection, authentication interactions among entities convey both rich topological information and clear temporal evolution. We therefore define the authentication graph as the quadruple G={V,E,T,ϕ}, where V is the set of all identity entities; E⊆V×V is the set of directed edges, with each (i,j)∈E representing a single authentication interaction from source entity i to target entity j; T:E→T⊆R is a timestamp mapping, such that T(i,j)=t indicates that the authentication event corresponding to the edge (i,j) occurred at time t; ϕ:E→A is an attribute mapping, where ϕ(i,j) denotes the attribute vector of the authentication event.

To preserve causal and temporal dependencies and supply the necessary context for newly arriving entities, we adopt an event-level incremental update strategy. Specifically, when a new event eijt arrives at timestamp t, we add the timestamped edge (i,j,t) to G and consider its one-hop neighborhood: N(eijt)={{ei,10,…,ei,nt−}∪{e1,j0,…,en,jt−}}∖{ei,j0,…,ei,jt−}, where {ei,10,…,ei,nt−} is the set of all historical interactions initiated by node i prior to t; {e1,j0,…,en,jt−} is the set of all historical interactions received by node j prior to t; {ei,j0,…,ei,jt−} is the set of all past events directly between i and j. By timestamping each new edge and updating node embeddings via their one-hop neighborhoods, the model preserves event-level temporal continuity, capturing network evolution while providing pseudo-neighborhood context for new interactions. This mechanism mitigates the cold-start problem by enriching each new edge with contextual information from its one-hop neighbors.

Additionally, to enhance each node's initial representation, we extract daily structural–temporal statistical features from the logs. For each host, we compute daily in-degree and out-degree counts and derive its average interaction frequency. These features capture activity fluctuations associated with lateral movement and expose latent infiltration patterns. We then integrate these statistics into each node's initial embedding, providing the downstream CTDG model with richer topological and temporal information.

3.3 Continuous-Time Dynamic Graph Enhancement Learning for Sparse Data

To address data sparsity and the cold-start problem in LM detection, we propose a data enhancement approach. This method generates augmented samples through uncertainty-driven representation-space augmentation following CTDG encoding and employs contrastive learning constraints to enhance the model's capacity to distinguish attack chain semantics. The detailed implementation of each sub-module is described below.

3.3.1 Continuous-Time Dynamic Graph Encoding

In lateral movement detection, authentication events not only determine connectivity between entities but also exhibit continuous, causally linked temporal evolution. Traditional static graphs or discrete-snapshot methods cannot simultaneously preserve fine-grained temporal and structural information. To overcome this, UGEA-LMD employs an event-driven continuous-time graph encoding strategy that incrementally updates each node's spatio-temporal embedding in real time. Gated recurrent unit (GRU) fuses historical states with temporal information for emerging authentication events, thereby preserving causal dependencies at the event level and generating stable embeddings. These embeddings serve as high-quality inputs for subsequent uncertainty-driven representation enhancement, offering significant improvements in modeling accuracy over existing methods.

Specifically, we represent the authentication graph G as a time-ordered sequence of events G={et0,et1,et2,…}. Each node i's hidden state mi(0) at t=0 is initialized to its base feature vector xi(0). When node i participates in an authentication event eij(t), we update its memory state as follows:

msrc(t)=msgsrc(msrc(t−1),mdst(t−1),∅(t−t′)),(1)

mdst(t)=msgdst(msrc(t−1),mdst(t−1),∅(t−t′)),(2)

where ∅(⋅) denotes an MLP, and message passing with a temporal embedding function msg(⋅), which is implemented using a GRU. The GRU integrates each node's previous hidden state with timestamp information to produce the temporal embedding. By accumulating a node's interaction history in its memory state, this update mechanism ensures that, whenever a node appears in a new event, its state reflects all previous related authentication records.

Based on the updated memory state, we generate a node's spatio-temporal embedding at time t. Let node i's current feature be vi(t) and its historical state be mi(t). Denote Nt(i) as the set of neighbors that interacted with i before t. We compute the final embedding xi(t) as

xi(t)=MLP(mi(t),vi(t),AGG(mj(t′)|j∈Nt(i))),(3)

where AGG(⋅) applies a multi-attention mechanism to aggregate neighbor information (see Fig. 2). The embedding xj(t) of node j is obtained in the same way.

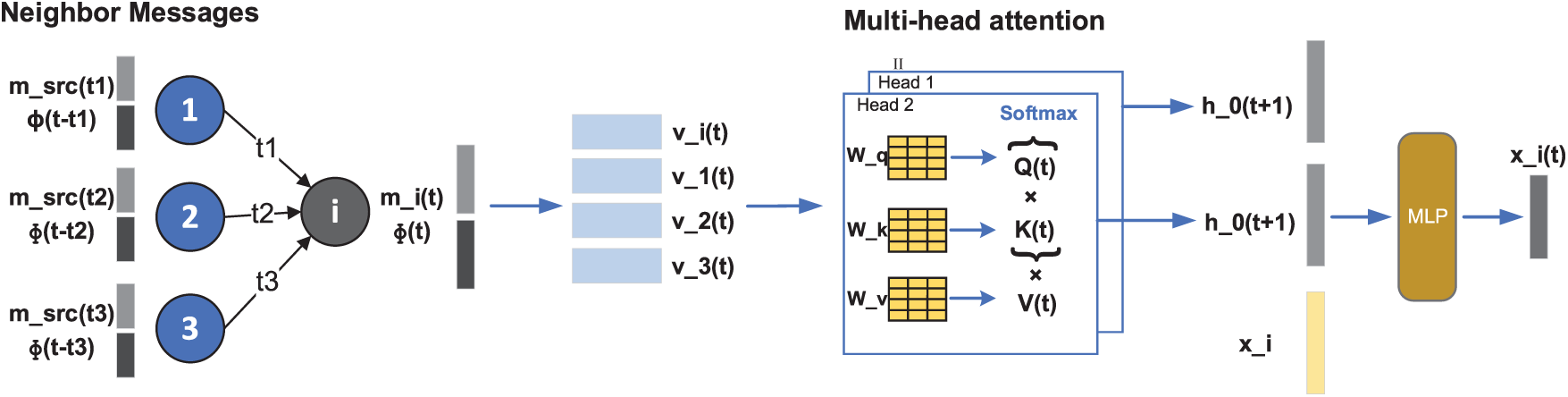
Figure 2: Neighbor aggregation strategy based on multi-head attention

Finally, the edge embedding for the event eij(t) is defined by concatenation: xij(t)=[xi(t)||xj(t)].

This continuous-time dynamic graph encoding module preserves event-level temporal details and interaction context, providing a stable initial representation for subsequent data enhancement.

3.3.2 Uncertainty-Driven Representation-Space Enhancement

In lateral movement detection, sparse malicious samples hinder effective representation learning. Existing data enhancement methods primarily operate in the input space via heuristic perturbations, which can increase sample count but ignore authentication events related to temporal order and disrupt causal continuity in attack paths. A few dynamic graph-oriented enhancement techniques consider both temporal and structural information, yet their strategies often depend on specific model modules, resulting in complex implementation and poor portability. In contrast, our method performs augmentation in the representation space; it preserves original spatio-temporal semantics while expanding the expressive space of potential attack patterns and remains architecture-agnostic—thereby significantly improving the model's generalization and robustness in sparse-sample scenarios.

As illustrated in Fig. 1D, following the acquisition of encoded embeddings, UGEA-LMD works as follows: first, the embedding matrix is normalized column-wise, and the empirical correlation matrix is calculated; next, matrix decomposition is carried out, and samples are taken from a standard normal distribution to create multivariate Gaussian perturbations that maintain dimensional correlations; these perturbations are adaptively adjusted by the introduction of trainable scaling and bias parameters, which are then combined with mask-based blending to produce a variety of augmented embeddings; and lastly, a contrastive loss aligns the original and augmented embeddings to maintain semantic consistency as the data is expanded.

First, let the node embedding matrix be X∈Rn×d, where n is the number of nodes and d is the embedding dimension. To ensure that each dimension is on a comparable scale, we normalize the X column-wise, as shown in Eqs. (4)–(6), where μεRd is the vector of per-dimension means, σεRd is the vector of per-dimension standard deviations, and the subtraction and division are performed element-wise.

Xnorm=(X−μ)σ,(4)

μj=1n∑i=1nXij,(5)

σj=1n∑i=1n(Xij−μj)2(j=1,…,d).(6)

Next, we compute the empirical correlation matrix R of the normalized embeddings, as defined in Eq. (7), and quantify the sample correlation coefficient between the i-th and j-th embedding dimensions.

R=1nXnormTXnorm,(7)

rij=1n∑k=1n(Xnorm)ki(Xnorm)kj.(8)

The Gaussian copula is a method that separates the dependence structure of a multivariate normal distribution from each dimension's marginal distribution [28]. Let Φ denote the cumulative distribution function (CDF) of the standard normal distribution, Φ−1 its inverse, and ΦR the CDF of a d-dimensional normal distribution with covariance matrix R.

The Gaussian copula is defined as Eq. (9), under this construction, any random vector (X1,…,Xd) is mapped to uniform variables Ui=Fi(xi) on [0, 1] via its marginal CDF Fi(xi). The copula CR then determines the joint distribution of (U1,…,Ud) independently of the original marginals, relying solely on the correlation matrix R.

CR(u1,…,ud)=ΦR(Φ−1(u1),…,Φ−1(ud)).(9)

By employing a Gaussian copula, we first estimate each dimension's marginal distribution, then impose the dependence encoded by R to construct the multivariate joint distribution. This approach flexibly preserves both the original marginal properties of each dimension and their inter-dimensional dependencies.

Cholesky decomposition factors a symmetric positive-definite matrix into a lower triangular matrix and its transpose, capturing inter-dimensional dependencies and providing a linear transform for sampling. Specifically, we decompose the correlation matrix R as R=LLT, L∈Rd×d (lower triangular).

Next, we sample a vector uεRd from the uniform distribution and transform it to a standard normal vector Z, applying the Cholesky transform LT yields a multivariate normal perturbation Zcorr with covariance R, it can be represented by Eqs. (10) and (11):

Z=Φ−1(u),Z∼N(0,I),(10)

Zcorr=ZLT,Zcorr∼N(0,R).(11)

To adaptively adjust these perturbations, we introduce trainable parameters β,γεRd, updated as Eq. (12), we then apply inverse standardization to Zcorr, producing the uncertainty-driven enhanced embedding Zun as Eq. (13):

β=μβ+εβ⊙σβ,γ=μγ+εγ⊙σγ,(12)

Zun=(Zcorr⊙σ+µ)⊙γ+β.(13)

To further diversify augmented samples while preserving local structure, we employ an adaptive mask-blending strategy. Let M∈{0,1}n×d be a binary mask where each element Mij~ Bernoulli (pj), with learnable probabilities pj initialized at 0.8 and constrained within [0.1, 0.9]. Let Zper be a randomly permuted embedding. The final augmented embedding is:

ZA=M⊙Zun+(1−M)⊙Zper.(14)

This random masking offers stochastic augmentation, and our Gaussian Copula framework (Eqs. (4)–(11)) preserves important dependency structures.

To ensure semantic consistency between original and augmented embeddings, we apply a contrastive learning constraint in representation space. We introduce a two-layer MLP projection head Proj:Rd→Rk that maps the original embedding X and the augmented embedding ZA into a shared low-dimensional space; see Eqs. (15)–(17):

Proj(u)=W2(Act(W1u+b1))+b2,(15)

P=Proj(X),(16)

PA=Proj(ZA).(17)

We then use the normalized temperature-scaled cross-entropy loss: for each node i, its projection Pi and its augmented projection PA,i form a positive pair. The contrastive loss is as shown in Eq. (18), where sim(Pi,PA,i) denotes cosine similarity, τ is a temperature parameter, and N is the total number of nodes. This loss minimizes the distance between each node's original and augmented representations while maximizing the distance between representations of different nodes, thus preserving semantic consistency and enhancing discriminative power.

Lc=−1N∑i=1Nlog⁡exp(sim(Pi,PA,i)/τ)∑j=1Nexp(sim(Pi,PA,j)/τ).(18)

Interactions in enterprise networks vary significantly across time and structure, leading different feature channels to encode distinct behavioral patterns. To address this, our mechanism applies adaptive, per-dimension updates that model each channel's diversity and dynamics during graph evolution while preserving the semantic integrity of critical attack paths. This targeted updating significantly enhances the model's robustness under sparse-sample conditions.

3.4 Model Training

We measure link prediction error via the binary cross-entropy loss as Eq. (19), where yi∈{0,1} is the true label for samples, yi^ is its predicted probability, and S is the total number of samples. The training objective combines the link prediction loss LP and the contrastive learning loss LC, as Eq. (20), where α is a balancing coefficient.

Lp=−1S∑i=1S(yilog⁡yi^+(1−yi)log⁡(1−yi^)),(19)

L=LP+αLC.(20)

By training the model end-to-end under this joint objective, we leverage the encoder's fine-grained temporal embeddings while mitigating data sparsity and cold-start issues through uncertainty-driven augmentation and contrastive constraints. This approach yields improved accuracy and robustness in LM detection.

4  Experimental Setup

4.1 Datasets and Configuration

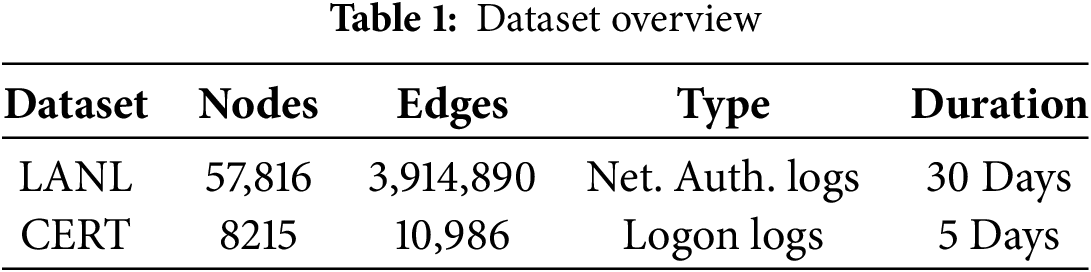
We evaluate UGEA-LMD on two large-scale real-world datasets: LANL [29] and CERT [30].

•   LANL: Released by Los Alamos National Laboratory, this dataset spans 58 days of multi-source security events from an enterprise network. It includes Windows host authentication logs, Active Directory domain-controller logon records, internal DNS queries, and router-captured network traffic, annotated with red-team attack activities. The compressed dataset is about 12 GB, comprising 12,425 users, 17,684 hosts, 62,974 processes, and 1.65 × 109 events.

•   CERT: The Carnegie Mellon CERT insider-threat dataset simulates employee logins and file accesses. We use version 6.2, which contains 3,530,286 login events and 2,014,884 file-access records. For our experiments, we extract a five-day window of interactions.

All experiments are implemented in PyTorch with PyTorch Geometric. Random seeds are fixed to ensure reproducibility. To simulate real-world malicious sample sparsity, we subsample 19,836 benign and 164 malicious events on LANL, and 17,000 benign and 400 malicious events on CERT. After converting logs into time-ordered interaction sequences, we split each dataset chronologically into 70% train, 15% validation, and 15% test sets. Further dataset statistics are presented in Table 1. To assess generalization, we randomly designate a subset of nodes as “unseen” during testing—ensuring they do not appear in training—to evaluate the model's adaptability to temporal evolution and its ability to detect lateral movement on previously unseen entities.

During manuscript preparation, we used GPT-4o (OpenAI; accessed 1 May—11 September 2025, version: GPT-4o) for English language polishing and stylistic revision. The tool was used only to improve language clarity and grammar; no new scientific claims, data, or figures were generated by the tool. All AI-generated text was carefully reviewed and edited by the authors, who take full responsibility for the final content.

4.2 Evaluation Metrics

To assess UGEA-LMD's performance and generalization in lateral movement detection, we employ four metrics (higher values indicate better performance):

•   AUC (Area Under the ROC Curve): Evaluates the model's ability to separate positive (malicious) and negative (benign) samples. To mitigate dataset imbalance, we select the decision threshold that maximizes the geometric mean of the True Positive Rate (TPR) and True Negative Rate (TNR) on the training set, yielding more robust classification.

•   Precision: The fraction of predicted malicious samples that are truly malicious, defined as Precision=TP/(FP+TP), where TP and FP denote true positives and false positives, respectively. High precision indicates a low false positive rate.

•   Recall: The fraction of actual malicious samples correctly identified, defined as Recall=TP/(TP+FN), where FN denotes false negatives. High recall indicates a low false negative rate.

•   AP (Average Precision): The area under the precision–recall curve, computed as a weighted sum of precisions at different recall levels, suitable for highly imbalanced scenarios: AP=∑n(Recalln−Recalln−1)×Precisionn.

4.3 Baseline Methods

To demonstrate UGEA-LMD's advantages in LM detection, we compare it against four state-of-the-art methods:

•   GAT [17]: A canonical static graph neural network employs a multi-head self-attention mechanism to learn per-neighbor weighting, thereby automatically capturing the relative importance of each node within the network topology.

•   GraphSAGE [16]: A scalable GNN that samples a fixed number of neighbors per node and aggregates their representations—via mean, pooling, or LSTM aggregators—to generate node embeddings, combining efficiency with expressive power on large graphs.

•   Euler [13]: A DTDG framework for LM detection. Authentication logs are partitioned into timestamped snapshots; a GNN model encodes each snapshot's topology, and a sequence model captures temporal dependencies across snapshots for edge prediction or anomaly detection.

•   Jbeil [14]: A TGN–based lateral movement detector featuring a temporal message-storage and memory-update mechanism, augmented by a sample enhancement module to address data sparsity. The public implementation omits the dataset-specific augmentation; therefore, we implemented the core TGN edge-prediction pipeline and replaced the undisclosed augmentation with SMOTE.

5  Results and Evaluation

In this section, we first evaluate UGEA-LMD against several representative models and frameworks to demonstrate its architectural effectiveness. Next, we conduct ablation studies to assess the contribution of each module within UGEA-LMD. We then analyze key hyperparameters experimentally to understand their impact on performance. Finally, we discuss the overall experimental findings and their implications.

5.1 Experimental Results

We evaluate UGEA-LMD under two settings: transductive and inductive [31]. For the Euler and Jbeil baselines, we strictly follow the detection pipelines and parameter settings reported in their original papers. To ensure fair replication of Euler’s results, we evaluate Euler only on the LANL dataset.

Transductive Setting: In this setting, test nodes are partially observable during training, allowing models to leverage graph structure information. Table 2 presents evaluation results across four metrics (Precision, Recall, AP, AUC) on both datasets. UGEA-LMD outperforms baseline methods on most evaluation metrics, achieving AUC 0.9254, Precision 93.95%, and Recall 91.00% on LANL and AUC 0.9176, Precision 89.16%, and Recall 95.24% on CERT.

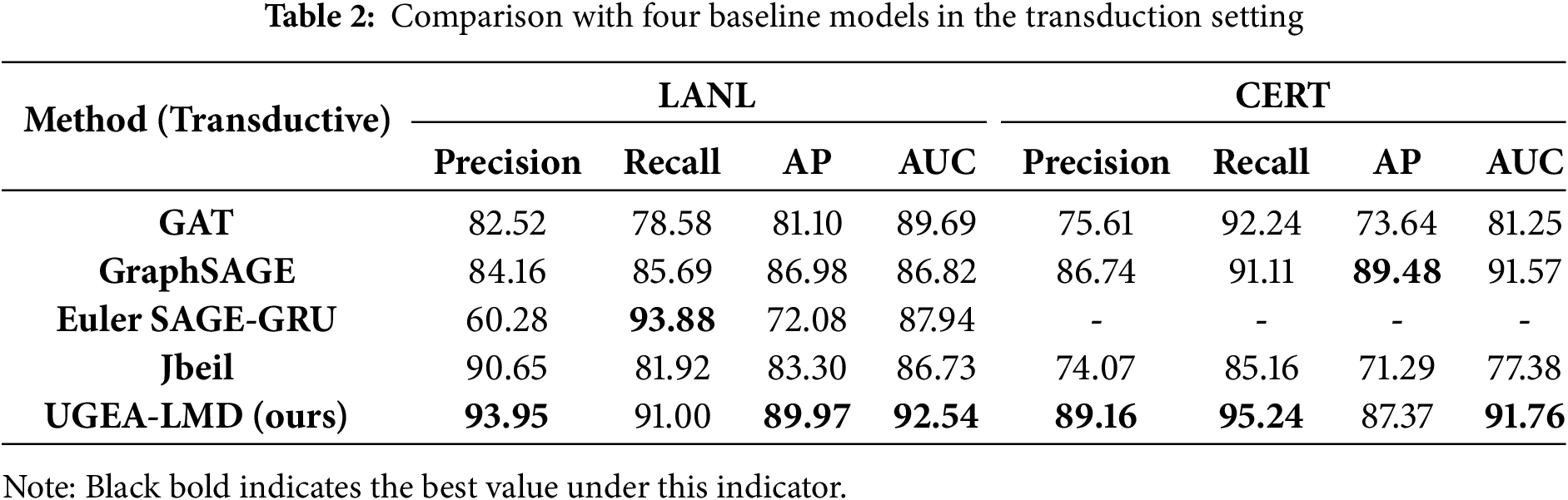
While achieving competitive precision on LANL (90.65%), Jbeil experiences substantial performance degradation on CERT (AUC 0.7738), indicating that SMOTE-based augmentation fails to model the intricate behavioral dynamics of synthetic datasets adequately. Euler demonstrates a pronounced precision-recall trade-off on LANL, achieving exceptionally high recall (93.88%) while suffering from severely compromised precision (60.28%), attributed to its discrete temporal snapshot approach, which amplifies noise and yields elevated false positive rates. GraphSAGE exhibits stable yet moderate performance across both datasets (AUC 0.8682–0.9157), while GAT demonstrates dataset-specific variability with enhanced recall on CERT (92.24%) but lower precision.

Inductive Setting: All methods show substantial performance degradation when models cannot access test nodes and must rely solely on representations learned from training subgraphs, as shown in Table 3. GAT and GraphSAGE exhibit severe drops with AUC scores of 0.6371−0.6601, as their neighborhood aggregation mechanisms fail when encountering unseen graph topology. Euler achieves moderate improvement on LANL (AUC 0.7667) through temporal modeling, yet suffers from reduced recall (59.54%), indicating that discrete temporal snapshots inadequately capture dynamics for generalizing to new attack patterns. Jbeil (with SMOTE augmentation) demonstrates notable dataset-dependent performance: modest results on LANL (AUC 0.7153) but substantially improved performance on CERT (AUC 0.8150), suggesting its continuous-time modeling suits datasets with regular temporal patterns.

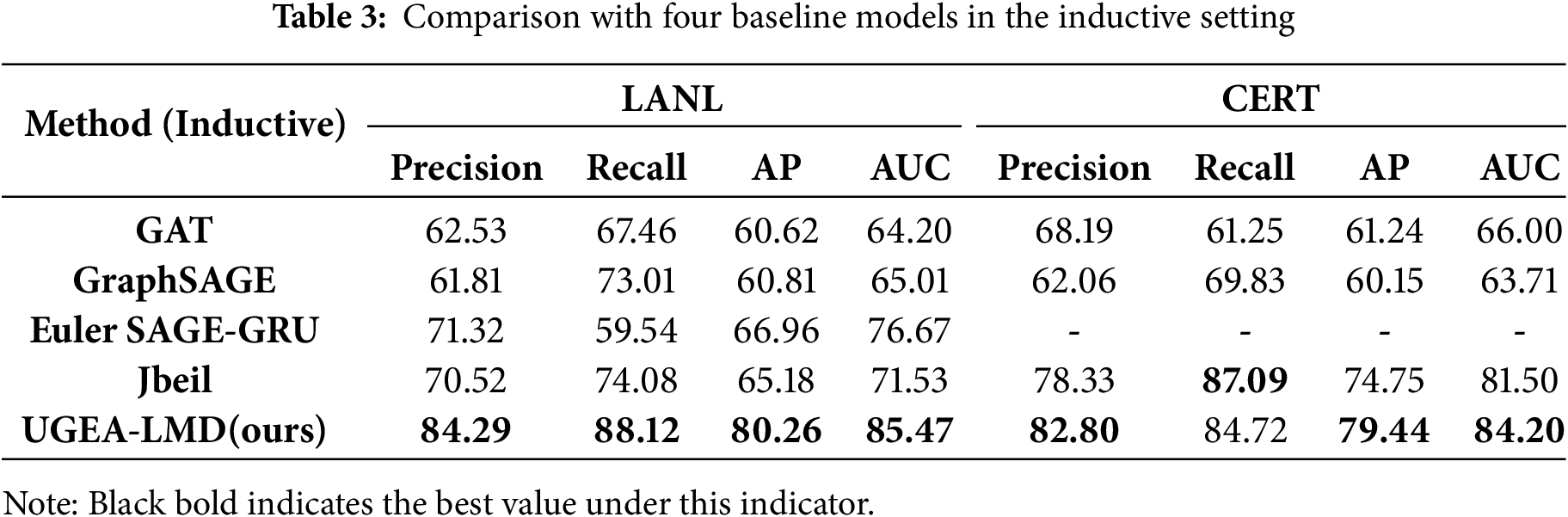
Overall, UGEA-LMD dominates across multidimensional metrics in both transductive and inductive settings, achieving AUC scores of 0.8547 (LANL) and 0.8420 (CERT) in the inductive setting. This capability stems from uncertainty-driven augmentation, which creates diverse training scenarios, and from contrastive learning, which promotes robust feature representations that generalize effectively to unseen entities.

5.2 Ablation Study

To accurately assess each module's contribution to UGEA-LMD's generalization, we conduct the ablation study exclusively under the inductive setting. We evaluate four variants on the LANL and CERT datasets and report Precision, Recall, AP, and AUC. The variants are defined as follows:

•   UGEA-LMD_U_C: Removes both uncertainty enhancement and contrastive learning, retaining only CTDG encoding and the basic link-prediction head.

•   UGEA-LMD_U: Removes uncertainty enhancement only, preserving contrastive learning.

•   UGEA-LMD_C: Removes contrastive learning only, preserving uncertainty enhancement.

•   UGEA-LMD: The full model.

Table 4 reports the ablation results in the inductive setting. The full model (UGEA-LMD) achieves the best overall performance, with AUC 0.8547 on LANL and AUC 0.8420 on CERT, approximately 10 percentage points higher than the strongest single variant. On LANL, the UGEA-LMD attains 84.29% precision and 88.12% recall for unseen nodes, substantially exceeding the baseline UGEA-LMD_U_C (69.67% precision, 73.93% recall). Fig. 3 shows t-SNE visualizations on a 6000-sample LANL subset (fewer than 1% outliers), illustrating a clear, progressive improvement in embedding separability. The silhouette coefficients are 0.01 for the baseline, 0.07 with uncertainty enhancement, 0.09 with contrastive learning, and 0.53 for the full model. Together, these visual and quantitative indicators confirm that the combined design substantially improves both discrimination and inductive generalization.

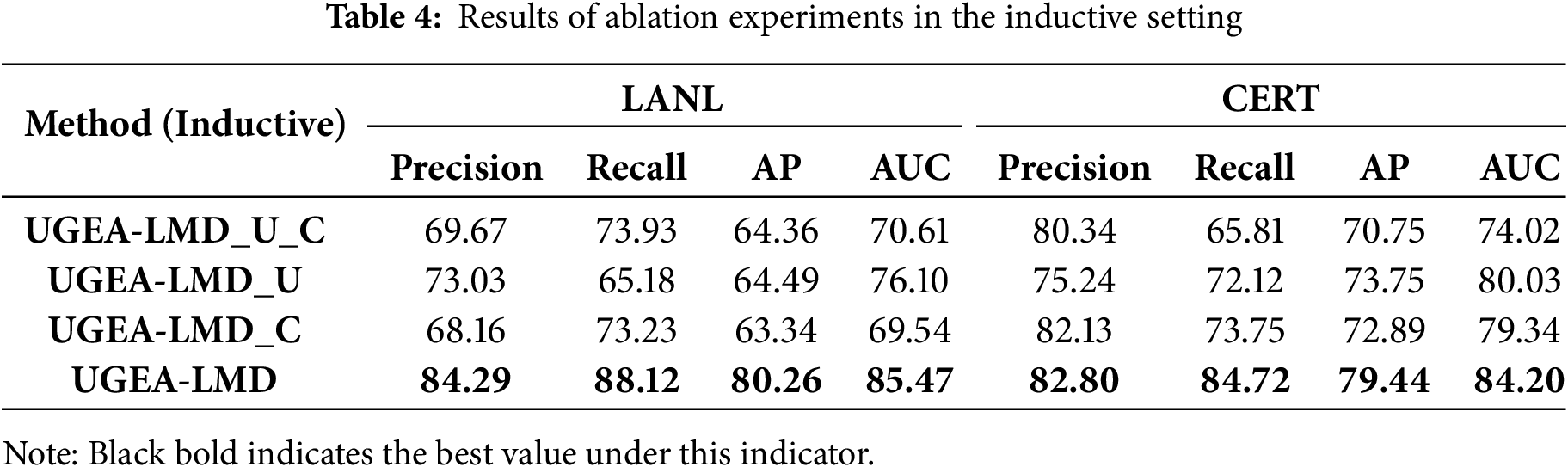
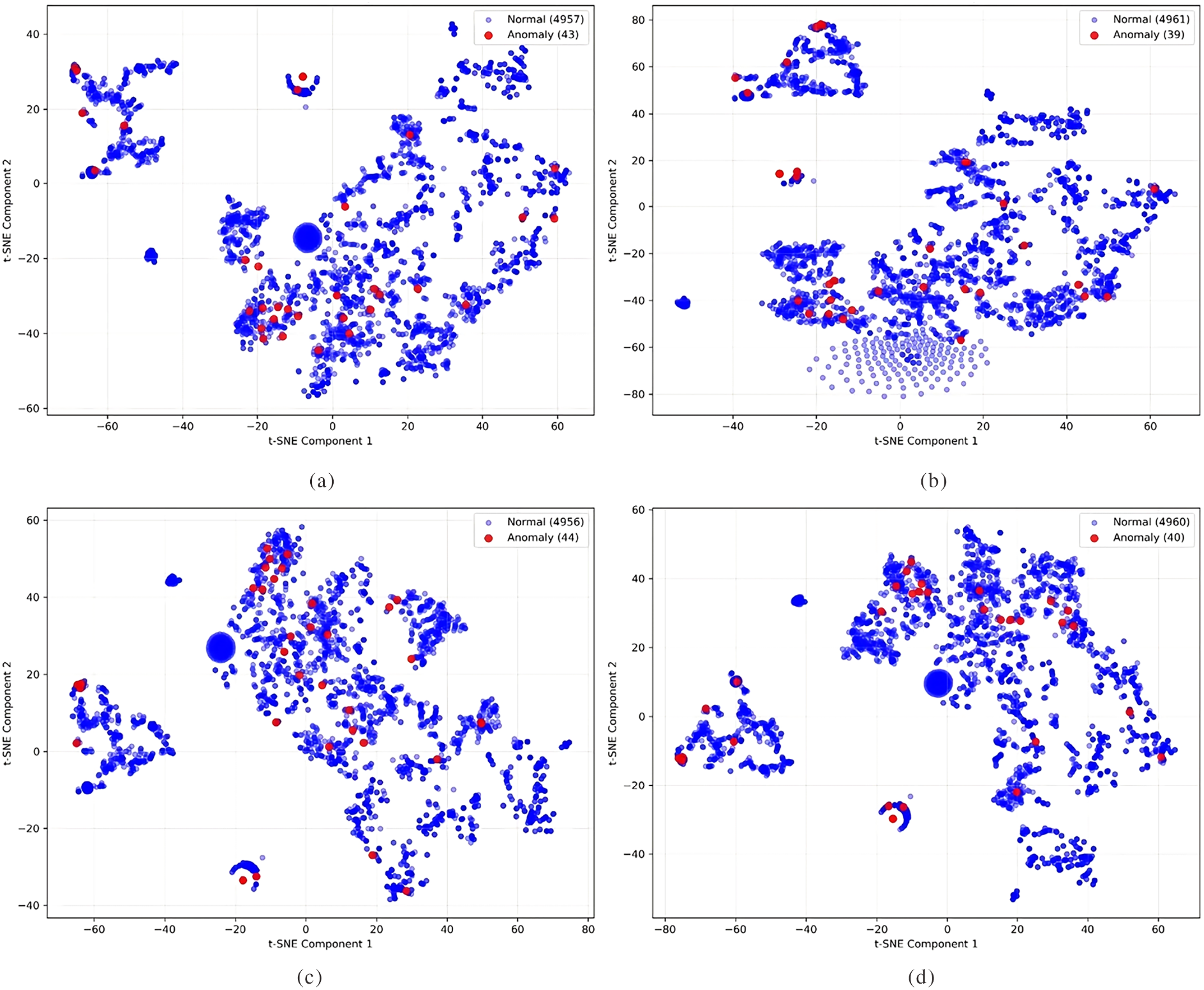
Figure 3: t-SNE visualizations for the UGEA-LMD ablation study: (a) Baseline only (silhouette = 0.01); (b) Baseline + Uncertainty Enhancement (silhouette = 0.07); (c) Baseline + Contrastive (silhouette = 0.09); (d) Full UGEA-LMD (Uncertainty + Contrastive) (silhouette = 0.53). The plots show progressive improvement in embedding separation as modules are added, with the complete model producing the most compact and well-separated anomaly clusters

The uncertainty enhancement module operates in representation space to produce controlled, parameterized perturbations around learned embeddings. By expanding local neighborhoods while preserving cross-dimension dependency and adaptively scaling perturbation magnitude, this module increases exposure to boundary cases and rare connectivity patterns, which improves sensitivity to anomalous structures and helps generalize to nodes with limited history. The main drawback is that augmentation can introduce variance when the true anomaly signal is extremely weak or when training signals are scarce, because some augmented samples may overlap with noise. The contrastive module enforces semantic consistency by pulling semantically similar pairs together and pushing dissimilar pairs apart, thereby reducing intra-class variance and improving global embedding geometry. As the downstream task optimizer for the uncertainty enhancement module, contrastive learning can only function in conjunction with it. Actually, the two modules are complementary: the uncertainty enhancement module diversifies candidate positive and negative pairs in the representation space, while the contrastive loss module anchors them onto a stable and discriminative manifold. As shown in Fig. 3, this synergy yields the most compact anomaly clusters in t-SNE visualizations.

However, coupling multiple objectives amplifies variance under extreme information loss, as shown by robustness tests on a smaller subset (Tables 5 and 6). Compared with the continuous-time graph backbone (UGEA-LMD_U_C), the uncertainty module transforms scarcity into augmented data under moderate sparsity but introduces variability at the most severe levels. The full model achieves the highest average AP under exceptionally sparse conditions and, despite greater fluctuations in extreme cases, consistently outperforms all variants across all evaluation metrics.

Overall, the ablation results confirm the effectiveness of each UGEA-LMD component and reveal that the collaborative interaction between uncertainty enhancement and contrastive learning is critical for high-performance link prediction in dynamic graphs.

5.3 Hyperparameter Settings

We evaluate the robustness and generalization of three key hyperparameters—uncertainty noise scale (μ), contrastive loss weight (α), and contrastive learning temperature (τ)—via systematic grid search on LANL and CERT. Fig. 4 shows how key hyperparameters affect the AP, AUC, Recall, and Precision of the model, and Table 7 summarizes the optimal configurations.

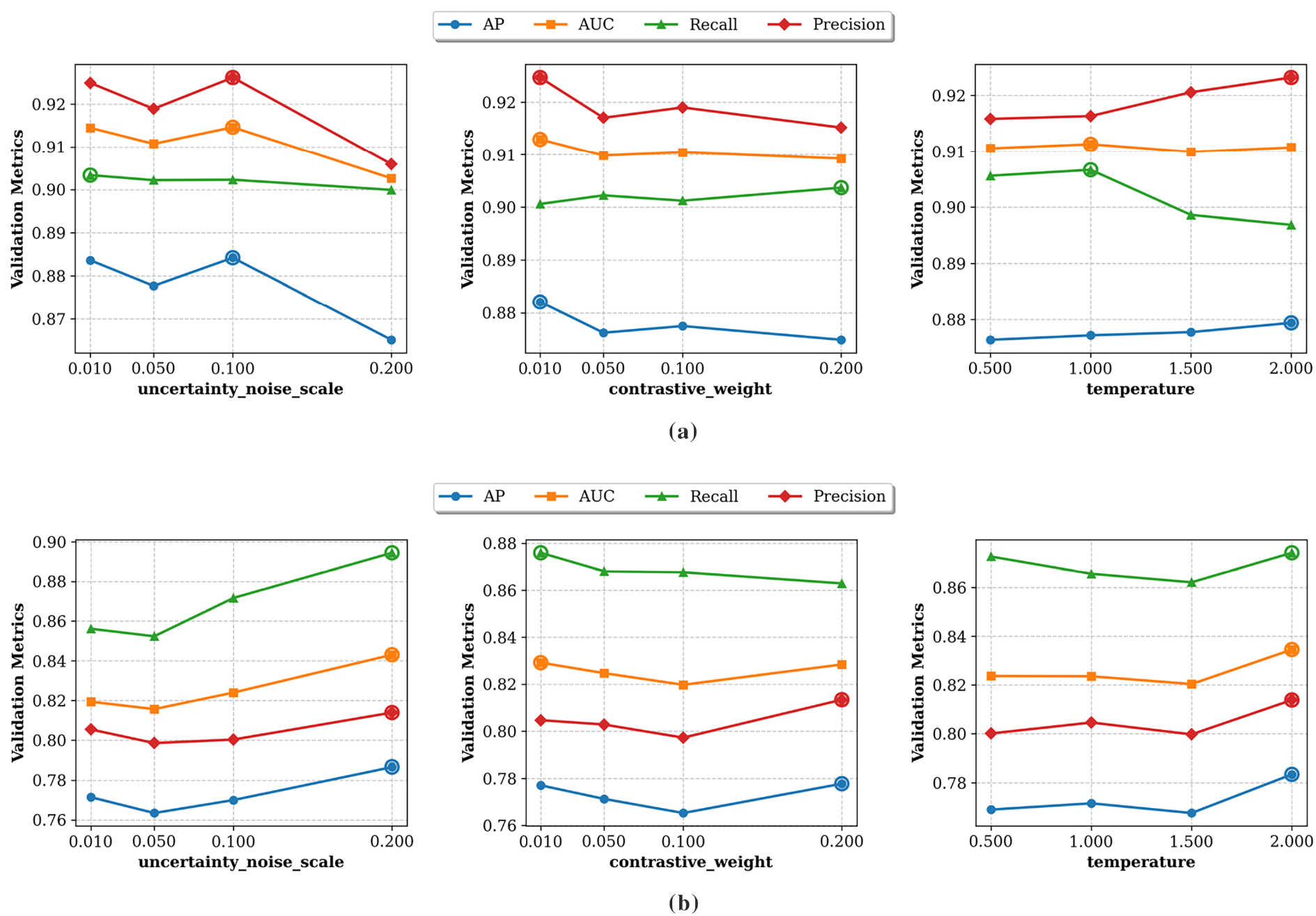
Figure 4: Sensitivity analysis of three hyperparameters—uncertainty noise scale (μ), contrastive loss weight (α), and contrastive temperature (τ)—on the (a) LANL and (b) CERT datasets

•   Uncertainty Noise Scale (μ): The optimal values are 0.10 for LANL and 0.20 for CERT, reflecting dataset-specific noise requirements. For the LANL dataset, small perturbations preserve node semantics while enhancing embedding diversity; values below 0.10 fail to introduce sufficient diversity for adversarial resilience, whereas higher values compromise embedding fidelity. For the CERT dataset, stronger noise is required to mitigate overfitting and reveal anomalous patterns; however, values above 0.20 cause gradient instability and hinder convergence.

•   Contrastive Loss Weight (α): For the LANL dataset, an α of 0.01 yields the highest AP and AUC and matches other settings on Recall and Precision; higher α values over-emphasize the contrastive loss and slightly destabilize link prediction. In contrast, for the CERT dataset, an α of 0.20 achieves the best precision gains and restores AP/AUC that dip at mid-range weights, indicating that CERT benefits from stronger contrastive regularization.

•   Contrastive Temperature (τ): All four metrics increase steadily with τ up to 2.0, reflecting that a “softer” distribution (higher temperature) improves contrastive separation without over-flattening the similarity scores. Although validation metrics increase monotonically with τ, we restrict the search to [0.5–2.0] to avoid confounding effects from its interaction with other hyperparameters.

Our parameter analysis revealed that CERT requires stronger perturbations than LANL. Therefore, we conducted a comprehensive sensitivity study across different uncertainty noise levels. Fig. 5 demonstrates this through a comprehensive sweep of noise intensity from 0.0 to 0.5. The results exhibit a classic inverted-U relationship, with optimal performance achieved at noise level 0.2 (AP = 0.82, AUC = 0.878). Insufficient noise (≤0.1) leads to suboptimal performance due to overfitting, while excessive noise (≥0.4) degrades performance by corrupting the underlying signal. The convergence analysis further validates this choice, showing that noise = 0.2 provides stable training dynamics with convergence in approximately 10 epochs, whereas both lower and higher noise levels result in unstable convergence patterns.

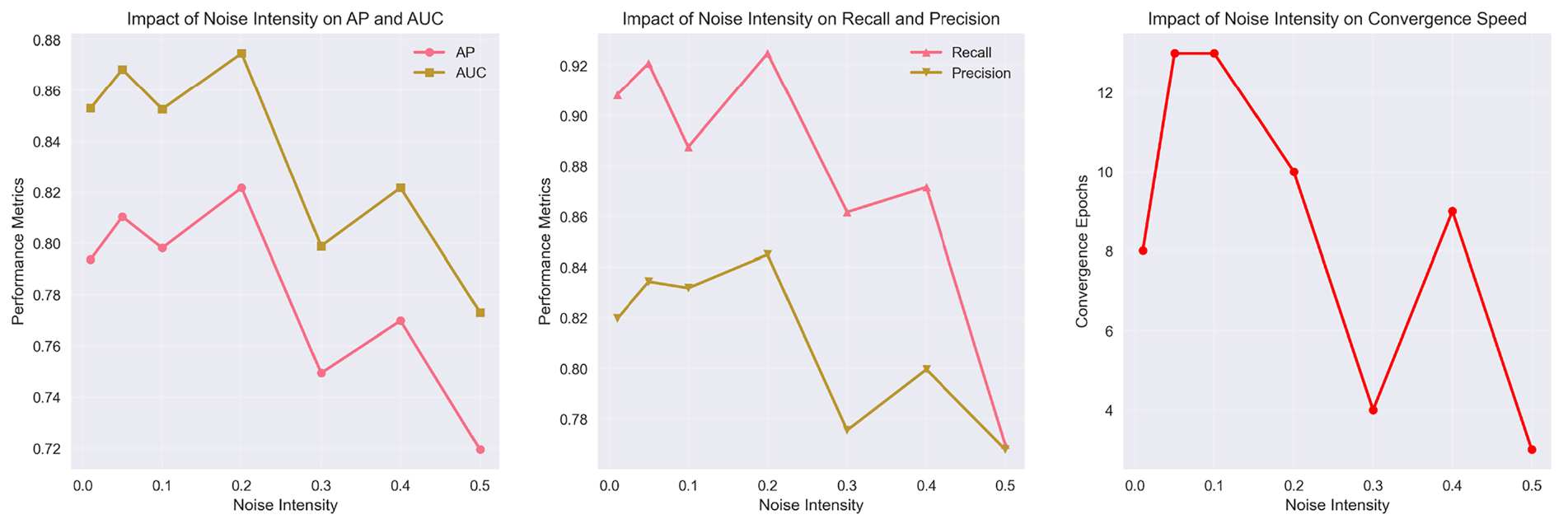
Figure 5: Sensitivity analysis of uncertainty noise intensity on CERT performance and convergence behavior

This analysis confirms the clear dataset dependence observed in our experiments: the LANL dataset benefits from a lower uncertainty noise scale and moderate contrastive weight, whereas the CERT dataset requires stronger perturbations and higher α to break overfitting pathways and surface anomalous patterns. Moreover, both datasets achieve optimal performance at a higher temperature, indicating that a softer similarity distribution enhances contrastive separation. Careful tuning of μ, α, and τ based on each dataset's noise characteristics and topological complexity is therefore essential for optimal detection performance.

5.4 Scalability and Runtime

We evaluated UGEA-LMD’s scalability on CERT dataset graphs ranging from 3228 to 11,365 edges. As shown in Fig. 6a, training time scales from 1.33 s to 4.84 s per epoch: training time increases by 3.6× for a 3.5× increase in edges, indicating near-linear growth. This scaling is comparable to GAT and outperforms Jbeil, demonstrating that our uncertainty and contrastive modules maintain computational efficiency. While static methods achieve faster absolute runtimes (0.63–0.93 s per epoch), the approximately 5–6× difference reflects the inherent overhead of temporal architectures, which must maintain memory states and process sequential dependencies.

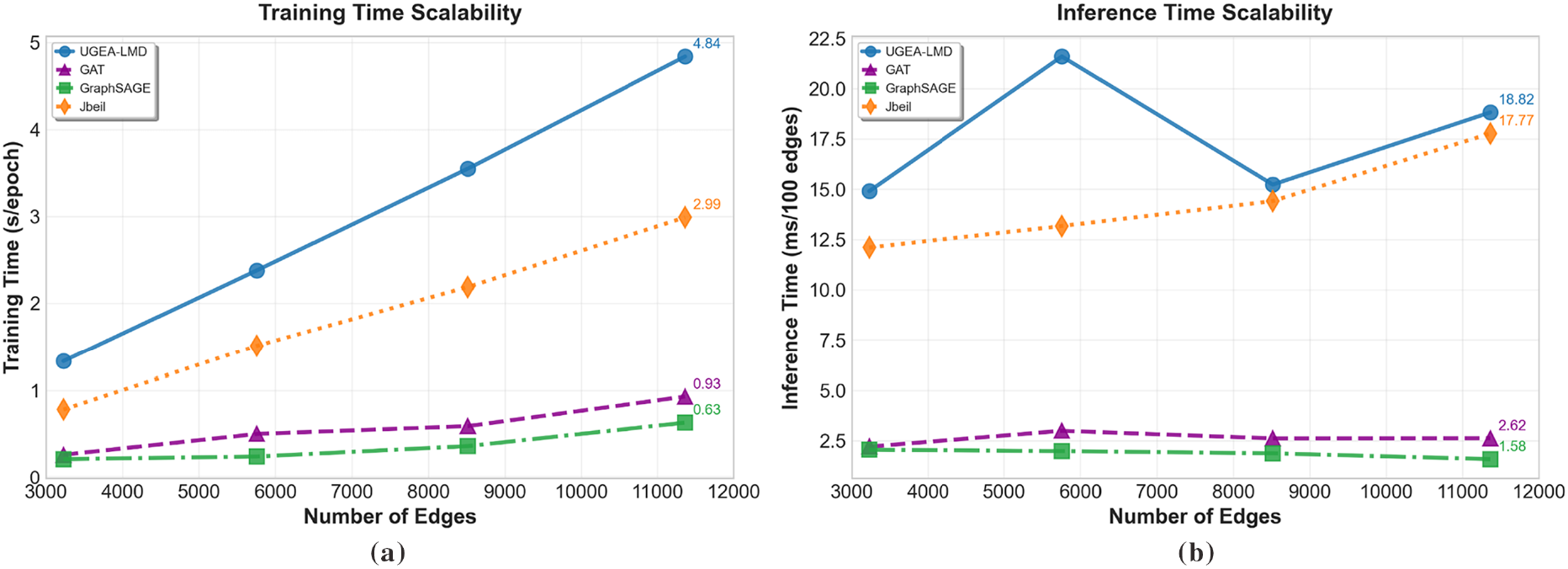
Figure 6: Training and inference scalability of UGEA-LMD compared to baseline methods (GAT, GraphSAGE, and Jbeil) on the CERT dataset with increasing graph sizes. Subfigure (a) reports training time, while (b) reports inference time

For inference performance (Fig. 6b), UGEA-LMD requires 14.90–18.82 ms per 100 edges, only 6% higher than Jbeil's 12.10–17.77 ms at the largest scale. This minimal inference overhead is crucial for real-time deployment scenarios. Substantial performance gains well justify the computational cost. In the inductive setting, UGEA-LMD achieves 80.26% AP compared to Jbeil's 65.18%—a 15.08 percentage point improvement. These results confirm that UGEA-LMD's modest computational overhead delivers significant detection improvements, particularly in challenging inductive settings.

6  Conclusion

We presented UGEA-LMD, a framework that addresses key challenges in lateral movement detection. By modeling authentication logs as a continuous-time dynamic graph and encoding event-level temporal dependencies, the model captures fine-grained user behaviors. An uncertainty-driven data-enhancement module injects structured noise to improve sensitivity to anomalous patterns, while a contrastive learning objective produces more discriminative node representations. Comprehensive experiments on two real-world cybersecurity datasets (LANL and CERT) demonstrate UGEA-LMD’s superiority. In the transductive setting, UGEA-LMD achieved AUC of 0.9254 (LANL) and 0.9176 (CERT), significantly outperforming state-of-the-art baselines. It also maintains strong performance in the inductive setting on unseen nodes, underscoring its practical applicability. UGEA-LMD therefore offers a novel, robust approach for detecting lateral movement detection that improves anomaly detection and generalization in dynamic network environments.

Acknowledgement: During the preparation of this manuscript, the authors utilized GPT-4o (OpenAI) for English language polishing and stylistic revision of the manuscript. The authors have carefully reviewed and revised the output and accept full responsibility for all content.

Funding Statement: This work was supported by the Zhongyuan University of Technology Discipline Backbone Teacher Support Program Project (No. GG202417); the Key Research and Development Program of Henan under Grant 251111212000.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jizhao Liu, Yuanyuan Shao, Shuqin Zhang, Fangfang Shan, and Jun Li; data collection: Yuanyuan Shao; analysis and interpretation of results: Jizhao Liu, Yuanyuan Shao, Shuqin Zhang, Fangfang Shan, and Jun Li; draft manuscript preparation: Jizhao Liu, Yuanyuan Shao, Shuqin Zhang, Fangfang Shan, and Jun Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The two datasets we use are publicly available: https://csr.lanl.gov/data/cyber1/ and https://kilthub.cmu.edu/articles/dataset/Insider_Threat_Test_Dataset/12841247 (accessed on 11 September 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Sharma A, Gupta BB, Singh AK, Saraswat VK. Advanced Persistent Threats (APTevolution, anatomy, attribution and countermeasures. J Ambient Intell Human Comput. 2023;14(7):9355–81. doi:10.1007/s12652-023-04603-y. [Google Scholar] [CrossRef]

2. Teichmann FM, Boticiu SR. The most impactful ransomware attacks in 2023 and their business implications. Int Cybersecur Law Rev. 2024;5(2):301–11. doi:10.1365/s43439-024-00115-3. [Google Scholar] [CrossRef]

3. Nassar M, Khoury J, Erradi A, Bou-Harb Eeditors. Game theoretical model for cybersecurity risk assessment of industrial control systems. In: 2021 11th IFIP International Conference on New Technologies, Mobility and Security (NTMS); 2021 Apr 19–21. doi:10.1109/NTMS49979.2021.9432668. [Google Scholar] [CrossRef]

4. Han X, Pasquier T, Bates A, Mickens J, Seltzer Meditors. Unicorn: runtime provenance-based detector for advanced persistent threats. In: Network and Distributed Systems Security (NDSS) Symposium 2020; 2020 Feb 23–26; San Diego, CA, USA. doi:10.14722/ndss.2020.24046. [Google Scholar] [CrossRef]

5. Ho G, Dhiman M, Akhawe D, Paxson V, Savage S, Voelker GM editors, et al. Hopper: modeling and detecting lateral movement. In: 30th USENIX Security Symposium (USENIX Security 21); 2021 Aug 11–13. [Google Scholar]

6. Bowman B, Laprade C, Ji Y, Huang HHeditors. Detecting lateral movement in enterprise computer networks with unsupervised graph {AI}. In: 23rd International Symposium on Research in Attacks, Intrusions and Defenses (RAID 2020); 2020. [Google Scholar]

7. Smiliotopoulos C, Kambourakis G, Barbatsalou K. On the detection of lateral movement through supervised machine learning and an open-source tool to create turnkey datasets from Sysmon logs. Int J Inform Secur. 2023;22(6):1893–919. doi:10.1007/s10207-023-00725-8. [Google Scholar] [CrossRef]

8. Bai T, Bian H, Salahuddin MA, Abou Daya A, Limam N, Boutaba R. RDP-based lateral movement detection using machine learning. Comput Commun. 2021;165(1):9–19. doi:10.1016/j.comcom.2020.10.013. [Google Scholar] [CrossRef]

9. Bian H, Bai T, Salahuddin MA, Limam N, Daya AA, Boutaba R. Uncovering lateral movement using authentication logs. IEEE Trans Netw Serv Manag. 2021;18(1):1049–63. doi:10.1109/TNSM.2021.3054356. [Google Scholar] [CrossRef]

10. Liu Q, Stokes JW, Mead R, Burrell T, Hellen I, Lambert Jeditors, et al. Latte: large-scale lateral movement detection. In: MILCOM 2018 - 2018 IEEE Military Communications Conference (MILCOM); 2018 Oct 29–31. doi:10.1109/MILCOM.2018.8599748. [Google Scholar] [CrossRef]

11. King IJ, Huang HH. Euler: detecting network lateral movement via scalable temporal link prediction. ACM Trans Priv Secur. 2023;26(3):35. doi:10.1145/3588771. [Google Scholar] [CrossRef]

12. Zhou J, Yao J, Chen X, Yu S, Xuan Q, Yang X. Lateral movement detection via time-aware subgraph classification on authentication logs. arXiv:2411.10279. 2024. doi:10.48550/arxiv.2411.10279. [Google Scholar] [CrossRef]

13. Khoury JĐK, Zanddizari H, Parra GDLT, Najafirad P, Bou-Harb E, editors. Jbeil: temporal graph-based inductive learning to infer lateral movement in evolving enterprise networks. In: 2024 IEEE Symposium on Security and Privacy (SP); 2024 May 19–23. doi:10.1109/SP54263.2024.00009. [Google Scholar] [CrossRef]

14. Bhatkar S, Gosavi P, Shelke V, Kenny J editors. Link prediction using graphSAGE. In: 2023 International Conference on Advanced Computing Technologies and Applications (ICACTA); 2023 Oct 6–7. doi:10.1109/ICACTA58201.2023.10393573. [Google Scholar] [CrossRef]

15. Velikovi P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. Graph attention networks. arXiv.1710.10903. 2017. doi:10.48550/arXiv.1710.10903. [Google Scholar] [CrossRef]

16. Caville E, Lo WW, Layeghy S, Portmann M. Anomal-E: a self-supervised network intrusion detection system based on graph neural networks. Knowl Based Syst. 2022;258(1):110030. doi:10.1016/j.knosys.2022.110030. [Google Scholar] [CrossRef]

17. Tong Zhao YL, Neves L, Woodford O, Jiang M, Shah Neditor. Data augmentation for graph neural networks. In: Proc AAAI Conf Artif Intell. 2021;35(12):11015–23. doi:10.1609/aaai.v35i12.17315. [Google Scholar] [CrossRef]

18. Wang Y, Cai Y, Liang Y, Ding H, Wang C, Bhatia S, et al. Adaptive data augmentation on temporal graphs. In: Proceedings of the 35th International Conference on Neural Information Processing Systems. Curran Associates Inc.; 2021. 111 p. [Google Scholar]

19. Bai H, Hou M, Wu L, Yang Y, Zhang K, Hong R, et al. Unified representation learning for discrete attribute enhanced completely cold-start recommendation. IEEE Transact Big Data. 2025;11(3):1091–102. doi:10.1109/TBDATA.2024.3387276. [Google Scholar] [CrossRef]

20. Zhang H, Jiang X. ConUMIP: continuous-time dynamic graph learning via uncertainty masked mix-up on representation space. Knowl Based Syst. 2024;306(70):112748. doi:10.1016/j.knosys.2024.112748. [Google Scholar] [CrossRef]

21. Duan G, Lv H, Wang H, Feng G, Li X. Practical cyber attack detection with continuous temporal graph in dynamic network system. IEEE Trans Inf Foren Secur. 2024;19(1):4851–64. doi:10.1109/TIFS.2024.3385321. [Google Scholar] [CrossRef]

22. Zhou J, Hu C, Chi J, Wu J, Shen M, Xuan Q. Behavior-aware account de-anonymization on ethereum interaction graph. IEEE Trans Inf Forens Secur. 2022;17:3433–48. doi:10.1109/TIFS.2022.3208471. [Google Scholar] [CrossRef]

23. Bilot T, Madhoun NE, Agha KA, Zouaoui A. Graph neural networks for intrusion detection: a survey. IEEE Access. 2023;11:49114–39. doi:10.1109/ACCESS.2023.3275789. [Google Scholar] [CrossRef]

24. Min S, Gao Z, Peng J, Wang L, Qin K, Fang B. STGSN—A Spatial–Temporal Graph Neural Network framework for time-evolving social networks. Knowl Based Syst. 2021;214(13):106746. doi:10.1016/j.knosys.2021.106746. [Google Scholar] [CrossRef]

25. Guo Z, Wang H. A deep graph neural network-based mechanism for social recommendations. IEEE Trans Indust Inf. 2021;17(4):2776–83. doi:10.1109/TII.2020.2986316. [Google Scholar] [CrossRef]

26. Liengaard BD, Becker J-M, Bennedsen M, Heiler P, Taylor LN, Ringle CM. Dealing with regression models’ endogeneity by means of an adjusted estimator for the Gaussian copula approach. J Acad Market Sci. 2025;53(1):279–99. doi:10.1007/s11747-024-01055-4. [Google Scholar] [CrossRef]

27. Cheng K, Ye J, Lu X, Sun L, Du B. Temporal Graph Network for continuous-time dynamic event sequence. Knowl Based Syst. 2024;304(1):112452. doi:10.1016/j.knosys.2024.112452. [Google Scholar] [CrossRef]

28. Zeng Z, Wang T. Neural Copula: a unified framework for estimating generic high-dimensional Copula functions; 2022. [Google Scholar]

29. LANL dataset. [cited 2025 Sep 1]. Available from: https://csr.lanl.gov/data/cyber1/. [Google Scholar]

30. Lindauer B. Insider threat test dataset 2020. [cited 2025 Sep 1]. Available from: https://kilthub.cmu.edu/articles/dataset/Insider_Threat_Test_Dataset/12841247. [Google Scholar]

31. Yang L, Chatelain C, Adam S. Dynamic graph representation learning with neural networks: a survey. IEEE Access. 2024;12(70):43460–84. doi:10.1109/ACCESS.2024.3378111. [Google Scholar] [CrossRef]