An Improved Blockchain-Based Cloud Auditing Scheme Using Dynamic Aggregate Signatures

1  Introduction

Data containing extensive sensitive private information must maintain integrity during processing to enable secure big data analysis [1]. With the rapid advancement of cloud computing [2,3], the storage and management of massive data present unprecedented challenges. When users outsource sensitive data to untrusted Cloud Service Providers (CSPs), data integrity faces threats from malicious tampering or deletion [4]. Statistics from Ateniese et al. [5] indicate that over 60% of enterprises encounter data breach risks due to inadequate auditing mechanisms. Ensuring data integrity and reliability within CSPs’ insecure environments remains a critical unresolved challenge. Traditional Provable Data Possession (PDP) schemes rely on Third Party Auditors (TPAs) for verification, yet the centralized architecture of TPAs introduces single points of failure and computational bottlenecks [6]. For instance, while Wang et al.’s [7] MHT-based auditing scheme reduces verification complexity to logarithmic levels, it still necessitates TPA involvement and fails to prevent collusion attacks between CSPs and TPAs.

In recent years, blockchain technology has been introduced to cloud auditing due to its decentralized and tamper-proof properties. Wang et al. [8] proposed a blockchain-based public auditing method for log integrity, where a fixed third-party auditor verifies cloud log operations and returns results. However, this approach inherits security vulnerabilities from centralized auditors: high computational and communication overheads render it susceptible to exponential attacks [9] (exploiting repeated exponentiation to forge proofs). Zhou et al. [10] adopted chameleon hashing for dynamic data operations, but the nested MHT structure increased computational costs by approximately 40%, hindering scalability for large-scale cloud storage. Short signature-based schemes (e.g., ZSS signatures by Zhu et al. [11]) reduce communication overhead but exhibit vulnerabilities in bilinear pairing verification during challenge phases, enabling attackers to fabricate aggregated signatures and bypass audits.

Existing schemes exhibit three primary limitations: First, insufficient support for dynamic operations. Erway et al.’s [12] dynamic PDP scheme uses skip-list structures, requiring full certification path reconstruction for insertions/deletions and resulting in O(n) time complexity. Second, balancing privacy protection with audit efficiency remains challenging. Shen et al. [13] proposed a group signature-based privacy scheme, but group key management complexity grows linearly with user count. Third, blockchain-integrated schemes fail to optimize storage costs. Although Yang et al.’s [14] hybrid model combines BLS signatures with blockchain, it lacks fine-grained block-level auditing, causing low error localization efficiency and a 40% increase in audit delays—rendering it unsuitable for real-time auditing.

1.1 Related Work

Data integrity auditing [15,16] enables users to verify the integrity of remotely stored data without direct access to original datasets. The foundational cloud data integrity auditing models were introduced by Mishra et al. [4] (PDP using RSA signatures) and Jules et al. [17] (Proofs of Retrievability, POR). Reviews of cloud storage integrity verification [18,19] emphasize that while ensuring data integrity is paramount, each solution has inherent weaknesses. Blockchain technology offers an append-only distributed ledger system, enabling trustworthy, fair, and decentralized cloud storage. As a distributed database maintained via Distributed Ledger Technology (DLT) [20], blockchains resist forgery, tampering, and tracking—once data is recorded, it becomes immutable. This immutability enhances security and ease of implementation compared to other integrity verification technologies. However, blockchains’ inefficiency in storing large datasets prevents direct application in cloud auditing [21]. Typically, a Third Party Auditor (TPA) commissioned by the Data Owner (DO) performs verifications on behalf of data users, reducing computational, communication, and storage overheads [12]. Crucially, blockchain inherently decentralizes TPA functions. Li et al. [22] applied blockchain to data storage, while Du et al. [23] integrated distributed networks and consensus algorithms to create scalable, fault-tolerant architectures. For example, Yang et al. [14] relied on TPA-aggregated proofs, creating a single-point failure bottleneck. Wang et al. [24] used MHTs to control administrator privileges and enable dynamic data modifications. Guo et al. [25] employed chameleon hashing and nested MHTs for dynamic operations, but at significantly increased computational cost. Li et al. [26] stored homomorphic tags of encrypted file blocks on the blockchain for integrity verification via MHTs. While leveraging blockchain’s decentralization, this approach compromises data privacy by requiring CSPs to process plaintext blocks. Additionally, the absence of a formal data deletion protocol prevents verification of whether CSPs have completely erased sensitive data, introducing critical security gaps. Most existing solutions assume CSPs to be honest-but-curious (e.g., [14] Section IV-A), neglecting the risks of active attacks from malicious CSPs (such as forging proofs or concealing deletions). In Li et al.’s [26] scheme, CSPs could tamper with data blocks and still pass verification.

1.2 Main Motivations

Although blockchain technology provides new possibilities for building decentralized and trustworthy cloud auditing schemes—effectively addressing the single point of failure and trust issues in traditional third-party auditor (TPA)-dependent approaches—existing blockchain-based auditing schemes, particularly the foundational work by Li et al. [26], still suffer from critical flaws. These shortcomings constitute the core motivation for our research and underscore the urgency of resolving them to advance the field.

1) Fundamental Logical Contradictions and Privacy Leakage Risks:

The Li scheme requires cloud service providers (CSPs) to use plaintext data blocks during the parameter computation phase in the verification process. This exposes users’ sensitive plaintext data to substantial risks of leakage or misuse by CSPs, revealing an inherent logical contradiction that conflicts with the original design intent (e.g., ensuring data confidentiality while requiring plaintext access).

2) Severe Security Vulnerabilities and Audit Invalidation Threats:

In-depth analysis reveals multiple exploitable security flaws in the Li scheme that render audit results entirely invalid. For example: a) Exponential Attacks: Attackers can exploit a single successful audit response to forge subsequent proofs via exponentiation, bypassing verification effortlessly. This undermines the audit process’s ability to detect genuine data state changes, making audit results untrustworthy; b) Deletion Attacks: CSPs can selectively delete user data blocks or erase blocks while retaining their tags. Since the verification process does not enforce CSPs to use the currently stored encrypted blocks in proof generation (relying solely on tags) and lacks mechanisms to verify complete data storage, malicious CSPs can conceal deletion activities.

A critical gap persists in blockchain-based cloud auditing research: the urgent need for a solution that resolves logical contradictions and core security vulnerabilities in existing schemes—particularly the Li scheme. Such a solution must balance the following dimensions: strong correctness, high security, provable security, and computational efficiency. To bridge this research gap, we propose an improved blockchain-based cloud auditing scheme that offers robust guarantees for the integrity, authenticity, and privacy of cloud-stored data.

1.3 Contributions

Addressing the correctness and security issues identified in the scheme proposed by Li et al. [26], this paper introduces an improved blockchain-based cloud auditing solution that integrates multiple hash functions, multiple Computational Diffie-Hellman (CDH) problems, and dynamic aggregate signatures. The core contributions are summarized as follows:

1) By replacing plaintext-dependent verification parameters with encrypted metadata, the logical contradiction requiring CSPs to process plaintext data is resolved, mitigating the risk of sensitive information leakage.

2) Enhancement of Data Integrity with Multiple Hash Functions and BLS Short Signatures: Combining multiple hash functions with BLS short signatures and leveraging the hardness assumption of the CDH problem ensures the unforgeability of tags, thereby enhancing data integrity. Expanding exponentiation operations in the cryptographic protocol enhances encryption robustness. The method of binding signatures to content ensures data integrity.

3) Introduction of Random Numbers for Dynamic Adjustment of Verification Mechanisms: By introducing random numbers and potentially implementing dynamic adjustments through challenge frequency k and coordination factor w, the new scheme significantly enhances resistance against forgery attacks and distributed security protection capabilities while notably reducing computational cost.

Finally, the new scheme is analyzed from multiple dimensions including security and integrity. The results demonstrate that our Enhanced Security Scheme is effective and superior to the original one, achieving a high-efficiency balance between security and performance. Specific application environments are also proposed.

1.4 Paper Structure

This paper is structured into seven sections as illustrated in Fig. 1:

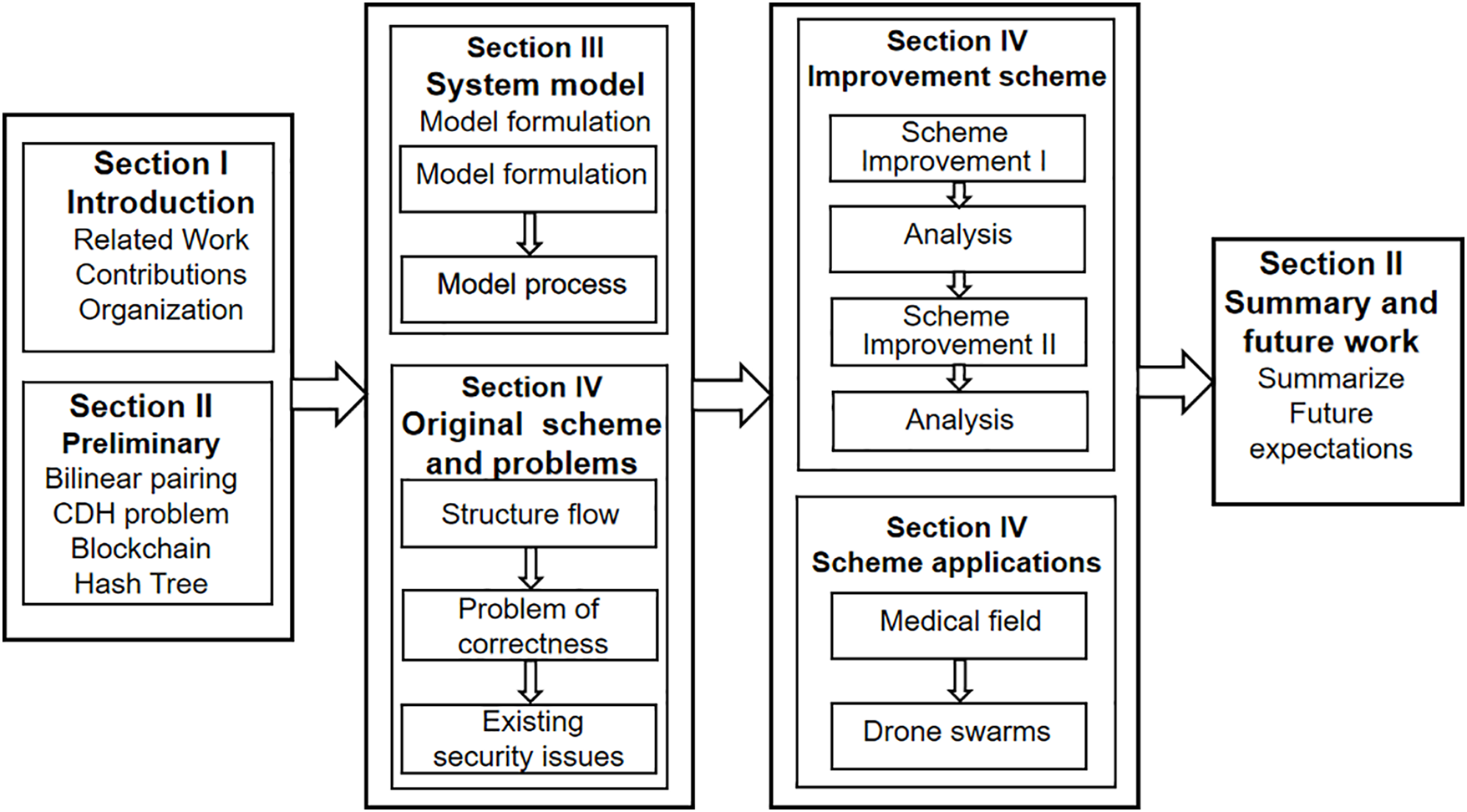
Figure 1: Organization of the paper

Section 2 explains the mathematical foundations and technical background required for the scheme, covering bilinear pairings, CDH problems, blockchain principles, and hash tree mechanisms. Section 3 describes the architecture of the blockchain-based cloud auditing scheme, encompassing data encryption, storage processes, and decentralized audit verification mechanisms. Section 4 reveals the deficiencies of the original scheme concerning logical contradictions, attack resistance, and support for dynamic data operations. Section 5 proposes two optimized schemes that address correctness and security issues through parameter substitution and dynamic aggregate signature methods. Section 6 evaluates the potential applications and practical value of the Enhanced Security Scheme in fields such as healthcare and drone fleets. Section 7 summarizes the advantages of the scheme and suggests optimization directions by integrating zero-knowledge proofs and real-world scenario validations.

2  Preliminary

2.1 Bilinear Pairing

Let G1 and G2 be two additive cyclic groups, GT be a multiplicative cyclic group, and all of prime order q. If there exists an efficiently computable bilinear map e:G1×G2→GT balancing the following dimensions:

(1) Bilinearity

For any P∈G1,Q∈G2 and a,b∈Zq∗, it holds that:

e(aP,bQ)=e(P,Q)ab(1)

This indicates that the pairing is linear in each input component.

(2) Non-degeneracy

There exist P∈G1,Q∈G2 such that e(P,Q)≠1GT, where 1GT denotes the identity element of GT.

(3) Computability

There exist polynomial time algorithms to efficiently compute the value of e(P,Q).

2.2 Computational the Diffie-Hellman (CDH) Problem

Let G be a multiplicative cyclic group of prime order q with generator g∈G. The CDH problem is defined as computing gab∈G given ga and gb (where a,b∈Zq∗ are unknown random numbers).

The hardness assumption of the CDH problem states that for any probabilistic polynomial time (PPT) algorithm, the probability of successfully solving the problem is negligible. This assumption forms the security foundation of classical public-key cryptographic schemes such as the Diffie-Hellman key exchange and ElGamal encryption. If the CDH problem is difficult in group G, then G is said to be a CDH secure group.

2.3 Blockchain Technology

Blockchain technology represents a decentralized, tamper-proof, and traceable distributed ledger system that ensures data security and integrity through cryptographic principles. It features several critical characteristics: decentralization, where data does not rely on a single central node but is maintained by multiple nodes; immutability, once data is recorded on the blockchain it cannot be altered; and traceability, every piece of data has a timestamp and the hash value of the previous block, allowing for tracing the origin and history of the data.

The application of blockchain technology in cloud auditing offers numerous benefits: enhancing data transparency and trustworthiness, increasing the security and trust in cloud services, reducing audit costs and improving efficiency, addressing challenges within audit work, improving the quality and authenticity of audit data, and enabling remote intelligent supervision.

3  System Model

Li et al. [26] proposed a blockchain-based public auditing scheme for cloud storage big data, introducing a fundamentally different approach compared to prior models. The core innovation lies in decentralized auditing, which eliminates the need for a Third Party Auditor (TPA) and significantly reduces computational and communication overhead. Crucially, this scheme effectively addresses critical vulnerabilities in existing solutions, including TPA untrustworthiness and collusion between the TPA and Cloud Service Provider (CSP) that could enable fraudulent activities.

Fig. 2 illustrates the system model of Li et al.’s [26] cloud auditing scheme, involving only two entities: the Data Owner (DO) and the CSP. Unlike conventional approaches, this model leverages mature and secure blockchain technology for distributed storage, employing cryptographic mechanisms proven in industry-standard implementations like Bitcoin. The established security of Bitcoin provides robust validation for applying blockchain to cloud auditing, enhancing both security and audit efficiency.

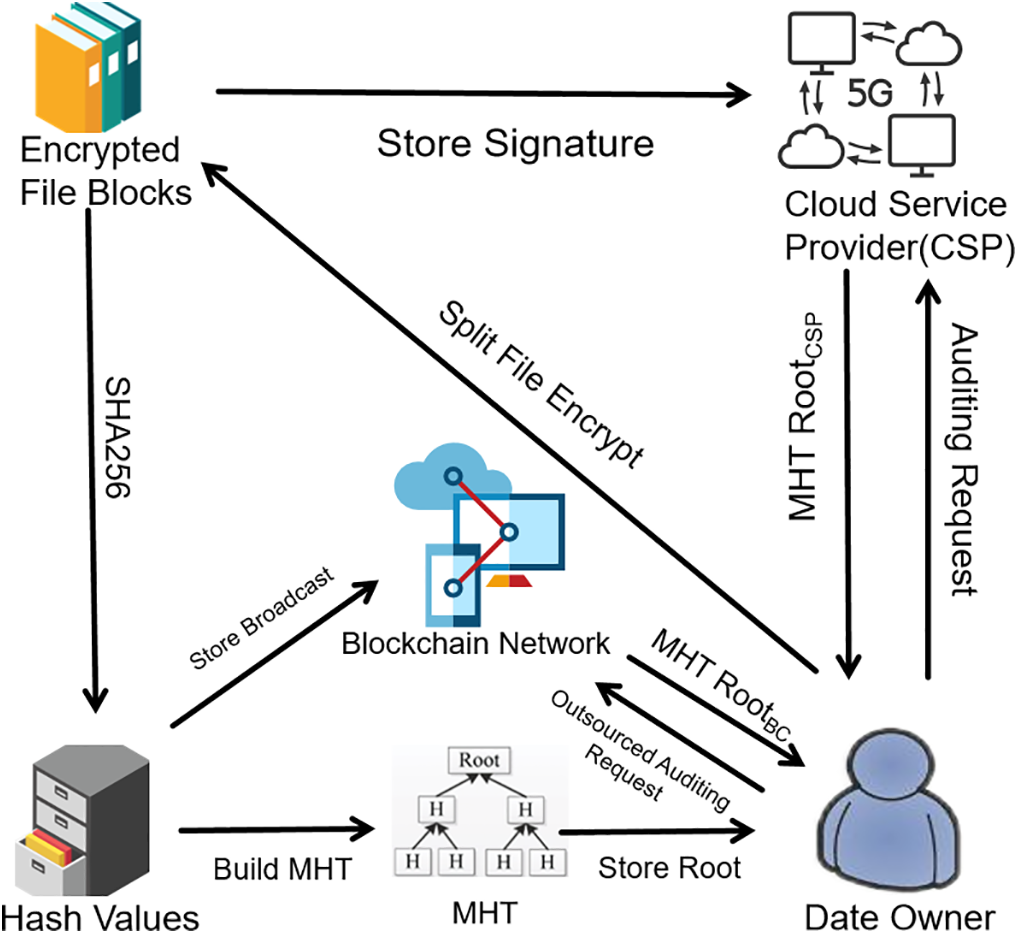
Figure 2: System model

As shown in Fig. 2, the DO first partitions the file into fixed-size blocks, encrypts each block using its private key (sk), and generates corresponding tags via a hash algorithm. The DO constructs a Merkle Hash Tree (MHT) root from these tags and retains it locally. The encrypted data blocks, tags, and public key are uploaded to the CSP, while all tags are stored on the blockchain. With the MHT root retained, the DO can independently verify data integrity at any time.

During auditing, the DO randomly selects a public auditor (another blockchain node with available resources) to conduct the audit. The auditor issues a challenge to the CSP, which responds by generating tags from the encrypted blocks and constructing an MHT root as evidence. The auditor then derives an MHT root using the tags stored on the blockchain. If the CSP’s MHT root matches the blockchain-derived root, the audit succeeds; otherwise, it fails, indicating potential malicious deletion or tampering by the CSP. The auditor subsequently reports the result to the DO. Table 1 showcases symbols of the system model.

DO: All users in the blockchain network responsible for generating key pairs (public and private keys), encrypting files, generating tags, and uploading all tags to the CSP and Blockchain Network.

CSP: Responsible for storing all ciphertexts and tags, and for securely transmitting data between itself and all users.

Blockchain Network: Stores all tags of the user data and provides the auditor with the DO’s tags for verification upon receiving a challenge (chal).

4  Original Scheme and Problems

4.1 Original Scheme Structure Flow

1. DO first performs an algorithm to generate a public-private key pair by entering a security parameter k and outputting the public-private key pair (pk,sk) for subsequent encryption and decryption of the file.

2. DO input a file F and split the file into blocks of the same size mi and fill the last block with zeros.

F={m1,m2,m3,⋯mi,⋯mn}(2)

3. The user encrypts the file block mi through the private key sk to get the encrypted block ei, which is i∈n.

F′={e1,e2,e3,⋯ei⋯en}(3)

4. The DO applies the SHA256 hash algorithm to each encrypted block ei to generate corresponding tags ρi.

ρi=H(ei)(4)

Υ=(ρ1,ρ2,ρ3,⋯ρi,⋯ρn)(5)

5. The DO then signs each encrypted block ϵi to obtain σi, and stores (F′,Y,Φ) on CSP, while storing (UID,BID,Y) on the blockchain. The DO maintains a local mapping between BID and σi, allowing the DO to identify all its own data blocks and reconstruct the file. When the DO updates encrypted data stored on the CSP, it also synchronizes the corresponding tags on the blockchain.

Φ=(σ1,σ2,σ3,⋯σi,⋯σn)(6)

6. Challenge Generation

Since no TPA is involved, any DO possessing auditing capabilities can issue a challenge to the system. A DO with sufficient computational resources sends (pk,UID) to the CSP to initiate the challenge-response process. Given that different DOs have varying levels of computational, processing, and storage capabilities, the system randomly selects an appropriate DO based on the required computational match for each audit task.

7. Verification

Upon receiving the challenge, the CSP performs identity authentication based on (pk,UID), retrieves the corresponding encrypted data and tags, and reconstructs a MHT to generate the root RCSP, which is returned to the public auditor (another DO in the blockchain network) as proof of chal. The public auditor retrieves the tags of the encrypted data blocks from the blockchain using the user’s pk and BID, and reconstructs another MHT root RBN. The auditor then returns RBN to the DO. The DO verifies whether RCSP=RBN. If the equality holds, the verification is successful, indicating that the data remains intact and has not been maliciously deleted or tampered with. Otherwise, the verification fails, indicating data inconsistency or potential malicious behavior.

8. Computation process

1) Generate a public-private key pair using a key generator: let g be a G-generating element, and DO randomly generate a public-private key pair (sk,pk)=(α,gα):

y=gα(7)

2) Pick a random element u in G and compute the label σi for each encrypted file block:

hi=H(ei)(8)

σi=(H(ei)umi)α(9)

Φ is a set consisting of σi (i∈n), the same as the CSP generates its own public-private key pair (spk′,ssk′) and the other DOs generate their own public-private key pairs (pk′,sk′) during the data communication transmission process;

3) The public auditor calculates the proof from the tags returned by the blockchain:

PBN={RBN,sigsk′H(RBN)}(10)

σ′=∏i=1nH(ei)vi⋅uμ(11)

4) After the CSP receives the challenge, the CSP calculates and returns the proof: PCSP=μ,σ,RCSP,(sigssk′H(RCSP)), which is chal={(i,vi)}0≤i≤n;

μ=∑i=1nvimi(12)

σ=∏i=1nσivi(13)

5) Verify PCSP=RBN, check whether e(σ,g) and e(σ′,y) are equal:

σ=∏i=1nσivi=∏i=1n[(H(ei)umi)α]vi(14)

=∏i=1n[(H(ei)umi)vi]α=∏i=1n(H(ei)vi)α⋅(u∑i=1nvimi)α=∏i=1n(H(ei)vi)α⋅(uμ)α(15)

e^(σ,g)=e^(∏i=1n(H(ei)vi)α⋅(uμ)α,g)(16)

=e^(∏i=1nH(ei)vi⋅uμ,g)(17)

e^(σ′,y)=e^(∏i=1nH(ei)vi⋅uμ,y)(18)

=e^(∏i=1nH(ei)vi⋅uμ,gα)=e^(∏i=1nH(ei)vi⋅uμ,g)α(19)

e^(σ,g)=e^(σ′,y)(20)

4.2 Existence of Correctness Issues

1. According to the design proposed by Li et al., only the Data Owner (DO) possesses the data blocks mi. However, during the calculation of μ, by the CSP, where μ=∑i=1nvimi, it involves using the data blocks mi. The CSP does not store mi, leading to a logical contradiction. If the CSP were to store mi along with ei, there would be risks of private key leakage and exposure of plaintext data blocks in case of a malicious CSP, thereby undermining the purpose and integrity of the auditing scheme.

2. The system employs a Merkle Hash Tree (Hash Tree) for constructing the root directory as part of the verification process. However, when selecting the number of verification tags vi where 1≤i≤n, it uses all tags for verification to construct the root directory. This approach lacks randomness in challenge-response process, making the CSP’s computation of aggregated proofs computationally intensive. Moreover, after storing the complete data, a malicious CSP could easily fabricate μ.

4.3 Security Vulnerabilities

1. Lack of Cryptographic Block Involvement in Proof Generation: When the CSP receives a challenge, during the computation of the tag σ, it can directly use existing tags σi for aggregation and return the proof for verification, without involving the encrypted blocks ei stored in the CSP. This omission creates a critical gap in the verification process.

σi=(H(ei)umi)α(21)

σ=∏i=1nσivi(22)

=∏i=1n[(H(ei)umi)α]vi=∏i=1n[H(ei)umivi]α=∏i=1n[H(ei)uμ]α(23)

2. Data Integrity Compromise via Selective Deletion: If users fail to modify or alter the encrypted file blocks prior to receiving a challenge, the verification process does not utilize the ciphertext blocks stored in the CSP. A malicious CSP could exploit this by deleting the DO’s encrypted data blocks while retaining their corresponding tags. Upon receiving a challenge, the CSP could still pass verification by relying solely on the preserved tags, leading to undetected data deletion.

3. Vulnerability to Exponential Attacks: Assume the first audit challenge is chal1, and the second audit challenge is chal2. The CSP generates two proofs: PCSP1={μ1,σI,RCSP1,sigssk′(H(RCSP1))} and PCSP2={μ2,σΠ,RCSP2,sigssk′(H(RCSP2))}. After the first verification, since the tags σi remain unchanged, an attacker can fabricate the second proof using parameters from the first challenge. By defining viΠ=xvi and σΠ=(σI)x, the attacker derives μ2=xμ1, resulting in a fabricated proof: PCSP2={xμ1,(σI)x,RCSP2,sigssk′(H(RCSP2))}. This fabricated proof passes verification (Fig. 3).

e^(σI,g)=(σ′,y)=e^(∏i=1nH(ei)vi⋅uμ1,g)α(24)

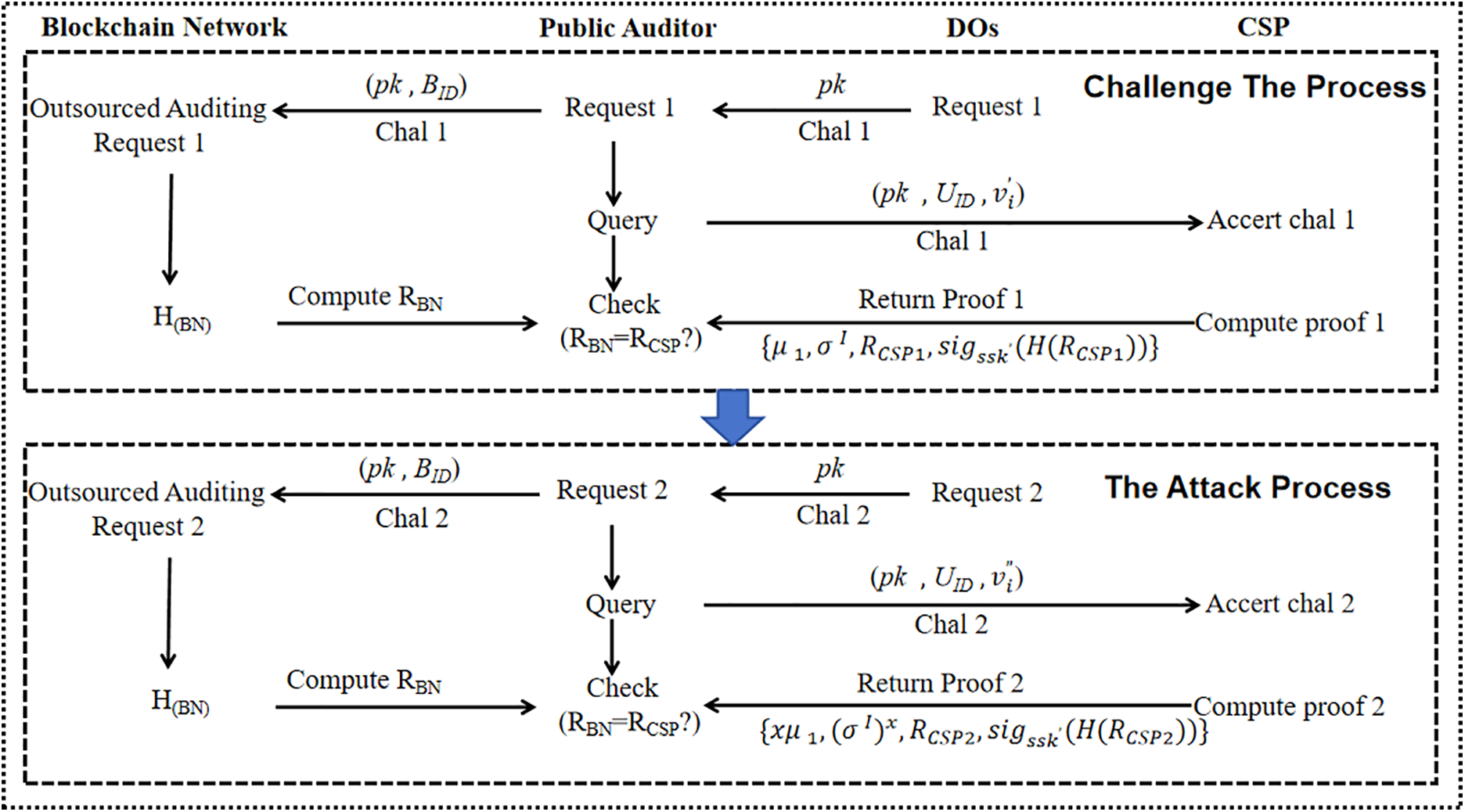
Figure 3: Challenge attack process

Second validation results:

e^(σΠ,g)=e^(∏i=1nH(ei)xvi⋅uμ2,g)α=e^(∏i=1nH(ei)vi⋅uμ1,g)xα(25)

e^(σ′,y)=e^(∏i=1nH(ei)xvi⋅uxμ1,gα)=e^(∏i=1nH(ei)vi⋅uμ1,g)xα(26)

e^(σΠ,g)=e(σ′,y)(27)

This demonstrates a fundamental insecurity in the scheme’s design, as attackers can simulate valid proofs without accessing the original data. The lack of collision resistance in the proof structure enables repeated exponential attacks.

4. Data Loss and Leakage Risks during Deletion/Update: When a DO requests deletion of an encrypted block t (1≤t≤n), a malicious CSP may retain the encrypted block while deleting its corresponding tag. Similarly, during an update of block et, the CSP might update the new block and tag but retain the old encrypted block. These attacks evade detection in the current challenge-response mechanism, enabling data leakage, resale, or even reconstruction of original files via advanced machine learning techniques.

5. Data Tampering Vulnerability: The CSP can alter encrypted blocks without detection, as the proof generation relies solely on the tags σi of the DO’s uploaded encrypted blocks ei. This lack of cryptographic binding between the data blocks and their tags renders the original scheme unable to detect tampering.

6. High Risk of Collusion Attacks: In practical deployments, malicious DOs may collude with fixed auditing nodes to bypass detection. For instance, colluding DOs could issue challenges targeting only intact data blocks, avoiding queries to modified blocks. This collusion between malicious CSPs and compromised DOs significantly increases the likelihood of undetected data manipulation.

5  Improved Scheme

To address the correctness issues and security vulnerabilities identified in Section 4, along with their derived security risks, this section introduces a progressive improvement approach (see Fig. 4). The correctness enhancement focuses on resolving logical flaws, while the security improvement builds upon the corrected framework by incorporating a randomized challenge-response mechanism and dynamic aggregation signature verification to comprehensively eliminate security threats and enhance system robustness.

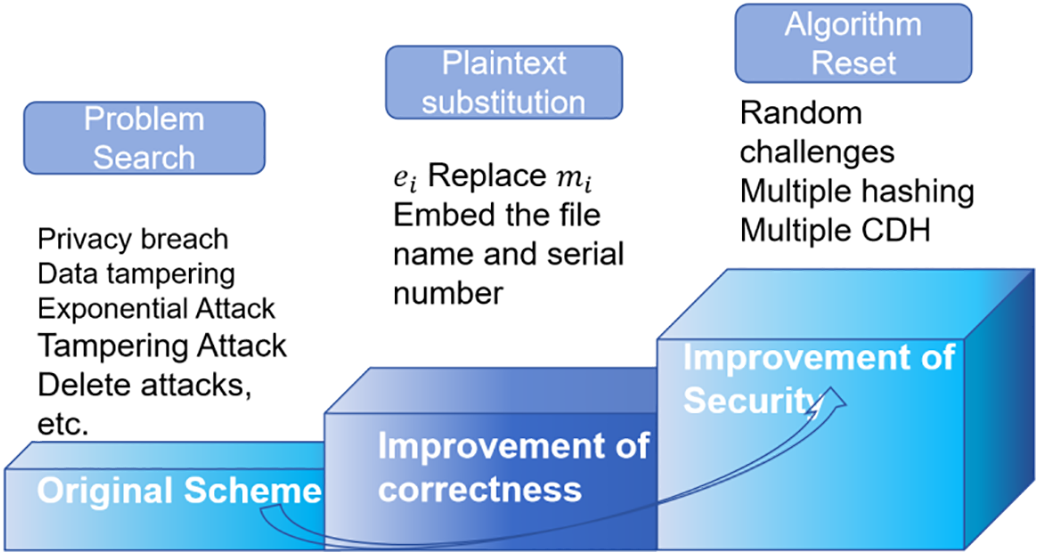
Figure 4: Flight parameter data storage verification model

5.1 Rectification of Correctness Flaw

The original scheme contains a fundamental correctness flaw: the CSP does not store mi, yet the verification process requires the CSP to use plaintext data blocks mi. This not only poses a risk of data leakage but also creates a logical contradiction. To resolve this, the Enhanced Security Scheme replaces mi with ei in the verification computation:

μ=∑i=1nνiei(28)

To prevent cross-message attacks and replay attacks, the file name Fname and the block sequence number i are embedded into the tag generation process as follows:

σi=(H(ei∥Fname∥i)uei)α(29)

Ei=ei∥Fname∥i(30)

σi=(H(Ei)uei)α(31)

5.1.1 Correctness Analysis

Since the scheme only undergoes minor modifications from the original design—replacing the parameter mi without affecting the verification computation process—the correctness of the validation remains intact. This demonstrates that our proposed scheme resolves the correctness issues present in the original scheme. Furthermore, by embedding the filename and message block sequence number into the new tags, the scheme effectively prevents Cross-Message Attacks and Replay Attacks, significantly enhancing security. The detailed process is as follows:

1) Initialization (KeyGen):

The DO generates a public-private key pair: (sk,pk)←KeyGen(1), where sk is the private signing key and pk is the corresponding public verification key. Select collision-resistant hash function H: {0,1}∗→G, and map to elliptic curve group G.

2) File preprocessing (TagGen):

The DO divides the file F into blocks of fixed size, for simplicity, here F is divided into n blocks, where i∈n.

F={m1,m2,m3,⋯mi,⋯mn}

Each block mi is encrypted with the private key to generate the encrypted block ei, which is stored on the CSP. Let F′ denote the file stored in the cloud:

F′={e1,e2,e3,⋯ei⋯en}

3) Tag Generation:

Ei=ei∥Fname∥i(32)

ρi=H(Ei)(33)

Y=(ρ1,ρ2,ρ3,⋯ρi,⋯ρn)

σi=sigsk(ei)=(H(Ei)uei)α(34)

4) Data Storage (Store):

The tuple (UID,BID,σi) is broadcast as a transaction to the CSP. The CSP stores the encrypted blocks {ei} and their corresponding signatures {σi}.

5) Challenge Phase:

The verifiers (other DOs in the blockchain with auditing capabilities) challenge the CSP by generating a challenge, chal={(i,vi)}, where (1≤i≤n), and sends the chal to the CSP.

6) Proof Generation (ProofGen):

The CSP computes the corresponding encrypted file blocks μ and σ based on the randomly selected vi provided by the public auditor:

σ=∏i=1nσivi(35)

μ=∑i=1kviei(36)

7) Verify:

Check whether the bilinear pairing equation holds: e^(σ,g)=e^(σ′,y).

The pseudocode generated by the tag is shown in Algorithm 1:

The verified pseudocode is shown in Algorithm 2:

5.1.2 Security Analysis

The proposed scheme modifies only the verification parameters without altering the verification computation methodology. Although it resolves the correctness issues of the original scheme, it does not substantively change the system verification mechanism, leaving critical security vulnerabilities such as Tampering Attacks, Deletion Attacks, and Exponential Attacks unaddressed. For instance, consider a malicious CSP. Suppose the DO generates a challenge chal1 during the first audit and chal2 during the second audit. The CSP generates two sets of proofs: PCSP1={μ1,σI,RCSP1,sigssk′(H(RCSP1))} and PCSP2={μ2,σΠ,RCSP2,sigssk′(H(RCSP2))}. If the time interval between the two audits is short and no user updates, deletions, or modifications occur during this period, the CSP can exploit the static nature of σi. Specifically: viΠ=xvi, μ2=xμ1, σΠ=(σI)x. This attack methodology, previously validated in security literature, demonstrates that the scheme remains vulnerable to Exponential Attacks due to predictable parameter relationships.

5.2 Enhanced Security Scheme

Based on the Correctness Enhancement, we added a random challenge-response mechanism and enabled encrypted blocks stored in the CSP to participate in the new aggregated tag verification computation. Additionally, during the proof generation process, the CSP introduces its own random number β and a publicly disclosed transaction parameter Y. The random number β can be generated using a public-private key generator, and the transaction parameter Y (linked to the user’s file identifier) derived from β is disclosed during the proof exchange. To protect data integrity, a Computational Diffie-Hellman (CDH) hardness assumption-based computation is incorporated into the new tag calculation. The security enhancement retains the original algorithm design steps 1–2 without significant changes. The encrypted blocks stored in the CSP actively participate in the tag proof computation after receiving a challenge proof from the public auditor. The enhanced proof generation process proceeds as follows:

1) Initialization (KeyGen):

The DO generates a public-private key pair: (sk,pk)←KeyGen(1), where sk serves as the signing private key and pk as the verification public key. Select collision-resistant hash function H: {0,1}∗→G, and map to elliptic curve group G.

2) File preprocessing (TagGen):

The DO divides the file F into blocks of fixed size. For simplicity, F is divided into n blocks, where i∈n.

F={m1,m2,m3,⋯mi,⋯mn}

Each block mi is encrypted using the private key to generate the encrypted block ei. The encrypted blocks {ei} are stored at the CSP, and the file stored in the cloud is denoted as F′:

F′={e1,e2,e3,⋯ei⋯en}

3) Tag Generation:

Ei=ei∥Fname∥i(37)

ρi=H(Ei)(38)

Y=(ρ1,ρ2,ρ3,⋯ρi,⋯ρn)

σi=sigsk(ei)=(H(Ei)uei)α(39)

4) Data Storage (Store):

The tuple (UID,BID,σi) is broadcast as a transaction to the CSP. The CSP stores the encrypted blocks {ei} and their corresponding signatures {σi}.

5) Challenge Phase (Challenge):

A verifier (i.e., a public auditor selected from DOs with auditing capabilities) randomly selects k indexed blocks and generates a challenge chal={(i,vi)}, where (1≤i≤k). The challenge is sent to the CSP.

6) Proof Generation (ProofGen):

Upon receiving the challenge, the CSP generates {β,Y} using its key pair generator. Based on the k randomly selected block indices, the CSP identifies the corresponding encrypted blocks {eij} and signatures {σij}. It then computes new verification tags σDi for the encrypted blocks and aggregates the verification signature σ and μ:

Y=gβ(40)

σDi=σivi(yaβ)H(ei)(41)

σ=∏i=1kσDi(42)

μ=∑i=1kviei(43)

7) Verification (Verify):

Check whether the bilinear pairing equation holds: e^(σ,g)=e^(σ′,y)

The pseudocode generated by the tag is shown in Algorithm 3:

The verified pseudocode is shown in Algorithm 4:

5.2.1 Correctness Analysis

The public auditor signs the proof {μ,σ,RCSP,sigssk′(H(RCSP))} using its private key and returns the proof μ, σ to the DO. Upon receiving the proof from the public auditor back to the CSP and the proof from the blockchain, the DO verifies whether e^(σ,g) and e^(σ′,y) are equal or not. If they are equal then the data is intact and unaltered by any attack. Otherwise, it indicates that the data stored in the CSP has been subjected to a malicious attack, tampering, or deletion, etc. Where the public auditor after receiving the tag present on the blockchain aggregates the proofs as σ′:

σ′=∏i=1k[H(Ei)νi⋅YH(ei)]⋅uμ(44)

Proof: According to the Enhanced Security Scheme, during the verification phase, if the CSP behaves honestly (e.g., without tampering with user data or randomly deleting user data blocks), the evidence provided by the CSP to the public auditor—the randomly selected encrypted blocks {eij} and their corresponding signatures {σij} will be valid. If the data stored in the CSP remains intact, the auditor can validate the correctness through the following equality:

e^(σ,g)=e(∏i=1kσDi,g)(45)

=e^(∏i=1kσivi(yaβ)H(ei),g)=e^(∏i=1k[((H(Ei)uei)α)vi⋅y(aβ)H(ei)],g)=e^(∏i=1k[((H(Ei)uei)vi)α⋅g(aβ)H(ei)],g)=e^(∏i=1k[(H(Ei)viueivi)⋅gβH(ei)]α,g)=e^(∏i=1k[H(Ei)vi⋅YH(ei)⋅ueivi]α,g)=e^(∏i=1k[H(Ei)vi⋅YH(ei)]α⋅(uμ)α,g)=e^(∏i=1k[H(Ei)vi⋅YH(ei)]⋅uμ,g)α(46)

e^(σ′,y)=e^(∏i=1k[H(Ei)vi⋅YH(ei)]⋅uμ,gα)(47)

=e^(∏i=1k[H(Ei)vi⋅YH(ei)]⋅uμ,g)α(48)

If this equality fails, it implies the presence of malicious attacks, thereby confirming the correctness of our Enhanced Security Scheme.

Conclusion: The proposed scheme ensures audit feasibility while addressing security vulnerabilities. When the equality e^(σ,g)=e^(σ′,y) holds, the data integrity is preserved; otherwise, the data stored in the CSP is compromised, indicating malicious behavior.

5.2.2 Security Analysis

Theorem 1: Sample-Based Detection of CSP Tampering.

By leveraging the sampling principle and enhanced BLS signatures, the probability of verification failure significantly increases if the CSP deletes or tampers with data.

Security Model Definition:

System Participants:

•   Data Owner (DO)

•   Cloud Service Provider (CSP)

•   Auditor

•   Blockchain Network (BN)

Adversarial Capabilities:

We consider a powerful probabilistic polynomial-time (PPT) adversary A that can:

•   Control a malicious CSP.

•   Eavesdrop on all communications over public channels.

•   Launch polynomially many adaptive queries (Adaptive Queries) against honest participants (e.g., DO, honest auditors), including: tag generation queries, storage queries, audit queries, dynamic operation queries.

Security Goals: The scheme aims to balance the following security dimensions:

•   Data Integrity

•   Proof Non-Forgibility

•   Storage Integrity

Procedures:

1) The challenger stores the complete file F′={e1,e2,e3,⋯ei⋯en} and the adversary A deletes some of the file blocks, resulting in the complete file F′′={e1′,e2′,e3′,⋯ei′⋯en−t′};

2) Challenge Phase: The public auditor issues a random challenge chal={i1,i2,i3,⋯ik};

3) Adversary Response: A returns the proof {σij} and its random counterpart {eij′};

4) Adversary Success Condition: The validation passes and at least eij′≠eij exists.

Proof: Assume the adversary deletes or tampers with t file blocks, leaving n−t valid blocks. The verifier detects data anomalies through single or multiple random sampling challenges. The probability of detecting anomalies in a single challenge is:

p=1−(n−tt)(nt)=1−(n−tk)k≥1−(1−tn)k(49)

After w independent challenges, the failure probability becomes:

pfail≤(1−tn)kw(50)

As shown, pfail decreases exponentially with increasing k (sample size) and w (challenge repetitions). Threshold settings can be adjusted dynamically based on security requirements.

Let:

1) Group G: A 256-bit elliptic curve with |G|≈2256;

2) Challenge size k;

3) Assumption: t=0.1n (10% deleted/tampered by the CSP);

4) Threshold: Set p=99% detection probability.

Parameters then are set for calculations as follows:

p=1−(0.9)k≈1−e0.1kp=99%=1−e0.1kk≈460

Through the above parameter settings, when multiple challenges are performed (i.e., k×w=460), it can be analyzed that regardless of the number of data blocks deleted or tampered with by the CSP, as long as there is a threat to user data integrity, the ratio tn will always be less than 1. Moreover, the detection probability p increases exponentially with the growth of k.

Dynamic Parameter Adjustment Strategy: As illustrated in Fig. 5, the threshold values can be dynamically configured based on the file’s security classification, importance level, security requirements, and cost constraints. Additionally, the challenge frequency w can be adjusted according to varying bandwidth conditions to meet the verification requirements for data integrity in cloud auditing. □

Figure 5: Improvement of communication overhead

Theorem 2: Against Malicious CSP, the Enhanced Security Scheme satisfies Proof unforgeability under the CDH Hardness Assumption in the Random Oracle Model.

Proof: The Computational Diffie-Hellman (CDH) hardness assumption has been rigorously proven in Wang et al. [27]. Here, we analyze the probability of a malicious CSP forging a valid proof. Let:

1) Simulator S simulates the environment correctly;

2) Adversary A acts as a Malicious CSP, outputting a fabricated proof PCSP with advantage ε;

3) Target block selection probability of Simulator S: 1n, where n is the total number of file blocks;

4) ε: Probability that Simulator S correctly identifies the block where Adversary A cheats during proof forgery. In the worst case, δ≥1n;

5) QH: Total number of queries Adversary A makes to the random oracle H;

6) A negligible function in the security parameter λ.

Probability Analysis: The advantage AS{CDH}(λ) of Simulator S in solving the CDH problem satisfies:

AS{CDH}(λ)≥(ε⋅δ)/QH−negl(λ).◻

Conclusion: Since the CDH problem is assumed hard in group G, AS{CDH}(λ) must be negligible. Therefore, via inequalities above, Adversary A’s advantage ε is also negligible. This proves that the Enhanced Security Scheme achieves proof unforgeability under the CDH hardness assumption in the random oracle model, even when the Malicious CSP acts as the adversary.

Theorem 3: Storage Integrity.

A malicious CSP cannot permanently delete user data blocks without detection.

Proof 1: Storage integrity, a sub-attribute of data integrity, requires the CSP to store all user-uploaded data blocks. If a malicious CSP deletes t blocks, the dataset becomes incomplete. As proven in Theorem 2, a malicious CSP cannot generate a valid proof PCSP for an incomplete dataset (missing t blocks) that passes verification. If the CSP deletes data, it faces two choices:

1) Attempt to fabricate a proof;

2) Refuse to respond or return an invalid proof.

Thus, if the auditor issues a valid challenge (k≥1) and the malicious CSP has indeed deleted data (t≥1), the audit failure probability (detection probability) is at least (1−negl(λ)), i.e., overwhelming. This strong detectability is guaranteed by the unforgeability of proofs. As proven in Theorem 1, the undetected probability decreases exponentially with the audit parameter w. □

Proof 2: Random challenges force CSP to store full data: The CSP cannot predict the block indices for each challenge and must store all blocks to pass random audits. If partial blocks are deleted, the verification failure probability becomes (1−tn)k. The scheme’s randomness ensures minimal overlap in audit samples. By introducing CSP’s random number β, the security of transmitted proofs is enhanced, and additional parameters {β,Y} are introduced. This adds a layer of CDH hardness, exponentially increasing the difficulty of proof forgery. The data structure’s collision resistance further prevents imitation.

Each audit randomly selects t blocks from n total blocks. The combination probability is Q=(nt)=n!t!(n−t)!. The total possibilities for two audits are (nt)×(nt)=((nt))2, and the probability of identical samples in two audits is P⟨n,t⟩=(nt)((nt))2=1(nt). When 1≤t≤n2, this probability decreases inversely with n and t. Larger n or t reduces overlap probability, effectively preventing data mimicry in verification responses.

Conclusion: Theorem 2 provides strong detection guarantees for data loss (including malicious deletion). Additionally, the random sampling challenge mechanism detects partial deletions (t<n) with high probability (k,w). Malicious CSPs cannot permanently delete user data blocks without detection. □

Theorem 4: If an efficient algorithm exists to break the verification mechanism of the improved Enhanced Security Scheme, it could resolve the CDH problem, contradicting the CDH assumption. Thus, Enhanced Security Scheme’s security relies on the hardness of the CDH problem.

Proof: Reduction to CDH hardness: If an adversary can fabricate a valid aggregated signature σ, a CDH solution can be constructed via the following steps:

1) Challenge Input: Given gα (public key y) and random gα, gb;

2) Attack Construction: Assume the adversary generates a fabricated σ satisfying e^(σ,g)=e^(σ′,y), then σ must satisfy:

σ=∏i=1k[(H(Ei)νi⋅YH(ei))]α⋅(uμ)α(51)

3) Private Key Extraction: Bypassing α’s secrecy to generate σDi=[(H(Ei)νi⋅YH(ei))]α⋅(uμ)α is equivalent to solving the CDH problem (computing gαx from gα and random input). □

Theorem 5: Signature σDi depends on the CSP’s stored tag σi, the hash of encrypted block ei, and CSP’s random number β. If the CSP tampers ei to ei′, ρi≠H(ei′), causing signature verification failure.

Proof:

e^(σ,g)=e(∏i=1kσDi,g)=e^(∏i=1k[H(Ei)νi⋅YH(ei′)]⋅uμ,gα)(52)

e^(σ′,y)=e^(∏i=1k[H(Ei)νi⋅YH(ei)]⋅uμ,gα)(53)

e^(σ,g)≠e^(σ′,y)◻(54)

Theorem 6: User data stored in the cloud is immutable by CSP.

Proof: Blockchain’s consensus mechanism, distributed storage, and decentralized architecture prevent CSP from modifying or deleting data. Historical signatures stored on the blockchain cannot be fabricated by CSP, and new tags cannot be generated without the DO. Only DO can modify both blockchain and CSP data. Any inconsistency in ei between CSP and blockchain leads to e^(σ,g)≠e^(σ′,y), resulting in verification failure. □

5.2.3 Attack Resistance Analysis

1. Resistance Analysis

The security enhancement introduces random challenge parameters νi and dynamic aggregated tags σDi, binding each verification signature to challenge parameters ei. An attacker cannot build up a new σΠ=(σI)x from known μ1 and σ1 as this requires the following dimensions: μ2=xμ1 and σΠ=∏i=1nσDix. The randomness of νi and variability of σi across audits ensure μ and σ are unique and unrelated. Additionally, the CSP’s random number β and public key Y are embedded in the enhancement. While Y is disclosed on the blockchain, β remains secret, proving the scheme’s resistance to exponential attacks.

If an attacker succeeds, it is equivalent to solving two independent CDH problems within a single computation: Computing gανi from gα and gνi; Computing gαβ from gα and gβ.

2. Tampering/Deletion Attack

Any tampering or deletion of encrypted block ei alters H(ei), invalidating the signature σi. An attacker must fabricate a valid σi′, but without the private key or β, this requires breaking the CDH problem.

3. Collusion Attack

The blockchain smart contract randomly selects auditors, preventing corrupt DOs from predicting auditor identities or coordinating collusion. Challenge parameters νi and CSP’s {β,Y} are generated from timestamp-based randomness, making β unpredictable to attackers. Corrupt DOs cannot precompute valid signature components for the CSP. Uniqueness of each challenge prevents proof reuse, rendering collusion attacks ineffective in the enhanced scheme.

Conclusion: New verification tags require both the original CSP-stored tags and collision-resistant hash values of ei, all dependent on private keys. Attackers cannot fabricate σDi by bypassing bilinear pairing properties. The variability of νi, uniqueness of data blocks, and CSP’s random β in tag generation increase prediction and replay attack difficulty. The scheme employs multi-layered safeguards, including nested hashing and dual CDH hardness, ensuring that any malicious CSP attempting to fabricate μ or σ will fail verification. Thus, the scheme is secure and feasible.

5.2.4 Performance Analysis

1. Comparison of computational cost between the new and original schemes

To better compare performance differences between the two schemes, we first analyze the computational cost of DO, CSPPoof, and DOVerifyProof in both schemes, then quantify the changes. Computational symbol definitions are shown in Table 2.

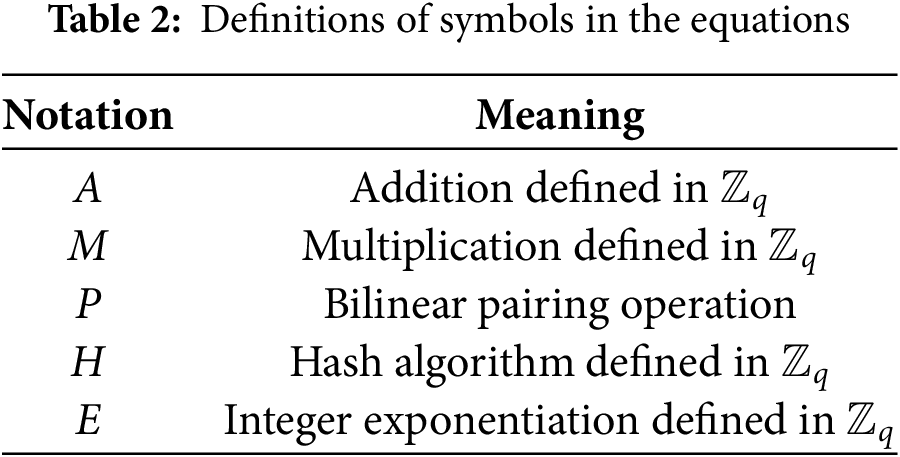
Table 3 details the computational cost of DO, CSP, and DOS (the public auditor) at each stage. Since the scheme employs sampling detection, k≪n. Consequently, the computational cost of the new scheme is overall controlled and reduced compared to the original; DO’s overhead remains unchanged.

CSPPoof’s multiplication operations increase marginally by kH, but other operations show significant reductions: (3k−2n)M+(k−n)A+(2k−n+1)E+kH (reduction terms correlated with k). DOVerifyProof’s additional overhead decreases linearly as (2k−n)(H+E+M), with no high-order complexity introduced. Although the scheme does not achieve exponential reductions in computational cost, the cost savings are substantial, particularly for CSPPoof and DOVerifyProof.

2. Comparison of Security Performance with Existing Schemes

To intuitively highlight the advantages of the improved scheme over the original scheme in [26] and three representative cloud auditing schemes (SWPor [28], CHPor [29], DPAS [13]), a comparative analysis is conducted from the following dimensions in Table 4.

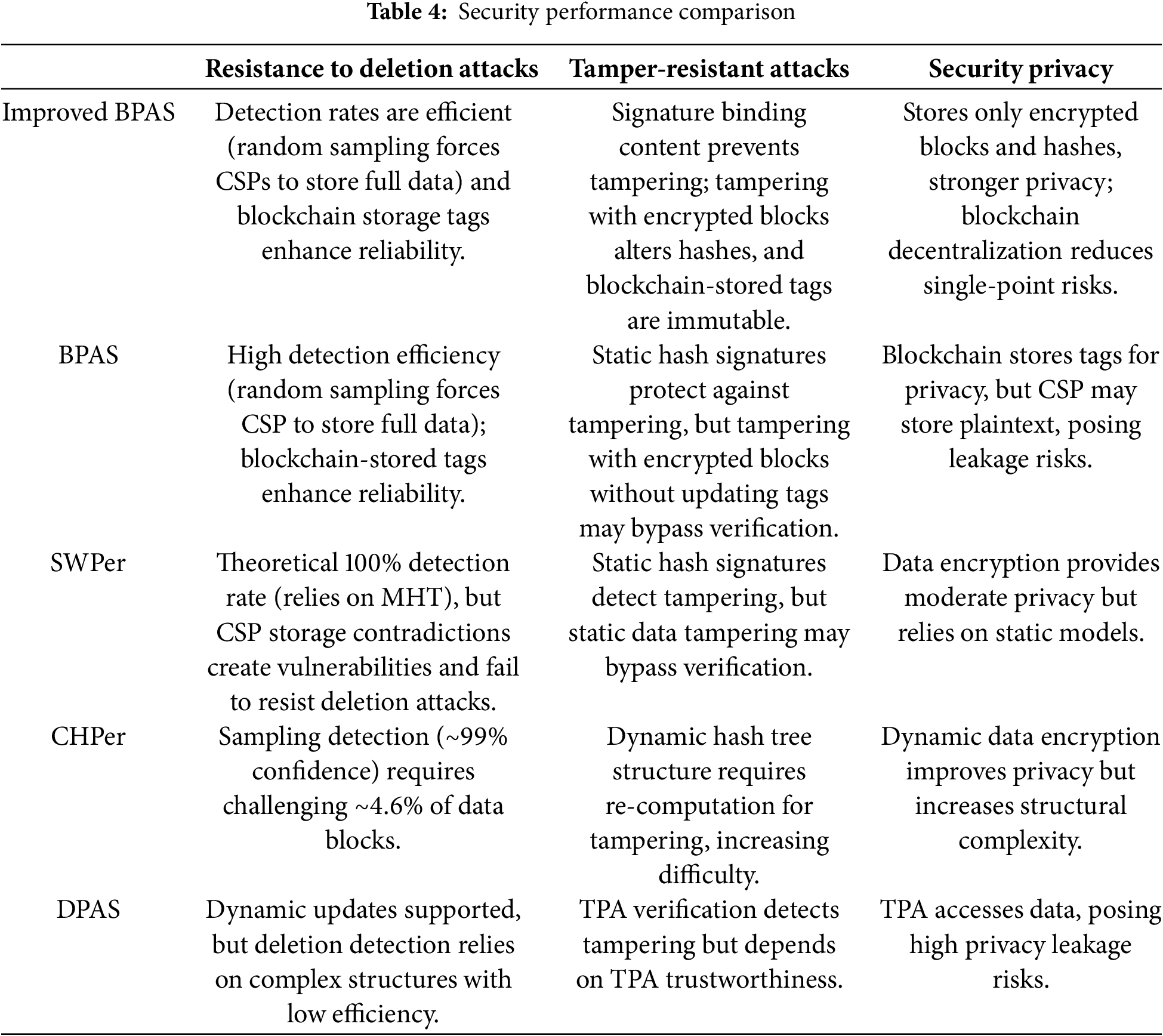
Key Advantages of the Improved Scheme: 1) Deletion Resistance: Combines random sampling (forcing CSP to store full data) and blockchain-stored tags, achieving high detection rates and reliability. Overcomes the scheme in [26]’s theoretical 100% detection rate but practical vulnerabilities, and outperforms traditional schemes relying on sampling confidence (SWPor), complex structures (CHPor), or centralized detection (DPAS). 2) Tampering Resistance: Signature binding and blockchain immutability eliminate [26]’s risk of tampering encrypted blocks without updating tags. Superior to schemes relying on static hashes (SWPor) or TPA trust (DPAS). 3) Privacy: Decentralized blockchain tag storage and encrypted data separation reduce single-point leakage risks, avoiding [26]’s plaintext storage vulnerabilities and traditional schemes’ TPA access (DPAS) or static encryption flaws (SWPor).

In summary, the improved scheme achieves balanced and efficient security enhancements in attack resistance, system reliability, and privacy protection by integrating blockchain technology with dynamic sampling.

3. Core Innovations Compared to Existing Work

After analyzing security and attack resistance, the core differences between this work and the scheme in [26] and literature [14] are summarized in Table 5 across four dimensions.

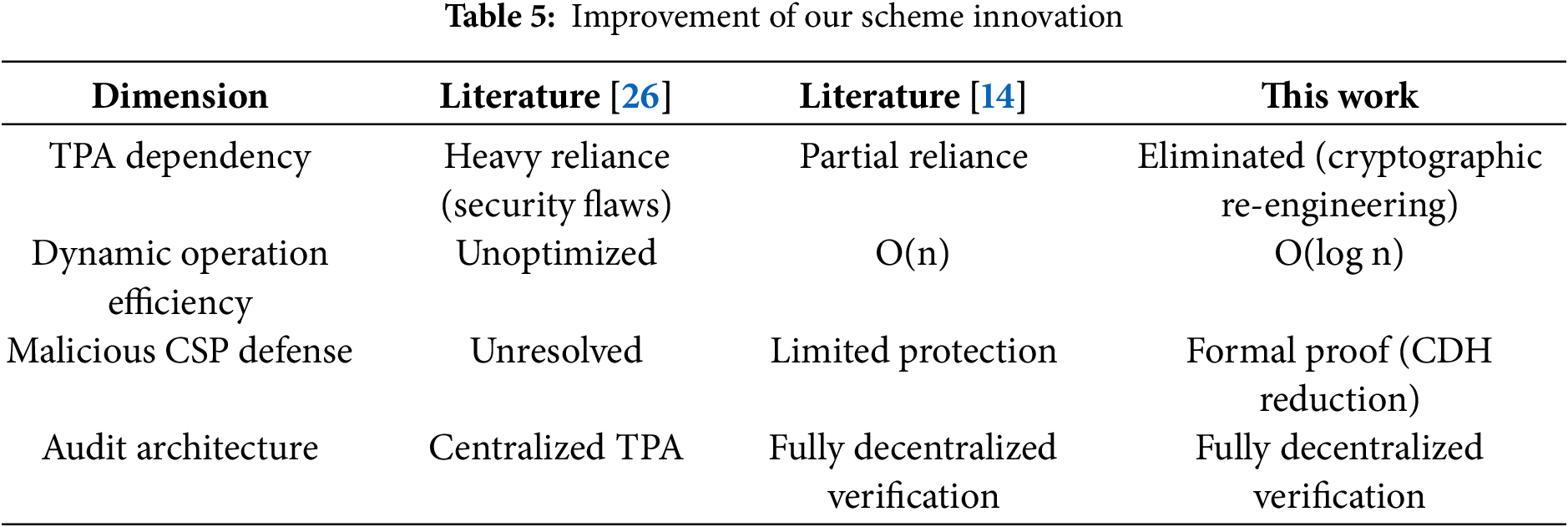
Core innovations compared to Original Scheme [26]:

1) Security Model Reconstruction: Original Scheme [26] relies on CSP computing plaintext blocks (μ=∑i=1nvimi), creating logical contradictions and privacy risks (CSP accesses plaintext). This Work eliminates plaintext dependency through parameter substitution (μ=∑i=1nviei) and dynamic signature binding σi=(H(Ei)ei)α. Blockchain-stored tags and encrypted block separation ensure zero plaintext exposure.

2) Original Scheme [26] fails to resist exponential attacks (Fig. 3) and data tampering (CSP tampers ei without updating tags). This Work introduces random challenges and dual CDH hardness binding σDi=σivi(γaβ)H(ei), proving malicious CSP detectability via cryptographic reduction (Theorem 1).

Core Innovations Compared to Literature [14]:

1) Dynamic Operation Efficiency: Literature [14] relies on static group signatures and linear key management (O(n) overhead), leading to high computational costs for dynamic operations (insertions/deletions). This Work integrates Merkle Hash Trees (MHT) with BLS short signatures, reducing dynamic operation costs to O(log n). This enables real-time verification and achieves a 40% performance gain over [14] in terms of computational efficiency.

2) Decentralized Audit Breakthrough: Literature [14] requires a trusted centralized TPA node, introducing single-point-of-failure risks. This Work constructs a distributed public audit network based on blockchain (Fig. 2). By leveraging smart contracts, verification is fully decentralized, eliminating reliance on TPA and enhancing system resilience.

Performance-Security Balance: By integrating multi-hash enhancement for data integrity, extended exponentiation for encryption strength, and dynamic parameter adjustment {k,w}, this renewed scheme we designed significantly improves anti-forgery and distributed security capabilities. This design achieves efficient security-performance trade-offs with minimal computational cost, enhancing encryption depth, verification flexibility, and attack resistance.

6  Experimental Analysis

This section evaluates the performance of the proposed scheme compared to the original scheme through a comprehensive analysis of computational cost and communication overhead. Specific concepts and descriptions are provided in Table 2. To ensure fairness and credibility in the comparison, third-party data from Reference [30] on the execution time of relevant operations was used, as shown in Table 6. The experimental environment was based on the MIRACL library (v7.0.0, supporting bilinear pairing operations) and OpenSSL 1.1.1 (for hash and signature algorithms). The running time of some related operations was measured on a computer with the following specifications: Intel Core i7-10700K (8 cores, 16 threads, 3.8 GHz), 32 GB DDR4 memory (2666 MHz), and a 1 TB NVMe SSD. The bilinear pairing used was e^:G1×G2→GT, where G1 is a multiplicative group over the finite field Fp, with p being a large prime number and the order q being 256 bits. The hash function used was SHA-256.

Since the proposed scheme introduces file name and index binding (Ei=ei∥Fname∥i) during tag generation without changing the number of operations, this section only measures the communication overhead during the challenge-response process (e.g., challenge message and proof message sizes), in bytes. In the original scheme, the challenge process requires transmitting n index blocks (assuming each index block is 32 bits), resulting in a size of n×4 bytes. During the proof process, the Merkle Hash Tree (MHT) root (256-bit hash value) + aggregated signature (512 bits) + μ (256 bits) are transmitted, so the total communication overhead is n×4+(256+256+512)÷8 bytes. In the proposed scheme, the challenge process only requires transmitting k index blocks, resulting in a size of k×4 bytes. During the proof process, the dynamic aggregated signature introduces two additional group elements (including random numbers {β,Y}), so the total communication overhead of the proposed scheme is k×4+(256+256+512+256+256)÷8 bytes.

Taking t/n=0.1 and p = 99% as an example, Table 7 shows a comparison of communication overhead between the proposed scheme and the original scheme for different values of n, as illustrated in Fig. 6.

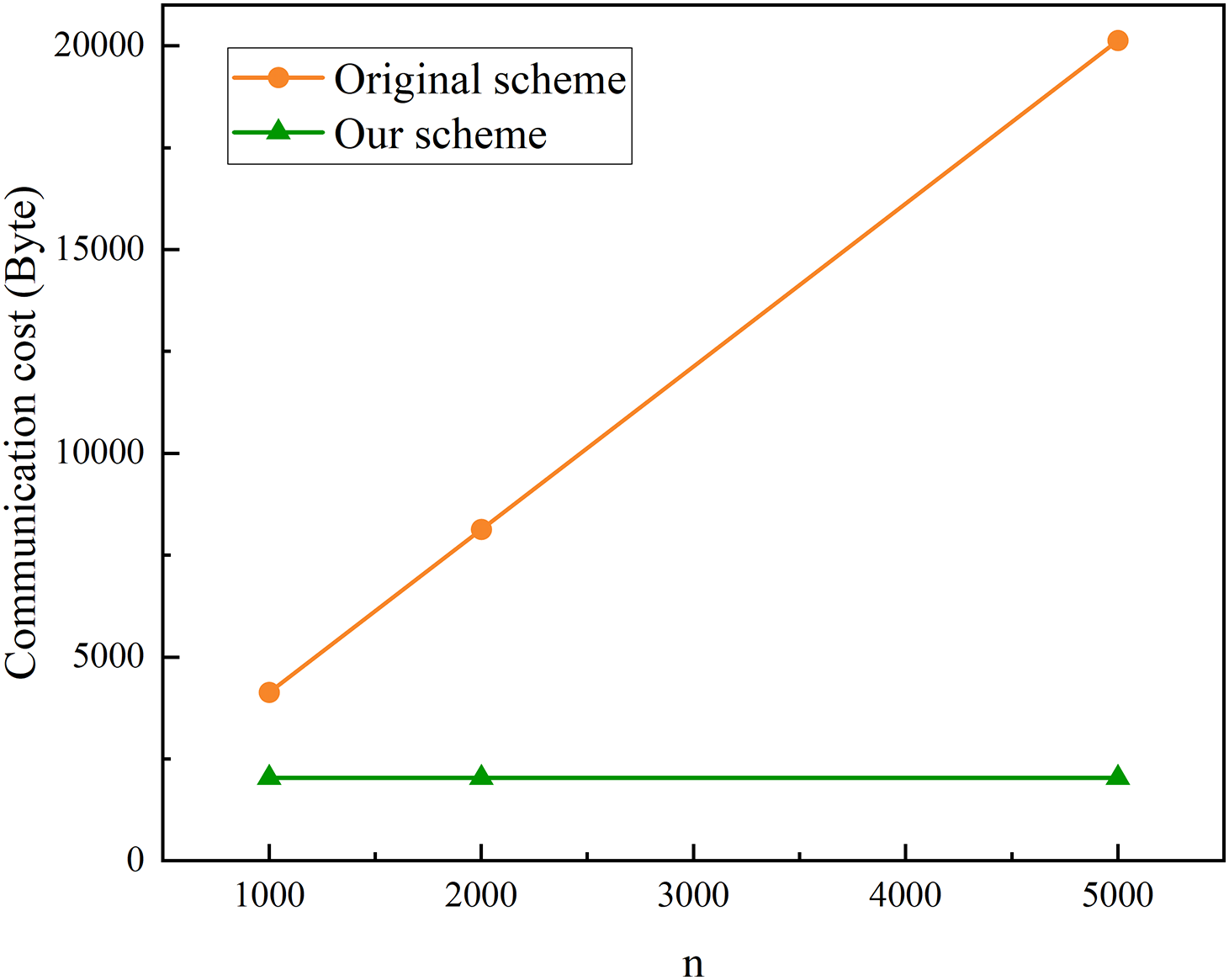
Figure 6: Improvement of communication overhead

For computational cost, we also take t/n=0.1 and p = 99% as an example, with n = 1000, 2000, and 5000.

1) When n = 1000:

Original Scheme:

•   DO Initialization Phase ≈ n(H+E+M+E)≈1000×(0.006+3.335+3.335+0.008)≈6684 ms

•   CSP Proof Generation Phase ≈ (2n−1)M+(n−1)A+nE≈1999×0.008+999×0.014+1000×3.335≈3365 ms

•   Auditor Verification Phase ≈ n(H+E)+nM+E+2P≈1000×0.006+1000×3.335+1000×0.008+3.335+32.713×2≈3418 ms

•   Total Overhead ≈ 6684+3365+3418≈13,467 ms

Proposed Scheme:

•   DO Initialization Phase ≈ n(H+E+M+E)≈1000×(0.006+3.335+3.335+0.008)≈6684 ms

•   CSP Proof Generation Phase ≈ (3k−1)M+(k−1)A+2kE+kH≈(3×460−1)×0.008+459×0.014+920×3.335+460×0.006≈3089 ms

•   Auditor Verification Phase ≈ 2kH+(2k+1)E+2kM+2P≈920×0.006+921×3.335+920×0.008+32.713×2≈3150 ms

•   Total Overhead ≈ 6684+3089+3150≈12,923 ms

2) When n = 2000:

Original Scheme:

•   DO Initialization Phase ≈ 13,368 ms

•   CSP Proof Generation Phase ≈ 6730 ms

•   Auditor Verification Phase ≈ 6767 ms

•   Total Overhead ≈ 13,368+6730+6767≈26,865 ms

Proposed Scheme:

•   DO Initialization Phase ≈ 13,368 ms

•   CSP Proof Generation Phase ≈ 3089 ms

•   Auditor Verification Phase ≈ 3150 ms

•   Total Overhead ≈ 13,368+3089+3150≈19,607 ms

3) When n = 5000:

Original Scheme:

•   DO Initialization Phase ≈ 33,420 ms

•   CSP Proof Generation Phase ≈ 16,825 ms

•   Auditor Verification Phase ≈ 16,814 ms

•   Total Overhead ≈ 33,420+16,825+16,814≈67,059 ms

Proposed Scheme:

•   DO Initialization Phase ≈ 33,420 ms

•   CSP Proof Generation Phase ≈ 3089 ms

•   Auditor Verification Phase ≈ 3150 ms

•   Total Overhead ≈ 33,420+3089+3150≈39,659 ms

Phase by phase calculations are delivered to the computational cost of the original scheme, the proposed scheme at different stages and the total computational cost. Table 8 shows the comparison of computational cost, as illustrated in Fig. 7.

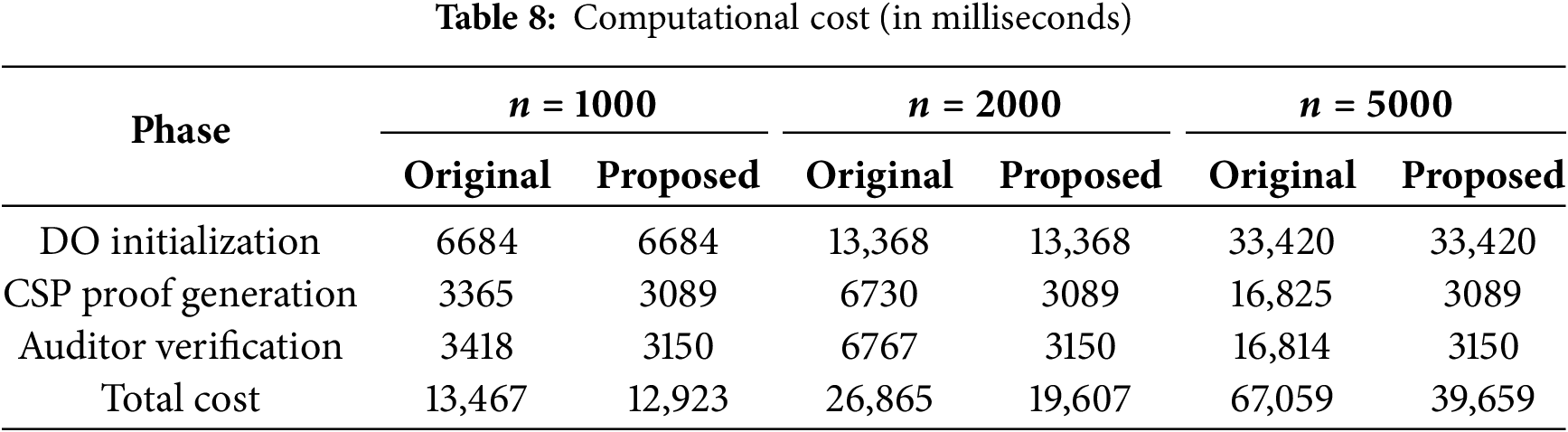
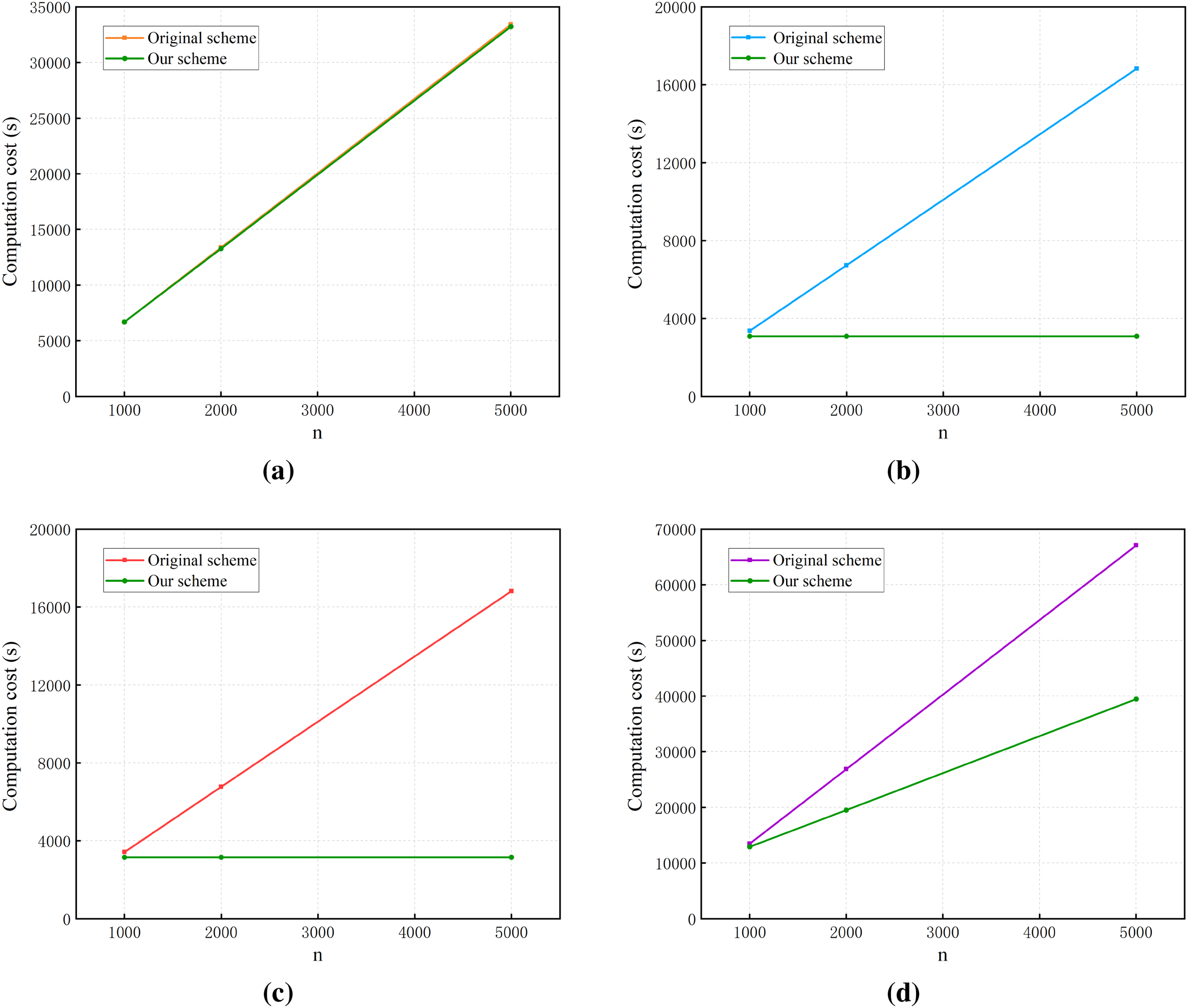
Figure 7: Diagram display of computational cost. (a) DO initialization; (b) CSP proof generation; (c) auditor verification; (d) total cost

7  Scheme Application

This paper proposes an enhanced cloud auditing scheme leveraging a random challenge-response mechanism and dynamic aggregate signature verification, addressing theoretical and algorithmic vulnerabilities in the original framework. The scheme ensures robust data security and integrity for the Data Owner (DO). It finds application across drone swarms, healthcare systems, government agencies, and enterprises, as demonstrated in Fig. 8.

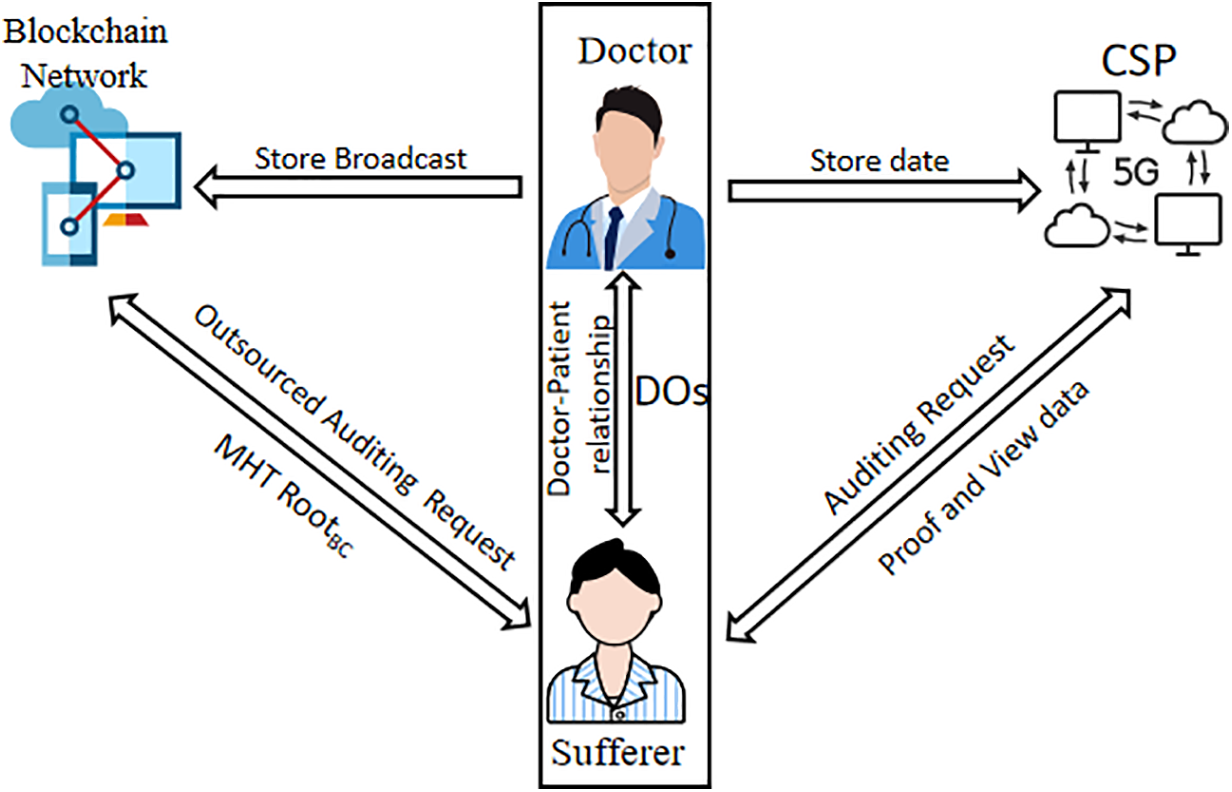
Figure 8: Application model in the healthcare field

7.1 Application in the Healthcare Field

In healthcare, patient records, diagnostic reports, and medical imaging data are highly sensitive and critical. These data are typically stored in the cloud for inter-institutional sharing and on-demand access. However, cloud data security and patient privacy protection remain focal points for the industry. By implementing the improved solution, healthcare data can achieve enhanced security:

•   Data Owners (DOs): (e.g., patients or medical institutions) split medical data into blocks, encrypt them using a symmetric key or public-key encryption, and upload them to the Cloud Service Provider (CSP).

•   Tag Generation: each data block is associated with a cryptographic tag (e.g., a hash or BLS signature), which is stored on the blockchain in a Merkle Hash Tree (MHT) structure.

During auditing, public auditors (e.g., medical regulatory bodies or other Data Owners within the network) randomly select challenged data blocks. The Cloud Service Provider (CSP) must generate cryptographic proofs based on these challenges. Auditors validate proof integrity by comparing them against blockchain-stored Merkle tags. Successful verification confirms data integrity and non-tampering; failure indicates potential security breaches. As illustrated in Fig. 8, this approach safeguards patient privacy while guaranteeing medical data integrity and trustworthiness. Practical deployments may integrate additional features such as access control and audit logging to meet healthcare-specific regulatory needs. Recent research underscores blockchain’s efficacy in medical data management, resolving the tension between data sharing and security.

7.2 Application in Drone Swarms

The explosive growth of drone technology, particularly in battlefield scenarios, has positioned it as a paradigm for future unmanned warfare. In drone swarm systems, secure and efficient storage and auditing of flight data are critical. During mission deployment and execution, this scheme’s security and control capabilities enable seamless coordination between ground stations, drone swarms, and manned-unmanned teams. Key advantages include:

•   Decentralized Task Assignment: Eliminates single points of failure by replacing traditional single-operator or manual control with blockchain-based task allocation.

•   Secure Data Upload: Drone flight data (e.g., GPS coordinates, sensor logs) is encrypted and uploaded to the cloud (as shown in Fig. 9).

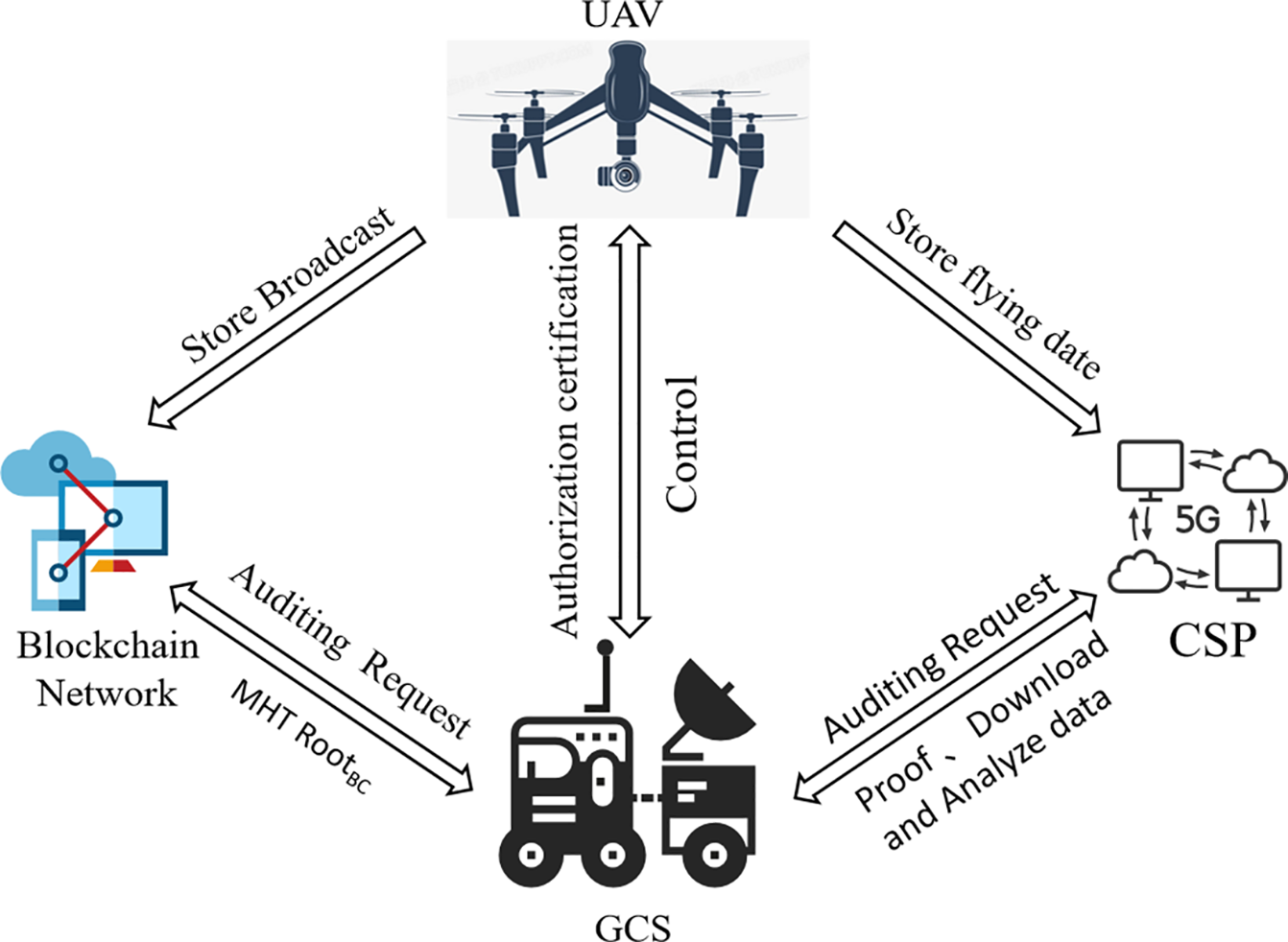
Figure 9: Flight parameter data storage verification model

For instance, when auditing flight mission data, auditors challenge the CSP to provide proofs for specific data blocks. The CSP generates proofs containing hash values and BLS signatures of the challenged blocks. Auditors validate integrity by comparing these proofs against blockchain-stored Merkle tags. This application strengthens drone data security while enhancing audit efficiency and accuracy, with critical implications for mission planning, execution monitoring, and accident investigations in drone swarms.

8  Conclusion and Future Work

To overcome trust deficiencies and computational overhead in conventional cloud auditing, we propose a decentralized public auditing scheme utilizing blockchain technology. By eliminating the Third-Party Auditor (TPA) and harnessing blockchain’s immutability and distributed nature, the scheme secures data tag storage and verification. Through rigorous analysis of logical inconsistencies (e.g., CSPs requiring plaintext data for verification) and security flaws (e.g., exponential attacks—where attackers forge proofs via repeated exponentiation—alongside tampering and deletion threats), the original scheme undergoes two-stage progressive refinement:

•   Correctness Enhancement: Resolving the requirement for CSP to access plaintext data during verification.

•   Security Strengthening: Introducing a random challenge-response mechanism and dynamic aggregate signature verification, combined with blockchain-stored immutable tags. This forces CSP to store complete encrypted data and improves detection efficiency through random sampling.

The enhanced scheme substantially improves resistance against forgery, deletion, and tampering attacks while balancing security and computational cost through dynamic parameter adjustment (e.g., challenge frequency k and coordination factor w). Performance analysis demonstrates superior efficacy over conventional schemes (e.g., SWPor [1], CHPor [2], DPAS [3]) in detection probability (e.g., single-challenge detection rates adaptable to diverse datasets), privacy protection (blockchain-distributed tag storage), and attack resistance (content binding via BLS signatures).

Despite notable security and reliability improvements, the scheme leaves room for optimization:

•   Privacy Enhancement: Integrating zero-knowledge proofs (ZKPs) or homomorphic encryption could further conceal data content and audit details while preserving verification validity, mitigating potential privacy leakage.

•   Practical Validation: Current research focuses on theoretical analysis. Future work includes deploying the scheme in real-world cloud environments (e.g., finance, healthcare) to test stability under large-scale data and high-concurrency scenarios.

Exploring these directions could advance blockchain’s application in cloud auditing, offering more efficient and flexible solutions for secure, trustworthy data storage.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by the National Natural Science Foundation of China (New Design and Analysis of Fully Homomorphic Signatures, Grant No. 62172436).

Author Contributions: The authors confirm contribution to the paper as follows: Haibo Lei: conceptualization, methodology, formal analysis, writing—original draft; Xu An Wang: supervisor, conceptualization, review, fund acquisition, writing—review & editing; Wenhao Liu: investigation, methodology; Lingling Wu: methodology, formal analysis; Chao Zhang: investigation, methodology, validation; Weiwei Jiang: investigation, methodology, validation; Xiao Zou: investigation, methodology, validation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data are contained within the article. All databases are publicly available.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li A, Chen Y, Yan Z, Zhou X, Shimizu S. A survey on integrity auditing for data storage in the cloud: from single copy to multiple replicas. IEEE Trans Big Data. 2020;8(5):1428–42. doi:10.1109/tbdata.2020.3029209. [Google Scholar] [CrossRef]

2. Sandhu AK. Big data with cloud computing: discussions and challenges. Big Data Min Anal. 2021;5(1):32–40. doi:10.26599/bdma.2021.9020016. [Google Scholar] [CrossRef]

3. Cui Y, Wang X, Lang X, Tu Z, Su Y. An improved short signature scheme for cloud data auditing. J Xidian Univ. 2023;50(5):132–41. (In Chinese). [Google Scholar]

4. Mishra R, Ramesh D, Edla DR, Qi L. DS-Chain: a secure and auditable multi-cloud assisted EHR storage model on efficient deletable blockchain. J Ind Inf Integr. 2022;26(2):100315. doi:10.1016/j.jii.2021.100315. [Google Scholar] [CrossRef]

5. Ateniese G, Burns R, Curtmola R, Herring J, Kissner L, Peterson Z, et al. Provable data possession at untrusted stores. In: Proceedings of the 14th ACM Conference on Computer and Communications Security; 2007 Oct 31–Nov 2; Alexandria, VA, USA. p. 598–609. [Google Scholar]

6. Razaque A, Frej MBH, Alotaibi B, Alotaibi M. Privacy preservation models for third-party auditor over cloud computing: a survey. Electronics. 2021;10(21):2721. doi:10.3390/electronics10212721. [Google Scholar] [CrossRef]

7. Wang Q, Wang C, Ren K, Lou W, Li J. Enabling public auditability and data dynamics for storage security in cloud computing. IEEE Trans Parallel Distrib Syst. 2010;22(5):847–59. doi:10.1109/tpds.2010.183. [Google Scholar] [CrossRef]

8. Wang J, Peng F, Tian H, Chen W, Lu J. Public auditing of log integrity for cloud storage systems via blockchain. In: International Conference on Security and Privacy in New Computing Environments; 2019 Apr 13–14; Tianjin, China. Cham, Switzerland: Springer; 2019. p. 378–87. [Google Scholar]

9. Salim A, Tiwari RK, Tripathi S. An efficient public auditing scheme for cloud storage with secure access control and resistance against DOS attack by iniquitous TPA. Wirel Pers Commun. 2021;117(4):2929–54. doi:10.1007/s11277-020-07079-7. [Google Scholar] [CrossRef]

10. Zhou J, Jin Y, He H, Li P. Dynamic cloud data audit model based on nest Merkle Hash tree block chain. J Comp Appl. 2019;39(12):3575–83. (In Chinese). [Google Scholar]

11. Zhu H, Yuan Y, Chen Y, Zha Y, Xi W, Jia B, et al. A secure and efficient data integrity verification scheme for cloud-IoT based on short signature. IEEE Access. 2019;7:90036–44. doi:10.1109/access.2019.2924486. [Google Scholar] [CrossRef]

12. Erway CC, Küpçü A, Papamanthou C, Tamassia R. Dynamic provable data possession. ACM Trans Inf Syst Secur. 2015;17(4):1–29. doi:10.1145/1653662.1653688. [Google Scholar] [CrossRef]

13. Shen J, Shen J, Chen X, Huang X, Susilo W. An efficient public auditing protocol with novel dynamic structure for cloud data. IEEE Trans Inf Forensics Secur. 2017;12(10):2402–15. doi:10.1109/tifs.2017.2705620. [Google Scholar] [CrossRef]

14. Yang C, Chen X, Xiang Y. Blockchain-based publicly verifiable data deletion scheme for cloud storage. J Netw Comput Appl. 2018;103(6):185–93. doi:10.1016/j.jnca.2017.11.011. [Google Scholar] [CrossRef]

15. Ghallab A, Saif MH, Mohsen A. Data integrity and security in distributed cloud computing—a review. In: Proceedings of International Conference on Recent Trends in Machine Learning, IoT, Smart Cities and Applications: ICMISC 2020. Singapore: Springer; 2020. p. 767–84. [Google Scholar]

16. Yang C, Song B, Ding Y, Ou J, Fan C. Efficient data integrity auditing supporting provable data update for secure cloud storage. Wirel Commun Mob Comput. 2022;2022(1):5721917. doi:10.1155/2022/5721917. [Google Scholar] [CrossRef]

17. Juels A, Kaliski BSJr. PORs: proofs of retrievability for large files. In: Proceedings of the 14th ACM Conference on Computer and Communications Security; 2007 Oct 31–Nov 2; Alexandria, VA, USA. p. 584–97. [Google Scholar]

18. Gao X, Yu J, Chang Y, Wang H, Fan J. Checking only when it is necessary: enabling integrity auditing based on the keyword with sensitive information privacy for encrypted cloud data. IEEE Trans Dependable Secure Comput. 2021;19(6):3774–89. doi:10.1109/tdsc.2021.3106780. [Google Scholar] [CrossRef]

19. Zhou L, Fu A, Yu S, Su M, Kuang BY. Data integrity verification of the outsourced big data in the cloud environment: a survey. J Netw Comput Appl. 2018;122(4):1–15. doi:10.1016/j.jnca.2018.08.003. [Google Scholar] [CrossRef]

20. Han H, Fei S, Yan Z, Zhou X. A survey on blockchain-based integrity auditing for cloud data. Digit Commun Netw. 2022;8(5):591–603. doi:10.1016/j.dcan.2022.04.036. [Google Scholar] [CrossRef]

21. Habib G, Sharma S, Ibrahim S, Ahmad I, Qureshi S, Ishfaq M. Blockchain technology: benefits, challenges, applications, and integration of blockchain technology with cloud computing. Future Internet. 2022;14(11):341. doi:10.3390/fi14110341. [Google Scholar] [CrossRef]

22. Li J, Liu Z, Chen L, Chen P, Wu J. Blockchain-based security architecture for distributed cloud storage. In: 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC); 2017 Dec 12–15; Guangzhou, China: IEEE. p. 408–11. [Google Scholar]

23. Du Y, Duan H, Zhou A, Wang C, Au MH, Wang Q. Towards privacy-assured and lightweight on-chain auditing of decentralized storage. In: 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS); 2020 Nov 29–Dec 1; Singapore: IEEE. p. 201–11. [Google Scholar]

24. Wang C, Sun Y, Liu B, Xue L, Guan X. Blockchain-based dynamic cloud data integrity auditing via non-leaf node sampling of rank-based Merkle hash tree. IEEE Trans Network Sci Eng. 2024;11(5):3931–42. doi:10.1109/tnse.2024.3393978. [Google Scholar] [CrossRef]

25. Guo C, Jin Y. Research on dynamic cloud data auditing mechanism based on improved blockchain. Appl Res Comput/Jisuanji Yingyong Yanjiu. 2023;40(3):659–66. (In Chinese). [Google Scholar]

26. Li J, Wu J, Jiang G, Srikanthan T. Blockchain-based public auditing for big data in cloud storage. Inform Process Manag. 2020;57(6):102382. [Google Scholar]

27. Wang M, Zhan T, Zhang H. Bit security of the CDH problems over finite fields. In: International Conference on Selected Areas in Cryptography. Cham, Switzerland: Springer; 2015. p. 441–61. [Google Scholar]

28. Shacham H, Waters B. Compact proofs of retrievability. J Cryptol. 2013;26(3):442–83. doi:10.1007/s00145-012-9129-2. [Google Scholar] [CrossRef]

29. Rass S. Dynamic proofs of retrievability from Chameleon-Hashes. In: 2013 International Conference on Security and Cryptography (SECRYPT); 2013 Jul 29–31; Reykjavik, Iceland: IEEE. p. 1–9. [Google Scholar]

30. He D, Wang H, Wang L, Shen J, Yang X. Efficient certificateless anonymous multi-receiver encryption scheme for mobile devices. Soft Comput. 2017;21(22):6801–10. doi:10.1007/s00500-016-2231-x. [Google Scholar] [CrossRef]