Smart Assessment of Flight Quality for Trajectory Planning in Internet of Flying Things

1  Introduction

In high-risk or high-intensity working environments, UAVs have gradually replaced human labor to perform tasks, improving work efficiency and reducing operational risks. For instance, the authors in [1] proposed a small UAV system capable of conducting inspection tasks in enclosed industrial environments. This system not only reduces the need for human involvement in hazardous tasks but also minimizes the downtime of industrial equipment. Currently, this research achievement has been extended to the exploration of indoor environments without GPS. Furthermore, intelligent UAVs are becoming an important direction for the future development of UAVs, especially in applications aimed at reducing operational costs and enhancing mission autonomy. The researchers in [2] explored the development opportunities and challenges of UAVs in civilian applications.

With the rapid development of drone technology, UAVs have demonstrated significant potential in various application scenarios, such as long-duration monitoring, long-distance patrolling, precision agriculture, and inspection of large-scale infrastructure. However, due to constraints like minimum turning radius, the path planning problem for certain types of UAVs is more complex than that of multi-rotor UAVs [3]. Moreover, most existing path planning methods focus on two-dimensional environments, while many UAVs typically operate in three-dimensional spaces. Therefore, optimizing flight trajectories in three-dimensional environments remains an important research question. It is important to note that the 2D trajectory planning component of this study has been previously presented [4]. This work builds upon it to extend the research into three-dimensional trajectory optimization.

On the other hand, the flight evaluation of UAVs is crucial for improving the quality of operator training and optimizing autonomous flight systems. Currently, many studies still primarily rely on flight attitude data without fully integrating trajectory matching analysis, which limits the accuracy and reliability of the evaluation. For example, the UAV flight trajectory evaluation method based on ADS-B (Automatic Dependent Surveillance-Broadcast) [5] has improved the accuracy of trajectory tracking to some extent, but it still faces significant noise interference in complex environments. Additionally, the advancement of artificial intelligence technology in recent years has provided new directions for UAV flight evaluation. Methods combining Recurrent Neural Networks (RNN) and Kalman Filters have been used to enhance the precision of flight data analysis [6]. Therefore, how to integrate flight trajectory and flight attitude data and use the latest intelligent algorithms to build a more accurate evaluation system is a significant motivation for this study. To address the aforementioned challenges, the main contributions of this paper are as follows:

•   Three-Dimensional Trajectory Optimization for UAVs: This paper introduces the MWPath3D algorithm, which optimizes the flight trajectory of UAVs in three-dimensional space by considering constraints such as turning radius and pitch angle. By integrating local search techniques with Bézier curve smoothing methods, the algorithm generates smoother UAV trajectories. Initially, the MWPath2D algorithm is used to plan the optimal path in two-dimensional space, followed by decoupling and integrating methods to generate smooth and flyable trajectories in three-dimensional space. Simulation results demonstrate that our algorithm’s results are fully consistent with discrete experiments, yet our algorithm is significantly faster.

•   Development of the Intelligent Trajectory and Attitude-Based Flight Evaluation (ITAFE) Algorithm: To more accurately assess the flight quality of UAV operators, this paper develops the ITAFE algorithm. By analyzing attitude and trajectory parameters during flight, and utilizing decision tree models for flight performance classification, the algorithm achieves accurate flight quality assessment. Experimental results show that the proposed algorithm not only rapidly generates optimal flight paths but also exhibits high accuracy and real-time performance in flight evaluation.

The rest of this article is organized in the following structure. Section 2 introduces the related work concerning trajectory optimization and intelligent flight evaluation algorithms for UAVs. Section 4 details the workflow and specifics of the MWPath2D, MWPath3D, and ITAFE algorithms proposed in this paper. Section 5 provides experimental validation and analysis of the methods presented. Finally, Section 6 summarizes the key findings of this study.

2  Related Works

With the rapid development of UAV technology, path planning and flight evaluation for UAVs have become research hotspots. The operational level of UAVs directly affects their mission execution capabilities, and improving UAV control skills primarily relies on efficient path planning and accurate flight evaluation [7]. The objective of path planning is to find the optimal or near-optimal flight trajectory under given constraints. The Traveling Salesman Problem (TSP) is a typical case [8–10], and traditional methods such as genetic algorithms, simulated annealing, and ant colony algorithms are commonly used. Moreover, human digital twin is a proper paradigm that bridges physical twins with powerful virtual twins for assisting complex task evaluation in human-centric services [11,12].

To address path planning for UAVs, researchers have emphasized Dubins trajectory optimization to satisfy the minimum turning radius constraint in the distant past [13]. Chen et al., addressing the issues of low tracking accuracy and weak interference resistance in three-dimensional path following control for small UAVs, designed a globally stable integral sliding mode function controller [14]. The authors in [15] proposed a path planning method based on enhanced gravitational search algorithm for UAV, by introducing the memory of the current optimal solution and chaotic levy flight perturbation, to balance between global and local search capabilities. Especially for the swarm UAV system, the authors in [16] designed a cost-effective system to improve communication range, processing power, autonomy, scalability, and energy efficiency, through salient features such as fortified communication, collaborative hardware integration, task distribution, optimized network topology, and efficient routing protocols. Although these methods can generate high-precision flight trajectories for specific scenarios, they become computationally expensive or infeasible when considering large, rapidly changing state spaces [17].

Flight evaluation for UAVs is crucial for assessing operator skill levels. Traditional evaluation methods mainly rely on manual observation or basic flight data statistics, which suffer from strong subjectivity and poor real-time performance, making it difficult to provide immediate and accurate feedback after training. Additionally, current methods often focus only on attitude data without considering trajectory matching between actual and target flight paths. The authors in [18] studied the correlation between indicators and pilot performance, making use of both local and global features based on convolutional neural network. The researchers in [19] proposed a three-stage machine learning-based evaluation method, achieving an assessment accuracy of 90%. Recently, automated flight evaluation systems have emerged. The authors in [20] conducted a flight test of flight path management to verify the automation’s core functions, providing positive indications in a future high-density air taxi environment. However, these methods still have limitations, as some studies focus solely on flight attitude parameters without comprehensively evaluating trajectory matching, and improvements in real-time assessment capabilities are still needed.

3  System Model

In this section, we introduce the motion model of UAVs in three-dimensional space constructed in this paper, as well as the models involved in intelligent flight quality assessment, paving the way for the methodology proposed in the next chapter.

The flight trajectory planning of UAVs must account for their kinematic constraints, among which the minimum turning radius and pitch angle are two critical factors influencing three-dimensional path optimization. Specifically, UAVs take off from a base and are required to pass through multiple mission waypoints during flight. The sets P={p1,p2,…,pm} and T={t1,t2,…,tn} represent the actual flight trajectory points and target flight trajectory points, respectively, with the lengths of the sets being m and n accordingly. The heading upon arrival at each mission waypoint can be arbitrary, and the UAV must ultimately land at the designated base.

We formulate a three-dimensional kinematic model for UAVs that satisfies their flight constraints. The model ensures the smoothness and feasibility of the optimized trajectory, with the starting and ending points represented as Ps(xs,ys,zs,φs,γs), Pf(xf,yf,zf,φf,γf), the intermediate mission waypoints are denoted as Pi(xi,yi,zi,φi∗,γi∗), where the subscript i indicates the order of arrival at the mission waypoint. The coordinates (xi,yi,zi) represent the position of the UAV in three-dimensional space, φi is the heading angle of the UAV, and γi is the pitch angle of the UAV, which is constrained within the interval [γmin,γmax]. The objective of path planning is to generate an optimal trajectory from the starting point Ps to the ending point Pf, ensuring that the UAV visits all mission waypoints in a prescribed order while satisfying the constraints of minimum turning radius and pitch angle. This can be formally expressed as follows:

Ltotalmin(φi∗,γi∗)=min{Ls[Ps(xs,ys,zs,φs,γs),Pi(xi,yi,zi,φi∗,γi∗)]+∑i=1m−1Li[Pi(xi,yi,zi,φi∗,γi∗),Pi+1(xi+1,yi+1,zi+1,φi+1∗,γi+1∗)]+Lf[Pi(xm,ym,zm,φm∗,γm∗),Pf(xf,yf,zf,φf,γf)]}.(1)

To simplify the global optimization, the 3D trajectory is decoupled into horizontal and vertical planes using the heading angle φi∗ and pitch angle γi∗, respectively. This enables independent optimization of the multi-waypoints trajectory in the horizontal plane.

Trajectory similarity measurement is widely used in recommendation systems. Currently, algorithms for calculating trajectory similarity are mainly divided into four categories: point-based, shape-based, segment-based, and task-specific. The matching effectiveness of different algorithms varies depending on the application scenario. Trajectory matching is crucial for evaluating the consistency between the UAV’s actual flight path and the predefined reference trajectory. To quantify the deviation between these trajectories, we employ three different metrics.

The first one is Dynamic Time Warping (DTW). The principle of DTW is to establish a correspondence between two elements based on the principle of matching the nearest distance, and it requires that the matching process be unidirectional along the time series. After the matching is completed, it is required that each point in one set has a corresponding point in the other set. The specific calculation is based on the idea of dynamic programming, and the formula is as follows:

Dd(pi,tj)={0,m=0 and n=0,∞,m=0 or n=0,dis(pi,tj)+min{Dd(pi−1,tj−1),Dd(pi,tj−1),Dd(pi−1,tj)},m≠0 and n≠0,(2)

where dis(pi,tj) represents the Euclidean distance between pi and tj. When the lengths of the target path and the actual path are both non-zero, a cumulative distance matrix can be constructed using (2) to obtain the matching value Dd, as shown in Fig. 1. The horizontal axis represents the target trajectory points, while the vertical axis represents the actual trajectory points. The yellow squares indicate matches between the target points and the actual trajectory points. The matching process proceeds from the bottom-left corner to the top-right corner. The value of D22 is obtained by adding dis(p2,t2) to the smallest value among D12, D21, and D11. This process is recursively applied up to Dnm, where Dnm represents the final matching result. A smaller Dnm indicates greater similarity between the two time series.

Figure 1: (a) The working principle of the DTW algorithm; (b) The improved DTW algorithm

The second metric is the Hausdorff distance, which is commonly used to represent the similarity between two point sets. It can be simply understood as the maximum of the shortest distances from the points in one set to the other set. It can be calculated by the following formula:

Dh=max{maxpi∈P⁡ minti∈T⁡‖pi−ti‖, maxti∈T⁡ minpi∈P⁡‖ti−pi‖}.(3)

As shown in Fig. 2, for each point in set P, match it to the point in set T with the shortest Euclidean distance, resulting in the matching set PTmin. Similarly, for each point in set T, match it to the point in set P with the shortest Euclidean distance, resulting in the matching set TPmin. Finally, the maximum value between the two sets is selected as the matching degree. The characteristics of the Hausdorff distance are that the sequences of the two sets are unordered, and it is relatively sensitive to outliers in the sequences. A single outlier may cause the distance between the sets to be very large.

Figure 2: Hausdorff distance

The last metric is the Longest Common Subsequence (LCSS) algorithm. Similar to the DTW algorithm, it is also based on the idea of dynamic programming. However, LCSS algorithm differs in that it directly skips and does not match some “outlier points.” Its computation process begins by matching the last elements of the two point sets. If a match is found, the matching value is incremented by one; if not, it takes the maximum value from the previous sequence matches. The longest common subsequence is ordered but not necessarily contiguous. The calculation formula is as follows:

LCSS(P,T)={0,m=0 or n=0,1+LCSS(pm,tn),dist(ai,bj)<δ,max(LCSS(pm−1,tn),LCSS(pm,tn−1)), otherwise, (4)

where δ is the threshold for determining whether points in the two point sets match. The Euclidean distance between two points can be used as the matching metric. When the distance between two points in the point sets is less than the threshold δ, these two points are considered to be matched. Since this paper involves matching multiple actual flight trajectories to a single target trajectory, for fairness, the matching degree between the actual flight trajectories and the target flight trajectory can be represented by the following formula:

DLCSS(P,T)=LCSS(P,T)n.(5)

As for attitude stability evaluation, we focus on the selection of flight performance parameters. As shown in Table 1, based on these selection principles and in conjunction with flight training regulations and the experience of senior pilots, we have refined the evaluation indicators for different flight phases. This study analyzes three distinct flight phases in relation to the mission trajectory. The climbing phase refers to the UAV’s ascent from the starting point to the first mission waypoint. The cruising phase involves the UAV flying sequentially from the first mission waypoint to the last, maintaining a stable altitude. The descending phase is the UAV’s landing from the last waypoint to the endpoint.

•   Comprehensiveness: The selected indicators should collectively reflect all operational skills of the UAV pilot and assess the entire flight process rather than a single phase.

•   Scientific validity: The indicators must accurately and reasonably reflect the true quality of flight.

•   Comparability: The indicators should highlight differences among pilots and be fair and measurable.

•   Practicality: The indicators should be easily obtainable and measurable.

The evaluation indicators for these three phases are largely consistent. Parameters such as climb and descent rates can be inferred from changes in altitude. Therefore, we unify the evaluation indicators for the entire flight process as follows: altitude, airspeed, heading angle, pitch angle, and roll angle.

After the simulated flight training, the UAV’s status can be categorized into three scenarios: 1) safe landing at the endpoint, 2) landing at the endpoint with damage, and 3) crash. These outcomes correspond to the trainee’s performance levels of excellent, satisfactory, and unsatisfactory, respectively.

4  Proposed Method

In this subsection, we introduce the multi-waypoint path optimization in a two-dimensional plane method named MWPath2D proposed in this paper, along with its extension, the multi-waypoint path optimization in a three-dimensional plane method named MWPath3D. Apart from this, we introduce an intelligent flight quality evaluation model called ITAFE. Next, we will present the implementation details of these methods.

4.1 Multi-Waypoint Trajectory Optimization for UAVs

This section investigates the optimal trajectory problem for UAVs to pass through multiple waypoints in sequence. By utilizing geometric knowledge and numerical analysis theory, the optimal heading angle range for multiple intermediate waypoints in a two-dimensional plane is determined. Subsequently, an interval optimization algorithm is employed to iteratively search for the target values of each heading angle within the optimal range to minimize the overall path length until convergence to the optimal solution. In three-dimensional space, the trajectory can be decoupled into curves on two orthogonal two-dimensional planes. Leveraging the pre-planned optimal multi-waypoint trajectories in the two-dimensional planes, the two-dimensional curves are extended to three-dimensional space using calculus.

In the previous section, we proposed the MWPath2D algorithm to compute a set of optimal heading values for task waypoints, enabling the UAV to achieve the shortest trajectory when passing through multiple waypoints in a 2D plane. For continuous smooth curves in 3D space, the trajectory can be projected onto the horizontal and vertical planes. The turning radius in the horizontal plane is denoted as rh, and the turning radius in the vertical plane is denoted as rv, as shown in Fig. 3.

Figure 3: Three-dimensional decoupling

The curvature expression formula for a curve in three-dimensional space can be written as:

κ=cos4⁡(γ)∗rv−2+rh−2,(6)

where γ represents the pitch angle in the vertical direction. According to the curvature constraint of Dubins curves κ≤Rmin−1, it can be concluded that:

cos4⁡(γ)∗rh−2+rv−2≤Rmin−2.(7)

Since Dubins curves are continuously differentiable, LH(t) denotes the projection of the UAV on the horizontal plane, and LH′ represents the first derivative of LH(t) in the two-dimensional horizontal plane. The path on the horizontal plane can be expressed as:

LH(t)=∫(xf,yf)(xs,ys)|LH′(t)|dt.(8)

The path in the vertical plane represents the trajectory from the starting point to the endpoint reached after flying horizontally over LH. The trajectory in the vertical plane can be expressed as:

LV(t)=∫(LH(f),zf)(LH(s),zs)|LV′(t)|dt.(9)

The pitch angle of the UAV in the vertical space is bounded. When the horizontal radius is sufficiently large, the pitch angle of the UAV during flight can be reduced. However, the total flight path becomes longer. We need to balance the values of rh and rv to minimize the total flight path. The objective equation is as follows:

minLtotal Vsubject tocos4⁡(γ)∗rh−2+rv−2≤Rmin−2,γ∈[γmin,γmax].(10)

First, we obtain the optimal path on the horizontal plane and the optimal heading for each mission waypoint using the MWPath2D algorithm. Then, we increase the turning radius to ensure that the three-dimensional trajectory meets the flight constraints of the UAV, while also updating the headings of the mission waypoints. After obtaining a three-dimensional trajectory that satisfies the flight constraints of the UAV, we reduce the turning radius to optimize the trajectory length. We refer to this multi-waypoint path optimization algorithm in three-dimensional space as MWPath3D. The key steps of the MWPath3D algorithm are as follows:

Step 1:   Set the minimum turning radius of the UAV, Rmin, as the turning radius rh on the horizontal plane, and input the two-dimensional data of the three-dimensional waypoint parameters into MWPath2D to obtain the optimal heading θbest for each waypoint on the horizontal plane.

Step 2:   Increase rh by an additional Rmin, and calculate rv using (7) until the constraint in (10) is satisfied. Initialize the iteration step size △.

Step 3:   Within the range rh∈[rh−Rmin,rh], iteratively update rh−△ to compute a more optimal LtotalV until convergence to the optimal solution.

4.2 Intelligent Flight Evaluation for UAVs

This section presents the ITAFE algorithm, which integrates trajectory matching, attitude analysis, and machine learning techniques to enhance the accuracy and objectivity of UAV flight assessment. The proposed method consists of three key components: trajectory matching analysis, attitude stability evaluation, and machine learning-based classification.

The evaluation process begins with flight data collection, where a UAV flight simulator (FlightGear) is used to generate flight logs. These logs contain key operational parameters, such as pitch angle, roll angle, and yaw angle, as well as positional information, including GPS coordinates and velocity.

Next, trajectory matching analysis is performed to assess flight path deviations. A trajectory matching algorithm computes the similarity between the intended trajectory and the actual flight trajectory, ensuring an objective measurement of path-following accuracy. At the same time, attitude stability evaluation is conducted by analyzing the fluctuations in flight attitude parameters, where the Bollinger Bands method is used to quantify stability.

Based on the extracted features, a flight dataset is constructed and used for machine learning-based classification. We employ models such as decision trees, logistic regression, and k-nearest neighbors (KNN) to categorize flight performance. The trained model then provides both pilot proficiency levels and quantitative performance scores, offering a comprehensive evaluation of UAV flight skills. Next, we introduce each component of ITAFE in detail.

In UAV trajectory matching, DTW is more adaptable than Hausdorff distance and LCSS. It dynamically aligns trajectory points, making it suitable for UAVs with varying speeds. Unlike Hausdorff, which ignores time order and is affected by outliers, and LCSS, which relies on a matching threshold, DTW provides a more accurate measure of overall trajectory similarity. DTW aligns all points, offering a stable metric, while LCSS needs a threshold δ that impacts results. However, standard DTW faces challenges like imbalanced matching points, high computational complexity O(mn), and local matching issues. To address these, we propose an improved DTW algorithm. It normalizes matching points, uses local mean matching strategies, and applies window constraints to reduce complexity, enhancing accuracy and efficiency.

As shown in Fig. 1b, for a planned waypoint Tt and multiple actual waypoints Pp1,Pp2,…,Ppk, the matching value is computed as the average Euclidean distance:

D(Tt,Pp1,Pp2,…,Ppk)=1k∑i=1kdist(Tt,Ppi),(11)

where dist(T−t,Ppi) is the Euclidean distance between the planned waypoint Tt and the actual waypoint Ppi. By ensuring a consistent number of matching pairs, the improved DTW algorithm eliminates bias caused by varying numbers of waypoints in the actual trajectory. The use of average distance for multiple matches reduces the impact of outliers, providing a more reliable measure of trajectory similarity. The improved DTW algorithm is particularly suitable for evaluating UAV flight trajectories, where precision and fairness in trajectory matching are critical.

In this study, we employ the Bollinger Bands algorithm to quantify the amplitude of parameter fluctuations. This algorithm consists of three main components: the upper band U(t), the middle band M(t), and the lower band D(t). The width of the data channel reflects the amplitude of parameter sequence fluctuations:

U(t)=1Wc∑i=t−Wc2t+Wc2+ m×1Wc∑i=t−Wc2t+Wc2(xi−e(i))2,M(t)=1Wc∑i=t−Wc2t+Wc2x(i),D(t)=1Wc∑i=t−Wc2t+Wc2x(i)−m×1Wc∑i=t−Wc2t+Wc2(xi−e(i))2.(12)

The Bollinger Bands algorithm employs a simple moving average method to calculate the average value of the parameter sequence x(i) within a window size Wc, where i≤N and N is the length of the parameter sequence. In this study, the window size Wc is set to 20, and the multiplier m is set to 2. The average width of the fluctuation channel represents the stability score of the UAV during flight, and it is calculated using the following formula:

s=∑i=1N|x(i)−M(i)|+|x(i)−D(i)|2N.(13)

A higher value of s indicates a greater amplitude of fluctuation. To verify the reliability of the Bollinger Bands channel, we analyzed pitch angle data from two groups of simulated flights: one group consisting of novice UAV operators who had recently started training, and the other comprising experienced UAV operators. The pitch angle data and corresponding fluctuations are shown in Fig. 4. The fluctuation channel diagrams reveal that the pitch angle variations for less skilled operators primarily range between [−20,20], while those for more skilled operators are confined within [−10,10]. Using (13), the stability scores for the two groups are calculated as 8.761 and 4.527, respectively. This indicates that the fluctuation amplitude for less skilled operators is approximately twice that of more skilled operators.

Figure 4: (a) Pitch angle sequence of less skilled operators. (b) Pitch angle fluctuation channel of less skilled operators. (c) Pitch angle sequence of more skilled operators. (d) Pitch angle fluctuation channel of more skilled operators

The fluctuation amplitude of UAV attitude data and the path matching value both indicate poorer controllability with higher values, making them inverse indicators. These do not require indicator normalization. However, due to the significant difference in the magnitude of these values, data need to be non-dimensionalized to address comparability issues. In this study, we use the range normalization method to standardize the data. Since all our indicators are inverse, we convert them to positive indicators for easier interpretation. The standardization formula is as follows:

x∗=xmax−xixmax−xmin,(14)

where xmax represents the maximum value of the indicator across all data groups, xmin is the minimum value, and x is the value of the indicator in the current data group.

Upon reviewing the UAV’s attitude and flight trajectory data for these misclassified samples, we found that stability and trajectory control were within acceptable ranges during climb and cruise phases. However, damage or crashes occurred during the final landing phase. This was often due to the pilot’s failure to reduce airspeed sufficiently, causing excessive impact forces upon landing, which damaged the UAV’s landing gear and fuselage. To address this issue, we added the UAV’s airspeed at landing as an additional evaluation metric. The updated confusion matrix indicates that this change significantly reduced the misclassification of “Qualify”. The specific scoring formula for simulated flight training is given by:

Score=ω⊤x,(15)

where ∑i=1nωi=1 represents the weight of each attribute calculated by the decision tree model, and 0⩽xi⩽1 is the normalized score of the flight evaluation indicators. From (15), it is evident that the maximum score for simulated flight training is 1, while the minimum score is 0. The final score is uniformly scaled within the interval [0,1], providing a more intuitive reflection of the trainee’s performance and facilitating subsequent comparisons. By examining the weights assigned to each indicator, it is observed that the path matching value carries significant weight. This highlights the necessity of incorporating precise trajectory control into the flight quality assessment metrics.

5  Simulations and Experiments

In this section, we conducted simulation experiments on the methods of Multi-waypoint Trajectory Optimization for UAVs and Intelligent Flight Evaluation for UAVs proposed in the previous subsection. The results demonstrate the effectiveness of the proposed methods.

We randomly initialized the coordinates of ten waypoints in three-dimensional space as follows: (0, 0, 0), (100, 200, 200), (250, 100, 300), (400, 200, 400), (600, 100, 500), (800, 300, 600), (600, 500, 700), (700, 800, 800), (900, 850, 900), and (1000, 1000, 1000). The headings at the starting and ending points were (0.0,0.0∘) and (0.0,60.0∘), respectively, where the first element of the tuple represents the horizontal heading and the second element represents the vertical heading, i.e., the pitch angle. The minimum turning radius of the UAV was set to 30m, and the pitch angle constraint range was [−60∘,60∘].

As shown in Fig. 5, the MWPath3D algorithm realizes the optimal trajectory for a UAV to fly from the starting point to the endpoint in three-dimensional space. The algorithm first determines the UAV’s approximate flight path on the horizontal plane, thereby enhancing the optimization efficiency in 3D space. It then optimizes the flight trajectory between adjacent waypoints by adjusting the turning radius to satisfy the pitch angle constraints during UAV flight. Compared with the traditional spiral ascent method, the proposed algorithm considers pitch angle constraints and generates trajectories that are more suitable for UAV operators. This makes it convenient for use as mission trajectories in flight training. Building on the idea of multi-waypoint path planning in two-dimensional space, this study connects the optimized trajectories between adjacent waypoints in 3D space, ultimately forming a smooth and feasible trajectory that meets the flight constraints of UAVs.

Figure 5: Three-dimensional path planning

The flight data used in this study were obtained from the FlightGear flight simulator, which features a robust I/O communication subsystem that supports the majority of current communication protocols. To acquire the desired flight parameters, we simply define them in XML format and transmit them over the network. The receiving host captures the transmitted data on its designated port. For ease of subsequent data analysis, the received data are saved in CSV format. Given that FlightGear employs the Global Positioning System (GPS), to ensure the efficiency of the path planning algorithm, the geodetic coordinates based on GPS positioning are simultaneously converted to three-dimensional Cartesian coordinates during data reception. As shown in Fig. 6, there are six sets of flight data. The green path represents the mission trajectory calculated using MWPath3D, while the red path depicts the actual flight trajectory of the trainee.

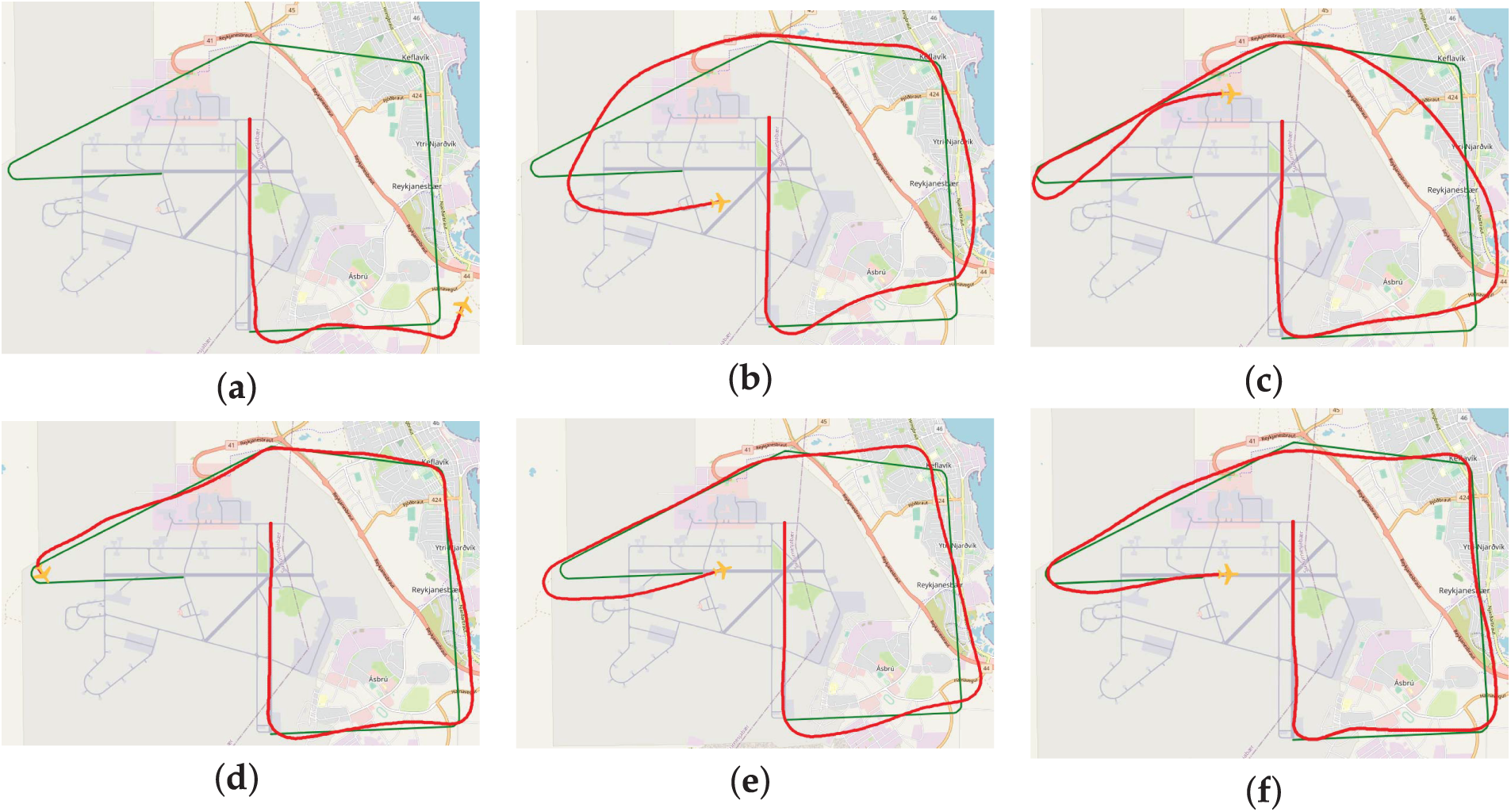
Figure 6: (a) Simulation of flight group 1 crashed in mid-flight with the worst match. (b) Simulation of flight group 2 completed the fight with bad match. (c) Simulation of flight group 3 completed the fight with match inference. (d) Simulation of flight group 4 crashed at the final turn. (e) Simulation of flight group 5 successfully reached the finish point. (f) Simulation of flight group 6 was the best match

We compared the improved DTW algorithm proposed in this paper with the Hausdorff distance algorithm and the LCSS algorithm to calculate the matching degree between the mission path and the actual flight trajectory. The improved DTW algorithm proposed in this paper maintains a consistent number of matching pairs between actual flight waypoints and mission waypoints relative to the total number of mission waypoints, ensuring fair matching results. As shown in Fig. 1b, when a mission waypoint Tt matches multiple actual flight waypoints Pp1, Pp2, and Pp3, we take the average of the Euclidean distances of these matching pairs as the current matching value. We provide a comprehensive comparison of the matching results from three algorithms, as shown in Table 2. The improved DTW algorithm, Hausdorff algorithm, and LCSS algorithm can all distinguish the degree of path similarity to some extent. However, in certain special cases, the results from the Hausdorff and LCSS algorithms do not align with our expectations.

To avoid discrepancies in the classification model arising from differences between the training and test datasets, we employed a five-fold cross-validation method. The data were equally divided into five subsets, with one subset used as the test set and the remaining four as the training set. This process was repeated five times to ensure that each sample served as both a test and training instance. To demonstrate the effectiveness of the decision tree model, we then compared the classification performance of logistic regression, decision tree, and KNN models in flight quality assessment using evaluation metrics such as Macro−F1 and accuracy.

Comparing their accuracy and Macro−F1 values, as shown in Fig. 7, the decision tree model consistently outperformed the others in both metrics. Furthermore, the decision tree exhibited greater stability, with less fluctuation in performance compared to logistic regression and KNN, which were more sensitive to data variations. The decision tree model demonstrated superior accuracy and stability.

Figure 7: (a) Comparison of accuracy; (b) Comparison of Macro−F1

6  Conclusions

In this paper, a novel algorithm MWPath3D is proposed by breaking down the large-scale multi-waypoints problem into smaller instances with fewer waypoints, to address the trajectory optimization issue for UAV in three-dimensional space. MWPath3D progressively extends the optimal solutions of these smaller problems to larger-scale problems. Moreover, an intelligent flight evaluation algorithm ITAFE is designed to assess the flight quality of UAV operators. By analyzing attitude and trajectory parameters during flight, ITAFE accurately evaluates flight quality employing a decision tree model to classify flight performance. Experimental results demonstrate that the proposed algorithms not only rapidly generate optimal flight paths, but also exhibit high accuracy and real-time performance in flight evaluation. Future works will explore the integration of reinforcement learning to enhance flight evaluation in cooperative UAV swarms. Through integrated simulation and real-world flight experiments, we will evaluate the scalability, robustness, and intelligence of these hybrid AI-driven approaches to advance the next generation of cooperative UAV operations. Based on more supports, it is also a very interesting issue to enhance the flight evaluation capabilities of cooperative UAV swarms by integrating expert pilot scoring with human-swarm interaction based on large language models, while closing the gap between human operators and complex swarm systems.

Acknowledgement: The authors are grateful to Prof. Jing Zhu and Prof. Xuedong Zhao at the Nanjing University of Aeronautics and Astronautics for helpful discussions.

Funding Statement: This research was funded in part by the Fundamental Research Funds for the Central Universities under Grant NS2023052, in part by the Natural Science Foundation of Jiangsu Province of China under Grants No. BK20231439 and No. BK20222012.

Author Contributions: Conceptualization, Weiping Zeng; Methodology, Weiping Zeng and Xiangping Bryce Zhai; Software, Cheng Sun; Validation, Cheng Sun and Yicong Du; Writing—original draft, Xiangping Bryce Zhai, Cheng Sun and Liusha Jiang; Writing—review & editing, Xiangping Bryce Zhai and Liusha Jiang; Supervision, Xuefeng Yan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Nikolic J, Burri M, Rehder J, Leutenegger S, Huerzeler C, Siegwart R. A UAV system for inspection of industrial facilities. In: 2013 IEEE Aerospace Conference; 2013 Mar 2–9; Big Sky, MT, USA. p. 1–8. [Google Scholar]

2. Shakhatreh H, Sawalmeh AH, Al-Fuqaha A, Dou Z, Almaita E, Khalil I, et al. Unmanned aerial vehicles (UAVsa survey on civil applications and key research challenges. IEEE Access. 2019;7:48572–634. doi:10.1109/access.2019.2909530. [Google Scholar] [CrossRef]

3. Yoon S, Jang D, Yoon H, Park T, Lee K. GRU-based deep learning framework for real-time, accurate, and scalable UAV trajectory prediction. Drones. 2025;9(2):142. doi:10.3390/drones9020142. [Google Scholar] [CrossRef]

4. Sun C, Zhai XB, Zhu J, Zhao X. Efficient path generation method for unmanned aerial vehicle via multiple waypoints. In: International Conference on Guidance, Navigation and Control. Cham, Switzerland: Springer; 2022. p. 552–61. [Google Scholar]

5. Li B, Ming X, Li G. Big data analytics platform for flight safety monitoring. In: IEEE 2nd International Conference on Big Data Analysis (ICBDA); 2017 Mar 10–12; Beijing, China. p. 350–3. [Google Scholar]

6. Hameed T, Wei W, Zhang R. Flying qualities specifications criteria and their determination for unmanned aerial vehicles. In: 2009 9th International Conference on Electronic Measurement & Instruments; 2009 Aug 16–9; Beijing, China. p. 3–557. [Google Scholar]

7. Jones M, Djahel S, Welsh K. Path-planning for unmanned aerial vehicles with environment complexity considerations: a survey. ACM Comput Surv. 2023;55(11):1–39. doi:10.1145/3570723. [Google Scholar] [CrossRef]

8. Roberge V, Tarbouchi M, Labonté G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans Ind Inform. 2012;9(1):132–41. doi:10.1109/tii.2012.2198665. [Google Scholar] [CrossRef]

9. Zhu Q, Yan Y, Xing Z. Robot path planning based on artificial potential field approach with simulated annealing. In: Sixth International Conference on Intelligent Systems Design and Applications; 2006 Oct 16–18; Jinan, China. p. 622–7. [Google Scholar]

10. Brand M, Masuda M, Wehner N, Yu XH. Ant colony optimization algorithm for robot path planning. In: 2010 Iternational Conference on Computer Design and Applications; 2010 Jun 25–27; Qinhuangdao, China. p. V3–436–40. [Google Scholar]

11. Yang Y, Shi Y, Yi C, Cai J, Kang J, Niyato D, et al. Dynamic human digital twin deployment at the edge for task execution: a two-timescale accuracy-aware online optimization. IEEE Trans Mob Comput. 2024;23(12):12262–79. doi:10.1109/tmc.2024.3406607. [Google Scholar] [CrossRef]

12. Okegbile SD, Cai J, Zheng H, Chen J, Yi C. Differentially private federated multi-task learning framework for enhancing human-to-virtual connectivity in human digital twin. IEEE J Sel Areas Commun. 2023;41(11):3533–47. doi:10.36227/techrxiv.23511720. [Google Scholar] [CrossRef]

13. Dubins LE. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am J Math. 1957;79(3):497–516. [Google Scholar]

14. Chen P, Zhang G, Li J, Chang Z, Yan Q. Path-following control of small fixed-wing UAVs under wind disturbance. Drones. 2023;7(4):253. doi:10.3390/drones7040253. [Google Scholar] [CrossRef]

15. Jiao K, Chen J, Xin B, Li L, Zheng Y, Zhao Z. Three-dimensional path planning with enhanced gravitational search algorithm for unmanned aerial vehicle. Robotica. 2024;42(7):2453–87. doi:10.1017/s0263574724000869. [Google Scholar] [CrossRef]

16. Bakirci M. A novel swarm unmanned aerial vehicle system: incorporating autonomous flight, real-time object detection, and coordinated intelligence for enhanced performance. Traitement Du Signal. 2023;40(5):2063–78. doi:10.18280/ts.400524. [Google Scholar] [CrossRef]

17. Yang Y, Xiong X, Yan Y. UAV formation trajectory planning algorithms: a review. Drones. 2023;7(1):62. doi:10.3390/drones7010062. [Google Scholar] [CrossRef]

18. Zhang S, Huo Z, Sun Y, Li F, Jia B. Pilot maneuvering performance analysis and evaluation with deep learning. Int J Aerosp Eng. 2023;2023(11):1–16. doi:10.1155/2023/6452129. [Google Scholar] [CrossRef]

19. Yuan W, Lu Z, Lu W, He S. Flight quality assessment based on machine learning. Sci Technol Eng. 2021;21(19):8262–9. [Google Scholar]

20. Ballin MG, Barrows BA, Nelson SL, Underwood MC, Fettrow TD, Wing DJ, et al. Flight evaluation of a flight path management system for high density advanced air mobility. In: AIAA Aviation Forum and Ascend; 2024 Jul 29–Aug 2; Las Vegas, NV, USA. [Google Scholar]