Structural and Helix Reversal Defects of Carbon Nanosprings: A Molecular Dynamics Study

1  Introduction

Carbon, an element in the fourth group of the periodic table, can form a wide variety of sp2 structures, including chiral structures that cannot be superimposed on their mirror images. Among them are the carbon microcoils/nanocoils [1,2], coiled carbon nanotubes [3–5], carbon nanocones [6], as well as the macromolecules composed of helicene and kekulene molecules [7–9]. The helical two-dimensional materials can be grown on nonplanar substrates [10]. The geometry of the coiled carbon nanotubes is controlled by the distribution of Stone-Wales and vacancy defects [11–13]. The helical graphene is actually a helical polymer [14–17] based on helicene and kekulene molecules. Helical CNTs can be designed through deformation induced by dislocation dipoles [18]. A graphene kirigami nanospring is an essential part of the nano-positioner offered in [19]. A carbon nanospring can act as a unit of an adsorbent model to control the capacity for gas adsorption [20]. Improvement of the thermoelectric properties can be achieved by using CNTs incorporating graphene nanosprings [21].

The helical graphene displays fascinating electronic properties [22–25], which are primarily determined by the interactions between layers [26,27]. The twisted nanoribbons can be used as nanocoils of inductance [28,29]. Coiled carbon nanotubes have potential in applications as nanoelectromechanical devices [30]. A change in the pitch of the helical graphene results in the metal-semiconductor transition [31]. The double-layer spiral graphene is metallic in an equilibrium state [32]. It has been determined that the electronic properties of helical graphene with armchair and zigzag edges differ significantly [33]. It has been shown experimentally and theoretically that DNA molecular springs modulate protein-protein interactions [34]. Various techniques are used for fabrication of nanospring: vapor phase synthesis, post-treatment techniques, templating methods, and molecular engineering [35]. The elastic properties of carbon and silicon based core-shell nanosprings have been found to be better than those of pure C and Si [36].

Helical carbon nanosprings are a unique material that combines the properties of single-layer nanoribbons and multilayer graphene. Due to their distinctive properties, they are of significant interest for nanotechnology. Not only electronic but also magnetic properties of helical graphene depend on the structure and elastic stretching [37]. Compression and stretching of helical graphene nanoribbons have been shown to cause a significant change in their thermal conductivity [38–41]. Tightly-wound helical carbon nanotubes exhibit giant elastic deformation under cyclic stretching and unloading and return to their original shape after more than doubling their length [42].

The mechanical properties of helical graphene nanoribbons have been analyzed in numerous studies. The nanosprings exhibit exceptional elasticity, with a maximum reversible tensile strain of hundreds percent [43,44]. The nanosprings, under tension, demonstrate a deviation from Hooke’s law due to the breaking of the van der Waals bonds between coils, which leads to non-homogeneous stretching [45]. Graphene nanoribbon nanosprings exhibit a distinctive force-strain relationship under tension, characterized by a constant force plateau across a broad range of tensile strain [9,46–48]. This phenomenon was explained in [9] by non-convex dependence of the potential energy of a structural unit of the nanospring as the function of tensile strain. A similar phenomenon has been observed for DNA [49–51] and for intermetallic NiAl and FeAl nanofilms [52–54].

Elastic and mechanical properties, the microscopic tensile deformation and fracture mechanisms of nanoentwined carbon nanocoils have been reported in the work [55]. Alternative terms are used for chiral extended metamaterials, including coiled and helical structures, whereas in the review [13] the term “spiral” has been chosen.

A comprehensive analysis of the mechanical and thermal properties of carbon nanosprings has been conducted, with a focus on tension and compression deformation [9,41,45,56–58]. Other modes of loading have not been addressed by the researchers, and here axial compression, bending, and twisting of the carbon nanosprings is analyzed using molecular dynamics simulations. The structures under consideration in this work can be divided into two categories: helicoids, Fig. 1a, and helical graphene nanoribbons, Fig. 1b. The chiral structures of the second type possess an inner channel, while the structures of the first type are devoid of such a feature.

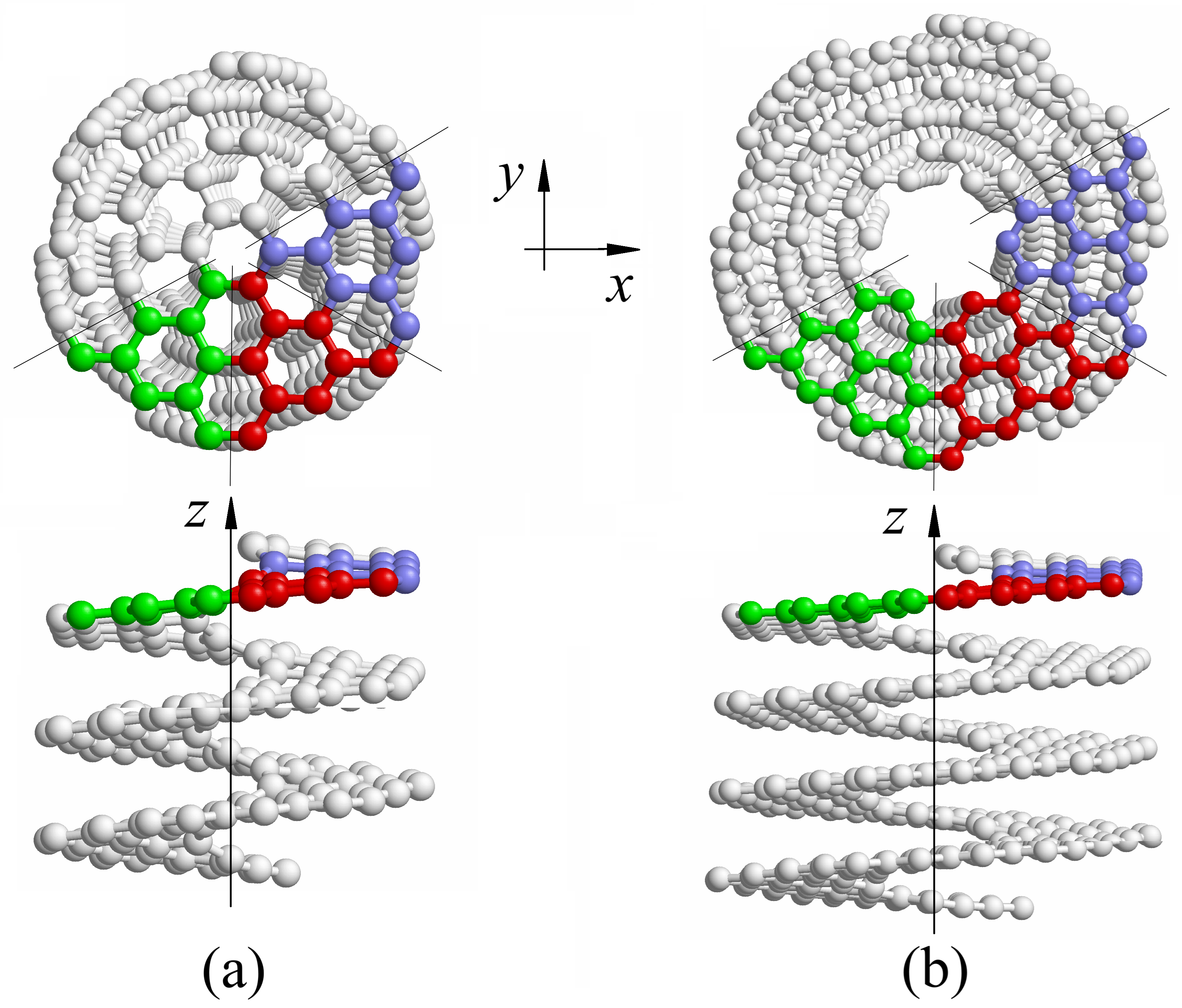
Figure 1: Atomic tructure of (a) helix l-helicene (C9H3)∞, l=3 and (b) helix l-kekulene (C15H5)∞, l=4. Three consecutive structural units are colored green, red, and blue. Hydrogen atoms bonded to surface carbon atoms are not shown here

In this work, we show that helical carbon nanosprings, in addition to their high tensile ability, have other unique mechanical properties. Thus, their compression can lead to the formation of stable folded structures with fractures, and their twisting can lead to the formation of structures with localized helix reversal defects separating parts of the nanospring with opposite chirality.

2  Model

Consider helical molecular structures derived from planar molecules l-kekulene C6(l2−1)Hl+1 (l≥3) and l-coronene C6l2H6l (l≥2) lying in the xy plane, by cutting them along the radius and further spiral extension along the z axis—see Fig. 1, where only carbon atoms are shown. In this work, the motion of hydrogen atoms is not modeled, but is taken into account by increasing the mass of carbon atoms of CH groups by the mass of the hydrogen atom, see Fig. 2, where the modified carbon atoms are shown in blue. The ground homogeneous state of such helical structures can be represented as successive shifts by Δz and rotations by angle Δϕ≈π/3 around the z-axis of a monomer of NC and NH carbon and hydrogen atoms (for l-kekulene NC=l2−1, NH=l+1, for l-coronene NC=l2, NH=l). Parameters Δz and Δϕ for different values of l are given in Table 1.

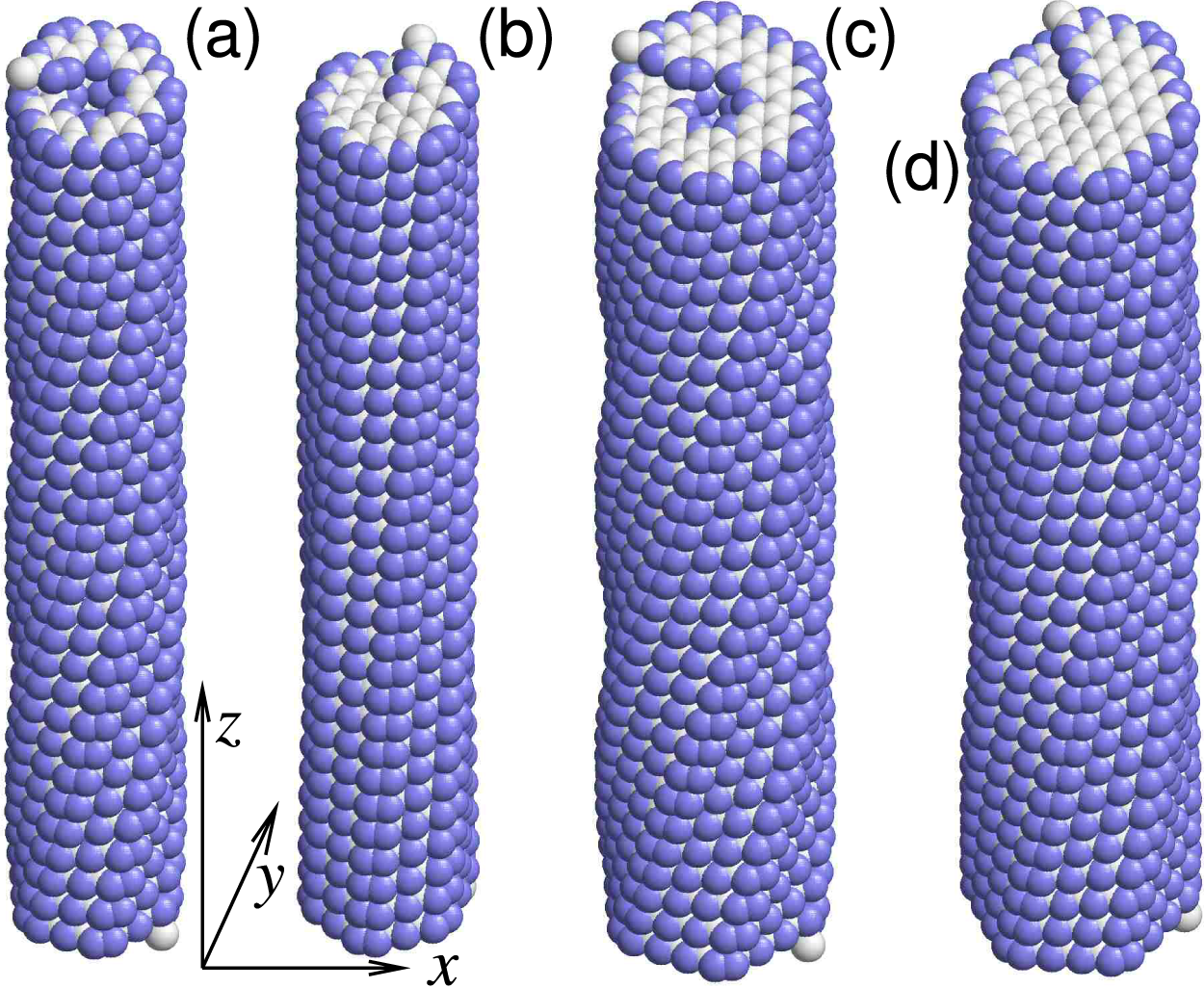
Figure 2: Spiral l-kekulene graphene nanoribbon (Cl2−1Hl+1)180 constructed from the l-kekulene molecule C6(l2−1)H6(l+1): (a) l=3 (helix kekulene); (c) l=4 (helix circumkekulene). Graphene helicoid (helix l-helicene) (Cl2Hl)180 built from l-coronene molecule C6l2H6l: (b) l=3 (helix circumhelicene); (d) l=4 (helix dicircumhelicene). The united CH atoms are shown in blue and the inner carbon atoms are shown in light gray. Recall that the united CH atoms are modeled by a single C atom, which has the combined mass of the C and H atoms. The nanosprings in (a) and (c) have an inner channel. Those in (b) and (d), however, do not

To simplify the modeling, valence-bonded CH groups of atoms at the edges of spiral structures are considered as a single carbon atom of mass M1=13mp, while all other inner carbon atoms have the mass M0=12mp, where mp=1.6601×10−27 kg is the proton mass. In this approach, each cell of the helix will consist of only NC−NH carbon atoms of mass M0 and NH united atoms of mass M1. In Fig. 2, the united atoms are shown in blue and the inner atoms are shown in light gray.

The coordinates of the carbon atoms of the n-th cell of the helix are completely determined by the by the coordinates of the atoms of the previous n−1 cell:

xn,j,1=xn−1,j,1cos⁡(Δϕ)−xn−1,j,2sin⁡(Δϕ),xn,j,2=xn−1,j,1sin⁡(Δϕ)+xn−1,j,2cos⁡(Δϕ),xn,j,3=xn−1,j,3+Δz, j=1,...,NC,(1)

where the vector xn,j=(xn,j,1,xn,j,2,xn,j,3) defines the coordinates of the jth atom of the nth unit cell, N is the number of unit cells (the length of the spiral L=(N−1)Δz). The longitudinal pitch is Δz≈0.58 AA, the angular pitch of the spiral is Δϕ≈61∘ [9].

A helical nanospring built from l-coronene molecules (helical l-helicene) has the chemical formula (Cl2Hl)N, where N is the number of structural units, l≥2. Such a l-coronene nanospring has the shape of a graphene helicoid, see Fig. 2b,d. A spiral nanospring built from l-kekulene molecules has the chemical formula (Cl2−1Hl+1)N, where l≥3. Such a l-kekulene nanospring has the shape of a spiral graphene nanoribbon, see Fig. 2a,c. Unlike the graphene helicoid, the spiral nanoribbon has an inner channel, which makes it a softer structure. A more detailed description of the structure of graphene nanospring is given in [9].

The deformation of nanosprings is modeled using the force field described in Ref. [9]. This force field accounts for the deformation of valence bonds and angles, as well as torsional and dihedral angles, and van der Waals interactions between atoms [59–64]. The Hamiltonian of a finite-length nanospring is given by

H=∑n=1N12(MX˙n,X˙n)+V(X1,...,XN)+∑n=1N−3∑k=n+3NW(Xn,Xk),(2)

where Xn={xn,j}j=1NC is the 3NC-dimensional vector with the coordinates of the atoms of the n-th structural unit and M is the diagonal matrix of the masses of the atoms. The first, second, and third terms on the right-hand side of the Hamiltonian (2) represent the kinetic energy, the valence interaction energy, and the van der Waals interaction energy, respectively.

The van der Waals interactions are described by the Lennard-Jones potentials

W(Xn,Xk)=∑j=1NC∑i=1NCULJ(rn,j;k,i),(3)

where the distance between the i-th atom of the k-th structural unit and the j-atom of the n-th structural unit is rn,j;k,i=|xk,i−xn,j|. Here the (6, 12) Lennard-Jones potential has the form

ULJ(r)=εc{[(rc/r)6−1]2−1},(4)

and the parameters are εc=0.002757 eV, rc=3.807 Å [65].

More complex reactive potentials have been developed to model the formation and breaking of covalent bonds between carbon atoms under thermomechanical loading, such as the Tersoff [66], ReaxFF [67], REBO [68] and AIREBO [69,70] potentials. These potentials describe the mechanical and elastic properties of carbon nanomaterials quite accurately [71–73]. However, they are more complex for numerical modeling and less accurately reproduce the phonon spectrum of graphene [66,74]. Therefore, their use is justified only when modeling processes involving changes in the topology of the valence bond network. It should be noted that the structural transformations of the nanosprings modeled in this work do not lead to the breaking or recovery of covalent bonds. Consequently, reactive force fields will lead to qualitatively the same results as the simple potential used in this work, since the interparticle distances change only slightly, and the reactive component of the potential is ineffective.

To find the ground state of the nanospring, the following potential energy minimization problem is numerically solved using the conjugate gradient method [75,76]:

Q=V(X1,...,XN)+∑n=1N−3∑k=n+3NW(Xn,Xk)→min:{Xn}n=1N.(5)

The ground states of the nanosprings of N=180 structural units (about 30 coils) are shown in Fig. 2.

The following system of Langevin equations is integrated numerically to model the thermal oscillations of the nanosprings:

MX¨n=−∂H∂Xn−γMX˙n−Ξn, n=1,...,N,(6)

with the initial conditions corresponding to the ground state

Xn(0)=Xn0, X˙n(0)=0, n=1,...,N,(7)

where {Xn0={(xn,j0,yn,j0,zn,j0)}j=1NC}n=1N is the solution to problem Eq. (5). Here γ=1/tr is the friction coefficient characterizing the intensity of interaction of the nanospring with the Langevin thermostat (the relaxation time of particle velocity is tr=10 ps), Ξn={(ξn,j,1,ξn,j,2,ξn,j,3)}j=1NC is the 3NC-dimensional vector of normally distributed random Langevin forces with correlation functions

⟨ξn,l,i(t1)ξk,m,j(t2)⟩=2MlkBTγδnkδlmδijδ(t1−t2),

with kB being the Boltzmann constant and T is the thermostat temperature.

The equations of motion Eq. (6) are solved numerically using the velocity Verlet method [77]. A time step of 1 fs is used in the simulations, since further reduction of the time step has no appreciable effect on the results.

Once equilibrium is reached between the molecular system and the thermostat, the mean energy E¯ and spring length L¯ are determined. The energy is given by the Hamiltonian (2), and the length is found as the distance between the centers of gravity of the first and last structural units. The temperature dependencies of the energy and length of the nanosprings are then obtained. Then the value of the dimensionless heat capacity coefficient is found c(T)=(3NNCkB)−1dE¯/dT and the axial thermal expansion coefficient of the nanospring α(T)=L¯−1dL¯/dT is determined.

Numerical modeling of nanosprings consisting of N=180 structural units (with a length of L0=10.4 nm) has shown their stability to thermal fluctuations within a wide temperature range 0<T<1300 K. An increase in temperature results in only a slight increase in the dimensionless heat capacity and an increase in helix length (see Fig. 3). The coefficient of axial thermal expansion is α≈5×10−5 K−1. The growth of the heat capacity and the increase in length are due to the soft anharmonicity of the van der Waals interactions between atoms (soft anharmonicity of the Lennard-Jones potential Eq. (4)). Thermal fluctuations do not lead to the formation of stable defects in the helix. It will be shown that such defects can be created by deforming the nanosprings through longitudinal compression, bending, and twisting.

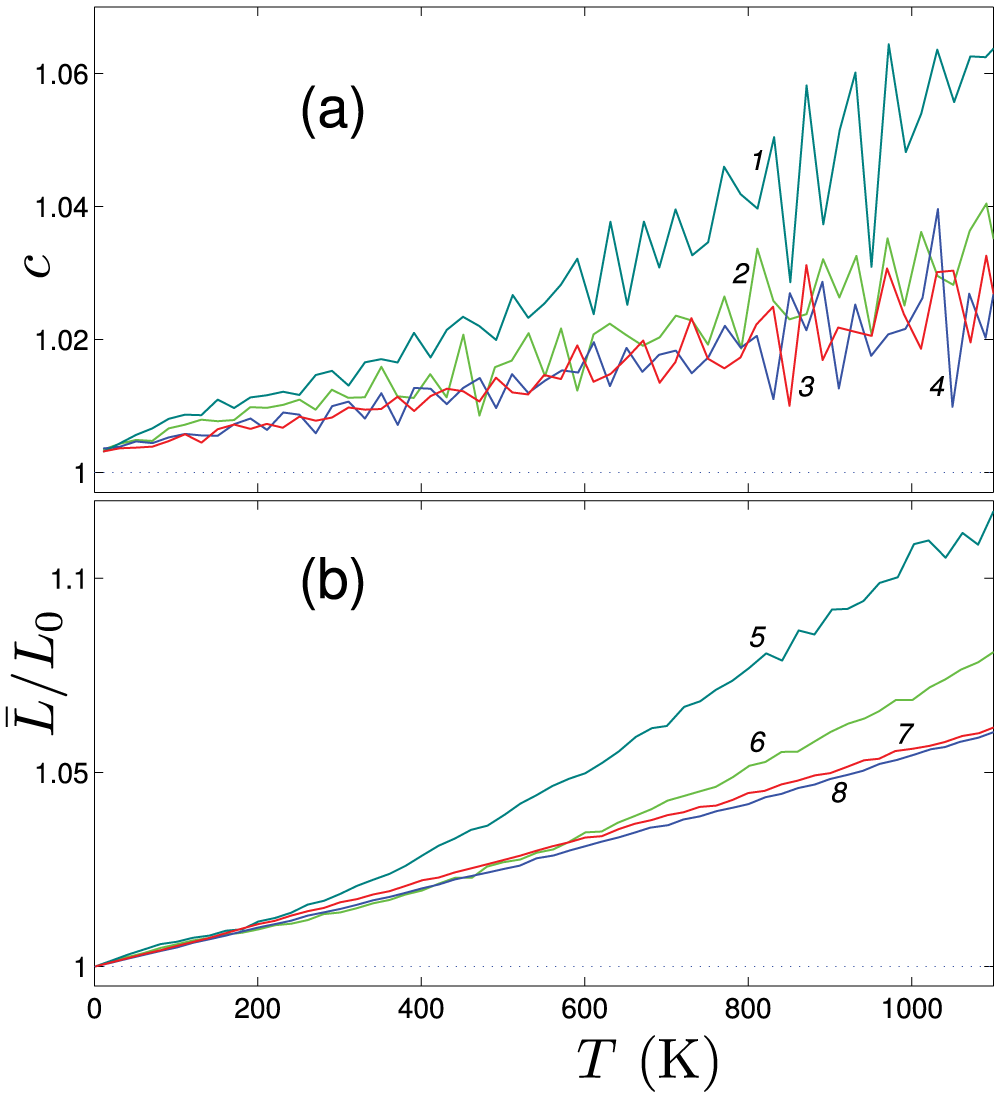
Figure 3: The temperature dependencies of (a) the dimensionless heat capacity c and (b) the relative elongation L¯/L0 of the helical l-kekulene nanosprings (curves 1, 2 and 5, 6 are for l=3, 4, respectively) and the helical l-coronene nanosprings (curve 3, 4 and 7, 8 are for l=3, 4, respectively). These nanosprings consist of N=180 structural units (L0 is the length of the molecule in the ground state)

3  Axial Compression of Nanosprings

The longitudinal compression of a nanosprings consisting of N=180 structural units is modeled. To do so, the ground state of the nanospring is used, and all the coordinates of the atoms in the first cell (n=1) and the x and y coordinates of the atoms in the last cell (n=N) are fixed. Conversely, the z coordinates of the last cell decrease at a constant speed, bringing the ends of the helix closer together. To achieve this, the system of equations of motion Eq. (6) is numerically integrated with the boundary conditions

X1≡X10, xN,j≡xN,j0, yN,j≡yN,j0,zN,j(t)=zN,j0−vt, j=1,...,NC,(8)

and initial conditions Eq. (7). The rate of compression is v=0.05 Å/ps and the simulation temperature is T=300 K.

After reaching the desired value of longitudinal dimensionless compression h(t0)=L(t0)/L(0) at time t=t0, the compression is stopped. Further modelling of the dynamics of the compressed nanospring with fixed edges is carried out by numerically integrating the system of equations of motion Eq. (6) with the boundary conditions

X1≡X10,XN≡XN(t0),(9)

and the initial conditions

Xn(0)=Xn(t0), X˙n(0)=X˙n(t0), n=1,2,...,N.(10)

After the system reaches the equilibrium with the thermostat, the mean value of its total energy E¯ is found. As the energy reference level it is convenient to take the energy of the ground state Em=E0+3(N−2)NCkBT. Here (N−2)NC is the total number of moving atoms of the nanospring, since motion of 2NC atoms in two structural units at the ends is constrained by the boundary conditions.

The energy E¯(h)−Em of the 4-coronene nanospring as the function of relative tension/compression h is shown in Fig. 4. Temperature has no significant effect on the shape of this function. As can be seen, changing the temperature from 1 K to 300 K only results in a slight upward shift of the curve. The change in shape of the nanospring under compression is shown in Fig. 5.

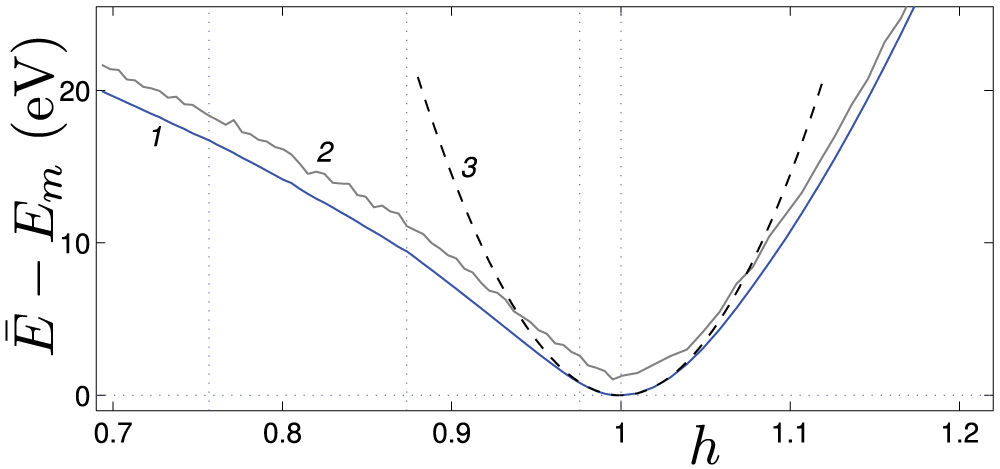
Figure 4: The dependence of the energy E¯−Em of the 4-coronene nanospring (C16H4)180 on the relative longitudinal tension/compression h. Curve 1 shows the dependence at a temperature of 1 K, while curve 2 at a temperature of 300 K. Curve 3 corresponds to the harmonic nanospring with a stiffness coefficient of K=4.4 N/m. The vertical dotted lines show the characteristic values of relative compression: h=0.757, 0.874, and 0.976

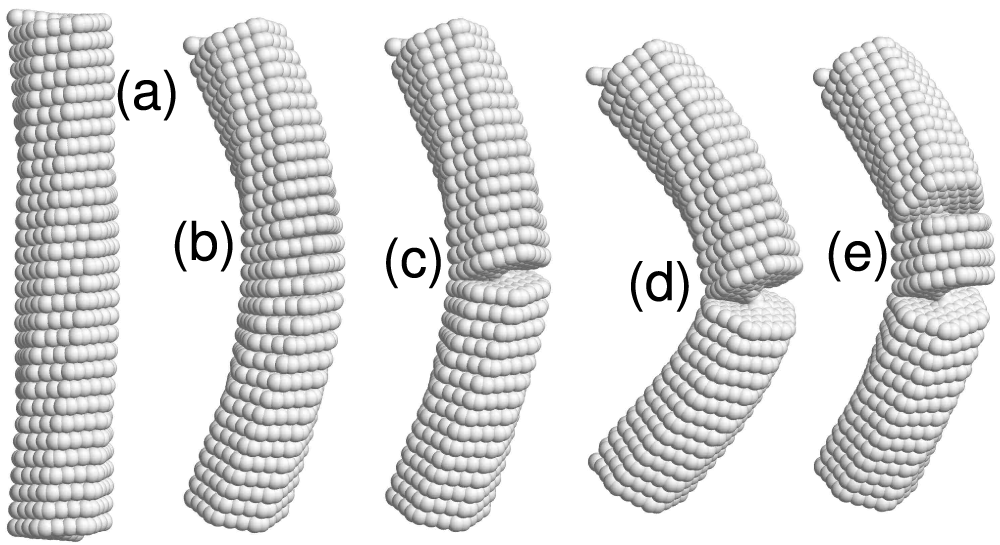
Figure 5: The 4-coronene nanospring (C16H4)180 under axial compression: (a) h=0.981, (b) 0.873, (c) 0.869, (d) 0.757, and (e) 0.752

At weak relative compression, 1>h≥h1=0.976, the nanospring energy grows proportionally to the parabola (h−1)2. Within this compression range, the nanospring axis remains straight, see Fig. 5a. At h=h1, the straight shape becomes unstable (Euler instability), and transverse bending occurs as the nanospring takes the form of a half-wave sinusoid, see Fig. 5b. Further compression increases the deviation of the nanospring axis from a straight line, and the energy growth of the compressed molecule follows an almost linear law. Thus, under axial compression, the nanospring behaves like a hinged rod. The half-wave sinusoidal shape loses stability at a relative compression of h=h2=0.874. At this point, the smooth bending of the nanospring ends, and a transverse crack appears in the middle, see Fig. 5c. Further compression increases the crack opening. At h=h3=0.757, a second crack appears in the nanospring, see Fig. 5d,e. It should be clarified that the formation of cracks occurs due to the rupture of only weak van der Waals bonds between the coils of the nanospring, while all covalent bonds remain intact, as noted in Section 2.

The energy E¯(h)−Em of the 4-kekulene nanospring (C15H5)180 as the function of relative axial tension/compression h is shown in Fig. 6. The change in the shape of this nanospring under compression is shown in Fig. 7. The nanospring behaves like a hinged Euler rod. At weak relative compression, 1>h≥h1=0.976, the nanospring axis remains straight, and its energy grows quadratically, see Fig. 7a. At h=h1=0.976, the straight configuration becomes unstable. The axis of the nanospring bends into the shape of a half-wave sinusoid, see Fig. 7b. Further compression increases bending and causes the energy of the compressed nanospring to increase almost linearly with h. Sinusoidal bending becomes unstable at h=h2=0.884, at which point a transverse crack appears in the middle, see Fig. 7c. Further compression occurs as the crack opens wider, as shown in Fig. 7d.

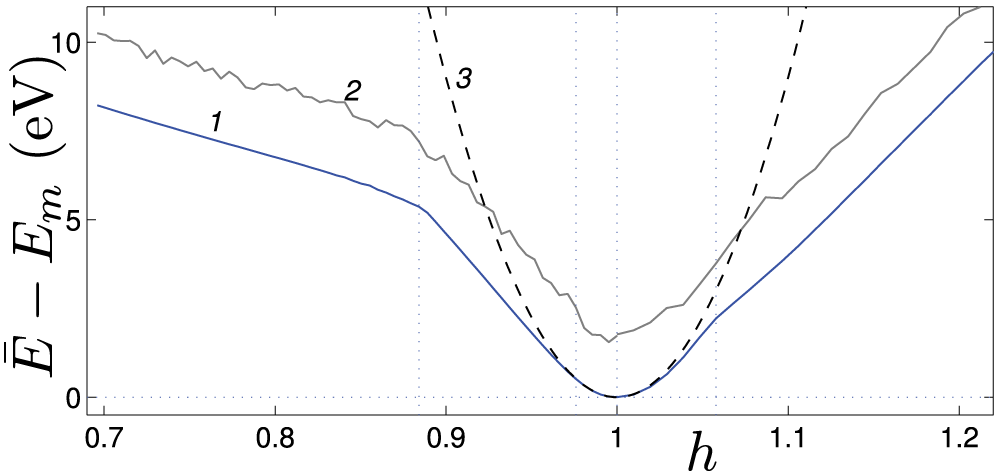
Figure 6: The dependence of the energy E¯−Em of the 4-kekulene nanospring (C15H5)180 on the relative longitudinal tension/compression h. Curve 1 shows the dependence at a temperature of 1 K, while curve 2 at a temperature of 300 K. Curve 3 corresponds to the harmonic nanospring with a stiffness coefficient of K=2.7 N/m. The vertical dotted lines show the characteristic values of relative compression: h=0.884, 0.976, and 1.058

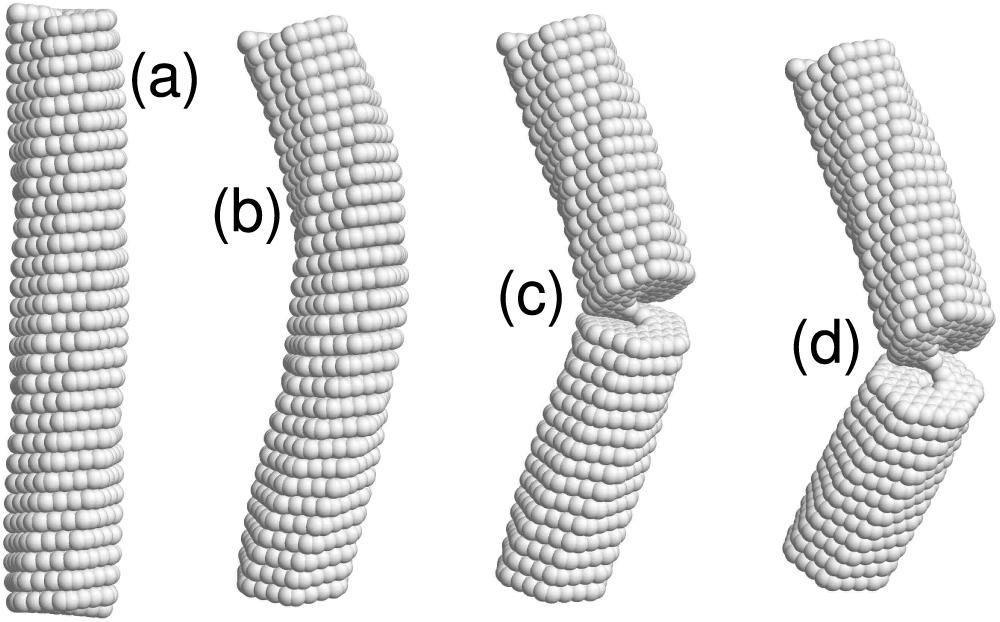
Figure 7: The 4-kekulene nanospring (C15H5)180 under axial compression: (a) h=0.981, (b) 0.889, (c) 0.884, and (d) 0.797

Note that, unlike the 4-coronene nanospring, compressing the 4-kekulene nanospring does not result in the formation of a second crack. Several cracks appear in the 4-coronene nanospring due to the presence of a rigid core that limits crack opening, making the formation of new cracks energetically preferable.

4  Bending and Fracture of Nanosprings

In order to bend the nanosprings, lateral forces must be applied in opposite directions to their ends and middle. This can be achieved by numerically integrating the following system of equations of motion

MX¨n=−∂H∂Xn−γMX˙n−Ξn+Ffn ex,n=1,2,...,N,(11)

where the index n numbers the structural units; F specifies the magnitude of the applied lateral force; the vector ex=(1,0,0) specifies the direction along the x-axis; and the coefficients f1=fN=1, fN/2=fN/2+1=−1, and fn=0 for the remaining values of n. Even though random forces in Eq. (11) are applied to all atoms of the nanospring, their effect on the motion of atoms constrained by the boundary conditions is zero, since their positions do not change when calculating the displacement increment at each time step.

Integrating the system of equations of motion Eq. (11) with the initial conditions Eq. (7) shows that there is a critical force, F=F0, at which the nanospring experiences irrecoverable fracture. When F<F0, the nanospring takes the form of an arc under the action of lateral forces. When the load is removed by setting F=0, the nanospring returns to its original ground state. When the force is equal to the critical value F=F0, the bending load leads to a fracture in the middle of the nanospring, and removing the load does not cause the nanospring to return to its initial ground state. After unloading, the nanospring can be in a folded steady state stabilized by van der Waals interactions between closely adjacent halves, see Figs. 8 and 9. Stable structures with a break angle of ϕd≈70∘ are also possible, see Fig. 10. These structures are stabilized by topological defect formed at the corner.

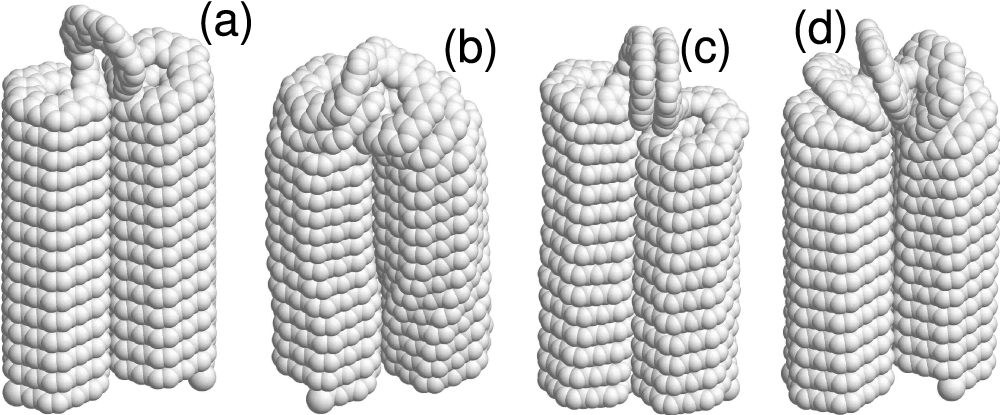
Figure 8: The equilibrium folded 3-kekulene nanosprings (C8H4)180 with energy (a) Ed=1.618, (b) 1.629, and (c) 2.202 eV, and (d) the equilibrium folded 3-coronene nanospring (C9H3)180 with energy Ed=17.433 eV. Energy is calculated relative to the ground state level, Ed=E−E0

Figure 9: The equilibrium folded 4-kekulene nanosprings (C15H5)180 with energy (a) Ed=7.080, (b) 8.072, (c) 8.628, (d) 9.428, (e) 10.247 eV, and (f) equilibrium folded 4-coronene nanospring (C16H4)180 with energy Ed=34.337 eV. The energy is counted from the ground state level, Ed=E−E0

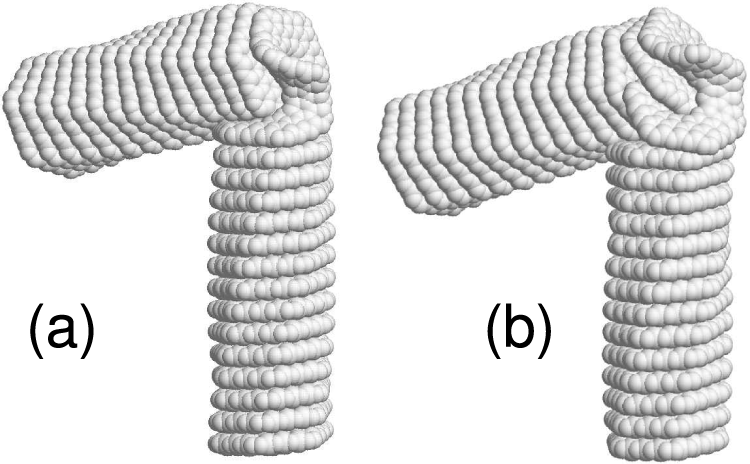
Figure 10: Stationary states of 4-kekulene nanospring (C15H5)180 with fracture with energy (a) Ed=6.974 and (b) 8.650 eV. The break angle is (a) ϕd=74∘ and (b) 70∘

For the 3-coronene nanospring (C9H3)180, the critical force is F0=0.036 eV/Å, while for the 4-coronene nanospring (C16H4)180 value F0=0.034 eV/Å. For F>F0, helix bending can only lead to the formation of stable folded states, see Figs. 8d and 9f. It can be seen that folding of the 3-coronene nanospring occurs by opening three coils, and folding of the 4-coronene nanospring occurs by opening four coils.

For the 3-kekulene nanospring (C8H4)180, the critical force value is F0=0.006 eV/Å, while for the 4-kekulene nanospring (C15H5)180 it is F0=0.012 eV/Å. Here one can talk about two closely located 90 degree cracks separated by one or a few coils, see Fig. 8a–c and Fig. 9a–e. All folded structures are stable, but the most energetically favorable is the folding of the helix with one coil separating the two cracks, see Figs. 8a and 9a. The 4-kekulene nanospring can also form stable structures with a break of angle ϕd≈70∘, see Fig. 10.

As mentioned above, the folded nanosprings shown in Figs. 8 and 9 are stabilized by van der Waals interactions between the adjacent halves. The energy of these interactions increases proportionally to the length of the nanospring, L. Therefore, very short nanosprings cannot remain in the folded state after unloading because the van der Waals energy is less than the elastic energy of bending. Conversely, for sufficiently long nanosprings, the folded structure is more favorable energetically than the straight configuration. Sufficiently long nanosprings will fold and form a bundle of adjacent parallel fragments of the same length, as often happens with α-helical regions of protein molecules [78,79].

5  Helix Reversal Defects in Nanosprings

Nanosprings in the form of helical macromolecules can exist in two equivalent ground states: a right-twisted helix or a left-twisted helix. A helix reversal defect occurs when one part of the macromolecule is a left-twisted helix and the other part is a right-twisted helix. This defect occurs at the boundary between these two regions, see Fig. 11. This structural defect describes a local change in the direction of rotation of the helix. Such defects are characteristic of helical polymer molecules. Helix reversal defects are present in polytetrafluoroethylene (PTFE) crystals, where they cause helical inversion [80], and in other helical polymers [15,81,82].

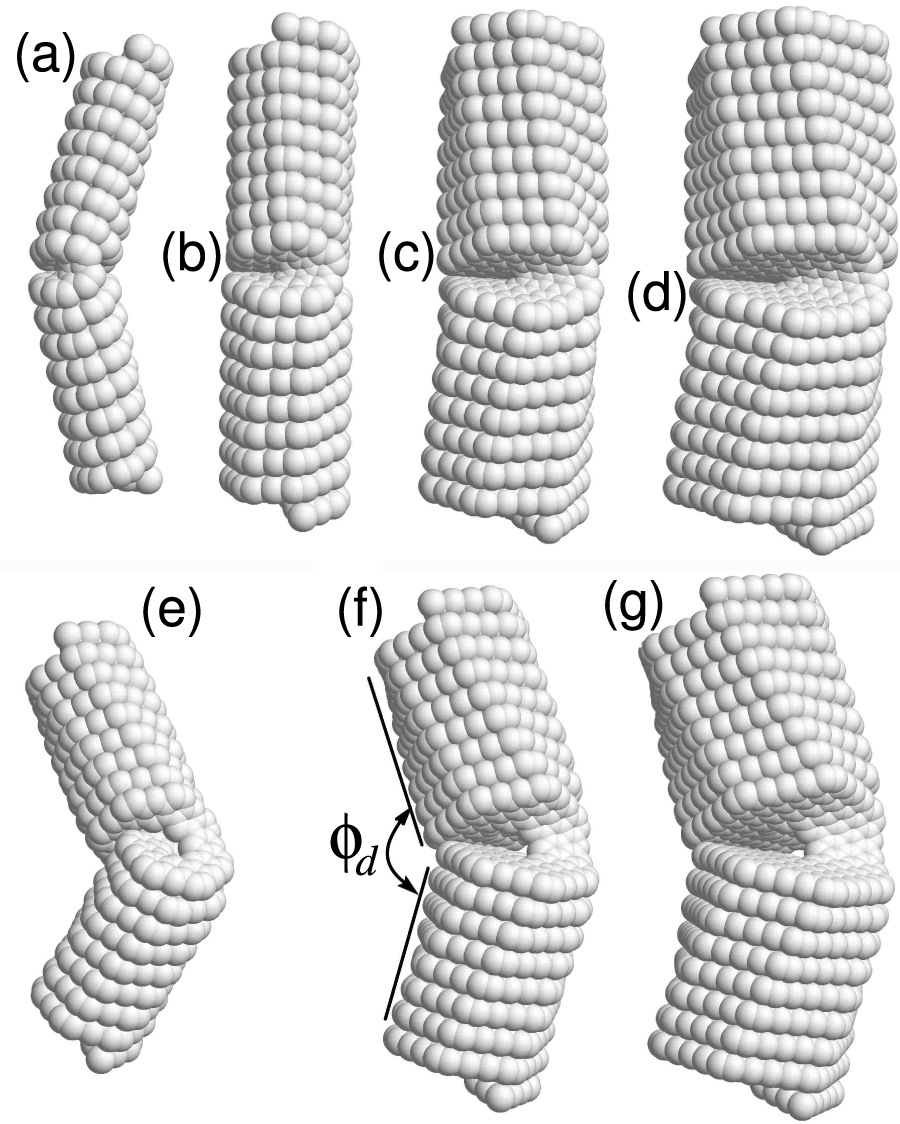
Figure 11: The helix reversal defects in l-coronene nanospring (in graphene helicoid) with (a) l=2, (b) l=3, (c) l=4, and (d) l=5, and in l-kekulene nanospring (in spiral graphene nanoribbon) with (e) l=3, (f) l=4, and (g) l=5. The angle between the axes of the two halves of the nanospring separated by the defect is denoted as ϕd

Solving the minimum potential energy problem Eq. (5) shows that the helix reversal defect is localized on two coils of the nanospring. The defect is characterized by the energy Ed=E1−E0, where E1 is the energy of the stationary state of the nanospring with the defect and E0 is the energy of the nanospring without the defect. The angle between the axes of the two halves of the nanospring separated by the defect is denoted as ϕd, see Fig. 11. The values of Ed and ϕd for different nanosprings are presented in Table 2.

6  Relaxation of a Highly Stretched Nanospring

The structural and helix reversal defects discussed above can form when nanosprings are rapidly relaxed after being stretched. To demonstrate this, the dynamics of a 4-kekulene nanospring (C15H17)400 is modeled. At time t=0, the stationary state of the stretched nanospring with a relative elongation h=L/L0=5.5 is considered. In this uniformly stretched state, the nanospring has length L=127.4 nm, and the axial and angular translational steps are Δz=3.19 Å and Δϕ=71∘, respectively. The number of helix coils is Nϕ=(N−1)Δϕ/2π=78.7. In the ground state (h=1), the nanospring has axial and angular steps Δz0=0.58 Å and Δϕ0=61∘, respectively, a length of L0=(N−1)Δz0=23.2 nm, and 67.6 coils.

To model the relaxation, the dynamics of a nanospring with free ends is considered. For this purpose the system of equations of motion (6) with the initial conditions

Xn(0)=Xn0,X˙n(0)=0,n=1,2,...,N,(12)

is numerically integrated, where the vector {Xn0}n=1N defines the stationary state of the initially stretched nanospring.

It is found that in the absence of interaction with the thermostat (at friction coefficient γ=0 and temperature T=0) the edges of the stretched nanospring converge with a constant velocity v=1866 m/s, see curve 1 in Fig. 12. The convergence occurs due to the formation of growing non-stretched regions with longitudinal Δz0 and angular pitch Δϕ0 at the ends of the helix. Without rotation of these end sections, their convergence would lead to the formation of Nϕ−Nϕ,0=11.6 coils with opposite twist inside the nanospring leading to the formation of helix reversal defects. In the absence of interaction with the thermostat, a very rapid contraction of the stretched nanospring is accompanied by a relatively slow rotation of the ends, which prevents the negative twist in the center of the chain from being fully eliminated. Consequently, two sections with negative twist form in the nanospring, see Fig. 13. Topological helix reversal defects form at the edges of these sections. In addition to these four defects, a structural defect (nanospring fracture) is formed.

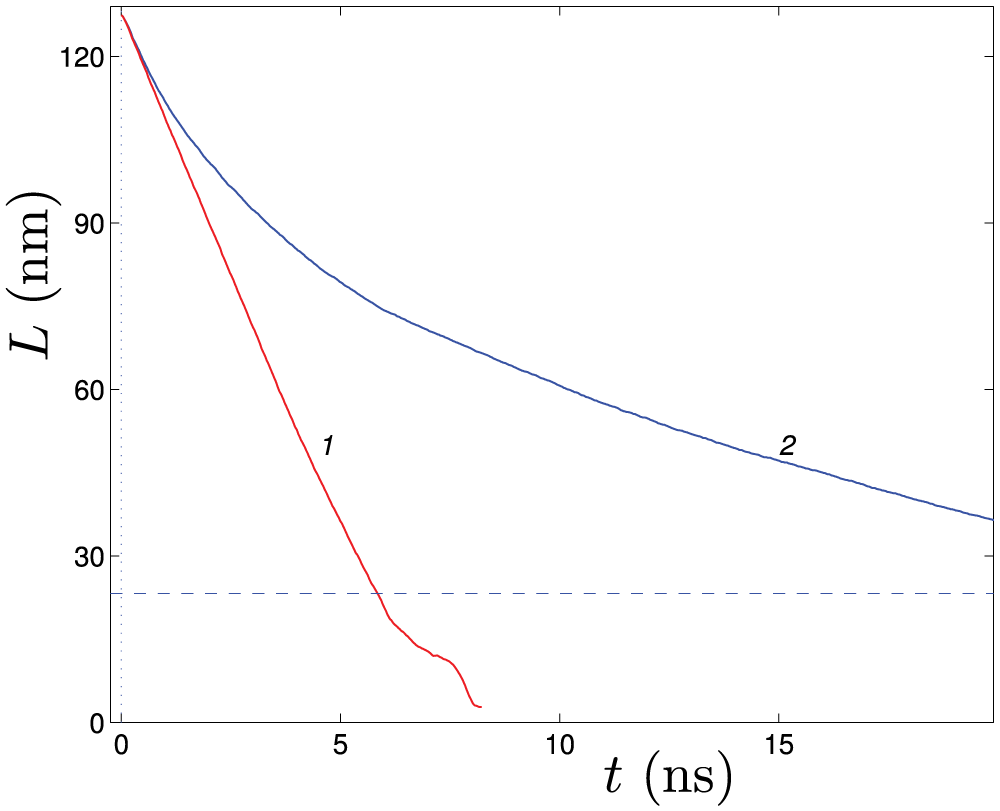
Figure 12: Relaxation of the 4-kekulene nanospring (C15H5)400 initially stretched up to h=5.5. The dependence of the nanospring length L on time t is shown. Curve 1 is obtained in the absence of interaction with the thermostat (γ=0, T=0), and curve 2 is obtained when the nanospring interacts with the thermostat (γ=0.1 ps−1, T=300 K). The dotted line shows the value of the equilibrium nanospring length L0

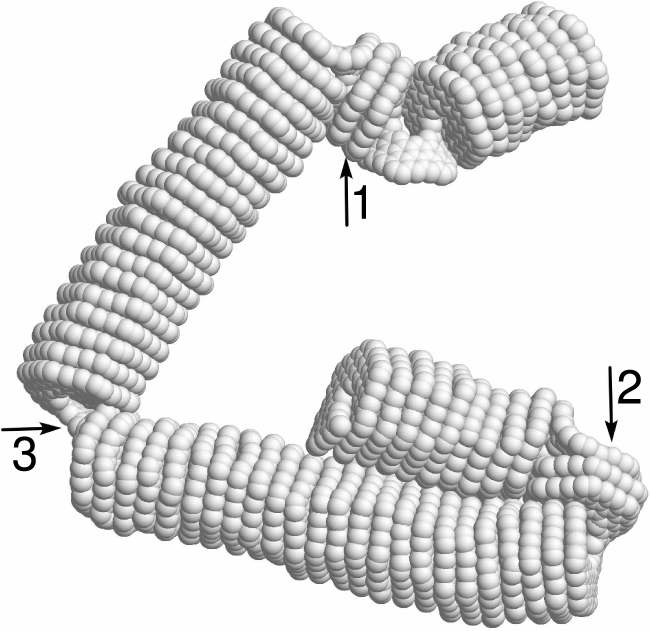
Figure 13: The structure of the initially stretched 4-kekulene nanospring (C15H5)400 after relaxation. The nanospring dynamics was simulated without considering the interaction with the thermostat. Arrows 1 and 2 show pairs of helix reversal defects, and arrow 3 shows the nanospring fracture

If the relaxation of the stretched nanospring takes place in a viscous medium, i.e., taking into account its interaction with the thermostat, viscosity leads to slowing down of the convergence of the ends, see curve 2 in Fig. 12. In this case, the convergence time is sufficient to remove the negative twist arising in the center of the nanospring due to the rotation of the ends. Therefore, the helix relaxes directly to its ground state and no defects are formed. Note that the friction coefficient value γ=0.1 ps−1 chosen for the simulation is relatively large and corresponds to the motion of the nanospring in water.

7  Twisting of Nanosprings

The helix reversal defect in a nanospring can also be obtained by twisting, which will be simulated for a nanospring of N=200 structural units starting with the ground state. The position of atoms of the first structural unit (n=1) are fixed, and the last structural unit (n=N) is rotated around the nanospring axis with a constant angular velocity. The system of equations of motion (6) is numerically integrate with the following boundary and initial conditions

X1(t)≡X10,xN,j(t)=cos⁡(ωt)xN,j0−sin⁡(ωt)yN,j0,yN,j(t)=sin⁡(ωt)xN,j0+cos⁡(ωt)yN,j0, j=1,...,NC,Xn(0)=Xn0, X˙n(0)=0,n=1,2,...,N,(13)

where ω defines the angular velocity of the last structural unit (n=N). The value |ω|=0.25 ps−1 is set.

The twisting of the nanospring starts at t=0 and ends at t=t0, when the twist angle ϕ=ωt0 is reached. Further modeling of the dynamics of the twisted nanospring with fixed values of x and y coordinates of the atoms of the last structural unit is carried out. After the system reached the equilibrium state, the average value of the total energy E¯ is found, and then the twisting energy of the helix is found

Et=E¯−E0−(3N−5)NCkBT,

where E0 is the ground state energy and T is the thermostat temperature.

The twist energy Et of the 4-kekulene and 4-coronene nanosprings as the function of the twist angle ϕ is shown in Fig. 14 by curves 1 and 2, respectively. For certainty, the nanosprings with a left-hand twist are taken; then for ϕ>0 the twist increases, while for ϕ<0 the nanospring is untwisted. When ϕ>0, the additional twist occurs uniformly with gradual decrease in the angular pitch of the nanospring and an increase in the axial pitch, see Fig. 15a. In this case, the energy of the nanospring increases with twist angle proportionally to ϕ2.

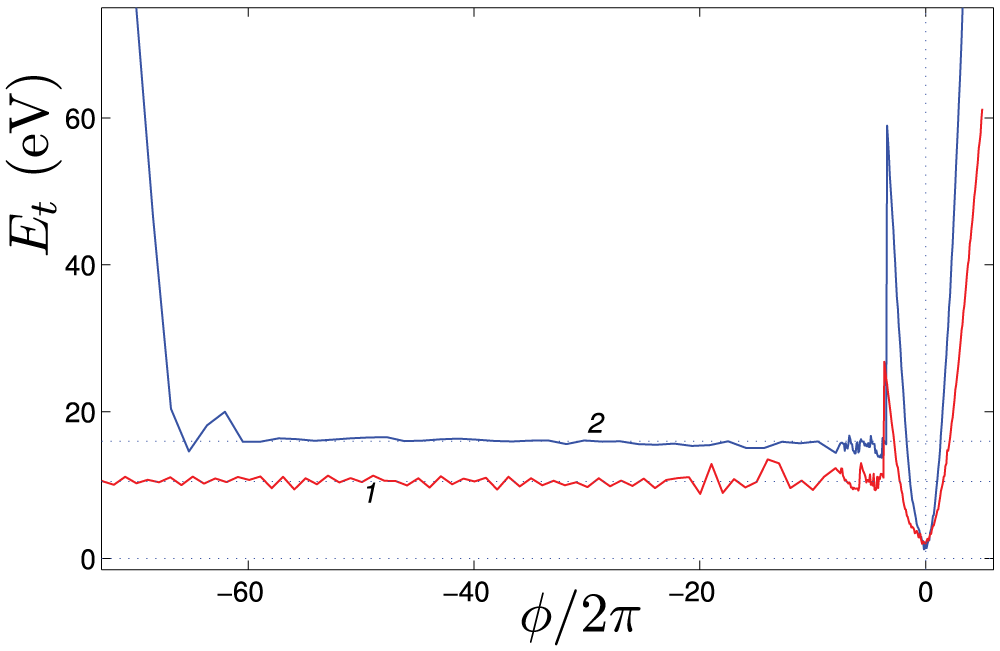
Figure 14: The energy Et of the twisted 4-kekulene (C15H5)200 (curve 1) and 4-coronene (C16H4)200 (curve 2) nanosprings as the function of the twist angle around the spiral axis. The dotted horizontal lines correspond to values Et=10.5 and 16 eV. The thermostat temperature is T=300 K

Figure 15: The structure of 4-coronene nanospring (C16H4)200 under twist angle ϕ: (a) ϕ=6.36π, (b) 0, (c) −6.36π, (d) −12.74π, (e) −51.0π, (f) −111.4π, and (g) −130.4π. The horizontal line at the bottom shows the fixation of the atoms of the first structural unit

When ϕ<0, the nanospring untwisting is also uniform at the beginning. The angular pitch increases and the longitudinal pitch decreases, see Fig. 15c. The energy of the nanospring increases proportionally to ϕ2 until it reaches a maximum value at ϕ=ϕ0 (for 4-coronene nanospring the critical value of the angle is ϕ0≈−7.2π), after which it drops sharply. At this point a helix reversal defect forms in the nanospring. A part of the macromolecule near its upper end obtains the right-handed twist and the remaining part maintains the left-handed twist, see Fig. 15d. Further unwinding practically does not lead to a change in the nanospring energy so that the dependence Et(ϕ) has a broad plateau, see Fig. 14. Further rotation of the upper end of the nanospring leads to the movement of the helix reversal defect toward the lower end of the nanospring. The propagation of the helix reversal defect occurs through the breaking and recovery of van der Waals bonds, and this process is discrete. However, the simulation is conducted in the presence of thermal fluctuations corresponding to 300 K, which smooth out the defect’s propagation. After complete transition of the nanospring from left- to right-handed shape, see Fig. 15d–g, the energy Et starts to grow proportionally to ϕ2, see Fig. 14.

8  Conclusion

A study was conducted to analyze the mechanical behavior of carbon nanosprings in the form of spiral macromolecules formed from l-kekulene and l-coronene molecules. This analysis was performed using molecular quasistatic (relaxational dynamics) and molecular dynamics simulations. The nanosprings were analyzed under axial compression, bending, and twisting. Earlier in the work [9], the peculiarities of tensile deformation were investigated.

The primary distinction between l-kekulene and l-coronene nanosprings lies in the presence or absence of the inner channel. Specifically, l-kekulene features an inner channel, while l-coronene does not. This structural difference results in a distinct mechanical response to external forces.

The primary findings of the present study can be outlined as follows.

•   The dimensionless heat capacity and the coefficient of axial thermal expansion were calculated in a wide range of temperatures, as shown in Fig. 3. The heat capacity increases with temperature linearly due to the soft anharmonicity of the van der Waals interactions between coils of the nanosprings. The coefficient of axial thermal expansion is as large as α≈5×10−5 K−1, which is significantly higher than that of many metals and alloys. This means that the use of carbon nanosprings in the production of temperature sensors is advantageous due to the thermal stability of l-kekulene and l-coronene molecules, which allows for sensors to function over a wide temperature range.

•   Nanosprings under axial compression have been shown to behave similarly to hinged elastic rods (see Fig. 5 for 4-coronene and Fig. 7 for 4-kekulene). They maintain a straight shape below the critical value of the compressive force, see panels (a), and demonstrate lateral buckling in the post-critical regime, see panels (b). It is evident from panels (c) that an even higher compressive force causes fracture of the nanosprings. As illustrated in Fig. 5a, 4-coronene nanosprings lacking an inner channel may exhibit multiple cracks. In contrast, Fig. 7d shows that for 4-kekulene, with an inner channel and consequently reduced bending stiffness, only a single crack is formed.

•   The bending of nanosprings initiates with their arching, which is elastic deformation, and ceases once the bending forces are eliminated. At a certain level of bending force, nanosprings undergo irreversible changes in shape. In Figs. 8 and 9, the folded equilibrium structures of the 3-kekulene and 4-kekulene nanosprings are shown. These structures are stabilized by the van der Waals interactions between the halves of the folded nanosprings. The folded structures exhibit even smaller potential energy than the straight nanosprings. In Fig. 10, another stable configuration of 4-kekulene nanospring is shown. This configuration is stabilized by the presence of a topological defect in the corner. This structure exhibits a higher potential energy than the straight nanospring.

•   Carbon nanosprings may exhibit helix reversal defects, separating the left-handed part from the right-handed part, as illustrated in Fig. 11. The energies of the equilibrium helix reversal defects and the angle between the axis of the adjacent halves of the nanosprings are given for l-coronene and l-kekulene nanosprings in Table 2.

•   Twisting of nanosprings increasing its twist, leads to quadratic growth of potential energy with twist angle. Twisting in the opposite direction is more interesting. The potential energy increases quadratically at first, but after reaching a specific twist angle, the energy of the nanospring drops sharply. At this stage, a helix reversal defect is formed, and a part of the nanospring acquires the opposite chirality. A subsequent twist leads to the movement of the helix reversal defect along the nanospring, ultimately resulting in a transformation of the entire structure to the opposite chirality. The structural transformation of the nanospring under twisting is illustrated in Fig. 15.

The results of this study show the unique behavior of carbon nanosprings when they are subjected to different types of deformation, such as compression, bending, and twisting. These deformation modes were not thoroughly explored in previous research. These results are particularly useful for the design of nanosensors that operate over a wide range of temperatures.

Acknowledgement: Sergey V. Dmitriev thanks the PRIORITY 2030 program of the Ufa State Petroleum Technological University (writing—review and editing, data curation).

Funding Statement: For Alexander V. Savin, the research work was funded by the Russian Science Foundation (RSF), grant No. 25-73-20038 (conceptualization, methodology, manuscript writing).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Alexander V. Savin; methodology, Alexander V. Savin; software, Elena A. Korznikova; investigation, Sergey V. Dmitriev; data curation, Sergey V. Dmitriev; writing—original draft preparation, Alexander V. Savin; writing—review and editing, Sergey V. Dmitriev. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yang S, Chen X, Motojima S. Morphology of the growth tip of carbon microcoils/nanocoils. Diam Relat Mater. 2004;13(11–12):2152–5. doi:10.1016/j.diamond.2004.06.014. [Google Scholar] [CrossRef]

2. Qian Y, Jiang S, Li Y, Yi Z, Zhou J, Tian J, et al. Water-induced growth of a highly oriented mesoporous graphitic carbon nanospring for fast potassium-ion adsorption/intercalation storage. Angew Chem. 2019;58(50):18108–15. doi:10.1002/anie.201912287. [Google Scholar] [PubMed] [CrossRef]

3. Ghaderi SH, Hajiesmaili E. Molecular structural mechanics applied to coiled carbon nanotubes. Comput Mater Sci. 2012;55:344–9. doi:10.1016/j.commatsci.2011.11.016. [Google Scholar] [CrossRef]

4. Poggi MA, Boyles JS, Bottomley LA, McFarland AW, Colton JS, Nguyen CV, et al. Measuring the compression of a carbon nanospring. Nano Lett. 2004;4(6):1009–16. doi:10.1021/nl0497023. [Google Scholar] [CrossRef]

5. Liu J, Lu YL, Tian M, Li F, Shen J, Gao Y, et al. The interesting influence of nanosprings on the viscoelasticity of elastomeric polymer materials: simulation and experiment. Adv Funct Mater. 2013;23(9):1156–63. doi:10.1002/adfm.201201438. [Google Scholar] [CrossRef]

6. Tang S, Ding G, Xie X, Chen J, Wang C, Ding X, et al. Nucleation and growth of single crystal graphene on hexagonal boron nitride. Carbon. 2012;50(1):329–31. doi:10.1016/j.carbon.2011.07.062. [Google Scholar] [CrossRef]

7. Nakakuki Y, Hirose T, Sotome H, Miyasaka H, Matsuda K. Hexa-peri-hexabenzo[7]helicene: homogeneously π-extended helicene as a primary substructure of helically twisted chiral graphenes. J Am Chem Soc. 2018;140(12):4317–26. doi:10.1021/jacs.7b13412. [Google Scholar] [PubMed] [CrossRef]

8. Nakakuki Y, Hirose T, Matsuda K. Synthesis of a helical analogue of kekulene: a Flexible π-expanded helicene with large helical diameter acting as a soft molecular spring. J Am Chem Soc. 2018;140(45):15461–9. doi:10.1021/jacs.8b09825. [Google Scholar] [PubMed] [CrossRef]

9. Savin AV, Dmitriev SV. Inhomogeneous elastic stretching of carbon nanosprings. Comput Mater Sci. 2024;244(14):113254. doi:10.1016/j.commatsci.2024.113254. [Google Scholar] [CrossRef]

10. Zhao Y, Zhang C, Kohler DD, Scheeler JM, Wright JC, Voyles PM, et al. Supertwisted spirals of layered materials enabled by growth on non-Euclidean surfaces. Science. 2020;370(6515):442–5. doi:10.1126/science.abc4284. [Google Scholar] [PubMed] [CrossRef]

11. Bie Z, Liu X, Tao J, Zhu J, Yang D, He X. Investigation of carbon nanosprings with the tunable mechanical properties controlled by the defect distribution. Carbon. 2021;179:240–55. doi:10.1016/j.carbon.2021.04.035. [Google Scholar] [CrossRef]

12. Bie Z, Deng Y, Liu X, Zhu J, Tao J, Shi X, et al. The controllable mechanical properties of coiled carbon nanotubes with Stone-Wales and vacancy defects. Nanomater. 2023;13(19):2656. doi:10.3390/nano13192656. [Google Scholar] [PubMed] [CrossRef]

13. Sharifian A, Fareghi P, Baghani M, Odegard GM, van Duin ACT, Rajabpour A, et al. Unveiling novel structural complexity of spiral carbon nanomaterials: review on mechanical, thermal, and interfacial behaviors via molecular dynamics. J Mol Struct. 2025;1321:139837. doi:10.1016/j.molstruc.2024.139837. [Google Scholar] [CrossRef]

14. Nakano T, Okamoto Y. Synthetic helical polymers: conformation and function. Chem Rev. 2001;101(12):4013–38. doi:10.1021/cr0000978. [Google Scholar] [PubMed] [CrossRef]

15. Yashima E, Maeda K, Iida H, Furusho Y, Nagai K. Helical Polymers: synthesis, structures, and functions. Chem Rev. 2009;109(11):6102–211. doi:10.1021/cr900162q. [Google Scholar] [PubMed] [CrossRef]

16. Ikai T, Miyoshi S, Oki K, Saha R, Hijikata Y, Yashima E. Defect-Free synthesis of a fully π-conjugated helical ladder polymer and resolution into a pair of enantiomeric helical ladders. J Mol Biol. 2023;62(20):e202301962. doi:10.26434/chemrxiv-2023-hqk71. [Google Scholar] [CrossRef]

17. Qiu Y, Wei X, Lam JWY, Qiu Z, Tang BZ. Chiral nanostructures from artificial helical polymers: recent advances in synthesis, regulation, and functions. ACS Nano. 2025;19(1):229–80. doi:10.1021/acsnano.4c14797. [Google Scholar] [PubMed] [CrossRef]

18. Lei X, Koyane J, Lu T, Matsuzaki K, Yan Y, Shi J, et al. Mechanical and geometric properties of nanosprings based on carbon nanotubes with dislocation dipoles. ACS Appl Nano Mater. 2025;8(18):9192–200. doi:10.1021/acsanm.5c00619. [Google Scholar] [CrossRef]

19. Feng H, Cai K, Shi J, Zhang Y. A high-frequency nanoscale positioner driven by an external electric field: a molecular dynamics study. Phys Chem Chem Phys. 2025;27(14):7326–35. doi:10.1039/d4cp04379k. [Google Scholar] [PubMed] [CrossRef]

20. Wan J, Cai K, Kang Y, Luo Y, Qin Q. Adjustable gas adsorption and desorption via a self-shrinking nanoscroll. Appl Phys Lett. 2023;123(23):233501. doi:10.1063/5.0175953. [Google Scholar] [CrossRef]

21. Xu X, Xiao H, Ouyang T, Zhong J. Improving the thermoelectric properties of carbon nanotubes through introducing graphene nanosprings. Curr Appl Phys. 2020;20(1):150–4. doi:10.1016/j.cap.2019.10.018. [Google Scholar] [CrossRef]

22. Avdoshenko S, Koskinen P, Sevincli H, Popov AA, Rocha CG. Topological signatures in the electronic structure of graphene spirals. Sci Rep. 2013;3(1):1632. doi:10.1038/srep01632. [Google Scholar] [PubMed] [CrossRef]

23. Tan J, Zhang X, Liu W, He X, Zhao M. Strain-induced tunable negative differential resistance in triangle graphene spirals. Nanotechnology. 2018;29(20):205202. doi:10.1088/1361-6528/aab1d9. [Google Scholar] [PubMed] [CrossRef]

24. Zhang X, Zhao M. Strain-induced phase transition and electron spin-polarization in graphene spirals. Sci Rep. 2014;4(1):5699. doi:10.1038/srep05699. [Google Scholar] [PubMed] [CrossRef]

25. Atanasov V, Saxena A. Helicoidal graphene nanoribbons: chiraltronics. Phys Rev B. 2015;92(3):035440. doi:10.1103/physrevb.92.035440. [Google Scholar] [CrossRef]

26. Xu X, Liu B, Zhao W, Jiang Y, Liu L, Li W, et al. Mechanism of mechanically induced optoelectronic and spintronic phase transitions in 1D graphene spirals: insight into the role of interlayer coupling. Nanoscale. 2017;9(27):9693–700. doi:10.1039/c7nr03432f. [Google Scholar] [PubMed] [CrossRef]

27. Korhonen T, Koskinen P. Electromechanics of graphene spirals. AIP Adv. 2014;4(12):127125. doi:10.1063/1.4904219. [Google Scholar] [CrossRef]

28. Porsev V, Evarestov R. Riemann surfaces of carbon as graphene nanosolenoids magnetic properties of zig-zag-edged hexagonal nanohelicenes: a quantum chemical study. Nanomater. 2023;13(3):415. doi:10.3390/nano13030415. [Google Scholar] [PubMed] [CrossRef]

29. Xu F, Yu H, Sadrzadeh A, Yakobson BI. Riemann surfaces of carbon as graphene nanosolenoids. Nano Lett. 2016;16(1):34–9. doi:10.1021/acs.nanolett.5b02430. [Google Scholar] [PubMed] [CrossRef]

30. Lin Y, Shi Q, Hao Y, Song Z, Zhou Z, Fu Y, et al. The effect of non-uniform pitch length and spiraling pathway on the mechanical properties of coiled carbon nanotubes. Int J Mech Sci. 2023;257:108532. doi:10.1016/j.ijmecsci.2023.108532. [Google Scholar] [CrossRef]

31. Liu ZP, Guo YD, Yan XH, Zeng HL, Mou XY, Wang ZR, et al. A metal-semiconductor transition in helical graphene nanoribbon. J Appl Phys. 2019;126:144303. [Google Scholar]

32. Thakur R, Ahluwalia PK, Kumar A, Sharma R. Stability and electronic properties of bilayer graphene spirals. Physica E. 2021;129:114638. doi:10.1016/j.physe.2021.114638. [Google Scholar] [CrossRef]

33. Zhou Z, Yan L, Wang XM, Zhang D, Yan JY. The sensitive energy band structure and the spiral current in helical graphenes. Results Phys. 2022;35(5696):105351. doi:10.1016/j.rinp.2022.105351. [Google Scholar] [CrossRef]

34. Zhang K, Duan J, Li C, Song C, Chen Z. How do DNA molecular springs modulate protein-protein interactions: experimental and theoretical results. Biochemistry. 2024;63(24):3369–80. doi:10.1021/acs.biochem.4c00280. [Google Scholar] [PubMed] [CrossRef]

35. Yang D, Huang R, Zou B, Wang R, Wang Y, Ang EH, et al. Unraveling nanosprings: morphology control and mechanical characterization. Mater Horiz. 2024;11(15):3500–27. doi:10.1039/d4mh00503a. [Google Scholar] [PubMed] [CrossRef]

36. Karabacak AY, Oguz HZ, Kart SO, Kart HHU. Mechanical properties of carbon and silicon core-shell nanosprings: a molecular dynamics simulation study. Physica B Condens Matter. 2025;716(3):417673. doi:10.1016/j.physb.2025.417673. [Google Scholar] [CrossRef]

37. Porsev VV, Bandura AV, Lukyanov SI, Evarestov RA. Expanded hexagonal nanohelicenes of zigzag morphology under elastic strain: a quantum chemical study. Carbon. 2019;152(3):755–65. doi:10.1016/j.carbon.2019.06.036. [Google Scholar] [CrossRef]

38. Zhan H, Zhang G, Yang C, Gu YT. Graphene helicoid: the distinct properties promote application of graphene related materials in thermal management. Phys Chem C. 2018;122(14):7605–12. doi:10.1021/acs.jpcc.8b00868. [Google Scholar] [CrossRef]

39. Norouzi S, Fakhrabadi MMS. Anisotropic nature of thermal conductivity in graphene spirals revealed by molecular dynamics simulations. J Phys Chem Solids. 2020;137(11):109228. doi:10.1016/j.jpcs.2019.109228. [Google Scholar] [CrossRef]

40. Sharifian A, Karbaschi T, Rajabpour A, Baghani M, Wu J, Baniassadi M. Insights into thermal characteristics of spiral carbon-based nanomaterials: from heat transport mechanisms to tunable thermal diode behavior. Int J Heat Mass Tran. 2022;189(6):122719. doi:10.1016/j.ijheatmasstransfer.2022.122719. [Google Scholar] [CrossRef]

41. Li H, Hassanzadeh afrouzi H, Zahra MMA, Bashar BS, Fathdal F, Hadrawi SK, et al. A comprehensive investigation of thermal conductivity in of monolayer graphene, helical graphene with different percentages of hydrogen atom: a molecular dynamics approach. Colloid Surface A. 2023;656(A):130324. doi:10.1016/j.colsurfa.2022.130324. [Google Scholar] [CrossRef]

42. Wu J, He J, Odegard GM, Nagao S, Zheng Q, Zhang Z. Giant stretchability and reversibility of tightly wound helical carbon nanotubes. J Am Chem Soc. 2013;135(37):13775–13785. doi:10.1021/ja404330q. [Google Scholar] [PubMed] [CrossRef]

43. Sestak P, Wu J, He J, J P, Zhang Z. Extraordinary deformation capacity of smallest carbohelicene springs. Phys Chem Chem Phys. 2015;17(28):18684–18690. doi:10.1039/c5cp02043c. [Google Scholar] [PubMed] [CrossRef]

44. Zhan H, Zhang Y, Yang C, Zhang G, Gu Y. Graphene helicoid as novel nanospring. Carbon. 2017;120(5496):18684–264. doi:10.1016/j.carbon.2017.05.044. [Google Scholar] [CrossRef]

45. Zhan H, Zhang G, Yang C, Gu Y. Breakdown of Hooke’s law at nanoscale-2D materials-based nanospring. Nanoscale. 2018;10(40):18961–8. doi:10.1039/c8nr04882g. [Google Scholar] [PubMed] [CrossRef]

46. Norouzi S, Fakhrabadi MMS. Nanomechanical properties of single- and double-layer graphene spirals: a molecular dynamics simulation. Appl Phys A. 2019;125(5):321. doi:10.1007/s00339-019-2623-8. [Google Scholar] [CrossRef]

47. Zhu C, Ji J, Zhang Z, Dong S, Wei N, Zhao J. Huge stretchability and reversibility of helical graphenes using molecular dynamics simulations and simplified theoretical models. Mech Mater. 2021;153:103683. doi:10.1016/j.mechmat.2020.103683. [Google Scholar] [CrossRef]

48. Sharifian A, Moshfegh A, Javadzadegan A, Afrouzi HH, Baghani M, Baniassadi M. Hydrogenation-controlled mechanical properties in graphene helicoids: exceptional distribution-dependent behavior. Phys Chem Chem Phys. 2019;21(23):12423–33. doi:10.1039/c9cp01361j. [Google Scholar] [PubMed] [CrossRef]

49. Savin AV, Kikot IP, Mazo MA, Onufriev AV. Two-phase stretching of molecular chains. Proc Natl Acad Sci U S A. 2013;110(8):2816–21. doi:10.1073/pnas.1218677110. [Google Scholar] [PubMed] [CrossRef]

50. Afanasyev AY, Onufriev AV. Stretching of long double-stranded DNA and RNA described by the same approach. J Chem Theory Comput. 2022;18(6):3911–20. doi:10.1021/acs.jctc.1c01221. [Google Scholar] [PubMed] [CrossRef]

51. Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271(5250):795–9. doi:10.1126/science.271.5250.795. [Google Scholar] [PubMed] [CrossRef]

52. Babicheva RI, Bukreeva KA, Dmitriev SV, Zhou K. Discontinuous elastic strain observed during stretching of NiAl single crystal nanofilms. Comp Mater Sci. 2013;79(2):52–5. doi:10.1016/j.commatsci.2013.06.007. [Google Scholar] [CrossRef]

53. Babicheva RI, B KA, Dmitriev SV, Mulyukov RR, Zhou K. Strengthening of NiAl nanofilms by introducing internal stresses. Intermetallics. 2013;43:171–6. doi:10.1016/j.intermet.2013.07.024. [Google Scholar] [CrossRef]

54. Bukreeva KA, Babicheva RI, Dmitriev SV, Zhou K, Mulyukov RR. Negative stiffness of the FeAl intermetallic nanofilm. Phys Solid State. 2013;55(9):1963–7. doi:10.1134/s1063783413090072. [Google Scholar] [CrossRef]

55. Wu J, Shi Q, Zhang Z, Wu H, Wang C, Ning F, et al. Nature-inspired entwined coiled carbon mechanical metamaterials: molecular dynamics simulations. Nanoscale. 2018;10(33):15641–15653. doi:10.1039/c8nr04507k. [Google Scholar] [PubMed] [CrossRef]

56. Dmitriev SV, Baimova JA, Savin AV, Kivshar YS. Ultimate strength, ripples, sound velocities, and density of phonon states of strained graphene. Comput Mater Sci. 2012;53(1):194–203. doi:10.1016/j.commatsci.2011.08.019. [Google Scholar] [CrossRef]

57. Liu R, Zhao J, Wang L, Wei N. Nonlinear vibrations of helical graphene resonators in the dynamic nano-indentation testing. Nanotechnology. 2020;31(2):025709. doi:10.1088/1361-6528/ab4760. [Google Scholar] [PubMed] [CrossRef]

58. Mokhalingam A, Gupta SS. Helical single-walled carbon nanotubes under mechanical and electrostatic loading. Carbon Trends. 2022;9(4):100204. doi:10.1016/j.cartre.2022.100204. [Google Scholar] [CrossRef]

59. Cornell WD, Cieplak WP, Bayly CI, Gould IR, Merz KM, Ferguson DM, et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. 1995;117(19):5179–5197. doi:10.1021/ja00124a002. [Google Scholar] [CrossRef]

60. Savin AV, Kivshar YS, Hu B. Suppression of thermal conductivity in graphene nanoribbons with rough edges. Phys Rev B. 2010;82(19):195422. doi:10.1103/physrevb.82.195422. [Google Scholar] [CrossRef]

61. Lisovenko DS, Baimova JA, Rysaeva LK, Gorodtsov VA, Rudskoy AI, Dmitriev SV. Equilibrium diamond-like carbon nanostructures with cubic anisotropy: elastic properties. Phys Status Solidi (B) Basic Res. 2016;253(7):1295–1302. doi:10.1002/pssb.201600049. [Google Scholar] [CrossRef]

62. Pavlov IS, Galiakhmetova LK, Kudreyko AA, Dmitriev SV. Mobility of dislocations in carbon nanotube bundles. Mater Today Commun. 2024;40(6348):110094. doi:10.1016/j.mtcomm.2024.110094. [Google Scholar] [CrossRef]

63. Ilgamov MA, Aitbaeva AA, Pavlov IS, Dmitriev SV. Carbon nanotube under pulsed pressure. Facta Univ Ser Mech Eng. 2024;22(2):275–92. doi:10.22190/fume230820049i. [Google Scholar] [CrossRef]

64. Andrukhova OV, Ovcharov AA, Andrukhova T, Morkina AY. Evolution of the single-wall carbon nanotubes bundle structure under compressive deformation. Mech Solids. 2025;60(2):872–82. doi:10.1134/s002565442460569x. [Google Scholar] [CrossRef]

65. Setton R. Carbon nanotubes-II. Cohesion and formation energy of cylindrical nanotubes. Carbon. 1996;34(1):69–75. doi:10.1016/0008-6223(95)00136-0. [Google Scholar] [CrossRef]

66. Lindsay LR, Broido DA. Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys Rev B. 2010;81(20):205441. doi:10.1103/physrevb.82.209903. [Google Scholar] [CrossRef]

67. Goverapet Srinivasan S, van Duin ACT, Ganesh P. Development of a ReaxFF potential for carbon condensed phases and its application to the thermal fragmentation of a large fullerene. J Phys Chem A. 2015;119(4):571–80. doi:10.1021/jp510274e. [Google Scholar] [PubMed] [CrossRef]

68. Brenner DW, Shenderova OA, Harrison JA, Stuart SJ, Ni B, Sinnott SB. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J Phys Condens Matter. 2002;14(4):783–802. doi:10.1088/0953-8984/14/4/312. [Google Scholar] [CrossRef]

69. Nikitin A, Ogasawara H, Mann DA, Denecke R, Zhang Z, Dai H, et al. Hydrogenation of single-walled carbon nanotubes. Phys Rev Lett. 2005;95(22):225507. doi:10.1103/physrevlett.95.225507. [Google Scholar] [PubMed] [CrossRef]

70. Stuart SJ, Tutein AB, Harrison JA. A reactive potential for hydrocarbons with intermolecular interactions. J Chem Phys. 2000;112(14):6472–86. doi:10.1063/1.481208. [Google Scholar] [CrossRef]

71. Polyakova PV, Murzaev RT, Baimova JA. Mechanical properties of diamane: orientation dependence of strength and fracture strain. Appl Surf Sci. 2025;681(3):161441. doi:10.1016/j.apsusc.2024.161441. [Google Scholar] [CrossRef]

72. Polyakova PV, Murzaev RT, Lisovenko DS, Baimova JA. Elastic constants of graphane, graphyne, and graphdiyne. Comput Mater Sci. 2024;244(3):113171. doi:10.1016/j.commatsci.2024.113171. [Google Scholar] [CrossRef]

73. Polyakova PV, Murzaev RT, Baimova JA. Determination of graphyne elasticity constants by the molecular dynamics method. J Appl Mech Tech Phys. 2023;64(6):1097–9. doi:10.1134/s0021894423060202. [Google Scholar] [CrossRef]

74. Bourque AJ, Rutledge GC. Empirical potential for molecular simulation of graphene nanoplatelets. J Chem Phys. 2018;148(14):144709. doi:10.1063/1.5023117. [Google Scholar] [PubMed] [CrossRef]

75. Fletcher R, Reeves C. Function minimization by conjugate gradients. Comput J. 1964;7(2):149–54. [Google Scholar]

76. Shanno DF, Phua KH. Algorithm 500: minimization of unconstrained multivariate functions [E4]. ACM Trans Math Software. 1976;2(1):87–94. doi:10.1145/355666.355673. [Google Scholar] [CrossRef]

77. Verlet L. Computer “Experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys Rev. 1967;159(1):98–103. doi:10.1103/physrev.159.98. [Google Scholar] [CrossRef]

78. Schafmeister CE, LaPorte SL, Miercke LJ, Stroud RM. A designed four helix bundle protein with native-like structure. Nat Struct Mol Biol. 1997;4:1039–46. [Google Scholar]

79. Liu J, Deng Y, Zheng Q, Cheng CS, Kallenbach NR, Lu M. A parallel coiled-coil tetramer with offset helices. Biochemistry. 2006;45(51):15224–31. doi:10.1021/bi061914m. [Google Scholar] [PubMed] [CrossRef]

80. Holt DB, Farmer BL. Modeling of helix reversal defects in polytetrafluoroethylene II. Molecular dynamics simulations. Polymer. 1999;40(16):4673–84. doi:10.1016/s0032-3861(99)00076-2. [Google Scholar] [CrossRef]

81. Rey-Tarrio F, Rodriguez R, Quinoa E, Freire F. Screw sense excess and reversals of helical polymers in solution. Nat Commun. 2023;14(1):1742. doi:10.1038/s41467-023-37405-z. [Google Scholar] [PubMed] [CrossRef]

82. Jeon Y, Goh B, Choi J. Nanomechanical investigation of deformation behavior of π–π stacked helical polymers. Int J Mech Sci. 2025;290:110100. doi:10.1016/j.ijmecsci.2025.110100. [Google Scholar] [CrossRef]