A Micromechanics-Based Softening Hyperelastic Model for Granular Materials: Multiscale Insights into Strain Localization and Softening

1  Introduction

Granular materials, such as sands, soils, and rocks, consist of discrete solid particles and interstitial voids, exhibiting significant heterogeneity, nonlinearity, and complex microscopic contact behaviors. These characteristics typically lead to intricate mechanical responses, including phenomena like strain localization and strain softening [1–3]. Such behaviors are closely related to the localized failure of granular materials, which is one of the primary causes of civil engineering structural failures and natural disasters like landslides and mudslides. Therefore, a thorough investigation and understanding of complex mechanical behaviors of granular materials remain critical tasks in the field of granular material mechanics.

To characterize the mechanical behaviors of granular materials, the elasto-plastic models [4–7] based on continuum mechanics have been developed, such as the Mohr-Coulomb, Drucker-Prager, and Lade-Duncan models. These models typically require some fundamental components, including the yield function, ultimate failure (plastic limit) surface, flow rule, and hardening/softening law. However, determining these components accurately often poses significant challenges. Therefore, in recent years, hyperelastic models [8–12] have also been employed to characterize the mechanical behaviors of granular materials. For instance, Houlsby et al. [8] developed a hyperelastic model that satisfies thermodynamic requirements by assuming the elastic modulus as a power function of the mean stress. Jiang and Liu [9] derived a generalized granular elastic model that accounts for yielding and dilatancy via thermodynamic instability and pressure-dependent elastic modulus. Xiao et al. [12] presented an anisotropic hyperelastic model for granular materials, predicting nonlinear elasticity and strength criterion through a unified thermodynamic approach. For the localized failure characteristics of granular materials, it is a critical challenge to accurately describe their strain localization and strain softening. Volokh [13,14] proposed a concept based on a hyperelastic model with softening, offering a novel approach based on the following principles: (1) there is a limit to the strain energy for real materials; (2) the strain energy of real materials is a function of the ideal material’s strain energy. As the strain increases (assuming it tends towards infinity), the strain energy of real materials will approach the limit value, and their stress-strain relationship will exhibit softening. Volokh’s model implements damage concepts through the energy threshold mechanism, eliminating the need for complex damage variables and evolution equations. It is noted that the Volokh softening hyperelastic model is specifically proposed for brittle materials or biological materials. Furthermore, considering that granular materials primarily have shear deformation and localized failure, Chang et al. [10] also proposed a softening hyperelastic model for granular materials based on Volokh’s model to simulate strain localization and strain softening. The softening hyperelastic models offer distinct advantages due to their clear conceptual framework, straightforward formulation, and ease of numerical implementation.

It is noted that the aforementioned models are predominantly macroscopic and phenomenological, and their parameters are typically calibrated to fit macroscopic stress-strain curves, lacking a direct, explicit connection to the underlying microstructure of granular materials. However, studies have proven that the mechanical behaviors of granular materials are profoundly influenced by their microstructural characteristics. For instance, the width of shear bands in granular materials is a function of the particle size [15]. Owing to the randomness and variety of the microstructure, it causes complex inter-particle interactions in the granular system, which give rise to complex macroscopic mechanical behaviors in turn, such as strain localization and strain softening. Therefore, to obtain a deeper understanding of macroscopic mechanical behaviors, it is essential to accurately characterize the influences of microstructural features at the micro scale.

To bridge the micro-macro scale, current strategies can be broadly categorized into three approaches: (1) the purely discrete approach, like the discrete element method (DEM) [16,17], (2) concurrent multiscale coupling, like FEM/DEM [18–20], and (3) microstructure-informed continuum models [6,21–23]. The DEM provides the most direct simulation of granular mechanics by explicitly describing particle interactions. However, its high computational cost severely limits its application to engineering-scale boundary value problems [15,18]. The coupled FEM/DEM approach aims to balance accuracy and cost by introducing DEM in critical regions into a continuum framework. Despite its potential, this technique requires complex operations like domain partitioning and cross-scale data exchange, limiting its practical application in engineering design. The microstructure-informed continuum model offers a distinct multiscale approach. It avoids the need to explicitly describe countless particles or manage complex concurrent coupling. Instead, it introduces key micromechanical characteristics directly into a computationally efficient continuum constitutive framework. This strategy achieves a balance, retaining a direct connection to granular micromechanics while enabling the simulation of large-scale geotechnical structures.

This paper considers a microstructure-informed approach by integrating macro-scale softening hyperelasticity with micromechanical characteristics, and first proposes a micromechanics-based softening hyperelastic model of granular materials. This model offers two key advantages: (1) within the hyperelastic framework, it has a clear conceptualization, straightforward formulation, and ease of numerical implementation; (2) it explicitly incorporates microstructural information at the micro scale to reveal its influences on macroscopic mechanical behaviors of granular materials. The formulation of the proposed model is derived by considering an isotropic directional contact distribution density and three specific microstructures of granular materials, with hyperelastic constitutive modulus tensors explicitly developed. Given the complexity of granular materials, this study establishes a foundational model by focusing on dry sands. This choice is strategic because dry sands exhibit a well-defined critical state. This aspect is central to their mechanical behavior, and the proposed model explicitly incorporates to describe the residual strength after softening. This focused scope needs deliberate simplifications, ignoring pore fluid, chemical bonding, or complex particle shapes, etc. Concentrating on dry, cohesionless sands, this study can more clearly investigate how basic microstructural parameters influence the critical state, including strain softening and localization, thus providing a benchmark for future extensions.

It should be noted that this study adopts a microstructure-informed method to construct a macroscopic constitutive model, which is fundamentally different from a strictly bottom-up, concurrent multiscale simulation. As noted by Talebi et al. [24], achieving fully consistent scale-bridging during localized failure is challenging. The proposed model offers a practical and complementary approach. It does not attempt to resolve this challenge in real-time but incorporates key microstructural information, such as the internal length and contact stiffness, into the model parameters. This strategy ensures high computational efficiency and engineering practicality, and retains its transparent connection between macroscopic responses and micro-parameters. However, its limitations also result from the idealized assumptions. The highly idealized microstructures limit the model’s capability to capture the complex fabric, particle shape distribution, and force chain evolution in natural soils or sands. Specifically, this simplification makes it challenging to spontaneously simulate the asymmetric initiation and propagation of shear bands often observed in natural materials due to initial fabric heterogeneity. Therefore, these limitations constitute the necessary compromise for achieving the model’s advantages in conceptual clarity and computational performance.

Furthermore, the machine learning alternatives [25] point to a promising paradigm for fracture modeling. These data-driven techniques offer distinct advantages in handling experimental noise, solving inverse problems, and naturally accounting for uncertainties. The physics-based path taken in this study and the data-driven approaches are not mutually exclusive but rather complementary. The proposed model provides transparent physical insights and microstructural relevance, while machine learning methods hold great potential for managing complexity and uncertainty. Integrating the key physical framework of the proposed model with machine learning techniques presents an important direction for future study.

Besides, the numerical implementation of this study is achieved by the User Material (UMAT) subroutine in the Abaqus framework. Numerical simulations are conducted to evaluate the model’s capability to capture strain localization and strain softening, as well as to investigate the influences of microstructural information on these phenomena.

2  The Micromechanics-Based Softening Hyperelastic Model

Volokh [13,14] presented a softening hyperelasticity approach for modeling brittle and soft material failure. In this approach, a strain energy density of hyperelastic materials with softening is defined by

ψ(W)=Φ−Φe−W/Φ(1)

where W is the strain energy density of an intact material and Φ is the critical failure energy density which indicates that materials have limited strain energy, and Eq. (1) can control material softening where ψ(W=∞)=Φ. In essence, Volokh’s model is a specialized mathematical realization of damage mechanics concepts. At the same time, it significantly simplifies and restructures traditional damage theories by using an energy threshold mechanism. This approach eliminates the need for explicit damage variables and complex evolution equations.

In previous studies [10,13,14], the strain energy density W is used for the isotropic Hookean model. However, owing to the discrete nature of granular materials at the micro scale, how to correlate the strain energy density W with the discrete information is a key challenge. In the micromechanical method of granular materials, it first considers a material point P as a microstructural representative volume element (RVE). Then, consider two particles m and n as shown in Fig. 1, with position coordinate vectors xim and xin, respectively. The displacement of particle m can be expressed using a Taylor series expansion of the displacement of particle n by

uim=uin+ui,jna(xjm−xjn)=uin+ui,jnaLja(2)

where uin and uim are respectively displacements of particles n and m, the superscript a denotes the a-th particle pair between particles n and m, and Lja is the branch vector connecting the centers of particles n and m. Then, the relative displacement between the two particles n and m can then be written as

Δui=uim−uin=ui,jnaLja=(εija+u[i,j]na)Lja(3)

where εija=1/2(ui,jna+uj,ina) is the particle-scale strain tensor, and u[i,j]na=1/2(ui,jna−uj,ina) represents the antisymmetric part of ui,jna. It is worth noting that the higher-order terms of the displacement are ignored here.

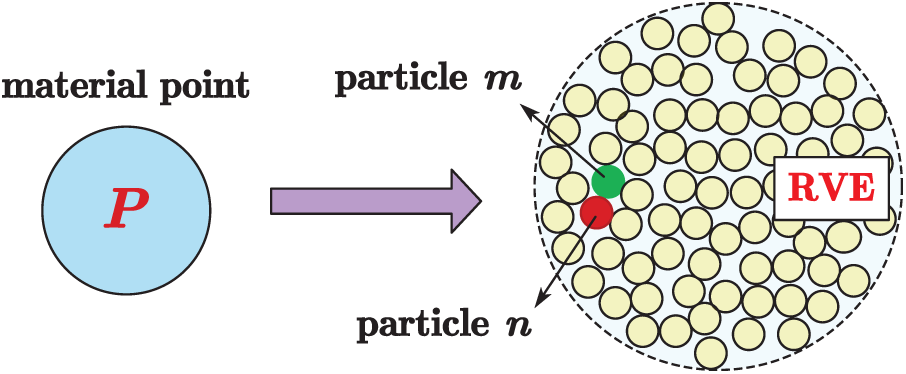
Figure 1: Schematic diagram for a material point P and its microstructural representative volume element V

In previous studies [6,23], a microscopic strain energy in the RVE is defined by

wa=12kn(Δuini)2+12kt(Δuiti)2+12ks(Δuisi)2(4)

where ni is a unit vector normal to the contact plane, and the other two orthogonal unit vectors, ti and si. kn, kt, ks are the normal, two tangential contact stiffness parameters, respectively. And the unit vectors ni, ti and si are written by

{n=cos⁡αe1+sin⁡αcos⁡βe2+sin⁡αsin⁡βe3t=dndα=−sin⁡αe1+cos⁡αcos⁡βe2+cos⁡αsin⁡βe3s=n×t=−sin⁡βe2+cos⁡βe3(5)

The macroscopic strain energy density W of material point P is a sum of the microscopic strain energy in its RVE, so the macroscopic strain energy density is expressed as the volume average of the microscopic strain energy:

W=1V∑a=1nwa(6)

where Σ is the sum over total contacts n in the RVE V. Then, substituting Eqs. (3) and (4) into Eq. (6), the macroscopic strain energy density can be written by

W=1V∑a=1n[12kn(Δuini)2+12kt(Δuiti)2+12kt(Δuiti)2](7)

Then, the constitutive modulus tensor of the micromechanics-based softening hyperelastic model are obtained by

Dijkl=∂2ψ(W)∂εij∂εkl(8)

where εij=1/2(ui,j+uj,i) is the macroscopic RVE strain tensor. It is necessary to establish the relationship between the particle-scale strain and the macroscopic RVE strain. However, it should be noted that to derive such a relationship, precise knowledge of the granular material’s microstructural characteristics is required, such as particle shape and size, particle boundaries, surface characteristics, particle contact mechanisms, and the initial and boundary conditions of the problem. Such detailed information is usually unavailable for most materials. However, this lack of information can be overcome through certain methods. Solving this problem neither require an exact and detailed solution nor precise knowledge of the motion of each particle in the RVE. The difference between the approximate average solution and the exact solution for each particle can be explained by the statistics of particle displacement fluctuations. Therefore, due to the problem’s complexity, statistical approximations are applicable, which are not influenced by the lack of information. In fact, what is sought is precisely those average solutions. Furthermore, it can be demonstrated that the fluctuation of displacement is inversely proportional to the size of the RVE. This implies that when using an RVE with a sufficient number of particles, the relative fluctuations of the average value determined from statistical approximations become increasingly negligible [26]. Based on this argument, the mean-field hypothesis, although approximate, provides a feasible method for deriving the constitutive relationship of the RVE and has been shown to describe some phenomena exhibited by granular materials [19,27,28]. Therefore, equating the particle-scale strain to the RVE strain, i.e., εija=εij, Eq. (8) can be derived as

Dijkl=∂2ψ(W)∂εij∂εkl=∂∂εkl∂∂εij(Φ−Φe−W/Φ)=∂∂εkl(e−W/Φ∂W∂εij)=∂∂εkl(e−W/Φ∂W∂εij)=e−W/Φ∂2W∂εij∂εkl+∂W∂εije−W/Φ(−1Φ)∂W∂εkl=e−W/Φ∂2(Wn+Wt+Ws)∂εij∂εkl+∂(Wn+Wt+Ws)∂εije−W/Φ(−1Φ)∂(Wn+Wt+Ws)∂εkl(9)

where Wn, Wt and Ws are respectively the first, second, and third right terms of W in Eq. (7). In order to derive Dijkl, it is only necessary to calculate all the first-order and second-order partial derivatives in Eq. (9). Then, it can be obtained by

∂2Wn∂εij∂εkl=1V∑a=1n12kn∂2(Δupnp)2∂εij∂εkl=1V∑a=1n12kn∂(Δupnp)∂(Δuqnq)∂εij∂εkl=1V∑a=1n12kn∂(up,mLmanp)∂(uq,nLnanq)∂εij∂εkl=1V∑a=1n12knLmanpLnanq∂(εpm+u[p,m])∂(εqn+u[q,n])∂εij∂εkl=1V∑a=1n12knLmanpLnanq∂εpmεqn+∂u[q,n]∂εpm+∂u[p,m]∂εqn+∂u[p,m]∂u[q,n]∂εij∂εkl=1V∑a=1n12knLmaLnanpnqδpiδmjδqkδnl=1V∑a=1n12knLjaLlanink(10)

It is noted that u[p,m] is the antisymmetric part of up,m, and it is the rigid body rotation which has no effect on the strain εij, i.e., the partial derivative of u[p,m] with respect to εij equals zero.

∂Wn∂εij=1V∑a=1n12kn∂(Δupnp)∂εij=1V∑a=1n12kn∂(up,mLmanp)∂εij=1V∑a=1n12knLmanp∂(εpm+u[p,m])∂εij=1V∑a=1n12knLmanpδpiδmj=1V∑a=1n12knLjani(11)

∂Wn∂εkl=1V∑a=1n12kn∂(Δuqnq)∂εkl=1V∑a=1n12kn∂uq,nLnanq∂εkl=1V∑c=1n12knLnanq∂(εqn+u[q,n])∂εkl=1V∑a=1n12knLnanqδqkδnl=1V∑a=1n12knLlank(12)

In the same way, ∂2Wt(s)∂εij∂εkl and ∂Wt(s)∂εij in Eq. (9) can be derived as the followings show

{∂2Wt∂εij∂εkl=1V∑a=1n12ktLjaLlatitk∂2Ws∂εij∂εkl=1V∑a=1n12ksLjaLlasisk∂Wt∂εij=1V∑a=1n12ktLjati∂Ws∂εij=1V∑a=1n12ksLjasi(13)

And for the spherical particle, kt and ks are seen to be equal, therefore, substituting Eqs. (10)–(13) into Eq. (9), it can be obtained by

Dijkl=∂2ψ(W)∂εij∂εkl=e−W/Φ2Vkn[∑a=1nLjaLlanink−kn2ΦV(∑a=1nLjani)(∑a=1nLlank)]+e−W/Φ2Vkt[∑a=1nLjaLla(titk+sisk)−kt2ΦV(∑a=1nLjati)(∑a=1nLlatk)−kt2ΦV(∑a=1nLjasi)(∑a=1nLlask)](14)

And the micromechanics-based softening hyperelastic constitutive relationship is obtained by

σij=Dijklεkl=∂2ψ(W)∂εij∂εklεkl=e−W/Φ2Vkn[∑a=1nLjaLlanink−kn2ΦV(∑a=1nLjani)(∑a=1nLlank)]+e−W/Φ2Vkt[∑a=1nLjaLla(titk+sisk)−kt2ΦV(∑a=1nLjati)(∑a=1nLlatk)−kt2ΦV(∑a=1nLjasi)(∑a=1nLlask)]εkl(15)

3  Identification of Constitutive Modulus Tensor

3.1 Isotropic Directional Density Distribution Function of Contacts

For an RVE V, contact stiffness parameters and internal lengths are usually different among contacts. To simplify the analysis, this study assumes that the material is isotropic, and Chang and Lun [22] proposed a directional density distribution function of contacts ξ(α,β)=1/4π, and (α,β) is shown in the local coordinate system in Eq. (5). And the radius of the particle is assumed to be equal: Lja=lnj where l is the distance of centers between two particles, i.e., the internal length. Therefore, the constitutive modulus tensor is written in integral form from the discrete summation form in Eq. (14):

Dijkl=e−W/Φ2knl2NV∫0π∫02πnjcnlcnink(1−knNV2Φ)ξsin⁡αdβdα+e−W/Φ2ktl2NV∫0π∫02πnjcnlc(titk+sisk)(1−ktNV2Φ)ξsin⁡αdβdα=e−W/Φ2knl2NV(1−knNV2Φ)∫0π∫02πnjcnlcninkξsin⁡αdβdα+e−W/Φ2ktl2NV(1−ktNV2Φ)∫0π∫02πnjcnlc(titk+sisk)ξsin⁡αdβdα(16)

where NV is the contact density in the RVE. Then, substituting Eq. (6) into Eq. (16), the constitutive modulus tensor of the micromechanics-based softening hyperelastic model is obtained by

{Diiii=l2NVe−W/Φ15[3kn(1−knNV2Φ)+kt(1−ktNV2Φ)]Diijj=Dijji=l2NVe−W/Φ15[kn(1−knNV2Φ)+kt(1−ktNV2Φ)]Dijij=l2NVe−W/Φ15[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]Dijkl=0, otherwise(17)

where i≠j.

3.2 Specific Microstructures

To incorporate more comprehensive microstructural details, this study considers three distinct three-dimensional microstructures characterized by different ordered particle arrangements, as shown in the previous study [29]. Each microstructure unit cell consists of a reference particle and a first ring of neighbors in contact. Fig. 2 shows the differences in particle arrangements, void ratios, and coordination numbers across these microstructures. Consequently, the three microstructures are categorized into one medium-dense and two dense configurations. It is noteworthy that this study initially considered a loose microstructure represented by a simple cubic arrangement; however, this configuration is deemed unrealistic due to its negligible resistance to shear deformation. Therefore, the loose microstructure is excluded from further analysis in this study. The medium-dense microstructure exhibits a hexagonal close-packed arrangement in the x-y plane and a cubic arrangement in x-z and y-z planes. The monodisperse dense microstructure is a hexagonal close-packed arrangement throughout. To construct the bidisperse dense microstructure, smaller particles are introduced to fill the voids in a simple cubic arrangement. These smaller particles, with a radius of (3−1)r, are tangent to the larger particles. Importantly, each microstructure must have a unit cell V as its minimum element, and a granular RVE is formed by the periodic arrangement of these unit cells, as depicted in Fig. 2. Table 1 summarizes the coordination numbers and void volume ratios for the three microstructures under investigation.

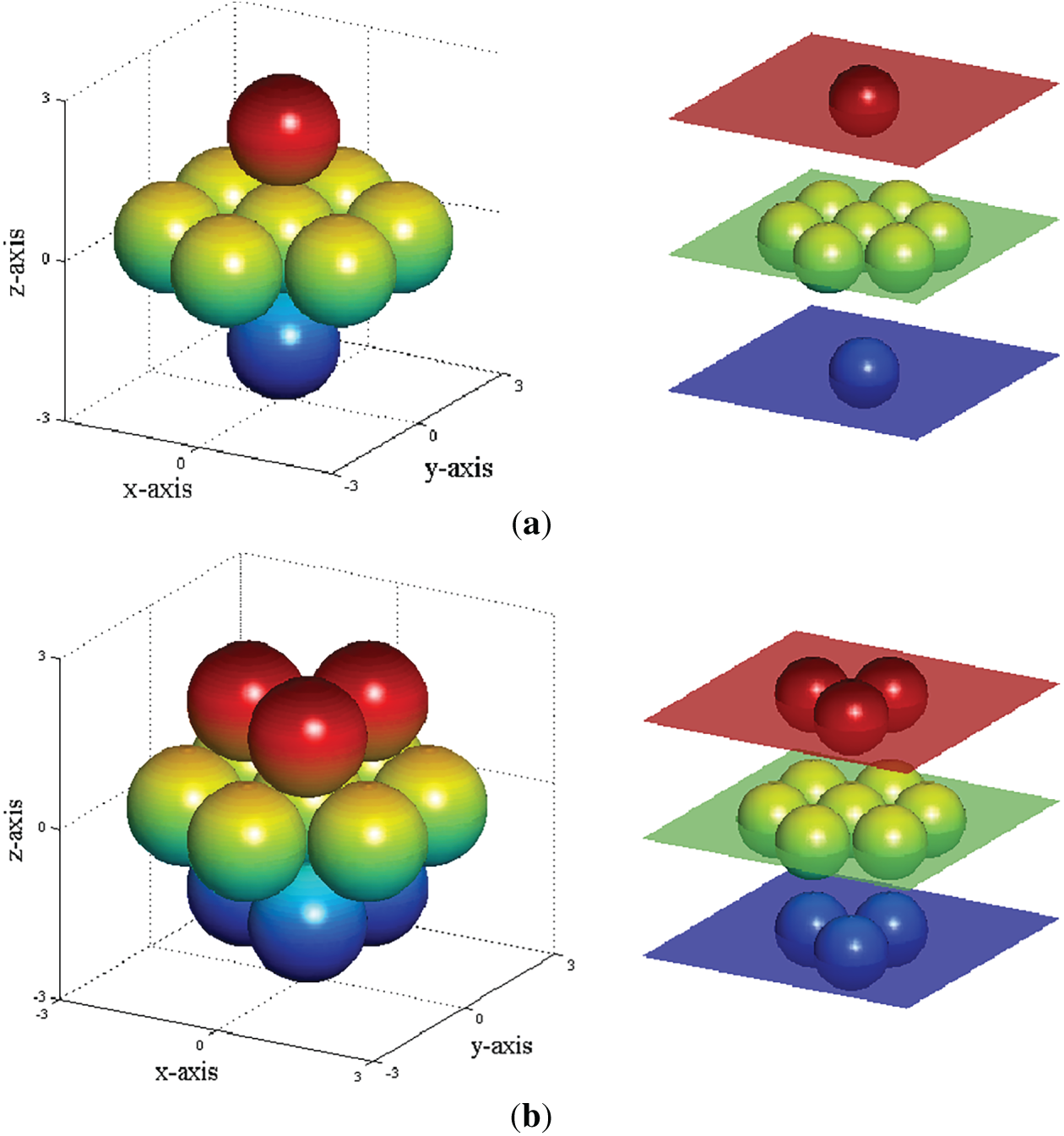
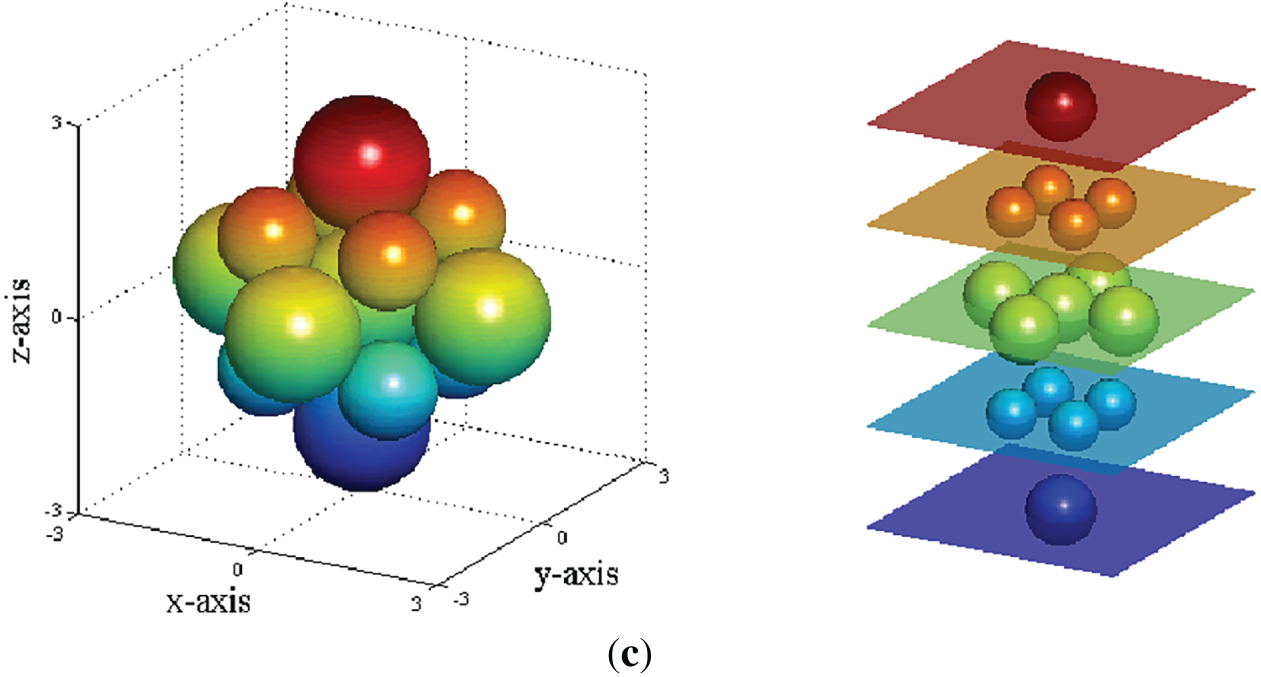
Figure 2: Schematic diagram for cells of three microstructures (a) cell of medium dense microstructure (b) cell of monodisperse dense microstructure (c) cell of bidisperse dense microstructure

Then, the constitutive modulus tensors of these granular materials with different microstructures can be obtained by directly solving the discrete summations as shown in Eq. (17), and the derivation process is provided in Appendix A. The constitutive modulus tensors are derived and presented as follows.

(1) Medium dense microstructure

{D1111=D2222=3l2e−W/Φ4V[3kn(1−knNV2Φ)+kt(1−ktNV2Φ)]D3333=2l2e−W/ΦV[kn(1−knNV2Φ)]D1122=D2211=3l2e−W/Φ4V[kn(1−knNV2Φ)+3kt(1−ktNV2Φ)]D1133=D2233=3l2e−W/ΦV[kt(1−knNV2Φ)]D3311=D3322=2l2e−W/ΦV[kt(1−knNV2Φ)]D1212=D1221=D2121=D2112=3l2e−W/Φ4V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]Dijkl=0,otherwise(18)

(2) Monodisperse dense microstructure

{D1111=4l2e−W/Φ3V[2kn(1−knNV2Φ)+kt(1−ktNV2Φ)]D2222=D3333=l2e−W/Φ2V[5kn(1−knNV2Φ)+3kt(1−ktNV2Φ)]D1122=D2211=D1133=D3311=2l2e−W/Φ3V[kn(1−knNV2Φ)+5kt(1−ktNV2Φ)]D3322=D2233=l2e−W/Φ6V[5kn(1−knNV2Φ)+19kt(1−ktNV2Φ)]D1212=D1221=D2121=D2112=2l2e−W/Φ3V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]D1313=D1331=D3131=D3113=2l2e−W/Φ3V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]D3232=D2323=D3223=D2332=5l2e−W/Φ6V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]Dijkl=0,otherwise(19)

(3) Bidisperse dense microstructure

{D1111=D2222=D3333=4l2e−W/Φ3V[2kn(1−knNV2Φ)+kt(1−ktNV2Φ)]D1122=D2211=D1133=D3311=D3322=D2233=2l2e−W/Φ3V[kn(1−knNV2Φ)+5kt(1−ktNV2Φ)]D1212=D1221=D2121=D2112=2l2e−W/Φ3V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]D1313=D1331=D3131=D3113=2l2e−W/Φ3V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]D3232=D2323=D3223=D2332=2l2e−W/Φ3V[kn(1−knNV2Φ)−kt(1−ktNV2Φ)]Dijkl=0,otherwise(20)

4  Critical State for the Micromechanics-Based Softening Hyperelastic Model

The micromechanics-based softening hyperelastic model derived above is based on the softening mechanism introduced by Volokh in Eq. (1); however, this softening mechanism is more applicable to brittle materials. Actually, it has been proven that granular materials like sands and soils have a critical state and residual strength [30]. Therefore, the mechanism that can describe the critical state and residual strength should be incorporated into the micromechanics-based softening hyperelastic model for granular materials. Then, a stress decomposition mechanism is proposed in Eq. (21), which states that the total stress is the sum of the stresses from the micromechanics-based linear and softening hyperelastic models.

σij=(1−α)σijN+ασijS(21)

where α is a proportional softening factor, ranging from 0 to 1, σijS is the stress in Eq. (18) for the complete softening situation, and σijN is the stress of the micromechanics-based hyperelastic model without softening. σijN is derived by

σijN=∂W∂εij(22)

in which W is the macroscopic strain energy density in Eq. (6), and it has no softening mechanism as shown in Eq. (1). When α=0, it refers to the condition where the material behaves as an ideal hyperelastic material, while α=1, it indicates that Eq. (21) describes brittle materials. In this study, the softening factor α plays an important role in characterizing the mechanical behaviors of granular materials, such as sands and soils, particularly in relation to their critical states. The investigation of α is essential for understanding complex interactions and stress-strain relationships within these materials, which are fundamental to geotechnical engineering applications.

5  Numerical Simulations

The micromechanics-based softening hyperelastic model is performed on Abaqus, and a user-defined material program is coded by the UMAT subroutine interface, and the numerical implementation process is given in Appendix B. The numerical simulations focus on the following issues: (1) capacity of modeling strain localization and strain softening for granular materials by the micromechanics-based softening hyperelastic model; (2) influences of softening factor, microstructures, and micro-/macroscopic parameters; (3) mesh sensitivity analysis; (4) simulation of slope instability.

5.1 Strain Localization and Strain Softening of Granular Materials Based on Isotropic Directional Density Distribution of Contacts

The numerical simulations concern a rectangular plate with a size of 0.6 m × 0.8 m (Fig. 3a), and an eight-node iso-parametric element with four integration points is used for the plane strain problem (Fig. 3b). The plate is subjected to compression under displacement-controlled loading with 30 mm displacement on the top. Nodes on the bottom boundaries are fixed, and those on the left and right boundaries are free. The material and microstructural parameters of the presented model are set in Table 2. And the plate is meshed by 24 × 32 in this example.

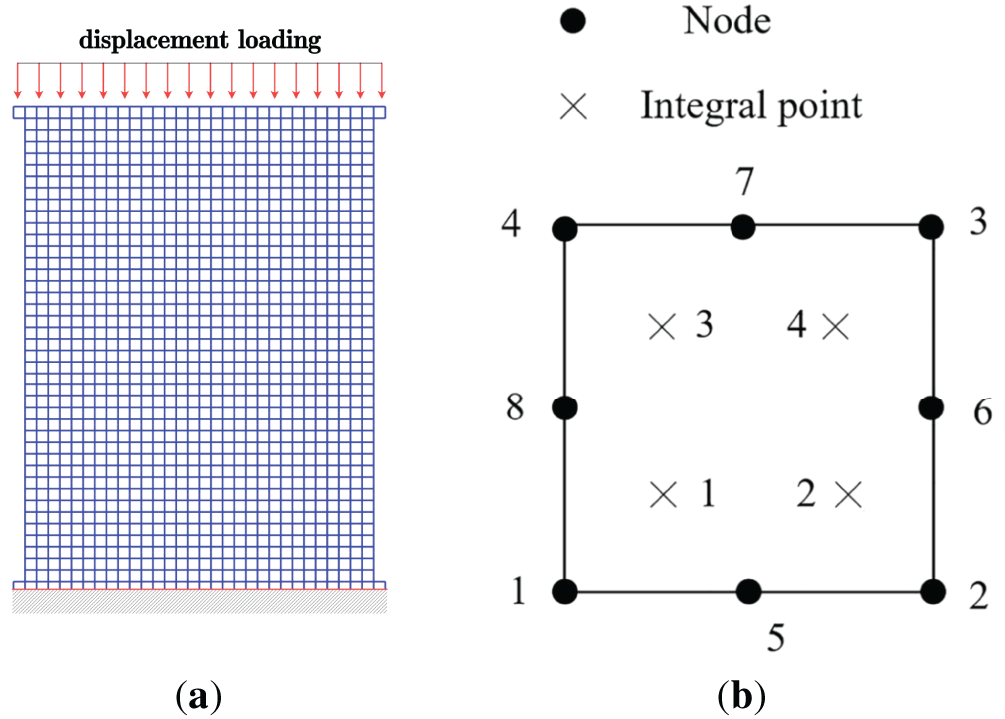
Figure 3: (a) Finite element mesh (b) plane strain element for the plate model

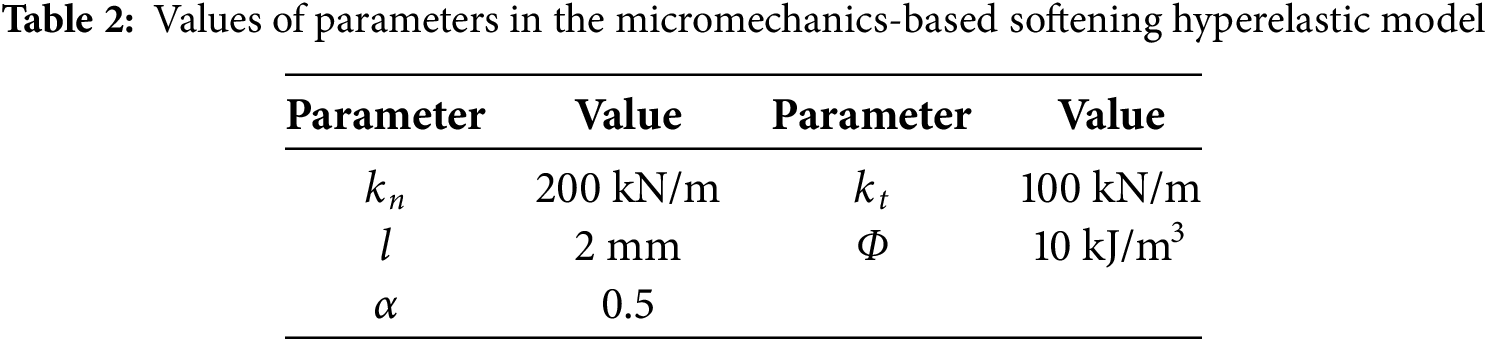
Fig. 4 illustrates the evolution process of the force-displacement curve strain localization of granular materials with isotropic directional contact density distribution simulated by the micromechanics-based softening hyperelastic model. The force-displacement curve shows a linear elastic stage, a hardening stage, a softening stage, and a critical state with the residual strength of approximately 661 kPa. This indicates that the critical state situation corresponds to geomaterials like dense sands and soils. The strain localization occurs during the hardening stage, prior to the ultimate strength, at a loading displacement of approximately 7.2 mm, corresponding to an axial strain of 0.9% (see Phase A in Fig. 4). It initiates at the four corners of the plate. As the displacement loading increases, it gradually spreads from the corners towards the center of the plate, ultimately forming a continuous X-shaped shear band with an inclination angle of approximately 53∘ (see Phases A to C). The formation of the continuous X-shaped shear band coincides with the lowest point of strain softening, which is approximately at an axial strain of 1.94% (see Phase D), marking the moment when the residual strength is reached. Subsequently, as the displacement loading progresses, the residual strength remains constant, thus establishing a critical state. During this process, both the degree and width of strain localization gradually increase.

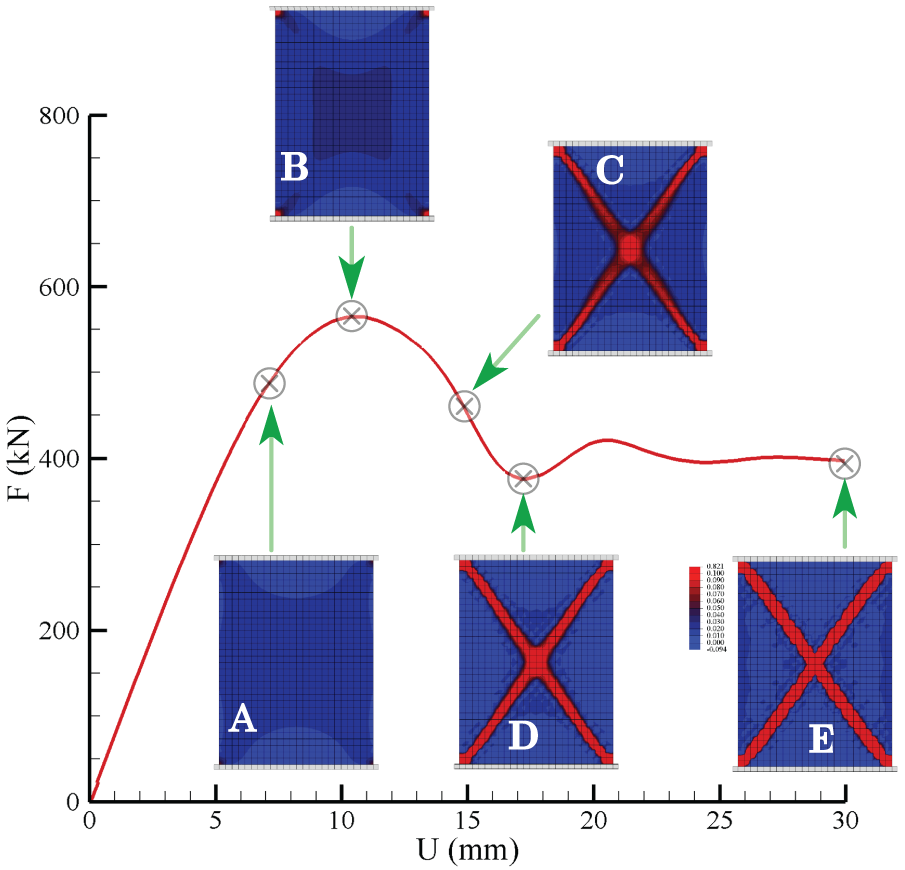
Figure 4: Evolution process of the force-displacement curve strain localization

Furthermore, to ascertain the validity of the proposed model, a comparative analysis is conducted with the results of the micromechanics-based softening hyperelastic model, the macro-scale models, and the experiment.

(1) Comparison with macro-scale Volokh softening hyperelastic model and Abaqus Drucker-Prager (DP) model

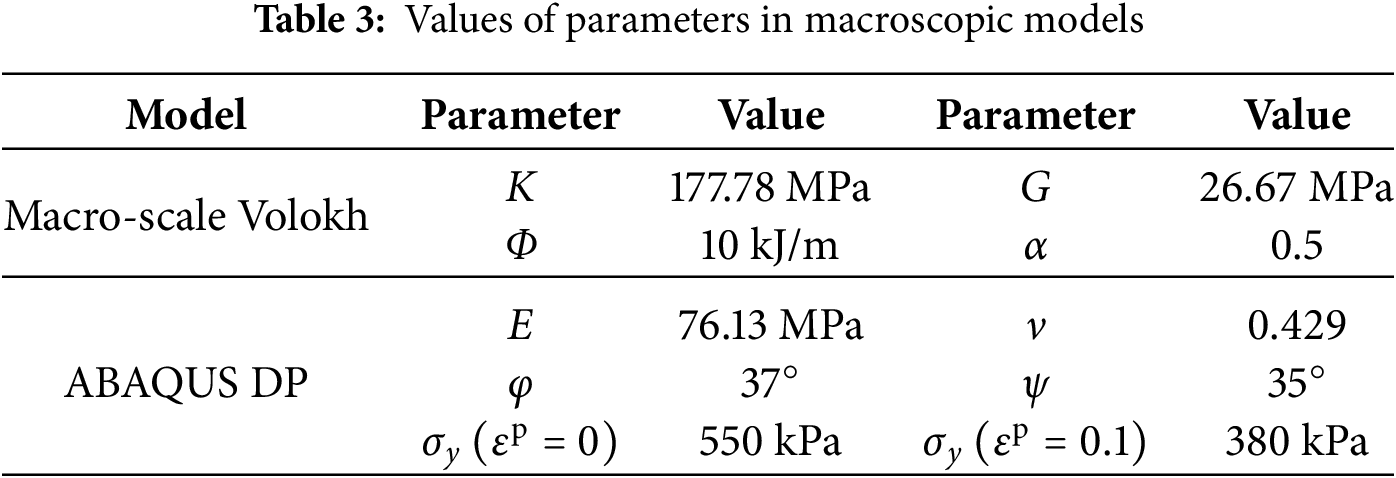
The comprehensive comparison ensures the model’s reliability in accurately representing the relevant mechanical behaviors. It is noteworthy that microscopic parameters used in this study can be identified as reported by Xiu and Chu [31]. Therefore, this study can obtain bulk modulus and shear modulus for the macro-scale Volokh softening hyperelastic model and the elastic modulus and Poisson’s ratio for the Abaqus DP model, as given in Table 3 below. However, the remaining elasto-plastic DP parameters cannot be directly identified from the microscopic ones. Consequently, these additional elasto-plastic parameters for the DP model, including the friction angle, dilatancy angle, initial yield stress, and subsequent yield stress, are also provided in Table 3 for the sake of completeness and clarity.

Figs. 5 and 6 respectively depict force-displacement curves and equivalent strain distributions simulated by the aforementioned models. It is evident from the comparison that the equivalent strain distributions and force-displacement curves simulated by the micromechanics-based softening hyperelastic model are nearly identical to those simulated by the macro-scale Volokh softening hyperelastic one. This similarity stems from the direct correlation between the macroscopic and microscopic parameters in both models. It is noted that the microscopic parameters are not related to the elasto-plastic DP parameters. Consequently, the appropriate values of the elasto-plastic DP parameters are obtained, as listed in Table 3, to achieve a force-displacement curve that closely approximates the one simulated by the micromechanics-based softening hyperelastic model. The DP force-displacement curve has identical elastic stage and ultimate strength, although the in-elastic hardening stage and the post-peak softening behavior do not align perfectly; however, it achieves the same residual strength. As a result, the equivalent strain distribution within the Abaqus DP model has a different mode, characterized by a 10% wider shear band and a higher degree of strain localization. Therefore, the presented micromechanics-based softening hyperelastic model is capable of simulating strain localization and strain softening of granular materials, with reliable results. Compared with complex elasto-plastic models, its numerical implementation is notably simpler. The most significant advantage of this model lies in its ability to consider the influences of microstructural information on macroscopic mechanical behaviors of granular materials, which will be discussed in detail in the subsequent section.

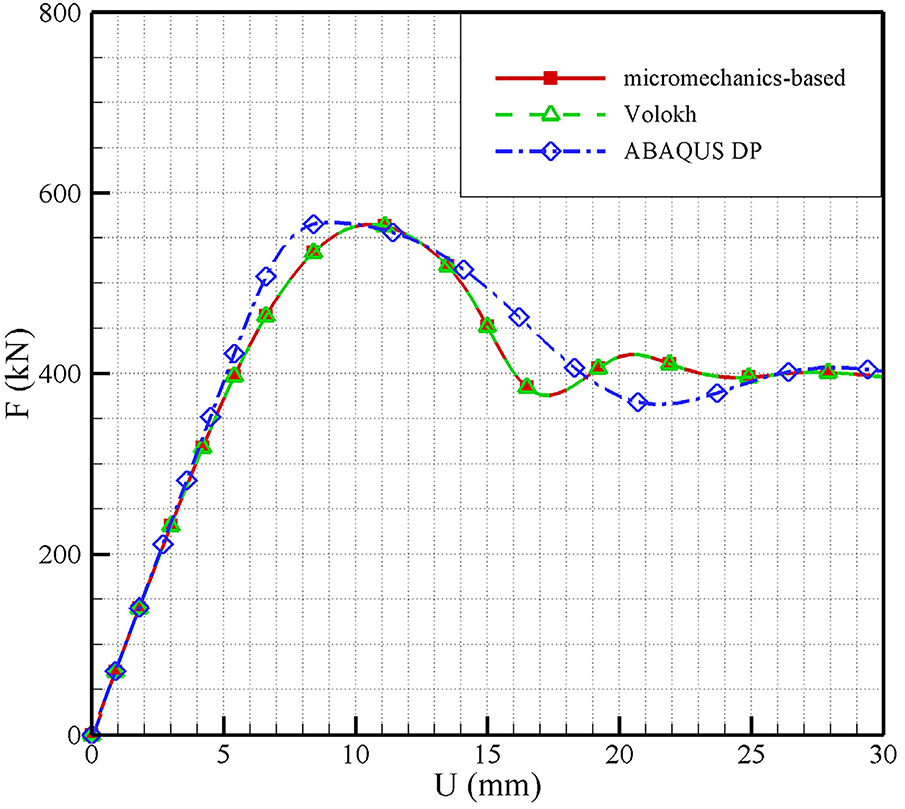
Figure 5: Force-displacement curves simulated by different models

Figure 6: Equivalent strain distributions simulated by (a) micromechanics-based softening hyperelastic model (b) macro-scale Volokh softening hyperelastic model (c) Abaqus Drucker-Prager model

(2) Comparison with the experiment

To further validate the reliability of the presented model, its results are compared with those of a biaxial test. The experimental granular system comprised glass beads with a diameter of 0.3 mm in a membrane of dimensions 85 mm height, 55 mm width, and 25 mm depth, as shown in Fig. 7a [32]. The confining pressure is fixed at 30 kPa. The stiffness of the entire system has been tested in a Hertz contact configuration and is found to be 730 kN/m. Therefore, the normal contact stiffness parameter in the numerical simulation should be valued as kn=730kN/m, and then kt=0.5kn accordingly. The internal length is set equal to the particle diameter as l=0.3 mm. A numerical simulation for the biaxial test is conducted (Fig. 7b): the upper boundary is subjected to compression under a 10% vertical strain, nodes on the bottom boundary are fixed in vertical and horizontal directions, and a 30 kPa confining pressure is applied to the left and right boundaries.

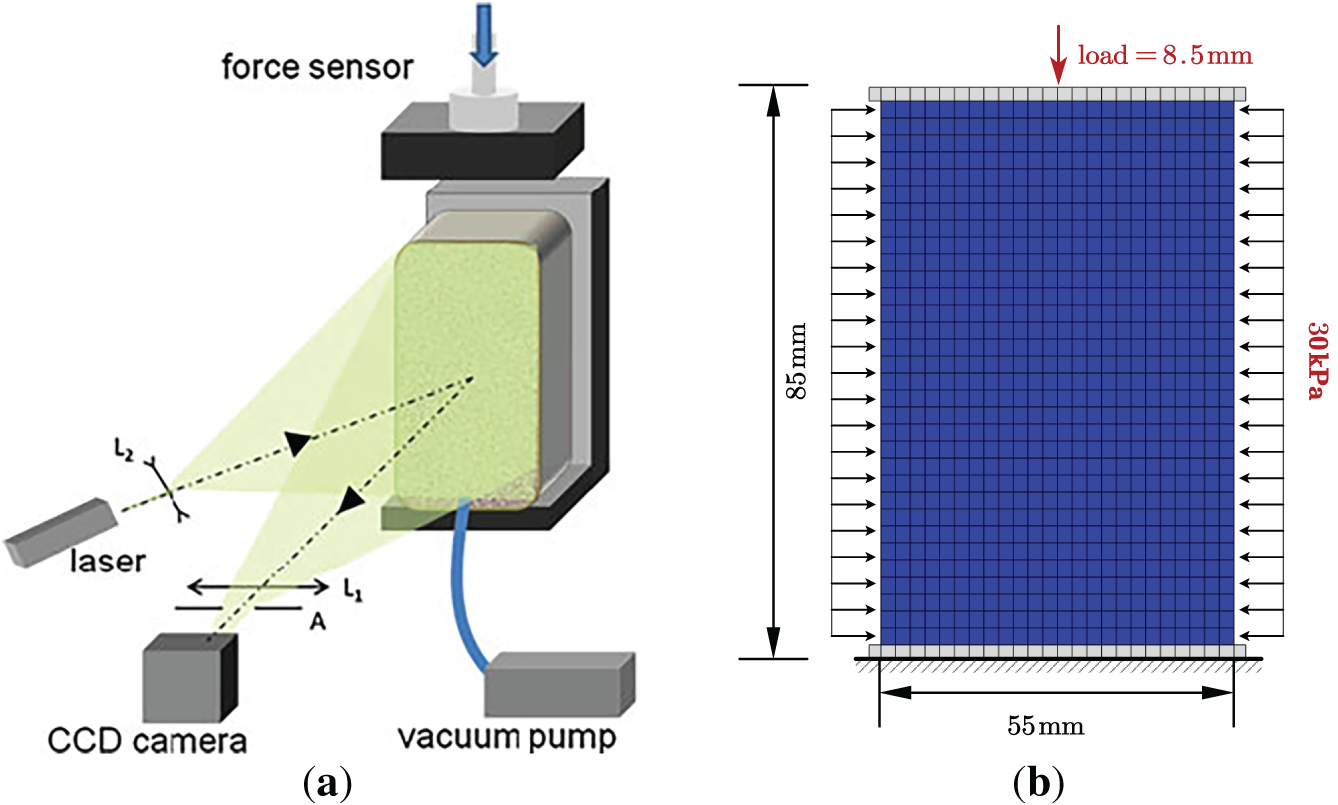
Figure 7: Schematics for a biaxial test by (a) experiment (b) numerical simulation

Figs. 8 and 9 present a direct comparison of stress-strain relationship curves and equivalent strain distributions between the model’s numerical predictions and the physical experimental results. It is important to note that, after using the micro-parameters directly derived from the experimental setup, the model required the specific macroscopic softening parameters, namely Φ=70kJ/m3 and α = 0.2 to replicate the macroscopic responses observed in the experiment. As shown in Fig. 8, with this parameter set, the simulated stress-strain relationship agrees well with the experimental measurement. Furthermore, the equivalent strain distribution in Fig. 9 demonstrates that the concentration of the X-shaped shear band predicted by the simulation is in close agreement with the dominant failure pattern observed experimentally. These comparisons confirm that, with appropriately determined macroscopic softening parameters, the proposed micromechanics-based model can effectively simulate both the macroscopic mechanical behavior and the strain localization failure pattern of real granular materials.

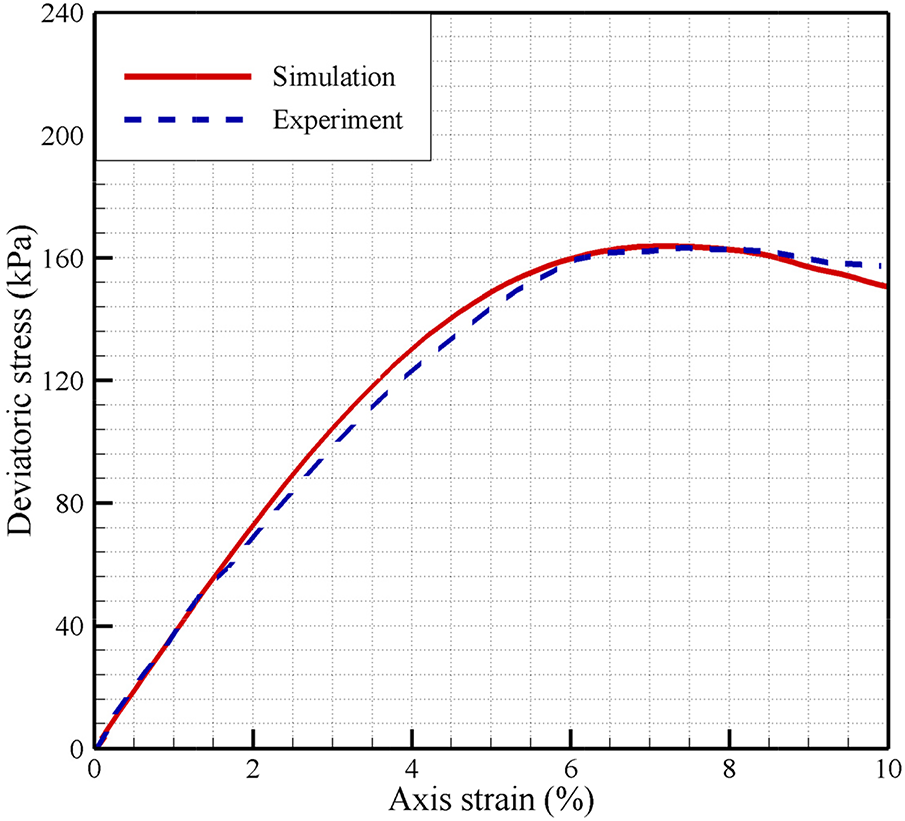
Figure 8: Stress-strain relationship curves predicted by the experiment and the numerical simulation

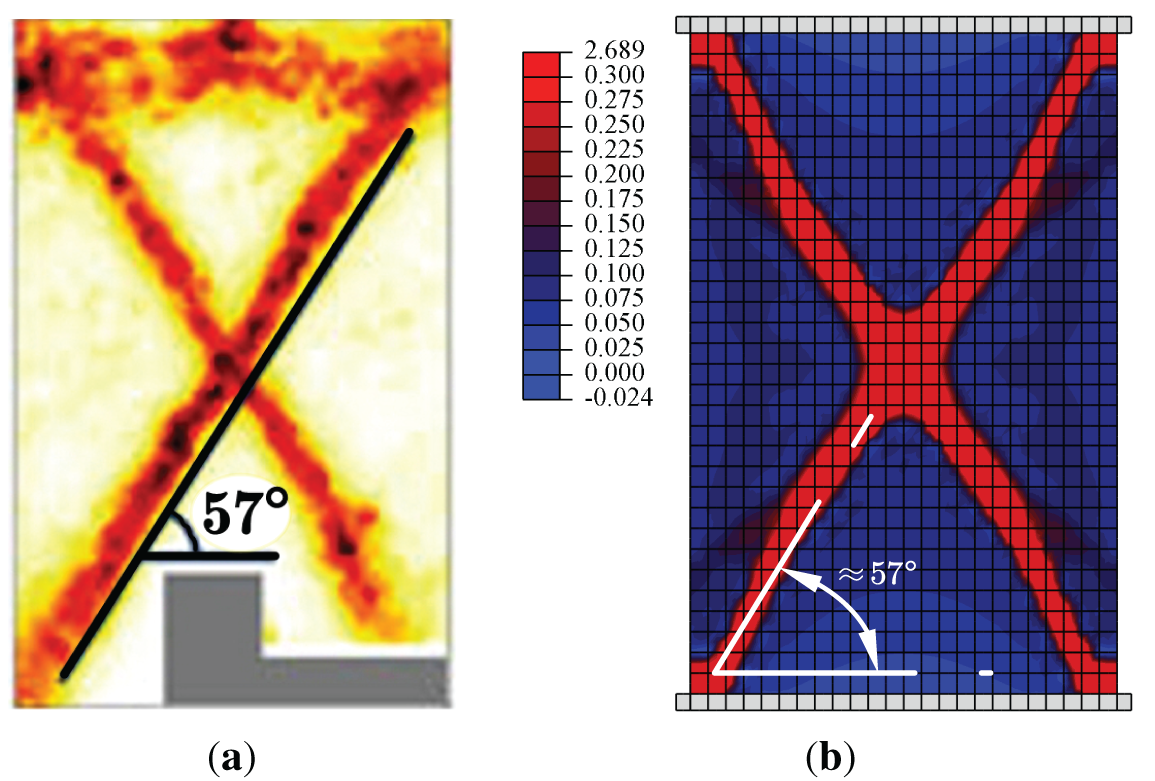
Figure 9: Equivalent strain distributions predicted by (a) the experiment [32] (b) the micromechanics-based softening hyperelastic model

5.2 Influences of Softening Factor on Strain Localization and Strain Softening

The softening factor α is crucial for characterizing the mechanical behaviors of granular materials like sands and soils, especially regarding their critical state. Investigating α is vital for understanding the complex stress-strain relationships in these materials, which are key to geotechnical engineering. In this section, the softening factor is analyzed by α=0.1,0.3,0.5,0.7,1, and other parameters are the same as those in Table 2.

Fig. 10 shows force-displacement curves under different softening factors. It can be observed that all the force-displacement curves coincide before 0.8% axial strain, which is the linear elastic stage. Subsequently, as the axial loading continues, cases with a smaller softening factor α exhibit a higher ultimate strength. When α is 0.1, the calculation fails to converge at the peak of the curve. When α is 1.0, the curve shows a complete strain softening state, that is, it reflects brittle failure behavior, corresponding to the stress-strain relationship of brittle granular materials. When α ranges from 0.3 to 0.7, the force-displacement curves can display strain softening and a critical state, and the residual strength in the critical state is inversely proportional to α. Fig. 11 presents equivalent strain distributions under different softening factors. Since the calculation fails to converge at the peak of the hardening stage when α is 0.1, strain localization cannot occur accordingly. However, when the value of α exceeds 0.3, a distinct X-shaped shear band can be observed in all cases. Moreover, when α ranges from 0.3 to 0.7, the width of the shear band remains consistent, approximately 45 mm. The degree of localization first decreases and then increases as α increases from 0.3 to 0.7. Specifically, when α equals 0.5, the degree of localization is at its minimum. When α equals 1.0, meaning it is in a complete strain softening state, the mode of the X-shaped shear band is slightly different. It exhibits a certain curvature, and its width is relatively smaller, approximately 40 mm.

Figure 10: Force-displacement curves simulated by the micromechanics-based softening hyperelastic model with different softening factors

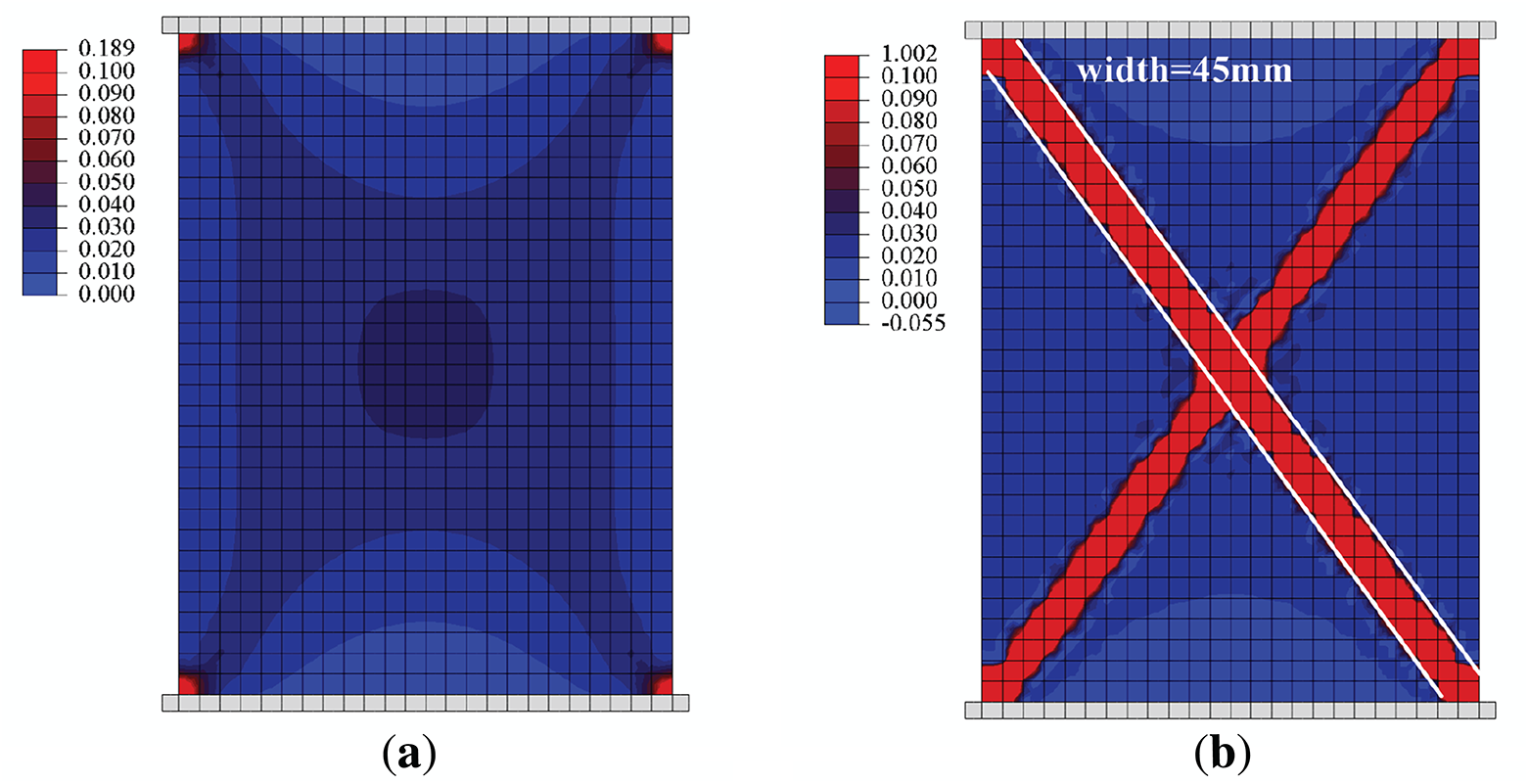
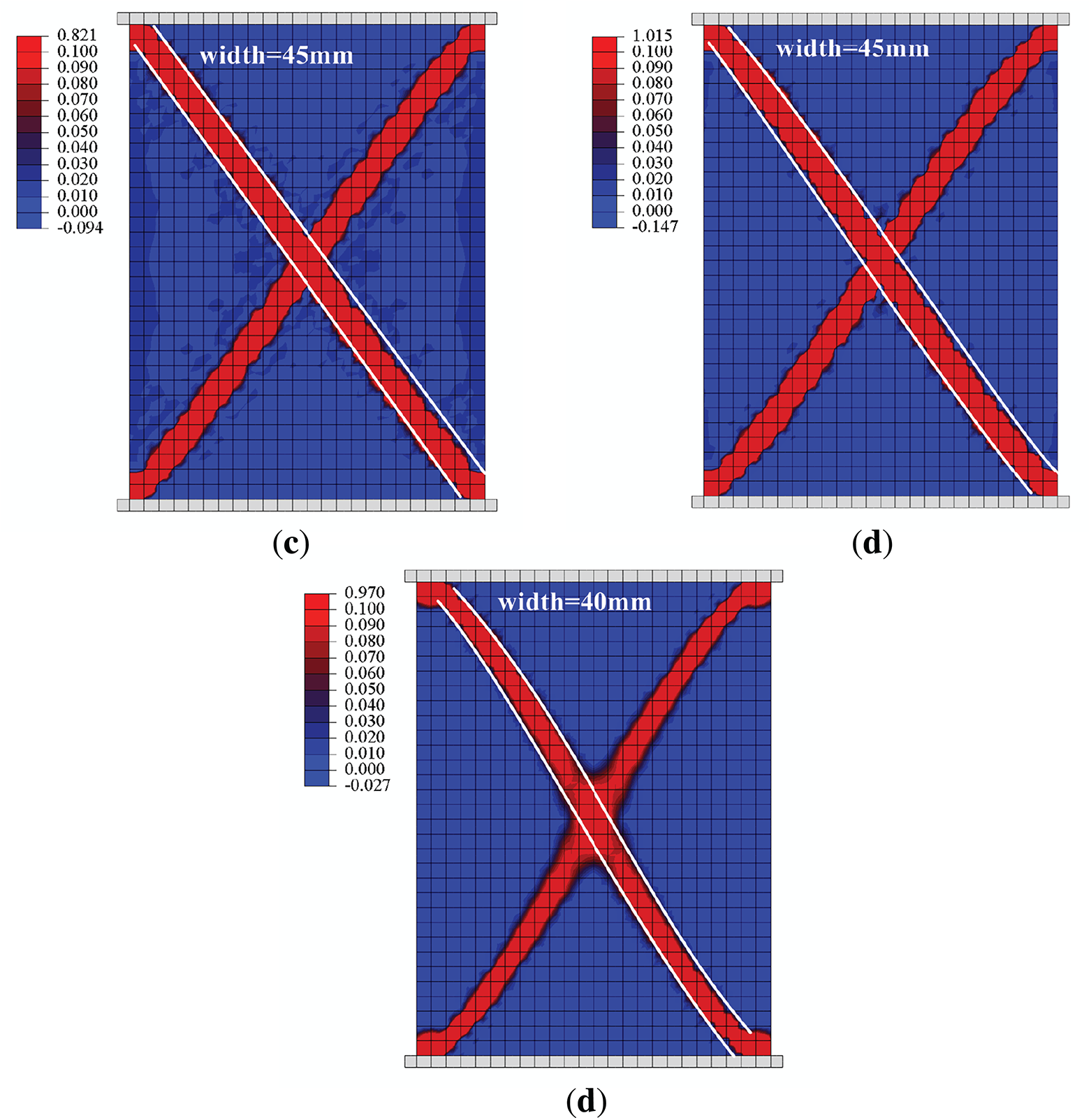
Figure 11: Equivalent strain distributions simulated by the micromechanics-based softening hyperelastic model with different softening factors (a) α=0.1 (b) α=0.3 (c) α=0.5 (d) α=0.7 (e) α=1.0

Therefore, in order to characterize the mechanical behaviors of granular materials with a critical state, it is recommended that the value of the softening factor α be in the range of 0.3–0.7, and the value of 0.5 taken in this paper is appropriate. In addition, considering the discrete nature of granular materials, the significance of α at the micro scale, or in other words, its connection with microstructural information, is also of great importance. This paper does not conduct an in-depth analysis, and relevant work will be continued in the subsequent study.

5.3 Influences of Microstructures on Strain Localization and Strain Softening

Fig. 2 shows three distinct and specific microstructures in granular materials. These microstructures, each with its own unique arrangement and configuration of particles, represent different states that granular materials can assume. The microstructure plays a pivotal role in the strength and deformation behavior of granular materials. This section has an in-depth discussion about the influences of these microstructures on strain localization and strain softening. Meanwhile, the results are compared with those of the case based on the isotropic directional distribution density of contacts mentioned previously. The parameters utilized in this analysis remain consistent with those in Table 2.

Figs. 12 and 13 respectively show force-displacement curves and equivalent strain distributions of granular materials with isotropic directional contact distribution density and different microstructures, simulated by the micromechanics-based softening hyperelastic model. As can be observed from Fig. 12, all the force-displacement curves can successively exhibit the linear elasticity, hardening, softening stages, and the critical state. However, the ultimate strengths and residual strengths under various cases are different. The case of isotropic directional contact distribution density (red line) has the maximum ultimate strength (706 kPa) and residual strength (661 kPa), followed by the case of monodisperse dense microstructure (blue line) and the case of bidisperse dense microstructure (black line) in turn. While the case of medium dense microstructure (green line) has the minimum ultimate strength (557 kPa) and residual strength (399 kPa). This result is presumed to be related to the porosity of the microstructure. The assumption of isotropic directional distribution density of contacts eliminates information about voids in microstructures. As a consequence, it has the maximum strength. Among the other three specific microstructures, their ultimate and residual strength are inversely proportional to the porosity of the microstructure. When the porosity is at its minimum, i.e., 26% in Table 1, the case of monodisperse dense microstructure exhibits greater strength and is quite close to the case of the isotropic assumption.

Figure 12: Force-displacement curves of granular materials with isotropic directional distribution density of contacts and different microstructures simulated by the micromechanics-based softening hyperelastic model

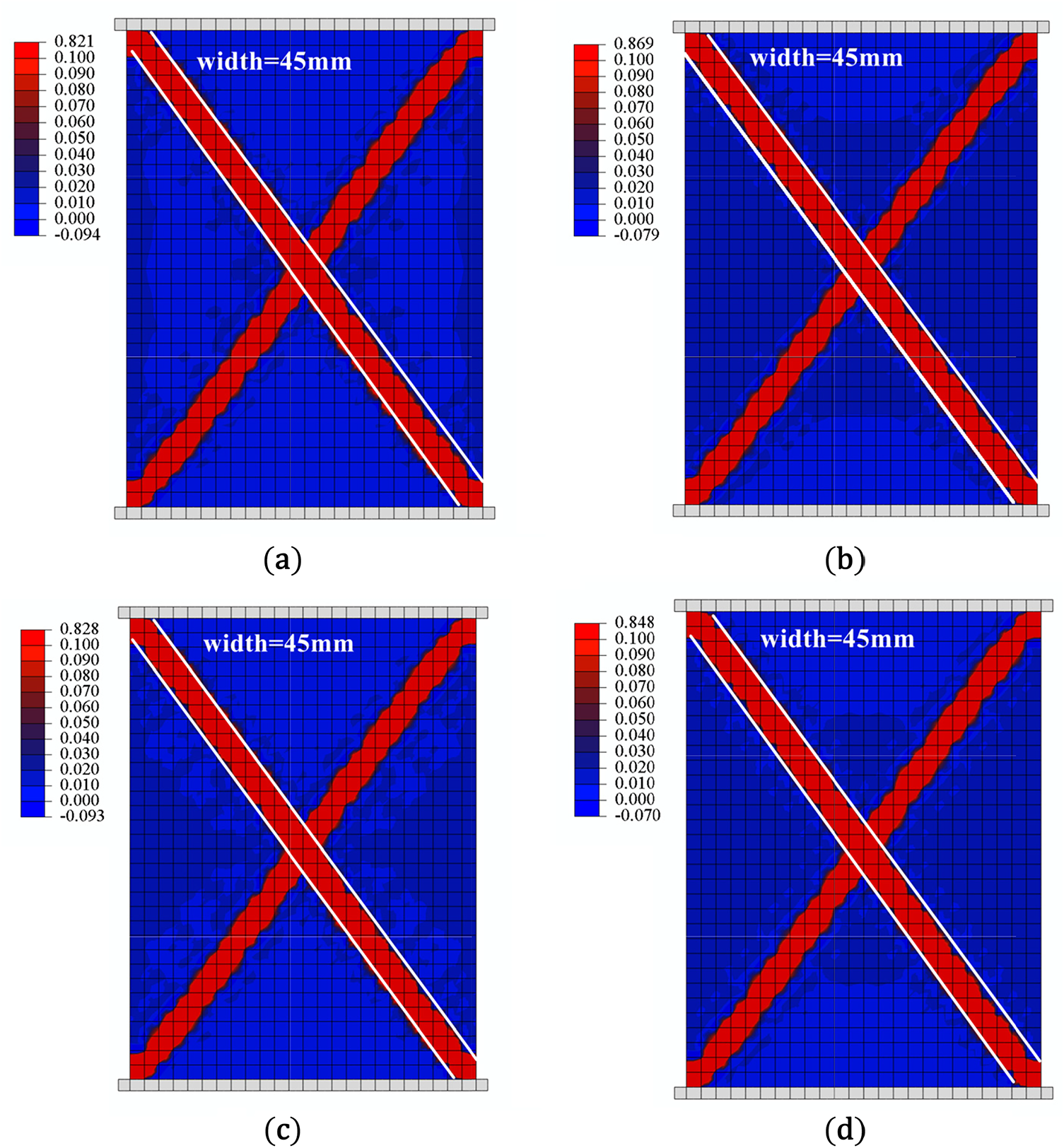
Figure 13: Equivalent strain distributions of granular materials with (a) isotropic directional density distribution of contacts (b) medium dense microstructure (c) monodisperse dense microstructure (d) bidisperse dense microstructure

Since all cases exhibit a critical state, the equivalent strain distributions as shown in Fig. 13 are quite similar. They all feature distinct X-shaped shear bands, with each shear band having a width of approximately 45 mm. However, the degree of localization is slightly different, which is consistent with the aforementioned rule regarding the force-displacement curves. Given that the case of medium dense microstructure has the minimum residual strength, it has the highest degree of localization, followed by the case of bidisperse dense microstructure, the case of monodisperse dense microstructure, and the case of isotropic assumption in turn.

It should be noted that the three microstructures in this paper are merely the most basic and easily constructed types of granular materials. In contrast, real granular materials (e.g., soils and rocks) possess extremely complex microstructures, featuring variations in particle size, shape, and arrangement. However, these complex microstructures can be regarded as being composed of simple and fundamental microstructural unit cells. Therefore, the investigation into the influences of the three proposed microstructures is also of great significance. It lays a foundation for subsequent studies on how complex microstructures affect macroscopic mechanical behaviors of granular materials.

5.4 Influences of Microscopic Parameters and Critical Failure Energy Density on Strain Localization and Strain Softening

This section discusses the influences of microscopic and macroscopic parameters in the micromechanics-based softening hyperelastic model on strain localization and strain softening, including contact stiffnesses, the particle size, and the critical failure energy density. And the micromechanics-based softening hyperelastic model is applied based on the isotropic directional density distribution of contacts.

5.4.1 The Influence of Ratio of Normal to Tangential Contact Stiffness

The normal and tangential contact stiffnesses are among the most important microscopic parameters for simulating and controlling the mechanical behaviors of granular materials. It is noteworthy that the normal contact stiffness is larger than the tangential contact stiffness [33], and the normal contact stiffness is typically set as twice the tangential contact stiffness in some numerical simulation studies [34]. To investigate the appropriate values and their influences for the normal and tangential contact stiffnesses, this study defines a ratio η of normal to tangential contact stiffness and presents different values of η, as shown in Table 4. The difference between groups A and B in the data is that the values in group A are larger than those in group B. Specifically, the tangential contact stiffness in group A is five times that of group B. Other parameters remain unchanged in Table 2.

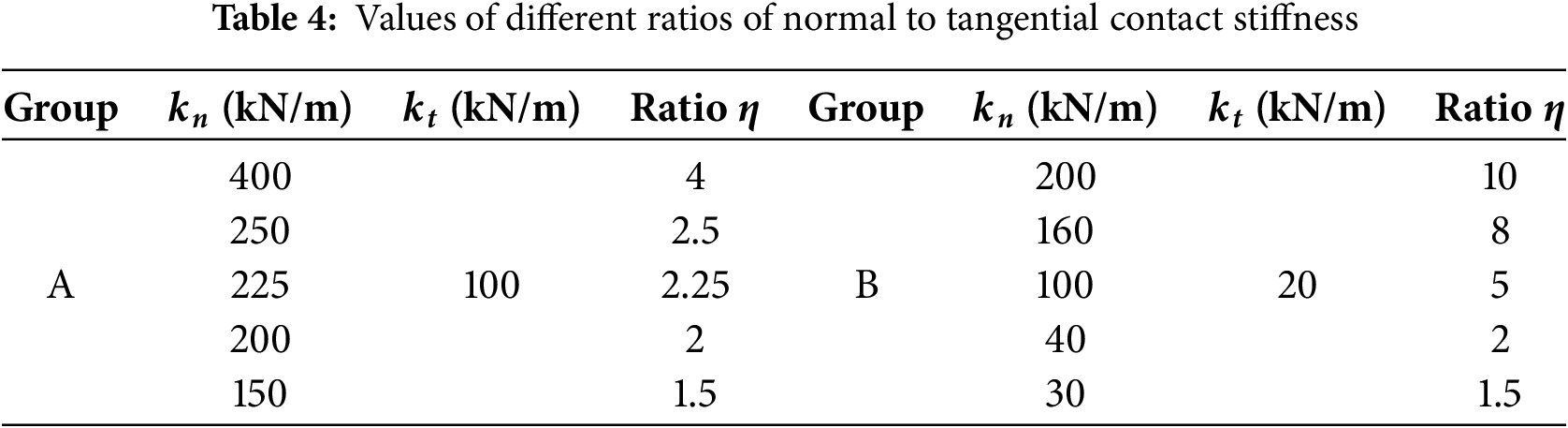
Fig. 14 gives force-displacement curves under different contact stiffness ratios η. From Fig. 14a,b, when the contact stiffness ratio η takes on a relatively large value as black lines show, the calculations no longer converge during the hardening stage. Meanwhile, by comparing Group A and Group B, it can be observed that for Group A, η must be below 2.25 to exhibit a complete linear elastic stage, hardening stage, softening stage, and critical state. However, for Group B, the range of η can be extended up to 8. This indicates that when the tangential contact stiffness kt is relatively high, such as 100 kN/m in Group A, the corresponding normal contact stiffness kn becomes more sensitive to its value. Meanwhile, it can also be observed that the ultimate strength gradually increases as η rises. Conversely, the axial strain at the point of reaching the ultimate strength gradually decreases with an increase in η. In other words, under cases of a larger contact stiffness ratio η, achieving the ultimate strength is more challenging, yet this strength can be achieved earlier. It is noted that the force-displacement curve has not reached the ultimate strength yet, when η=1.5 in Fig. 14b, and achieving the ultimate strength may require a relatively large displacement, exceeding the 30 mm loading displacement used in this paper.

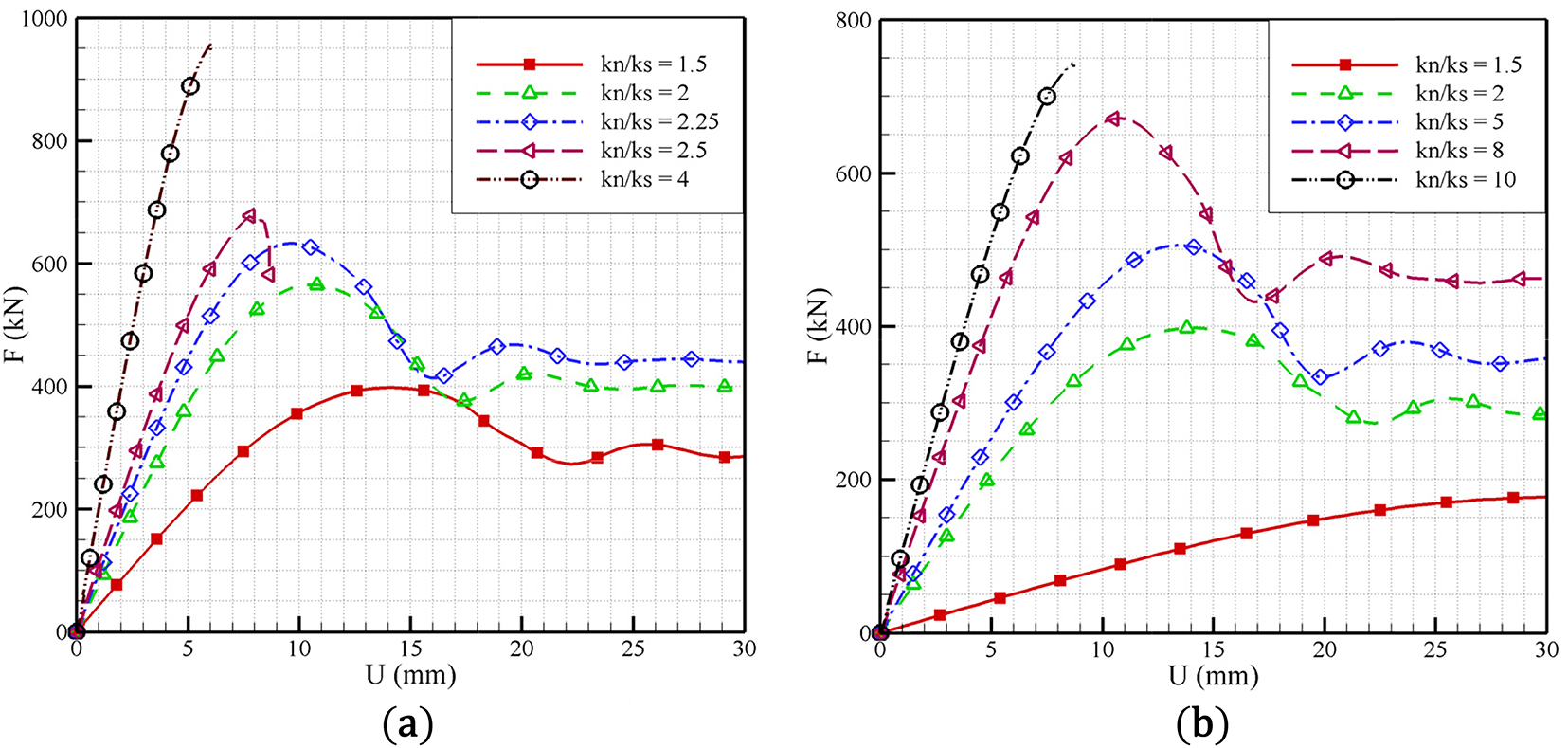
Figure 14: Force-displacement curves under different ratios of normal to tangential contact stiffness (a) group A: η=1.5,2,2.25,2.5,4 (kt=100) (b) group B: η=1.5,2,5,8,10 (kt=20)

Figs. 15 and 16 present equivalent strain distributions under different contact stiffness ratios for Group A and Group B in Table 4, respectively. In Fig. 15, X-shaped shear bands can be simulated when η≤2.25 for Group A, and the degrees and widths of strain localization also do not differ significantly. While η is 2.5, a partial double X-shaped shear band appears in the middle of the plate. When η further increases to 4, the localization phenomenon cannot be observed. Comparing the equivalent strain distributions presented in Fig. 16 for Group B to those in Fig. 15 for Group A, there are certain differences in the forms of shear bands. X-shaped shear bands can be presented when η≤8. However, as η decreases, the shear band will exhibit a certain curvature, as seen in the case when η=2. And the strain localization is not obvious, presenting a relatively homogeneous distribution instead when η=1.5. This is because the force-displacement curve is still in the hardening stage.

Figure 15: Equivalent strain distributions under η=1.5,2,2.25,2.5,4 (kt=100)

Figure 16: Equivalent strain distributions under η=1.5,2,5,8,10 (kt=20)

Based on the comprehensive analysis, when the values of normal and tangential contact stiffnesses are generally higher, it is recommended that the contact stiffness ratio η be approximately 2. On the other hand, when the values of normal and tangential contact stiffness are generally lower, the recommended range for η is 2–8.

5.4.2 The Influence of Internal Length

The internal length l is an important microscopic parameter in the proposed model, which represents the length connecting the centers of the particles, i.e., the particle diameter. It should be noted that in the macroscopic continuum models of granular material mechanics, higher-order models such as the Cosserat model are usually used. The constitutive relationships of these models include a characteristic length lc that describes the size of the microstructure. The characteristic length lc corresponding to the internal length in this model can be expressed as

lc∝l2V∝1l(23)

It indicates that the characteristic length lc is inversely proportional to the internal length l. This part discusses the influence of internal length l on strain localization and strain softening, and other parameters are also used in Table 2.

Fig. 17 gives force-displacement curves under different internal lengths l. When the internal length l is smaller, the force-displacement curve has a higher strength, and its ultimate strength can be reached earlier. It is noted that the internal length l is inversely proportional to the characteristic length lc. This implies that in situations where lc is larger, the ultimate strength is greater and is achieved earlier. This result agrees with existing conclusions [6,35]. The complete linear elastic, hardening, softening stages, and the critical state can only be exhibited when l=2,4mm. When l≥8mm, the occurrence of the critical state requires a larger loading displacement than the 30 mm in this paper. Fig. 18 presents equivalent strain distributions under different internal lengths l. It can be seen that distinct X-shaped shear bands only appear when the value of l is in the range of 2–8 mm. Among them, the shear band exhibits a certain degree of curvature when l=8mm. Therefore, the recommended value range for the internal length l, i.e., the particle diameter, is 2–4 mm in the micromechanics-based softening hyperelastic model.

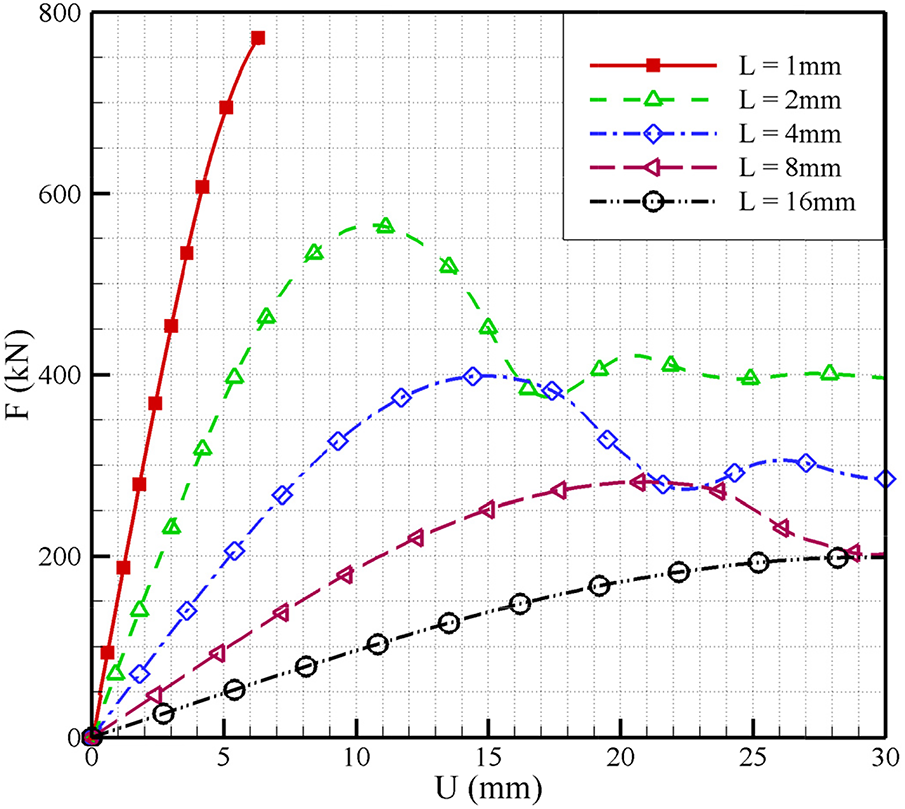
Figure 17: Force-displacement curves under different internal lengths

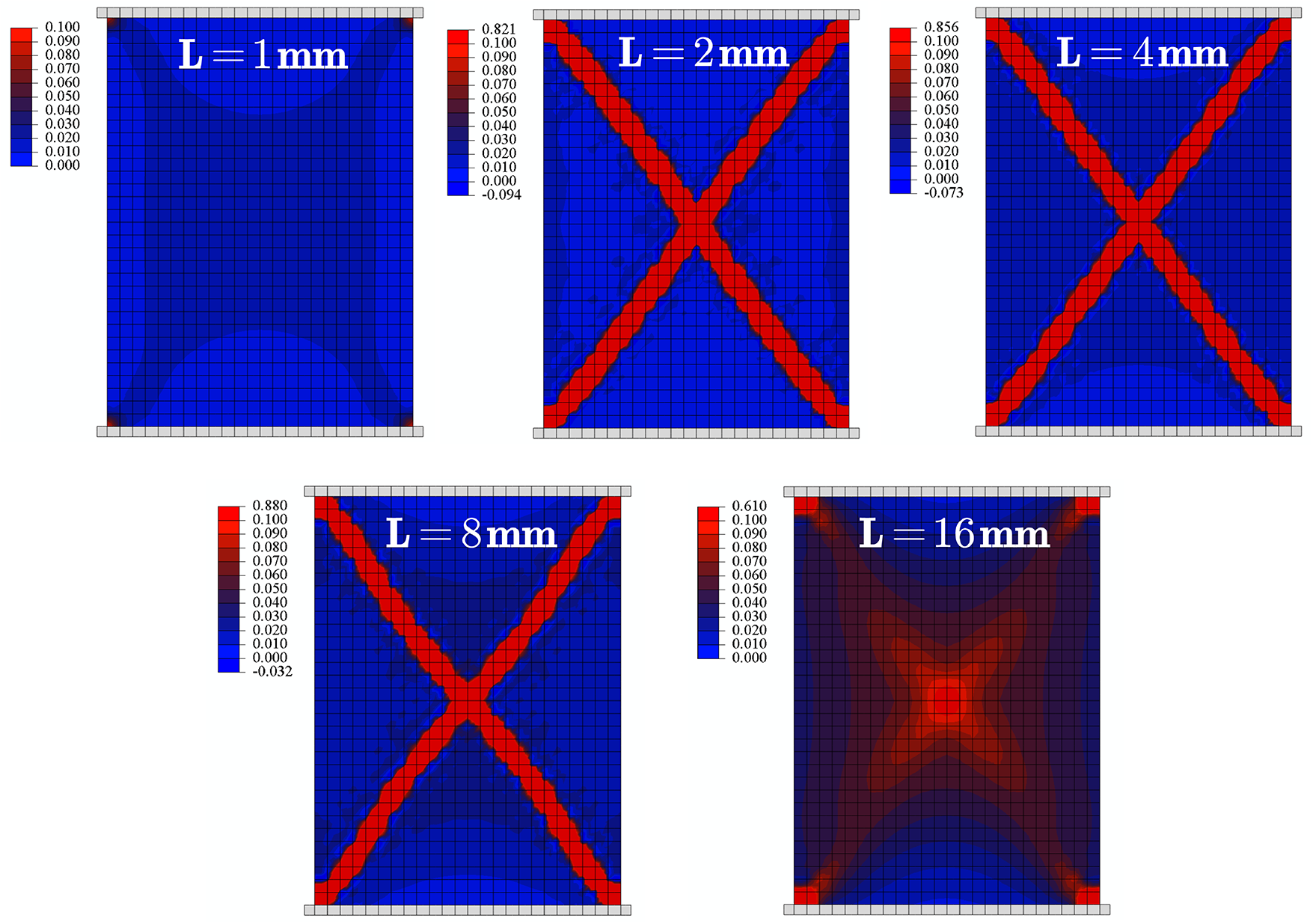
Figure 18: Equivalent strain distributions under different internal lengths

5.4.3 The Influence of Critical Failure Energy Density

The critical failure energy density Φ is given in Eq. (1), and it can determine whether granular materials enter the softening stage. Therefore, it is meaningful to discuss its influence. In this part, Φ is valued by 1,3,10,30,50kJ/m3, respectively, and other parameters are the same with those in Table 2.

Figs. 19 and 20 present the force-displacement curves and equivalent strain distributions, respectively, simulated by the micromechanics-based softening hyperelastic model under different critical failure energy densities. The results demonstrate that Φ has an important influence on the macroscopic mechanical behaviors of granular materials, underscoring the physical role of an energy threshold in the material failure process. Specifically, when Φ is low (≤10 kJ/m3), the stored strain energy in the system rapidly reaches this low critical threshold, leading to prematurely trigger inelastic mechanisms. Macroscopically, this shows as obvious strain softening, distinct residual strengths, and well-developed X-shaped shear bands (shown in Fig. 20). It is noteworthy that as Φ decreases, the shear bands become narrower and more intensely localized. This indicates that energy dissipation is concentrated within a more confined zone and characterizes a more brittle failure mode. Conversely, when Φ increases to 30 kJ/m3 and above, the system can sustain higher strain energy without instability, causing the macroscopic response to approach ideal hyperelasticity or perfect plasticity; therefore, it fails to capture realistic softening and localization.

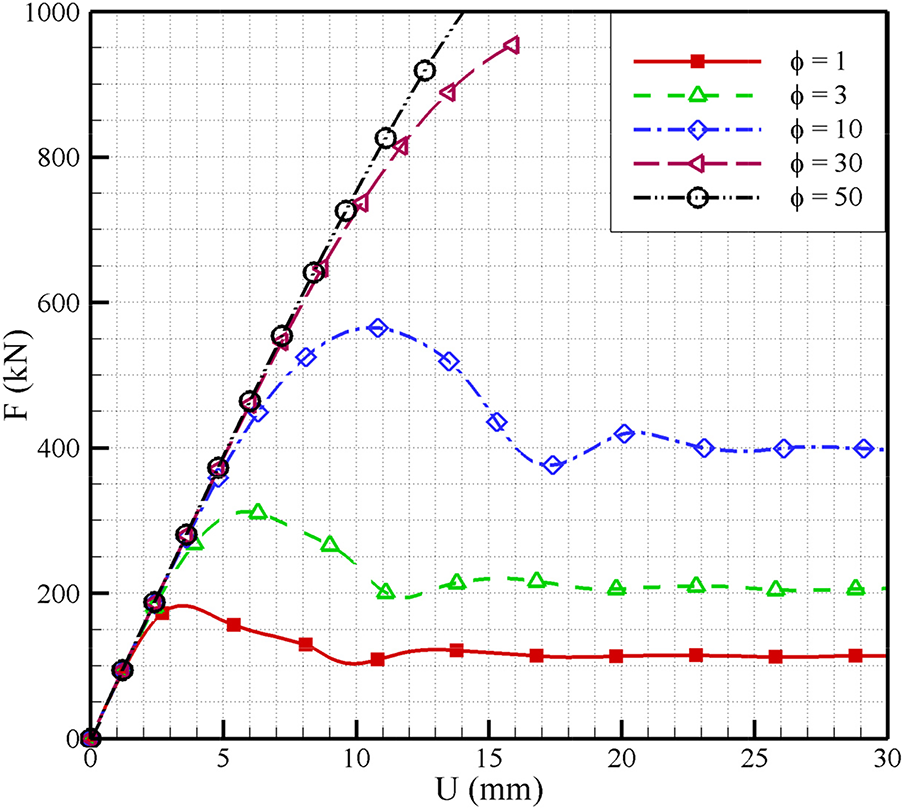
Figure 19: Force-displacement curves under different critical failure energy densities

Figure 20: Equivalent strain distributions under different critical failure energy densities

This study identifies that a value of Φ on the order of 10 kJ/m3 enables the model to simulate key granular material behaviors, including complete stress-strain responses with strain softening and the development of obvious X-shaped shear bands. The parametric study reveals the model’s high sensitivity to Φ, underscoring its role as a constitutive parameter that intrinsically controls the material’s macroscopic energy dissipation capacity. While the current study establishes this clear macro-scale phenomenological link, quantitatively connecting this critical energy density to specific micro-scale mechanisms (such as inter-particle friction and fabric evolution) remains a valuable objective for future study. Nonetheless, compared with empirical parameters in conventional models, the critical failure energy density provides a more physically intuitive basis for simulating failure.

5.5 Mesh Independence Analysis

Owing to the existence of the internal length that describes the microstructural size of granular materials in this model, a regularization mechanism is provided, which helps to avoid pathological mesh dependency. In order to investigate the mesh independence of the proposed model, Fig. 21 gives four finite element meshes: 18 × 24, 24 × 32, 30 × 40 and 60 × 80. Parameters are used in Table 2.

Figure 21: Different finite element meshes for the plate model (a) 18 × 24 (b) 24 × 32 (c) 30 × 40 (d) 60 × 80

Fig. 22 shows force-displacement curves under four different meshes. For the coarsest mesh 18 × 24, the curve exhibits non-convergence after the linear elastic stage; therefore, strain localization cannot be presented simultaneously. As the mesh size decreases, all cases can basically converge to the same force-displacement curve. For further quantitative analysis, a relative error in the L2-norm for the load-displacement curves is proposed in this study. The result from the finest mesh (60 × 80) is taken as the reference solution. The relative L2 error er for a coarser mesh is computed by

er=‖Fcoarse−Ffine‖L2‖Ffine‖L2(24)

where F denotes the force vector. The calculated errors are summarized in Table 5. It shows that refining the mesh from 18 × 24 to 24 × 32 reduces the relative L2 error markedly from 8.52% to 1.73%. Further refinement to 30 × 40 only slightly lowers the error to 1.18%, indicating full convergence. The 24 × 32 mesh, with an error below 2%, meets engineering accuracy requirements while saving substantial computational cost. Besides, Fig. 23 gives equivalent strain distributions under four different meshes. The observed variation in shear band width (from 45.0 to 42.5 to 40.3 mm) indeed occurs during the initial refinement stages. However, the key point is the convergence trend. The relative change in shear band width decreases significantly with each refinement: a 5.6% reduction from the 24 × 32 to the 30 × 40 mesh, and a further 5.2% reduction to the 40 × 60. It indicates that the simulation by the proposed model is robust with respect to mesh refinement, as the force-displacement curve and shear band width are not significantly affected by the reduction in mesh size. Therefore, the 24 × 32 mesh used in the previous parts is appropriate, which can save a considerable amount of computation time, representing the optimal balance.

Figure 22: Force-displacement curves under different meshes

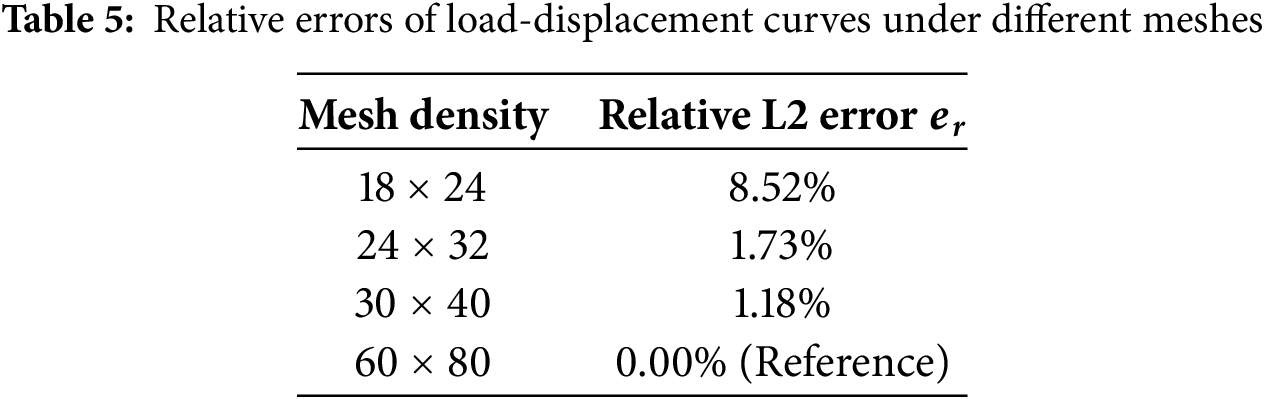
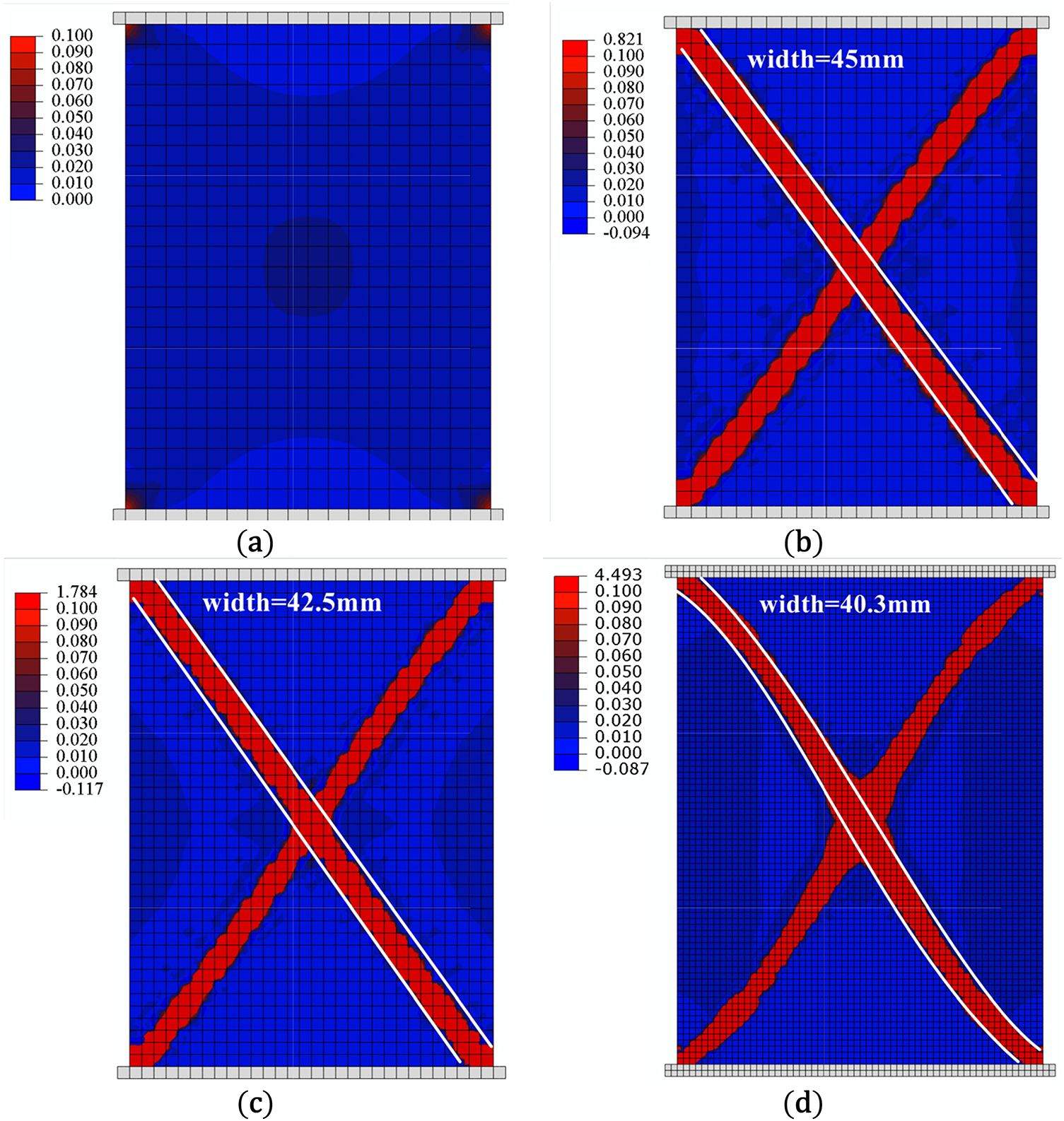
Figure 23: Equivalent strain distributions under different meshes (a) 18 × 24 (b) 24 × 32 (c) 30 × 40 (d) 60 × 80

5.6 Simulations of Slope Instability Issue

This section uses the micromechanics-based softening hyperelastic model to simulate and analyze the slope instability issue.

5.6.1 Simulation on the Slip Surface of the Slope

A 19.2 m × 9.6 m slope model with 24 × 24 mesh and its boundary conditions are given in Fig. 24. The slope is subjected to an eccentric compression load through the rigid slab on the top, and the eccentricity is 0.6 m. And a 0.4 m vertical displacement loads at the eccentric point. Table 6 gives the parameters for the slope model; different contact stiffness ratios are investigated in this part.

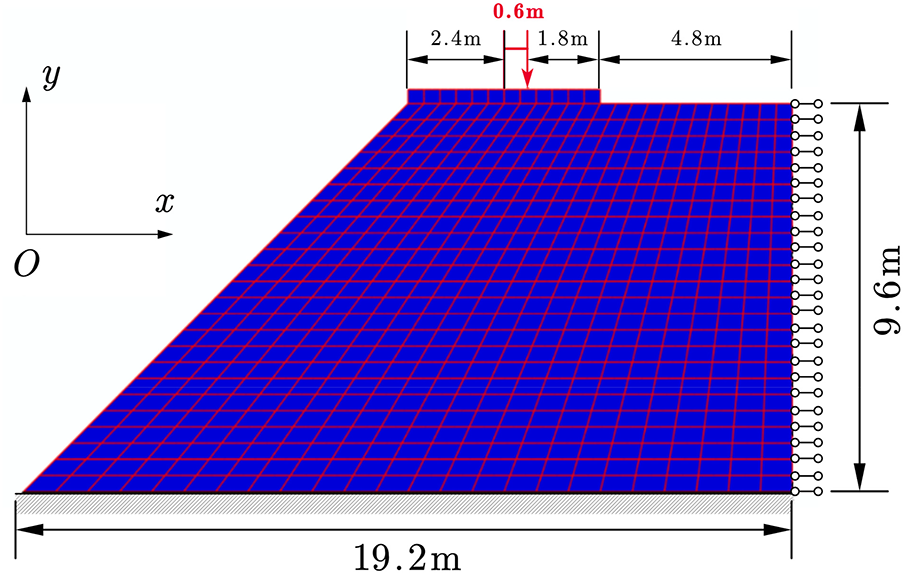
Figure 24: Schematic diagram of the slope model

Fig. 25 gives force-displacement curves for the slope model under different contact stiffness ratios η. It can be seen that the overall pattern is similar to that presented in Fig. 14, i.e., the ultimate strength is positively related to η. The key difference is that the critical state is more significantly influenced by the contact stiffness ratio η. The situations with η=4,8 cannot present critical states. And equivalent strain distributions are correspondingly given in Fig. 26. The strain localization zones represent the slip surfaces of slopes, which appear as penetrating narrow-band zones from the right of the rigid slab to the middle left of the slope, as shown in Fig. 26a,b. And the widths of both slip surfaces are approximately 0.7 m. The contact stiffness ratio η has a significant influence on the shape of the slip surface. The penetrating slip surfaces cannot be presented when η=4,8, because the critical states are not simulated in these situations. And the length of the slip surface is negatively related to η. Therefore, in numerical simulations, it is suggested to avoid larger values for the contact stiffness ratio η, with a typical recommended value of 2.

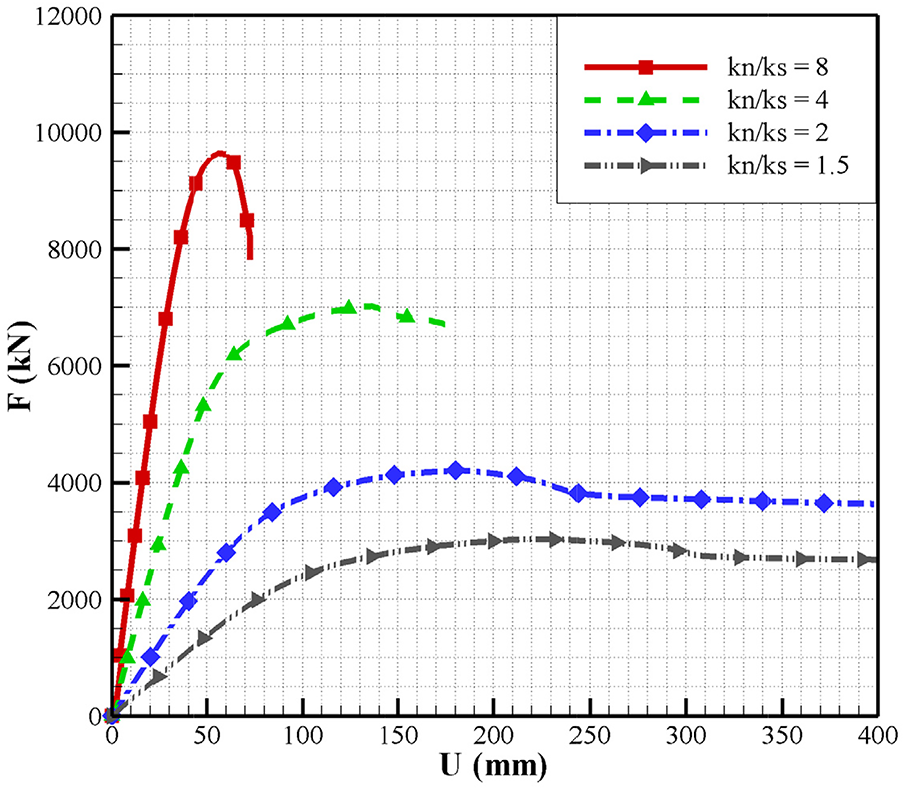
Figure 25: Force-displacement curves for the slope model under different contact stiffness ratios

Figure 26: Equivalent strain distributions for the slope model under different contact stiffness ratios (a) η=1.5 (b) η=2 (c) η=4 (d) η=8

Furthermore, this study investigates the evolution process of the slip surface, considering the case when η=2, as shown in Fig. 27. It is noted that the strain distribution diagrams are magnified by a factor of 3 to highlight the slip surfaces more clearly. It shows that the strain localization first occurs near the right of the rigid slab at the end of the linear elastic stage, and it gradually develops downwards with strain hardening and softening. When the loading displacement reaches approximately 250 mm, i.e., the end of the softening stage, the strain localization forms a penetrating narrow-band zone to the middle left of the slope, which corresponds to the initial form of the slip surface. After entering the critical state, as the degree of strain localization increases, the slip surface ultimately forms for the slope.

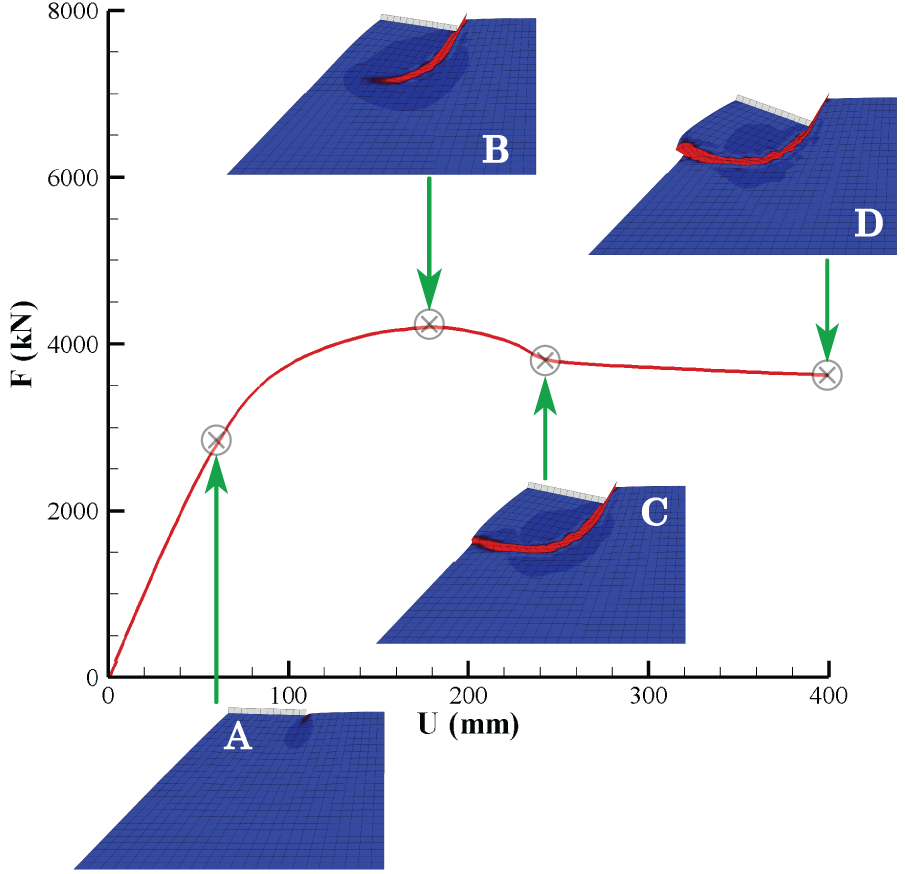
Figure 27: Evolution process of slip surface of slope when contact stiffness ratio η=2

5.6.2 Comparative Analysis between Micromechanics-Based Softening Hyperelastic and Abaqus DP Models

Then, a comparative analysis is conducted with results of the micromechanics-based softening hyperelastic model and Abaqus DP model for simulating the slip surface of slope. The parameters are used in Table 7, and the contact stiffness ratio η is set to 2 as indicated above.

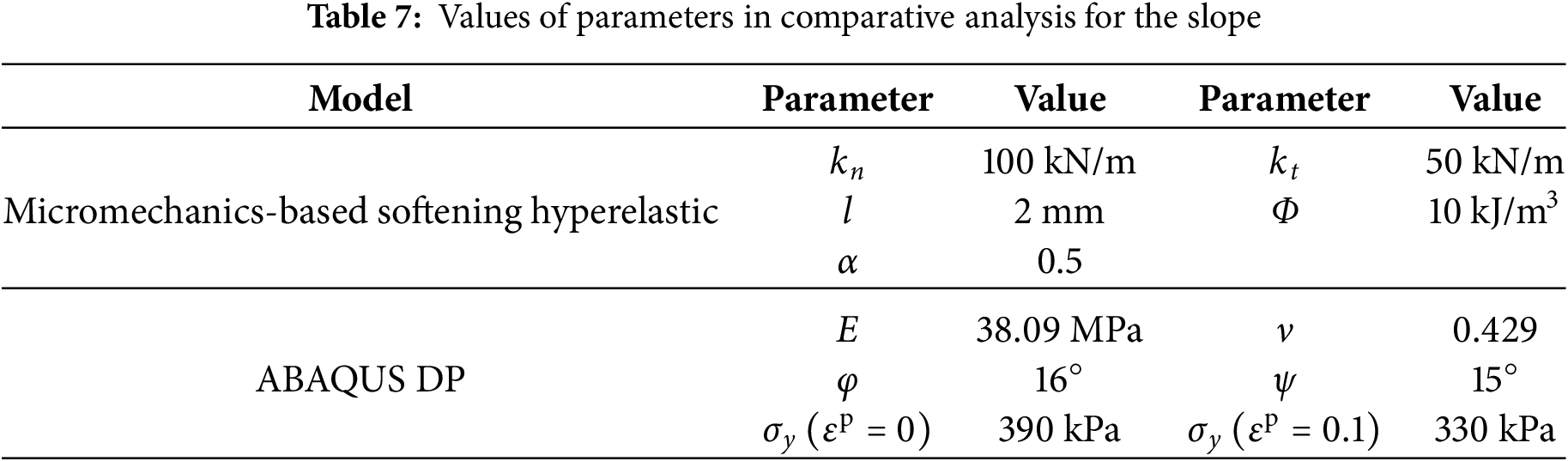
Fig. 28 gives force-displacement curves for the slope simulated by micromechanics-based softening hyperelastic and Abaqus DP models. Using the parameters in Table 7, the curves show good agreement in the elastic stage, hardening stage, and ultimate strength. However, the post-peak softening degree in the DP model is significantly less than that in the micromechanics-based model. This discrepancy originates from their fundamental constitutive frameworks. The softening in the presented model is a result of continuous evolution, naturally derived from a single hyperelastic potential function embedded with microstructural information, where the sharp strength drop reflects the physical essence of microstructural instability. In contrast, the DP model is a staged, phenomenological model whose softening mainly relies on the definition of the yield surface and a user-prescribed softening law that lacks a direct connection to micromechanisms. Therefore, the observed difference is an inevitable manifestation of these two modeling approaches in describing material instability, arising from intrinsic theoretical distinctions. Furthermore, Fig. 29 presents the equivalent plastic strain distributions for the slope from both models. Although the shapes of the slip surfaces and the degrees of strain localization are generally similar, the slip surface in the DP model is about 0.1 m wider than that in the micromechanics-based model. This difference results from the intrinsic distinctions in how the two theoretical frameworks describe the localization process. The micromechanics-based model, through its internal length scale, provides a physical constraint on the concentration of the strain localization band. In contrast, the DP model, as a macroscopic phenomenological theory, lacks such an internal scale related to micro-geometric characteristics within its framework. This results in a different representation in controlling the localization band width compared with the micro-mechanics-based approach.

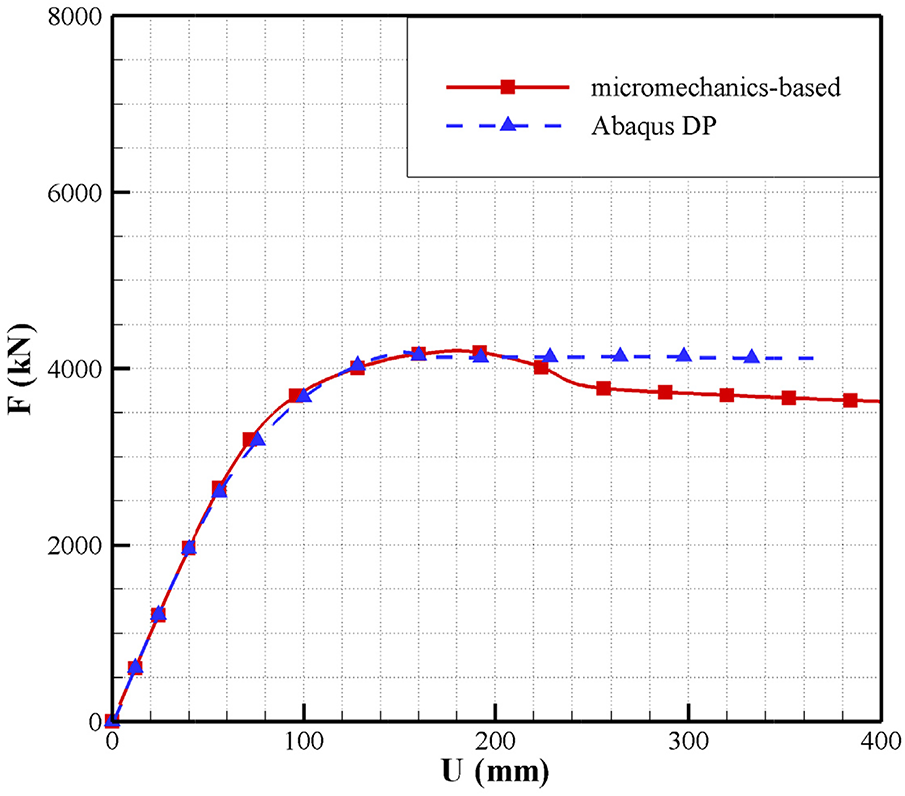
Figure 28: Force-displacement curves simulated by different models for the slope model

Figure 29: Equivalent strain distributions of the slope model simulated by (a) micromechanics-based softening hyperelastic model and (b) Abaqus Drucker-Prager model

5.6.3 The Influence of Softening Factor

In the previous section, the influence of the softening factor on strain localization and strain softening is discussed for the flat plate compression numerical test. This part continues to investigate its influence on the slope instability issue. The microscopic parameters are the same with those in Table 7.

Figs. 30 and 31 respectively show force-displacement curves and equivalent strain distributions for the slope model under different softening factors. Fig. 31 exhibits certain patterns similar to those in Fig. 10, but there are also distinct differences. The force-displacement curves can demonstrate the complete process from the linear elastic stage to the critical state, only when α=0.5,0.7. Correspondingly, the penetrating slip surfaces only appear when α=0.5,0.7. It tends to show a form of double slip surfaces when α=0.1,0.3. However, due to the non-convergence of calculations, the slip surfaces cannot continue to expand. When α is 1.0, it corresponds to the complete softening state. However, the calculation also fails to converge; therefore, the slip surface does not penetrate either.

Figure 30: Force-displacement curves for the slope model under different softening factors

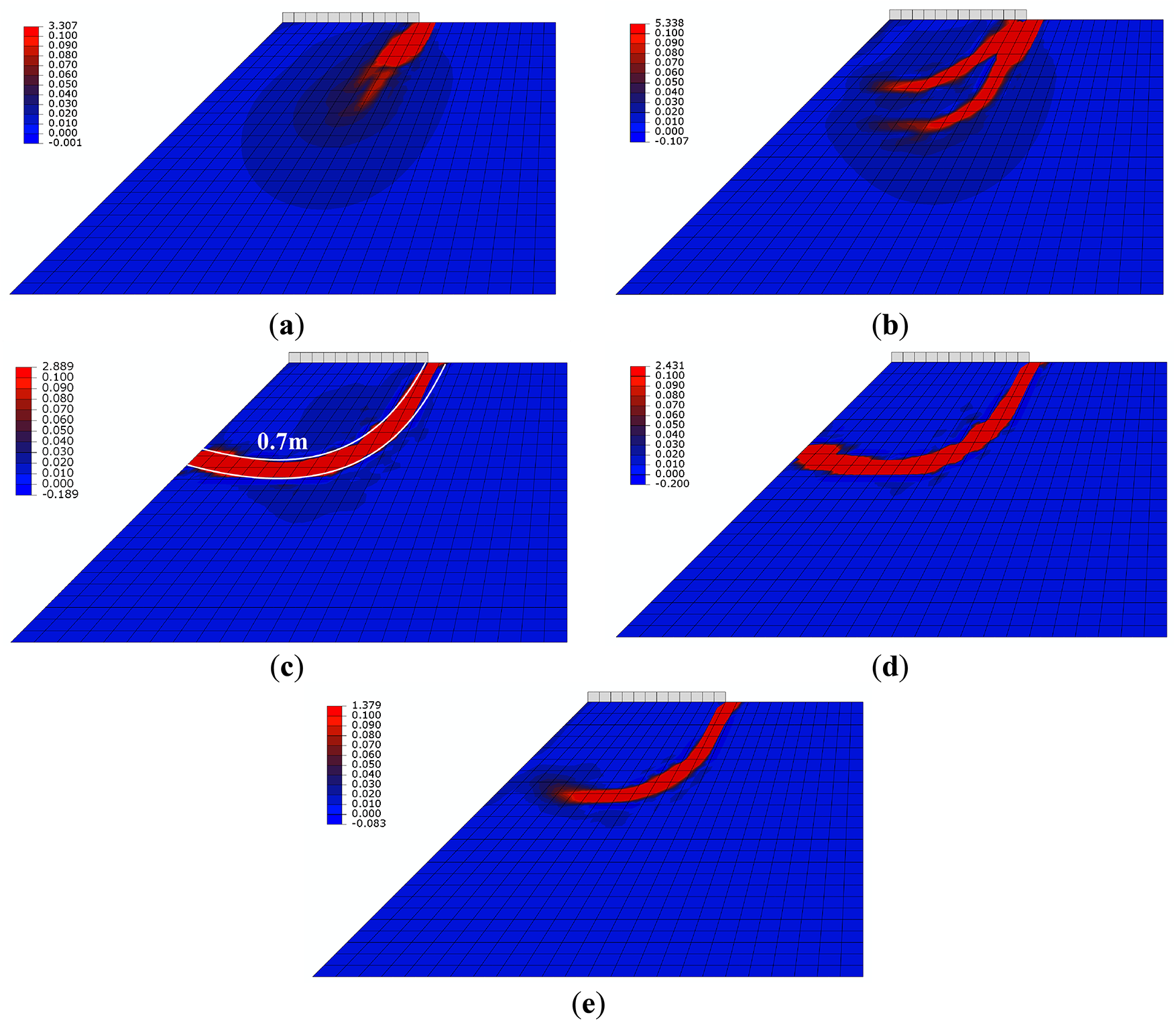
Figure 31: Equivalent strain distributions of the slope model simulated by the micromechanics-based softening hyperelastic model with different softening factors (a) α=0.1 (b) α=0.3 (c) α=0.5 (d) α=0.7 (e) α=1.0

5.6.4 Slip Surface of Slope under Different Microstructures

The discussion in the preceding text has validated the influence of microstructure on strain localization and strain softening for granular materials, through the flat plate compression numerical test.

Figs. 32 and 33 respectively give force-displacement curves and equivalent strain distributions of granular materials with isotropic directional contact distribution density and different microstructures for the slope model. The overall pattern of the force-displacement curves is basically consistent with that presented in Fig. 12. However, for granular materials with different microstructures in Fig. 32, their critical states are not clearly enough defined, compared with the case of isotropic directional contact distribution density. Correspondingly, their degrees of localizations are lower than that of the case of isotropic directional distribution density, as shown in Fig. 33. For cases with different microstructures, the widths of their slip surfaces are basically the same, all around 0.6 m, which is smaller than that in the case of isotropic directional contact distribution density.

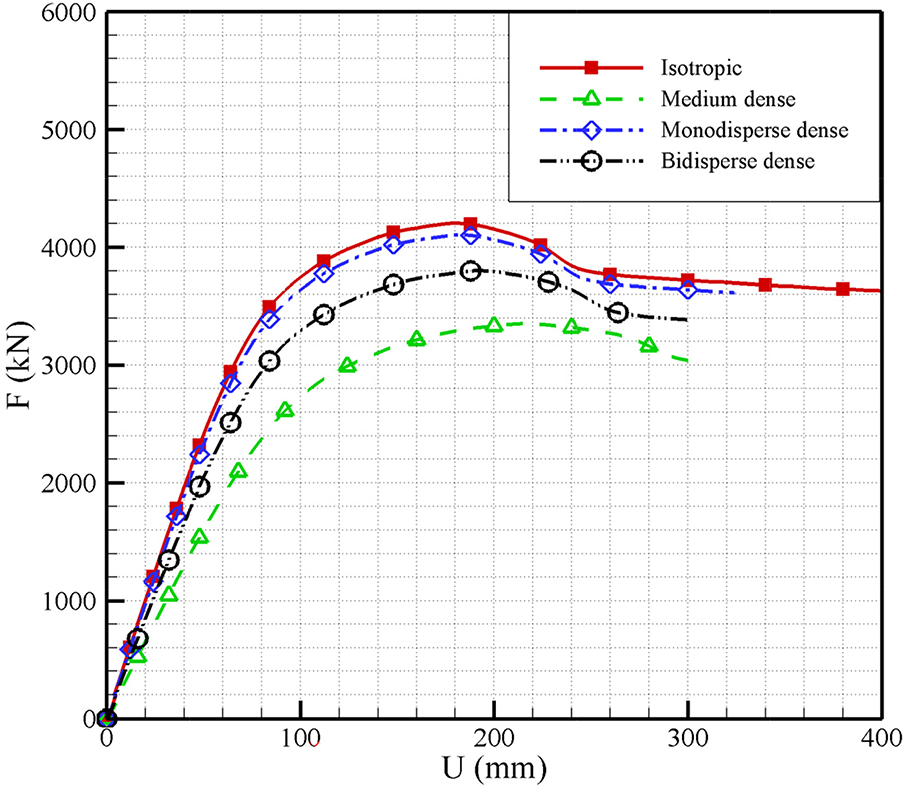
Figure 32: Force-displacement curves of granular materials with different microstructures for the slope model

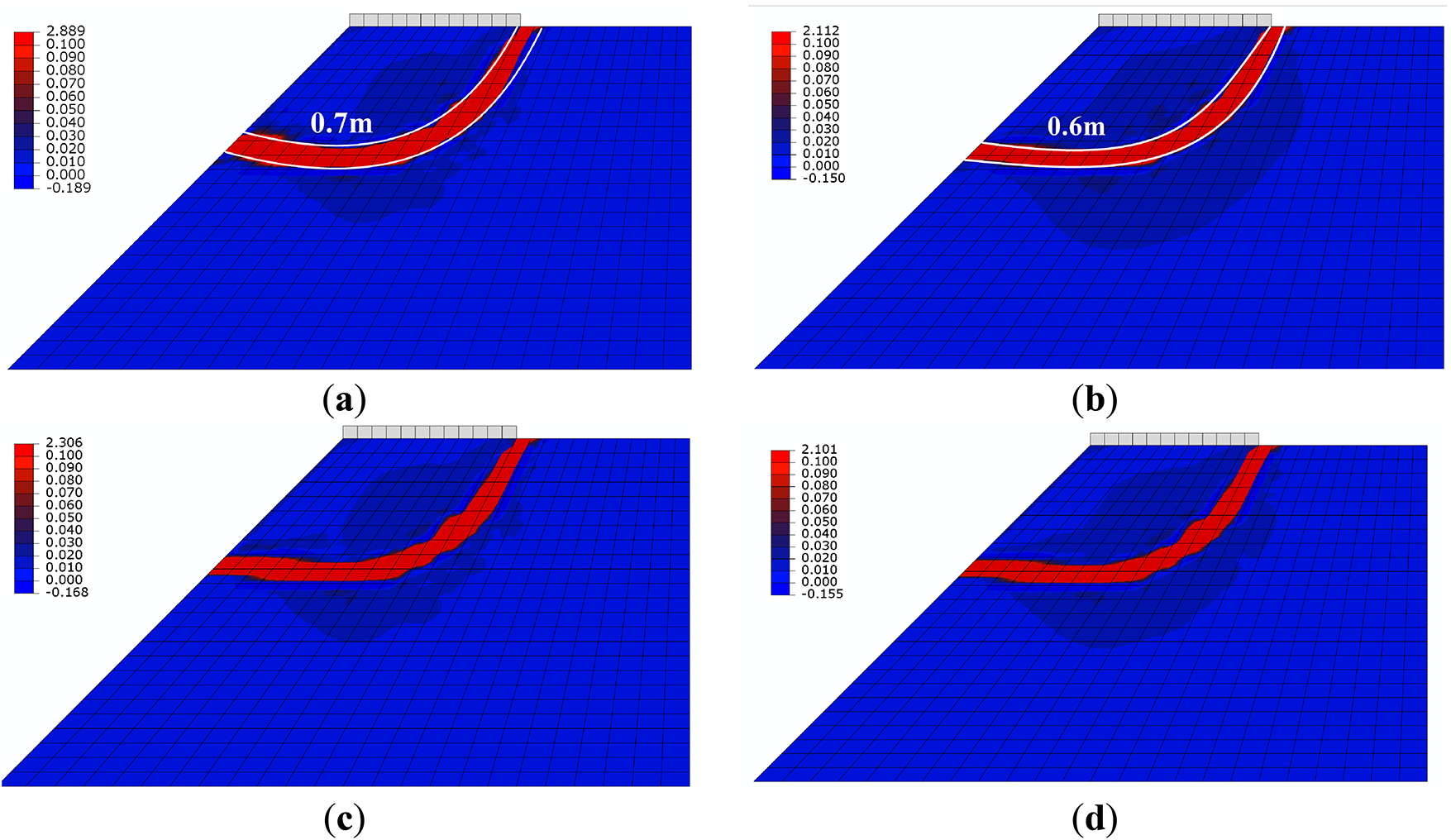
Figure 33: Equivalent strain distributions of granular materials with (a) isotropic directional density distribution (b) medium dense microstructure (c) monodisperse dense microstructure (d) bidisperse dense microstructure

6  Conclusions

This paper presents a novel micromechanics-based softening hyperelastic model for granular materials, integrating softening hyperelasticity with microstructural insights. It considers an isotropic directional contact distribution density and three specific microstructures for granular materials, and the hyperelastic constitutive modulus tensors are explicitly derived. The proposed model offers two key advantages: First, it has a clear conceptualization, straightforward formulation, and ease of numerical implementation under the hyperelastic framework. Second, it effectively incorporates micro-scale microstructural information to reveal its influences on macroscopic mechanical behaviors of granular materials. A softening factor is introduced to describe the critical state, and numerical implementation is achieved via the User Material (UMAT) subroutine in Abaqus. The model successfully simulates strain localization and strain softening, with the influences of microstructural information are thoroughly investigated. The principal conclusions are summarized as follows:

(1)   By introducing the critical state, the proposed model can capture a complete mechanical response process of a linear elastic stage, a hardening stage, a softening stage, and a critical state with the residual strength. The continuous X-shaped shear bands are simulated, and the evolution process of strain localization is obtained under the consideration of the critical state. Results by the micromechanics-based softening hyperelastic model are compared with the macro-scale Volokh softening hyperelastic model, Abaqus Drucker-Prager model, and the experiment to verify the validity of the proposed model.

(2)   The influence of the softening factor α is investigated, with a recommended range of 0.3–0.7 for accurately describing strain softening, the critical state, and strain localization.

(3)   Microstructural porosity significantly affects the mechanical behaviors of granular materials. Simulations using a micromechanics-based softening hyperelastic model reveal that strength characteristics vary with microstructure porosity. The isotropic directional contact distribution density assumption, ignoring voids, yields the highest strength, while the monodisperse dense microstructure, with minimal porosity, approaches this strength. In contrast, the medium dense microstructure, with higher porosity, shows the lowest strength. These results highlight the critical role of porosity in determining macroscopic mechanical responses of granular materials.

(4)   The influences of important parameters—normal to tangential contact stiffness ratio (η), internal length (l), and critical failure energy density (Φ)—are analyzed. For η, a value of 2 is recommended for high-stiffness cases and 2–8 for low-stiffness ones. A higher η increases ultimate strength but delays its attainment, while also influencing shear band formation. The internal length l, inversely proportional to the characteristic length, is optimal in the range of 2–4 mm, with smaller l leading to higher and earlier-reached ultimate strength. For Φ, cases of values ≤10kJ/m3 enable the complete process from the linear elastic stage to the critical state with the distinct X-shaped shear band. Φ=10kJ/m3 is an appropriate value for describing granular material behaviors.

(5)   The mesh independence for numerical simulations based on this proposed model is discussed. As the model introduces an internal length describing the microstructural size, it can basically eliminate the pathological mesh dependency.

(6)   The model is applied to simulate slope instability, capturing the evolution of the slip surface and corresponding force-displacement curve. The slip surface of the slope presents a penetrating narrow-band zone to the middle left of the slope. Compared with the Abaqus DP model, the proposed model shows minor differences during the softening stage. Influences of softening factor α, contact stiffness ratio η and microstructures are similar to those observed for the plate model.

Acknowledgement: Not applicable.

Funding Statement: This work is supported by the National Natural Science Foundation of China through grant numbers 12002245 and 12172263, the Science and Technology Research Program of Chongqing Municipal Education Commission through grant number KJQN202300742, the National Natural Science Foundation of Chongqing Municipality through grant number CSTB2025NSCQ-GPX0841, and Chongqing Jiaotong University through grant number F1220038.

Author Contributions: Chenxi Xiu: Conceptualization, Funding acquisition, Supervision, Investigation, Methodology, Software, Writing—original draft, Writing—review & editing. Xihua Chu: Conceptualization, Methodology, Funding acquisition, Writing—review & editing. Ao Mei: Investigation, Writing—review & editing. Liangfei Gong: Software, Writing—review & editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A Identification Procedure of Constitutive Modulus Tensor:

This appendix shows how to get the specific constitutive tensor (Eq. (18)) from the general formula (Eq. (14)) for the medium dense microstructure. The general constitutive modulus tensor is given in Eq. (14). To find the tensor for a specific microstructure, the discrete sums over all contacts in the RVE must be calculated. For the medium dense structure (coordination number = 8), it assumes equal-sized particles, so the branch vector is Lja=lnj. The sums now depend only on the contact directions (ni, ti, si). Then, the sums are calculated for all 8 contacts in the unit cell, taking D1111 as an example.

Let i=j=k=l, and the general formula of D1111 becomes

D1111=e−W/Φ2Vkn[∑a=18L1aL1an1n1−kn2ΦV(∑a=18L1an1)2]+e−W/Φ2Vkt[∑a=18L1aL1a(t1t1+s1s1)−kt2ΦV(∑a=18L1at1)2−kt2ΦV(∑a=18L1as1)2](A1)

Substitute L1a=ln1:

D1111=e−W/Φ2Vknl2[∑a=18(n1)4−knl22ΦV(∑a=18(n1)2)2]+e−W/Φ2Vktl2[∑a=18(n1)2((t1)2+(s1)2)−ktl22ΦV(∑a=18n1t1)2−ktl22ΦV(∑a=18n1s1)2](A2)

Then, the sums in Eq. (A2) can be obtained as

∑a=18(n1)4=92,∑a=18(n1)2((t1)2+(s1)2)=32,∑a=18n1t1=∑a=18n1s1=32(A3)

Substituting back to Eq. (A3), the final component is obainted:

D1111=3l2e−W/Φ4V[3kn(1−knNV2Φ)+kt(1−ktNV2Φ)](A4)

Repeating this process for all index combinations (i,j,k,l) and the applying symmetry of the medium dense structure, The full constitutive tensor can be derived in Eq. (18).

The constitutive modulus tensors for the monodisperse dense and bidisperse dense microstructures (Eqs. (19) and (20)) are derived in the same manner, differing only in the specific contact orientations and coordination numbers used in the discrete summations. Their detailed derivations are omitted here for brevity.

Appendix B Numerical Implementation:

The governing equation for the quasi-static mechanical response of granular materials is the equilibrium equation in the strong form:

∇⋅σ+b=0 in Ω(A5)

where σ is the Cauchy stress tensor derived from the proposed micromechanics-based softening hyperelastic model (Eq. (15)), b and is the body force vector. The boundary conditions are:

u=u¯ on Γu(A6)

σ⋅n=t¯onΓt(A7)

where u¯ and t¯ are prescribed displacements and tractions, respectively, and n is the unit outward normal vector.

The weak form is derived using the principle of virtual work:

∫Ωσ:δεdV=∫Ωb⋅δudV+∫Γtt¯⋅δudS(A8)

where δu is the virtual displacement field, and δε=12[∇(δu)+(∇(δu))T] is the virtual strain tensor.

The domain Ω is discretized into finite elements. The displacement field u is approximated as:

u≈Nue(A9)

where N is the matrix of shape functions and ue is the nodal displacement vector of element e. The strain tensor is then:

ε≈Bue(A10)

where B is the strain-displacement matrix.

Substituting into the weak form yields the discrete system of equations:

KU=F(A11)

where K is the global stiffness matrix, U is the global nodal displacement vector, and F is the global force vector. The element stiffness matrix and force vector are:

Ke=∫ΩeBTDBdV,Fe=∫Ωeb⋅δudV+∫ΓteNTt¯dS(A12)

here, D is the constitutive modulus tensor defined in Eq. (14) and further specified for different microstructures in Eqs. (17)–(20). The softening evolution is embedded in D through the energy term W and the softening factor α in Eq. (21).

The nonlinear system is solved using the Newton-Raphson method, and the UMAT subroutine in Abaqus is used to update D and σ at each integration point based on the current strain state.

References

1. Yuan J, Zhang Q, Li B, Zhao X. Experimental analysis of shear band formation in plane strain tests on Shanghai silty clay. Bull Eng Geol Environ. 2013;72(1):107–14. doi:10.1007/s10064-012-0453-4. [Google Scholar] [CrossRef]

2. Lu D, Dong H, Lin Q, Guo C, Gao Z, Du X. A method for characterizing the deformation localization in granular materials using the relative particle motion. Comput Geotech. 2023;156:105262. doi:10.1016/j.compgeo.2023.105262. [Google Scholar] [CrossRef]

3. Phan QT, Bui HH, Nguyen GD, Nicot F. Strain localization in the standard triaxial tests of granular materials: insights into meso- and macro-scale behaviours. Num Anal Meth Geomech. 2024;48(5):1345–71. doi:10.1002/nag.3687. [Google Scholar] [CrossRef]

4. Li N, Ma B, Wang H, Sun W. Development of elasto-plastic constitutive model for unbound granular materials under repeated loads. Transp Geotech. 2020;23:100347. doi:10.1016/j.trgeo.2020.100347. [Google Scholar] [CrossRef]

5. Tang H, Wei W, Liu F, Chen G. Elastoplastic Cosserat continuum model considering strength anisotropy and its application to the analysis of slope stability. Comput Geotech. 2020;117:103235. doi:10.1016/j.compgeo.2019.103235. [Google Scholar] [CrossRef]

6. Xiu C, Chu X. A micromorphic elastoplastic model and finite element simulation on failure behaviors of granular materials. Num Anal Meth Geomech. 2020;44(4):484–515. doi:10.1002/nag.3034. [Google Scholar] [CrossRef]

7. Tian J, Lai Y, Liu E, He C. A thermodynamics-based micro-macro elastoplastic micropolar continuum model for granular materials. Comput Geotech. 2023;162:105653. doi:10.1016/j.compgeo.2023.105653. [Google Scholar] [CrossRef]

8. Houlsby GT, Amorosi A, Rojas E. Elastic moduli of soils dependent on pressure: a hyperelastic formulation. Géotechnique. 2005;55(5):383–92. doi:10.1680/geot.55.5.383.66021. [Google Scholar] [CrossRef]

9. Jiang Y, Liu M. A brief review of granular elasticity: why and how far is sand elastic? Eur Phys J E Soft Matter. 2007;22(3):255–60. doi:10.1140/epje/e2007-00009-x. [Google Scholar] [PubMed] [CrossRef]

10. Chang J, Chu X, Xu Y. A softening hyperelastic model and simulation of the failure of granular materials. Geomech Eng. 2014;7(4):335–53. doi:10.12989/gae.2014.7.4.335. [Google Scholar] [CrossRef]

11. Amorosi A, Rollo F, Houlsby GT. A nonlinear anisotropic hyperelastic formulation for granular materials: comparison with existing models and validation. Acta Geotech. 2020;15(1):179–96. doi:10.1007/s11440-019-00827-5. [Google Scholar] [CrossRef]

12. Xiao Y, Zhang Z, Wang J. Granular hyperelasticity with inherent and stress-induced anisotropy. Acta Geotech. 2020;15(3):671–80. doi:10.1007/s11440-019-00768-z. [Google Scholar] [CrossRef]

13. Volokh KY. Hyperelasticity with softening for modeling materials failure. J Mech Phys Solids. 2007;55(10):2237–64. doi:10.1016/j.jmps.2007.02.012. [Google Scholar] [CrossRef]

14. Volokh KY. Softening hyperelasticity for modeling material failure: analysis of cavitation in hydrostatic tension. Int J Solids Struct. 2007;44(14–15):5043–55. doi:10.1016/j.ijsolstr.2006.12.022. [Google Scholar] [CrossRef]

15. Lei D, Huang J, Xu W, Wang W, Zhang P. Deformation analysis of shear band in granular materials via a robust plane shear test and numerical simulation. Powder Technol. 2018;323:385–92. doi:10.1016/j.powtec.2017.10.027. [Google Scholar] [CrossRef]

16. Zhu H, Zhou WH, Yin ZY. Deformation mechanism of strain localization in 2D numerical interface tests. Acta Geotech. 2018;13(3):557–73. doi:10.1007/s11440-017-0561-1. [Google Scholar] [CrossRef]

17. Cao W, Mei J, Yang X, Zhou W, Chang X, Ma G. A network-based investigation on static liquefaction of sheared granular materials. Granul Matter. 2024;26(3):60. doi:10.1007/s10035-024-01433-3. [Google Scholar] [CrossRef]

18. Guo N, Yang Z, Yuan W, Zhao J. A coupled SPFEM/DEM approach for multiscale modeling of large-deformation geomechanical problems. Num Anal Meth Geomech. 2021;45(5):648–67. doi:10.1002/nag.3175. [Google Scholar] [CrossRef]

19. Li X, Liu Q, Zhang J. A micro-macro homogenization approach for discrete particle assembly-Cosserat continuum modeling of granular materials. Int J Solids Struct. 2010;47(2):291–303. doi:10.1016/j.ijsolstr.2009.09.033. [Google Scholar] [CrossRef]

20. Zhao S, Zhao J, Liang W, Niu F. Multiscale modeling of coupled thermo-mechanical behavior of granular media in large deformation and flow. Comput Geotech. 2022;149:104855. doi:10.1016/j.compgeo.2022.104855. [Google Scholar] [CrossRef]

21. Chang CS, Ma L. Modeling of discrete granulates as micropolar continua. J Eng Mech. 1990;116(12):2703–21. doi:10.1061/(asce)0733-9399(1990)116:12(2703). [Google Scholar] [CrossRef]

22. Chang CS, Lun M. Elastic material constants for isotropic granular solids with particle rotation. Int J Solids Struct. 1992;29(8):1001–18. doi:10.1016/0020-7683(92)90071-Z. [Google Scholar] [CrossRef]

23. Xiu C, Chu X, Wang J, Wu W, Duan Q. A micromechanics-based micromorphic model for granular materials and prediction on dispersion behaviors. Granul Matter. 2020;22(4):74. doi:10.1007/s10035-020-01044-8. [Google Scholar] [CrossRef]

24. Talebi H, Silani M, Bordas SPA, Kerfriden P, Rabczuk T. A computational library for multiscale modeling of material failure. Comput Mech. 2014;53(5):1047–71. doi:10.1007/s00466-013-0948-2. [Google Scholar] [CrossRef]

25. Goswami S, Anitescu C, Chakraborty S, Rabczuk T. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture. Theor Appl Fract Mech. 2020;106:102447. doi:10.1016/j.tafmec.2019.102447. [Google Scholar] [CrossRef]

26. Kanit T, Forest S, Galliet I, Mounoury V, Jeulin D. Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int J Solids Struct. 2003;40(13–14):3647–79. doi:10.1016/S0020-7683(03)00143-4. [Google Scholar] [CrossRef]

27. Chang CS, Misra A. Packing structure and mechanical properties of granulates. J Eng Mech. 1990;116(5):1077–93. doi:10.1061/(asce)0733-9399(1990)116:5(1077). [Google Scholar] [CrossRef]

28. Li X, Zhang S, Duan Q. Effective hydro-mechanical material properties and constitutive behaviors of meso-structured RVE of saturated granular media. Comput Geotech. 2020;127:103774. doi:10.1016/j.compgeo.2020.103774. [Google Scholar] [CrossRef]

29. Xiu C, Chu X, Wang J. The micromorphic constitutive parameters and dispersion behaviors in different granular crystals. Powder Technol. 2021;392:325–43. doi:10.1016/j.powtec.2021.07.021. [Google Scholar] [CrossRef]

30. Yilmaz N, Yildizdag ME, Fabbrocino F, Placidi L, Misra A. Emergence of critical state in granular materials using a variationally-based damage-elasto-plastic micromechanical continuum model. Num Anal Meth Geomech. 2024;48(13):3369–91. doi:10.1002/nag.3795. [Google Scholar] [CrossRef]

31. Xiu C, Chu X. Finite element simulations on failure behaviors of granular materials with microstructures using a micromechanics-based cosserat elastoplastic model. Comput Model Eng Sci. 2024;138(3):2305–38. doi:10.32604/cmes.2023.030194. [Google Scholar] [CrossRef]

32. Le Bouil A, Amon A, Sangleboeuf JC, Orain H, Bésuelle P, Viggiani G, et al. A biaxial apparatus for the study of heterogeneous and intermittent strains in granular materials. Granul Matter. 2014;16(1):1–8. doi:10.1007/s10035-013-0477-x. [Google Scholar] [CrossRef]

33. Kruyt NP, Agnolin I, Luding S, Rothenburg L. Micromechanical study of elastic moduli of loose granular materials. J Mech Phys Solids. 2010;58(9):1286–301. doi:10.1016/j.jmps.2010.06.003. [Google Scholar] [CrossRef]

34. Durán O, Kruyt NP, Luding S. Micro-mechanical analysis of deformation characteristics of three-dimensional granular materials. Int J Solids Struct. 2010;47(17):2234–45. doi:10.1016/j.ijsolstr.2010.04.014. [Google Scholar] [CrossRef]

35. Li X, Tang H. A consistent return mapping algorithm for pressure-dependent elastoplastic Cosserat continua and modelling of strain localisation. Comput Struct. 2005;83(1):1–10. doi:10.1016/j.compstruc.2004.08.009. [Google Scholar] [CrossRef]