Constraint Intensity-Driven Evolutionary Multitasking for Constrained Multi-Objective Optimization

1  Introduction

Constrained multi-objective optimization problems (CMOPs) frequently arise in practical scenarios, including portfolio optimization, resource scheduling, and engineering system design, where multiple conflicting objectives must be optimized simultaneously under a set of nonlinear inequality and equality constraints [1,2]. In contrast to unconstrained problems, CMOPs introduce structural complexity by partitioning the search space into feasible and infeasible regions, often resulting in fragmented and irregular solution landscapes. Such complexity poses substantial difficulties for evolutionary algorithms in maintaining convergence, feasibility, and diversity within the feasible domain.

To address these challenges, various constraint-handling techniques(CHT) have been proposed, including penalty-based approaches, constraint dominance principles (CDP), and ε-constraint strategies [3–6]. These methods attempt to guide the search process toward feasible and high-quality regions by penalizing constraint violations, prioritizing feasible solutions, or relaxing constraints within controlled thresholds. While effective in certain single-objective or low-dimensional settings, their performance often deteriorates when applied to high-dimensional or tightly constrained multi-objective problems. Penalty-based methods are typically sensitive to the choice of penalty coefficients, which can be challenging to calibrate across diverse problem instances. CDP-based strategies may overemphasize feasibility, thereby limiting search diversity and leading to premature convergence. Similarly, ε-constraint methods require extensive parameter tuning and impose significant computational overhead to maintain a delicate balance between feasibility and optimality [7]. These limitations underscore the need for more adaptive and context-aware optimization frameworks that can effectively handle the heterogeneous characteristics of CMOPs without relying heavily on manual parameter adjustments or problem-specific heuristics.

Motivated by these limitations, recent studies have explored evolutionary multitasking (EMT) as a promising paradigm for enhancing constrained optimization. The EMT framework aims to leverage inter-task knowledge transfer by simultaneously solving multiple related tasks, thereby improving convergence efficiency and solution diversity [8,9]. In the context of CMOPs, multitasking strategies often incorporate auxiliary tasks, typically those with relaxed constraints or unconstrained objectives, to support the optimization of the primary constrained task. By sharing potentially useful solutions across tasks, these approaches seek to accelerate the discovery of feasible and high-quality solutions.

However, existing multitasking-based CMOPs algorithms face several persistent challenges. Many assume implicit compatibility among tasks and overlook the constraint-induced heterogeneity that may exist between search spaces. When the unconstrained Pareto front (UPF) and the constrained Pareto front (CPF) exhibit minimal overlap or structural dissimilarity, unfiltered knowledge transfer may introduce detrimental guidance that compromises search effectiveness. Moreover, most current methods lack adaptive mechanisms to evaluate the contribution of transferred solutions in real time. These limitations reduce the robustness and scalability of EMT approaches in solving CMOPs with diverse constraint landscapes. This observation underscores the need for a more flexible and empirically informed multitasking framework—one that dynamically recognizes problem structure, guides task-specific strategy design, and selectively transfers knowledge based on its actual utility to the optimization process.

In response to these challenges, this study proposes a novel algorithm named Constraint-Intensity Driven Evolutionary Multi-Tasking (CIDEMT), which explicitly incorporates constraint landscape characteristics into the design of multitasking strategies for CMOPs. Specifically, the proposed method is designed to:

(1)   Develop a two-task, three-task co-evolutionary framework that integrates multiple constraint-handling principles to support both global exploration and local exploitation;

(2)   Construct a constraint-intensity-based (i.e., the degree of overlap between the distributions of CPF and UPF)classification mechanism that differentiates CMOPs according to the degree of overlap between the constrained and unconstrained Pareto fronts, thereby enabling adaptive, task-specific strategy selection;

(3)   Implement a dynamic knowledge transfer strategy that quantitatively evaluates the contribution of auxiliary solutions to the primary task, promoting beneficial transfer while suppressing negative influence;

(4)   Validate the proposed algorithm through comprehensive experiments on benchmark and real-world CMOPs, assessing performance in terms of convergence accuracy, feasibility rate, and solution diversity.

Together, these efforts yield a robust and generalizable optimization framework that effectively bridges constraint modeling with evolutionary multitasking, advancing the state of the art in solving CMOPs under complex and heterogeneous constraint conditions.

2  Literature Relevant

2.1 Constraint-Handling Techniques

Constrained multi-objective optimization problems (CMOPs) involve the simultaneous optimization of multiple conflicting objectives subject to complex nonlinear constraints. Existing constraint-handling Techniques (CHT) can be broadly categorized into three main categories: (1) penalty-based approaches, which embed constraint violations into the objective function via penalty terms but often require careful and problem-dependent tuning of penalty parameters [8]; (2) CDP-based methods, which promote feasible solutions by leveraging dominance relationships but may reduce population diversity and lead to premature convergence [9]; and (3) ε-constraint techniques, which incrementally relax constraints to facilitate exploration across infeasible regions, typically at the cost of increased computational overhead [10]. Or, the aforementioned combination constraint strategy formed by CHT can be used to balance the feasible solutions and the infeasible solutions [11]. Although these approaches have shown effectiveness in single-objective problems, their scalability and robustness degrade significantly when addressing CMOPs with complex constraint landscapes.

2.2 Multi-Stage and Multi-Population Strategies

To address the limitations of traditional constraint-handling methods, researchers have investigated advanced evolutionary frameworks, particularly those based on multi-stage and multi-population designs. Multi-stage approaches aim to sequentially exploit different search dynamics to improve performance. For example, Fan et al. proposed the push-pull search (PPS) to solve CMOPs. In the framework, which alternates between unconstrained global exploration (push stage) and constrained local refinement (pull stage) [12]. Qiao [13] uses dynamic constraint adjustment to maximize the improvement in population feasibility. In contrast, LR [14] leverages Gaussian processes to enhance the quality of offspring generation. Ma et al. introduced a three-phase model comprising a learning phase, a classification phase, and an evolutionary phase. This framework leverages knowledge of the constraint landscape to guide the search direction more effectively [15]. Similarly, Feng et al. developed the Adaptive Trade-off Evolutionary Algorithm (ATEA), which integrates exploratory, trade-off, and developmental phases to dynamically balance convergence, diversity and feasibility [16].

In parallel, Unlike a single population that utilizes different strategies to enhance the performance of the algorithm [17], multiple populations are more about cooperation among the different populations. Utilizing multi-population co-optimization strategies have been designed to enhance search robustness and solution feasibility. Tian et al. proposed the Constrained Cooperative Multi-Objective Optimization (CCMO) framework, which employs weakly coupled constrained and unconstrained populations that evolve towards the CPF and UPF, respectively. These populations interact through an adaptive environmental selection mechanism [18]. To further enhance cooperation, Wang et al. presented a bidirectional search framework that coordinates dual populations via a dynamic selection strategy [19]. Qiao et al. [20] introduced a co-evolutionary approach featuring a dynamic constraint-handling mechanism and a feedback-driven resource allocation scheme, enabling efficient use of computational resources across populations. Additionally, Ming proposed the Constrained Multi-Objective Evolutionary Strategy (CMOES), which identifies promising feasible regions and adaptively tunes ε to enhance solution diversity and feasibility [21].

2.3 Evolutionary Multitasking for CMOPs

Evolutionary multitasking (EMT) has emerged as a promising optimization paradigm in which multiple related tasks are tackled simultaneously through inter-task knowledge transfer. Unlike conventional multi-population methods that typically focus on population-level interactions, EMT emphasizes task-level information sharing to enhance optimization efficiency. Qiao et al. introduced evolutionary multitasking (EMT)-based constrained multiobjective optimization (EMCMO), which dynamically explores useful information for the primary task through a trial-and-error mechanism [22]. Ming et al. proposed CMOEMT, which formulates a CMOPs as a three-tasks multitasking model, enabling knowledge sharing to accelerate convergence and improve solution diversity [23].

Despite their demonstrated potential, EMT-based methods still encounter several critical challenges. First, they often assume implicit transferability of solutions across tasks, overlooking potential dissimilarities between the CPF and the UPF. Second, most existing approaches lack adaptive transfer mechanisms that can assess the relevance and utility of shared solutions in real-time. Third, inappropriate or negative knowledge transfer may misguide the search process, impair convergence, and lead to inefficient resource usage. These issues underscore the need for more flexible and problem-aware EMT frameworks tailored to the characteristics of individual CMOPs.

2.4 Discussion and Insights

One of the pivotal developments in constrained multi-objective problem (CMOP) research is the classification of problem types based on the relationship between the CPF and the UPF. Ma and Wang [24] proposed a four-category taxonomy to describe these relationships, as shown in Fig. 1. This taxonomy provides critical guidance for the design and selection of constraint-handling techniques and knowledge transfer mechanisms, as different CPF-UPF configurations entail distinct optimization challenges.

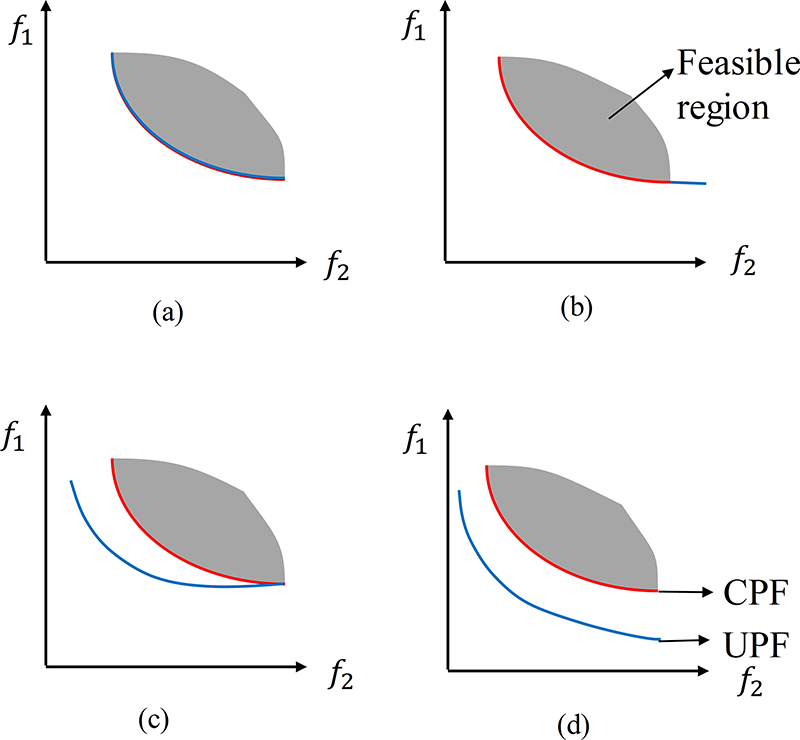
Figure 1: Four relationships CPF and UPF, where the grey area denotes the feasible region, the blue line denotes the UPF, and the red line denotes the CPF. (a) CPF coincides with UPF, (b) CPF is a subset of UPF, (c) CPF and UPF partially overlap, and (d) CPF and UPF are completely disjoint

As illustrated in Fig. 1, recognizing the CPF-UPF relationship early in the search process enables the selection of more suitable evolutionary strategies for each scenario. This not only improves algorithmic robustness but also helps avoid inefficient search paths or detrimental knowledge transfers.

Additionally, Fig. 2 illustrates the impact of knowledge transfer between tasks with similar constraint structures. Specifically, feasible and non-dominated solutions obtained from a source task with a comparable CPF can provide superior initialization for the target task, thereby accelerating convergence and enhancing search efficiency. Conversely, when irrelevant or mismatched solutions are transferred without filtering, they may misguide the search process or lead to performance degradation. These observations underscore the need for adaptive knowledge transfer mechanisms that prioritize effective and contextually relevant information while minimizing negative transfers.

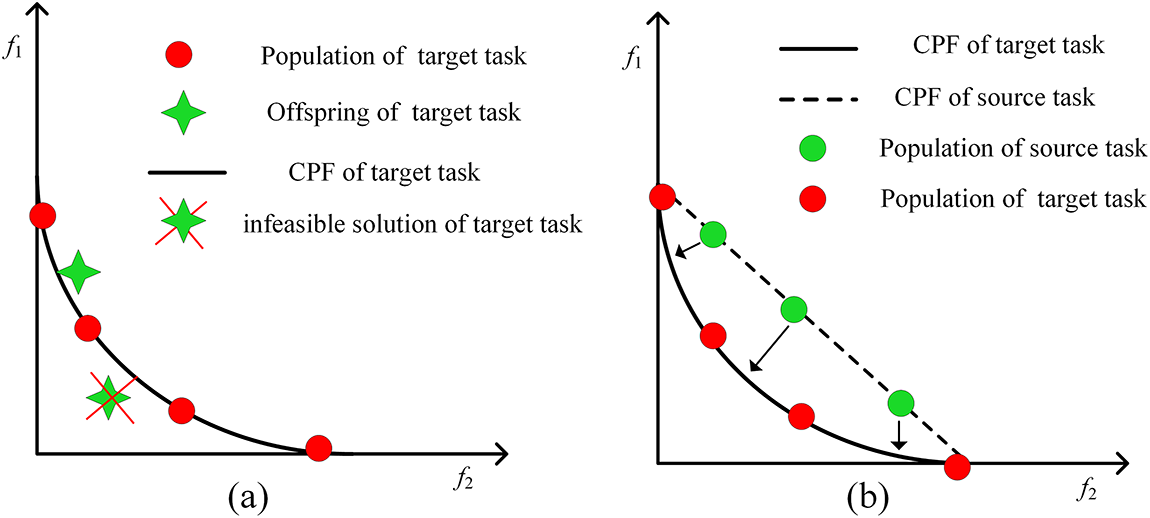
Figure 2: The functions of multitasking and knowledge transfer in solving CMOP. (a) Target task without knowledge transfer assistance. (b) The target task is assisted by knowledge transfer from the source task

Collectively, these insights reinforce the motivation for a multitasking framework that not only incorporates CPF-UPF structural awareness but also integrates adaptive transfer strategies tailored to the characteristics of constraints. These considerations form the foundation for developing the proposed CIDEMT algorithm.

3  The Proposed Algorithm

3.1 Framework Overview

The proposed Constraint-Intensity Driven Evolutionary Multi-Tasking (CIDEMT) algorithm employs a two-stage, three-task evolutionary multitasking framework (see Fig. 3) to address CMOPs, characterized by complex and heterogeneous constraint landscapes. In the first stage, three cooperative tasks are initialized: T1, the primary task governed by the CDP; T2, an auxiliary task employing Pareto dominance; and T3, an auxiliary task utilizing an ε-constraint mechanism. These three tasks implement different strategies based on the intensity of constraints (i.e., the degree of overlap between the distributions of CPF and UPF), collaboratively explore diverse regions of the decision space and generate complementary knowledge of solutions.

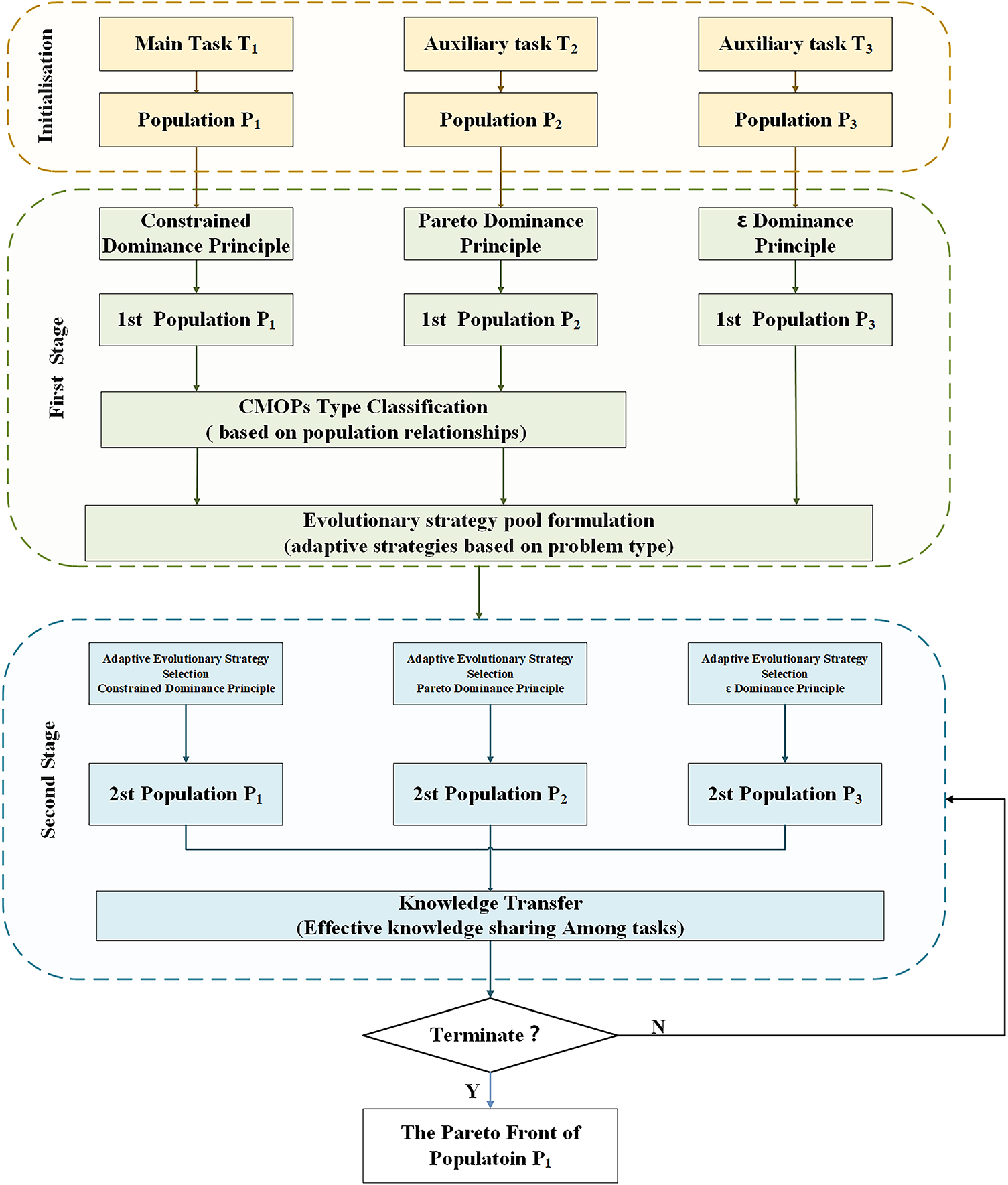
Figure 3: Schematic diagram of CIDEMT

Algorithm 1 describes the detailed implementation of CIDEMT. The process begins by initializing the population of the three tasks based on a predetermined population size, NP. In the first stage, each of the three tasks generates its own children, utilizing CDP, the Pareto dominance principle, and the ε-constraint relaxation principle to initialize populations. In the ε-constraint relaxation principle, theε parameter is set to ε0, which is defined as the maximum constraint value of the auxiliary task population T2 based on the ε-constraint relaxation principle. We use the parameter λ to control the transition from the first stage to the second stage,at the end of the first stage, the constraint intensity is determined based on the degree of overlap between UPF and CPF to determine the problem type (see Algorithm 2), and an evolutionary strategy is constructed for the second stage (see Section 3.2.2).

In the second stage, offspring are generated using adaptive selection of evolutionary strategies. Additionally, to more effectively find beneficial solutions and reduce computational resources, a τ-driven knowledge transfer mechanism evaluates and integrates solutions from auxiliary tasks into the primary task (T1) (as described in Algorithm 3), ensuring only effective solutions contribute to the main search process. And the population will be updated through the SPEA2 environmental strategy [25].

Our approach differs from previous multi-task algorithms, such as CMOEMT and those that use Gaussian processes to generate offspring. Instead, we leverage the specific characteristics of the problem to define operators for offspring generation. Furthermore, we introduce dynamic adjustment and a pull-push search mechanism for task T3. This enables a more effective exploration of the decision space. This two-stage architecture is designed to facilitate broad global exploration in the early phase and focused, adaptive exploitation in the later phase, with the aim of enhancing convergence accuracy, solution diversity, and feasibility preservation across complex CMOP scenarios.

3.2 Constraint Intensity-Driven Optimization Strategy

3.2.1 CPF-UPF-Based Problem Classification Mechanism

To tailor search strategies to problem characteristics, CIDEMT classifies CMOPs based on the Constraint Intensity—structural overlap between the CPF and the UPF. Three problem types are defined: Type I: CPF and UPF completely overlap; Type II: CPF and UPF partially overlap; Type III: CPF and UPF are disjoint.

The classification is achieved via Algorithm 2, which analyzes the feasibility proportions under CDP and Pareto dominance in merged populations from tasks T1 and T2. A set of threshold-based rules, incorporating an error-tolerant parameter α, determines the final type.

Rationale for Problem Reclassification, the reclassification of problem types is motivated by the need to tailor evolutionary strategies based on the structural relationship between the CPF and the UPF. As illustrated in Fig. 1a,b, when CPF and UPF completely overlap, the primary task T1 can effectively degenerate into the auxiliary task T2. In such cases, solving task T2 implicitly addresses task T1, thereby reducing computational overhead. Therefore, these scenarios are categorized as Type I problems.

In contrast, Fig. 1d represent cases where CPF and UPF are non-overlapping. To address these, the algorithm must exploit the non-intersecting regions to generate solutions beneficial for task T1, leading to their classification as Type III problems.

Fig. 1c presents a hybrid case in which CPF and UPF partially overlap. Here, it is essential to maintain exploration around the UPF (T2) while leveraging the shared region to support the feasiblity of T1. Due to this dual nature, it is assigned to a separate category—Type II. This classification enables the algorithm to apply more targeted and effective evolutionary strategies depending on the CPF-UPF relationship.

3.2.2 Evolutionary Strategies Pool Constructed

These types are not only descriptive but also directly impact the design of evolutionary strategies (Table 1). For instance, Type I problems are simplified due to constraint equivalence, while Type III problems require targeted exploitation from non-overlapping auxiliary fronts. This optimization-aware classification bridges the gap between problem structure and algorithmic behavior.

The formulation of evolutionary strategies is guided by the CPF-UPF relationship identified in the problem classification. As detailed in Table 1, for Type I problems, where the CPF is entirely coincident with the UPF, both tasks T1 and T2 adopt the Genetic Algorithm (GA) framework, employing Simulated Binary Crossover (SBX) [26] and Polynomial Mutation (PM) [27] as their primary variation operators. In parallel, task T3 utilizes the DE/current-to-opbest/1 operator [28].

As shown in Fig. 4a, for Type I problems, Given the complete overlap between CPF and UPF, these problems essentially reduce to unconstrained multi-objective optimization problems, thus eliminating the need for complex constraint-handling mechanisms. T2 utilizes GA to ensure a balance between global exploration and local exploitation while maintaining high computational efficiency. Furthermore, since task T3 is positioned in regions aligned with constraint boundaries, high-quality solutions from task T2 are leveraged to guide the generation of offspring beneficial to task T1. This inter-task guidance promotes knowledge transfer and improves convergence toward the true CPF.

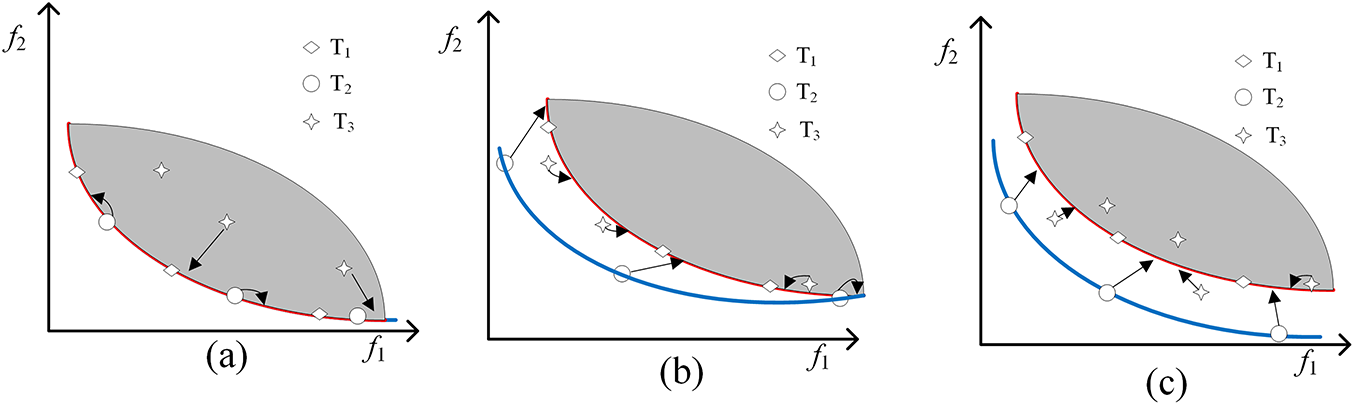
Figure 4: (a) In Type I problems, tasks T2 and T3 are auxiliary processes of T1. (b) In Type II problems, tasks T2 and T3 are auxiliary processes of T1. (c) In Type III problems, tasks T2 and T3 are auxiliary processes of T1. Red represents CPF, and blue represents UPF, grey area represents the feasible region

For Type II Problem’s Strategy Formulation, task T1 employs a combination of the GA and DE/rand/1 [29], while task T2 utilizes GA, DE/transfer, and DE/current-to-pbest/1 [28]. Task T3 utilizes standard GA operators. These problems are characterized by partial overlap between CPF and UPF, often situated near the boundary between feasible and infeasible regions. As such, the evolutionary strategy must strike a balance between global exploration and local convergence.

GA provides baseline search capabilities across all tasks. The DE/rand/1 operator enhances exploration by using purely stochastic vector differences, effectively preventing premature convergence near the UPF and enabling the discovery of promising feasible regions in its vicinity. The DE/transfer operator facilitates knowledge transfer from task T2 to T1, thereby accelerating convergence in the overlapping CPF-UPF zones. Meanwhile, DE/current-to-pbest/1 leverages elite-based guidance to improve optimization performance near the constraint boundaries, particularly useful for navigating fragmented or broken Pareto fronts.

Task T3, operating in complementary regions, performs local search using GA to provide feasible candidate solutions for task T1. The overall cooperative mechanism is illustrated in Fig. 4b, highlighting how each task contributes distinct yet synergistic search capabilities to improve performance under partially overlapping constraint scenarios.

For Type III Problem’s Strategy Formulation. For the strategy largely retains the operator configurations used in Type II for tasks T1 and T3. However, task T2 is specifically assigned the DE/current-to-opbest/1 operator. This modification targets optimization scenarios where CPF and UPF are adjacent but disjoint, posing significant challenges in navigating the decision space. The key objective under this setting is to efficiently identify feasible solutions near the infeasible UPF region, which may still offer valuable guidance for task T1. The use of DE/current-to-opbest/1 in task T2 enhances search effectiveness in these borderline areas by leveraging directional guidance toward optimal solutions in similar landscapes. The overall cooperative procedure for Type III is illustrated in Fig. 4c, demonstrating how the designed operator assignments facilitate knowledge transfer and improve convergence in the absence of CPF-UPF intersection.

3.3 τ-Driven Adaptive Knowledge Transfer

After each task generates offspring based on the designed evolutionary operators, the challenge arises in selecting the solutions that are most beneficial to the main task from among all the individuals. To address this, we propose the following methods:

In our framework, the original CMOP is designated as the main task, while auxiliary tasks are treated as concurrent source tasks for potential knowledge transfer. The subsequent analysis focuses on two representative problem types illustrated in Fig. 5: Type I and Type II. In both cases, the CPF is partially or wholly surrounded by a large infeasible region. Under such circumstances, solutions from source tasks can enhance convergence and diversity of the main task by contributing valuable information, as indicated by the blue and green regions.

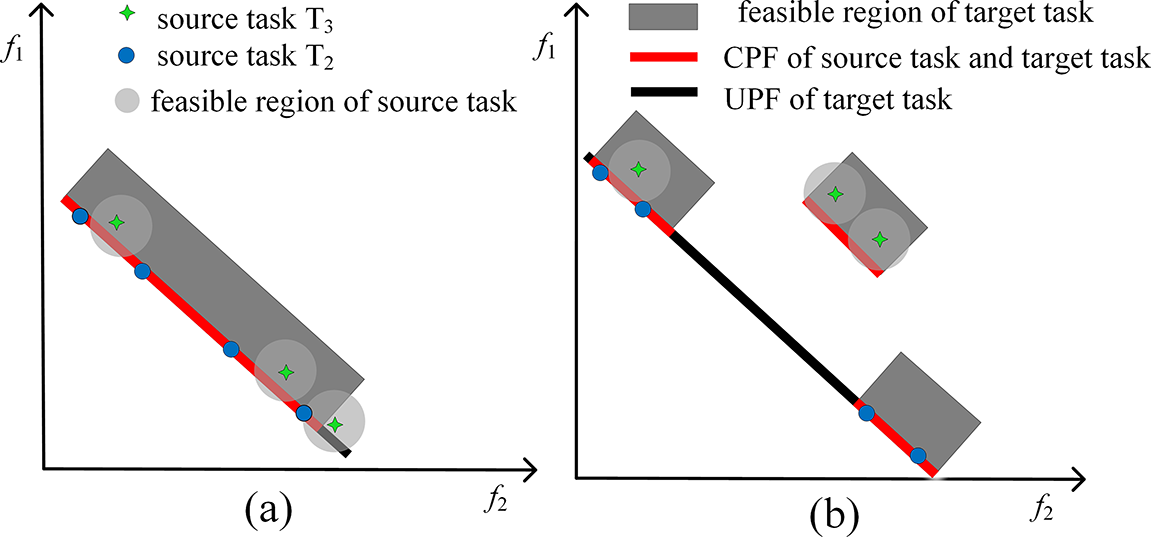
Figure 5: (a) Example of the impact of knowledge transfer on the main task in Type I problems; (b) Example of the impact of knowledge transfer on the main task in Type II problems

For Type I problems (Fig. 5a), if the source task’s solutions have already reached the CPF while the main task’s solutions have not, the CPF-aligned solutions from the source task can serve as a promising initialization, guiding the main task toward feasible regions more efficiently. For Type II problems (Fig. 5b), where the feasible region of the source task partially overlaps with that of the main task, feasible non-dominated solutions from the source task can assist the main task by uncovering unexplored feasible areas. Additionally, relaxed auxiliary tasks may traverse into the feasible region of the main task, further expanding the search space. In these illustrations, light-colored regions represent the relaxed feasible boundaries

The specific design is as follows: In the second stage, further optimization is achieved through a τ-driven adaptive knowledge transfer strategy. To enhance optimization efficiency, the algorithm calculates the proportion of solutions in each source task that are effective (i.e., have an effectiveness factor τ = 1) for the target task. Knowledge transfer is then guided by this proportion, ensuring that only relevant and beneficial solutions are incorporated into the target task, as detailed in Algorithm 3.

The effectiveness of a solution x with respect to task Ti (where i = 1, 2, 3) is determined using a task-specific effectiveness factor τ, defined as follows:

(1)   For T1 (the primary constrained task): If the solution satisfies all constraints and is non-dominated, i.e., CV(x) = 0 and NF(x) = 1, then τ1 = 1; otherwise, τ1 = 0;

(2)   For T2 (the unconstrained auxiliary task): If the solution is non-dominated, i.e., NF(x) = 1, then τ2 = 1, otherwise τ2 = 0.

(3)   For T3 (the ε-relaxed task): If the solution violates constraints within a tolerance ε and is non-dominated, i.e., CV(x) ≤ ε and NF(x) = 1, otherwise, τ3 = 0.

Here, CV(x) denotes the constraint violation value of solution x, and NF(x) indicates whether x belongs to the non-dominated front. After evaluating all candidate solutions, a transfer ratio is computed from the t-th task population to the k-th population based on the relative abundance of effective solutions. This ratio is formally defined in Eq. (1) and used to control the flow of knowledge, thereby reducing negative transfer and improving convergence performance in the target task.

pt=∑x∈Ttτk(x)|Tt|(1)

where t represents the t−th source task, k represents the kth target task, the one with a larger transfer ratio is considered more suitable for the kth task, where only the solution with τk=1 is recognised as useful knowledge to be transferred to the kth task, and the effective knowledge solutions are selected to participate in the knowledge transfer of the task Tk according to the ratio, so that negative knowledge transfer and reduction of time complexity can be avoided and effectively reduced.

3.4 Cooperation Mechanisms among Tri-Task

To sum up, the CIDEMT framework integrates intra-task optimization with inter-task knowledge sharing to effectively address complex constraint landscapes in CMOPs. Within each task, evolutionary operators are customized based on the task’s constraint characteristics. Moreover, CIDEMT selects corresponding evolutionary operations based on the characteristics of its problem constraints.

At the inter-task level, a τ-driven adaptive knowledge transfer mechanism enables the selective reuse of high-quality solutions across tasks. Specifically, the primary task (T1) assimilates knowledge from auxiliary tasks (T2 and T3) when their solutions demonstrate high feasibility and relevance. To further enhance the effectiveness of this transfer, an improved ε-dynamic adjustment strategy (Eqs. (2) and (3)) is employed to progressively guide T2 and T3 toward feasible regions while maintaining diversity at the search boundaries.

{ε0, if is frist stage ε0⋅(1−gGmax)(−log⁡(ε0+6)log⁡(1−β)), other (2)

ε0=CVmax(x)(3)

In this context, ε0 represents the maximum contract value at the initialization of the population, g denotes the current evaluation count, Gmax indicates the maximum evaluation count, and β is a control parameter set to 0.5.

This hybrid mechanism not only accelerates convergence under complex constraints but also enhances the population’s adaptability and robustness during evolutionary search.

3.5 Computational Complexity Analysis

The computational complexity of CIDEMT primarily stems from mating selection, evolutionary operators, population classification, and adaptive knowledge transfer. In the first stage, the three task populations evolve independently, with each task contributing O (NP⋅D) operations, where NP is the population size and D is the dimension of the decision variable. Stage two introduces additional complexity due to τ−driven knowledge transfer, necessitating O (NP2) operations for validity computation and filtering. The classification of problem types based on UPF and CPF relationships adds O (M⋅NP2) complexity. Despite these steps, CIDEMT employs selective knowledge transfer and task-specific operator application, which significantly reduces redundant computation. Hence, the overall computational complexity remains O (M⋅NP2), consistent with state-of-the-art CMOEAs. Regarding the space complexity, it depends on the number of populations, so the space complexity is O(NP). Although the complexity of CIDEMT is the same as that of many other algorithms, its optimization effect on CMOPs is superior to the latest algorithms. This is specifically verified in Sections 4.3–4.5.

4  Results

4.1 Experimental Setting

To comprehensively evaluate the performance of the proposed CIDEMT algorithm, it is experimentally compared with six state-of-the-art algorithms: CMOES [21], EMCMO [22], CMOEMT [23], MTCMO [13], APSEA [30], and IMCMOEAD [14]. The comparisons are conducted on three benchmark test suites-DOC [31], LIRCMOP [32], and DASCMOP [33]-as well as eight real-World constrained multi-objective optimization problems: Pressure Vessel Design (PVD) [34], Gear Train Design (GTD) [35], Car Side Impact Design (CSID) [36], Water Resources Management(WRM), Simply Supported I-beam Design (SID) [37], Gear Box Design (GBD) [38], Bulk Carrier Design (BCD) [39], Multi-product Batch Plant (MBP) [40], Haverly’s Pooling Problem (HPP) [41], Reactor Network Design (RND) [42], Process Synthesis Problem (PSP) [43], Synchronous Optimal Pulse-width Modulation of 3-level Inverters (SOPM) [44] and Optimal Droop Setting for Minimizing Active and Reactive Power Loss (MARP) [45]. All experiments were performed on the Platemo [46] platform. To assess the statistical significance of performance differences, the Wilcoxon rank sum test is applied at a 0.05 significance level. Test outcomes are represented by the symbols ‘+’, ‘–’ and ‘=’, denoting that the benchmark algorithm performs significantly better than, worse than, or comparably to CIDEMT, respectively.

4.2 Performance Indicators and Parameter Settings

4.2.1 Performance Indicators

•   Inverted Generational Distance (IGD) [47]

The IGD metric evaluates algorithm performance with respect to both convergence and diversity. Its formal definition is provided below:

{IGD(P∗,A)=∑y∗∈P∗d(y∗,A)|P∗|d(y∗,A)=miny∈A{∑i=1m(yi∗−yi)2}(4)

where P∗ is the set of representative solutions sampled from the true Pareto front (PF) and A is the set of approximated solutions obtained by the algorithm under evaluation. Specifically, P∗ consists of 10,000 uniformly sampled points from the actual PF. The number of objectives is denoted by m. A lower IGD value indicates better performance in terms of both convergence and diversity.

•   Hypervolume (HV) [48]

HV metric measures the proximity of the obtained non-dominated solution set to the true PF. A larger HV value indicates that the solution set is closer to the true PF, reflecting superior performance in terms of convergence and diversity.

HV(S)=VOL(Ux∈S[f1(x),Z1r]×…×[fm(x),Zmr])(5)

where VOL(∙) is the Lebesgue measure, m is the number of targets, and Zr=(z1r,z2r…zmr) is a user-defined reference point in the target space. In particular, larger HV values indicate better performance in terms of diversity and convergence

4.2.2 Parameter Settings

To ensure the fairness and reproducibility of the experiments, all algorithms were configured according to the parameter settings specified in their original publications. A consistent configuration was applied across all compared methods. Specifically, the population size for each task was set to NP = 100. The maximum number of function evaluations was limited to Gmax = 300,000, and the number of runs is set to 30. The control parameter for the first-stage evolution was set to λ=1/3. In the problem type determination of Algorithm 2, the parameter α is set to 0.1. The scaling factor F and crossover rate CR were randomly selected from the sets F ∈{0.6,0.8,1.0} and CR ∈{0.1,0.2,1.0}, respectively. A more detailed discussion on the λ and α parameter can be found in Supplementary Material Tables S8–S11.

4.3 Experiments Analysis

In this section, we analyze the performance of the CIDEMT model with respect to the benchmark models in terms of IGD and HV metrics for the LIRCMOP, DASCMOP and DOC problems.

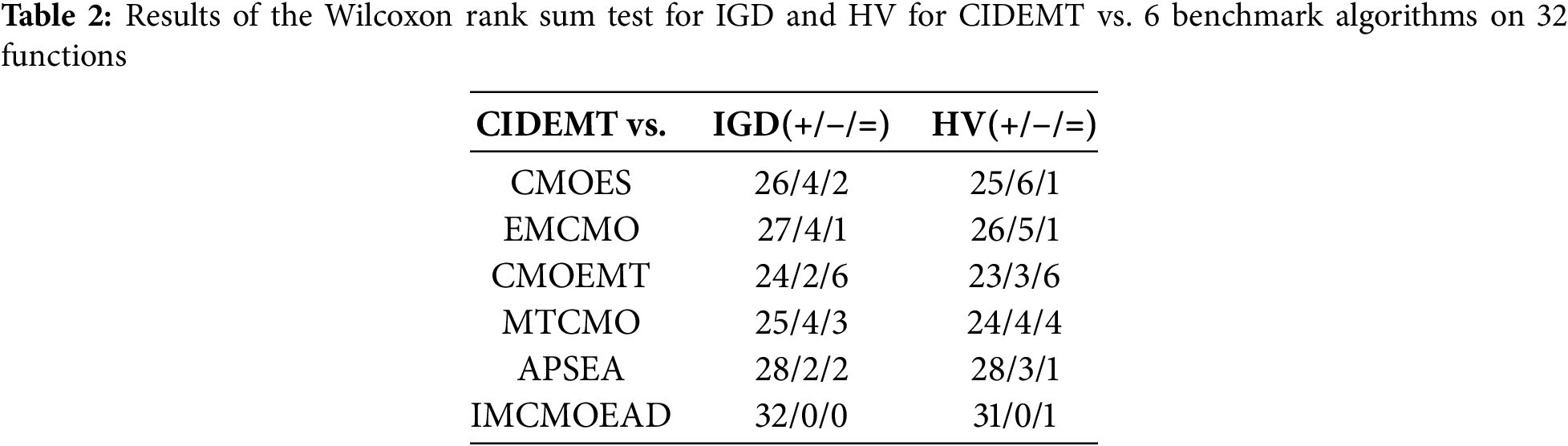
As summarized in Table 2, CIDEMT consistently outperforms the compared algorithms in most cases. Specifically, against CMOES, CIDEMT yields 26 superior, 2 comparable, and 4 inferior IGD results, demonstrating improved convergence and solution quality. Compared to EMCMO, CIDEMT achieves 27 better, 1 equal, and 4 worse IGD scores, again indicating robust improvement in the approximation of the Pareto front. Furthermore, CIDEMT obtains 32 superior IGD values compared to IMCMOEAD, underscoring its stability and competitiveness. In terms of HV, CIDEMT also performs favorably. It achieves 25 better, 1 equal, and 6 worse HV results than CMOES, reflecting enhanced diversity and solution spread. The comparison with APSEA is particularly notable: CIDEMT surpasses APSEA in 28 cases, demonstrating superior coverage across the boundaries.

Although CIDEMT performs well on most benchmark problems, it exhibits certain limitations when tackling complex problems with specific structural characteristics. For example, in problems with narrow feasible regions and high dimensionality (e.g., LIRCMOP1, LIRCMOP13, and LIRCMOP14), the use of ε-constraint relaxation and the CDP principle during population initialization struggles to effectively cover critical areas in the sparse feasible space, resulting in poor feasibility and reduced search efficiency. In problems with complex constraints and discrete or discontinuous constraint Pareto fronts (e.g., DASCMOP4 and DASCMOP5), the algorithm’s knowledge transfer mechanism lacks the ability to effectively explore multiple feasible regions, often leading to premature convergence in local areas. To overcome these challenges, future improvements may focus on enhancing density estimation and incorporating surrogate models to better identify feasible regions and improve global search efficiency, thereby strengthening the algorithm’s performance on complex constrained problems. More detailed results and analysis are presented in Supplementary Materials Tables S1–S6.

Although CIDEMT is not specifically designed for high-dimensional constrained multi-objective problems, we have conducted scalability tests on such problems to further demonstrate the generality of the algorithm. The experimental results show that CIDEMT performs well in terms of scalability compared to the benchmark algorithms, effectively handling high-dimensional constrained multi-objective optimization tasks while maintaining stable performance. Detailed results and analysis can be found in Tables S14 and S15 of the supplementary materials, where readers can refer for more comprehensive insights.

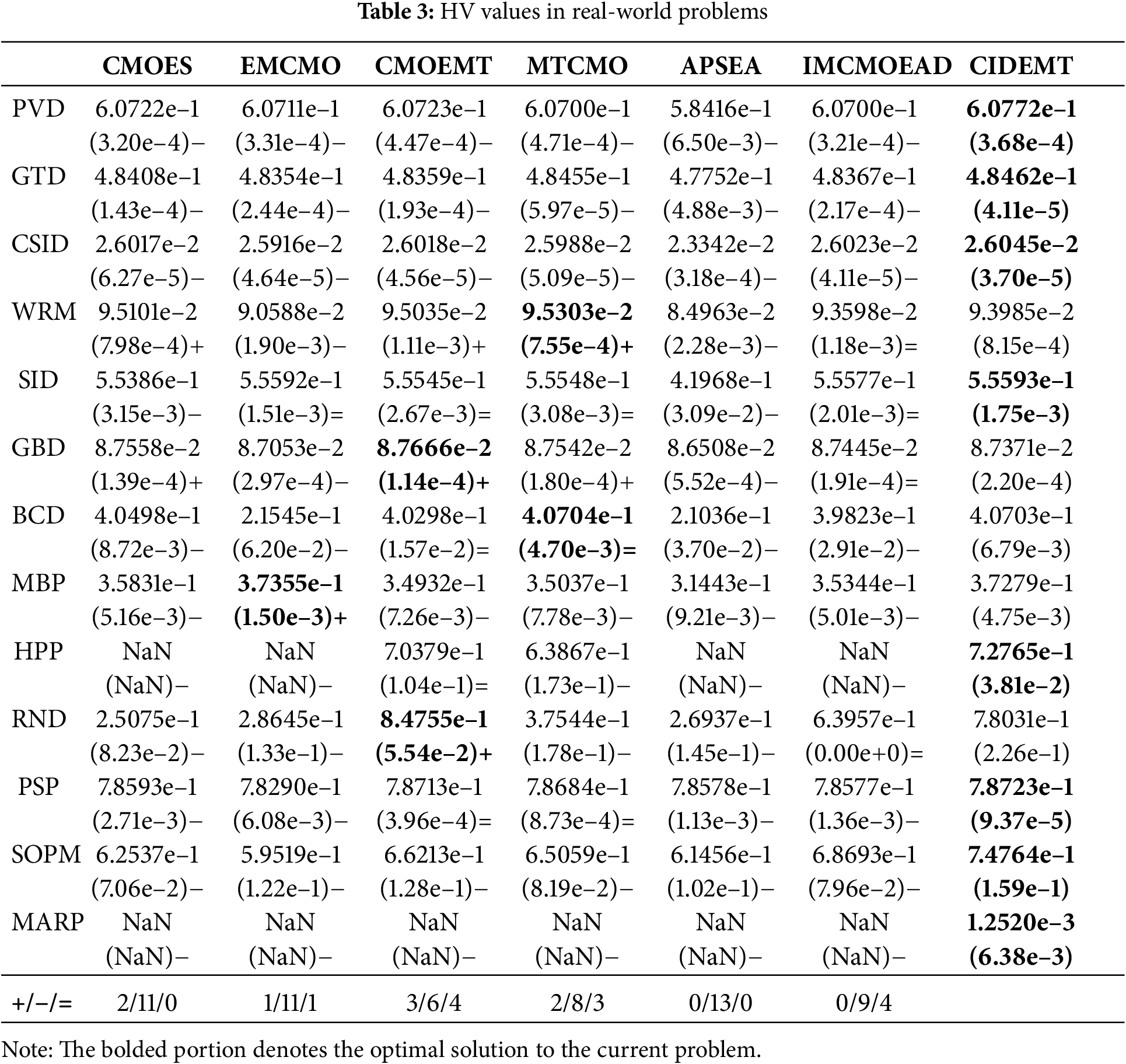
Regarding real-world constrained multi-objective problems, as shown in Table 3, CIDEMT attains the highest HV values in 8 out of 13 test cases. In contrast, EMCMO, CMOEMT, and MTCMO secure the best HV performance in only 1, 2, and 2 cases, respectively. In some real-world CMOPs, numerous objectives and complex constraints result in a highly discrete and heterogeneous feasible space. This makes it difficult for CIDEMT to capture scattered feasible regions, especially when they are sparse or fragmented, limiting its convergence and distribution performance. Nonetheless, it remains competitive compared to benchmark algorithms.

To better visualize the solution quality, Fig. 6 presents the final solution distributions of CIDEMT and and the CMOEMT algorithm, which also addresses three tasks, at both the mid-term and final stages across three different problem types. On the LIRCMOP6 problem of type I, both CIDEMT and CMOEMT showed good convergence, but their convergence speeds were not as fast as that of CIDEMT. For LIRCMOP11 and LIRCMOP2, which belong to type II and type III problems, compared to CMOEMT and CIDMET, due to the collaboration among tasks, each task achieves better convergence, thereby enhancing the excellent performance of the final solution. Furthermore, as shown in Fig. 7, for the three types of problems, when the number of iterations is the same, CIDEMT converges faster than the benchmark algorithm. One limitation is that, due to the complex computations involved in the knowledge transfer process, the running time is somewhat disadvantaged compared to the baseline algorithm. Future efforts will focus on optimizing the runtime to improve efficiency. More detailed results are presented in Supplementary Materials Figs. S1–S8 and Table S7.

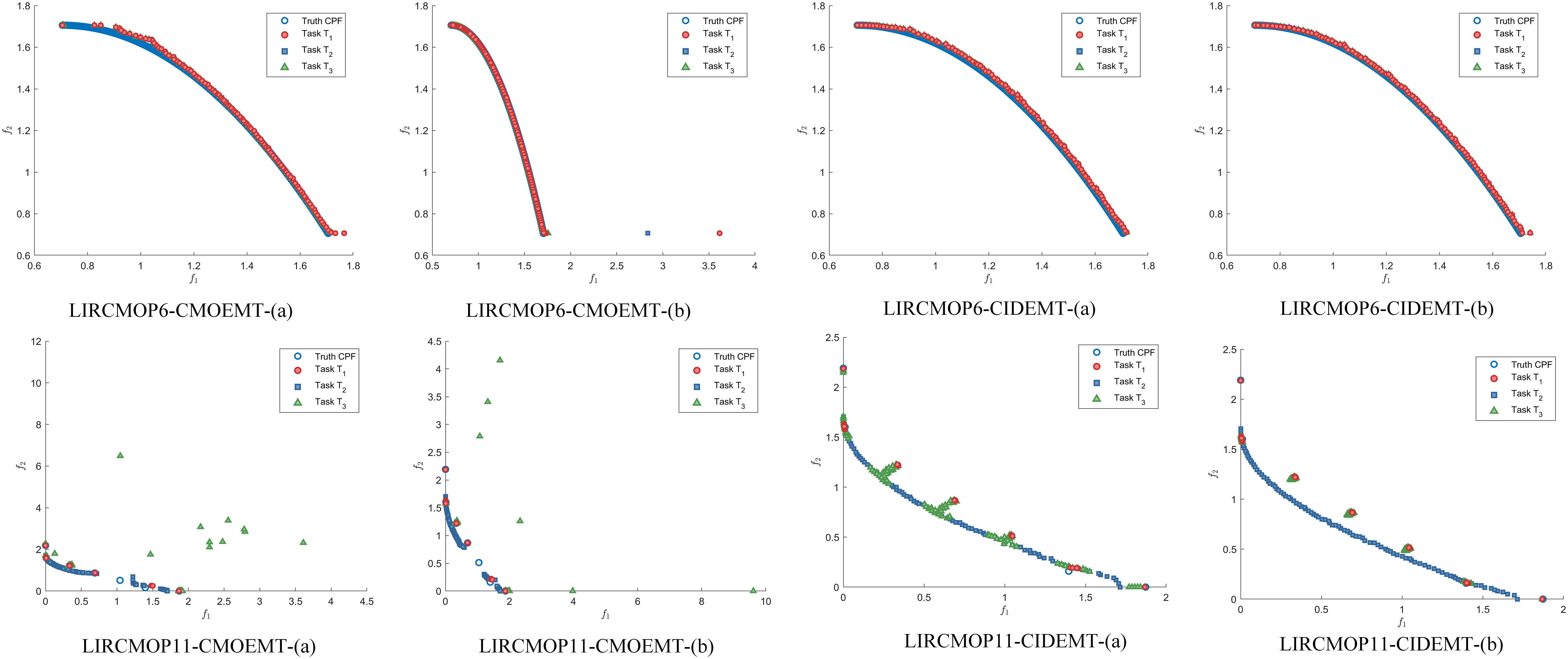
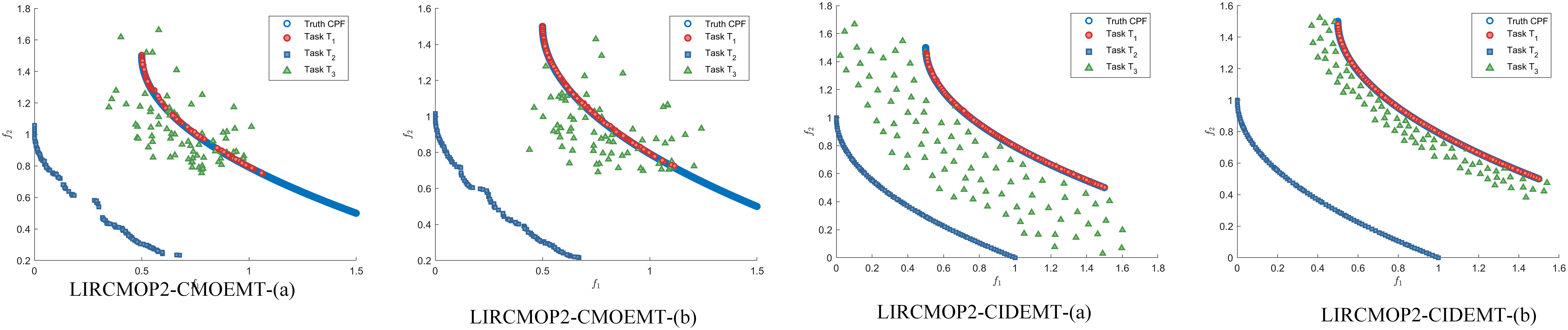
Figure 6: Distribution of mid-term and final solutions of CIDEMT and CMOEMT across three different problem types. (a) indicates the intermediate solution, (b) indicates the final solution

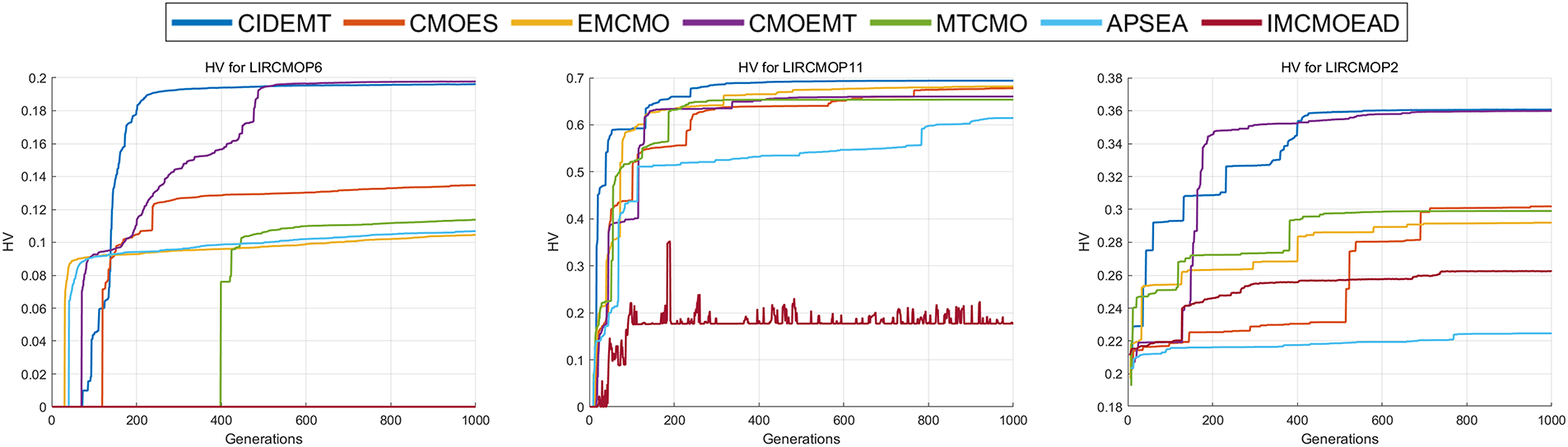
Figure 7: Comparison of convergence speeds of different algorithms

Overall, CIDEMT exhibits strong and consistent performance across both synthetic and real-world CMOPs. Its advantage in terms of IGD and HV metrics validates the effectiveness of the proposed multi-tasking and knowledge transfer mechanisms. Future work could further enhance CIDEMT’s generalizability by integrating hybrid strategies or extending its application to broader domains of multi-objective optimization.

4.4 Effectiveness Analysis of CIDEMT and Benchmark Algorithms

Table 4 presents the results of the Wilcoxon signed-rank test across 32 benchmark functions. All p-values are below 0.05, indicating statistically significant differences between CIDEMT and the compared algorithms. Furthermore, the R+ values are consistently and substantially greater than the R- values, further validating the superior performance of CIDEMT.

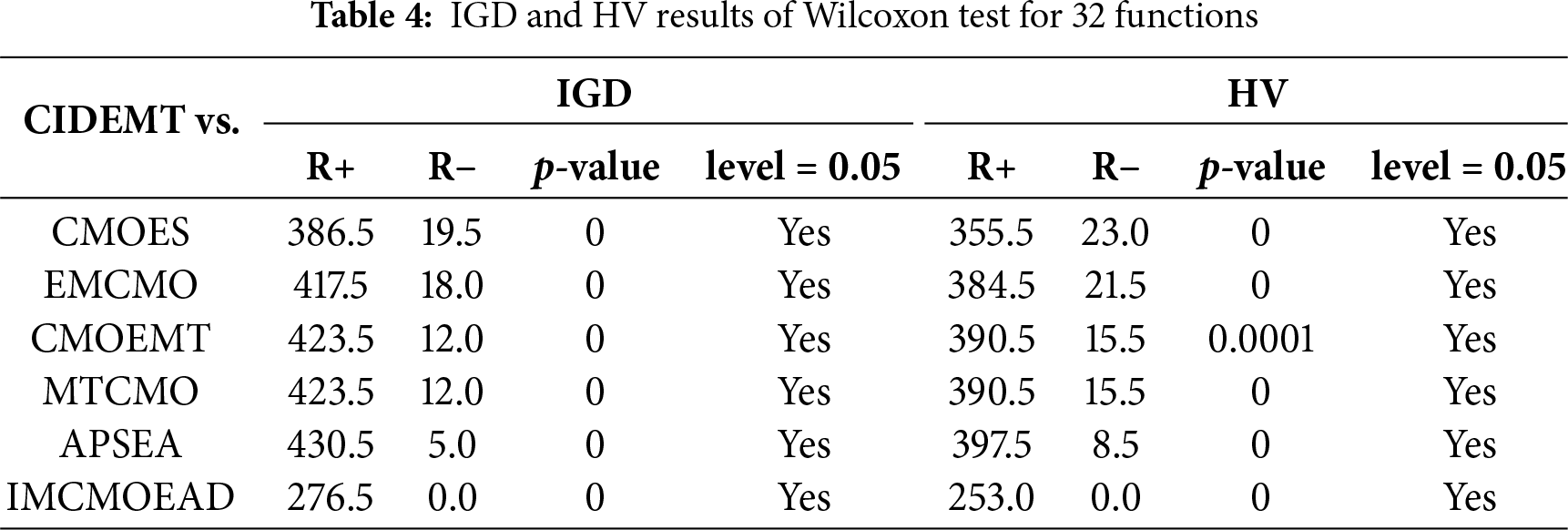
As shown in Table 4, CIDEMT consistently outperforms the benchmark algorithms in terms of both IGD and HV metrics. Notably, CIDEMT demonstrates significant advantages over CMOES, EMCMO, CMOEMT, MTCMO, APSEA, and IMCMOEAD. The corresponding p-values for these comparisons are all zero, confirming that CIDEMT achieves statistically better or equivalent performance across these tests.

4.5 Ablation Study

As shown in Table 5, an ablation study was conducted to further validate the effectiveness of the proposed adaptive evolution strategy pool (ESP) based on problem type, as well as the enhanced knowledge transfer mechanism. Two variants of CIDEMT were designed for comparison. CIDEMT-1 employs only the improved knowledge transfer strategy without utilizing adaptive strategies from the problem-type-based ESP. Conversely, CIDEMT-2 adopts adaptive strategies from the ESP during the optimization process but excludes the knowledge transfer mechanism.

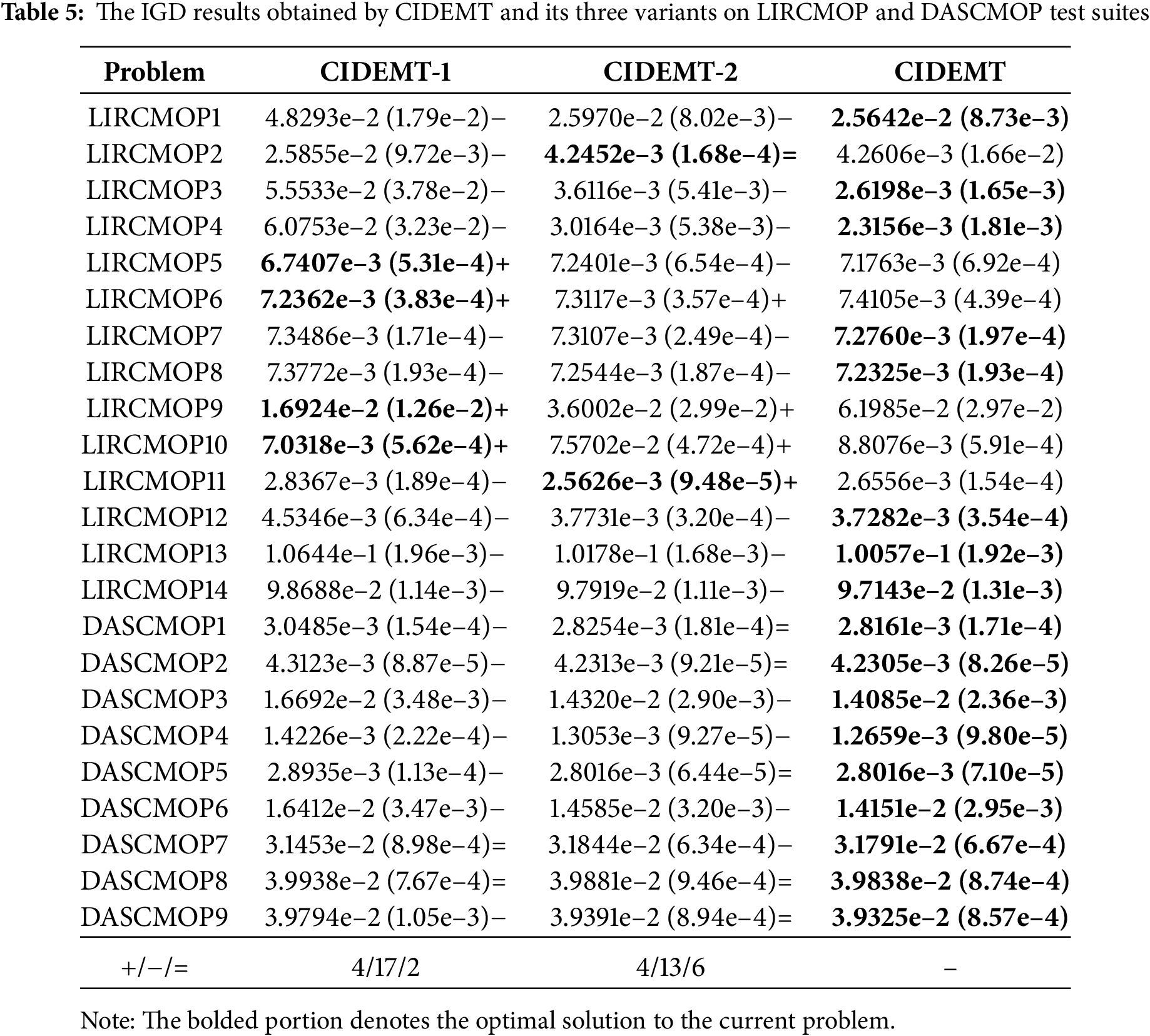
According to the results summarized in Table 5, CIDEMT achieved the best IGD averages across all DASCMOP benchmark problems and obtained eight optimal IGD values on the LIRCMOP benchmark, indicating overall superior performance. To illustrate the impact of knowledge transfer, we recorded the transfer process from auxiliary tasks T2 and T3 to T1 during the transfer stage, as shown in Fig. 8. For type I and II problems, transfer from T2 to T1 occurred at a lower rate due to the overlap between CPF and UPF, making the source and target tasks highly similar, with redundant information that did not effectively enhance learning. In contrast, for type III, since CPF and UPF do not intersect, knowledge transfer from T2 to T1 is more likely to select individuals meeting the constraints, leading to more effective transfer. For T3, its ε constraint is located near the CPF boundary, making it more likely to provide valuable information. Furthermore, as shown in Fig. 7, the convergence situation of CIDEMT during the same period indicates that, due to the effectiveness of the knowledge transfer strategy, the negative knowledge was well eliminated and did not lead to performance decline.

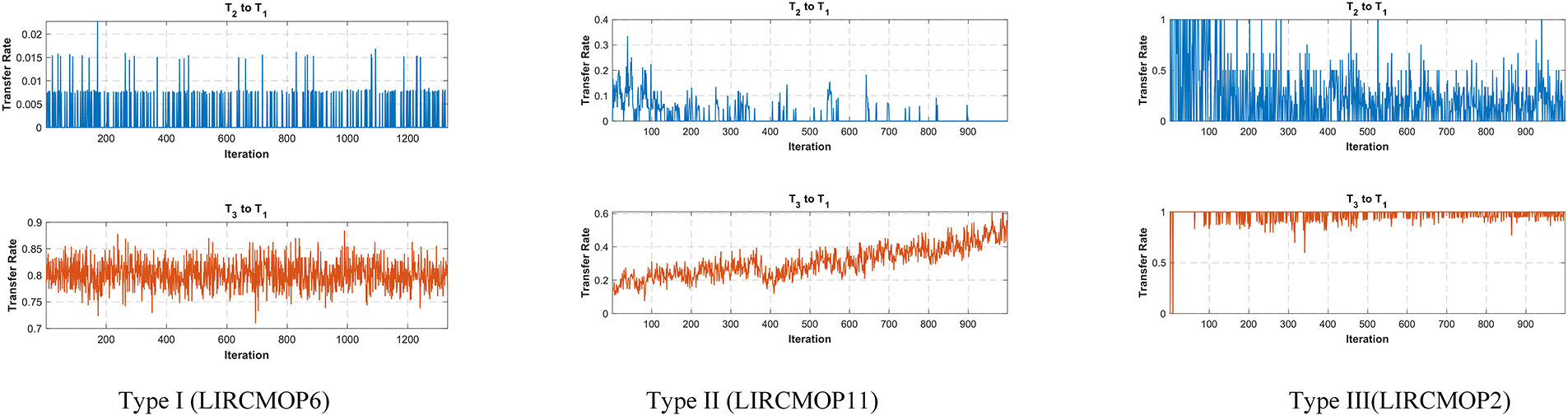
Figure 8: The CIDEMT in the knowledge transfer rates across the three types of problems

To further validate the effectiveness of its components, we conducted the Wilcoxon rank sum test. The results show that CIDEMT achieved statistically significant advantages over CIDEMT-1 and CIDEMT-2 on 17 and 14 benchmark problems, respectively. These experimental results confirm that both the problem-type-aware strategy selection and the enhanced knowledge transfer significantly contribute to improved convergence and diversity, thereby validating the effectiveness of the full CIDEMT framework.

5  Conclusion

This study proposes a two-stage, tri-task optimization algorithm—CIDEMT (Constraint-Intensity Driven Evolutionary Multi-Tasking)—which leverages the structural relationships between the constrained Pareto front (CPF) and the unconstrained Pareto front (UPF) to address constrained multi-objective optimization problems (CMOPs). By dynamically integrating auxiliary tasks, CIDEMT assists the main task in escaping local optima through adaptive strategy evolution and a τ−driven knowledge transfer mechanism. The framework is structured in two stages. In the first stage, the main task and two auxiliary tasks evolve toward the CPF, the UPF, and the ϵ−relaxed constraint boundary, respectively. Based on the detected CPF-UPF relationship, the problem is classified, and a tailored evolutionary strategy pool is constructed. In the second stage, each task selects appropriate strategies from this pool for further evolution. Simultaneously, an improved knowledge transfer mechanism is applied to enhance solution quality by evaluating the suitability of shared individuals.

Extensive experiments conducted on three benchmark suites and eight real-world problems demonstrate that CIDEMT significantly outperforms six state-of-the-art algorithms in terms of IGD, HV, and statistical significance (Wilcoxon rank-sum test). These results confirm CIDEMT’s effectiveness and robustness in solving CMOPs with complex constraint structures.

Despite its strong empirical performance, CIDEMT still faces challenges in handling high-dimensional CMOPs, particularly regarding convergence speed and computational efficiency. As the number of objectives increases, identifying an accurate CPF becomes more difficult, potentially leading to longer optimization times. Future research will focus on enhancing CIDEMT’s scalability by incorporating multi-agent models to address operator selection in multitasking scenarios, thereby enabling more efficient search strategies. These improvements aim to broaden CIDEMT’s applicability and strengthen its performance in solving large-scale, real-world multi-objective optimization problems.

Acknowledgement: Not applicable.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant No. 61972040, and the Science and Technology Research and Development Project funded by China Railway Material Trade Group Luban Company.

Author Contributions: Leyu Zheng conceptualized the study and wrote the manuscript. Mingming Xiao contributed to the concept, idea of the study and the revision of the manuscript. Ke Li contributed to the review of the manuscript. Yi Ren contributed to the review of the manuscript. Chang Sun review of experimental data of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available within the article or its supplementary materials.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Supplementary Materials: The supplementary material is available online at https://www.techscience.com/doi/10.32604/cmc.2025.072036/s1.

References

1. Hemici M, Zouache D. A multi-population evolutionary algorithm for multi-objective constrained portfolio optimization problem. Artif Intell Rev. 2023;56(Suppl 3):3299–340. doi:10.1007/s10462-023-10604-2. [Google Scholar] [CrossRef]

2. Pan JS, Yu N, Chu SC, Zhang A, Yan B, Watada J. Innovative approaches to task scheduling in cloud computing environments using an advanced willow catkin optimization algorithm. Comput Mater Contin. 2025;82(2):2495–520. doi:10.32604/cmc.2024.058450. [Google Scholar] [CrossRef]

3. Song S, Zhang K, Zhang L, Wu N. A dual-population algorithm based on self-adaptive epsilon method for constrained multi-objective optimization. Inf Sci. 2024;655(6):119906. doi:10.1016/j.ins.2023.119906. [Google Scholar] [CrossRef]

4. Ming F, Gong W, Wang L, Gao L. A constraint-handling technique for decomposition-based constrained many-objective evolutionary algorithms. IEEE Trans Syst Man Cybern Syst. 2023;53(12):7783–93. doi:10.1109/tsmc.2023.3299570. [Google Scholar] [CrossRef]

5. Zhu Q, Zhang Q, Lin Q. A constrained multiobjective evolutionary algorithm with detect-and-escape strategy. IEEE Trans Evol Comput. 2020;24(5):938–47. doi:10.1109/tevc.2020.2981949. [Google Scholar] [CrossRef]

6. Yang W, Chen L, Li Y, Zhang J. A constrained multi/many-objective particle swarm optimization algorithm with a two-level balance scheme. IEEE Access. 2021;9:122509–31. doi:10.1109/access.2021.3107284. [Google Scholar] [CrossRef]

7. Lagaros ND, Kournoutos M, Kallioras NA, Nordas AN. Constraint handling techniques for metaheuristics: a state-of-the-art review and new variants. Optim Eng. 2023;24(4):2251–98. doi:10.1007/s11081-022-09782-9. [Google Scholar] [CrossRef]

8. Ray T, Tai K, Seow KC. Multiobjective design optimization by an evolutionary algorithm. Eng Optim. 2001;33(4):399–424. doi:10.1080/03052150108940926. [Google Scholar] [CrossRef]

9. Deb K, Pratap A, Agarwal S, Meyarivan TAMT. A fast and elitist multiobjective genetic algorithm: nSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–97. doi:10.1109/4235.996017. [Google Scholar] [CrossRef]

10. Takahama T, Sakai S. Constrained optimization by the ε constrained differential evolution with an archive and gradient-based mutation. In: Proceedings of the IEEE Congress on Evolutionary Computation; 2010 Jul 18–23; Barcelona, Spain. Piscataway, NJ, USA: IEEE; 2010. p. 1–9. [Google Scholar]

11. Wang W, Xu L, Chau K. Cε-LDE: a lightweight variant of differential evolution algorithm with combined ε constrained method and Lévy flight for constrained optimization problems. Expert Syst Appl. 2023;211:118644. doi:10.1016/j.eswa.2022.118644. [Google Scholar] [CrossRef]

12. Fan Z, Li W, Cai X, Li H, Wei C, Zhang Q, et al. Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol Comput. 2019;44(1):665–79. doi:10.1016/j.swevo.2024.101728. [Google Scholar] [CrossRef]

13. Qiao K, Yu K, Qu B, Liang J, Song H, Yue C, et al. Dynamic auxiliary task-based evolutionary multitasking for constrained multiobjective optimization. IEEE Trans Evol Comput. 2023;27(3):642–56. doi:10.1109/tevc.2022.3175065. [Google Scholar] [CrossRef]

14. Farias LR, Araújo AF. An inverse modeling constrained multi-objective evolutionary algorithm based on decomposition. In: Proceedings of the 2024 IEEE International Conference on Systems, Man, and Cybernetics (SMC); 2024 Oct 6–9; Kobe, Japan. Piscataway, NJ, USA. p. 3727–32. [Google Scholar]

15. Ma Y, Shen B, Pan A, Xue J. Constraint landscape knowledge assisted constrained multiobjective optimization. Swarm Evol Comput. 2024;90(2):101685. doi:10.1016/j.swevo.2024.101685. [Google Scholar] [CrossRef]

16. Feng J, Liu S, Yang S, Zheng J, Liu J. An adaptive tradeoff evolutionary algorithm with composite differential evolution for constrained multi-objective optimization. Swarm Evol Comput. 2023;83(3):101386. doi:10.1016/j.swevo.2023.101386. [Google Scholar] [CrossRef]

17. Wang J, Wang W, Chau K. An improved golden jackal optimization algorithm based on multi-strategy mixing for solving engineering optimization problems. J Bionic Eng. 2024;21(2):1092–115. doi:10.1007/s42235-023-00469-0. [Google Scholar] [CrossRef]

18. Tian Y, Zhang T, Xiao J, Zhang X, Jin Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans Evol Comput. 2020;25(1):102–16. [Google Scholar]

19. Wang Y, Huang K, Gong W, Ming F. Bi-directional search based on constraint relaxation for constrained multi-objective optimization problems with large infeasible regions. Expert Syst Appl. 2024;239(1):122492. doi:10.1016/j.eswa.2023.122492. [Google Scholar] [CrossRef]

20. Qiao K, Chen Z, Qu B, Yu K, Yue C, Chen K, et al. A dual-population evolutionary algorithm based on dynamic constraint processing and resource allocation for constrained multi-objective optimization problems. Expert Syst Appl. 2024;238(3):121707. doi:10.1016/j.eswa.2023.121707. [Google Scholar] [CrossRef]

21. Ming F, Gong W, Jin Y. Even search in a promising region for constrained multi-objective optimization. IEEE/CAA J Autom Sin. 2024;11(2):474–86. doi:10.1109/jas.2023.123792. [Google Scholar] [CrossRef]

22. Qiao K, Yu K, Qu B, Liang J, Song H, Yue C. An evolutionary multitasking optimization framework for constrained multiobjective optimization problems. IEEE Trans Evol Comput. 2022;26(2):263–77. doi:10.1109/tevc.2022.3145582. [Google Scholar] [CrossRef]

23. Ming F, Gong W, Wang L, Gao L. Constrained multiobjective optimization via multitasking and knowledge transfer. IEEE Trans Evol Comput. 2024;28(1):77–89. doi:10.1109/tevc.2022.3230822. [Google Scholar] [CrossRef]

24. Ma Z, Wang Y. Evolutionary constrained multiobjective optimization: test suite construction and performance comparisons. IEEE Trans Evol Comput. 2019;23(6):972–86. doi:10.1109/tevc.2019.2896967. [Google Scholar] [CrossRef]

25. Zitzler E, Laumanns M, Thiele L. SPEA2: improving the strength Pareto evolutionary algorithm. In: TIK-report. Vol. 103. Zürich, Switzerland: ETH Zurich; 2001. doi:10.3929/ethz-a-004284029. [Google Scholar] [CrossRef]

26. Deb K, Agrawal RB. Simulated binary crossover for continuous search space. Complex Syst. 1995;9(2):115–48. [Google Scholar]

27. Deb K, Goyal M. A combined genetic adaptive search (GeneAS) for engineering design. Comput Sci Inform. 1996;26:30–45. [Google Scholar]

28. Liang J, Qiao K, Yuan M, Yu K, Qu B, Ge S, et al. Evolutionary multi-task optimization for parameters extraction of photovoltaic models. Energy Convers Manage. 2020;207:112509. doi:10.1016/j.enconman.2020.112509. [Google Scholar] [CrossRef]

29. Tan KC, Feng L, Jiang M. Evolutionary transfer optimization—a new frontier in evolutionary computation research. IEEE Comput Intell Mag. 2021;16(1):22–33. doi:10.1109/mci.2020.3039066. [Google Scholar] [CrossRef]

30. Tian Y, Wang R, Zhang Y, Zhang X. Adaptive population sizing for multi-population based constrained multi-objective optimization. Neurocomputing. 2025;621(1):129296. doi:10.1016/j.neucom.2024.129296. [Google Scholar] [CrossRef]

31. Liu ZZ, Wang Y. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces. IEEE Trans Evol Comput. 2019;23(5):870–84. doi:10.1109/tevc.2019.2894743. [Google Scholar] [CrossRef]

32. Fan Z, Li W, Cai X, Huang H, Fang Y, You Y, et al. An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions. arXiv:1707.08767. 2017. [Google Scholar]

33. Fan Z, Li W, Cai X, Li H, Wei C, Zhang Q, et al. Difficulty adjustable and scalable constrained multiobjective test problem toolkit. Evol Comput. 2020;28(3):339–78. doi:10.1162/evco_a_00259. [Google Scholar] [PubMed] [CrossRef]

34. Kannan BK, Kramer SN. An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J Mech Des. 1994;116(2):405–11. doi:10.1115/1.2919393. [Google Scholar] [CrossRef]

35. Ray T, Liew KM. A swarm metaphor for multiobjective design optimization. Eng Optim. 2002;34(2):141–53. doi:10.1080/03052150210915. [Google Scholar] [CrossRef]

36. Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: handling constraints and extending to an adaptive approach. IEEE Trans Evol Comput. 2013;18(4):602–22. doi:10.1109/tevc.2013.2281534. [Google Scholar] [CrossRef]

37. Huang HZ, Gu YK, Du X. An interactive fuzzy multi-objective optimization method for engineering design. Eng Appl Artif Intell. 2006;19(5):451–60. doi:10.1016/j.engappai.2005.12.001. [Google Scholar] [CrossRef]

38. Steven G. Evolutionary algorithms for single and multicriteria design optimization. A. Osyczka. Springer Verlag, Berlin, 2002, ISBN 3-7908-1418-01. Struct Multidisc Optim. 2002;24(1):88–9. [Google Scholar]

39. Parsons MG, Scott RL. Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods. J Ship Res. 2004;48(1):61–76. doi:10.5957/jsr.2004.48.1.61. [Google Scholar] [CrossRef]

40. Dhiman G, Kumar V. Multi-objective spotted hyena optimizer: a multi-objective optimization algorithm for engineering problems. Knowl Based Syst. 2018;150(6):175–97. doi:10.1016/j.knosys.2018.03.011. [Google Scholar] [CrossRef]

41. Floudas CA, Pardalos PM. A collection of test problems for constrained global optimization algorithms. Berlin/Heidelberg, Germany: Springer; 1990. [Google Scholar]

42. Ryoo HS, Sahinidis NV. Global optimization of nonconvex NLPs and MINLPs with applications in process design. Comput Chem Eng. 1995;19(5):551–66. doi:10.1016/0098-1354(94)00097-2. [Google Scholar] [CrossRef]

43. Kocis GR, Grossmann IE. A modelling and decomposition strategy for the MINLP optimization of process flowsheets. Comput Chem Eng. 1989;13(7):797–819. doi:10.1016/0098-1354(89)85053-7. [Google Scholar] [CrossRef]

44. Rathore AK, Holtz J, Boller T. Synchronous optimal pulsewidth modulation for low-switching-frequency control of medium-voltage multilevel inverters. IEEE Trans Ind Electron. 2010;57(7):2374–81. doi:10.1109/tie.2010.2047824. [Google Scholar] [CrossRef]

45. Kumar A, Jha BK, Dheer DK, Singh D, Misra RK. Nested backward/forward sweep algorithm for power flow analysis of droop regulated islanded microgrids. IET Gen Trans Distrib. 2019;13(14):3086–95. doi:10.1049/iet-gtd.2019.0388. [Google Scholar] [CrossRef]

46. Tian Y, Cheng R, Zhang X, Jin Y. PlatEMO: a MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput Intell Mag. 2017;12(4):73–87. doi:10.1109/mci.2017.2742868. [Google Scholar] [CrossRef]

47. Bosman PA, Thierens D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans Evol Comput. 2003;7(2):174–88. doi:10.1109/tevc.2003.810761. [Google Scholar] [CrossRef]

48. Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput. 2002;3(4):257–71. doi:10.1109/4235.797969. [Google Scholar] [CrossRef]