Framework for Secure Substitution Box Construction and Its Application in Image Encryption

1  Introduction

Nowadays, protecting private information and confidential data from unauthorized sources is a significant challenge. Due to modern technology, access to information is easy for anyone from anywhere at any time, as various modern technology mediums, such as computer networks, software, and the internet, have made this possible. Almost all information is shared online through the internet, and the sharing of private information through insecure networks is a big problem. It is necessary to ensure the security of private data while transferring it through insecure networks. The said task can be fulfilled via different approaches. That is why, with the rapid advancement in information technology, cryptosystems are frequently developed to ensure the security of private information from unauthorized users. There are various methods employed in modern cryptography, including S-boxes, pseudo-random numbers, and encryption techniques, to secure information. However, the substitution box (S-box) is one of the crucial and fundamental components of well-known block ciphers, such as the Data Encryption Standard (DES) and the Advanced Encryption Standard (AES). A well-designed S-box algorithm can be used for a real-time application if it meets the following conditions: (i) Low computation cost, (ii) strong resistance against well-known attacks, including algebraic, differential, linear, and Boolean function attacks, and (iii) the ability to generate highly dynamic S-boxes. Furthermore, the proposed S-boxes can also be utilized in various cryptographic applications.

1.1 Related Work

Many researchers developed various new S-box algorithms to enhance the security of private information against modern attacks. These enhancements are based on diverse mathematical structures. Recently, chaotic systems have mostly been utilized in cryptography for designing secure cryptosystems. The reasons are their unpredictable behavior, ease of implementation, and sensitivity to initial conditions. For example, Lai et al. [1] proposed an S-box construction technique to enhance the cryptographic properties utilizing a new chaotic system. Ding and Xue [2] designed an efficient method to generate dynamic S-boxes for the encryption of images. Zhu et al. [3] utilized chaotic mappings to propose an S-box algorithm and a lightweight encryption scheme with better security. Liu et al. [4] developed an efficient method for the generation of S-boxes with strong nonlinearity that relies on a third-order nonlinear digital filter. Gupta and Chauhan [5] employed an S-box and a pseudo-random number generator based on a four dimensional (4D) hyperchaotic system in a secure image encryption approach. Gao et al. [6] designed a three dimensional (3D) encryption scheme and random numbers algorithm utilizing chaotic maps. Vijayakumar and Ahilan [7] designed an optimized chaos-based S-box for a real-time image encryption technique. Alexan et al. [8] proposed a secure algorithm for an image cryptosystem using different mathematical structures such as multiple base modulo operations, Chen-based binary quantization S-box, Fourier DNA coding, and a hyperchaotic system. Sani et al. [9] designed an S-box algorithm for a watermarking application based on a piecewise chaotic map. Brahim et al. [10] designed an image encryption technique utilizing multi-specific S-boxes and a hyperchaotic system. Tian and Su [11] developed a new virtual image enciphering method by integrating a chaotic S-box. Gan et al. [12] proposed an efficient and novel image encryption scheme using an S-box and a chaotic system. Zaghir et al. [13] used a novel three-dimensional hyperchaotic system to analyze and generate S-boxes for the AES algorithm. Khompysh et al. [14] designed an S-box algorithm based on a Galois field for protecting confidential information. Gao et al. [15] proposed a new 3D memristive cubic map using dual memristors and demonstrated its application to image encryption. The encryption scheme has strong confusion and diffusion properties. Lai and Chen [16] introduced an efficient and robust bit-level image encryption technique using chaotic maps. Aribilola et al. [17] proposed a technique for constructing robust S-boxes based on Möbius transformation combined with bit-wise shift permutation to improve the security of Internet of Things multimedia applications. The schemes based on a simple action of the Möbius transformation over a Galois field face the following challenges: (i) such a scheme can be easily predictable by the reverse engineering due to the bijective characteristic of said transformation, (ii) the aforesaid algebraic construction is limited to a small number of S-boxes and hence has the dynamic behaviour of a small degree, and (iii) has low resistance to the key related attacks due to the small number of utilized parameters. Bilal et al. [18] designed a dynamic S-box generator using a Mordell elliptic curve (MEC) with a combination of Möbius transformation. Further, the proposed S-boxes are utilized in image encryption. Dougherty et al. [19] introduced a new approach to image encryption utilizing signature-dependent S-boxes based on Latin squares and the Playfair cryptographic technique. Hua et al. [20] designed a novel S-box algorithm using a complete Latin square to encrypt images. Abd-El-Atty [21] employed quantum walks and particle swarm optimization to present an efficient S-box algorithm and used it in an image cryptosystem. Furthermore, Wang et al. [22] introduced an optical image enciphering technique that utilizes a quantum S-box. Gao et al. [23] designed a 3D hyperchaotic map, which is used to construct a pseudo-random number generator and a multi-image encryption scheme with robust cryptographic properties. Farah et al. [24] applied a Jaya optimization approach to enhance the performance of the chaotic-based S-box. Zamli [25] introduced a novel optimization technique to form an S-box that surpasses other optimization algorithms in two major benchmarks, namely nonlinearity and the strict avalanche criteria, while maintaining the desired performance in other metrics. Alhadawi et al. [26] presented a new S-box generation method combining a discrete chaotic map and nomadic people optimization. Artuger [27] developed a method to produce S-boxes with high nonlinearity based on a chaotic system and the whale optimization algorithm. Jawed and Sajid [28] designed an optimal S-box generation algorithm using an algebraic-heuristic algorithm, affine mapping, Galois field, and chaotic system. Additionally, the proposed S-box is utilized for both encryption and decryption of images. Qobbi et al. [29] used a genetic operator to construct a dynamic S-box to design a chaotic encryption scheme for medical images.

From the past few decades, elliptic curves (ECs) are playing a significant role in the area of cryptography due to their strong algebraic and cryptographic properties. Particularly, the sensitivity to initial parameters and the underlying algebraic structures. Furthermore, when the ordered EC is transformed through some maps, the dynamic behaviour and ordered points of the ECs make it difficult for the intruders to discover the utilized scheme for the generation of cryptographic components. Firstly, Miller utilized the EC in the field of cryptography [30] and stated that EC based cryptosystem is twenty times faster than the Diffie-Hellman scheme with identical key size. The ECs offer strong security with a smaller key size when compared to existing classical cryptosystems [31]. Liu and Liu [32] developed a cryptographic system based on a cyclic EC. When compared to other traditional cryptosystems, the aforesaid cryptosystems provide more security, but searching of a generator for such kind of ECs is a time consuming task. Silva-Garcia et al. [33] proposed a new symmetric cryptosystem using an EC with strong resistance against linear cryptanalysis. The proposed cryptosystem has a large key space to resist key related attacks. However, the proposed work includes the search for a generator point. In addition, AbdElHaleem et al. [34] designed an EC-based cryptosystem. The proposed cryptosystem is computationally intensive due to the group law operations. Furthermore, Pali et al. [35] introduced a scheme to generate an S-box using a supersingular EC over a finite field. The suggested scheme generates an S-box with high nonlinearity. However, the proposed technique does not have enough strength against key cryptanalysis due to the small size of its keyspace. Ye et al. [36] designed a safe cryptosystem for protecting digital data by utilizing an EC for the key exchange process. A generator point and three parameters each having a large number of bits are used for sharing keys. Consequently, the suggested cryptosystem consumes time in the computation of points from the generator and has small key space for the key exchange process.

Recently, some new S-box construction techniques have been designed based on finite ECs. For example, Hayat et al. [37] firstly used ECs for the generation of S-boxes. Hayat and Azam [38] developed an S-box algorithm using a totally ordered EC over a finite field. Khan et al. [39] developed a new S-box construction technique that uses ECs to construct secure and dynamic S-boxes. This technique computes the points on an EC using group law operations, which takes time to produce S-boxes. Ibrahim and Abbas [40] developed a method for generating dynamic S-boxes using ordered ECs over prime of different bit lengths. Furthermore, Hayat et al. [41] developed an efficient algorithm for generating strong S-boxes against different cryptanalyses using EC over finite rings. In [42] an S-box scheme is proposed for block ciphers based on ordered EC over finite rings to generate dynamic S-boxes for image encryption. The methods developed in [42–45] utilize ordered MECs to construct strong S-boxes with a low time complexity. Nevertheless, all the techniques mentioned in [42–45] have a common fact. That is, the proposed schemes are difficult to apply with ECs over large prime. The reason is the generation of all points on ECs to generate S-boxes. As the methods in [42–45] use MECs with two parameters b and p. Due to the limited number of input parameters, the suggested algorithms have small key spaces and are vulnerable to key related attacks. Additionally, it is noted that these schemes cannot produce S-boxes for significantly small primes. Thus, there is still a need to generate dynamic S-boxes with strong cryptographic properties. The above discussion concludes the following research gaps for the motivation of this study.

1.2 Research Gaps and Motivation

The research gaps, novelty, and base for the current study are summarized as follows:

•   Despite that all of the discussed schemes have their own importance to develop nonlinear components, but all of them either need the whole EC or the EC at least of the length 2n to design an n×n S-box. Thus, the need is to focus on generating the S-box of the same length in an optimized manner. The current scheme is optimized by reducing the number of points of the EC to 2n−1, which is half the length of the S-box. Furthermore, these points are not fixed as in the former schemes. This property makes our scheme not only fast but also flexible in selecting points.

•   The former schemes concentrate on the efficiency of the generation of the EC based S-box, but the time interval gets larger when a large number of S-boxes are required. To the best of our knowledge, no study has yet discussed the efficiency of the scheme for a large number of distinct S-boxes, taking into account the computation time of the underlying EC. The current scheme addresses this research gap by introducing an efficient scheme based on the MEC over the complex field.

•   Similarly, the aforementioned schemes require a prime larger than the size of the S-box. Naturally, the question arises whether the newly developed scheme performs for those primes for which the others do not. The authors answer this question by experimentally showing the performance of the current scheme for those primes where others are restricted. The new algorithm is also suitable for application in a constrained environment.

1.3 Contribution

To overcome the deficiencies in existing state-of-the-art S-box construction techniques, we designed a novel S-box construction algorithm. Our main contributions are:

•   We select a MEC with p≡3(mod4), and a complex algebraic structure Fp[i] rather than a real finite field or ring. The aim of choosing such a conditional prime is to get a field. As for each prime p, Fp[i] is not a field. The elements of the chosen field are complex numbers, which consist of both real and imaginary parts. The nature of points of an MEC generated over such a field is not easy to understand, as in the case of real fields.

•   The new scheme does not require generating all the points of the MEC; however, to optimize the scheme, the points required by the scheme are fixed and are half the length of the proposed S-box. In addition, any such points may be selected on the chosen EC, which is not the case in [40,41,43,44]. This property makes it more difficult to determine the utilized points by brute-force search.

•   In the current scheme, we do not impose a condition on the size of the underlying prime. Therefore, the scheme also works for primes of restricted size if the number of points on the MEC for that prime is at least half the length of the S-box. However, the schemes in [39,41,43,44] require primes with a sufficiently large size. Thus, in this respect, our scheme is optimal than the schemes [39,41–44] to output an S-box. Apart from this, the current scheme is more efficient than the methods in [42–44] in generating a significant number of dynamic S-boxes.

•   In the presented scheme, we form a vector by merging the real and imaginary parts of a coordinate of the naturally ordered points. The aim of doing this is to form a row vector with more diffusion in the acquired entries, which is not possible in the existing schemes based on the ECs generated over real finite fields or rings.

•   As the MEC consists of only two parameters. So, the key space is enhanced by applying the linear fractional transformation by preserving the existing order, and the key space of the current scheme becomes larger than that of existing schemes.

•   The randomness in elements of an S-box and the non-singularity of an algorithm are necessary to design an S-box. The stated objectives are achieved by selecting the indices of numbers in the formed vector. In a mathematical result, we show that the proposed algorithm has no singular points.

•   To achieve an S-box with the desired level of cryptographic properties, we permuted the initial S-box using a random permutation π of length 2n. The permuted S-box outperforms existing optimal S-boxes in different cryptographic properties.

•   It is essential to evaluate the potential of an algorithm regarding the generation of S-boxes. Therefore, we theoretically find the exact number of the proposed S-boxes. Furthermore, we mathematically classify the S-boxes that do not qualify for the desired level of security.

•   The recently developed EC based schemes are not capable of giving an output for the significantly small primes. Therefore, we experimentally prove that the newly developed algorithm can generate a large number of highly non-linear S-boxes for small primes.

1.4 Paper Organization

The rest of the paper is organized as follows: The preliminaries for the finite field, EC, and Möbius transformation are discussed in Section 2. The complete point-wise description of the proposed S-box algorithm is detailed in Section 3. The cryptographic properties of the proposed S-box algorithm are analyzed in Sections 4 and 5, while the application of the proposed S-box is presented in Section 6. Finally, the concluding remarks of the study are drawn in Section 7.

2  Paper Methodology

The proposed cryptographic system consists of three main phases: The selection of an appropriate finite field, an EC, and a transformation. As finite field are carefully chosen for developing a cryptosystem. The proposed study chooses the appropriate prime to construct a finite field. Then an MEC is generated based on the chosen finite field. To optimize the scheme, the specific points of the MEC based on the chosen field are generated instead of generating the whole EC. The generated points are naturally ordered. Lastly, we transform only one coordinate of the points by a linear fractional transformation. The indices of the transformed coordinate result in an S-box. We define all the related concepts in the following subsections.

2.1 Finite Field

If n is a prime number, then the set Fn={0,1,2,…,n−1} is a finite field [46]. Otherwise, it is a ring of integers and denoted by Zn [46]. It is important to note that, for each prime p, there exists a finite field Fp with p elements. Furthermore, the set Zp[i]={a+bi:a,b∈Zp} with i=−1 is a ring with p2 elements. In a ring Zp[i], the addition and multiplication operations are performed using standard complex numbers under the modulo p operation. If a condition is imposed on prime p, then Zp[i] becomes a field Fp[i]. Let us discuss this condition in the auxiliary result stated in Lemma 1 as follows.

Lemma 1: Let p be a prime number. Then Fp[i] is a field if and only if p≡3(mod4) [47].

2.2 Elliptic Curve

ECs are widely utilized in cryptography due to their strong security. The ECs may be defined over fields and rings. We give a brief introduction of ECs over different algebraic structures in the following.

An EC over a finite field Fp with a,b ∈ Fp is the set of points defined as,

Ep,a,b={(x,y)∈Fp×Fp:y2≡x3+ax2+b(modp)}∪{𝒪}.(1)

The prime p, and integers a,b are called the parameters of the EC Ep,a,b, while the point 𝒪 represents the point at infinity. Let #Ep,a,b represent the number of points on an EC, then in [48], the upper bound on the #Ep,a,b is computed by Hasse’s Theorem 1.

Theorem 1 (Hasse’s Theorem): Suppose Ep,a,b is an EC over the field Fp. The upper bound for #Ep,a,b is given by:

|#Ep,a,b−(p+1)|≤2p.

An EC is known as an MEC if the parameter a is set as zero while keeping the other parameter b non-zero. Mathematically, the MEC over the Fp is defined as:

Ep,b={(x,y)∈Fp×Fp:y2≡x3+b(modp)}∪{O}.(2)

The remarkable result regarding the number of points on an MEC is stated in the following Lemma 2.

Lemma 2: If p≡2(mod3) is a prime with p≥3, then the MEC Ep,b comprises precisely (p+1) points, with the unique y-coordinates, and for each y∈[0,p−1], ∃ an x∈[0,p−1] such that (x,y)∈Ep,b.

The points of an EC may be ordered in numerous ways, but Azam et al. [43] defined some well-known orderings on the ECs. For instance, the natural ordering ON on an EC is explained as follows. Let (x1,y1) and (x2,y2) be any two points on an EC, then

(x1,y1)≺N(x2,y2)⇔{eitherx1<x2,orx1=x2,andy1<y2.

When an ordering is defined on an EC, then it is known as an ordered EC.

If an EC Ep,a,b is defined over the field Fp[i], where p is a prime number and satisfying the condition p≡3(mod4). The expression in 1 becomes:

Ep,a,b={(x,y)∈Fp[i]×Fp[i]:y2≡x3+ax+b(modp)}∪{O}.

Similarly, the MEC 2 changes to the form:

Ep,0,b={(x,y)∈Fp[i]×Fp[i]:y2≡x3+b(modp)}∪{O}.

As the field Fp[i] is finite. Thus, there exists a finite number of points on the EC Ep,a,b. In this version of EC, the points appear in the form a+bi for a,b∈Fp.

The points on an EC may be generated in more than one way. We explain two methods, the group law method and the simple search method. Both are briefly explained as follows:

•   The group law: In this method, one needs to know one non-identity P point of an EC Ep,a,b, and the other n points are generated by the binary operation +. For any two points P(xp,yp) and Q(xQ,yQ) of an EC, the addition + is defined as follows:

P(xp,yp)+Q(xQ,yQ)=R(xR,yR), where xR=λ2−xp−xQ, and yR=λ(xp−xQ)−yp, where the scalar λ is obtained as,

λ={yQ−ypxQ−xp if P≠Q3xp2+a2yp if P=Q.

It is necessary to mention that in a cyclic EC, only one point is sufficient to generate the whole EC, but the case differs in an ordinary EC.

•   Search method: The first significance of a search method is that one does not need to know any point to generate any EC Ep,a,b. Secondly, any EC can be generated by a search method. In the said method, we just find those values of x and y that satisfy the algebraic representation of an EC. To explain this method, let us consider the EC E5,1,3:y2≡x3+x2+3(mod5), and consider the following Table 1.

It is visible from the Table 1, that (1, 0), (4, 1), (4, 4) are points of the EC E5,1,3.

2.3 Möbius Transformation

Möbius transformation based on algebraic structures and chaotic systems are widely used in literature to design highly secure cryptosystems [12,17]. The cryptographic algorithms based on Möbius transformation have strong resistance against various security attacks, including linear and differential attacks. In our framework, we design a cryptographic algorithm by combining an EC and Möbius transformation over the field Fp[i]. A Möbius transformation (or fractional linear transformation) g is a rational map of complex numbers Z because the map f is the ratio of two linear maps, which is mathematically expressed as follows:

g(Z)=cZ+deZ+f,(3)

where the complex coefficients c, d, e, and f∈Fp[i]. Now, we explain two important conditions of Möbius transformation: when cf−de≠0 and when cf−de=0.

(i)   When cf−de≠0, then g is said to be a non-singular map and is bijective. Thus, g is invertible [49].

(ii)   When cf−de=0, then g is called a singular map and not invertible. Thus, the transformation becomes constant [49].

3  The Proposed S-Box Description

Our scheme is concerned with the generation of S-boxes by integrating three mathematical structures: the finite field of Fp[i], the MEC Ep,b, and the Möbius transformation. The basic steps in generating the resulting S-box are described as follows:

(i)   To get the field Fp[i], it is necessary to select the appropriate prime p. As for each prime p, Fp[i] is not a field. It becomes a ring for some primes, for example, 13, 17, and 29. Keeping in view this reason, we choose the prime p such that p≡3(mod4), so that Fp[i] becomes a field [47]. Selecting a ring instead of a field may result zero more than once in the denominator of the Möbius transformation, whereas in a field there exists a unique case causing the Möbius transformation to be undefined. So, in the case of fields, excluding such a case consumes less time than in the case of rings. Moreover, the prediction of the MEC over the proposed field Fp[i] needs 𝒪(p4) time, whereas in case of the field Fp one can search the whole MEC in time 𝒪(p2). That is, the selected field enhances the complexity of the brute-force attacks.

(ii)   Recently, in [42–44], MECs over the finite field Fp are widely used due to the commonly recognized property explained by Lemma 2 in Section 2. But we select the MEC Ep,b over the chosen field Fp[i] in the Step 3 To generate an n×n S-box, we do not need to generate the all possible points of the Ep,b, but only 2n−1 points are sufficient to design the proposed S-box. Regardless of the approach, one may obtain any 2n−1 points of the Ep,b, but we select the initial 2n−1 naturally ordered points of EC over Fp[i].

(iii)   After achieving the desired number of points, we proceed to arrange them by natural ordering. The significance of ordering is to distort the natural sequence of the points of the MEC. We do not specify the nature of points, whether they are different or similar. Thus, in what follows, Ep,b is a naturally ordered MEC over Fp[i] with 2n−1 points unless it is specified.

(iv)   Next, we continue by selecting four parameters c,d,e,f∈Fp[i] and apply the Möbius transformation g for these parameters on only one coordinate of the generated Ep,b. Currently, the y-coordinate is transformed by the transformation g. Keeping in view that the parameters c,d,e,f∈Fp[i] are chosen by excluding the value for which the map g becomes undefined. Otherwise, the transformation may be applied to any parameters.

(v)   Now form a row vector Ag(y) by respectively allocating the odd and even indices to the real and imaginary parts of the acquired values of g(y). So that the length of Ag(y) is 2n.

(vi)   To design the proposed S-box, we define and apply a mathematical rule as:

σ(i)={r−1 if mr=max(Ag(y))s−1 if mr=ms and r>s,

where 1≤r,s≤2n and σ(i)≠σ(j) for i≠j.

(vii)   Finally, to disrupt the obtained S-box and make it harder for an adversary to exploit the resultant S-box, we permute the σ by a random permutation π to obtain a permuted S-box σπ with enhanced cryptographic properties.

The above described steps are explicitly summarized in the following Algorithm 1 and Fig. 1.

Figure 1: Flowchart of our proposed S-box generation process

To have a clear view of the scheme, we explain the steps of the whole scheme by illustrating an example of a 4×4 S-box in the Fig. 2.

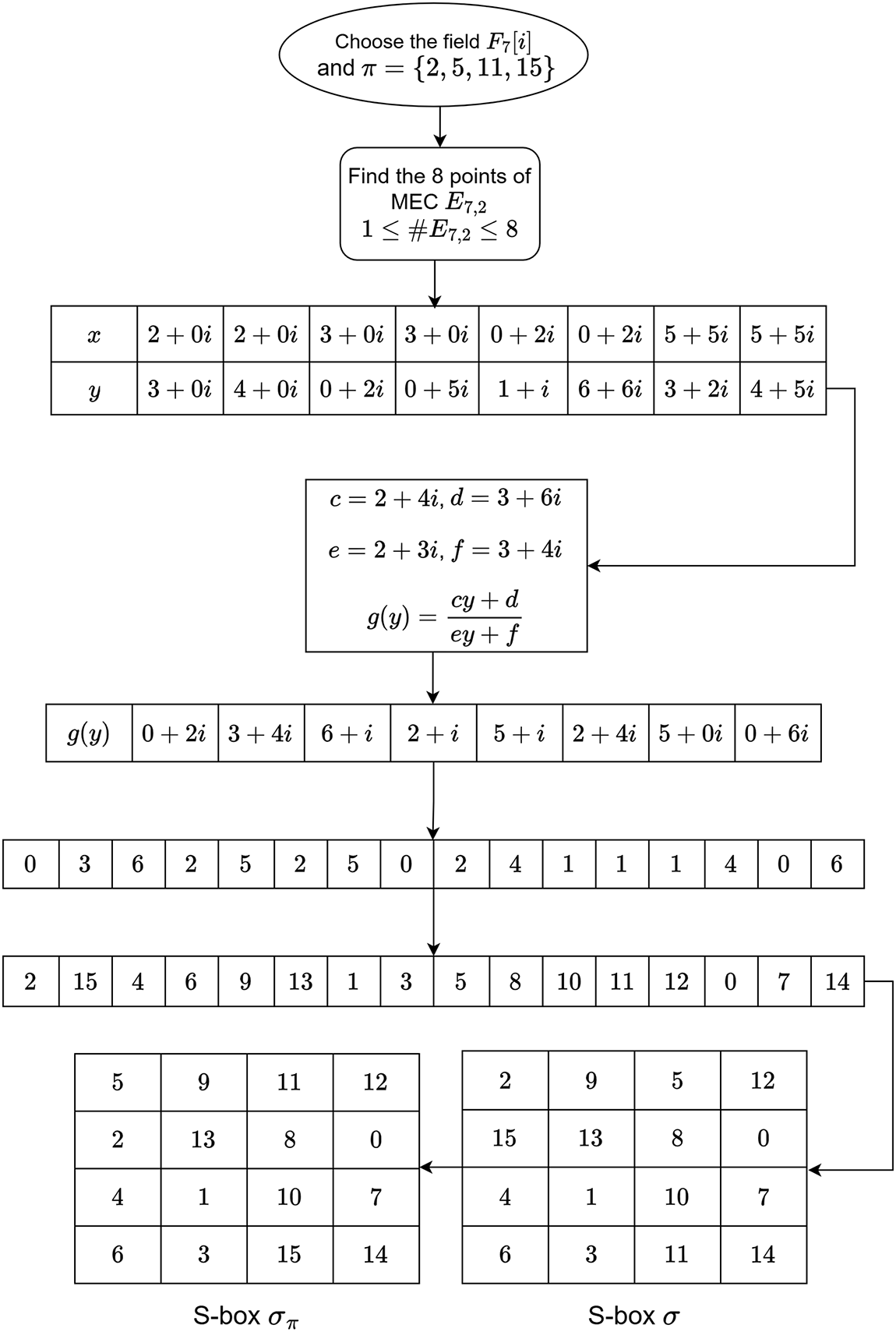
Figure 2: Generation of the sample S-boxes by the proposed scheme

Let us mathematically assess the probability of obtaining the proposed S-box and determine whether it is injective. We assert that the likelihood of the proposed algorithm is certain in generating injective S-boxes. For this, consider the following Lemma 3.

Lemma 3: The presented S-box algorithm is nonsingular, then the resultant S-box is injective.

Proof: From Algorithm 1, Step 19, it follows that the cardinality of the data set Ag(y) is 2n, possibly consists of some repeated values. So, by designing σ, we have σ(i)=r−1 if mr=max(Ag(y)) and σ(i)=s−1 if  mr=ms and r>s for 1≤i≤2n. That is σ(i) represents the index of max(Ag(y)) in Ag(y) preceding to all other possible repetitions in Ag(y), and indices may not be repeated. Thus, the probability Pr(σ(i)) of each σ(i) is 12n. As σ(i) is 2n in number and σ(i), σ(j) for i≠j are mutually exclusive. Then

Pr(σ)=⋃i=12nPr(σ(i))=∑i=12nPr(σ(i))=Pr(σ(1))+Pr(σ(2))+Pr(σ(3))+…+Pr(σ(2n))=12n+12n+12n+…+12n=2n2n=1.

The Pr(σ)=1, ensures the output of an S-box for valid input parameters, thereby confirming the nonsigularity of the proposed algorithm. Now, to prove that the proposed S-box is injective. Let us assume that i≠j, where σ(i)=r−1 if mr=max(Ag(y)) and σ(j)=s−1 if ms=max(Ag(y)). Here, we discuss two cases:

(i)   If mr≠ms, then either mr>ms or mr<ms and r<s or r>s. Then in both cases r≠s, that is r−1≠s−1 and hence σ(i)≠σ(j)

(ii)   Suppose that mr=ms, as mr,ms∈Ag(y), and Ag(y) is a row (or column) vector. So, r<s or s<r depends on the selection of i and j. Thus r≠s in both the cases, and σ(i)≠σ(j) as in the preceding case.

Thus in both the cases, it follows that the newly developed algorithm outputs injective S-boxes with the maximum probability. ◻

To evaluate an S-box generator, it is necessary to check the capability of such a generator with respect to the generation of total S-boxes. The answer to the aforementioned query is provided in Lemma 4.

Lemma 4: For a fixed prime p, the total number of the proposed n×n S-boxes from 2n−1 points of MEC Ep,b is:

(i) p4(p2−m)(p2−1), if ∃m points (xi,yi)∈Ep,b with eyi=−f.

(ii) 0, if for some i, yi=0, and f=0.

Proof: From Algorithm 1, it may be observed that the proposed n×n S-box needs 2n−1 values of the y-coordinate. That is 2n−1 points of the MEC Ep,b are sufficient to get the desired output. For the chosen prime p, Fp[i] becomes a field, and hence a group under both binary operations multiplication and addition. Thus, in Step 10 of the Algorithm 1, we have eyi+f=0 either if (i) eyi and f are additive inverses of each other or (ii) for some i,yi=0, and f=0. In the former case, if we have m such values of f for which eyi becomes additive inverse of f. The eyi cannot be equal to zero. As Fp[i]∖{0} is the multiplicative group, then we need to skip m such values of e to get the set et Ag(y), and hence we are left with p2−m choices for e, p2 choices for each c, d and p2−1 possible values for f. That is the number of S-boxes becomes p4(p2−m)(p2−1). It is mentioned that, for each yi in a chosen set of points, there exists e and f in a field Fp[i] such that eyi and f become additive inverses, that bounds the maximum such occurrences by m≤2n−1. In the later case, the transformation g will undefined for all choices of c, d, e, and hence we are unable to form the vector Ag(y) from undefined values. Consequently, the Pr(σ(i)) is not defined, and hence in such a special case the number of S-boxes will be zero. ◻

Corollary 1: If the points (xi,yi) are chosen on the mentioned MEC in such a way that for any i, eyi+f≠0(modp), then the total number of the proposed S-boxes is p4(p2−1)2.

Proof: In such a case eyi+f=0(modp) if and only if e=f=0. Then by excluding these two values, we obtain the total number of S-boxes p4(p2−1)2. ◻

The presented algorithm is capable of generating cryptographically strong S-boxes, but we specify some cases that should be avoided when constructing the proposed S-box. That is, the resultant S-boxes for such specific parameters are not cryptographically good. More precisely, the minimum nonlinearity becomes zero for such S-boxes. The following Lemma 5 is useful to recognize such S-boxes before generating them by their input parameters.

Lemma 5: If c,d,e,f∈Fp[i] such that e≠0 and cf−de=0. Furthermore, for (x,y)∈Ep,b∄y with cy+f=0, then the minimum nonlinearity of the resultant S-box will be zero.

Proof: Since g(y)=cy+dey+f, and after division algorithm we can write is as g(y)=ce+de−cfe(cy+f). But we have cf−de=0, which implies that de−cf=0. Then we can write g(y)=ce, and hence g is independent of y. That is g is a constant transformation, and the proposed S-box S a naturally ordered symbol set of elements [0,2n−1]. Then the first 2n−1 bits of the component Boolean function S1 are zeros, and last 2n−1 bits of the S1 are ones. Choose u∈GF(2n) having zero at the places of n−1 bits except the first one. Then u.xi=0 for xi∈GF(2n), i=1,2,…,2n−1, as first bit of the mentioned xi is zero. Thus S1⊕u.xi=0⊕0=0, and hence (−1)Sl⊕u.xi=1, for i=1,2,…,2n−1. Similarly, the first bit in the remaining 2n−1 elements xi is one. Then for the selected u, we have u.xi=1, that is S1⊕u.xi=1⊕1=0, and (−1)Sl⊕u.xi=1, for i=2n−1+1,2n−1+2,…,2n. Then,

WS1(u)=∑x∈F2n(−1)S1(x)⊕u⋅x=∑x∈F2n1=2n,

which is the maximum value for the Boolean function S1. So that, the NL(S1)=2n−1−12(2n)=0, which is the required result. ◻

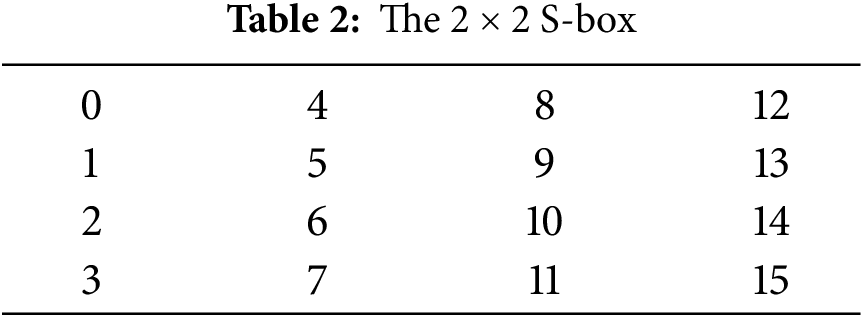
To clearly understand the above Lemma 5, we insert an example of such a 2×2 S-box over GF(24) and explicitly mention the necessary details. For this choose the c=e≠0 and d=f=0, then cf−de=0 and in such a case for any possible (x,y)∈Ep,b, we have g(y)=ce=1, and hence the corresponding S-box is shown in Table 2. For the said S-box u=1000, S1=0000000011111111 and GF(24)={0000,0001,0010,0011,0100,0101,0110,0111,1000,1001,1010,1011,1100,1101,1110,1111}. After some calculations, we have WS1(1000)=16, and hence NL(S1)=24−1−12(16)=0.

4  The Analyses against Cryptographic Attacks

To assess the cryptographic properties of our scheme, we first test a sample of S-boxes generated by the proposed method using a well-known set of standard tests. In the following, each test is explained in detail, and the results for the sample S-boxes are presented along with the relevant test. Each cryptographic test assesses different aspects of S-box resistance against linear, differential, Boolean function, and algebraic attacks. Furthermore, a detailed comparison of the presented method is carried out with the recently developed schemes.

Experimental framework: To complete the said tasks, we perform the experiments using MATLAB R2016a on a LENOVO machine with an AMD A6−6310 APU with AMD Radeon R4 Graphics, 1800 MHz, 4 Core(s), 4 Logical Processor(s), and 6.00 GB RAM installed. The proposed S-boxes σ and σπ as shown in Tables 3 and 4 are generated for the parameters p=107,b=4,c=1+46i,d=32+46i,e=3+4i and f=5+6i. Further, the parameters chosen for 100 S-boxes are p=47, b=1, c=[2,46+46i] with the step size 2, d=[2,4], e=17+37i, and f=19+17i.

4.1 Tests and Results

4.1.1 Nonlinearity

In [50], Willi and Othmar first proposed the idea of nonlinearity (NL) for an S-box S. The NL evaluates the linear relation between the inputs and outputs of an S-box. Mathematically, NL(S) of an S-box can be computed by:

NL(S)=min{2n−1−12maxu≠0|∑x∈GF(2n)(−1)Si(x)⊕u⋅x|},

where, u∈GF(2n), and Si represents the coordinate Boolean function of S, while “⋅” and “⊕” denote the dot product and addition over GF(2), respectively. The higher value of the NL stands for high resistance to linear attacks. The optimal value of NL for an n×n S-box is 2n−1−2(n/2)−1. The NL value of the S-boxes outlined in Tables 3 and 4 are 106 and 112, respectively. These NL results are high enough to thwart the attacks.

4.1.2 Linear Approximation Probability

Matsui presented the idea of linear approximation probability (LAP) in [51] for evaluating the strength of the S-box against linear attacks. To analyze the security of S, LAP is used to quantify the linear characteristics and correlation between the input and output bits. The following expression is used to compute the LAP of an S-box:

LAP⁡(S)=12n(maxρ,σ|#{x∈GF(2n):ρ⋅x=σ⋅S(x)}−2n−1|),

where, ρ∈GF(2n), σ∈GF(2n)∖{0}, and “⋅” denotes the dot product over GF(2). The lower value of the LAP indicates high resistance against linear attacks. The LAP results of the S-boxes demonstrated in Tables 3 and 4 are 0.0312 and 0.0078, respectively, which are very low.

4.1.3 Differential Approximation Probability

In [52], Biham and Shamir first provided the differential approximation probability (DAP) test. The DAP is a well-known test used to determine the security of an S-box against differential attacks. The DAP measures the probability of the precise difference between input and output bits. That is, it quantifies the probability of a specific differential characteristic occurring within the S-box S. The DAP can be calculated by the following equation:

DAP(S)=12n(maxΔs1, Δs2#{x∈GF(2n):S(x)⊕S(x⊕Δs1)=Δs2}),

here, Δs1 and Δs2 belong to GF(2n), and “⊕” represents the bit-wise addition over GF(2). For the low value of DAP, the S-box is considered more strong against differential attacks. The DAP of the S-boxes exhibited in Tables 3 and 4 are 0.0390 and 0.0156, respectively, which are very low.

4.1.4 Strict Avalanche Criterion

The concept of strict avalanche criterion (SAC) was first proposed by Webster and Tavares in [53]. The SAC is a useful tool to determine the security of S against Boolean function attacks by quantifying the substantial change in an S-box output bit when a single input bit is varied. For the Boolean functions Si, and ρp∈GF(2n), the SAC is computed using an n×n dependence matrix N=[dij], whose entry dij is calculated as follows:

dij=12n(∑x∈GF(2n)w(Si(x⊕ρj)⊕Si(x)) ),

where w(r), for r∈GF(2n), denotes the number of non-zero bits in the vector r. The S-box S is said to satisfy the SAC and has high cryptographic strength against Boolean function attacks if every off-diagonal entry of N is close to the optimal value of 0.50. The SAC values of the S-boxes in Tables 3 and 4 are 0.4218, 0.5937 and, 0.4531, 0.5625, respectively. These values are sufficiently close to the optimal value 0.50, exhibiting strong avalanche properties.

4.1.5 Bit Independence Criterion

The idea of the Bit independence criterion (BIC) was given by Webster and Tavares in [53]. The BIC is also used to determine the security of S against Boolean function attacks by measuring the variation in a pair of S-box output bits when a single input bit is changed. Let D be a BIC matrix and defined as D=[zqr], where zqr is computed by:

zqr=12n(∑x∈GF(2n)1≤q≠ℓ≤nw(Sq(x⊕ρr)⊕Sq(x)⊕Sℓ(x⊕ρr)⊕Sℓ(x))).

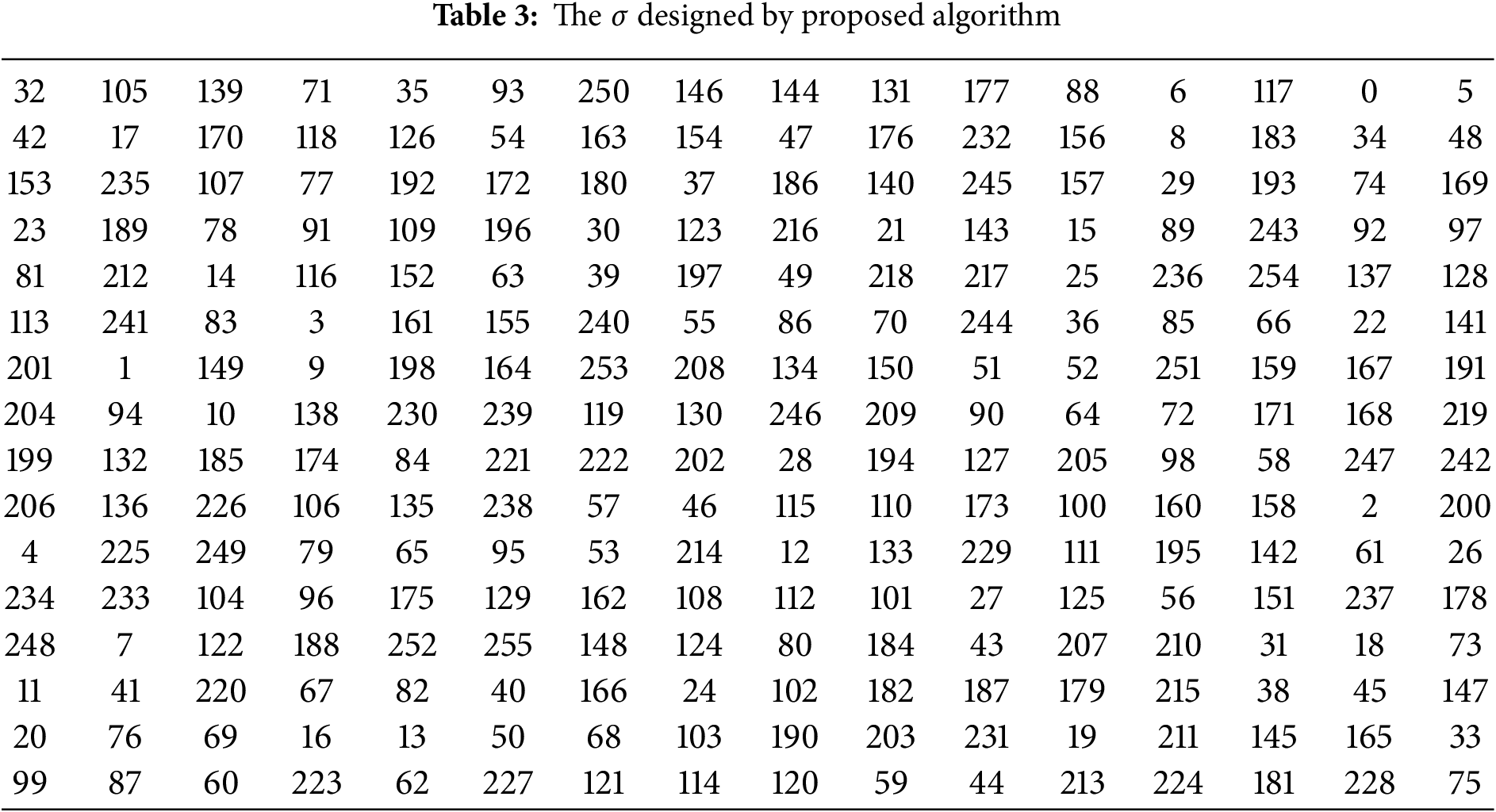
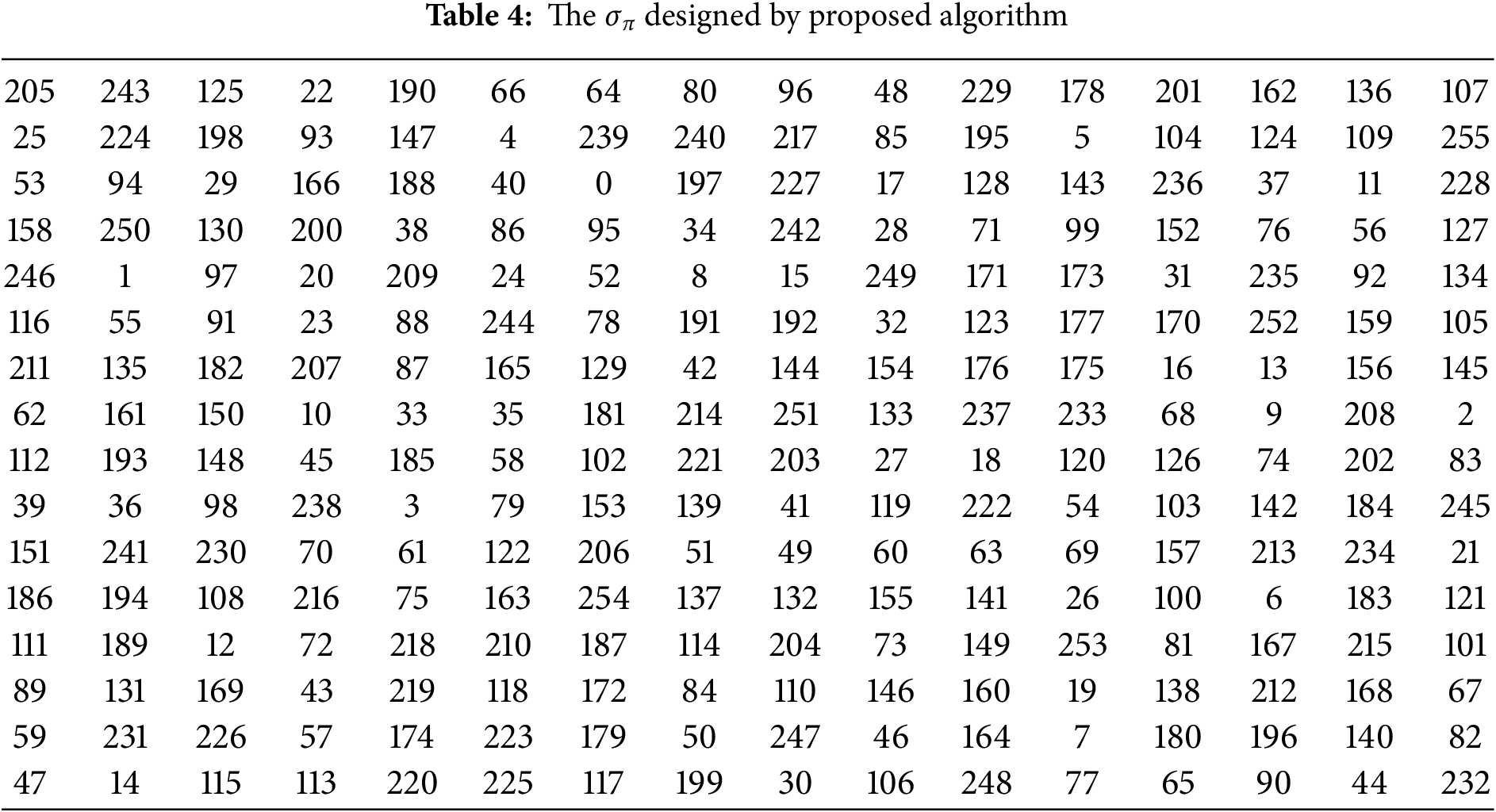
The S-box is considered to fulfill the BIC criteria and provide good cryptographic strength against Boolean function attacks if every off-diagonal entry in the matrix D is close to the optimal value of 0.50. The BIC values of the Tables 3 and 4 are 0.4707, 0.5293, 0.4883, and 0.5234, respectively, which are extremely close to the optimal value 0.50.

4.1.6 Algebraic Complexity

Sakall et al. [54] proposed the concept of algebraic complexity (AC) to test the resistance of an S-box against an algebraic attack. The AC represents the number of non-zero terms in the linear polynomial representation of an S-box. As 2n−1 is the optimal value of the AC for any n×n S-box. The AC of the S-boxes in Tables 3 and 4 attains the optimal value 255.

It follows from the above-attained values of the proposed S-boxes that the presented algorithm has strong cryptographic strength. However, to rigorously analyze the new algorithm, a comparison with recently developed schemes is conducted below.

5  The Comparison Based Analysis

This section provides a rigorous analysis of our algorithm and checks its cryptographic strength against the well-known attacks. The Table 5 presents a detailed comparison of our proposed S-boxes and S-boxes generated by the state-of-the-art techniques based on various mathematical structures. Furthermore, we prepared the Tables 6 and 7 based on the data available in Table 5. The ‘Remark’ column summarizes the resistance of the reference techniques against the respective attacks, contrasted with that of the proposed scheme.

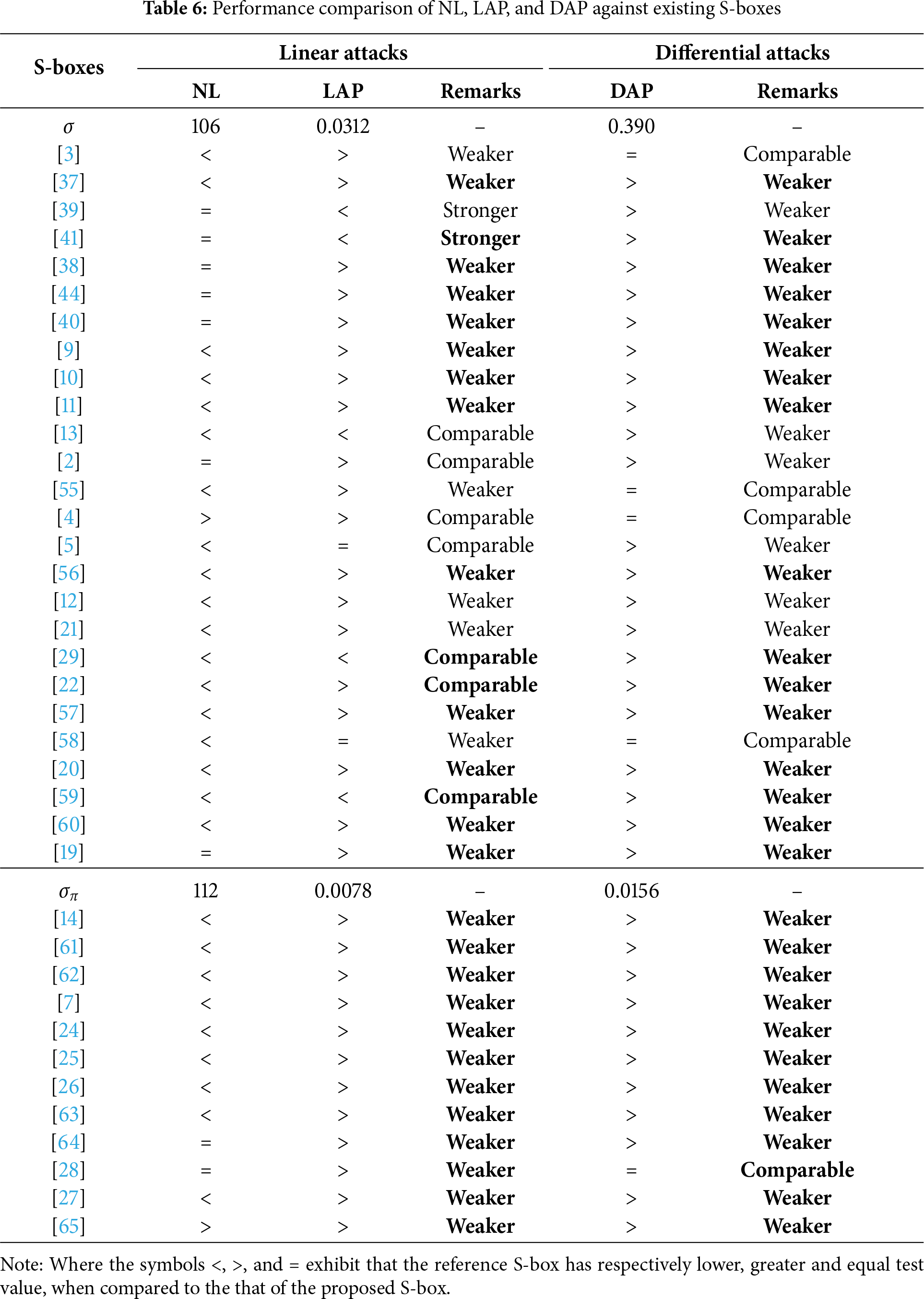
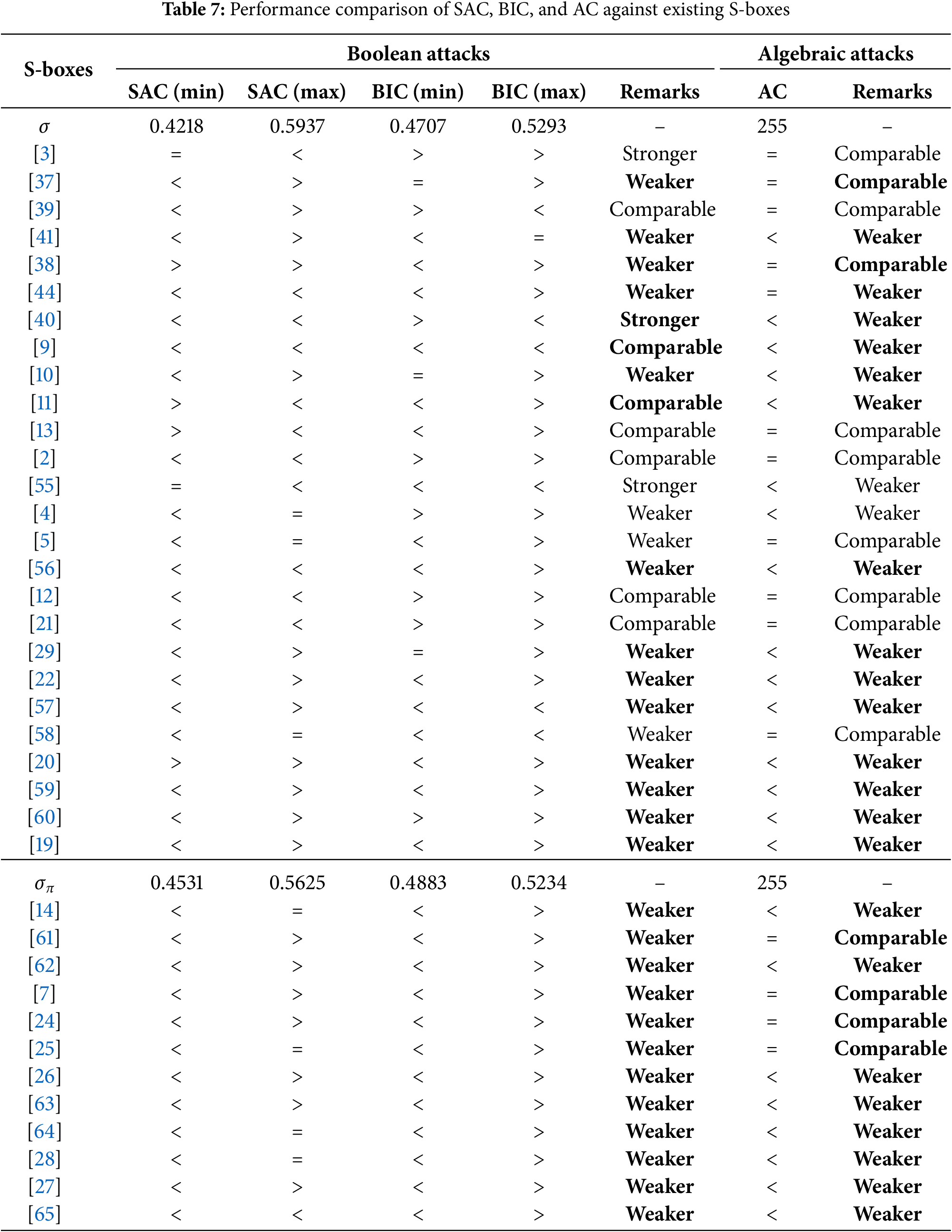
The current scheme demonstrates superior performance across all analyzed attacks, as observed in Tables 6 and 7, when compared to the reference schemes highlighted in bold.

5.1 Side-Channel Attack Analysis

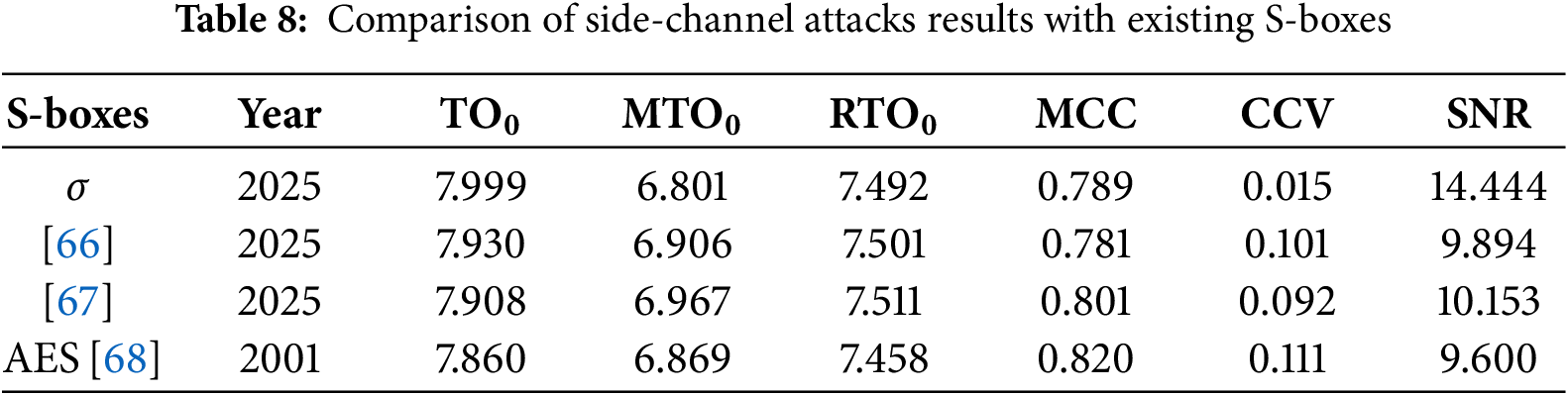
Beyond testing conventional cryptographic criteria, it is important to assess the S-box resistance against side-channel attacks. Side-channel attacks, unlike conventional mathematical attacks that focus on the algorithmic framework, exploit physical leaks such as power consumption during cryptographic operations. Even a mathematically and cryptographically strong algorithm can become vulnerable if its implementation exposes exploitable information, so evaluating its resistance to such attacks is crucial. As a result, side-channel analysis is essential for designing cryptosystems that are both theoretically secure and resistant to real-world exploitation. We applied several well-known and commonly used parameters, including Normalized Transparency Order (TO), Mean Normalized Transparency Order (MTO), and Relative Transparency Order (RTO), along with supplementary measurements such as Maximum Correlation Coefficient (MCC), Correlation Coefficient Variance (CCV), and Signal-to-Noise Ratio (SNR) to our generated S-box in Table 3. However, these analyses provide a foundation for evaluating how effectively an S-box reduces leakage that can be exploited by power analysis. To conduct a fair comparison between the proposed S-box and other related techniques based on a real finite field, and experimental results are demonstrated in Table 8. The results show that the proposed algorithm’s outputs closely align with those of AES and other recent, robust, and highly nonlinear state-of-the-art S-box methods. Since the variation between our method and other generators is very low, it can be assumed that the proposed S-box algorithm and the majority of modern S-box algorithms are theoretically equally resilient to basic side-channel attacks. These findings demonstrate that the cryptographic strength of our S-box does not compromise its resistance to side-channel leakage, preserving a robust trade-off between implementation security and cryptographic strength.

5.2 Performance Analysis

An S-box generator is considered cryptographically favorable if it can generate a large number of distinct S-boxes in a short span of time, and the number of fixed points in the generated S-boxes is as small as possible. Furthermore, it should be nonsingular [61]. In this subsection, we analyze the presented algorithm regarding its capability to generate S-boxes, fixed points, singularity, execution time, and distribution of NL values. Furthermore, we compare the current algorithm with similar algorithms [42–44] in terms of the aforementioned criteria.

5.2.1 Generation Efficiency

We run the algorithms [42–44] for initial valid values of prime p and b to generate the first 1000 S-boxes using the MEC y2≡x3+b(modp), and the experimental results are shown in Table 9. The results indicate that the presented scheme needs fewer input points, a smaller value of prime than the schemes in [42–44] to generate a comparable number of distinct S-boxes. The number of total possible proposed S-boxes is greater than those of [42–44] for every initial valid underlying primes. More explicitly, the current algorithm begins to perform for very small primes, whereas the mentioned schemes are incapable of generating a single S-box for primes less than 257.

5.2.2 Fixed Points Evaluation

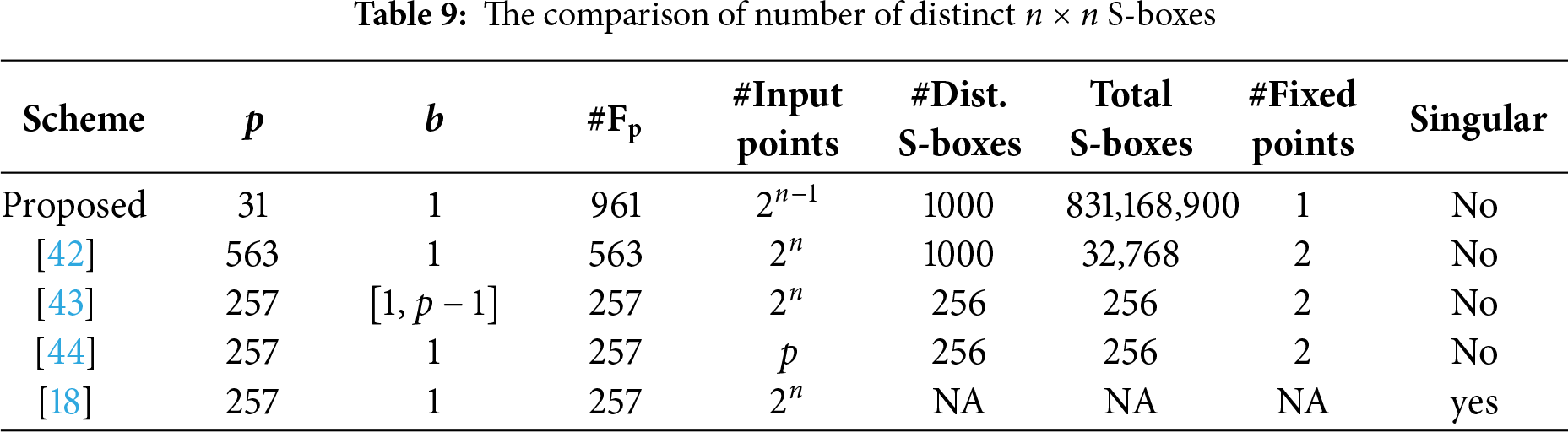
Apart from the generation of a large number of distinct S-boxes, an S-box generator is considered to have good dynamic behavior if the mean value of the fixed points in the generated S-boxes is considerably small [61]. The round-off mean values of the fixed points (#Fixed points) for the proposed S-box generator and the generators presented in [42–44] are drawn in Table 9. It is obvious that the proposed algorithm has comparatively more dynamic behavior than those of [42–44].

5.2.3 Analysis of Singular Points

An S-box algorithm is said to have singular points if it does not generate an S-box for a valid input parameter, and hence, the algorithm becomes singular. An S-box generator is considered favorable for cryptographic applications if it is nonsingular. The comparison of the presented algorithm with respect to the singular points is presented in Table 9. It can be verified that the current algorithm is also nonsingular.

5.2.4 Assessment of the Execution Time

An S-box generator is promising for cryptographic applications if it can efficiently generate the resulting S-box [40]. More precisely, for a favorable S-box construction method, it is necessary to frequently output dynamic S-boxes in a minimal time. We analyzed the computation time of the current and some recent schemes for generating the above 1000 S-boxes. The experimental results are shown in Fig. 3.

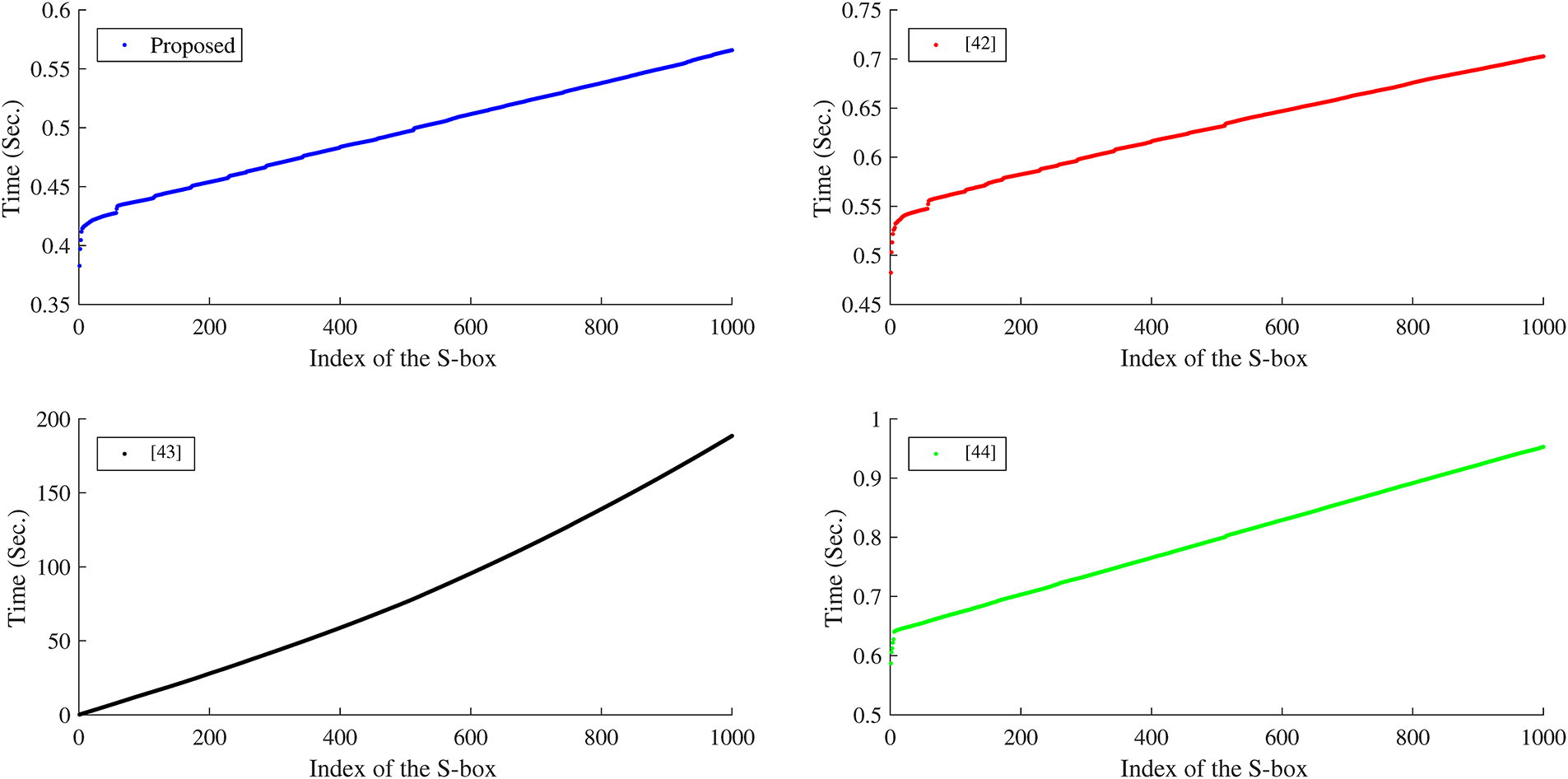
Figure 3: The comparison of execution time of new and existing algorithms [42–44]

It is clear that the average time for the proposed S-box is 0.50 s, whereas the average time required for the S-boxes [42–44] is 0.63, 82.76 and 0.80 s, respectively. Furthermore, the current scheme takes only 0.57 s to generate 1000 S-boxes, whereas the schemes in [42–44] require 0.70, 188.50, and 0.95 s, respectively, to generate the same number of S-boxes. Consequently, our algorithm is faster than those of our competitors. The speed of the current algorithm is superior to that of the algorithm in [43] because the newly developed method does not require generating all points for S-box generation.

5.2.5 The NL Distribution

Apart from this, we picked only the first 100 S-boxes generated by the new scheme and the aforesaid schemes. The NL ranges for the proposed scheme and the schemes in [42–44] are [86, 104], [86, 104], [90, 104], and [90, 102], respectively. Thus, the range for the proposed scheme is comparable with the ranges of the scheme [42,44]. However, if we choose a bit larger prime for the current algorithm and the chosen parameters illustrated in Section 4, then the NL range for the proposed technique becomes [92,104] and hence the number of S-boxes for each NL value in the corresponding range is shown in Fig. 4. It follows that the minimum NL value (92) for the proposed algorithm is greater than the minimum NL values (86,90,90, respectively) attained by the schemes [42–44]. In addition, the current scheme generates more S-boxes of NL = 104 than the schemes in [42–44]. Hence, the proposed algorithm is more capable of generating highly non-linear S-boxes with small input parameters.

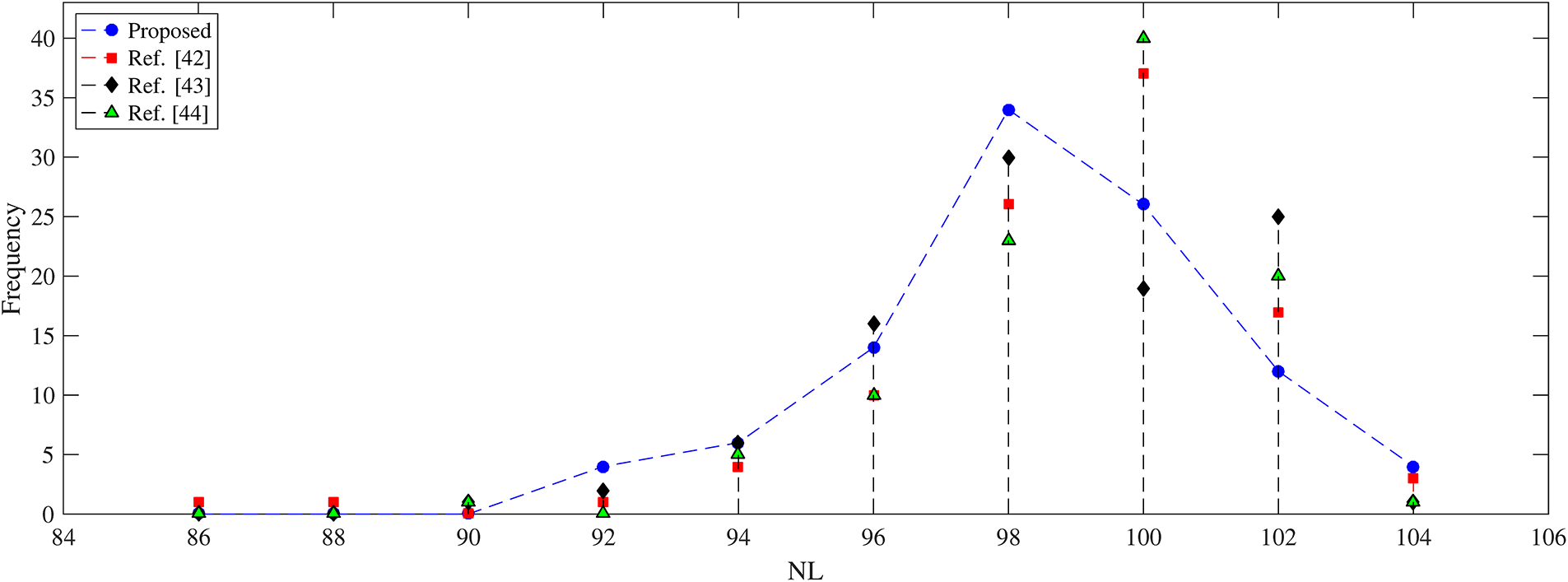
Figure 4: The comparison of NL distribution by the new and existing algorithms [42–44]

5.2.6 Analysis Based on Repeated Trails

To validate the effectiveness of our S-box generator, we conducted independent repeated trials to produce 100 S-boxes using the various parameters described in Section 4. For each generated S-box, we calculated cryptographic properties using standard metrics, including LAP, DAP, BIC, and SAC, and outlined the results in Fig. 5. The LAP values for 100 S-boxes are shown in Fig. 5a, falling in the range [0.0156, 0.0937] with an average of 0.0497, which are low, indicating that our generator produces secure S-boxes against linear attacks. Similarly, the DAP results for the same set of 100 S-boxes are depicted in Fig. 5b. The range of the DAP is [0.0390, 0.0625], having average of 0.0442. That is low, and these findings confirm that constructed S-boxes exhibit high resistance to differential attacks. Moreover, the SAC (min) and SAC (max) test results for 100 S-boxes are presented in Fig. 5c. The ranges [0.3437, 0.4375] and [0.5468, 0.6562] correspond to the SAC (min) and SAC (max) values, indicating averages of 0.3982 and 0.6053, respectively, which are closer to the desired value of 0.5. Likewise, the BIC (min) and BIC (max) test outcomes of 100 S-boxes are depicted in Fig. 5d. The BIC ranges [0.4433, 0.4882] and [0.5156, 0.5566] with average BIC (min) and BIC (max) values 0.4710 and 0.5330, respectively, which are close to the ideal value 0.5, indicating that our generator can produce S-boxes with the desired confusion and secure against Boolean attacks. As a result of the repeated-trial analysis, the suggested method consistently generates dynamic S-boxes with satisfactory cryptographic properties and is independent of specific parameter choices. Hence, the proposed S-box framework offers considerable resistance against various cryptographic attacks.

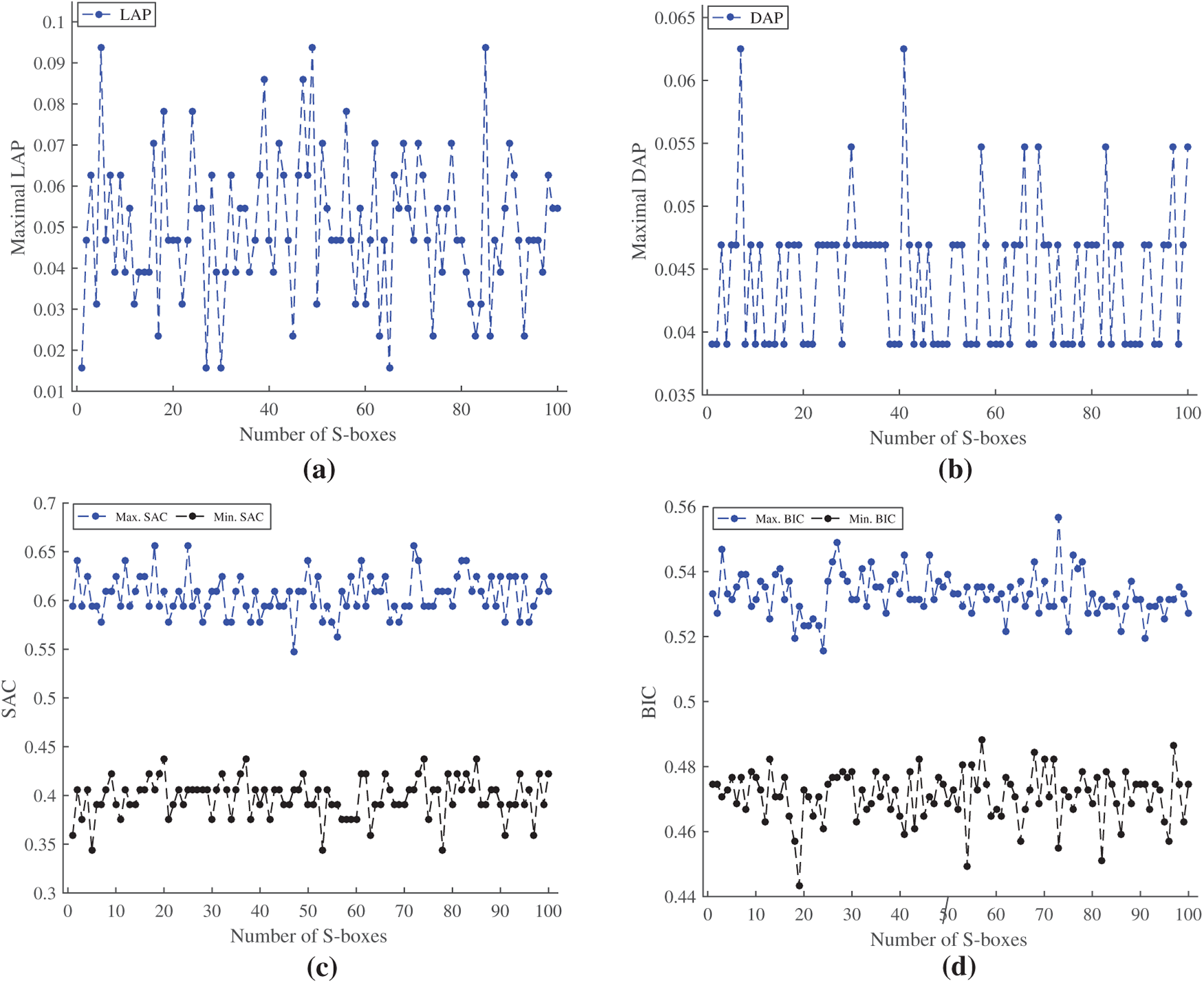
Figure 5: Distribution of 100 S-boxes cryptographic results. (a) Maximal LAP. (b) Maximal DAP. (c) Minimum and Maximum values of SAC. (d) Minimum and Maximum values of BIC

5.3 Key Space Analysis

The security of any encryption algorithm is based on its key space, and hence, keyed S-boxes are cryptographically more favorable regarding the security against key cryptanalysis [40]. In this section, we analyze the size of the key space and, hence, the sensitivity of each key of the proposed S-box generator.

5.3.1 Size of Key Space

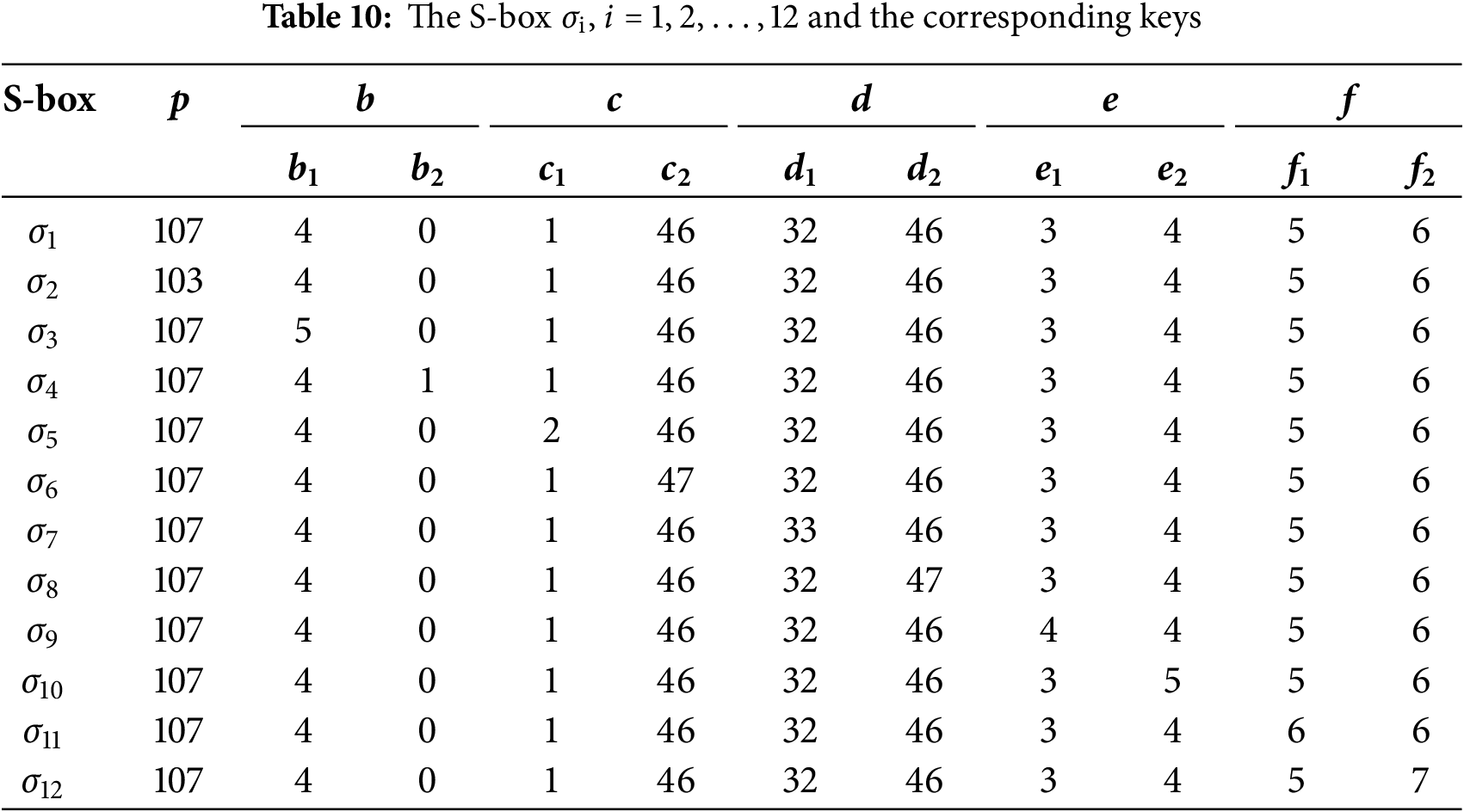
Since the proposed algorithm uses six keys that are p,b,c,d,e and f. In which only p is real, while the remaining five keys consist of two parts. The proposed algorithm is implemented by choosing p of eight bits. However, the number of bits may be increased by selecting a large p. In general, if p consists of μ bits, then the key space of the proposed cryptosystem is 211μ, which is much larger than the key spaces 22μ,23μ,24μ,29μ,29μ of the schemes [39–42,44], respectively. Thus, the new scheme offers more security to thwart unauthorized attempts of attackers.

5.3.2 Key Sensitivity

A cryptosystem is considerably secure to key-related attacks if a minor change in any key results in a different output. To analyze this property of the presented algorithm, we generate S-boxes against different altered keys, as listed in Table 10. We have 12 S-boxes, where σ1 is the one for unchanged keys, as shown in Table 3, and σi,i=2,3,…,12, for the slightly changed keys, are shown in Table 10.

Then we compute the correlation coefficient (CC) between each pair (σi,σj) for i≠j of S-boxes generated by the original keys and slightly changed keys. The CC must be close to zero for a highly key sensitive S-box algorithm. The results are shown in Fig. 6, where the average CC (0.0085) indicates that a minor change in any key produces a completely uncorrelated and different output.

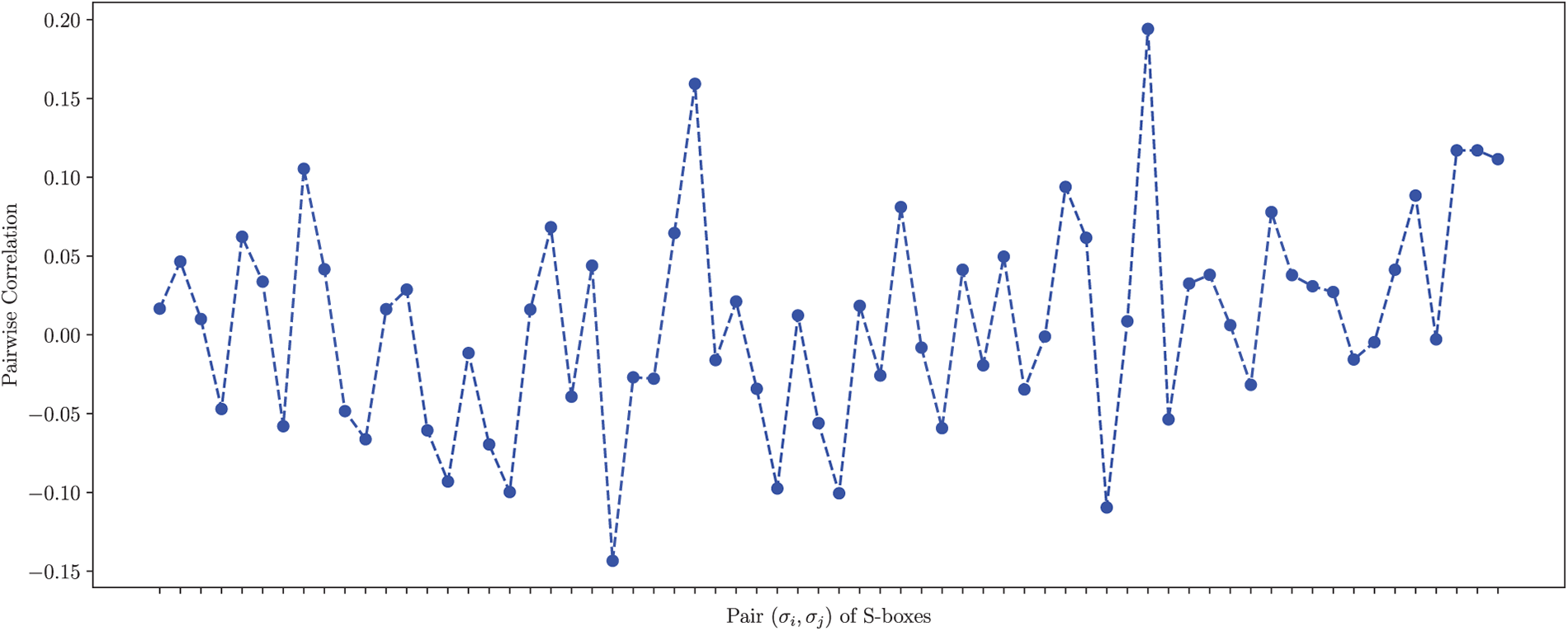
Figure 6: The CC of the S-boxes generated by slightly different keys

6  Application of Proposed S-Box

The presented S-box algorithm can be utilized in diverse security fields such as steganography, encryption, and watermarking. Nowadays, in the area of cryptography, the security of confidential images has emerged as a prominent research topic. In this paper, we used our S-box generator for strong and secure image encryption. The S-box provides diffusion and confusion, which enhances the security of the image cryptosystem. Traditional image cryptosystems, particularly cryptosystems that depend on a static S-box, are insufficient to assure the security of images.

6.1 Application in Image Encryption

In this subsection, we demonstrate the potential application of our S-box generator by integrating it into the image encryption technique designed by Hayat et al. [41]. The encryption technique presented by Hayat et al. [41] is based on an EC over a finite ring and comprises three phases, namely the masking phase, diffusion phase, and confusion phase. In the confusion phase, image based S-boxes are employed to permute the pixels of the diffused image in the encryption process to obtain a cipher image. Although the utilized S-boxes in the said encryption scheme present promising results and show strong security against well-known attacks. However, the presented S-box scheme uses a large EC and has a low key space. In order to analyze the security and efficiency of the image encryption algorithm, we replace the S-box designed by Hayat et al. [41] with the proposed S-box. The encryption scheme and replacement process are detailed in Algorithm 2. A comprehensive analysis of the results obtained is presented in the following subsections.

6.2 A Detailed Performance Analysis

In this section, we examined the effectiveness of the encryption scheme based on different generated S-boxes. To do this, we first substituted our proposed S-box and performed all standard security tests. Likewise, we substituted the other well-known S-boxes of algorithms [42,68] with NL = 112 in the same encryption scheme. Using the same system and the parameters listed in Section 4, we encrypted standard images of Resolution chart256×256, Chemical plant256×256, Herringbone weave512×512, and San diego512×512, respectively. The encrypted images obtained using the presented S-box are shown in Fig. 7.

Figure 7: Results of encryption process: (a–d) plain images; (e–h) corresponding cipher images

6.2.1 Discussion of Results

In this part of the article, we compare and discuss the results of the encrypted images obtained by the current and existing S-boxes.

6.2.2 Differential Attacks

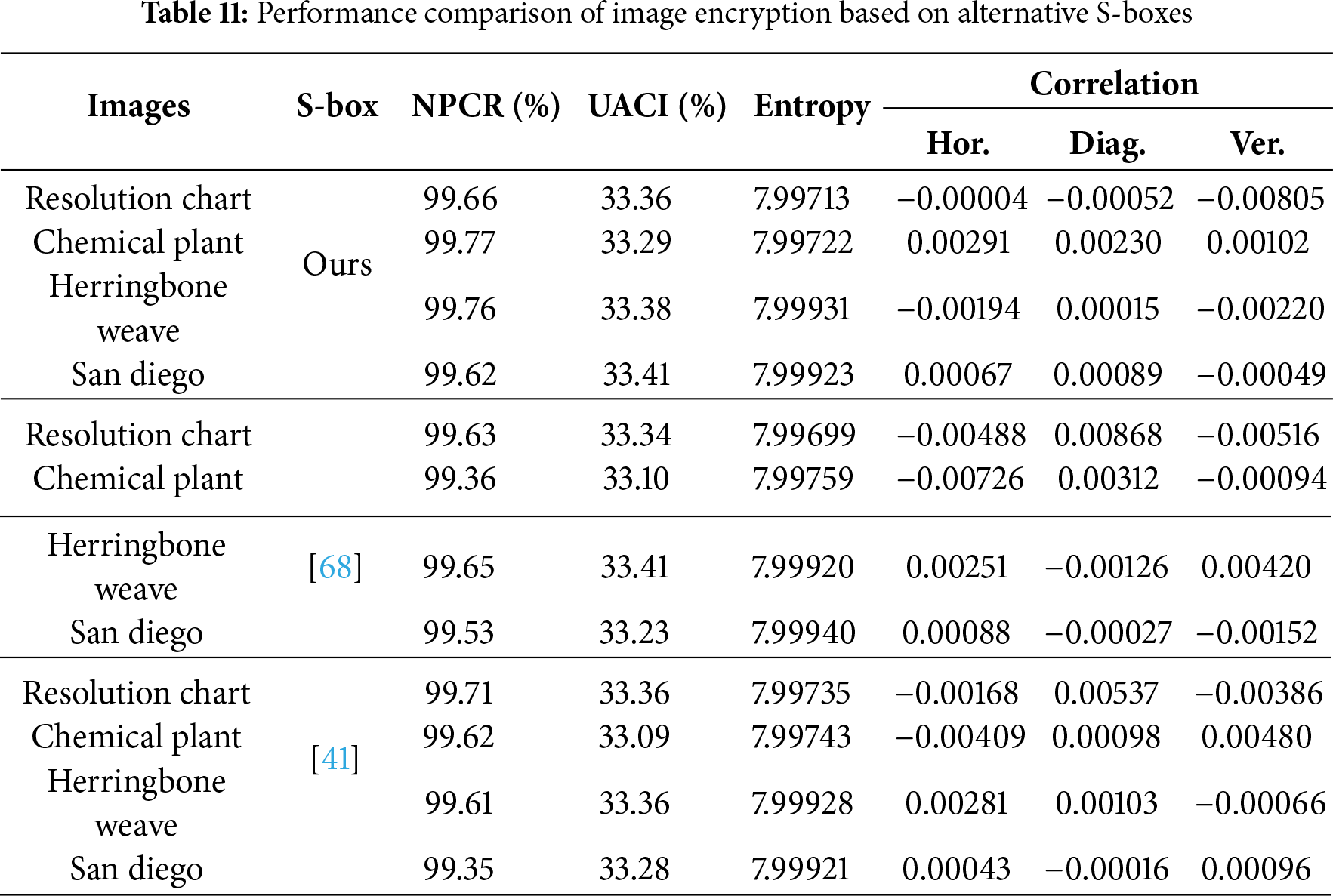
If an encryption approach can produce considerably distinct encrypted images from two slightly distinct plain images, then it is assumed to be secure against differential attacks. The resilience of an encryption technique against a differential attack is quantified by two metrics: NPCR (Number of Pixels Changed Rate) and UACI (Unified Average Changing Intensity). The theoretical values of NPCR and UACI for the images of size 256×256 and 512×512 are 99.5693, [33.2824, 33.6447] and 99.5893, [33.3730, 33.5541], respectively. For the aforesaid images, we computed the NPCR and UACI values as listed in Table 11. It may be observed that the NPCR values for the Resolution chart, Chemical plant, Herringbone weave, and San diego are according to the theoretical values and better than the results acquired by the [42,68]. Similarly, the UACI results of the images based on our S-box fall in the theoretical ranges and are better than results based on the S-boxes of [42,68]. Therefore, the encryption approach using our S-box shows stronger resistance against differential attacks than the results for the S-boxes of [42,68].

6.2.3 Statistical Attacks

A secure encryption algorithm must be capable of effectively resisting all kinds of statistical attacks. We applied various tests, including histograms, correlation, and entropy tests, to evaluate the robustness of the presented image cryptosystem against such attacks.

6.2.4 Information Entropy

Entropy is a statistical metric used to quantify the randomness of secret data. It depicts the intensity distribution and unpredictability among the image pixels. An encrypted image with a higher entropy can protect more information when compared to an encrypted image with a lower entropy. The ideal value of entropy for an encrypted image is 8. We computed the entropy of all cipher images shown in Fig. 7 and the results are depicted in Table 11. It follows that entropy results for images such as the Resolution chart and Chemical plant when ciphered by the new S-box are comparable with images encrypted by the S-box in [68] and are close to the entropy obtained due to the S-box in [41]. Likewise, for encrypted images, Herringbone weave and San diego, entropy results for the current S-box are better than those of the S-box in [68] and are comparable with those of [41]. Consequently, the encryption method using our S-box exhibits stronger resilience to statistical attacks than [68] and achieves comparable resistance with [41].

6.2.5 Correlation Coefficient

The pixels of a plain image are significantly connected to the adjacent pixels. A secure encryption algorithm must generate encrypted images with extremely low inter-pixel correlation between their pixels. Ideally, bring it close to zero so that no information may be obtained by a cryptanalyst. We employed correlation analysis to compute the correlation coefficient in horizontal, diagonal, and vertical directions to examine the pixel correlation in the enciphered images. The outcomes obtained by the correlation test are depicted in Table 11. It follows that correlation results for cipher images of the Resolution chart and Chemical plant along three different dimensions, such as horizontal, diagonal, and vertical, using our presented S-box, are better than results obtained from the S-boxes of [41,68]. Alike, for encrypted images such as Herringbone weave and San diego, correlation results using the new S-box are better than the S-box in [68] and are comparable with the S-box of the scheme [41]. The encryption approach using the newly designed S-box demonstrates stronger resilience to statistical attacks than utilizing the S-boxes in [41,68].

6.2.6 Histogram Analysis

The uniformity of the histogram of encrypted images demonstrates the level of security of an image encryption scheme. An encrypted image with a uniformly distributed histogram can effectively resist statistical attacks. The histograms of the cipher images are exhibited in Fig. 8. It is evident that the histograms of the enciphered images generated using our S-box generator in the proposed encryption scheme are uniform. As a result, an improved cryptosystem provides robust security against statistical attacks and successfully passes the histogram analysis.

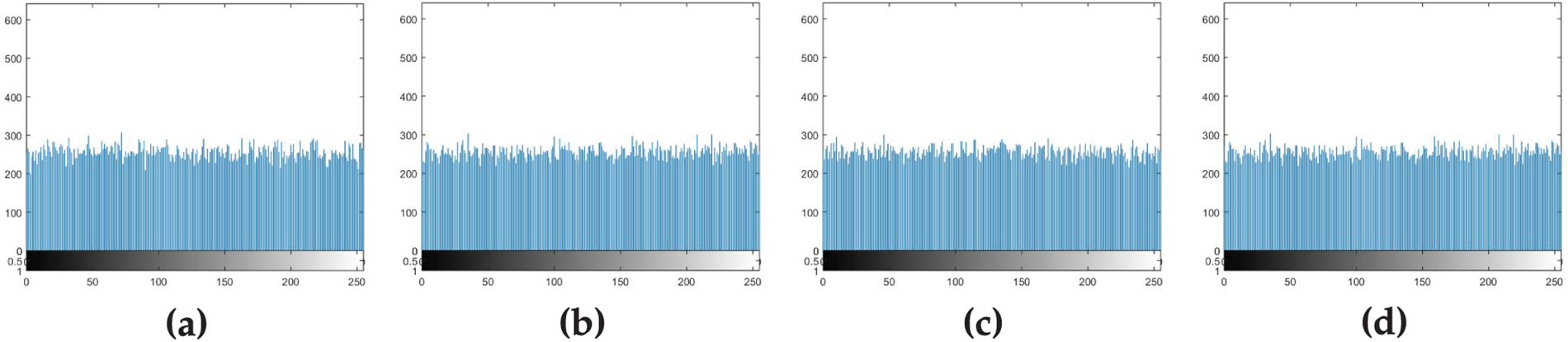
Figure 8: (a–d) Histograms of encrypted images in Fig. 7 (e–h)

6.2.7 Key Space

The key space refers to the total number of distinct keys that can be utilized during the encryption process. It is important to recognize that the security of a cryptographic system is strongly correlated with the size of its key space. If the key space is large, then the attacker will find it more difficult to break the cryptosystem using a brute-force attack. The S-box algorithm proposed by Hayat et al. [41] has a key space 24μ, and our S-box generator has a key space 211μ. Thus, the encryption algorithm using our S-box generator has strong security against key attacks.

6.2.8 NIST SP 800–22 Analysis

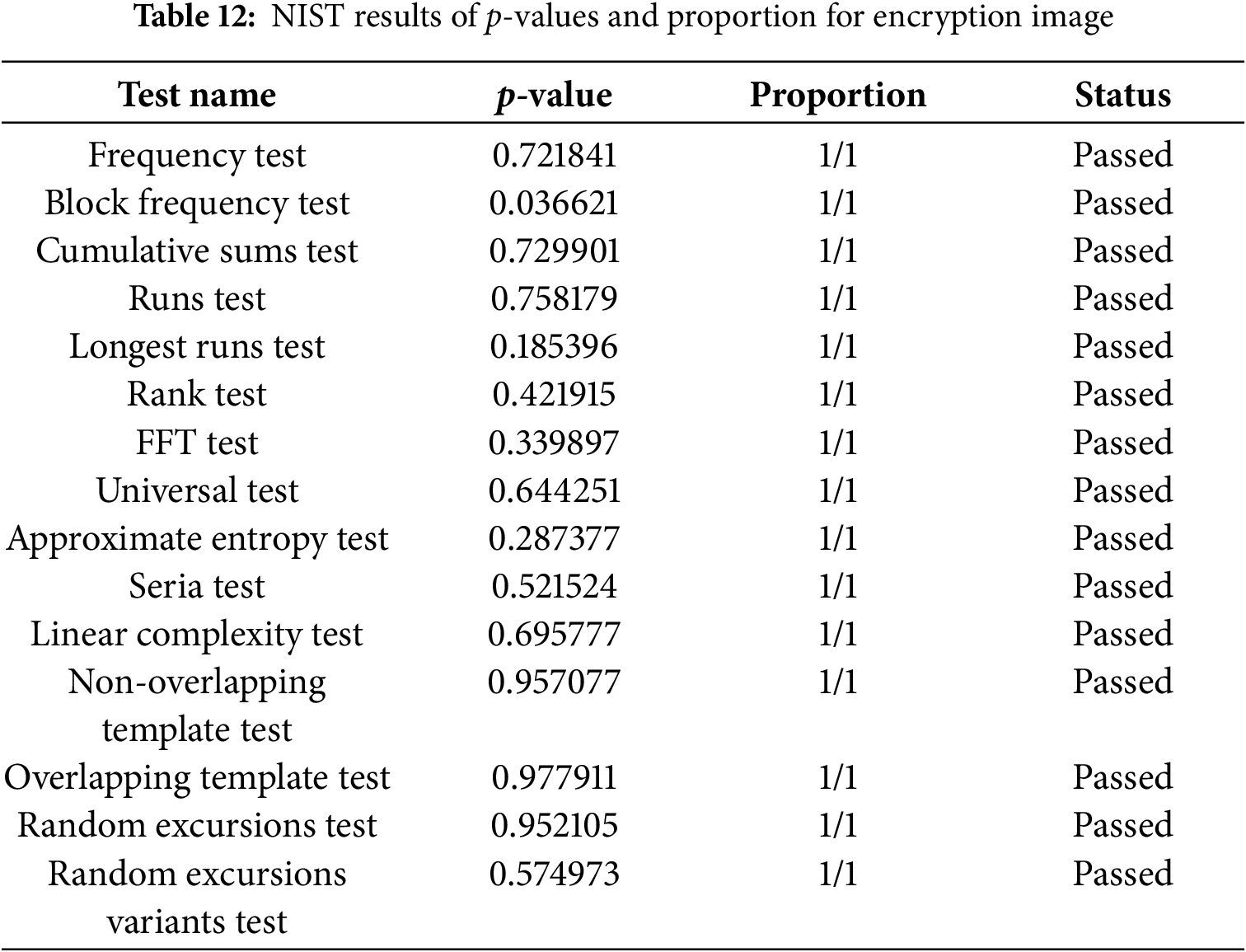
To evaluate the randomness and cryptographic robustness of the proposed scheme, after its integration into our S-box generator, the National Institute of Standards and Technology (NIST) Statistical Test Suite (SP 800–22) [69] is employed to an arbitrary encrypted image. The NIST test suite is a collection of widely recognized, standardized tests which is used to assess the randomness of binary sequences generated by cryptographic schemes. These metrics ensure that cryptographic algorithms produce outputs that are unpredictable and maintain cryptographic security, thereby preventing statistical inference and pattern-based attacks. The results obtained after successfully applying the NIST test suite are demonstrated in Table 12. The test results indicate that the probability (p-values) of all tests exceed the accepted significance threshold of 0.01, demonstrating that they successfully pass each NIST test suite and achieved good randomness. These consistent p-values verify that the encrypted image meets the criteria of statistical randomness, free from detectable patterns or structural biases, which is essential for cryptography. Therefore, the presented S-box algorithm exhibits strong resistance against statistical and pattern-based attacks, proving highly suitable for securing image data with high randomness.

6.2.9 Robustness Analyses

To examine the encryption performance of the presented scheme, three fundamental quantitative metrics are utilized in this study: the Peak Signal-to-Noise Ratio (PSNR), the Structural Similarity Index (SSIM), and the Bit Correct Ratio (BCR). The PSNR is a widely used, standard metric for assessing image quality by comparing the original and decrypted images. A higher PSNR value indicates a more precise decryption process and a higher-quality decrypted image, reflecting that the decrypted image is more similar to the original plain image. The PSNR is quantified utilizing the Mean Square Error (MSE) between the original plain and its decrypted image. On the other hand, the SSIM measures the degree of structural information preserved after decryption. It computes visual similarity, contrast, and structural correlation in plain and ciphered images. Likewise, the BCR quantifies decryption accuracy by computing the ratio of accurately retrieved bits to the total number of bits compared between the plain and encrypted images. It offers a numerical measure of decryption accuracy and the overall encryption process. We computed the MSE, PSNR, SSIM, and BCR values for the plain Cameraman image and the corresponding decrypted image, and summarized the results in Table 13. Under the noise-free scenario, it is evident from Table 13 that the decrypted image generated using the proposed algorithm is exactly similar to the plain image. As a result, the MSE output is zero, the PSNR outcome approaches ∞, and both the SSIM and BCR results are equal to 1. Higher scores for these metrics indicate a more effective encryption process, revealing that negligible data loss occurs during decryption. Hence, the encryption approach, after using our S-box algorithm, removes the visual and structural features of the original plain images.

6.2.10 Noise Attack Test

During transmission, some image data may be lost due to noise. An encryption algorithm must possess strong anti-noise properties, maintain security even in noisy transmission scenarios, and ensure reliable image decryption. To evaluate the robustness of the encryption scheme against noise interference, a Cameraman256×256 test image is chosen. We add Salt-and-pepper noise to the encrypted image at varying noise densities of 0.01, 0.05, 0.1, and 0.2, respectively. The performance of the presented algorithm against a noise attack is illustrated in Fig. 9. From Fig. 9, we observe that the decrypted images are visually recognizable across distinct noise densities, preserving the essential visual content of the plain images even after sufficient noise is added. This reveals that the generator exhibits strong resilience and high efficiency against noise-based attacks.

Figure 9: The encrypted Cameraman image with different levels of noise densities: (a) 0.01 noise, (b) 0.05 noise, (c) 0.10 noise, (d) 0.20 noise. Corresponding decrypted images of the noisy images in (a–d) are shown in (e–h), respectively

6.2.11 Crop Attack Test

In addition to noise interference, partial data loss may also occur during image transmission over networks. For a reliable encryption scheme, it is necessary to recover as much information as possible from encrypted images even in the presence of such losses. To examine the robustness of the presented scheme under these conditions, the ciphered image of Cameraman256×256 is cropped at varying rates of 1/16%, 1/8%, 1/4%, and 1/2% of the total pixels, and the resulting cropped images are decrypted. The performance results are demonstrated in Fig. 10. It is evident from Fig. 10 that, even with substantial data loss in the ciphered image, the decrypted images successfully reconstruct the primary visual content of the original image. These findings confirm that the proposed algorithm has strong resistance to cropping attacks, demonstrating its ability to effectively recover key image information even when partial data is missing. These results collectively validate the high security and robustness of the proposed encryption method against data loss attacks.

Figure 10: The encrypted Cameraman image with different levels of cropings: (a) 1/16%, (b) 1/8%, (c) 1/4%, (d) 1/2%. Corresponding decrypted images of data lost images in (a–d) are shown in (e–h), respectively

7  Conclusions

The current work highlights the significance of MECs when combined with fractional transformation in generating dynamic S-boxes. More explicitly, the focus of the new work is to demonstrate an MEC based algorithm, when 2n−1 points are generated and combined with the fractional transformation, which efficiently generates a large number of dynamic S-boxes with the required level of security. However, the key outcomes of this study are: (i) The new algorithm needs exactly 2n−1 points on the MEC, unlike the existing EC based algorithms, where at least 2n points are required to generate an S-box. (ii) One time generation of the said points resulting in a number of new S-boxes faster than other matching schemes. (iii) The scheme is more generalized, as it has significantly large outputs for those primes as well, whereas the comparable schemes do not have a single output. (iv) The empirical results reveal that the current algorithm is highly efficient and secure for the generation of S-boxes. Additionally, we tested the presented scheme by incorporating the newly designed S-box into an existing encryption algorithm. The results of the encrypted images using our newly designed S-box and the S-boxes of [42,68] reveal that the new algorithm is capable of generating S-boxes with comparable performance to existing S-boxes of high nonlinearity in securing image data.

Lastly, the theoretical and experimental analyses exhibit the robustness and potential of the newly designed algorithm. Moreover, the combination of ECs with other algebraic structures leads to a new area of research, developing more efficient and innovative techniques for generating secure dynamic S-boxes with high nonlinearity.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Umar Hayat and Ikram Ullah; methodology, Umar Hayat, Ikram Ullah and Muhammad Bilal; project management, Umar Hayat; supervision, Umar Hayat; data analysis, Ikram Ullah; data visualization, Muhammad Bilal; software, Muhammad Bilal; writing original draft, Ikram Ullah and Muhammad Bilal; writing and editing final draft, Umar Hayat. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not Applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Lai Q, Akgul A, Li C, Xu G, Çavuşoğlu Ü. A new chaotic system with multiple attractors: dynamic analysis, circuit realization and S-box design. Entropy. 2017;20(1):12. doi:10.3390/e20010012. [Google Scholar] [PubMed] [CrossRef]

2. Ding C, Xue R. Signal-sensing dynamic S-box image encryption with 2D Griewank–sin map. Nonlin Dynam. 2023;111(24):22595–620. doi:10.1007/s11071-023-08985-8. [Google Scholar] [CrossRef]

3. Zhu D, Tong X, Wang Z, Zhang M. A novel lightweight block encryption algorithm based on combined chaotic system. J Inf Secur Appl. 2022;69(2):103289. doi:10.1016/j.jisa.2022.103289. [Google Scholar] [CrossRef]

4. Liu X, Tong X, Wang Z, Zhang M. Efficient high nonlinearity S-box generating algorithm based on third-order nonlinear digital filter. Chaos Solitons Fractals. 2021;150:111109. doi:10.1016/j.chaos.2021.111109. [Google Scholar] [CrossRef]

5. Gupta MD, Chauhan RK. Secure image encryption scheme using 4D-hyperchaotic systems based reconfigurable pseudo-random number generator and S-box. Integration. 2021;81:137–59. doi:10.1016/j.vlsi.2021.07.002. [Google Scholar] [CrossRef]

6. Gao S, Wu R, Wang X, Wang J, Li Q, Wang C, et al. A 3D model encryption scheme based on a cascaded chaotic system. Signal Process. 2023;202:108745. doi:10.1016/j.sigpro.2022.108745. [Google Scholar] [CrossRef]

7. Vijayakumar M, Ahilan A. An optimized chaotic S-box for real-time image encryption scheme based on 4-dimensional memristive hyperchaotic map. Ain Shams Eng J. 2024;2024:102620. doi:10.1016/j.asej.2023.102620. [Google Scholar] [CrossRef]

8. Alexan W, El-Damak D, Gabr M. Image encryption based on fourier-DNA coding for hyperchaotic chen system, chen-based binary quantization S-box, and variable-base modulo operation. IEEE Access. 2024;12:21092–113. doi:10.1109/access.2024.3363018. [Google Scholar] [CrossRef]

9. Sani RH, Behnia S, Ziaei J. Construction of S-box based on chaotic piecewise map: watermark application. Multim Tools Appl. 2023;82(1):1131–48. doi:10.1007/s11042-022-13278-0. [Google Scholar] [CrossRef]

10. Brahim AH, Pacha AA, Said NH. A new image encryption scheme based on a hyperchaotic system & multi specific S-boxes. Inf Secur J A Glob Perspect. 2023;32(2):59–75. [Google Scholar]

11. Tian P, Su R. A novel virtual optical image encryption scheme created by combining chaotic S-box with double random phase encoding. Sensors. 2022;22(14):5325. doi:10.3390/s22145325. [Google Scholar] [PubMed] [CrossRef]

12. Gan Z, Chai X, Yuan K, Lu Y. A novel image encryption algorithm based on LFT based S-boxes and chaos. Multim Tools Applicat. 2018;77:8759–83. doi:10.1007/s11042-017-4772-0. [Google Scholar] [CrossRef]

13. Zghair HK, Manaa ME, Al-Murieb SSA, Abd Al-Razaq FJ. Analysis and description S-box generation for the AES algorithm-a new 3D hyperchaotic system. Bull Electr Eng Inform. 2023;12(3):1639–47. doi:10.11591/eei.v12i3.4824. [Google Scholar] [CrossRef]

14. Khompysh A, Kapalova N, Algazy K, Dyusenbayev D, Sakan K. Design of substitution nodes (S-boxes) of a block cipher intended for preliminary encryption of confidential information. Cogent Eng. 2022;9(1):2080623. doi:10.1080/23311916.2022.2080623. [Google Scholar] [CrossRef]

15. Gao S, Iu HHC, Erkan U, Simsek C, Toktas A, Cao Y, et al. A 3D memristive cubic map with dual discrete memristors: design, implementation, and application in image encryption. IEEE Trans Circuits Syst Video Technol. 2025;35(8):7706–18. doi:10.1109/tcsvt.2025.3545868. [Google Scholar] [CrossRef]

16. Lai Q, Chen Y. Effect of electromagnetic radiation on double-loop neural networks and its application to image encryption. Chaos Solit Fract. 2025;194:116208. doi:10.1016/j.chaos.2025.116208. [Google Scholar] [CrossRef]

17. Aribilola I, Lee B, Asghar MN. Möbius transformation and permutation based S-box to enhance IoT multimedia security. IEEE Access. 2024;12:140792–808. doi:10.1109/access.2024.3466930. [Google Scholar] [CrossRef]

18. Bilal M, Murtaza G, Demir B, Bustamante MD, Hayat U. An efficient algorithm to generate dynamic substitution-boxes and its applications in image encryption. Alex Eng J. 2025;116:214–31. doi:10.1016/j.aej.2024.11.014. [Google Scholar] [CrossRef]

19. Dougherty ST, Sahinkaya S, Ustun D. A novel method for image encryption using time signature-dependent S-boxes based on latin squares and the playfair system of cryptography. Multim Tools Appl. 2024;83(2):4167–94. doi:10.1007/s11042-023-15240-0. [Google Scholar] [CrossRef]

20. Hua Z, Li J, Chen Y, Yi S. Design and application of an S-box using complete Latin square. Nonlin Dynam. 2021;104(1):807–25. doi:10.1007/s11071-021-06308-3. [Google Scholar] [CrossRef]

21. Abd-El-Atty B. Efficient S-box construction based on quantum-inspired quantum walks with PSO algorithm and its application to image cryptosystem. Comp Intell Syst. 2023;9(5):4817–35. doi:10.1007/s40747-023-00988-7. [Google Scholar] [CrossRef]

22. Wang J, Chen J, Wang F, Ni R. Optical image encryption scheme based on quantum S-box and meaningful ciphertext generation algorithm. Opt Commun. 2022;525:128834. doi:10.1016/j.optcom.2022.128834. [Google Scholar] [CrossRef]

23. Gao S, Ding S, Ho-Ching Iu H, Erkan U, Toktas A, Simsek C, et al. A three-dimensional memristor-based hyperchaotic map for pseudorandom number generation and multi-image encryption. Chaos Interdiscip J Nonlinear Sci. 2025;35(7):073105. doi:10.1063/5.0270220. [Google Scholar] [PubMed] [CrossRef]

24. Farah MB, Farah A, Farah T. An image encryption scheme based on a new hybrid chaotic map and optimized substitution box. Nonlin Dynam. 2020;99(4):3041–64. doi:10.1007/s11071-019-05413-8. [Google Scholar] [CrossRef]

25. Zamli KZ. Optimizing S-box generation based on the adaptive agent heroes and cowards algorithm. Expert Syst Appl. 2021;182:115305. doi:10.1016/j.eswa.2021.115305. [Google Scholar] [CrossRef]

26. Alhadawi HS, Ahmad M, Salih SQ. A novel bijective substitution box design based on nomadic people optimizer and discrete chaotic map. Knowl Based Syst. 2025;325:113977. doi:10.1016/j.knosys.2025.113977. [Google Scholar] [CrossRef]

27. Artuğer F. A new S-box generator algorithm based on 3D chaotic maps and whale optimization algorithm. Wirel Pers Commun. 2023;131(2):835–53. doi:10.1007/s11277-023-10456-7. [Google Scholar] [CrossRef]

28. Jawed MS, Sajid M. COBLAH: a chaotic OBL initialized hybrid algebraic-heuristic algorithm for optimal S-box construction. Comput Stand Interf. 2025;91:103890. doi:10.1016/j.csi.2024.103890. [Google Scholar] [CrossRef]

29. Qobbi Y, Abid A, Jarjar M, El Kaddouhi S, Jarjar A, Benazzi A. Adaptation of a genetic operator and a dynamic S-box for chaotic encryption of medical and color images. Sci Afr. 2023;19:e01551. doi:10.1016/j.sciaf.2023.e01551. [Google Scholar] [CrossRef]

30. Miller VS. Use of elliptic curves in cryptography. In: Advances in cryptology—CRYPTO ‘85 proceedings. Berlin/Heidelberg, Germany: Springer; 1985. p. 417–26. [Google Scholar]

31. Koblitz N. A course in number theory and cryptography. Vol. 114. Berlin/Heidelberg, Germany: Springer Science & Business Media; 1994. [Google Scholar]

32. Liu H, Liu Y. Cryptanalyzing an image encryption scheme based on hybrid chaotic system and cyclic elliptic curve. Opt Laser Technol. 2014;56:15–9. doi:10.1016/j.optlastec.2013.07.009. [Google Scholar] [CrossRef]

33. Silva-Garcia VM, Flores-Carapia R, González-Ramírez MD, Vega-Alvarado E, Villarreal-Cervantes MG. Cryptosystem based on the elliptic curve with a high degree of resistance to damage on the encrypted images. IEEE Access. 2020;8:218777–92. doi:10.1109/access.2020.3042475. [Google Scholar] [CrossRef]

34. AbdElHaleem SH, Abd-El-Hafiz SK, Radwan AG. A generalized framework for elliptic curves based PRNG and its utilization in image encryption. Sci Rep. 2022;12(1):13278. doi:10.1038/s41598-022-17045-x. [Google Scholar] [PubMed] [CrossRef]

35. Pali IA, Soomro MA, Memon M, Maitlo AA, Dehraj S, Umrani NA. Construction of an S-box using suppersingular elliptic curve over finite field. J Hunan Univ Nat Sci. 2023;50(7):43–51. [Google Scholar]

36. Ye G, Liu M, Wu M. Double image encryption algorithm based on compressive sensing and elliptic curve. Alex Eng J. 2022;61(9):6785–95. doi:10.1016/j.aej.2021.12.023. [Google Scholar] [CrossRef]

37. Hayat U, Azam NA, Asif M. A method of generating 8 × 8 substitution boxes based on elliptic curves. Wirel Pers Commun. 2018;101(1):439–51. doi:10.1007/s11277-018-5698-1. [Google Scholar] [CrossRef]

38. Hayat U, Azam NA. A novel image encryption scheme based on an elliptic curve. Signal Process. 2019;155:391–402. doi:10.1016/j.sigpro.2018.10.011. [Google Scholar] [CrossRef]

39. Khan MAM, Azam NA, Hayat U, Kamarulhaili H. A novel deterministic substitution box generator over elliptic curves for real-time applications. J King Saud Univ-Comput Inf Sci. 2023;35(1):219–36. doi:10.1016/j.jksuci.2022.11.012. [Google Scholar] [CrossRef]

40. Ibrahim S, Abbas AM. Efficient key-dependent dynamic S-boxes based on permutated elliptic curves. Inf Sci. 2021;558:246–64. doi:10.1016/j.ins.2021.01.014. [Google Scholar] [CrossRef]

41. Hayat U, Ullah I, Azam NA, Azhar S. A novel image encryption scheme based on elliptic curves over finite rings. Entropy. 2022;24(5):571. doi:10.3390/e24050571. [Google Scholar] [PubMed] [CrossRef]

42. Ullah I, Azam NA, Hayat U. Efficient and secure substitution box and random number generators over Mordell elliptic curves. J Inf Secur Appl. 2021;56(3):102619. doi:10.1016/j.jisa.2020.102619. [Google Scholar] [CrossRef]

43. Azam NA, Hayat U, Ullah I. Efficient construction of a substitution box based on a Mordell elliptic curve over a finite field. Front Inf Technol Electron Eng. 2019;20(10):1378–89. doi:10.1631/FITEE.1800434. [Google Scholar] [CrossRef]

44. Azam NA, Hayat U, Ullah I. An injective S-box design scheme over an ordered isomorphic elliptic curve and its characterization. Secur Commun Netw. 2018;2018:1–9. [Google Scholar]

45. Azam NA, Hayat U, Ayub M. A substitution box generator, its analysis, and applications in image encryption. Signal Process. 2021;187:108144. doi:10.1016/j.sigpro.2021.108144. [Google Scholar] [CrossRef]

46. Swamy U, Murthy A. Algebra: abstract and modern. Chennai, India: Pearson India; 2012. [Google Scholar]

47. Gallian J. Contemporary abstract algebra. New York, NY, USA: Chapman and Hall/CRC; 2021. [Google Scholar]

48. Washington LC. Elliptic curves: number theory and cryptography. New York, NY, USA: Chapman and Hall/CRC; 2008. [Google Scholar]

49. Beardon AF. Algebra and geometry. Cambridge, UK: Cambridge University Press; 2005. [Google Scholar]

50. Meier W, Staffelbach O. Nonlinearity criteria for cryptographic functions. In: Workshop on the theory and application of cryptographic techniques. Berlin/Heidelberg, Germany: Springer; 1989. p. 549–62. doi:10.1007/3-540-46885-4_53. [Google Scholar] [CrossRef]

51. Matsui M. Linear cryptanalysis method for DES cipher. In: Workshop on the theory and application of cryptographic techniques. Berlin/Heidelberg, Germany: Springer; 1993. p. 386–97. doi:10.1007/3-540-48285-7_33. [Google Scholar] [CrossRef]

52. Biham E, Shamir A. Differential cryptanalysis of DES-like cryptosystems. J Cryptol. 1991;4(1):3–72. doi:10.1007/bf00630563. [Google Scholar] [CrossRef]

53. Webster AF, Tavares SE. On the design of S-boxes. In: Advances in cryptology—CRYPTO ‘85 proceedings. Berlin/Heidelberg, Germany: Springer; 1985. p. 523–34. [Google Scholar]

54. Sakall MT, Aslan B, Buluş E, Mesut AŞ, Büyüksaraçoğlu F, Karaahmetoğlu O. On the algebraic expression of the AES S-box like S-boxes. In: The Second International Conference on Networked Digital Technologies, NDT 2010; 2010 Jul 7–9; Prague, Czech Republic. Berlin/Heidelberg, Germany: Springer; 2010. p. 213–27. [Google Scholar]

55. Özkaynak F, Çelik V, Özer AB. A new S-box construction method based on the fractional-order chaotic Chen system. Signal Image Video Process. 2017;11:659–64. doi:10.1007/s11760-016-1007-1. [Google Scholar] [CrossRef]

56. Wang X, Çavuşoğlu Ü, Kacar S, Akgul A, Pham VT, Jafari S, et al. S-box based image encryption application using a chaotic system without equilibrium. Appl Sci. 2019;9(4):781. doi:10.3390/app9040781. [Google Scholar] [CrossRef]

57. Zheng J, Zeng Q. An image encryption algorithm using a dynamic S-box and chaotic maps. Appl Intell. 2022;52(13):15703–17. doi:10.1007/s10489-022-03174-3. [Google Scholar] [CrossRef]

58. Hoseini R, Behnia S, Sarmady S, Fathizadeh S. Construction of dynamical S-boxes based on image encryption approach. Soft Comput. 2022;26(24):13985–97. doi:10.1007/s00500-022-07443-8. [Google Scholar] [CrossRef]

59. Gautam A, Gaba GS, Miglani R, Pasricha R. Application of chaotic functions for construction of strong substitution boxes. Indian J Sci Technol. 2015;8(28):1–5. doi:10.17485/ijst/2015/v8i28/71759. [Google Scholar] [CrossRef]

60. Wen H, Feng Z, Bai C, Lin Y, Zhang X, Feng W. Frequency-domain image encryption based on IWT and 3D S-box. Phys Scr. 2024;99(5):055254. doi:10.1088/1402-4896/ad30ec. [Google Scholar] [CrossRef]

61. Haider T, Azam NA, Hayat U. Substitution box generator with enhanced cryptographic properties and minimal computation time. Expert Syst Appl. 2024;241:122779. doi:10.1016/j.eswa.2023.122779. [Google Scholar] [CrossRef]

62. Zhao M, Yuan Z, Li L, Chen XB. A novel efficient S-box design algorithm based on a new chaotic map and permutation. Multim Tools Appl. 2024;83(24):64899–918. doi:10.1007/s11042-023-17720-9. [Google Scholar] [CrossRef]

63. Zhou L, Chen H, Zhou X, Yuan Y, Zhu W, Zhou M. A smart agriculture image protection scheme based on annealing algorithm and affine transformation is optimized for S-box generated by chaos. Nonlin Dynam. 2025;113(10):12263–87. doi:10.1007/s11071-024-10677-w. [Google Scholar] [CrossRef]

64. Su Y, Tong X, Zhang M, Wang Z. A new S-box three-layer optimization method and its application. Nonlin Dynam. 2023;111(3):2841–67. doi:10.1007/s11071-022-07956-9. [Google Scholar] [CrossRef]

65. Dimitrov MM. A framework for fine-grained nonlinearity optimization of Boolean and vectorial Boolean functions. IEEE Access. 2021;9:124910–20. doi:10.1109/access.2021.3110761. [Google Scholar] [CrossRef]

66. Duong PP, Dang TK, Hoang TT, Pham CK. Compact 8-bit S-boxes based on multiplication in a galois field GF (24). Cryptography. 2025;9(2):21. doi:10.3390/cryptography9020021. [Google Scholar] [CrossRef]

67. Duong PP, Pham CK. Constructing 8× 8 S-boxes with optimal boolean function nonlinearity. Cryptography. 2025;9(4):67. doi:10.3390/cryptography9040067. [Google Scholar] [CrossRef]

68. Pub NF. 197: advanced encryption standard (AES). Fed Inf Process Stand Publ. 2001;197:0311. [Google Scholar]

69. Rukhin A, Soto J, Nechvatal J, Smid M, Barker E. A statistical test suite for random and pseudorandom number generators for cryptographic applications. Gaithersburg, MD, USA: National Institute of Standards and Technology; 2001. [Google Scholar]