An Efficient Certificateless Authentication Scheme with Enhanced Security for NDN-IoT Environments

1  Introduction

The Internet of Things (IoT) has seamlessly integrated into our daily lives, transforming industries and urban infrastructure with its interconnected smart systems. However, the widespread interconnection of IoT devices and the rapid growth of data volume pose significant challenges to the security and efficiency of communication systems. To tackle these problems, named data networking (NDN) has gained recognition as an innovative content-centric communication framework, distinguished by its unique strengths [1,2]. Departing from conventional address-centric network models, NDN adopts a data-centric paradigm enabled by name-driven routing protocols, delivering superior flexibility, scalability, and native security features. In short, NDN shifts the model from host-to-host communication, like the current Internet Protocol (IP), to a data-centric model where users request content by name. However, integrating NDN and IoT contexts introduces multifaceted security complexities. Recall that data is the core resource of NDN-IoT applications, necessitating robust protective measures to safeguard its security. In real-world scenarios, however, data frequently traverses insecure public networks, and faces numerous security threats [3,4]. A key security requirement involves verification mechanisms where data receivers must validate the source’s trustworthiness and confirm the data integrity throughout its transmission path [5]. In addition, an observer in NDN may be able to monitor which content names are being requested, potentially revealing sensitive information. Therefore, user’s privacy should also not be ignored.

Digital signatures is an essential cryptographic mechanism for guaranteeing both data integrity and source authentication. Moreover, in high-throughput applications such as vehicular ad hoc networks and named data networking (NDN) networks, there are a large number of digital signatures that require efficient validation, which puts higher performance requirements on digital signatures. The aggregate signature scheme, initially put forward by Boneh et al. [6], presents an optimal solution by enabling the compression of n individual signatures into one consolidated form. This approach facilitates batch verification while significantly reducing bandwidth consumption.

Boneh et al.’s framework relies on public key infrastructure (PKI), and its actual deployment faces challenges due to the substantial overhead associated with key management. Alternative aggregate signature schemes using identity-based cryptography have emerged [7] to address PKI’s limitations; however, identity-based setting suffers from the inherent key-escrow issue. The certificateless paradigm [8] elegantly resolves both concerns by employing a hybrid key generation model: the key generation center (KGC) supplies partial secret information while users independently select additional secret components, with public keys derived from the user’s public information [9]. Due to its merits, recent years have witnessed significant academic interest in certificateless aggregate signature (CLAS) schemes for IoT applications [10,11].

1.1 Related Work & Motivation

To date, a number of CLAS schemes have been designed for IoT applications. Early schemes were designed based on bilinear pairing [12,13], requiring expensive computational costs. Cui et al. [14] designed a pairing-free CLAS scheme for vehicular ad hoc networks. However, their design cannot resist malicious-but-passive KGC attacks (i.e., called as Type 2 attacks) [15]. Xu et al. [16] put forward another CLAS scheme without pairings for VANETs. Zhu et al. [17] pointed out the security vulnerability of [16] in resisting the Type 2 attack and constructed a new scheme with enhanced security. However, their work was further pointed out by Yang et al. [18] to have a security vulnerability of the public-key replacement attack (i.e., called as Type 1 attacks). In [18], Yang et al. then proposed an improved CLAS scheme with new aggregate algorithm, which ensures the validity of all individual signatures participating in the aggregation. But the performance is a weakness of their design. In addition, Zhu and Guan [19] put forward an authentication scheme with conditional privacy protection for vehicular ad-hoc networks based on a CLAS scheme. However, their work cannot achieve Type 1 security [20]. A recent comprehensive survey of CLAS schemes can be found in [21].

More recently, Yue et al. [22] proposed a CLAS scheme for VANETs. However, their design is computationally inefficient and cannot ensure resistance to Type 1 attacks, where an adversary can systematically generate fraudulent signatures for arbitrary messages (refer to Appendix A). This vulnerability fundamentally compromises the unforgeability property, which is a core security requirement for any CLAS schemes. In addition, Wang et al. [23] designed a CLAS scheme for NDN-IoT environments. Wang et al. initially asserted the security of their CLAS construction. Our analysis reveals, however, that their implementation remains vulnerable to public-key replacement attacks. That is, their schemes can not ensure data integrity, thus cannot be deployed in real-world NDN-IoT applications.

Contribution. To solve data security and efficiency problems in NDN-IoT applications, we put forward a new CLAS scheme. The key contributions of this work are outlined below:

1.   By presenting a concrete public-key replacement attack, we explored the security vulnerability of a very recent CLAS scheme in [23] proposed for NDN-IoT environments.

2.   We systematically examine the root causes behind the vulnerability in [23] and propose an improved CLAS design.

3.   We prove the security of our design based on the cryptographic assumption, and analyze its performance. The performance comparison results demonstrate that the improved CLAS scheme not only has better security but also has desirable computational and communication costs. Therefore, our design is suitable for NDN-IoT environments.

4.   As an additional contribution, in Appendix A, we analyze the security flaw of a very recent CLAS construction in [22] and propose targeted countermeasures to enhance its security.

Organization. The subsequent sections of this paper are structured as the following: Section 2 introduces the foundational concepts and preliminaries. In Section 3, we review Wang et al.’s scheme in [23] and put forward our security analysis. In Section 4, we introduce our enhanced design with its rigorous security analysis. We evaluate the performance of our proposal in Section 5 and conclude the work in Section 6. In Appendix A, we provide a retrospective analysis of Yue et al.’s construction in [22], including identified security weaknesses and proposed response strategies.

2  Preliminaries

Here, we introduce some required preliminaries, such as notations and elliptic curve discrete logarithm problem (ECDLP).

2.1 Notations

Some notations are listed in Table 1.

2.2 ECDLP

Let G be an q-order cyclic elliptic curve group and P be a generator of G. Given (P,αP)∈G for some unknown α∈Zq∗, the ECDLP is to find α.

3  Security Attack to Wang et al.’s CLAS Scheme in [23]

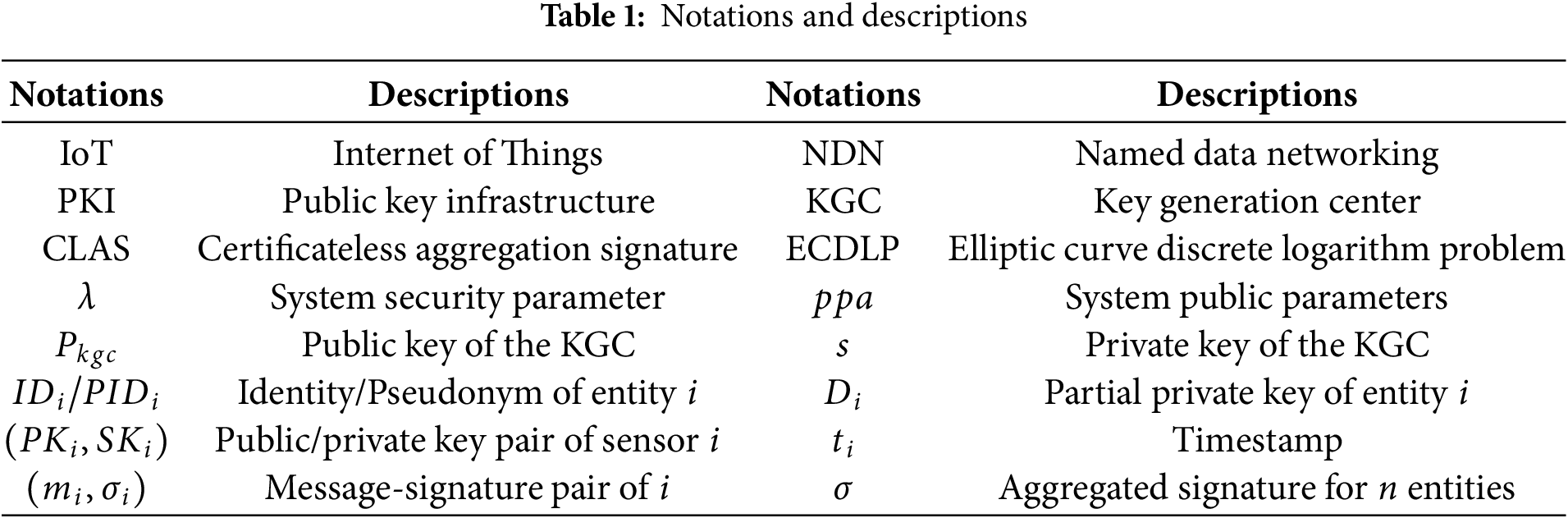
As shown in Fig. 1, there are several entities in [23]. The KGC is responsible for building the system. An end device (ED) can register as a producer or consumer in the network system by interacting with KGC. Acting as a vital element for secure data forwarding, the NDN router checks the integrity of data packets during transmission. It conducts signature verification on the embedded producer details within the data packets. Moreover, it supports batch processing of multiple signatures from multiple end devices. As a data requester, the consumer can send Interest packets to request needed data or services. In addition, the producer, which corresponds to the producer entity in NDN, is in charge of generating data in the NDN-IoT environment. It employs sensor devices to gather information like soil moisture levels, vehicle locations, and indoor temperatures.

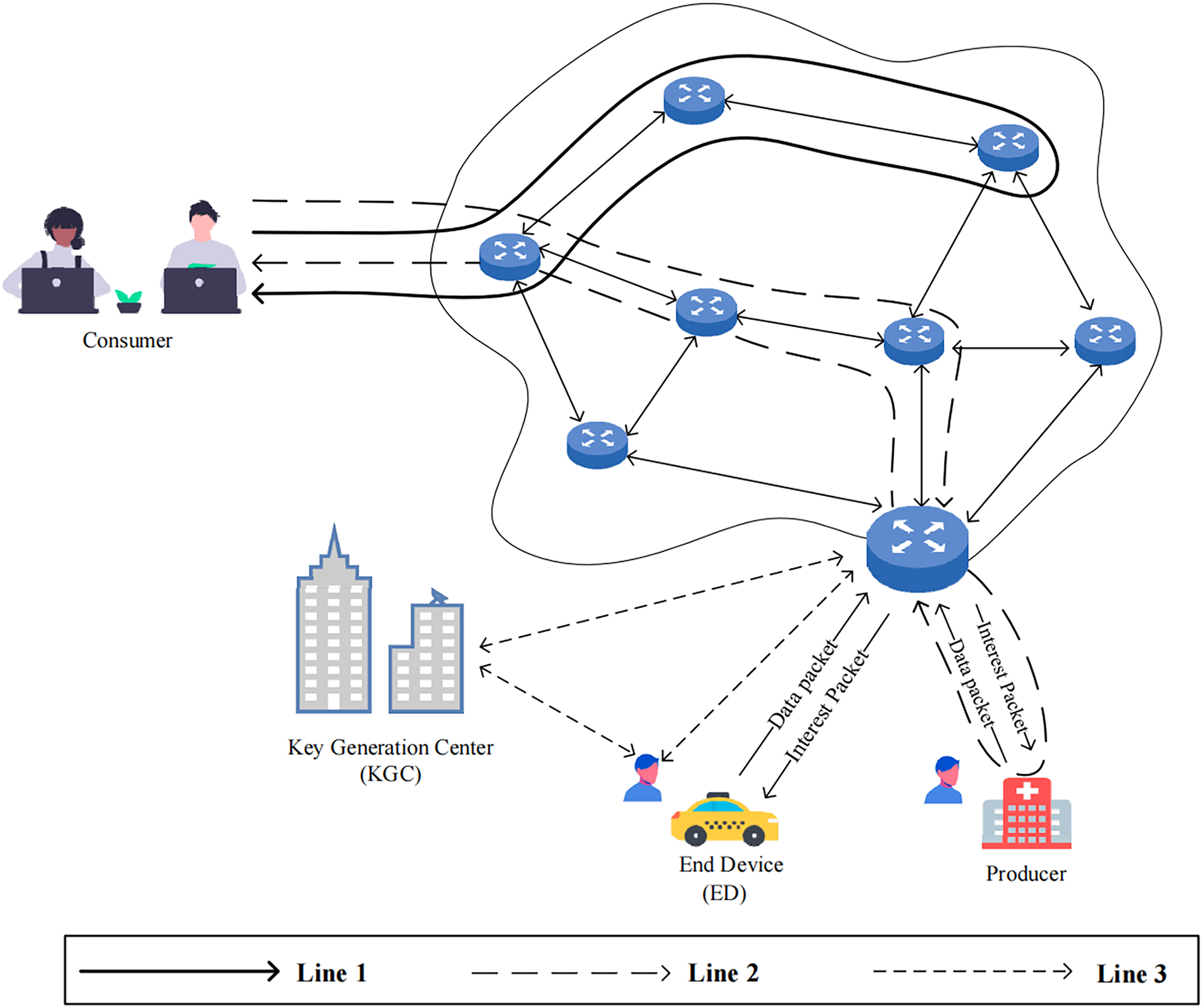
Figure 1: Wang et al’s system structure. The figure is adopted from [23]. Line 1 depicts an instance of how a consumer seeks data forwarding from an NDN router. Line 2 showcases the procedure where a consumer requests data packets from multiple producers. Line 3 presents the interaction between terminal devices and the KGC for registration purposes, along with the process of creating an aggregate signature and sending data packets through the NDN router

The CLAS scheme proposed by Wang et al. [23] mainly formed by the following algorithms: System Setup, Device Pseudonym Generation, Device Keys Generation, Signing, Single Signature Verification, and Aggregated Signature Verification. We now briefly review their algorithms to support our analysis.

1.   System Setup: Taking a security parameter ζ as input, the KGC sets up the system as below:

(a)   Define an q-order cyclic group G=⟨P⟩.

(b)   Randomly select a master private key α∈Zq∗ and calculate a public key PKkgc=αP.

(c)   Choose three hash functions Hi:{0,1}∗→Zq∗, i=1,2,…,3.

(d)   Store α secretly and publish public parameters ppa={G,P,q,PKkgc,Hi}.

2.   Device Pseudonym Generation: In this algorithm, a terminal device EDi with real identity IDi interacts with KGC to generate a pseudonym PIDi={AIDi2,Ti} for a validity period Ti.

(a)   EDi randomly picks ei∈Zq∗ and computes Ei=eiP, Fi=eiPkgc, and AIDi1=IDi⊕Fi. Then, it sends {Ei,Fi,AIDi1} to the KGC.

(b)   KGC recovers IDi=AIDi1⊕Ei, computes AIDi2=H1(Ti,αAIDi1)⊕IDi, and sends PIDi={AIDi2,Ti} to EDi.

3.   Device Keys Generation:

(a)   EDi randomly picks xi∈Zq∗ and computes Xi=xiP.

(b)   KGC picks ri∈Zq∗ at random, computes Ri=riP, hi(2)=H2(PIDi,Ri,Pkgc), di=ri+αhi(2), and provides EDi with the partial private key Di=(di,Ri).

(c)   EDi computes hi(2)=H2(PIDi,Ri,Pkgc), Ki=hi(2)Xi+Ri, and sets its private key SKi=di+hi(2)xi and public key PKi=(Ki,Ri).

4.   Signing: To sign a message mi∈{0,1}∗ at time ti, EDi performs the following:

(a)   Pick ui∈Zq∗ at random and calculate Ui=uiP and hi(3)=H3(mi,PIDi,PKi,Ui,ti).

(b)   Compute Vi=ui+hi(3)SKi and set σi=(Ui,Vi) as the signature.

5.   Single Signature Verification: Given {PIDi,PKi,mi,σi,ti}, the verifier verifies the freshness of ti, recovers hi(2)=H2(PIDi,Ri,Pkgc), and hi(3)=H3(mi,PIDi,PKi,Ui,ti). It accepts the signature if ViP=Ui+hi(3)(Ki+hi(2)Pkgc) and rejects otherwise.

6.   Signature Aggregation: For n messages {PIDi,PKi,mi,σi,ti} from n EDi, the verifier computes an aggregated signature σag=(U,V), where U=∑i=1nUi and V=∑i=1nVi.

7.   Aggregation Verification: To check the validity of σag=(U,V), verifier verifies first checks whether ti is fresh. Then, it recovers hi(2) and hi(3) for i=1,2,…,n. It accepts the signature if VP=U+∑k=1nhi(3)((Ki+hi(2)Pkgc) and rejects otherwise.

3.1 Security Analysis to [23]

The first five algorithms in [23] naturally form a CLS scheme and the remaining algorithms are used to perform batch verification of multiple signatures. For ease presentation, our analysis focuses on their CLS scheme. For a CLS scheme, two distinct types of attackers should be considered, i.e., public-key replacement attacker (called as Type 1 attacker) and malicious-but-passive KGC (called as Type 2 attacker). In particular, a Type 1 attacker knows a target user’s secret value. However, the attacker cannot access the user’s partial private key. A Type 2 attacker knows the KGC’s private key but does not allowed to access the target user’s secret value. For more security definitions and security models, please refer to [23].

In [23], Wang et al. stated that their design can achieve both Type 1 and Type 2 security. In the following, we show that a Type 1 attacker ℱ1 possesses the capability to produce a verifiable signature for any fraudulent message, thereby compromising the unforgeability property inherent in their cryptographic construction. Let the device EDi with pseudonym PIDi be the target device attacked by ℱ1. Given public parameters ppa={G,P,q,PKkgc,Hi} and EDi’s public key PKi=(Ki,Ri), ℱ1 can also access EDi’s secret value xi. Suppose that ℱ1 tries to generate a forgery σi∗ on a message mi∗ at time ti, as shown in Fig. 2, ℱ1 operates as follows:

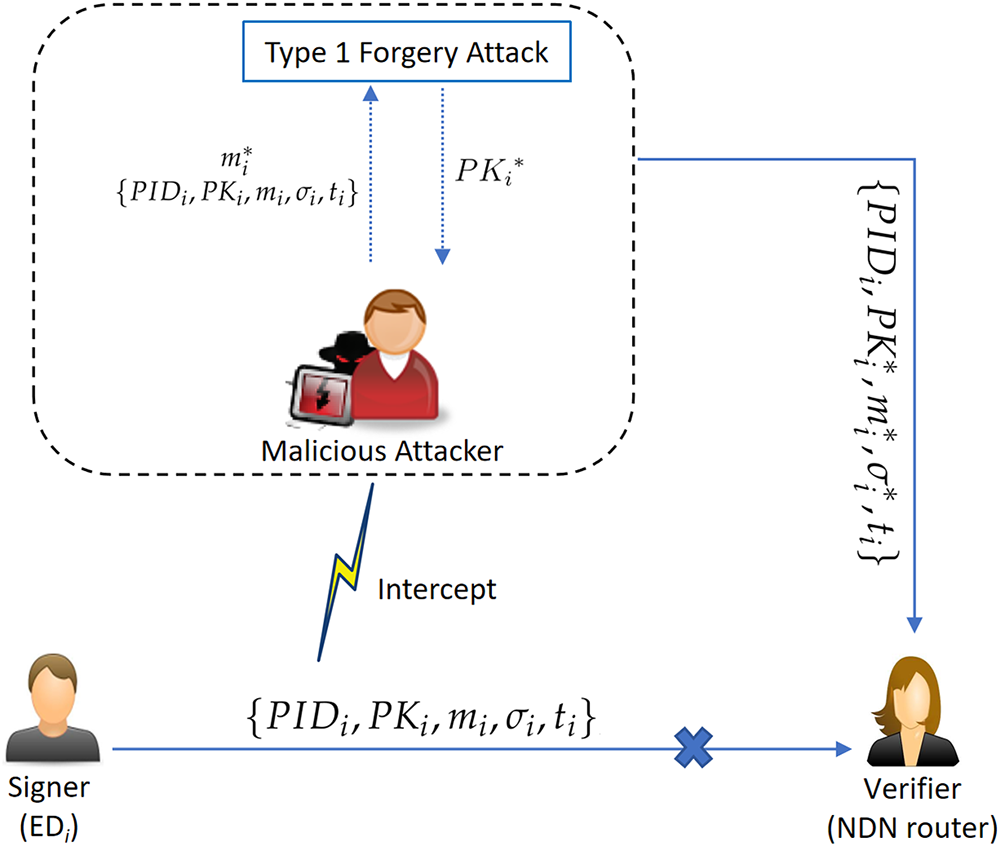
Figure 2: An example of the Type 1 attack

(1)   Compute hi(2)=H2(PIDi,Ri,Pkgc).

(2)   Pick β∈Zq∗ at random and set Ki∗=βP−hi(2)Pkgc.

(3)   Set PKi∗=(Ki∗,Ri) as the replaced public key.

(4)   Select ui∗∈Zq∗ at random and compute Ui∗=ui∗P, hi(3)∗=H3(mi∗,PIDi,PKi∗,Ui∗,ti), and Vi∗=ui∗+hi(3)∗β.

(5)   Set σi∗=(Ui∗,Vi∗) as the forged signature.

Now, the correctness of σi∗ is checked by:

Vi∗P=(ui∗+hi(3)∗β)P=ui∗P+hi(3)∗βP=Ui∗+hi(3)∗(Ki∗+hi(2)Pkgc).

Since the underlying CLS scheme is insecure, the CLAS construction is therefore cannot achieve unforgeability.

4  Our Improvement

In [23], a verifier checks a received signature through the equation ViP=Ui+hi(3)(Ki+hi(2)Pkgc). However, due to the lack of binding between Ki and hi(2), a ℱ1 attacker can use the algebraic relationship in the equation to bypass the KGC’s private key α (corresponding to Pkgc).

To patch this vulnerability, our improvement is as follows:

1.   The algorithms System Setup and Device Pseudonym Generation are the same as the original scheme.

2.   Device Keys Generation:

(a)   EDi randomly picks xi∈Zq∗ and computes Xi=xiP.

(b)   KGC picks ri∈Zq∗ at random, computes Ri=riP, hi(2)=H2(PIDi,Xi,Ri,Pkgc), di=ri+αhi(2), and securely provides EDi with the partial private key Di=(di,Ri).

(c)   EDi sets its private key SKi=(xi,di) and public key PKi=(Xi,Ri).

3.   Signing: To generate a signature on message mi∈{0,1}∗ at time ti, EDi performs the following:

(a)   Randomly pick ui∈Zq∗ and calculate Ui=uiP and hi(3)=H3(mi,PIDi,PKi,Ui,ti).

(b)   Compute Vi=ui+hi(3)(xi+di) and set the signature σi=(Ui,Vi).

4.   Single Signature Verification: Given {PIDi,PKi,mi,σi,ti}, the verifier checks whether ti is fresh. It then recovers hi(2)=H2(PIDi,Xi,Ri,Pkgc) and hi(3)=H3(mi,PIDi,PKi,Ui,ti). It accepts the signature if ViP=Ui+hi(3)(Xi+Ri+hi(2)Pkgc) and rejects otherwise. The correctness:

ViP=(ui+hi(3)(xi+di))P=uiP+hi(3)(xi+di))P=Ui+hi(3)(xiP+diP)=Ui+hi(3)(Xi+Ri+hi(2)Pkgc).

5.   Signature Aggregation: The algorithm is the same as the original scheme.

6.   Aggregation Verification: To check the validity of σag=(U,V), the verifier checks whether ti is fresh. Then, it recovers hi(2) and hi(3) for i=1,2,…,n. It accepts the signature if VP=U+∑i=1nhi(3)(Xi+Ri)+(∑i=1nhi(3)hi(2))Pkgc and rejects otherwise. The correctness:

VP=(∑i=1nVi)P=∑i=1n(ui+hi(3)(xi+di))P=∑i=1n(Ui+hi(3)(Xi+Ri+hi(2)Pkgc))=∑i=1nUi+∑i=1nhi(3)(Xi+Ri+hi(2)Pkgc)=U+∑i=1nhi(3)(Xi+Ri)+(∑i=1nhi(3)hi(2))Pkgc.

Following Wang et al.’s proof approach in [23], the modified scheme can be easily proven to be secure. To avoid a lot of repetitive proof work, we omit the proof process here. Compared to the original scheme, the improvement adds one point multiplication, one point addition, and a general hash operation. This is acceptable since the modification achieves greater security.

4.1 Security Proof

Here, we proof the security of our improved design. Note that for ease presentation, our proof directly focuses on our underlying CLS scheme. Following the proof idea in [23,24], the improved CLS design is resistant to forgery attacks against Type 1 and Type 2 adversaries.

Theorem 1: The improved CLS scheme is secure against any Type 1 adversary if ECDLP is hard.

Proof: This theorem demonstrates that if a Type 1 adversary A1 compromises the underlying CLS scheme, there must exist an adversary B capable of resolving the ECDLP. Now, A1 and B performs the following:

•   Stage-1: ℬ operates as System Setup to obtain system parameters ppa={G,P,q,PKkgc,Hi}, where Pkgc=αP for some unknown α∈Zq∗. It sends ppa to 𝒜1. For simplicity, let PIDi∗ be 𝒜1’s target identity. During the forgery game, 𝒜1 keeps a series of lists to store the query results. In the initial stage, all lists are empty.

•   Stage-2: In this stage, ℬ responds to 𝒜1’s adaptive queries as below.

H2-Query: For a H2 query on (PIDi,Ri,Pkgc), if the item (PIDi,Xi,Ri,Pkgc,hi(2)) can be found in the list LH2, ℬ returns hi(2) to 𝒜1. Otherwise, ℬ picks hi(2)∈RZq∗, inserts (PIDi,Xi,Ri,Pkgc,hi(2)) to LH2, and responds hi(2) to 𝒜1.

H3-Query: For a H3 query on (mi,PIDi,PKi,Ui,ti), if the item (mi,PIDi,PKi,Ui,ti,hi(3)) exists in the list LH3, ℬ returns hi(3) to 𝒜1. Otherwise, ℬ picks hi(3)∈RZq∗, inserts (mi,PIDi,PKi,Ui,ti,hi(3)) to LH3, and responds hi(3) to 𝒜1.

Secret value-Query: 𝒜1 can issue such query on PIDi. ℬ searches the tuple (PIDi,xi,Xi) from the list Lsv and sends it to 𝒜1. Otherwise, ℬ selects xi∈RZq∗, stores (PIDi,xi,Xi) to Lsv, and responds xi to 𝒜1.

Partial private key-Query: 𝒜1 can issue any partial secret key query regarding PIDi. If PIDi=PIDi∗, ℬ aborts. Otherwise, ℬ searches the list Lpsk to find (PIDi,di,Ri) and send it to 𝒜1. If the tuple (PIDi,di,Ri) does not exist in Lpsk and the tuple (PIDi,Xi,Ri,Pkgc,hi(2)) does not exist in LH2, ℬ selects di,hi(2)∈RZq∗, computes Ri=diP−hi(2)Pkgc, and sets hi(2)=H2(PIDi,Xi,Ri,Pkgc). 𝒜 updates lists LH2 and Lpsk and provides 𝒜1 with (PIDi,di,Ri). Public key-Query: Once ℬ receives 𝒜1’s query on PIDi (PIDi=PIDi∗), ℬ checks if (PIDi,xi,Xi,di,Ri) exists in the list Lkey. If it exists, ℬ returns (Xi,Ri). Otherwise, ℬ runs as Secret value-Query and Partial private key-Query to generate and update (PIDi,xi,Xi,di,Ri), and then returns (Xi,Ri).

Public key replacement-Query: Once ℬ receives a query for some (IDi,PKi,PKi′) from 𝒜1, ℬ searches the tuple (IDi,PKi) from Lkey and replaces it with (PIDi,⊥,Xi′,di,Ri).

Signing-Query: Upon receiving 𝒜1’s query on (mi,PIDi), ℬ performs as below. If PIDi≠PIDi∗, ℬ scans the lists to obtain the required parameters and runs as Signing to produce a signature σi=(Ui,Vi) as the response. Otherwise, ℬ picks hi(2), hi(3),Vi∈RZq∗, sets Ui=ViP−hi(3)(Xi+Ri+hi(2)Pkgc), and returns σi=(Ui,Vi).

•   Stage-3: Eventually, ℱ1 either admits failure or returns its forgery σi∗=(Ui∗,Vi∗) on mi∗.

If σi∗ is a valid forgery under (PIDi∗,mi∗), then Vi∗P=Ui∗+hi(3∗)(Xi∗+Ri+hi(2∗)Pkgc) holds. By applying the forking lemma in [25], ℬ replays 𝒜1 with the same random tape, but provides two distinct values of H3. 𝒜1 can output another valid signature σi∗=(Ui∗,Vi∗′). Hence, we have Vi∗′P=Ui∗+hi(3∗)(Xi∗+Ri+hi(2∗′)Pkgc). Therefore, ℬ calculates α=(Vi∗−Vi∗′)(hi(3∗)(hi(2∗)−hi(2∗′)))−1 as a solution to ECDLP. ◻

Theorem 2: The improved CLS scheme is secure against any Type 2 adversary if ECDLP is hard.

Proof: The proof follows a similar approach to that of Theorem 1 and is thus omitted for brevity. ◻

Theorem 3: The improved CLS scheme achieves conditional privacy-preserving.

Proof: In our design, the anonymity of the end device is assured by the pseudonym PIDi. Recall that PIDi={AIDi2,Ti}, where AIDi2=H1(Ti,αAIDi1)⊕IDi, AIDi1=IDi⊕Fi, Fi=eiPkgc, Ei=eiP, ei∈Zq∗, and Ti is the valid period. To extract the real identity IDi, the attacker must compute H1(Ti,αAIDi1). However, computing H1(Ti,αAIDi1) means that the attacker must know α and AIDi1. Note that α is the private key of the KGC. Meanwhile, according to the above equation, to compute AIDi1, the attacker needs to recover ei from Ei=eiP, which is solving the ECDLP. Due to the hardness of the ECDLP, it is evident that no such attacker can reveal IDi. However, in scenarios where an end device fails to operate correctly or triggers an operational issue, the KGC can trace IDi to take appropriate action in a timely manner.

In Signing, to generate a signature on a message, three distinct random numbers ei,xi, and ui are generated by the end device. The inherent randomness of these random numbers ensures that the attacker cannot correlate anonymous identities or associate disparate signatures produced by the same end device, thereby achieving unlinkability in our improvement. The combination of the above properties implies the proof. ◻

5  Performance Analysis

This section analyzes the performance of our design by comparing its computational and communication costs with recent schemes in [17,22,23]. We adopt the experiment parameters provided in [23] for our analysis, which was tested on a Raspberry Pi 3B+ device under the Curve25519 elliptic curve, achieving 128-bit security level. Specifically, the running time for different operations is as follows: general hash Th=0.0729 ms, point addition operation Tpa=0.1652 ms, and point multiplication operation Tpm=23.4405 ms.

Computational costs. Taking the algorithm Signing in our improved scheme as an example, it executes one point multiplication operation and one general hash operation to generate the signature. Hence, the total computational cost is Tpm+Th=23.5134 ms. Similarly, we count the cost for the remaining schemes and record the computational costs in Table 2.

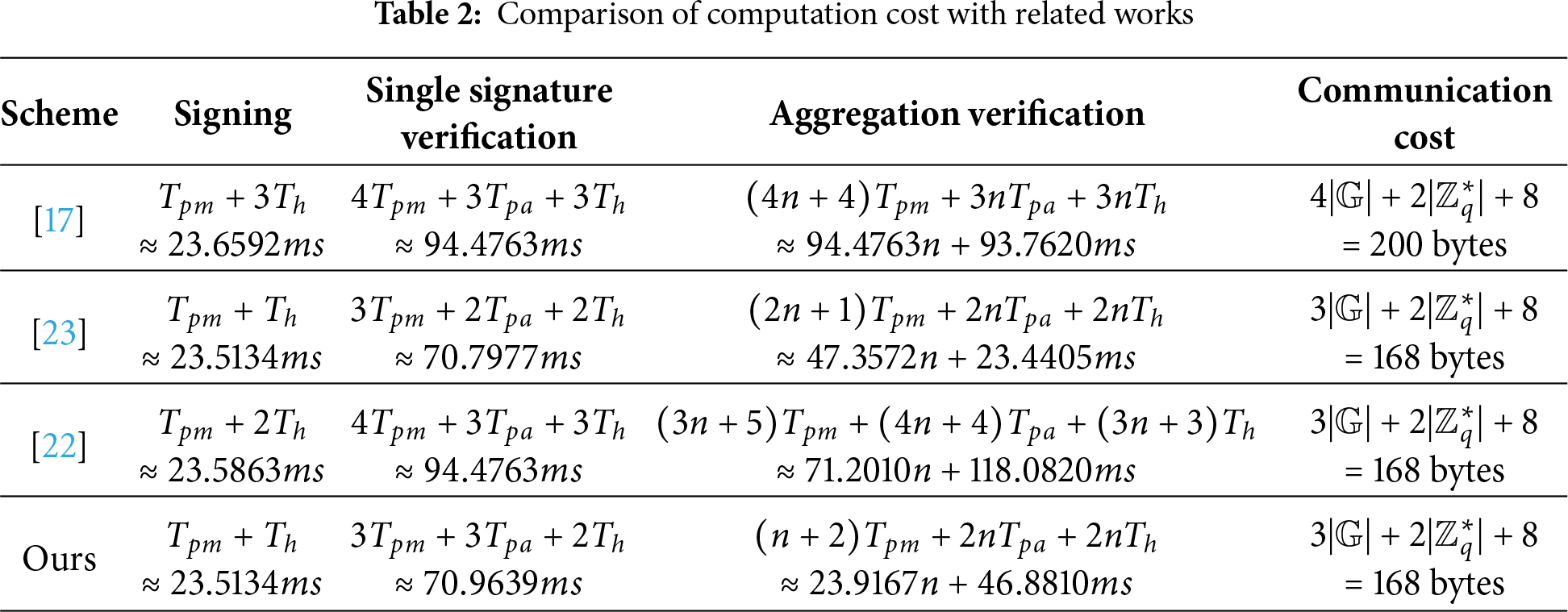
In Signing, the cost of our design is the same as that of [23] and lower than that of [17] (i.e., 23.6592 ms) and [22] (i.e., 23.5863 ms). In Verification, the schemes in [17,22] require a relatively high computational cost. Though the cost of our scheme is slightly higher than that of [23], the gap between them is quite small (i.e., 0.1652 ms). In addition, as can be seen from the table and Fig. 3, our scheme achieves the smallest computational cost in Aggregate Verification. Therefore, our scheme has better security and desirable computational cost.

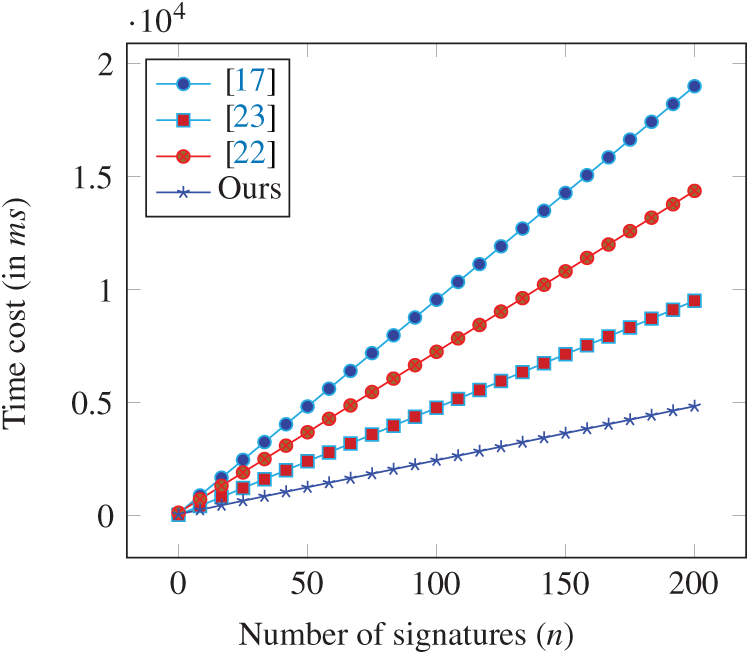
Figure 3: Computational costs comparison between the improved CLAS scheme and [17,22,23] in aggregation verification phase

Communication costs. Based on the above curve parameters, the length of G and Zq∗ can be represented by 32 bytes and 32 bytes, respectively [26,27]. We assume that the size of both the identity and the timestamp is 4 bytes. In our design, the signer needs to send {PIDi,PKi,mi,σi,ti} to the verifier, where PIDi={AIDi2,Ti}, PKi=(Xi,Ri), and σi=(Ui,Vi). Since Xi,Ri,Ui∈G and AIDi2,Vi∈Zq∗, the cost is 3|G|+2|Zq∗|+8=32×5+8=168 bytes. Similarly, Table 2 counts the communication costs of these schemes. The above results indicate that the communication cost required for the scheme in [17] is 200 bytes, while other schemes, including ours, only require 168 bytes.

In summary, our improved scheme not only has better security but also has desirable computational and communication costs.

Discussion

In Wang et al.’s design in [23], the main reason why their proposal has the security vulnerability under Type 1 attack is that the verification equation ViP=Ui+hi(3)(Ki+hi(2)Pkgc) in the verification algorithm has some special algebraic relationship (i.e., Ki and hi(2) are independent and do not affect each other). As we analyzed in Section 3.1, the Type 1 attacker uses such an algebraic relationship to replace Ki by setting Ki∗=βP−hi(2)Pkgc, where the random β∈Zq∗. Hence, the attacker can bypass the KGC’s private key α (corresponding to Pkgc=αP).

In our improvement, we have made corresponding adjustments to the device private-public key pair generation method, signature generation process, and verification equation, avoiding the problems found in Wang et al.’s design. The above performance analysis shows that compared with existing work, our improvement has reached the optimal state in signature generation, signature batch verification processing, and communication cost. However, our work cannot not achieve optimal performance in terms of single signature verification. This is a cost for our solution in achieving high security. To address this limitation, a feasible approach is to combine certificateless cryptosystems with lightweight hash-based message authentication code [28] to construct new privacy preserving authentication schemes. However, However, this may require a new security model.

6  Conclusion

In this effort, we explored the security vulnerability of a very recent CLAS scheme in [23] proposed for NDN-IoT environments. By presenting a specific Type 1 attack, our analysis demonstrates how attackers can use their scheme to forge legitimate signatures for fraudulent environmental data. This manipulation allows malicious actors to deceive consumers, thereby guiding them to make wrong decisions. In view of this, we have systematically examined the root causes behind the vulnerability in [23] and proposed an improved CLAS design to secure NDN-IoT applications. We proved its security based on the cryptographic assumption, and analyzed its performance. The performance comparison results showed that our improved scheme not only has better security but also has desirable computational and communication costs. Finally, as an additional contribution, we analysed the security vulnerability of a very recent CLAS scheme in [22] and proposed targeted countermeasures to enhance its security.

Acknowledgement: None.

Funding Statement: This work was supported in part by the Hubei Engineering Research Center for BDS-Cloud High-Precision Deformation Monitoring Open Funding (No. HBBDGJ202507Y), in part by the National Natural Science Foundation of China (No. 62377037).

Author Contributions: Conceptualization, Feihong Xu, Fei Zhu, Saru Kumari; Methodology, Jianbo Wu, Qing An; Writing—original draft, Feihong Xu and Fei Zhu; Writing—review & editing, Feihong Xu, Jianbo Wu, Qing An, Zhaoyang Han, and Saru Kumari. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A Cryptanalysis and Improvement of Yue et al.’s CLAS scheme in [22]

Appendix A.1 Review of the Original Scheme: The CLAS scheme introduced by Yue et al. [22] consists of the following algorithms: System Setup, Pseudonym Identity Generation, Partial Private Key Generation, Vehicle Key Generation, Individual Signature Generation, Single Signature Verification, Aggregated Signature Generation, and Aggregated Signature Verification. For ease of presentation, we only briefly review their first six algorithms to support our analysis, which naturally form a CLS scheme.

1.   System Setup: Taking a security parameter ζ as input, the KGC and TA generate below system parameters:

(a)   Define an q-order cyclic group G=⟨P⟩.

(b)   Choose hash functions Hi:{0,1}∗→Zq∗, i=0,1,…,4.

(c)   (KGC:) Randomly select a private key a∈Zq∗ and calculate a public key PKkgc=aP.

(d)   (TA:) Randomly select a private key b∈Zq∗ and calculate a public key PKta=bP.

(e)   KGC and TA store a and b, respectively, and publish public parameters ppa={G,P,q,PKkgc,PKta,Hi}.

2.   Pseudonym Identity Generation: A vehicle Vi with real identity RIDi interacts with TA to generate a pseudonym PIDi for a validity period Ti.

(a)   Vi randomly picks xi∈Zq∗ and calculates Xi=xiP, TIDi=RIDi⊕H0(xiTpub), and submits {Xi,TIDi} to TA.

(b)   TA extracts RIDi=TIDi⊕H0(bXi), computes pseudonym PIDi=RIDi⊕H1(bXi,Ti,ti), and sends {PIDi,Xi,Ti,ti} to KGC, where Ti is the validity period for PIDi and ti is current timestamp.

3.   Partial Private Key Generation: After checking the validity of Ti and ti, the KGC randomly picks ri∈Zq∗ and computes Ri=riP, hi(2)=H2(PIDi,Ri,PKkgc,Xi,Ti), di=ri+ahi(2), and Di=di⊕H0(aXi). Then, it sends the tuple {PIDi,Di,Ri,Ti,ti} to Vi.

4.   Vehicle Key Generation: Vi recovers di=Di⊕H0(xiPKkgc) and hi(2)=H2(PIDi,Ri,PKkgc,Xi,Ti). Note that di can be checked by diP=Ri+hi(2)PKkgc. If and only if di is valid, Vi accepts its private key SKi=(xi,di) and public key PKi=(Xi,Ri).

5.   Signing: To sign a message mi∈{0,1}∗ at time ti, Vi performs the following:

(a)   Select ui∈Zq∗ at random and calculate Ui=uiP.

(b)   Calculate hi(3)=H3(mi,PIDi,PKi,PKkgc,ti) and hi(4)=H4(mi,PIDi,PKi,Ui,ti).

(c)   Compute si=ui+dihi(3)+xihi(4) and set the signature σi=(Ui,si).

6.   Single Signature Verification: Given {PIDi,PKi,mi,σi,Ti,ti}, the verifier checks the freshness of ti. Then it recovers hi(2)=H2(PIDi,Ri,PKkgc,Xi,Ti), hi(3)=H3(mi,PIDi,PKi,PKkgc,ti), and hi(4)=H4(mi,PIDi,PKi,Ui,ti). It accepts the signature if siP=Ui+hi(3)(Ri+hi(2)Pkgc)+hi(4)Xi and rejects otherwise.

Appendix A.2 Security Analysis to [22]: In [22], Yue et al. stated that their design is secure against both Type 1 and Type 2 attackers. Here, we show that a Type 1 attacker ℱ1 possesses the capability to produce a verifiable signature for any fraudulent message, thereby compromising the unforgeability property inherent in their cryptographic construction. Let the vehicle Vi with pseudonym PIDi be the target device attacked by ℱ1. Given public parameters ppa={G,P,q,PKkgc,PKta,Hi} and Vi’s public key PKi=(Xi,Ri), ℱ1 can also access Vi’s secret value xi. Suppose that ℱ1 wants to generate a forgery σi∗ on a message mi∗ at time ti, as shown in Fig. A1, ℱ1 operates as follows:

(1)   Compute hi(2)=H2(PIDi,Ri,PKkgc,Xi,Ti) and hi(3)=H3(mi,PIDi,PKi,PKkgc,ti).

(2)   Pick β∈Zq∗ at random and set Ui∗=βP−hi(3)(Ri+hi(2)Pkgc).

(3)   Compute hi(4)∗=H4(mi∗,PIDi,PKi,Ui∗,ti) and si∗=β+hi(4)xi.

(4)   Set its forgery σi∗=(Ui∗,si∗).

Figure A1: An example of the Type 1 attack

Now, the correctness of σi∗ is checked by:

si∗P=(β+hi(4)xi)P=βP+hi(4)xiP=Ui∗+hi(3)(Ri+hi(2)Pkgc)+hi(4)Xi.

Due to the insecurity of the underlying CLS scheme, their CLAS construction cannot achieve unforgeability.

Appendix A.3 Improvement: In [22], a verifier checks a received signature through the equation siP=Ui+hi(3)(Ri+hi(2)Pkgc)+hi(4)Xi. However, due to the lack of binding between Ui and hi(3), the attacker ℱ1 can use the algebraic relationship in the equation to bypass the KGC’s private key a (corresponding to Pkgc=aP).

To patch this vulnerability, a simple suggestion is to include Ui in computing hi(3). That is, hi(3)=H3(mi,PIDi,PKi,PKkgc,Ui,ti). Following Yue et al.’s proof approach in [22], the modified scheme can be easily proven to be secure. The modification does not add any additional computational cost.

References

1. Daniel E, Tschorsch F. IPFS and friends: a qualitative comparison of next generation peer-to-peer data networks. IEEE Commun Surv Tutorials. 2022;24(1):31–52. doi:10.1109/comst.2022.3143147. [Google Scholar] [CrossRef]

2. Benmoussa A, Kerrache CA, Lagraa N, Mastorakis S, Lakas A, Tahari AEK. Interest flooding attacks in named data networking: survey of existing solutions, open issues, requirements, and future directions. ACM Comput Surv. 2023;55(7):139:1–37. doi:10.1145/3539730. [Google Scholar] [CrossRef]

3. Mazhar T, Irfan HM, Haq I, Ullah I, Ashraf M, Shloul TA, et al. Analysis of challenges and solutions of IoT in smart grids using AI and machine learning techniques: a review. Electronics. 2023;12(1):242. doi:10.3390/electronics12010242. [Google Scholar] [CrossRef]

4. Mazhar T, Talpur DB, Shloul TA, Ghadi YY, Haq I, Ullah I, et al. Analysis of IoT security challenges and its solutions using artificial intelligence. Brain Sci. 2023;13(4):683. doi:10.3390/brainsci13040683. [Google Scholar] [PubMed] [CrossRef]

5. Zhu F, Yi X, Abuadbba A, Luo J, Nepal S, Huang X. Efficient hash-based redactable signature for smart grid applications. In: ESORICS 2022. Copenhagen, Denmark; 2022 Sep 26–30. Vol. 13556. Cham, Switzerland: Springer; 2022. p. 554–73. [Google Scholar]

6. Boneh D, Gentry C, Lynn B, Shacham H. Aggregate and verifiably encrypted signatures from bilinear maps. In: EUROCRYPT 2003. Warsaw, Poland; 2003 May 4–8. Vol. 2656. Cham, Switzerland: Springer; 2003. p. 416–32. [Google Scholar]

7. Shen L, Ma J, Liu X, Wei F, Miao M. A secure and efficient ID-based aggregate signature scheme for wireless sensor networks. IEEE Internet Things J. 2017;4(2):546–54. doi:10.1109/jiot.2016.2557487. [Google Scholar] [CrossRef]

8. Al-Riyami SS, Paterson KG. Certificateless public key cryptography. In: ASIACRYPT 2003. Taipei, Taiwan; 2003 Nov 30–Dec 4. Vol. 2894. Cham, Switzerland: Springer; 2003. p. 452–73. [Google Scholar]

9. Shim K. A secure certificateless signature scheme for cloud-assisted industrial IoT. IEEE Trans Ind Informatics. 2024;20(4):6834–43. doi:10.1109/tii.2023.3343437. [Google Scholar] [CrossRef]

10. Yang W, Wang S, Mu Y. An enhanced certificateless aggregate signature without pairings for E-healthcare system. IEEE Inter Things J. 2021;8(6):5000–8. doi:10.1109/jiot.2020.3034307. [Google Scholar] [CrossRef]

11. Aljarwan AZA, Ngadi MA. Review of certificateless authentication scheme for vehicular ad hoc networks. IEEE Access. 2025;13:100074–94. doi:10.1109/access.2025.3576926. [Google Scholar] [CrossRef]

12. Mei Q, Xiong H, Chen J, Yang M, Kumari S, Khan MK. Efficient certificateless aggregate signature with conditional privacy preservation in IoV. IEEE Syst J. 2021;15(1):245–56. doi:10.1109/jsyst.2020.2966526. [Google Scholar] [CrossRef]

13. Cahyadi EF, Su T, Yang CC, Hwang M. A certificateless aggregate signature scheme for security and privacy protection in VANET. Int J Distributed Sens Networks. 2022;18(5). doi:10.1177/15501329221080658. [Google Scholar] [CrossRef]

14. Cui J, Zhang J, Zhong H, Shi R, Xu Y. An efficient certificateless aggregate signature without pairings for vehicular ad hoc networks. Inf Sci. 2018;451–452:1–15. doi:10.1016/j.ins.2018.03.060. [Google Scholar] [CrossRef]

15. Kamil IA, Ogundoyin SO. An improved certificateless aggregate signature scheme without bilinear pairings for vehicular ad hoc networks. J Inf Secur Appl. 2019;44(1):184–200. doi:10.1016/j.jisa.2018.12.004. [Google Scholar] [CrossRef]

16. Xu G, Zhou W, Sangaiah AK, Zhang Y, Zheng X, Tang Q, et al. A security-enhanced certificateless aggregate signature authentication protocol for InVANETs. IEEE Netw. 2020;34(2):22–9. doi:10.1109/mnet.001.1900035. [Google Scholar] [CrossRef]

17. Zhu F, Yi X, Abuadbba A, Khalil I, Huang X, Xu F. A security-enhanced certificateless conditional privacy-preserving authentication scheme for vehicular ad hoc networks. IEEE Trans Intell Transp Syst. 2023;24(10):10456–66. doi:10.1109/tits.2023.3275077. [Google Scholar] [CrossRef]

18. Yang W, Fan J, Song K, Zheng Y, Zhang F. An efficient and practical conditional privacy-preserving aggregate authentication for vehicular ad-hoc networks. IEEE Trans Intell Transp Syst. 2024;25(12):20256–67. doi:10.1109/tits.2024.3474210. [Google Scholar] [CrossRef]

19. Zhu D, Guan Y. Secure and lightweight conditional privacy-preserving identity authentication scheme for VANET. IEEE Sensors J. 2024;24(21):35743–56. doi:10.1109/jsen.2024.3431557. [Google Scholar] [CrossRef]

20. Zhu F, Hu Y, Ren Y, Han B, Yang X. Public-Key replacement attacks on lightweight authentication schemes for resource-constrained scenarios. Cyber Secur Applicat. 2025;3:100102. doi:10.1016/j.csa.2025.100102. [Google Scholar] [CrossRef]

21. Verma RK, Khan AJ, Kashyap SK, Chande MK. Certificateless aggregate signatures: a comprehensive survey and comparative analysis. J Univers Comput Sci. 2024;30(12):1662–90. doi:10.3897/jucs.116249. [Google Scholar] [CrossRef]

22. Yue Q, Jiang W, Lei H. A lightweight certificateless aggregate signature scheme without pairing for VANETs. Sci Rep. 2025;15(1):23663. doi:10.1038/s41598-025-08656-1. [Google Scholar] [PubMed] [CrossRef]

23. Wang C, Wu H, Gan Y, Zhang R, Ma M. ECAE: an efficient certificateless aggregate signature scheme based on elliptic curves for NDN-IoT environments. Entropy. 2025;27(5):471. doi:10.3390/e27050471. [Google Scholar] [PubMed] [CrossRef]

24. Xu F, Liu S, Yang X. An efficient privacy-preserving authentication scheme with enhanced security for IoMT applications. Comput Commun. 2023;208:171–8. doi:10.1016/j.comcom.2023.06.012. [Google Scholar] [CrossRef]

25. Pointcheval D, Stern J. Security arguments for digital signatures and blind signatures. J Cryptol. 2000;13(3):361–96. doi:10.1007/s001450010003. [Google Scholar] [CrossRef]

26. Sasdrich P, Güneysu T. Implementing Curve25519 for side-channel-protected elliptic curve cryptography. ACM Trans Reconfigurable Technol Syst. 2015;9(1):3:1–15. doi:10.1145/2700834. [Google Scholar] [CrossRef]

27. Tanksale V. Efficient elliptic curve diffie-hellman key exchange for resource-constrained IoT devices. Electronics. 2024;13(18):3631. doi:10.3390/electronics13183631. [Google Scholar] [CrossRef]

28. Katz J, Lindell Y. Introduction to modern cryptography. 2nd ed. Philadelphia, PA, USA: CRC Press; 2014. [Google Scholar]