Heterogeneous User Authentication and Key Establishment Protocol for Client-Server Environment

1  Introduction

With the rapid advancement of Internet technologies, the client-server architecture has become a cornerstone of modern information systems [1]. It finds extensive application in mission-critical domains such as the Internet of Things (IoT) [2], wireless body area networks (WBANs) [3], and industrial control systems (ICS) [4]. However, the inherent openness and heterogeneity of this architecture introduce significant security challenges to data transmission. These challenges manifest as vulnerabilities to man-in-the-middle attacks, data tampering, and privacy breaches [5], particularly in lightweight IoT communications and critical WBAN medical data transmissions where security failures can have dire consequences [6]. To mitigate these risks and ensure confidentiality, integrity, and non-repudiation, authentication and key establishment (AKE) protocols are widely employed to establish trusted identities and negotiate secure session keys [7].

Current research has yielded numerous AKE protocols based on elliptic curve cryptography (ECC) [8], public key infrastructure (PKI) [9], identity-based cryptography (IBC) [10], and certificateless cryptography (CLC) [11]. However, existing solutions still face critical bottlenecks in adapting to heterogeneous environments, which can be framed as two core conflicts.

Efficiency vs. Resource Constraints. Traditional security protocols, such as those based on Diffie-Hellman (DH) key exchange, often require multiple rounds of interaction, leading to significant communication and computational overhead. In resource-constrained environments like IoT terminals or WBAN devices, this high overhead can degrade real-time performance and drastically shorten device lifespan due to excessive energy consumption. This creates a fundamental conflict between achieving robust security and maintaining the operational viability of lightweight devices.

Architectural Trade-Offs in Heterogeneous Trust Models. A second, more nuanced conflict arises from the architectural trade-offs between different cryptographic systems. On one hand, resource-limited clients are best served by lightweight systems like IBC, which eliminates the prohibitive certificate management overhead of traditional PKI. On the other hand, servers demand robust security without single points of failure. The inherent key escrow vulnerability of IBC, where a key generation center (KGC) knows all client private keys, is an unacceptable risk for a trusted server. While CLC mitigates this key escrow problem, existing protocols predominantly adopt a single, homogeneous system. This approach fails to address the conflicting requirements of clients (who need simplicity) and servers (who need security without escrow), creating a critical need for innovative heterogeneous designs that can harmonize these competing demands.

To address these challenges, this paper proposes a signcryption-based heterogeneous user authentication and key establishment protocol (HUAKE). Signcryption, a cryptographic primitive that integrates digital signatures and encryption within a single logical step, provides confidentiality, integrity, non-repudiation, and authentication for sensitive data. By leveraging signcryption, the HUAKE protocol reduces communication rounds while enhancing security. In this protocol, clients adopt IBC, where public keys are directly derived from unique identifiers (e.g., device IDs), eliminating certificate management burdens. Servers adopt CLC, where partial private keys are generated by the KGC and combined with server-specific secret values to form complete private keys. This hybrid approach circumvents IBC’s key escrow risks while avoiding reliance on PKI’s complex certificate chains.

Furthermore, HUAKE integrates identity authentication, key agreement, and data encryption into 1.5 communication rounds through signcryption, significantly reducing interaction complexity and communication overhead. Theoretical analysis and experimental results demonstrate that HUAKE ensures resistance to forgery, replay, key compromise impersonation (KCI) attacks, while achieving superior communication efficiency compared to existing schemes. This makes HUAKE particularly suitable for lightweight secure interactions between resource-constrained devices (e.g., IoT) and servers in client-server environments.

1.1 Contribution

The contributions of this work are fourfold.

•   We construct a novel HUAKE protocol based on signcryption, in which IBC-based clients resolve public key certificate management issues, while CLC-based servers simultaneously address certificate management and key escrow risks.

•   We formally demonstrate the security of our protocol by mBR model. Security proof revealed that the proposed protocol enables user authentication, key authentication, key establishment, mutual authentication. Moreover, it can also resist forgery, replay, and KCI attacks.

•   We demonstrate how HUAKE transitions from a key transport mechanism to a DH-based construction, offering flexibility in AKE protocol design.

•   Comparative evaluations against five protocols confirm that HUAKE achieves the lowest communication overhead, making it a practical solution for secure communications in client-server environments.

1.2 Organization

We characterize the existing literature in Section 2. In the next Section, we focus on the preliminaries. We describe the security model of this protocol in Section 4. In Section 5, we describe our protocol. Then, we illustrate security and performance in sections 6 and 7. Finally, we make a conclusion of the paper.

2  Related Work

Public key cryptosystems are broadly categorized into three types based on their authentication mechanisms: PKI, IBC, and CLC [12]. PKI [13] relies on a Certificate Authority (CA) to bind public keys to identities, but the associated certificate management overhead makes it cumbersome for resource-constrained mobile environments. To address this, Shamir introduced IBC [10], which simplifies key management by deriving public keys from identity strings. However, IBC introduces the key escrow problem, as a central private key generator (PKG) knows all users’ private keys. CLC [11] was later proposed to resolve both issues; it eliminates PKI’s complex certificates and mitigates IBC’s key escrow risk by having users contribute a secret value to their full private key, making it well-suited for large-scale networks.

Numerous AKE protocols have been developed for mobile client-server (MCS) environments. However, many early schemes were proven to be vulnerable to security threats like reflection, parallel session, and tracking attacks [14,15]. Other works have explored symmetric encryption techniques [16] or CLC-based multi-server authentication [17], but often lacked a heterogeneous design or incurred significant communication overhead [18].

More recent research has continued to refine AKE protocols. For instance, Qiu et al. [19] proposed a lightweight ECC-based protocol, which was nevertheless found vulnerable during its password update phase. Other schemes have focused on achieving anonymity [20] or provable security against specific threats like KCI attacks [21]. A critical limitation of many of these advanced protocols, including those by Tsobdjou et al. [22] and Rana et al. [23], is their operation within homogeneous environments. While some heterogeneous protocols exist, such as the IBC-to-PKI scheme by Li et al. [24], they do not fully solve the certificate management problem due to their reliance on a PKI-based server. Most recently, Daniel et al. [25] developed a pairing-free ID-AKE protocol with strong security in the enhanced eCK security model, while Ma et al. [26] improved a CL-AKE protocol by Cheng et al. [27] to achieve perfect forward secrecy and reduce computational overhead. While significant, these state-of-the-art solutions do not address the specific challenge of creating a secure, efficient, and truly certificateless heterogeneous link between an IBC-based client and a CLC-based server. Recently, the field of heterogeneous signcryption authentication has seen a surge in research targeting specific application scenarios. For example, Khalafalla et al. [28] designed a cross-domain mutual authentication scheme for Vehicular Ad Hoc Networks (VANETs) that combines CLC and IBC, leveraging blockchain technology for decentralized trust management. Another work [29] enhances the security of a heterogeneous CLC-PKI scheme by introducing a cryptographic reverse firewall to prevent data leakage.

3  Preliminaries

In this paragraph, we describe the network model, threat model and security goals, bilinear pairings as well as syntax, respectively.

3.1 Network Model

The client-server network architecture supported by our proposed protocol, as depicted in Fig. 1, consists of three core entities: a Registration Center (RC), a server, and multiple clients such as industrial IoT devices. Within this framework, clients and servers interact through wired or wireless communication channels. The RC functions as the central trusted authority, playing a dual role within this heterogeneous framework. For the IBC-based clients, it acts as a PKG, creating their full private keys. For the CLC-based servers, it acts as a KGC, responsible for generating their partial private keys. Beyond key generation, the RC assumes the critical responsibility of managing the credential lifecycle and security. To handle cases where a client’s private key is compromised before its expiration date, the RC maintains and periodically publishes a digitally signed Revocation List (RL). This list contains the unique identifiers of all invalidated credentials, serving as an authoritative source for the server to verify a client’s real-time status. While the RC is inherently trusted due to its custody of client private keys, a distributed RC architecture could optionally be implemented to alleviate key escrow concerns. To initiate communication with a server, the client and server first undergo a registration process with the RC. Subsequently, the client transmits an authenticated message to the target server, which then verifies the client’s legitimacy. Upon successful authentication, both parties engage in ephemeral session key negotiation to establish secure communication.

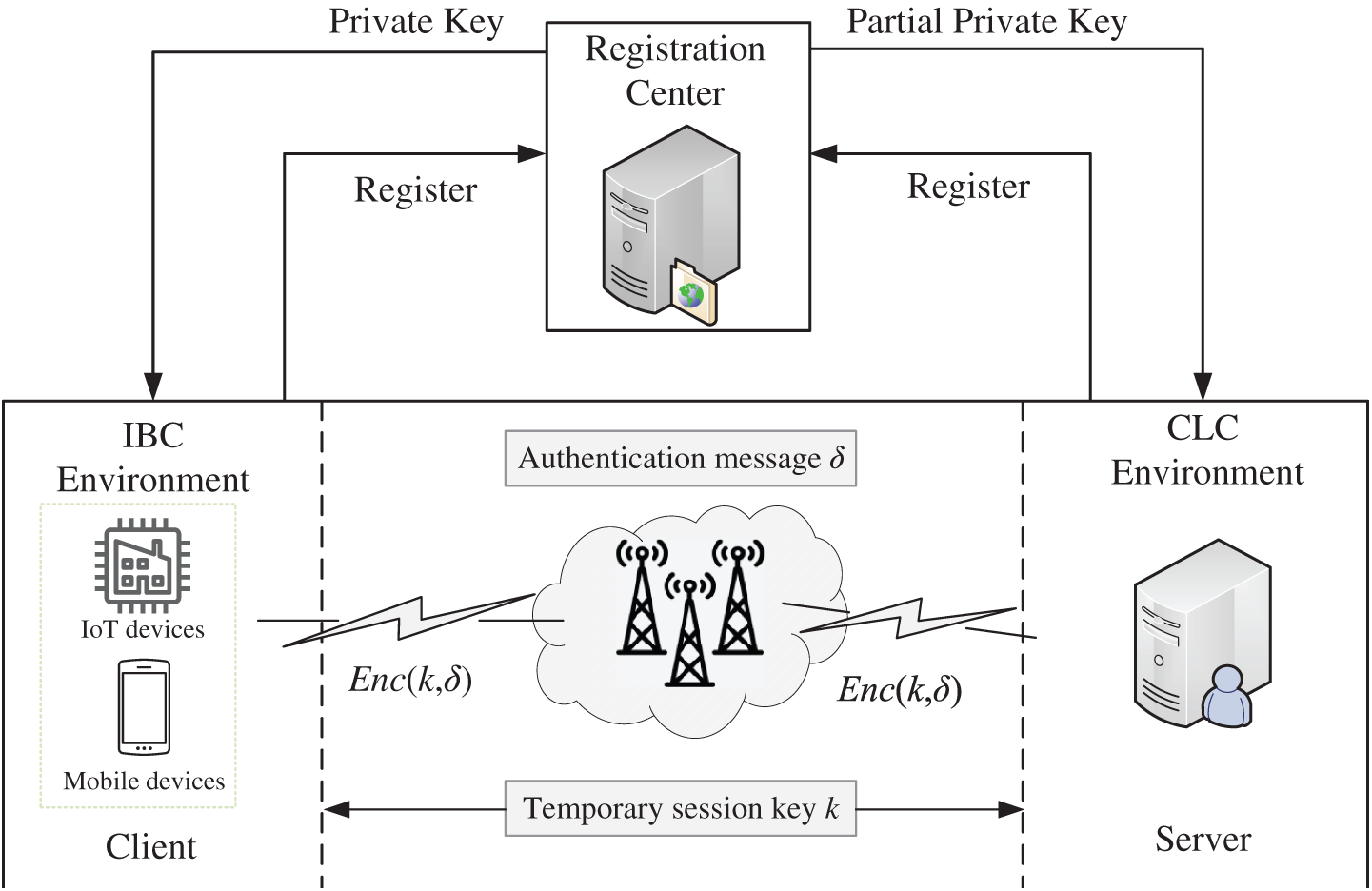
Figure 1: Network model

3.2 Bilinear Pairings

Assume the existence of two groups G1 and G2. G1 is an additive group and G2 is a multiplicative group with the same prime order p, a generator P of G1. We say that e:G1×G1→G2 with the three features. 1) Bilinearity: ∀r,c∈Zp∗, ∀Q,R∈G1, e(rQ,cR)=e(Q,R)rc. 2) Non-degeneracy: ∃Q,R∈G1 such that e(Q,R)≠1. 3). There exists a feasible algorithm to find e(Q,R), ∀Q,R∈G1.

We now demonstrate security concepts for the HUAKE protocol.

Definition 1: Upon receiving groups G1 (the generator is P) and G2 with same order p, and a bilinear pairing is a map e:G1×G1→G2.

•   The computational Diffie-Hellman (CDH) problem in G1 is to find xyP by giving (P,xP,yP).

•   The gap Diffie-Hellman (GDH) problem in (G1,G2,e) is to find xyP by giving (P,xP,yP) with the help of the DBDH oracle that can decide whether DBDH (P,xP,yP,zP,T) = ⊤ or ⊥.

•   The bilinear computational Diffie-Hellman (BDH) problem in (G1,G2,e) is to find T=e(P,P)xyz by giving (P,xP,yP,zP).

•   The decisional bilinear Diffie-Hellman (DBDH) problem in (G1,G2,e) is determine whether or not T=e(P,P)xyz by giving (P,xP,yP,zP,T), where T∈G2. If T=e(P,P)xyz, then DBDH(P,xP,yP,zP,T)=⊤. Otherwise, we represent it by DBDH(P,xP,yP,zP,T)=⊥.

•   The gap bilinear Diffie-Hellman (GBDH) problem in (G1,G2,e) is to find T=e(P,P)xyz by giving (P,xP,yP,zP) with the help of the DBDH oracle that can decide if DBDH(P,xP,yP,zP) = ⊤ or ⊥.

3.3 Security Goals

The main security goals achieved in this paper are as follows.

–   Forgery Attack: No attacker can establish communication with a client disguised as a legitimate server.

–   Replay Attack: This means that adversaries cannot send previous authentication messages to the server for authentication.

–   Key Compromise Impersonation Attack: An attacker who has compromised the client Ci’s long-term private key must not be able to use it to impersonate the server Sj to the client Ci.

–   Session Key Security: In this context, we must ensure that adversaries cannot recover the session key from the information transmitted on public channels.

3.4 Syntax

The syntax of our protocol includes the below seven algorithms.

System Initialization: This phase is executed by RC. It takes a security parameter μ as input, and returns a master private key s and parameters that contain the master public key Ppub.

Identity-Based-Key-Extraction (IB-KE): This happens in IBC environment. This phase is carried out by RC to create a public/private pair (QIDi/SIDi) with an identity IDi as input.

Partial-Private-Key-Extract (PPKE): This phase happens in CLC environment. This phase is carried out by RC to generate a partial private key DIDj with an identity IDj as input.

Set-Secret-Value (SSV): A user with an identity IDj randomly chooses xj∈Zp∗ as its secret value.

Set-Private-Key (SPK): This phase is executed by a user with DIDj and xj as input, it returns the corresponding full private key SIDj.

Public-Key-Extract (PKE): This phase is executed by a user with system parameters and xj as input, it outputs the corresponding public key PKIDj.

Key-Establishment: The two communicating parties complete the authentication and key establishment functions according to this protocol. Finally, a common temporary security session key kij=kji=k is established between the two communicating parties.

4  Security Model

Our HUAKE protocol is constructed using signcryption technology. The security of a signcryption scheme primarily requires demonstrating the confidentiality of the message and its unforgeability. Therefore, our proof methodology is based on standard signcryption security proofs. However, as our protocol is designed for authenticated key agreement, we have adapted the proof logic by referencing the model in [30] to fit the context of a key agreement protocol. The security proof is modeled as a game between a challenger 𝒞, and a probabilistic polynomial time (PPT) adversary 𝒜, who controls all communication channels and can modify, relay, or delete messages. Since the server in our protocol operates within a certificateless environment, we must consider two distinct types of adversaries to fully capture the security requirements. 1) Type I (𝒜ℐ): Can perform public key replacement (PKR) queries but cannot obtain the system master private key. 2) Type II (𝒜ℐℐ): Can obtain the master private key but cannot perform PKR queries.

The adversary 𝒜 interacts with oracles, which represent the n-th communication session (∏i,jn) between parties i and j. 𝒜 can adaptively issue a series of queries to these oracles, including a single Test query, to challenge the protocol’s security.

IB-KE(IDi): 𝒜 sends an identity IDi to 𝒞, 𝒞 gives the public key QIDi, private key SIDi to 𝒜.

Create(IDj): 𝒜 transmits an identity IDj to 𝒞, 𝒞 gives the public/private key pair for IDj.

PKE(IDj): 𝒜 transmits an identity IDj to 𝒞, 𝒞 gives the public key PKIDj to 𝒜.

PPKE(IDj): 𝒜 transmits an identity IDj to 𝒞, 𝒞 gives the partial private key DIDj to 𝒜.

Corrupt(IDj): 𝒜 transmits an identity IDj to 𝒞, 𝒞 gives the full private key SIDj to 𝒜.

PKR(IDj): This algorithm allows 𝒜ℐ to replace the public key PKIDj with PKIDj′. The replaced public key PKIDj′ is recorded by 𝒞.

Send(∏i,jn, M): Suppose that the communication parties are i and j. After receiving this query, 𝒜 can initiate a query to oracle ∏i,jn with a message M. If M = ‘begin’, the oracle is an initiator oracle and initiates a new session. Otherwise, it is a response oracle.

Reveal(∏i,jn): 𝒜 can require a specific oracle to disclose the session key it presently holds (if it is) to 𝒜.

Test(∏i,jn): When 𝒞 receipts of a Test query started by 𝒜, it selects b∈(0,1) and outputs the actual temporary session key if b=0. If b=1, 𝒞 randomly selects a temporary session key g∈(0,1)l1 and outputs it.

Definition 2: Matching conversation: Two oracles ∏i,jn and ∏j,in are defined as matching conversation if the two oracles share the common session identifier.

Definition 3: Fresh oracle: We say an oracle ∏i,jn is a fresh oracle if it satisfies the four requirements. ∏i,jn has produced a session key. The adversary has not made a Reveal query on ∏i,jn. If there is a matching conversation exists for ∏i,jn, the adversary has not made a Reveal query on it. If the adversary is 𝒜ℐℐ, it has not made a PKR query on IDj.

The adversary may repeat all queries besides Test query, but these queries are limited by the three conditions. It cannot make a Reveal query on ∏i,jn or ∏j,in, which has a matching conversation with ∏i,jn (if it exists). It cannot execute a Corrupt query on identity IDj. If the adversary is 𝒜ℐℐ, it cannot execute a PKR query on IDj.

Finally, 𝒜 has to export a surmise bit b′. We say that the adversary wins if b′ = b and the advantage of it to win this game is defined as Adv(𝒜)=|P(b′=b)−12| where P(b′=b) represents the probability that b′=b.

Definition 4: A user authentication key establishment protocol may be considered secure if it satisfies the tow requirements. 1) In the existence of a passive attacker on ∏i,jn and ∏j,in, the two oracles always concur over the common session key. In addition, this key is uniformly distributed. 2) For each adversary, Adv(𝒜) is negligible.

5  The Proposed Protocol

We mainly introduce an efficient HUAKE protocol for a client-server environment in this segment. The following four algorithms show the detailed construction of this protocol. Table 1 explains the main notations.

5.1 Initialization Phase

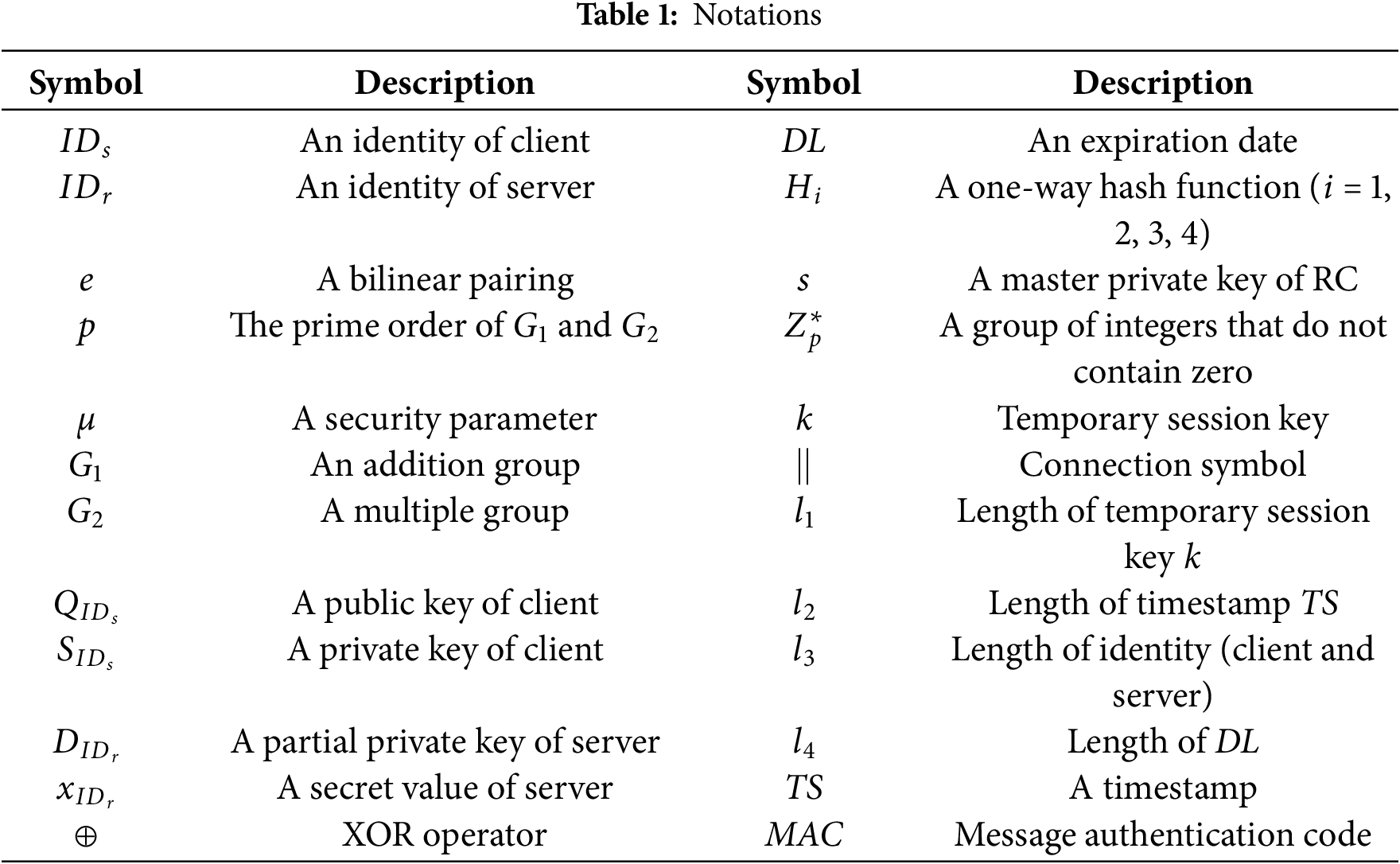
System Initialization: A security parameter μ is provided to RC to produce a bilinear map, e:G1×G1→G2. Here, P∈G1 is the generator of G1, G1 is an additive group and G2 is a multiplicative group with the same prime order p. RC chooses four hash functions: H1:{0,1}l1×{0,1}l4→G1, H2:(G1)2×G2×{0,1}l3→{0,1}l1+l2+l3+l4,H3:(G1)2×{0,1}l1+l2+l3+l4×{0,1}l3→G1,H4:(G1)2×{0,1}l1+l2+l3+l4×{0,1}l3→Zp∗. Functionally, H1 maps identities to public key, H2 provides confidentiality by generating the encryption mask, and H3 and H4 collectively ensure integrity and unforgeability by producing components for the signature. RC randomly selects a master private key s∈Zp∗, calculates Ppub=sP as system master public key. Finally, RC publishes system parameters {G1,G2,e,P,Ppub,H1,H2,H3,H4} but retains s secret.

5.2 Registration Phase

Both clients and the server need to complete registration on RC before they communicate with each other.

•   IB-KE: A client Ci in IBC transmits its identity IDs∈{0,1}l3 to RC. RC picks a deadline DL∈{0,1}l4 and calculates public key QIDs=H1(IDs||DL), private key SIDs=sQIDs for Ci, as well as sends (SIDs,DL) to Ci over a secure and authenticated channel. This channel is assumed to provide confidentiality and integrity for the transmitted key. Similar to Wu et al. [31], we can achieve this through methods such as offline delivery or online protocols like Transport Layer Security (TLS).

•   PPKE: A server Sj in CLC submits its identity IDr∈{0,1}l3 to RC. Then RC calculates QIDr=H1(IDr||DL), partial private key DIDr=sQIDr for Sj, as well as sends (DIDr,DL) to Sj in a secure way.

•   SSV: A server Sj with an identity IDj randomly selects xIDr∈Zp∗ as its secret value.

•   SPK: Given a secret value xIDr and a partial private key DIDr, Sj calculates its full private key SIDr=(xIDr,DIDr).

•   PKE: Given a secret value xIDr, Sj calculates its public key PkIDr=xIDrP.

5.3 User Authentication and Key Establishment Phase

In the following steps, both the encryption and signature components share a common random number r. Specifically, the encryption of the session key k is realized by using r and the server’s public key to derive the T, which is then hashed to create a mask h for encrypting the key. The subsequent steps, culminating in the generation of V, form the signature component, which provides authenticity and integrity, preventing an adversary from forging a valid message.

1)   Randomly selects k∈{0,1}l1,r∈Zp∗

2)   Computes U=rP,T=e(Ppub,QIDr)r

3)   Computes h=H2(U,T,IDr,rPKIDr)

4)   Computes C=(k||TS||IDs||DL)⊕h

5)   Computes W=H3(U,C,IDr,PKIDr)

6)   Computes f=H4(U,C,IDr,PKIDr)

7)   Computes V=rW+fSIDs. Finally, Ci sends the authentication message (U,C,V,TS) to Sj.

When Sj receives the authentication message (U,C,V,TS) from Ci, it first checks the validation of TS by Time-TS< △T, in which △T is the maximum time threshold of accepting messages and Time is the current time received message. This check presupposes that the client and server maintain reasonably synchronized clocks, with any potential clock drift accommodated within the threshold △T. If it is true, Sj performs the next steps:

1) Computes W=H3(U,C,IDr,PKIDr)

2) Computes f=H4(U,C,IDr,PKIDr)

3) Checks if e(P,V)=e(U,W)e(Ppub,QIDs)f holds. If yes, proceed to step 4. Otherwise, Sj rejects the authentication message and outputs an error symbol ⊥

4) Computes T=e(U,DIDr)

5) Computes h=H2(U,T,IDr,xIDrU)

6) Recovers the temporary session key k, computes (k||TS||IDs||DL)=C⊕h. Then, the server Sj computes QIDs′=H1(IDs||DL). Then, Sj verifies the expiration date DL and consults its cached RL. If the DL is expired or QIDs′ is found on the RL, Sj must reject the authentication message and return an error symbol ⊥.

At this point, Ci and Sj have successfully established a temporary session key k. This HUAKE protocol also supports key confirmation property in which Sj continues to compute tag=MACk(TS) and sends it to Ci. When receiving the tag from Sj, Ci computes tag′=MACk(TS), then verifies whether tag′=tag holds. If it holds, Ci confirms that Sj has correctly recovered the temporary session key k. Otherwise, Ci rejects the temporary session key and stops. This process is summarized in Fig. 2.

Figure 2: User authentication and key establishment process

We commonly use two methods to establish a temporary session key. The first method is Differ-Hellman key exchange protocol where both Ci and Sj determine the temporary session key together. The second one is key transport protocol which permits Ci in selecting a session key to pass it to Sj. Although our protocol is the second one, but it can also be modified to the first way, which only requires Sj to select another temporary session key k′∈(0,1)l1 and computes tag=MACk⊕k′(TS), then, sends (tag,k′) to Ci. Ci continues to compute tag′=MACk⊕k′(TS), then Verifies whether tag′=tag holds. If it holds, the temporary session key is k⊕k′. Otherwise, Ci rejects this temporary session key and returns an error symbol ⊥. The default key transport mode offers maximum efficiency with 1.5 communication rounds, making it ideal for latency-sensitive applications. The optional key exchange modification ensures the session key is derived from the mutual contributions of both parties, which enhances the key’s collaborative generation.

5.4 Revocation Mechanism

Real-time certificate queries, such as the online certificate status protocol (OCSP), add a synchronous network round-trip to each authentication, which degrades the performance of lightweight protocols. To implement a near-real-time key revocation mechanism, the RC maintains a dynamically updated Revocation List (RL), which is digitally signed with its master key. This list records all client credentials that have been confirmed as compromised or are otherwise invalidated.

To avoid imposing a burden on resource-constrained clients, the responsibility for fetching and verifying revocation status is entirely shifted to the more powerful server. The server actively and asynchronously polls the RC at a configurable, fixed interval (e.g., every few minutes, depending on the specific application scenario) to fetch the latest signed RL and caches it locally. When processing a client’s authentication request, the server first validates the client’s signature. Following successful signature validation, the server proceeds to decrypt the authentication message, recovering the session key k, the client’s identity IDs, and the expiration date DL. It is only after this recovery step that the mandatory “hard-fail” security check is performed. The server uses the recovered IDs and DL to compute the specific credential identifier (QIDs′), which is then checked against the local RL cache. If the credential is found on the revocation list, the server must discard the recovered session key k and abort the protocol, even though the digital signature was initially valid. Once the RC updates the RL, the server learns of the change within the next polling cycle. This allows the system to block the use of a compromised key within a short time window determined by the polling period, thereby achieving near-real-time revocation capability.

While this mechanism introduces additional communication overhead, this cost is primarily borne by the server for its periodic communication with the RC and does not add latency to the client authentication handshake. This trade-off is deemed acceptable, as the server typically possesses a more stable network connection and greater processing power.

6  Analysis of the Protocol

6.1 Correctness

We know PKIDr=xIDrP,DIDr=sQIDr, we have T=e(U,DIDr), =e(rP,sQIDr), =e(Ppub,QIDr)r. Also on account of U=rP,V=rW+fSIDs,SIDs=sQIDs, so we have e(U,W)e(Ppub,QIDs)f=e(U,W)e(P,sQIDs)f=e(P,rW)e(P,fSIDs)=e(P,rW+fSIDs)=e(P,V).

6.2 Security

The security proof of our HUAKE protocol follows the standard methodology for signcryption schemes, which primarily involves proving confidentiality and unforgeability. However, since our protocol is designed for authenticated key establishment, we have adapted the proof logic from the standard model to fit the context of a key agreement protocol. We use i and j (e.g., IDi, IDj) to represent any participant in the system. These indices correspond to the client the server roles described in Section 5. The security analysis of our protocol is as follows. The following lemmas formalize the security guarantees.

Lemma 1: There exists a begin adversary on ∏i,jn and ∏j,in, the two oracles always reach agreement over the common session key as if there was no adversary. In addition, this key is uniformly distributed.

This Lemma aims ensuring that in the absence of an active adversary, both parties will always agree on the same, uniformly random session key.

Proof of Lemma 1: In this HUAKE protocol, suppose that two participants Ci and Sj follow the protocol and 𝒜 is benign. According to the above correctness analysis in Section 6.1, it can be concluded that two participants may establish a shared temporary session key. It is uniformly distributed over {0,1}l1, because r is a random value and hash functions h,W,f are also random. □

Lemma 2: If there exists a PPT adversary 𝒜ℐ having advantage ς to succeed the security of the HUAKE protocol under the mBR model at time t with qμ IB-KE queries, qpke PKE queries, qppk PPK queries, qc Corrupt queries, qpkr PKR queries, qs Send queries, and qHi(i=1,2,3,4) hash queries, then there exists an algorithm 𝒞 that can resolve the GBDH problem with a non-negligible advantage ς′≥ςqH1(1−qs(qs+qH3)2μ) in a time t′≤t+O(qs)tp, where μ is a security parameter and tp represents the cost of a pairing operation.

This Lemma establishes the confidentiality of the session key k. It demonstrates that no adversary can break the confidentiality of the ciphertext without solving the GBDH problem.

Proof of Lemma 2: In this proof, we demonstrate how 𝒞 utilizes 𝒜ℐ as a subroutine to resolve a random example (P,xP,yP,zP) of the GBDH problem in the following content.

Initial: 𝒞 runs the System Initialization algorithm to generate the master public key Ppub=xP, where the corresponding private key x is unknown to 𝒞. The specific process is as follows:

In this game, 𝒞 maintains lists L1, L2, L3 and L4 to save hash queries. Furthermore, 𝒞 also keeps an empty list Lk to store public key. We assume that H1 query is different from other hash queries, 𝒜ℐ will do H1(ID) query before using ID. Through the irreflexive assumption, we assume that the sender and receiver identities are different. 𝒞 randomly selects ξ∈{1,2,…,qH1} to answer the queries of 𝒜ℐ.

H1 queries: 𝒜ℐ sends an identity to 𝒞. For the ξ-th query, 𝒞 computes H1(IDξ)=yP to answer this query, and inserts the tuple (IDξ,⊥) into L1. For the i-th query (i≠ξ), 𝒞 picks di∈Zp∗ at random and sends H1(IDi)=diP to 𝒜ℐ, then, inserts the tuple (IDi,di) into the list L1.

H2 queries: 𝒞 executes the below procedure: If (xP,yP,zP,Tj)=⊤, 𝒞 returns Tj and stops; if the list L2 includes a tuple (Uj,∗,IDj,R,hj) that makes DBDH(xP,yP,Uj,Tj)=⊤, 𝒞 sends hj and renews the notation ∗ to Tj. At this point, IDj=IDξ; if 𝒞 reaches this point of execution, it selects a random value, then sends it to 𝒜ℐ. After this, the random value must be saved in L2 by 𝒞. H3 queries: When 𝒜ℐ initiates a H3 query, 𝒞 first checks whether (Uj,Cj,IDj,PKIDj,tj,tjP) exists in the list L3. If it exists, 𝒞 gives tjP to 𝒜ℐ. Otherwise, 𝒞 selects t∈Zp∗ ati random, inserts the tuple (Uj,Cj,IDj,PKIDj,t,tP) into the list L3, then gives tP to 𝒜ℐ.

H4 queries: 𝒞 first checks whether the tuple (Uj,Cj,IDj,PKIDj,fj) exists in the list L4. If it exists, 𝒞 sends fj to 𝒜ℐ. Otherwise, 𝒞 selects f∈Zp∗ at random, inserts the tuple (Uj,Cj,IDj,PKIDj,f) into the list L4 and returns f to 𝒜ℐ.

IB-KE(IDi): 𝒞 fails and stops if IDi=IDξ. Otherwise, 𝒞 invokes H1 oracle for acquiring the tuple (IDi,di) and sends private key SIDi=dixP to 𝒜ℐ.

Create(IDj): 𝒞 maintains an empyt list Lc. when receiving IDj from 𝒜ℐ, 𝒞 will fail if IDj=IDξ. Otherwise, 𝒞 runs H1 oracle to get (IDj,dj), then 𝒞 randomly selects xIDj∈Zp∗ and computes PKIDj=xIDjP. Then, 𝒞 inserts (IDj,PKIDj,xIDj) and (IDj,PKIDj,xIDj,djxP) into Lk and Lc.

PKE(IDj): 𝒞 finds the tuple indexed by IDj in the list Lk, and returns PKIDj to 𝒜ℐ.

PPKE(IDj) queries: 𝒞 first checks if IDj=IDξ. If yes, 𝒞 will fail. Otherwise, 𝒞 invokes H1 oracle for acquiring the tuple (IDj,dj), then sends DIDj=djxP to 𝒜ℐ.

Corrupt(IDj): 𝒞 first checks if IDj=IDξ. If yes, 𝒞 will fail. Otherwise, 𝒞 looks for a tuple indexed by IDj in the list Lc, and returns (xIDj,djxP) to 𝒜ℐ.

PKR(IDj): 𝒜ℐ can replace the public key PKIDj with a random value PKIDj′ that it chooses. For a PKR query, 𝒞 should replace the corresponding tuple (IDj,PKIDj) in the list Lk with (IDj,PKIDj,⊥), where ⊥ indicates an unknown secret value.

Send(∏i,jn,M): We define ∏S,jn denotes the n-th session between a sender S and a receiver j, ∏R,in denotes the n-th session between a receiver R and a sender i. 𝒞 maintains a list Ls to store internal state information.

An oracle can be in one of several states: Accepted: Oracle accepts a session key after receiving the appropriate messages. Rejected: In the absence of a session key, an oracle will reject this protocol run and abort it. ∗: This oracle is in state ∗ if it has not decided whether to accept or reject. Opened: The state is opened if an oracle replies to a reveal query and Corrupted: The state is corrupted if an oracle replies to a corrupt query. To complete this simulation process, there are three cases that need to be considered.

(1) When ∏i,jn=∏S,jn, M = begin, IDi=IDξ, 𝒞 selects u,v∈Zp∗ at random, defines U=vxP, T=e(U,DIDj), V=uxP and H3(U,C,IDj,PKIDj) as v−1(uP−fjQIDj). 𝒞 fails if H3 is already defined but this situation only occurs with probability (qs+qH3)/2μ. 𝒞 runs H2 oracle to obtain the value of h and computes C=(k||TS||IDi||DL⊕h). Finally, 𝒞 transmits this authentication message δ=(U,C,V) to 𝒜ℐ and inserts the tuple (n,S,j,k||TS||IDi||DL,δ,∗) into the list Ls.

(2) When ∏i,jn=∏R,in, M=δ, IDj≠IDξ, 𝒞 runs Corrupt(IDj) oracle to acquire the partial private key DIDj of the receiver and calculations T=e(U,DIDj). Then 𝒞 invokes H2 oracle for acquiring the value of h and computes (k||IDi||TS||DL)=C⊕h. At this time, 𝒞 marks the state of ∏R,in as Accepted, then inserts the tuple (n,R,i,k||IDi||TS||DL,δ,Accept) into the list Ls. Finally, 𝒞 returns tag=MACk(TS) to 𝒜ℐ. If 𝒞 outputs an error symbol ⊥, the status of ∏R,in is marked as Rejected and the tuple (n,R,i,δ,Rejected) is inserted into the list Ls by 𝒞. 𝒞 returns Rejected to 𝒜ℐ.

(3) When ∏i,jn=∏R,in, M=δ, IDj=IDξ, 𝒞 is unable to acquire the partial private key DIDj of the receiver, in which situation T fails to be calculated. In order to reply with a consensus response, 𝒞 queries the tuple (U,T,IDj,h) in the list L2, for different values of T such that DBDH(xP,yP,U,T)=⊤. If the tuple exists in the list L2, which implies that we have found the correct T. 𝒞 continues to compute (k||TS||IDi||DL)=C⊕h. Note that, if there is no tuple (U,T,IDj,h) in the list L2 for different values of T such that DBDH(xP,yP,U,T)=⊤. 𝒞 places the tuple (U,∗,IDj,PKIDj,h) for a random h in the list L2 and computes (k||TS||IDi||DL)=C⊕h. The notation ∗ represents an unclear value of T. At this point, the constant component of all entries with the symbol ∗ is IDξ. After completing this calculation, 𝒞 marks the state of ∏R,in as Accepted and inserts the tuple (n,R,i,(k||TS||IDi||DL,δ,Accepted) into the list Ls, then returns tag=MACk(TS) to 𝒜ℐ. If 𝒞 outputs a error symbol ⊥, which indicates this session is Rejected. 𝒞 gives Rejected to 𝒜ℐ and adds the tuple (n,R,i,⊥,δ,Rejected) into the list Ls.

Reveal(∏i,jn): 𝒞 starts by examining if the tuple (n,i,j) exists in the list Ls. Since a Reveal inquiry can only be initiated when the session state is signs Accept, which means that L2 must include a tuple (n,i,j). Otherwise, this query is invalid. 𝒞 gives this session key to 𝒜ℐ, then renews the tuple (n,i,j,k||TS||IDi||DL,δ,Accepted) into (n,i,j,k||TS||IDi||DL,δ,Opened). Before Test query, 𝒞 examines whether a tuple (n,S,R,n,i,j,k||TS||IDi||DL,δ,Accepted) such that no tuple contains (n,S,R) exists in the list Ls. If yes, 𝒞 can output a forged authentication message δ∗=(U∗,V∗,C∗). To generate δ∗, 𝒞 randomly selects a hash value h∗, defines U∗=cP, C∗=(k∗||TS||IDi||DL)⊕h∗,V∗=tcP+fSIDs.

Test(∏i,jn): At this stage, if ∏i,jn≠∏S,Rn, 𝒞 stops. Otherwise, 𝒞 outputs the real session key if b=0. If b=1, 𝒞 picks g∈{0,1}l1 at random as well as outputs it.

The success of this simulation is contingent on the challenger 𝒞 correctly guessing the target identity IDξ at the start of the game, an event which occurs with a probability of at most 1/qH1 since the list L1 contains at most qH1 elements. As described in the simulation of the IB-KE query, the game aborts if the adversary requests the private key for this specific identity. This is precisely why the simulation’s success probability is bounded, linking this potential failure condition directly to the 1/qH1 factor in our final advantage calculation. Assuming this event occurs (i.e., the guess is correct and the simulation does not abort), the simulation is perfect unless 𝒜I performs an H2 query on the challenge-related tuple (U∗,T∗,IDξ). 𝒜I will have no advantage if this tuple is absent from L2, since the hash function H2 is modeled as a random oracle. However, if this event occurs, 𝒞 will resolve the GBDH problem because of the first step in the simulation of H2. 𝒞 can make at most qH22+qH2qs DBDH queries in the whole process. □

Lemma 3: If there exists a PPT adversary 𝒜ℐ having advantage ς to succeed the security of the HUAKE protocol under the mBR model at time t with qμ IB-KE queries, qpke PKE queries, qppk PPK queries, qc Corrupt queries, qpkr PKR queries, qs Send queries, and qHi(i=1,2,3,4) hash queries, then there exists an algorithm 𝒞 that can resolve the GDH problem with a non-negligible advantage ς′≥ςqH1(1−qs(qs+qH3)2μ) in a time t′≤t+O(qs)tp, where μ is a security parameter and tp denotes the cost of one pairing operation.

This lemma establishes the unforgeability of the protocol message against a Type I adversary. It proves that no Type I adversary can forge a valid authentication message without solving the GDH problem, thus ensuring message integrity and authenticity.

Proof of Lemma 3: Initial: 𝒞 executes the System Initialization algorithm with a security parameter μ as input to generate the system parameters that contain a master public key Ppub=xP. Note that x emulates the master private key of RC, and it is unknown for 𝒞.

𝒞 performs the same procedure as in Lemma 2 to answer the queries of 𝒜ℐ, except for H2.

H2 queries: 𝒞 starts by checking whether the tuple (Uj,Tj,IDj,Rj,hj) exists in the list L2. If yes, 𝒞 gives hj to 𝒜ℐ. If it does not exist in the list L2, 𝒞 randomly selects h∈{0,1}l1+l2+l3+l4 and returns it to 𝒜ℐ, then inserts the tuple (Uj,Tj,IDj,Rj,h) into the list L2.

𝒜ℐ exports a forged authentication message δ∗=(U∗,V∗,C∗), a sender’s identity IDs, a receiver’s identity IDr. 𝒞 examines whether IDs = IDξ. If not, 𝒞 stops. Otherwise, 𝒞 obtains t and f by inquiring L3 and L4, respectively. If 𝒜ℐ wins the game, the authentication message δ∗ must be valid, which means that we can compute e(P,V∗)=e(U∗,tP)e(Ppub,QIDs)f=e(U∗,tP)e(xP,yP)f. Therefore, 𝒞 can compute xyP=f−1(V∗−tU∗). At this time, IDs=IDξ, QIDs=yP.

The probability of an adversary guessing correctly by a non-negligible advantage is related to the following events. 1) E1: 𝒜ℐ does not select identity IDξ. 2) E2: 𝒜ℐ has performed a Corrupt query on IDξ. 3) E3: 𝒜ℐ has performed a IB-KE query at some stage. 4) E4: 𝒞 stops in a send query due to a collision on H3.

Clearly, Pr[⌝E] = 1/qH1 and Pr[E4] ≤qs(qs+qH3)/2k. Furthermore, we know that ⌝E1 means ⌝E2 and ⌝E3. So, we have ς′≥ςqH1(1−qs(qs+qH3)2μ). □

Lemma 4: If there exists a PPT adversary 𝒜ℐℐ having advantage ς to succeed the security of the HUAKE protocol under the mBR model at time t with qc Corrupt queries, qpke PKE queries, qs Send queries and qHi(i=1,2,3,4) hash queries, then there exists an algorithm 𝒞 that can resolve the CDH problem with a non-negligible advantage ς′≥ςqc+qpke+qs+1(1−qs(qs+qH3)2μ) in a time t′≤t+O(qs)tp, where μ is a security parameter and tp denotes the cost of one pairing operation.

Proof of Lemma 4: Initial: 𝒞 executes the System Initialization algorithm with a security parameter μ as input to generate the system parameters that contain a master public key Ppub=sP. In this game, s is randomly chosen by 𝒞 which emulates the master private key of RC.

This lemma completes the unforgeability proof by addressing the Type II adversary. It demonstrates that even a malicious KGC cannot forge a valid message without solving the CDH problem, thus securing the protocol against insider threats.

In this game, 𝒞 randomly selects ξ∈{1,2,…,qc+qpke+qs+1} to answer the queries of 𝒜ℐℐ. 𝒞 performs the same procedure as in Lemma 2 to answer the queries of 𝒜ℐℐ, but except for the following queries:

H1 queries: 𝒞 starts by checking whether the tuple (IDi,ei) exists in the list L1. If yes, 𝒞 returns eiP to 𝒜ℐℐ. If the tuple does not exist in the list L1, 𝒞 randomly selects e∈Zp∗ and returns eP to 𝒜ℐℐ, then inserts the tuple (IDi,e) into the list L1.

H3 queries: 𝒞 starts by checking whether the tuple (Uj,Cj,IDj,PKIDj,tj,tjyP) exists in list L3. If yes, 𝒞 returns tjyP to 𝒜ℐℐ. If the tuple does not exist in list L3, 𝒞 randomly selects t∈Zp∗ and returns tyP to 𝒜ℐℐ, then inserts the tuple (Uj,Tj,IDj,PKIDj,t,tyP) into the list L3.

Create(IDj) queries: 𝒞 maintains a list Lc with an empty initial value. After receiving an identity IDj from 𝒜ℐℐ, 𝒞 fails if IDj=IDξ. Otherwise, 𝒞 runs the H1 oracle to obtain the tuple (IDj,dj), then 𝒞 randomly selects xIDj∈Zp∗ and computes PKIDj=xIDjP. Then, 𝒞 inserts the two tuples (IDj,PKIDj,xIDj) and (IDj,PKIDj,xIDj,djsP) into the list Lk and Lc, respectively.

PKE(IDj): 𝒞 looks for PKIDj indexed by IDj in the list Lk, then gives it to 𝒜ℐℐ.

Corrupt(IDj): 𝒞 starts by examining if IDj=IDξ. If yes, 𝒞 fails. Otherwise, 𝒞 looks for a tuple indexed by IDj in the list Lc, and returns (xIDj,djsP) to 𝒜ℐℐ.

𝒜ℐℐ exports a forged authentication message δ∗=(U∗,V∗,C∗), a sender’s identity IDs, a receiver’s identity IDr. At this point, let U∗=xP, 𝒞 examines whether IDs = IDξ. If not, 𝒞 stops. Else, 𝒞 obtains t and y from the list L3 and L4, respectively. If 𝒜ℐℐ wins the game, the authentication message δ∗ must be valid, which means that we can compute e(P,V∗)=e(U∗,tyP)e(Ppub,QIDs)f=e(U∗,tyP)e(sP,QIDs)f. Therefore, 𝒞 can compute xyP=t−1(V∗−fsQIDs).

The probability of an adversary guessing correctly by a non-negligible advantage is related to the following events. 1) E1: 𝒜ℐℐ does not select identity IDξ. 2) E2: 𝒜ℐℐ has performed a Corrupt query on IDξ. 3) E3: 𝒞 stops in a send query due to a collision on H3.

It is obvious that Pr[⌝E] = 1/(qc+qpke+qs+1) and Pr[E3] ≤qs(qs+qH3)/2μ. Furthermore, we know that ⌝E1 means ⌝E2, the maximum of the list Lk is (qc+qpke+qs+1), So, we have ς′≥ςqc+qpke+qs+1(1−qs(qs+qH3)2μ). □

6.3 Informal Security Analysis

The security requirements met by the HUAKE protocol are as follows.

•   Forgery Attack: This type of attack means that an adversary can masquerade as a legitimate server. If the adversary is 𝒜ℐ, it can perform a public key replacement attack but cannot obtain the master private key s. To obtain a full private key of Sj, 𝒜ℐ needs to obtain s from Ppub=sP. However, if it is able to obtain s that means the CDH hard problem is solvable, which is not correspond to the fact. If the adversary is 𝒜ℐℐ, it can obtain the master private key of RC but fails to execute a public key replacement attack. To obtain a full private key of Sj, 𝒜ℐℐ needs to obtain xIDr from PKIDr. We known the public key PKIDr=xIDrP, 𝒜ℐℐ cannot obtain xIDr because the CDH hard problem is intractable.

•   Replay Attack: Our protocol can resist replay attacks by taking a timestamp. When Sj receives the authentication message (U,C,V,TS) from Ci, it first checks the validation of TS by Time−TS<△T, in which △T is the maximum time threshold of accepting messages and Time is the current time received message. In other words, if an adversary performs a replay attack using the previous authentication information, the timestamp TS will not be verified successfully.

•   Key Compromise Impersonation Attack: We consider a scenario where an adversary compromises the client’s long-term private key SIDs and then attempts to impersonate the server Sj to that same client. The attack proceeds as follows: the client Ci initiates a session by sending the message (U,C,V,TS) to the adversary (believing it is the server). To successfully impersonate the server, the adversary must respond with a valid confirmation tag, which is computed as MACk(TS). To generate this tag, the adversary must first know the session key k. According to our protocol, the session key k is encrypted within C and can only be decrypted by the legitimate server Sj using its own long-term secrets (the partial private key DIDr and the secret value xIDr). Therefore, possession of SIDs provides no advantage to the adversary in deriving the server’s secrets or the session key k. Unable to compute the correct k, the adversary cannot forge a valid tag. The client Ci will reject the session upon failing to verify the tag, thus thwarting the KCI attack.

•   Session Key Security: The attacker wants to recover session keys from the information exchanged on public data and communication channels. In this paper, the session key k is a random value chosen by Ci and it is also encrypted for transmission. Therefore, there is no possibility for an adversary to retrieve k from the public information.

It is important to note that the HUAKE protocol, in its current form as a key transport scheme, does not provide forward secrecy. A compromise of the server’s long-term keys would allow an adversary to decrypt previously captured sessions.

7  Performance

In this section, we evaluate the performance of our proposed HUAKE protocol against five existing protocols: HA [18], TL [22], RS [23], DMR [25], and MA [26]. The evaluation focuses on computational and communication overheads. Table 2 summarizes the theoretical cryptographic operations for each scheme. The notation PC signifies a bilinear pairing operation, PM denotes a point multiplication operation on G1, EC represents an exponential operation on G2, and |x| indicates the bit length of x. Cheaper operations like XOR and point addition are omitted for clarity. Operations marked with () can benefit from pre-computation using known public information. For a fair comparison, a deadline DL has been incorporated into the communication overhead of the compared protocols. It should be noted that the ∣k∣ in our communication overhead formula accounts for the size of the key confirmation tag sent from the server back to the client.

7.1 Computational Overhead

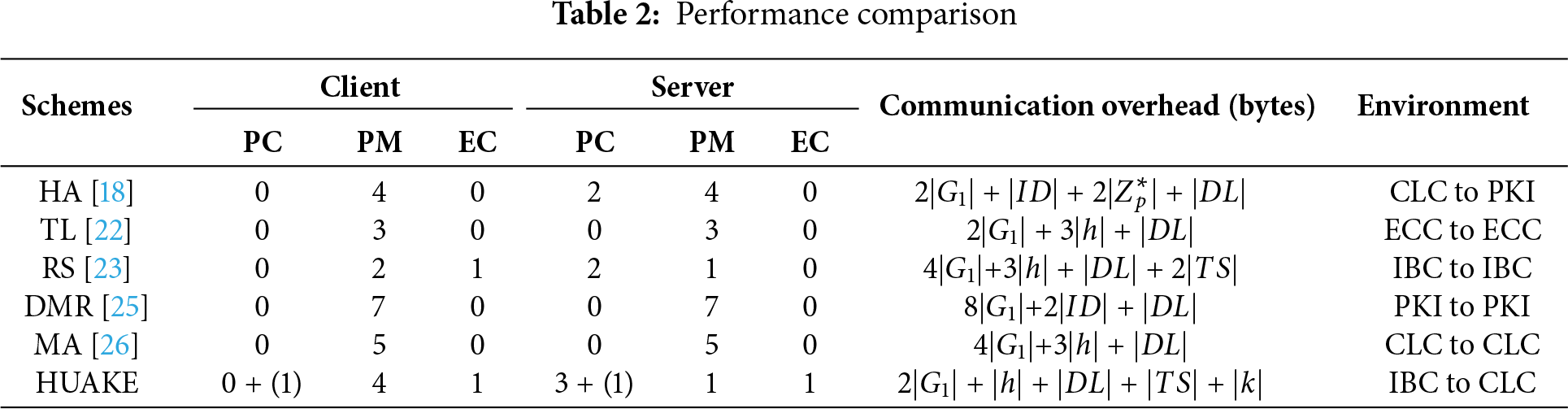
To empirically assess the computational overhead, we utilized the JPBC library, which is a widely adopted standard for prototyping and benchmarking pairing-based protocols. We selected Type A pairings for our tests due to their noted computational efficiency, making them a suitable choice for evaluating performance in resource-aware environments. The pairing is built on the elliptic curve y2≡(x3+x)(modq) where q is a prime (q≡3(mod4)), the embedding degree is two, and p is the order of G1 [32]. Three security levels were adopted, namely 80-bit security with a 512-bit q and a 160-bit p, 112-bit security with a 1024-bit q and a 224-bit p, and 128-bit security with a 1536-bit q and a 256-bit p. The client-side experiments were conducted on a Xiaomi 10 smartphone (CPU Snapdragon 865, 2.84 GHz, 8 GB RAM, Android 12.0), while the server-side experiments were performed on an HP computer (Intel Core i7-7700HQ, 2.80 GHz, 8 GB RAM). The experiments were implemented using the JPBC library (version 2.0.0) running on an OpenJDK 17.0.7 Java development environment. All tests were executed with the default Java Virtual Machine (JVM) runtime parameters. To ensure the fairness and accuracy of the results while minimizing the impact of random errors, especially given that the computation times are sensitive at the millisecond level, each performance test in this study was independently repeated 500 times. All computational times presented in the final figures are the average values of these 500 measurements.

Client-side computational overhead is detailed in Fig. 3. While our protocol’s client-side computation is slightly higher than the lightweight homogeneous schemes TL [22] and RS [23], it remains highly competitive and often superior to other schemes like DMR [25]. More importantly, this moderate computational cost at the client facilitates a crucial advantage: our protocol’s heterogeneous architecture. This allows resource-constrained clients operating in an IBC environment to securely interact with servers in a CLC environment, a flexibility not offered by the purely homogeneous schemes. The slight increase in client-side operations is a well-justified trade-off for this enhanced interoperability and practicality in diverse real-world scenarios.

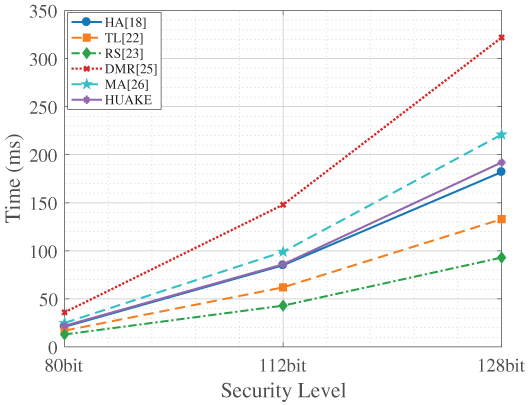
Figure 3: Computational time of the client for each scheme [18,22, 23,25,26]

Fig. 4 illustrates the server-side computational overhead. Here, our protocol demonstrates a distinct and significant advantage. Across all tested security levels, Ours consistently exhibits the lowest computational time on the server. This superior server-side efficiency becomes even more pronounced at higher security levels. While server resources are generally more abundant, this notable efficiency contributes to reduced operational costs and better scalability for service providers.

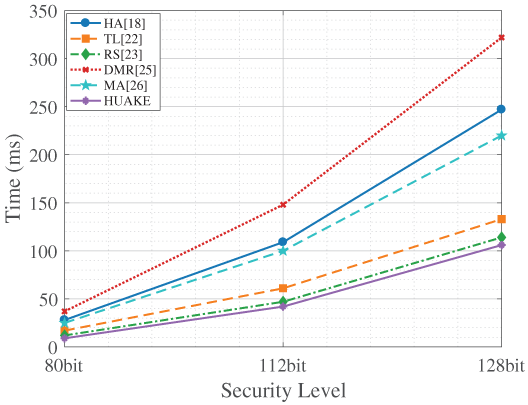
Figure 4: Computational time of the server for each scheme [18,22, 23,25,26]

When considering the total computational overhead (client + server), as shown in Fig. 5, our protocol achieves an excellent balance. Ours is demonstrably more efficient in total computation time than HA [18], DMR [25], and MA [26] across all security levels. While the total time for TL [22] and RS [23] can be marginally lower in some instances, these schemes do not offer the heterogeneous environment support that is a core strength of our protocol.

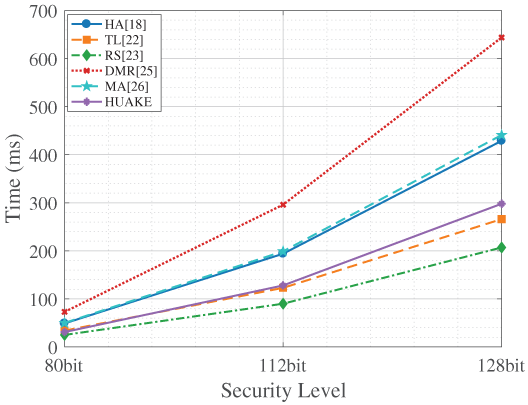
Figure 5: Total computational time for each scheme [18,22,23,25,26]

7.2 Communication Overhead

The efficiency of data transmission is paramount, especially for resource-constrained devices. We analyzed the communication overhead of all six protocols, with the following parameters. |ID|=160 bits, |TS|=32 bits, |DL|=112 bits. An element in G1 is compressed to 65 bytes [33]. Hash output sizes (|h|) are 160-, 224-, and 256-bit for the respective security levels. For our protocol, a symmetric key or nonce |k| is 80 bits. The detailed byte values for each scheme at 80-, 112-, and 128-bit security levels are visually presented in Figs. 6–8, respectively. The communication overhead analysis in this paper considers only the size of the cryptographic payload transmitted at the application layer and does not include the overhead from lower-level network protocol headers (e.g., TCP/IP).

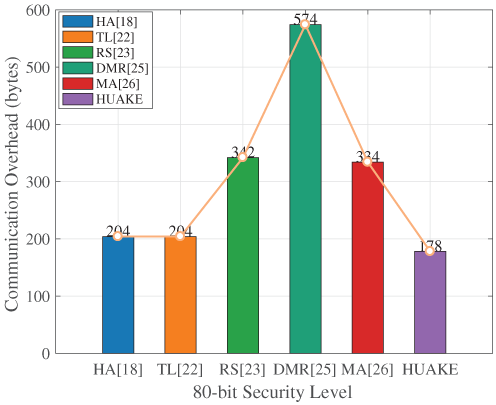
Figure 6: Total communication over head with 80-bit security [18,22,23,25,26]

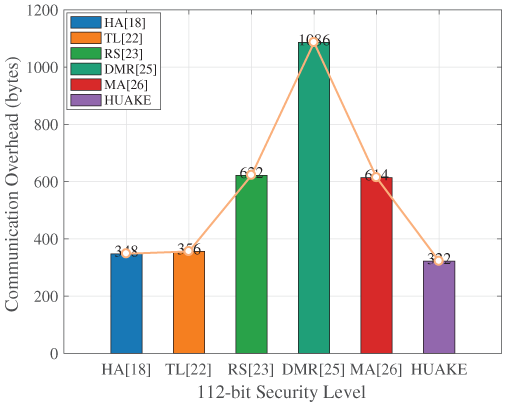
Figure 7: Total communication over head with 112-bit security [18,22,23,25,26]

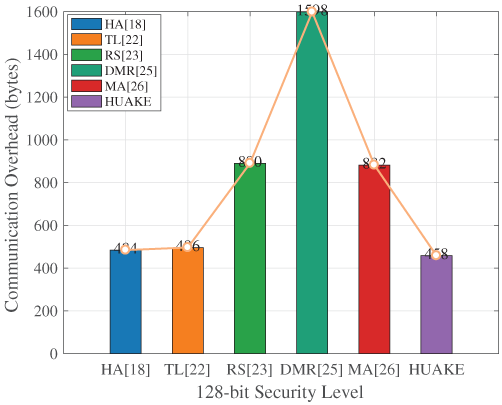
Figure 8: Total communication overhead with 128-bit security [18,22,23,25,26]

A consistent and striking observation from Figs. 6–8 is that our protocol unequivocally achieves the lowest communication overhead across all evaluated security levels. This superior performance is not marginal but represents a substantial improvement over the compared schemes.

For instance, at the 80-bit security level in Fig. 6, our protocol’s communication cost is significantly lower than all other protocols. Even compared to HA [18] and TL [22], which are relatively efficient, our scheme offers a notable reduction. The advantage becomes even more pronounced when compared to RS [23], MA [26], and particularly DMR [25]. This trend of superior communication efficiency continues and is often amplified at higher security settings. As seen in Figs. 7 and 8, while the absolute communication costs increase for all protocols to ensure stronger security, our protocol maintains its leading position with the smallest data transmission size. The percentage reduction in communication overhead offered by our protocol is substantial, as detailed in Table 3. Our scheme consistently cuts down data transfer by a significant margin compared to HA [18], TL [22], RS [23], MA [26], and especially DMR [25], with advantages often exceeding 45% against several protocols and reaching over 70% against DMR [25].

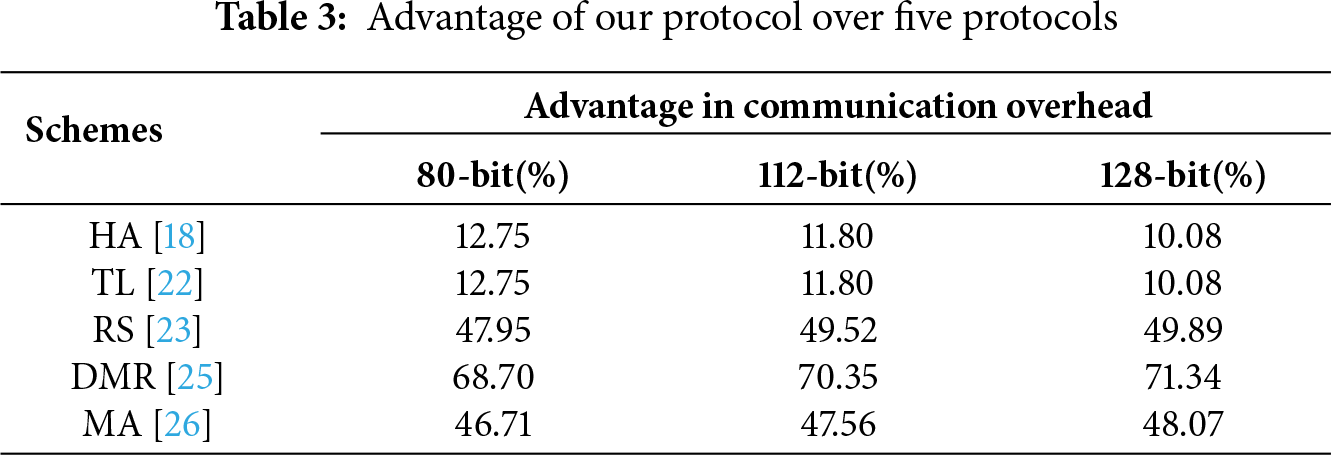
This pronounced efficiency in communication overhead is a key advantage of our protocol. By minimizing the amount of data exchanged, Our scheme significantly reduces bandwidth consumption, latency, and energy usage on client devices. This makes our protocol exceptionally well-suited for deployment in bandwidth-sensitive and power-constrained environments, such as mobile networks, IoT ecosystems, and other scenarios where efficient communication is critical. The empirical data strongly supports the theoretical communication cost analysis presented in Table 2, confirming our protocol’s design for optimal communication performance.

7.3 Discussion on Practical Application Scenarios

While its client-side computational overhead is not the lowest, this protocol’s extremely low communication overhead makes it a superior choice in environments where communication is the dominant cost, such as battery-reliant IoT devices on low-power wide-area networks (LPWAN) or implantable wearable medical devices (WBANs). In these scenarios, minimizing data transmission is critical for extending multi-year battery life, rendering the brief, one-time computational cost for authentication a well-justified trade-off for device longevity.

8  Conclusion

We designed an efficient and secure HUAKE protocol using signcryption for heterogeneous MCS communication. In this protocol, the client belongs to the IBC and the server belongs to the CLC, which is quite applicable to heterogeneous networks. In addition, we proved the security of the proposed HUAKE protocol in the mBR model and described its resilience against other attacks using heuristic analysis. Our performance evaluation indicates that the protocol achieves the least communication overhead compared to the associated protocols. While the protocol excels in communication efficiency, its computational overhead is not optimal, and it does not provide forward secrecy. Future work will focus on achieving forward secrecy by incorporating a key exchange mechanism, while simultaneously optimizing the new construction to reduce computational overhead.

Acknowledgement: Not applicable.

Funding Statement: This work was supported by the Key Project of Science and Technology Research by Chongqing Education Commission under Grant KJZD-K202400610 and the Chongqing Natural Science Foundation General Project Grant CSTB2025NSCQ-GPX1263.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Huihui Zhu and Fei Tang; methodology, Fei Tang; validation, Ping Wang; formal analysis, Huihui Zhu; investigation, Ping Wang; resources, Fei Tang; writing—original draft preparation, Huihui Zhu; writing—review and editing, Huihui Zhu and Chunhua Jin; funding acquisition, Fei Tang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable. For studies not involving humans or animals.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ali S, Alauldeen R, Ruaa A. What is client-server system: architecture, issues and challenge of client-server system. Recent Trends Cloud Comput Web Eng. 2020;2(1):1–6. [Google Scholar]

2. Yousefi S, Karimipour H, Derakhshan F. Data aggregation mechanisms on the internet of things: a systematic literature review. Internet Things. 2021;15:100427. doi:10.1016/j.iot.2021.100427. [Google Scholar] [CrossRef]

3. Preethichandra D, Piyathilaka L, Izhar U, Samarasinghe R, De Silva LC. Wireless body area networks and their applications—a review. IEEE Access. 2023;11:9202–20. doi:10.1109/access.2023.3239008. [Google Scholar] [CrossRef]

4. Conti M, Donadel D, Turrin F. A survey on industrial control system testbeds and datasets for security research. IEEE Communicat Surv Tutorials. 2021;23(4):2248–94. doi:10.1109/COMST.2021.3094360. [Google Scholar] [CrossRef]

5. Thankappan M, Rifà-Pous H, Garrigues C. Multi-Channel Man-in-the-Middle attacks against protected Wi-Fi networks: a state of the art review. Expert Syst Appl. 2022;210:118401. doi:10.1016/j.eswa.2022.118401. [Google Scholar] [CrossRef]

6. Aski VJ, Dhaka VS, Parashar A, kumar S, Rida I. Internet of Things in healthcare: a survey on protocol standards, enabling technologies, WBAN architectures and open issues. Phys Commun. 2023;60:102103. doi:10.1016/j.phycom.2023.102103. [Google Scholar] [CrossRef]

7. Blake-Wilson S, Johnson D, Menezes A. Key agreement protocols and their security analysis. In: IMA international conference on cryptography and coding; Berlin/Heidelberg, Germany: Springer; 1997. p. 30–45. [Google Scholar]

8. Koblitz N, Menezes A, Vanstone S. The state of elliptic curve cryptography. Des Codes Cryptogr. 2000;19:173–93. doi:10.1023/a:1008354106356. [Google Scholar] [CrossRef]

9. Maurer U. Modelling a public-key infrastructure. In: Computer Security—ESORICS 96: 4th European Symposium on Research in Computer Security; Sep 25–27; Rome, Italy. Berlin/Heidelberg, Germany: Springer; 1996. p. 325–50. [Google Scholar]

10. Shamir A. Identity-based cryptosystems and signature schemes. In: Workshop on the theory and application of cryptographic techniques. Berlin/Heidelberg, Germany: Springer; 1984. p. 47–53 doi: 10.1007/3-540-39568-7_5. [Google Scholar] [CrossRef]

11. Girault M. Self-certified public keys. In: Workshop on the theory and application of of cryptographic techniques. Berlin/Heidelberg, Germany: Springer; 1991. p. 490–7. [Google Scholar]

12. Braeken A. Public key versus symmetric key cryptography in client-server authentication protocols. Int J Inf Secur. 2022;21(1):103–14. doi:10.1007/s10207-021-00543-w. [Google Scholar] [CrossRef]

13. Alrawais A, Alhothaily A, Cheng X, Hu C, Yu J. SecureGuard: a certificate validation system in public key infrastructure. IEEE Trans Veh Technol. 2018;67(6):5399–408. doi:10.1109/tvt.2018.2805700. [Google Scholar] [CrossRef]

14. Wang D, Ma Cg. Cryptanalysis of a remote user authentication scheme for mobile client-server environment based on ECC. Inf Fusion. 2013;14(4):498–503. doi:10.1016/j.inffus.2012.12.002. [Google Scholar] [CrossRef]

15. Hsieh WB, Leu JS. An anonymous mobile user authentication protocol using self-certified public keys based on multi-server architectures. J Supercomput. 2014;70(1):133–48. doi:10.1007/s11227-014-1135-8. [Google Scholar] [CrossRef]

16. Dey S, Sampalli S, Ye Q. MDA: message digest-based authentication for mobile cloud computing. J Cloud Comput. 2016;5(1):1–13. doi:10.1186/s13677-016-0068-6. [Google Scholar] [CrossRef]

17. Liu B, Zhou Y, Hu F, Li F. User authentication and key agreement protocol for mobile client-multi-server environment. J Cryptol Res. 2018;5(2):111–25. (In Chinese). [Google Scholar]

18. Hassan A, Eltayieb N, Elhabob R, Li F. An efficient certificateless user authentication and key exchange protocol for client-server environment. J Ambient Intell Human Comput. 2018;9(6):1713–27. doi:10.1007/s12652-017-0622-1. [Google Scholar] [CrossRef]

19. Qiu S, Xu G, Ahmad H, Xu G, Qiu X, Xu H. An improved lightweight two-factor authentication and key agreement protocol with dynamic identity based on elliptic curve cryptography. KSII Trans Internet Inf Syst. 2019;13(2):978–1002. [Google Scholar]

20. Jegadeesan S, Azees M, Kumar PM, Manogaran G, Chilamkurti N, Varatharajan R, et al. An efficient anonymous mutual authentication technique for providing secure communication in mobile cloud computing for smart city applications. Sustain Cities Soc. 2019;49:101522. doi:10.1016/j.scs.2019.101522. [Google Scholar] [CrossRef]

21. Xu S, Reng X, Chen C, Yuan F, Yang Z. Provably secure certificateless two-party authenticated key agreement Protocol. J Cryptol Res. 2020;7(6):886–98. (In Chinese). doi:10.1109/cis.2009.152. [Google Scholar] [CrossRef]

22. Tsobdjou LD, Pierre S, Quintero A. A new mutual authentication and key agreement protocol for mobile client—Server environment. IEEE Trans Netw Serv Manag. 2021;18(2):1275–86. doi:10.1109/tnsm.2021.3071087. [Google Scholar] [CrossRef]

23. Rana S, Obaidat MS, Mishra D, Mishra A, Rao YS. Efficient design of an authenticated key agreement protocol for dew-assisted IoT systems. J Supercomput. 2022;78(3):3696–714. doi:10.1007/s11227-021-04003-z. [Google Scholar] [CrossRef]

24. Li F, Wang J, Zhou Y, Jin C, Islam S. A heterogeneous user authentication and key establishment for mobile client-server environment. Wireless Netw. 2020;26(2):913–24. doi:10.1007/s11276-018-1839-4. [Google Scholar] [CrossRef]

25. Daniel RM, Thomas A, Rajsingh EB, Silas S. A strengthened eCK secure identity based authenticated key agreement protocol based on the standard CDH assumption. Inf Comput. 2023;294:105067. doi:10.1016/j.ic.2023.105067. [Google Scholar] [CrossRef]

26. Ma Y, Ma Y, Liu Y, Cheng Q. A secure and efficient certificateless authenticated key agreement protocol for smart healthcare. Comput Stand Interf. 2023;86:103735. doi:10.1016/j.csi.2023.103735. [Google Scholar] [CrossRef]

27. Cheng Q, Li Y, Shi W, Li X. A certificateless authentication and key agreement scheme for secure cloud-assisted wireless body area network. Mobile Netw Applicat. 2022;27(1):346–56. doi:10.1007/s11036-021-01840-3. [Google Scholar] [CrossRef]

28. Khalafalla W, Zhu WX, Elkhalil A, Yan C. An efficient cross-domain mutual authentication scheme for heterogeneous signcryption in VANETs. Cluster Comput. 2025;28(13):838. doi:10.1007/s10586-025-05333-w. [Google Scholar] [CrossRef]

29. Khalafalla W, Zhu WX, Elkhalil A, Khokhar S. Efficient authentication scheme for heterogeneous signcryption with cryptographic reverse firewalls for VANETs. Int J Inf Secur. 2025;24(3):1–18. doi:10.1007/s10207-025-01021-3. [Google Scholar] [CrossRef]

30. Bellare M, Rogaway P. Entity authentication and key distribution. In: Annual International Cryptology Conference. Berlin/Heidelberg, Germany: Springer; 1993. p. 232–49. [Google Scholar]

31. Wu TY, Tseng YM. An efficient user authentication and key exchange protocol for mobile client-server environment. Comput Netw. 2010;54(9):1520–30. doi:10.1016/j.comnet.2009.12.008. [Google Scholar] [CrossRef]

32. De Caro A, Iovino V. jPBC: java pairing based cryptography. In: 2011 IEEE Symposium on Computers and Communications (ISCC); 2011 Jun 28–Jul 1; Kerkyra, Greece: IEEE; 2011. p. 850–5. [Google Scholar]

33. Shim KA. An efficient conditional privacy-preserving authentication scheme for vehicular sensor networks. IEEE Trans Veh Technol. 2012;61(4):1874–83. doi:10.1109/tvt.2012.2186992. [Google Scholar] [CrossRef]