Video Transmission Secrecy Improvement Based on Fractional Order Hyper Chaotic System

1  Introduction

In the conventional method of video capture, the data acquisition requires a sampling rate of a minimum of at least double the signal’s greatest frequency for exact reconstruction. In applications where the data rate is high, such as video processing in the internet of video things, the Nyquist rate results in too many samples. Compressive Sensing is an emerging technology that takes advantage of the signal’s sparse nature, signal can be obtained from smaller measurements if it is sparsely or near to sparse in any region [1–3]. Video signals have large numbers of temporal and spatial redundancies, which can be well used to represent the signals sparsely [4–6]. Therefore, the application of CS to videos has outstanding potential.

In the world of multimedia communication, that handles a massive volume of videos, it becomes necessary to provide secure transmission. Encryption is the most trustworthy method in the transfer of video signals. Recent research [7–9] has shown that encryption techniques based on chaotic systems are efficient. Extreme unpredictability is one of the features of a chaotic system, unpredictable nature, vulnerability to the initial values and configuration parameters that make it predominant in video encryption. The hyper chaotic system has been viewed with fast-growing concern over the last decades. A chaotic systems with numerous positive Lyapunov coefficients is called hyper chaotic. Given, that hyper chaotic systems have better outcomes than conventional chaotic systems, such as affluent chaos and complexity, several researchers used hyper chaotic systems in encryption algorithms [10–14]. In [15] the proposed encryption algorithm consists of three steps: the input image decomposed into the primary color channels, R, G, & B. The confusion and diffusion operations are performed for each channel independently. The 4D hyperchaotic Chen system of fractional orders generates random numbers to permit pixel positions. We split the permitted image into 2 × 2 blocks where the Fibonacci Q-matrix diffused each of them. Experiments performed where the obtained results ensure the efficiency of the proposed encryption algorithm and its ability to resist attacks. In Ding et al. (2020) [16], the authors utilize the Cycle-GAN network as the primary learning network to encrypt and decrypt the medical image. Ding et al. (2021) [17] proposed a new deep learning-based stream cipher generator, DeepKeyGen, designed to generate the private key to encrypt medical images.

Zhao utilized the improper fractional order chaotic system [18]. Focusing on the extreme parallelism and exceptional characteristics of DNA molecules, various authors combined DNA operations with chaos to develop extremely competent and efficient encryption systems. K. Zhan proposed an encryption method incorporates DNA operations with hyper chaotic systems. A Lorenz system and DNA computing based image encoding method is proposed by Li. we concentrated on picture compression and encryption techniques [19]. This study proposes a video compressive encryption algorithm based on partial order hyper chaotic systems and Nucleotide Sequences processes, which performs compression better than existing methods.

The following is how the paper is structured: The second segment delves into the foundations of video security. The Section 3 discusses reconstruction algorithms and video proposals. Sensing that is compressed Section 4 discusses the encryption approach, Section 5 elaborates on the experimental results, and Section 6 summarises the paper’s overall findings.

2  Preliminaries

2.1 Compressive Sensing

According to CS, even with a lesser amount of measurements, the signal can be reconstructed if the signal is on any field, enough insufficient. Assume x € RN characterizes an N-dimensional signal, and x € RMN represents a matrix of measurement. The CS acquisition process is then represented in Eq. (1)

Y=ΦX (1)

where y ∈ RM denotes the compressive sensing measurements. Here Y << N, which makes the system underdetermined.

Let X is an one-dimensional signal represented in an N × N basis Ψ, then x is defined as x = Ψ x′. If x′ has large coefficients K of small numbers less than N, it can be assumed that x in the domain is K sparse. The signal x is retrievable from y through optimization if the basis and measurement matrix obeys restricted isometry property and are incoherent enough.

In a high-dimensional signal, such as videos, the dense measurement matrix’s storing and processing imposes a large memory and computational complexity burden. Additionally, the reconstruction procedure will be tedious if the dimensionality is enormous. Hence, the video is captured frame by frame through Block-based CS (BCS) as in [20] and [21,22]. An N pixel video frame blocks size is divided into B × B, each of which is obtained using a size MB × B2 measurement matrix ΦB. The CS measurements are given in Eq. (2),

yi=ΦBxi (2)

where xi is the ith block column vector of the image, and ΦB is a measurement matrix of size MB × B2. S = MB/B2 gives sub rate of BCS. By incorporating Smoothed Projected Landweber (SPL) with Dual Discrete Wavelet Transform (BCS-SPL) and Multi Scale Variant (MS-BCS-SPL) [23], the reconstruction quality is improved. For video, Multiple Hypothesis (MH) based prediction is proposed to improve the reconstruction quality. MH incorporates Motion Compensation (MC) and Motion Estimation (ME) [24].

2.2 Fractional Order Hyper Chaotic System

A new hyper chaotic Chen scheme based on the Chen system. By swapping the standard difference operators with the fractions difference operators as shown in equation, the partial hyper-chaotic chensystem is created in Eq. (3)

dq1x1dtq1=β(x2−x1)+x4,dq2x2dtq2=γx1−x1x2+λx2, dq3x3dtq3=x1x2−αx3, dq4x4dtq4=x2x3+rx4 (3)

where λ, q, β, α, γ, r, are the control system parameter.

A system shows a hyperchaotic behaviour, when the initial values are (2,2,1,−1) and the control parameter is β = 35, λ= 12, γ = 7, α = 3, r = 0.5, qi = 0.96 (i = 1,2,3,4). The phasor diagrams are shown in Fig. 1.

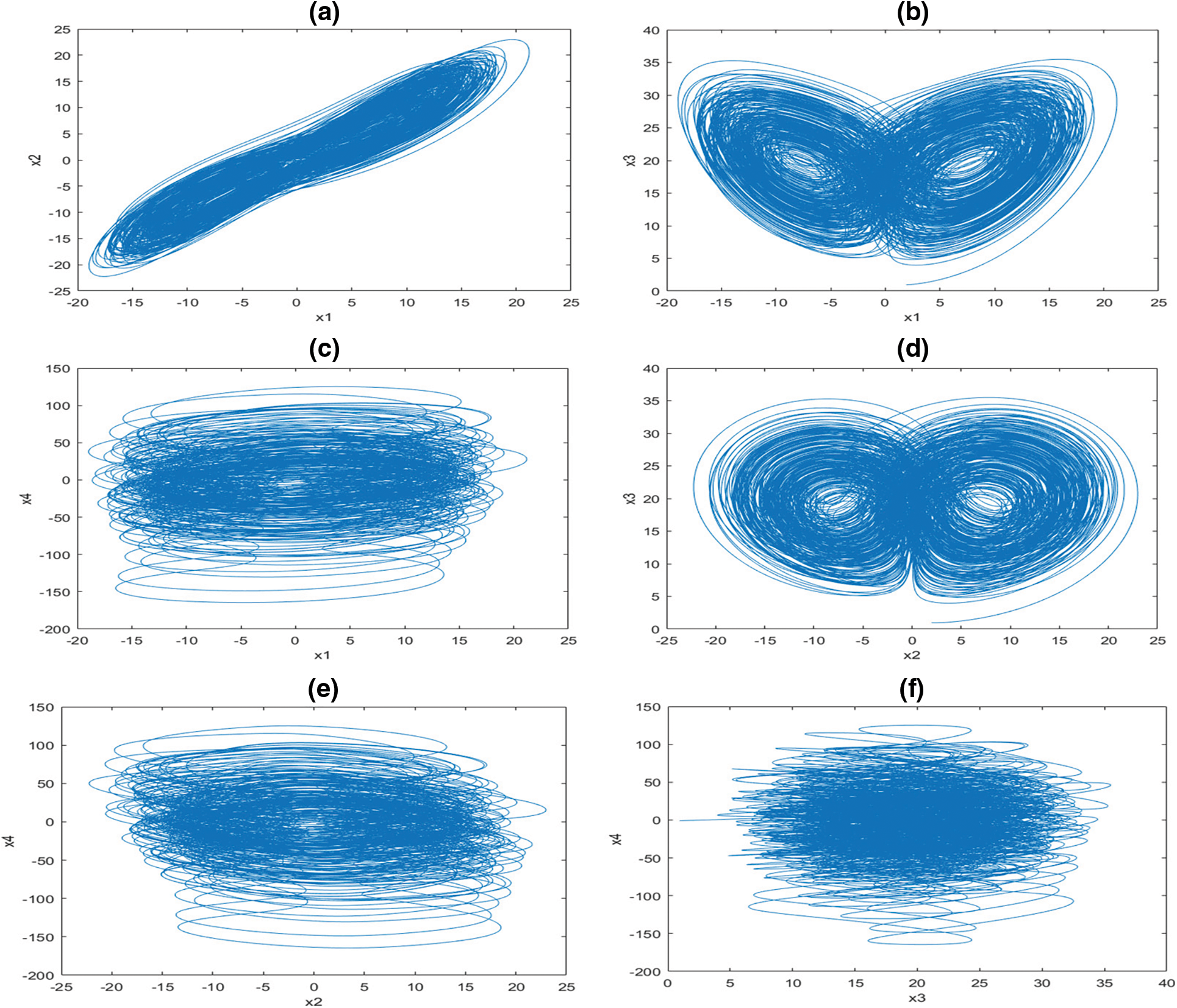
Figure 1: Phase diagram (a) x1, x2 (b) x1, x3 (c) x1, x4 (d) x2, x3 (e) x2, x4 (f) x3, x4

2.3 Nucleotide Sequences

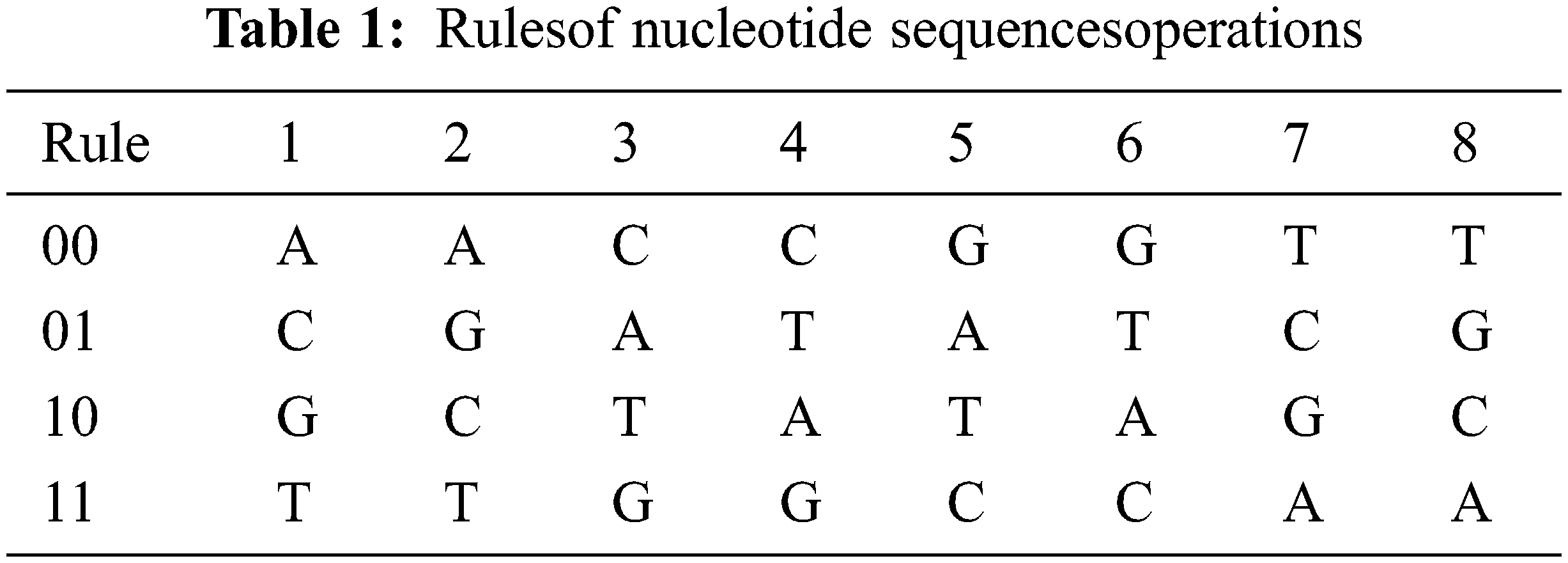
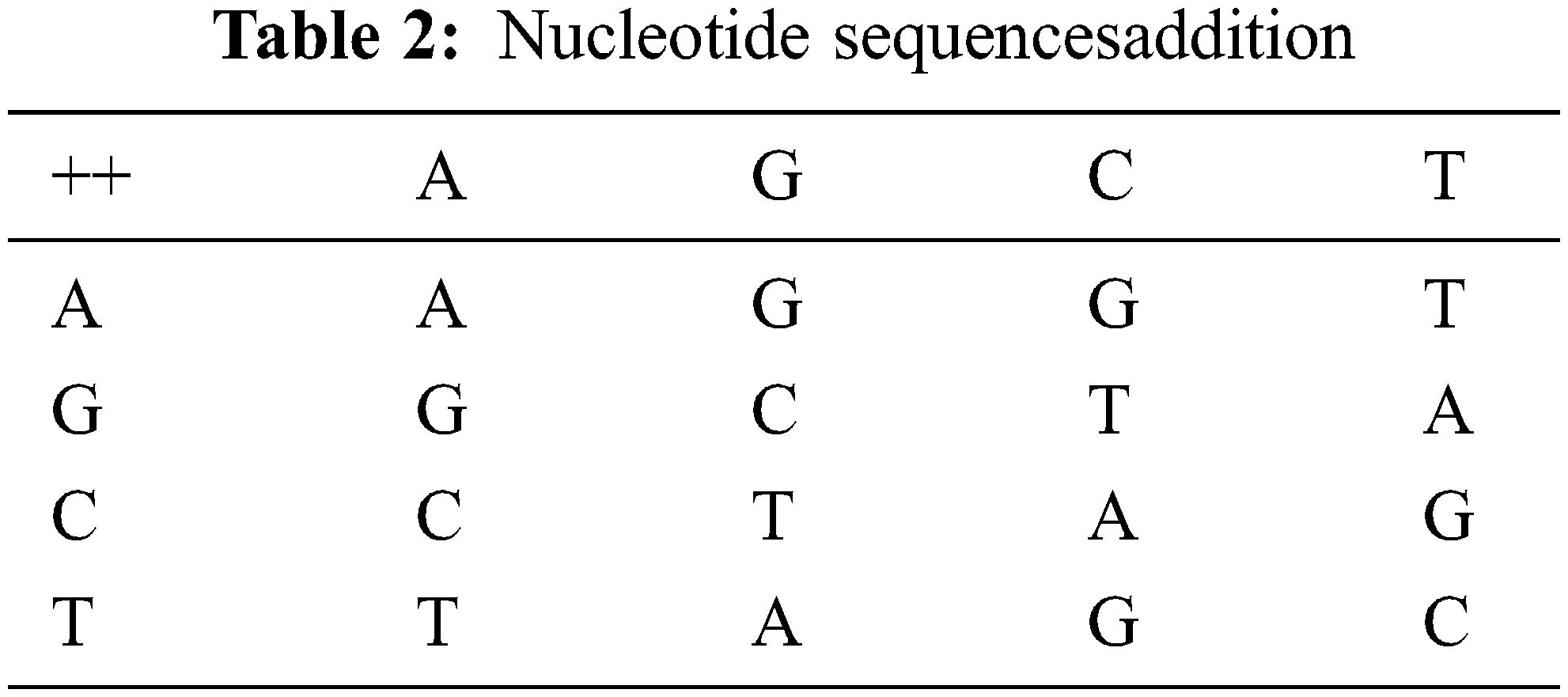
A Nucleotide Sequence is made up of four distinct nucleic acid bases and carbohydrates. Adenine, Guanine, and Thymine are the four nucleotides that make up DNA. T is complimented by A, and C is complimented by G. There are 4! Combinations of encoding rules shown in Table 1. agree with the laws of base pair. For binary schemes, the “0” and “1” complement one another; thus 00, 01, 10, 11 represent the digits 0, 1, 2, 3, respectively. The Nucleotide addition, subtraction is shown in Tables 2 and 3.

3  Reconstruction Algorithm

In recent years, several researchers proposed video compressive sensing reconstruction algorithms [25]. In the proposed work, the reconstruction algorithm contains of two stages, the first stage utilizes intra-frame similarity and offers strong preliminary retrieval for each frame. Stage two iteratively improves reconstruction efficiency by integrating interframe MH estimation, reweighted residual sparsity modeling, and l1 regularization Minimization [26,27]. Residual coefficient weights are adjusted based on the MH prediction in each iteration using a statistical procedure. The weighted l1 minimization issue is solved using an iteration algorithm based on the Split Bregman method. The key elements are sampled at a higher substrate to produce greater compression, while the non-key elements are sampled at a lower substrate to achieve better compression. In phase one,due to the higher subframe rate, key frames have more excellent retrieval than non-key. They are not handled further during the stage two, but instead act as hint frames for the non-key frames. An accuracy of non-key frames is improved in stage two by using a reweighted residual sparsity model that takes use of the temporal connection among key and non-key frames.

4  Proposed Method: Video Compressive Sensing Encryption

In this chapter, we’ll go over the proposed compression and encryption mechanism, Fig. 2. Shown a block diagram.

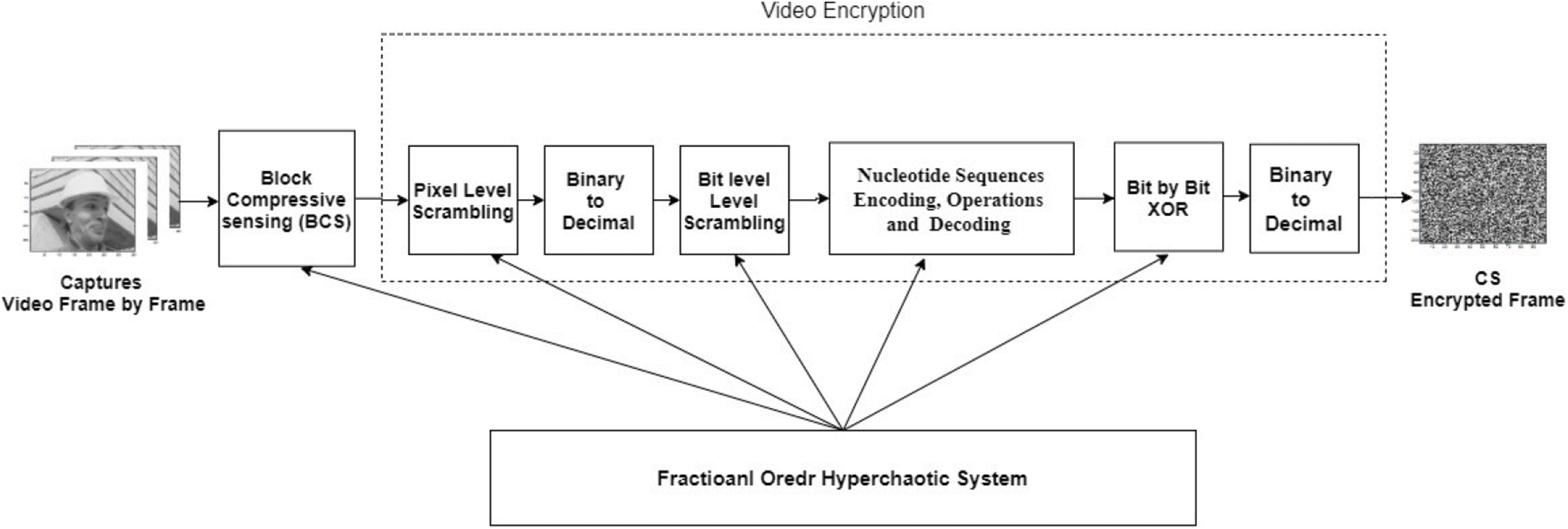
Figure 2: Block diagram-compressive sensing encryption method

4.1 Measurement Matrix Generation

The Fractional order hyper chaotic Chensystem is predicated N0 times to avoid transit pseudo randomness and increase stability. The procedure is repeatedly iterated M * N times. t iteration produces four state values {p1t,p2t,p3t,p4t} . Two different key values are generated in each iteration as follows in Eqs. (4)–(6)

(Zla)t=modulo{floor[(|plt|−floor(|plt|))×1015108],256},l=1,2,3,4 (4)

(Zlb)t=modulo(floor(modulo{[(|plt|−floor(|plt|))×1015],108}),256),l=1,2,3,4 (5)

A vector is formed by joining these two key variables zt as given below,

zt=[(z1a)t,(z2a)t,(z3a)t,(z4a)t,(z1b)t,(z2b)t,(z3b)t,(z4b)t] (6)

The morals of at every iterationzt are joined to form the series z is z = [z1, z2…, zMxN],

The letter z can be used to represent an element in the z-series zq, q∈[1,8MN].

Successive M * N Fractional order hyper chaotic series z forms the measurement matrix.

4.2 BCS on Video Frames

The CS measurements y can be obtained by performing frame by frame video captures by using BCS.

4.3 PixelLevel Scrambling

The measurement pixel values are scrambled to resist plain text attack. The pixel level scrambling is accomplished in two steps.

Step 1: generates the pixels of intermediate chipper frame in Eqs. (7) and (8).

G(1)=Mod(y(1)+z(2)+G0,256)⊕Mod(z(1)+G0,256) (7)

G(i)=(Mod(y(i)+z(i+1),256)⊕Mod(z(i)+G(i−1),256) (8)

where i=1,2,3..mn,G0∈[0,255],here G0=74

Step 2: generates the pixels of final chipper frame in Eqs. (9) and (10).

H(i)=(Mod(G(1)+z(2),256)⊕Mod(z(1)+C(mn),256) (9)

H(i)=(Mod(G(i)+z(i+1),256)⊕Mod(z(i)+H(i−1),256) (10)

where i=1,2,3..mn

4.4 BitLevel Scrambling

ByScrambling the intensity values of the pixel level scrambling values bit by bit, the correlation amongadjacent pixels minimized. The scrambling is done bit by bit in two measures.

Step 1: Each measurement’s intensity is translated into its binary value and organized as a binary series in ascending order. In an increasing order the hyperchaotic sequence z is ordered to obtain an index sequence zq.

Step 2: The binary sequence B0 is scrambled based on the index sequence zq.

4.5 The Nucleotide Sequences Generation

Step 1:Scramble a little at a time, as described in D) on pixel-level scrambling of the measurements to obtain a binary sequence B1.

Step 2: Apply Nucleotide decoding rule 1 on sequence B1 to get the Nucleotide sequence D1.

Step 3: Apply Nucleotide addition on D1 elementsto find Nucleotide sequence D2, considering the initial condition as D0 = ‘A’.

Step 4: M × N decimal hyperchaotic sequences are extracted from the sequence z, aszs = [z1, z2…zMN]. The decimal order zs is converted to binary sequence and Nucleotide coding rule 3 is applied to obtain the sequence Dk according.

Step 5: Apply Nucleotide addition on D2 and Dk to find sequence D3.

Step 6: Apply Mask sequence γ from the as specified in the Eq. (11) and D3 as follows, if f(γ) = 1, Di4 can be produced by combining two or more similar di3 , Eventually, nothing changes to obtain Nucleotide sequence D4.

f(γ)={0,0≤τ255<0.5,1,0.5≤τ255≤1 (11)

Step 7:ApplyNucleotide coding rule 1 to decode D4 to obtain the binary sequence B2.

Step 8:Applybitwise XOR between Dk and B2 to get binary chipper sequence B3.

Step 9:Convert B3 to decimal to obtain the encrypted image Q.

F) Decoding is the encryption method’s inverse process, and reconstruction is carried out by combining MH estimation and reweighted residual sparsity model.

5  Performance Analysis

Various simulation findings are provided in this section to analyze the proposed video compressive sensing encryption algorithm’s performance. The experiments were carried out on a Windows 10 operating system using MATLAB 2016, 64-bit Lenovo computer with intel core i3, 7th generation processor. The experiment is performed on 17 subsequent video frames of five standard video sequences such as Silent, Foreman, Mother daughter, Akiyo, and Carphone.

5.1 Key Space Analysis

The proposed video compressive sensing encryption algorithm has four initial values as a security key. Size of key space for an initial value with precision value of 10−16 is calculated as 1016 x 4 = 1064 which is nearly equal to 2212, which is greater than 2100. Hence, the designedalgorithm’s keyspace is competent of resist brute force attack.

5.2 Sensitivity to Secret Key

A simple change in the security key should make the encryption technique vulnerable. To test the algorithm’s performance, a somewhat alternative key is employed x10=2+10−15,x20=2,x30=1,x40=−1 ., which results in a different decrypted video than the original input video. The results are shown in Fig. 3.

Figure 3: Decrypted video frame first column: reconstructed frame no.7 with correct security key. Second column: reconstructed frame no.7 with incorrect security key

5.3 Histogram Analysis

Histogram is a method for justifying the encryption algorithm. It computes the spread of pixel values in input and encrypted video frame. Fig. 4 displays the histogram for input video and encrypted video. Fig. 4 indicates that the input video histogram is irregularly distributed while the encrypted video is uniformly distributed. The analysis implies the encryption algorithm prevents attacks on the histograms.

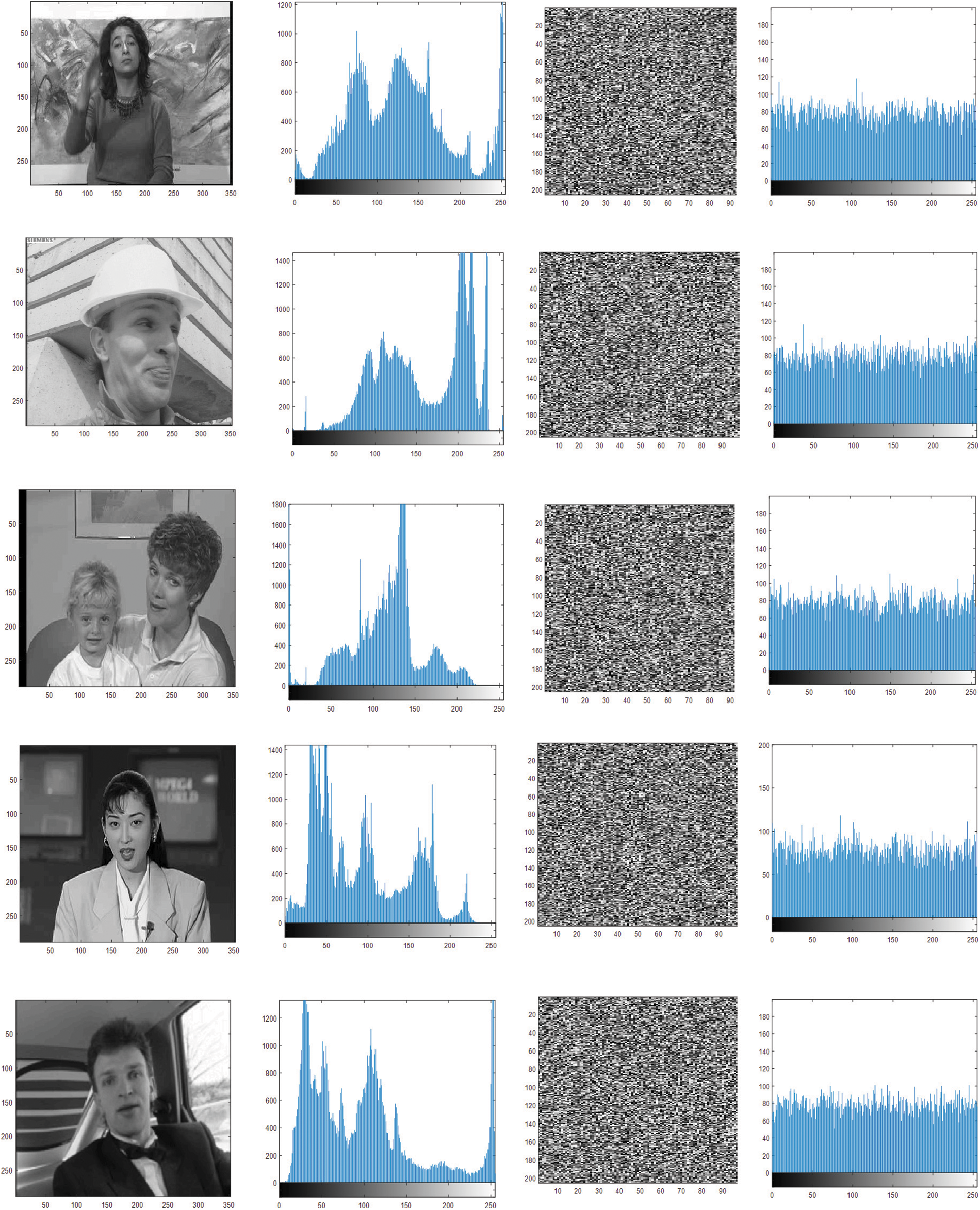
Figure 4: Histogram of video frame and their corresponding encryptedframe

5.4 Correlation Coefficient

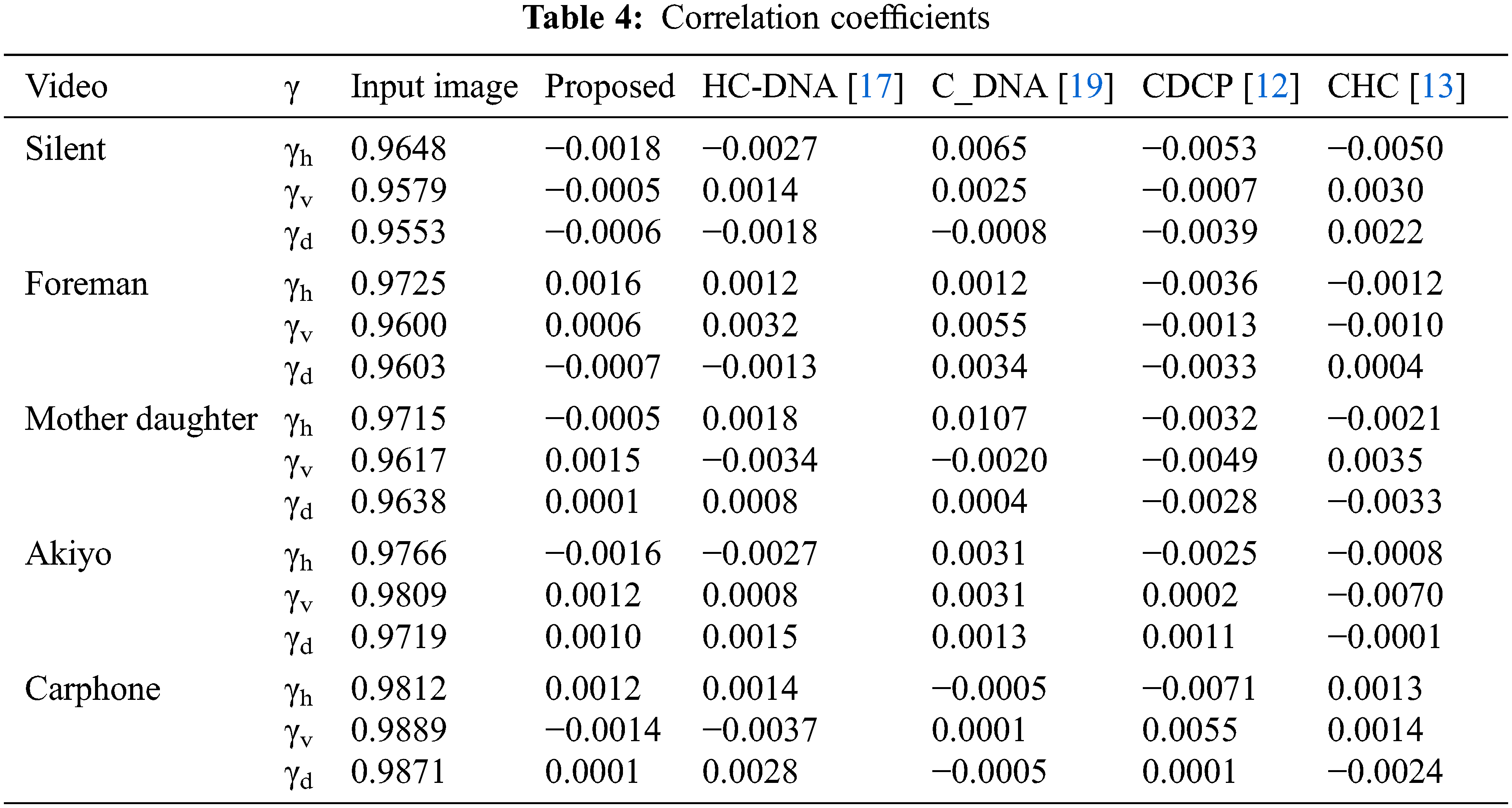
A correlation coefficient is a system of measurement to find the association of the neighboring pixel. An effective encryption algorithm’s correlation coefficient should have values practically equal to zero.

The correlation coefficient [28] is formulated as in Eqs. (12)–(15)

E(p)=1N∑i=1Npia, (12)

D(p)=1N∑i=1N(pia−E(pa))2, (13)

cov(pa,pb)=1N∑i=1N(pia−E(pa))(pib−E(pb)), (14)

γ=cov(pa,pb)D(pa)D(pb), (15)

where piaandpib represents the intensity values of neighboring pixels in an image.

Table 4 Shows the correlated coefficients of the input video frame and the encrypted frame. The findings indicate that the coefficients of correlation of the input video frames are roughly equivalent to one, while the correlation values of correlation of the encrypted video frames are approximately equal zero.

5.5 Information Entropy

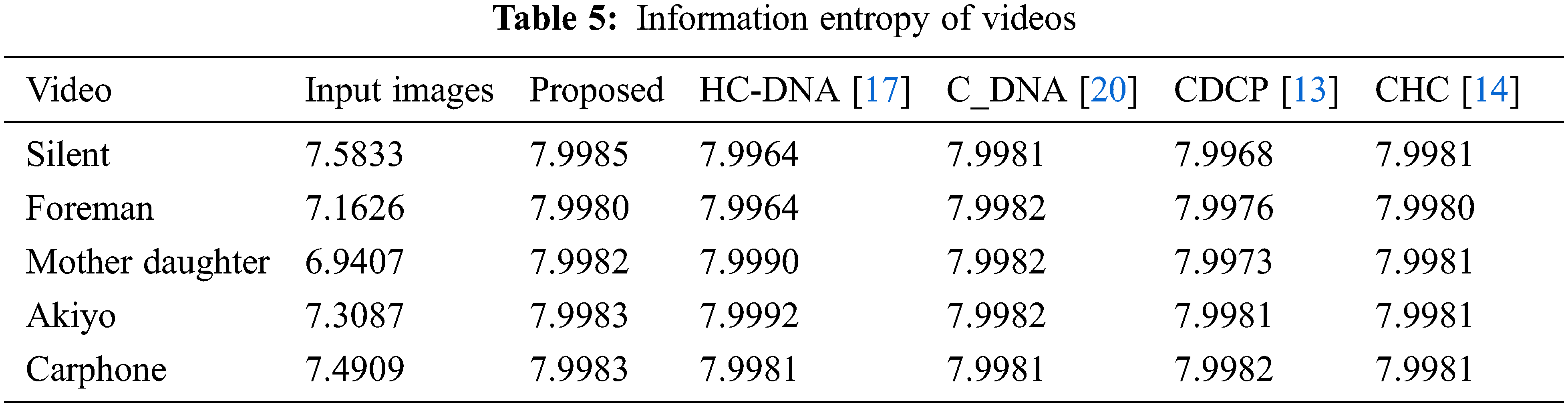
IEP (information entropy) measures the random nature of an frame. The IEP is calculated as below for an eight-bit grayscale frame which is represented in Eq. (16),

IEP=−∑i=0255probl(Pi)log2(probl(Pi)) (16)

where probl refers to the pixel value probability. Table 5 tabulates the values of IEP for the proposed algorithm. It is clear from the result that the IEP of the original frame is less than 8 when the encrypted frame has value equal to the ideal value 8.

5.6 Differential Attack Analysis

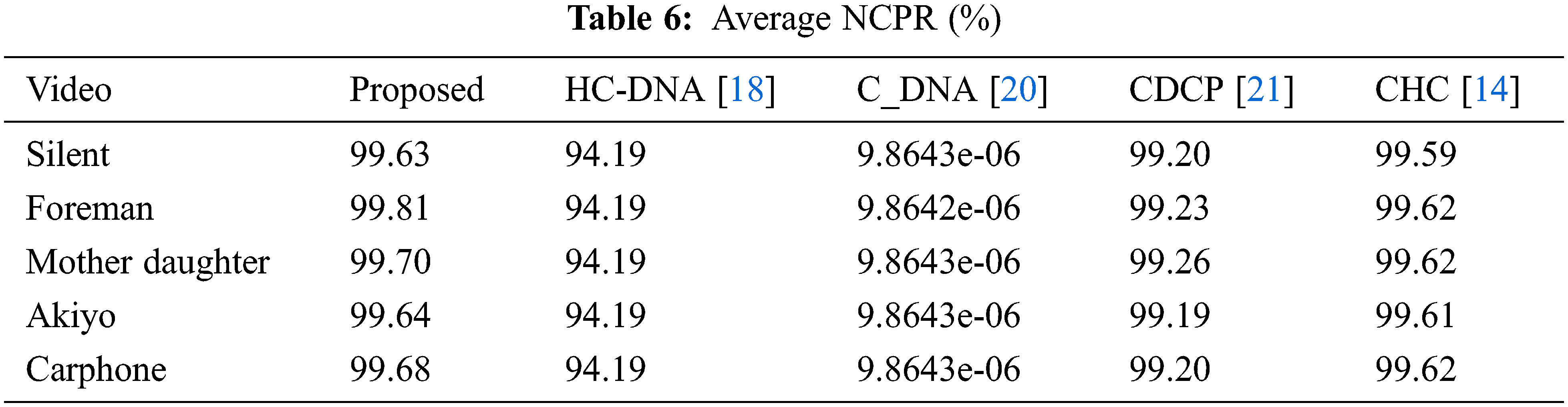
An effective encryption method would be susceptible to the input frame and lead to a different encrypted video frame for a little change in the input video frame. Two essential methods of study of the differential attack are the Unified Average Change Intensity (UACI) and the Number of Pixel Change Rate (NCPR) [28].

Let q1 be the input p1 encrypted frame of size h × w, and shift a bit p1 randomly to p2. Q2 is the input p2 encrypted frame. NPCR and UACI are formulated as in Eqs. (17) and (18).

NPCR=1MN∑i=1h∑j=1wδij×100% (17)

where,

δij={0,qij1=qij2,1,qij1≠qij2;

UACI=1MN∑i=1h∑j=1w|qij1−qij2|255×100% (18)

qij1 and qij2 represent pixel intensity at (i, j) of the original frame’s compressive encryption and compressive encryption of one bit changed frame, respectively. The theoretical value of UACI for an eight-bit Gray scale image is 33.4635 percent, while NPCR is 99.6094 percent. Tables 6 and 7 show that the values of NPCR and UACI are effective in resisting differentiated attacks.

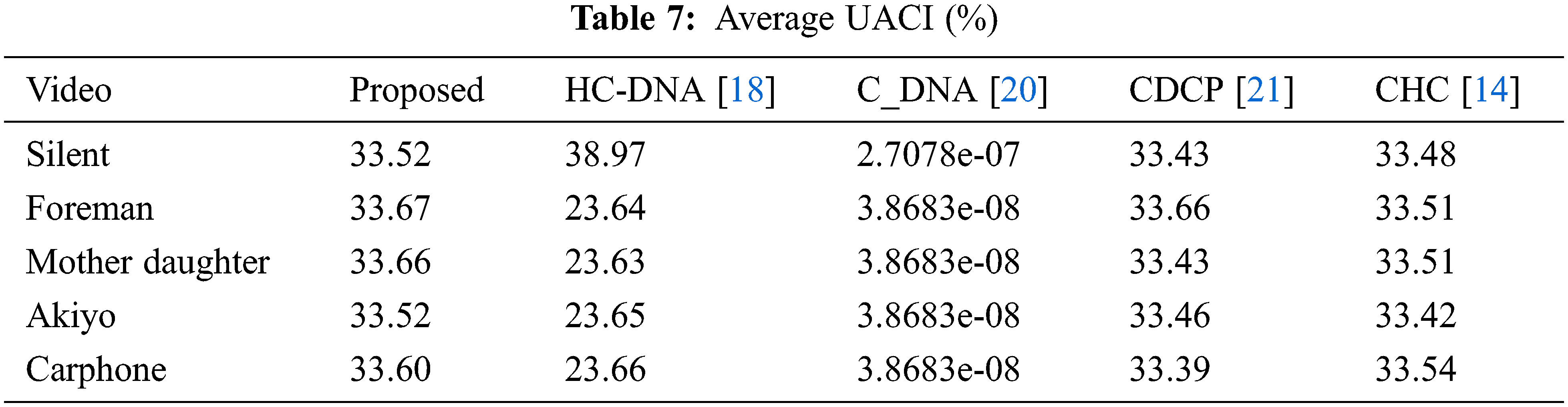
5.7 Reconstruction Performance

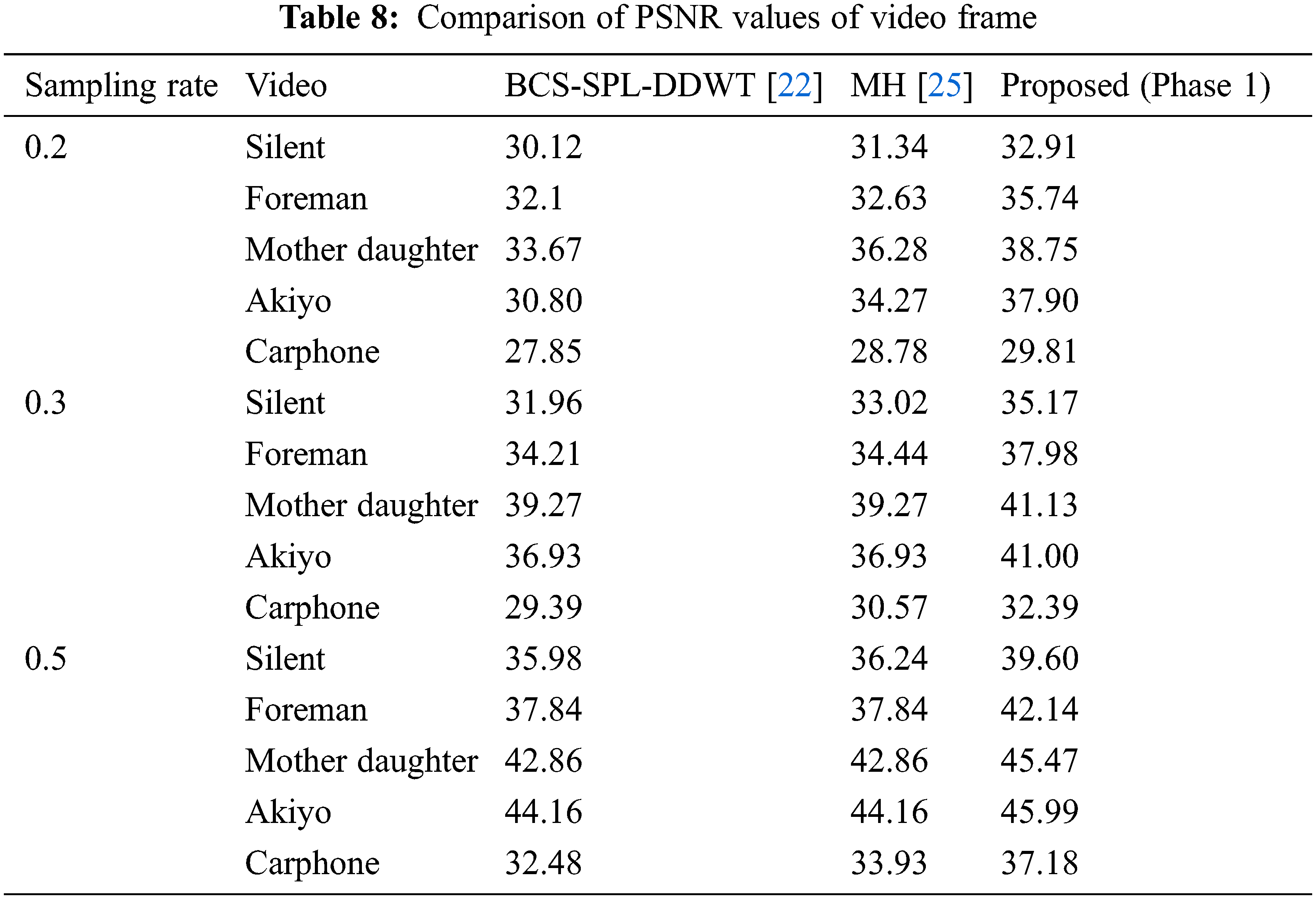
Reweighted residual sparsity modeling and l1 regularization suggested approach uses the minimization method to recreate the video frames. Experiments are performed on five different videos Foreman, silent, mother daughter, Akiyo and carphone. The frame size is 352 × 288, with a key frame sample rate of 0.7 and a non-key frame sample rate of 0.2. The performance of the reconstruction algorithm is measured as given in Eqs. (19) and (20).

PSNR=10log10(maxpixelvalue2Meansquareerror) (19)

Mean square error=1NXN∑l=1N∑m=1N(input(h,g)−estimated(h,g))2 (20)

where the pixel values of the input and reconstruction frames are represented by input (h, g) and estimate (h, g), correspondingly.

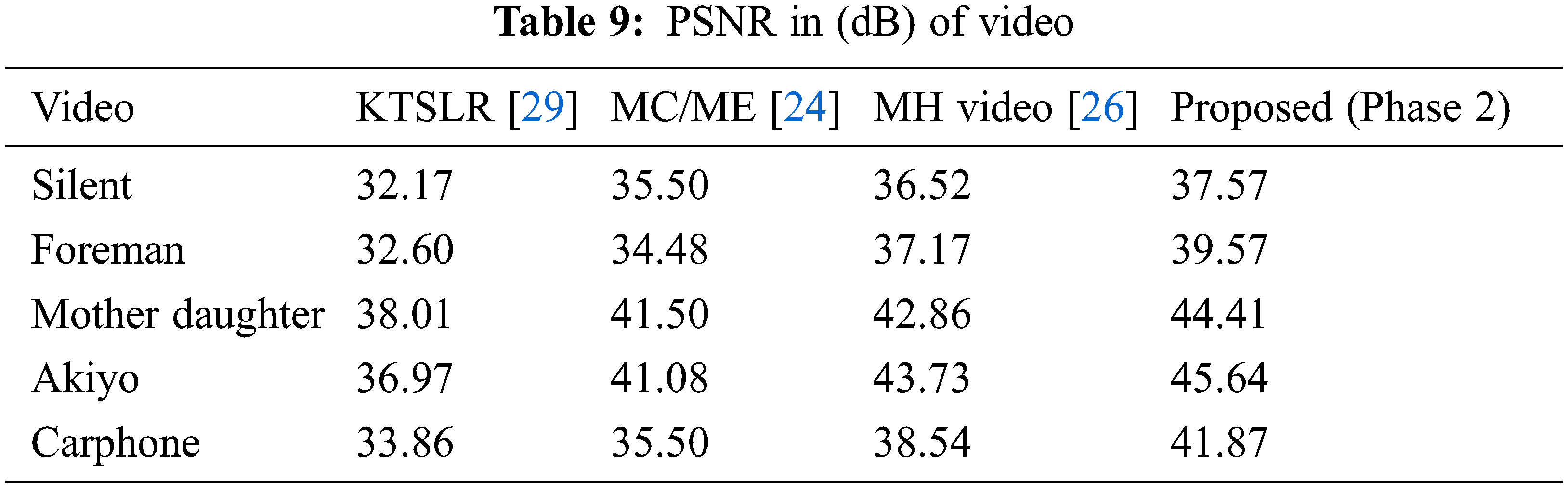
Table 8 shows the comparison of PSNR values of frame 7 of video with the available image recovery methods [22,25] for the different sampling rates. The results show that the phase 1 result exceeds the other methods. Table 9 shows the PSNR values of video compares with the existing methods [24,26,29]. The results are evident that strong reconstruction efficiency is retained in the proposed compression encryption method.

6  Conclusion

The proposal is for a compelling video compressive sensing encryption method based on fractional order hyperchaotic chen system, pixel level, bit level scrambling, and Nucleotide Sequences functions. The proposed approach guarantees effective video compression as well as improved security. The reconstruction technique includes two stages, the first stage of which utilizes intra-frame similarity and offers strong preliminary retrieval for each frame, and the stage two iteratively improves the efficiency of reconstruction by integrating inter frame MH estimation and weighted residual sparsity modeling. The experimental findings indicate that the method proposed preserves the robustness of compressive sensing with improved security. As an extension in the future, the proposed work could be employed for color video and extended to real-time implementation.

Acknowledgement: We thank anonymously reviewers for their helpful suggestions.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. Donoho, “Compressed sensing,” IEEE Transactions on Information Theory, vol. 52, no. 4, pp. 1289–1306, 2006. [Google Scholar]

 2.  R. Baraniuk, “Compressive sensing [lecture notes],” IEEE Signal Processing Magazine, vol. 24, no. 4, pp. 118–121, 2007. [Google Scholar]

 3.  A. Ahamed, C. Eswaran and R. Kannan, “Lossy image compression based on vector quantization using artificial bee colony and genetic algorithms,” Advanced Science Letters, vol. 24, no. 2, pp. 1134–1137, 2018. [Google Scholar]

 4.  C. Zhao, S. Ma and W. Gao, “Video compressive sensing via structured Laplacian modelling,” in Proc. IEEE Visual Communications and Image Processing Conf., Valletta, Malta, pp. 402–405, 2014. [Google Scholar]

 5.  J. Y. Park and M. B. Wakin, “A multiscale framework for compressive sensing of video,” in Proc. Picture Coding Symp., Chicago, IL, USA, pp. 1–4, 2009. [Google Scholar]

 6.  J. Angel Ida Chellam, P. V. Kavitha and M. SenthamilSelvi, “Live video watermarking using lab view,” International Journal of Pure and Applied Mathematics, vol. 119, no. 18, pp. 287–297, 2018. [Google Scholar]

 7.  X. Huang, “Image encryption algorithm using chaotic Chebyshev generator,” Nonlinear Dynamics, vol. 67, no. 4, pp. 2411–2417, 2012. [Google Scholar]

 8.  N. K. Pareek, V. Patidar and K. K. Sud, “Image encryption using chaotic logistic map,” Image and Vision Computing, vol. 24, no. 9, pp. 926–934, 2006. [Google Scholar]

 9.  S. Lian, J. Sun and Z. Wang, “A block cipher based on a suitable use of the chaotic standard map,” Chaos Solitons and Fractals, vol. 26, no. 1, pp. 117–129, 2005. [Google Scholar]

10. B. Norouzi, S. Mirzakuchaki, S. M. Seyedzadeh and R. M. Mosavi, “A simple, sensitive and secure image encryption algorithm based on hyperchaotic system with only one round diffusion process,” Multimedia Tools and Applications, vol. 71, no. 3, pp. 1469–1497, 2014. [Google Scholar]

11. X. Wang and H. Zhang, “A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems,” Nonlinear Dynamics, vol. 1, pp. 333–346, 2016. [Google Scholar]

12. Y. Li, W. K. S. Tang and G. R. Chen, “Generating hyperchaos via state feedback control,” International Journal of Bifurcation and Chaos in Applied Sciences and Engineering, vol. 15, no. 10, pp. 3367–3375, 2005. [Google Scholar]

13. C. Zhu, Y. Hu and K. Sun, “New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern,” Journal of Electronics & Information Technology, vol. 34, no. 7, pp. 1735–1743, 2012. [Google Scholar]

14. C. Zhu and K. Sun, “Cryptanalysis and improvement of a class of hyperchaos based image encryption algorithms,” Acta Physica Sinica, vol. 61, no. 12, pp. 120503, 2012. [Google Scholar]

15. K. M. Hosny, S. T. Kamal and M. M. Darwish, “Novel encryption for color images using fractional-order hyperchaotic system,” Journal of Ambient Intelligence and Humanized Computing, vol. 8, no. 3, pp. 1–16, 2022. [Google Scholar]

16. Y. Ding, G. Wu, D. Chen, N. Zhang, L. Gong et al., “DeepEDN: A deep-learning-based image encryption and decryption network for internet of medical things,” IEEE Internet of Things Journal, vol. 8, no. 3, pp. 1504–1518, 2020. [Google Scholar]

17. Y. Ding, F. Tan, Z. Qin, M. Cao, K. K. R. Choo et al., “DeepKeyGen: A deep learning-based stream cipher generator for medical image encryption and decryption,” IEEE Transactions on Neural Networks and Learning Systems, pp. 1–15, 2021. [Google Scholar]

18. K. Zhan, D. Wei, J. Shi and J. Yu, “Cross-utilizing hyperchaotic and DNA sequences for image encryption,” Journal of Electronic Imaging, vol. 26, no. 1, pp. 13021, 2017. [Google Scholar]

19. T. Li, M. Yang, J. Wu and X. Jing, “A novel image encryption algorithm based on a fractional-order hyperchaotic system and dna computing,” Complexity, vol. 2017, no. 11, pp. 1–14, 2017. [Google Scholar]

20. X. Wang and C. Liu, “A novel and effective image encryption algorithm based on chaos and DNA encoding,” Multimedia Tools and Applications, vol. 76, no. 5, pp. 6229–6245, 2017. [Google Scholar]

21. S. Kayalvizhi and S. Malarvizhi, “A novel encrypted compressive sensing of images based on fractional order hyper chaotic Chen system and DNA operations,” Multimedia Tools and Applications, vol. 79, no. 5, pp. 3957–3974, 2019. [Google Scholar]

22. S. Mun and J. Fowler, “Block compressed sensing of images using directional transforms,” in 16th IEEE Int. Conf. on Image Processing (ICIP), Cairo, Egypt, pp. 3021–3024, 2009. [Google Scholar]

23. J. E. Fowler, S. Mun and E. W. Tramel, “Block-based compressed sensing of images and video,” Foundations and Trends in Signal Processing, vol. 4, no. 4, pp. 297–416, 2012. [Google Scholar]

24. S. Mun and J. E. Fowler, “Residual reconstruction for block-based compressed sensing of video,” in Proc. Data Compression Conf., (DCC), Snowbird, UT, USA, pp. 183–192, 2011. [Google Scholar]

25. C. Chen, E. W. Tramel and J. E. Fowler, “Compressed-sensing recovery of images and video using multihypothesis predictions,” in Proc. Conf. Record Of The Forty Fifth Asilomar Conf. On Signals, Systems And Computers (ASILOMAR), Pacific Grove, CA, USA, pp. 1193–1198, 2011. [Google Scholar]

26. E. W. Tramel and J. E. Fowler, “Video compressed sensing with multihypothesis,” in Proc. IEEE Data Compression Conf. (DCC), Snowbird, UT, USA, pp. 193–202, 2011. [Google Scholar]

27. C. Zhao and S. Ma, “Video compressive sensing reconstruction via reweighted residual sparsity,” IEEE Transactions on Circuits and Systems For Video Technology, vol. 27, no. 6, pp. 1182–1195, 2017. [Google Scholar]

28. G. Chen, Y. Mao and C. K. Chui, “A symmetric image encryption scheme based on 3D chaotic cat maps,” Chaos Solitons Fractals, vol. 21, no. 3, pp. 749–761, 2004. [Google Scholar]

29. S. G. Lingala, Y. Hu, E. DiBella and M. Jacob, “Accelerated dynamic MRI exploiting sparsity and low-rank structure: K-t SLR,” IEEE Transactions On Medical Imaging, vol. 30, no. 5, pp. 1042–1054, 2011. [Google Scholar]