 Open Access
Open Access
ARTICLE
Reinforcement Learning with an Ensemble of Binary Action Deep Q-Networks
1
Department of Electronics & Communication Engineering, Institute of Technology, University of Kashmir, Srinagar, J&K,
190006, India
2
Department of Computer Science, Faculty of Computers and Information, South Valley University, Qena, Egypt
3
College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, Alkhrj, KSA
4
Department of Computer Science, Faculty of Computers and Information, Luxor University, Luxor, Egypt
* Corresponding Author: M. Hassaballah. Email:
Computer Systems Science and Engineering 2023, 46(3), 2651-2666. https://doi.org/10.32604/csse.2023.031720
Received 25 April 2022; Accepted 29 June 2022; Issue published 03 April 2023
Abstract
With the advent of Reinforcement Learning (RL) and its continuous progress, state-of-the-art RL systems have come up for many challenging and real-world tasks. Given the scope of this area, various techniques are found in the literature. One such notable technique, Multiple Deep Q-Network (DQN) based RL systems use multiple DQN-based-entities, which learn together and communicate with each other. The learning has to be distributed wisely among all entities in such a scheme and the inter-entity communication protocol has to be carefully designed. As more complex DQNs come to the fore, the overall complexity of these multi-entity systems has increased many folds leading to issues like difficulty in training, need for high resources, more training time, and difficulty in fine-tuning leading to performance issues. Taking a cue from the parallel processing found in the nature and its efficacy, we propose a lightweight ensemble based approach for solving the core RL tasks. It uses multiple binary action DQNs having shared state and reward. The benefits of the proposed approach are overall simplicity, faster convergence and better performance compared to conventional DQN based approaches. The approach can potentially be extended to any type of DQN by forming its ensemble. Conducting extensive experimentation, promising results are obtained using the proposed ensemble approach on OpenAI Gym tasks, and Atari 2600 games as compared to recent techniques. The proposed approach gives a stateof-the-art score of 500 on the Cartpole-v1 task, 259.2 on the LunarLander-v2 task, and state-of-the-art results on four out of five Atari 2600 games.Keywords
Following the success of deep learning [1–10], Deep Q-Networks (DQNs) [11–13] were used in many AI-based decision making systems like Multi-agent systems (MAS) [14,15] for Reinforcement Learning (RL) [16–21]. The DQN helps solve many complex sequential decision making problems. In MAS, the emphasis is put on data-sharing schemes, inter-entity communication, and novelty of the Q-Network. However the complexity of these systems is increasing rapidly, leading to issues like difficulty in training, need for more computational and time resources, difficulty in fine-tuning, etc. An upcoming approach which has been applied successfully to machine vision tasks is deep ensemble learning [22–24]. Parallelization seems to be one of nature’s best approaches for massive computation and decision making, as found in the human brain. If this line of action is followed, much progress can be made in machine learning and other related tasks. Taking a cue from the same, in order to address these problems, we propose a simple but efficient DQN-based ensemble RL approach. The DQNs in the proposed approach share the state and the reward, but have their own local binary actions, which are updated in their experience replay pools.
Using ensembles in deep RL is rare as has been done in [25], where Q-learning agents have been used in an ensemble for a time series prediction task. In the same work, different agents are trained over different epochs leading to varied exposure and hence they have varied decision-making abilities. This tendency may not be suitable in the long run. In addition, if the time series is too long, the number of agents in the ensemble grows exponentially. In order to address these issues, the proposed approach is used in Deep Q-Network ensembles (DQN ensembles) and applied to core RL decision-making tasks. In experiments on some notable OpenAI Gym tasks, Atari 2600 games, etc., the proposed approach shows advantages like robustness, faster convergence and better performance as compared to state-of-the-art techniques, including various conventional Deep Q-Network techniques. The proposed approach achieves state-of-the-art results on the tasks.
The rest of this paper is organized as follows. Section 2 discusses the background of the paper. Section 3 briefly discusses related works. Section 4 describes details of the proposed approach. Section 5 gives the implementation details, experimental results, limitations and future work. Finally, Section 6 concludes the paper.
Deep neural network [11] for approximation of the optimal action-value function from Q-learning can be expressed by:
where the expression gives the maximum sum of rewards rtusing discounting factor γ for each timestep t which is achieved by a behavior policy π = P(a|s), for state s and action a after making an observation of the same.
It is well known that conventional reinforcement learning (RL) algorithms would become unstable or even show divergence when non-linear functions were used as in the case of neural network being used for representation of Q (i.e., the action-value function). In [11], authors discussed some notable reasons. Firstly, it is due to the correlations present in the observation sequence of the state s. In RL applications, there is an autocorrelation in the sequence state observations, which is a time-series. However, this could be true also for the applications of deep networks for modeling of time series data. Secondly, small updates to Q can significantly alter the policy π, and can hence alter the distribution of data. Finally, there may be correlations between the action values, Q and the values of the targets, i.e., r + γmaxa’Q(s’, a’). In [10], they firstly randomize data hence removing correlations in the observation sequence of the state s, and smooth any changes in the distribution of data. Secondly, they also use an iteration based update rule which adjusts the action values Q towards the target values Q′ which are only updated periodically hence reducing target correlations. As it turns out, there can be many techniques of approximation for the action value function Q(s, a) using a deep network. The sole input to the DQN is the state representation. Also, its output layer has a different output for every action. Each output unit corresponds to the predicted Q-values of the separate action in the input state. The input of the DQN consists of an image (84 × 84 × 4) which is produced by using a preprocessing map ϕ. The DQN has 4hidden layers out of which 3 are Convolutional and the last one is fully connected (i.e., dense). All layers use a ReLU activation function. The output layer of the DQN is also a fully connected layer with one output for every action. The Q-learning iterative update of the DQN uses the loss function as:
where Li is the loss function, E is the error function, r is the reward, s is the old state, s′ is the new state, γ is the discount factor in the horizon of the entity, θi comprises of the parameters of the DQN for the ith iteration, and
The max operator used in Deep Q-Networks uses the same values both for selection and evaluation of an action. This leads it to being more inclined towards selection of overestimated values. This issue results in over-optimistic estimation of values. In order to prevent this, Hasselt, et al. [12] decouples the selection component from the evaluation component. This is the motivation behind Double Q-learning. In the basic Double Q-learning technique, two functions are learned by assigning every experience randomly for updating of any one of these two value functions, in a manner that there will be two sets of weights, θ and θ`. For every update, one weight-set is used for the greedy policy determination and the other is used for its value determination. Decoupling the selection component and the evaluation component in Q-learning and rewriting the target error
where the variables have their usual connotations as given above.
The error of the Double Q-learning algorithm
where, the second set of weights
2.3 Return-based Deep Q-Networks
In [13], authors proposed a general framework for combination of a Deep Q-Network and the return-based RL algorithm called Return-Based Deep Q-Network (R-DQN). They showed that the traditional DQN performance can be significantly improved by introduction of the return-based algorithm. For further improvement in R-DQN, they designed a strategy having two measurements for the quality of the policy discrepancy. They conducted experiments on various OpenAI Gym tasks and Atari 2600 games, achieving state-of-the-art performance validating the effectiveness of R-DQN. The transitions (xt, at, rt, xt + 1,…, xt + k) are borrowed from the replay memory. The sequences of these transitions are used by R-DQN for computation of the value of the state estimate and TD error. The loss L is given by
where θjis the representation of R-DQN parameters at step j. Also, the target error Y(xt, at) is given by
where k is the number of transitions and
R-DQN uses experience replay [11,26]. The two main differences between R-DQN [27] and DQN [17] w.r.t. experience replay are that: 1) In the R-DQN, for a state x, the behavior policy μ(⋅|x) is stored in R-DQN. 2) In the R-DQN, the replay memory samples are sequential.
To deal with non-stationary issues in RL systems, Palmer, et al. [27] developed a technique named Lenient-DQN (LDQN), which applies leniency with decaying temperature values for adjustment of policy updates, which are sampled from the experience replay pool. This technique has been applied to the coordinated multi-entity systems and the performance of this work has been compared with the Hysteretic-DQN (HDQN) [28]. Experimentation demonstrates that LDQN is better than HDQN. The concept of leniency coupled with a replay strategy has also been used in the Weighted Double Deep Q-Network (WDDQN) [29] to deal with non-stationarity. Experimentation showed that WDDQN performs better than Double DQN in two multi-entity environments. Hong et al. [30] introduced a Deep Policy Inference Q-Network (DPIQN) for modeling of MAS and also the enhanced version viz. Deep Recurrent Policy Inference Q-Network (DRPIQN) for coping with partial observability. Experiments show better performance of both DPIQN and DRPIQN over their respective baselines, viz. DQN and DRQN [31]. However, these deep network approaches suffer from complexity issues and are difficult to implement, train and tune.
Gupta et al. [32] examined three separate training techniques: centralized learning, concurrent learning and parameter sharing. Centralized policy gives a joint action using joint observations of all the entities in the environment while as the concurrent learning trains entities together with the help of the joint reward signal. In concurrent learning, each entity learns its private policy, which is independent and is based on private observation. In the parameter-sharing scheme, entities are trained simultaneously using their experiences together although each of them has unique observations. Our approach is not as complex as these, as it uses a robust ensemble scheme. It involves sharing a common state and common reward, with the exception of the action which is locally updated in the experience replay pool of each DQN. As a result, significant time and resources are saved during training and execution, because of the reduced complexity. However, it should be noted that the proposed approach does not go in the direction of multi-entity based RL systems due to its parallel nature and other aspects; hence, no comparison is made with them. RL-based ensemble learning is rare, as found in a work using deep Q-learning agent ensembles for time series prediction [25]. The Q-learning agents are trained over different epochs. This mechanism has the disadvantage that the exposure of the agents to the environment is varied and hence different decision-making abilities may be acquired. Also, this issue may not be suitable for obtaining the optimum behavior of the ensemble. Also, if the data series is long, the number of agents in the ensemble grows exponentially. To the best of our knowledge, the proposed technique is the first one to use DQN ensembles and apply them to RL decision-making tasks like OpenAI Gym tasks, Atari 2600 games, and maze traversal.
DQNs [11] are typical deep RL representations, which use Convolutional Neural Networks (CNNs) [33] as models trained with variants of Q-learning [34]. Experiments showed that DQNs surpass their previous algorithms on almost the entire Atari 2600 suite of games [35] and perform almost as well and even better than humans. DQNs have been found to be adaptable and versatile [36]. Subsequent to the success of DQNs many efficient techniques have been proposed. DDQNs [12] reduce over-estimation bias risks of Q-learning as explained above. Due to limitations of CNNs, Long Short Term Memory Networks (LSTMs) or other Auto-encoders, DQNs exhibit other problems like lack of long term memory. Hausknecht, et al. [31] also investigated the effect of adding recurrence in DQNs. Wang, et al. [37] have since expanded DQNs using a dueling architecture by generalizing actions. Multistep bootstrapped targets [17,38] used for the Asynchronous Advantage Actor Critic (A3C) [39] shift the variance-bias tradeoff and help to propagate the rewards faster. Noisy DQNs [40] use stochastic layer sin the network for exploration. Distributed Q-learning [41] uses learning based on categorical distributions of the returns. Rainbow [42] combines various types of DQNs since they use a common framework. Experiments showed that rainbow achieves good performance on the Atari 2600 games benchmark. After looking closer at Rainbow, it was observed that priority identification was an important factor for the performance of the agent. Schaul, et al. [43] used one actor for data collection, leading to efficiency issues. Ape-X [44] used a distributed deep RL architecture having hundreds of actors for data collection for obtaining a large number of replay-buffers. Experiments showed that ApeX doubles the performance of rainbow with lesser training time. The success of techniques like ApeX, reveals the efficacy of distributed computing in deep RL and its importance in the field. However, it seems that using the technique wherein a large number of agents are used without proper consideration for the holistic as well as individual behavior(s), needs some improvement. Continuing in this line of distributed computing, the closest work to the proposed technique is that of [25], wherein Q-learning based agents are used in an ensemble for time series prediction. Here the agents are trained over distinct epochs, which may lead to different exposure in turn leading to overall varied decision-making abilities. This issue may create long term problems. Also, for a long time series, the number of ensemble agents increases exponentially. To address these issues, we propose a simplified, robust and efficient DQN ensemble based technique.
The proposed technique utilizes the ensemble of Deep Q-Networks for deciding the task action by using a consensus-based decision structure. The DQNs in the ensemble propose their local actions, which are taken up by the decision structure. The ensemble DQNs have shared state and common reward, but with DQN local-action update using experience replay [43]. The task environment is either explored by selecting a random action from the task action set A or is exploited by formulating a consensus action acons using the DQN ensemble. The freedom of the decision maker to choose between exploration or exploitation is a well-known concept in RL and it depends on probabilistic parameters. If exploitation is chosen, an ensemble consensus action aconsis formulated using a decision structure based on a chain of if-else statements feeding on local actions suggested by each of the ensemble DQNs. Otherwise a random action is chosen from the action set A of the task. Once the final action afinalis applied to the environment, the reward or penalty is obtained depending upon success or failure of the action taken. This reward or penalty is passed on to each DQN in the ensemble along with the final action value afinalof the DQN ensemble. The final action is then decomposed into n local actions by a decomposition structure. This decomposition ensures a binary action space for every DQN based entity presented in the ensemble. This new feature in turn ensures the following:
1. Straightforward and faster learning due to limited action space.
2. Reduced resource requirement for training or learning.
3. Lesser learning burden on each entity by using a simple load distribution scheme.
For n DQN entities in the ensemble, it can be stated that the mary task action space to be taken up by the ensemble, e.g., given by A = { a1, a2, a3,…, am} is decomposed into n binary action spaces for n DQNs, all being present in the proposed ensemble. Thus,
Having a binary action space is also useful for faster convergence due to lesser entity-learning load, as has been demonstrated experimentally in the subsequent section. Proceeding further with the discussion of the proposed approach, next each DQN updates its state using experience replay [43] using its local action and the common reward. Subsequently task error, score, etc. is calculated and the training loop keeps running till error decreases below a certain threshold. Fig. 1 illustrates the working of the proposed approach. Algorithm 1 summarizes steps for training the DQN ensemble using the proposed approach.
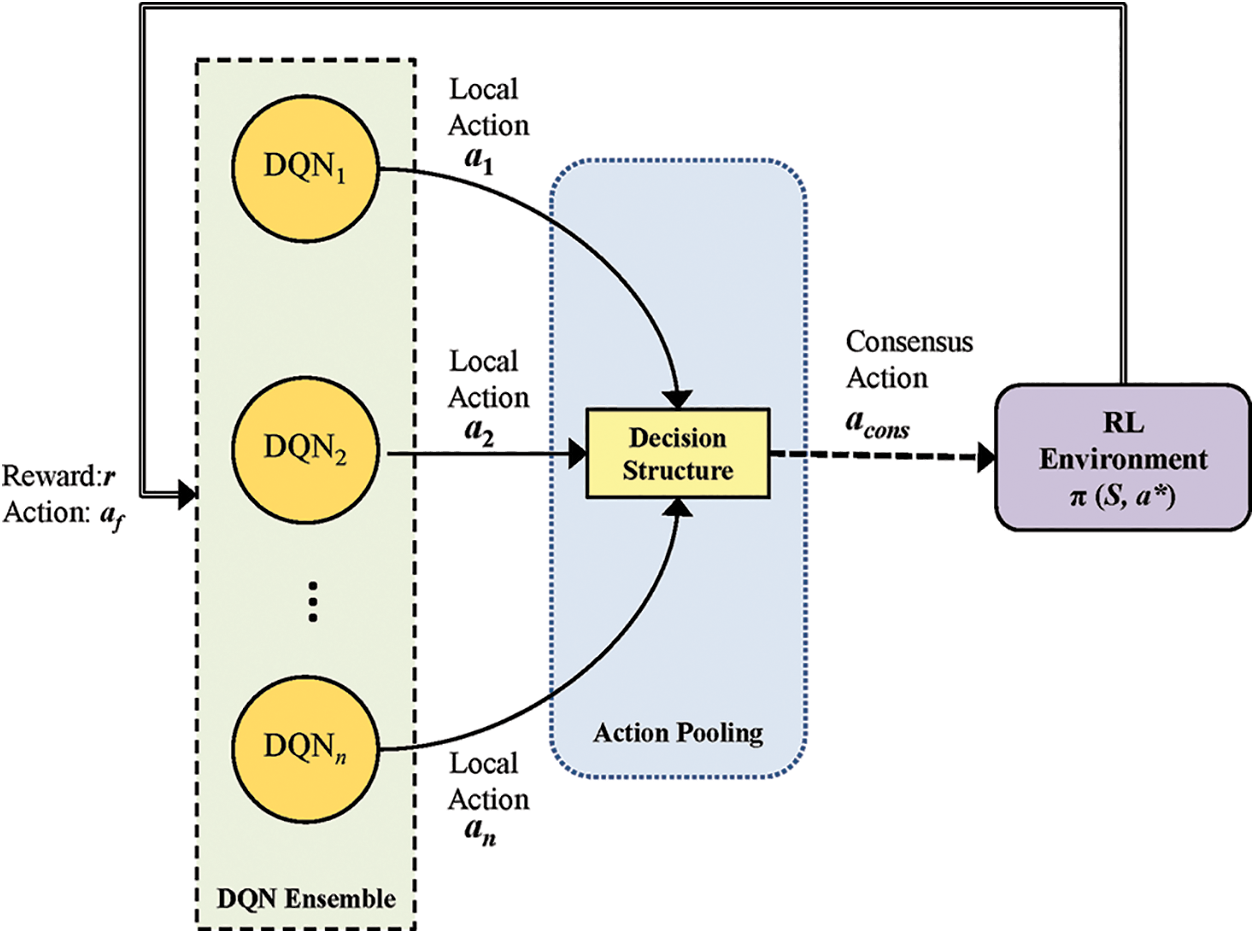
Figure 1: Illustration of the proposed approach

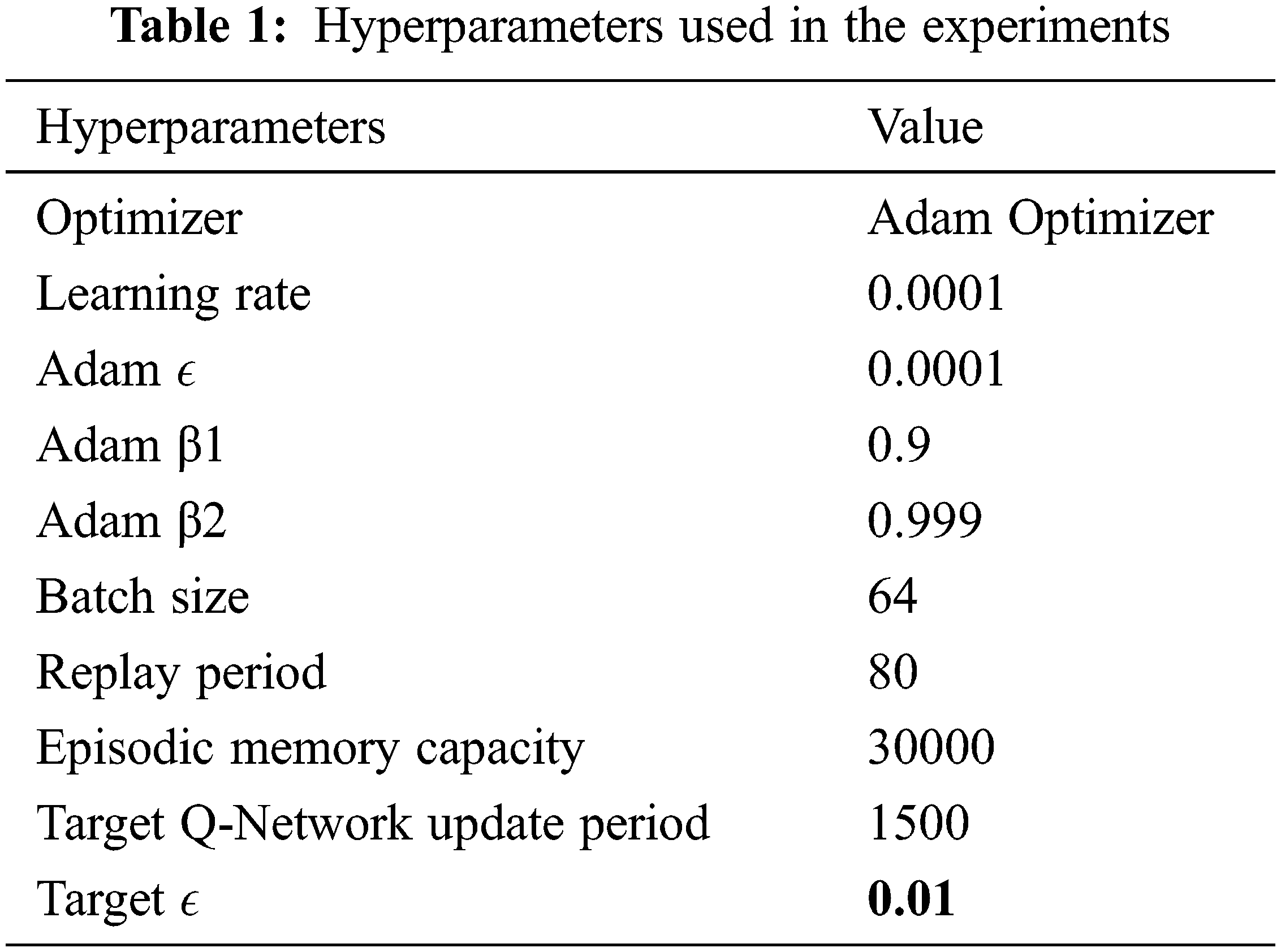
This section describes the experiments undertaken during the course of this project. Experimentation was done on the Python platform using TensorFlow with an Intel Xeon (2 Core) processor, with 26.75 GB RAM and 16 GB GPU (Nvidia T4). The hyperparameters used in the experiments are similar to those used in [45] as listed in Table 1.
5.1 RL Environments Used for Testing
We investigate the proposed approach using ensembles of some existing Deep Q Networks viz. DQN, DDQN and RDQN [11–13], on two notable OpenAI Gym tasks viz. Cartpole-v1 and LunarLander-v2, on a custom maze traversal task and on five Atari 2600 games. The DQNs in the proposed ensembles follow their original papers with regards to their respective implementations. The standard tasks are chosen because they can be conveniently used by the proposed approach, besides being extensively benchmarked as follows:
In this OpenAI Gym environment, a pole is attached to a cart by an un-actuated joint, which is moving along a frictionless track. The whole system is controlled by application of a force of + 1 or −1 to the cart. Initially the pendulum is upright, and the goal of the governing algorithm is to prevent the pendulum from falling over. The reward is + 1 for each time step for which the pole remains upright. The episode ends if the standing pole is more than 15° from the vertical, or if the cart moves beyond 2.4 units from the center. The available actions are move left (0) and move right (1). The above environment is based on the cart-pole problem discussed by Barto, Sutton, and Anderson [46].
In this OpenAI Gym environment, the landing pad is located at coordinates (0,0) corresponding to the first two numbers in state vector. The reward for landing safely on the landing pad with zero speed is about 100 to 140 points. The episode ends if the lander crashes or comes to rest. These actions lead to additional −100 or + 100 points respectively. Each leg ground contact gives + 10 points. Firing main engine leads to −0.3 points each frame. Solved task has 200 points. There is infinite fuel in the lander, so it can learn to fly and then land on its first attempt. Four discrete actions are available, i.e., do nothing (0), fire left orientation engine(1), fire main engine (2) and fire right orientation engine (3).
This is a customized framework for a Markov Decision Process (MDP) and consists of amaze environment (with 8 × 8 cells) and a DQN based entity. The environment is a square maze with three types of cells i.e., occupied cells, free cells and the target cell. The DQN based entity is a self-maneuverable entity which is allowed to move only on free cells, and whose goal is to get to the target cell. The DQN based entity is encouraged to find the shortest path to the target cell by a simple reward scheme. Four discrete actions are available i.e., move left (0), move up (1), move right (2) and move down (3). The rewards are floating points ranging from −1.0 to 1.0. A move from a cell to another will be rewarded by a positive or a negative amount. A move from a cell to an adjacent one will cost the entity −0.04 points. This discourages the entity from wandering around and encourages it to get to the target in the shortest route possible. Maximum reward of 1.0 points is given when the entity arrives at the target cell. Entering a blocked cell costs the entity −0.75 points. An attempt to move to a blocked cell is invalid and is not executed. However, this attempt will incur a −0.75 points penalty. The same rule holds for an attempt to move outside the maze boundaries i.e., −0.8 points penalty. The entity is also penalized by −0.25 points for moving to a cell which it has already visited. To avoid infinite loops and wandering, the game ends if the total reward of the entity is below a negative threshold i.e., −0.5 × Maze-size. It is assumed that under this threshold, the entity has lost its way and has made too many errors from which it has learned enough, and should proceed to a new episode.
We also investigate the performance of the proposed technique on computer games. For this, we choose five Atari 2600 games [35] using end-to-end RL vision setup, since its games are popular and contain varied challenge sets. Fig. 2 shows rendering screenshots for some of the tasks.
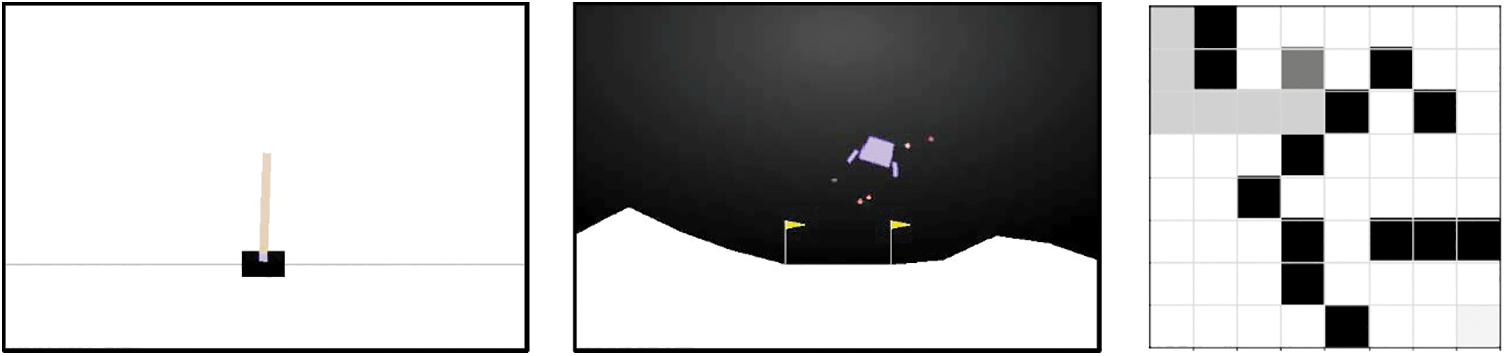
Figure 2: Screenshots of the three tasks. Left: Cartpole-v1, middle: LunarLander-v2, right: Maze traversal
For evaluation of consistency with earlier benchmarking on the tasks used here, the interpretability metric M is used as in [47]:
where l is formula size, no is the number of operations, nnao is the number of non-arithmetical operations, and nnaoc is the number of consecutive compositions of non-arithmetical operations. For assessing the statistical repeatability in the experiments, 10 independent runs are performed for every setting.
5.2.1 Performance on the CartPole-v1 Task
Fig. 3 shows the reward v/s episode variation for Cartpole-v1 for DQN [11] and that of its proposed ensemble. The red horizontal line corresponds to reward for solving the task. The dark brown and light brown vertical lines correspond to the episode number for which the task is solved by the original and proposed techniques, respectively. Fig. 4 shows the results within same environment and set of rules using DDQN [12] for the conventional and proposed approaches respectively. The horizontal red, vertical light-brown and vertical dark-brown lines have the same meanings as the previous Fig. 3. It is noted from Figs. 3 and 4 that the proposed approach converges much earlier (in 125 episodes) as compared to the conventional approach (in 146 episodes). After training, both of the competing techniques are allowed to run to evaluate their respective performances, which stay well above the minimum reward line. Table 2 shows the state-of-the-art results including those of our technique. It can be seen that the proposed ensemble R-DQN ensemble achieves the highest task score as shared by two other state-of-the-art techniques, while it achieves the second rank for the interpretability metric (M) among various competing techniques.
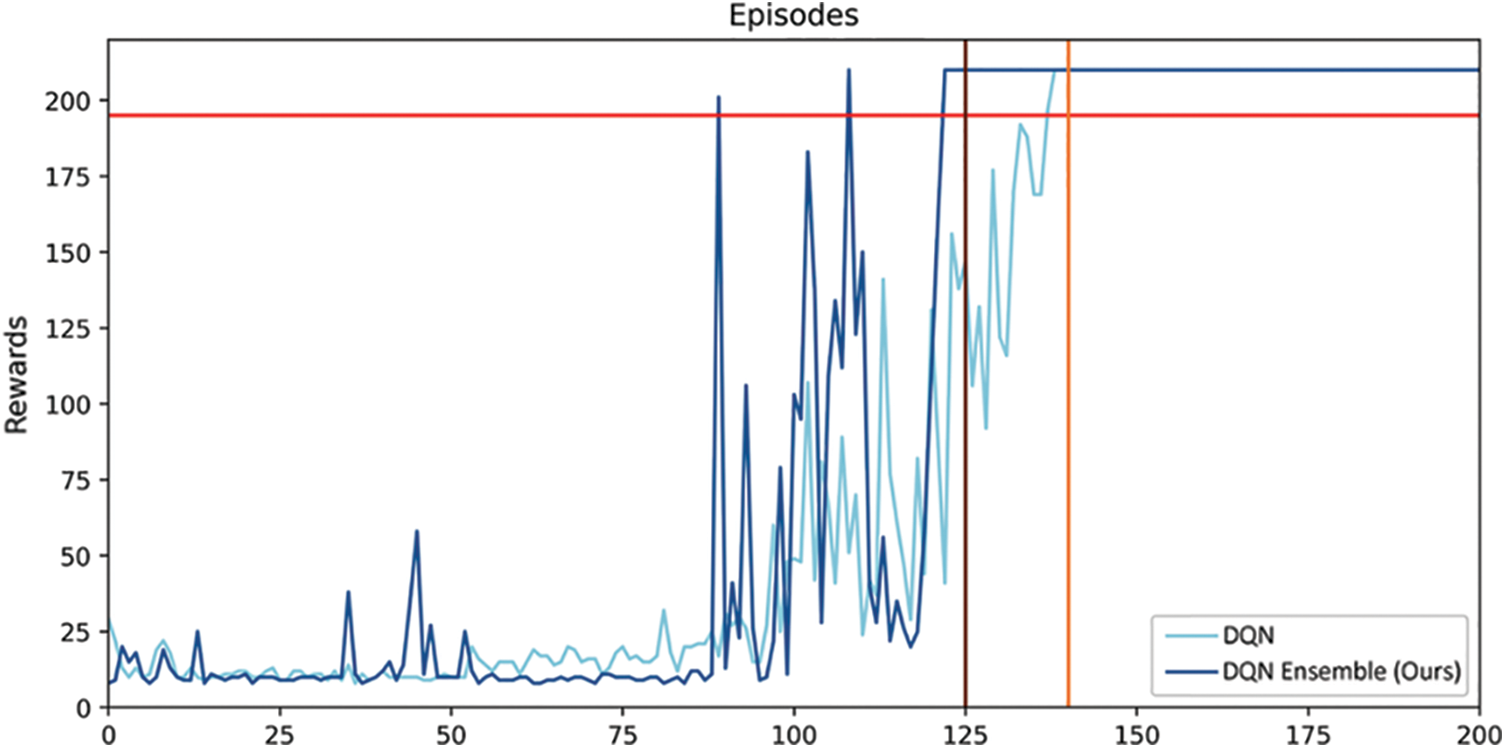
Figure 3: Rewards v/s Episodes obtained using DQN and the proposed DQN ensemble for Cartpole-v1
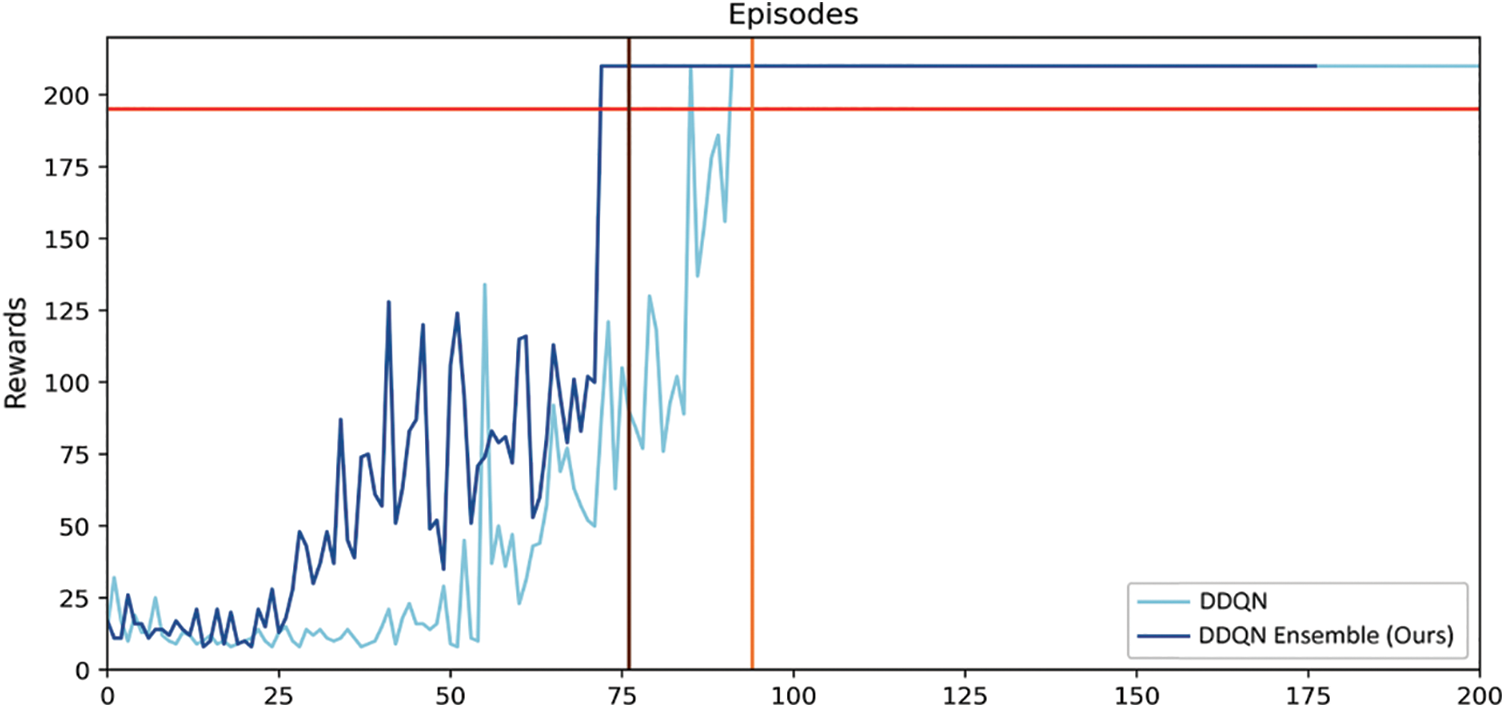
Figure 4: Rewards v/s Episodes obtained by using single DDQN and the proposed DDQN ensemble for Cartpole-v1
5.2.2 Performance on the LunarLander-v2 Task
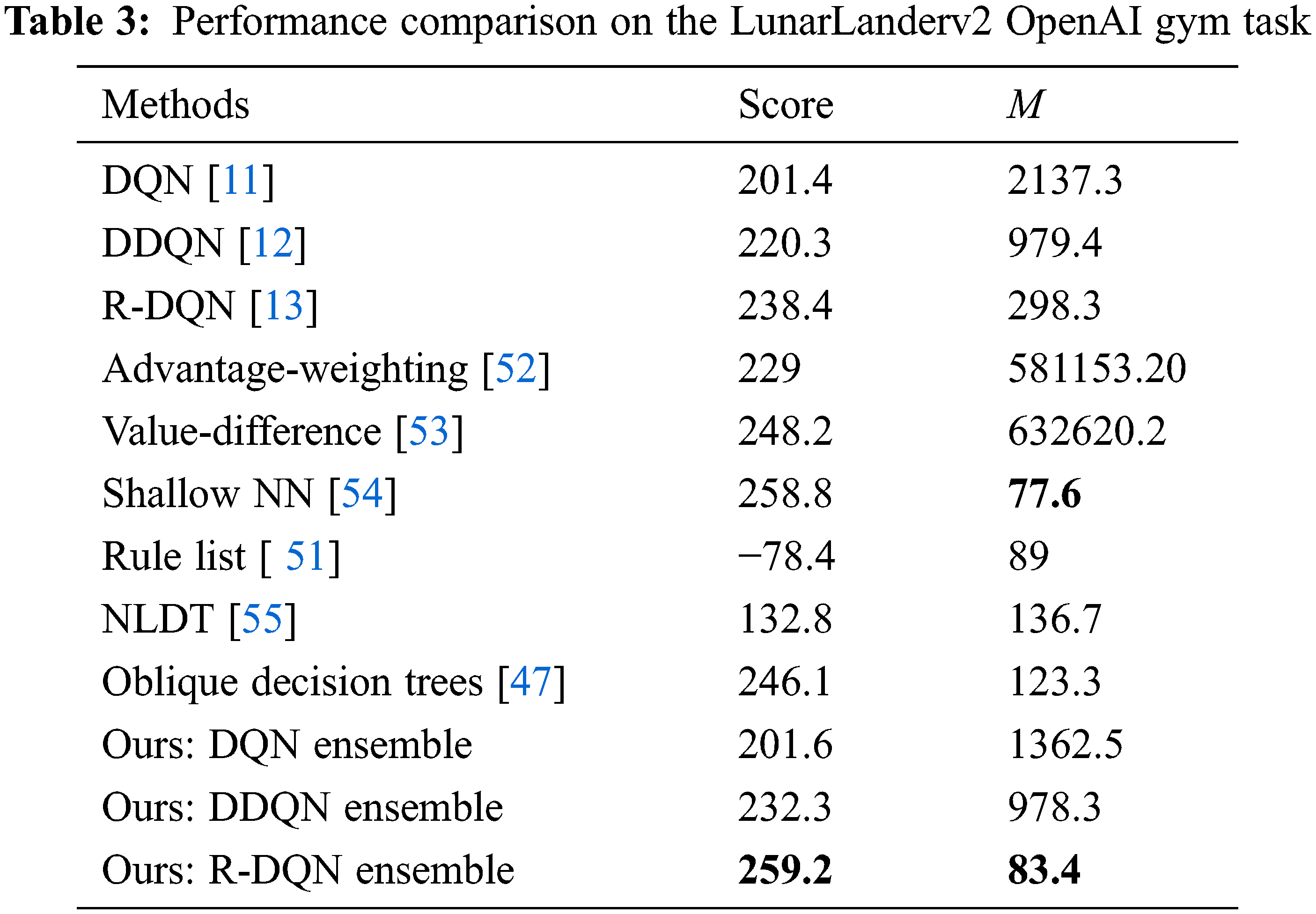
Fig. 5 shows the episode score v/s episodes for DQN and its proposed ensemble on the LunarLander-v2 task. It should be noted that the proposed ensemble is able to outperform the conventional DQN approach by converging in 671 episodes, whereas the conventional DQN approach lags behind by converging in 749 episodes. The performance of the state-of-the-art techniques including ours on the Lunarlander-v2 task is shown in Table 3. It can be seen from the table that the proposed R-DQN ensemble achieves first rank for the task score, and the second rank for the interpretability metric M among various competing techniques, respectively.
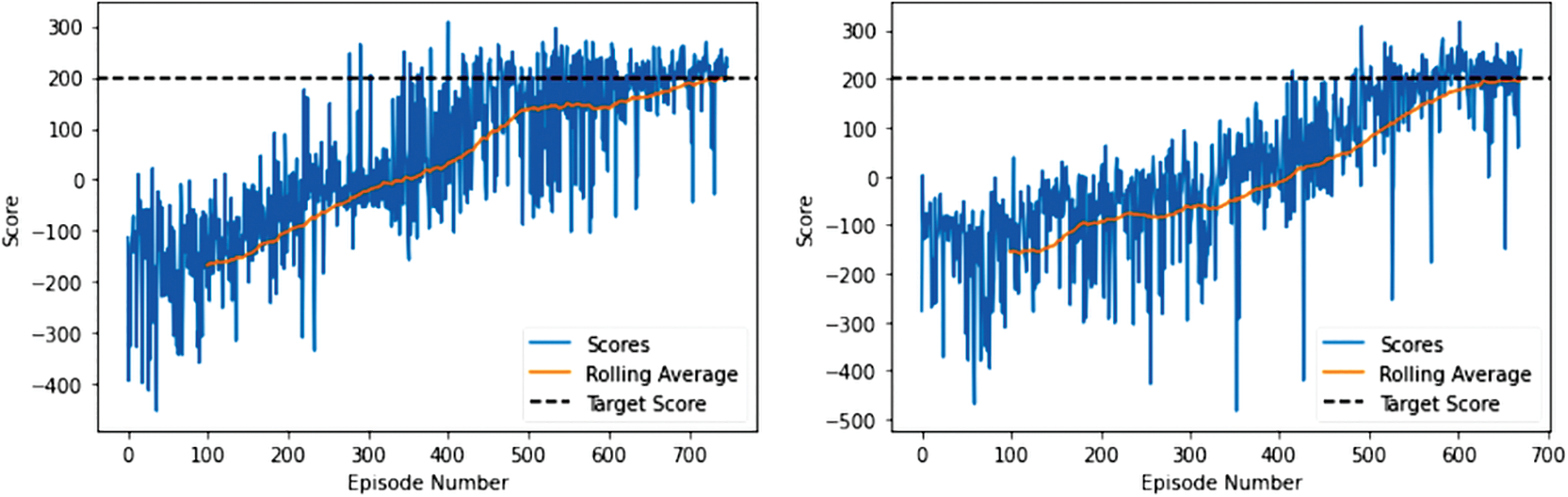
Figure 5: Score v/s episode performance on the LunarLander-v2 task. Left: For DQN and right for the proposed DQN ensemble
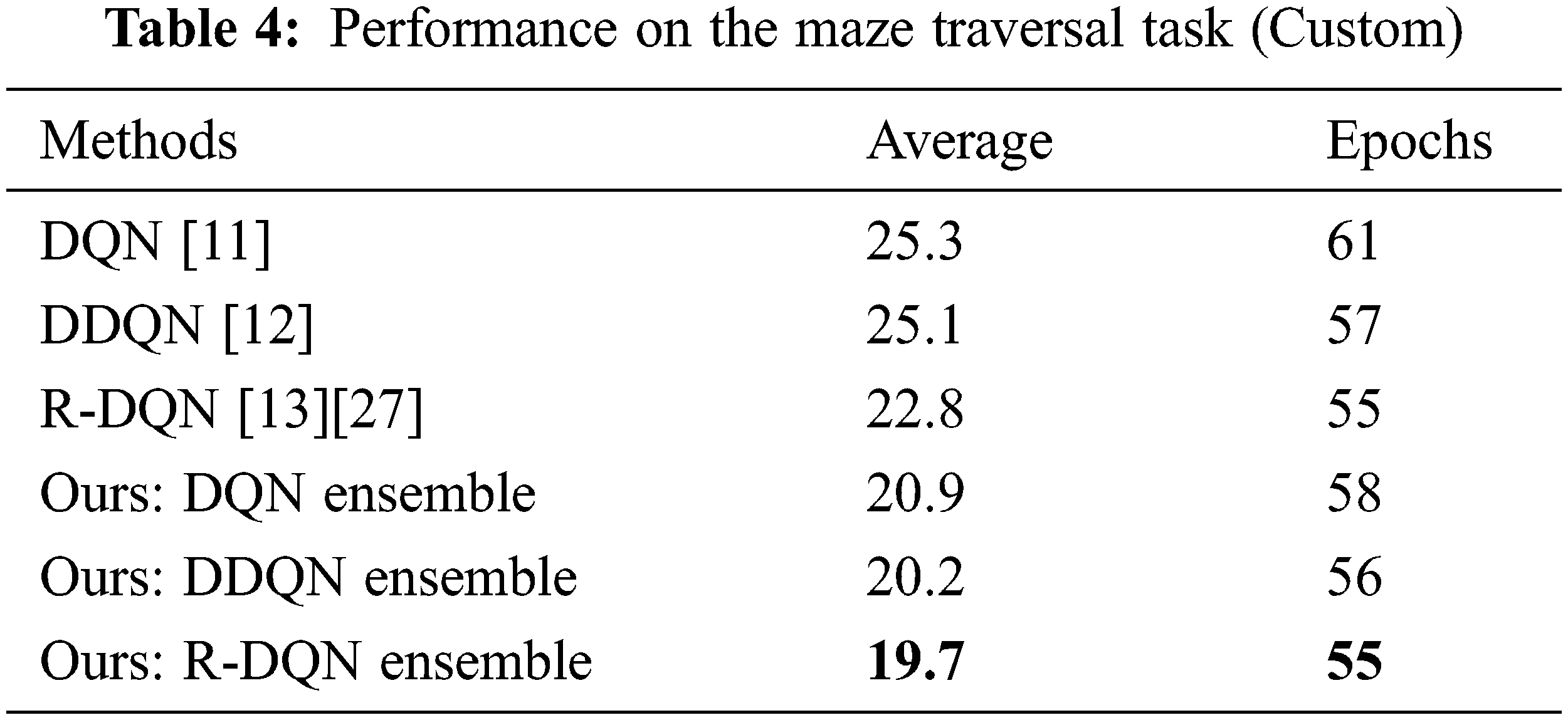
5.2.3 Performance on the Maze Traversal Task
For the custom maze traversal task, Fig. 6 shows the episode length per epoch v/s epochs for DQN and the proposed DQN ensemble respectively. The lesser the episode length, the lesser is the number of steps which the entity takes to reach the target cell for the particular epoch. The training stops when the win-rate becomes one. It should be noted that the proposed DQN ensemble approach converges in lesser number of epochs viz. 58, as compared to the conventional approach viz. 61 epochs which is an indication of the robustness of the proposed technique. Convergence takes place in this task when win-rate becomes one. Fig. 7 shows the total win count for both approaches till win-rate becomes one. Note that the total win count towards the end of training is higher for the proposed DQN ensemble compared to the original [11]. Table 4 shows the performance of DQNs on the Maze Traversal task, along with that of their respective proposed ensembles. The values are obtained till win-rate for the task becomes one. The proposed R-DQN ensemble achieves best results among various competing techniques. At this point, we would like to emphasize that the better performance of our ensemble technique can be attributed to parallelization of the decision-making, which offers distributed decision-making, allowing for more liberty per DQN entity, which in turn makes it more aware and efficient by reducing its load as compared to conventional single entity based techniques. All deep Q-Networks used in the proposed ensemble technique are as per their respective papers [17,26,27].
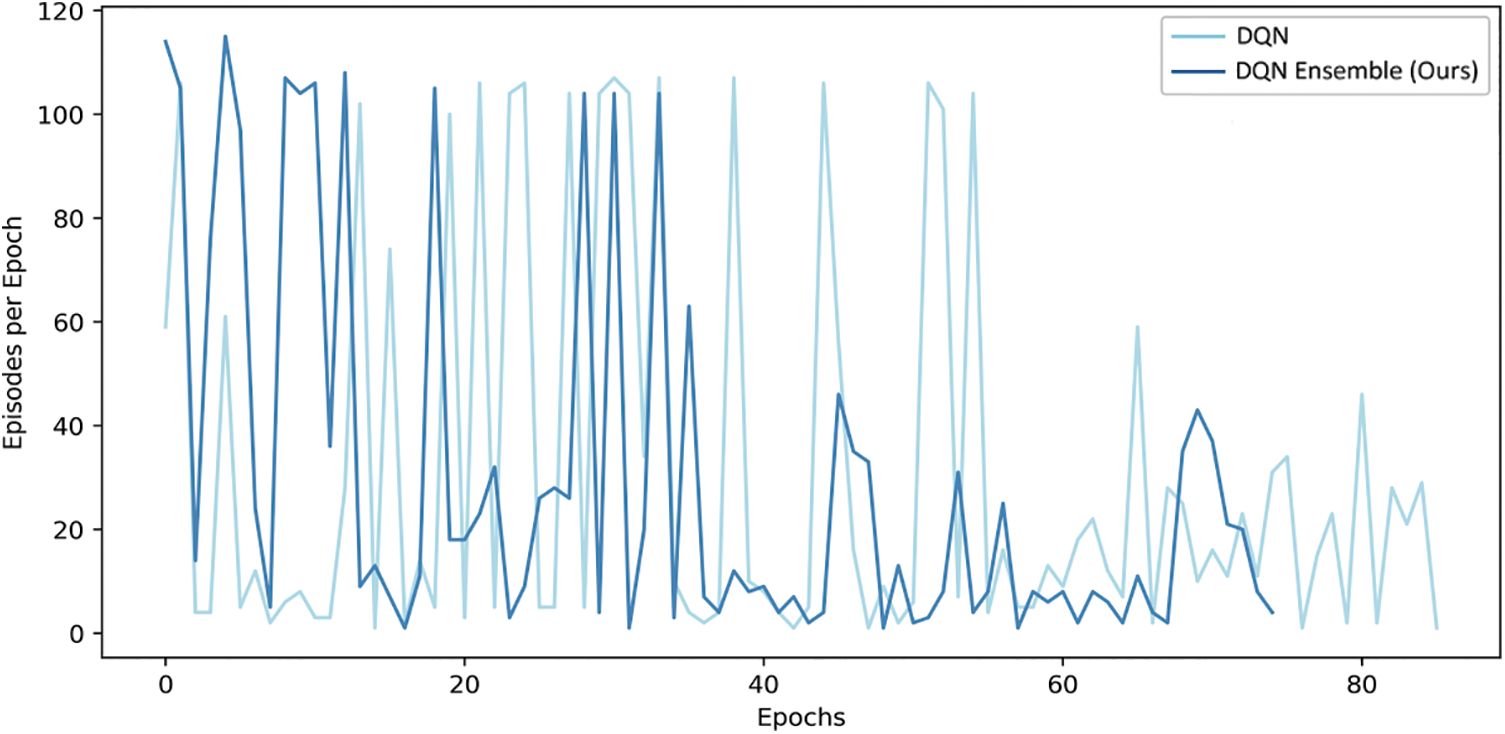
Figure 6: Episode length v/s epochs for maze traversal task using DQN [17] and the proposed DQN
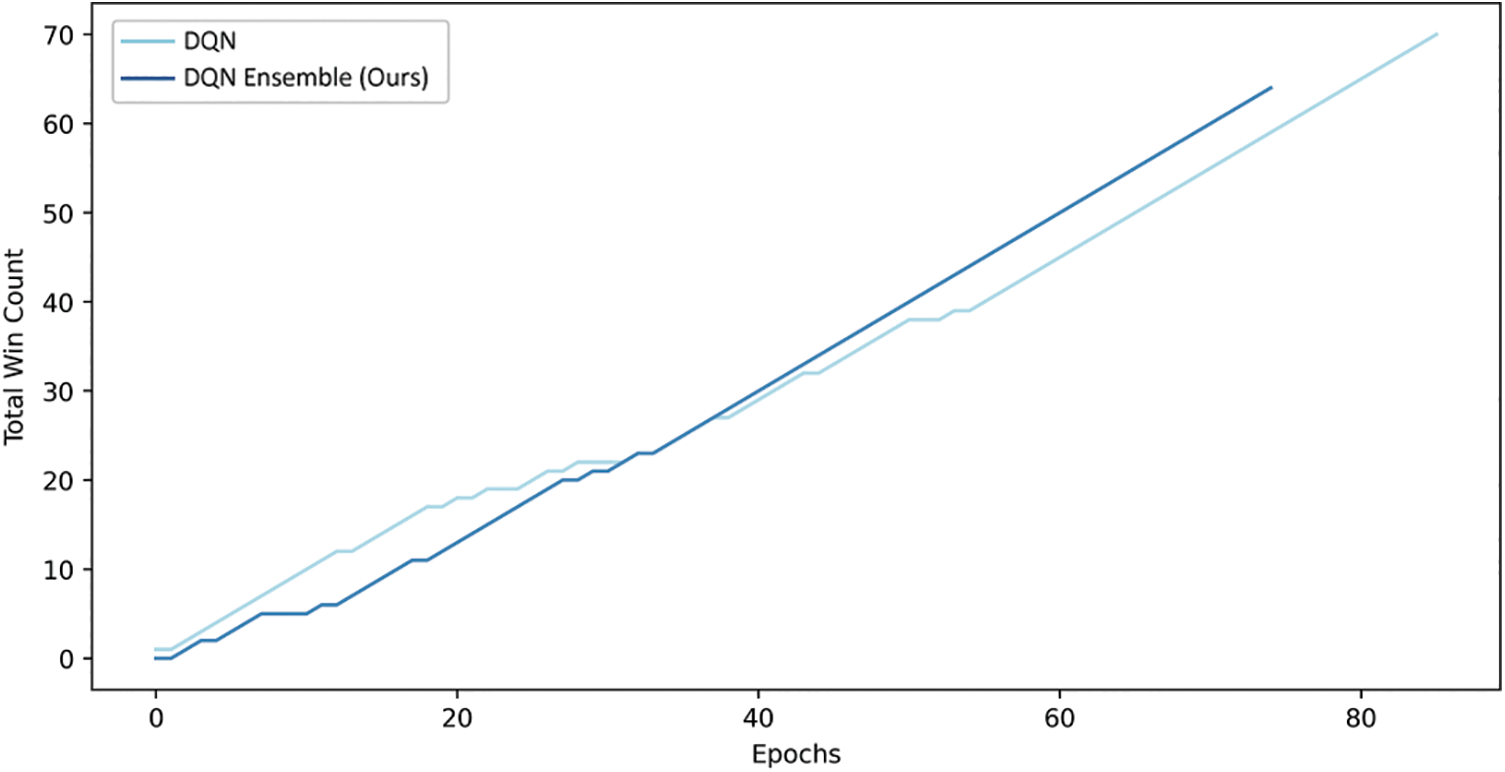
Figure 7: Total win count v/s epochs for the maze traversal task using DQN [17] and the proposed DQN
5.2.4 Performance on Atari 2600 Games
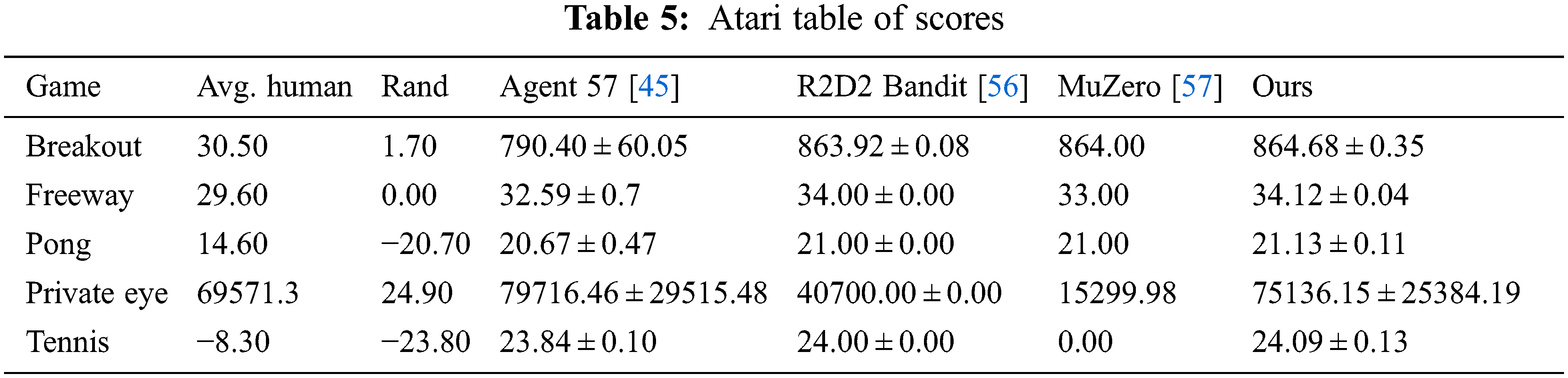
Experimentation for five Atari 2600 games [49] is also been done using an R-DQN based ensemble because of its superior performance. The results of the competing state-of-the-art techniques are from [45] and are shown in Table 5. It can be seen that the proposed the R-DQN ensemble generally outperforms other state-of-the-art techniques and achieves top results on 4 out of 5 Atari 2600 games.
Coming to the limitations of the proposed approach, it should be noted that the ensemble approach can perform many times faster using parallel processing hardware for better distribution of the load as mandated by the ensemble approach. Also, due to use of a limited local action space for every DQN in the ensemble and straightforward action decomposition rule, the performance can be improved if these aspects are improved. Also, finding better and more efficient DQNs for the proposed ensemble technique will be a fruitful exercise. Further using a larger action spaces can hopefully enrich the technique. We intend to take up these issues in the future. Another task which we intend to take up is applying the technique to real-world tasks like robotics and financial predictions.
In this paper, the efficacy of using parallel decision making in the DQN based systems for reinforcement learning has been highlighted in light of the difficulties faced by the contemporary techniques, like training issues and limited performance. Consequently a simple but efficient DQN ensemble technique is proposed using an ensemble of binary action based DQNs. For experimentation, ensembles of DQN, DDQN (Double Q-learning) and R-DQN have been used. The performances of the single DQNs, their respective ensembles, and other state-of-the-art techniques have been compared. The proposed Deep Q-network ensemble technique is able to outperform other state-of-the-art techniques on different RL tasks. For example, the proposed technique achieves first rank on scores of the Cartpole-v1 task, of the LunarLander-v2 task, and of four out of five Atari 2600 games. Issues associated with the proposed approach include having a limited local action space for each DQN-based entity in the ensemble. This action space needs to be augmented with richer information for more complex tasks. In addition, the action decomposition structure needs to be made more accommodating for extended decision-making in more complex tasks. Future work would involve applying the proposed approach to tasks that have a large action space and that are more complex, such as those found in real-world environments like robotics and others.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.
References
1. M. Hassaballah and A. I. Awad, in Deep Learning in Computer Vision: Principles and Applications, Boca Raton, FL: CRC Press, 2020. [Online]. Available: https://www.routledge.com/Deep-Learning-in-Computer-Vision-Principles-and-Applications/Hassaballah-Awad/p/book/9781032242859 [Google Scholar]
2. A. Amanat, M. Rizwan, A. R. Javed, M. Abdelhaq, R. Alsaqour et al., “Deep learning for depression detection from textual data,” Electronics, vol. 11, no. 5, pp. 676–689, 2022. [Google Scholar]
3. M. Hina, M. Ali, A. R. Javed, F. Ghabban, L. A. Khan et al., “SeFACED: Semantic-based forensic analysis and classification of e-mail data using deep learning,” IEEE Access, vol. 9, pp. 98398–98411, 2021. [Google Scholar]
4. F. Sajid, A. R. Javed, A. Basharat, N. Kryvinska, A. Afzal et al., “An efficient deep learning framework for distracted driver detection,” IEEE Access, vol. 9, pp. 169270–169280, 2021. [Google Scholar]
5. J. Zhang, J. Sun, J. Wang and X. -G. Yue, “Visual object tracking based on residual network and cascaded correlation filters,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 8, pp. 8427–8440, 2021. [Google Scholar]
6. S. Zhou and B. Tan, “Electrocardiogram soft computing using hybrid deep learning CNN-ELM,” Applied Soft Computing, vol. 86, pp. 105778, 2020. [Google Scholar]
7. S. Zhou, M. Ke and P. Luo, “Multi-camera transfer GAN for person re-identification,” Journal of Visual Communication and Image Representation, vol. 59, pp. 393–400, 2019. [Google Scholar]
8. W. Wei, J. Yongbin, L. Yanhong, L. Ji, W. Xin et al., “An advanced deep residual dense network (DRDN) approach for image super-resolution,” International Journal of Computational Intelligence Systems, vol. 12, no. 2, pp. 1592–1601, 2019. [Google Scholar]
9. X. Zhang, X. Chen, W. Sun and X. He, “Vehicle re-identification model based on optimized DenseNet121 with joint loss,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3933–3948, 2021. [Google Scholar]
10. D. Zhang, J. Hu, F. Li, X. Ding, A. -K. Sangaiah et al., “Small object detection via precise region-based fully convolutional networks,” Computers,” Materials & Continua, vol. 69, no. 2, pp. 1503–1517, 2021. [Google Scholar]
11. V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness et al., “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, 2015. [Google Scholar] [PubMed]
12. H. van Hasselt, A. Guez and D. Silver, “Deep reinforcement learning with double Q-learning,” in Proc. AAAI Conf. on Artificial Intelligence, Phoenix, Arizona USA, vol. 30, no. 1, 2016. [Google Scholar]
13. W. Meng, Q. Zheng, L. Yang, P. Li and G. Pan, “Qualitative measurements of policy discrepancy for return-based deep Q-network,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 10, pp. 4374–4380, 2020. [Google Scholar] [PubMed]
14. T. T. Nguyen, N. D. Nguyen and S. Nahavandi, “Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications,” IEEE Transactions on Cybernetics, vol. 50, no. 9, pp. 3826–3839, 2020. [Google Scholar] [PubMed]
15. P. Hernandez-Leal, B. Kartal and M. E. Taylor, “A survey and critique of multiagent deep reinforcement learning,” Autonomous Agents and Multi-Agent Systems, vol. 33, no. 6, pp. 750–797, 2019. [Google Scholar]
16. M. Toromanoff, E. Wirbel and F. Moutarde, “End-to-end model-free reinforcement learning for urban driving using implicit affordances,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 7153–7162, 2020. [Google Scholar]
17. R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, MIT Press, Cambridge, Massachusetts London, England, 2018. [Google Scholar]
18. B. Uzkent, C. Yeh and S. Ermon, “Efficient object detection in large images using deep reinforcement learning,” in Proc. IEEE Winter Conf. on Applications of Computer Vision, Seattle, WA, USA, pp. 1824–1833, 2020. [Google Scholar]
19. D. Zhang, J. Han, L. Zhao and T. Zhao, “From discriminant to complete: Reinforcement searching-agent learning for weakly supervised object detection,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 12, pp. 5549–5560, 2020. [Google Scholar] [PubMed]
20. R. Furuta, N. Inoue and T. Yamasaki, “Fully convolutional network with multi-step reinforcement learning for image processing,” in Proc. Thirty-Third AAAI Conf. on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conf. and Ninth AAAI Symp. on Educational Advances in Artificial Intelligence, Honolulu, Hawaii, USA, pp. 3598–3605, 2019. [Google Scholar]
21. M. Botvinick, S. Ritter, J. X. Wang, Z. Kurth-Nelson, C. Blundell et al., “Reinforcement learning, fast and slow,” Trends in Cognitive Sciences, vol. 23, no. 5, pp. 408–422, 2019. [Google Scholar] [PubMed]
22. A. M. Hafiz and G. M. Bhat, “Fast training of deep networks with one-class CNNs,” in Modern Approaches in Machine Learning and Cognitive Science: A Walkthrough: Latest Trends in AI, vol. 2, Springer International Publishing, Switzerland AG, pp. 409–421, 2021. [Google Scholar]
23. A. M. Hafiz and G. M. Bhat, “Deep network ensemble learning applied to image classification using CNN trees,” arXiv preprint arXiv:2008.00829, 2020. [Google Scholar]
24. A. M. Hafiz and M. Hassaballah, “Digit image recognition using an ensemble of one-versus-all deep network classifiers,” in Proc. Information and Communication Technology for Competitive Strategies, Springer, Singapore, 2021. [Google Scholar]
25. S. Carta, A. Ferreira, A. S. Podda, D. Reforgiato Recupero and A. Sanna, “Multi-DQN: An ensemble of deep Q-learning agents for stock market forecasting,” Expert Systems with Applications, vol. 164, pp. 113820, 2021. [Google Scholar]
26. L. J. Lin, “Scaling up reinforcement learning for robot control,” in Proc. Tenth Int. Conf. on Machine Learning, Amherst, MA, USA, Morgan Kaufmann Publishers Inc., pp. 182–189, 1993. [Google Scholar]
27. G. Palmer, K. Tuyls, D. Bloembergen and R. Savani, “Lenient multi-agent deep reinforcement learning,” arXiv preprint arXiv:1707.04402, 2017. [Google Scholar]
28. S. Omidshafiei, J. Pazis, C. Amato, J. P. How and J. Vian, “Deep decentralized multi-task multi-agent reinforcement learning under partial observability,” in Proc. 34th Int. Conf. on Machine Learning, Sydney, Australia, pp. 2681–2690, 2017. [Google Scholar]
29. Y. Zheng, Z. Meng, J. Hao and Z. Zhang, “Weighted double deep multiagent reinforcement learning in stochastic cooperative environments,” in Proc. PRICAI 2018: Trends in Artificial Intelligence, Cham: Springer International Publishing, pp. 421–429, 2018. [Google Scholar]
30. Z. -W. Hong, S. -Y. Su, T. -Y. Shann, Y. -H. Chang and C. -Y. Lee, “A deep policy inference q-network for multi-agent systems,” arXiv preprint arXiv:1712.07893, 2017. [Google Scholar]
31. M. Hausknecht and P. Stone, “Deep recurrent q-learning for partially observable MDPs,” in Proc. AAAI Fall Symp. Series, The Westin Arlington Gateway, Arlington, Virginia, pp. 29–37, 2015. [Google Scholar]
32. J. K. Gupta, M. Egorov and M. Kochenderfer, “Cooperative multi-agent control using deep reinforcement learning,” in Proc. AAMAS, Cham: Springer International Publishing, pp. 66–83, 2017. [Google Scholar]
33. A. Krizhevsky, I. Sutskever and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” in Proc. Advances in Neural Information Processing Systems, Lake Tahoe, Nevada, United States, vol. 25, 2012. [Google Scholar]
34. B. J. Krose, “Learning from delayed rewards,” Robotics and Autonomous Systems, vol. 4, no. 15, pp. 233–235, 1995. [Google Scholar]
35. M. G. Bellemare, Y. Naddaf, J. Veness and M. Bowling, “The arcade learning environment: An evaluation platform for general agents,” Journal of Artificial Intelligence Research, vol. 47, no. 1, pp. 253–279, 2013. [Google Scholar]
36. S. Gu, T. Lillicrap, I. Sutskever and S. Levine, “Continuous deep Q-learning with model-based acceleration,” in Proc. 33rd Int. Conf. on Machine Learning, New York, NY, USA, pp. 2829–2838, 2016. [Google Scholar]
37. Z. Wang, T. Schaul, M. Hessel, H. V. Hasselt, M. Lanctot et al., “Dueling network architectures for deep reinforcement learning,” in Proc. 33rd Int. Conf. on Machine Learning, New York, NY, USA, pp. 1995–2003, 2016. [Google Scholar]
38. R. S. Sutton, “Learning to predict by the methods of temporal differences,” Machine Learning, vol. 3, no. 1, pp. 9–44, 1988. [Google Scholar]
39. V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Lillicrap et al., “Asynchronous methods for deep reinforcement learning,” in Proc. 33rd Int. Conf. on Machine Learning, New York City, NY, USA, pp. 1928–1937, 2016. [Google Scholar]
40. M. Fortunato, M. G. Azar, B. Piot, J. Menick, I. Osband et al., “Noisy networks for exploration,” arXiv preprint arXiv:1706.10295, 2017. [Google Scholar]
41. M. G. Bellemare, W. Dabney and R. Munos, “A distributional perspective on reinforcement learning,” in Proc. 34th Int. Conf. on Machine Learning, International Convention Centre, Sydney, Australia, pp. 449–458, 2017. [Google Scholar]
42. M. Hessel, J. Modayil, H. Van Hasselt, T. Schaul, G. Ostrovski et al., “Rainbow: Combining improvements in deep reinforcement learning,” in Proc. Thirty-Second AAAI Conf. on Artificial Intelligence, New Orleans, Louisiana USA, pp. 3215–3222, 2018. [Google Scholar]
43. T. Schaul, J. Quan, I. Antonoglou and D. Silver, “Prioritized experience replay,” arXiv preprint arXiv:1511.05952, 2015. [Google Scholar]
44. D. Horgan, J. Quan, D. Budden, G. Barth-Maron, M. Hessel et al., “Distributed prioritized experience replay,” arXiv preprint arXiv:1803.00933, 2018. [Google Scholar]
45. A. P. Badia, B. Piot, S. Kapturowski, P. Sprechmann, A. Vitvitskyi et al., “Agent57: Outperforming the atari human benchmark,” in Proc. 37th Int. Conf. on Machine Learning, Virtual, pp. 507–517, 2020. [Google Scholar]
46. A. G. Barto, R. S. Sutton and C. W. Anderson, “Neuronlike adaptive elements that can solve difficult learning control problems,” IEEE Transactions on Systems, Man, and Cybernetics, vol. SMC-13, no. 5, pp. 834–846, 1983. [Google Scholar]
47. L. L. Custode and G. Iacca, “Evolutionary learning of interpretable decision trees,” arXiv preprint arXiv:2012.07723, 2020. [Google Scholar]
48. H. P. van Hasselt, “Insights in reinforcement learning: Formal analysis and empirical evaluation of temporal-difference learning algorithms,” Ph.D. dissertation, Utrecht University, 2011. [Google Scholar]
49. J. Xuan, J. Lu, Z. Yan and G. Zhang, “Bayesian deep reinforcement learning via deep kernel learning,” International Journal of Computational Intelligence Systems, vol. 12, pp. 164–171, 2018. [Google Scholar]
50. R. Beltiukov, “Optimizing Q-learning with K-FAC algorithm,” in Proc. AIST, Cham: Springer International Publishing, pp. 3–8, 2019. [Google Scholar]
51. A. Silva, M. Gombolay, T. Killian, I. Jimenez and S. -H. Son, “Optimization methods for interpretable differentiable decision trees applied to reinforcement learning,” in Proc. 23rd Int. Conf. on Artificial Intelligence and Statistics, pp. 1855–1865, 2020. [Google Scholar]
52. X. B. Peng, A. Kumar, G. Zhang and S. Levine, “Advantage-weighted regression: Simple and scalable off-policy reinforcement learning,” arXiv preprint arXiv:1910.00177, 2019. [Google Scholar]
53. Z. Xu, L. Cao and X. Chen, “Deep reinforcement learning with adaptive update target combination,” The Computer Journal, vol. 63, no. 7, pp. 995–1003, 2020. [Google Scholar]
54. M. Malagon and J. Ceberio, “Evolving neural networks in reinforcement learning by means of UMDAc,” arXiv preprint arXiv:1904.10932, 2019. [Google Scholar]
55. Y. Dhebar, K. Deb, S. Nageshrao, L. Zhu and D. Filev, “Interpretable-AI policies using evolutionary nonlinear decision trees for discrete action systems,” arXiv preprint arXiv:2009.09521, 2020. [Google Scholar]
56. S. Kapturowski, G. Ostrovski, J. Quan, R. Munos and W. Dabney, “Recurrent experience replay in distributed reinforcement learning,” in Proc. Int. Conf. on Learning Representations, Vancouver Canada, 2018. [Google Scholar]
57. J. Schrittwieser, I. Antonoglou, T. Hubert, K. Simonyan, L. Sifre et al., “Mastering atari, Go, chess and shogi by planning with a learned model,” Nature, vol. 588, no. 7839, pp. 604–609, 2020. [Google Scholar] [PubMed]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF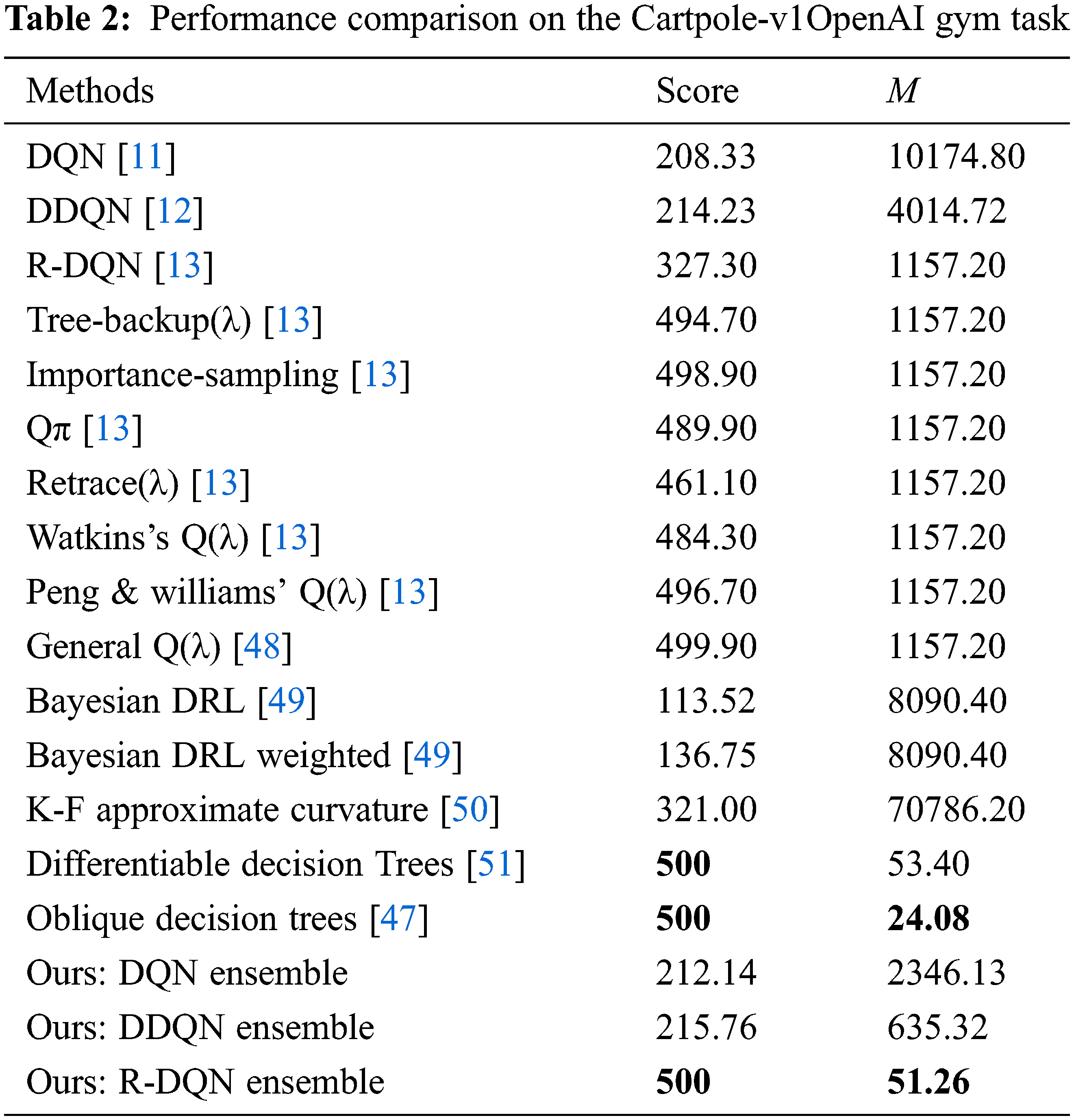
 Downloads
Downloads
 Citation Tools
Citation Tools