High-Imperceptibility Data Hiding Scheme for JPEG Images Based on Direction Modification

1  Introduction

With the development of the Internet and portable digital products, multimedia data, such as images and videos, have become the main medium for transmitting information. More and more users are choosing to store their personal data by using public network platforms, such as Weibo, WeChat, and Cloud-disk [1], which bring certain threats to the security of users’ private data. Data hiding [2–7], is an important data protection technology that is based on insensitivity of the human visual system (HVS) and the redundancy of the image itself to embed the data that are needed to be protected into another open carrier. The carrier that contains the embedded data is visually indistinguishable from the original carrier, and this ensures the security of the data that are being protected. In this paper, the carrier that contains the embedded data is called the marked image.

The early DH schemes were based mostly on uncompressed images. However, with the increasing demand for information, compressed images are more suitable for transmission and storage in the network. Currently, the JPEG [8] is one of the most extensively used image compression format. It can control the sizes of images by using a variable compression ratio, thereby saving the transmission bandwidth and storage space of the images. However, compared with uncompressed images, JPEG images have some weaknesses, such as less redundancy, limited embedding capacity, and higher visual distortion caused by the modification of arbitrary data. Therefore, data hiding for JPEG images is more challenging [9–13], and this has become one of the major studies in the field of DH.

Existing DH schemes for JPEG images can be summarized into three kinds, i.e., (1) schemes that modify the huffman code [14–16], (2) schemes that modify the quantization table [17–20], and (3) schemes that modify the quantized DCT coefficient [21–29]. In the first kind, Mobasseri et al. [14] were the first to propose embedding the secret data by building the mapping between a used variable length code (VLC) and an unused VLC in the code-table. This scheme ensures the advantage of file size increment, but it has a low embedding capacity. Subsequently, Hu et al. [15] improved the performance of Mobasseri et al.’s scheme by making full use of an unused VLC by specific mapping strategies to increase the embedding capacity. Although this kind of schemes can guarantee the visual quality and file size increment of the marked JPEG images, the embedding capacities of such schemes are quite limited.

The second kind of schemes was proposed first by Fridrich et al. [17] in 2002, and it was extended by Wang et al. [20]. In this extended scheme, the embedded space was made by decreasing certain the quantization step and increasing the corresponding quantized DCT coefficients to achieve higher embedding capacity and better visual quality. But the reduction of the quantization steps leads to a decrease in the compression rate, and the file size increment may increase appreciably. For the second kind of schemes, changes to the quantization table break the balance between the image quality and the file size increment during the compression process, and this leads to the obviously increase in file size increment of the marked JPEG image.

The third kind of schemes that modify the quantized DCT coefficients can obtain a balance among the quality of the image, the embedding capacity, and the file size increment, so it has become the mainstream of current research in data hiding for JPEG images. Xuan et al. [21] proposed reversible data hiding (RDH) for JPEG based on histogram of the DCT coefficient-pairs, this approach designed the optimal search strategy to improve the image quality. Nikolaidis [23] used the zero value of the quantized DCT coefficients to hide the secret data. Compared with many schemes that modify the non-zero quantization coefficients, this scheme obtains better image quality while maintaining the same embedding capacity. In 2016, RDH for JPEG images proposed by Huang et al. [26] designed one-dimensional (1D) histogram shifting rules of DCT coefficients, and selected the AC coefficients with absolute values of 1 to hide the secret data, and shifted the remaining AC coefficients to assist the embedding operation. Moreover, the optimization strategy that preferentially selects DCT blocks with more zero coefficients for embedding both improves the embedding capacity and maintains the file size. Subsequently, Hou et al. [27] extended Huang et al.’s scheme [26] by introducing a frequency selection and block sorting strategy in order to reduce distortion. After that, Li et al. [28] built a 2D histogram by pairing every two non-consecutive-zero AC coefficients in the same frequency, and they designed an effective 2D mapping rule to modify coefficient-pair in order to hide the secret data. This scheme improved the image quality and reduced the file size increment, but the amplitude relationship between coefficients is not considered during the process of pairing the coefficients, thus the optimal rate distortion performance could not be obtained. Therefore, the adaptive RDH for JPEG images based on coefficient pairing was proposed by Wu et al. [29] to improve Li et al.’s scheme [28]. This scheme pairs the small AC coefficients to construct a 2D reversible mapping rule and to select coefficients with different frequencies in each block by combining the adaptive frequency strategy to hide the secret data. The experimental results show that this scheme has obvious advantages in image quality and file size increment when it is compared with previous schemes.

Although the schemes mentioned above strive to improve visual image quality and the embedding capacity while reducing the file size increment, the results are not satisfactory. Thus, we propose a high-imperceptibility data hiding for JPEG image based on direction modification. In our scheme, all of the quantized DCT blocks are sorted, and non-consecutive-zero AC coefficients (NCAC) with absolute values less than or equal to 1 at the same frequency position in two adjacent blocks were selected to complete the pairing. According to the guidance of the randomly filled reference matrix, the 2-bit secret data can be hidden into a selected coefficient-pair by using the designed direction modification rules. Because the rule of direction modification restricts the DCT coefficients to switch only among −1, 0, and 1, the proposed scheme obtained a higher visual image quality of the marked JPEG image and a smaller file size increment.

The rest of this paper is organized as follows: In Section “Related works”, the overview of JPEG compression and the two related schemes are presented. Our scheme is described in Section “Proposed scheme”. And then, the experimental results and discussion in comparison with existing schemes are described in Section “Experimental results and analysis”. Section “Conclusion” is addressed at the end of this paper.

2  Related Works

2.1 Overview of JPEG Compression

As shown in Fig. 1, the JPEG compression process includes mainly three parts, i.e., the DCT transform, quantization and entropy coding.

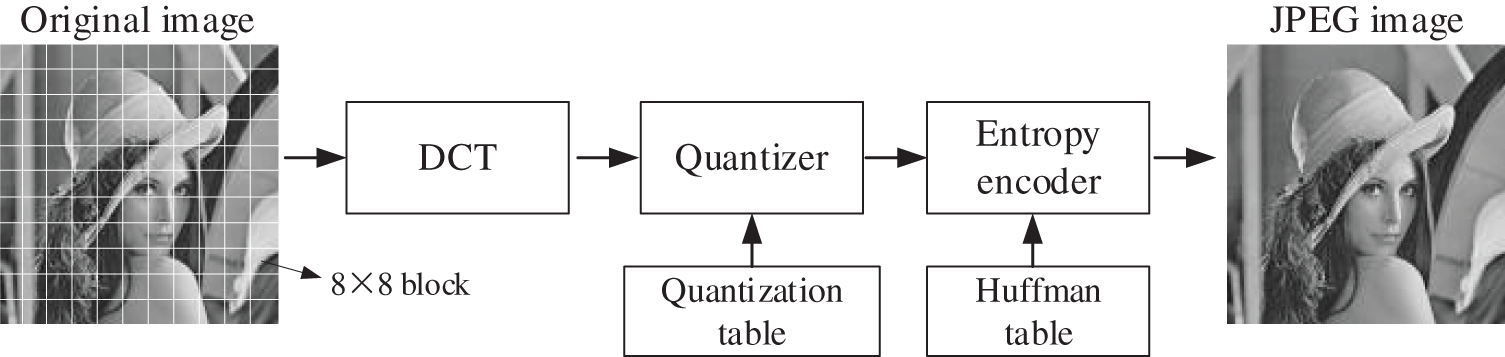
Figure 1: The encoding process of JPEG images

The JPEG encoding process is as follows:

(1) Divide the original image into non-overlapping 8 × 8 image blocks;

(2) For each block, Eq. (1) is used for DCT transformation to convert the original image into the frequency domain:

P(a,b)=r(a)r(b)4∑i=07∑j=07p(i,j)cos⁡((2i+1)aπ16)cos⁡((2j+1)bπ16)(1)

where, r(a)={12,a=01, others, p(i,j) represents the pixel value of the original image on coordinate (i, j), and P(a,b) is the DCT coefficient value in the frequency domain, whose frequency coordinate is {a, b};

(3) An 8 × 8 quantization table was used to quantify the obtained DCT coefficients, and the quantized DCT coefficients were obtained by Eq. (2):

h(a,b)=Round(P(a,b)g(a,b))(2)

where, g(a,b) is the quantization step at the corresponding frequency (a, b) in the quantization table, and h(a, b) is the quantized DCT coefficient;

(4) Entropy coding was used on the quantized direct current (DC) coefficient and the encoded AC coefficient to get the compressed bit stream; then, the JPEG image is obtained.

2.2 Huang et al.’s Scheme

Huang et al. [26] selected the quantized AC coefficients values of “±1” in smooth blocks defined by Eq. (3) for extended embedding.

Tk=#{j:djk=0,1≤j≤63}(3)

where Tk denotes the smoothness of the kth block, # is the cardinality of a set, i.e., the number of zero AC coefficients in each block.

The histogram is generated from non-zero AC coefficients in the quantized DCT blocks, and the secret bit s to be embedded determines whether or not the histogram is shifted when embedding. The embedding process of the secret bit is described by Eq. (4):

d^jk={djk+s, if djk=1djk−s, if djk=−1djk, if djk=0djk+1, if djk>1djk−1, if djk<−1(4)

where d^jk denotes the modified non-zero AC coefficient, and s∈{0,1} indicates the secret bit to be embedded. The embedding operation occurs only on the smoothest first t blocks, where t indicates the number of the selected blocks that can provide sufficient embedding capacity.

2.3 Wu et al.’s Scheme

The detailed depiction of Wu et al.’s scheme [29] is given as follows:

First, all of the quantized DCT coefficient blocks were arranged in descending order according to the number of zero-coefficient, and they were divided into 4 sets with different texture complexity, i.e., R1={B1,…,B⌊N/4⌋}, R2={B⌊N/4⌋+1,…,B⌊N/2⌋}, R3={B⌊N/2⌋+1,…,B⌊3N/4⌋}, R4={B⌊3N/4⌋+1,…,BN}, where R1 represents the smoothest blocks, R4 represents the blocks that have the most texture, and N is the number of the quantized DCT blocks.

Second, a frequency selection strategy was designed according to the texture complexity of each block. For any given block Bi(1≤i≤N), the sequence of AC coefficients obtained by Zig-zag scanning is (d1i,d2i,…,d63i). Suppose that the sequence of AC coefficients selected for pairing is (dmi,…,dni), where 1≤m≤n≤63, and the starting frequency m and the cut-off frequency n are determined according to Eq. (5):

{m=⌈iN×T1⌉n=T2(5)

where ⌈⋅⌉ means round up. T1 and T2 (1≤T1,T2≤63) are two parameters that can obtain optimal starting and cut-off frequencies. The optimal parameters, T1 and T2, can be obtained by minimizing the mean squared error (MSE) between the marked image and the original image, as shown in Eq. (6).

{(T1∗,T2∗)=argminED(T1,T2)T1,T2subject to EC(T1,T2)≥P.(6)

where P is a given embedded capacity, ED(T1,T2) and EC(T1,T2) are expressed as distortion and embedding capacity, respectively. The optimal parameter (T1∗,T2∗) can be obtained by exhaustive search.

Finally, non-zero AC coefficients with absolute values that are not greater than k in the selected frequency band are selected for pairing, and secret data are embedded according to the two-dimensional mapping rule, while non-zero AC coefficients dji with absolute values greater than k are shifted using to Eq. (7).

d⌢ji={dji+1, if dji>kdji−1, if dji<−k(7)

3  Proposed Scheme

Fig. 2 shows a framework of our scheme, and the process of data hiding is applied in the quantized DCT coefficients, and it includes three stages, i.e., block sorting, coefficient pairing and data embedding. All of the digital symbols used in our scheme are shown in Table 1.

Figure 2: Framework of our scheme

3.1 Block Sorting

In the JPEG compression process, each 8 × 8 quantized DCT coefficient block is scanned in zig-zag order to obtain the coefficient sequence Di=(d0i,d1i,…,d63i). We divided the AC coefficients into two parts, i.e., non-consecutive-zero AC coefficients (NCAC) and consecutive-zeros AC coefficients. Because modification of DC and consecutive-zeros AC coefficients may reduce the image quality drastically while increasing the file size, they are not used in our scheme. Therefore, the coefficient sequence that can be used for pairing and embedding data is expressed as D⌢i=(d1i,…,dki).

In order for our scheme to obtain better performance, all of the quantized DCT blocks (D⌢1,D⌢2,…,D⌢N are sorted in ascending order, and a new block sequence (D⌢γ(1),D⌢γ(2),…,D⌢γ(N) is generated, and γ:{1,2,…,N}→{1,2,…,N} is the unique one-to-one mapping, such that kγ(1)≤⋯≤kγ(N), and γ(i)<γ(j) if kγ(i)=kγ(j) with i<j.

In our scheme, the advantages of sorting the blocks are reflected mainly in the following two aspects:

1) Sorting in ascending order can ensure that more coefficients in low frequency are used preferentially, thus reducing the distortion in the embedding process.

2) Reducing the difference of kγ(i) and kγ(i+1) in two adjacent DCT blocks can achieve more valid coefficient-pair for embedding, thus improving the embedding capacity. Fig. 3 gives an example indicating that large differences of kγ(i) and kγ(i+1) lead to pair failure.

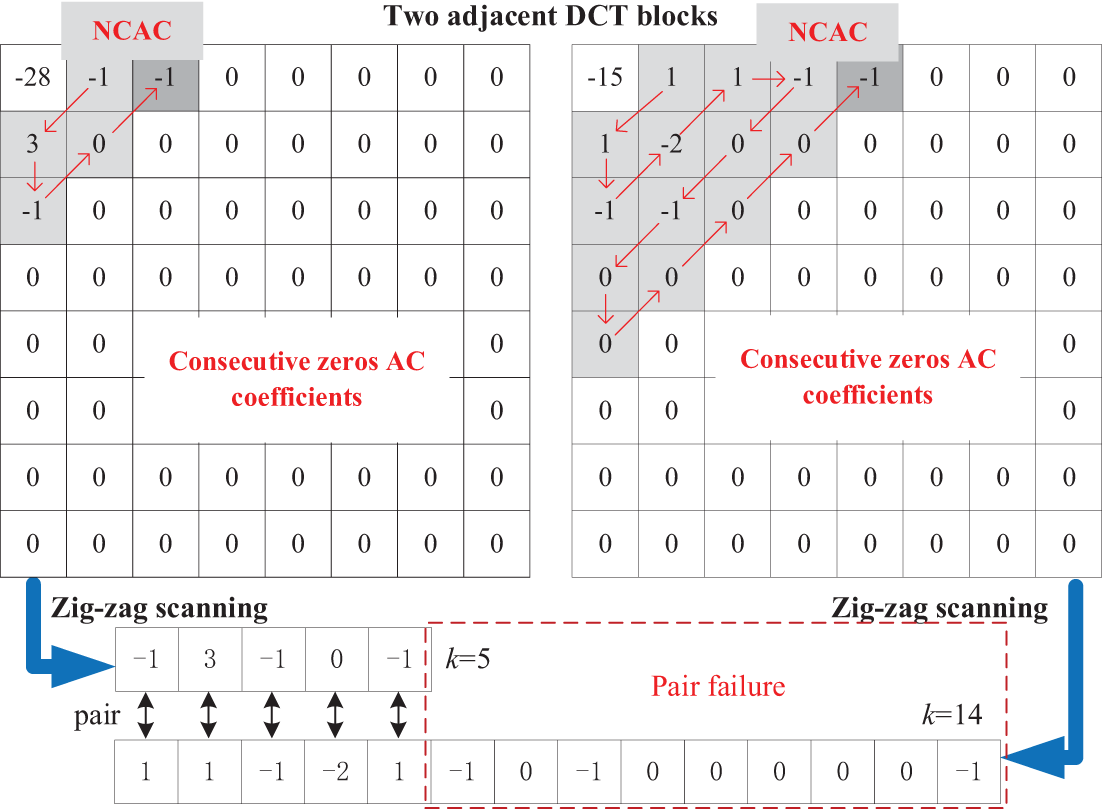
Figure 3: Example showing that large differences of k lead to pair failure

3.2 Coefficient Pairing

Fig. 4 gives an example of an AC coefficient histogram at the same frequency position for Lena when the QF is equal to 70, 80, and 90, respectively. This figure shows that the AC coefficients at the same frequency position are mainly concentrated in −1, 0, 1. Based on this, our scheme selects NCAC with high occurrence frequency and absolute value less than or equal to 1 in two adjacent blocks for pairing in order to obtain more coefficient-pairs for embedding. The sorted sequence is (D⌢γ(1),D⌢γ(2), . . . , D⌢γ(N)), and the pairing process is shown in Eq. (8).

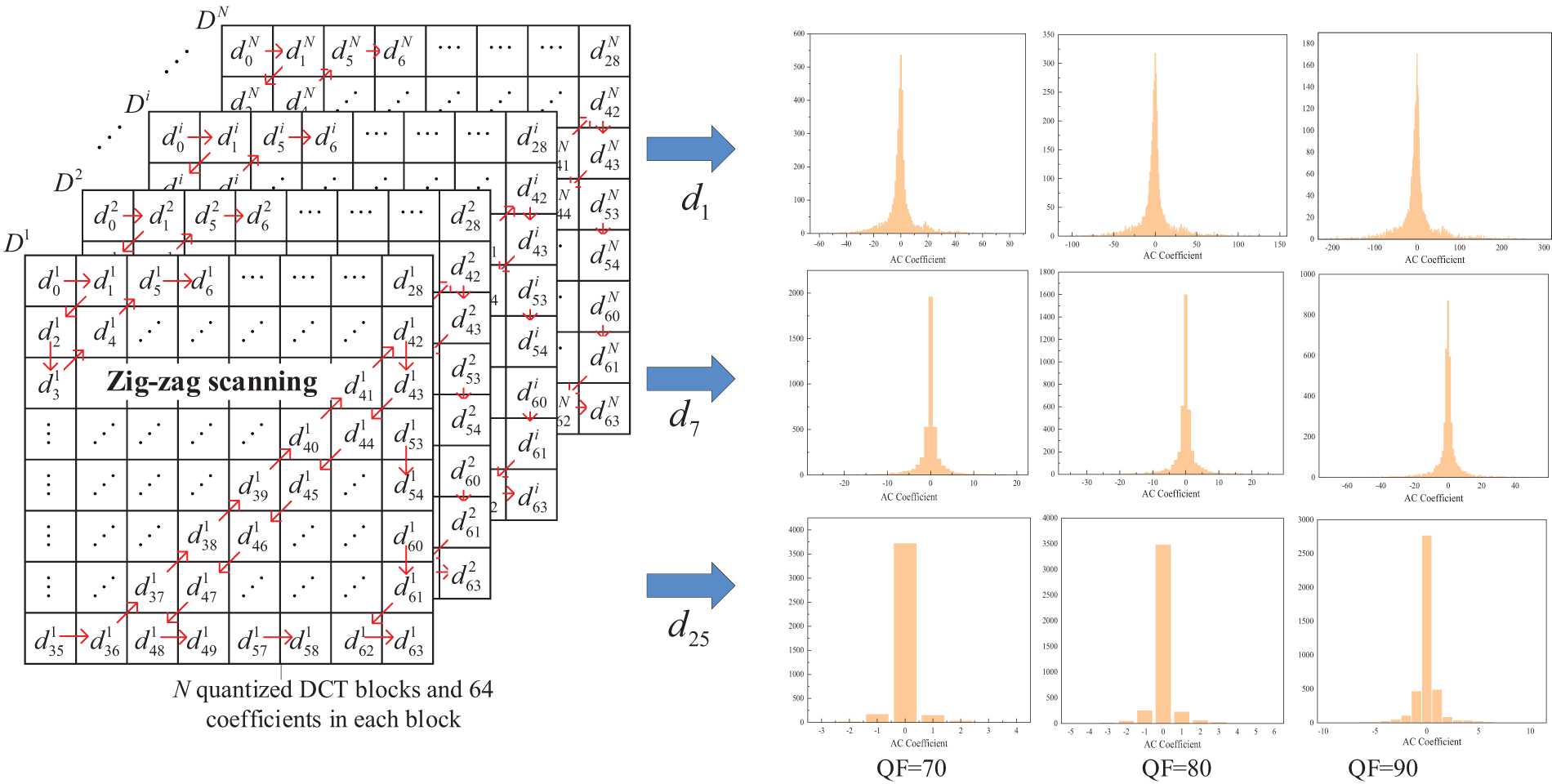
Figure 4: The distribution of the quantized DCT blocks and AC coefficient histogram at the same frequency position for Lena

C={(djγ(p),djγ(p+1)):−1≤djγ(p),djγ(p+1)≤1,1≤j≤kγ(p)}(8)

where p is odd, djγ(p), djγ(p+1) are coefficients at the jth frequency position of two adjacent blocks.

Fig. 5 shows the two-dimensional distribution of the coefficient-pair of “Lena” and “Baboon” at QF = 80 in our scheme, where the horizontal and vertical coordinates represent the values of the coefficients. This histogram shows that the peak points appear on the coefficient-pair (0, 0), and the surrounding position centered at (0, 0), i.e., (−1, −1), (−1, 0), (−1, 1), (0, −1), (0, 1), (1, −1), (1, 0), and (1, 1), their number also is greater than the number of the other coefficient-pairs.

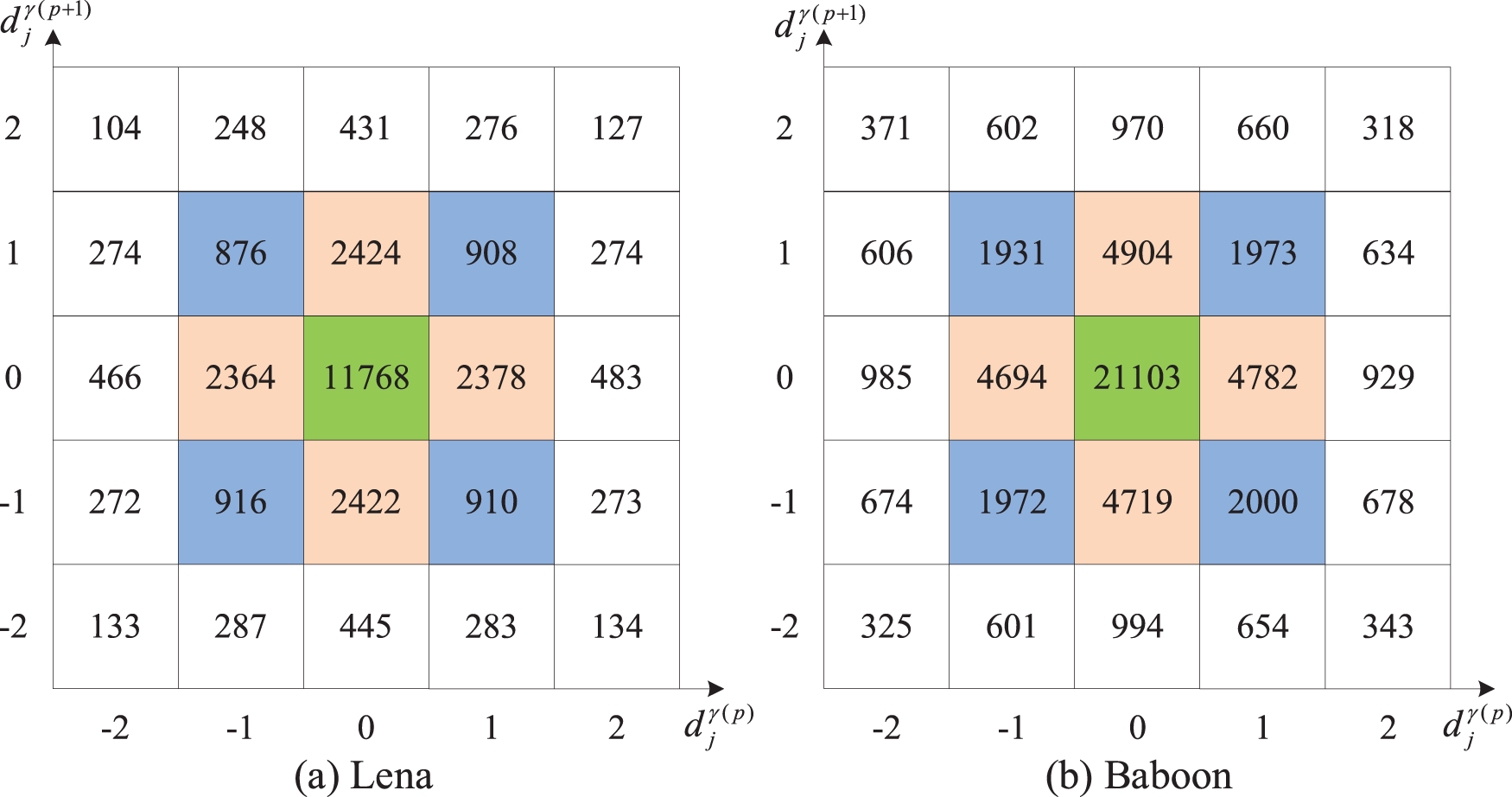
Figure 5: The 2D histogram of coefficient-pair at QF = 80 in our scheme

3.3 Data Embedding

In order to ensure the embedding capacity while considering the performances of both the image quality and the file size increment, we selected the nine coefficient-pairs with the highest frequency, i.e., (0, 0), (−1, −1), (−1, 0), (−1, 1), (0, −1), (0, 1), (1, −1), (1, 0), (1, 1) to embed the secret data.

First, we divided the coefficient-pair (djγ(p),djγ(p+1)) into the following three types:

Type A: (djγ(p),djγ(p+1)) = {(−1, −1), (−1, 1), (1, −1), (1, 1)};

Type B: (djγ(p),djγ(p+1)) = {(−1,0), (0, −1), (1, 0), (0, 1)};

Type C: (djγ(p),djγ(p+1)) = {(0, 0)}.

Also, as shown in Fig. 6, we designed the direction modification rule of every type. The coefficient-pairs in type A are changed from ±1 to 0, thus reducing the file size increment, but a diagonal shift result in a maximum coefficient modification of 2. In type B, coefficient-pairs (−1, 0) and (1, 0) have diagonal modification, but the balanced conversion of 0 and ±1 does not result in an increase in the file size. For type C, the maximum modification is only 1, so images with better qualities can be obtained; but more modification of 0 to ±1 will cause file size to increase. Therefore, users can balance the relationship among embedding capacity, image quality, and file size increment according to their requirements, and they can optimally select the different types of the coefficient-pair to obtain better performance.

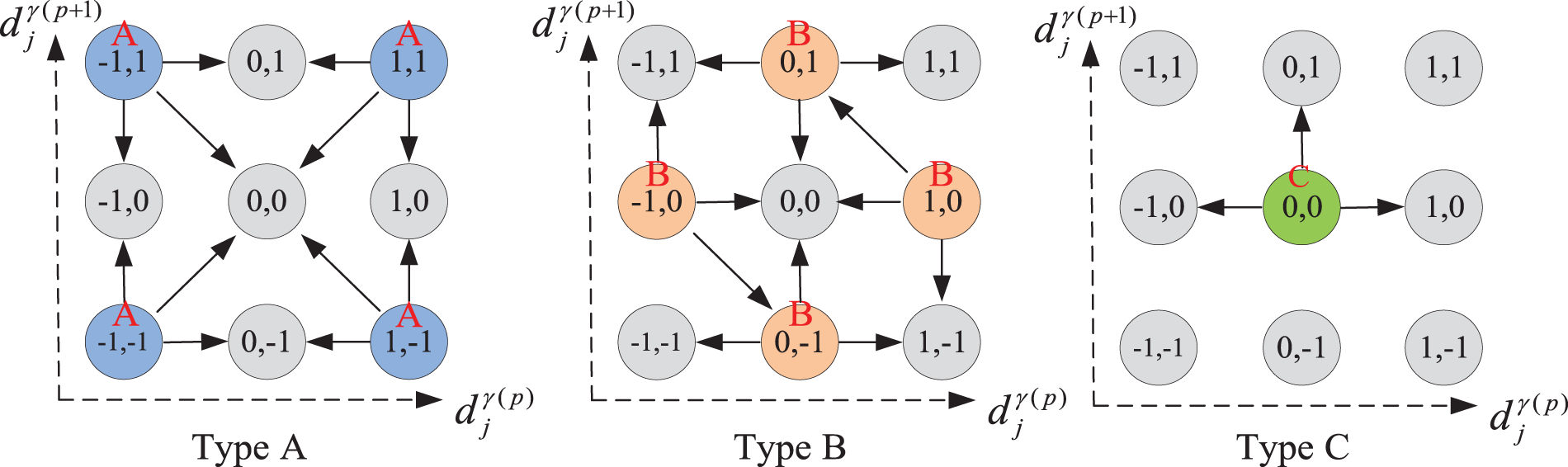
Figure 6: Direction modification rule for different types of coefficient-pairs

Then, we randomly filled the reference digit R with 4-ary notational system into the corresponding position of the coefficient-pair (djγ(p),djγ(p+1)) to generate a reference matrix,as shown in Fig. 7. This reference matrix is used to guide the embedding of secret data into a selected coefficient-pair. The filled data must meet the following two requirements: (1) In the same row, the difference value between the two adjacent digit is 1 (modulo 4); (2) In the same column, the difference value between the two adjacent digit is 2 (modulo 4). Random filling operations can improve the security of our scheme, and the filled rules ensure that every digit can find all other reference digit in its neighborhood.

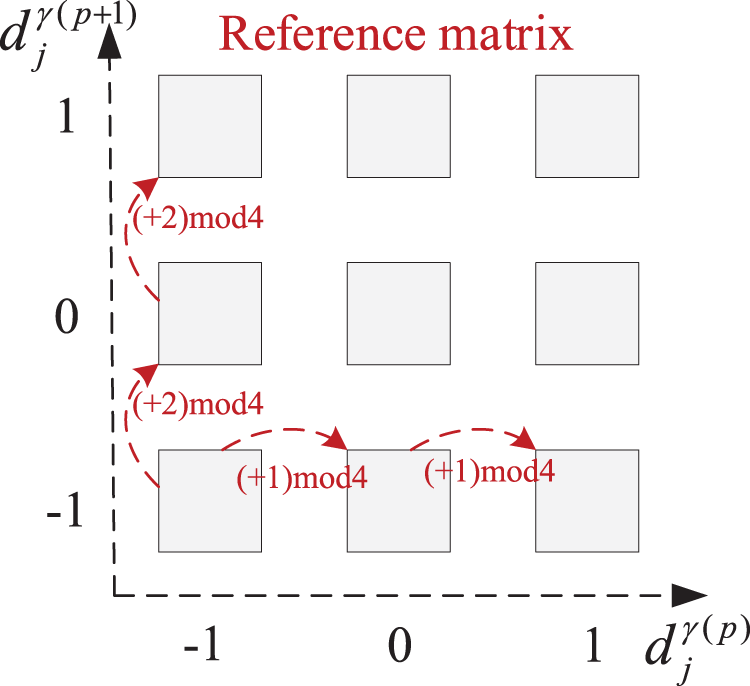
Figure 7: Filling rules of reference data with 4-ary notational system

Finally, based on the relationship of the secret data to be embedded S and the reference digit R, 2-bit secret data can be hidden into a coefficient-pair by direction modification rules. The detailed operations are as follows:

(1) Determine the type of the selected coefficient-pair (djγ(p),djγ(p+1)) . If S is not equal to R of the corresponding coefficient-pair position, the coefficient-pair is modified according to the direction of the arrows in Fig. 6 so that S=R is satisfied.

(2) If S is equal to R of the corresponding coefficient-pair position, the direction does not change, i.e., the coefficient-pair is not modified in any way.

Take the coefficient-pair (1, 1) as an example, and suppose the filled reference digit is 2. Obviously, the type of coefficient-pair (1, 1) belongs to Type A, so if S = 2, the coefficient-pair is not modified, and if S = 0, the direction is corrected downward and the coefficient-pair is modified to (0,1), and if S = 1, the direction is corrected horizontally and the coefficient-pair is modified to (1, 0), and if S = 3, the direction is corrected to the diagonal direction and the coefficient-pair is modified to (0, 0).

According to the above direction modification rules, the distortion generated by the embedding process can be divided into two kinds, i.e., 1) the distortion ED1 generated by the diagonal modification, including type A and (1, 0), (−1, 0) in type B; 2) the distortion ED2 generated by the horizontal or vertical modification, including (0, 1), (0, −1) in type B and type C. Suppose the number of coefficient-pairs of distortion in the first kind is N1 and the number of coefficient-pairs of distortion in the second kind is N2. It is known from Fig. 5 that N1 < N2, then:

ED1=14×(1+1+2)N1=N1(9)

ED2=14×(1+1+1)N2=34N2(10)

Also, because each coefficient-pair can be embedded into two secret bits, i.e., the embedding capacity is 2 bits, then

EC1=2N1(11)

EC2=2N2(12)

Therefore, the rate distortion [28] that the ratio of the average embedding capacity to the average distortion can be obtained, and larger rate distortion indicates less image distortion:

R1=EC1ED1=2N1N1=2(13)

R2=EC2ED2=2N23N2/4=83(14)

Obviously, R1<R2. That is, if the coefficient-pair of (0, −1), (0, 1) in type B and type C are selected preferentially to embed the secret data, a higher image visual quality will be obtained. But the file size also will increase slightly or remain unchanged as the zero coefficients decrease. On the contrary, if the coefficient-pair of type A and (1, 0), (−1, 0) in type B are preferentially selected to embed the secret data, the probability of −1 or 1 becoming 0 will be increased due to the directional modification, and thus the file size increment will be reduced significantly, while the small modification of coefficient-pair will not cause large distortion of the image.

3.4 Data Extracting

In the data hiding scheme, it should be ensured that the embedded bits can be completely extracted, and the specific extraction steps are as follows:

Step 1: The marked JPEG image is divided into overlapping 8 × 8 blocks, and all blocks are entropy decoded to obtain the quantized DCT blocks.

Step 2: Scanning each quantized DCT block in zig-zag order and sorting them in ascending order according to the number of NCAC.

Step 3: Complete the NCAC coefficient pairing and use the coefficient-pair to locate the reference digit in Fig. 7. In our scheme, the reference digit is the embedded secret data.

Step 4: Repeat the above steps until all of the secret bits has been extracted.

4  Experimental Results and Analysis

In experiment, three state-of-the-art and similar schemes, i.e., Huang et al.’s scheme [26], Hou et al.’s scheme [27], and Wu et al.’s scheme [29] were selected as the comparison schemes. To demonstrate the advantages of our scheme, we selected the same five 512 × 512 standard test images in the USC-SIPI dataset [30], as shown in Fig. 8. In the process of the experiment,the IJG tool [31] was used to convert the test images into JPEG images with QF = 70, QF = 80 and QF = 90. The secret data to be embedded were generated by a random generator. Our experimental results were implemented by MATLAB 2019a on a Windows 10 workstation with an Intel® Core™ i5 CPU running at 3.0 GHz and 16.00 GB of RAM.

Figure 8: The standard test images

Peak-signal-to-noise ratio (PSNR), the structural similarity index measurement (SSIM) [32], embedding capacity (EC), and increased file size (IFS) were used to evaluate the performance of the schemes. PSNR is used to evaluate the visual quality of the image, as shown in Eq. (15):

{ PSNR=10log10(2552MSE)MSE=1K×L∑i=1k∑j=1L(Iij−Iij')2(15)

where K × L is the size of the test image, I is the original JPEG image, I' is the marked JPEG image. EC denotes the total number of embedded secret bits. IFS is used to measure the change of file size for the JPEG image before and after the secret data are embedded, as shown in Eq. (16):

IFS=P′−P(16)

where P′ is the file size of the JPEG image after embedding the secret bits, and P is the file size of the original JPEG image.

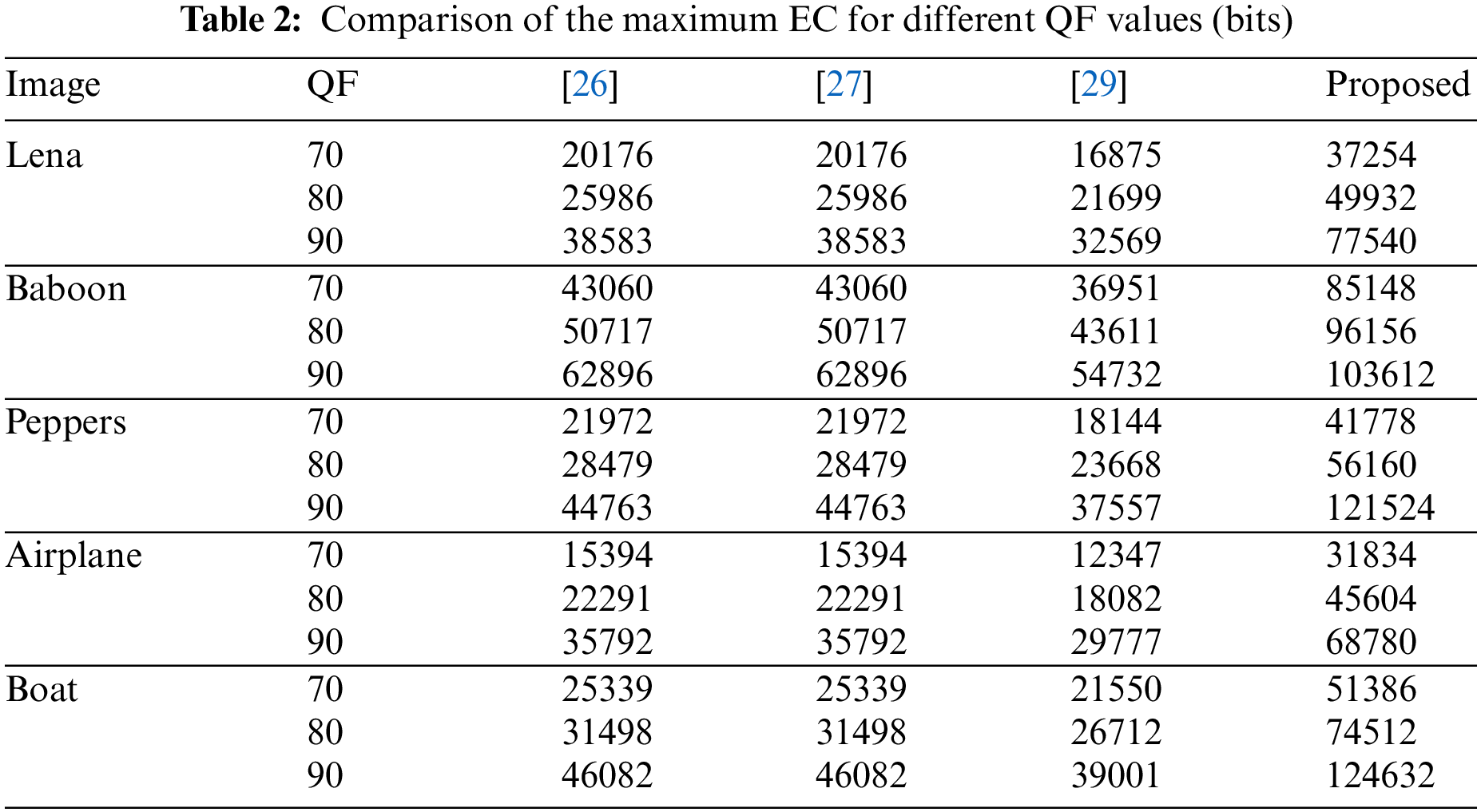
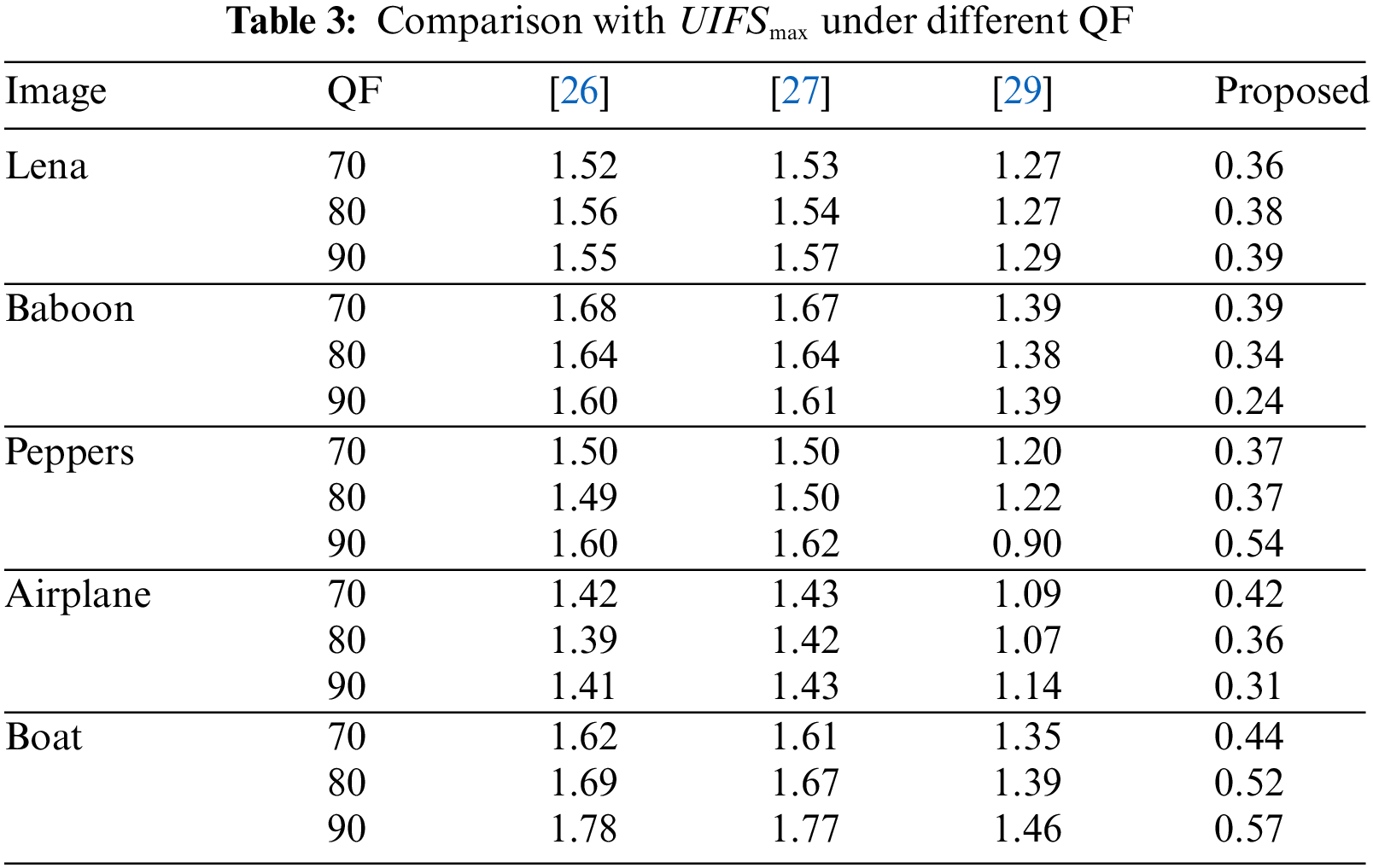
4.1 Performance Comparison at Maximum EC

Table 2 gives the maximum EC of the proposed scheme and the comparison scheme for different QF values, respectively. In this table, it is apparent that there are similar maximum EC in [26,27]. This is because the scheme in [27] improved the performance of [26] by optimization strategies of block sorting and frequency selection, but the effect of these optimization strategies disappears when the EC reaches the maximum. The strategy of the coefficient pairing in [29] reduces the use of small non-zero AC coefficients to a certain extent, so the maximum EC decreases compared to schemes in [26,27]. The proposed scheme selects the coefficients −1, 0, 1 that have the highest occurrence at the same frequency position in the quantized DCT block to pair, so more coefficient-pairs are obtained to hide the secret bits. Therefore, the maximum EC improves significantly compared with three state-of-the-art schemes.

In order to compare the IFS under the maximum EC, we define the unit maximum embedding increment UIFSmax, which is the ratio of the file size increment to the maximum EC, as shown in Eq. (17).

UIFSmax=IFSECmax(17)

Obviously, the smaller UIFSmax is better. Table 3 gives UIFSmax of our scheme and the comparison schemes under the different QF, and it can be seen from this table that the performance improvement of our scheme is significant. Taking “Lena” as an example, the UIFSmax of the comparison scheme is 1.56, 1.54, and 1.27, respectively, but our scheme decreases to 0.38, which shows that our scheme can obtain the smallest IFS even at the maximum EC.

4.2 Performance Comparison at the Fixed EC

Fig. 9 compares the average PSNR of the five test images under different QF and the fixed EC. The horizontal axis represents the EC, and the vertical axis represents the average PSNR. When QF = 70 and QF = 80, the visual quality of the marked JPEG images in our scheme is significantly better than that of three state-of-the-art schemes, and this advantage is more obvious as the EC increases. When QF = 90, the visual quality of our scheme is still better than that of schemes in [26,27]. Compared with [29], our scheme is slightly inferior at low EC. That’s because the quantization step of the high-frequency region increases when the QF is larger, and even the small modification of AC coefficients results in larger distortion. When the EC increases, our scheme is better than [29].

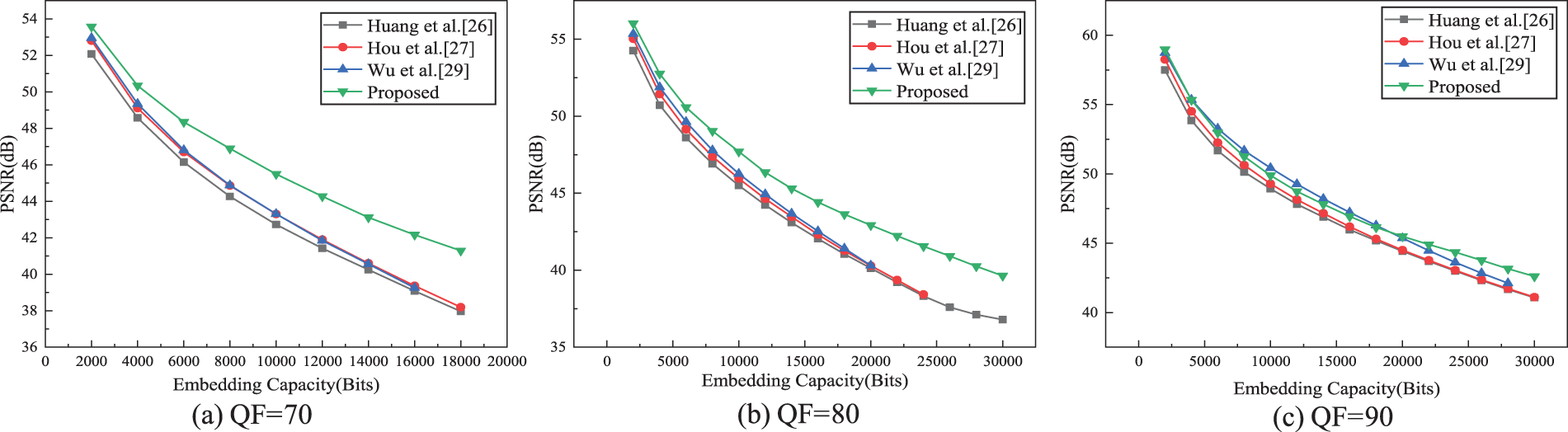
Figure 9: Comparison of average PSNR of the test images under fixed EC

Fig. 10 provides a comparison of the average IFS of the five test images under different QF and the fixed EC. Fig. 10 clearly shows that our scheme obtains the lowest IFS at any EC irrespective of the value of QF. The main reason is that the modification of the AC coefficients always is restricted to −1, 0, 1 by using direction modification rules, and the embedding process of secret bits may increase the frequency of zero coefficients, thus improving the efficiency of run-length encoding and obtaining a better compression ratio.

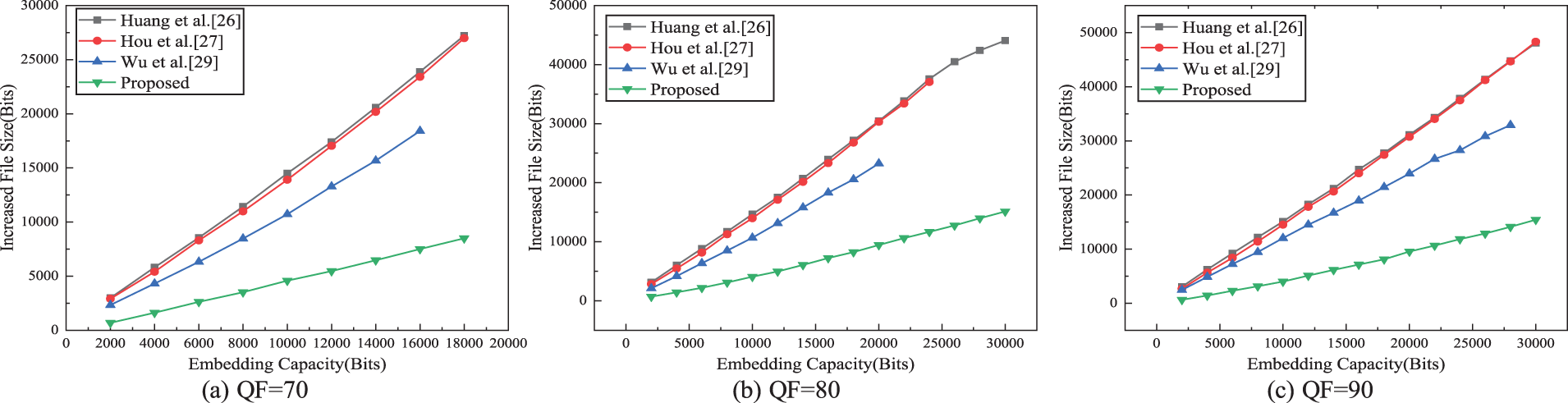
Figure 10: Comparison of average IFS of the test images under fixed EC

Table 4 compares the results of PSNR, SSIM and IFS for five test images with fixed EC at QF = 80. The table shows that our scheme can obtain better image quality and smaller IFS under the fixed embedding capacity than three state-of-the-art schemes in [26,27,29]. Taking “Baboon” as an example, when the embedding capacity is 16000 bits, the PSNR of our scheme is 1.7 dB, 1.49 dB and 0.62 dB higher than that of three state-of-the-art schemes in [26,27,29], while the IFS is 18248, 18128 and 12656 bits lower than that of three state-of-the-art schemes in [26,27,29], respectively.

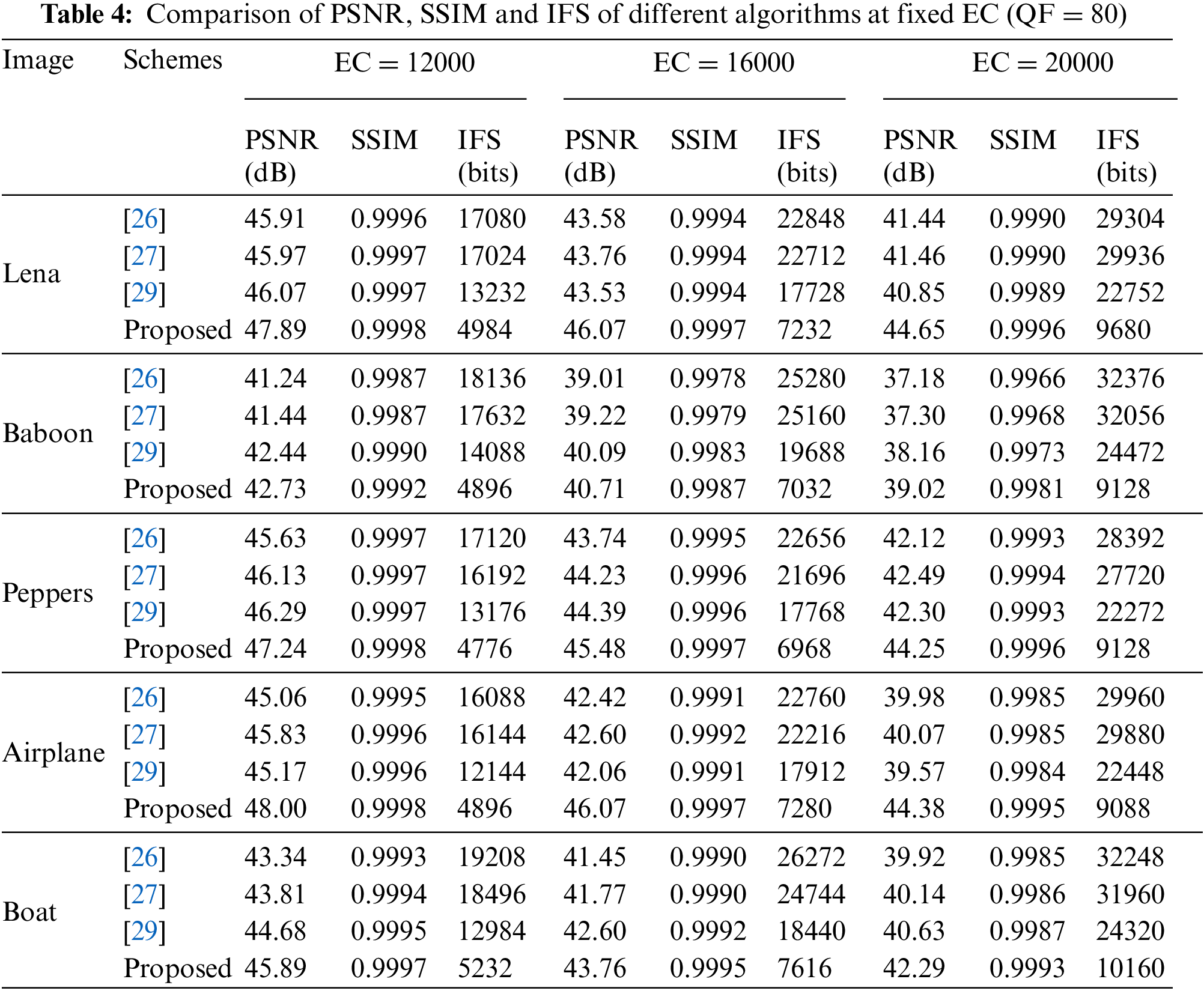
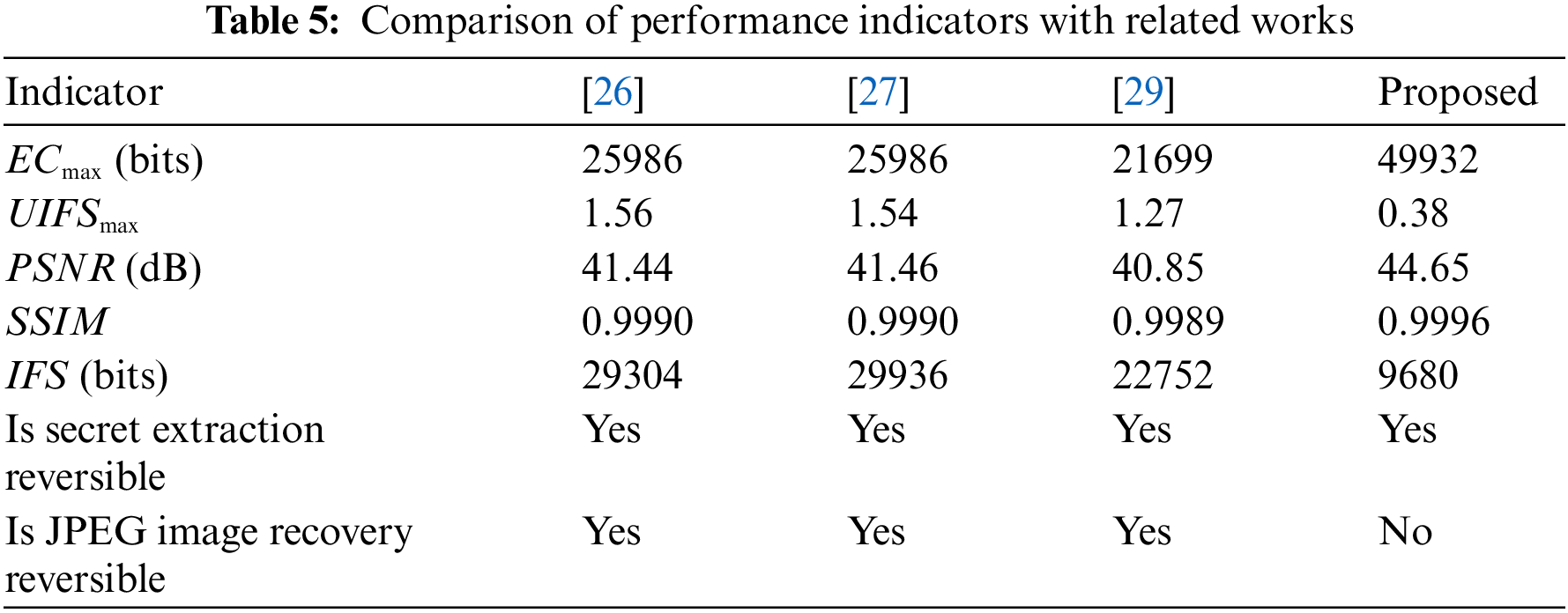
Table 5 compares the performance indicators of our scheme with the performance indicators of [26,27,29]. Part of the data in this table are from “Lena” with QF = 80 and an EC of 20000 bits. It is apparent that the maximum EC of our scheme is almost double that of three comparison schemes. Most important of all, the IFS of our scheme is only one fifth of that of [26], one fifth of that of [27], and one fourth of that of [29]. In terms of the visual quality of the marked JPEG image, our scheme also is significantly higher than the visual qualities of comparison schemes. Although our scheme cannot lossless recover JPEG images, the distortion is insignificant compared with the distortion of the JPEG compression process. It is worth the small loss in exchange for other significant performance improvements.

4.3 Performance Comparison Based on Datasets

The experiments were performed on 1000 randomly selected images from the dataset BOSSbase in order to verify the generality of our scheme. Figs. 11 and 12 compare the average PSNR and the average IFS at the fixed EC when the QF is 70, 80 and 90, respectively. The figures show that the visual quality of the proposed scheme was improved by 1~4 dB on average compared to comparison schemes in [26,27,29], and the maximum decrease of IFS was about 15% of that of the comparison schemes.

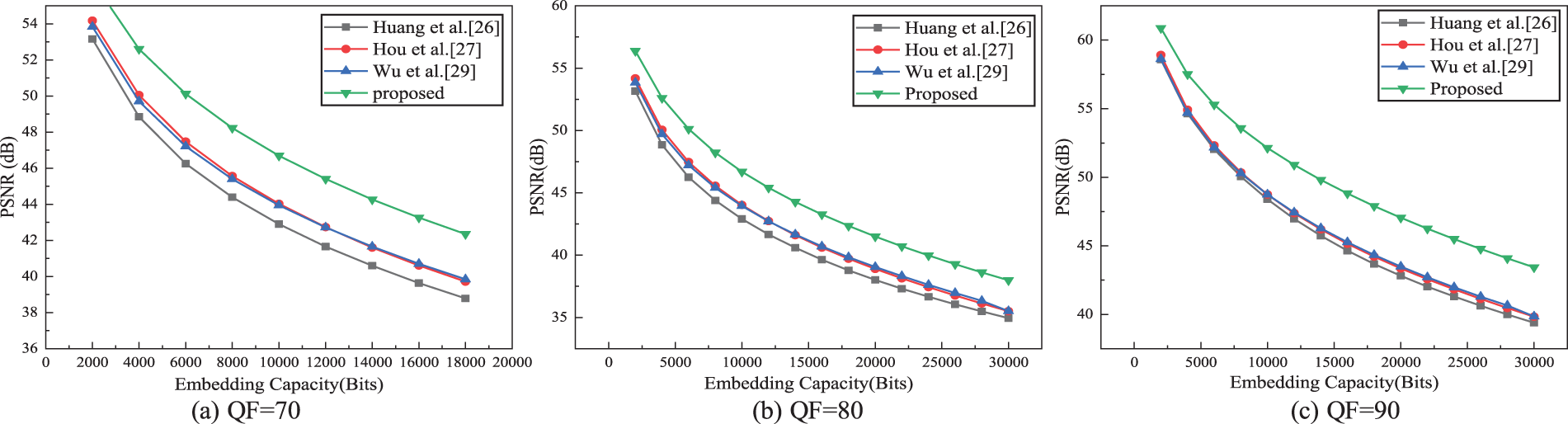
Figure 11: Comparison of average PSNR of the dataset images under fixed EC

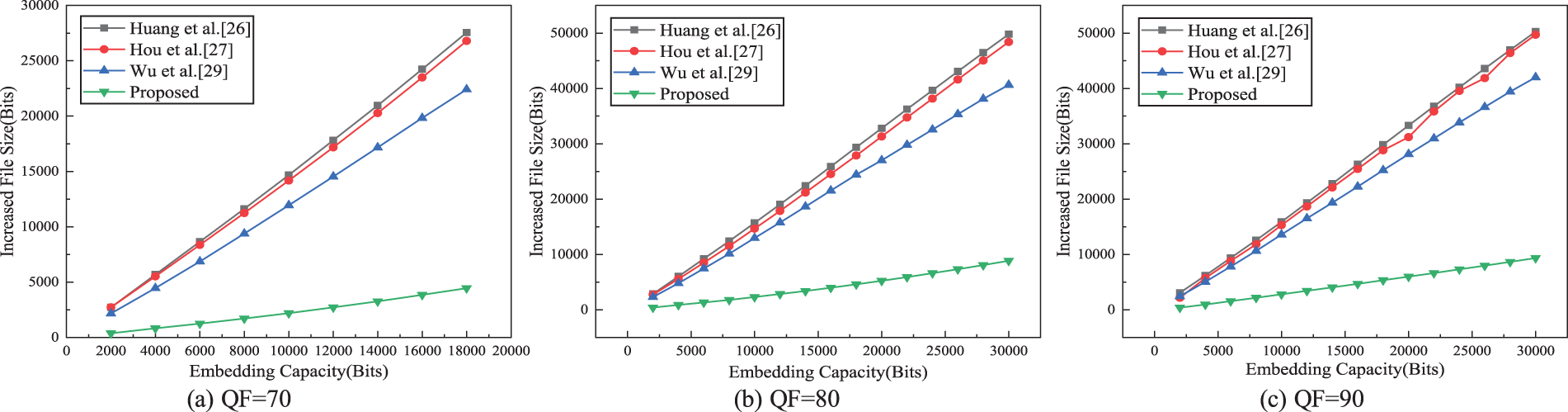
Figure 12: Comparison of average IFS of the dataset images under fixed EC

5  Conclusion

In this paper, we propose a high-imperceptibility data hiding scheme for JPEG images based on direction modification. The main advantages of our scheme are reflected in the following four aspects: (1) block sorting ensures that more coefficients in low frequency are used preferentially, and increases the number of valid coefficient-pair; (2) Strategy of the coefficient pairing obtains more coefficient-pairs for embedding; (3) The randomly filled reference matrix improves the security of our scheme; and (4) The designed direction modification rules reduces the distortion and the file size increment of the marked JPEG images. The experimental results showed that the visual quality of our scheme is improved by 1~4 dB compared with the comparison schemes, and the file size increment is reduced at most to 15% of the comparison schemes. In our next work, we will conduct an in-depth study of the reversible problem in order to propose an RDH scheme with better performance to meet the practical needs.

Funding Statement: This research is supported by the National Natural Science Foundation of China (62072325), Shanxi Scholarship Council of China (HGKY2019081), Fundamental Research Program of Shanxi Province (202103021224272), TYUST SRIF (20212039).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Song, D. Zhang, Q. Tang, S. Tang and K. Yang, “Local and nonlocal constraints for compressed sensing video and multi-view image recovery,” Neurocomputing, vol. 406, no. 2, pp. 34–48, 2020. [Google Scholar]

2. Y. Q. Shi, X. L. Li, X. P. Zhang, H. T. Wu and B. Ma, “Reversible data hiding: Advances in the past two decades,” IEEE Access, vol. 4, pp. 3210–3237, 2016. [Google Scholar]

3. S. Solak, “High embedding capacity data hiding technique based on EMSD and LSB substitution algorithms,” IEEE Access, vol. 8, pp. 166513–166524, 2020. [Google Scholar]

4. P. Puteaux, S. Y. Ong, K. S. Wong and W. Puech, “A survey of reversible data hiding in encrypted images the first 12 years,” Journal of Visual Communication & Image Representation, vol. 77, pp. 103085, 2021. [Google Scholar]

5. L. Liu, L. F. Wang and C. C. Chang, “Separable reversible data hiding in encrypted images based on flexible preservation of the differences,” Multimedia Tools & Applications, vol. 80, no. 5, pp. 6639–6659, 2021. [Google Scholar]

6. X. Y. Chen, H. D. Zhong and A. Q. Qiu, “Reversible data hiding scheme in multiple encrypted images based on code division multiplexing,” Multimedia Tools & Applications, vol. 78, no. 6, pp. 7499–7516, 2019. [Google Scholar]

7. F. Peng, Y. Zhao, X. Zhang, M. Long and W. Q. Pan, “Reversible data hiding based on RSBEMD coding and adaptive multi-segment left and right histogram shifting,” Signal Processing: Image Communication, vol. 81, pp. 115715, 2020. [Google Scholar]

8. G. K. Wallace, “The JPEG still picture compression standard,” Communications of the ACM, vol. 34, no. 4, pp. 30–44, 1991. [Google Scholar]

9. J. H. He, J. X. Chen and S. H. Tang, “Reversible data hiding in JPEG images based on negative influence models,” IEEE Transactions on Information Forensics & Security, vol. 15, pp. 2121–2133, 2019. [Google Scholar]

10. Y. Y. Wang, H. J. He, F. Chen and S. J. Zhang, “Reversible data hiding in JPEG images based on distortion-extension cost,” Journal of Computer Research & Development, vol. 57, no. 11, pp. 2271–2282, 2020. [Google Scholar]

11. Z. X. Yin, Y. Ji and B. Luo, “Reversible data hiding in JPEG images with multi-objective optimization,” IEEE Transactions on Circuits & System for Video Technology, vol. 30, no. 8, pp. 2343–2352, 2020. [Google Scholar]

12. S. W. Weng, Y. Zhou and T. C. Zhang, “Adaptive reversible data hiding for JPEG images with multiple two-dimensional histograms,” Journal of Visual Communication & Image Representation, vol. 85, no. 8, pp. 103487, 2022. [Google Scholar]

13. F. Y. Li, L. M. Zhang, C. Qin and K. Wu, “Reversible data hiding for JPEG images with minimum additive distortion,” Information Sciences, vol. 595, no. 6, pp. 142–158, 2022. [Google Scholar]

14. B. G. Mobasseri, R. J. Berger, M. P. Marcinak and Y. J. NaikRaikar, “Data embedding in JPEG bitstream by code mapping,” IEEE Transactions on Image Process, vol. 19, no. 4, pp. 958–966, 2010. [Google Scholar]

15. Y. J. Hu, K. Wang and Z. M. Lu, “An improved VLC-based lossless data hiding scheme for JPEG images,” Journal of Systems & Software, vol. 86, no. 8, pp. 2166–2173, 2013. [Google Scholar]

16. Y. Q. Qiu, H. He, Z. X. Qian, S. Li and X. P. Zhang, “Lossless data hiding in JPEG bitstream using alternative embedding,” Journal of Visual Communication & Image Representation, vol. 52, no. 2, pp. 86–91, 2018. [Google Scholar]

17. J. Fridrich, M. Goljan and R. Du, “Lossless data embedding for all image formats,” in Proc. of Security and Watermarking of Multimedia Contents IV, Bellingham, Washington, USA: SPIE, pp. 572–583, 2002. [Google Scholar]

18. C. C. Chang, C. C. Lin, C. S. Tseng and W. L. Ta, “Reversible hiding in DCT-based compressed images,” Information Sciences, vol. 177, no. 13, pp. 2768–2786, 2007. [Google Scholar]

19. L. S. Chen, S. J. Lin and J. C. Lin, “Reversible JPEG-based hiding method with high hiding-ratio,” International Journal of Pattern Recognition & Artificial Intelligence, vol. 24, no. 3, pp. 433–456, 2010. [Google Scholar]

20. K. Wang, Z. M. Lu and Y. J. Hu, “A high capacity lossless data hiding scheme for JPEG images,” Journal of Systems & Software, vol. 86, no. 7, pp. 1965–1975, 2013. [Google Scholar]

21. G. R. Xuan, Y. Q. Shi, Z. C. Ni, P. Q. Chai, X. Cui et al., “Reversible data hiding for JPEG images based on histogram pairs,” in Proc. of Int. Conf. Image Analysis & Recognition, Berlin, Springer, pp. 715–727, 2007. [Google Scholar]

22. X. Lu and F. J. Huang, “Reversible data hiding in JPEG images based on two-dimensional histogram modification,” Cyberspace Security, vol. 10, no. 8, pp. 55–64, 2019. [Google Scholar]

23. A. Nikolaidis, “Reversible data hiding in JPEG images utilizing zero quantized coefficients,” IET Image Processing, vol. 9, no. 7, pp. 560–568, 2015. [Google Scholar]

24. S. Kim, F. J. Huang and H. J. Kim, “Reversible data hiding in JPEG images using quantized DC,” Entropy, vol. 21, no. 9, pp. 835, 2019. [Google Scholar]

25. M. Y. Xiao, X. L. Li, B. Ma, X. P. Zhang and Y. Zhao, “Efficient reversible data hiding for JPEG images with multiple histograms modification,” IEEE Transactions on Circuits & Systems for Video Technology, vol. 31, no. 7, pp. 2535–2546, 2020. [Google Scholar]

26. F. J. Huang, X. C. Qu, H. J. Kim and J. W. Huang, “Reversible data hiding in JPEG images,” IEEE Transactions on Circuits & Systems for Video Technology, vol. 26, no. 9, pp. 1610–1621, 2016. [Google Scholar]

27. D. D. Hou, H. Q. Wang, W. M. Zhang and N. H. Yu, “Reversible data hiding in JPEG image based on DCT frequency and block selection,” Signal Processing, vol. 148, no. 8, pp. 41–47, 2018. [Google Scholar]

28. N. Li and F. J. Huang, “Reversible data hiding for JPEG images based on pairwise nonzero AC coefficient expansion,” Signal Processing, vol. 171, no. 2, pp. 107476–107483, 2020. [Google Scholar]

29. T. Y. Wu and F. J. Huang, “Adaptive reversible data hiding in JPEG images based on coefficient pairing,” Journal of Software, vol. 33, no. 2, pp. 725+728–739, 2022. [Google Scholar]

30. The USC-SIPI Image Database, 2022. [Online]. Available: http://sipi.usc.edu/database/ [Google Scholar]

31. Independent jpeg group, 2019. [Online]. Available: http://www.ijp.org [Google Scholar]

32. Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–614, 2004. [Google Scholar] [PubMed]