Economic Power Dispatching from Distributed Generations: Review of Optimization Techniques

1  Introduction

Distributed generation (DG) is gaining popularity due to its environmental and economic benefits. DGs can assist to reduce greenhouse gas emissions, enhance energy efficiency, and boost the dependability of power systems. However, integrating DGs into power networks involves a number of issues, such as coordinating DG unit dispatch with other generators in the system [1]. According to a forecast published in 2022 by the International Renewable Energy Agency (IRENA), DG might contribute for up to 40% of worldwide power output by 2050. Grid stability and a consistent and well-balanced energy supply depend on the efficient management of power generation from DGs in tandem with traditional high-capacity power generation. Economic power dispatching from DGs in coordination with conventional high capacity power generations is a complex task with the following technical challenges: (i) Intermittent and unpredictable nature of renewable energy, (ii) Bidirectional power flow, (iii) Lack of visibility and control. It may be challenging in some circumstances to gain real-time visibility into the output of DGs and govern their functioning. This can make ensuring the stability and security of the electrical infrastructure more complex. Power system operators can enable effective integration of DGs into the power grid and reap the benefits of these technologies, such as reduced greenhouse gas emissions, improved air quality, and increased energy security and reliability, by addressing the technical challenges associated with DG dispatch.

Economic power dispatching is a strategy for determining the best generating schedule for a set of power plants in order to satisfy load demand at the lowest cost. Optimisation approaches are critical in economical power dispatching, particularly in power systems incorporating DGs. Complex economic dispatching issues with various limitations, such as capacity limits, ramp rate limits, and voltage constraints, can be solved using optimisation approaches [2]. Because of recent economic, environmental, and technological advancements, distributed energy generation is now being employed efficiently [3]. Energy system designers and operators are required to integrate solar photovoltaics (PV), wind power plants, combined heat and power (CHP) units, and other technologies with traditional power generating units in order to fulfil the distributed demand [4]. The role of renewable energy sources is to meet sustainable development goals [5]. Power supply management from dispatchable energy sources faces technological and economic issues as a result of increasing DGs [6]. The power generation mix for global electrical energy production in 2022 is shown in Fig. 1 [7]. The integration of a large number of DGs into the power network causes several technical challenges (such as voltage quality, power quality, power line losses, techno-economic operations, and so on) [8]. Economic power dispatching from DGs necessitates the use of optimisation techniques in order to increase efficiency, reduce costs, and provide a steady supply of electricity [9]. Optimisation techniques may be employed in a variety of ways to optimise economic power dispatching from DGs, including: (i) Coordinate the dispatch of DGs with conventional power generation; (ii) Maximise DG utilisation; (iii) Reduce the demand for spinning reserve; and (iv) Improve power grid dependability and stability. The role of optimisation approaches in economic power dispatching from DGs is discussed in this article. It addresses the many optimisation strategies that may be used for economic dispatching with DGs.

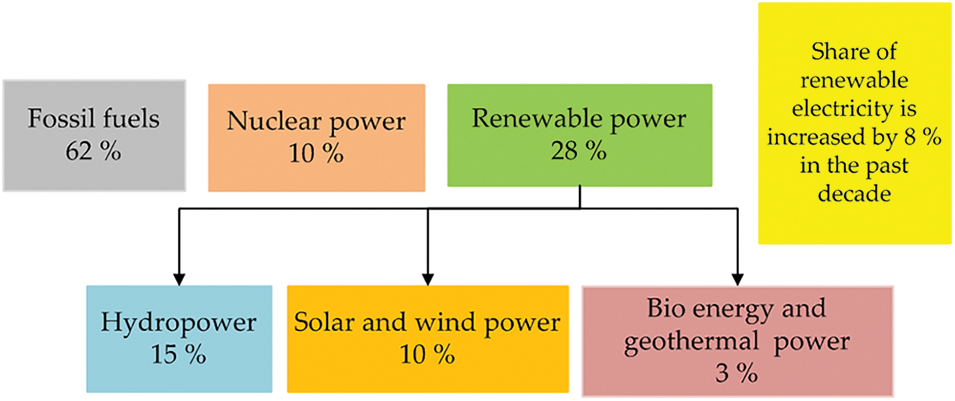
Figure 1: Estimated percentage of renewable energy in world power generation by the end of 2022

1.1 Distributed Energy Generation Concept

Distributed energy resources (DER) consist of distributed generation (DG) units, distributed energy storage (DES) and controllable loads, which are connected through the point of common coupling (PCC) to the main power grid. DGs maycontain solar PV, wind turbines, fuel cells and microturbines [10]. The main objective of the DER unit is to combine the benefits of intermiiteant renewable energy source and combine with the dispacthable DG (e.g., combined heat and the power (CHP) unit). Selection of the DGs is based on the local available resources. Also, DGs’ sustainability is ensured by the local energy scenario, reginal energy policies.

In the traditional power generation system the flow of both electricity and information is uni-directional. Electrical power flows seamlessly from centralized sources to distributed networks in conventional systems, traversing through transmission lines and distribution networks to reach end-users efficiently (Fig. 2). However in DER system, the power flow can be optimally managed throgh DGs shown in Fig. 3.

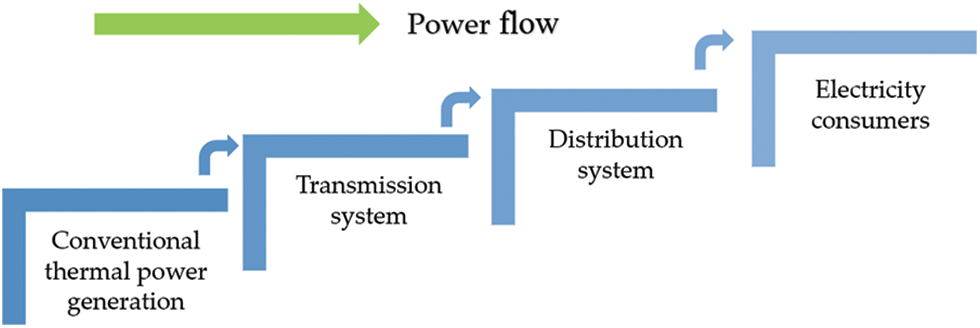
Figure 2: Traditional power system grid

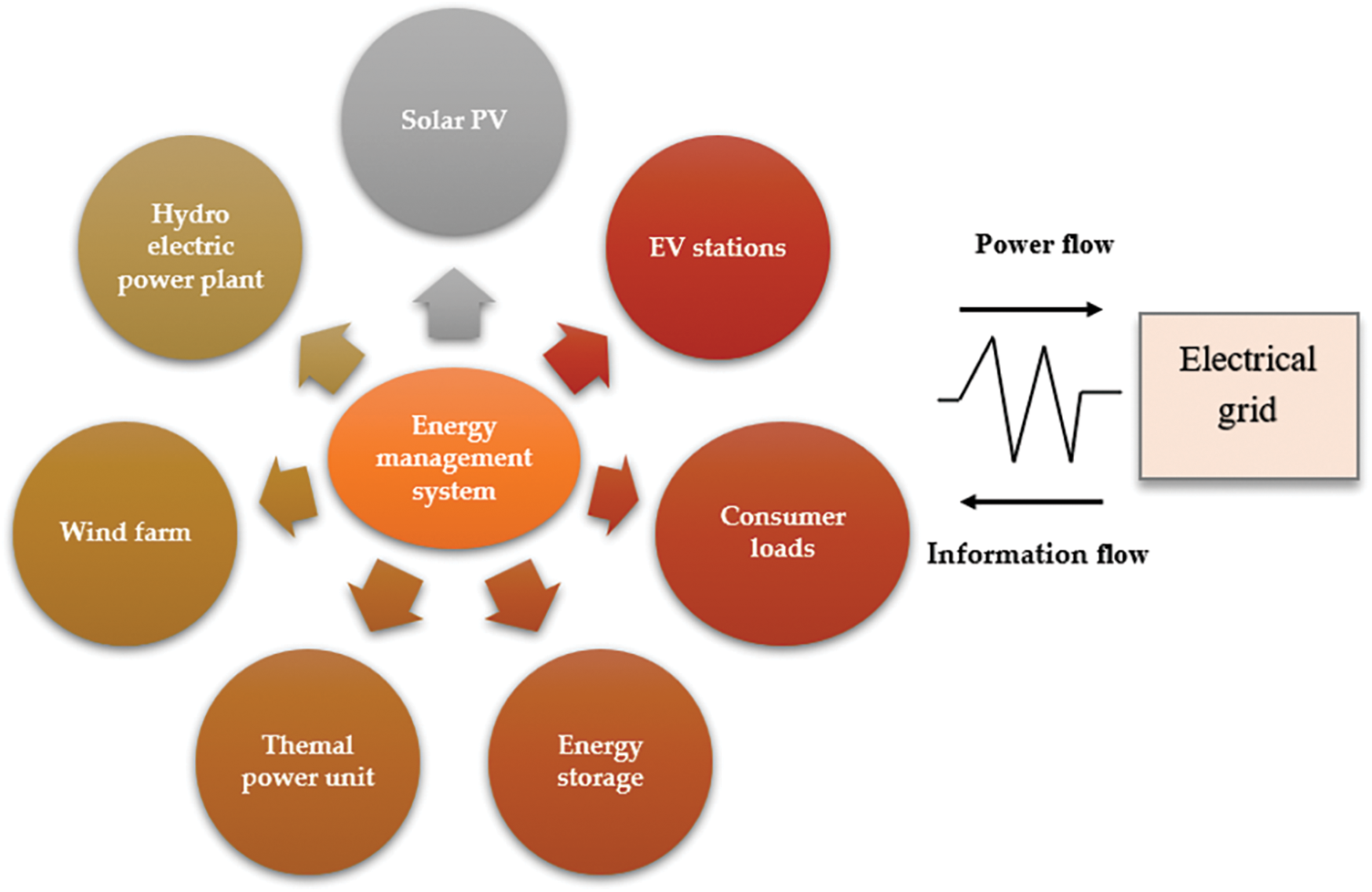
Figure 3: Distributed energy resource structure

DERs complete their operation in grid-connected, islanded, or changeover among these two modes. In the grid-connected mode, it absorbs or delivers the power to the main grid. Whereas in the islanded mode, power generation would be self-regulated and used to maintain voltage and frequency [11,12]. Synchronized operations of renewable energy units in distributed power generation have the benefit of improved system reliability and high power quality [13]. It can provide appropriate control and energy management strategy for power networks in terms of economics [14]. The power generation from solar PV and wind turbines is very intermittent. These difficulties need to develop spinning reserves and energy storage devices. The energy storage system (ESS), plays a vital role in deciding to purchase and sell electricity to the main grid. That’s why for operational requirements, DERs are required to realize synchronized control and optimum management of the energy system, even though ensuring minimize the cost of operation and maintenance.

1.2 Energy Management System

It provides reliable and efficient operation and plays a significant role to direct the flow of energy between generation points to utilities while satisfying definite objectives and limitations of the power networks [15]. Although DERs can increase resiliency, consistency, and power superiority but suffer from the internment nature of renewable energy due to the following reasons:

1. Limited power generation capacity compared to the load requirement [16].

2. There is a significant difference between generation and demand meeting due to the high integration of renewable power, followed by a problematic load task [17].

3. DERs contain either dynamic or non-linear loads and the security depends upon generation set values, mainly in isolated mode of operation [18].

Energy management is an efficient process to achieve the energy demand within the power networks and communicate with the grid to satisfy technical, environmental and economic operations [19]. It is responsible to produce the followings operations:

•   Determine the total sum of energy generated/consumed by generating system/load.

•   Ensure the power balance between the existing sources.

•   Minimize overall maintenance and operational costs.

•   Certify the agreement and operating rules to handle distributed system.

Islanded mode of operation requires the EMS, but the grid-connected operation improves the reliability and maximizes the revenue of power generation [20]. Also, in centralized power generation, energy management system faces some technical challenges due to the following reasons:

•   A dedicated energy management system is not available.

•   The computational burden is higher due to congested controlling resources

•   Due to geographical extent, communication requirements increase.

•   A frequent reform of the model due to variation in any unit affects the central control unit.

•   A common point failure occurs several times due to reliability and security weakness.

Hence, the operation of centralized power generation was found problematic with the real-time control applications. Thus distributed energy generation is suitable to deliver essential functionality [21]. It ensures communication among the units. Allocating the control task toward different units based on operation in different time intervals constitutes an idea of control hierarchy (primary, secondary, and tertiary controls) [22,23].

1.3 Economic Dispatch

For efficient operation of DERs, economic dispatch formulation is required to operate the system without any constraint violations. The economic dispatch improves several predefined objective functions and specified different constraints to get numerous decision-making variables. It is one of the crucial optimization tasks and is mainly concerned with fossil-fired power-generating plants [24]. The objective is to allocate the load demand amongst dedicated generators cost-effectively, while all physical and operational constraints remain satisfied. According to this, power system generation, operation and planning can be done by one or several central decision control units. For economic dispatch formulations, the cost function is taken as an objective function [25]. A convex piecewise linear cost function and quadratic cost function can be used for DERs [26]. Several approaches have been technologically advanced to explain the ED problem in the conventional centralized power system, like lambda iteration, gradient search method, Newton’s method and dynamic programming [27]. The heuristic optimization approaches, like genetic algorithm, particle swarm optimization, neural network, biogeography and differential evolution-based methods are situated for the economic dispatch problem in conventional power systems [28]. Because of the economic and operational difficulties met with centralized power plants, researchers are concentrated on distributed generation systems [29]. The DERs are capable of improving their operation. For example, minimizing the energy cost, and additional charges, ensuring less maintenance costs of generation, employing demand meet and use to protect the environment [30].

This paper introduces first time economic dispatch optimization formulations and techniques of DER. The design, installation, and operation of the DERs met several environmental and technical challenges to satisfy the economic operation and load demand. As a result, due to these problems, the planning and operation of DER become difficult. In this review paper, researchers get benefited based on economic aspects. That is why this paper is appealing to a popular or scientific audience because this paper motivates us to research the new approaches to find optimization techniques of distributed generation schemes in real-world scenarios which will be helpful for the researchers in academics as well as industry people.

This review paper is organized as follows: Section 2 surveys computational optimization problem formulations that must be met for optimization variables for economic dispatch and energy management. Section 3 is about computational optimization techniques for DERs economic dispatch optimization. Section 4 gives the tools used for optimization purposes, Section 5 includes the discussion and Section 6 contains the conclusion and future trends.

2  Optimization Problem Formulations

The economic dispatch formulation of DERs is including objective function (minimization or maximization) and different equality or inequality constraints of different generating units. Detailed explanations are given under.

2.1 Objective Functions

The objective function can be minimization and maximization in nature. A detailed description of various objective functions is explained under.

2.1.1 Total Operating Cost

ED is most important optimization problem in the power system networks, which is targeted to minimize the total economic cost. It includes:

•   The fuel cost of the generation unit while satisfying the constraints. It is either a linear or quadratic function of output power [31,32]. Sometimes emission is considered with fuel cost which is multi-objective but converted to a single objective function by using some parameters [33].

•   The cost of DGs is dispatchable or non-dispatchable in nature. It includes the cost of solar PV, wind energy fuel cells, natural gas, microturbine, energy storage batteries, diesel generator, etc. [34].

•   Optimizing the operation and maintenance costs of DGs is required to minimize while meeting the load demand [35].

•   It includes the cost of energy purchased from the utility when DERs are unable to supply its load demand. If it is connected to the main grid then they are capable to inject power into the main grid, which is economically beneficial [36].

•   It includes the depreciation cost of the battery and energy exchange cost [37].

•   During operation and maintenance, installation costs is another important parameter that affects the overall economy [38].

•   Startup or start-down cost represents the generator’s working conditions and is represented by an exponential cost curve [39].

•   It includes the penalty cost, due to higher emissions, renewable energy curtailment, lack of thermal supply as well as deviations after day-ahead power exchange and load shedding [40].

2.1.2 Network Losses

Economic load dispatch optimization strongly emphasized the minimization of network losses [41]. It is represented through B-coefficients having a linear and constant term given by Kron’s loss formula [42]. The transmission losses are measured around 3% to 5% of the full load. As a result, the transmission losses are approximately characterized by multiplying the full load demand by 5% [43]. These losses do not belong to any generating unit. They are the result of how power is dispatched [44]. Active power and reactive power losses are also considered along with transmission losses [45].

2.1.3 Carbon Emmision

To maximize the benefits and the environmental concern, it is necessary to reduce the emission of pollutant gases NOx, COx, SOx, etc. [46]. DERs are playing a significant role concerning environmental hazards. As a result, many optimization formulations seek to minimize the emissions and pollutants emitted in power system networks [47]. One of the optimization techniques based on the weighting factor price penalty factor approach [48], also shows the mathematical relationship between the loading level of DG units and the associated amount of pollutant emissions.

2.1.4 Effective Load Distribution

The standalone system can maximize the load served effectively when voltage and frequency variations are restricted by certain boundaries. The optimal operation strategy increases the load served [49] like battery energy storage system capacity [50] and allocates the range of renewable power variation into multiple scenes. So that the power output of traditional generation units along with their spinning reserve is optimized as well as the energy management system performs better [51].

2.1.5 Voltage Fluctuation

In economic operations, voltage fluctuation problems are considered multi-objective optimal operations. To enhance the economic operations and power quality it is necessary to minimize the voltage deviation [52]. It can be optimized by keeping the voltage stability index minimal. Efficient voltage regulation accomplished to facilitate the output voltage is maintained near the optimal values [53]. Sometimes these voltage variations are above or below the limits. However, the minimization of voltage is also addressed in V/F control methods [54]. The power management technique also retains the voltage within a safe limit. DER gives technical and regulatory challenges due to voltage variations and offers solutions to distributed system operators [55].

2.1.6 Frequency Variations

A frequency control method is designed to maintain the power balance by regulating the power generation, which keeps the frequency to its nominal value of 50 Hz. If power disturbances occur, then it creates frequency oscillations from its nominal value. A voltage frequency management technique keeps the frequency to the desired amount [56]. Droop control is another way to maintain frequency deviations [57]. The maximum frequency deviations are 3% or 4% for less than 2 s, designed for continuous and transient operations, respectively.

2.1.7 Reliable Operating Condition

This is the overall ability of the system to generate and supply electric power. Various planning studies and parameters have been used to handle this situation. A feeder addition, which refers to an optimization problem, improves reliability by increasing the redundancy in a system [58]. Most importantly, multi-scene load shedding and dynamic energy management also improve the reliability [59]. The droop control method is another way to enhance reliability by reducing communication nodes. On the other hand, in some reliability optimization problems, it increases by decreasing the outage cost using an energy storage system. Optimal DG allocation and sizing in distribution systems also guarantee reliable operation [60].

2.2 Constraints

In economic dispatch formulation, there are two types of constraints: equality constraints and inequality constraints. The detailed survey of constraints is as follows.

2.2.1 Equality Constraints

This is the most common constraint of the economic dispatch optimization technique. It includes active and reactive power balance equations in economic dispatch operations.

•   It includes total active power generation plus purchased power from the external grid must balance the predicted power demand plus the sold power to the main grid.

•   It also represents the constraint that is related to various generating units.

2.2.2 Inequality Constraints

Several inequality constraints are considered to solve economic dispatch problems. It is explained in the following points:

•   For stable operation of the generator, the real power generation is controlled by the generator’s lower and upper margins [61].

•   The DG capacity limit represents the minimum and maximum operating limits of DERs like solar PV, wind, fuel cells, etc. [62,63].

•   It is found that the active power output of generators must lie between its lower and upper boundaries. This shows the physical limitations for stable operation Another related constraint is the limitations of reactive power injection/absorption into the power system given by its maximum and minimum values [64,65].

•   The physical operating constraint is termed the ramp rate of DG and is measured in MW/min or kW/min. This is specified as ramp-up and ramp-down limits for each generating unit. In the context of the small generator unit ramp up from 0 to full load in several minutes, so cannot reach hourly scheduling operations and sometimes it follows the load shedding or curtailing the renewable for power balance [66].

•   Minimum up/down time limits of generator constraints is related to the operating limits of DG, concerned with unit commitment optimization problems. Once a DG is set to an on state, it requires functioning continuously for a certain number of times before it can be switched to an off state [67].

•   Energy storage systems (ESS) show the charging and discharging of batteries. Charging and discharging the battery regularly increases the life span of ESS. There is a limitation of state of charge (SOC) limit, which lies between minimum and maximum values [68].

•   Voltage limits relate to maintaining the voltage limits at all the generators to avoid voltage variations to protect the electrical devices. Frequency has certain limits to improve the power-sharing accuracy and to avoid large instability when the load varies from 0% to 100% [69].

•   It shows the thermal limits in the form of transmission line constraints, line flow limits, and real power transition among the DERs and main grid [70].

For stable operation, spinning and nonspinning reserve constraints are derived and those are considered reserves for fluctuated load demand for islanded operation. Operation and control of DERs are uncontrollable due to renewable energy integration. Load shedding limits prevent the unstable behavior of the system by using controllable loads which can be interrupted during the islanding mode of operations.

Sections 2.1 and 2.2 are well explained the different objective functions and constraints for the economic dispatching of DERs. To find the optimal solution for the objective function, various methods have been adopted, which are explained in Section 3.

3  Optimization Techniques

For improving the planning and dispatch problems, several optimization techniques are considered. They are categorized as classical techniques, nature-inspired techniques, stochastic optimization techniques, artificial intelligence and rule-based techniques, recent optimization techniques, and some other methods. A detailed explanation of each optimization method is discussed as follows.

3.1 Conventional Optimization Techniques

The conventional optimization techniques for economic load dispatch analysis is explained as under.

3.1.1 Linear Programming

Economic dispatch of DERs with a linear technique is quite often employed. In reference [59], multiple scenes are generated by dividing the range of wind power fluctuations in the security-constrained economic dispatch (SCED) problem. The spinning reserve and the reliability are optimized and guaranteed for stable operation. Another energy management with a rolling horizon scheme integrated with renewable energy sources has been formulated using linear programming. It reduces operating costs and penalties. It also minimizes the cost of electricity usage [71]. While in reference [72], the total operating cost is minimized using a branch and cut algorithm for combined cooling heating and power (CCHP) system based on mixed-integer linear programming (MILP).

An alternative way is combined heat and power where electric load and heat load are both considered together, and generation scheduling is formulated when DER is either operated or not. It minimizes the operating cost and maximizes the selling benefits as well [67]. However, a benders decomposition with mixed-integer second-order cone programming (MISOCP) is formulated, which increases the degree of security, efficiency, reliability, and sustainability of operation [55].

3.1.2 Non-Linear Programming

Mixed-integer non-linear programming technique is adopted to minimize the operating costs and controllable operations of DERs [73]. A model predictive control technique designed to solve ED problems considering several uncertainties in a real-time scenario on an hourly basis. Which leads to non-linear optimal power flow (OPF) due to the nonconvex characteristics of the system [53].

Another probability-based concept in reference [74] has been explained. It reduces the emission and forecasts errors using a duality-based approach with mixed-integer non-linear programming. While in reference [35], mesh adaptive direct search (MADS) algorithm is designed for non-linear optimization formulation for environmental, and economic dispatch problems. However, a stable operation of a grid-connected system ensures after islanding using a modified direct search method [70]. A non-linear objective function for Pareto optimality of procedure and emission cost is taken for islanded DERs operation and solved using mixed-integer non-linear programming (MINLP) [46].

3.1.3 Non-Differential Programming

For stable and reliable economic dispatch formulation, the author explains a dual decomposition-based non-differential optimization solution technique to minimize the net cost of DERs [75].

3.1.4 Quadratic Programming

In reference [46], the operating cost and emission cost are minimized in an isolated mode of operation. It is taken as a quadratic function and solved using mixed-integer quadratic programming (MIQP).

3.2 Nature Inspired Algorithms

The mathematical methods described above, are well suited to converge and obtain an accurate solution in a limited number of iterations. However, they were struggling to handle the non-convex fuel cost function efficiently. Metaheuristic algorithms overcome the issues addressed by mathematical methods. Metaheuristic algorithms shows the strong search ability that allows them to formulate non-convex, non-differentiable and non-continuous objective cost functions. Some of the nature inspired algorithms are explained below.

3.2.1 Differential Evolution (DE)

DE is a universal and straightforward optimization solution strategy based on population satisfying all the constraints using its different crossover steps. A multi-objective function is formulated for the minimization of fuel cost and emission and maximizes the stability of DER [33].

3.2.2 Partial Swarm Optimization (PSO)

The objective behind the PSO algorithm is aggressive particle movement. Based on this, the optimal area and size of DER are identified by the loss sensitivity index (LSI). While in [33], authors have explained PSO-based multi-grid formulations for minimization of cost using the Weibull distribution factor. However, a modified particle swarms optimization (MPSO) in the short-horizon operation stage holds the frequency and voltage in a prescribed limit using a multilayer scheme and energy management [40]. To improve the reliability and ensure the environmental, and economic dispatch, an improved quantum particle swarm optimization (IQPSO) has been explained by the authors in reference [76]. While in reference [45], operating cost and environmental issues were minimized by constrained optimization and annealing mutation PSO.

3.2.3 Genetic Algorithm (GA)

In GA, a population of the individual chromosome is included, which converts an accurate solution to the optimization problem and smart energy management [64]. A mathematical model of the DERs structure was explained in [42] with the help of a chaotic quantum genetic algorithm (CQGA). Another feature is the addition of a feeder in a radial system, which makes it partially meshed to maximize the utility of renewable energy distributed generation, from grid-connected mode to islanded operating conditions [58]. In reference [36], authors produced a genetic algorithm to minimize the operating cost of DERs. A new memory-based GA (MGA), is formulated to reduce the cost of production by optimal sharing of power demand among the system [77]. A multi-objective function is also modeled in reference [78], where power generation and load both are taken at the same period to maximize the operational benefits and minimize the environmental cost with an improved quantum genetic algorithm. In addition to these, the optimal allocation of distributed generation is given by an improved adaptive genetic algorithm (IAGA), which is a multi-objective formulation using the bi-level planning method. A nano cogenerator unit in a residential pilot is simulated to show an energy saving of around 25%–30% [79].

3.2.4 Hybrid Approach

The hybrid method is widely used to solve the dispatch optimization of DERs. A differential evolution-based particle swarm optimization method (DE-PSO) calculates loss coefficients considering diverse demand configurations [80]. In reference [52], a multi-objective security-constrained dispatch structure projected for both grid-connected and isolated modes of operation to minimize generation cost and maximize reliability while satisfying steady-state and dynamic constraints with Pareto concavity elimination transformation (PaCcET) [81], non-dominated-sorting-genetic-algorithm II (NSGA-II) [82] and multi-objective particle swarm optimization (MOPSO) [83]. However, in reference [57] author formulated a fuzzy-based particle swarm optimization to decrease the fuel cost and system damping and push the most dominant eigenvalue away from the imaginary axis to the left of the s-plane. While in [39], two genetic algorithms were included with the fuzzy experts to control the power output of the storage system. Where the first GA performs the generation scheduling, and the second GA tunes the membership function.

3.3 Stochastic Optimization Technique

The large dimension matrix creates computational burdens such as the curse of dimensionality to dynamic programming. Approximate dynamic programming (ADP) overcomes these challenges and deals with uncertainties. In reference [84], the authors formulated energy storage operations through ADP with a piecewise linear function approximation technique. While in reference [68], ADP with the Monte Carlo (MC) method is assumed to perform the economic dispatch (ED) of a grid-connected system. Whereas in reference [61], battery energy storage system optimizes using a model predictive control and quadratic programming method. It satisfies the network constraints to control the flow due to the large integration of renewable energy sources. In reference [34], the authors considered renewable energy fluctuations to formulate the ED problem by two-stage stochastic mixed-integer programming. In reference [50], the authors generated the uncertainties of renewable energy sources using different probabilistic scenarios to solve optimal battery energy storage systems (BESS). It minimizes the costs of operation and installation. However, stochastic optimization models assume zero degradation cost of BESS to estimate the battery life span, considering the linear function of the depth of discharge. Still, it produces additional calculation fault [85] and become nonconvex as well as computationally challenging [86]. Reinforcement learning found a better solution approach, but it suffers from the balance of exploration and exploitation [87].

However in reference [88], a reinforcement learning solution with Monte-Carlo tree search and Q-learning was considered, but the life span of BESS is affected by charging and discharging. It converts the objective function into nonconvex nature. Significant research work is still required to decrease the computational cost of reinforcement learning without using a central control technique. In reference [38], authors explained function approximation to achieve the lowest price of distributed economic dispatch in a grid-connected mode, where diffusion strategy organizes the action among multiple agents. Another approach for economic and environmental dispatch is the combined heat and power (CHP) system, which delivers electricity and heat together. In reference [89], the economical optimal operation of the CHP-based grid-connected system was considered using chance-constrained programming (CCP) and particle swarm optimization (PSO) to handle the uncertainties based adequately on stochastic simulation.

3.4 Artificial Intelligence and Rule-Based Technique

Artificial intelligence and rule-based techniques have an inherent characteristic to formulate the calculations in limited time intervals. Rule-based systems include fuzzy-based approaches. Related work was carried out in reference [32] where fuzzy experts minimized the cost of operation and emission level synchronized with the energy management system (EMS). The intelligent methods in reference [90] remained inadequate for energy management among solar PV and energy-storing devices. This difficulty was overcome in reference [60]. An intelligent adaptive dynamic energy management system improves the operations on the minute to the minute time interval and ensures the optimal dispatch of energy. In recent years of advancement, renewable energy penetration played a vital role in developing global optimization of DERs using a recurrent neural network (RNN) to calculate optimal power supplied by each source [91]. For stable operation frequency controllers are designed for active power balance constraints in dynamic economic dispatch formulations and are further improved when frequency control methods include consensus-based dynamic ED where it is distributed in nature [92]. Another approach is the alternating direction method without a central controller for economic dispatch in multi-area in an active distribution network considering the network losses [93].

3.5 Recent Optimization Techniques

Some of the latest technologies are explained below for the analysis of DER economic scheduling.

3.5.1 Model Predictive Control (MPC) Based Approach

The rolling optimization method is understood by the model predictive control (MPC) technique [31], where operation is performed based on a future forecast of renewable energy generation and power consumption. While in reference [94], a model predictive control strategy included mixed-integer non-linear optimal power flow and second-order cone programming to reduce the adverse effects of uncertainties. It is used to improve real-time DERs power dispatch. As part of various demand-side management (DSM) and demand response (DR) arrangements, consumers can join in energy management by load shifting [95] or load shaving [96] throughout the peak load periods which in turn, improves the reliability, but it not includes pollutant emission. To overcome this, in reference [46], authors provided an energy management system (EMS) where the equivalent CO2 emission model is taken, Where the dispatch problem solved considering the updated forecast of the generation from renewables at every 5-min time interval.

3.5.2 Multi-Agent System-Based Approach

In recent years, researchers are interested in distributed algorithms for the economic dispatch problem because they are more scalable and robust. Most of the existing distributed algorithms are based on consensus theory for a multi-agent system. In this way novel, consensus-based approach solves the energy management for an isolated mode where incremental cost is taken. As the consensus variable of each agent through limited communication between neighboring agents, the proposed approach converges quickly to find the optimal solution in terms of social welfare [97]. In reference [41], authors solved a consensus-based distributed algorithm running in parallel, including transmission losses and DG constraints. While in reference [98], the authors included the impact of time delay on the information transmission network. In the practical communication network, the time delay may destabilize the system. So the author obtained the allowable delay bound in islanded distributed ED (Economic dispatch) in coordination with the generalized Nyquist criterion [99]. It converges slowly and potentially enhances the generation cost. To avoid this author present a heterogeneous wireless network architecture.

In reference [100], the authors found a common virtual node to distribute the load with a constant feedback gain of the communication network, which converges the algorithm fast. To meet the power balance, the local mismatch between supply and demand is considered as feedback in a fully distributed algorithm for different time-varying variables [101]. While in reference [37], authors have proposed frequency deviations to reduce the power imbalance, but it takes a long convergence time. Still, the convergence time is too less. In sequence with this, a two-layer model was proposed in reference [54], which ensures the supply and load balance as well as minimization of the operating cost of the system. Here centralized or leader agents are not required, only local agents are considered.

The complexity of multi-area dynamic economic dispatch is overcome by a consensus algorithm based on a fully decentralized optimization technique [102]. It is further improved by a prime dual consensus algorithm for a multi-distributed energy resources structure and designed for respective agents [65]. This complex behavior of dynamic dispatch also uses a decomposition-based strategy that overcomes the dynamic coupling between decision and stochastic variables in a centralized dispatch formulation [103]. In reference [104], the authors found a new consensus algorithm-based adaptive control for optimal dispatch. It reduces the investment and increases the reliability and dynamic performance of the network. For the solution of a single-time step, as well as a multi-time step author produces a constrained optimization which included consensus plus innovation-based technique in reference [105] with first-order optimality equation (Karush-Kuhn-Tucker conditions). In reference [106], energy management was calculated using an incremental welfare consensus-based method which reduces the central energy coordination and leader unit.

3.5.3 Droop Control-Based Approach

The ED problem is efficiently resolved using consensus algorithms in a distributed manner without using a centralized coordinator. The consensus algorithms are employed through asynchronous or synchronous communications. For example, the agents in the communication system are updated and replaced along with other agents. It reduces the convergence speed. Furthermore, the consensus algorithms are excessively dependent upon the communication system for information exchange and malfunction of communication links. Hence, the liabilities of the consensus algorithms motivated the attention of droop control systems. Non-linear droop schemes are added with generation costs to minimize the cost of DG and produce more power [69]. While in reference [107], linear droop control is considered for a reduction in generation cost. In addition to this, a cost-based droop scheme is projected as an equal incremental cost principle to minimize the total active power generation in islanded mode [43]. It offers to handle single-point failure [42]. However, in DC distributed generation system, voltage is the only control parameter, hence, voltage droop cannot deliver outstanding power control. To deal with this problem a frequency-based control technique was offered in reference [53]. However, an incremental cost (IC) based droop control approach was suggested to optimize the operating cost in a decentralized manner, and it was implemented for autonomous AC, DC, and hybrid AC/DC distributed energy resources [37].

3.5.4 Real-Time Algorithm

In real-world online algorithms give a satisfactory performance. The penetration of uncontrollable and intermittent renewable energy sources introduces insecurity into generation scheduling. Since centralized control is generally expensive for implementation and responsible for a single-point failure. Related work was carried out in reference [108], where generation and demand mismatches emphasize the need for online formulations. A peak-aware strategy is adopted in DERs economic scheduling operations for minimizing operating costs while satisfying the constraints using a divide-and-conquer approach. These observations inspire us to examine a new distributed gradient algorithm based on multi-agent online scheduling approaches [109]. For reliable system operations, the energy management system can ensure power balance, therefore, a novel optimal approach based on more accurate online forecasts is proposed, which removes the system outage based on the day ahead approach [110]. However, in reference [111], authors offered optimal scheduling of wind turbines and energy-storing devices by using artificial neural networks and fuzzy rules to minimize costs of operation and emission.

3.6 Other Techniques

Another formulation algorithm proposed backcasting algorithm, which evaluates future price calculations based on the previous week’s data and considered the operational limits like power capacity, variable efficiency, energy storage, and energy ratings. It is suitable for both grid-connected and islanded modes of operation. They can also be used to formulate appropriate power dispatch of an energy storage system. Its available energy is dependent on the charging/discharging pattern from previous time horizons [112]. Multi-objective dispatch problems are also taken into consideration via the interval optimization (IO) approach to satisfy economic conditions, power quality, and security constraints under renewable data presented as interval variables [113,114].

From the above explanations, it is easier to find out the techniques which are applied to get an optimized solution of economic dispatch. It is beneficial for researchers to set new benchmark in the field of optimization techniques.

4  Tool Used for ED Analysis

Distributed generation is very complex and it has non-linear dynamics. The use of tools enhances the reliability of the optimization process. The different tools are used by several authors for the optimization of DER’s economic dispatch and energy management problems. It is described in Table 1, where the detailed description and application areas of multiple solvers like Multiport power electronic interface (MPEI), DSpace, Cplex, Interior-point-based solver, MATLAB YALMIP, MATPOWER, MOSEK, GAMS, PSCAD/EMTDC, Digsilent power factory and MATLAB are given.

5  Discussion

The detailed survey of economic dispatch of DGs has been studied based on different minimization and maximization of an objective function, various constraints and different optimization algorithms and tools used out of 84 articles based on [31–114]. The analysis of various objective function parameters is shown in Fig. 4, where it has been clear that the 39 articles have been used to minimize of fuel cost of the thermal unit and this is the dominant parameter among all others. 32 articles of operation and maintenance cost and 28 articles of power purchased cost are other parameters that are used several times in the form of minimization of the objective function. However, in Fig. 5, different constraints analysis has been given, where 58 articles have been addressed as power balance constraints which is important during the optimization process. As well as 44 articles have been proposed by the authors for generator limit, which shows a valuable impact during economic dispatch analysis. The analysis of various optimization algorithms proposed by different authors is given in Fig. 6, where 31 articles are related to recent optimization techniques like model predictive control-based approach, multi-agent system-based approach, and droop control-based approach. These methods overcome all other algorithms due to their fast convergence and less computational time.

Figure 4: Analysis of objective function parameters

Figure 5: Analysis of constraints

Figure 6: Analysis of optimization techniques

6  Conclusion and Future Trends

A crucial component of guaranteeing an effective, dependable, and cost-effective power supply is economic power dispatching from distributed energy resources (DERs). In this review, we looked at the optimization methods applied to DER-based economic power dispatching.

We observed that the most often employed optimization methods are linear programming and quadratic programming models. These models are capable of managing difficult optimization issues in large-scale systems, taking into account restrictions like network capacity, voltage, and frequency, and incorporating several renewable energy sources. When the issue becomes too complex for conventional optimization techniques, metaheuristic optimization algorithms like genetic algorithms, particle swarm optimization, and ant colony optimization are also helpful.

The scope and depth of the issue, as well as the precision of the incoming data, determine how effective these strategies are. However, applying these optimization techniques can lower costs, increase cost-effectiveness, and significantly improve the efficiency and reliability of power supply from DERs. Economic power dispatching from DERs will become more important in maintaining an efficient, dependable, and cost-effective power supply as the demand for renewable energy sources rises. Therefore, more investigation is required to create novel and creative optimization techniques that can address the difficulties of economically dispatching power from DERs and guarantee a secure and sustainable energy future.

Acknowledgement: None.

Funding Statement: This research work has no external funding.

Author Contributions: Paramjeet Kaur: writing the original draft; Krishna Teerth Chaturvedi: writing-review & editing, supervision; Mohan Lal Kolhe: writing-review & editing, co-supervision. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Joao, C. P. S. (2012). Advanced forecasting techniques and optimal generation scheduling. USA: CRC Press. [Google Scholar]

2. Kolhe, M. (2012). Smart grid: Charting a new energy future: Research, development and demonstration. The Electricity Journal, 25(2), 88–93. [Google Scholar]

3. Kaur, P., Chaturvedi, K. T., Kolhe, M. L. (2023). Economic dispatch of combined heat and power plant units within energy network integrated with the wind power plant. Processes, 11, 1232. [Google Scholar]

4. Aguero, J. R., Takayesu, E., Novosel, D., Masiello, R. (2017). Modernizing the grid: Challenges and opportunities for a sustainable future. IEEE Power Energy Magagement, 15, 74–83. [Google Scholar]

5. Østergaard, P. A., Duic, N., Noorollahi, Y., Kalogirou, S. (2022). Renewable energy for sustainable development. Renewable Energy, 199, 1145–1152. [Google Scholar]

6. Konara, K. M. S. Y., Kolhe, M. L. (2016). Charging management of grid integrated battery for overcoming the intermittency of RE sources. IEEE International Conference on Information and Automation for Sustainability, pp. 1–6. Galle, Sri Lanka. [Google Scholar]

7. REN22 Secretariat (2022). Renewables 2022 global status report. https://www.ren21.net/gsr-2022/ (accessed on 01/05/2023). [Google Scholar]

8. Saeed, M. H., Fangzong, W., Kulwar, B. A., Iqbal, S. (2021). A review on microgrids challenges and perspective. IEEE Access, 9, 166502–1665179. [Google Scholar]

9. Jirdehi, M. A., Tabar, V. S., Ghassemzadeh, S., Tohidi, S. (2020). Different aspects of microgrid management: A comprehensive review. Journal of Energy Storage, 30, 101457. [Google Scholar]

10. Hatziargyriou, N., Asano, H., Iravani, R., Marnay, C. (2007). Microgrids: An overview of ongoing research and development and demonstration projects. IEEE Power Energy Management, 5, 78–94. [Google Scholar]

11. Wang, Y., Shiwen, M. R., Nelms, M. (2015). Online algorithms for optimal energy distribution in microgrids. Auburn AL, USA: Springer Briefs in Applied Sciences and Technology. [Google Scholar]

12. Al-Ismail, F. S. (2021). DC microgrid planning, operation, and control: A comprehensive review. IEEE Access, 9, 36154–36172. [Google Scholar]

13. Hirsch, A., Parag, Y., Guerrero, J. (2018). Microgrids: A review of technologies, key drivers, and outstanding issues. Renewable and Sustainable Energy Reviews, 90, 402–411. [Google Scholar]

14. Zhang, Z., Li, G., Zhou, M. (2010). Application of microgrid in distributed generation together with the benefit research. IEEE PES General Meeting Providence, pp. 25–29. Providence, RI, USA. [Google Scholar]

15. Yamashita, D. Y., Vechiu, I., Gaubert, J. P. (2020). A review of hierarchical control for building microgrids. Renewable Sustainable Energy Reviews, 118, 109523. [Google Scholar]

16. Mashayekh, S., Butler-Purry, K. L. (2015). An integrated security-constrained model-based dynamic power management approach for isolated microgrids in all-electric ships. IEEE Transactions on Power Systems, 30, 2934–2945. [Google Scholar]

17. Roslan, M. F., Hannan, M. A., Jern, P., Uddin, M. N. (2019). Microgrid control methods toward achieving sustainable energy management. Applied Energy, 240, 583–607. [Google Scholar]

18. Sarfi, V., Livani, H. (2017). A novel multi-objective security-constrained power management for isolated microgrids in all-electric ships. IEEE Electric Ship Technologies Symposium (ESTS), Arlington, VA, USA. [Google Scholar]

19. Altaf, M. F., Arif, M. T., Islam, S. N., Haque, M. E. (2022). Microgrid protection challenges and mitigation approaches–A comprehensive review. IEEE Access, 10, 38895–38922. [Google Scholar]

20. Hatziargyriou, N. (2014). Microgrids: Architectures and control. New York: John Wiley & Sons. [Google Scholar]

21. Guan, Y., Wei, B., Guerrero, J. M., Vasquez, J. C. (2022). An overview of the operation architechture and energy management system for multiple microgrid clusters. iEnergy, 1(3), 306–314. [Google Scholar]

22. Kim, H. J., Kim, M. K. (2023). A novel deep learning-based forecasting model optimized by heuristic algorithm for energy management of microgrid. Applied Energy, 332, 120525. [Google Scholar]

23. Mahmoud, M. S. (2017). Microgrid advanced control methods and renewable energy system integration. Elsevier: USA. [Google Scholar]

24. Wood, A. J., Wollenberg, B. F. (1996). Power generation, operation, and control. New York: John Wiley & Sons. [Google Scholar]

25. Wood, A. J., Wollenberg, B. F., Sheblle, G. B. (2013). Power generation, operation, and control. New York: John Wiley & Sons. [Google Scholar]

26. Kaur, P., Chaturvedi, K. T., Kolhe, M. L. (2022). Techno economic power dispatching of combined heat and power plant considering prohibited operating zones and valve point loading. Processes, 10, 81727. [Google Scholar]

27. Kaur, P., Chaturvedi, K. T., Kolhe, M. L. (2023). Combined heat and power economic dispatching within energy network using hybrid metaheuristic technique. Energies, 16, 1221. [Google Scholar]

28. Zheng, H. F. (2019). Dynamic economic dispatch based on improved differential evolution algorithm. Cluster Computing, 22, 8241–8248. [Google Scholar]

29. Alanazi, M. S. (2021). A modified teaching learning-based optimization for economic load dispatch considering both wind power and load demand uncertainties with operational constraints. IEEE Access, 9, 101665–101680. [Google Scholar]

30. Sattar, M. A., Ahmad, A., Fayyaz, S., Haq, S. S. U., Saddique, M. S. (2020). Ramp rate handling strategies in dynamic economic load dispatch (DELD) problem using grey wolf optimizer (GWO). Journal of Chinese Institute of Engineers, 43, 200–213. [Google Scholar]

31. Parisio, A., Rikos, E., Tzamalis, G., Glielmo, L. (2014). Use of model predictive control for experimental microgrid optimization. Applied Energy, 115, 37–46. [Google Scholar]

32. Chaouachi, A., Kamel, R. M., Andoulsi, R., Nagasaka, K. (2013). Multi-objective intelligent energy management for a microgrid. IEEE Transaction on. Industrial Electronics, 60, 1688–1699. [Google Scholar]

33. Basu, A. K., Bhattacharya, A., Chowdhury, S. (2012). Planned scheduling for economic power sharing in a CHP-based micro-grid. Power Systems. IEEE Transaction of Power System, 27, 30–38. [Google Scholar]

34. Talari, S., Yazdaninejad, M., Haghifam, M. R. (2015). Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages, and responsive loads. IET Generation Transmission and Distribution, 9, 498–509. [Google Scholar]

35. Mohamed, F. A., Koivo, H. N. (2012). Multiobjective optimization using Mesh Adaptive Direct Search for power dispatch problem of microgrid. International Journal of Electrical Power Energy System, 42, 728–735. [Google Scholar]

36. Li, C., Bosio, F. D., Chen, F., Chaudhary, S. K., Vasquez, J. C. et al. (2017). Economic Dispatch for operating cost minimization under real-time pricing in droop-controlled DC microgrid. IEEE Journal of Emerging and Selected Topics in Power Electronics, 5, 587–595. [Google Scholar]

37. Xu, Q., Xiao, J., Wang, P., Wen, C. (2017). A decentralized control strategy for economic operation of autonomous AC, DC, and hybrid AC/DC microgrids. IEEE Transaction on Energy Conversion, 32, 1345–1355. [Google Scholar]

38. Liu, W., Zhuang, P., Liang, H., Peng, J., Huang, Z. (2018). Distributed economic dispatch in microgrids based on cooperative reinforcement learning. IEEE Transaction on Neural Networks Learning Systems, 29, 2192–2203. [Google Scholar]

39. Fossati, J. P., Galarza, A., Martín-Villate, A., Echeverría, J. M., Fontan, L. (2015). Optimal scheduling of a microgrid with a fuzzy logic-controlled storage system. International Journal of Electrical Power Energy Systems, 68, 61–70. [Google Scholar]

40. Shoeb, M. A., Shahnia, F., Shafiullah, G. M. (2019). A multilayer and event-triggered voltage and frequency management technique for microgrid's central controller considering operational and sustainability aspects. IEEE Transaction on Smart Grid, 10, 5136–5151. [Google Scholar]

41. Binetti, G., Davoudi, A., Lewis, F. L., Naso, D., Turchiano, B. (2014). Distributed consensus-based economic dispatch with transmission losses. IEEE Transaction on Power Systems, 29, 1711–1720. [Google Scholar]

42. Binetti, G., Davoudi, A., Naso, D., Turchiano, B., Lewis, F. L. (2014). A distributed auction-based algorithm for the nonconvex economic dispatch problem. IEEE Transaction on Industrial Information, 10, 1124–1132. [Google Scholar]

43. Chen, F. (2017). Cost-based droop schemes for economic dispatch in islanded microgrids. IEEE Transaction on Smart Grid, 8, 63–74. [Google Scholar]

44. Li, Q., Gao, D. W., Zhang, H., Wu, Z., Wang, F. (2019). Consensus-based distributed economic dispatch control method in power systems. IEEE Transaction on Smart Grid, 10, 941–954. [Google Scholar]

45. Jiang, H., Ning, S., Ge, Q. (2019). Multi-objective optimal dispatching of microgrid with large-scale electric vehicles. IEEE Access, 7, 145880–145888. [Google Scholar]

46. Solanki, B. V., Bhattacharya, K., Canizares, C. A. (2017). A sustainable energy management system for isolated microgrids. IEEE Transaction on Sustainable Energy, 8, 1507–1517. [Google Scholar]

47. Abou Houran, M., Chen, W., Zhu, M., Dai, L. (2019). Economic dispatch of grid-connected microgrid for smart building considering the impact of air temperature. IEEE Access, 7, 70332–70342. [Google Scholar]

48. Wu, H., Zhuang, H., Zhang, W., Ding, M. (2016). Optimal allocation of microgrid considering economic dispatch based on hybrid weighted bilevel planning method and algorithm improvement. International Journal on Electrical Power Energy Systems, 75, 28–37. [Google Scholar]

49. Liang, H., Choi, B. J., Abdrabou, A., Zhuang, W., Shen, X. (2012). Decentralized economic dispatch in microgrids via heterogeneous wireless networks. IEEE Journal on Selected Areas Communication, 30, 1061–1074. [Google Scholar]

50. Alharbi, H., Bhattacharya, K. (2018). Stochastic optimal planning of battery energy storage systems for isolated microgrids. IEEE Transaction on Sustainable Energy, 9, 211–227. [Google Scholar]

51. Die, W. (2019). Optimal approach in the EMS of microgrids based on online forecasts. Journal of Engineering, 2019, 1645–1648. [Google Scholar]

52. Sarfi, V., Livani, H. (2018). An economic-reliability security-constrained optimal dispatch for microgrids. IEEE Transaction on Power Systems, 33, 6777–6786. [Google Scholar]

53. Babazadeh-Dizaji, R., Hamzeh, M., Hekmati, A. (2020). A frequency-based economical-sharing strategy for low-voltage DC microgrids. International Journal on Electrical Power Energy System, 118, 105822. [Google Scholar]

54. Xia, H. (2018). Distributed control method for economic dispatch in islanded microgrids with renewable energy sources. IEEE Access, 6, 21802–21811. [Google Scholar]

55. Zhao, Y., Yu, J., Ban, M., Liu, Y., Li, Z. (2018). Privacy-preserving economic dispatch for an active distribution network with multiple networked microgrids. IEEE Access, 6, 38802–38819. [Google Scholar]

56. Mudumbai, R., Dasgupta, S., Cho, B. B. (2012). Distributed control for optimal economic dispatch of a network of heterogeneous power generators. IEEE Transaction on Power Systems, 27, 1750–1760. [Google Scholar]

57. Maulik, A., Das, D. (2019). Stability constrained economic operation of islanded droop-controlled DC microgrids. IEEE Transaction on Sustainable Energy, 10, 569–578. [Google Scholar]

58. Brown, H. E., Suryanarayanan, S., Member, S., Natarajan, S. A., Rajopadhye, S. (2012). Improving reliability of islanded distribution energy resources. IEEE Transaction on Smart Grid, 3, 2028–2038. [Google Scholar]

59. Shen, X., Zheng, J., Zhu, S., Wang, X. (2014). Multi-scene security-constrained economic dispatch with rational wind power curtailment in micro-grid. IEEE Power and Energy Society General Meeting, pp. 27–31. National Harbor, MD, USA. [Google Scholar]

60. Venayagamoorthy, G. K., Sharma, R. K., Gautam, P. K., Ahmadi, A. (2016). Dynamic energy management system for a smart microgrid. IEEE Transaction on Neural Networks Learning System, 27, 1643–1656. [Google Scholar]

61. Giorgio, A. D., Liberati, F., Lanna, A., Pietrabissa, A., Priscoli, F. D. (2017). Model predictive control of energy storage systems for power tracking and shaving in distribution grids. IEEE Transaction on Sustainable Energy, 8, 496–504. [Google Scholar]

62. Liao, G. C. (2012). Solve environmental economic dispatch of Smart Micro-Grid containing distributed generation system–Using chaotic quantum genetic algorithm. International Journal on Electrical Power Energy System, 43, 779–787. [Google Scholar]

63. Ross, M., Abbey, C., Bouffard, F., Joos, G. (2018). Microgrid economic dispatch with energy storage systems. IEEE Transaction on Smart Grid, 9, 3039–3047. [Google Scholar]

64. Chen, C., Duan, S., Cai, T., Liu, B., Hu, G. (2011). Smart energy management system for optimal microgrid economic operation. IET Renewable Power Generation, 5, 258–267. [Google Scholar]

65. He, X., Yu, J., Huang, T., Li, C. (2019). Distributed power management for dynamic economic dispatch in the multimicrogrids environment. IEEE Transaction on Control System Technology, 27, 1651–1658. [Google Scholar]

66. Zhang, Y., Gatsis, N., Giannakis, G. B. (2013). Robust energy management for microgrids with high-penetration renewables. IEEE Transaction on Sustainable Energy, 4, 944–953. [Google Scholar]

67. Sohn, J. M. (2016). Generation applications package for combined heat power in on-grid and off-grid microgrid energy management system. IEEE Access, 4, 3444–3453. [Google Scholar]

68. Shuai, H., Fang, J. Ai, Tang, X., Wen, Y., He, J. et al. (2019). Stochastic optimization of economic dispatch for microgrid based on approximate dynamic programming. IEEE Transaction on Smart Grid, 10, 2440–2452. [Google Scholar]

69. Nutkani, I. U., Loh, P. C., Blaabjerg, F. (2014). Droop scheme with consideration of operating costs. IEEE Transaction on Power Electronics, 29, 1047–1052. [Google Scholar]

70. Ahn, S. J., Nam, S. R., Choi, J. H., Moon, S. (2013). Power scheduling of distributed generators for economic and stable operation of a microgrid. IEEE Transaction on Smart Grid, 4, 398–405. [Google Scholar]

71. Silvente, J., Kopanos, G. M., Pistikopoulos, E. N., Espuna, A. (2015). A rolling horizon optimization framework for the simultaneous energy supply and demand planning in microgrids. Applied Energy, 155, 485–501. [Google Scholar]

72. Wang, J., Zhong, H., Xia, Q., Kang, C. Du, E. (2017). Optimal joint-dispatch of energy and reserve for CCHP-based microgrids. IET Generation Transmission and Distribution, 11, 785–794. [Google Scholar]

73. Malysz, P., Sirouspour, S., Emadi, A. (2014). An optimal energy storage control strategy for grid-connected microgrids. IEEE Transaction on Smart Grid, 5, 1785–1796. [Google Scholar]

74. Battistelli, C., Agalgaonkar, Y. P., Pal, B. C. (2017). Probabilistic dispatch of remote hybrid microgrids including battery storage and load management. IEEE Transaction on Smart Grid, 8, 1305– 1317. [Google Scholar]

75. Nikmehr, N., Ravadanegh, S. N. (2015). Optimal power dispatch of multi-microgrids at future smart distribution grids. IEEE Transaction on Smart Grid, 6, 1648–1657. [Google Scholar]

76. Zhao, X. C., Zhang, Z. Q., Xie, Y. M., Meng, J. (2020). Economic-environmental dispatch of microgrid based on improved quantum particle swarm optimization. Energy, 195, 117014. [Google Scholar]

77. Askarzadeh, A. (2018). A memory-based genetic algorithm for optimization of power generation in a microgrid. IEEE Transaction on Sustainable Energy, 9, 1081–1089. [Google Scholar]

78. Shan, H. (2019). Economic optimization of microgrid based on improved quantum genetic algorithm. Journal of Engineering, 2019, 1167–1174. [Google Scholar]

79. Shehzad, M. F., Dan, M., Mariani, V., Srinivasan, S., Liuzza, D. et al. (2021). A heuristic algorithm for combined heat and power system operation management. Energies, 14, 1–22. [Google Scholar]

80. Mojica-Nava, E., Rivera, S., Quijano, N. (2017). Game-theoretic dispatch control in microgrids considering network losses and renewable distributed energy resources integration. IET Generation Transmission and Distribution, 11, 1583–1590. [Google Scholar]

81. Yliniemi, L., Tumer, K. P. (2014). PaCcET: An objective space transformation to iteratively convexify the pareto front. In: SEAL 2014: Simulated evolution and learning, pp. 204–215. Dunedin, New Zealand. [Google Scholar]

82. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182–197. [Google Scholar]

83. Zhao, B., Cao, Y. J. (2005). Multiple objective particle swarm optimization technique for economic load dispatch. Journal of Zhejiang University–Science A, 6, 420–427. [Google Scholar]

84. Nascimento, J., Powell, W. B. (2013). An optimal approximate dynamic programming algorithm for concave, scalar storage problems with vector-valued controls. IEEE Transaction Automatic Control, 58, 2995–3010. [Google Scholar]

85. Liu, C., Wang, X., Wu, X., Guo, J. (2017). Economic scheduling model of microgrid considering the lifetime of batteries. IET Generation Transmission and Distribution, 11, 759–767. [Google Scholar]

86. Li, Y., Wang, P., Gooi, H. B., Ye, J., Wu, L. (2019). Multi-objective optimal dispatch of microgrid under uncertainties via interval optimization. IEEE Transaction on Smart Grid, 10, 2046–2058. [Google Scholar]

87. Wei, Q., Liu, D., Shi, G. (2015). A novel dual iterative Q-learning method for optimal battery management in smart residential environments. IEEE Transaction Industrial Electronics, 62, 2509–2518. [Google Scholar]

88. Shang, Y. (2020). Stochastic dispatch of energy storage in microgrids: An augmented reinforcement learning approach. Applied Energy, 261, 114423. [Google Scholar]

89. Wu, Z., Gu, W., Wang, R., Yuan, X., Liu, W. (2011). Economic optimal schedule of CHP microgrid system using chance constrained programming and particle swarm optimization. IEEE Power Energy Society General Meeting, Detroit, MI, USA. [Google Scholar]

90. Welch, R. L., Venayagamoorthy, G. K. (2010). Energy dispatch fuzzy controller for a grid-independent photovoltaic system. Energy Conversion Management, 51, 928–937. [Google Scholar]

91. Gamez Urias, M. E., Sanchez, E. N., Ricalde, L. J. (2015). Electrical microgrid optimization via a new recurrent neural network. IEEE Systems Journal, 9, 945–953. [Google Scholar]

92. Lasseter, R. H., Paigi, P. (2004). Microgrid: A conceptual solution. IEEE 35th Annual Power Electronics Conference, Aachen, Germany. [Google Scholar]

93. Zheng, W., Wu, W., Zhang, B., Li, Z., Liu, Y. (2015). Fully distributed multi-area economic dispatch method for active distribution networks. IET Generation Transmission and Distribution, 9, 1341–1351. [Google Scholar]

94. Du, Y., Pei, W., Chen, N., Ge, X., Xiao, H. (2017). Real-time microgrid economic dispatch based on model predictive control strategy. Journal of Modern Power Systems and Clean Energy, 5, 787–796. [Google Scholar]

95. Palma-Behnke, R., Benavides, C., Lanas, F., Severino, B., Reyes, L. et al. (2013). A microgrid energy management system based on the rolling horizon strategy. IEEE Transaction on Smart Grid, 4, 996–1006. [Google Scholar]

96. Parisio, A., Rikos, E., Glielmo, L. (2014). A model predictive control approach to microgrid operation optimization. IEEE Transaction on Control System, 22, 1813–1827. [Google Scholar]

97. Tang, Z., Hill, D. J., Liu, T. (2018). A novel consensus-based economic dispatch for microgrids. IEEE Transactions on Smart Grid, 9, 3920–3922. [Google Scholar]

98. Chen, G., Ren, J., Feng, E. N. (2017). Distributed finite-time economic dispatch of a network of energy resources. IEEE Transactions on Smart Grid, 8, 822–832. [Google Scholar]

99. Chen, G., Zhao, Z. (2018). Delay effects on consensus-based distributed economic dispatch algorithm in microgrid. IEEE Transaction on Power System, 33, 602–612. [Google Scholar]

100. Yang, S., Tan, S., Xu, J. X. (2013). Consensus based approach for economic dispatch problem in a smart grid. IEEE Transaction on Power Systems, 28, 4416–4423. [Google Scholar]

101. Wang, R., Li, Q., Zhang, B., Wang, L. (2019). Distributed consensus based algorithm for economic dispatch in a microgrid. IEEE Transaction on Smart Grid, 10, 3630–3640. [Google Scholar]

102. Zhao, W., Liu, M., Zhu, J., Li, L. (2016). Fully decentralised multi-area dynamic economic dispatch for large-scale power systems via cutting plane consensus. IET Generation Transmission and Distribution, 10, 2486–2495. [Google Scholar]

103. Mahmoodi, M., Shamsi, P., Fahimi, B. (2015). Economic dispatch of a hybrid microgrid with distributed energy storage. IEEE Transactions on Smart Grid, 6, 2607–2614. [Google Scholar]

104. Hu, J., Duan, J., Ma, H., Chow, M. Y. (2018). Distributed adaptive droop control for optimal power dispatch in DC microgrid. IEEE Transaction Industrial Electronics, 65, 778–789. [Google Scholar]

105. Hug, G., Kar, S., Wu, C. (2015). Consensus + innovations approach for distributed multiagent coordination in a microgrid. IEEE Transactions on Smart Grid, 6, 1893–1903. [Google Scholar]

106. Zhang, Z., Chow, M. Y. (2012). Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid. IEEE Transactions on Power Systems, 27, 1761–1768. [Google Scholar]

107. Nutkani, I. U., Loh, P. C., Wang, P., Blaabjerg, F. (2017). Decentralized economic dispatch scheme with online power reserve for microgrids. IEEE Transactions on Smart Grid, 8, 139–148. [Google Scholar]

108. Zhang, Y., Hajiesmaili, M. H., Cai, S., Chen, M., Zhu, Q. (2018). Peak-aware online economic dispatching for microgrids. IEEE Transactions on Smart Grid, 9, 323–335. [Google Scholar]

109. Zhang, W., Liu, W., Wang, X., Liu, L., Ferrese, F. (2015). Online optimal generation control based on constrained distributed gradient algorithm. IEEE Transaction Power System, 30, 35–45. [Google Scholar]

110. Xu, Q., Li, L., Chen, X., Huang, Y., Luan, K. et al. (2019). Optimal economic dispatch of combined cooling, heating and power-type multi-microgrids considering interaction power among microgrids. IET Transactions on Smart Grid, 2, 391–398. [Google Scholar]

111. Zhang, Z., Chow, M. Y. (2012). Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid. IEEE Transaction on Power System, 27, 1761–1768. [Google Scholar]

112. Zhao, B., Shi, Y., Dong, X., Luan, W., Bornemann, J. (2014). Short-term operation scheduling in renewable-powered microgrids: A duality-based approach. IEEE Transaction on Sustainable Energy, 5, 209–217. [Google Scholar]

113. Liu, W., Zhuang, P., Liang, H., Peng, J., Peng, Z. (2018). Distributed economic dispatch in microgrids based on cooperative reinforcement learning. IEEE Transaction Neural Network Learning Systems, 29, 2192–2203. [Google Scholar]

114. Motevasel, M., Seifi, A. R. (2014). Expert energy management of a microgrid considering wind energy uncertainty. Energy Conversion and Management, 83, 58–72. [Google Scholar]