 Open Access
Open Access
REVIEW
Optimal Location of Renewable Energy Generators in Transmission and Distribution System of Deregulated Power Sector: A Review
1 Department Electrical Engineering, Government Polytechnic College, BTE Lucknow, Etah, 207120, India
2 University of Nevada, Reno, NV 89557, USA
3 Department of Computer Science, Zarqa University, Zarqa, 13110, Jordan
4 Department of Interdisciplinary Courses in Engineering, Chitkara University Institute of Engineering & Technology, Chitkara University, Chandigarh, 160002, India
5 Jadara University Research Center, Jadara University, Irbid, 00962, Jordan
6 Department of Industrial Engineering, Al Zawiya University, Al-Zawiya, P.O. Box 16418, Libya
7 Applied Science Research Center, Applied Science Private University, Amman, 11931, Jordan
8 Department of Biosciences, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, 602105, India
* Corresponding Authors: Mohammad Aljaidi. Email: ; Manish Kumar Singla. Email:
Energy Engineering 2025, 122(3), 823-859. https://doi.org/10.32604/ee.2025.059309
Received 03 October 2024; Accepted 17 December 2024; Issue published 07 March 2025
Abstract
The literature on multi-attribute optimization for renewable energy source (RES) placement in deregulated power markets is extensive and diverse in methodology. This study focuses on the most relevant publications directly addressing the research problem at hand. Similarly, while the body of work on optimal location and sizing of renewable energy generators (REGs) in balanced distribution systems is substantial, only the most pertinent sources are cited, aligning closely with the study’s objective function. A comprehensive literature review reveals several key research areas: RES integration, RES-related optimization techniques, strategic placement of wind and solar generation, and RES promotion in deregulated power markets, particularly within transmission systems. Furthermore, the optimal location and sizing of REGs in both balanced and unbalanced distribution systems have been extensively studied. RESs demonstrate significant potential for standalone applications in remote areas lacking conventional transmission and distribution infrastructure. Also presents a thorough review of current modeling and optimization approaches for RES-based distribution system location and sizing. Additionally, it examines the optimal positioning, sizing, and performance of hybrid and standalone renewable energy systems. This paper provides a comprehensive review of current modeling and optimization approaches for the location and sizing of Renewable Energy Sources (RESs) in distribution systems, focusing on both balanced and unbalanced networks.Keywords
Nomenclature
| Coefficient of the generators | |
| Generation power | |
| Emission coefficients of the generators | |
| ith | Bus Number |
| αj, βj λj | Demand bidding coefficient |
Energy constitutes a fundamental driver of economic growth and social development across nations, with sources broadly classified into renewable and non-renewable categories. The ongoing proliferation of renewable energy sources (RESs), encompassing wind, solar, small hydro, geothermal, bio-power, and waste-to-energy, is experiencing rapid acceleration due to their inherent characteristics of cleanliness, sustainability, and abundance. These freely accessible sources are increasingly acknowledged as crucial to global initiatives aimed at expanding energy capacity, bolstering energy security, mitigating environmental concerns, and fostering the burgeoning renewable energy market. Consequently, RESs are positioned as the vanguard of green energy, poised to supplant less environmentally benign energy sources in the future. This paradigm shift towards renewables represents a significant trend in the global energy landscape, with far-reaching implications for policy formulation, technological innovation, and environmental sustainability. The growing energy demand, driven by rising population, industrialization, and urbanization, places significant pressure on energy supplies. Electrical energy, which constitutes a substantial portion of total energy consumption, faces a notable shortfall due to high consumption rates and insufficient supply [1]. Centralized power generation systems are often inadequate to meet energy demands due to limitations in transmission capacity, voltage stability, and economic constraints. Conventional energy sources contribute to various environmental problems, including health issues, premature mortality, and significant economic costs, amounting to billions of dollars annually. The integration of renewable energy sources and distributed generation systems offers a promising solution to mitigate these challenges.
Renewable Energy Sources (RESs) offer a highly effective and efficient alternative for power generation. In recent years, the growing demand for power and increasing environmental concerns have driven the expanded use of RESs, positioning them as key players in power generation, sustainable development, and the mitigation of environmental issues. Historically, the RESs cost has been higher than conventional energy sources, limiting their competitiveness in deregulated power markets. However, recent trends show a continuous decline in the costs of RESs, particularly solar power, which is expected to reach parity with conventional electricity generation costs in the near future. As a result, RESs are now leading new capacity installations for electrical power generation in India and globally. Renewable energy sources and associated technologies hold significant potential to address longstanding energy challenges and help bridge the gap between electricity generation and demand, particularly in developing countries.
This paper examines research on the strategic placement of Renewable Energy Generators (REGs) in power grids. We consider factors like social impact, power losses, voltage stability, emissions, and REG size to optimize their location and capacity. Proper REG placement can alleviate the strain on traditional power sources, improve network efficiency, and reduce energy waste. This paper also reviews current methods for optimally placing and sizing Renewable Energy Sources (RESs) in balanced and unbalanced distribution networks. We examine optimization techniques like Particle Swarm Optimization (PSO) and Genetic Algorithms (GA) to identify challenges and knowledge gaps in RES integration, particularly for hybrid and standalone systems. The findings emphasize the need to consider multiple optimization criteria, including power losses, emissions, and system reliability, to maximize performance and efficiency.
2 Position of Renewable Energy in India and Worldwide
Global renewable energy (RE) capacity has significantly increased over the past decade. Wind power remains the leading RE source, followed by solar photovoltaic (PV) power. As shown in Fig. 1 [2], wind power accounts for 370 GW of the total 673 GW installed RE capacity worldwide. India ranks 5th globally in wind power capacity with 22.6 GW. For solar power, the global capacity is 177 GW, with India ranking 11th at 4 GW.
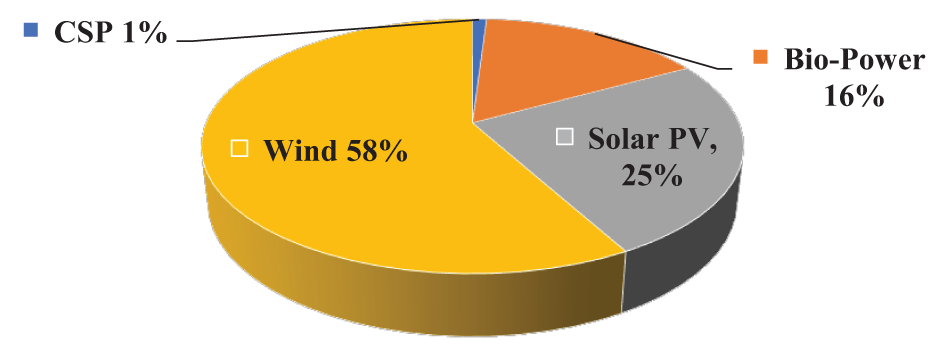
Figure 1: Renewable energy capacity around the world. Reprinted from Ref. [2]
China dominates the global wind power landscape, leading with an installed capacity of 114.6 GW. The United States follows in second place, with a wind power capacity of 65.9 GW. Germany and Spain occupy the third and fourth positions, respectively. India holds the fifth position worldwide, contributing 22.6 GW to the global wind power capacity. This global distribution of wind power capacity is illustrated in Fig. 2.
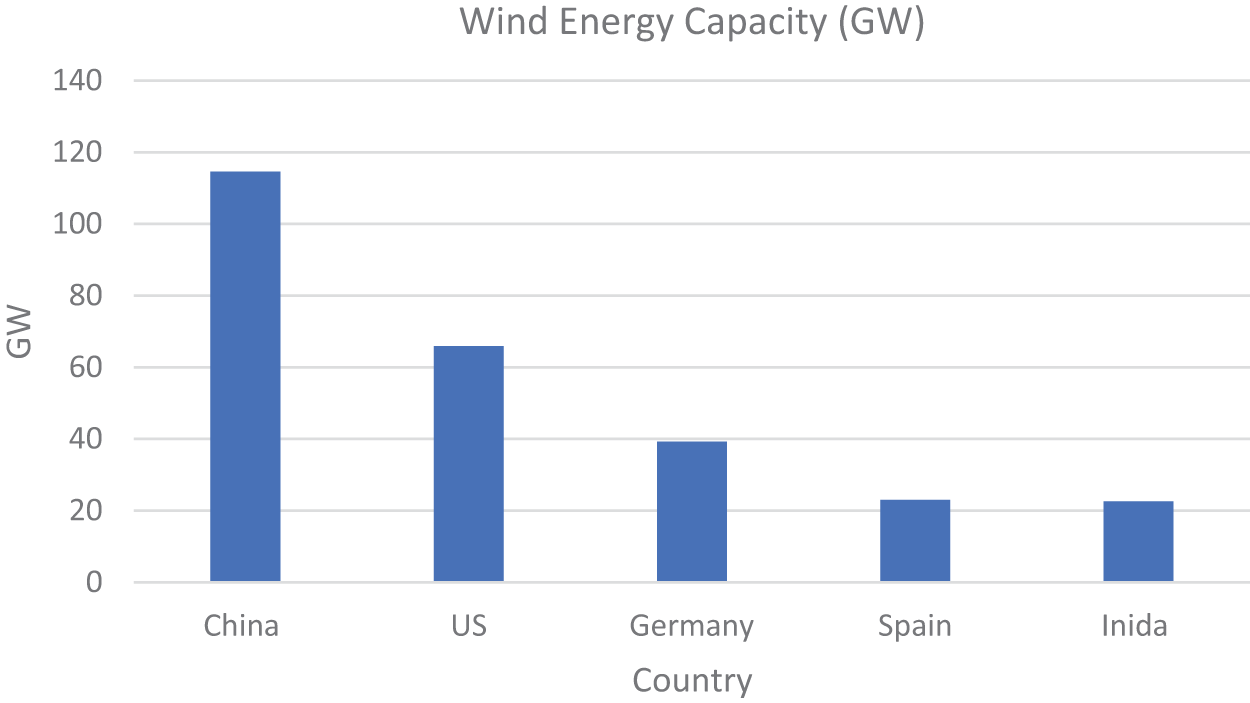
Figure 2: Installed wind energy capacity (GW)
Germany holds the top position globally in solar power installed capacity, with 38.2 GW. It is followed by China with 28.2 GW, Japan with 23.3 GW, Italy with 18.5 GW, and the United States with 18.2 GW, ranking second through fifth, respectively India has demonstrated substantial growth in solar power installations over the past five years, achieving an installed capacity exceeding 4 GW by the conclusion of 2015.
2.1 March 2015 Wind Energy Growth Path Across Indian States
According to the Centre for Wind Energy Technology (CWET), India’s current installed wind power capacity is 22,645 MW. The estimated wind power potential varies with hub height: at 50 m, it is assessed at 49,130 MW, while at 80 m, the potential increases significantly to 102,788 MW. Fig. 3 illustrates the geographical distribution of wind energy potential across various Indian states. CWET has established ambitious targets for future wind power installations, projecting 32,352 MW by 2016–17 and 60,000 MW by 2021–22.
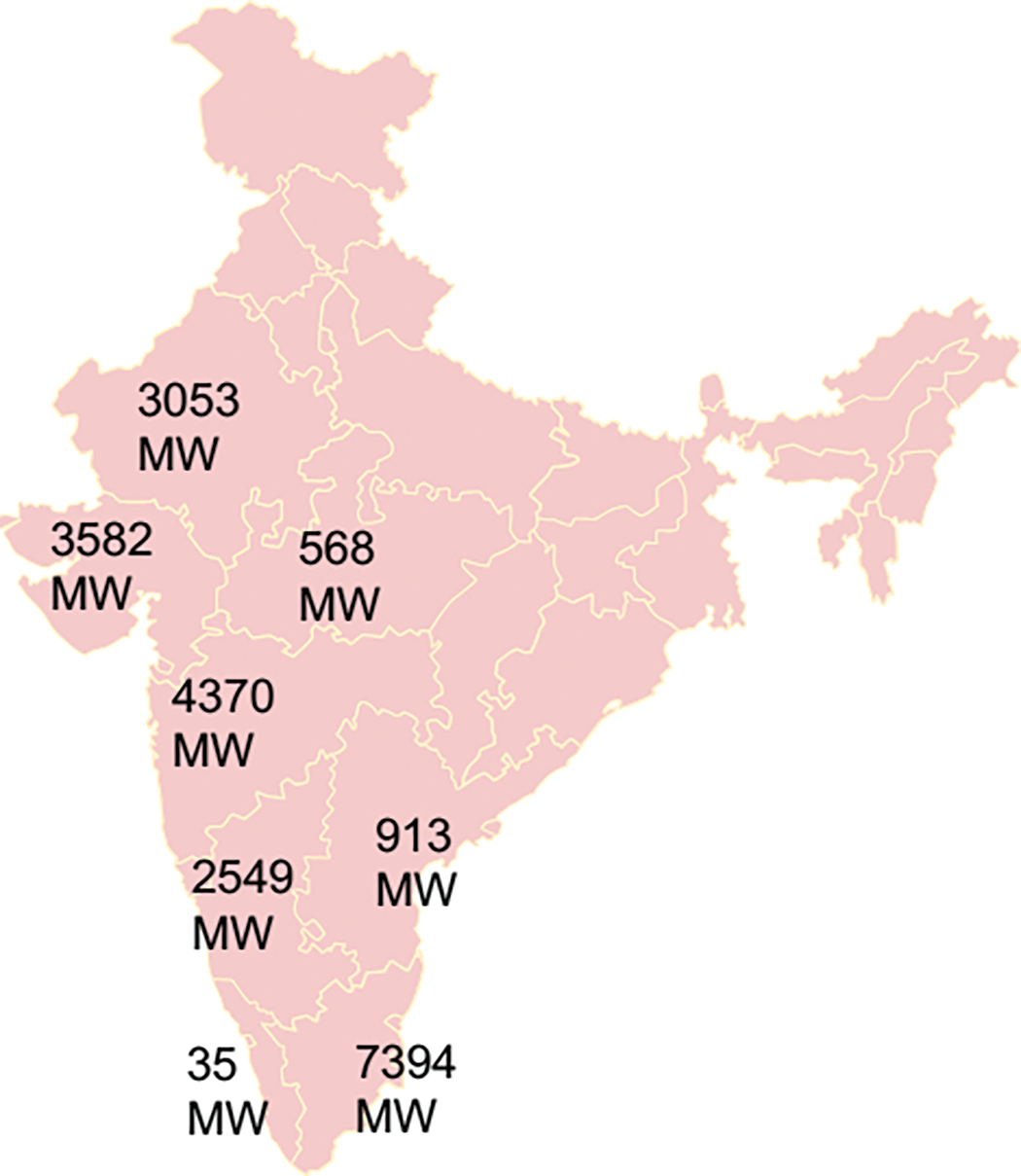
Figure 3: State-wise wind power locations in India
The aggregate installed wind power capacity across Europe, China, the United States, and India totals approximately 297 GW [3]. China has consistently maintained its global leadership in wind power capacity over the past eight years, with an installed capacity exceeding 91 GW. As of October 2015, India’s cumulative installed wind power capacity surpassed 24 GW [4]. The primary contributors to wind power generation in India are the states of Tamil Nadu, Maharashtra, Gujarat, Rajasthan, Karnataka, and Andhra Pradesh.
2.2 Solar Energy Growth in Indian States through March 2015
Several states in India receive abundant solar radiation, making them particularly suitable for solar power generation, with Rajasthan, Gujarat, Tamil Nadu, and Maharashtra being notable examples. The installation of solar power plants across India has been a collaborative effort between state governments and the Government of India. Fig. 4 illustrates the solar power installed capacities in various Indian states as of March 2015 [5]. By the conclusion of 2015, six states had emerged as frontrunners in solar power generation in India: Gujarat, Rajasthan, Madhya Pradesh, Maharashtra, Andhra Pradesh, and Tamil Nadu.
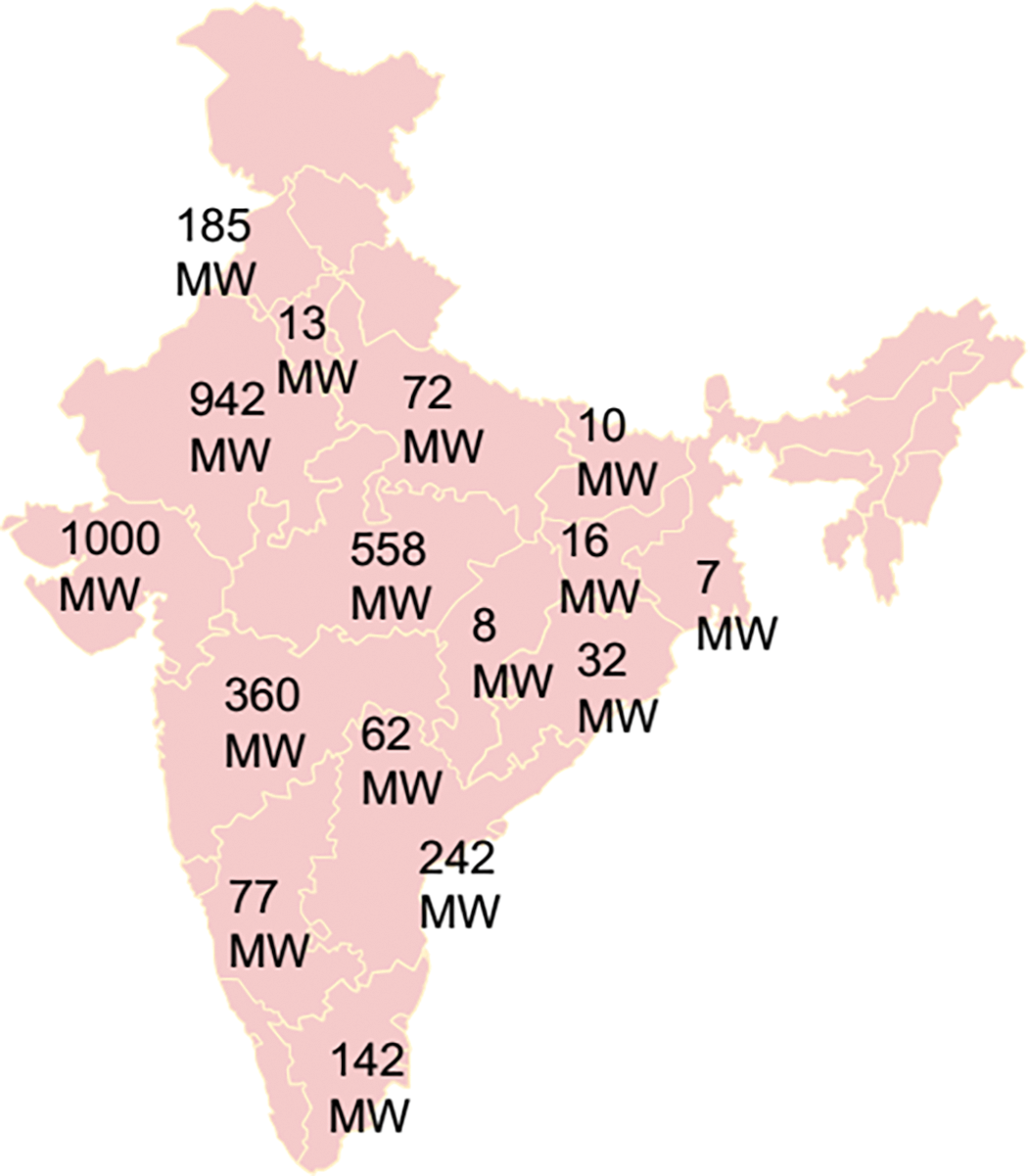
Figure 4: State-wise solar power sites in India. Reprinted from Ref. [5]
1) The status and revised targets for renewable energy (RE) in India during the financial years 2007 to 2015 (FY 2007-15) demonstrate a substantial increase in installed capacity. Over this period, renewable energy installations surged from 9389 MW in 2007 to 34,351 MW by 2015, as depicted in Fig. 5. This significant growth underscores India’s efforts to scale up its renewable energy capacity across various sources.
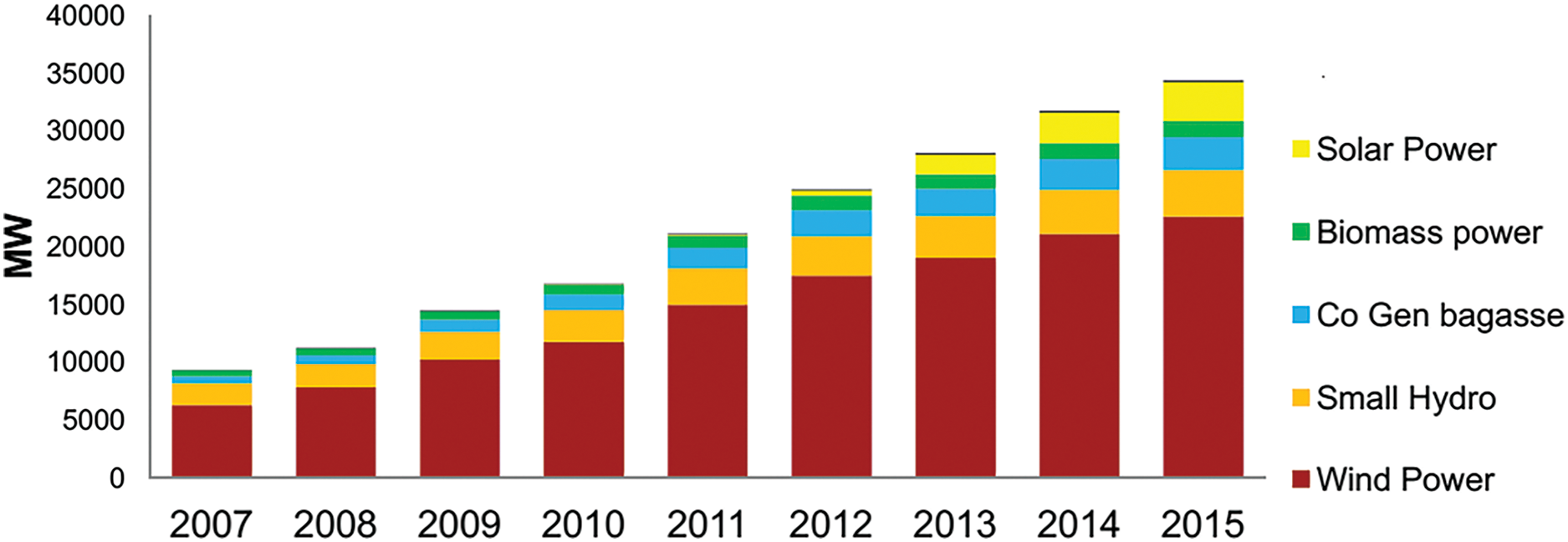
Figure 5: Renewable energy progress through 2015
2) The total installed power generation capacity in India is 272.50 GW, with renewable energy (RE) contributing 35.78 GW. This accounts for 13% of the total installed capacity and approximately 7% of the electricity produced in the country [5].
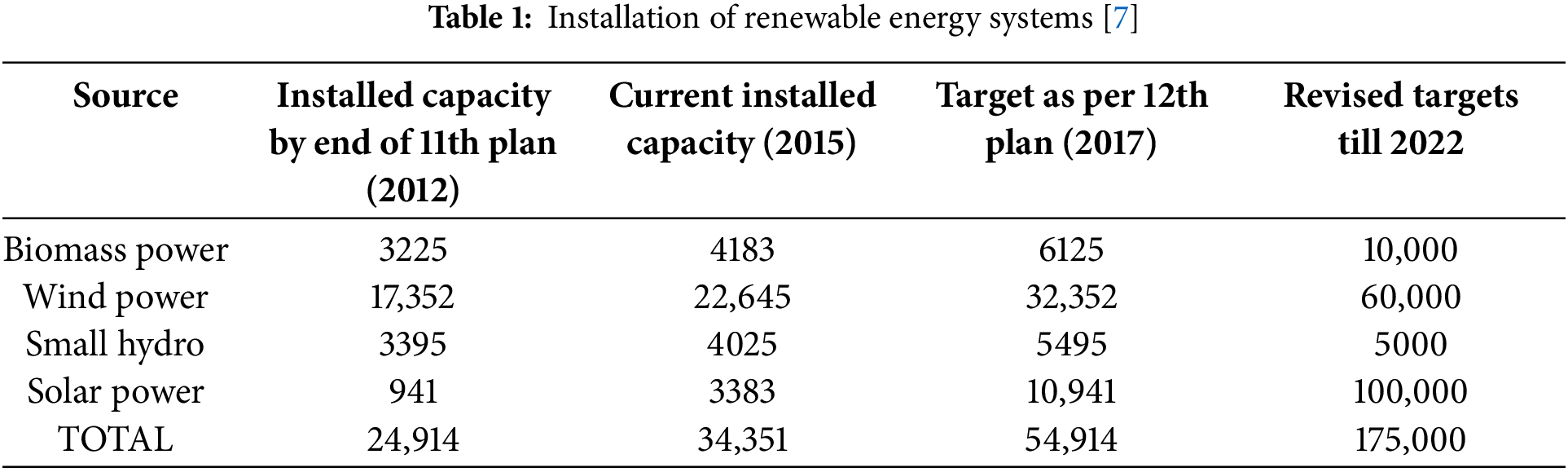
3) India’s new vision for renewable energy targets by 2022 delineates an ambitious plan for significant capacity expansion. Currently, under the National Action Plan for Climate Change, the installed renewable energy capacity is 34.5 GW. The plan projects an increase to 142.3 GW by 2020, with an ultimate target of 175 GW by 2022. This target is disaggregated as follows: 100 GW from solar power, 60 GW from wind power, 10 GW from biomass, and 5 GW from small hydro projects [6]. Table 1 provides detailed information on the installation of off-grid renewable energy systems.
The Renewable Purchase Obligation (RPO) mandates that a certain percentage of the power consumed must come from renewable energy sources, with specific targets set for each state. The current target is 7%, but it is aimed to increase to 15% by 2020 and further to 18.9% (corresponding to 175 GW) by 2022 [7], as shown in Fig. 6. Achieving these targets is crucial for India’s transition to a greener energy mix and reducing its dependence on fossil fuels.
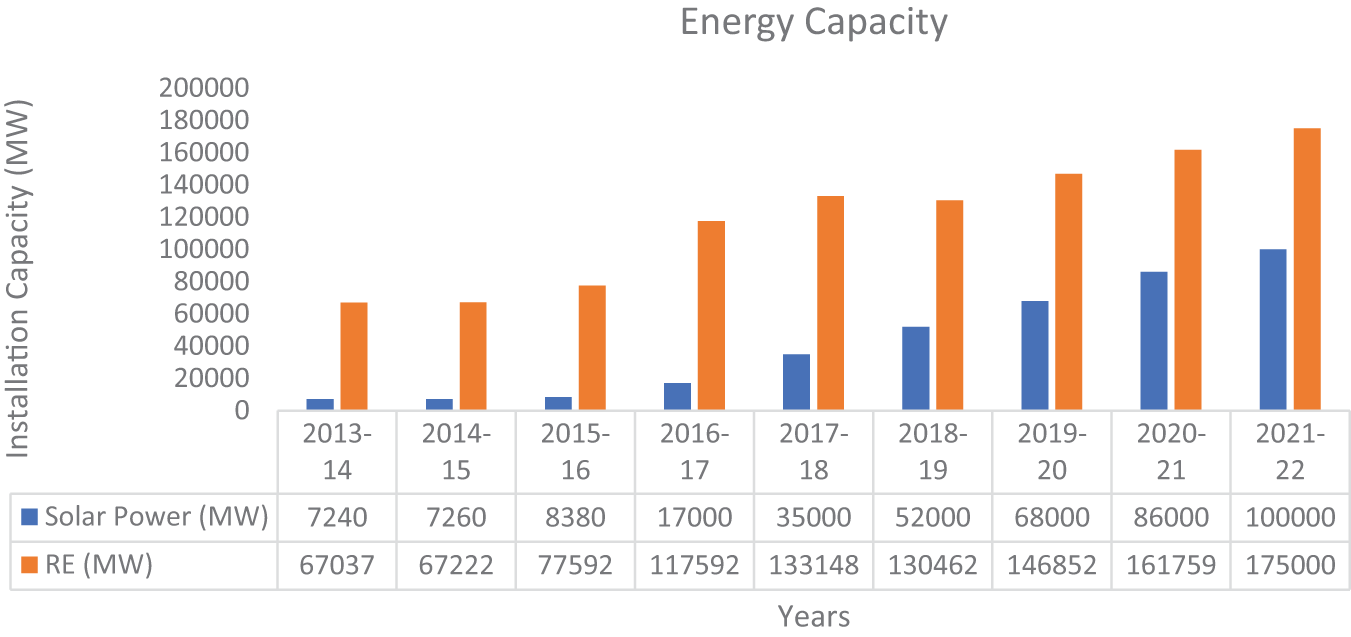
Figure 6: Projected renewable energy capacity of 175 GW by 2022
3 Renewable Energy Source Breakdown
Renewable energy sources, like solar, wind, hydro, geothermal, biomass, biogas, and ocean wave power, can be replenished naturally. Unlike finite fossil fuels, these sources are continuously renewed. While humans have utilized renewable energy for centuries, significant growth occurred in the 20th century due to technological advancements, economic factors, and global shifts [7]. The increasing concern over fossil fuel-related environmental issues, energy security, and geopolitical tensions has driven the surge in renewable energy adoption. In recent years, fossil fuels have continued to dominate the global energy landscape despite rising oil prices and their detrimental impact on the environment, particularly in terms of air pollution. Nevertheless, the adoption of renewable energy, recognized for its critical environmental, social, and economic benefits, is increasingly viewed as a necessary alternative to conventional fossil fuels.
The shift towards renewable energy sources (RESs) is particularly important in deregulated power markets, where environmental and social concerns associated with conventional energy generation are more pronounced. The integration of RESs into the power grid is primarily driven by ecological policies that promote sustainable energy resources and reduce carbon emissions. Technological advancements have significantly contributed to the growth of RESs, and many countries now recognize these technologies as essential for the future. Solar, wind, and hydropower offer a reliable and inexhaustible supply of renewable energy, unlike fossil fuels, which are subject to resource limitations and political uncertainties [8]. Renewable energy and associated technologies hold great promise in addressing the energy crises developing countries like India face. Solar and wind energy, in particular, play a central role in India’s energy strategy by adding new capacity and enhancing energy security, addressing environmental concerns, and driving the substantial market for renewable energy [9].
Photovoltaic (PV) technology directly converts sunlight into electricity. This process, known as photovoltaic generation, uses semiconductor materials to transform solar energy into direct current (DC) electricity. The International Energy Agency (IEA) categorizes PV applications into four main types: off-grid domestic, off-grid non-domestic, grid-connected centralized, and grid-connected distributed systems. PV modules typically consist of approximately 36 or 72 cells connected in series and encapsulated within an aluminum frame, with the configuration varying based on the specific application and cell technology [8,9]. The widespread adoption of PV technology in renewable energy is attributable to its silent operation, non-toxic production processes, and minimal maintenance requirements [10]. The power sector, a key driver of economic development, must actively participate in research projects with relevant stakeholders to ensure that the benefits of technological advancements reach end consumers [11]. In the 1990s, many electric utilities globally were required to shift from vertically integrated structures to open market models to enhance efficiency and competitiveness. The extensive use of fossil fuels has caused considerable environmental harm due to various emissions, with human activities releasing an estimated 8 billion metric tonnes of carbon into the atmosphere annually, including 6.5 billion tonnes from fossil fuel combustion and 1.5 billion tonnes from deforestation [12]. In response to global power sector transformations, India established regulatory commissions in 1998 to promote competition, efficiency, and economic operations. This restructuring began with the Orissa State Electricity Board and has since expanded to several other states. India is now the sixth-largest electricity generator globally, with 274 GW of installed capacity [13]. While thermal power dominates at 65%, there’s a growing emphasis on renewable energy sources, which contribute around 12% [14]. Despite significant growth, a substantial gap persists between electricity generation and demand, necessitating additional power plants, especially those utilizing renewable energy [10].
The IEEE bus system under consideration includes three generators and two dispatch able loads. The generators are located at specific bus numbers. Dispatch able loads are situated at certain bus numbers, while a fixed load is assigned to a particular bus. The bid function for each generation unit is defined as
Similarly, the demand biding function has been taken as
The emission function is presented by the following quadratic equation:
where
Due to significant environmental concerns associated with fossil fuel-based electricity generation, renewable energy sources are gaining prominence. Mitigating these environmental and social impacts is a key focus in policy-making, project development, and operational practices. In India, particularly, the poor quality of coal, often with high ash content, exacerbates the environmental impact of coal-fired power plants [15]. Approximately one-third of these plants generate large amounts of ash, along with harmful gases like CO2, SO2, and NOx. As the economy expands, energy demand is anticipated to rise sharply, and continued dependence on traditional energy sources is likely to lead to increased emissions of harmful gases and a surge in greenhouse gas (GHG) emissions [16]. To address these challenges, the development of renewable energy sources (RESs) is crucial. RESs are abundant, can improve energy security by diversifying the energy supply, reduce reliance on fossil fuel imports, and provide energy access to rural areas. As India strives for sustainable and environmentally responsible energy solutions, transitioning to renewable energy is essential.
3.1 Overview of Renewable Energy Generation Capacity in India
India has witnessed exponential growth in renewable energy consumption over the past decade [17]. The share of renewables in the country’s total installed grid-connected capacity has increased at an average rate of 25% per year, currently accounting for 13% of India’s overall electricity generation capacity. When large hydroelectric generation is included, this share rises to 28% [18]. As of March 2015, India’s total installed power generation capacity reached 272 gigawatts (GW), with 36 GW derived from grid-connected renewable energy sources (RESs) [19]. Wind energy was the dominant renewable source, contributing 24 GW, followed by biomass power at 4.4 GW and small hydroelectric power at 4 GW. Although relatively new, solar photovoltaic (PV) capacity had experienced rapid growth, increasing from 0.035 GW in 2010 to 4 GW by March 2015 [20]. In terms of overall grid-connected electricity generation capacity in 2015, RESs made a significant impact, with wind energy maintaining the highest share at 66% and solar energy accounting for 12% [21].
3.2 Assessing Renewable Energy Targets, Potential, and Regulations in India
Regulatory support has been instrumental in promoting investment in solar energy, significantly contributing to the sector’s growth. The Indian government’s ambitious renewable energy target of 175 GW has created a favorable environment for accelerated solar energy investment. Market research by Deutsche Bank indicates that annual capital investment in the solar energy sector is projected to exceed coal by 2019–20, driven by a commitment of US$35 billion from global investors [22].
The report projects that annually adding 5 GW of solar power from 2016 to 2020 could decrease India’s coal reliance by 8%, reducing coal imports and GHG emissions. To accelerate renewable energy adoption, state electricity regulators must implement measures like preferential tariffs and open access to the grid. India’s 2008 National Action Plan on Climate Change set a 15% solar energy penetration goal by 2020, strengthening Renewable Purchase Obligations (RPOs) to mandate renewable electricity procurement by distribution companies and consumers [23].
India has significantly increased its renewable energy targets. The 2022 goal is 175 GW, including 100 GW of solar power (40 GW from rooftop installations), 60 GW of wind, 10 GW of biomass, and 5 GW of small hydro. This is a substantial increase from the initial 20 GW target under the Jawaharlal Nehru National Solar Mission [24]. Additionally, the 12th Five-Year Plan aims to add 30 GW of new renewable energy capacity by 2017 [25]. The realization of these ambitious goals is estimated to necessitate an investment of approximately US$200 billion. These targets constitute a crucial component of India’s national climate plan, which was submitted to the United Nations Framework Convention on Climate Change (UNFCCC) in December 2015, in preparation for the United Nations Conference of the Parties on Climate Change in Paris (COP21) [26]. This heightened policy commitment has revitalized confidence in the solar energy sector, underscoring its growth potential and making it an increasingly attractive area for investment [27,28]. India’s current renewable energy potential is summarized in Table 2.
3.3 India’s Initiatives for Promoting Solar Energy
In June 2008, the National Action Plan on Climate Change (NAPCC) formally acknowledged the developmental trajectory of solar energy technologies in India, leading to the establishment of the National Solar Mission (NSM) [29,30]. With the objective of achieving grid parity with conventional power tariffs by 2022, the Government of India launched the “Jawaharlal Nehru National Solar Mission” (JNNSM) in November 2009. This initiative was primarily focused on promoting the development and widespread adoption of solar energy technologies across the nation [31,32]. The significance of solar energy has been substantially amplified in recent years, driven by escalating energy demand and the imperative to minimize environmental impacts. Solar energy, characterized by its clean, secure, and low-maintenance attributes, presents an appealing option for sustainable energy development. As of June 2015, India’s total installed solar power capacity had attained 4.011 GW, as detailed in Table 3.
3.4 Techniques for Optimizing Renewable Energy Systems
Optimizing the exploitation of renewable energy sources (RESs) across multiple sites to maximize profits poses significant challenges for energy operators. These challenges include efficiently dispatching available power sources at the lowest possible cost while navigating the complexities of large-scale RES integration into electrical systems. The increased utilization of RESs offers substantial societal benefits, such as local availability, sustainability, and renewable resource usage. However, incorporating large amounts of RES-generated energy into the grid requires advanced operational tools and techniques.
Optimizing new generation assets in deregulated markets has become increasingly critical, especially considering regulatory frameworks and emerging factors like carbon credits and emission trading. Various modern optimization techniques have been developed and analyzed by researchers worldwide to improve the operation of RESs within electric power systems. These analyses focus on hydro, wind, and solar energy production, including cooperative efforts between different technologies, regional dispatching, and integration solutions.
Akella et al. proposed a method for optimizing the utilization of renewable energy sources (RESs) in remote areas [34]. Another study [35] employed a linear programming-based energy model to minimize the use of agricultural residues as biomass energy by optimally allocating land for crop cultivation in a region of South India. The optimization of both individual RESs and hybrid systems involves selecting the best components, determining their optimal sizes, and developing operation strategies to ensure cost-effective, efficient, and reliable energy generation. For instance, Zhu et al. [36] presented the simulation and design of standalone hybrid systems for electricity generation from RESs, highlighting the critical role of component selection and sizing [37,38].
A strategy utilizing multiple control variables, optimized through Genetic Algorithms (GA), was introduced for managing standalone hybrid renewable electrical systems [39]. Another study [40] proposed a GA-based optimization technique for the optimal sizing of solar PV-wind hybrid energy systems, aiming to minimize total system costs while keeping the loss of power supply probability below a defined threshold. Furthermore, an enhanced GA-based method was developed to optimize hybrid renewable energy systems, factoring in the system’s operational lifespan [41]. Other studies have reported multi-objective optimization techniques for the optimal unit sizing of hybrid power generation systems [42,43], including the optimization of hybrid solar-wind energy systems using genetic algorithms [44].
Razak et al. focused on hybrid system optimization with an emphasis on minimizing excess energy and overall energy costs [45]. The Hybrid Optimization Model for Electric Renewables (HOMER) software has been widely employed to determine optimal system sizing and minimize costs for hybrid power systems with specific load demands [46–48]. For example, researchers used HOMER to optimize a hybrid PV/diesel generator system with battery backup for a village in Saudi Arabia, utilizing hourly solar energy data [49]. Muselli et al. [50] proposed that the optimal configuration of hybrid systems should aim to minimize the cost per kilowatt-hour (kWh). Additional studies have optimized the sizing of hybrid PV/diesel systems in various regions, such as Malaysia [51].
The growing importance of RESs is driven by factors like deregulation, power system restructuring, global warming, and the depletion of fossil fuel reserves. Hammons [52] examined the challenges and potential solutions for integrating new renewable energy sources into European power grids, including applying wind power prediction tools. Researchers have also developed optimization models for RESs using binary particle swarm optimization and fuzzy logic [53].
Differential evolution-based optimization techniques have been employed to enhance electric energy production through RESs [54]. A study [55] focused on integrating and optimizing renewable energy sources (RESs) in a remote region, recommending the energy hub concept as a modeling framework for optimal power flow (OPF) problems in integrated energy systems with multiple energy carriers [56]. Liu et al. proposed a particle swarm optimization-based maximum power point tracking algorithm for photovoltaic systems operating under partially shaded conditions [57]. Other studies [58] have optimized new hybrid standalone renewable energy systems using Particle Swarm Optimization (PSO), simulating scenarios with hourly data on wind speed, solar radiation, water flow, and energy demand, such as shown the literature Tables 4 and 5 as per the optimization technique and objective according to stand alone systema and case studies as per deferent area of the world.
Numerous studies have investigated the potential of renewable energy solutions. An optimization model was developed to fulfill the energy requirements of Lemnos Island through the utilization of renewable energy sources (RESs), taking into account factors such as environmental impacts, energy demand, energy costs, and resource availability [59]. Another study [60] examined a hybrid photovoltaic (PV)/diesel generator system for remote electrification in rural areas. Researchers have also conducted techno-economic evaluations of hybrid solar PV-wind power generation systems [61] and grid-connected hybrid renewable energy systems [62]. A standalone hybrid energy system, combining biomass gasifier-based power generation, picohydro, and solar photovoltaic (PV) technologies, was proposed [63], with studies focusing on optimal sizing for remote village clusters in Uttarakhand to ensure a reliable power supply with minimal environmental impact [64]. Milan et al. developed a linear programming-based model for the optimal sizing of renewable supply systems, aiming to minimize overall system costs [65].
4 Site Selection for Efficient Wind Power Generation
Wind energy has emerged as one of the most significant sources of renewable energy in recent years. Its availability and ability to reduce reliance on carbon-based energy sources like coal and oil make it a crucial component in the global transition to cleaner energy. The rapid development of wind energy worldwide underscores its potential for supplying energy, particularly in rural and remote regions. Determining optimal locations for wind energy systems is crucial for maximizing their efficiency and utility.
The deployment of large-scale wind energy systems is being considered by numerous utilities, with a range of optimization techniques, encompassing both classical and artificial intelligence-based methods, being developed to determine optimal locations for renewable energy sources (RESs). The identification of the optimal location and sizing of RESs within the deregulated power sector presents a complex optimization challenge. For instance, Singh et al. [66] utilized mixed integer nonlinear programming (MINLP) to identify optimal sites for combining fuel cells and RESs, while the analytic hierarchy process was employed for decision-making related to the placement of RESs.
In another study, researchers formulated an optimization approach for determining the optimal sizing and placement of RESs on electrical distribution feeders, considering both technical and economic factors [67]. However, these studies often did not include social benefit maximization as an objective. Another investigation utilized MINLP for the economic evaluation of the optimal generation capacity of a wind park, focusing on maximizing expected generation profit while minimizing risks associated with uncertain wind speeds [68]. Additionally, a methodology based on MINLP was proposed to optimally allocate various types of renewable distributed generation (DG) units in distribution systems to minimize annual energy losses [69].
The integration of renewable energy into electricity generation, with a specific focus on CO2 reduction, has been extensively studied. Musi et al. [70] developed a model for the optimal planning of renewable energy-integrated electricity generation using mixed integer linear programming (MILP). Other researchers, such as Alberto et al. [71], have analyzed the optimal utilization of renewable energy sources (RESs) and energy storage systems (ESS) using multi-period alternating current optimal power flow (AC-OPF). Advanced techniques, including Complex-Valued Neural Networks (CVNN) and Time Domain Power Flow (TDPF), have been implemented to optimize the placement and sizing of storage systems in transmission and distribution networks [72].
To minimize losses, traditional Big Bang-Big Crunch algorithms have been applied for the optimal placement of renewable energy generators (REGs) in systems with dispatchable generation [73]. Cheng et al. [74] presented a case study on “Wang-An Island,” utilizing the energy PLAN model to simulate energy demands and the potential of renewable energy sources (RESs), optimizing their integration. However, these studies often neglected to consider models of deregulated power systems.
Various methodologies have been employed to optimize the placement and sizing of RESs, including mixed integer nonlinear programming (MINLP) [75], linear programming [76], and step-controlled primal-dual interior point methods [77,78]. Nevertheless, many of these studies have not prioritized the minimization of pollutant emissions. Efforts to enhance voltage regulation and reduce energy losses through optimal placement of REGs for profit maximization have also been explored [79]. Muis et al. [80] investigated renewable energy-integrated electricity generation planning with targets for CO2 reduction using MILP. Multi-objective artificial bee algorithms have been utilized to minimize fuel costs and emissions from thermal units by adjusting the size and location of solar farms, while incorporating power system security constraints [81–84]. Yet, these studies have often overlooked social benefit maximization.
Several methods have been proposed for the optimal placement of wind turbines, employing approaches such as step-controlled primal-dual interior point methods [85–88], probabilistic load flow analysis [89,90], and Newton-Raphson methods for load flow studies [91]. Research has also focused on minimizing fuel and emission costs [92,93], utilizing techniques like the Ant Colony Optimization model [94–96], Tabu search optimization [97], and hybrid Fuzzy-GA methods [98]. These approaches have been applied to optimize DG placement for enhanced reliability, loss reduction, and voltage improvement [99–103].
Other studies have examined strategies for integrating wind power into existing power systems [104–107], with a focus on operational efficiency, economic performance, and system reliability [108–110]. Particle Swarm Optimization (PSO) algorithms have been applied to optimize the placement of wind turbines to maximize power generation [111–114], while genetic algorithms have been used to optimize electric power systems incorporating offshore wind farms [115–119].
In addition, various techniques have been explored for optimizing wind turbine placement and sizing within wind farms, including simulated annealing optimization, distributed genetic algorithms [120–123], and Artificial Neural Networks (ANN) [124–128]. These methods aim to enhance wind farm efficiency, reduce costs, and improve the overall reliability of power systems [129–131], such as shown the in the Table 6 (Techniques for Optimal Wind Turbine Placement) and Table 7 (Techniques for Optimizing Wind Turbine Placement and Sizing Within Wind Farms) for optimal wind turbine placement [132–134].
Overall, wind energy’s importance in the electricity markets continues to grow, driven by its environmental, economic, and fuel independence benefits. As wind power integration increases, various optimization techniques will be crucial in addressing the challenges associated with this growth, such as investment in grid infrastructure, efficiency losses, and ensuring a competitive electricity market [135–138].
5 Optimal Locations for Solar Farm Development
Solar energy, derived from the sun’s radiation, is one of the most promising renewable energy sources globally [139–142]. In many regions worldwide, direct solar radiation is considered a highly potent energy source. The growth of photovoltaic (PV) technology is largely driven by the increasing demand for renewable energy, particularly as fossil fuel reserves deplete. PV systems offer a secure and clean energy source, although their high costs have prompted significant research aimed at improving efficiency and reducing expenses [143–145]. The optimal location and sizing of solar energy systems are crucial factors, as the utilization of solar radiation varies across different locations within a country [146–148].
Solar energy can be harnessed in various forms, such as water heating and electricity generation, through both direct and indirect conversions. Research has focused on different aspects of optimizing solar energy systems, particularly grid-connected PV systems, which are influenced by the intermittent nature of renewable energy generation. For instance, authors in [149] investigated the significance of grid-connected PV systems, emphasizing the need for compliance with grid codes given the variability of PV generation. In another study [150], several parameters, such as shading analysis, wire losses, and the optimal orientation and tilt angle, were optimized for grid PV systems in Spain, though PV array size optimization was not addressed.
An in-depth economic and environmental analysis of grid-connected photovoltaic (PV) systems in Malaysia was performed in [151], evaluating multiple scenarios that account for variations in interest rates and initial cost incentives. The methodology for identifying optimal sites for PV grid-connected systems was further investigated in [152]. Shen [153] concentrated on the size optimization of solar arrays and batteries in standalone PV systems, to minimize system costs while ensuring load demand fulfillment and maintaining an acceptable loss of power supply probability.
Several studies [154,155] have developed analytical models focused on optimal sizing for standalone PV systems, emphasizing cost minimization and achieving predetermined reliability levels to satisfy load requirements. For grid-connected systems, optimization models have been proposed to determine the appropriate PV array size, orientation, tilt angle, and inverter sizing ratio [156,157]. An economic analysis integrated with optimization strategies for PV grid-connected systems was presented in [158], concentrating on selecting optimal PV module types, numbers, arrangements, and tilt angles.
Artificial intelligence (AI) techniques are gaining prominence as alternatives to traditional approaches in PV system sizing. A comprehensive review of AI-based sizing methods is provided in [159], highlighting their application in forecasting meteorological data, system modeling, simulation, and control [160]. In [161], an Artificial Neural Network-Genetic Algorithm (ANN-GA) model was introduced to generate sizing curves for standalone PV systems, specifically addressing various loss of load probabilities across different locations in Algeria.
Kornelakis et al. [162,163] applied Particle Swarm Optimization (PSO) to multi-objective optimization problems aimed at maximizing the economic and environmental performance of photovoltaic grid-connected systems. Another study [164] utilized Binary Particle Swarm Optimization (BPSO) to determine the optimal location and size of Solar Photovoltaic Grid-Connected Systems (PVGCS) for distributed power generation, considering technical constraints such as maximum installed peak power capacity.
Medina [165] proposed a multi-objective optimization framework for the optimal allocation and sizing of photovoltaic grid-connected systems (PVGCSs) in distribution networks, evaluating both technical and economic impacts. The influence of PV system placement on power quality in distribution systems was examined in [166], which included a measurement setup for a grid-connected PV system. Kirmani et al. [167] introduced a methodology for identifying the optimal size and location for solar photovoltaic (SPV) systems in radial distribution networks to minimize power losses. The strategic placement of solar PV systems for power loss reduction and voltage profile enhancement was further recommended in [168].
6 Site Selection for Effective Hybrid Renewable Systems
Several modern optimization techniques have emerged to enhance the efficiency of solar and wind energy combinations in electrical systems. For example, in [169], a graphical sizing curve method was employed to determine the optimal configuration of solar and wind generators that could meet energy demands throughout the year, such as shown in Table 8 of optimization technique for optimal solar energy system. Another study [170] presented a methodology for calculating the optimal size of a PV array in a standalone hybrid wind/PV system, using the least squares method to find the best positioning for PV arrays and wind turbines relative to a given load.
The use of real meteorological data vs. generic analytical models for sizing PV and wind systems was examined in [171]. Garcia and Weisser [172] applied linear programming (LP) and fixed dispatch methods to optimize the size and dispatch of grid units in a wind-diesel hybrid system with hydrogen storage, utilizing a year-long hourly time series of wind speed and electricity demand data to minimize costs. In [173], an optimization procedure was discussed for sizing a hybrid system that integrates wind generators, batteries, and hydrogen storage based on real wind data and average residential demand. Additionally, a genetic algorithm (GA) was introduced in [174] for the optimal sizing of standalone PV-wind systems, aimed at selecting the ideal number and type of units to minimize costs while meeting full load energy requirements.
Renewable energy sources such as solar and wind power present substantial challenges in deregulated power markets, particularly in terms of grid flexibility, capacity adequacy, and the integration of these generators into energy markets. Both solar and wind energy are abundant, especially in remote areas, making them key components of global renewable energy strategies. However, due to their intermittent nature, neither energy source can provide a consistent supply on its own, given seasonal and periodic variations [175–177]. To overcome this issue, hybrid energy systems, which integrate multiple renewable resources, have been developed to enhance the reliability of energy supply by balancing the strengths of each source. These systems are particularly effective in ensuring a stable electricity supply across diverse locations worldwide.
Other studies have also employed GA to optimize hybrid solar-wind configurations, including battery banks, by considering factors such as the number of PV modules, wind turbines, battery storage capacity, the tilt angle of PV panels, and the installation height of wind turbines [175]. An evolutionary algorithm (EA) was used in [176] to design and control a complex hybrid PV-wind-diesel-battery-hydrogen system, yielding effective solutions with minimal computational effort.
In [177], a multi-objective GA was applied to optimize the sizing of a solar-wind-battery hybrid system for the northern coast of Senegal, also evaluating how load profiles influence the system’s configuration. Masoum et al. [178] proposed a GA-based method to optimally place hybrid PV-wind systems (HPWS) and determine the ideal wind/solar power ratio, with total HPWS capacity based on estimated annual power demand, average wind speed, and solar radiation.
A mathematical model for sizing a PV/wind system, incorporating solar energy, wind speed, wind turbines, PV modules, and battery storage, was proposed in [179]. Simulated Annealing (SA) was applied in a response surface meta-model (RSM) to optimize a hybrid PV/wind system in Turkey, addressing two different load types [180]. Another study [181] optimized the sizing of a PV/wind hybrid system with battery storage, accounting for varying loads and auxiliary energy source costs, using a simulation-based optimization procedure called OptQuest.
Research on hybrid PV/wind systems for an island in Malaysia [182] utilized hourly solar radiation, wind speed, and load demand data to optimize system size. Studies for specific regions [183,184] used mathematical models, hourly radiation, and wind speed records to optimize standalone solar PV and hybrid PV/wind systems. A technical review by Jamil et al. [185] assessed the economic feasibility of solar photovoltaic power generation.
Hybrid PV-wind systems were examined for multiple locations in Sweden, assessing system costs, energy generation costs, and the potential cost reductions of hybrid systems compared to standalone PV systems [186]. Optimal site selection for hybrid renewable energy installations on a hill in an island’s eastern region was discussed in [187]. Manas et al. [188] developed a methodology for optimally sizing autonomous hybrid PV/wind systems to ensure system reliability with the lowest levelized cost of energy, also shown the Table 9 of Optimization Techniques for hybrid Energy Systems.
An optimization algorithm for PV arrays with battery storage in standalone solar-wind hybrid systems was developed in [189], utilizing long-term hourly solar radiation and peak load demand data. Studies conducted in various locations worldwide consistently show that hybrid PV-wind systems are often more cost-effective than standalone PV or wind systems [190–193].
7 Optimal Sites for REGs in Distribution Networks
In traditional power systems, high-voltage lines form the backbone of the transmission network, with loads connected at medium and low voltage levels. However, this conventional structure is evolving due to the integration of renewable energy sources into the grid. Renewable Portfolio Standards (RPS) set by various regions mandate that a percentage of electricity must be sourced from renewables, while subsidies from governments, including India’s, promote renewable energy installations for both individuals and communities. These incentives have accelerated the development of sustainable distributed generations (REGs), which are small-scale plants directly connected to the distribution network.
One significant challenge in such systems is voltage management. In conventional radial distribution feeders, voltage tends to drop toward the end of the feeder due to load-induced voltage drops. However, when REGs are introduced, reverse power flow can occur, disrupting existing protection mechanisms and raising the voltage at the point of REG connection. This change in voltage profile has led researchers to investigate optimal location and sizing techniques for REGs in distribution networks.
For instance, the authors in [194] utilized small load pick-up conditions to optimally allocate distributed generation (DG) units to improve voltage deviations. As most distribution system components (e.g., transformers, motors) are inductive, they result in a lagging power factor, as noted in [195]. Studies such as [196,197] have examined the role of shunt capacitors in boosting system capacity, improving voltage profiles, and reducing losses. In [198], optimization techniques successfully reduced energy losses and enhanced reliability and power quality in distribution networks.
Various approaches have been proposed for the optimal placement and sizing of DGs in distribution systems. Studies have focused on expanding distribution networks [199], identifying optimal DG technologies and locations [200], and ensuring compatibility with existing systems, including protection schemes [201]. Determining optimal DG locations involves technical, regulatory, economic, and environmental considerations, as explored in [202], with techniques tailored to specific scenarios [203,204].
Optimization tools, including artificial intelligence (AI)-based methods, have been employed for placing multiple DGs, as outlined in [205–207]. Genetic algorithms (GA) have been widely used for determining optimal DG placement and sizing, as demonstrated in [208], while particle swarm optimization (PSO) was used in [209] to minimize real power losses through optimal DG and capacitor placement. Some studies also integrated simultaneous DG and capacitor placement to further reduce losses under time-varying loads [210].
Advanced techniques like the reinitialized social configuration PSO algorithm were proposed in [211] for locating multiple REGs in microgrids, aiming to minimize active power loss. Griffin et al. [212] presented a load-balancing approach for optimal DG placement. Research has also focused on combining real and reactive power injection strategies to optimize voltage profiles and reduce losses through DG placement [205–208]. Certain models only account for real or reactive power injection alongside capacitor placement [210–212].
To quantify the benefits of DG placement, several studies have developed optimization techniques that address REG penetration thresholds, such as the analytical method proposed in [213], which minimized power losses in primary distribution systems. While some approaches considered the reliability improvements from DGs, they did not incorporate reliability as a direct optimization criterion for DG placement [214]. Other methods, such as [215], preset DG capacities and locations before applying optimization to minimize real power losses, with novel approaches like the Harmony Search Algorithm setting penetration limits for DGs [216].
A loss sensitivity approach, combined with optimal siting and sizing strategies, was used in [217], focusing on power loss reduction. Additionally, reference [218] proposed region-specific optimization goals based on emissions reduction. GAs have also been applied to optimize DG placement and sizing to minimize losses and balance the power supply to the grid [219]. Studies like [220] investigated DG placement in voltage-sensitive areas to prevent collapse.
In hybrid optimization methods, GA and PSO have been combined to achieve optimal DG placement, as shown in [221–223], while algorithms such as the imperialist competitive algorithm have been applied for both DG and capacitor placement [224]. Some researchers proposed integrating network reconfiguration with DG placement for improved system efficiency [225–227]. In restructured distribution systems, the GA-based Tabu Search method was employed to solve the DG allocation problem [228]. The Voltage Stability Index (VSI) has been used to identify weak nodes for DG placement in radial networks [229,230].
Other approaches include using a price-area zonal method to determine the optimal DG size and location [231,232], as well as market-simulation methods for assessing DG impacts on transmission expansion [233]. Hengsritawat et al. [234] used a probabilistic method to size PV-DG systems, minimizing active power losses while considering power quality constraints. Differential evolution (DE) and the loss sensitivity factor simulated annealing (LSFSA) method have been applied in larger distribution systems to optimize DG placement, minimize losses, and improve voltage stability [235,236].
Several algorithms, such as Tabu Search [237] and continuation power flow analysis [238], have been introduced to minimize power losses and enhance voltage profiles in distribution systems. An artificial neural network (ANN)-based model for determining the appropriate DG size and location was tested on a 52-bus system by Kayal et al. [239], illustrating the effectiveness of ANN in optimizing DG placement and sizing. Optimal placement and sizing of REG units can significantly enhance the performance of distribution networks. Various optimization techniques, including classical optimization methods, metaheuristic algorithms, and artificial intelligence, can be employed to achieve optimal solutions. Real-world factors such as load profiles, network topology, and regulatory constraints must be carefully considered during the optimization process. By effectively applying these techniques, it is possible to harness the benefits of renewable energy while ensuring the reliability and efficiency of distribution networks, such as shown in Table 10.

7.1 Optimal Renewable Source Selection Criteria
The selection of the most appropriate renewable energy source is commonly addressed as a multiple attribute decision-making (MADM) problem, requiring consideration of various criteria. To tackle this complexity, a fuzzy-based MADM algorithm has been proposed, incorporating intuitionistic fuzzy sets to handle the inherent imprecision and vagueness in the decision-making process. This method was specifically applied to the Indian state of Tamil Nadu, demonstrating its effectiveness in evaluating renewable energy options [240].
Another approach for prioritizing and ranking renewable energy potential integrates a geographical information system (GIS) with the analytical hierarchy process (AHP). In this technique, weights are assigned based on multiple criteria and used as inputs for GIS-based spatial analysis. GIS tools are then utilized to generate maps showing wind speed, geothermal potential, and solar irradiance. This method was applied across 30 provinces in Indonesia, with the results indicating that geothermal energy was the most viable, followed by solar and wind energy [241].
Optimal location selection for renewable energy installations has also been achieved using meteorological data, which provides key insights into renewable energy potential. Combined with land use analysis, the total available space for generation units is calculated, identifying potential expansion sites while accounting for geographical and social constraints that might limit usable land. After completing the meteorological and land use analyses, an economic evaluation compares the investment costs for different renewable energy sources to inform the final decision [242].
7.2 Modeling Approaches for Renewable Energy Sources
The authors developed a time series analysis method to model uncertainties inherent in the availability of solar and wind energy. This approach involved adjusting historical hourly solar irradiance and wind speed data to fit autoregressive moving average (ARMA) models, thereby simulating variations in resource availability. To further evaluate design candidates, Monte Carlo simulations were employed, with a focus on total system cost and reliability [243]. In a separate study, a mathematical model was formulated by combining numerical and analytical methods to address the limitations associated with simpler models. The Lambert W function was utilized to calculate the output current of photovoltaic (PV) modules, while the Newton-Raphson method was applied for voltage calculations. The derived algebraic equations determined the shape factor, and the model was validated against manufacturer-rated PV output, yielding an error margin of ±2% [244].
An evolutionary programming (EP) algorithm was also proposed for modeling PV power output. The EP algorithm optimized the fill factor to accurately predict PV system power output, and its effectiveness was confirmed by comparing results with measured power values from PV systems [245].
Another study [246] introduced an aggregate model that integrates multiple forecasting models, offering improved performance compared to problem-specific individual models. The model includes three groups of backpropagation neural network (BPNN) models: a multivariate model, a hybrid ARIMA-BPNN model, and a univariate BPNN model. Each was used for forecasting, with fuzzy theory combining their outputs to produce final results. Additionally, a model for estimating PV system power production with solar tracking, based on temperature and solar irradiance data, was developed and validated using the Photovoltaic Geographical Information System (PVGIS) and data from a PV test facility. The study also addressed factors influencing solar power output [247].
Finally, an improvement to the Grey prediction model was proposed by incorporating an exponential smoothing method. When compared to the standard Grey prediction model using actual PV output data, the improved model demonstrated higher accuracy and effectiveness, making it a more reliable and straightforward method for predicting PV output [248].
7.3 Energy Loss in Power Systems
The authors developed an analytical expression for determining the optimal size of distributed generation (DG) units, along with an effective method for identifying the best location for DG placement, aiming to minimize total power losses in distribution systems. This methodology is based on an exact loss formula, forming the foundation for the analytical expression. The study thoroughly examines how DG unit size and location affect system losses within the distribution network [249,250].
Additionally, the authors proposed an efficient analytical method to optimize the installation of multiple DG units and calculate their optimal power factor, focusing on minimizing power losses. This approach also incorporates the allocation of an optimal mix of DG types, each with varying generation capabilities. By combining an Evolutionary Algorithm (EA) with optimal power flow techniques, the authors introduced a novel method that effectively handles system constraints, offering a robust solution for optimizing DG placement and operation within power distribution networks [251].
7.4 Voltage Distribution Across the Network
The authors proposed a method that considers active power losses and imposes penalties for voltage deviations to optimize the placement of generation units. Binary variables are used to define generation locations, employing a classical optimization approach. This method enables the identification of optimal generation sites while accounting for both power losses and voltage stability [252].
In addition, the authors introduced a Particle Swarm Optimization (PSO) technique for the optimal placement of Distributed Generators (DGs) with the dual objectives of reducing power losses and improving the voltage profile. A violation coefficient is incorporated into the voltage profile to formulate the objective function. The results show that this method significantly reduces power losses, reinforces the minimum voltage profile, and improves the overall voltage stability across the system [253].
Furthermore, a novel methodology based on a fuzzy adaptive hybrid PSO was proposed for optimal voltage and reactive power control. The primary goal is to minimize a comprehensive cost function that includes operational costs for transformers and capacitors, power losses, and various constraints such as reactive power limits, the maximum number of switching operations allowed per day, and voltage deviation limits. Fuzzy adaptive inference is employed to refine the search process, resulting in more efficient and effective optimization outcomes [254].
7.5 Assessing Reliability in Power Systems
In [255], the authors proposed a method to calculate the impact of Distributed Generators (DGs) on the reliability of distribution systems, using a typical utility feeder from Calicut, Kerala, as a case study. The findings revealed that while the integration of a single DG enhances system reliability, the addition of multiple DGs may have an adverse effect. The reliability of the system was evaluated using specific reliability indexes [256].
Furthermore, a methodology for the optimal location and sizing of DGs was developed, focusing on reducing power losses and improving system reliability [256–259]. The problem was formulated as a Mixed Integer Nonlinear Programming (MINLP) model and solved using a Genetic Algorithm (GA) [259–262]. The methodology also included the calculation of interruption costs and losses associated with renewable-based DGs [263–265]. Additionally, factors such as load variations, renewable energy input, and hourly energy costs were incorporated into the optimization process to ensure a thorough analysis [265–267].
7.6 Ensuring Voltage Stability in Power Systems
In [268], an optimal Distributed Generation (DG) placement strategy was developed with a primary emphasis on voltage stability as a critical security measure. This approach integrates continuous power flow analysis and modal analysis into a hierarchical placement algorithm. To address the issue of reactive power shortages, a modified version of the equivalent reactive compensation method was utilized to create a priority list of potential DG locations. Simulations conducted on a 33-bus radial distribution network demonstrated the efficacy of the proposed method in maintaining voltage stability.
Similarly, another method has been introduced for optimal DG allocation and sizing, aimed at reducing losses while enhancing voltage stability. This approach employs bifurcation analysis to identify the buses most prone to voltage instability, which are then selected as prime locations for DG placement. The number of DGs is determined to ensure that the voltage profile remains within acceptable limits. A dynamic programming search is subsequently utilized to find the global optimum size for the DGs. Additionally, the consideration of reactive power limits on DG units influences voltage stability bifurcation, which in turn affects the size, location, and number of DGs required [269].
7.7 Emission Monitoring and Reduction Strategies
In [270], a planning strategy for advancing low-carbon sustainability in distribution systems was presented. This strategy utilizes an integrated method that incorporates both demand response (DR) and renewable distributed generation (RDG). The problem is addressed using a two-stage model that co-optimizes renewable and non-renewable distributed generation units, along with smart metering, with the goal of minimizing both carbon emissions and total economic costs. The stochastic nature of renewable energy sources and the price responsiveness of customers are modeled through various probabilistic scenarios. To implement this methodology, an efficient hybrid algorithm is employed, which effectively manages the complexities of the co-optimization process. The results from this approach show significant improvements in system efficiency and reductions in carbon emissions, demonstrating its potential to support sustainable energy transitions in distribution networks.
The optimal placement and sizing of REG in distribution networks is a complex optimization problem with significant implications for the reliability, efficiency, and sustainability of power systems. A variety of optimization techniques, including classical optimization methods, metaheuristic algorithms, and artificial intelligence, can be employed to address this challenge. While classical optimization techniques are well-suited for simple problems, metaheuristic and artificial intelligence-based techniques offer greater flexibility and can handle complex, real-world scenarios. Hybrid approaches that combine multiple techniques can further enhance the performance of optimization models, such as shown in Table 11.

The further optimize renewable energy systems, future research should focus on several key areas. One promising direction is the development of advanced hybrid optimization algorithms that combine machine learning and metaheuristic techniques to improve the accuracy and efficiency of renewable energy placement and sizing, especially in complex and dynamic environments. Additionally, integrating energy storage systems with renewable energy sources can enhance grid balance, particularly in regions with high renewable energy penetration. Research should also explore the optimization of renewable energy systems in deregulated power markets, considering market dynamics and policy changes. Furthermore, there is a need to investigate the scalability of optimization models for large-scale power systems and the socioeconomic impacts of transitioning to renewable energy-based distribution systems. Lastly, ensuring the resilience of renewable energy systems under extreme weather conditions and developing real-time optimization strategies are crucial for reliable and efficient renewable energy systems. A multidisciplinary approach, involving experts from electrical engineering, economics, and environmental science, is essential to address these complex challenges and accelerate the transition to a sustainable energy future.
Renewable energy sources (RESs) are green energy options capable of generating large amounts of power at lower costs and with minimal emissions compared to non-renewable energy sources. RESs have become an integral component of modern electrical power systems, and their share in total power generation is expected to grow rapidly with ongoing advancements in related technologies. This review discusses in detail the selection and modeling techniques for RESs, general optimization criteria such as power losses, emissions, and reliability, as well as techniques for the optimal positioning and sizing of Renewable Energy Generators (REGs) using methods like Particle Swarm Optimization (PSO), Genetic Algorithms (GA), Evolutionary Programming (EP), Monte Carlo Simulation-Optimal Power Flow (MCS-OPF), and others. The review also covers hybrid and standalone systems, providing an overview of different methods used to determine optimal performance, location, and size of RESs. According to the findings, conducting a detailed analysis of RESs at the initial stage and considering a wide range of optimization criteria is crucial for achieving optimal placement and sizing of RESs to enhance overall system performance. Transitioning to hybrid systems, rather than relying on a single RES, can improve reliability. Additionally, standalone systems offer a viable alternative for power supply in remote areas, often proving more effective than extending the existing transmission network.
In conclusion, the optimal placement and sizing of RESs are crucial for enhancing system performance and reliability in modern electrical grids. This review highlights that hybrid systems offer improved resilience over standalone solutions, particularly in remote areas. Future research should focus on developing more sophisticated optimization models that integrate energy storage and account for deregulated market dynamics. By addressing these challenges, future work can significantly advance the efficient integration of RESs into power systems, contributing to a more sustainable and reliable energy future.
Acknowledgement: The authors would like to thanks the department DICE, CUIET, Chitkara University, Punjab for providing useful infrastructure and support to carry out various studies related to this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Digambar Singh, Ramesh Kumar and Manish Kumar Singla; data collection: Mohammad Aljaidi; analysis and interpretation of results: Najat Elgeberi and Rabia Emhamed Al Mamlook; draft manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Chen H, Xia Y, Wei W, Zhou Y, Zhao B, Zhang L. Safety and efficiency problems of hydrogen production from alkaline water electrolyzers driven by renewable energy sources. Int J Hydrogen Energy. 2024;54:700–12. [Google Scholar]
2. Global wind energy council launched. Refocus. 2005;6(2):11. doi:10.1016/s1471-0846(05)00313-6. [Google Scholar] [CrossRef]
3. GWEC-Global Wind Energy Council. Global wind energy council. [Internet] [cited 2024 Nov 10]. Available from: https://www.gwec.net. [Google Scholar]
4. Ministry of New & Renewable Energy-Government of India, Mnre.gov.in; 2020. [Internet] [cited 2024 Nov 10]. Available from: https://www.mnre.gov.in. [Google Scholar]
5. Sargsyan G, Bhatia M, Banerjee SG, Raghunathan K, Soni R. Unleashing the potential of renewable energy in India. Washington, DC, USA: World Bank Publications; 2011. [Google Scholar]
6. IRENA. Global renewables outlook: energy transformation 2050. Abu Dhabi, United Arab Emirates: International Renewable Energy Agency (IRENA); 2020. [Google Scholar]
7. International Energy Agency. World energy outlook 2019. France: International Energy Agency; 2019. [Google Scholar]
8. Barzegarkhoo R, Lee SS, Siwakoti YP, Khan SA, Blaabjerg F. Design, control, and analysis of a novel grid-interfaced switched-boost dual T-type five-level inverter with common-ground concept. IEEE Trans Ind Electron. 2021;68(9):8193–206. doi:10.1109/TIE.2020.3018073. [Google Scholar] [CrossRef]
9. Bollipo RB, Mikkili S, Bonthagorla PK. Critical review on PV MPPT techniques: classical, intelligent and optimization. IET Renew Power Gener. 2020;14(9):1433–52. doi:10.1049/iet-rpg.2019.1163. [Google Scholar] [CrossRef]
10. Saini KK, Sharma P, Mathur H, Gautam AR, Bansal RC. Techno-economic and reliability assessment of an off-grid solar-powered energy system. Appl Energy. 2024;371:123579. [Google Scholar]
11. Ramaiah V, Jayasankar V. Performance assessment of Indian electric distribution utilities using data envelopment analysis (DEA). Int J Electr Electron Eng Telecommun. 2022;11(3):192–202. doi:10.18178/ijeetc.11.3.192-202. [Google Scholar] [CrossRef]
12. Patel AK, Mathew L. Ga integrated OPF approach for optimal procurement of energy under competitive environment. In: AIP Conference Proceedings; 2024; Woodbury, Long Island, NY, USA: AIP Publishing. Vol. 2900, no. 1. [Google Scholar]
13. Singh A. Power sector reform in India: current issues and prospectus. Energy Policy. 2006;34:2480–90. [Google Scholar]
14. Ministry of Power. Welcome to Government of India | Ministry of Power. Powermin.nic.in; 2020. [Internet] [cited 2024 Nov 10]. Available from: http://www.powermin.nic.in. [Google Scholar]
15. Kumar N, Prabhansu. Renewable energy technologies: advances and emerging trends for sustainability. Hoboken, NJ, USA: John Wiley & Sons; 2022. doi:10.1002/9781119827634. [Google Scholar] [CrossRef]
16. Government of India. Annual report 2009–10. New Delhi, India: Ministry of New and Renewable Energy; 2010. [Google Scholar]
17. Data Management & Load Forecasting Division. Growth of electricity sector in India from 1947–2015. CEA Booklet. [Internet] [cited 2024 Nov 10]. Available from: http://www.cea.nic.in/reports/planning/dmlf/growth-2015.pdf. [Google Scholar]
18. Central Electricity Authority (CEA). All India installed capacity (in MW) of power stations located in the regions of mainland and islands. CEA Monthly Report; 2015. [Internet] [cited 2024 Nov 10]. Available from: http://cea.nic.in/reports/monthly/installedcapacity/2015/installed_capacity-03.pdf. [Google Scholar]
19. Ministry of New and Renewable Energy (MNRE). Scheme wise physical progress in 2015–16; 2015. [Internet] [cited 2024 Nov 10]. Available from: http://www.mnre.gov.in/mission-and-vision2/achievements/program. [Google Scholar]
20. De A, Mercados AF. Current trends/status in solar power market. MNRE Workshop on Challenges and Issues in Solar RPO Compliance; 2013. [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/file-manager/UserFiles/presentations-23052013/MERCADOS.pdf. [Google Scholar]
21. Abhishek P. India 2020: utilities & renewable. Deutsche Bank Markets Research; 2015. [Internet] [cited 2024 Nov 10]. Available from: https://www.db.com/cr/en/docs/Deutsche-Bank-report-Make-way-for-the-Sun.pdf. [Google Scholar]
22. Abas N, Kalair A, Khan N. Review of fossil fuels and future energy technologies. Futures. 2015;69(6):31–49. doi:10.1016/j.futures.2015.03.003. [Google Scholar] [CrossRef]
23. Ministry of New and Renewable Energy (MNRE). Renewable energy regulatory framework. [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/information/renewable-energy-regulatory-framework. [Google Scholar]
24. Ministry of New and Renewable Energy (MNRE). Loan for installation of grid interactive rooftop solar PV plants. Press Release. [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/file-manager/UserFiles/Press-Release-Grid-Interactive-Solar-Rooftop.pdf. [Google Scholar]
25. International Energy Agency (IEA). Twelfth five year plan (2012–2017) in Planning Commission Government of India. [Internet] [cited 2024 Nov 10]. Available from: http://www.iea.org/policiesandmeasures/pams/india/name-42436-en.php. [Google Scholar]
26. Singh R, Upadhyay A. Cheap power or clean energy, India’s $200 billion dilemma. Bloomberg Business; 2015. [Internet] [cited 2024 Nov 10]. Available from: http://www.bloomberg.com/news/articles/2015-07-29/cheap-power-or-clean-energy-india-s-200-billion-dilemma. [Google Scholar]
27. National Institute of Solar Energy. State wise estimated solar power potential in the country; 2014. [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/file-manager/UserFiles/State-wise-Solar-Potential-NISE.pdf. [Google Scholar]
28. Gomathinayagam S. India’s wind power potential. Centre for Wind Energy Technology; 2004. [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/file-manager/UserFiles/Presentations-NWM-09012014/Gomathinaygam.pdf. [Google Scholar]
29. Ministry of New and Renewable Energy (MNRE). Biomass power and cogeneration program. [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/schemes/grid-connected/biomass-powercogen. [Google Scholar]
30. Ministry of New and Renewable Energy (MNRE). State wise numbers and aggregate capacity of SHP projects (up to 25 MW). [Internet] [cited 2024 Nov 10]. Available from: http://mnre.gov.in/file-manager/UserFiles/SHP-potential.pdf. [Google Scholar]
31. Government of India. Union budget 2015–16. [Internet] [cited 2024 Nov 10]. Available from: http://www.pppinindia.com/sector-power.php. [Google Scholar]
32. Martinot E, Chaurey A, Lew D, Moreira JR, Wamukonya N. Renewable energy markets in developing countries. Annu Rev Energy Environ. 2002;27(1):309–48. doi:10.1146/annurev.energy.27.122001.083444. [Google Scholar] [CrossRef]
33. India Achieves 4 GW Installed Solar Power Capacity. CleanTechnica; 2015. [Internet] [cited 2024 Nov 10]. Available from: https://cleantechnica.com/2015/06/22/indias-achieves-4-gw-installed-solar-power-capacity. [Google Scholar]
34. Kamal MM, Ashraf I, Fernandez E. Optimal sizing of standalone rural microgrid for sustainable electrification with renewable energy resources. Sustain Cities Soc. 2023;88:104298. doi:10.1016/j.scs.2022.104298. [Google Scholar] [CrossRef]
35. Bhuiyan MRA. Overcome the future environmental challenges through sustainable and renewable energy resources. Micro Nano Lett. 2022;17(14):402–16. doi:10.1049/mna2.12148. [Google Scholar] [CrossRef]
36. Zhu W, Guo J, Zhao G. Multi-objective sizing optimization of hybrid renewable energy microgrid in a stand-alone marine context. Electronics. 2021;10(2):174. doi:10.3390/electronics10020174. [Google Scholar] [CrossRef]
37. Mayer MJ, Szilágyi A, Gróf G. Environmental and economic multi-objective optimization of a household level hybrid renewable energy system by genetic algorithm. Appl Energy. 2020;269:115058. doi:10.1016/j.apenergy.2020.115058. [Google Scholar] [CrossRef]
38. Rehman S, Habib HUR, Wang S, Buker MS, Alhems LM, Al Garni HZ. Optimal design and model predictive control of standalone HRES: a real case study for residential demand side management. IEEE Access. 2020;8:29767–814. doi:10.1109/ACCESS.2020.2972302. [Google Scholar] [CrossRef]
39. Zhou X, Yu N, Wu Z, Maleki A. Energy control and design optimization of a hybrid solar-hydrogen energy storage system using various solar panel technologies. J Energy Storage. 2024;94:112389. [Google Scholar]
40. Singla MK, Safaraliev M, Gupta J, Aljaidi M, Odinaev I, Kumar R, et al. Optimizing proton exchange membrane fuel cell parameter identification using enhanced hummingbird algorithm. Int J Hydrogen Energy. 2024;89:342–52. [Google Scholar]
41. Singh S, Chauhan P, Aftab MA, Ali I, Hussain SMS, Ustun TS. Cost optimization of a stand-alone hybrid energy system with fuel cell and PV. Energies. 2020;13(5):1295. [Google Scholar]
42. Ramli MAM, Bouchekara HREH, Alghamdi AS. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew Energy. 2018;121:400–11. [Google Scholar]
43. Thirunavukkarasu M, Sawle Y, Lala H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew Sustain Energ Rev. 2023;176:113192. [Google Scholar]
44. Chu S, Majumdar A. Opportunities and challenges for a sustainable energy future. Nature. 2022;488(7411):294–303. doi:10.1038/nature11475. [Google Scholar] [PubMed] [CrossRef]
45. Medghalchi Z, Taylan O. A novel hybrid optimization framework for sizing renewable energy systems integrated with energy storage systems with solar photovoltaics, wind, battery and electrolyzer-fuel cell. Energy Convers Manag. 2023;294:117594. [Google Scholar]
46. Raza A, Chen Y, Li M, Abouzeid SI, Abdelhameed EH. Feasibility and optimal size analysis of off grid hybrid AC-DC microgrid system: case study of El Kharga Oasis, Egypt. J Energy Storage. 2024;97:112721. [Google Scholar]
47. Khan MJ, Iqbal MT. Pre-feasibility study of stand-alone hybrid energy systems for applications in Newfoundland. Renew Energy. 2005;30(6):835–54. [Google Scholar]
48. National Renewable Energy Laboratory. HOMER getting started guide version 2.1. Golden, CO, USA: NREL; 2005. [Google Scholar]
49. Garg A, Ratnesh RK. Solar cell trends, and the future: a review. J Pharm Negat Results. 2022;13:2051–60. [Google Scholar]
50. Pandey PK, Kumar R, Gupta V, Kanungo A, Diwania S. An innovative hybrid controller-based combined grid-connected hybrid renewable energy system. Elect Eng. 2024;106(6):7055–72. doi:10.1007/s00202-024-02363-2. [Google Scholar] [CrossRef]
51. Khatib T, Mohamed A, Sopian K, Mahmoud M. Optimal sizing of the energy sources in hybrid PV/diesel systems: a case study for Malaysia. Int J Green Energy. 2013;10(1):41–52. [Google Scholar]
52. Farghali M, Osman A, Chen Z, Abdelhaleem A, Ihara I, Mohamed IMA, et al. Social, environmental, and economic consequences of integrating renewable energies in the electricity sector: a review. Environ Chem Lett. 2023;21(3):1381–418. [Google Scholar]
53. Ebrahimi A, Ramezani MR, Moieni M. Optimal operation of distribution network considering renewable energy sources by binary particle swarm optimization and fuzzy theory. In: Proceedings of IEEE; 2012 May 29–30. p. 1–4. [Google Scholar]
54. Garrido OC, Stumberger G, Vorsic J. Optimizing production of electric energy from renewable sources by differential evolution. In: Proceedings of ICREPQ; 2007; UK. p. 1–4. [Google Scholar]
55. Roy D. Modelling an off-grid hybrid renewable energy system to deliver electricity to a remote Indian island. Energy Convers Manag. 2023;281:116839. [Google Scholar]
56. Buonomano A, Papa GDel, Giuzio GF, Palombo A, Russo G. Future pathways for decarbonization and energy efficiency of ports: modelling and optimization as sustainable energy hubs. J Clean Prod. 2023;420:138389. [Google Scholar]
57. Abdulaziz S, Atlam G, Zaki G, Nabil E. Cuckoo search algorithm and particle swarm optimization-based maximum power point tracking techniques. Indones J Electr Eng Comput Sci. 2022;26(2):605. doi:10.11591/ijeecs.v26.i2.pp605-616. [Google Scholar] [CrossRef]
58. Hassanein WS, Ahmed MM, Abed O, Ashmawy MG, Mosaad MI. Performance improvement of off-grid hybrid renewable energy system using dynamic voltage restorer. Alex Eng J. 2020;59(3):1567–81. doi:10.1016/j.aej.2020.03.037. [Google Scholar] [CrossRef]
59. Papakonstantinou M. Challenges and opportunities of a Greek island on the journey to renewable energy: the case of Ikaria. In: Skupchenko JK, editor. Towards circular: analysis of the coastal areas of Greece. Italy and Spain: Think Tank AlterContacts [Internet]; 2024 [cited 2024 Nov 10]. Available from: https://www.altercontacts.org/publications/towards-circular-2024/gr-sd-5. [Google Scholar]
60. Phuangpornpitak N, Kumar S. PV hybrid systems for rural electrification in Thailand. Renew Sustain Energ Rev. 2007;11(7):1530–43. [Google Scholar]
61. Dursun B, Gokcol C, Umut I, Ucar E, Kocabey S. Techno-economic evaluation of a hybrid PV-wind power generation system. Int J Green Energy. 2013;10(2):117–36. [Google Scholar]
62. Li Y, Xiao D, Chen H, Cai W, Prado JCD. Analyzing the wind-dominant electricity market under coexistence of regulated and deregulated power trading. Energy Eng. 2024;121(8):2093–127. doi:10.32604/ee.2024.049232. [Google Scholar] [CrossRef]
63. Kumaravel S, Ashok S. An optimal stand-alone biomass/solar-PV/Pico-hydel hybrid energy system for remote rural area electrification of isolated village in Western-Ghats Region of India. Int J Green Energy. 2012;9(5):398–408. [Google Scholar]
64. Dawood F, Shafiullah G, Anda M. Stand-alone microgrid with 100% renewable energy: a case study with hybrid solar PV-battery-hydrogen. Sustainability. 2020;12(5):2047. doi:10.3390/su12052047. [Google Scholar] [CrossRef]
65. Milan C, Bojesen C, Nielsen MP. A cost optimization model for 100% renewable residential energy supply systems. Energy. 2012;48(1):118–27. [Google Scholar]
66. Singh AK, Panda SK. Combined optimal placement of solar, wind and fuel cell-based DGs using AHP. In: Proceedings of World Renewable Energy Congress-Sweden; 2011; Sweden. p. 3113–20. [Google Scholar]
67. Henrique LF, Silva WN, Silva CCA, Dias BH, Oliveira LW, de Almeida MC. Optimal siting and sizing of distributed energy resources in a Smart Campus. Elect Power Syst Res. 2023;217:109095. [Google Scholar]
68. Kongnam C, Nuchprayoon S, Premrudeepreechacham S, Uatrongjit S. Decision analysis on generation capacity of a wind park. Renew Sustain Energ Rev. 2009;13(8):2126–33. [Google Scholar]
69. Atwa YM, El-Saadany EF, Salama MMA, Seethapathy R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans Power Syst. 2010;25(1):360–70. doi:10.1109/tpwrs.2009.2030276. [Google Scholar] [CrossRef]
70. Muis ZA, Hashim H, Manan ZA, Taha FM, Douglas PL. Optimal planning of renewable energy-integrated electricity generation schemes with CO2 reduction target. Renew Energy. 2010;35(11):2562–70. doi:10.1016/j.renene.2010.03.032. [Google Scholar] [CrossRef]
71. Liu J, Hu H, Yu SS, Trinh H. Virtual power plant with renewable energy sources and energy storage systems for sustainable power grid-formation, control techniques and demand response. Energies. 2023;16(9):3705. [Google Scholar]
72. Motalleb M, Reihani E, Ghorbani R. Optimal placement and sizing of the storage supporting transmission and distribution networks. Renew Energy. 2016;94(12):651–9. doi:10.1016/j.renene.2016.03.101. [Google Scholar] [CrossRef]
73. Abdelaziz AY, Hegazy YG, El-Khattam W, Othman MM. Optimal allocation of stochastically dependent renewable energy based distributed generators in unbalanced distribution networks. Elect Power Syst Res. 2015;119:34–44. doi:10.1016/j.epsr.2014.09.005. [Google Scholar] [CrossRef]
74. Yue C-D, Chen C-S, Lee Y-C. Integration of optimal combinations of renewable energy sources into the energy supply of Wang-An Island. Renew Energy. 2016;86(D12110):930–42. doi:10.1016/j.renene.2015.08.073. [Google Scholar] [CrossRef]
75. Singh AK, Parida SK. A novel hybrid approach to allocate renewable energy sources in distribution system. Sustain Energy Technol Assess. 2015;10:1–11. doi:10.1016/j.seta.2015.01.003. [Google Scholar] [CrossRef]
76. Keane A, O’Malley M. Optimal allocation of embedded generation on distribution networks. IEEE Trans Power Syst. 2005;20(3):1640–6. doi:10.1109/TPWRS.2005.852115. [Google Scholar] [CrossRef]
77. Mokryani G, Siano P, Piccolo A. Social welfare maximization for optimal allocation of wind turbines in distribution systems. In: Proceedings of the 11th International Conference on Electrical Power Quality and Utilization; 2011; Lisbon, Portugal. p. 1–6. [Google Scholar]
78. Sharma NK, Sood YR. Strategy for optimal location and rating of wind power generator with maximization of social welfare in double auction competitive power market. J Renew Sustain Energy. 2014;6(1):013123. doi:10.1063/1.4863089. [Google Scholar] [CrossRef]
79. Gautam D, Mithulananthan N. Optimal DG placement in deregulated electricity market. Elect Power Syst Res. 2007;77(12):1627–36. doi:10.1016/j.epsr.2006.11.014. [Google Scholar] [CrossRef]
80. Mhanna S, Saedi I, Mancarella P. Optimal integrated planning of electricity and hydrogen infrastructure for large-scale renewable energy transport. SSRN Electron J. 2023. doi:10.2139/ssrn.4479052. [Google Scholar] [CrossRef]
81. Phonrattanasak P, Sakamoto MMO. Optimal placement of solar farm on the power system network. In: Proceedings of the Department of Electrical Engineering; 2013; Thailand: North Eastern University. p. 1–6. [Google Scholar]
82. Teng J-H. Power flow and loss allocation for deregulated transmission systems. Int J Electr Power Energy Syst. 2005;27(4):327–33. doi:10.1016/j.ijepes.2004.12.005. [Google Scholar] [CrossRef]
83. Baghayipour M, Foroud AA, Soofiabadi A. A comprehensive fair nodal pricing scheme, considering participants’ efficiencies and their rational shares of total cost of transmission losses. Electr Power Energy Syst. 2014;63:30–43. doi:10.1016/j.ijepes.2014.05.022. [Google Scholar] [CrossRef]
84. Zhong J, Bhattacharya K. Reactive power management in deregulated electricity markets-a review. In: Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting; 2002; New York, NY, USA. p. 1–6. doi:10.1109/pesw.2002.985223. [Google Scholar] [CrossRef]
85. Shukla UK, Thampy A. Analysis of competition and market power in the wholesale electricity market in India. Energy Policy. 2011;39(5):2699–710. doi:10.1016/j.enpol.2011.02.039. [Google Scholar] [CrossRef]
86. Suresh N, Thirunavukkarasu NR, Karthik NN. Optimization of energy storage unit size and location in a radial distribution network to minimize power loss using firefly algorithm. J Adv Res Appl Sci Eng Technol. 2023;31(3):25–42. doi:10.37934/araset.31.3.2542. [Google Scholar] [CrossRef]
87. Atwa YM, El-Saadany EF. Probabilistic approach for optimal allocation of wind-based distributed generation in distribution systems. IET Renew Power Gener. 2009;5(1):79–88. doi:10.1049/iet-rpg.2009.0011. [Google Scholar] [CrossRef]
88. Dawn S, Tiwari PK. Maximization of social welfare by optimal allocation of UPFC with wind power generator in deregulated electricity market. In: Proceedings of 2014 International Conference on Advanced Computing, Communication and Networks (ICACCT); 2014; Ramanathapuram, India. p. 1–6. doi:10.1109/icaccct.2014.7019454. [Google Scholar] [CrossRef]
89. Holttinen H. Wind integration: experience, issues, and challenges. Wiley Interdis Rev: Energy Environ. 2012;1(3):243–55. doi:10.1002/wene.18. [Google Scholar] [CrossRef]
90. Burke DJ, O’Malley MJ. Optimal wind power location on transmission systems IM a probabilistic load flow approach. In: Proceedings of IEEE Power Engineering Society Meeting; 2008; Rincon, PR, USA. p. 1–8. [Google Scholar]
91. Ghosh S, Ghoshal SP, Ghosh S. Optimal sizing and placement of distributed generation in a network system. Int J Electr Power Energy Syst. 2010;32(8):849–56. doi:10.1016/j.ijepes.2010.01.029. [Google Scholar] [CrossRef]
92. Velamuri S, Sreejith S. Economic dispatch and cost analysis on a Power system network interconnected with Solar Farm. Int J Renew Res. 2015;5(4):1098–105. doi:10.20508/ijrer.40671. [Google Scholar] [CrossRef]
93. Kaabeche A, Belhamel M, Ibtiouen R. Optimal sizing method for stand-alone hybrid PV/wind power generation system. In: Proceedings of Revue des Energies Renouvelables (SMEE’70); 2010; Bou Ismail, Algeria. p. 205–13. [Google Scholar]
94. Taheri SI, Davoodi M, Ali MH. A simulated-annealing-quasi-oppositional-teaching-learning-based optimization algorithm for distributed generation allocation. Computation. 2023;11(11):214. doi:10.3390/computation11110214. [Google Scholar] [CrossRef]
95. Wu H, Zheng X. Optimizing receiving transformer capacity assessment decision-making through strategy and implementation of ant colony algorithm. In: 2024 5th International Conference on Electronics and Sustainable Communication Systems (ICESC); 2024; Coimbatore, India. p. 1338–43. [Google Scholar]
96. Wang L, Singh C. Reliability-constrained optimum placement of reclosers and distributed generators in distribution networks using an ant colony system algorithm. IEEE Trans Syst Man Cybern Part C (Appl Rev). 2008;38(6):757–64. doi:10.1109/TSMCC.2008.2001573. [Google Scholar] [CrossRef]
97. Wang CN, Nhieu NL, Viet TAP. Enhancing efficiency in PCB assembly for the leading global electronics manufacturing services firm: a TRIZ and ant colony optimization approach. Int J Adv Manuf Technol. 2024;133(11):5529–52. doi:10.1007/s00170-024-14025-5. [Google Scholar] [CrossRef]
98. Nara K, Hayashi Y, Ikeda K, Ashizawa T. Application of tabu turbines by dynamic ant colony search algorithm power systems. IEEE Trans Power Syst. 2007;22(2):580–7. doi:10.1109/TPWRS.2007.894861. [Google Scholar] [CrossRef]
99. Afriany R, Sinaga R, Samsinar S. Fuzzy employee placement suitability assessment using mamdani fuzzy method. Berkala SAINSTEK. 2022;10(2):109. doi:10.19184/bst.v10i2.30280. [Google Scholar] [CrossRef]
100. Khalili M, Aliasghari TP, Najmi ES, Abdelaziz AY, Abu-Siada A, Nowdeh SA. Optimal allocation of distributed thyristor controlled series compensators in power system considering overload, voltage, and losses with reliability effect. Energies. 2022;15(20):7478. doi:10.3390/en15207478. [Google Scholar] [CrossRef]
101. Jain R, Mahajan V. Impact of multiple DG penetration in energy market. In: Proceedings of the 2020 International Conference on Clean Energy (ICCE); 2020; Berlin, Germany. doi:10.1109/icce50343.2020.9290738. [Google Scholar] [CrossRef]
102. Pradhan P, Mishra S, Raut U. A novel framework for implementing optimal power distribution network planning approaches. Int J Syst Assur Eng Manage. 2024;15(6):2411–30. doi:10.1007/s13198-024-02255-5. [Google Scholar] [CrossRef]
103. Wang C, Nehrir MH. Analytical approaches for optimal placement of distributed generation sources in power systems. IEEE Trans Power Syst. 2004;19(4):2068–76. doi:10.1109/TPWRS.2004.836189. [Google Scholar] [CrossRef]
104. Wei B, Guoqing H, Wenhui S, Kaihui F, Weiran Z. Distributed wind generation siting and sizing considering fluctuating wind resources. In: Proceedings of IEEE; 2012; Tianjin, China. p. 1–7. [Google Scholar]
105. Sultana U, Khairuddin AB, Sultana B, Rasheed N, Qazi SH, Malik NR. Placement and sizing of multiple distributed generation and battery swapping stations using grasshopper optimizer algorithm. Energy. 2018;165, part A:408–21. doi:10.1016/j.energy.2018.09.083. [Google Scholar] [CrossRef]
106. Hadjsaid N, Canard J-F, Dumas F. Dispersed generation impact on distribution networks. IEEE Comput Appl Power. 1999;12(2):22–8. doi:10.1109/67.755642. [Google Scholar] [CrossRef]
107. Kalantari M, Kazemi A. Placement of distributed generation unit and capacitor allocation in distribution systems using genetic algorithm. In: Proceedings of IEEE; 2011; Rome, Italy. [Google Scholar]
108. Kansal S, Sai BBR, Tyagi B, Kumar V. Optimal placement of distributed generation in distribution networks. Int J Eng Sci Technol. 2011;3(3). doi:10.4314/ijest.v3i3.68421. [Google Scholar] [CrossRef]
109. Xu M, Zhuan X. Optimal planning for wind power capacity in an electric power system. Renew Energy. 2013;53:280–6. [Google Scholar]
110. Alnowibet KA, Alrasheedi AF, Alshamrani AM. Integrated stochastic transmission network and wind farm investment considering maximum allowable capacity. Elect Power Syst Res. 2023;215:108961. doi:10.1016/j.epsr.2022.108961. [Google Scholar] [CrossRef]
111. Ala A, Mahmoudi A, Mirjalili S, Simic V, Pamucar D. Evaluating the performance of various algorithms for wind energy optimization: a hybrid decision-making model. Expert Syst Appl. 2023;221:119731. [Google Scholar]
112. Bazzi AM, Fares DA. GSI-based wind firm site selection in Lebanon. In: Proceedings of IEEE; 2008; Ames, IA, USA. p. 201–4. [Google Scholar]
113. Chowdhury S, Messac A, Zhang J, Castillo L, Lebron J. Optimization of the unrestricted placement of turbines of differing rotor diameters in a wind farm for maximum power generation. In: Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; 2010; Montreal, QC, Canada. p. 1–16. [Google Scholar]
114. Pookpunt S, Ongsakul W. Optimal placement of wind turbines within a wind farm using binary particle swarm optimization with time-varying acceleration coefficients. Renew Energy. 2013;55:266–76. [Google Scholar]
115. Azadeh A, Ghaderi SF, Nasrollahi MR. Location optimization of wind plants in Iran by an integrated hierarchical data envelopment analysis. Renew Energy. 2011;36(5):1621–31. doi:10.1016/j.renene.2010.11.004. [Google Scholar] [CrossRef]
116. Aras H, Erdoğmuş Ş., Koç E. Multi-criteria selection for a wind observation station location using analytic hierarchy process. Renew Energy. 2004;29(8):1383–92. doi:10.1016/j.renene.2003.12.020. [Google Scholar] [CrossRef]
117. El-Zonkoly AM. Optimal placement of multi-distributed generation units including different load models using particle swarm optimisation. IET Generat, Trans Distrib. 2011;5(7):760–8. doi:10.1049/iet-gtd.2010.0676. [Google Scholar] [CrossRef]
118. Marmidis G, Lazarou S, Pyrgioti E. Optimal placement of wind turbines in a wind park using Monte Carlo simulation. Renew Energy. 2008;33(7):1455–60. doi:10.1016/j.renene.2007.09.004. [Google Scholar] [CrossRef]
119. Liu R, Peng L, Huang G, Zhou X, Yang Q, Cai J. A Monte Carlo simulation method for probabilistic evaluation of annual energy production of wind farm considering wind flow model and wake effect. Energy Convers Manag. 2023;292(2):117355. doi:10.1016/j.enconman.2023.117355. [Google Scholar] [CrossRef]
120. Saavedra-Moreno B, Salcedo-Sanz S, Paniagua-Tineo A, Prieto L, Portilla-Figueras A. Seeding evolutionary algorithms with heuristics for optimal wind turbines positioning in wind farms. Renew Energy. 2011;36(11):2838–44. doi:10.1016/j.renene.2011.04.018. [Google Scholar] [CrossRef]
121. Ekonomou L, Lazarou S, Chatzarakis GE, Vita V. Estimation of wind turbines optimal number and produced power in a wind farm using an artificial neural network model. Simul Model Pract Theory. 2012;21(1):21–5. doi:10.1016/j.simpat.2011.09.009. [Google Scholar] [CrossRef]
122. Jónsson T, Pinson P, Madsen H. On the market impact of wind energy forecasts. Energy Econ. 2010;32(2):313–20. doi:10.1016/j.eneco.2009.10.018. [Google Scholar] [CrossRef]
123. Zhao M, Chen Z, Blaabjerg F. Optimization of electrical system for offshore wind farms via genetic algorithm. IEEE Trans Renew Power Generat. 2009;3(2):205–16. doi:10.1049/iet-rpg:20070112. [Google Scholar] [CrossRef]
124. Li DD, He C, Fu Y. Optimization of internal electric connection system of large offshore wind farm with hybrid genetic and immune algorithm. In: Proceedings of IEEE; 2008; Nanjing, China. p. 2476–81. [Google Scholar]
125. Zhao M, Chen Z, Hjerrild J. Analysis of the behavior of genetic algorithm applied in optimization of electrical system design for offshore wind farms. In: Proceedings of IEEE; 2006; Paris, France. p. 2335–40. [Google Scholar]
126. Wu Y, Zhang S, Wang R, Wang Y, Feng X. A design methodology for wind farm layout considering cable routing and economic benefit based on genetic algorithm and GeoSteiner. Renew Energy. 2019;146(3):687–98. doi:10.1016/j.renene.2019.07.002. [Google Scholar] [CrossRef]
127. Dong LD, He C, Shu HY. Optimization of electric distribution system of large offshore wind farm with improved genetic algorithm. In: Proceedings of IEEE; 2008; Pittsburg, PA, USA. p. 1–6. [Google Scholar]
128. Sisbot S, Turgut O, Tunc M, Camdali U. Optimal positioning of wind turbines on Gokceada using multiobjective genetic algorithm. Wind Energy. 2010;13(4):297–306. doi:10.1002/we.339. [Google Scholar] [CrossRef]
129. Abou El-Ela AA, Allam SM, Shatla MM. Maximal optimal benefits of distributed generation using genetic algorithms. Electr Power Syst Res. 2010;80(7):869–77. doi:10.1016/j.epsr.2009.12.021. [Google Scholar] [CrossRef]
130. Mosetti G, Poloni C, Diviacco B. Optimization of wind turbine positioning in large wind farms by means of a genetic algorithm. J Wind Eng Ind Aerodyn. 1994;51(1):105–16. doi:10.1016/0167-6105(94)90080-9. [Google Scholar] [CrossRef]
131. Grady SA, Hussaini MY, Abdullah MM. Placement of wind turbines using genetic algorithms. Renew Energy. 2005;30(2):259–70. doi:10.1016/j.renene.2004.05.007. [Google Scholar] [CrossRef]
132. Verma M, Ghritlahre HK, Chaurasiya PK, Ahmed S, Bajpai S. Optimization of wind power plant sizing and placement by the application of multi-objective genetic algorithm (GA) in Madhya Pradesh, India, Sustainable Computing. Inform Syst. 2021;32(10):100606. doi:10.1016/j.suscom.2021.100606. [Google Scholar] [CrossRef]
133. Gilani SH, Afrakhte H, Ghadi MJ. Probabilistic method for optimal placement of wind-based distributed generation with considering reliability improvement and power reduction. In: Proceedings of IEEE; 2012; Tehran, Iran. p. 1–6. [Google Scholar]
134. Kirchner-Bossi N, Porté-Agel F. Wind farm power density optimization according to the area size using a novel self-adaptive genetic algorithm. Renew Energy. 2024;220(5):119524. doi:10.1016/j.renene.2023.119524. [Google Scholar] [CrossRef]
135. Chen R, Zhang Z, Hu J, Zhao L, Li C, Zhang X. Grouping-based optimal design of collector system topology for a large-scale offshore wind farm by improved simulated annealing. Prot Control Mod Power Syst. 2024;9(1):94–111. doi:10.23919/PCMP.2023.000151. [Google Scholar] [CrossRef]
136. Gupta SC, Kumar Y, Agnihotri G. Optimal sizing of solar-wind hybrid system. In: IET-UK International Conference on Information and Communication Technology in Electrical Sciences (ICTES 2007); 2007; England and Wales. p. 282–7. [Google Scholar]
137. Wu Y-K, Lee C-Y, Chen C-R, Hsu K-W, Tseng H-T. Optimization of the wind turbine layout and transmission system planning for a large-scale offshore wind farm by AI technology. In: Proceedings of IEEE; 2012; Las Vegas, NV, USA. p. 1–9. [Google Scholar]
138. Neshat M, Nezhad M, Abbasnejad E, Mirjalili S, Groppi D, Heydari A, et al. Wind turbine power output prediction using a new hybrid neuro-evolutionary method. Energy. 2021;229(1):120617. doi:10.1016/j.energy.2021.120617. [Google Scholar] [CrossRef]
139. Kusiak A, Zheng H, Song Z. Power optimization of wind turbines with data mining and evolutionary computation. Renew Energy. 2010;35(3):695–702. doi:10.1016/j.renene.2009.08.018. [Google Scholar] [CrossRef]
140. Kusiak A, Zhang Z, Li M. Optimization of wind turbine performance with data-driven models. IEEE Trans Sustain Energy. 2010;1(2):62–76. doi:10.1109/TSTE.2010.2046919. [Google Scholar] [CrossRef]
141. Abreu LVL, Shahidehpour M. Wind energy and power system inertia. In: Proceedings of IEEE; 2006; Montreal, QC, Canada. p. 1–6. [Google Scholar]
142. Faia R, Lezama F, Soares J, Pinto T, Vale Z. Local electricity markets: a review on benefits, barriers, current trends and future perspectives. Renew Sustain Energ Rev. 2024;190:114006. [Google Scholar]
143. Lee BL, Wilson C, Simshauser P, Majiwa E. Deregulation, efficiency and policy determination: an analysis of Australia’s electricity distribution sector. Energy Econ. 2021;98(1):105210. doi:10.1016/j.eneco.2021.105210. [Google Scholar] [CrossRef]
144. Feng D, Xu Z, Ostergaard J. Redesign electricity market for the next generation power system of renewable energy and distributed storage technologies. In: Proceedings of IEEE; 2010; Minneapolis, MN, USA. p. 1–8. [Google Scholar]
145. Banerjee B, Islam S. Reliability-based optimum location of distributed generation. Int J Electr Power Energy Syst. 2011;33(8):1470–8. doi:10.1016/j.ijepes.2011.06.029. [Google Scholar] [CrossRef]
146. Cunial SS. Policy legacies and energy transitions: greening policies under sectoral reforms in Argentina and Chile. Energy Policy. 2024;188:114059. [Google Scholar]
147. Zicmane I, Kovalenko S, Beryozkina S, Berzina K, Sobolevskis A. Evaluation of Latvian power system static stability according to a new development strategy until 2025. Sustainability. 2021;13(12):6860. [Google Scholar]
148. Lopes JAP. Technical and commercial impacts of the integration of wind power in the Portuguese system having in mind the Iberian electricity market. In: Proceedings of IEEE; 2005; St. Pittursburg, Russia. p. 1–3. [Google Scholar]
149. Lydia M, Kumar SS. A comprehensive overview on wind power forecasting. In: Proceedings of IEEE; 2010; Singapore. p. 268–73. [Google Scholar]
150. Eltawil MA, Zhao Z. Grid-connected photovoltaic power systems: technical and potential problems—a review. Renew Sustain Energ Rev. 2010;14(1):112–29. doi:10.1016/j.rser.2009.07.015. [Google Scholar] [CrossRef]
151. Fernández-Infantes A, Contreras J, Bernal-Agustín JL. Design of grid-connected PV systems considering electrical, economical and environmental aspects: a practical case. Renew Energy. 2006;31(13):2042–62. doi:10.1016/j.renene.2005.09.028. [Google Scholar] [CrossRef]
152. Karnali SK, Mekhilef S. Evaluation study on grid-connected PV system at University of Malaya. In: Proceedings of IEEE; 2009; Kuala Lumpur, Malaysia. p. 1–7. [Google Scholar]
153. Vasita J, Shakhiya Q, Modi J. Feasibility study and performance evaluation of a grid-connected rooftop solar PV system. In: 2017 International Conference on Information, Communication, Instrumentation and Control (ICICIC); 2017; Indore, India. doi:10.1109/icomicon.2017.8279067. [Google Scholar] [CrossRef]
154. Shen WX. Optimally sizing of solar array and battery in a standalone photovoltaic system in Malaysia. Renew Energy. 2009;34(1):348–52. [Google Scholar]
155. Jakhrani AQ, Othman A-K, Rigit ARH, Samo SR, Kamboh SA. A novel analytical model for optimal sizing of standalone photovoltaic systems. Energy. 2012;46(1):675–82. [Google Scholar]
156. Khatib T, Mohamed A, Sopian K, Mahmoud M. A new approach for optimal sizing of standalone photovoltaic systems. Int J Photoenergy. 2012;2012(13):1–7. doi:10.1155/2012/391213. [Google Scholar] [CrossRef]
157. Notton G, Lazarov V, Stoyanov L. Optimal sizing of a grid-connected PV system for various PV module technologies and inclinations, inverter efficiency characteristics and locations. Renew Energy. 2010;35(2):541–54. doi:10.1016/j.renene.2009.07.013. [Google Scholar] [CrossRef]
158. Mondol JD, Yohanis YG, Norton B. Comparison of measured and predicted long term performance of grid a connected photovoltaic system. Energy Convers Manag. 2007;48(4):1065–80. doi:10.1016/j.enconman.2006.10.021. [Google Scholar] [CrossRef]
159. Abo-Khalil AG, Sayed K, Radwan A, El-Sharkawy IA. Analysis of the PV system sizing and economic feasibility study in a grid-connected PV system. Case Stud Therm Eng. 2023;45(2):102903. doi:10.1016/j.csite.2023.102903. [Google Scholar] [CrossRef]
160. Rekha Y, Jamuna V, Christopher IW, Narmadha TV. Application of artificial intelligence techniques in grid-tied photovoltaic system-an overview. IoT Anal Renew Energy Syst. 2023;1:281–99. doi:10.1201/9781003331117. [Google Scholar] [CrossRef]
161. Feng C, Liu Y, Zhang J. A taxonomical review on recent artificial intelligence applications to PV integration into power grids. Int J Electr Power Energy Syst. 2021;132(6):107176. doi:10.1016/j.ijepes.2021.107176. [Google Scholar] [CrossRef]
162. Garud KS, Jayaraj S, Lee M. A review on modeling of solar photovoltaic systems using artificial neural networks, fuzzy logic, genetic algorithm and hybrid models. Int J Energy Res. 2020;45(1):6–35. doi:10.1002/er.5608. [Google Scholar] [CrossRef]
163. Kornelakis A. Multi-objective particle swarm optimization for the optimal design of photovoltaic grid-connected systems. Sol Energy. 2010;84(12):2022–33. doi:10.1016/j.solener.2010.10.001. [Google Scholar] [CrossRef]
164. Kornelakis A, Marinakis Y. Contribution for optimal sizing of grid-connected PV-systems using PSO. Renew Energy. 2010;35(6):1333–41. doi:10.1016/j.renene.2009.10.014. [Google Scholar] [CrossRef]
165. Gomez M, Lopez A, Jurado F. Optimal placement and sizing from standpoint of the investor of photovoltaics grid-connected systems using binary particle swarm optimization. Appl Energy. 2010;87(6):1911–8. doi:10.1016/j.apenergy.2009.12.021. [Google Scholar] [CrossRef]
166. Ali A, Keerio U, Laghari JM. Optimal site and size of distributed generation allocation in radial distribution network using multi-objective optimization. J Mod Power Syst Clean Energy. 2021;9(2):404–15. [Google Scholar]
167. Srisaen N. Effects of PV grid-connected system location on a distribution system. In: Proceedings of IEEE; 2006; Singapore. p. 852–5. [Google Scholar]
168. Kirmani S, Jamil M, Rizwan M. Optimal placement of SPV based DG system for loss reduction in radial distribution network using heuristic search strategies. In: Proceedings of IEEE; 2011; Bhubaneshwar, India. p. 1–4. [Google Scholar]
169. Mohammadi E, Esmaeili S. A novel optimal placement of solar PV system for loss reduction and voltage profile improvement. Tech Phys Prob Eng. 2012;4(13):11–46. [Google Scholar]
170. Bansal AK. Sizing and forecasting techniques in photovoltaic-wind based hybrid renewable energy system: a review. J Clean Prod. 2022;369:133376. [Google Scholar]
171. Rajkumar RK, Ramachandaramurthy VK, Yong BL, Chia DB. Techno-economical optimization of hybrid pv/wind/battery system using Neuro-Fuzzy. Energy. 2011;36(8):5148–53. [Google Scholar]
172. Shivam K, Tzou J-C, Wu S-C. Multi-objective sizing optimization of a grid-connected solar-wind hybrid system using climate classification: a case study of four locations in Southern Taiwan. Energies. 2020;13(10):2505. [Google Scholar]
173. Yang H, Wei Z, Chengzhi L. Optimal design and techno-economic analysis of a hybrid solar-wind power generation system. Appl Energy. 2009;86(2):163–9. doi:10.1016/j.apenergy.2008.03.008. [Google Scholar] [CrossRef]
174. Jamil M, Kirmani S, Rizwan M. Techno-economic feasibility analysis of solar photovoltaic power generation: a review. Smart Grid Renew Energy. 2012;3(4):266–74. doi:10.4236/sgre.2012.34037. [Google Scholar] [CrossRef]
175. Fiedler F, Pazmino V, Berruezo I, Maison V. PV-wind hybrid systems for swedish locations. In: Proceedings of IEEE; 2008; Glyfada, Greece. p. 1–8. [Google Scholar]
176. Darus ZM, Hashim N, Manan S, Rahman MAA, Maulud KNA, Karim O. The development of hybrid integrated renewable energy system (wind and solar) for sustainable living at Perhentian Island, Malaysia. Eur J Soc Sci. 2009;11(2):198–204. [Google Scholar]
177. Diaf S, Diaf D, Belhamel M, Haddadi M, Louche A. A methodology for optimal sizing of autonomous hybrid PV/wind system. Energy Policy. 2007;35(11):5708–18. doi:10.1016/j.enpol.2007.06.020. [Google Scholar] [CrossRef]
178. Borowy BS, Salameh ZM. Methodology for optimally sizing the combination of a battery bank and PV array in a wind/PV hybrid system. IEEE Trans Energy Convers. 1996;11(2):367–75. doi:10.1109/60.507648. [Google Scholar] [CrossRef]
179. Celik AN. Optimisation and techno-economic analysis of autonomous photovoltaic-wind hybrid energy systems in comparison to single photovoltaic and wind systems. Energy Convers Manag. 2002;43(18):2453–68. doi:10.1016/S0196-8904(01)00198-4. [Google Scholar] [CrossRef]
180. Silva LMR, Beluco A, Daronco G. A wind PV diesel hybrid system for energizing a sewage station in Santa Rosa, in Southern Brazil. IEEE Lat Am Trans. 2020;18(4):773–80. doi:10.1109/TLA.2020.9082221. [Google Scholar] [CrossRef]
181. Anoune K, Ghazi M, Bouya M, Laknizi A, Ghazouani M, Ben Abdellah A, et al. Optimization and techno-economic analysis of photovoltaic-wind-battery based hybrid system. J Energy Storage. 2020:101878. doi:10.1016/j.est.2020.101878. [Google Scholar] [CrossRef]
182. Ardakani FJ, Riahy G, Abedi M. Optimal sizing of a grid-connected hybrid system for North-West of Iran—case study. In: Proceedings of IEEE; 2010; Prague, Czech Republic. p. 29–32. [Google Scholar]
183. Bathe C. A method for allocating renewable energy source subsidies among final energy consumers. Energy Policy. 2011;39(5):2586–95. doi:10.1016/j.enpol.2011.02.027. [Google Scholar] [CrossRef]
184. Rehman S, Mahbub Alam Md, Meyer JP, Al-Hadhrami LM. Feasibility study of a wind-PV–diesel hybrid power system for a village. Renew Energy. 2012;38(1):258–68. doi:10.1016/j.renene.2011.06.028. [Google Scholar] [CrossRef]
185. Pradhan C, Senapati MK, Malla SG, Nayak PK, Gjengedal T. Coordinated power management and control of standalone PV-hybrid system with modified IWO-based MPPT. IEEE Syst J. 2021;15(3):3585–96. doi:10.1109/jsyst.2020.3020275. [Google Scholar] [CrossRef]
186. Asmae B, Rachid EM. Hybrid energy system models. Amsterdam, Netherlands: Academic Press; 2020. [Google Scholar]
187. Teferra DM, Ngoo LM, Nyakoe GN. Fuzzy-based prediction of solar PV and wind power generation for microgrid modeling using particle swarm optimization. Heliyon. 2023;91:e12802. [Google Scholar] [PubMed]
188. Manas M, Sharma SK, Reddy S, Srivastava A. A critical review on techno-economic analysis of hybrid renewable energy resources-based microgrids. J Eng Appl Sci. 2023;70(1):148. doi:10.1186/s44147-023-00290-w. [Google Scholar] [CrossRef]
189. Kirim Y, Sadikoglu H, Melikoglu M. Technical and economic analysis of biogas and solar photovoltaic (PV) hybrid renewable energy system for dairy cattle barns. Renew Energy. 2022;188:873–89. doi:10.1016/j.renene.2022.02.082. [Google Scholar] [CrossRef]
190. Shao X, Fang T. Performance analysis of government subsidies for photovoltaic industry: based on spatial econometric model. Energy Strategy Rev. 2021;34:100631. [Google Scholar]
191. Branker K, Pearce JM. Financial return for government support of large-scale thin-film solar photovoltaic manufacturing in Canada. Energy Policy. 2010;38(8):4291–303. [Google Scholar]
192. Sivaraman D, Moore MR. Economic performance of grid-connected photovoltaics in California and Texas (United Statesthe influence of renewable energy and climate policies. Energy Policy. 2012;49:274–87. [Google Scholar]
193. Burkart CS, Arguea NM. Efficient scale for photovoltaic systems and Florida’s solar rebate program. Energy Policy. 2012;48:470–8. [Google Scholar]
194. Walters R, Walsh PR. Examining the financial performance of microgeneration wind projects and the subsidy effect of feed-in tariffs for urban locations in the United Kingdom. Energy Policy. 2011;39:5167–81. [Google Scholar]
195. Kumar V, Kumar R, Gupta I, Gupta HO. DG integrated approach for service restoration under cold load pickup. IEEE Trans Power Deliv. 2010;25(1):398–406. [Google Scholar]
196. Gallego RA, Monticelli AJ, Romero R. Optimal capacitor placement in radial distribution networks. IEEE Trans Power Syst. 2001;16(4):630–7. [Google Scholar]
197. Ng HN, Salama MMA, Chikhani AY. Classification of capacitor allocation techniques. IEEE Trans Power Deliv. 2000;15:387–92. [Google Scholar]
198. Chians HD, Wang JC, Cockings O, Shin HD. Optimal capacitor placement in distribution systems: part I, part II. IEEE Trans Power Deliv. 1990;5(2):643–7. [Google Scholar]
199. Pecas Lopes JA, Hatziargyriou N, Mutale J, Djapic P, Jenkins N. Integrating distributed generation into electric power systems: a review of drivers, challenges and opportunities. Electr Power Energy Syst Res. 2007;77:1189–203. [Google Scholar]
200. Abdelkader MA, Osman ZH, Elshahed MA. New analytical approach for simultaneous feeder reconfiguration and DG hosting allocation in radial distribution networks. Ain Shams Eng J. 2021;12(2):1823–37. doi:10.1016/j.asej.2020.09.024. [Google Scholar] [CrossRef]
201. Kansal S, Kumar V, Tyagi B. Optimal placement of different types of DG sources in distribution networks. Electr Power Energy Syst. 2013;53(1):752–60. doi:10.1016/j.ijepes.2013.05.040. [Google Scholar] [CrossRef]
202. Akbar MI, Kazmi SAA, Alrumayh O, Khan ZA, Altamimi A, Malik MM. A novel hybrid optimization-based algorithm for the single and multi-objective achievement with optimal DG allocations in distribution networks. IEEE Access. 2022;10:25669–87. doi:10.1109/ACCESS.2022.3155484. [Google Scholar] [CrossRef]
203. Gozel T, Hocauglu MH. An analytical method for the sizing and siting of distributed generators in radial systems. Electr Power Syst Res. 2009;79(6):912–8. doi:10.1016/j.epsr.2008.12.007. [Google Scholar] [CrossRef]
204. Shaheen AM, Elsayed AM, El-Sehiemy RA, Abdelaziz AY. Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Appl Soft Comput. 2021;98(17):106867. doi:10.1016/j.asoc.2020.106867. [Google Scholar] [CrossRef]
205. Castiblanco-Pérez R, Toro-Rodríguez DE, Montoya OD, Giral-Ramírez DA. Optimal placement and sizing of D-STATCOM in radial and meshed distribution networks using a discrete-continuous version of the genetic algorithm. Electronics. 2021;10(12):1452. [Google Scholar]
206. Celli G, Ghiani E, Mocci S, Pilo F. A multiobjective evolutionary algorithm for the sizing and siting of distributed generation. IEEE Trans Power Syst. 2005;20(2):750–7. doi:10.1109/TPWRS.2005.846219. [Google Scholar] [CrossRef]
207. Ould Bilal B, Sambou V, Ndiaye PA, Kébé CMF, Ndongo M. Optimal design of a hybrid solar-wind-battery system using the minimization of the annualized cost system and the minimization of the loss of power supply probability (LPSP). Renew Energy. 2010;35(10):2388–90. doi:10.1016/j.renene.2010.03.004. [Google Scholar] [CrossRef]
208. Hung DQ, Mithulananthan N, Bansal RC. Multiple distributed generators placement in primary distribution networks for loss reduction. IEEE Trans Ind Electron. 2013;60(4):1700–8. doi:10.1109/TIE.2011.2112316. [Google Scholar] [CrossRef]
209. Salgotra R, Sharma P, Raju S, Gandomi AH. A contemporary systematic review on meta-heuristic optimization algorithms with their MATLAB and Python code reference. Arch Comput Methods Eng. 2023;31(3):1749–822. doi:10.1007/s11831-023-10030-1. [Google Scholar] [CrossRef]
210. Kansal S, Kumar V, Tyagi B. Composite active and reactive power compensation of distribution networks. In: Proceedings of IEEE; 2012; Chennai, India. p. 1–6. [Google Scholar]
211. Sajjadi SM, Haghifam MR, Salehi J. Simultaneous placement of distributed generation and capacitors in distribution networks considering voltage stability index. Int J Electr Power Energy Syst. 2013;46:366–75. doi:10.1016/j.ijepes.2012.10.027. [Google Scholar] [CrossRef]
212. Prommee W, Ongsakul W. Optimal multiple distributed generation placement in microgrid system by improved reinitialized social structures particle swarm optimization. Eur Trans Electr Power. 2011;21(1):489–504. doi:10.1002/etep.456. [Google Scholar] [CrossRef]
213. Gampa SR, Jasthi K, Goli P, Das D, Bansal RC. Grasshopper optimization algorithm based two-stage fuzzy multi-objective approach for optimum sizing and placement of distributed generations, shunt capacitors, and electric vehicle charging stations. J Energy Storage. 2020;27:101117. [Google Scholar]
214. Naresh A, Pukar M, Mithulananthan N. An analytical approach for DG allocation in primary distribution network. Electr Power Energy Syst. 2006;28(10):669–78. doi:10.1016/j.ijepes.2006.02.013. [Google Scholar] [CrossRef]
215. Selim A, Kamel S, Jurado F. Efficient optimization technique for multiple DG allocation in distribution networks. Appl Soft Comput. 2020;86(9):105938. doi:10.1016/j.asoc.2019.105938. [Google Scholar] [CrossRef]
216. Gandomkar M, Vakilian M, Ehsan M. A genetic-based tabu search algorithm for optimal DG allocation in distribution networks. Electr Power Comp Syst. 2005;33(12):1351–62. doi:10.1080/15325000590964254. [Google Scholar] [CrossRef]
217. Parizad A, Khazali AH, Kalantar M. Siting and sizing of distributed generation through harmony search algorithm for improving voltage profile and reduction of THD and losses. In: Proceeding of 23rd Canadian Conference on Electrical and Computer Engineering (CCECE); 2010; Calgary, AB, Canada. p. 1–6. [Google Scholar]
218. Sheth AP, Larson JA. Federated database systems for managing distributed, heterogeneous, and autonomous databases. ACM Comput Surv. 2020;22(3):183–236. doi:10.1145/96602.96604. [Google Scholar] [CrossRef]
219. Celli G, Mocci S, Pilo F, Soma GG. A multiobjective approach for the optimal distributed generation allocation with environmental constraints. In: Proceeding of 10th International Conference Probabilistic Methods Applied to Power Systems (PMAPS); 2008; Rincon, PR, USA. p. 1–8. [Google Scholar]
220. Singh RK, Goswami SK. Optimum siting and sizing of distributed generations in radial and networked systems. Electr Power Compon Syst. 2009;37(2):127–45. doi:10.1080/15325000802388633. [Google Scholar] [CrossRef]
221. Suresh MCV, Edward JB. A hybrid algorithm-based optimal placement of DG units for loss reduction in the distribution system. Appl Soft Comput. 2020;91(6):106191. doi:10.1016/j.asoc.2020.106191. [Google Scholar] [CrossRef]
222. Ziari I, Ledwich G, Ghosh A, Cornforth D, Wishart M. Optimal allocation and sizing of DGs in distribution networks. In: Proceedings of IEEE; 2010; Minneapolis, MN, USA. p. 1–8. [Google Scholar]
223. Moradi MH, Abedini M. A combination of genetic and particle swarm optimization for optimal DG location and sizing in distribution systems. Electr Power Energy Syst. 2012;34(1):66–74. doi:10.1016/j.ijepes.2011.08.023. [Google Scholar] [CrossRef]
224. Safari A, Jahani R, Shayanfar HA, Olamaei J. Optimal DG allocation in distribution network. Electr Electron Eng. 2010;4(8):550–3. [Google Scholar]
225. Leghari ZH, Kumar M, Shaikh PH, Kumar L, Tran QT. A critical review of optimization strategies for simultaneous integration of distributed generation and capacitor banks in power distribution networks. Energies. 2022;15(21):8258. [Google Scholar]
226. Sicong T, Xin XJ, Kumar PS. Optimization of distribution network incorporating distributed generators: an integrated approach. IEEE Trans Power Syst. 2013;28(3):2421–32. [Google Scholar]
227. Pavlos SG, Nikos DH. Optimal distributed generation placement in power distribution networks: models, methods, and future research. IEEE Trans Power Syst. 2013;28(3):3420–8. [Google Scholar]
228. Moradi MH, Abedini M. Optimal placement of multitypes DG as independent private sector under pool/hybrid power market using GA-based tabu search method. Electr Power Energy Syst. 2013;51:43–53. [Google Scholar]
229. Mekhamer SF, Shehata RH, Abdelaziz AY, Al-Gabalawy MA. Enhancing radial distribution system performance by optimal placement of DSTATCOM. Int J Electr Comput Eng. 2020;10(3):2850–60. [Google Scholar]
230. Eminoglu U, Hocaoglu MH. Network topology-based voltage stability index for radial distribution networks. Electr Power Energy Syst. 2009;29(2):131–43. doi:10.2316/Journal.203.2009.2.203-4280. [Google Scholar] [CrossRef]
231. Singh D, Singh D, Verma KS. Multiobjective optimization for DG planning with load models. IEEE Trans Power Syst. 2009;24(1):427–36. doi:10.1109/TPWRS.2008.2009483. [Google Scholar] [CrossRef]
232. Kumar A, Gao W. New price area zonal-based approach for optimal location of distributed generation in hybrid electricity markets. Electr Power Compon Syst. 2009;37(6):672–92. doi:10.1080/15325000802705638. [Google Scholar] [CrossRef]
233. Zhao JH, Foster J, Dong ZY, Wong KP. Flexible transmission network planning considering distributed generation impacts. IEEE Trans Power Syst. 2011;26(3):1434–43. doi:10.1109/TPWRS.2010.2089994. [Google Scholar] [CrossRef]
234. Hengsritawat V, Tayjasanant T, Nimpitiwan N. Optimal sizing of photovoltaic distributed generators in a distribution system with consideration of solar radiation and harmonic distortion. Electr Power Energy Syst. 2012;39(1):36–47. doi:10.1016/j.ijepes.2012.01.002. [Google Scholar] [CrossRef]
235. Nayak MR, Dash SK, Rout PK. Optimal placement and sizing of distributed generation in radial distribution system using differential evolution algorithm. Swarm Evol Memetic Comput Lect Notes Comput Sci. 2012;7677:133–42. [Google Scholar]
236. Kumar IS, Kumar NP. A novel approach to identify optimal access point and capacity of multiple DGs in small, medium and large scale radial distribution systems. Electr Power Energy Syst. 2013;45(1):142–51. doi:10.1016/j.ijepes.2012.08.043. [Google Scholar] [CrossRef]
237. Dong Z, Zhengcai F, Liuchun Z. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems. Electr Power Syst Res. 2007;77(5):685–94. doi:10.1016/j.epsr.2006.06.005. [Google Scholar] [CrossRef]
238. Ghaffarzadeh N, Sadeghi H. A new efficient BBO based method for simultaneous placement of inverter-based DG units and capacitors considering harmonic limits. Int J Electr Power Energy Syst. 2016;80(4):37–45. doi:10.1016/j.ijepes.2016.01.030. [Google Scholar] [CrossRef]
239. Kayal P, Chanda KC. A simple and fast approach for allocation and size evaluation of distributed generation. Energy Environ Eng. 2013;4(7):1–9. [Google Scholar]
240. Grandhi S, Wibowo S. The selection of renewable energy alternative using the fuzzy multiattribute decision making method. In: Proceeding of 12th International Conference on Fuzzy Systems Knowledge Discovery (FSKD); 2015; Zhangjiajie, China. p. 195–200. [Google Scholar]
241. Rumbayan M, Nagasaka K. Prioritization decision for renewable energy development using analytic hierarchy process and geographic information system. In: Proceeding of International Conference on Advanced Mechatronic Systems; 2012; Tokyo, Japan. p. 36–41. [Google Scholar]
242. Kraemer C, Goldermann K, Breuer C, Awater P, Moser A. Optimal positioning of renewable energy units. In: Proceeding of Energytech; 2013; Cleveland, OH, USA. p. 1–5. [Google Scholar]
243. Kamjoo A, Maheri A, Putrus G. Wind speed and solar irradiance variation simulation using ARMA models in design of hybrid wind-PV battery system. Clean Energy Technol. 2013;1:14–7. [Google Scholar]
244. Jakhrani AQ, Samo SR, Kamboh SA, Labadin J, Rigit ARH. An improved mathematical model for computing power output of solar photovoltaic modules. Photoenergy. 2014;2014(1–4):1–9. doi:10.1155/2014/346704. [Google Scholar] [CrossRef]
245. Huang CJ, Huang MT, Chen CC. A novel power output model for photovoltaic systems. Smart Grid Clean Energy. 2013;2(2):39–147. doi:10.12720/sgce.2.2.139-147. [Google Scholar] [CrossRef]
246. Zhang Q, Lai KK, Niu D, Wang Q. A fuzzy group forecasting model based on BPNN for wind power output. In: Proceeding of 5th International Conference Business Intelligence and Financial Engineering (BIFE); 2012; Lanzhou, China. p. 1–5. [Google Scholar]
247. Coelho A, Castro R. Modeling and validation of PV power output with solar tracking. In: Proceeding of International Conference on Power Engineering, Energy and Electrical Drives (POWERENG); 2011; Malaga, Spain. p. 1–6. [Google Scholar]
248. Li Y, Zhang J, Xiao J, Tan Y. Short-term prediction of the output power of PV system based on improved grey prediction model. In: Proceeding of International Conference on Advanced Mechatronic Systems; 2014; Kumamoto, Japan. p. 547–51. [Google Scholar]
249. Singh D, Meena RK, Punia PK. Optimal location of renewable energy generator in deregulated power sector. In: Sharma H, Pundir A, Yadav N, Sharma A, Das S, editors. Recent trends in communication and intelligent systems. Singapore: Springer; 2020. doi:10.1007/978-981-15-0426-6_4. [Google Scholar] [CrossRef]
250. Elgerd IO. Electric energy system theory: an introduction. New York, NY, USA: McGraw-Hill; 1971. [Google Scholar]
251. Mahmoud K, Yorino N, Ahmed A. Optimal distributed generation allocation in distribution systems for loss minimization. IEEE Trans Power Syst. 2016;31(2):960–9. doi:10.1109/TPWRS.2015.2418333. [Google Scholar] [CrossRef]
252. Zulpo RS, Leborgne RC, Bretas AS. Optimal siting and sizing of distributed generation through power losses and voltage deviation. In: Proceeding of 16th International Conference Harmonics Quality Power (ICHQP); 2014; Bucharest, Romania. p. 871–5. [Google Scholar]
253. Hasan IJ, Ghani MRA, Gan CK. Optimum distributed generation allocation using PSO in order to reduce losses and voltage improvement. In: Proceeding of 3rd IET International Conference Clean Energy Technology (CEAT); 2014; Kuching, Malaysia. p. 1–6. [Google Scholar]
254. Chen S, Hu W, Su C, Zhang X, Chen Z. Optimal reactive power and voltage control in distribution networks with distributed generators by fuzzy adaptive hybrid particle swarm optimisation method. IET Gener Transm Distrib. 2015;9(11):1096–103. doi:10.1049/iet-gtd.2014.1059. [Google Scholar] [CrossRef]
255. Mathew RK, Ashok S, Kumaravel S. Analyzing the effect of DG on reliability of distribution systems. In: Proceeding of IEEE; 2015; Coimbatore, India. p. 1–4. [Google Scholar]
256. Brown RE. Electrical power distribution reliability. New York, NY, USA: Marcel Dekker; 2002. [Google Scholar]
257. Shaaban MF, El-Saadany EF. Optimal allocation of renewable DG for reliability improvement and losses reduction. In: Proceeding of IEEE; 2012; San Diego, CA, USA. p. 1–8. [Google Scholar]
258. Aljaidi M, Samara G, Singla MK, Alsarhan A, Hassan M, Safaraliev M. A particle swarm optimizer-based optimization approach for locating electric vehicles charging stations in smart cities. Int J Hydrogen Energy. 2024;87(25):1047–55. doi:10.1016/j.ijhydene.2024.09.029. [Google Scholar] [CrossRef]
259. Singla MK, Gupta J, Alsharif MH, Kim MK, Aljaidi M, Safaraliev M. A robust multi-objective optimization algorithm for accurate parameter estimation for solar cell models. Soft Comput. 2024;28(19):11265–77. doi:10.1007/s00500-024-09888-5. [Google Scholar] [CrossRef]
260. Hamdare S, Brown DJ, Cao Y, Aljaidi M, Kaiwartya O, Yadav R, et al. EV charging management and security for multi-charging stations environment. IEEE Open J Veh Technol. 2024;5(1):807–24. doi:10.1109/OJVT.2024.3418201. [Google Scholar] [CrossRef]
261. Kumar Tiwari P, Prakash S, Tripathi A, Aljaidi M, Kumar Shukla N, Kaiwartya O, et al. A novel model for vehicular delay tolerant networks using deterministic bundle relaying scheme. IEEE Access. 2024;12:68916–25. doi:10.1109/ACCESS.2024.3400408. [Google Scholar] [CrossRef]
262. Kumar Bairappaka S, Ghosh A, Kaiwartya O, Aljaidi M, Cao Y, Kharel R. A novel design of broadband circularly polarized rectenna with enhanced gain for energy harvesting. IEEE Access. 2024;12:65583–94. doi:10.1109/ACCESS.2024.3397016. [Google Scholar] [CrossRef]
263. Ghori MR, Wan TC, Sodhy GC, Aljaidi M, Rizwan A, Sadiq AS, et al. Enhancing reliability and stability of BLE mesh networks: a multipath optimized AODV approach. Sensors. 2024;24(18):5901. doi:10.3390/s24185901. [Google Scholar] [PubMed] [CrossRef]
264. Manderna A, Kumar S, Dohare U, Aljaidi M, Kaiwartya O, Lloret J. Vehicular network intrusion detection using a cascaded deep learning approach with multi-variant metaheuristic. Sensors. 2023;23(21):8772. doi:10.3390/s23218772. [Google Scholar] [PubMed] [CrossRef]
265. Saied O, Kaiwartya O, Aljaidi M, Kumar S, Mahmud M, Kharel R, et al. LiNEV: visible light networking for connected vehicles. Photonics. 2023;10(8):925. doi:10.3390/photonics10080925. [Google Scholar] [CrossRef]
266. Yaduwanshi R, Kumar S, Kumar A, Kaiwartya O, Deepti D, Aljaidi M, et al. Efficient route planning using temporal reliance of link quality for highway IoV traffic environment. Electronics. 2023;12(1):130. doi:10.3390/electronics12010130. [Google Scholar] [CrossRef]
267. Ahmad A, Khalid M, Ullah Z, Ahmad N, Aljaidi M, Malik FA, et al. Electric vehicle charging modes, technologies and applications of smart charging. Energies. 2022;15(24):9471. doi:10.3390/en15249471. [Google Scholar] [CrossRef]
268. Ettehadi M, Ghasemi H, Vaez-Zadeh S. Voltage stability-based DG placement in distribution networks. IEEE Trans Power Del. 2013;28(1):171–8. doi:10.1109/TPWRD.2012.2214241. [Google Scholar] [CrossRef]
269. Esmaili M, Firozjaee EC, Shayanfar HA. Optimal placement of distributed generations considering voltage stability and power losses with observing voltage-related constraints. Appl Energy. 2014;113:1252–60. doi:10.1016/j.apenergy.2013.09.004. [Google Scholar] [CrossRef]
270. Mina-Casaran JD, Echeverry DF, Lozano CA. Demand response integration in microgrid planning as a strategy for energy transition in power systems. IET Renew Power Gener. 2021;15(4):889–902. doi:10.1049/rpg2.12080. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF




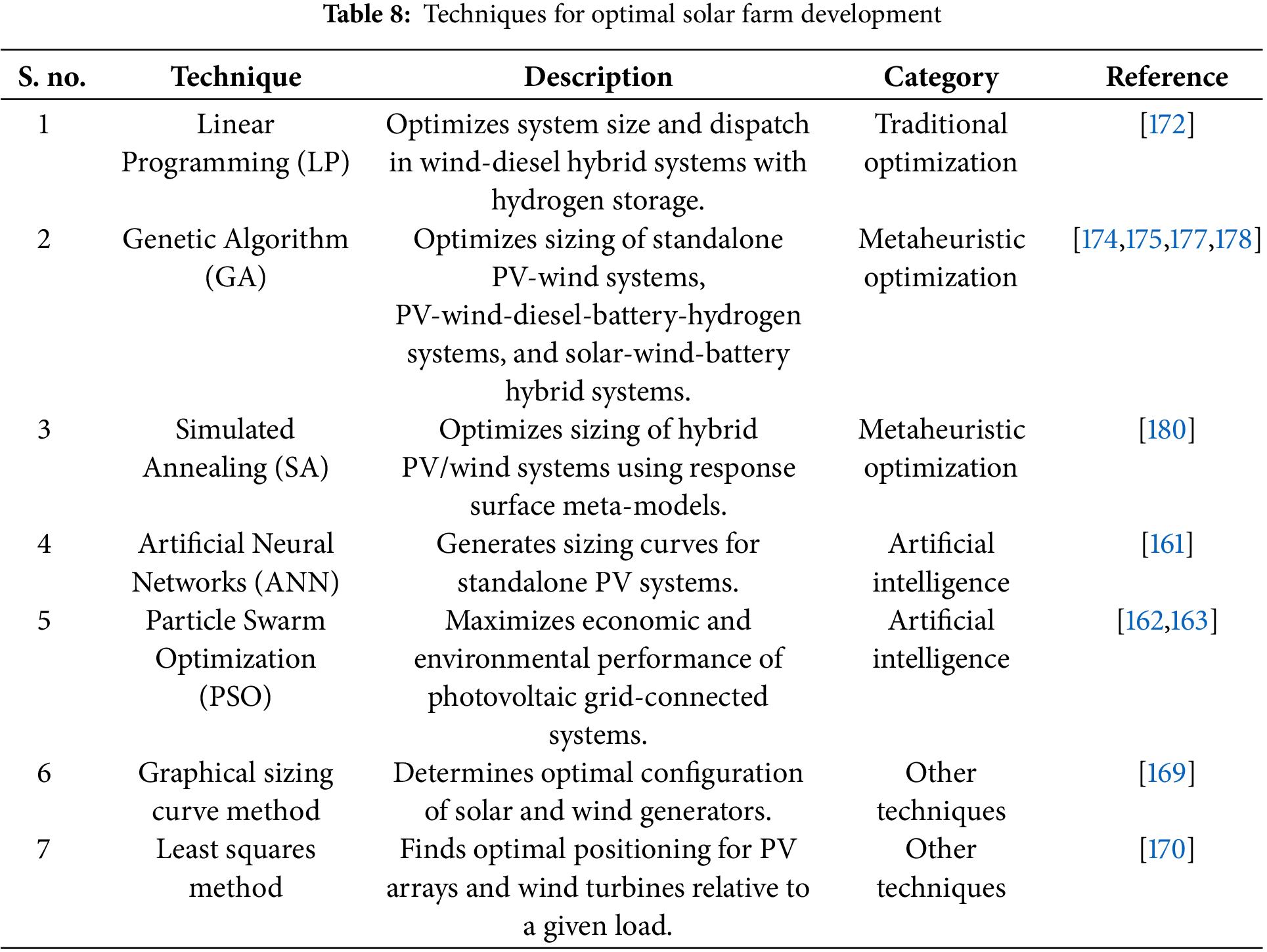

 Downloads
Downloads
 Citation Tools
Citation Tools