Study on the Seepage Characteristics of Deep Tight Reservoirs Considering the Effects of Creep

1  Introduction

With the rapid development of the global economy, the demand for oil and gas re-sources has been steadily increasing, prompting a shift in exploration and production from conventional to unconventional reservoirs [1–3]. Deep tight oil and gas reservoirs, as a significant type of unconventional resource, have emerged as a critical frontier for in-creasing reserves and production in recent years [4,5]. Accurate characterization of the flow properties in tight reservoirs is essential for identifying hydrocarbon-rich zones, designing exploration and development strategies, optimizing well patterns, and determining well placement. Unlike conventional reservoirs, the flow characteristics of deep tight reservoirs under “three high” conditions (high temperature, high pressure, and high stress) are influenced by coupled effects of multiple fields, including stress and fluid flow [6]. Moreover, these reservoirs exhibit pronounced creep behavior during hydrocarbon extraction [7]. Consequently, numerous studies have been conducted to investigate these phenomena. For example, Bowden et al. [8] performed shear creep experiments on shale and observed significant creep deformation when loading was applied perpendicular to the bed-ding planes. Zvonko [9] conducted laboratory creep tests on marl to describe time-dependent deformation after loading or unloading. Karev et al. [10] studied the time-dependent deformation of strata under complex stress conditions during oil and gas field development using true triaxial creep experiments and established time-dependent relationships for stepwise loading conditions. Wang et al. [11] conducted a series of triaxial compression tests on low-porosity sandstone, involving loading-unloading cycles and permeability measurements. They investigated the deformation behavior of the rock and the evolution of its permeability. Liang et al. [12] conducted a series of triaxial creep experiments on rock samples under high temperature, constant axial pressure, and unloading confining pressure conditions.

Based on the experimental findings mentioned above, scholars have proposed various theoretical models and conducted numerical simulations to reveal the underlying mechanisms. Qiao et al. [13] developed a creep constitutive model considering the effects of temperature on rock creep properties. Li et al. [14] proposed a stress intensity model for crack tips considering pore pressure and validated its applicability in analyzing the effects of pore pressure on crack propagation and strain during rock creep. Lei et al. [15] utilized numerical simulations to explore the influence of fracture aperture and surface roughness on rock permeability. Xu et al. [16] systematically analyzed the evolution of mechanical properties of granite, including uniaxial compressive strength, elastic modulus, creep deformation, steady-state creep rate, and long-term strength, under thermo-mechanical coupling conditions. Cao et al. [17] based on the nonlinear damage creep characteristics of rock and the damage variable, defined a new nonlinear damage creep constitutive model for high-stress soft rock by serially combining the improved Burgers model, Hooke model, and St. Venant model. Xu et al. [18] based on the capillary model theory, linked permeability to tortuosity and porosity, proposing the K-C permeability model expressed as a function of porosity. Lastly, Wang [19] developed a multi-field coupling control equation for temperature, fluid flow, and rheology in deep rock masses, analyzing the time-dependent evolution of borehole wall deformation and permeability under coupled rheological and fluid flow conditions.

Although significant progress has been made in understanding reservoir flow characteristics, research on the flow behavior of deep tight reservoirs considering creep effects remains limited. This gap is particularly evident due to the considerable burial depth of such reservoirs, the pronounced coupling of multiple physical fields, and the notable creep behavior exhibited during hydrocarbon production. To address this issue, a comprehensive study integrating theoretical analysis, laboratory experiments, and numerical simulations has been conducted to investigate the evolution of flow characteristics in deep tight reservoirs under the influence of creep. This research aims to provide technical sup-port for the efficient exploration and development of deep tight oil and gas resources.

In this study, we have undertaken a comprehensive investigation of the seepage characteristics of deep tight reservoirs, with a particular focus on the effects of creep. The research methodology employed in this study is multifaceted, combining theoretical analysis, experimental validation, and numerical simulation to provide a robust understanding of the seepage behavior under creep conditions.

The study commenced with an extensive review of the existing literature to identify the current state of knowledge and to pinpoint the gaps that this research aims to fill. Subsequently, a series of laboratory experiments were meticulously designed and executed. These experiments were aimed at determining the mechanical and hydraulic properties of the reservoir rocks under various stress and temperature conditions, which are crucial for understanding the seepage behavior. Building on the experimental data, a detailed theoretical framework was developed. This framework includes the formulation of governing equations that describe the seepage characteristics, taking into account the time-dependent deformation due to creep. The constitutive relationships were established based on the experimental results, ensuring that the models accurately reflect the behavior of the reservoir rocks. To further validate and refine the theoretical models, advanced numerical simulations were conducted. These simulations allowed for a comprehensive analysis of the seepage behavior under different scenarios, providing valuable insights into the complex interactions between the reservoir rocks and the flowing fluids. The numerical results were compared with the experimental data to ensure the accuracy and reliability of the models. Through this integrated approach, this study not only provides a deeper understanding of the seepage characteristics of deep tight reservoirs but also offers practical guidance for the optimization of reservoir management strategies. The findings of this research are expected to contribute significantly to the field of reservoir engineering and to enhance the efficiency of hydrocarbon recovery from deep tight reservoirs.

2  Physical Characteristics of Dense Reservoirs

The study area is located within a deep reservoir in western China. Statistical analysis of Well M1, Well M2, and Well M3 was conducted using drilling and logging data, yielding the frequency distribution of porosity and permeability in the study area, as shown in Fig. 1. The porosity of the three wells in the study area is generally below 15%, with the primary porosity frequency distribution for Wells M1, M2, and M3 concentrated in the range of <5%. The permeability values are less than 10 mD, with the main permeability frequency distribution ranges for Wells M1, M2, and M3 being 1–10 mD, <1 mD, and <1 mD, respectively.

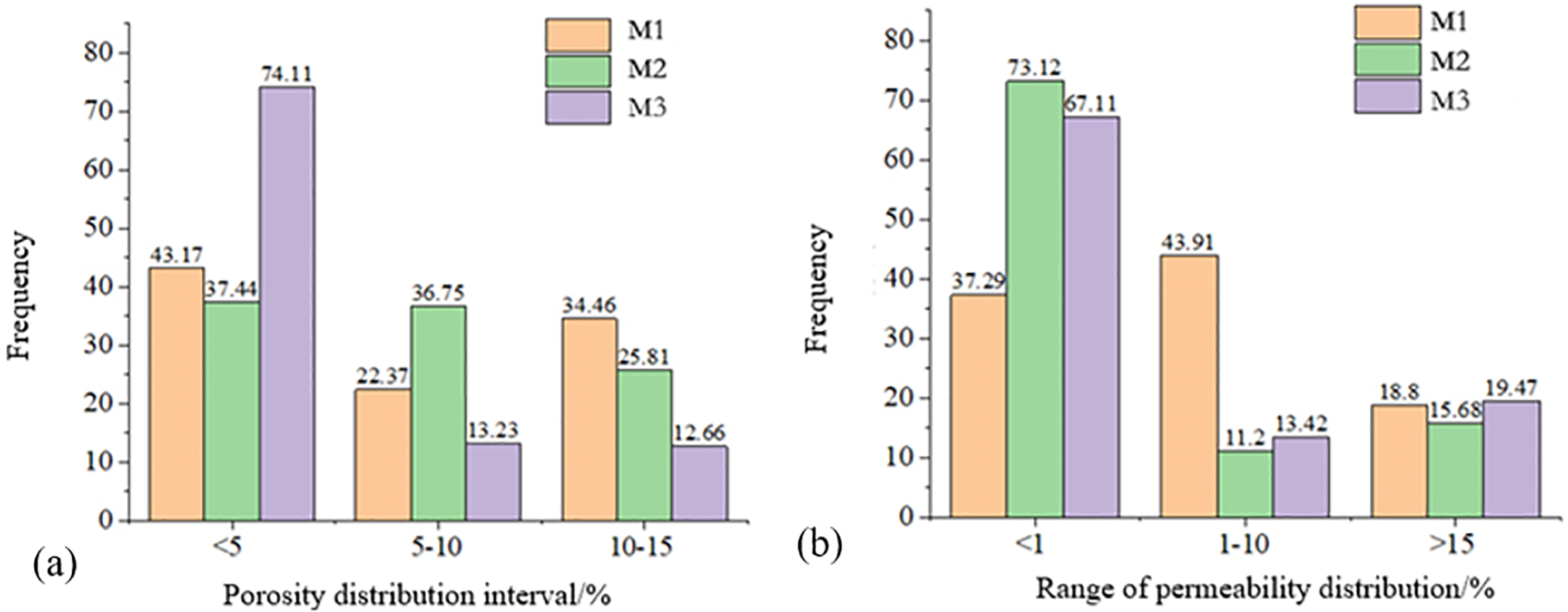
Figure 1: Frequency distribution of shale physical properties in the study area. (a) Frequency distribution of shale porosity in the study area; (b) Frequency distribution of shale permeability in the study area

The average porosity values for Wells M1, M2, and M3 are 2.417%, 4.152%, and 1.675%, respectively, all below 5%. The average permeability values for these wells are 0.314, 0.218, and 0.167 mD, all less than 1 mD. Therefore, the study area is characterized as an ultra-low porosity and ultra-low permeability reservoir.

Shale reservoirs exhibit marked spatial and temporal variability due to differences in porosity, permeability, mineral composition, and the presence of natural fractures, as well as changes over time in factors such as fluid injection, temperature, and chemical reactions. Spatially, areas with higher porosity and permeability may undergo greater deformation due to higher fluid pressure, enhancing creep, while regions with lower values could become stress concentration points, potentially leading to fractures. The distribution of minerals like clay, quartz, and calcite also affects mechanical properties, with clay-rich areas showing more ductility and creep, and quartz-rich areas being more brittle. Natural fractures act as fluid flow pathways, boosting seepage and concentrating stress, which can cause localized creep and new fractures. Temporally, fluid injection and production alter the stress state and pore pressure, impacting effective stress and creep rates. Temperature changes can increase creep rates by reducing rock viscosity, while chemical reactions between injected fluids and reservoir rock modify mineral composition and porosity, affecting both mechanical properties and seepage. These spatial and temporal variations lead to non-uniform deformation and seepage, with some areas experiencing more significant creep and seepage than others. They also result in time-dependent changes in creep and seepage behavior, as factors like fluid injection, temperature, and chemical reactions evolve over time, altering the reservoir’s mechanical and hydraulic properties. Understanding these influences is vital for predicting reservoir performance and optimizing production strategies.

3  Test of Mechanical Properties of Deep Dense Reservoir Rocks

3.1 Test System and Rock Samples

Fig. 2 illustrates the triaxial and creep tests conducted using a high-temperature and high-pressure rock testing system. The system is capable of applying axial loads up to 2000 KN and a maximum confining pressure of 200 MPa, enabling the simulation of the stress, pore pressure, and temperature conditions present in deep reservoirs.

Figure 2: High temperature and high pressure rock comprehensive test system

The test samples were collected from a deep reservoir in western China. Following the standards recommended by the International Society for Rock Mechanics, 11 sets of standard cores with dimensions of Φ25 mm × 50 mm were prepared. Among these, seven sets were designated for triaxial compression tests, labeled as HS11-1, HS11-2, HS11-3, HS11-4, HS11-5, HS11-6, and HS11-7. The remaining six sets were allocated for creep tests, labeled as R-1, R-2, R-3, R-4, R-5, and R-6. The specific rock samples are shown in Fig. 3. Table 1 shows the physical characteristics of the three Wells in the study area.

Figure 3: Core specimen for test

3.2 Triaxial Compression Test of Dense Reservoir Rocks

Triaxial compression tests were conducted on the rock samples under confining pressures of 0, 20, 30, 35, 40, 45, and 50 MPa. Axial pressure was applied in a strain-controlled manner at a loading rate of approximately 2 × 10−5 s−1 until the rock samples failed. During the experiments, axial stress, axial displacement, and lateral displacement were recorded. The Burgers model’s ability to distinctly separate elastic, viscoelastic, and viscous deformation mechanisms is crucial for shale, where microfracture closure and mineral reorientation occur during creep. This is consistent with the triaxial test results (Fig. 4), which highlighted crack compaction and delayed elasticity as prominent features. Models that omit these stages would likely underestimate both strain accumulation and permeability reduction. The complete stress-strain curves of the core samples under these conditions are presented in Fig. 4.

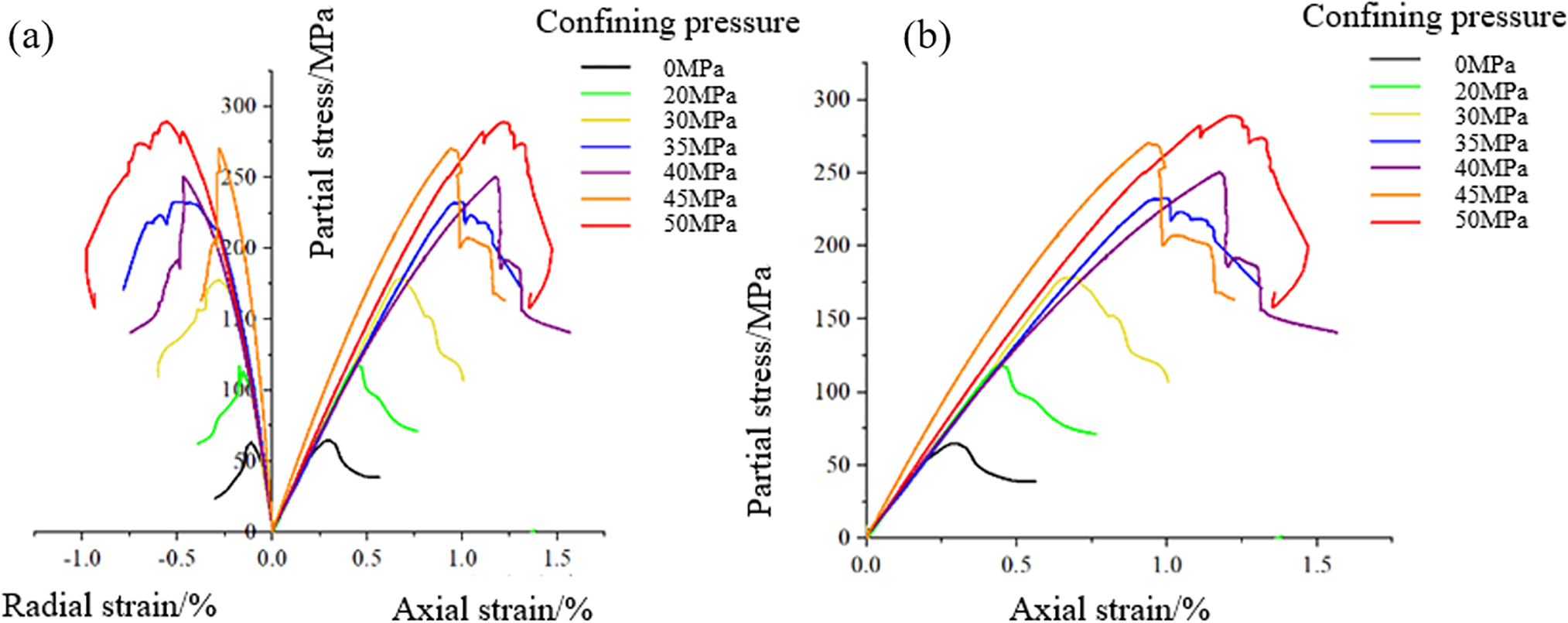
Figure 4: Stress-strain diagrams of rock specimens under different circumferential pressures. (a) Stress-strain diagrams of rock specimens under different circumferential pressures; (b) Axial stress-strain diagram of rock sample under different confining pressures

Fig. 4 demonstrates significant variations in rock deformation behavior under different confining pressures. The stress-strain relationship curves can be divided into four stages: crack compaction, linear deformation, viscoelastic deformation, and yielding de-formation. From the stress-strain curves, parameters such as elastic modulus and Pois-son’s ratio were determined for each core sample. The elastic modulus was calculated as the slope of the linear portion of the stress-strain curve, while Poisson’s ratio was deter-mined as the absolute value of the ratio between the radial deformation rate and the axial deformation rate. The results are presented in Table 2.

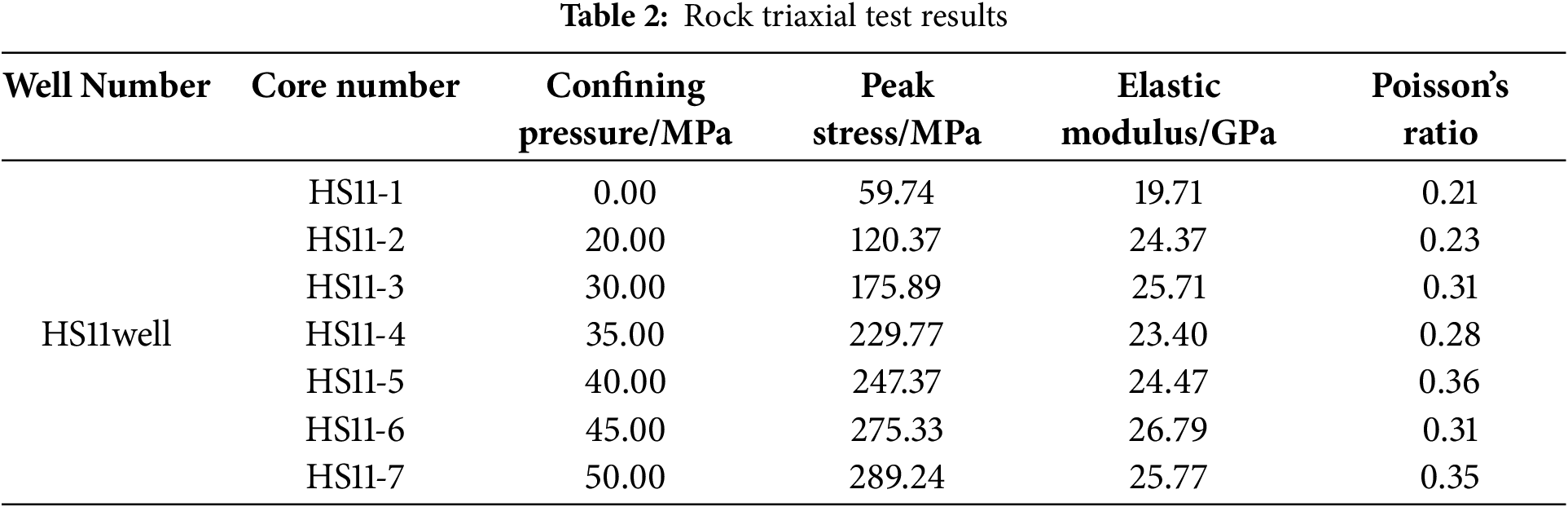
Fig. 5 illustrates the variation trends of peak strength and elastic modulus for seven rock samples under different confining pressures. It can be observed that the peak strength of the rock increases with the rise in confining pressure. At lower confining pressures (≤35 MPa), the peak strength exhibits significant increases, whereas beyond 35 MPa, the incremental growth becomes less pronounced. This behavior can be attributed to the inhibitory effect of confining pressure on the propagation and evolution of micropores and fractures within the rock samples. Higher confining pressures provide greater resistance, thereby requiring higher stress levels for the samples to fail. The elastic modulus of reservoir rocks shows substantial fluctuations with increasing confining pressure. At low confining pressures (≤30 MPa), the elastic modulus increases as the confining pressure rises. However, beyond 30 MPa, the elastic modulus begins to decrease and continues to exhibit significant variability as confining pressure increases. This phenomenon may be due to the heterogeneity of the rock samples, which originate from different stratigraphic depths.

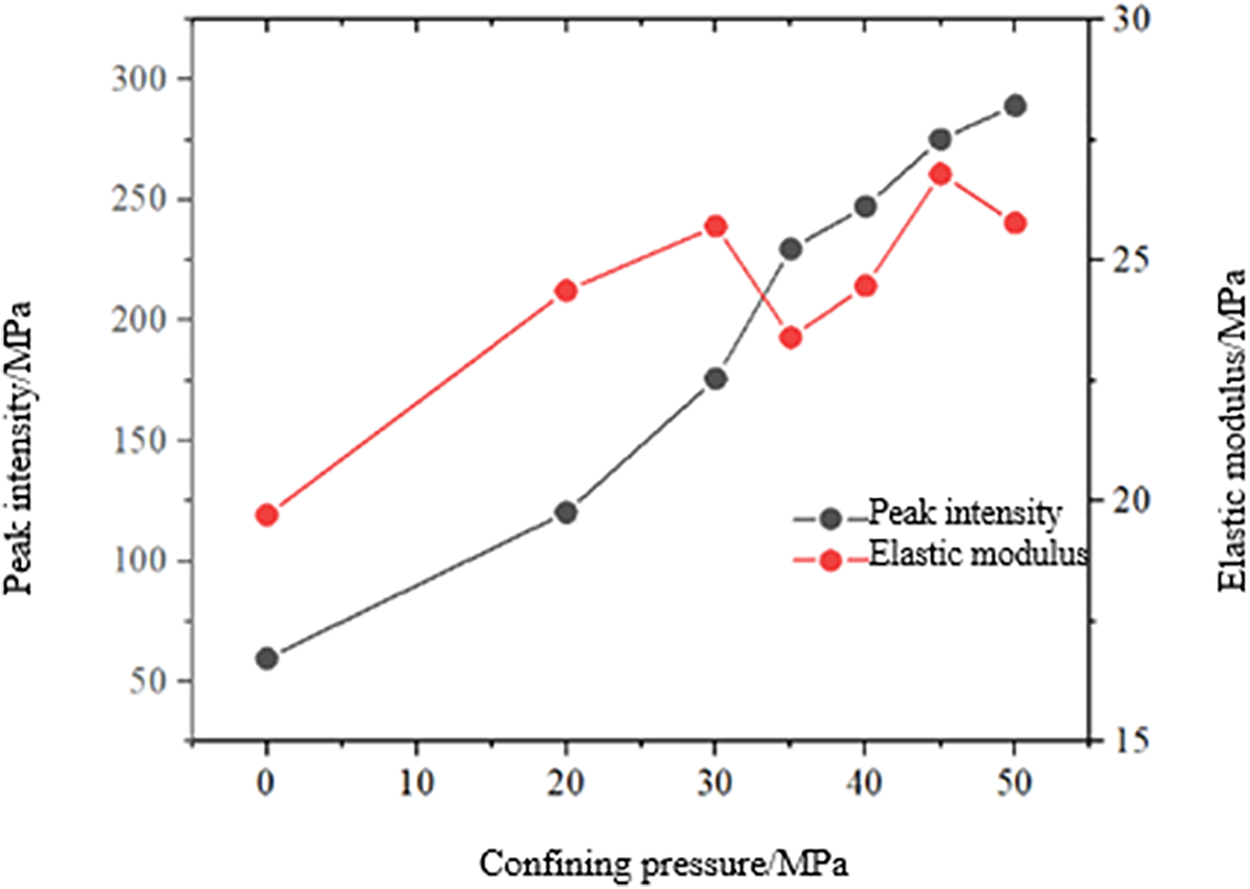
Figure 5: Trend of peak strength and modulus of elasticity of rock specimens

Triaxial compression tests were performed to determine the stress-strain relationship of the reservoir rocks under various confining pressures. The tests involved applying a confining pressure to the rock samples and then subjecting them to a uniaxial compressive stress until failure. The stress-strain curves were recorded to identify the different deformation stages, including crack compression, linear deformation, delayed elastic deformation, and yield deformation. The peak stress and elastic modulus were measured, and their variations with confining pressure were analyzed. These tests helped to establish the mechanical properties of the rocks, which are essential for modeling the seepage behavior.

4  Dense Reservoir Rock Creep Test and Model Research

4.1 Experimental Plan

The experiments conducted were uniaxial creep tests, where six rock samples were subjected to stress levels corresponding to 60%, 70%, 75%, 80%, 85%, and 90% of their uniaxial compressive strength at peak stress (35.84, 41.82, 44.81, 47.79, 50.78, and 53.77 MPa, respectively). Creep was considered to reach a stable state when the axial deformation of the sample remained less than 0.001% over a 10-h period. The detailed experimental plan is shown in Table 3.

4.2 Test Results and Analysis

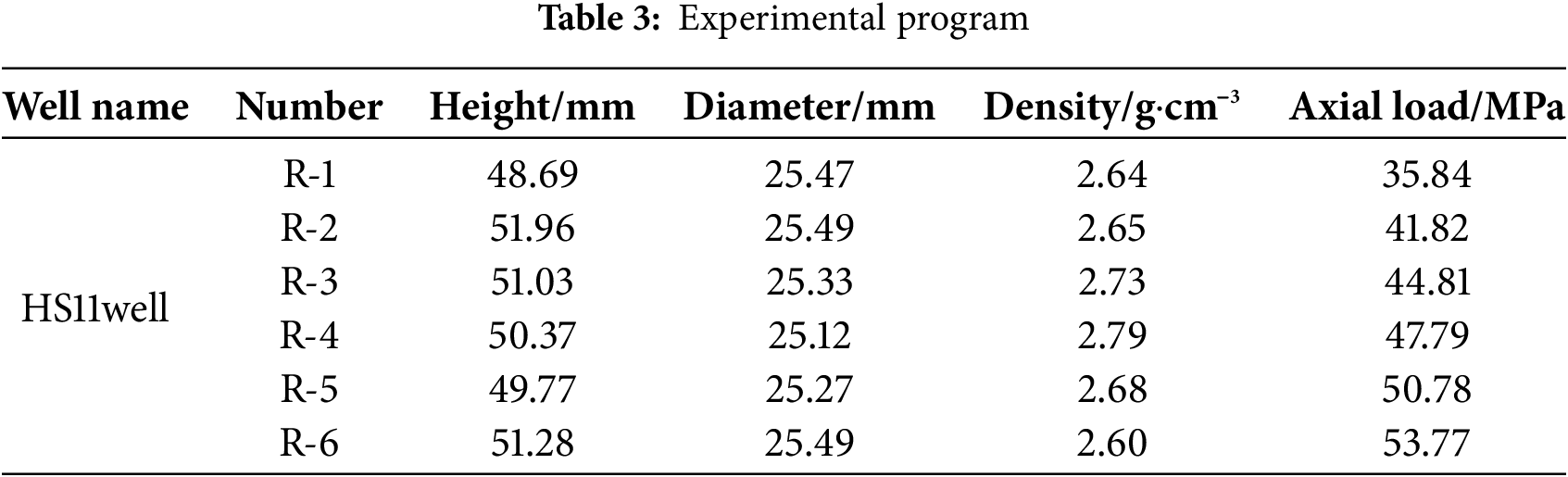
Fig. 6 presents the creep curves of the rock samples under different stress levels, based on the experimental data. As the stress increases, the instantaneous elastic strain of the rock samples also increases, causing the creep curves to shift upward. The strain in the rock samples increases, and the time required for the creep curve to stabilize decreases. Furthermore, the strain rate during the steady-state creep phase increases with increasing load, and the time required for rock failure shortens. When the applied stress is relatively low, the strain of the rock gradually stabilizes at a specific value under load, and the rate of strain increase tends toward zero, indicating that the rock has entered a stable creep state. However, at higher stress levels, the rock strain undergoes uniform growth for a certain period before entering an accelerated growth phase, continuing until excessive de-formation causes the sample to lose its load-bearing capacity.

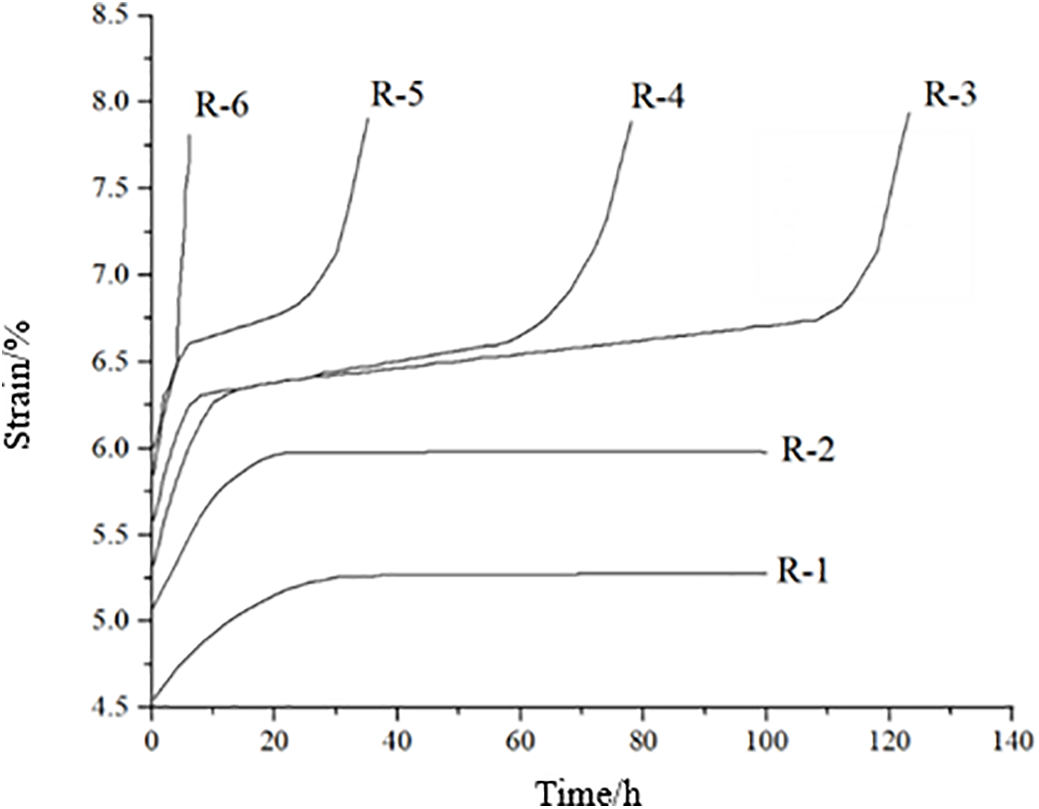
Figure 6: Creep test curve

The Burgers model, comprising a Kelvin model (which captures delayed elasticity) and a Maxwell model (which accounts for viscous flow) that characterized by four constants: E1, E2, η1 and η2, was selected due to its capability to represent both transient and steady-state creep behaviors. Shale exhibits multi-stage creep characteristics under prolonged stress, including an instantaneous elastic deformation phase, a decelerating creep phase, and a steady-state phase. While simpler models, such as the Maxwell model (series spring-dashpot) or the Kelvin-Voigt model (parallel spring-dashpot), can describe individual stages (e.g., steady-state creep for Maxwell or transient creep for Kelvin-Voigt), they are inadequate for capturing the full creep evolution observed in shale. For example, the Maxwell model fails to account for transient creep behavior, while the Kelvin-Voigt model cannot describe steady-state viscous flow. The Burgers model uniquely integrates these characteristics, making it well-suited for simulating time-dependent strain accumulation and permeability evolution in deep tight reservoirs under multi-field coupling [20].

The intrinsic equation [21,22] of the Burgers model is:

η1η2E1ε¨+η2ε˙=η1η2E1E2σ¨+(η1E2+η1E1+η2E2)σ˙+σ(1)

The transformed creep equation is:

ε(t)=σ0[1E1+1η1+1E2(1−e−E2η2t)](2)

The data obtained from the creep tests were fitted using Origin software [23], resulting in model fitting curves. Since the Burgers model provides a good fit for both the decaying and steady-state creep stages, only the decaying and steady-state creep portions of samples R-1, R-2, and R-3 were fitted. The fitting results and comparisons are shown in Fig. 7. The correlation coefficients of the fitting curves were 0.994, 0.989, and 0.997, respectively, indicating a good fitting performance.

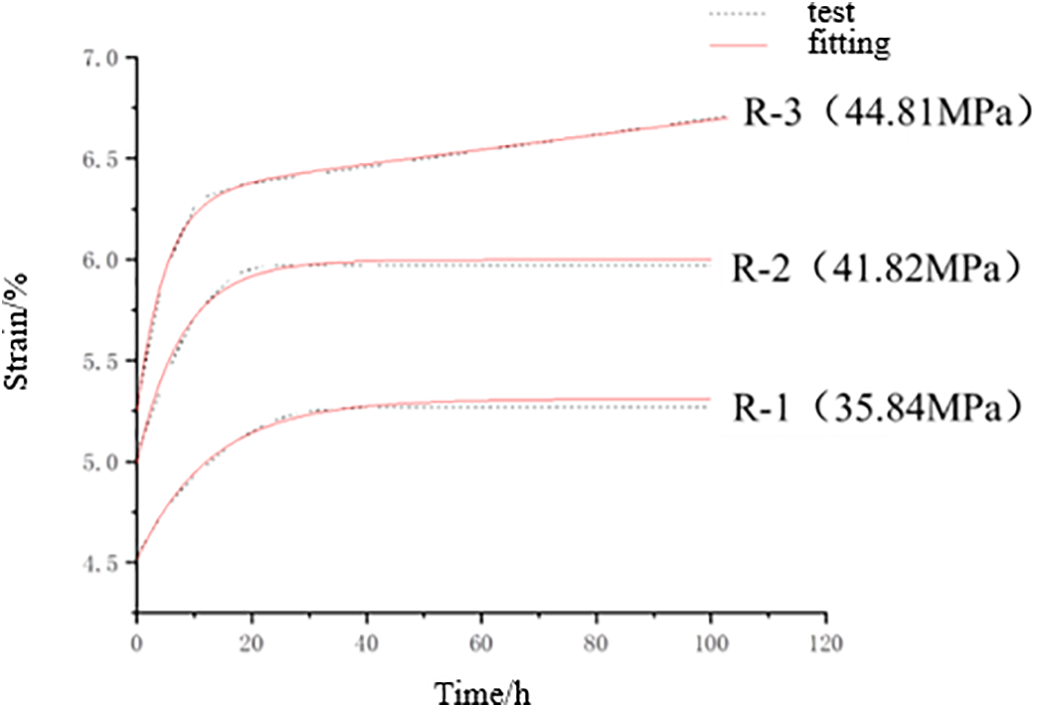
Figure 7: Test and fitting curves

Table 4 presents the fitting parameters of the Burgers model obtained from the fitting curves under different load conditions.

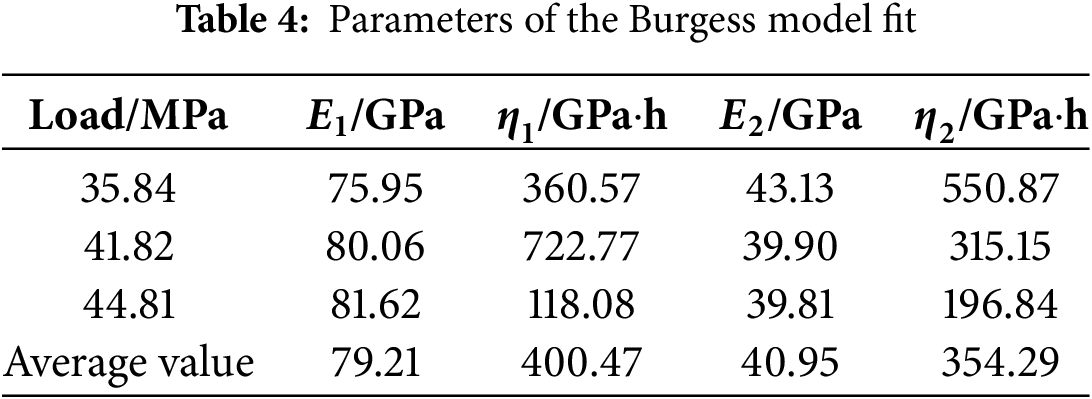
Creep tests were conducted to study the time-dependent deformation of the reservoir rocks under constant stress conditions. The tests involved applying a constant stress to the rock samples and monitoring the strain over time. The creep behavior was analyzed to develop a Burgers creep model, which was used to describe the viscoelastic properties of the rocks. The creep tests provided valuable data on the deformation characteristics of the rocks, which are critical for understanding the long-term seepage behavior.

5  Study on Seepage Characteristics of Deep Tight Reservoirs Considering Creep Effects

5.1 Creep-Seepage Coupling Model for Tight Reservoir Rocks

To facilitate the analysis of the interrelationships between various physical fields during oil and gas extraction, the following simplifying assumptions are made: the continuity assumption, the small deformation assumption, the phase homogeneity assumption, and the assumption that the temperature of the rock layers and the gas within them does not change during the coupled movement process.

5.1.1 Stress Field State Equation Considering Creep Effects

Under the action of external forces, the rock mass experiences stress and strain. The fluids present in the pores and fractures generate pore pressure, causing deformation of the rock skeleton, while temperature variations induce expansion or contraction of the rock skeleton, resulting in thermal strain. Therefore, it is assumed that the rock mass be-haves as a porous elastic medium, and the stress-strain relationship is expressed as:

σij=2Gεij+2Gυ1−2υεvolδij−αPδij−KβTTδij(3)

where σij is the stress tensor (positive for tension), εij is the strain tensor, G=E/2(1+μ) is the shear modulus, υ is Poisson’s ratio, εvol is the volumetric strain, δij is the Kronecker tensor symbol, α is the Biot coefficient, P is the fluid pore pressure, K is the bulk modulus of the rock, βT is the thermal expansion coefficient of the rock material, and T is the temperature of the rock material.

According to the theory of elasticity, the relationship between rock strain and dis-placement is expressed as:

εij=12(ui,j+uj,i)(4)

And the static equilibrium equation for the rock under external loading is:

σij,j+fi=0(5)

Substituting Eqs. (4) and (5) into Eq. (3) yields the Navier equation containing displacement and temperature variables:

Gui,jj+G1−2υuj,ji+αp,i+KβTTi+F,i=0(6)

where ui and uj are the components of displacement in the i and j directions, respectively, and Fi is the component of the body force in the i direction.

The Laplace transform of the Burgers model constitutive equation gives the rheological modulus as:

E(t)=E11+E1η1t+E1E2[1−exp⁡(−E2η2t)](7)

Replacing E in Navier’s equation with the creep modulus E(t) yields the equilibrium equation considering effective stress changes due to pore pressure, creep, and temperature changes:

G(t)ui,jj+G(t)1−2υuj,ji+αp,i+KβTTi+F,i=0(8)

where G(t)=E(t)2(1+2υ),K(t)=E(t)3(1−2υ) is assumed that Poisson’s ratio v does not change during creep.

5.1.2 Equation of State for the Seepage Field

Deep rock mass is composed of a rock skeleton, pores, and fractures, containing a large amount of mobile gas and a certain amount of moisture, making it a typical porous multiphase medium. To simplify calculations, this simulation does not consider the in-fluence of moisture on the mechanical properties of the rock mass and gas flow. The mass conservation equation for rock mass seepage is:

∂m∂t+∇⋅(ρgqg)=Qp(9)

where m is the mass of fluid inside the rock mass, t is time, ρg is the fluid density in the rock mass, qg is the fluid seepage velocity in the rock mass, and Qp is the mass source term.

Ignoring the adsorption and desorption of tight gas, the fluid content in the rock mass is expressed as:

m=φρg(10)

Then the partial derivative of the first term of conservation of mass, the fluid mass m, with respect to time t is:

∂m∂t=φ∂ρg∂t+ρg∂φ∂t=ρg(φKw+1−φKs)∂p∂t(11)

where φ is porosity, ρg is fluid density, Kw is the bulk modulus of the fluid, and Ks is the bulk modulus of the rock particles, named S=φ/Kw+(1−φ)/Ks is the stativity coefficient.

Meanwhile, considering the basic assumption that fluid seepage satisfies Darcy’s law, the velocity equation for fluid flow is:

qg=−kμw∇p(12)

Substituting Eqs. (11) and (12) into Eq. (9) yields the continuity equation for fluid within the rock:

S∂p∂t−∇⋅(Kμw∇p)=Qp(13)

5.1.3 Permeability Model

The Kozeny-Carman model, based on the capillary bundle theory, initially established a relationship between permeability and porosity, specific surface area, shape factor, and tortuosity, while neglecting changes in the matrix surface area. The resulting equation for rock permeability, considering the coupling effects of the stress field and the flow field, is given by:

k=k01+εv[1+εvφ0+φ0−1φ0(εs−εp)]3(14)

In the extraction of tight oil and gas, deep reservoirs undergo creep deformation due to long-term exposure to physical fields such as temperature and stress. Therefore, to study the variation of reservoir permeability, the impact of creep must be considered. By substituting the creep constitutive Eq. (7) into Eq. (14), the multi-field coupled permeability control equation that takes into account the effects of stress, flow, and creep can be derived as follows:

k=k01+εv(t)[1+εv(t)φ0+φ0−1φ0(εs−εp)]3(15)

5.2 Simulation of Seepage Characteristics in Deep Tight Reservoirs Considering Creep Effects

Based on the aforementioned rock mechanics properties of tight reservoirs and the established multi-field coupled control equations, a simulation study of deep tight reservoir permeability characteristics considering the effects of creep was conducted using COMSOL Multiphysics software.

5.2.1 Geometric Model

Fig. 8 presents a three-dimensional numerical model of a horizontal well in a tight reservoir, with dimensions of 1.0 m × 1.0 m × 2.0 m, where the diameter of the horizontal well is 0.2 m. The horizontal principal stresses σx and σy, as well as the vertical stress σz, are applied on the three faces of the model to simulate the in-situ layer pressure, representing the horizontal earth stress and the overburden pressure, respectively. The other boundaries are constrained with roller supports. The initial formation pore pressure is set to p0, and the wellbore boundary is modeled with an unsupported condition and a flow boundary, with the flow pressure set to p and the fluid temperature set to T. All other outer boundaries are set as no-flow boundaries. To obtain the distribution and variation of physical quantities in the reservoir under multi-field coupling, measurement lines are set on the YZ plane (with the X-axis coordinate at 1 m). Four measurement points are placed along the line, at distances of 0.1, 0.2, and 0.3 m from the wellbore, as well as at the wellbore wall.

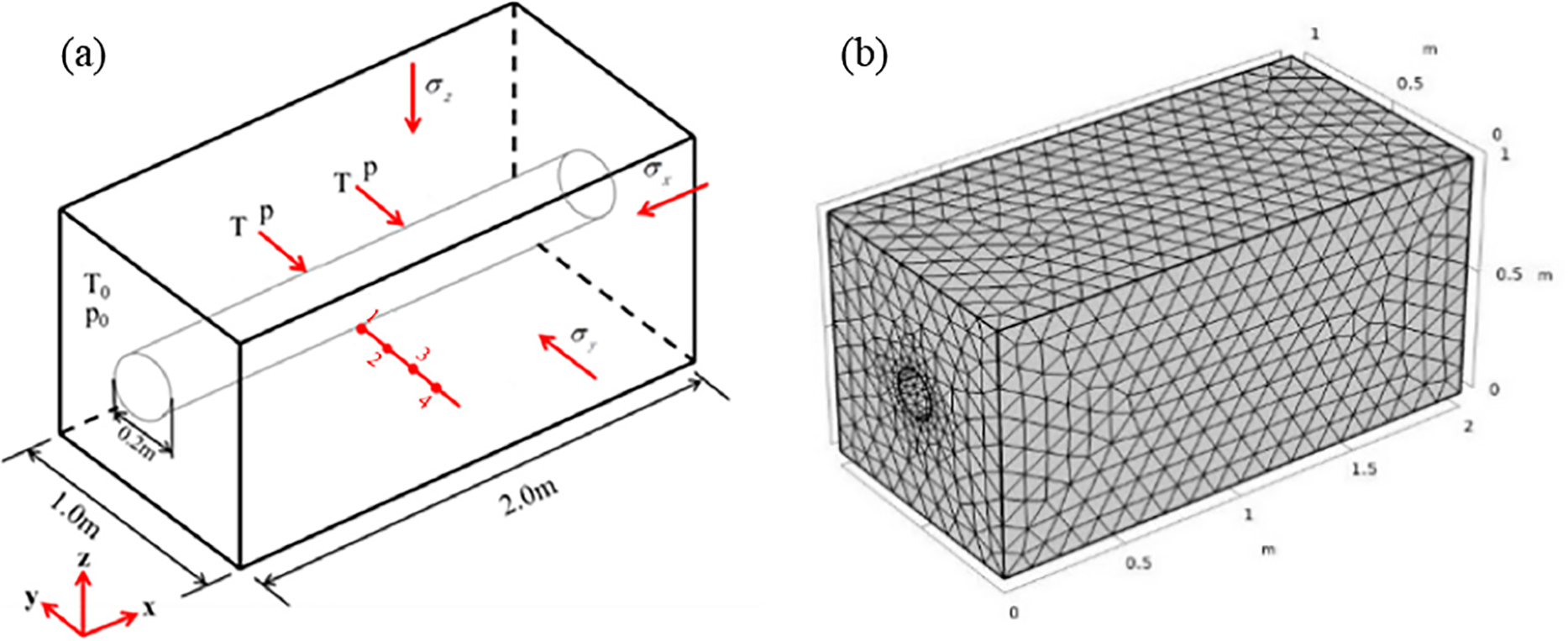
Figure 8: Geometric model and grid division of horizontal wells in tight reservoirs. (a) Geometric model of horizontal wells in tight reservoirs; (b) Grid division of horizontal wells in tight reservoirs

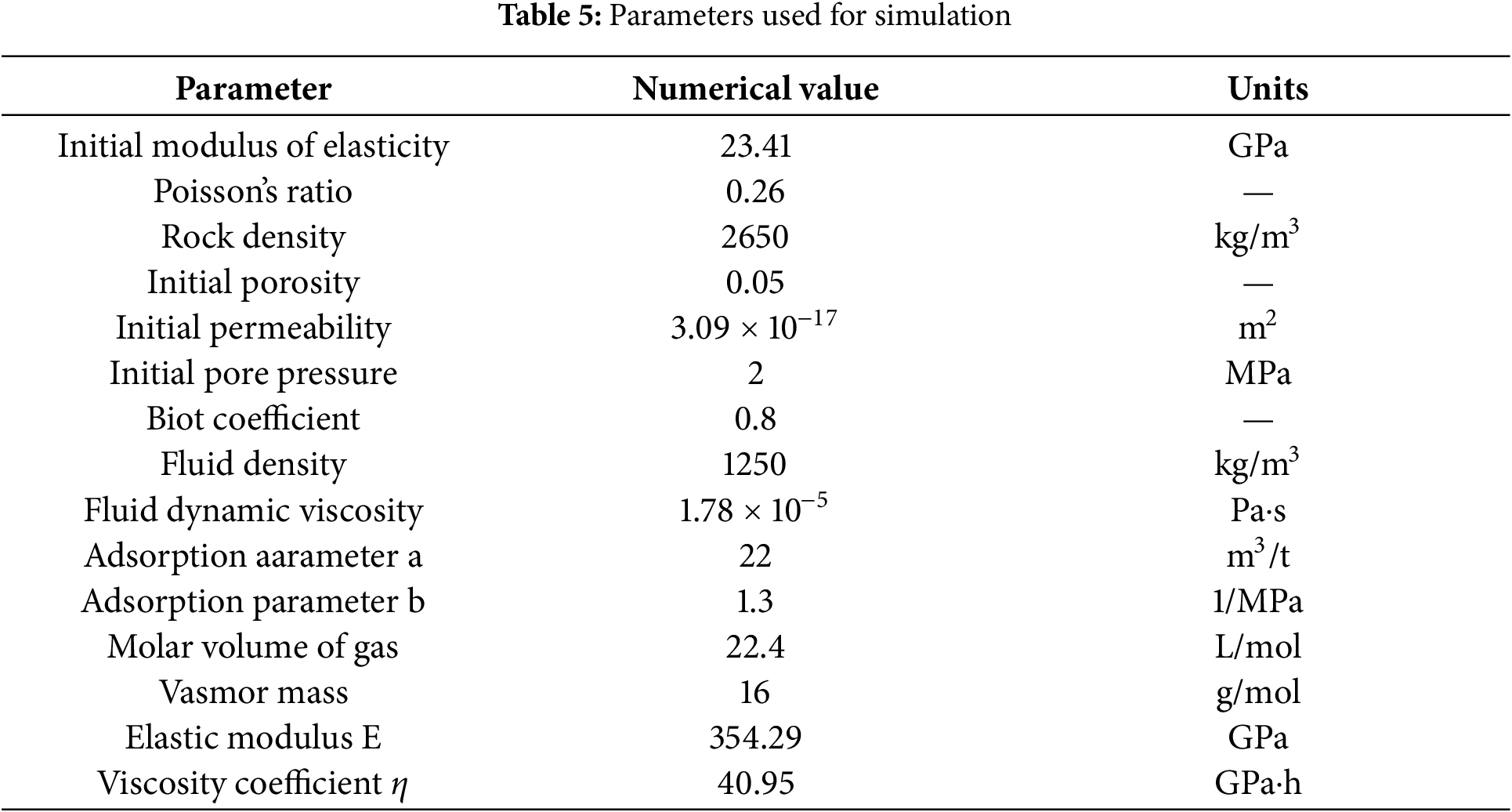
5.2.2 Parameter Settings and Measurement Point Layout

The initial conditions for the simulation are as follows: horizontal earth stresses σx = 15 MPa, σy = 25 MPa, vertical stress σz = 25 MPa, flow pressure p = 0.1 MPa, and fluid temperature T = 293.15 K. The relevant model parameters are provided in Table 5.

5.2.3 Variation Patterns of Volumetric Strain in Tight Reservoir Rocks

Four different in-situ stress conditions were set for the numerical simulation study, with vertical stresses σz = 25, 30, 40, and 50 MPa. During the simulation, the flow pressure at the wellbore was kept constant at 0.1 MPa, and the fluid temperature was maintained at 323.15 K. The variation of strain with time at the four measurement points under these different conditions is recorded and shown in Fig. 9.

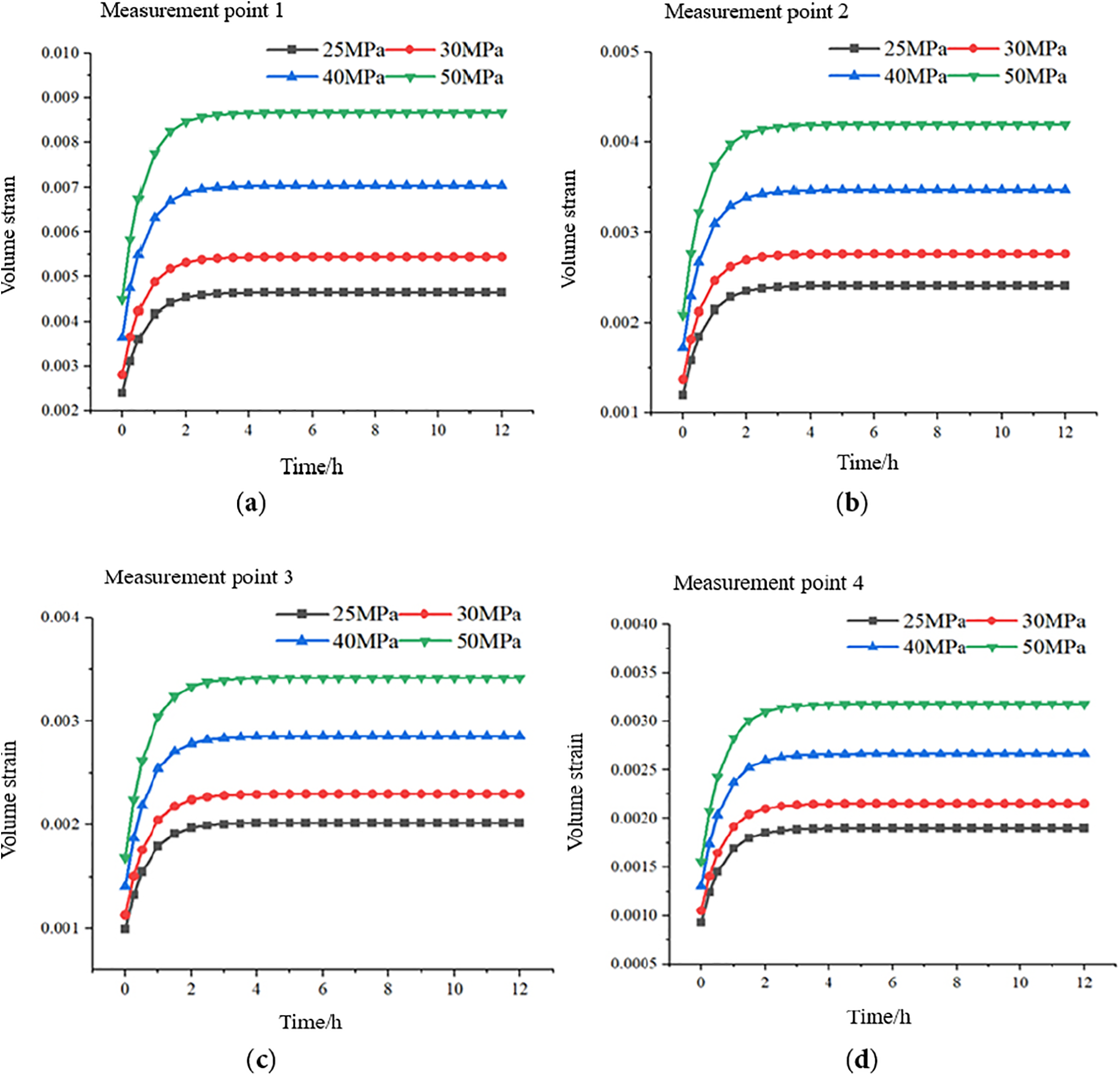
Figure 9: Strain-time curves of measured points under different ground stresses. (a) Strain-time curves of measuring point 1 under different ground stresses; (b) Strain-time curves of measuring point 2 under different ground stresses;(c) Strain-time curves of measuring point 3 under different ground stresses; (d) Strain-time curves of measuring point 4 under different ground stresses

Fig. 9 illustrates the time-dependent volumetric strain at the four measurement points within the reservoir. The absolute value of strain increases rapidly during the initial creep phase, then gradually increases at a slower rate. After approximately 4 h, the strain stabilizes. Analyzing the strain behavior at Measurement Point 1 under the four vertical stress conditions, when the vertical stress is 25 MPa, the stable strain is 0.0046; at 30 MPa, the stable strain is 0.0054; at 40 MPa, the stable strain is 0.0071; and at 50 MPa, the stable strain is 0.0087. The strain value increases as the in-situ stress increases. This is because, with the flow pressure and temperature remaining constant, the effective stress on the sample increases as the in-situ stress rises, ultimately leading to a larger strain value. When the vertical stress is 25 MPa, the stable strains at Measurement Points 1, 2, 3, and 4 are 0.0046, 0.0024, 0.002, and 0.0019, respectively. The closer the measurement point is to the wellbore, the larger the volumetric strain.

Fig. 10 shows the variation curves of the initial volumetric strain of the rock at different measurement points with vertical stress. As the vertical stress increases, the initial volumetric strain at all four measurement points shows varying degrees of increase. This indicates that with the increase in reservoir depth, the greater stress accelerates the creep deformation of the rock, with the wellbore wall being the most significantly affected.

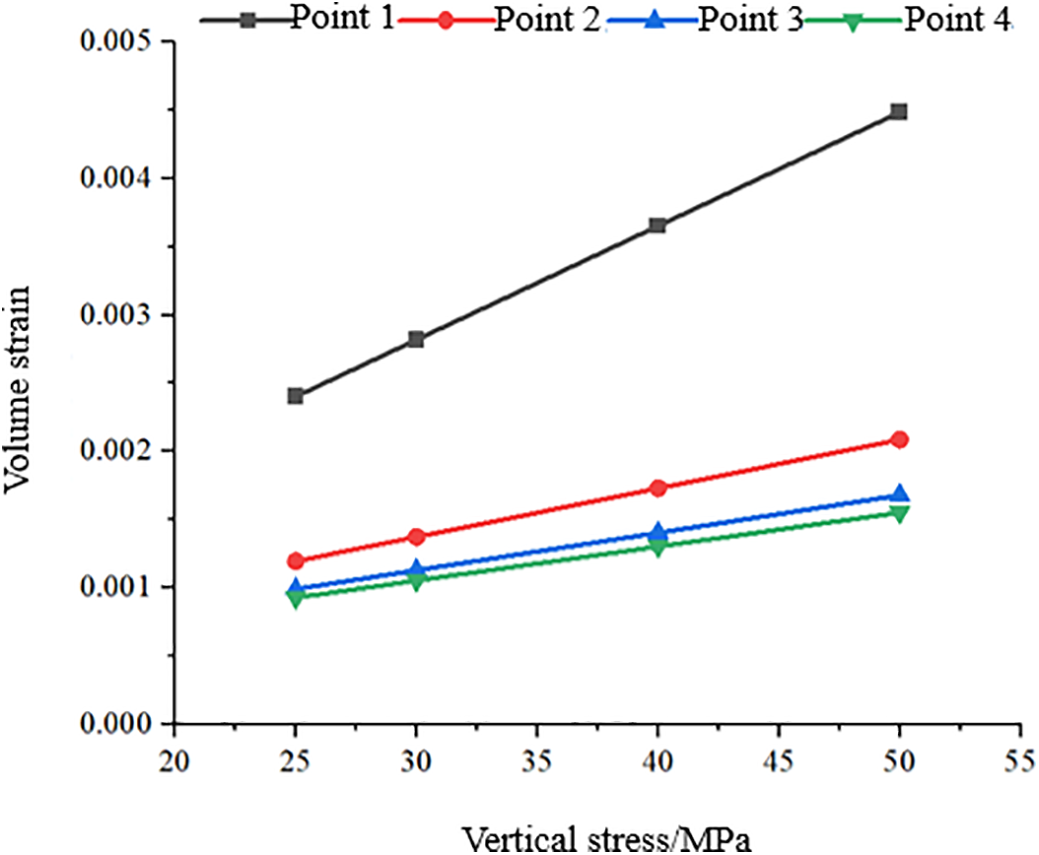
Figure 10: Initial volumetric strain of rock under different geostresses

5.2.4 Variation Patterns of Permeability in Tight Reservoirs

Fig. 11 shows the permeability of the tight reservoir under different vertical stress conditions. As the vertical stress increases, the permeability of the surrounding rock at the wellbore wall gradually increases. Additionally, the permeability is dependent on the distance from the wellbore: the closer to the wellbore, the higher the permeability. Fig. 12 illustrates the changes in the overall permeability of the model under vertical stresses of 25, 30, 40, and 50 MPa. From 0 to 4 h, the rock is in the initial creep stage, where the compression of rock fractures leads to a rapid decrease in porosity, which in turn causes a decrease in permeability. After 4 h, in the stable creep phase, the rock undergoes no further deformation, and the change in permeability gradually stabilizes. Comparing the permeability values at the same time point reveals that, as the vertical stress increases, the permeability gradually decreases.

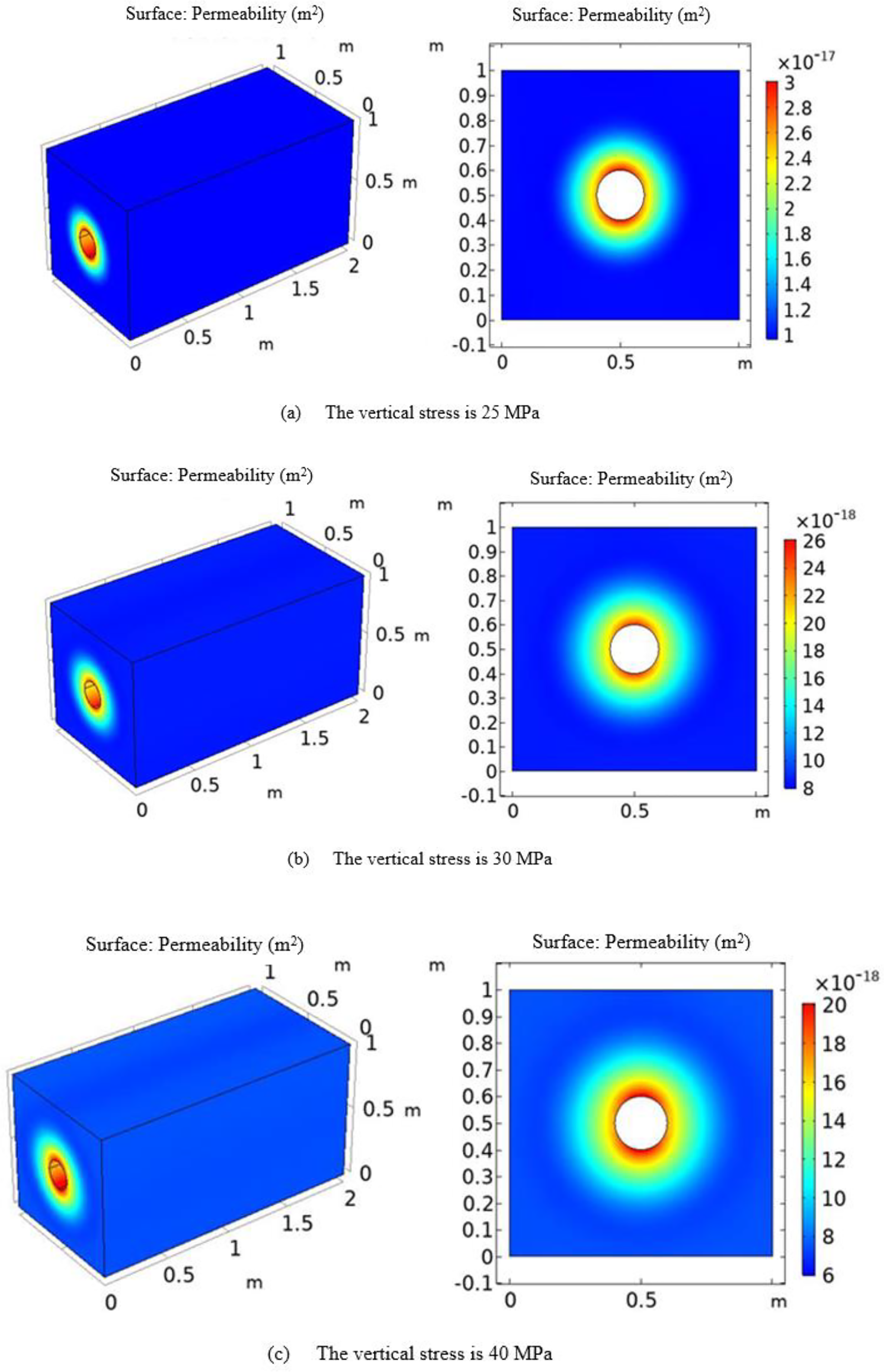
Figure 11: Modeled permeability distribution under different ground stresses

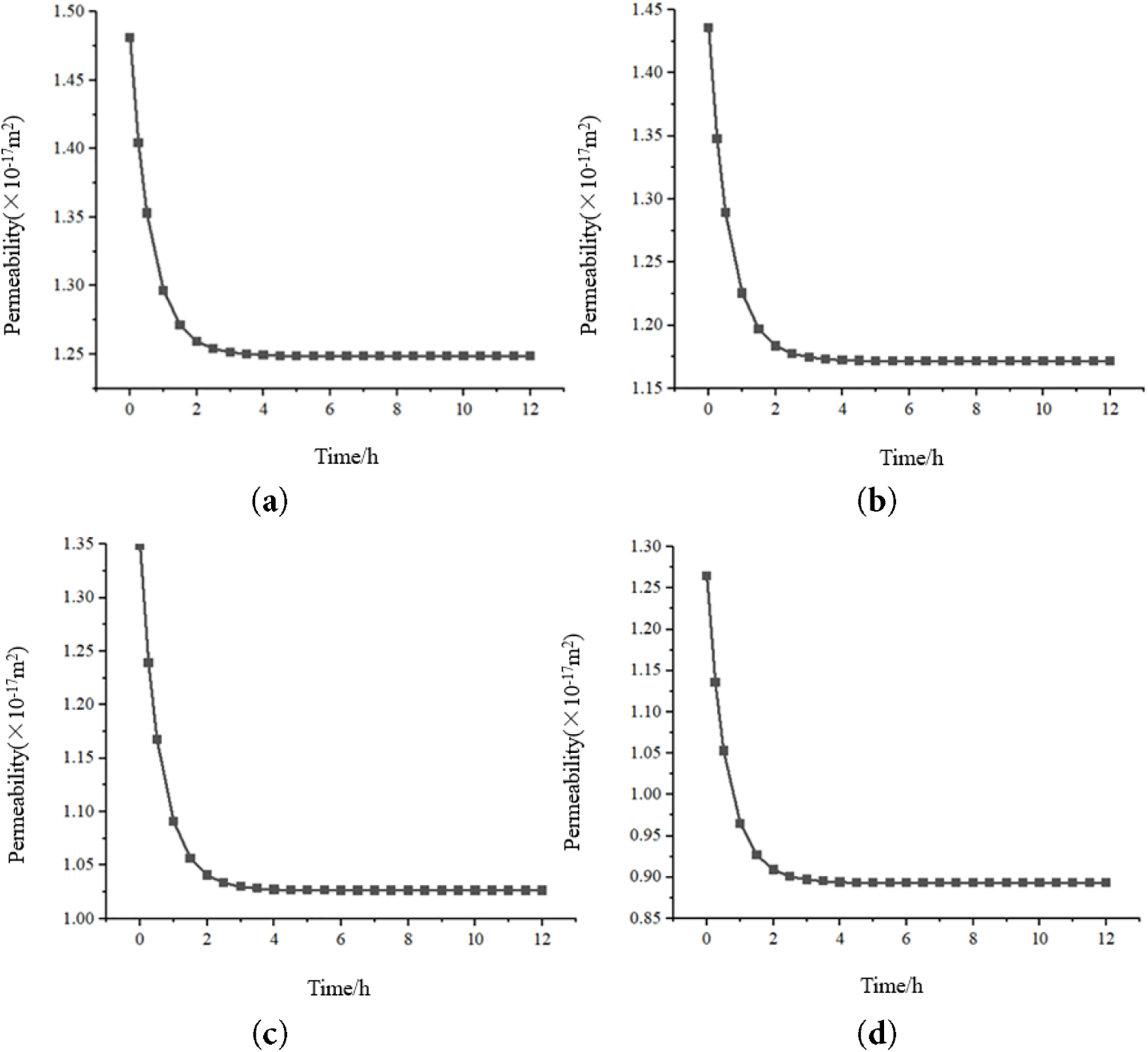
Figure 12: Changing law of permeability with time under different geostresses. (a) The vertical stress is 25 MPa; (b) The vertical stress is 30 MPa; (c) The vertical stress is 40 MPa; (d) The vertical stress is 50 MPa

From the comparison of Figs. 9–12, it can be observed that the changes in permeability during the creep process of the tight reservoir under different in-situ stress conditions follow a similar pattern to that of volumetric strain: From 0 to 4 h, the reservoir is in the decelerating creep phase, where the volumetric strain increases rapidly. Permeability and porosity decrease sharply, as the rock skeleton continues to compress, causing a rapid reduction in porosity and consequently a decrease in permeability. From 4 to 12 h, the reservoir enters the stable creep phase. During this phase, the pores and fractures within the rock are further compressed, and the change in permeability slows down until it stabilizes.

Our study developed a coupled flow-creep control equation to account for the effects of creep on tight reservoir permeability. Similarly, the 2025 study by Yang et al. established a fluid—solid coupling model using a digital core of tight sandstone, which was built using Computed Tomography (CT) scanning [24]. Both studies emphasize the significance of fluid—solid coupling in understanding the seepage behavior of tight reservoirs. However, our model focuses on the time—dependent deformation due to creep, while the 2025 study emphasizes the micro—scale seepage characteristics.

Our findings reveal that permeability and porosity decrease significantly during the decelerating creep phase, resulting in a sharp decline in reservoir productivity. Yang et al. [24] similarly observed that permeability decreases with increasing confining pressure, following a first-order exponential function.

This aligns with our results, reinforcing the critical influence of reservoir rock mechanics on permeability and porosity.

The models and findings from our research have significant implications for the economic and operational aspects of tight reservoir development. A deeper understanding of seepage behavior and creep effects allows for optimized reservoir management strategies, ultimately enhancing recovery efficiency and improving the economic feasibility of deep tight reservoirs. Furthermore, Zhao et al. (2023) highlight the importance of accurate permeability prediction in boosting oil production, further validating the practical applications of our research [25].

A comprehensive sensitivity analysis was conducted to evaluate the impact of key parameters, including creep coefficients, stress levels, and fluid properties, on the seepage behavior of deep tight reservoirs. The analysis revealed that higher creep coefficients lead to increased deformation and stress relaxation, enhancing the seepage rate by creating additional pathways, while lower coefficients result in reduced deformation and a lower seepage rate due to a more rigid rock structure. Stress levels were found to significantly affect permeability, with higher stress reducing permeability and seepage rates, and lower stress increasing permeability and enhancing seepage. Fluid properties, such as viscosity and density, also play a crucial role, where higher viscosity reduces seepage rates due to increased flow resistance, and lower viscosity enhances seepage by allowing easier fluid flow. Higher fluid density can increase buoyancy effects, which may either enhance or reduce seepage depending on specific conditions, while lower density results in reduced buoyancy and more uniform seepage. The combined effects of these parameters were analyzed, showing that the model is most sensitive to creep coefficients, followed by stress levels and fluid properties, confirming the robustness of the model across a range of parameter values. These findings provide practical insights for optimizing fluid injection and production strategies, adjusting stress levels to control permeability, and accurately determining creep coefficients to improve model reliability, ultimately guiding reservoir management decisions to enhance production efficiency and reservoir performance.

6  Conclusion

(1)   Triaxial compression tests showed the stress-strain curve has four stages: crack compression, linear deformation, delayed elastic deformation, and yield deformation. Peak stress and elastic modulus generally rise with confining pressure, but fractures or uneven mineral distribution can cause exceptions.

(2)   A Burgers creep model for tight reservoirs was created, along with a coupled flow-creep control equation to consider creep effects on permeability.

(3)   Volumetric strain in the reservoir increases rapidly initially, then slows, stabilizing after about 4 h. Deeper reservoirs experience faster creep deformation, especially around the wellbore wall.

(4)   Creep significantly affects tight reservoir permeability. During the decelerating creep phase, rapid volumetric strain increases lead to sharp declines in permeability and porosity. In the stable creep phase, further pore and fracture compression gradually reduces permeability until it stabilizes.

This study comprehensively investigates the seepage characteristics of deep tight reservoirs, with a particular focus on the significant impacts of creep. The innovative aspects of this research are highlighted in three key areas. First, we have developed an innovative mathematical model that precisely describes the complex seepage behavior under creep conditions. This model comprehensively considers various factors, including the mechanical properties of reservoir rocks, fluid flow dynamics, and time-dependent deformation. Second, extensive experimental and numerical simulations have been conducted to validate the proposed model. The results demonstrate that our model can effectively predict seepage behavior and provide valuable insights into reservoir performance. Third, we have proposed novel methods for optimizing production strategies of deep tight reservoirs based on the seepage characteristics and creep effects. These methods are expected to enhance the recovery efficiency and economic benefits of such reservoirs. In summary, this paper addresses the existing research gap in the seepage characteristics of deep tight reservoirs and provides a robust theoretical foundation and practical guidance for their development.

Acknowledgement: The authors received funding from the National Natural Science Foundation of China, the Re-search Fund of PetroChina Tarim Oilfield Company, and the Research Fund of China National Petroleum Corporation Limited. We gratefully acknowledge these contributions.

Funding Statement: This work was financially supported by the National Natural Science Foundation of China (Grant Nos. 42472195 and 42272153), the Research Fund of PetroChina Tarim Oilfield Company (Grant No. 671023060003) and Technology Projects of China National Petroleum Corporation (Grant No. 2023ZZ16YJ02).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jing Li, Yongfu Liu; data collection: Haitao Zhao, Xingliang Deng; model construction and calculation: Xingliang Deng, Chengqiang Yang; analysis and interpretation of results: Jing Li, Guipeng Huang; draft manuscript preparation: Chengqiang Yang, Baozhu Guan; manuscript revision: Jing Li, Yongfu Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting the conclusions of this study can be obtained from the corresponding authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zou CN, Yang Z, Zhu RK, Zhang GS, Hou LH, Wu ST, et al. Progress in China's unconventional oil & gas exploration and development and theoretical technologies. Acta Geol Sin. 2015;89(3):979–1007. doi:10.1111/1755-6724.12491. [Google Scholar] [CrossRef]

2. He ZL, Ma YS, Zhu DY, Duan TZ, Geng JH, Zhang JT, et al. Theoretical and technological progress and research direction of deep and ultra-deep carbonate reservoirs. Oil Gas Geol. 2021;42(3):533–46. doi:10.11743/ogg20210301. [Google Scholar] [CrossRef]

3. Deziel NC, Brokovich E, Grotto I, Clark CJ, Itzhaki ZB, Broday D, et al. Unconventional oil and gas development and health outcomes: a scoping review of the epidemiological research. Environ Res. 2020;182:109124. doi:10.1016/j.envres.2020.109124. [Google Scholar] [PubMed] [CrossRef]

4. Lei Q, Xu Y, Yang ZW, Cai B, Wang X, Zhou L, et al. Progress and development directions of stimulation techniques for ultra-deep oil and gas reservoirs. Pet Explor Dev. 2021;48(1):221–31. doi:10.1016/S1876-3804(21)60018-6. [Google Scholar] [CrossRef]

5. Deziel NC, Clark CJ, Casey JA, Bell ML, Plata DL, Saiers JE. Assessing exposure to unconventional oil and gas development: strengths, challenges, and implications for epidemiologic research. Curr Envir Health Rpt. 2022;9(3):436–50. doi:10.1007/s40572-022-00358-4. [Google Scholar] [PubMed] [CrossRef]

6. Selvadurai APS, Zhang DJ, Kang YL. Permeability evolution in natural fractures and their potential influence on loss of productivity in ultra-deep gas reservoirs of the Tarim Basin. China J Nat Gas Sci Eng. 2018;58(1892):162–77. doi:10.1016/j.jngse.2018.07.026. [Google Scholar] [CrossRef]

7. Xie YT, Li J, Liu HM, Zhang KH, Li JL, Li CH, et al. Study on hydro-mechanical-damage coupling seepage in digital shale cores: a case study of shale in Bohai Bay Basin. Energy. 2023;268(9):126759. doi:10.1016/J.ENERGY.2023.126759. [Google Scholar] [CrossRef]

8. Bowden RK, Curran JH. Time-dependent behavior of joints in shale. In: 25th U.S. Symposium on Rock Mechanics (USRMS); 1984 Jun 20–23; Evanston, IL, USA. [Google Scholar]

9. Zvonko T. Rheological model of soft rock creep based on the tests on marl. Mech Time-Depend Mater. 2006;10(2):317–35. doi:10.1007/s11043-006-9005-2. [Google Scholar] [CrossRef]

10. Karev VI, Kilmov DM, Kovalenko YF, Ustinov KB. Experimental study of rock creep under true triaxial loading. Mech Solids. 2019;54(8):44–63. doi:10.3103/S0025654419080041. [Google Scholar] [CrossRef]

11. Wang W, Duan XL, Jia Y, Cao YJ, Zhu QZ, Liu SF. Deformation characteristics, gas permeability and energy evolution of low-permeability sandstone under cyclic loading and unloading path. Bull Eng Geol Env. 2022;81(9):369. doi:10.1007/s10064-022-02858-x. [Google Scholar] [CrossRef]

12. Liang C, Liu J, Yang JX, Yang HN, Chen ZW, Ran L. A creep model for ultra-deep salt rock considering thermal-mechanical damage under triaxial stress conditions. J Rock Mech Geotech Eng. 2024;16(2):588–96. doi:10.1016/j.jrmge.2023.06.009. [Google Scholar] [CrossRef]

13. Qiao LP, Wang ZC, Liu J, Wei L. Internal state variable creep constitutive model for the rock creep behavior. Bull Eng Geol Env. 2022;81(11):456. doi:10.1007/s10064-022-02921-7. [Google Scholar] [CrossRef]

14. Li X, Ban L, Qi C. Study on the mechanical model of macro-mecro creep under high seepage pressure in brittle rocks. Rock Soil Mech. 2020;41(12):3987–95. doi:10.16285/j.rsm.2020.0453. [Google Scholar] [CrossRef]

15. Lei G, Shen ZZ, Xiao M. Experimental investigation of seepage characteristics in porous rocks with a single fracture. Hydrogeol J. 2020;28(8):2933–46. doi:10.1007/s10040-020-02224-9. [Google Scholar] [CrossRef]

16. Xu ZH, Zhong XP, Zhang SL, Wang YF, Liu KY, Liu X, et al. Experimental study on mechanical damage and creep characteristics of Gonghe granite under real-time high temperature. Geothermics. 2024;123(9):103100. doi:10.1016/j.geothermics.2024.103100. [Google Scholar] [CrossRef]

17. Cao P, Wen YD, Wang YX, Yuan HP, Yuan BX. Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ Earth Sci. 2016;75(10):900. doi:10.1007/s12665-016-5699-x. [Google Scholar] [CrossRef]

18. Xu P, Yu B. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry. Adv Water Resour. 2008;31(1):74–81. doi:10.1016/j.advwatres.2007.06.003. [Google Scholar] [CrossRef]

19. Wang L. Modeling approach to creep-seepage-temperature coupling in deep coal. Beijing, China: China University of Minning & Technology-Beijing; 2020. [Google Scholar]

20. Ivins ER, Caron L, Adhikari S, Larour E. Notes on a compressible extended Burgers model of rheology. Geophy J Int. 2022 Mar;228(3):1975–91. doi:10.1093/gji/ggab452. [Google Scholar] [CrossRef]

21. Li XM, Wang MW, Shen FQ. A three-dimensional nonlinear rock damage creep model with double damage factors and residual strength. Nat Hazards. 2023;115(3):2205–22. doi:10.1007/s11069-022-05634-y. [Google Scholar] [CrossRef]

22. Wei J, Wang YY, Qi J, Li JG. Mathematical model of seepage in porous medium on account of solid-fluid coupling and creep effect. J Liaoning Tech Univ Nat Sci. 2011;30(5):726–9. [Google Scholar]

23. Liu C, Qu XF, Li J, Xie YT, Zhang JT. Creep experiment and model study of tight sandstone. J Exp Mech. 2020;35(6):1023–9. doi:10.7520/1001-4888-19-166. [Google Scholar] [CrossRef]

24. Yang H, Cai Z, Zhang H, Sun C, Li J, Meng X, et al. Study on the fluid-solid coupling seepage of the deep tight reservoir based on 3D digital core modeling. Energy Eng. 2025;122(2):537–60. doi:10.32604/ee.2024.058747. [Google Scholar] [CrossRef]

25. Zhao XY, Li MF, Yan K, Yin L. Revolutionizing tight reservoir production: a novel dual-medium unsteady seepage model for optimizing volumetrically fractured horizontal wells. Energy Eng. 2023;120(12):2933–49. doi:10.32604/ee.2023.041580. [Google Scholar] [CrossRef]