Smart Grid Peak Shaving with Energy Storage: Integrated Load Forecasting and Cost-Benefit Optimization

1  Introduction

The rapid development of science and technology, coupled with societal progress, has led to a significant increase in global electricity demand. However, traditional thermal power generation remains a dominant yet environmentally detrimental energy source. Meanwhile, challenges such as the COVID-19 pandemic in 2019, evolving international political-economic dynamics, and domestic requirements for economic transformation toward high-quality development further complicate energy planning. During China’s 14th Five-Year Plan period, electricity consumption is projected to grow steadily despite these complexities [1]. In addition, electric cars have become increasingly popular in recent years. The grid connection of electric vehicles increases the pressure on the power grid [2]. As can be seen, the growing burden on the power system’s electrical output has led to a widening gap between supply and demand [3].

The energy storage system can be used for power peaking, avoiding the cost of waste caused by installing generator sets to meet the peak load. The energy storage system can fully utilize the power at the trough of the bag to provide a short-time power supply in the face of unexpected situations, reducing the pressure of grid operation [4]. Therefore, the excellent configuration of the capacity of the energy storage system is a current issue that needs to be studied urgently.

The literature [5] proposed a multi-scenario cost optimization modeling approach to address energy storage configuration challenges in Indonesia’s national grid for achieving the 100% renewable energy target. By developing an integrated optimization framework encompassing power supply-demand dynamics, transmission networks, renewable energy sources, and multi-configuration energy storage systems, it resolves critical issues in balancing temporal variability and spatial distribution of renewable generation at scale. The literature [6] proposed a two-stage optimization method that considers the application of demand response and energy storage, and the combination of these two methods effectively reduces the impact of source load bias. The study also achieves optimal scheduling by optimizing the purchase and sale price of energy. The literature [7] proposed an optimal allocation method for energy storage systems based on economic optimality. The method calculates the energy storage capacity configuration to maximize net present value by analyzing the operation status of photovoltaic power plants and wind farms and using the time-by-time data of solar and wind energy resources, the unit cost of the energy storage system, charging and discharging efficiency, operation cost, electricity selling price and the number of years of operation of the energy storage system as the boundary conditions, but if the electricity price subsidy is given with the wind farm supporting the construction of energy storage system or with the participation of energy storage system in frequency regulation. If issued following the feed-in tariff accounting of the energy storage system, it will be able to improve the economics of the energy storage system. The literature [8] considered the depletion of global fossil-fuel-based energy resources and the impending energy crisis, proposing energy management strategies to optimize power production and consumption methods and solutions to enhance the reliability of electrical power systems, addressing the limitations of previous approaches. At this stage, domestic and foreign research on power load forecasting technology has been relatively mature, classical predicting methods have the advantages of simple calculation and high reliability, but the predicting accuracy and the use of predicting range are always limited [9]. As the power industry continues to develop, the demand for predicting accuracy is increasing, which requires the improvement or use of entirely new predicting methods that significantly improve predicting accuracy and extend the range of predicting applications with an appropriate increase in computational effort [10].

The literature [11] proposed an improved sparrow search algorithm optimized BP neural network for the short-term load predicting model, improved the foraging behavior of the finder in the sparrow search algorithm from jumping to moving, optimized the initial weights and thresholds of the BP neural network, and verified the accuracy of the predicting model with the electricity load data of a particular place, compared with the standard sparrow search algorithm optimized BP neural network, the improved sparrow algorithm optimized BP. The average error of the prediction model of the enhanced sparrow algorithm optimized BP neural network was reduced by 4.80% compared with the standard sparrow search algorithm optimized BP neural network. However, prediction accuracy is difficult to guarantee by using a single prediction method, and there is still much room for improvement in prediction accuracy and stability. The literature [12] proposed a stacking integration algorithm of CNN, BiLSTM, Attention Mechanism, and XGBoost to address the limitations of traditional short-term load forecasting methods in capturing long-term dependencies and deep-seated features in unknown datasets, thereby improving their generalization ability. The literature [13] uses a combination of the traditional grey GM(1,1) model and a time series approach, first fitting the non-linear growth trend of the electrical load with a grey model, then characterizing the seasonality and periodicity in the load change with a time series model, the two algorithms combining to compensate for the shortcomings of the individual algorithms, and finally correcting the predict results using Markov chains. The method requires only a small amount of data to predict electrical loads, but the accuracy is not high.

Although current electricity load prediction is relatively mature, various methods have drawbacks. A combined predicting model that combines different models is needed to accurately predict complex electricity load data.

In this paper, the application of power load forecasting technology to the capacity allocation of energy storage power stations is discussed. We combine grey model forecasting, optimal BP neural network forecasting, and multiple linear regression forecasting to establish a reliable and reasonable grey regression neural network power load forecasting model. To further enhance the prediction accuracy, we introduce the Informer model, which integrates with the grey regression neural network model using a stacking strategy, forming a new combined prediction model. By obtaining load prediction curves, we are able to identify electricity consumption peaks and valleys. The objective of this study is to reduce the difference between peak and valley loads, alleviate pressure on the power grid, and enhance economic returns. The overall research framework is illustrated in Fig. 1.

Figure 1: Overall research roadmap

2  Methods

2.1 Electricity Load Predicting the Technology

This paper uses the grey predicting model, optimized BP neural network predicting model, and multiple linear Regression predicting models to obtain optimal results by taking the strengths and weaknesses of various predicting models and determining the weights of each single predicting model using the inverse variance method.

2.1.1 Grey Prediction Model

The grey prediction model is simple, fast, and efficient. It does not require the sample data to satisfy the normal distribution and independence assumptions, nor does it require a large amount of data and a linear relationship between variables, suitable for various types of data. The modeling mechanism of grey models is one of the leading research elements of grey systems theory [14]. The grey prediction model was constructed in the following steps: firstly, the original data were generated cumulatively to weaken the randomness of the data; secondly, a first-order differential equation model was established for the cumulatively generated series; finally, the relevant parameters in the first-order differential equation model were estimated using the least squares method to obtain the specific formula for the GM(1,1) prediction model.

The grey prediction model obtained by simplification is as follows:

xa(k+1)=[xa(1)−u^a^]e−a^k+u^a^(1)

In addition, to improve the prediction accuracy of the grey model, this paper transforms the original series before cumulative generation. It changes the original series into a steadily growing series in an exponential form whenever possible. The original series is assumed to be X={x1,x2,…,xn} and is then modified by adding policy factors to the original series. The expression of the conversion sequence is Xz={x1z,x2z,…,xnz}, as shown in the equation:

xiz=1n−i+1(xi+xi+1+…+xn)(2)

2.1.2 ICS-BP Neural Network Prediction Model

Back Propagation (BP) Neural network is a machine learning method, which trains sample data sets to build a model, enabling it to learn and adapt to data rules, can deal with complex problems with nonlinear relationships and adapt to multiple data types.

The CS algorithm has the advantage of improving the local and global search of the algorithm, etc. To enhance the dependence of the BP neural network on the initial weights and thresholds [15]. By applying the CS algorithm to BP neural networks, the initial network weights and points are searched for before the network is trained, and the optimal solution is then assigned to the web for training, which can effectively avoid the problem of BP neural networks falling into local minima due to the initial weights and thresholds, and improve the convergence speed of BP neural networks [16].

In order to improve the performance of the CS algorithm, this paper improves the CS algorithm and proposes an improved cuckoo ICS optimization algorithm. In this paper, the fixed-value Pa in the algorithm is improved by using a random discovery probability instead of a fixed discovery probability so that smaller random probabilities and larger random probabilities occur randomly, thus balancing the algorithm’s ability of global search and local development, improving the convergence speed of the algorithm, and increasing the population diversity.

The improved formulae are shown as follows:

Pr=Pamin+(Pamax−Pamin)×rand×τ(1,2)×k(3)

Pr∈[0.15,0.55](4)

where Pr is the random probability, Pamin and Pamax are the maximum and minimum values of Pa respect, rand is a random number in the range (0,1), τ(1,2) is a gamma-distributed random number obeying a shape parameter of 1 and a scale parameter of 2, and k is used to control the degree of deviation between the inertia weights and the expected value.

Adding inertia weights to the path and position update formula of cuckoo nest finding to balance the relationship between global search and local search can make the algorithm have strong global search capability in the early stage while having strong local exploitation capability in the later stage, improving the convergence speed and merit finding accuracy of the algorithm:

Xi(t+1)=ω(t)Xi(t)+a⊕Levy(λ),i=1,2,…,n(5)

ω(t)=rmax−η×(rmax−rmin)×logTmaxt−φ×β(6)

where t is the current number of iterations; Tmax is the maximum number of iterations; rmin and rmax are the minimum and maximum values of the inertia weights, respectively; η is the log deviation factor; φ is the inertia adjustment factor, and β is the random number of asymmetric distributions between (0,1) generated by the beta distribution.

2.1.3 Multiple Linear Regression Predicting

Multiple linear Regression predicting is a popular and intuitive among many predicting methods. The key to using multiple linear regression predicting is to determine the multiple linear regression equation [17]. When the prediction object y is influenced by more than one factor x1,x2,…,xm, if the correlation between each influencing factor xj(j=1,2,…,m) and y can be approximated linearly, then the prediction can be analyzed by establishing a multiple linear regression model, the general form of the multiple linear regression model is shown in the following equation:

y0=b0+b1x1i+b2x2i+…+bmxmi+εi(i=1,2,…,n)(7)

εi=yi−y^i(i=1,2,…,n)(8)

where bj(j=1,2,…,m) denotes the model regression coefficient; εi denotes the random variable generated by yi in addition to the effect of the independent variable xj(j=1,2,…,m), called the random error.

2.1.4 Grey Regression Neural Network Prediction (GRNN)

This paper combines grey predicting with neural networks, making reasonable use of the ability of artificial neural networks to approximate arbitrary functions and the ability of grey predicting methods to predict the overall trend of electricity load changes. Regression predicting combines time series and Regression predicting to enhance predicting accuracy. A combination of multiple load-predicting models was used to obtain a prediction result with the lowest root mean square error.

This paper uses the inverse of the variance method to assign greater weights to the more accurate prediction values. The weighted average value is the final value to improve the prediction results. Take the three predicting methods selected in this paper as an example. The expressions for calculating the weight wi are derived as follows:

wi=ei−1∑i=1mei−1(9)

f1, f2, f3 do the three predicting methods obtain the predicted values, respectively, w1, w2 and w3 are the weighting coefficients, and w1+w2+w3=1. fc is the weighted average, e1, e2, e3 and ec denote the squared prediction error corresponding to f1, f2, f3 and fc. The specific expression is shown in the following equation:

fc=w1f1+w2f2+w3f3(10)

ec=w1e1+w2e2+w3e3(11)

ei=(y−y^i)2(12)

The grey regression neural network prediction process used in this paper is shown in Fig. 2.

Figure 2: Flow chart of the technical route for electricity load predicting

2.1.5 Informer-Grey Regression Neural Network Prediction (IGRNN)

To further improve the prediction accuracy, this paper also introduces the Informer model, which adopts a stacking strategy and fuses it with the grey regression neural network model to form a new combined prediction model. The Informer model is a sequence prediction model based on the self-attention mechanism [18]. It is mainly used in time series prediction and natural language processing tasks. The model is an extension and improvement of the Transformer model, allowing it to capture long-distance dependency information in the time series through the multi-layer self-attention mechanism and improve the prediction accuracy [19].

The key feature of the Informer model is the introduction of a new attention mechanism called the Globally Attentive Temporal Mechanism (GATM), which uses the Globally Attentive Temporal LSTM [20]. Unlike the traditional self-attention mechanism, the Globally Attentive Temporal LSTM computes the attention of the entire historical sequence at each time step, thus capturing the global dependencies in the sequence more effectively [21]. Additionally, the Informer model incorporates a structure of Long Short-Term Memories (LSTMs) to extract long-term and short-term patterns in the sequence data. By utilizing both global attention and LSTMs in the model, the Informer model effectively models the multi-scale and multi-granularity features of time series data [22].

The stacking strategy utilizes a meta-machine learning model to combine different base learning models, aiming to enhance the overall accuracy of generalization [23]. The strategy involves combining multiple basic predictive models and learning their respective predictions to generate a final prediction. This is achieved by using a meta-model, often a simple linear model, to integrate these predictions [24]. By combining the strengths of different models, the stacking strategy enhances prediction accuracy, overcomes the limitations of individual models, and improves the generalization ability of the overall model [25].

2.2 Research on the Capacity Allocation of Photovoltaic Energy Storage Plants

In this paper, we find the peak and trough periods of electricity consumption through the prediction results, cut the mountains and fill the tracks through the power load curve of the PV storage power plant, and construct a capacity allocation model according to the effect of peak and trough cutting, the cost of the storage power plant and the failure rate of the storage battery, and use the multi-objective snake optimization algorithm to solve the model to get the optimal capacity allocation method, the capacity allocation method of the storage power plant is shown in Fig. 3.

Figure 3: Capacity allocation method diagram for energy storage plants

2.2.1 Modelling the Cost of Energy Storage Plants

The investment in energy storage plants and the extended operating period require consideration of the necessary costs for operation and maintenance, end-of-life recycling, etc., throughout the plant’s life cycle [26]. They established a cost model for energy storage plants and optimized the allocation of storage plants to maximize annual net returns.

(1)   Energy storage investment costs: the cost of energy storage is mainly used to purchase batteries and other equipment at the beginning of the project and requires a one-time investment in start-up capital, mainly for the purchase of battery capacity and battery power equipment required for energy storage power plants [27]. The formula for calculating the average annual investment cost of energy storage can be expressed as:

C1=α(r,Y)(CP×Pe+Ce×Ee)(13)

α(r,Y)=r(1+r)Y(1+r)Y−1(14)

where CP and Ce are the cost per unit of power and capacity of the energy storage plant, respectively, Pe and Ee are the power and ability of the energy storage plant, respectively, Y is the operational life of the energy storage, and r is the base discount rate. α(r,Y) It is the equal annual value of the capital regression coefficient and n is the entire life cycle of the investment project.

(2)   Operation and maintenance costs, in the whole life planning years of the investment of energy storage power plant, operation, and maintenance costs, are the costs invested in maintaining the safe and stable operation of the energy storage power plant during the life years, which generally include the costs of overhaul, maintenance, installation, labor, wear and tear and maintenance of energy storage equipment, etc. The specific costs are related to the power size and capacity of the energy storage power plant. The calculation formula is as follows:

C2=Ck×Pe+Cv×Ee(15)

where Ck and Cv are the unit price of operation and maintenance per unit of power and capacity of the energy storage plant, respectively, Pe and Ee are the power size and breadth of the energy storage plant, respectively.

(3)   Battery end-of-life cost refers to the cost of the harmless disposal of lithium iron phosphate batteries after the loss of lithium iron phosphate batteries to a limited value during the whole life cycle of the energy storage plant. The calculation formula is shown below:

C3=β(r,Y)EcPk(16)

β(r,Y)=(1+r)−Y(17)

where Pk is the cost per unit capacity of lithium battery at end-of-life, β(r,Y) is the capital discount factor, and Y is the energy storage’s operational life; is the battery capacity size.

(4)   Auxiliary equipment costs include the cost of purchasing cables, communication and networking control equipment, servers and other equipment, as well as the cost of purchasing lithium battery capacity, power components and inverter equipment for the energy storage plant [28]. The calculation formula is shown below:

C4=α(r,Y)CzEe(18)

where Cz represents the auxiliary cost per unit of lithium battery capacity.

Total Cost of Ownership Model:

C=∑i=1nCi(19)

2.2.2 Modelling the Failure Rate of Energy Storage Unit Batteries

Failure of energy storage can severely affect the capacity allocation of the storage device. If an energy storage device fails, greater storage capacity may be required to cope with unexpected situations or more extended periods of power supply. An energy storage failure may result in the energy storage station being unable to charge and discharge as planned, leading to an unstable energy supply. Additional energy storage capacity may be required to compensate for this instability to ensure a reliable supply. Energy storage failures may require higher maintenance and repair costs. If the capacity of the energy storage device is not configured correctly, it may result in increased time and resources required for maintenance and repair.

Battery failure rate refers to the ratio of failed cells to the total number of individual cells in a lithium iron phosphate energy storage cell during the evaluation period [29]. The calculation formula is as follows:

FR=ILBLB(20)

where FR is the rate of a cell failure, ILB is the number of cells that failed during the evaluation period, and LB is the total number of cells in the electric storage unit.

2.2.3 Modelling the Effects of Peak Shaving and Valley Filling

Battery storage power stations are used for peak and valley reduction so that they can be charged at low load times and discharged at peak load times, which not only effectively reduces the peak-to-valley difference between day and night, smoothes the load, relieves the peak load on the transmission and distribution line expansion requirements, but also allows for direct profits from “low storage and high generation” through the time-sharing tariff system [30]. Therefore, the capacity of energy storage plants can be configured by their peak-shaving effect on the load curve.

This paper constructs a model of the effect of peak shaving as shown below:

S=λ1Pmax−PminPmax×ω+λ21n∑i=1n(Pi−P¯)2(21)

where S is an evaluation indicator reflecting the effect of peak shaving, Pmax and Pmin are the peak and trough values of the load, respectively, Pi denotes the load value of the predicted data at the moment i, P¯ denotes the average value of the predicted load data, ω is the balance parameter, and λ1, λ2 are the weighting factors satisfying λ1+λ2=1.

2.3 Multi-Objective Optimization Algorithms

The Multi-Objective Snake Optimization (MOSO) algorithm is a multi-objective optimization approach extended from the single-objective Snake Optimization (SO) method. It draws inspiration from the behavioral patterns of snakes in natural environments. The algorithm mimics snakes’ responses to ambient temperature variations and their food-seeking patterns to achieve global optimization in multi-objective problems.

This paper uses the multi-objective snake optimization algorithm MOSO to solve the capacity allocation model, incorporating the idea of multi-objective optimization into the snake optimization algorithm [31].

The mathematical expression for the multi-objective optimization algorithm is shown below:

min/maxy=f(x)=(f1(x),f2(x),⋯,fM(x))(22)

st.{x=(x1,x2,⋯,xD)∈Xy=(y1,y2,⋯,yM)∈Y(23)

where x denotes the decision vector, X denotes the decision space, y denotes the target vector, Y denotes the target space, D denotes the decision variable and M denotes the target quantity.

The technical route of the capacity configuration of the energy storage power station proposed in this paper is shown in Fig. 4.

Figure 4: Technology roadmap for capacity configuration of energy storage plants

3  Analysis of Experimental Results

Fig. 5 shows the overall idea of this paper. In this paper, the power load data of a chemical park in the Jiangsu region for half a year is processed and analyzed. The chemical park has a maximum power load of more than 860 kW in six months, while the minimum power load is just under 650 kW, which will cause more significant pressure on the power grid. A suitable power load prediction model is established. The results of the power load prediction are used as the basis for the capacity configuration of the photovoltaic energy storage plant. The prediction curve is shaved to fill the valley, and the difference between the peak and the valley is reduced. The power load of the chemical park is controlled at about 800 kW, which improves the energy utilization rate and reduces the pressure of power grid operation.

Figure 5: Block diagram of the overall research idea

3.1 Data Preprocessing

The dataset for this paper is based on daily power load data from an industrial park in Jiangsu Province. After removing outliers, there are 937 power load data points in total. The dataset is divided into training and testing sets in a 3:7 ratio. The model’s initial weights are set within the interval [−1, 1], with five hidden layers. A metaheuristic algorithm is employed for 100 iterations to optimize the model’s hyperparameters. The error threshold is set to 1 × 10−6, and the learning rate is 0.01.

For visualization, the model is called M1, M2, M3, etc., as shown in Table 1.

3.2 Electricity Load Prediction Results

This paper uses root mean square error (RMSE), mean absolute error (MAE), and the coefficient of determination (R2) to comprehensively evaluate the prediction model’s performance. The formulas are as follows:

RMSE=1n∑i=1n(y^i−yi)2(24)

MAE=1n∑i=1n|y^i−yi|(25)

R2=1−∑i=1n(y^i−yi)2∑i=1n(y¯i−yi)2(26)

where y^i is the predicted value of the electrical load on day one, yi is the actual value of the electrical load on day one, y¯i is the average value of the electrical load, and n is the array amount of the test set.

The time series forecasting models have a standard approach of collecting historical data for predicting load [32]. In this study, the performance of several models for electricity load forecasting is compared, including LSTM, BiLSTM, CNN, and BP neural networks. The prediction results are shown in Fig. 6.

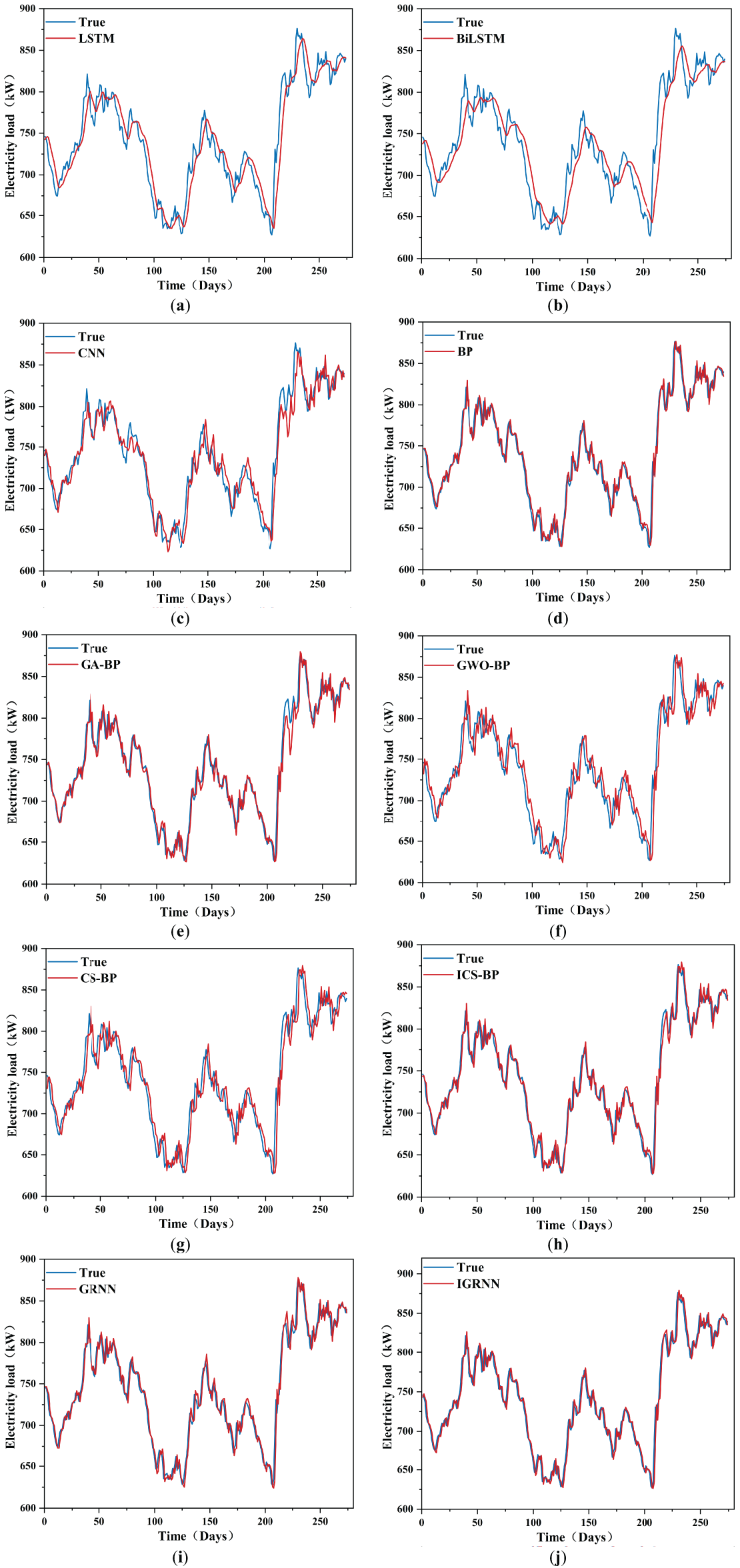
Figure 6: Prediction results of each model. (a) Prediction results of the LSTM model; (b) Prediction results of the BiLSTM model; (c) Prediction results of the CNN model; (d) Prediction results of the BP model; (e) Prediction results of the GA-BP model; (f) Prediction results of the GWO-BP model; (g) Prediction results of the CS-BP model; (h) Prediction results of the ICS-BP model; (i) Prediction results of the GRNN model; (j) Prediction results of the IGRNN model

Table 2 shows the comparison of the prediction error index of the proposed model and the control group model, and Fig. 7 shows the visualization of the table. The experimental results indicate that the BP neural network achieves the best performance with an RMSE of 11.7222, an R2 of 96.56%, and an MAE of 8.8685. Subsequently, the BP neural network is optimized using GA, GWO and CS algorithms. Among these optimization methods, the CS algorithm stands out and significantly improves the model’s performance, resulting in an RMSE of 11.5243, an R2 of 96.68%, and an MAE of 8.6829 for the CS-BP model. Further improvements are made by introducing the ICS algorithm, which enhances the CS algorithm and leads to an RMSE of 11.5119, an R2 of 96.69%, and an MAE of 8.6951 for the ICS-BP model. Finally, the Informer-grey regression neural network model is introduced, achieving an RMSE of 11.1361, an R2 of 96.90%, and an MAE of 8.264, further validating the effectiveness of the proposed model. These results demonstrate that the proposed model has high accuracy and stability in electricity load forecasting and can provide a reliable basis for capacity configuration of energy storage systems in smart grids.

Figure 7: Comparison table of each index. (a) Comparison table of RMSE; (b) Comparison table of R2; (c) Comparison table of MAE

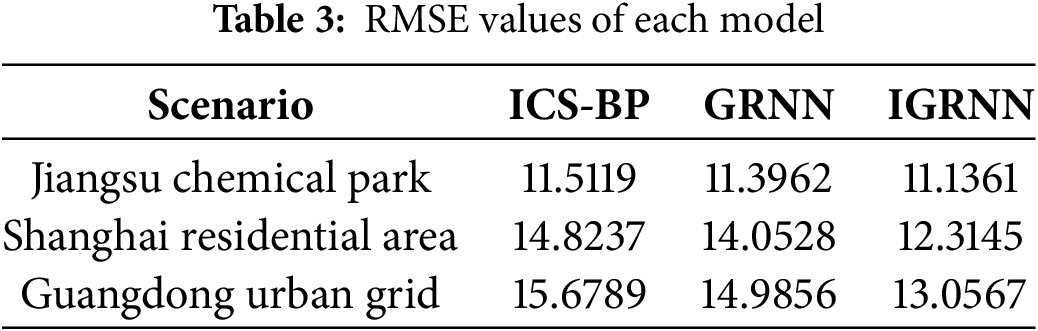
To evaluate the robustness of our methodology across diverse contexts, we conducted additional experiments on two distinct datasets: residential load data from a Shanghai community (2023) with distinct daily patterns, and urban grid data from a Guangdong mixed-use grid (2023) with high renewable penetration.

As shown in Table 3, the comparative analysis of three scenario datasets reveals the significant advantages of the IGRNN model. In three typical application scenarios—Jiangsu Chemical Park, Shanghai Residential Area, and Guangdong Urban Grid—the IGRNN achieves RMSE values of 11.1361, 12.3145, and 13.0567, respectively. Compared to the ICS-BP model, it reduces errors by 3.3%, 16.9%, and 16.7%, while achieving error reductions of 2.3%, 12.4%, and 12.9% compared to the GRNN model. These results demonstrate that the model effectively enhances prediction accuracy and scenario generalization performance.

3.3 Capacity Allocation Results for Energy Storage Plants

As shown in Fig. 8, the capacity allocation model constructed in this paper was used to experiment with more than 1000 historical data from a chemical park in the Jiangsu region, and the effect of peak shaving was apparent, with the load data fluctuating around 800 kW every day, which showed that the power load curve rose rapidly from 840.625 to 1169.5125 kW between the 410th and 478th days; and then fell from 1169.5125 to 879.675 kW between the 478th and Such a drastic change in load has increased the burden on the grid to a large extent. By optimizing the configuration of the storage plant to participate in peak regulation, the bag is kept between 752.775 and 898.7125 kW from day 400 to day 500, with the difference between peak and valley reduced from 321.2125 to 145.9875 kW, which has a significant effect on the load curve and effectively reduces the pressure on the grid.

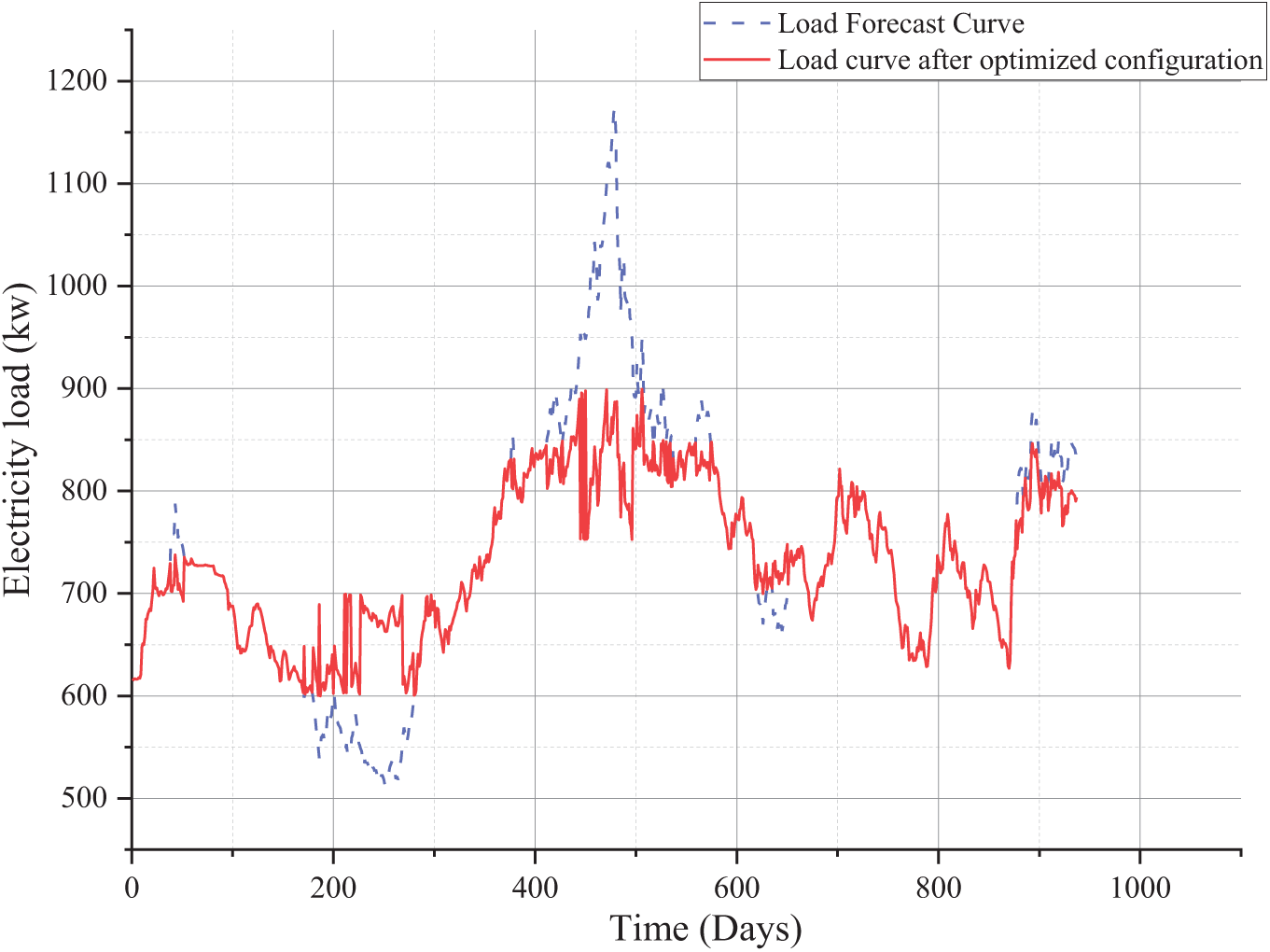
Figure 8: Graph showing the effect of peak shaving on the total load curve

As shown in Fig. 9, the peak value of the original load curve is reduced from 876.3625 to 804.4632 kW, the valley value is increased from 626.95 to 667.45 kW, the peak-to-valley difference is reduced from 249.4125 to 137.0132 kW, and the variance of the load predict curve is reduced from 4128.952 to 923.103 (kW)2, with a significant reduction in friction, indicating that There was a substantial reduction in the conflict of the curve, indicating a reduction in the steepness of the curve; between days 71 and 138 and days 200 and 265, there was a significant reduction in the peak-to-valley effect. Between days 71 and 138, the peak load valley value increased from 629.225 to 725.5125 kW, and the peak-valley difference decreased from 150.023 to 100.027 kW; between days 200 and 265, the peak load value decreased from 876.3621 to 804.3625 kW, and the peak-valley difference decreased from 249.4136 to 89.673 kW, significantly reducing This reduces the pressure on the grid and effectively improves energy efficiency. Fig. 10 shows the effect of peak shaving on the load prediction curve. After the energy storage station participates in peak regulation, the peak value of the original load curve decreases from 876.3625 to 804.4632 kW, and the valley value increases from 626.95 to 667.45 kW. The peak-valley difference decreases from 249.4125 to 137.0132 kW, and the variance of the load forecasting curve decreases from 4128.952 to 923.103 (kW)2, indicating a reduction in the steepness of the curve. The peak—shaving and valley—filling effects are significant between day 71 and day 138 and between day 200 and day 265. Between day 71 and day 138, the load valley increases from 629.225 to 725.5125 kW, reducing the peak—valley difference from 150.023 to 100.027 kW. Between day 200 and day 265, the load peak decreases from 876.3621 to 804.3625 kW, and the peak-valley difference reduces from 249.4136 to 89.673 kW, significantly alleviating grid operation pressure and improving energy utilization efficiency.

Figure 9: Graph showing the effect of peak shaving on the load-predicting curve

Figure 10: Cumulative costs vs. benefits

3.4 Economic Assessment

The cost-effective solution in any domain is a considerable factor [33]. As is shown in Fig. 10, through the cumulative cost and cumulative revenue comparison can be seen, this paper’s photovoltaic energy storage power plant construction cost is about 2.45 million yuan, the annual maintenance cost of 1–3 million yuan, the yearly profit varies between 120,000–250,000 yuan, from the cumulative cost and cumulative revenue difference can be seen, energy storage power plant operation for about 15 years, the incremental revenue can exceed the accumulative cost.

4  Conclusion

This paper proposes a capacity allocation method for energy storage plants based on power load forecasting technology, combining the grey predicting method with the neural network, making reasonable use of the ability of the BP neural network to approximate arbitrary functions and the ability of grey predicting method better to predict the general trend of power load changes. At the same time, the BP neural network requires multiple samples to train the neural network, while the grey predicting method can use fewer samples for modelling and predicting. The two can complement each other’s strengths and weaknesses. The integration of multiple linear regression prediction on the above basis, combining time series prediction with regression prediction, further reduces the prediction error, effectively improves prediction accuracy, and provides a reliable basis for the capacity allocation of energy storage plants.

The experiments show that the Informer-grey regression neural network model proposed in this paper achieves achieving an RMSE of 11.1361, an R2 of 96.90%, and an MAE of 8.264. Compared to the benchmark models, it has the smallest RMSE and MAE, and the R2 closest to 1, indicating the best prediction performance.

In this paper, the capacity allocation method of energy storage power station is used to construct a capacity allocation model of energy storage power station by studying the resulting curve of power load prediction, and the multi-objective snake optimization algorithm is used to solve the model and obtain the optimal capacity allocation of energy storage power station. After the power station participates in peak regulation, the effect of peak shaving and valley filling is significant, and the cost is relatively low. While meeting the regular operation of the chemical park relieves the pressure of grid operation and improves the economic return.

While our experiments primarily focused on a chemical park, the additional validations on residential and urban grids confirm the model’s applicability to diverse scenarios. Future work will explore integration with real-time weather forecasts and policy-driven constraints to further enhance practical relevance.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by Huaian Hongeng Group Co., Ltd. Relying on the project “Research on Key Technologies of Integrated Photovoltaic and Energy Storage Electric Vehicle Charging Stations” (Project Number: SGTYHT/23-JS-001), acknowledges with gratitude the financial and logistical support it has received. This study would not have been possible without the generous backing provided by the project sponsors.

Author Contributions: Study conception and design: Cong Zhang, Chutong Zhang, Jie Ji; data collection: Lei Shen, Renwei Guo; analysis and interpretation of results: Wan Chen; draft manuscript preparation: Hui Huang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Jie Ji, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Symbol Description:

This paper summarizes the symbols and definitions used in the text, as shown in table below.

References

1. Wu X, Xu C, Ma T, Xu J, Zhang C. Carbon emission of China’s power industry: driving factors and emission reduction path. Environ Sci Pollut Res Int. 2022;29(52):78345–60. doi:10.1007/s11356-022-21297-5. [Google Scholar] [PubMed] [CrossRef]

2. İnci M, Çelik Ö, Lashab A, Bayındır KÇ, Vasquez JC, Guerrero JM. Power system integration of electric vehicles: a review on impacts and contributions to the smart grid. Appl Sci. 2024;14(6):2246. doi:10.3390/app14062246. [Google Scholar] [CrossRef]

3. Hao G, Xianyu J. Short-term load forecasting based on improved manta ray algorithm to optimize neural network. J Phys Conf Ser. 2022;2189(1):012019. doi:10.1088/1742-6596/2189/1/012019. [Google Scholar] [CrossRef]

4. Masenga B, Byiringiro J, Kagiri C, Tafara E, Ngoma D, Aristid G. Design and development of wind-solar hybrid power system with compressed air energy storage for voltage and frequency regulations. J Power Energy Eng. 2023;11(2):1–24. doi:10.4236/jpee.2023.112001. [Google Scholar] [CrossRef]

5. Amiruddin A, Liebman A, Dargaville R, Gawler R. Optimal energy storage configuration to support 100% renewable energy for Indonesia. Energy Sustain Dev. 2024;81(6):101509. doi:10.1016/j.esd.2024.101509. [Google Scholar] [CrossRef]

6. Ma L, Xie L, Ye J, Bian Y. Two-stage dispatching strategy for park-level integrated energy systems based on a master-slave-cooperative hybrid game model. Renew Energy. 2024;232(4):120971. doi:10.1016/j.renene.2024.120971. [Google Scholar] [CrossRef]

7. Wang D, Xue J, Sun R, Tao Y, Zhao D, Gao B. Configuration optimization of energy storage power station considering failure cost. In: Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC); 2020 Sep 20–23; Nanjing, China. doi:10.1109/appeec48164.2020.9220676. [Google Scholar] [CrossRef]

8. Khan MR, Haider ZM, Malik FH, Almasoudi FM, Alatawi KSS, Bhutta MS. A comprehensive review of microgrid energy management strategies considering electric vehicles, energy storage systems, and AI techniques. Processes. 2024;12(2):270. doi:10.3390/pr12020270. [Google Scholar] [CrossRef]

9. Jia Y, Zuo T, Li Y, Bi W, Xue L, Li C. Finite-time economic model predictive control for optimal load dispatch and frequency regulation in interconnected power systems. Glob Energy Interconnect. 2023;6(3):355–62. doi:10.1016/j.gloei.2023.06.009. [Google Scholar] [CrossRef]

10. Yuan J, Wang L, Qiu Y, Wang J, Zhang H, Liao Y. Short-term electric load forecasting based on improved extreme learning machine mode. Energy Rep. 2021;7(17):1563–73. doi:10.1016/j.egyr.2021.09.067. [Google Scholar] [CrossRef]

11. Guo S, Ba Y, Li C. Power load forecasting model based on improved SSA algorithm and optimized BP neural network. J Heilongjiang Sci Technol Univ. 2022;32(3):401–5. (In Chinese). doi:10.3969/j.issn.2095-7262. [Google Scholar] [CrossRef]

12. Luo S, Wang B, Gao Q, Wang Y, Pang X. Stacking integration algorithm based on CNN-BiLSTM-Attention with XGBoost for short-term electricity load forecasting. Energy Rep. 2024;12:2676–89. doi:10.1016/j.egyr.2024.08.078. [Google Scholar] [CrossRef]

13. Yang X, Wang S, Peng Y, Chen J, Meng L. Short-term photovoltaic power prediction with similar-day integrated by BP-AdaBoost based on the Grey-Markov model. Electr Power Syst Res. 2023;215(3):108966. doi:10.1016/j.epsr.2022.108966. [Google Scholar] [CrossRef]

14. Lu X, Pan D, Wang K, Bi J. Grey time series power load forecasting method based on Markov modification. Autom Technol Appl. 2022;3:132–6. (In Chinese). doi:10.3969/j.issn.1003-7241.2022.03.029. [Google Scholar] [CrossRef]

15. Wei J, Niu H. A ranking-based adaptive cuckoo search algorithm for unconstrained optimization. Expert Syst Appl. 2022;204(2):117428. doi:10.1016/j.eswa.2022.117428. [Google Scholar] [CrossRef]

16. Lu J, She S, Wei X. Lithium battery state of charge prediction based on cuckoo search optimized neural network. Autom Comput Meas. 2021;29(8):5. (In Chinese). doi:10.16526/j.cnki.11-4762/tp.2021.08.010. [Google Scholar] [CrossRef]

17. Chen S, Zhou X, Zhou G, Fan C, Ding P, Chen Q. An online physical-based multiple linear regression model for building’s hourly cooling load prediction. Energy Build. 2022;254(1):111574. doi:10.1016/j.enbuild.2021.111574. [Google Scholar] [CrossRef]

18. Sun Y, Hou L, Lv Z, Peng D. Informer-based intrusion detection method for network attack of integrated energy system. IEEE J Radio Freq Identif. 2022;6:748–52. doi:10.1109/JRFID.2022.3215599. [Google Scholar] [CrossRef]

19. Zhou H, Li J, Zhang S, Zhang S, Yan M, Xiong H. Expanding the prediction capacity in long sequence time-series forecasting. Artif Intell. 2023;318(1):103886. doi:10.1016/j.artint.2023.103886. [Google Scholar] [CrossRef]

20. Zhou H, Zhang S, Peng J, Zhang S, Li J, Xiong H, et al. Informer: beyond efficient transformer for long sequence time-series forecasting. Proc AAAI Conf Artif Intell. 2021;35(12):11106–15. doi:10.1609/aaai.v35i12.17325. [Google Scholar] [CrossRef]

21. Tian R, Li X, Ma Z. LD former: a parallel neural network model for long-term power forecasting. Front Inf Technol Electron Eng. 2023;24(9):1287–301. doi:10.1631/fitee.2200540. [Google Scholar] [CrossRef]

22. Gong M, Zhao Y, Sun J, Han C, Sun G, Yan B. Load forecasting of district heating system based on informer. Energy. 2022;253(10):124179. doi:10.1016/j.energy.2022.124179. [Google Scholar] [CrossRef]

23. Hajihosseinlou M, Maghsoudi A, Ghezelbash R. Stacking: a novel data-driven ensemble machine learning strategy for prediction and mapping of Pb-Zn prospectivity in Varcheh district, west Iran. Expert Syst Appl. 2024;237(3):121668. doi:10.1016/j.eswa.2023.121668. [Google Scholar] [CrossRef]

24. Wang W, Wang Q, Zhong R, Chen L, Shi X. Stacking sequence optimization of arbitrary quadrilateral laminated plates for maximum fundamental frequency by hybrid whale optimization algorithm. Compos Struct. 2023;310(3):116764. doi:10.1016/j.compstruct.2023.116764. [Google Scholar] [CrossRef]

25. Shah SAH, Ahmed U, Bilal M, Khan AR, Razzaq S, Aziz I, et al. Improved electric load forecasting using quantile long short-term memory network with dual attention mechanism. Energy Rep. 2025;13(5):2343–53. doi:10.1016/j.egyr.2025.01.058. [Google Scholar] [CrossRef]

26. Buratynskyi I, Nechaieva T. The least-cost optimization of PV-station DC/AC equipment using battery energy storage system. Latv J Phys Tech Sci. 2022;59(1):53–62. doi:10.2478/lpts-2022-0006. [Google Scholar] [CrossRef]

27. Karamov D, Ilyushin P, Minarchenko I, Filippov S, Suslov K. The role of energy performance agreements in the sustainable development of decentralized energy systems: Methodology for determining the equilibrium conditions of the contract. Energies. 2023;16(6):2564. doi:10.3390/en16062564. [Google Scholar] [CrossRef]

28. Li Z. Optimal allocation of energy storage in distribution network considering microgrid cluster and system economic operation. J Phys Conf Ser. 2023;2474(1):012082. (In Chinese). doi:10.1088/1742-6596/2474/1/012082. [Google Scholar] [CrossRef]

29. Won Hwang S, Hong DK. Performance evaluation of composite electrolyte with GQD for all-solid-state lithium batteries. Comput Mater Contin. 2023;74(1):55–66. doi:10.32604/cmc.2023.028845. [Google Scholar] [CrossRef]

30. Zhang H, Zhou S, Gu W, Zhu C, Chen XG. Optimal operation of micro-energy grids considering shared energy storage systems and balanced profit allocations. CSEE J Power Energy Syst. 2023;9(1):254–71. doi:10.17775/CSEEJPES.2020.04760. [Google Scholar] [CrossRef]

31. Zhou L, Ma T. Analysis of energy storage operation configuration of power system based on multi-objective optimization. J Electron Res Appl. 2022;6(4):13–38. doi:10.26689/jera.v6i4.4272. [Google Scholar] [CrossRef]

32. Yousaf A, Asif RM, Shakir M, Rehman AU, Adrees MS. An improved residential electricity load forecasting using a machine-learning-based feature selection approach and a proposed integration strategy. Sustainability. 2021;13(11):6199. doi:10.3390/su13116199. [Google Scholar] [CrossRef]

33. Yousaf A, Asif RM, Shakir M, Rehman AU, Alassery F, Hamam H, et al. A novel machine learning-based price forecasting for energy management systems. Sustainability. 2021;13(22):12693. doi:10.3390/su132212693. [Google Scholar] [CrossRef]