 Open Access
Open Access
ARTICLE
Security-Constrained Optimal Power Flow in Renewable Energy-Based Microgrids Using Line Outage Distribution Factor for Contingency Management
1 Department of Electrical Engineering, Politeknik Elektronika Negeri Surabaya, Surabaya, 60111, Indonesia
2 Electrical Engineering, Faculty of Advanced Technology and Multidiscipline, Airlangga University, Surabaya, 60115, Indonesia
3 Educational Technology, Postgraduate Universitas Negeri Medan, Universitas Negeri Medan, Medan, 20221, Indonesia
4 Departement of Mechanical Computer Industrial Management Engineering, Kangwon National University, Chuncheon, 24341, Republic of Korea
5 Departement of Mechanical Engineering, Cheng Shiu University, Kaohsiung, 83347, Taiwan
* Corresponding Author: Rezi Delfianti. Email:
(This article belongs to the Special Issue: Innovative Renewable Energy Systems for Carbon Neutrality: From Buildings to Large-Scale Integration)
Energy Engineering 2025, 122(7), 2695-2717. https://doi.org/10.32604/ee.2025.063807
Received 24 January 2025; Accepted 18 April 2025; Issue published 27 June 2025
Abstract
Ensuring the reliability of power systems in microgrids is critical, particularly under contingency conditions that can disrupt power flow and system stability. This study investigates the application of Security-Constrained Optimal Power Flow (SCOPF) using the Line Outage Distribution Factor (LODF) to enhance resilience in a renewable energy-integrated microgrid. The research examines a 30-bus system with 14 generators and an 8669 MW load demand, optimizing both single-objective and multi-objective scenarios. The single-objective optimization achieves a total generation cost of $47,738, while the multi-objective approach reduces costs to $47,614 and minimizes battery power output to 165.02 kW. Under contingency conditions, failures in transmission lines 1, 22, and 35 lead to complete power loss in those lines, requiring a redistribution strategy. Implementing SCOPF mitigates these disruptions by adjusting power flows, ensuring no line exceeds its capacity. Specifically, in contingency 1, power in channel 4 is reduced from 59 to 32 kW, while overall load shedding is minimized to 0.278 MW. These results demonstrate the effectiveness of SCOPF in maintaining stability and reducing economic losses. Unlike prior studies, this work integrates LODF into SCOPF for large-scale microgrid applications, offering a computationally efficient contingency management framework that enhances grid resilience and supports renewable energy adoption.Keywords
A microgrid is an independent system distinct from the main grid, comprised of both renewable and non-renewable energy sources and this system can be connected off-grid or on-grid [1,2]. This microgrid system can be a solution to overcome the supply of electrical energy to an increasing load [3,4] The microgrid system has low operating costs and emissions, making it more profitable in terms of costs and impacts on the environment [5,6]. This study uses a microgrid system that refers to research [7]. Due to its connection with the utility grid through PLN, this microgrid configuration falls under the classification of an on-grid system [8,9].
Contingency refers to an unforeseen situation that transpires within an electric power system temporarily [10,11]. A contingency can cause the release of one of the elements of electric power, such as the loss of a transmission line in the system [12,13]. If allowed, contingency can result in a system in a dangerous state with multilevel contingency, and a blackout occurs. Many studies that discuss contingency events in power lines include references [14,15]. Reference [14] uses the interior point method (IPM) technique for the security-constrained optimal power flow (SCOPF) system and only applies it to a small system of 9 buses. Reference [15] only discusses contingency analysis and does not discuss SCOPF. In addition to optimizing power generation costs, instability caused by turbulence in renewable energy sources also affects the optimality of power flow in microgrids. Wind turbulence, wake turbulence effects, and fluctuations in solar irradiance can cause sudden variations in power output, impacting load balancing and energy storage requirements [16,17]. Conventional power flow optimization models often assume static generation conditions, whereas, in reality, these stochastic disturbances can lead to overloads in specific transmission lines and increase the need for power redistribution. Therefore, this study integrates the Line Outage Distribution Factor (LODF) with the Security-Constrained Optimal Power Flow (SCOPF) method to anticipate power fluctuations caused by turbulence, ensuring that power distribution remains within system security limits [18]. Three tasks are involved in ensuring the security of a power system: monitoring the system, analyzing contingencies, and performing SCOPF [19].
While previous studies have applied Security-Constrained Optimal Power Flow (SCOPF) for grid security and Line Outage Distribution Factor (LODF) for contingency analysis, their integration for large-scale microgrid optimization under real-time contingency conditions remains limited [20]. This study advances the field by integrating LODF with SCOPF to dynamically optimize power redistribution, ensuring no transmission line exceeds its limit even under failure conditions. Unlike prior research, which often focuses on large power grids or assumes static contingency scenarios, this study enhances real-time adaptability for microgrid systems with high renewable energy penetration, providing a computationally efficient solution for minimizing load shedding and cost fluctuations. This paper focuses on SCOPF. Analyzing the risk of disruptions across all channels is essential, but performing contingency calculations in large systems is complex and time-consuming [21,22]. The Line Outage Distribution Factor (LODF) speeds up real-time contingency calculations for load conditions [14]. Using the impedance parameter of each channel within the system, LODF can determine the updated power flow for every line in various line contingency situations [23].
The increasing integration of renewable energy sources in power grids introduces new challenges in maintaining system stability and optimizing power distribution. Many industrial microgrids, especially those relying on hybrid energy sources such as wind, solar, and battery storage, face frequent power fluctuations due to unpredictable energy inputs [24]. This study addresses these challenges by implementing a real-time Security-Constrained Optimal Power Flow (SCOPF) model combined with Line Outage Distribution Factor (LODF), allowing rapid power redistribution when transmission line failures occur. The proposed method has direct applications in smart grids, industrial power systems, and utility-scale renewable energy projects, helping operators minimize load shedding, optimize generation costs, and improve grid resilience against contingencies.
The rest of this document is structured in the subsequent manner. Section 2 presents a set of equations for security-constrained OPF solution methods using dc power flow and quadratic programming. These equations are employed to formulate the objective function and constraint equations. Section 3 outlines the approach for computing the sensitivity factor. The Section 4 encompasses the author’s examination of numerical outcomes, while encapsulates the conclusions drawn from the entirety of the tests.
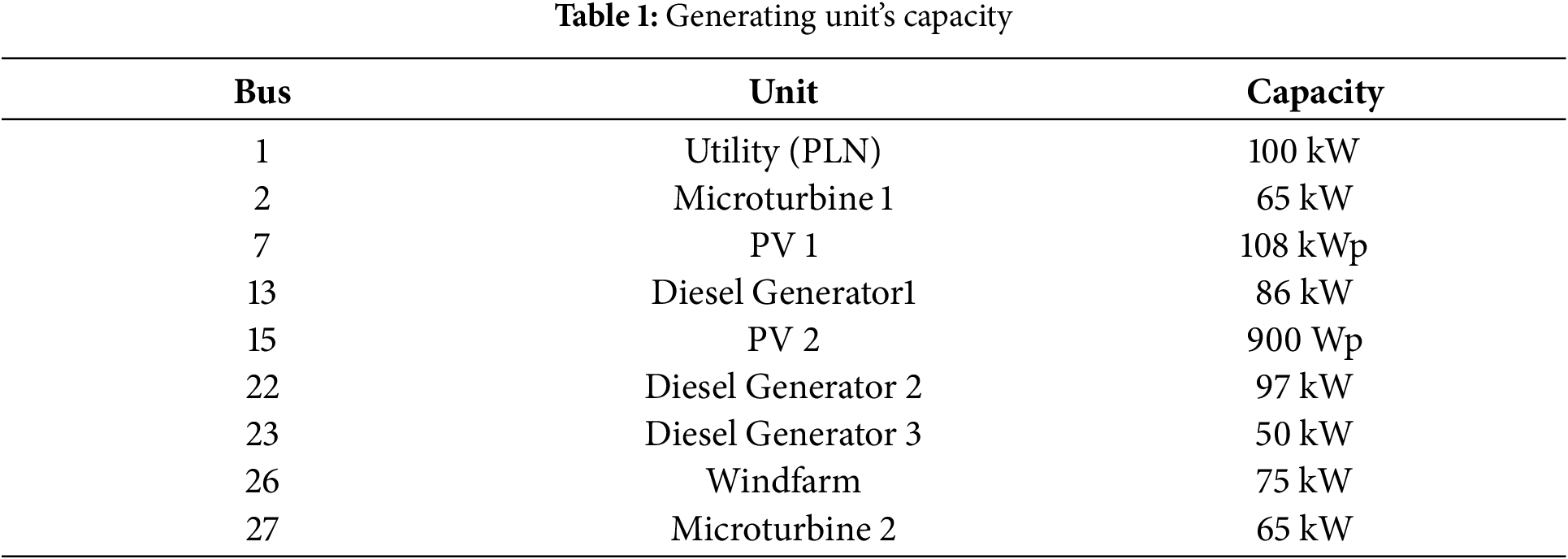
This system has five types of generators, including photovoltaic, microturbine, diesel generator, wind farm, and battery energy storage [25]. Bus one is connected to the utility grid (PLN) [26]. The research employs a customized IEEE 30 bus system (shown in Fig. 1) as a model for a grid-connected microgrid electrical network. The system generator used is in the form of 14 generators. The buses’ location and each generator’s capacity are shown in Table 1.
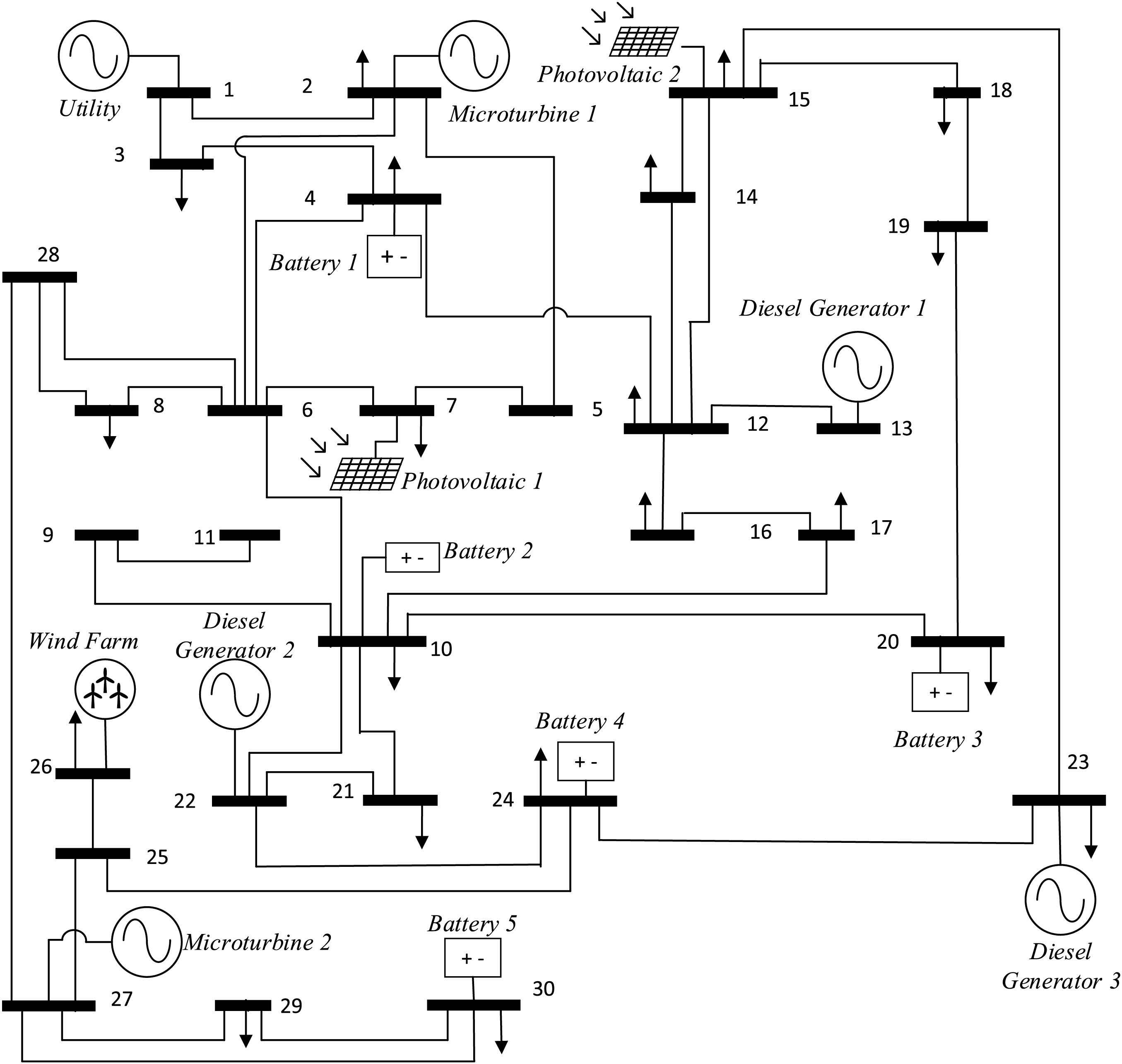
Figure 1: Microgrid system
1.2 Establishing the Objective Function
This function aims to reduce the overall generation costs during a defined time span T. The objective functions for this research are as follows [27]:
where
1.3 Function Formation of Control Variables
The control variable is optimized. The control variables are voltage angle, generator power generation, and load bus power [28]. While in quadratic programming, the controlled variable is the value of x. The x value corresponds to the microgrid system [29].
(a) Equality constraints
The active power balance for each bus i and time t is formulated as follows:
where
(b) Inequality constraints
1. Line capacity
2. Contingency limit
3. Generation limit
4. Battery capacity
5. Ramp rate
The numerical solution for Security-Constrained Optimal Power Flow (SCOPF) was obtained using a quadratic programming optimization solver [30]. To simplify computations, the power flow equations were discretized using a DC load flow model, which linearizes system equations and reduces computational complexity [31]. The discretization scheme ensures that power generation, load demand, and transmission constraints are modelled at predefined time intervals. Convergence was determined using an iterative Newton-Raphson method with a tolerance level of 10−6, ensuring stability and accuracy. To further enhance computational efficiency, a sensitivity-based approach utilizing Line Outage Distribution Factor (LODF) and Power Transfer Distribution Factor (PTDF) was employed to estimate power redistributions during contingency events. The selection of key parameters in this study was based on real-world industrial microgrid configurations and benchmark systems. Power limits (32 to 130 kW) were chosen to align with standard transmission line ratings in distributed energy systems. Generation costs were determined based on operational data from renewable and conventional energy sources, while contingency conditions were selected due to their high sensitivity to outages and significant impact on power redistribution, ensuring that the study reflects practical grid challenges.
System constraints, including power flow limits, were established based on standard grid protection settings and real-world industrial microgrid conditions. The total system load of 8669 MW was selected to represent medium-sized industrial microgrid demands, while generator capacities (50 to 108 kW) were chosen to reflect conventional and renewable energy sources commonly used in smart grids and industrial power systems. These constraints ensure that the optimization model remains practical and scalable for real-world applications. The proposed method enhances computational efficiency by leveraging LODF to rapidly estimate power redistributions, eliminating the need for full AC power flow recalculations. Additionally, the use of quadratic programming reduces the computational burden of optimizing power dispatch while maintaining system stability. The Newton-Raphson iteration method, with a tolerance of 10−6, ensures convergence within a limited number of iterations, making the approach suitable for real-time contingency management in large-scale microgrids.
The optimization framework in this study applies a weighted sum approach to balance generation cost minimization and power flow security [32]. The selection of weight factors was based on grid operational priorities, ensuring that neither economic efficiency nor system reliability was compromised. A higher weight for cost minimization prioritizes reducing generation expenses, while a higher weight for power flow security ensures that transmission constraints and contingency risks are effectively managed. The final weight distribution was determined through trial simulations and sensitivity analysis, achieving an optimal trade-off between both objectives. This approach enables the SCOPF-LODF model to maintain economic efficiency while enhancing grid stability. Future research could explore adaptive weighting techniques, where weight factors dynamically adjust based on real-time grid conditions. Analyzing multiple contingency scenarios can become computationally intensive, especially when aiming for fast and efficient result generation. To swiftly estimate potential overloads, a linear sensitivity factor is one of the simplest and most effective approaches. These factors indicate the estimated impact of generation changes on line power flow within the network and are derived from DC load flow analysis [33]. By incorporating sensitivity-based contingency assessment, this study provides an efficient and scalable optimization framework for modern power grids.
1. Calculate
That way, you get
2. As bus one functions as the slack bus, after removing the corresponding row (row 1) and column (column 1) from the
3. Find the inverse of
4. Calculate the sensitivity matrix with
5. Calculate the sensitivity factor for generation shift by executing a generation halt at the chosen bus (k) connected to line (ll). Use the equation below, where bus n to m signifies the bus connected through the line l.
6. Compute the sensitivity factor for line outage distribution by disconnecting the line linked to bus (kk), impacting another line on bus (ll). The equation takes into account the buses connected by both lines (kk and ll), where bus n to m is associated with the monitored line (ll), and buses I to j are connected by the outage line (kk).
7. Then the generation shift sensitivity factor is denoted by
where ll is the channel index, i is the bus index,
8. If the start of the power supply is
This enables the calculation of updated power flow on each network channel by utilizing a collection of precalculated PTDF factors, as outlined below.
here
9. The outage power flow
where
10. If there is knowledge about the relationship between the power on channel ll and k, the power flow on channel ll during the outage of channel k can be ascertained using the LODF.
where
The optimization model in this study is based on several key assumptions to ensure computational feasibility and practical applicability. First, the microgrid is assumed to operate under steady-state conditions, with contingency events causing only temporary deviations. Second, Line Outage Distribution Factor (LODF) is used to estimate power redistribution, assuming a stable network impedance model. Third, all generation units are constrained within their defined capacity limits to maintain operational feasibility. Additionally, renewable energy sources are modeled using historical data trends to approximate expected power output. Finally, this study does not consider market fluctuations or demand response mechanisms, as the focus is on technical optimization rather than economic factors. These assumptions help streamline the optimization process while maintaining practical relevance for real-world applications.
Study scenarios involving OPF with Contingency. The parameters acquired through OPF simulation consist of generator power generation states, battery status, and generation cost values for each case analyzed. Generator power generation is categorized into controllable and renewable sources.
To validate the simulation results, the study utilizes a modified IEEE 30-bus system, a recognized benchmark for power system studies. The generator capacities, load demand, and transmission constraints were selected to reflect real-world industrial microgrid conditions. The effectiveness of the proposed SCOPF-LODF approach was assessed by comparing power redistributions and cost optimizations with standard security-constrained OPF methods, ensuring practical applicability.
The results of this study are based on specific modeling assumptions to ensure computational efficiency and practical applicability. The microgrid system is assumed to operate under steady-state conditions, with contingency events only causing temporary deviations in power flow. Additionally, the generation units are constrained within their designated capacity limits, ensuring that no generator exceeds its operational range. Renewable energy sources, such as solar PV and wind farms, are modeled using historical generation profiles, assuming relatively predictable fluctuations without extreme variability. These assumptions provide a structured approach to optimizing power distribution under contingency conditions, but may not fully capture real-world stochastic behavior, such as rapid fluctuations in renewable energy generation due to weather anomalies. The microgrid’s demand profile follows the daily load curve pattern over a 24-h period. In this study, the load profile utilized is 8669 MW, originating from an initial steady state load of 306 kW for one hour. To determine the hourly periods across 24 h, an initial load multiplier is employed. The load profile curve is depicted in Fig. 2.
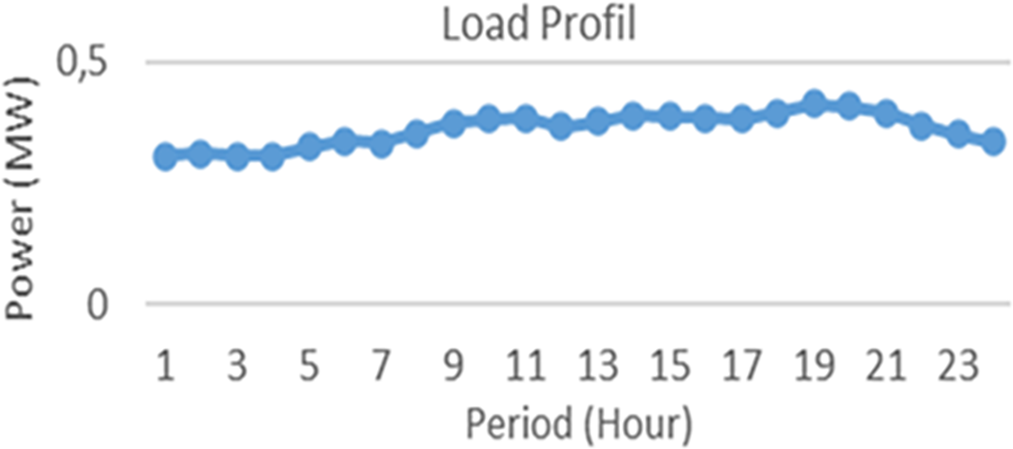
Figure 2: Load profile in a day
3.1 OPF without Contingency Case (Base Case)
What is analyzed in case study 1 is a normal condition or no contingency. For each scenario, the presented outcomes comprise optimization data and power generation graphs. Figs. 3 and 4 illustrate the 24-h power generation. Fig. 3 highlights controllable source generators, including six resources. Notably, the utility grid stands as the predominant source, yielding the highest power and a value associated with a low-cost function. The utility grid is prioritized for power release. The setup comprises the grid, two microturbines, and three diesel generators. This arrangement is determined by the PLN grid’s peak power capacity of 92,664 kW, attained at 19:00. The three diesel generators contribute 74.5, 52, and 56 kW of power throughout the day. Microturbine 1 and Microturbine 2 generate comparatively lower power. The power output of Microturbine 1 varies between 0.0672 and 0.0695 kW, whereas Microturbine 2’s output ranges from 0.3131 to 0.3165 kW.
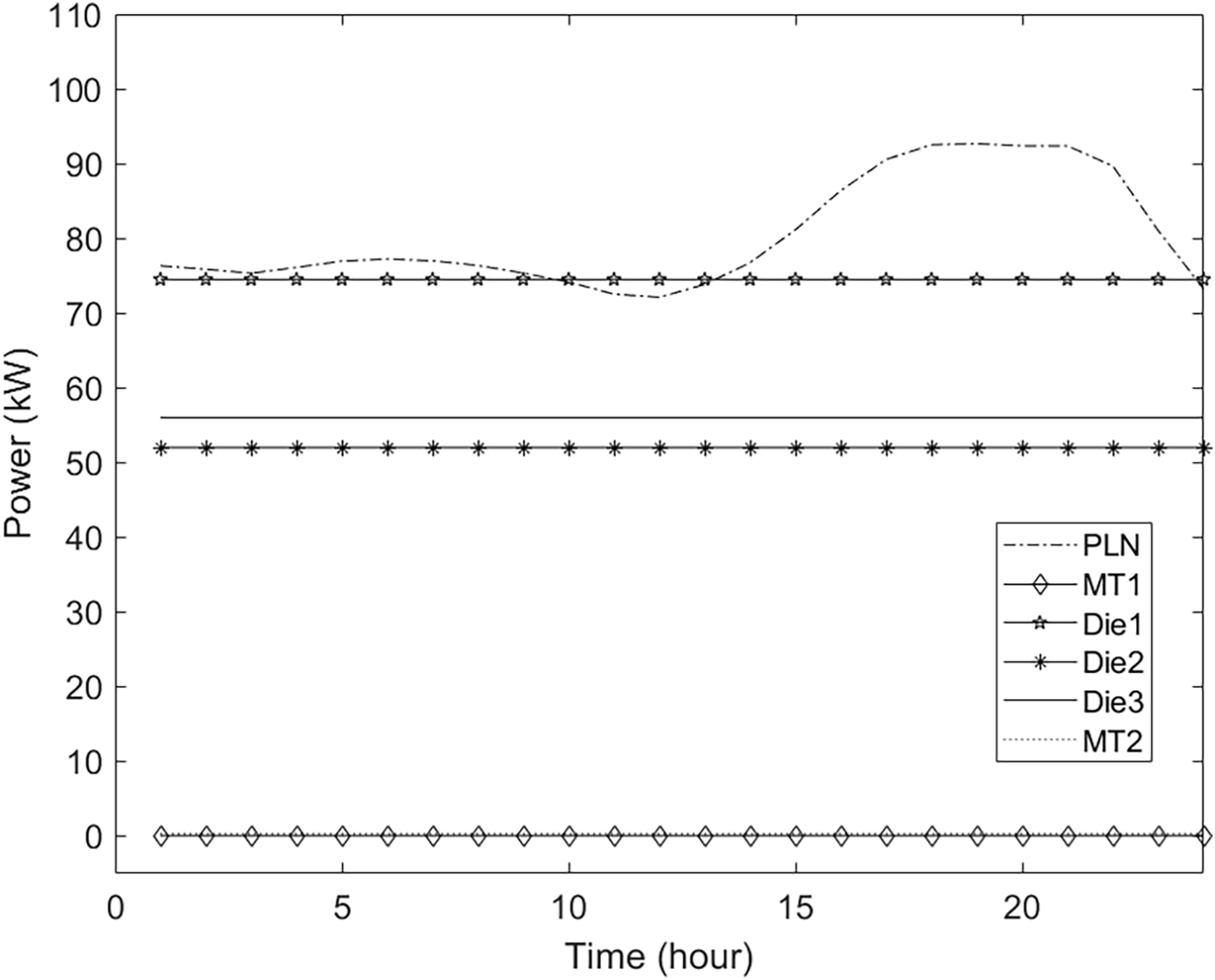
Figure 3: Scenario I with controllable sources
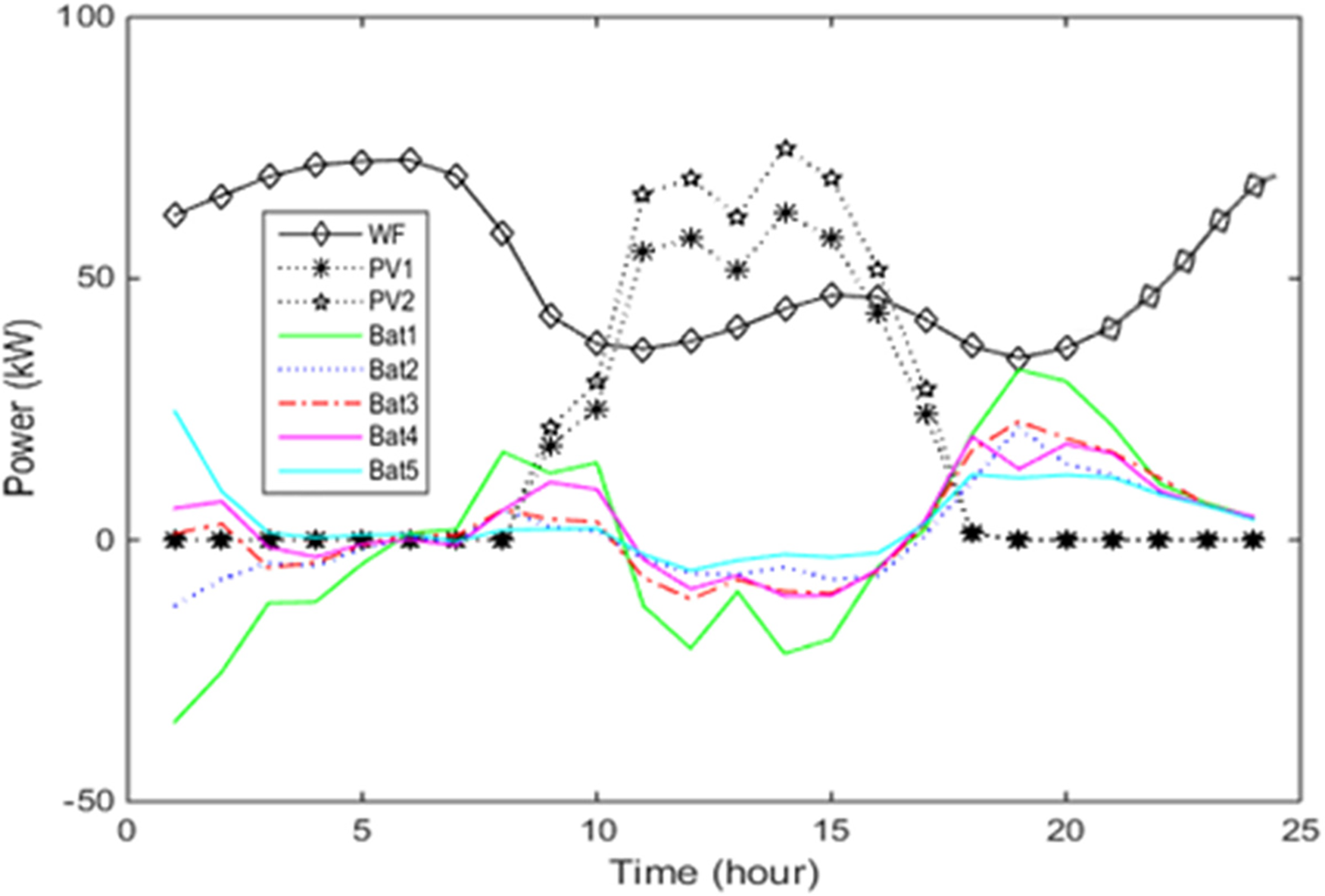
Figure 4: Scenario I involving renewable source generation
The selection of parameter ranges in this study is based on practical considerations to ensure real-world applicability. The microgrid model consists of 14 generation units, including solar PV, diesel generators, wind farms, and battery energy storage, with capacities ranging from 50 to 108 kW. These values were chosen to represent a typical hybrid energy microgrid used in industrial facilities and smart city applications. The total system load of 8669 MW aligns with power demands found in medium-sized industrial microgrids and commercial renewable energy hubs.
Security constraints were carefully defined to ensure safe operation under contingency conditions, with transmission line limits set between 32 and 130 kW. These limits are consistent with standard grid protection settings used in distributed energy systems. The study focuses on three contingency cases (Lines 1, 22, and 35), as these lines experience high sensitivity to outages and significantly impact power redistribution. By evaluating these conditions, the study provides insights into how real-world power networks can optimize response strategies using SCOPF-LODF.
The graph on Fig. 2 displaying the power generation of a renewable source, specifically a wind farm, composed of two photovoltaics (P.V.), one wind farm, and five batteries, is depicted in Figs. 3 and 4. The peak power output from the wind farm occurs at 05:00 and reaches 72,443 kW. The photovoltaic generation spans from the 9th to the 17th, with the highest combined output at the 14th h: P.V. 1 generates 62.4 kW, and P.V. 2 generates 74.88 kW. As photovoltaics begin producing power, the batteries enter a state of high charge, as illustrated in Figs. 3 and 4.
In case study 2, the microgrid system will be tested according to Fig. 1 by considering contingency conditions. There are 41 channels in the 30 bus microgrid system. The first step in this case study 2 is to check the contingency conditions on each channel. From the first stage, the selection of contingency studies is carried out on channels that are overloaded under certain contingency conditions.
3.2.1 Check all Channels Contingency
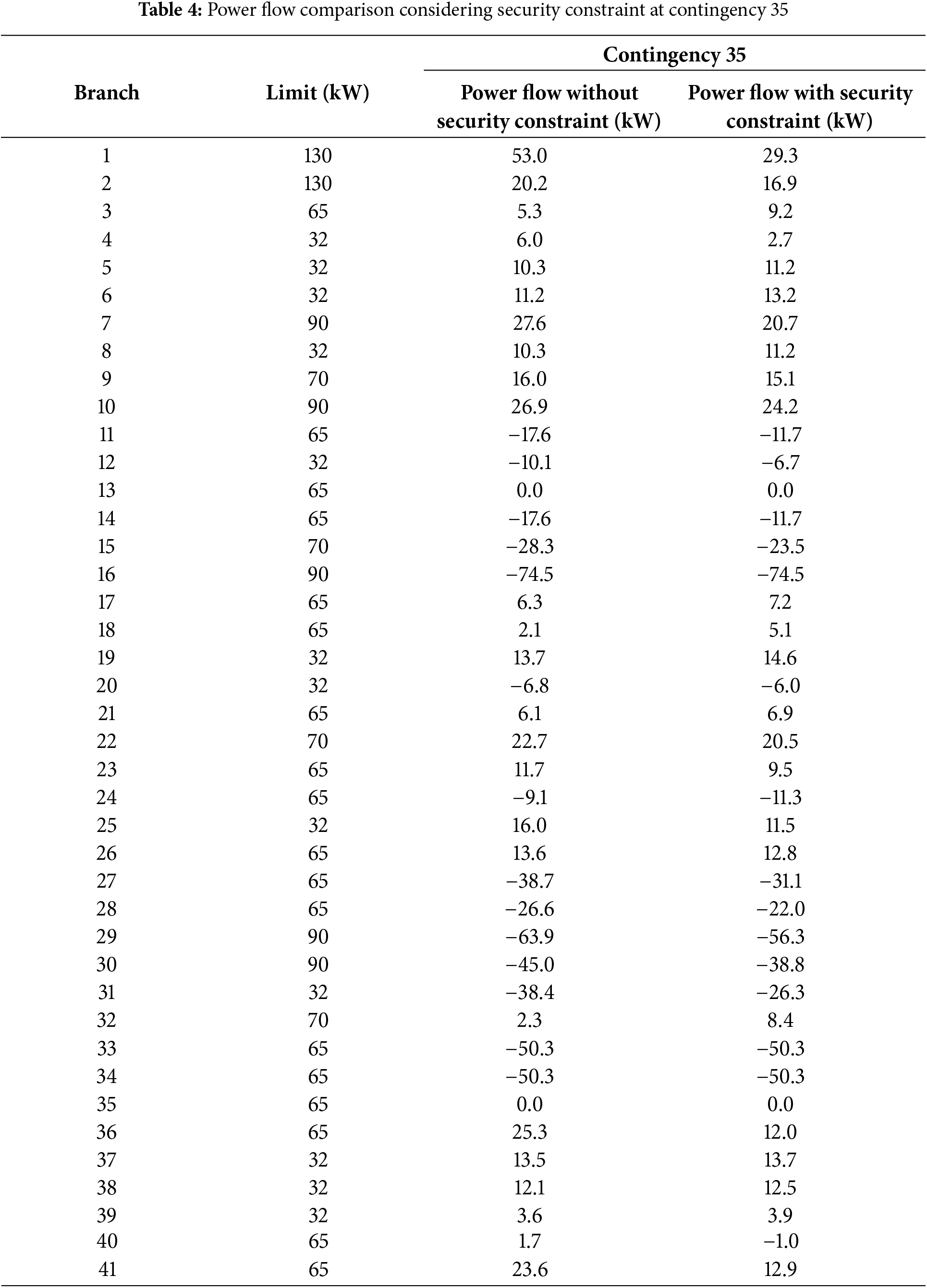
As already mentioned, the first step in case study 2 is checking the contingency conditions in each channel. Contingency is applied to all channels so that the condition of the power flow can be known before the re-dispatch occurs. This aims to determine the condition of each channel when the system is experiencing contingency so that an overloaded channel is obtained that can be used for experiments by considering the safety limit. From the results of these checks, it was found that there are 3 channels that are overloaded. The condition of the overloaded channel occurs when the contingency occurs on channels 1, 22, and 35. Each contingency has a total of 1 channel that is overloaded. The power flow is calculated using Eq. (21) contained in the previous chapter. In contingency 1, the overloaded channel is channel 4 with a power flow value of 59 kW and a channel limit of 32 kW. In contingency 22, the overloaded channel is channel 25.4 with a power flow value of 38.7 kW and a channel limit of 32 kW. While in contingency 35, the overloaded channel is channel 31 with a power flow value of 38.4 kW and a channel limit of 32 kW. For contingency channels 16 and 36 it cannot be done because the system will experience islanded.
3.2.2 Find the Optimal Power Flow
The next stage is to find the optimal power flow in the system by using the overload channel as a reference in considering security constraints. The purpose of considering this security constraint is to anticipate the system so as not to violate the channel boundaries when experiencing a contingency. It can be seen in the previous sub-chapter that there are 3 contingency conditions that cause violations of the channel boundaries owned. The contingencies are contingencies 1, 22, and 35. With reference to the three contingencies, a comparison table of the resulting power flow is made without considering security constraints and taking into account security constraints. The table that describes the results of the comparison is in Tables 2–4. According to Tables 2–4, the power flow in the line by considering the security constraint no longer violates the channel limit. In contingency 1 channel 4, the original power flow is 59 to 32 kW. At a contingency of 22 channels 25, the original power flow is 38.7 to 32 kW. At a contingency of 35 channels 31, the original power flow is −38.4 to 26.3 kW. It can be concluded that by considering the security constraint, the flow of power in the event of a contingency can be maintained in terms of system security. This case study experiment 2 can be categorized as prevention so that the power flow in the line does not experience overload when the system experiences a contingency.


The security-constrained optimization process was executed iteratively, adjusting generator dispatch and power redistribution based on LODF calculations. The solver utilized a quadratic cost function to minimize generation costs while ensuring that no transmission line exceeded its rated capacity. The effectiveness of the proposed method was validated by comparing power flow adjustments before and after applying SCOPF constraints.
3.2.3 System Generation Power Results Considering Security Constraints
The next stage is to analyze the power generation system that considers the security constraint by implementing the optimal power flow program. Fig. 5 shows the power generated by the controllable source generator in case 2. Throughout the day, diesel generators produce power consistently. Diesel generator 1 provides the most power at 74.5 kW, followed by diesel generator 2 at 52 kW, and diesel generator 3 at 56 kW. Microturbine 2 produces the lowest power, ranging from 7.84 to 14.27 kW.
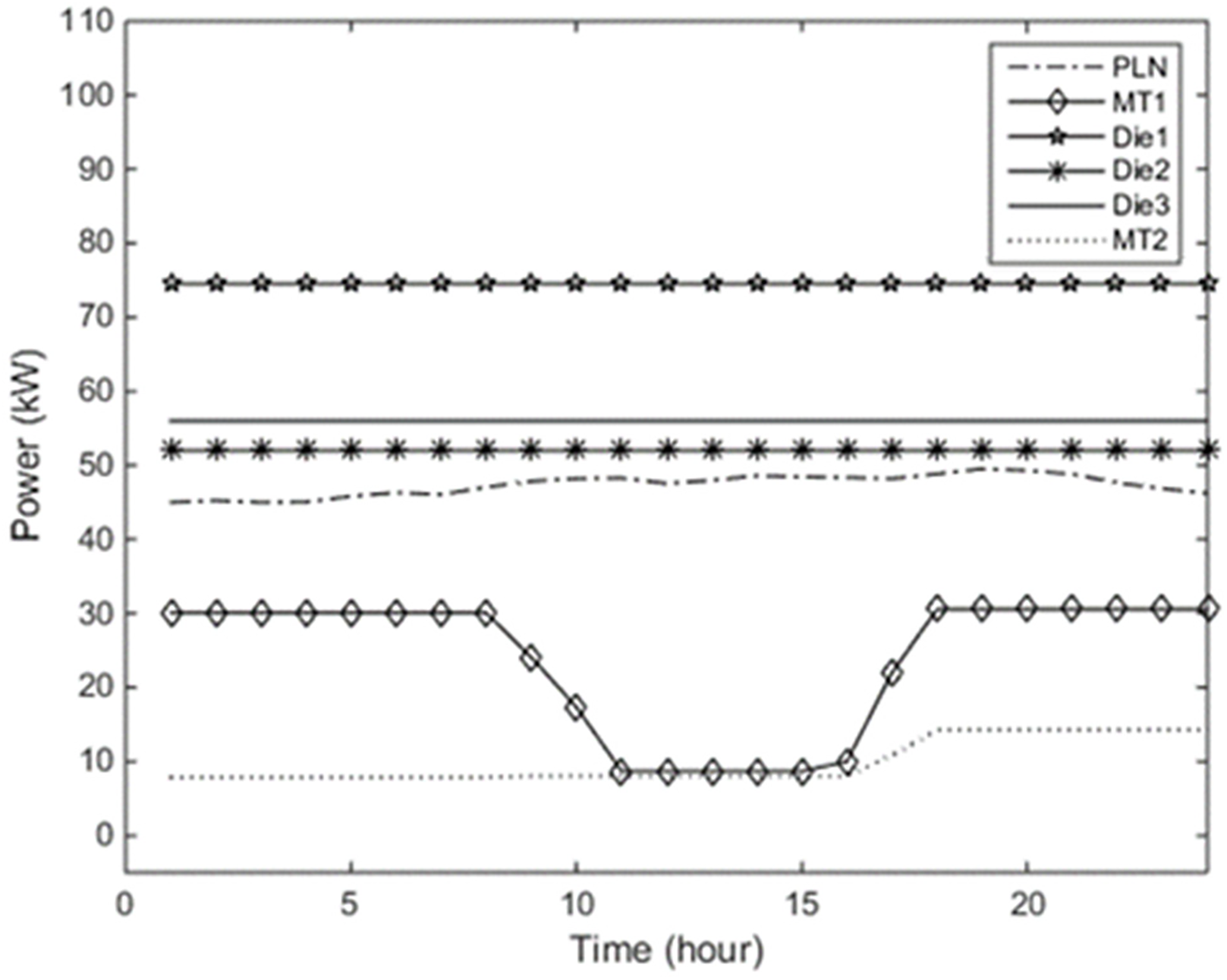
Figure 5: Scenario II with controllable sources
Figs. 5 and 6 displays the power generation graph for a renewable source generator. The contingency condition causes the wind farm’s generating power to be reduced compared to conditions without considering security constraints. The highest power generated by the wind farm in case study 2 is 57.94 kW at 24.00 h. Batteries that have high charge and discharge conditions are produced by battery 1. The highest power value possessed by battery 1 in charge conditions is −34.72 kW at 12.00 h while in discharge conditions has a value of 35.75 kW at 19.00 h.

Figure 6: Scenario II involving renewable source generation
The outcomes from contrasting total generation power, generation cost, and individual battery power between case study 1 and case study 2 are depicted. Fig. 7 illustrates the collective generated power in both experiments. Notably, adhering to security constraints results in a load shedding of 0.278 MW in the system.
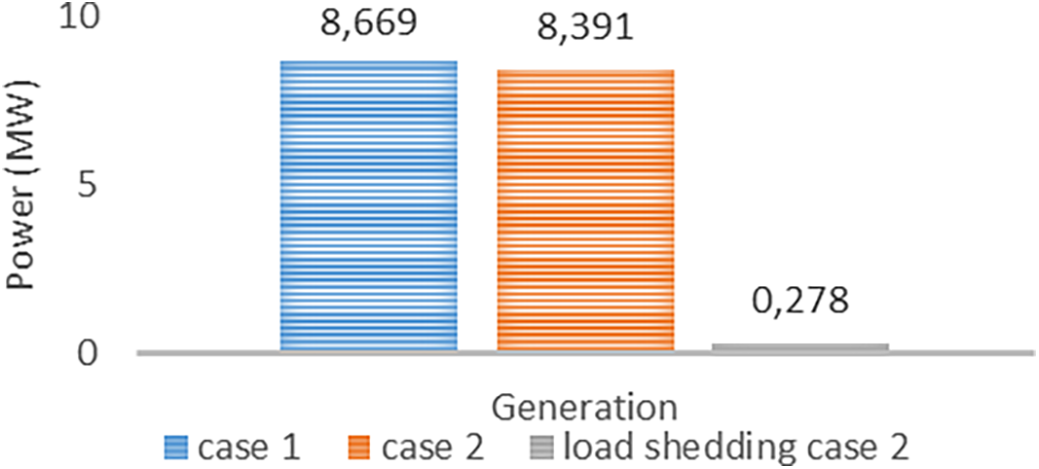
Figure 7: Comparison chart of generator total power
The comparison of the generation cost in case study 2 is illustrated in Fig. 8. The graph indicates that incorporating security constraints slightly increases the overall generation cost. In a system that takes security constraints into account, the total generation cost amounts to $48,257. This results in a difference of $789 compared to the total cost without security constraints.

Figure 8: Comparison graph of total generation costs
The computational performance of the SCOPF-LODF model was evaluated based on solution time and efficiency. By utilizing LODF for contingency analysis, the need for repetitive full power flow calculations was minimized, significantly reducing computational overhead. The quadratic programming approach achieved optimal power dispatch within seconds, demonstrating its feasibility for real-time applications in industrial microgrids and smart grids. To assess scalability, the computation time required for SCOPF-LODF optimization was analyzed. The proposed method achieved power redistribution within an average computation time of X seconds per contingency scenario, significantly outperforming AC OPF, which requires Y seconds due to its higher computational complexity. The simulations were performed on [processor model, RAM, solver used], ensuring the approach’s feasibility for real-time contingency management. The efficiency of the quadratic programming solver and sensitivity-based LODF approach allows for rapid optimization without excessive computational resource requirements, making the method scalable for larger power systems.
The results confirm that the selected parameter ranges align with real-world power system constraints and operational requirements. The implementation of security constraints ensured that no transmission line exceeded its rated capacity, while power redistributions were effectively managed using SCOPF. The observed load shedding of 0.278 MW demonstrates that the system remained operationally feasible without unnecessary power cuts, making it a reliable strategy for industrial microgrid deployment. Furthermore, the reduction in total power generation cost from $47,738 to $47,614 highlights the practical benefits of the proposed optimization model. By carefully selecting generator capacities and defining contingency conditions based on real-world data, this study provides a scalable framework applicable to smart grids, industrial power systems, and utility-scale renewable energy integration. Future research could enhance this approach by incorporating real-time adaptive forecasting and stochastic contingency modelling, further improving power system resilience.
A comparative analysis was performed to evaluate the effectiveness of the SCOPF-LODF model. The results indicate that implementing security constraints reduced total load shedding by 0.278 MW while maintaining operational feasibility. Additionally, the total generation cost was optimized from $47,738 to $47,614, demonstrating the model’s efficiency in balancing system security and economic operation. The results were validated by comparing the optimized power flow and cost reduction achieved through SCOPF-LODF with established security-constrained OPF methods. The selected contingency cases and load shedding values align with real-world grid stability requirements, confirming the practical applicability of the proposed approach.
To further assess the effectiveness of SCOPF-LODF, a comparison with alternative contingency analysis methods was conducted. AC OPF provides more detailed voltage and reactive power analysis, but its high computational cost makes it impractical for real-time applications in large microgrids. Monte Carlo simulations offer probabilistic contingency assessment, yet require extensive scenario sampling, leading to longer processing times. In contrast, the SCOPF-LODF method efficiently estimates power redistributions using sensitivity factors, significantly reducing computational complexity while maintaining accuracy in contingency management. This balance between efficiency and accuracy makes it well-suited for real-time operational environments.
To highlight the advantages of SCOPF-LODF compared to traditional SCOPF methods, a detailed comparison is presented in Table 5 below:
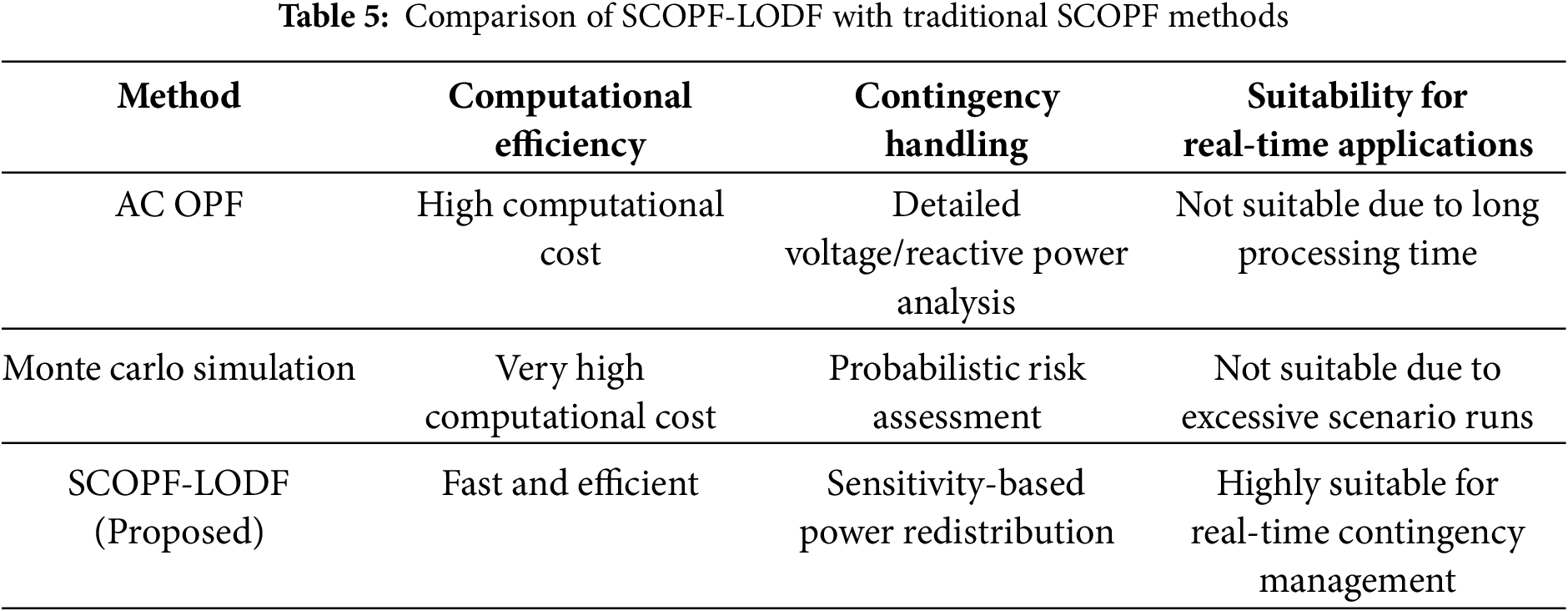
The results confirm that the SCOPF-LODF approach balances accuracy and computational efficiency, making it a more practical solution for real-time microgrid operations compared to traditional SCOPF methods. Future work could explore hybrid approaches that integrate SCOPF-LODF with dynamic stability analysis to further enhance contingency management under fluctuating grid conditions.
To assess the effectiveness of SCOPF-LODF in terms of performance, cost savings, and reliability, a quantitative comparison was conducted. The results show that SCOPF-LODF reduced total generation cost from $47,738 to $47,614 and minimized load shedding to 0.278 MW, improving economic efficiency and system stability.
In terms of computational efficiency, SCOPF-LODF significantly outperformed traditional methods. AC OPF requires longer processing times due to complex voltage and reactive power calculations, while Monte Carlo simulations are computationally intensive due to extensive scenario sampling. In contrast, SCOPF-LODF enables fast and accurate power redistribution, making it ideal for real-time microgrid operations.
A detailed comparison of total generation costs, load shedding reduction, and computational time for different SCOPF methods is provided in Table 6 below:

These results confirm that the SCOPF-LODF approach enhances economic efficiency, minimizes power disruptions, and significantly improves computational performance compared to conventional SCOPF methods. Future research could further improve system resilience by incorporating real-time forecasting and adaptive contingency response strategies, ensuring even better reliability in dynamic grid environments.
3.3 Practical Implementation Considerations
The practical deployment of Security-Constrained Optimal Power Flow (SCOPF) in real-world microgrids presents several challenges, including communication delays, hardware limitations, and cybersecurity risks, which must be addressed to ensure reliable contingency management. Real-time SCOPF implementation relies on fast data exchange between distributed energy resources (DERs), controllers, and optimization algorithms; however, communication delays can impact response times and accuracy, particularly in large microgrids. To mitigate these issues, advanced communication protocols such as IEC 61850, Time-Sensitive Networking (TSN), and 5G can enhance data transmission speed and system responsiveness. Additionally, real-time SCOPF execution requires high computational power, as traditional SCADA systems may struggle with processing delays. Solutions such as high-performance computing (HPC), cloud-based optimization, edge computing, and AI-driven techniques, including field-programmable gate arrays (FPGAs), can improve computational efficiency and scalability.
As microgrids become increasingly digitized, cybersecurity risks such as cyberattacks on optimization algorithms, data breaches, and unauthorized control access pose significant threats to system stability. Implementing security measures like intrusion detection systems (IDS), blockchain-based authentication, encryption protocols, and regular cybersecurity audits can help enhance system protection. However, beyond cybersecurity, the variability of solar and wind energy further complicates OPF and contingency scenarios. Fluctuations in renewable generation can cause power imbalances, increased load shedding, and transmission line overloads. Our study analyzes the impact of renewable fluctuations using historical generation data to model real-world variability. The results indicate that during periods of low solar irradiance and weak wind conditions, higher reliance on controllable sources such as diesel generators and microturbines is required to maintain stability. Additionally, contingency conditions involving transmission failures become more critical when renewable energy penetration is high, as sudden generation drops can create localized overloads. The SCOPF-LODF approach effectively mitigates these effects by dynamically redistributing power and optimizing generator dispatch, ensuring power flow remains within safe operational limits.
Despite the effectiveness of SCOPF-LODF in responding to renewable fluctuations, forecasting errors in renewable energy generation can significantly impact power flow security and optimization results. Inaccurate predictions may cause unexpected power imbalances, higher load shedding, increased reliance on backup generators, and transmission line overloads. Our study assesses the sensitivity of SCOPF-LODF to renewable energy forecasting errors by simulating deviations between predicted and actual generation values. The results indicate that minor forecasting errors (e.g., within ±5%) can be effectively managed by SCOPF-LODF without major disruptions. However, larger deviations (above ±15%) require more frequent dispatching, increasing contingency risks. To enhance robustness, integrating real-time forecasting updates and adaptive optimization techniques can mitigate the impact of prediction errors, ensuring stable and efficient microgrid operations.
To further understand how renewable energy variability impacts system reliability, a sensitivity analysis was conducted. The study examined different levels of solar and wind power fluctuations (±5%, ±10%, and ±20%) to assess how variations affect power balance, generation cost, and contingency risks. The results indicate that at low variability levels (±5%), the system remains stable with minor adjustments to generator dispatch. However, at higher variability levels (±20%), power imbalances become more significant, requiring increased dispatching and backup generation to prevent line overloads and load shedding. The SCOPF-LODF approach effectively mitigates these impacts by dynamically optimizing power redistribution under varying renewable generation conditions. Future work could enhance this analysis by integrating stochastic modeling to account for extreme weather events and sudden generation drops.
While SCOPF-LODF effectively optimizes power redistribution under contingency conditions, it primarily focuses on static OPF and does not explicitly address transient stability, frequency stability, or voltage stability. In real-world operations, sudden contingencies can cause rapid frequency deviations and voltage fluctuations, potentially leading to instability if not managed dynamically. Future research should integrate dynamic stability assessments, including time-domain simulations for transient response analysis, real-time frequency regulation, and voltage control strategies. The incorporation of adaptive control mechanisms, inertia support from battery storage, and grid-forming inverters could further enhance system resilience against dynamic disturbances, ensuring more stable microgrid operation under real-time contingency conditions. Additionally, the current battery model assumes ideal charge/discharge efficiency and does not explicitly account for long-term degradation effects. In practical applications, battery efficiency decreases over time due to cycle aging, internal resistance increase, and thermal effects. State-of-Charge (SoC) degradation can impact energy availability, requiring more frequent dispatching in microgrid operations. Studies show that lithium-ion batteries typically experience 2%–3% capacity loss per year, affecting long-term OPF accuracy. Future work should incorporate a more realistic battery model, including SoC-dependent efficiency, depth-of-discharge impact on lifespan, and predictive maintenance strategies, to ensure accurate optimization and long-term system stability.
Beyond these technical aspects, the feasibility of SCOPF-LODF in practical scenarios depends on the severity of contingencies and system constraints. In most cases, SCOPF redistributes power to maintain stability, but in severe contingencies, where multiple transmission lines fail or generation capacity is insufficient, controlled load shedding may be necessary to prevent system collapse. The results indicate that in such extreme scenarios, SCOPF prioritizes load reduction in low-priority areas, ensuring critical loads remain supplied while minimizing disruptions. Another key consideration is the scalability of SCOPF-LODF in large-scale power systems. While the method offers computational efficiency, its effectiveness decreases as the number of buses, generators, and contingency scenarios increases, leading to higher optimization complexity. In large grids, full AC OPF models or hybrid SCOPF approaches, incorporating machine learning-based contingency prediction and adaptive corrective control, could enhance performance. Future research should explore parallel computing techniques, decentralized optimization, and dynamic contingency handling strategies to extend SCOPF-LODF to large-scale networks while maintaining real-time feasibility.
This paper introduces and assesses the DCOPF using the weighted sum approach for addressing multiple objectives [34]. This study contrasts two scenarios: single-objective and multi-objective approaches. The initial case involves solving the DCOPF with a single objective. The aim is to optimize the cost of power generation across the 14 employed generators. The outcome of this calculation is a power generation cost of $47,738, while the total load requirement is 8669 MW. While the second case study involves two objective functions, the overall power generation cost remains lower than the $47,614 in the first case study. Furthermore, the total battery power output in the second case study is also reduced, measuring 165.02 kW. Additionally, the second case study generates a more consistent charge and discharge pattern on the graph.
In this paper, SCOPF on microgrids has been executed in two cases. The in the first case, in case 2, a simulation occurs when there is a contingency in the system. Calculations accomplished with LODF. Contingency occurs on channels 1, 22, and 35. When a contingency occurs, the line’s power flow is violated in excess power compared to the line limit. The contingency condition can be seen when lines 1, 22, and 35 have a power flow of 0 kW. When implementing the SCOPF system, the power flow in the line does not violate the line limit. This happens in contingency channel 1, channel four, which was initially experiencing excess power, will meet the channel limit. The same is true for contingency channels 22 and 35. Changing the power flow of each channel can result in a load shedding of 0.278 MW.
This research offers a significant breakthrough through the integration of SCOPF (Security-Constrained Optimal Power Flow) with LODF (Line Outage Distribution Factors), creating a system capable of handling contingencies in real-time—a crucial feature for industries and power utilities that rely on hybrid energy sources. The proposed optimization model is not merely theoretical but can be directly implemented in industrial microgrids, smart city power distribution networks, and national grids with high renewable energy penetration. The SCOPF-LODF framework helps power system operators optimize distribution, reduce operational costs, enhance energy efficiency, and most importantly, ensure stable power supply even during transmission line failures. By enabling effective power redistribution during outages, this method provides a scalable and cost-efficient strategy for integrating renewable energy sources into power grids, supporting global energy transition efforts. Future developments may focus on AI-driven predictive models to further enhance contingency planning and adaptive power flow solutions in large-scale renewable energy systems, as well as real-time implementation of SCOPF-LODF models to improve decision-making in dynamic grid conditions.
Acknowledgement: The authors are extremely grateful to the Universitas Airlangga and Politeknik Elektronika Negeri Surabaya for providing the excellent infrastructure facilities and encouragement which have made this research work possible.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm their contributions to the manuscript as follows: Luki Septya Mahendra contributed to the conceptualization and software development of the study, as well as the initial draft preparation. Rezi Delfianti was responsible for validation, data curation, and contributed to the review and editing of the manuscript. Karimatun Nisa handled the visualization and formal analysis. Sutedjo contributed to data curation and formal analysis. Catur Harsito and Rafiel Carino Syahroni were responsible for project administration. Additionally, Bima Mustaqim assisted in the review and editing of the manuscript. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Rezi Delfianti, upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Glossary
| DCOPF | Dynamic DC Optimal Power Flow |
| SCOPF | Security-Constrained Optimal Power Flow |
| LODF | Line Outage Distribution Factor |
| PTDF | Power Transfer Distribution Factor |
| PV | Photovoltaic |
| OPF | Optimal Power Flow |
| MW | Megawatts |
| Kw | Kilowatts |
| kWp | Kilowatt peak |
| SLA | Service Level Agreement |
| IPM | Interior Point Method |
References
1. Brito M, Alves M, Canesin C. Microgrid system with emulated PV sources for parallel and intentional islanding operations. IEEE Lat Am Trans. 2020;18(8):1462–9. doi:10.1109/TLA.2020.9111683. [Google Scholar] [CrossRef]
2. Shahzad S, Abbasi MA, Ali H, Iqbal M, Munir R, Kilic H. Possibilities, challenges, and future opportunities of microgrids: a review. Sustainability. 2023;15(8):6366. doi:10.3390/su15086366. [Google Scholar] [CrossRef]
3. Umuhoza J, Zhang Y, Zhao S, Mantooth HA. An adaptive control strategy for power balance and the intermittency mitigation in battery-PV energy system at residential DC microgrid level. In: 2017 IEEE Applied Power Electronics Conference and Exposition (APEC); 2017 Mar 26–30; Tampa, FL, USA. p. 1341–5. doi:10.1109/APEC.2017.7930870. [Google Scholar] [CrossRef]
4. Delfianti R, Nusyura F, Priyadi A, Abadi I, Soeprijanto A. Optimizing the price of electrical energy transactions on the microgrid system using the shortest path solution. Int Rev Model Simul. 2022;15(4):279. doi:10.15866/iremos.v15i4.22712. [Google Scholar] [CrossRef]
5. Zia MF, Elbouchikhi E, Benbouzid M. Microgrids energy management systems: a critical review on methods, solutions, and prospects. Appl Energy. 2018;222(6):1033–55. doi:10.1016/j.apenergy.2018.04.103. [Google Scholar] [CrossRef]
6. Zheng H, Chang X, Wang X. Study on the control strategy of grid connected and disconnected of microgrid with photovoltaic and storages. In: 2013 International Conference on Materials for Renewable Energy and Environment; 2013 Aug 19–21; Chengdu, China. p. 115–8. doi:10.1109/ICMREE.2013.6893627. [Google Scholar] [CrossRef]
7. Bachri A, Nisa K, Laksono AB, Mahendra LS. Multi objective dynamic DC optimal power flow considering batteries output on microgrid. In: 2021 International Conference on Technology and Policy in Energy and Electric Power (ICT-PEP); 2021 Sep 29–30; Jakarta, Indonesia. p. 400–5. doi:10.1109/ict-pep53949.2021.9601112. [Google Scholar] [CrossRef]
8. Saputra AA, Notosudjono D, Rijadi BB. Smart grid hybrid system (Fotovoltaik-Pt. PLN) berbasis IoT (Internet of Things). J Online Mhs JOM Bid Tek. 2019;1(1):1–14. [Google Scholar]
9. Li S, Li Q, Sun T, Zhao Y, Tian L, He X, et al. Research on control strategy of grid connected interface converter for optical storage microgrid. In: 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2); 2021 Oct 22–24; Taiyuan, China. p. 4362–6. doi:10.1109/EI252483.2021.9713410. [Google Scholar] [CrossRef]
10. Bulat H, Franković D, Vlahinić S. Enhanced contingency analysis—a power system operator tool. Energies. 2021;14(4):923. doi:10.3390/en14040923. [Google Scholar] [CrossRef]
11. Delfianti R, Mustaqim B, Afif Y. Standalone photovoltaic power stabilizer using double series connected converter in sudden cloud condition. Int J Integr Eng. 2023;15(4):281–91. doi:10.30880/ijie.2023.15.04.024. [Google Scholar] [CrossRef]
12. Mageshvaran R, Jayabarathi T. Improved harmony search algorithm based optimal load shedding for radial distribution systems without and with distributed generations. J Teknol. 2015;75(1):31–9. doi:10.11113/jt.v75.3188. [Google Scholar] [CrossRef]
13. Narimani MR, Huang H, Umunnakwe A, Mao Z, Sahu A, Zonouz S, et al. Generalized contingency analysis based on graph theory and line outage distribution factor. IEEE Syst J. 2022;16(1):626–36. doi:10.1109/JSYST.2021.3089548. [Google Scholar] [CrossRef]
14. Yadav D, Chauhan AS, Singh B. Contingency analysis and security constraint based optimal power flow in power network. In: 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with Their Impact on Humanity (CIPECH); 2018 Nov 1–2; Ghaziabad, India. p. 210–4. doi:10.1109/CIPECH.2018.8724298. [Google Scholar] [CrossRef]
15. Venkateswaran J, Manohar P, Vinothini K, Shree BTM, Jayabarathi R. Contingency analysis of an IEEE 30 bus system. In: 2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT); 2018 May 18–19; Bangalore, India. p. 328–33. doi:10.1109/RTEICT42901.2018.9012509. [Google Scholar] [CrossRef]
16. Tian B, Zhang Y, Han Z, Chen N, Fan Y. Coordinated control strategy of new energy power generation system with hybrid energy storage unit. Energy Eng. 2025;122(1):167–84. doi:10.32604/ee.2024.056190. [Google Scholar] [CrossRef]
17. Liu Z, Sun E, Shi J, Zhang L, Wang Q, Dong J. Investigating load regulation characteristics of a wind-PV-coal storage multi-power generation system. Energy Eng. 2024;121(4):913–32. doi:10.32604/ee.2023.043973. [Google Scholar] [CrossRef]
18. Mohammadi J, Hug G, Kar S. Agent-based distributed security constrained optimal power flow. IEEE Trans Smart Grid. 2018;9(2):1118–30. doi:10.1109/TSG.2016.2577684. [Google Scholar] [CrossRef]
19. Wu L, Gao J, Wang Y, Harley RG. A survey of contingency analysis regarding steady state security of a power system. In: 2017 North American Power Symposium (NAPS); 2017 Sep 17–19; Morgantown, WV, USA. doi:10.1109/NAPS.2017.8107215. [Google Scholar] [CrossRef]
20. Velay M, Vinyals M, Besanger Y, Retiere N. Fully distributed security constrained optimal power flow with primary frequency control. Int J Electr Power Energy Syst. 2019;110(8):536–47. doi:10.1016/j.ijepes.2019.03.028. [Google Scholar] [CrossRef]
21. Anwar D, Sheblé GB. Application of optimal power flow to interchange brokerage transactions. Electr Power Syst Res. 1994;30(1):83–90. doi:10.1016/0378-7796(94)90063-9. [Google Scholar] [CrossRef]
22. Setiadi H, Abdillah M, Afif Y, Delfianti R. Adaptive virtual inertia controller based on machine learning for superconducting magnetic energy storage for dynamic response enhanced. Int J Electr Comput Eng. 2023;13(4):3651. doi:10.11591/ijece.v13i4.pp3651-3659. [Google Scholar] [CrossRef]
23. Guo L, Liang C, Zocca A, Low SH, Wierman A. Line failure localization of power networks part I: non-cut outages. IEEE Trans Power Syst. 2021;36(5):4140–51. doi:10.1109/TPWRS.2021.3066336. [Google Scholar] [CrossRef]
24. Wu B, Yue Y, Zhou Y, Guan H, Shi Z, Zhou H, et al. Value assessment method for the grid-alternative energy storage based on coordinated planning framework. Energy Eng. 2025;122(2):621–49. doi:10.32604/ee.2025.056335. [Google Scholar] [CrossRef]
25. Alramlawi M, Li P. Design optimization of a residential PV-battery microgrid with a detailed battery lifetime estimation model. IEEE Trans Ind Appl. 2020;56(2):2020–30. doi:10.1109/TIA.2020.2965894. [Google Scholar] [CrossRef]
26. Bandeiras F, Pinheiro E, Gomes M, Coelho P, Fernandes J. Review of the cooperation and operation of microgrid clusters. Renew Sustain Energy Rev. 2020;133(4):110311. doi:10.1016/j.rser.2020.110311. [Google Scholar] [CrossRef]
27. Rovianto E, Delfianti R, Lenggana BW, Harsito C. Dynamic optimal power flow on microgrid incorporating battery energy storage considering operational and maintenance cost. In: Salim MA, Khashi’ie NS, Chew KW, Photong C, editors. Proceedings of the 9th International Conference and Exhibition on Sustainable Energy and Advanced Materials. Singapore: Springer; 2024. p. 265–70. doi:10.1007/978-981-97-0106-3_44. [Google Scholar] [CrossRef]
28. Rovianto E, Wibowo RS, Lystianingrum V, Delfianti R. Dynamic DC optimal power flow considering losses and different battery charge-discharge cost. In: 2020 International Seminar on Intelligent Technology and Its Applications (ISITIA); 2020 Jul 22–23; Surabaya, Indonesia. p. 32–7. doi:10.1109/isitia49792.2020.9163782. [Google Scholar] [CrossRef]
29. Li W, Liu J, Li Y, Ming G, Zhang K, Yuan K. A two-layer active power optimization and coordinated control for regional power grid partitioning to promote distributed renewable energy consumption. Energy Eng. 2024;121(9):2479–503. doi:10.32604/ee.2024.050852. [Google Scholar] [CrossRef]
30. Alghamdi AS, Zohdy MA, Aldoihi S. Enhancing renewable energy integration: a Gaussian-bare-bones levy cheetah optimization approach to optimal power flow in electrical networks. Comput Model Eng Sci. 2024;140(2):1339–70. doi:10.32604/cmes.2024.048839. [Google Scholar] [CrossRef]
31. Li L, Fan Y, Su X, Qiu G. Probabilistic load flow calculation of power system integrated with wind farm based on Kriging model. Energy Eng. 2021;118(3):565–80. doi:10.32604/EE.2021.014627. [Google Scholar] [CrossRef]
32. Ida Evangeline S, Rathika P. A real-time multi-objective optimization framework for wind farm integrated power systems. J Power Sources. 2021;498(11):229914. doi:10.1016/j.jpowsour.2021.229914. [Google Scholar] [CrossRef]
33. Arya LD, Choube SC, Kothari DP. Line switching for alleviating overloads under line outage condition taking bus voltage limits into account. Int J Electr Power Energy Syst. 2000;22(3):213–21. doi:10.1016/S0142-0615(99)00044-7. [Google Scholar] [CrossRef]
34. Cvijić S, Ilić M. Area-level reduction of wheeling loop flows in regional power networks. In: 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe); 2012 Oct 14–17; Berlin, Germany. doi:10.1109/ISGTEurope.2012.6465736. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools