Improved Multi-Fusion Black-Winged Kite Algorithm for Optimizing Stochastic Configuration Networks for Lithium Battery Remaining Life Prediction

1  Introduction

With the rapid development of renewable energy and electric vehicles, Li-ion batteries, as key energy storage devices, are widely used in various electronic products and electric vehicles. The State of Health (SOH) of Li-ion batteries not only directly affects their performance and lifetime [1], but also directly affects the safety and economic efficiency of electric vehicles. Therefore, the development of an efficient and reliable SOH estimation method is of great theoretical and practical significance.

Model-based estimation and data-driven estimation are currently the two major approaches utilized to calculate Li-ion batteries’ SOH. Model-based approaches often use physical models of the battery, but because of the intricacy of battery properties and the operating environment, these models’ accuracy is frequently constrained [2]. Data-driven approaches, such as machine learning and deep learning techniques, on the other hand, are able to extract features from historical data, providing more flexible estimation capabilities [3]. Deep learning can be applied for both prediction and classification tasks [4]. The method extracts parameters such as current, voltage, and capacity as health factors (HF) in charging and discharging historical data and is used as inputs to the SOH estimation model [5]. Liu et al. [6] utilized an artificial bee colony (ABC) algorithm and long short-term memory (LSTM) network combined with a dropout technique to estimate the Li-ion battery. Wang et al. [7] used Cheetah optimization (CO) and Extreme learning machine (ELM) to predict the remaining life of Li-ion batteries. Li et al. [8] used (the Grey Wolf Optimizer Algorithm Grey Wolf Optimizer, GWO) and Gated Recurrent Unit (GRU) to estimate the battery’s remaining life and obtained good results. While the optimization algorithm’s ability to find the optimal solution and the model’s learning style and generalization ability are important factors in SOH estimation, the combination of algorithm and model effectively increases the accuracy of SOH estimation. The optimization algorithm’s ability to find the optimum and the model’s learning style and generalization ability play a key role in the estimation of SOH [9]. However, there are some limitations in practical applications, among which the LSTM neural network is more sensitive to the setting of model parameters, ELM neural network has limited generalization ability and is sensitive to noise which may lead to the degradation of model performance, and the GRU model has a longer training time and more complex parameter tuning.

In 2017, Wang and Li [10] proposed a stochastic configuration network (SCN) for the first time. Compared with LSTM and GRU models, SCN adopted an incremental learning approach and introduced a supervisory mechanism to adjust the network structure and weights during the learning process to achieve adaptive modeling of the data, and this flexibility makes it more advantageous when dealing with complex and nonlinear data of lithium batteries. Zhang and Ding [11] combined the Sparrow Search Algorithm (SSA) with the Stochastic Configuration Network (SCN) and proved the feasibility and effectiveness of their proposed method. Guo et al. [12] proposed an SOH estimation method combining the parameter-optimized multivariate variational mode decomposition (MVMD) and stochastic configuration network (SCN) and achieved good measurement accuracy.

Black winged kite algorithm (BKA) [13] is a novel meta-heuristic algorithm proposed in 2024. Compared with learning algorithms such as Particle Swarm Optimization (PSO) [14], Grey Wolf Optimizer (GWO) [15], Ant Colony Optimization (ACO) [16], BKA shows stronger optimization ability and higher efficiency on benchmark functions. However, an analysis of the process of BKA reveals that there are defects in the global search phase, including cases of falling into local optimal solutions. While the main feature of chaos is that it does not repeat the previous behavior [17]. Therefore, the SBKA algorithm is proposed by incorporating chaotic mapping to improve the initialization of the population phase.

In conclusion, this study suggests the SBKA-CLSCN model as a solution to the issues of determining the ideal hyperparameters and enhancing the model’s capacity for generalization. The black-winged kite population is initialized using Sine chaotic mapping to increase the algorithm’s convergence speed, and the global searching capability is enhanced using the golden sine strategy [18]. The Cauchy distribution approach is also applied to optimize the model’s weights and biases, and the regularization technique is employed to enhance the model’s capacity for generalization. Tests show that SBKA-CLSCN produces satisfactory regression results. The main contributions of this paper are: (1) HI sequences are extracted from the constant-current charging stage of the battery; (2) the global search capability of the BKA algorithm is enhanced and the SBKA algorithm is proposed; (3) the generalization capability of the SCN model is enhanced and the CLSCN model is proposed; and (4) the SBKA-CLSCN prediction model has been developed and experimentally compared.

2  Data Processing

2.1 Battery Data Set

Four battery samples (No. CS2_35, CS2_36, CS2_37, and CS2_38) were chosen as experimental data for this research from CALCE’s battery dataset. The precise procedure for charging and discharging the batteries is as follows:

(1)   Charging: 1.1 Ah battery with a rated capacity, charged first at 0.5 C constant current, switched to constant voltage charging when terminal voltage reached 4.2 V, and then cut to constant voltage charging until charging current was less than 0.05 A.

(2)   Discharge: Continue to discharge at a steady 0.5 C current until the terminal voltage falls to 2.7 V, marking the conclusion of the single charge/discharge cycle.

(3)   The aging experiment was terminated when the batteries reached the cut-off life after repeated charging and discharging operations. The CALCE failure threshold in this study is set at 80% of the rated capacity or when the capacity meets the 0.85 Ah failure threshold. Fig. 1 displays the four batteries’ full-cycle capacity decline trends.

Figure 1: Battery capacity decay curve

2.2 Battery HI Extraction

The resistance of CS2 is depicted in Fig. 2a,b, along with the variation of the curves of constant current charging time (CCCT) and constant voltage charging time (CVCT), respectively. As the number of charging and discharging cycles increases, the internal resistance of the batteries rises, and the charging time for constant voltage gradually rises while the charging time for constant current gradually decreases. These changes indicate that the batteries’ performance is deteriorating. Thus, HF1 and HF2 are chosen to symbolize the charging times with constant voltage and current, respectively.

Figure 2: Constant current voltage charging time

2.3 Correlation Analysis

In this paper, the HI of the battery is evaluated using the Pearson correlation coefficient [19], which is calculated as follows:

Person=∑i=1n(xi−x¯)(yi−y¯)∑i=1n(xi−x¯)2∑i=1n(yi−y¯)2,(1)

the formula uses xi and yi to represent the data’s ith value and x¯ and y¯ to represent the variables’ mean value. The correlation coefficient indicates the relationship between the two data sets; the closer the Pearson is to 1, the stronger the correlation. The correlation coefficients of HF1 and HF2 in CALCE’s CS2 dataset with capacity, respectively, are shown in Table 1.

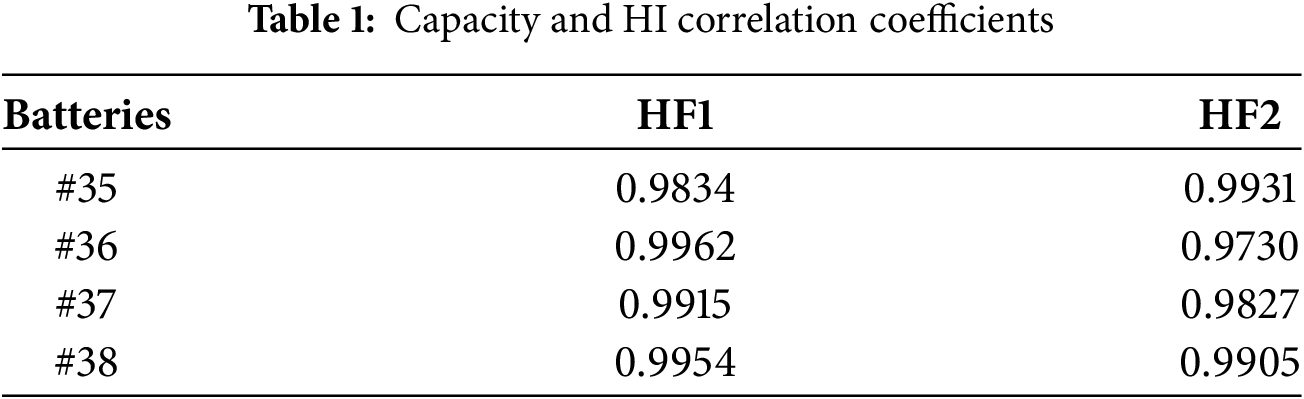
Table 1 shows that the extracted health variables and the capacity have a good link, and they can be chosen as the capacity’s health factors because all of the Pearson coefficients fall between 0.9 and 1.0.

3  Research on Related Technologies

3.1 Randomized Network Configuration

SCN is a randomized weight neural network, similar to a feed-forward neural network; both contain input, hidden, and output layers [20]. The supervisory method is used to randomly set the input weights and bias of the nodes in the hidden layer so that the model can be completed, progressively increase the number of nodes in the hidden layer, and determine the output weights using the least squares approach [21]. The topology of the SCN network structure is shown in Fig. 3.

Figure 3: SCN network structure topology diagram

The process of constructing the SCN network model is as follows:

Given the dataset, X={x1,x2,⋯,xN} denotes feature data, xi={xi,1,xi,2,⋯,xi,d}∈Rd; Y={y1,y2,⋯,yN} denotes labeled data, yi={yi,1,yi,2,⋯yi,m}∈Rm; i=1,2,⋯,N.

Step 1: Given the objective function f:Rd→Rm, assuming that L−1 nodes of the SCN implicit layer have been generated, the current network output is calculated by the formula as in Eq. (2):

fL−1(X)=∑j=1L−1βjgj(wjTX+bj),L=1,2,…Lmax,f0=0,(2)

where βj denotes the output weight of the node j in the implicit layer, g(⋅) denotes the activation function, wj and bj denotes the input weight and bias of the jth node in the implicit layer, respectively, j=1,2,⋯Lmax. Since the value of the sigmoid function between 0 and 1 conforms to the probability distribution, is conductible everywhere, and changes rapidly near 0, the sigmoid function of Eq. (3) is chosen as the activation function.

g(x)=11+exp⁡(−x).(3)

Step 2: Calculate the current network residual vector formula as in Eq. (4):

eL−1=f−fL−1(X)=[eL−1,1(X),eL−1,2(X),…,eL−1,m(X)]T∈RN×m.(4)

Step 3: If ‖eL−1‖2 does not reach the preset error ε or does not reach the maximum number of nodes Lmax, then increase the L implicit layer node, and according to the formula supervision mechanism determine the input weight and bias as in Eq. (5); at this time the SCN output model is:

fL=fL−1+βLgL,(5)

ξL,q=(eL−1,qT⋅hL)2hLThL−(1−r−μL)‖eL−1,q‖2,q=1,2⋯,m,(6)

ξL=∑q=1mξL,q≥0,(7)

hL=[gL(wLTx1+bL),gL(wLTx2+bL),…gL(wLTxN+bL)]T∈RN.(8)

Step 4: Determine the implicit layer node output weights as in Eq. (9):

β=arg⁡minβ‖Hβ−Y‖2=H+Y,(9)

where H+ denotes the generalized inverse of H and H=[h1,h2,⋯,hL].

Step 5: Calculate the model output f as in Eq. (10).

f=Hβ.(10)

3.2 BKA Optimization Algorithm

The main principle behind heuristic algorithms, which are search and optimization techniques used to solve complicated problems, is to identify the best answer by searching the solution space within a given time frame. Because of its exceptional adaptability to changes in the target location and environment, the black-winged kite algorithm combines the two mutation strategies of Cauchy and Leader, improving the algorithm’s searching ability and speed of convergence. The attack and migration patterns of black-winged kites served as the model for this optimization algorithm.

Step 1: Initialize the population

BK=[BK1,1BK1,2⋯BK1,dimBK2,1BK2,2⋯BK2,dim⋮⋮⋮⋮BKpop,1BKpop,2⋯BKpop,dim],(11)

initialize the random solution and the above matrix represents the position of each black-winged kite. pop is representing the number of solutions, dim is the size of the dimension of the given problem, and BKi,j refers to the ith black-winged kite and the jth dimension, which is needed to distribute the position of each black-winged kite equally.

Xi=BKlb+rand(BKub−BKlb),(12)

the lower and upper limits are represented by the lb and ub, while the rands are randomly selected values between zero and one. The i stands for the integers between 1 and 0. At initiation, the most adapted individual should be chosen because the Leader XL in the population is regarded as the best position among them.

fbest=min(f(Xi)),(13)

Xi=X(find(fbest==f(Xi))).(14)

Step 2: Offensive behavior

The black-winged kite uses a technique that may be used for global search. The mathematical model of its attack behavior can be represented as follows: it monitors its prey, changes the angle of its wings and tail in flight based on the speed of the wind, and then swiftly swoops to attack.

yt+1i,j={yti,j+n(1+sin⁡(r))×yti,jp<ryti,j+n×(2r−1)×yti,jelse,(15)

n=0.05×e−2×(tT)2,(16)

in the jth and (t + 1) iteration steps, respectively, yti,j and yt+1i,j indicate the location of the ith black-winged kite. p is a constant of 0.9, while r is a random number between 0 and 1. T is the number of iterations that have been finished thus far, and T is the total number of iterations.

Step 3: Migratory behavior

In order to adjust to seasonal variations, birds create migratory movements, which are often guided by a leader. Assuming that the current fitness is less than the stochastic fitness, the leader ceases leading and joins the migrating population, indicating that it is unfit to lead. This is the Leader policy that is incorporated into the BKA algorithm. The leader is in charge of the population’s migration if the present fitness is higher than the stochastic fitness. This tactic actively chooses capable leaders to guarantee the migration’s success, and the attack behavior’s mathematical model can be written as follows:

yt+1i,j={yti,j+C(0,1)×(yti,j−Ltj)Fi<Friyti,j+C(0,1)×(Ltj−m×yti,j)else,(17)

m=2×sin⁡(r+π/2),(18)

where yti,j represents the top scorer of the black-winged kite of dimension j in the tth iteration thus far. Any black-winged kite’s jth dimensional current position in the tth iteration is indicated by the Fi, represents the fitness value of each black-winged kite in the tth iteration’s jth dimensional random point. The following is the formula for the Cauchy distribution’s probability density function:

f(x,δ,μ)=1πδδ2+(x−μ)2,−∞<x<∞,(19)

when δ = 1 and μ = 0, the standard form of the probability density function is as follows:

f(x,δ,μ)=1π1x2+1,−∞<x<∞.(20)

4  SBKA-CLSCN

4.1 Improvement Strategies for the Black-Winged Kite Optimization Algorithm

The BKA method randomly creates the starting population, resulting in an uneven distribution and a lack of diversity in the solution space. This, in turn, reduces the accuracy and speed of convergence. This is the first of two primary improvement efforts. The second issue is the imbalance between global search and local development. The BKA algorithm improves its ability to find the optimal solution by combining the Cauchy mutation and the Leader strategy. However, this imbalance still exists and can lead to local optimal solution problems.

1. Sine Chaos Mapping Initialization Population

This paper uses Sine chaotic mapping to initialize the population in order to address the issue of randomly generating the initial population, which leads to uneven distribution and a lack of diversity in the solution space. This method has good coverage ability and avoids the problem of concentrating in a particular region, increasing search diversity and maintaining a large variable range during the search process, which aids in finding a more optimal solution to complex problems.

Sine chaotic mapping is defined as follows:

Yi+1=rsin⁡(πYi),(21)

Xi,d=Ld+(1+Yi,dUd−Ld2),(22)

where Yi∈[−1,1] is the chaotic sequence, r is the control parameter, and Ud and Ld represent the upper and lower limits of the d-dimensional search range.

Sine mapping is extremely chaotic and is controlled by r, Fig. 4 which shows the bifurcation diagram of sine mapping. From the figure, it can be seen that the chaotic performance is in the optimal state when the control parameter r is constantly approaching −1 and 1, which enables Yi to be uniformly distributed between them, and therefore in the subsequent experiments r = −1.

Figure 4: Sine chaotic mapping bifurcation map

2. Gold Sine Strategy

In order to achieve a balanced state of global search and local exploitation, GSA uses the sinusoidal function, which is a mathematical function with a strong global search capability, for iterative optimization. At the same time, it introduces the golden section in the iterative update of the position information, allowing the algorithm to search the local area fully.

The improved position update formula is as follows:

yt+1i,j={yti,j∗|sin⁡(r1)|+|sin⁡(r2)|∗n∗(1+sin⁡(r))∗|x1∗Ljt−x2∗yti,j|p<ryti,j∗|sin⁡(r1)|+|sin⁡(r2)|∗n∗(2r−1)∗|x1∗Ljt−x2∗yti,j|else,(23)

where r1 is the random number between [0,2π], r2 is the random number between [0,π], r1 represents the distance of moving, r2 represents the direction of moving; Ljt denotes the black-winged kite’s ideal attack position in the t iteration’s jth dimension; x1 and x2 are the coefficients obtained by the introduction of the golden section, τ is the golden section coefficient (5−1)/2, and the computational formulas are shown as follows:

x1=−π+(1−π)∗2π,(24)

x2=−π+τ∗2π.(25)

4.2 Improvement of SCN

In the original SCN, the input weights w and biases b of the hidden layer nodes are randomly generated from a predefined uniform distribution. However, experimental results show that different input weights and biases lead to varying degrees of reduction in network residuals, which in turn affects the convergence speed and structural compactness of the model. To address this issue, this paper proposes an improved stochastic configuration network, called the Cauchy and Laplace Stochastic Configuration Network (CLSCN).

1. Kersey distribution

It is important to discuss the optimal randomization of the weights and biases in SCN algorithms because, for the original SCN model, where the weights w and biases b are randomly generated from a uniform distribution, randomly generating different weights and biases affects the variation of the network residuals. A neural network architecture that randomly assigns the weights well can greatly outperform a more flawed architecture that finely tunes the weights.

The Cauchy distribution is used in this study for bias and weight selection at random. The Cauchy distribution approach is used for optimization, where the following is the conventional Cauchy distribution probability density function:

F(x)=1πarctan⁡(2(x−μc)σ)+12,(26)

where μc is the position parameter and σ is the scale parameter.

2. Laplace regularization

To further improve the robustness of SCN, Laplace regularized SCN is used in this paper.

β∗=arg⁡minβ‖HLβ−Y‖F2+α2Tr((Hβ)TLHβ),(27)

where L denotes the Laplace matrix and α denotes the Laplace regularization factor. Taking the derivatives of both sides of the equation of Eq. (27) simultaneously gives:

β=(HTH+αHTLH)−1HTY.(28)

Furthermore, the Laplace matrix can be computed as:

L=D−12⋅(D−S)⋅D−12.(29)

The similarity matrix S is built with a Gaussian radial basis function:

Sij=exp⁡(−0.5∗‖xi−xj‖2).(30)

D is the diagonal matrix:

Dii=∑j=1NSij.(31)

The flowchart of the CLSCN algorithm is shown in Fig. 5:

Figure 5: The flowchart of CLSCN algorithm

4.3 Implementation of SBKA-CLSCN

The performance of the stochastic configuration network is directly impacted by the hyperparameter settings in the SCN model; however, the parameters r and λ are constrained by the predefined range. This study optimizes the regularization parameters r and the scale factor λ in the stochastic configuration network model, known as SBKA-CLSCN, using an enhanced black-winged kite optimization algorithm to increase the accuracy and efficiency of SCN. In the meantime, Fig. 6 proposes the SBKA-CLSCN associated flowchart.

Figure 6: The flowchart of SBKA-CLSCN algorithm

The steps to achieve this are as follows:

Step 1: Initialize SBKA-CLSCN parameters

Initialize the population size (pop), the number of dimensions (D), the upper bound (ub) and lower bound (lb) of r and λ, the control parameter (µ), the maximum number of hidden nodes (Lmax), the maximum number of candidate nodes (Tmax), the maximum number of iterations (T), the tolerance error (ε), and the Laplace regularization factor α.

Step 2: Build and train SCN models

Individuals of the randomly initialized population are used as initialization parameters r and λ, and the CLSCN model is constructed and trained according to the above equation.

Step 3: Update regularization parameters and scale factors

The regularization parameters and scale factors are updated according to the formula.

Step 4: Calculate the fitness value

The root mean square error (RMSE) is selected as the fitness function to evaluate the SBKA-CLSCN as in Eq. (32):

ffitness=∑n=1N(ym−y^m)2/N,(32)

where N represents the number of samples, ym represents the sample true value and y^m represents the sample output value.

Step 5: Output SBKA-CLSCN test results

When the specified tolerance is met, or the maximum number of iterations is reached, then the adaptation value is optimal, thus obtaining the optimal hyperparameters and outputting the resultant values. The flowchart of the SBKA-CLSCN algorithm is shown in Fig. 6.

5  Experimental Results and Comparative Analysis

5.1 Error Evaluation Indicators

The optimization algorithm’s performance was examined through experiments using the average (Ave) and standard deviation (Std). The following formulas were utilized to assess and examine the model estimation effect utilizing the mean absolute error (MAE) and root mean square error (RMSE) error metrics:

Std=1n∑i=1n(xi−x¯)2,(33)

RMSE=1n∑i=1n(y^−yi)2,(34)

MAE=1n∑i=1n|y^i−yi|,(35)

where n stands for the number of samples, sample value, overall sample mean, sample predicted value, and sample true value.

5.2 SBKA Performance Testing

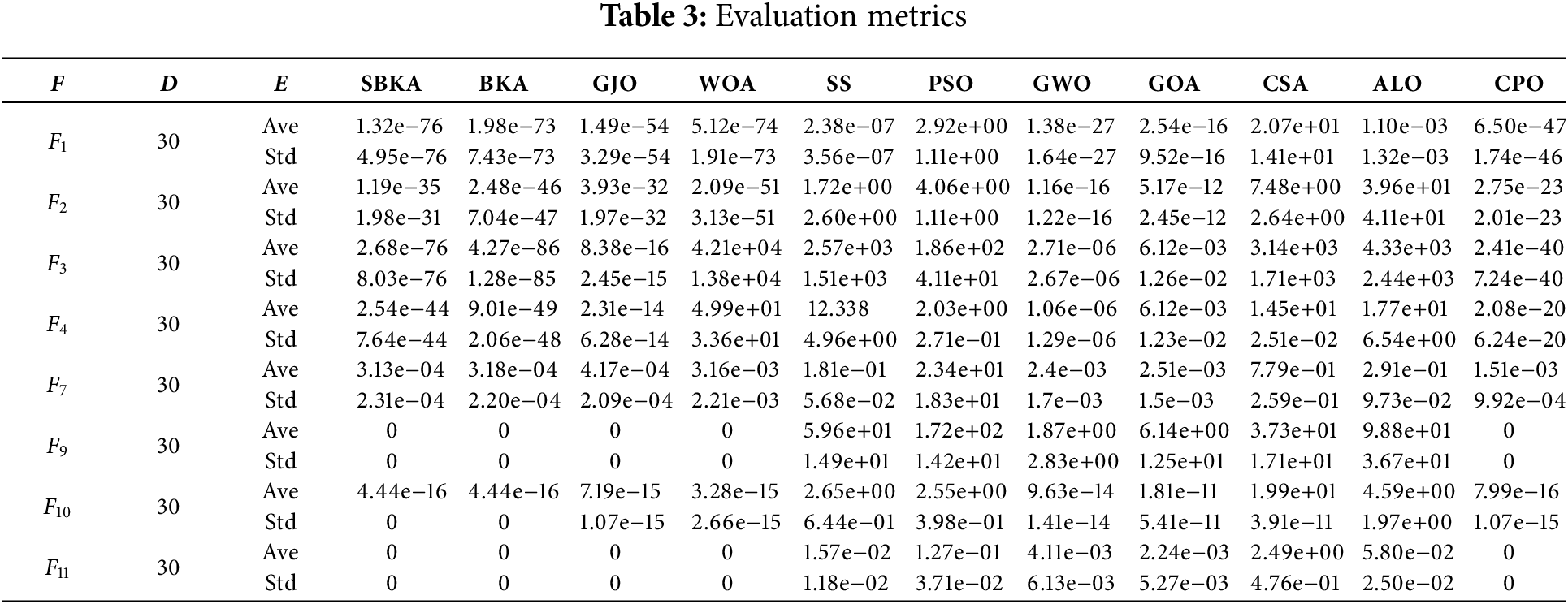
SBKA is tested and compared with ten optimization algorithms of BKA, CPO, ALO, CSA, GOA, GWO, PSO, SS, WOA, and GJO. The nine types of objective functions are displayed in the table. Eight types of benchmark functions are chosen for this experiment, as indicated in Table 2, of which one is a single-peak function. The other is a multidimensional function, as indicated in Table 1. The experiment’s rationality is ensured by setting the parameters of all the algorithms to the same values and 500 iterations with a population size of N = 30. Fig. 7 displays the convergence curve for each optimization procedure.

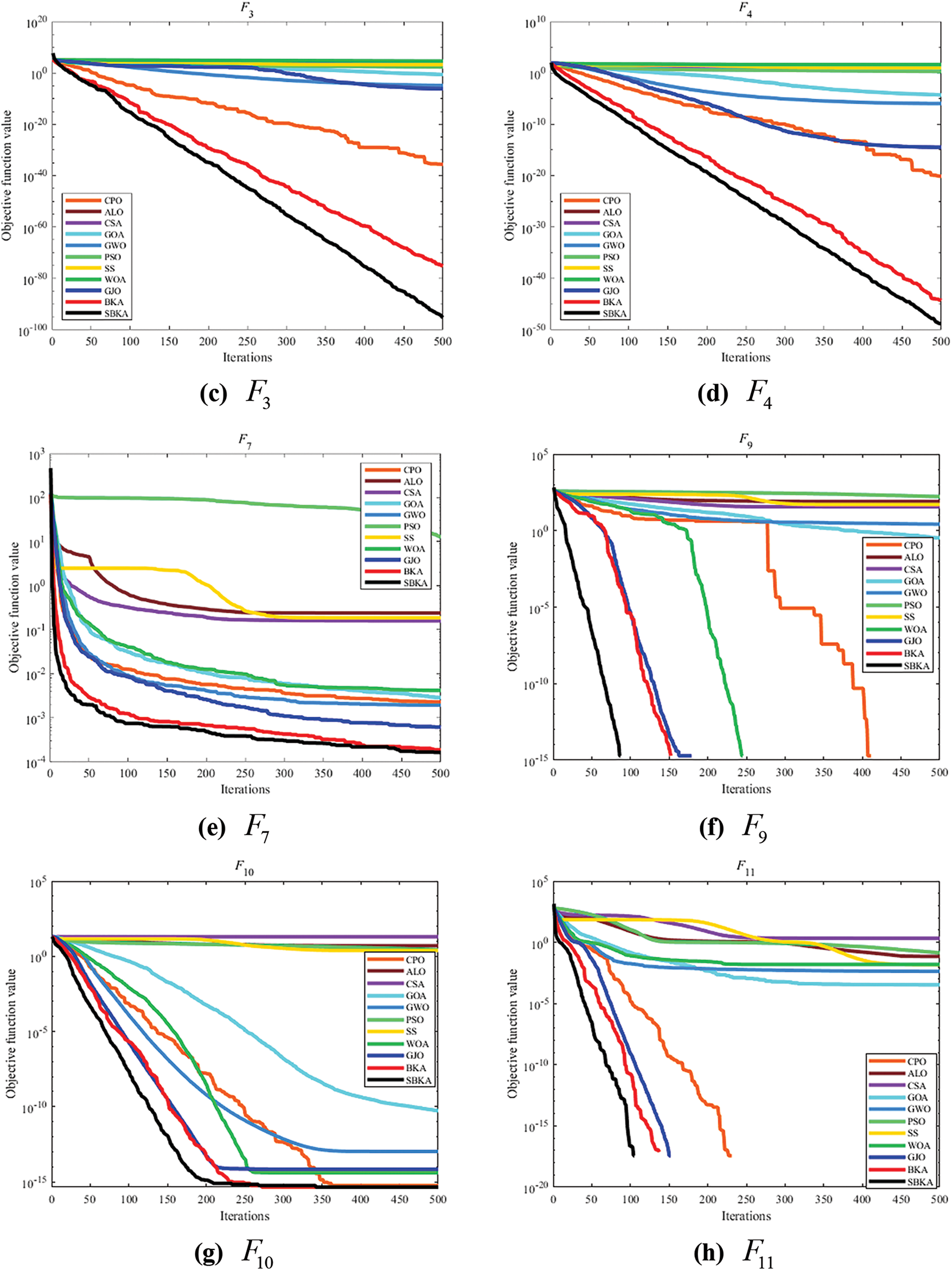
Figure 7: Convergence curve of optimization algorithm

Under consistent parameters, BKA converges faster than other optimization algorithms, and the improved SBKA also demonstrates superior convergence speed compared to other algorithms, as shown in Fig. 7. As shown in Table 3, SBKA achieves the highest testing accuracy across various basis functions among all optimization algorithms, with the lowest standard deviation, indicating its stability. It typically converges to the global optimal solution of each basis function. In contrast, other algorithms all fall into the local optimal solution, which SBKA avoids by introducing the Sine mapping and the golden sine strategy. The experimental findings demonstrate SBKA’s high capacity for identifying the best answer.

5.3 CL-SCN Performance Test

CALCE is used to evaluate CL-SCN’s performance and compare it to the original SCN to determine its effectiveness. Comparison trials are carried out in two scenarios with maximum numbers of hidden layer nodes of 25 and 50, and the results are averaged over 20 experiments. The parameters of both models are set identically, with a maximum number of candidate nodes L = 100 and an acceptable error r = 0.001. The average training error convergence curves for SCN and CL-SCN on the CALCE dataset are shown in the figure. It is evident from Fig. 8 that CL-SCN performs better than SCN due to its quicker rate of convergence.

Figure 8: Average training results of SCN and CL-SCN on CALCE

5.4 Analysis of Experimental Results

This study compares SBKA-CLSCN with alternative approaches using the CALCE CS series dataset. Capacity is the model’s output, and the health features HF1 and HF2 are its inputs. The first 400 and 500 CS data sets are used as training sets, while the remaining data sets are used as test sets. Fig. 9 displays the capacity estimation curves for several test sets using various techniques. The table displays the estimation errors. This study uses the CALCE CS series dataset to compare SBKA-CLSCN with other methods. The model’s inputs are the health characteristics HF1 and HF2, and its output is capacity. The remaining data sets are utilized as test sets for trials, while the first 400 and 500 CS data sets are used as training sets. The capacity estimation curves for several test sets and methodologies are shown in Fig. 9. The estimation errors are shown in the table.

Figure 9: Prediction curves of lithium-ion batteries for five methods (first 400 cycles data as training samples)

The SBKA-CLSCN algorithm’s experimental curve has the best traceability, as shown in Fig. 9 and Table 4, and the table shows that the error is the smallest and tends to be close to 0. This indicates that the optimization effect of Sine chaotic mapping and the golden sine strategy on the BKA algorithm can effectively prevent BKA from entering the local optimum during optimization, allowing it to find the global optimum and produce a better training result. By optimizing SCN parameters, SBKA successfully reduces the issue of inadequate model prediction accuracy in the latter stages of the cycle and enhances the model estimation effect. The more training data available for the CS2 dataset, the higher the estimation accuracy. With the most precise prediction, all of the optimized RMSEs in the table stay under 0.1%, and they outperform the unoptimized SCN model by a wide margin. It demonstrates how the SBKA-CLSCN algorithm’s accuracy and resilience have significantly increased.

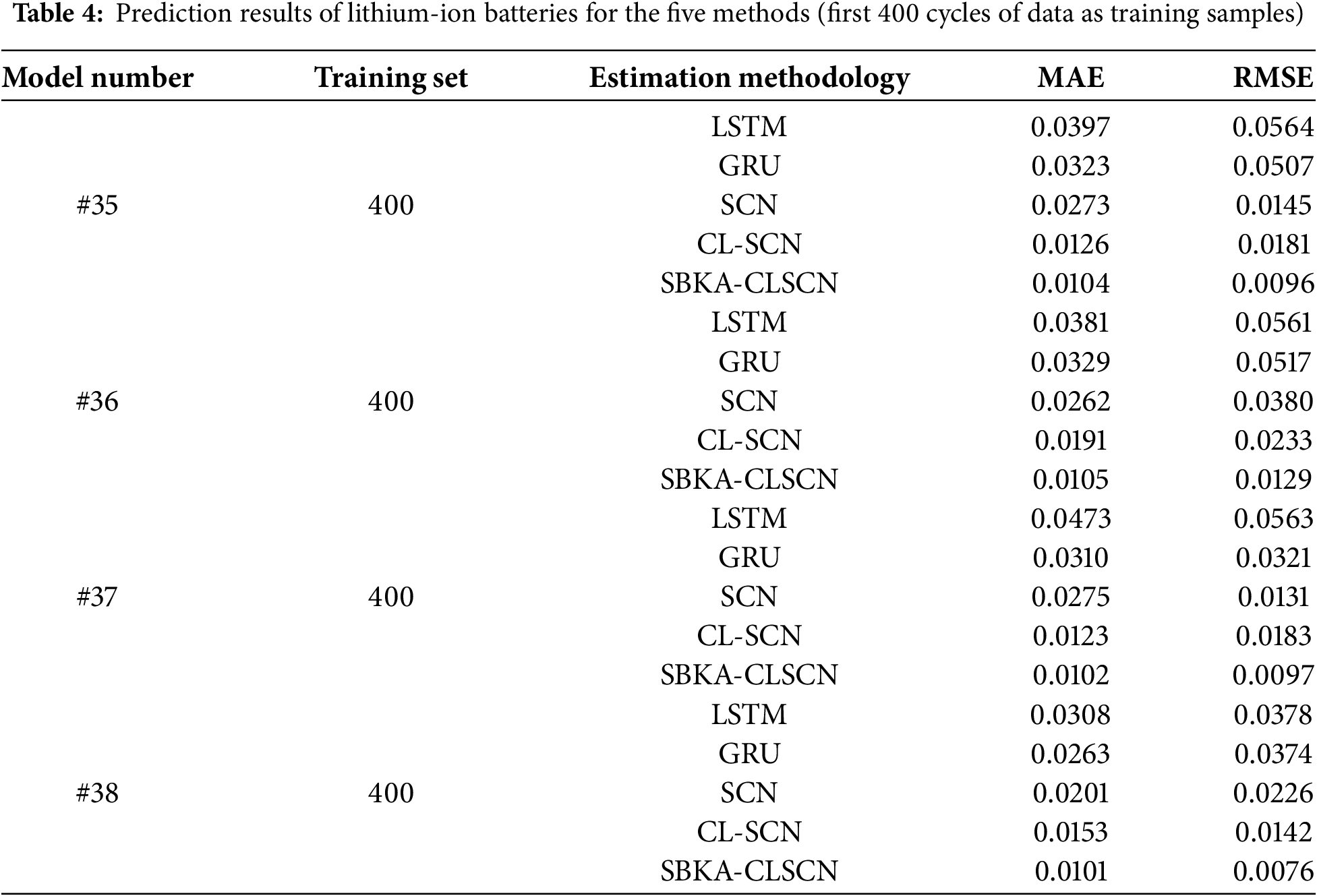
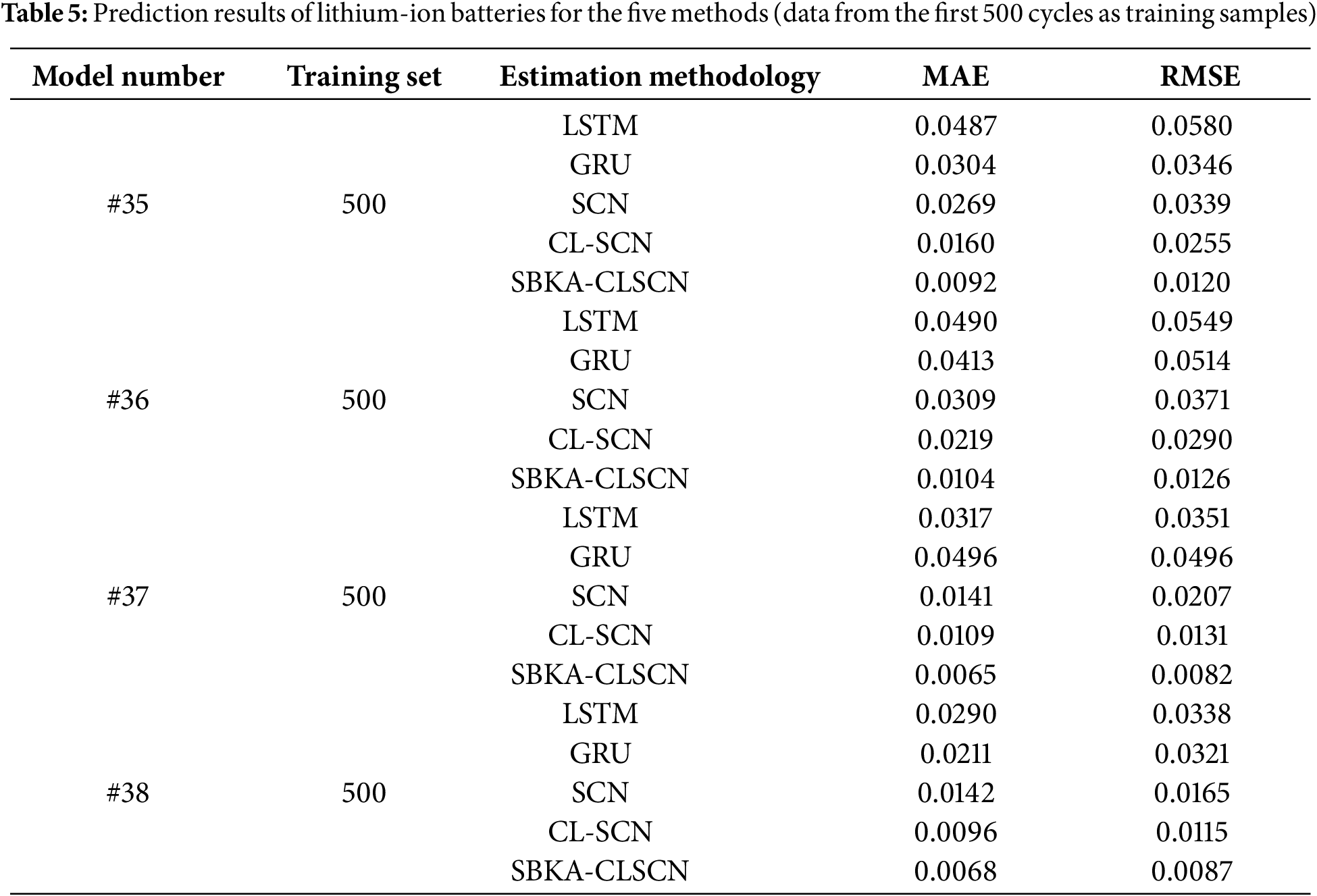
It is evident from Fig. 10 and Table 5 that the more training data there is for the CS2 dataset, the higher the model estimation accuracy. In general, 500 datasets work better as a training set than 400 datasets. Compared to LSTM and GRU, SCN has reduced curve fluctuation; however, the error is still greater, and the estimation accuracy is poor. When comparing predicted images on various datasets using various techniques, SBKA-CLSCN produces the best estimation effect, the best fit to the real curve, and an RMSE that is 0.0219 and 0.0135 lower than that of the original SCN and CLSCN models.

Figure 10: Prediction curves of lithium-ion batteries for five methods (first 500 cycles data as training samples)

6  Conclusion

In this study, an SBKA-CLSCN approach for predicting the residual usable life (RUL) of lithium batteries is proposed. In the process of charging and discharging lithium batteries, the indirect health factor that may indicate deterioration in battery performance is extracted and used as input to the RUL estimation model. The degree of correlation between the health factor and the battery’s state of health is determined using the Pearson coefficient. With the use of golden sine strategy and sine mapping, the BKA algorithm is enhanced. The Laplace transform is used to increase the accuracy and resilience of the SCN. When the two are tuned, an accurate estimation model is created, eventually leading to the precise calculation of RUL for lithium batteries. The SBKA-CLSCN produces the best estimation effect on various datasets and has superior estimation accuracy and stability when comparing the estimation results of the suggested technique with those of other methods on the CALCE dataset.

To extend the battery’s lifespan, it is advisable to avoid charging the battery to 100%. The charging limit can be set between 80% and 90% to reduce battery stress. Regular charging and discharging cycles should be conducted to prevent prolonged states of full charge or discharge. Additionally, installing a Battery Management System (BMS) can help monitor the battery’s status and prevent overcharging, deep discharging, and overheating.

In future research, the impact of various complex operating conditions on the estimation of the battery’s State of Health (SOH) will be considered, along with the effects of many complex lithium-ion battery operating scenarios, to achieve a more accurate and comprehensive estimation of SOH. This will enable dynamic adjustments to the charging method based on the battery’s condition, thereby extending battery life. By enhancing battery performance and health management, this approach will promote the widespread application of electric vehicles and renewable energy storage systems, contributing to the transition to green energy.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Yuheng Yin, Lin Wang; Data collection: Lin Wang; Analysis and interpretation of results: Yuheng Yin, Lin Wang; Draft manuscript preparation: Lin Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Lin Wang, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhao H, Han C, Cheng XL, Hao W, Xu HY, Geng MM, et al. Study on the capacity degradation mechanism of lithium-ion batteries with high rate aging using anode pre-lithiation technology. Energy Storage Sci Technol. 2021;10(2):454. doi:10.19799/j.cnki.2095-4239.2020.0340. [Google Scholar] [CrossRef]

2. Sun Z, Wang Z, Liu P. A review on the fault diagnosis of power battery system in new energy vehicles. J Mech Eng. 2021;57(14):87–104. [Google Scholar]

3. Zuo C, Feng SJ, Zhang XY. Computational imaging with deep learning: current status, challenges and future. Acta Opt Sin. 2020;40(1):0111003. doi:10.3788/AOS202040.0111003. [Google Scholar] [CrossRef]

4. Vismaya VS, Nair BV, Muni SS. Deep learning for prediction and classifying the dynamical behaviour of piecewise-smooth maps. Frankl Open. 2024;9(4):100180. doi:10.1016/j.fraope.2024.100180. [Google Scholar] [CrossRef]

5. Dong G, Han W, Wang Y. Dynamic bayesian network-based lithium-ion battery health prognosis for electric vehicles. IEEE Trans Ind Electron. 2021;68(11):10949–58. doi:10.1109/tie.2020.3034855. [Google Scholar] [CrossRef]

6. Liu Y, Yu H, Liu D, Mu Y, Wang Y, Zhang X. Remaining service life prediction of lithium-ion battery based on ABC-LSTM model. Energy Storage Sci Technol. 2025;14(1):331–45. doi:10.1109/irce59430.2023.10254780. [Google Scholar] [CrossRef]

7. Wang P, Zhou J, Wu X, Liu T. Improved Sine chaotic mapping CO-ELM RUL prediction for lithium-ion batteries. Energy Storage Sci Technol. 2025;14(4):1603 1–17. (In Chinese). [Google Scholar]

8. Li Y, Zhuo XJ, Liu Y, Li CY. Remaining service life prediction of lithium-ion battery based on PCA-GWO-GRU. Min Metall Eng. 2024;44(4):95–9. [Google Scholar]

9. Wang ZP, Wang QS, Liu P, Zhang ZS. A review of big data-driven methods for power battery health state estimation. J Mech Eng. 2023;59(2):151–68. [Google Scholar]

10. Wang D, Li M. Stochastic configuration networks: fundamentals and algorithms. IEEE Trans Cybern. 2017;47(10):3466–79. doi:10.1109/tcyb.2017.2734043. [Google Scholar] [PubMed] [CrossRef]

11. Zhang C, Ding S. A stochastic configuration network based on chaotic sparrow search algorithm. Knowl-Based Syst. 2021;220(10):106924. doi:10.1016/j.knosys.2021.106924. [Google Scholar] [CrossRef]

12. Guo XF, Huang YH, Shan D, Yuan BL, Ning L. Improved global ZOA optimization of lithium battery SOH estimation for MVMD-SCN. Electron Meas Technol. 2024;47(5):22–30. [Google Scholar]

13. Wang J, Wang WC, Hu XX, Qiu L, Zang HF. Black-winged kite algorithm: a nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif Intell Rev. 2024;57(4):98. doi:10.1007/s10462-024-10723-4. [Google Scholar] [CrossRef]

14. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95–International Conference on Neural Networks; 1995 Nov 27–Dec 1; Perth, WA, Australia. Piscataway, NJ, USA: IEEE; 2020. p. 1942–8. [Google Scholar]

15. Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi:10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

16. Dorigo M, Birattari M, Stutzle T. Ant colony optimization. IEEE Comput Intell Mag. 2007;1(4):28–39. doi:10.1109/mci.2006.329691. [Google Scholar] [CrossRef]

17. Rafiq MN, Rafiq MH, Alsaud H. Chaotic response, multistability and new wave structures for the generalized coupled Whitham—Broer–Kaup—Boussinesq–Kupershmidt system with a novel methodology. Chaos Solitons Fractals. 2025;190(7):115755. doi:10.1016/j.chaos.2024.115755. [Google Scholar] [CrossRef]

18. Yu JF, Liu S, Wang J. An ant-lion optimization algorithm integrating Lévy flight and golden sine. Appl Res Comput /Jisuanji Yingyong Yanjiu. 2020;37(8):2349–53. (In Chinese). [Google Scholar]

19. Cohen I, Huang Y, Chen J, Benesty J, Benesty J, Chen J, et al. Pearson correlation coefficient. Noise Reduct Speech Process. 2009;2:1–4. doi:10.1007/978-3-642-00296-0_5. [Google Scholar] [CrossRef]

20. Yan AJ, Yu X. Optimization of stochastic configuration network parameters based on chaotic feedback ocelot optimization algorithm. J Beijing Univ Technol. 2023;49(7):749–57. (In Chinese). [Google Scholar]

21. Zhang CL, Ding SF, Guo LL, Zhang J. Advances in randomized configuration networks. J Softw. 2024;35(5):2379–99. (In Chinese). [Google Scholar]