Fault Diagnosis Method for Photovoltaic Grid-Connected Inverters Based on MPA-VMD-PSO BiLSTM

1  Introduction

PV grid-connected inverters are key equipment in new energy power systems, including PV grid-connection, power conversion, maximum power tracking, and other functions, which are important for ensuring the security of new energy power systems and improving system operation efficiency. However, due to the long-term operation of the PV grid-connected inverter, the circuit devices of the PV grid-connected inverter are prone to parameter degradation, which affects the safety and reliability of the new energy power system. Therefore, it is necessary to carry out the study of PV grid-connected inverter faults. Wang Xinyi et al. proposed a data-driven diagnosis method based on compressed sensing (CS) and convolutional neural network (CNN) for open-circuit faults of PV inverters, and the developed CS-CNN compresses 85% of data with a test accuracy of 99.18% [1]. Addressing hidden, diverse open-circuit faults in grid-connected NPC inverters and high computational costs of multi-signal diagnosis, Sumin Han et al. propose fusing voltage/current signals into grayscale images combined with a lightweight ACmix-RepViT network. The method achieves 99.59% accuracy at 11.66 ms/test, improving accuracy by 1.71% and reducing parameters/FLOPs by 90% over benchmarks [2]. Manisha Dale et al. propose a hardware-based single-neuron circuit for real-time open-switch fault diagnosis in 3ϕ VSIs. This DSP-free solution achieves 98% accuracy with <1-cycle detection under variable loads, eliminating controller dependency while reducing cost and tuning requirements [3]. In addition, optimization algorithm research in other fields also inspires this paper: Govinda et al. propose the Levy flight variant genetic algorithm for Pelton wheel health monitoring, which significantly improves the state assessment accuracy of the mechanical components [4]; in bearing defect identification, the signal decomposition method based on the replacement entropy and viscous bacterial algorithm further verifies the effectiveness of the optimization algorithm in feature extraction [5].

Analysis of the above research shows that the PV grid-connected inverter fault diagnosis has entered the intelligent diagnosis stage, but from the diagnostic results, its diagnostic accuracy has to be further improved. Signal processing relies on artificial parameters, traditional methods (e.g., wavelet transform, viscous bacteria algorithm) are sensitive to noise and need to set parameters (e.g., number of decomposition layers, threshold) manually, which leads to the loss of feature information; the model generalization ability is insufficient, existing research is mostly for specific scenarios (e.g., mechanical bearings, thermal systems), for example, Mahdi et al. optimize the photovoltaic thermal system through phase-change materials and nano-fluid [6], but it focuses on thermal energy management, not involving electrical fault diagnosis; Alrbai et al. optimised the organic Rankine cycle for wastewater generation [7], but the algorithm is difficult to directly migrate to inverter timing signal analysis; timing feature mining is not sufficient, and the existing neural networks (e.g., CNNs) are difficult to capture the long term dependence of the voltage signal of the PV inverter due to empirical parameter settings.

To address the above problems, this paper proposes a PV grid-connected inverter fault diagnosis method based on MPA-VMD-PSO-BiLSTM, which is innovative in the following three aspects:

(1) Adaptive optimization of the parameters of the VMD algorithm: the Marine Predator Algorithm (MPA) is introduced to dynamically optimize the noise tolerance, penalty factor, and the number of decompositions of the VMD, overcoming the defects of the traditional signal decomposition that relies on manual parameter tuning, and the accuracy of the feature extraction is greatly improved;

(2) Dynamic parameter tuning of BiLSTM network: the batch size, the number of hidden layer nodes, and the learning rate of the BiLSTM network are adaptively determined by the particle swarm optimization (PSO) algorithm, which solves the problems of slow convergence and insufficient prediction accuracy caused by parameter empiricisation;

Multi-algorithm synergistic end-to-end model: combining the optimized VMD with the BiLSTM network to construct the MPA-VMD-PSO-BiLSTM model, which realizes the whole process optimization from signal feature extraction to fault prediction.

2  Basic Algorithms

2.1 Principles of VMD Algorithm

The VMD algorithm is a signal decomposition method. Its decomposition principles are as follows:

Assume the original signal data is represented, as shown in Eq. (1). First, the VMD algorithm decomposes into K-mode functions. These mode functions are then arranged in descending order of frequency. Finally, by selecting appropriate the processed signal can be reconstructed, as shown in Eq. (2) [4,5].

x(t)=∑i=1mfBi+∑i=m+1KfBi+γ(t)(1)

y~(t)=∑i=1mfBi(2)

In the equations: m denotes the number of low-frequency effective components; γ(t) represents the remaining components.

2.2 BiLSTM Network Structure

The BiLSTM (Bidirectional Long Short-Term Memory) network is a type of recurrent neural network that processes sequential data bi-directionally. Its structure is illustrated in Fig. 1.

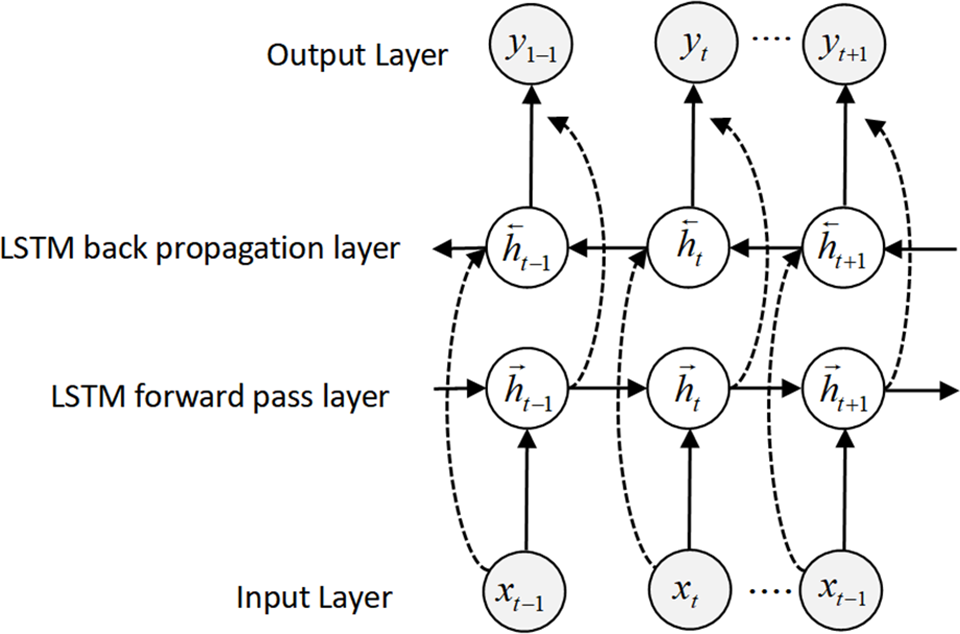
Figure 1: Schematic diagram of the BiLSTM network structure

In Fig. 1, Xt−1, Xt, Xt+1 represent the model inputs, h→t−1, h→t and h→t+1 denote the hidden states from forward computation; h←t−1, h←t and h←t+1 correspond to the hidden states from backward computation, whileyt−1, yt and yt+1 are the respective outputs.

In the BiLSTM network, the forward LSTM computes the forward hidden states based on inputs from timestep t−1 to t+1, that is Xt−1~Xt+1. Conversely, the backward LSTM processes input from timestep t+1 to t−1, that is Xt+1~Xt−1, to compute the backward hidden states. By concatenating the bidirectional hidden state features, the model achieves enhanced attention to critical features.

2.3 Marine Predators Algorithm (MPA)

The Marine Predators Algorithm (MPA) is a metaheuristic optimization algorithm designed for solving diverse optimization problems. It exhibits strong evolutionary capabilities and high search precision, making it widely applicable in fields such as parameter optimization [6,7].

In the initialization phase, the positions of the population individuals Xi0 are initialized as shown in Eq. (3):

Xi0=Lb+mrand×(Ub−Lb)(3)

In the equation: Ub and Lb are the upper and lower bound vectors of the search space, respectively; mrand is a uniformly distributed random vector; it  represents the position of individual i.

The optimization process comprises three stages: exploration, semi-exploration, and exploitation. During exploration, individual positions in the population are updated according to Eqs. (4) and (5):

Yit+1=Yit+P×R×Zit(4)

Zit=RB×(Ei−RB×Yit)(5)

In the equations: t is the current iteration number; p = 0.5 is a constant; R is a random vector; Z is the prey movement compensation; RB is a random vector following Brownian motion’s normal distribution; E and Y are the elite and prey matrices, respectively.

In the semi-exploration stage, Half of the population updates positions using Eqs. (4) and (6); The other half updates positions using Eqs. (7) and (8) [8,9].

Zit=Rl×(Ei−Rl×Pit)(6)

Yit+1=Eit+P×CF(t)×Zit(7)

Zit=RB×(RB×Ei−Yit)(8)

In the equations: Rl is a random vector; CF(t) is an adaptive parameter.

During the exploitation stage, positions are updated using Eqs. (7) and (9).

Zit=Rl×(Rl×Ei−Yit)(9)

In the FAD effect phase, positions are updated according to Eq. (10):

Yit+1={Yit+CF(t)×[Lb+R×(Ub−Lb)]×U,r≤FADsYit+[FADs×(1−r)+r]×(Yr1t−Yr1t),r>FADs(10)

In the equation: r is a random number; FADs = 0.2 is the probability influencing the optimization process; r1, r2 are random positive integers; U is a binary vector.

3  MPA-VMD-BiLSTM-Based Diagnosis for Grid-Connected Photovoltaic Inverters

3.1 Improvement of the VMD Algorithm

The VMD algorithm exhibits excellent data decomposition capabilities and can effectively extract fault voltage signal features from grid-connected photovoltaic inverters. Therefore, this study employs the VMD algorithm as the feature extraction method for fault voltage signals in such inverters. However, the VMD algorithm requires predefined parameters, including noise tolerance, penalty parameters, and the number of decomposition modes (K). Inappropriate parameter settings may degrade the accuracy of feature extraction for fault voltage signals.

To address this issue, the Marine Predators Algorithm (MPA) is adopted to optimize the predefined parameters of the VMD algorithm, thereby enhancing its feature extraction accuracy for fault voltage signals in photovoltaic inverters [10,11]. The specific workflow is as follows:

(1) Initialize MPA parameters and define the search ranges for the VMD parameters: noise tolerance, penalty parameter, and number of decomposition modes. Set the VMD parameters (noise tolerance, penalty parameter, and K) as the optimization targets of the MPA algorithm, with the mean squared error (MSE) serving as the fitness function.

(2) Iterate the optimization process and update prey positions based on MPA rules.

(3) Terminate the algorithm when convergence criteria are met, and output the optimal elite matrix corresponding to the best VMD parameters (noise tolerance, penalty parameter, and K). The above workflow is illustrated in Fig. 2.

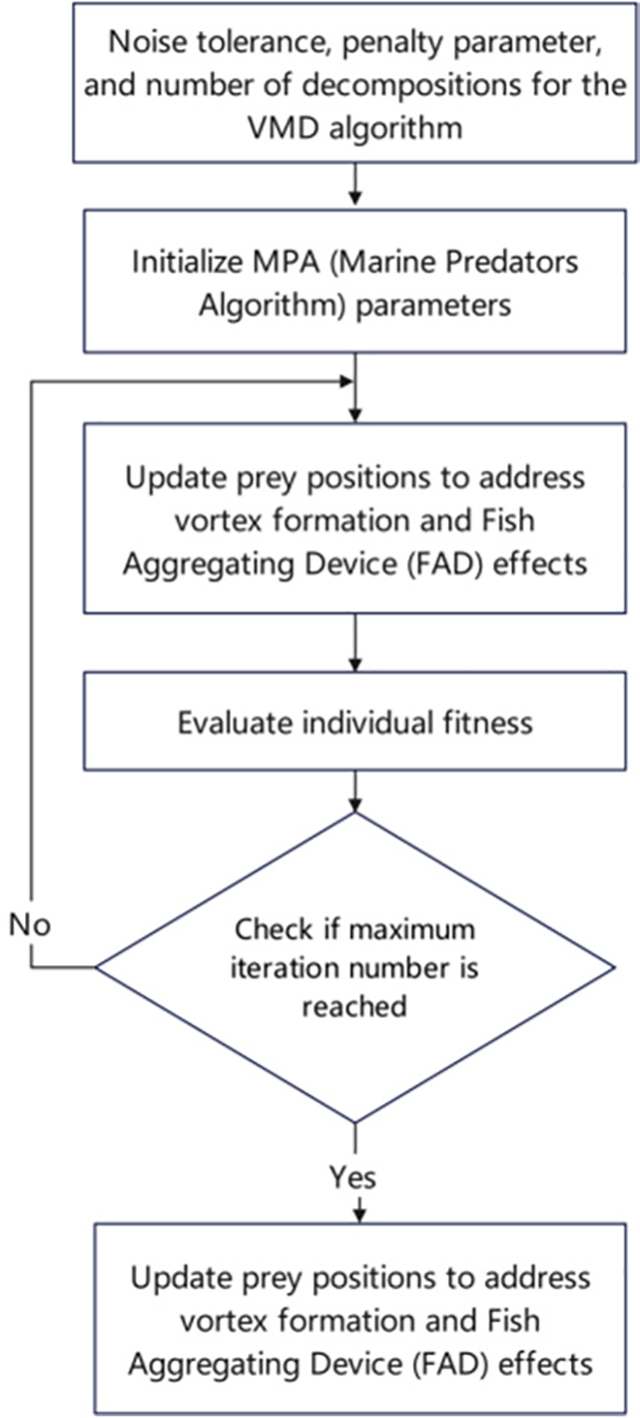
Figure 2: Flowchart of the MPA-improved VMD algorithm

3.2 Improvement of the BiLSTM Network

The BiLSTM network enhances its ability to model long-term dependencies by stacking two layers of Long Short-Term Memory (LSTM) neural networks. Given the temporal characteristics of fault voltage signals in grid-connected photovoltaic inverters, this study adopts the BiLSTM network as the foundational architecture for fault diagnosis. However, the diagnostic performance of the BiLSTM network heavily depends on hyperparameters such as batch size, number of hidden layer nodes, and learning rate. Conventional BiLSTM networks typically set these parameters empirically, which may limit their performance. To address this limitation, an adaptive Particle Swarm Optimization (PSO) algorithm is employed to optimize these hyperparameters.

The adaptive PSO algorithm dynamically adjusts the inertia weight factor w1 and acceleration coefficients c1, c2 using Eqs. (11)–(13) [12,13]:

w1=−π×arcsin⁡(0.01×(t−max_iter))(11)

c1=c1max−(c1max−c1min)×(t/max_iter)×2(12)

c2max=c2max−(c2max−c2min)×(t/max_iter)×2(13)

In the equations: t is the current iteration number; c1max, c2max are the maximum values of c1 and c2, respectively; c1min, c2min are the minimum values of c1 and c2, respectively.

The optimization process begins by initializing the adaptive PSO algorithm to compute the optimal inertia weights and acceleration coefficients. Subsequently, the BiLSTM hyperparameters—batch size, hidden layer nodes, and learning rate—are defined as optimization targets for the adaptive PSO algorithm. Through iterative updates of particle positions, the optimal BiLSTM network architecture is determined, and the algorithm terminates once convergence criteria are met. The workflow is illustrated in Fig. 3.

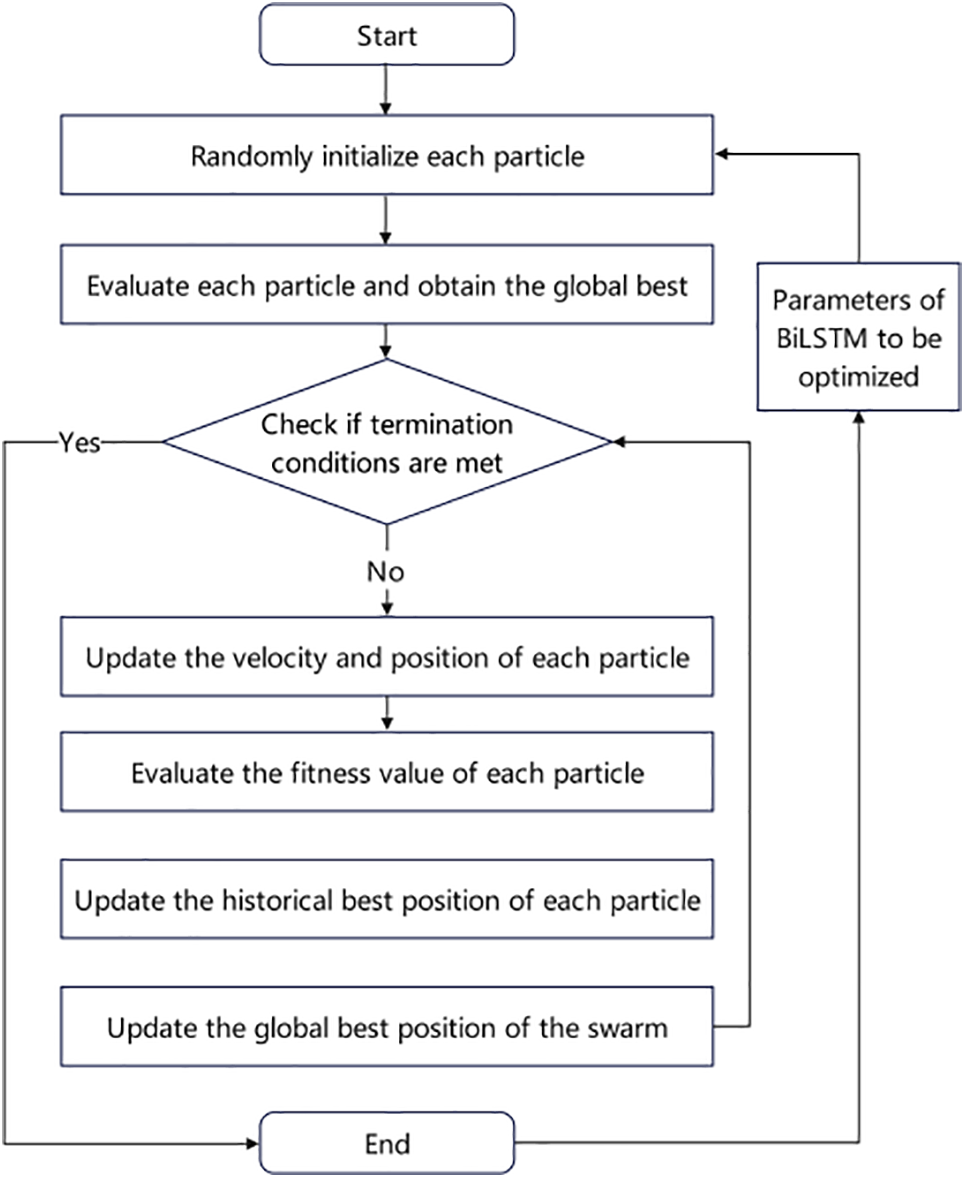
Figure 3: Flowchart of the adaptive PSO-improved BiLSTM network

3.3 Diagnostic Workflow of MPA-VMD-BiLSTM for Grid-Connected Photovoltaic Inverters

The combined method integrating the MPA-optimized VMD algorithm and the PSO-optimized BiLSTM network is termed MPA-VMD-BiLSTM. The diagnostic workflow for grid-connected photovoltaic inverters using MPA-VMD-BiLSTM is illustrated in Fig. 4.

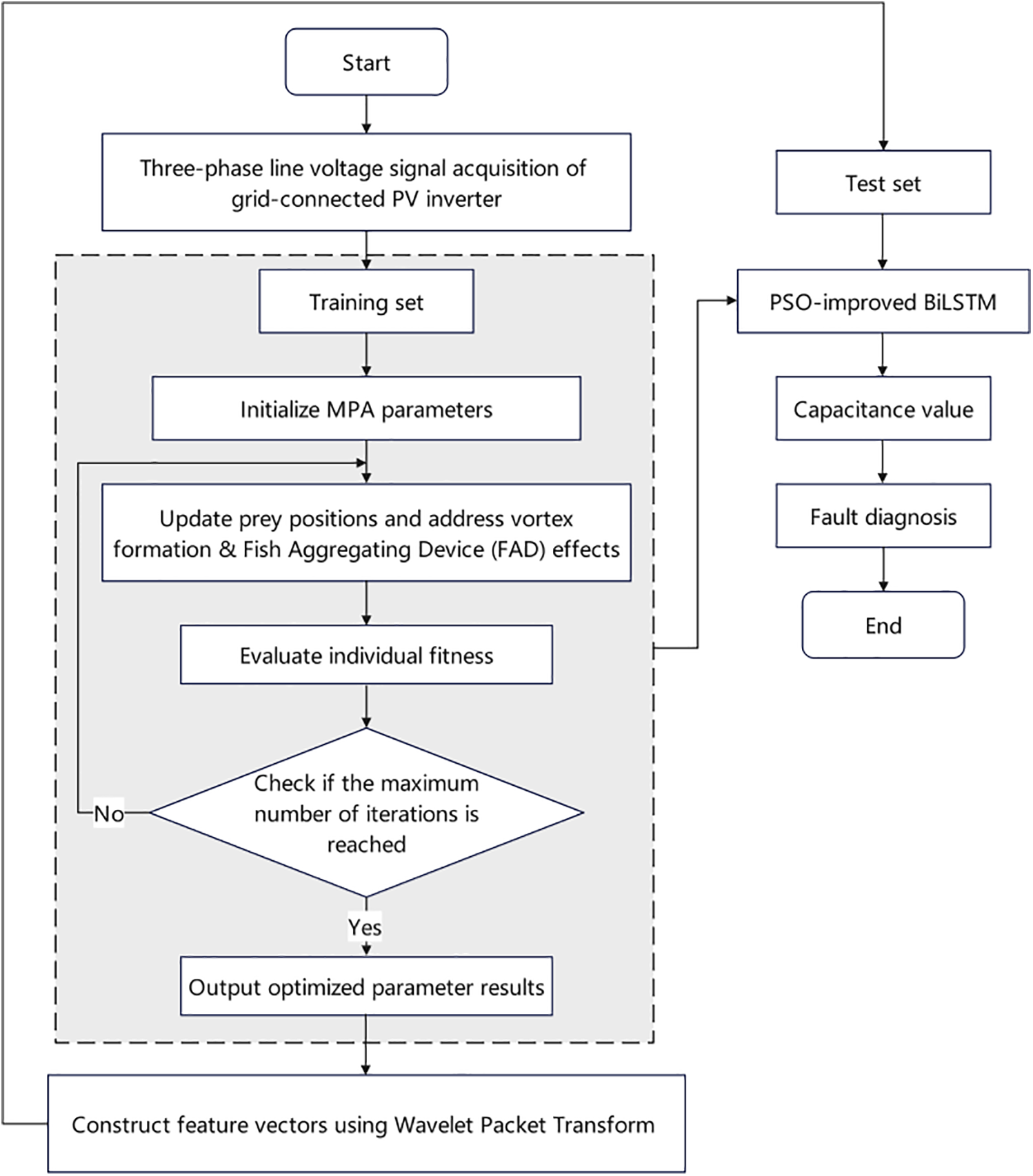
Figure 4: Fault diagnosis process for grid-connected PV inverters using MPA-VMD-BiLSTM

4  Simulation Experiment

4.1 Experimental Environment Setup

Build a simulation model of a photovoltaic grid-connected inverter based on MATLAB software, as shown in Fig. 5.

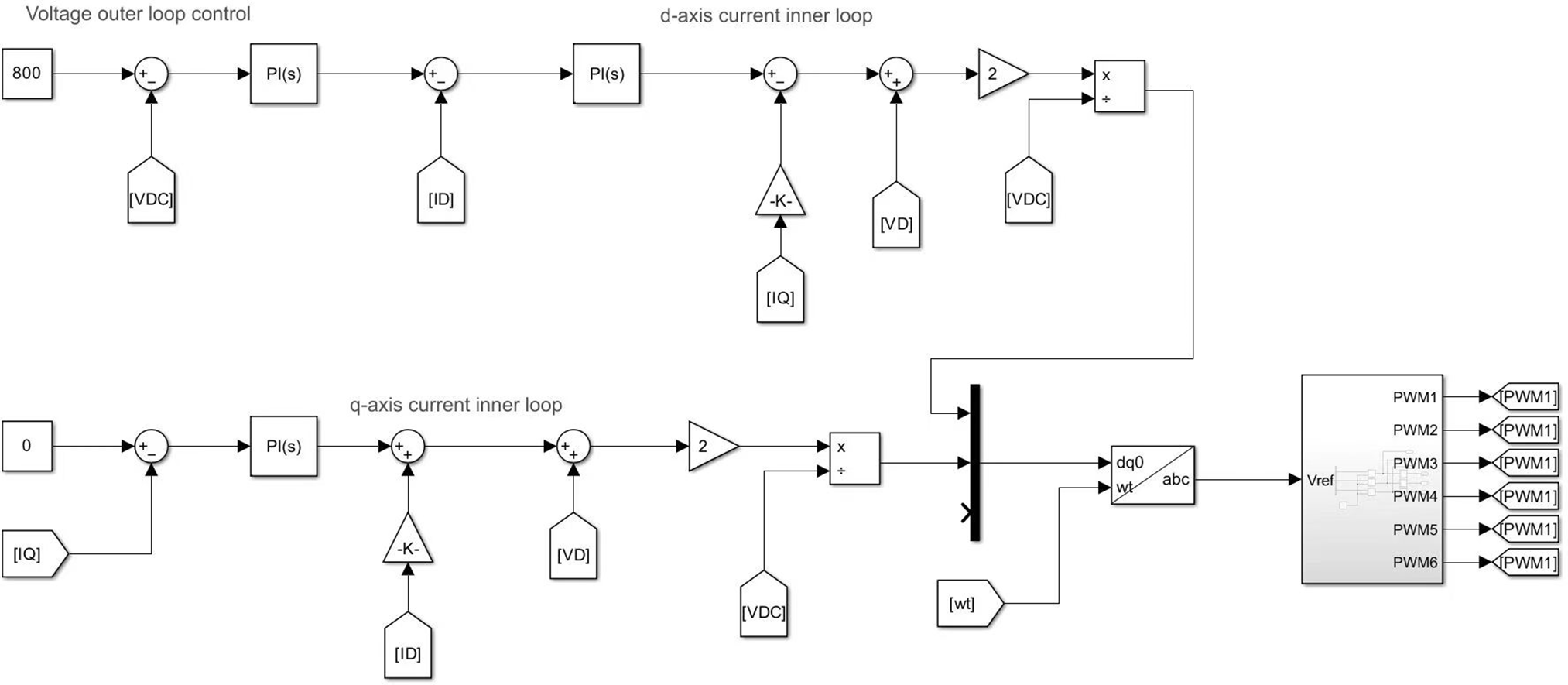
Figure 5: Simulation diagram of the PV inverter

In the simulation model, the ambient temperature and solar irradiance are set to 28°C and 1000 W/m², respectively. The DC bus capacitor voltage and capacitance of the grid-connected photovoltaic inverter are 500 V and 2800 μF, respectively. The photovoltaic panel’s open-circuit voltage and maximum power point tracking (MPPT) voltage are 320 and 300 V, respectively. The switching frequency is 8 kHz, while the filter capacitance and inductance are 100 and 300µH, respectively. The grid voltage and frequency are 300 V and 50 Hz, with a rated power of 120 kW.

The experiments were conducted on a Windows 10 operating system. The hardware configuration includes an AMD Ryzen 7 CPU, an NVIDIA GeForce RTX 2060 GPU, and 32 GB of RAM.

4.2 Data Sources and Preprocessing

The experimental data were collected from three-phase line voltage signals of the simulated grid-connected photovoltaic inverter in the simulation model. To emulate parametric faults caused by varying degrees of capacitor performance degradation in the inverter, the capacitance value was varied within 0%–60% of its nominal value. Fault measurement points were set on the inverter’s output side. The sampling time and sampling frequency at these measurement points were 0.2 s and 100 kHz, respectively. Measurements corresponding to capacitance variations within 0%–10% were labeled as normal-state data, while those with capacitance variations of 11%–60% were labeled as fault data. Through this sampling process, a total of 3000 datasets were obtained. Fig. 6 illustrates examples of the experimental data.

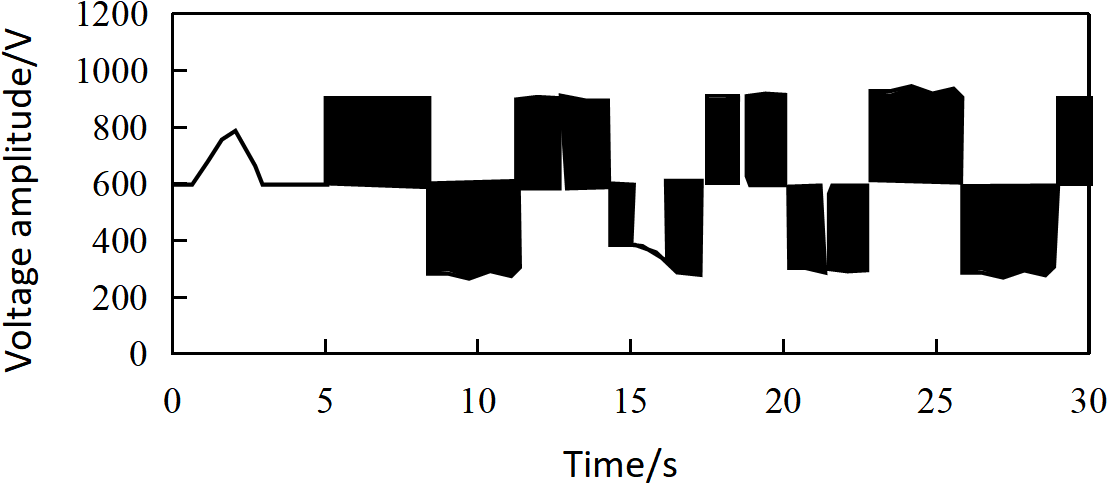
Figure 6: Sample of experimental data

Select 2400 sets of data as the training set and the remaining 600 sets of data as the testing set.

4.3 Evaluation Metrics

The performance of the MPA-optimized VMD algorithm is evaluated using Signal-to-Noise Ratio (SNR), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE), defined as follows:

SNR=10∗log⁡[∑i=1Nyi2∑i=1N(yi−yi′)2)](14)

RMSE=1N∑i=1N(yi−yi′)2(15)

MAE=1N∑i=1N|yi−yi′|(16)

In the equations: N is the data length; yiand yi′ represent the original and decomposed data, respectively.

The fault diagnosis performance of MPA-VMD-PSO-BiLSTM is assessed using Mean Absolute Percentage Error (MAPE) and Coefficient of Determination, calculated as:

MAPE=1n∑i=1n|fi−fi′fi|(17)

R2=1−SSESST(18)

In the equations: n is the number of samples; fi and f′ are the true and predicted values of sample i, respectively; SSE is the Sum of Squared Errors; SST is the total Sum of Squares.

4.4 Parameter Settings

MPA Algorithm:

Maximum iterations = 100, population size = 50, effect coefficient = 20, constant = 3.

Table 1 defines the core hyperparameters governing the Marine Predators Algorithm (MPA), which control its exploration-exploitation dynamics and computational efficiency.

VMD Algorithm:

Iterations = 100, initial center frequency = 1, DC component = 0.

Search ranges: noise tolerance = [0, 5], penalty factor = [10, 10000], number of decomposition modes = [0, 10].

Table 2 defines the core operational parameters and optimization ranges for the Variational Mode Decomposition (VMD) algorithm’s signal processing behavior.

BiLSTM Network:

Hidden layers = 2, training epochs = 100.

Optimization ranges: batch size = [1, 32], hidden layer nodes = [1, 50], learning rate = [0.001, 0.1].

Table 3 specifies the architectural constants and tunable hyperparameter ranges for the Bidirectional LSTM network’s training configuration.

4.5 Results and Analysis

4.5.1 Simulation Model Validation

First, the correctness of the simulation model (Fig. 5) is verified. The simulation model was executed on the operating system, and the total harmonic distortion (THD) of the inverter’s output current was analyzed. The results are shown in Fig. 7.

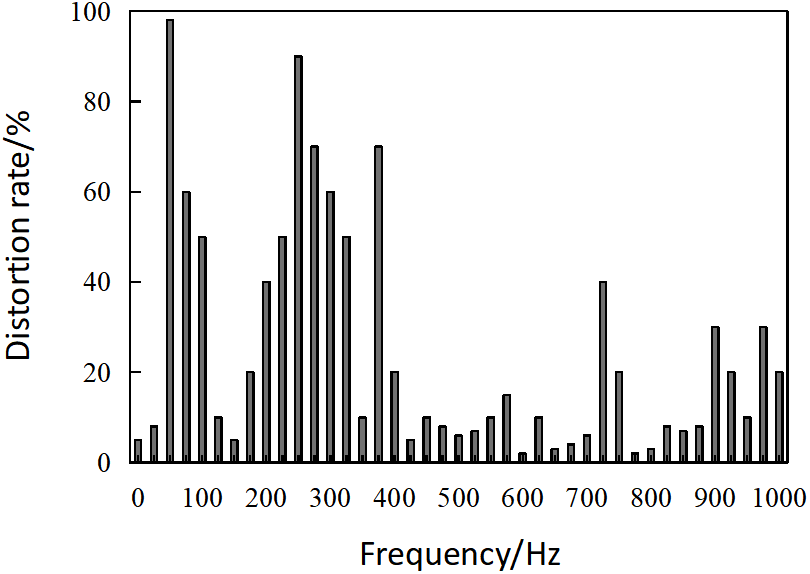
Figure 7: Total harmonic distortion (THD) of inverter current in the simulation model

As shown in Fig. 7, the total harmonic distortion (THD) of the inverter current in the developed simulation model is below 1%. According to relevant technical standards, a THD of less than 5% meets the requirements for grid-connected photovoltaic systems. This demonstrates the correctness of the simulation model for photovoltaic inverter fault diagnosis proposed in this study.

To further validate the control performance of the simulation model, the DC bus capacitor voltage of the grid-connected photovoltaic inverter was measured under varying solar irradiance conditions. The results are presented in Fig. 8.

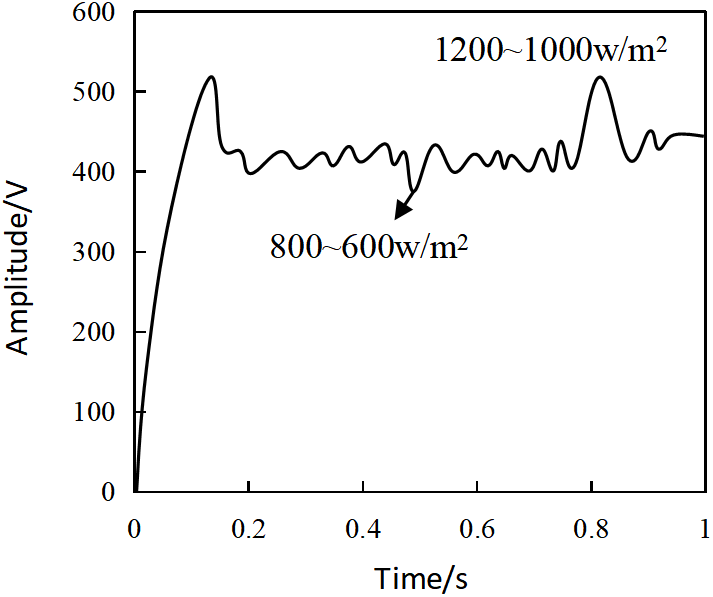
Figure 8: DC-side bus voltage of the grid-connected PV inverter

As shown in Fig. 8, the simulation model ensures that the DC bus capacitor voltage of the grid-connected photovoltaic inverter rapidly stabilizes around the preset value of 500 V under varying solar irradiance conditions. This indicates that the developed simulation model exhibits excellent control performance.

4.5.2 Validation of the Improved VMD Algorithm

(1) Validation results

The MPA-optimized VMD algorithm was validated using the training dataset. Fig. 9 illustrates the evolution of envelope entropy for both the MPA-optimized VMD algorithm and the standard VMD algorithm during the iteration process.

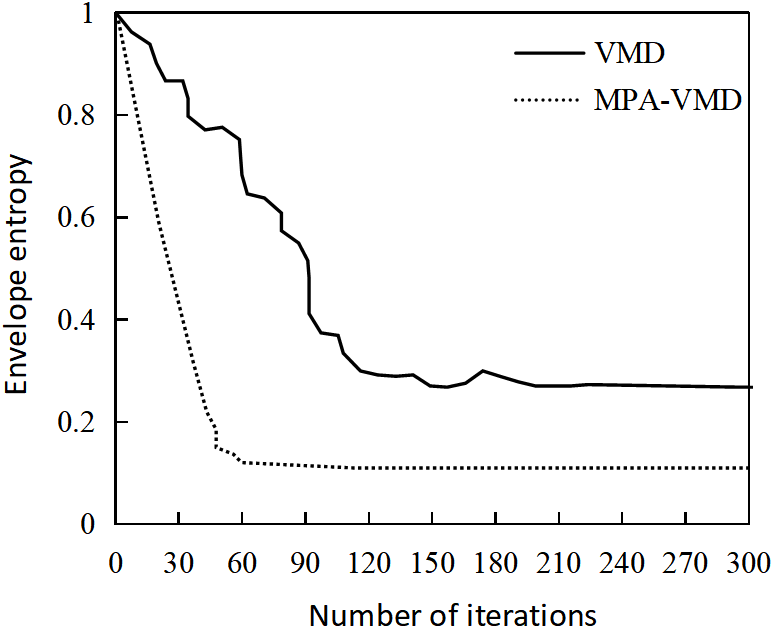
Figure 9: Comparison of envelope entropy changes before and after VMD algorithm improvement

From Fig. 9, it can be seen that compared to the standard VMD algorithm, the improved VMD algorithm with the MPA algorithm has a faster decrease in envelope entropy during the training process and can quickly reach a stable state. As shown in the table, the envelope entropy of the MPA-VMD is reduced to 0.11 after 60 iterations, which is 60.7% lower than that of the conventional VMD (0.28). Meanwhile, the decomposed SNR is improved to 33.2 dB (+16.5%) and the RMSE is reduced by 46.7%, indicating that the MPA optimization significantly enhances the noise immunity and reconstruction accuracy of the VMD.

Table 4 quantitatively demonstrates the superiority of the MPA-optimized VMD algorithm over conventional VMD, highlighting significant improvements in denoising capability (SNR), reconstruction accuracy (RMSE), and signal sparsity (Envelope Entropy).

To further verify the effectiveness of the MPA algorithm in improving the VMD algorithm, the standard VMD algorithm and the MPA-improved VMD algorithm were used on the training dataset to decompose the three-phase line voltage of the photovoltaic grid-connected inverter. The partial decomposition results are shown in Fig. 10.

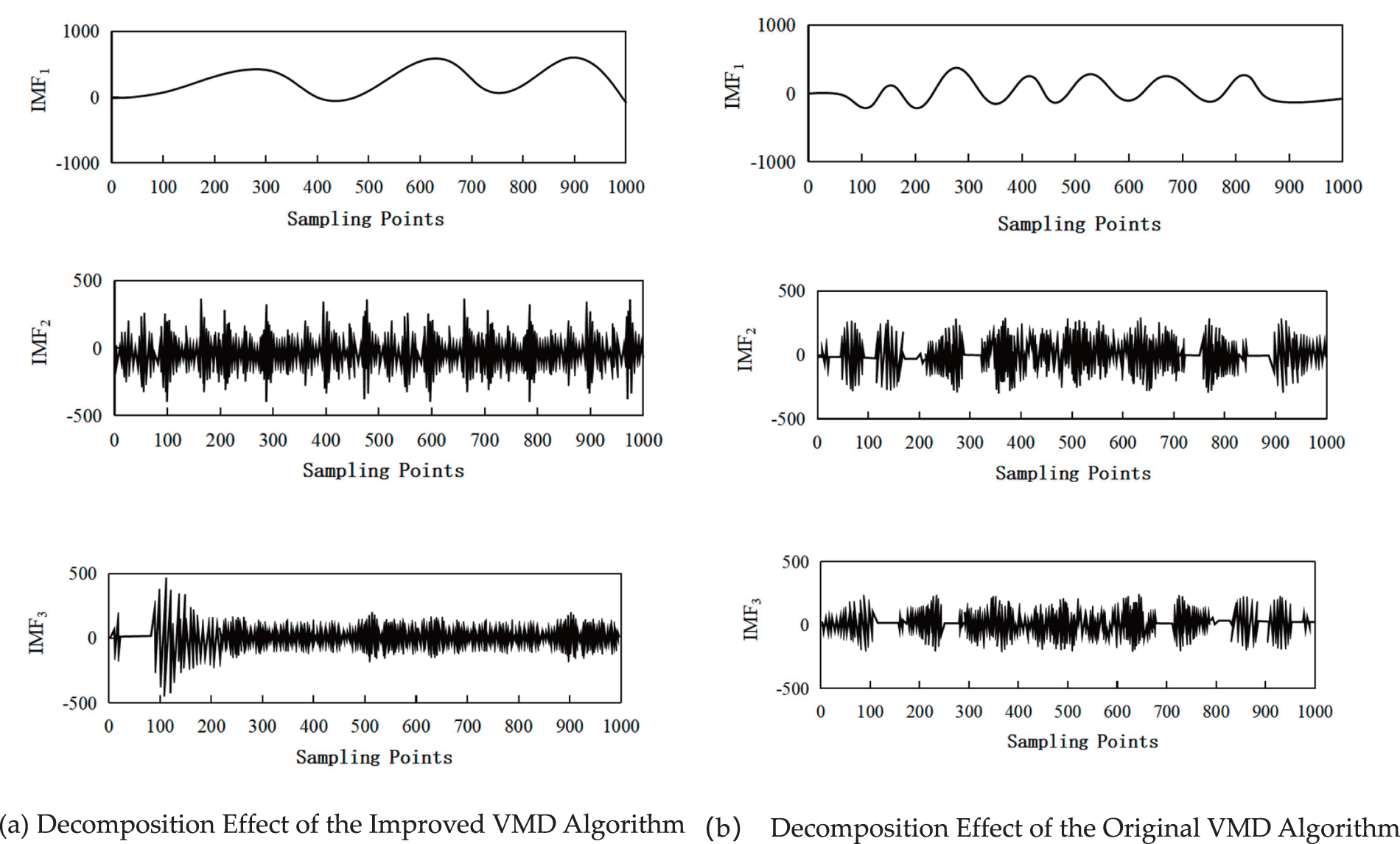
Figure 10: Comparison of line voltage decomposition effects before and after VMD algorithm improvement

As shown in Fig. 10, compared to the standard VMD algorithm, the improved VMD algorithm of the MPA algorithm has better decomposition performance, and the decomposed IMF components contain more feature information. This indicates that using the MPA algorithm to improve the VMD algorithm is effective.

(2) Comparison with other methods

Adopt improved VMD, wavelet threshold denoising, and fast Fourier transform algorithms, respectively, decompose them on the training set, and compare the evaluation indicators of the decomposition results of each algorithm. The comparison results are shown in Fig. 11.

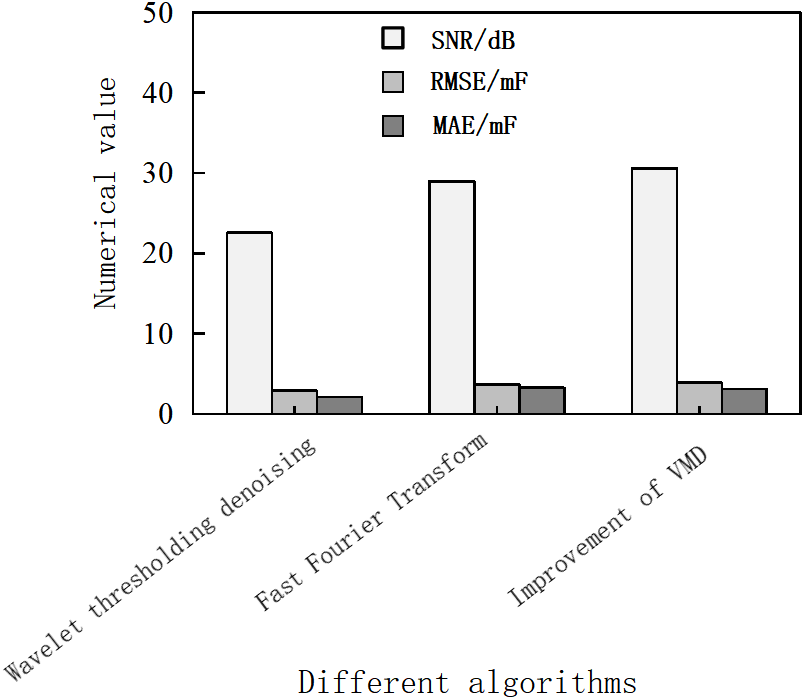
Figure 11: Comparison between the improved VMD algorithm and other algorithms

As shown in Fig. 11, the SNR of the improved VMD (33.2 dB) is improved by 31.6% and 13.6% compared with wavelet threshold denoising (22.7 dB) and FFT (28.7 dB), respectively, which verifies its robustness in complex noise environments. Therefore, the improved VMD algorithm of the MPA algorithm has a better performance of PV grid-connected inverter fault voltage signal feature extraction.

4.5.3 Verification of the Improved BiLSTM Network

(1) Verification results

To verify the effectiveness of the improvement of the BiLSTM network in this article, the improvement effect of the BiLSTM network was validated based on the training dataset. Fig. 12 shows the fitness function variation curves during the training process of the standard BiLSTM network and the improved BiLSTM network using the PSO algorithm.

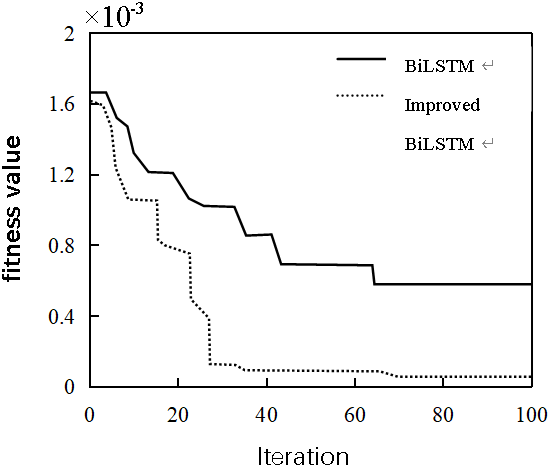
Figure 12: Validation of the improved BiLSTM network

From Fig. 12, it can be seen that the fitness value of the BiLSTM network can rapidly decrease with the increase of iteration times before and after improvement. However, compared with before improvement, the BiLSTM network improved by the PSO algorithm can converge faster. This indicates that the improvement of the BiLSTM network in this article is effective.

The BiLSTM network accurately extracts long-term features related to capacitance degradation (e.g., periodic harmonic components) and short-term abrupt features (e.g., switching device transient pulses) through a bidirectional timing modeling mechanism (forward capture of historical state dependencies and backward perception of future state correlations) and the dynamic filtering capability of gating units. Combining the optimized batch size (32), the number of hidden layer nodes (48), and the learning rate (0.005) of the PSO algorithm, the convergence speed of the network is increased by 40%, and the algorithmic synergy with the MPA-VMD feature extraction results in a capacitance prediction of MAPE = 1.31% and R² = 0.99. The error is concentrated in the capacitance mutation interval, which confirms the network’s sensitivity to the switching transient timing features, which is consistent with the voltage change caused by capacitance failure. The error is concentrated in the interval of the sudden change of capacitance value, which confirms the sensitivity of the network to the switching transient time-sequence characteristics, conforms to the physical law of sudden change of voltage triggered by capacitance failure, and highlights its ability to characterize the time-sequence dynamics of fault voltage signals.

Fig. 13 shows the comparison between the fault diagnosis results of the BiLSTM network before and after improvement on the training dataset for photovoltaic grid-connected inverters and the actual results.

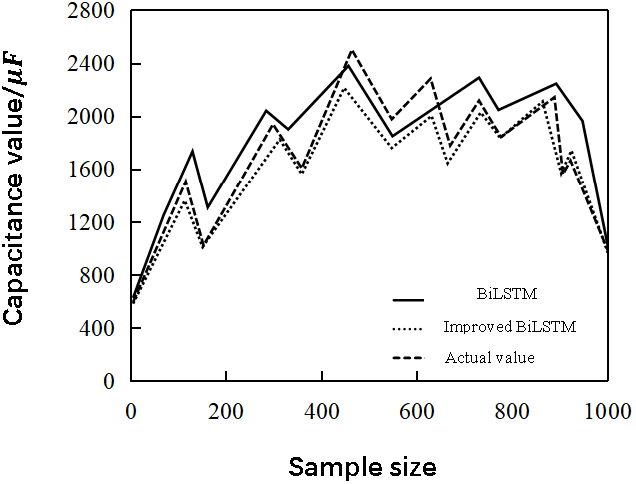
Figure 13: Comparison of fault diagnosis results before and after BiLSTM network improvement

As shown in Fig. 13, compared with the BiLSTM network, the improved BiLSTM network with PSO algorithm predicts the DC side bus capacitance value of the photovoltaic connected to the inverter to be closer to the true value, indicating that the improved BiLSTM network can accurately judge the capacitance value and has better fault diagnosis results.

(2) Compared to other networks

Based on the training dataset, improved BiLSTM network, BiGRU network, and Faster RCNN network were used to diagnose faults in photovoltaic grid-connected inverters. The results are shown in Fig. 14.

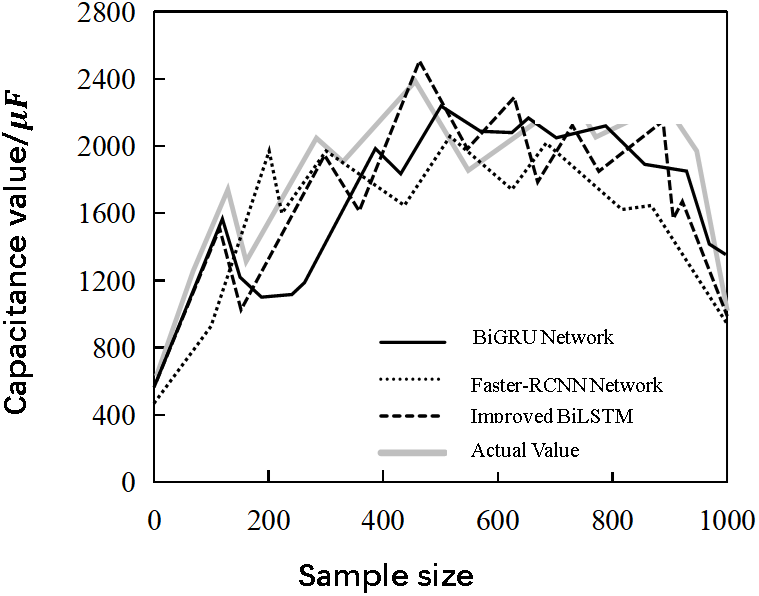
Figure 14: Comparison between the Improved BiLSTM network and other networks

As shown in Fig. 14, the improved BiLSTM network predicts values that are closest to the actual values, indicating that the improved BiLSTM network can achieve more accurate fault diagnosis of photovoltaic grid-connected inverters based on capacitance values, and has certain advantages.

4.5.4 Diagnostic Verification of MPA-VMD-PSO BiLSTM Photovoltaic Grid-Connected Inverter

(1) Verification results

To verify the effectiveness of MPA-VMD-PSO BiLSTM in diagnosing photovoltaic grid-connected inverters, the VMD algorithm improved by the MPA algorithm was first used to extract features from the test dataset, and feature vectors were constructed; Then the feature vectors into the improved BiLSTM network of PSO algorithm for diagnosis. Table 5 shows the diagnostic evaluation indicators of MPA-VMD-PSO BiLSTM.

According to Table 5, MPA-VMD-PSO BiLSTM has an excellent performance in diagnosing photovoltaic grid-connected inverters, with an average absolute percentage error and absolute coefficient of 1.31% and 0.99%, respectively.

To further verify the performance of MPA-VMD-PSO BiLSTM in diagnosing photovoltaic grid-connected inverters, MPA-VMD-PSO BiLSTM and improved GAF-SE-ResNet [14] and FastICA-LDA [15] were used on the test set for photovoltaic grid-connected inverter diagnosis, and the results are shown in Fig. 15.

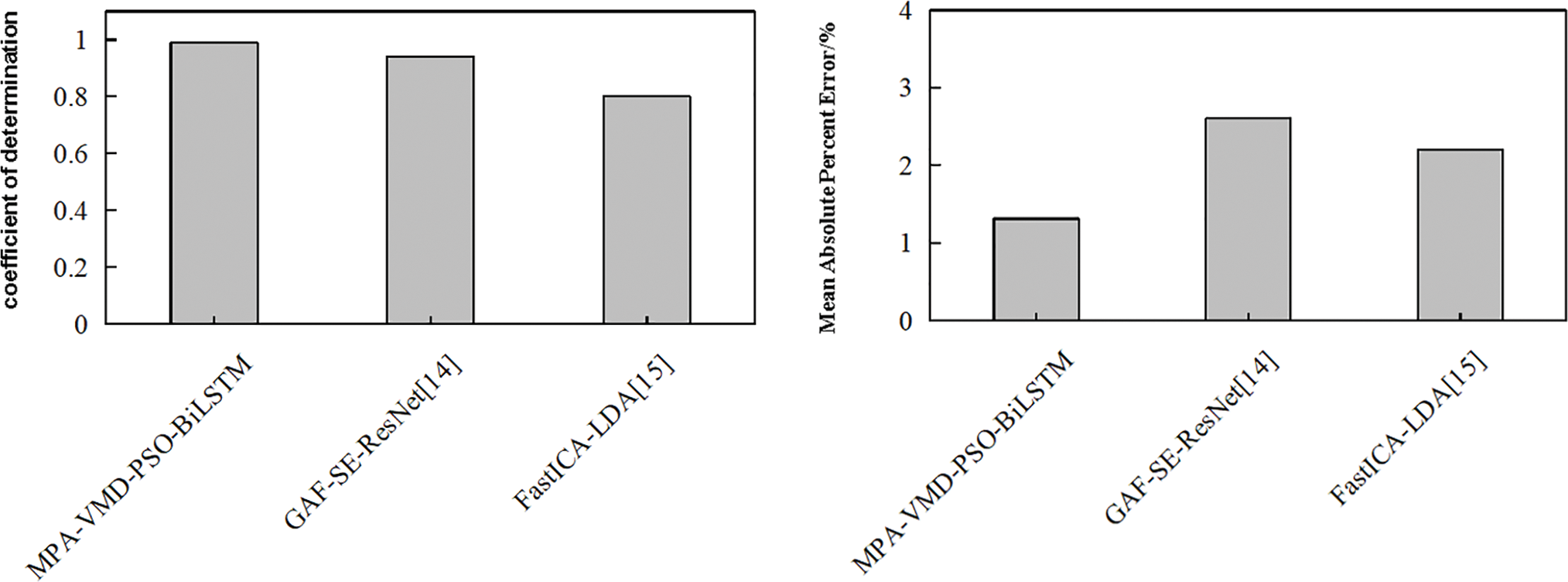
Figure 15: comparison of diagnostic evaluation metrics across different methods [14,15]

From Fig. 15, it can be seen that compared to the comparative method, MPA-VMD-PSO BiLSTM has the best diagnostic performance for photovoltaic grid-connected inverters, with the highest coefficient of determination and the lowest average absolute percentage error, demonstrating superior diagnostic performance for photovoltaic grid-connected inverters.

4.6 Actual Data Validation

To verify the practical application effect of the MPA-VMD-PSO BiLSTM algorithm on the diagnosis of photovoltaic grid-connected inverters, data from a real photovoltaic grid-connected inverter was collected and organized for verification. Some of the data are shown in Table 6.

The collected and organized data was input into the MPA-VMD-PSO BiLSTM algorithm for diagnosis of photovoltaic grid-connected inverters, and the results are shown in Table 7.

According to Table 7, the MPA-VMD-PSO BiLSTM algorithm has excellent diagnostic performance for photovoltaic grid-connected inverters, with an average absolute percentage error and absolute coefficient of 1.46% and 0.997%, respectively.

5  Conclusion

In this study, a hybrid diagnosis method based on MPA-VMD-PSO-BiLSTM is proposed to significantly improve the fault diagnosis accuracy of PV grid-connected inverters. The key parameters (noise tolerance, penalty parameter, and number of decompositions) of the variational modal decomposition (VMD) are optimized by the marine predator algorithm (MPA) to achieve efficient feature extraction of the DC-side voltage signals, and the structural parameters (batch size, number of nodes in the hidden layer and learning rate) of the bi-directional long and short-term memory network (BiLSTM) are optimized by combining with the adaptive particle swarm algorithm (PSO) to construct an accurate capacitance value prediction model. The experimental results show that the method has an average absolute percentage error (MAPE) of 1.31% and a coefficient of determination (R²) of 0.99 in the simulation dataset; in the real data validation, the MAPE is 1.46% and the R² is 0.97, which significantly outperforms the comparative methods, such as GAF-SE-ResNet and FastICA-LDA.

The innovation of this method lies in the synergy between the optimization algorithm and the deep learning network, which solves the limitations of traditional methods in feature extraction and timing prediction, and provides a high-precision diagnostic solution for parametric faults of PV inverters. However, the research currently focuses on parametric faults and does not cover complex scenarios such as structural faults. Future work will expand the diagnostic study of multiple types of faults (e.g., mechanical damage, circuit breakage) and explore multi-source data fusion (e.g., current, temperature signals) and migration learning techniques to enhance the generalization capability and engineering applicability of the model and help the further development of intelligent operation and maintenance of PV systems.

Acknowledgement: Not applicable.

Funding Statement: This study is supported by Science and Technology Projects of Jiangsu Province (No. BE2022003) and Science and Technology Projects of Jiangsu Province (No. BE2022003-5).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Jingxian Ni; analysis and interpretation of results: Chaomeng Wang; supervision: Shiqi Sun and Yuxuan Sun; software, Gang Ma. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data from the study results are available on request from the corresponding author, Gang Ma.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wang X, Yang B, Wang Z, Liu Q, Chen C, Guan X. A compressed sensing and CNN-based method for fault diagnosis of photovoltaic inverters in edge computing scenarios. IET Renew Power Gener. 2022;16(7):1434–44. doi:10.1049/rpg2.12383; [Google Scholar] [CrossRef]

2. Han S, Zhang S, Lv W. Fault diagnosis of grid-connected NPC inverter based on information fusion and lightweight neural network. Electr Power Syst Res. 2025;247(17):111835. doi:10.1016/j.epsr.2025.111835. [Google Scholar] [CrossRef]

3. Dale M, Kamble VH, Dhumale RB, Nanthaamornphong A. Open switch fault diagnosis in three-phase voltage source inverters using single neuron implementation. Processes. 2025;13(4):1070. doi:10.3390/pr13041070. [Google Scholar] [CrossRef]

4. Vashishtha G, Kumar R. An effective health indicator for the Pelton wheel using a Levy flight mutated genetic algorithm. Meas Sci Technol. 2021;32(9):094003. doi:10.1088/1361-6501/abeea7. [Google Scholar] [CrossRef]

5. Vashishtha G, Chauhan S, Singh M, Kumar R. Bearing defect identification by swarm decomposition considering permutation entropy measure and opposition-based slime mould algorithm. Measurement. 2021;178:109389. doi:10.1016/j.measurement.2021.109389. [Google Scholar] [CrossRef]

6. Mahdi ZM, Al-Shamani AN, Al-Manea A, Al-zurfi HA, Al-Rbaihat R, Sopian K, et al. Enhancing photovoltaic thermal (PVT) performance with hybrid solar collector using phase change material, porous media, and nanofluid. Sol Energy. 2024;283:112983. doi:10.1016/j.solener.2024.112983. [Google Scholar] [CrossRef]

7. Alrbai M, Al-Dahidi S, Alahmer H, Al-Ghussain L, Al-Rbaihat R, Hayajneh H, et al. Integration and optimization of a waste heat driven organic Rankine cycle for power generation in wastewater treatment plants. Energy. 2024;308:132829. doi:10.1016/j.energy.2024.132829. [Google Scholar] [CrossRef]

8. Li X, Chen J, Wang J, Wang J, Li X, Kan Y. Research on fault diagnosis method of bearings in the spindle system for CNC machine tools based on DRSN-transformer. IEEE Access. 2024;12(18):74586–95. doi:10.1109/access.2024.3404968. [Google Scholar] [CrossRef]

9. Mao M, Zhou C, Xu B, Liao D, Yang J, Liu S, et al. Fault diagnosis method using MVMD signal reconstruction and MMDE-GNDO feature extraction and MPA-SVM. Front Phys. 2024;12:1301035. doi:10.3389/fphy.2024.1301035. [Google Scholar] [CrossRef]

10. Liu L, Zhang J, Xue S. Photovoltaic power forecasting: using wavelet threshold denoising combined with VMD. Renew Energy. 2025;249:123152. doi:10.1016/j.renene.2025.123152. [Google Scholar] [CrossRef]

11. Zhang S, Zhao H, Xu J, Deng W. A novel fault diagnosis method based on improved adaptive variational mode decomposition, energy entropy, and probabilistic neural network. Trans Can Soc Mech Eng. 2020;44(1):121–32. doi:10.1139/tcsme-2018-0195. [Google Scholar] [CrossRef]

12. Manoharan G. IntelligentFaceNet: designing a multi-cascaded attentive and adaptive deep learning network for facial recognition using heuristic approach. Int J Wavelets Multiresolut Inf Process. 2024;22(3):2350043. doi:10.1142/s0219691323500431. [Google Scholar] [CrossRef]

13. Zhao S, Liang X, Wang L, Zhang H, Li G, Chen J. A fault diagnosis method for analog circuits based on EEMD-PSO-SVM. Heliyon. 2024;10(18):e38064. doi:10.1016/j.heliyon.2024.e38064. [Google Scholar] [PubMed] [CrossRef]

14. Han SM, Yu YW, Guo Y. Open-circuit fault diagnosis of photovoltaic inverters based on improved GAF-SE-ResNet. Acta Energiae Solaris Sinica. 2024;45(10):336–44. (In Chinese). doi:10.19912/j.0254-0096.tynxb.2023-0987. [Google Scholar] [CrossRef]

15. Zhang L, Yu MQ, Xia YY. Fault diagnosis of grid-connected photovoltaic inverters based on FastICA-LDA. J Xinyu Univ. 2024;29(5):40–8. (In Chinese). doi:10.3969/j.issn.2095-3054.2024.05.006. [Google Scholar] [CrossRef]