A Non-Unit Protection Based on Propagation of Fault Traveling Wave for Transmission Line Connected to Wind Power Plant

1  Introduction

The accelerated depletion of carbon-intensive resources, coupled with the escalating climate crisis, has catalyzed exponential expansion in harvesting renewable energy resources, particularly within modernized power systems [1–4]. However, the grid-scale proliferation of renewable generation—predominantly inverter-interfaced wind and solar resources—introduces novel fault signatures, undermining the efficacy of conventional line protection schemes designed for synchronous machine-dominated systems [5–9]. For example, due to the weak feed characteristic of the current, the sensitivity of the current differential protection is reduced, and the ability of the power frequency quantity distance protection to resist transient resistance is decreased. Affected by the control strategies of the renewable energy sources, their equivalent impedance changes, leading to a decrease in the reliability of the directional elements based on the impedance of the backside system, and even misjudgments may occur. Therefore, it is necessary to study protection methods that can be applied to the transmission lines of renewable energy.

Currently, scholars have carried out studies on transmission line protection methods for power grids that accommodate the integration of renewable energy sources. These studies can be divided into two categories: one involves improved methods for traditional protections, and the other explores new principles for protections.

In terms of improving traditional protection methods, authors in [10] proposed a fault current classification method to enhance the calculation accuracy of measured impedance. But this method is still based on frequency-domain information. Its operation speed is constrained by frequency deviations and harmonic distortions in wind plant-connected transmission line fault currents, attributed to the transient response characteristics of power electronics. In [11], a new distance protection based on positive sequence voltage was introduced. However, this protection method is only applicable to phase-to-phase faults. In [12], a distance protection with an adaptive time delay based on frequency estimation was proposed. The method in [13] adapted the operating zone of distance protection based on the dynamic response of renewable energy sources, effectively mitigating both overreach and under-reach issues. Although these two methods advance conventional distance protection adaptability to renewable energy sources, they still exhibit drawbacks, including inadequate transient response characteristics and slow operation speed in complex fault situations. An adaptive distance protection is proposed in [14]. However, zone II of the proposed protection may fail to achieve coordination with zone I on the adjacent line. Authors in [15] proposed an improved current differential protection based on wideband quantities. Though the enhanced method performs well under different fault situations, it imposes special requirements on CT, which limits its practical application. In [16], an artificial neural network is applied to adaptively adjust the setting values of distance protection criteria based on different fault scenarios. However, considering that the artificial neural network requires a large amount of correct and reliable data for training, the practical usability of the method proposed in [16] needs further discussion. Authors in [17] propose a new solution method for differential equations of the R-L model to optimize the performance of time-domain distance protection. However, the method in [17] ignores the effects of the distributed capacitance of the line, resulting in limited performance of the proposed method in long transmission lines. Then, authors in [18] analyzed the error of the time-domain fault location method based on the R-L model and presented an improved scheme unaffected by distributed capacitance.

In terms of studies on new protection principles, authors in [19] introduced a localized protection scheme that utilizes current and voltage signals for precise fault detection. Nevertheless, voltage-dependent protection methods exhibit inherent drawbacks, including slow operating speed and reduced sensitivity to high-resistance faults. References [20,21] developed impedance-based differential protection schemes. These schemes, however, impose stringent synchronization requirements for data acquisition from both line terminals. Reference [22] utilized transient high-frequency impedance characteristics for fault detection, providing valuable insights for new energy transmission line protection. Authors in [23,24] employed current cosine similarity and bilateral waveform correlation analysis to develop pilot protection schemes. While demonstrating strong tolerance to fault resistance, these schemes necessitate stringent synchronization of dual-terminal measured data. Reference [25] introduced a pilot protection scheme utilizing the similarity and squared error of multi-band (10–200 Hz) components of currents from both ends of the line. However, the performance of the protection is potentially limited by inverter control interactions within this frequency range. In [26], a pilot protection based on the sequence current ratio was introduced. The proposed method only utilizes the amplitude feature, thereby requiring lower time synchronization. References [27,28] introduced an innovative inter-harmonic-based differential protection method, where inverters are controlled to inject specific inter-harmonic components into the power system. Fault discrimination is achieved by analyzing the differential characteristics of harmonic distributions across transmission line terminals.

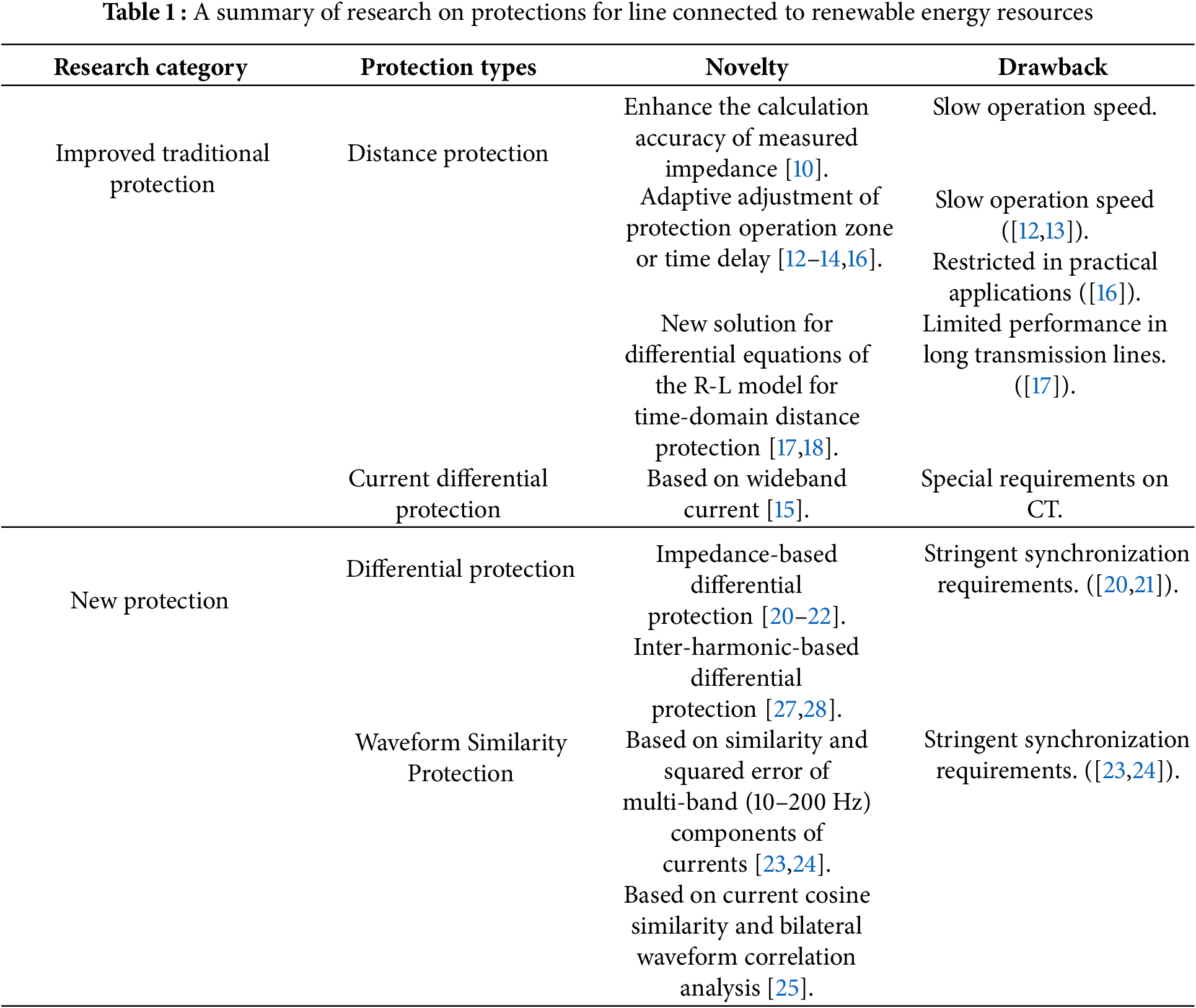
Based on the preceding analysis, a summary is presented in Table 1. As shown in Table 1, despite significant research efforts devoted to various protection schemes that demonstrate effectiveness, they still exhibit limitations.

In this paper, a transmission line protection unaffected by renewable energy sources is proposed, and simulation tests based on PSCAD have been done to validate the performance of the proposed protection.

The remainder of the paper is organized as follows: the fault traveling wave propagation characteristics are introduced in Section 2. Section 3 introduces the proposed protection, including its fundamental principle, criteria, and the flow chart. Section 4 shows different simulation tests. Section 5 is the conclusion part.

2  Traveling Wave Propagation Characteristics

Based on the two-terminal system shown in Fig. 1, the positive direction is designated as the orientation from the bus toward the line. For point M, the blue arrow denotes the forward traveling wave, propagating in the positive direction; the red arrow indicates the backward-propagating wave, whose propagation direction is opposite to the positive direction.

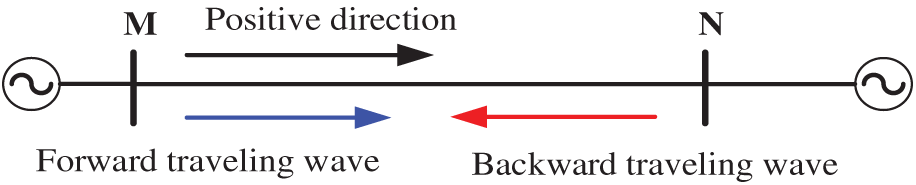
Figure 1: The two-terminal system

Upon the inception of an internal fault, the fault traveling wave emanates from the fault point and propagates bidirectionally toward terminals M and N. When the fault traveling wave arrives at point M, the fault backward traveling wave is detected at point M for the first time, while the surge impedance discontinuity at this junction simultaneously induces wave refraction and reflection phenomena. Then, the reflected wave continues to propagate backward to the fault point. Upon reaching the fault point, refraction and reflection occur again due to the surge impedance disparity at this discontinuity interface. And the refracted traveling wave continues to propagate to point N, and the reflected traveling wave propagates backward to point M. For point N, there is a similar propagation process.

As mentioned above, the initial detection of the fault backward traveling wave at point M occurs at the first arrival of the fault traveling wave generated at the fault point. However, the second detection bifurcates into two distinct scenarios.

In the first scenario, as shown in Fig. 2, the fault location is on segment ON, and point O is the midpoint of transmission line MN. From Fig. 2, the fault backward wave detected for the second time at point M is the arrival of ub2 in Fig. 2, which is the refraction wave of the traveling wave propagating from point N.

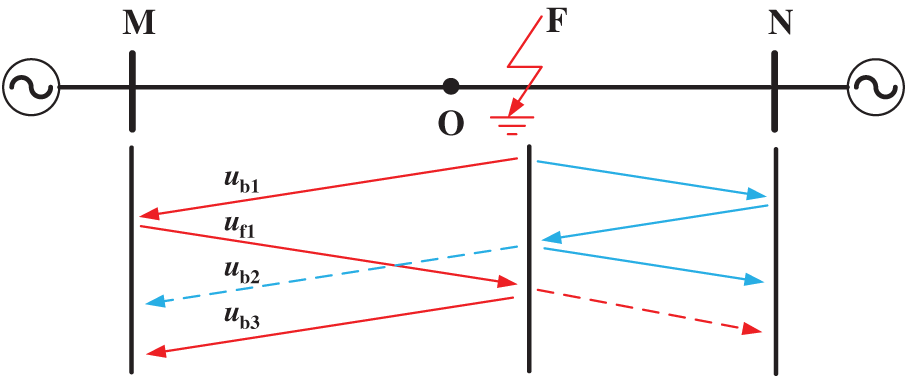
Figure 2: The propagation process of the fault traveling wave in the first internal fault scenario

In the second scenario, as shown in Fig. 3, the fault location is on segment MO, and point O is the midpoint of transmission line MN. From Fig. 3, the second detection of the fault backward traveling wave at point M is the arrival ub2 in Fig. 3, which is the refraction wave of the traveling wave uf1 in Fig. 3.

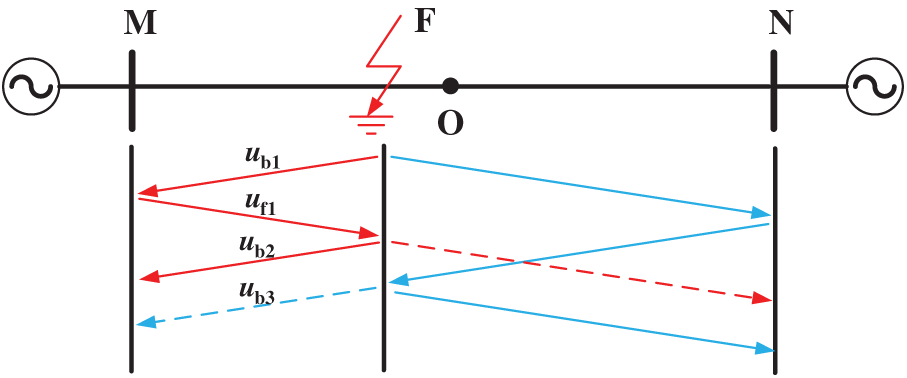
Figure 3: The propagation process of the fault traveling wave in the second internal fault scenario

For the external faults, the fault situations can be divided into two situations.

Fig. 4 shows one of the external fault situations. When the fault occurs at the position shown in Fig. 4, the fault traveling wave generated at the fault point is refracted at point N, and the refracted traveling wave propagates from point N to point M. When the refracted traveling wave reaches point M, the fault backward traveling wave ub1 is detected for the first time at point M. At the same time, the refracted traveling wave is reflected at point M. Then, the reflected traveling wave uf1 propagates backward to point N. When uf1 reaches point N, it is reflected again at point N and propagates to point M again. Point M detects the fault traveling wave for the second time once the reflected traveling wave ub2 reaches point M again.

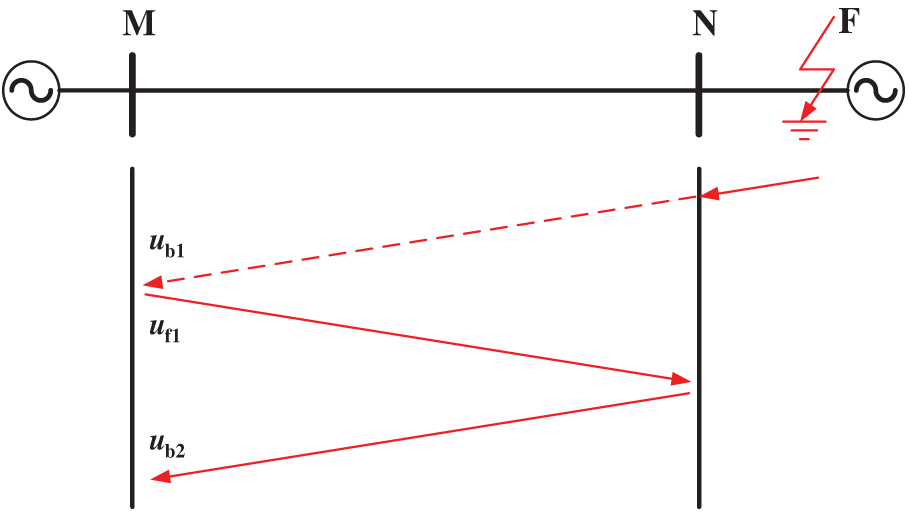
Figure 4: The propagation of the fault traveling wave under an external fault

Fig. 5 shows another external fault situation. The fault position is on the dorsal side of point M. When the fault occurs, the fault traveling wave is refracted at point M, and the refracted traveling wave uf1 continues to propagate to point N. When uf1 reaches point N, it is reflected at point N, and the reflected traveling wave ub1 propagates backward to point M. When ub1 reaches point M, the reflection occurs again, and the fault backward traveling wave is detected for the first time at point M. Then the reflected traveling wave uf2 propagates backward to point N. After reaching point N, uf2 is reflected again, and the reflected wave ub2 propagates from point N to point M. When it reaches point M, the fault backward traveling wave is detected for the second time at point M.

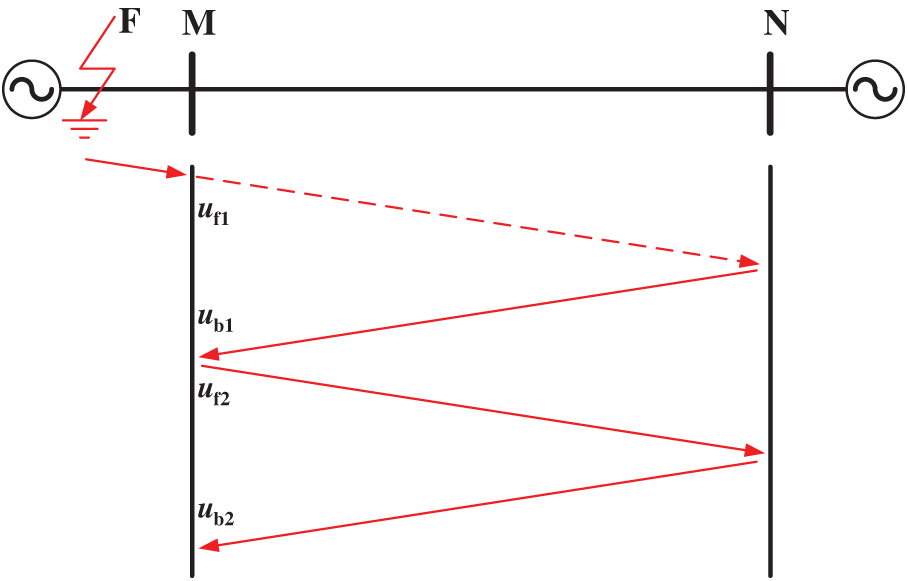
Figure 5: The propagation of the fault traveling wave under an external fault

From the analysis above, the temporal interval between the initial and secondary arrivals of the fault backward traveling wave can be used to determine whether the fault occurred on the protected transmission line.

Suppose the propagation speed of the fault traveling wave is vc, the temporal interval between the initial and secondary arrivals of the fault backward traveling wave is ΔT, the total length of the transmission line is l, and the distance from the fault point to point M is lF.

For the first case of internal fault, based on Fig. 2, the relationship of vc, ΔT, l and lF can be expressed as:

lF=l−12vcΔT.(1)

Based on Fig. 2, the relationship of vc, ΔT, l and lF under the second case of internal fault can be expressed as:

lF=12vcΔT<l.(2)

Based on Figs. 3 and 4, the relationship of vc, ΔT, l and lF under external fault can be expressed as:

lF=12vcΔT.(3)

From (1) and (2), for the internal faults, the calculation result of vcΔT/2 is less than l. For the external faults, the calculation result of vcΔT/2 is equal to l. Therefore, using the calculation result of vcΔT/2 can distinguish between internal faults and external faults.

3  The Transmission Line Protection Method

3.1 Obtainment of Fault Backward Traveling Wave

The three-phase lines are coupled with each other. To avoid such effects, the three-phase voltage and current need to be decoupled. The phase-mode transformation is employed to deal with the three-phase current and voltage. Taking voltage as an example, the transformation of voltage is:

[u0uαuβ]=13[1111−1010−1][uAuBuC].(4)

In (4), the subscripts A, B, and C denote the three-phase quantities, the subscripts 0, α, and β denote the zero-mode component, α-mode component, and β-mode component, respectively.

Based on (4), the α-mode components used to obtain the fault backward traveling wave are calculated by:

{Δiα=13(ΔiA−ΔiB)Δuα=13(ΔuA−ΔuB),(5)

where, ΔiA and ΔiB are the current fault components of phase A and phase B, respectively, ΔuA and ΔuB are the voltage fault components of phase A and phase B, respectively.

After obtaining Δiα and Δuα, the fault backward traveling wave is calculated by:

Δubα=Δuα−ZCΔiα,(6)

where, ZC represents the surge impedance of the transmission line.

Based on the transmission line whose structure is shown in Fig. 6, the fault backward traveling wave during an internal fault is calculated here. The α-mode surge impedance of the transmission line required for the calculation process varies with frequency, as shown in Fig. 7. As Fig. 7 illustrates, the α-mode surge impedance does not vary much at different frequencies. Therefore, the surge impedance used in (7) can be set to 350 Ω.

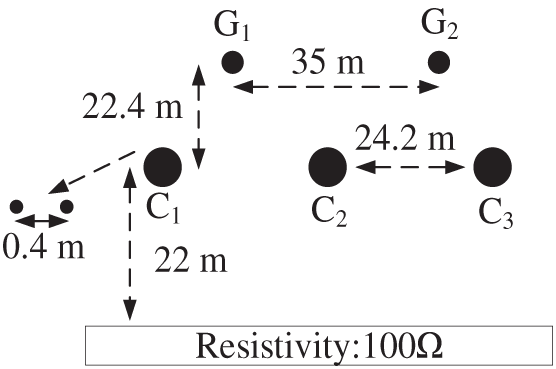
Figure 6: The structure of the transmission line

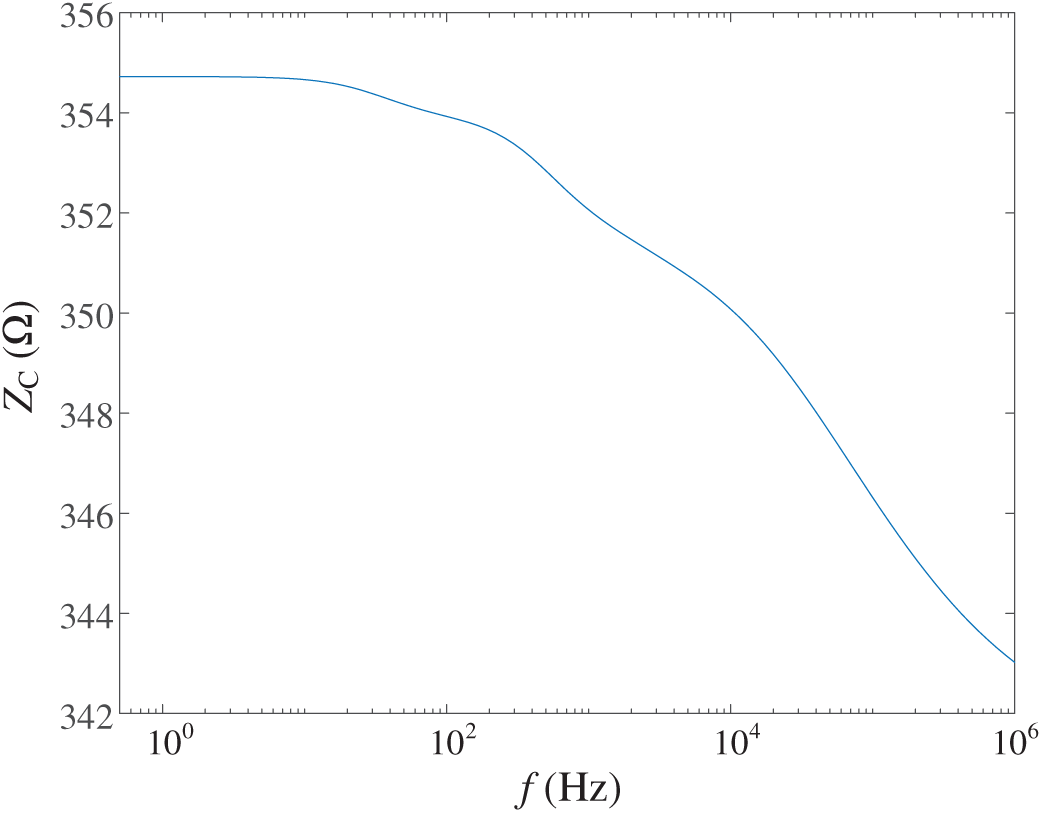
Figure 7: The surge impedance of the transmission line under different frequencies

The calculation result is shown in Fig. 8. Before the fault occurs, there is no fault component, and consequently no fault backward traveling wave, corresponding to the waveform near zero in the first half of Fig. 8. After the fault occurs, a fault backward traveling wave is generated, corresponding to the waveform in the latter half of Fig. 8. From Fig. 8, the fault backward traveling wave exhibits multiple step mutations (as marked by the red dashed rectangles in the figure) after the fault occurs. And these mutations are caused by the fault backward traveling waves reaching the measurement point.

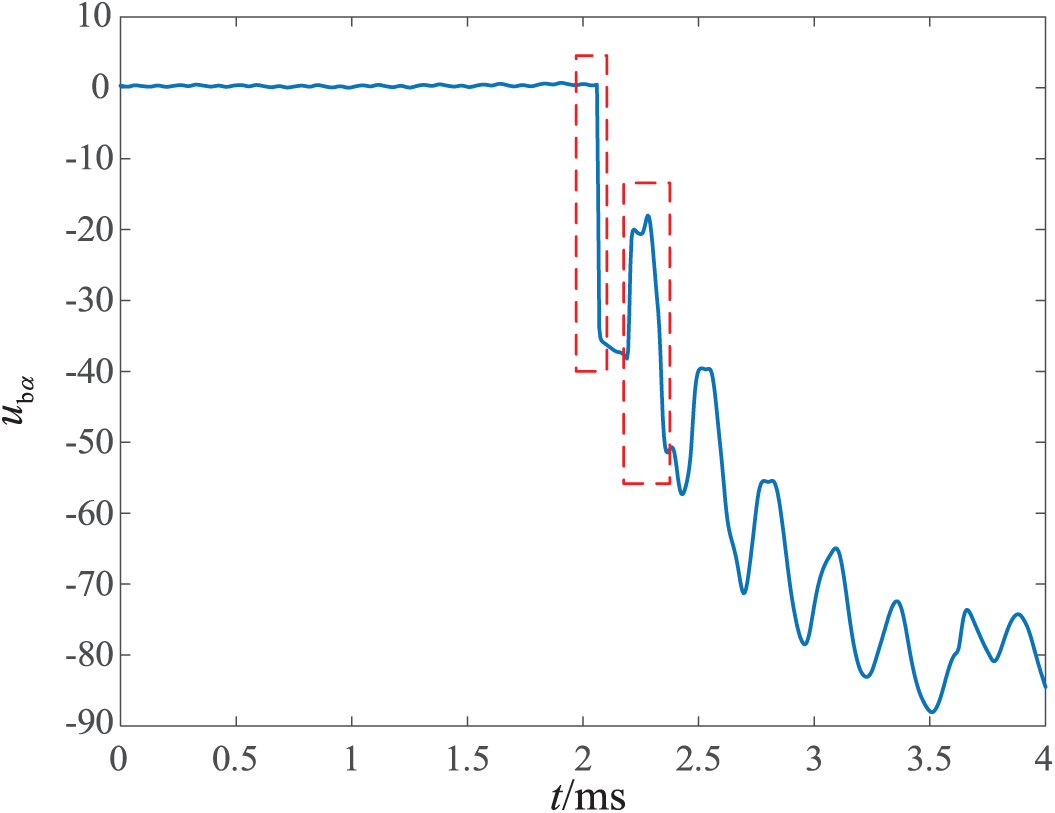
Figure 8: The calculated fault backward traveling wave

Since each step mutation in the waveform represents the arrival of the fault backward traveling wave at the measurement point, quantitative identification of these step mutations enables determination of ΔT, which is defined as the temporal interval between the initial and secondary arrivals of the fault backward traveling wave in Section 2. Then, the calculation result of vcΔT/2 can be used to form the protection criterion.

3.2 Identification of Step Mutations

As demonstrated in Section 3.1, finding a method to accurately quantify and identify step mutations of the fault backward traveling wave is essential for reliably distinguishing between internal faults and external faults. The Teager Energy Operator (TEO) is employed to deal with the fault backward traveling wave to find step mutations.

TEO is a nonlinear signal processing operator that quantifies the instantaneous energy. Its expression can be written as:

ψ[x(t)]=x˙2(t)−x(t)x¨(x),(7)

where, x(t) represents the pending signal, x˙(t) and x¨(t) represent the first-order differential and second-order differential of x(t), respectively.

Take a cosine signal as an example to characterize the properties of TEO. Define x(t) as Acos⁡(ωt+φ), (7) can be rewritten as:

ψ[x(t)]=A2ω2.(8)

It can be seen from (8) that TEO considers both the amplitude and frequency of a signal when tracking the energy changes of the signal. Compared to conventional instantaneous energy signal processing methods that solely consider amplitude information, TEO possesses an inherent advantage in describing the characteristics of step mutations in a signal more clearly, as step mutations exhibit not only drastic amplitude variations but also contain abundant high-frequency components.

Using TEO, the fault backward traveling wave shown in Fig. 8 is processed here. And the processing result is presented in Fig. 9. In Fig. 9, the blue solid line represents the processed result of the fault backward traveling wave in Fig. 8, while the green dashed line is the waveform shown in Fig. 8. As evidenced in Fig. 9, the TEO processing has significantly enhanced the characterization of the step mutations in the fault backward traveling wave shown in Fig. 8. This improvement is manifested through more distinct waveform spikes in Fig. 9 (as highlighted by the red dashed rectangles).

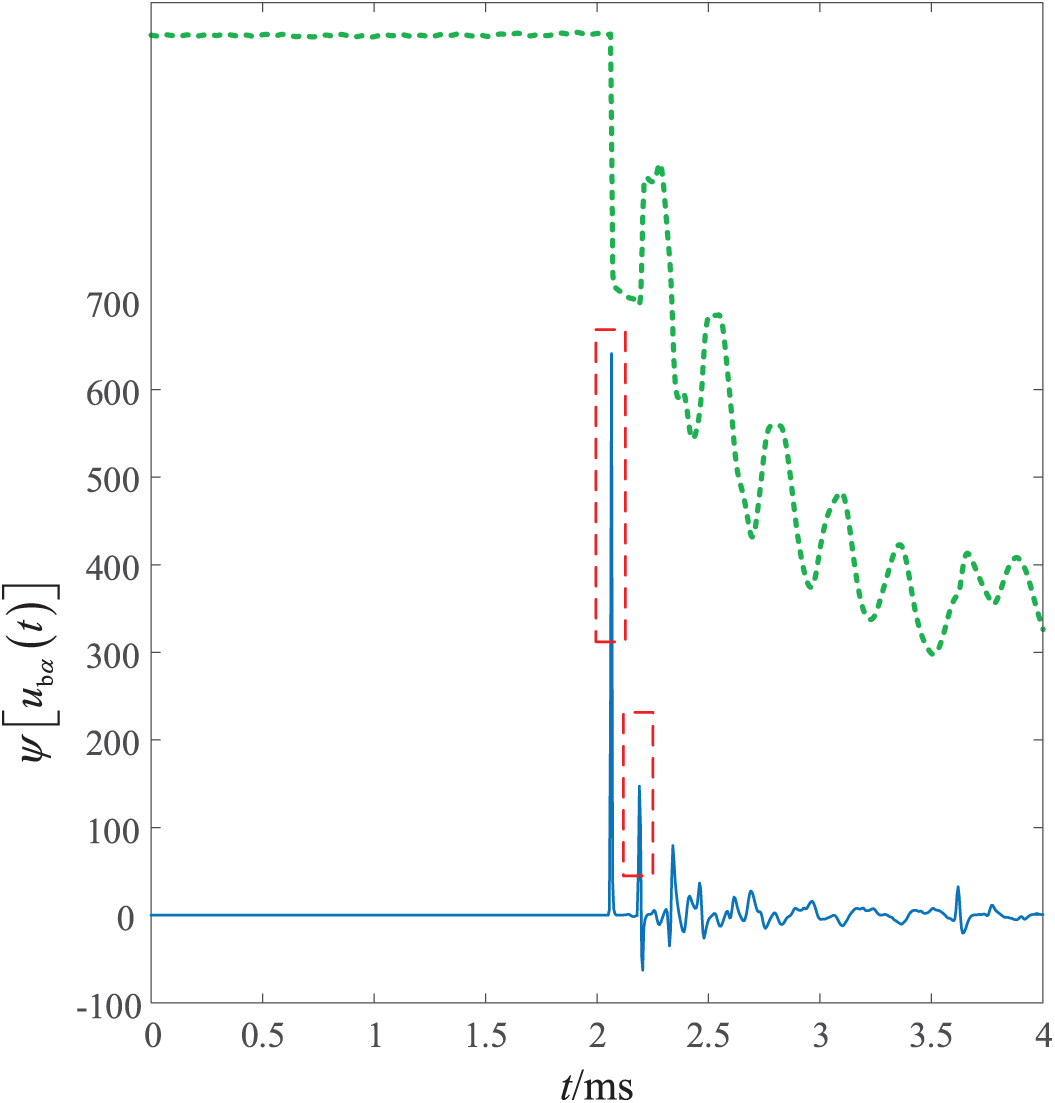
Figure 9: The results of processing the fault backward traveling wave

3.3 The Criterion and Flow Chart

Based on the introduction of Section 3.1, define iα(kΔt) and uα(kΔt) as:

{Δiα(kΔt)=13[ΔiA(kΔt)−ΔiB(kΔt)]Δuα(kΔt)=13[ΔuA(kΔt)−ΔuB(kΔt)],(9)

where, Δt is the sampling interval, k=1,2,⋯,N and N is the number of sample points in a sampling window. And the sampling time window spans a total of 4 ms, with 2 ms allocated before and 2 ms after the start of the protection. The start criterion is:

Uφ<0.8UN,(10)

where Uφ is the amplitude of phase voltage and φ=A,B,C, UN is the rate value of phase voltage.

Substituting (9) into (6) gives:

Δubα(kΔt)=Δuα(kΔt)−ZCΔiα(kΔt).(11)

As the sampling signal is discrete, the discrete TEO is needed. For a discrete signal x[n], the TEO is formulated as a nonlinear functional mapping:

ψ[x[n]]=x2(n)−x[n−1]x[n+1].(12)

Based on (11) and (12), calculate S(kΔt) as:

S(kΔt)=ubα2(kΔt)−ubα[(k−1)Δt]ubα[(k+1)Δt].(13)

After obtaining S(kΔt), compare S(kΔt) with a set threshold value Sset. Start counting when S(kΔt) is larger than Sset for the first time, stop counting when S(kΔt) is larger than Sset for the second time, and get the count result N1.

12vcN1Δt<lset,(14)

where, lset is the threshold. Considering the reliability, lset can be set to 0.9l, l is the total length of the transmission line. When (14) is satisfied, the fault occurs on the transmission line, and vice versa.

The flow chart of the protection is shown in Fig. 10. As illustrated in Fig. 10, when the start criterion is satisfied, S(kΔt) is calculated within a sampling window. After obtaining S(kΔt), each element in S(kΔt) is compared with Sset in turn. When the first element greater than Sset appears, starts counting until the second element greater than Sset stops counting, and the counting result N1 is obtained. Then, compare the calculation result of vcN1Δt/2 with lset. If vcN1Δt/2 is less than lset, there is a fault occurring on the transmission line, and the protection operates. Besides, if only one element in S(kΔt) is greater than Sset or all the elements in S(kΔt) are less than Sset, it is concluded that no fault has occurred on the transmission line.

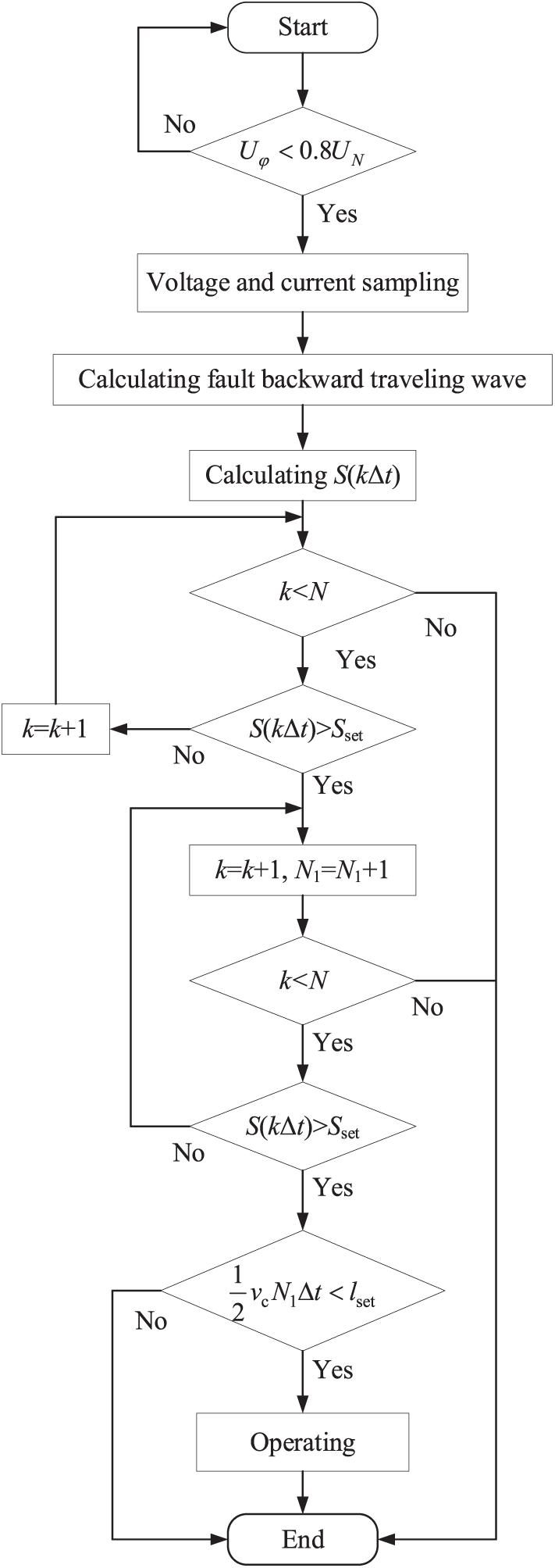
Figure 10: The flow chart

4  Simulation Tests

The performance evaluation of the proposed protection was conducted using a simulation system built in PSCAD/EMTDC, as shown in Fig. 11. In the figure, the conventional AC grid is connected to the left terminal of the transmission line, while the wind power plants are connected to the right terminal.

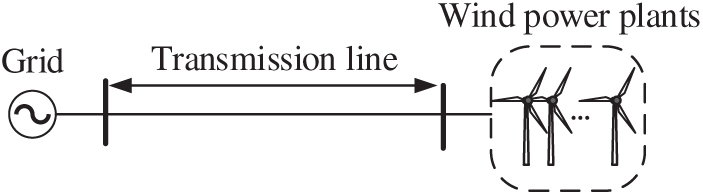
Figure 11: The structure of the simulation system

The speed of the α-mode traveling wave at different frequencies is shown in Fig. 12. As seen in Fig. 12, the speed of the α-mode traveling wave remains relatively constant across various frequencies. And the speed vc can be set to 2.92×105 km/s.

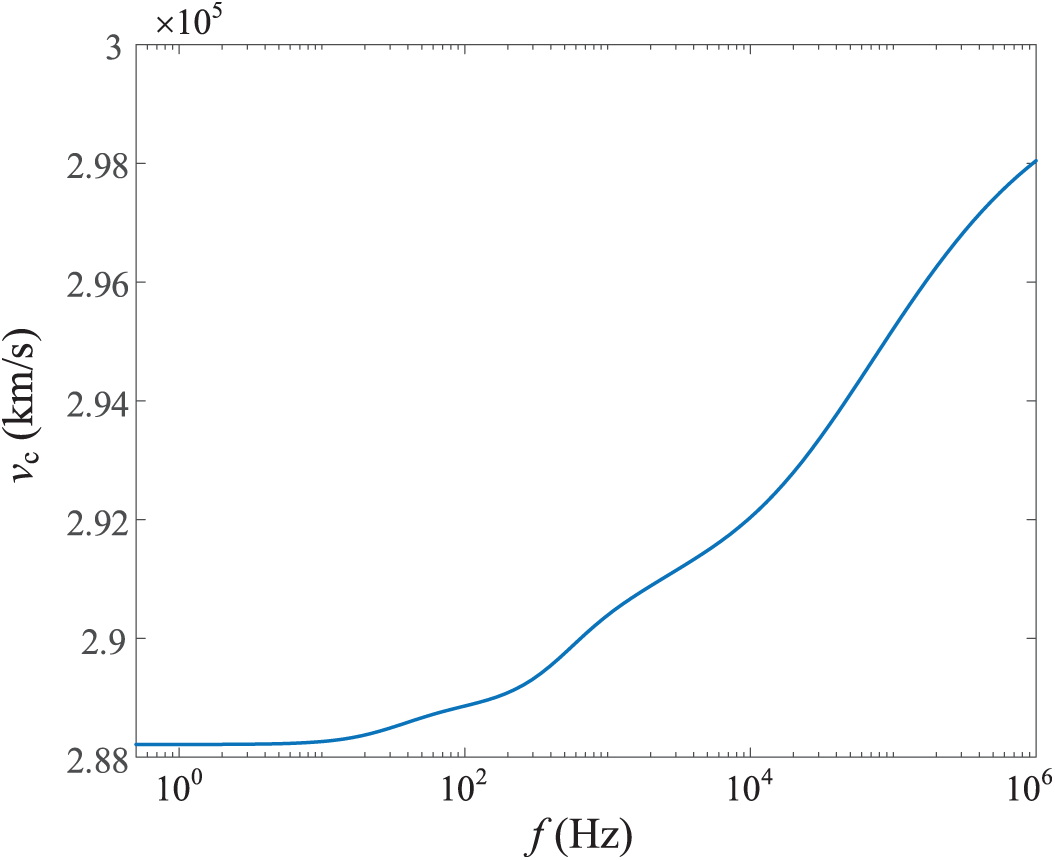
Figure 12: The speed of the α-mode traveling wave under different frequencies

4.1 Performance Evaluation under Different Fault Types

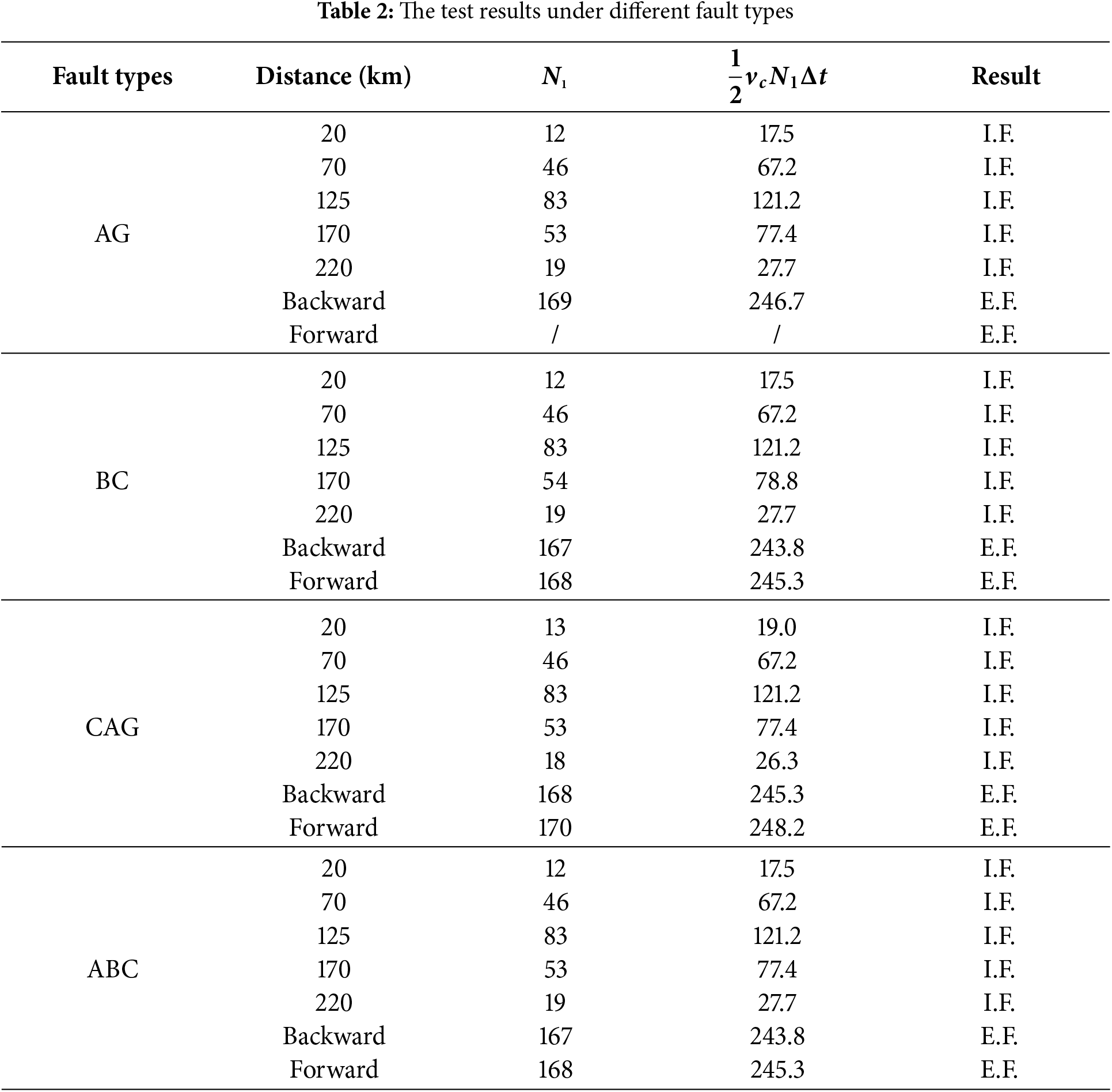
The performance of the proposed protection is validated through multi-type fault emulations within the simulation system. Table 2 shows the test results. Table entries “AG”, “BC”, “CAG”, and “ABC” denote single-phase grounding fault on phase A, phase-to-phase short-circuit fault on phase B and C, phase-to-phase short-circuit grounding fault on phase C and A, and three-phase short-circuit fault, respectively. “Distance” denotes the distance from the fault point to the bus of the wind power plant side, and the “Backward” and “Forward” represent two cases of external faults. “I.F.” and “E.F.” denote the determination results of the proposed protection, with “I.F.” indicating an internal fault and “E.F.” representing an external fault. As evidenced in Table 2, the proposed protection achieves reliable discrimination of diverse internal and external fault scenarios

4.2 Discussion about the Influence of Fault Time

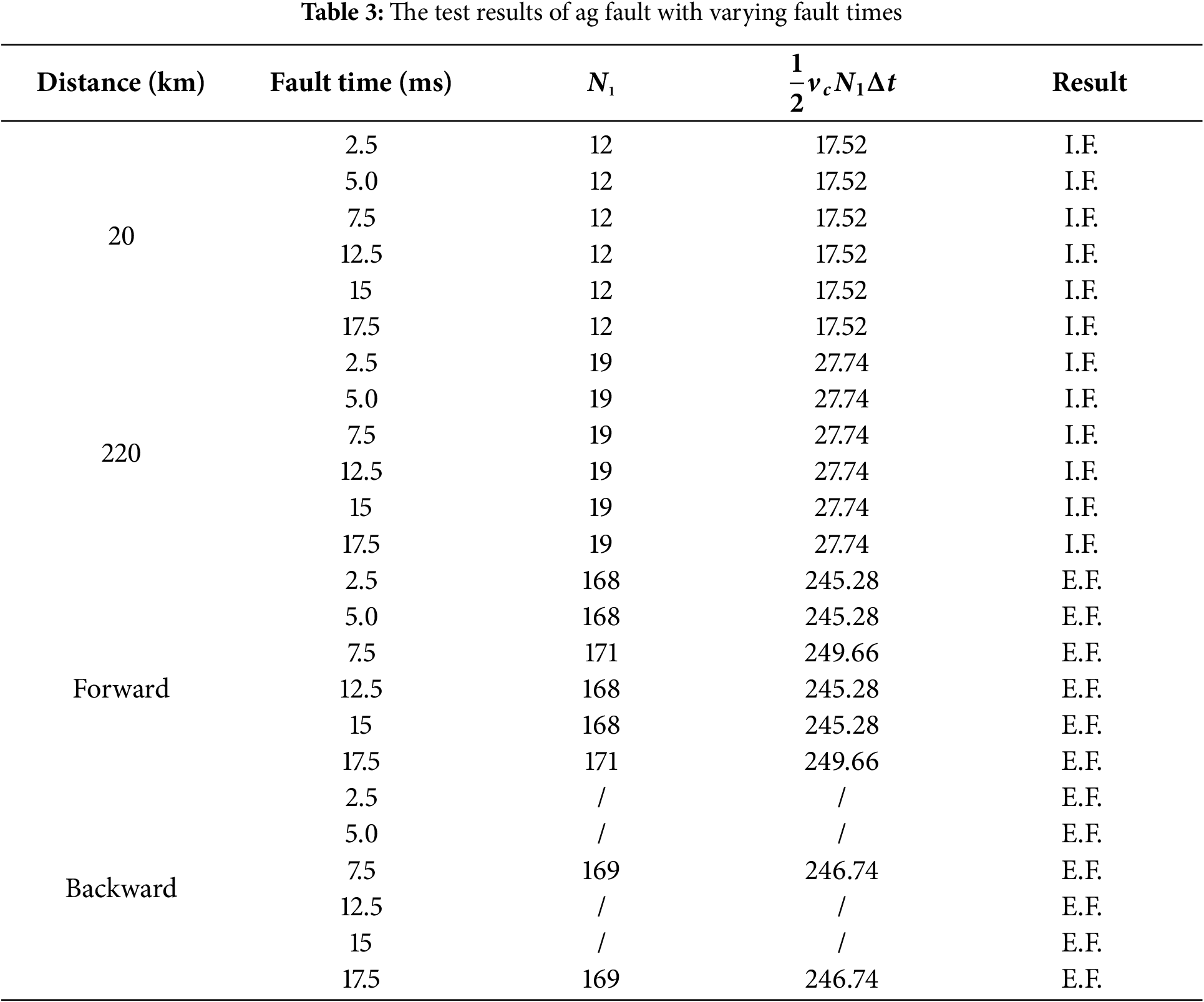
The transient response of AC transmission line faults exhibits significant dependence on fault time. Multiple AG fault scenarios with varying fault times are emulated to validate the performance of the proposed protection. Table 3 shows the test results. Table 3 confirms the immunity to fault timing variations of the proposed protection, enabling consistent internal and external fault identification.

4.3 Discussion about the Influence of Measuring Noise

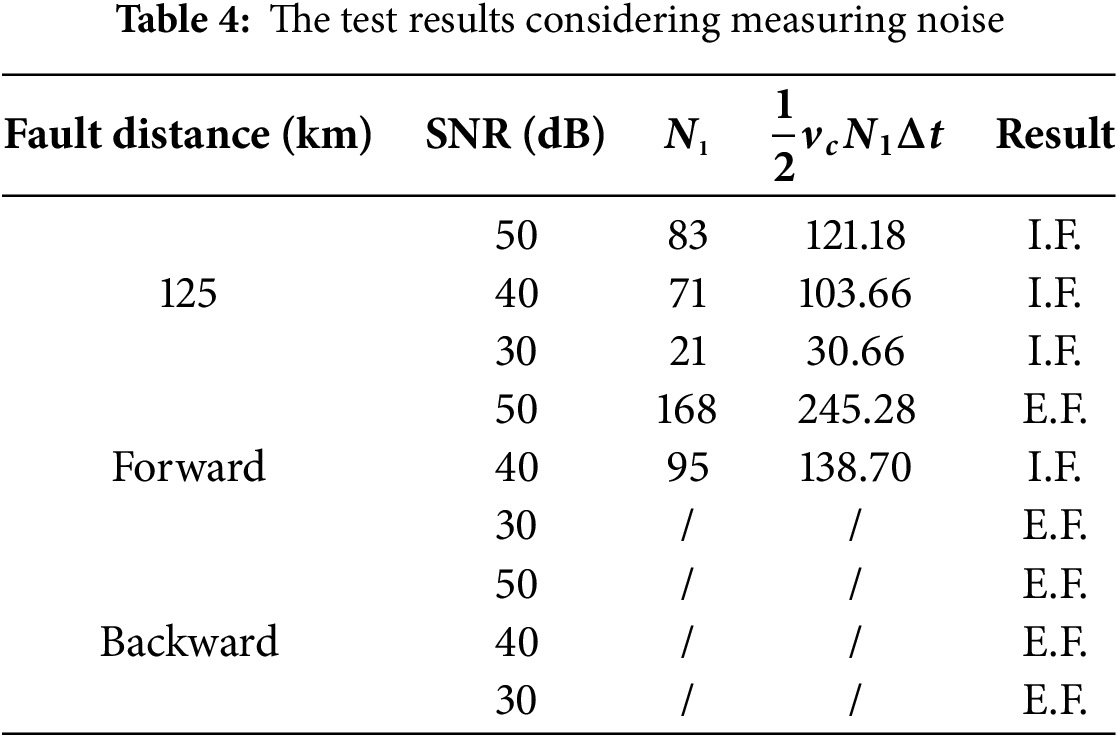
To investigate the impact of measurement noise on the performance of the proposed protection, Gaussian white noise was added to the current and voltage sampling signals in simulated phase A grounding fault scenarios with varying fault distances, thereby validating the performance of the proposed method. Table 4 shows the test results. In the table, “SNR” denotes the signal-to-noise ratio, and a smaller SNR value indicates higher measurement noise. From Table 4, the proposed protection scheme is susceptible to noise interference. As the SNR decreases, while the protection can still correctly identify internal faults occurring at the line midpoint, its performance gradually deteriorates. More critically, maloperation cases even happen due to external faults. Therefore, to further enhance the reliability of the proposed protection, incorporating filtering devices to operate in conjunction with the protection could be considered.

5  Conclusions

A non-unit protection method based on the propagation process of the fault traveling wave is proposed here. After a fault occurs, a fault traveling wave emanates from the fault point and propagates bidirectionally toward terminals. Analysis shows that the temporal interval between the initial and secondary arrivals of the fault backward traveling wave at the measurement point can reflect the fault location. Based on the analysis, the temporal interval between the initial and secondary arrivals of the α-mode component fault backward traveling wave is used to form the protection criterion, and the Teager energy operator is applied to obtain the time difference. Different fault scenarios are simulated in PSCAD to test the performance of the proposed method.

Theoretical analysis and simulation verification demonstrate that the proposed method can effectively identify internal and external faults under different fault scenarios, while offering the following advantages:

(a)   The proposed protection method requires only a sampling time window of 2 ms before and after protection initiation, ensuring a fast operation speed.

(b)   Within the required 4 ms sampling time window, the control strategies of renewable energy sources will not be activated. The changes in fault current and voltage depend solely on the inherent system topology, rendering the proposed protection immune to the influence of integrating renewable energy sources.

(c)   The proposed protection algorithm involves only simple counting and basic arithmetic operations, making it easy to implement.

The proposed protection is suitable for us as the main protection for transmission lines. Indeed, the proposed protection still has certain limitations, such as susceptibility to measurement noise. To enhance the reliability of the proposed protection, consideration could be given to incorporating a filter to cooperate with it.

Acknowledgement: Not applicable.

Funding Statement: This research was funded in part by Science and Technology Project of State Grid Sichuan Electric Power Company under Grant 521997230003.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Hao Wang; methodology, Hao Wang; software, Yiping Luo; validation, Wenyue Zhou; writing—original draft preparation, Hao Wang; writing—review and editing, Wenyue Zhou and Yiping Luo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yang Z, Wang H, Liao W. Protection challenges and solutions for AC systems with renewable energy sources: a review. Prot Control Mod Power Syst. 2025;10(1):18–39. doi:10.23919/PCMP.2023.000279. [Google Scholar] [CrossRef]

2. Zheng X, Chao C, Weng Y, Ye H, Liu Z, Gao P, et al. High-frequency fault analysis-based pilot protection scheme for a distribution network with high photovoltaic penetration. IEEE Trans Smart Grid. 2023;14(1):302–14. doi:10.1109/TSG.2022.3203392. [Google Scholar] [CrossRef]

3. Chen F, Xue M, Qiu Y, Yang L, Chen Q, Yu C, et al. Multi-terminal wireless differential protection method for offshore wind power collection lines. IEEE Access. 2024;12(5):58789–800. doi:10.1109/ACCESS.2024.3392570. [Google Scholar] [CrossRef]

4. Quispe JC, Orduña E. Transmission line protection challenges influenced by inverter-based resources: a review. Prot Control Mod Power Syst. 2022;7(3):1–17. doi:10.1186/s41601-022-00249-8. [Google Scholar] [CrossRef]

5. Muljadi E, Samaan N, Gevorgian V. Different factors affecting short circuit behavior of a wind power plant. IEEE Trans Ind Appl. 2013;49(1):284–92. doi:10.1109/TIA.2012.2228831. [Google Scholar] [CrossRef]

6. Saleh SA, Aljankawey AS, Abu-Khaizaran MS. Influences of power electronic converters on voltage–current behaviors during faults in DGUs—part I: wind energy conversion systems. IEEE Trans Ind Appl. 2015;51(4):2819–31. doi:10.1109/TIA.2014.2387477. [Google Scholar] [CrossRef]

7. Saleh SA, Aljankawey AS, Alsayid B. Influences of power electronic converters on voltage–current behaviors during faults in DGUs—part II: photovoltaic systems. IEEE Trans Ind Appl. 2015;51(4):2832–45. doi:10.1109/TIA.2014.2387482. [Google Scholar] [CrossRef]

8. Chandrasekar S, Gokaraju R. Dynamic phasor modeling of type 3 DFIG wind generators (including SSCI phenomenon) for short-circuit calculations. IEEE Trans Power Deliv. 2015;30(2):887–97. doi:10.1109/TPWRD.2014.2365587. [Google Scholar] [CrossRef]

9. Howard DF, Habetler TG, Harley RG. Improved sequence network model of wind turbine generators for short-circuit studies. IEEE Trans Energy Convers. 2012;27(4):968–77. doi:10.1109/TEC.2012.2213255. [Google Scholar] [CrossRef]

10. Hooshyar A, Azzouz MA, El-Saadany EF. Distance protection of lines connected to induction generator-based wind farms during balanced faults. IEEE Trans Sustain Energy. 2014;5(4):1193–203. doi:10.1109/TSTE.2014.2336773. [Google Scholar] [CrossRef]

11. Zhou Z, Yu S, Wang X. A new distance protection method using calculated voltage as polarization voltage for renewable energy system. In: Proceedings of the 18th International Conference on Developments in Power System Protection; 2025 Jan 8–11; Hong Kong, China. p. 278–82. doi:10.1049/icp.2025.0481. [Google Scholar] [CrossRef]

12. Li B, Sheng Y, He J. Improved distance protection for wind farm transmission line based on dynamic frequency estimation. Int J Electr Power Energy Syst. 2023;153(1):109382. doi:10.1016/j.ijepes.2023.109382. [Google Scholar] [CrossRef]

13. Mishra P, Pradhan AK, Bajpai P. Adaptive distance relaying for distribution lines connecting inverter-interfaced solar PV plant. IEEE Trans Ind Electron. 2021;68(3):2300–9. doi:10.1109/TIE.2020.2975462. [Google Scholar] [CrossRef]

14. Ma K, Høidalen HK, Chen Z. Improved zone 1 top line tilting scheme for the polygonal distance protection in the outgoing line. CSEE J Power Energy Syst. 2023;9(1):172–84. doi:10.17775/CSEEJPES.2021.07870. [Google Scholar] [CrossRef]

15. Zhang Y, Zhang G, Wang G, Mo C, Liu Z, Sun Y, et al. Algorithm for pilot current differential protection based on wideband quantities. In: Proceedings of the 2025 7th International Conference on Information Science, Electrical and Automation Engineering; 2025 Apr 18–20; Harbin, China. p. 1094–7. doi:10.1109/ISEAE64934.2025.11041905. [Google Scholar] [CrossRef]

16. Sadegh H. A novel method for adaptive distance protection of transmission line connected to wind farms. Int J Electr Power Energy Syst. 2012;43(1):1376–82. doi:10.1016/j.ijepes.2012.06.072. [Google Scholar] [CrossRef]

17. Chen Y, Wen M, Yin X. Distance protection for transmission lines of DFIG-based wind power integration system. Int J Electr Power Energy Syst. 2018;100(6–7):438–48. doi:10.1016/j.ijepes.2018.02.041. [Google Scholar] [CrossRef]

18. Hu Z, Li B, Zheng Y, Wu T, He J, Yao B, et al. Fast distance protection scheme for wind farm transmission lines considering RL and Bergeron models. J Mod Power Syst Clean Energy. 2023;11(3):840–52. doi:10.35833/MPCE.2021.000423. [Google Scholar] [CrossRef]

19. Singh P, Pradhan A. A local measurement-based protection technique for distribution system with photovoltaic plants. IET Renew Power Gener. 2020;14(6):996–1003. doi:10.1049/iet-rpg.2019.0996. [Google Scholar] [CrossRef]

20. Huang W, Nengling T, Zheng X, Fan C, Yang X, et al. An impedance protection scheme for feeders of active distribution networks. IEEE Trans Power Deliv. 2014;29(4):1591–602. doi:10.1109/TPWRD.2014.2322866. [Google Scholar] [CrossRef]

21. Chen G, Liu Y, Yang Q. Impedance differential protection for active distribution network. IEEE Trans Power Deliv. 2020;35(1):25–36. doi:10.1109/TPWRD.2019.2919142. [Google Scholar] [CrossRef]

22. Jia K, Xuan Z, Feng T. Transient high-frequency impedance comparison-based protection for flexible DC distribution systems. IEEE Trans Smart Grid. 2020;11(1):323–33. doi:10.1109/TSG.2019.2921387. [Google Scholar] [CrossRef]

23. Li Z, Xiao R, Du Y, Ren S, Tang P, Yan X. Fault transient analysis and protection for transmission lines with integration of centralized photovoltaic. Autom Electr Power Syst. 2019;43(18):120–8. doi:10.7500/AEPS20181231004. [Google Scholar] [CrossRef]

24. Jia K, Yang Z, Wei C. Pilot protection based on spearman rank correlation coefficient for transmission line connected to renewable energy source. Autom Electr Power Syst. 2020;44(15):103–11. (In Chinese). doi:10.7500/AEPS20190630001. [Google Scholar] [CrossRef]

25. Zheng L, Jia K, Bi T. Comprehensive criteria of pilot protection based on structural similarity and square error for outgoing line from renewable power plants. Power Syst Technol. 2020;44(5):1788–95. (In Chinese). doi:10.13335/j.1000-3673.pst.2019.0934. [Google Scholar] [CrossRef]

26. Yang Z, Liao W, Bak CL. Comprehensive current amplitude ratio based pilot protection for line with converter-interfaced sources. Energy Rep. 2022;8(2):420–30. doi:10.1016/j.egyr.2022.05.170. [Google Scholar] [CrossRef]

27. Soleimanisardoo A, Karegar H, Zeineldin H. Differential frequency protection scheme based on off-nominal frequency injections for inverter-based islanded microgrids. IEEE Trans Smart Grid. 2019;10(2):2107–14. doi:10.1109/TSG.2017.2788851. [Google Scholar] [CrossRef]

28. EL-Sayed W, EL-Saadany E, Zeineldin H. Interharmonic differential relay with a soft current limiter for the protection of inverter-based islanded microgrids. IEEE Trans Power Deliv. 2021;36(3):1349–59. doi:10.1109/TPWRD.2020.3006791. [Google Scholar] [CrossRef]