 Open Access
Open Access
ARTICLE
Numerical Study of Natural Convective Heat Transfer in an Air Filled Square Cavity Heated from Below and Symmetrically Cooled from the Sides with a Partition in the Hot Wall
Laboratoire des Sciences et Ingénierie Maritimes, Faculté de Génie Mécanique, USTO-MB, BP 1505 El M’naouer, Oran, 31000, Algérie
* Corresponding Author: Farah Zemani-Kaci. Email:
(This article belongs to the Special Issue: Materials and Energy an Updated Image for 2021)
Fluid Dynamics & Materials Processing 2023, 19(2), 513-539. https://doi.org/10.32604/fdmp.2022.021974
Received 15 February 2022; Accepted 22 March 2022; Issue published 29 August 2022
Abstract
A two-dimensional numerical study of laminar natural convection in a square enclosure filled with air with a wall partially heated on the bottom is presented. The heat source is located on the lower wall with different heated widths varied from 20 to 80%(ε = 0.2–0.8) of the total width of the lower wall and different heights h = H/4 and H/2 of the partition. The effect of the partition height on the main system dynamics is investigated through solution of the two-dimensional Navier–Stokes equations and the energy equation by means of a finite volume method based on the SIMPLE algorithm. The influence of the Rayleigh number (Ra = 103 to 106) and the hot wall length is also examined. It is shown that the average Nusselt number grows when ε increases and when h decreases. For a given value of ε and h, the average Nusselt number increases as Ra increases. It is concluded that the partition height causes a decrease in the average Nusselt number.Graphic Abstract
Keywords
Nomenclature
| g | gravitational acceleration (m/s2) |
| H | height of caterpillar curve shape |
| W | width (m) |
| L | width of the enclosure (m) |
| Nu | Nusselt number |
| P | pressure (N/m2) |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| T | temperature (K) |
| Th | temperature of the hot surface (K) |
| Tc | temperature of the cold surface (K) |
| ΔT | temperature variation, Th–Tc (k) |
| U | velocity component in x direction (m/s) |
| V | velocity component in y-direction (m/s) |
| x, y | cartesian coordinates (m) |
| X,Y | dimensionless coordinates |
| l | hot wall length (m) |
| Greek Symbols | |
| k | thermal conductivity of fluid (W/mK) |
| α | thermal diffusivity (m2/s) |
| β | coefficient of volumetric expansion (1/K) |
| θ | dimension less temperature, (T-To) |
| μ | dynamic viscosity (N s/m2) |
| ρ | fluid density (kg/m3) |
| ε | dimension less length of heated wall (ε = l/L) |
| Subscripts | |
| C | Cold |
| H | Hot |
| 0 | Initial |
| M | Mean |
The study of natural convection in enclosures has been the subject of a very large works, both theoretical and experimental. The interest of such studies remains in its involvement in many industrial applications such as the electronic components cooling, the thermal of buildings, the metallurgical industry, the growth of crystals for the semiconductor industry, and the case of accidental heat generation due to a fire in a nuclear reactor building, etc. The convective heat transfer in the square enclosures has been studied widely on natural convection in cavities and can be seen in Ostrach [1]. However, Natural convection in a square cavity heated from below and cooled from one side has been studied by Anderson et al. [2]. Yao [3] was the first to study natural convection along a wavy surface; a decrease in heat transfer along the undulating surface comparing with the flat surface is remarked. One of their main results is the reduction of the heat exchange between the corrugated wall of the cavity and the fluid. Chu et al. [4] studied experimentally and numerically natural convection in an enclosure with localized heating below to simulate convective heat transfer in a chamber of magma.
Sharif et al. [5] studied natural convection in a rectangular enclosure, using a finite volumes method. They considered a constant bottom heating and isothermal cooling of the side walls while the upper wall is adiabatic. The length of the heat source was varied from 20% to 80% of the bottom length of the enclosure for the range of Grashof number from 103 to 106. They found that the average Nusselt number and the maximum temperature are functions of the elongation of the enclosure and of the heat source length. While Calcagni et al. [6] investigated numerically and experimentally the development of the heat transfer phenomenon in a square enclosure partially heated from below. The heat source is located on the bottom surface of the cavity and its length range from 1/5 to 4/5 of the side (H); the two lateral walls are cooled while the other surfaces are considered adiabatic. Also, laminar natural convection inside air-filled rectangular enclosures, heated from below and cooled from above, with the lower portions of both sidewalls maintained at the temperature of the bottom wall, and the remaining upper portions of the sidewalls maintained at the temperature of the top wall, is studied numerically Caronna et al. [7]. While a natural convection in cubical enclosure with hot surface geometry and partial partitions has been analyzed by Zemani et al. [8]. The geometry is a cube with a wavy hot surface (three undulations) and three partitions. The results obtained show that the hot wall geometry with partitions affects the flow and the heat transfer rate in the cavity. It has been found also that the mean Nusselt number decreases compared with the heat transfer in the undulated cubical cavity without partitions. It was found that the flow pattern observed in 3D enclosure is very similar in the 2D case already studied in reference [9] which they treated similar cavity in two dimensional study. Steady-state laminar free convection of power-law fluids in a square enclosure with partial heating from below and symmetrical cooling from sides has been investigated by Yigit et al. [10] based on numerical simulations. It has been found that the mean Nusselt number Nu increases with increasing values of nominal Rayleigh number due to the strengthening of advective transport for shear thinning, Newtonian and shear thickening fluids. However, the mean Nusselt number is found to be insensitive in the change of the Prandtl number for all the values of Ra.
Also, Torabi et al. [11] did a comprehensive investigation of natural convection inside a partially differentially heated cavity with a thin fin using two-set lattice Boltzmann distribution functions, The results indicated that by choosing the appropriate position for the fin, the average Nu could be increased by more than 150%.
Mebarek-Oudina [12] investigated a natural convection heat transfer stability in cylindrical annular with discrete isoflux heat source of different lengths, he found that the increase of heat source length ratio decreases the critical Rayleigh number and that the flow stability and heat transfer rate can be controlled in varying of the length of heat source. Also, Zaim et al. [13] analyzed a Galerkin finite element of magneto-hydrodynamic natural convection of Cu-water nanoliquid in a baffled U-shaped enclosure, they determined that the heat transfer rate enhances with Rayleigh number and volume fraction and when decreasing the nanoparticle volume fraction the average Nusselt number augmented where Ra > 105 and Ha > 20.
The literature review gives confirmation that studies on enclosures with a partition in the hot wall contribute a significant role in the heat transfer reduction. The partition has several practical applications in flat-plate solar collectors, microelectronic devices, and refrigeration systems for example.
The purpose of this work is to conduct a numerical study and simulation of laminar natural convection in a square enclosure, with partial heating of the lower wall and cooling of the side walls. This study simulates the case of accidental heat generation due to a fire in a nuclear reactor building, for example, or the partial heating at the lower surface simulated electronic components such as chips.
The most part of our simulation is to show the partition length effects and the influence of the heat source length with a partial partition on the laminar natural convection.
Simulations are performed for different values of the Rayleigh number Ra in the range between 103 and 106, of the different heater locations (ε = 0.2 to 0.8) and for different partition height (h = 0.25 L to 0.5 L). Correlations have been developed to predict heat transfer rates from the enclosure as a function of the dimensionless heated length height, heat source length and Ra.
The numerical model considered is shown schematically in Fig. 1. It is a square cavity filled with air heated from below in two dimensions with a side equal to L, which represents the length of the cavity. The heat source is located in the center of the lower surface and its length ε varies from 0.2 to 0.8 of L, with a partition in its center, the height of the partition is varied from 0.25 L to 0.5 L. The cooling is achieved by the two vertical walls. The Prandtl number is equal to 0.71. The numerical study was carried out using a two-dimensional model and the Boussinesq approximation for air. The investigation concerns cases with Rayleigh numbers ranging from 103 to 106. The heat sources have a temperature Th= 323 K whereas the cooling walls have a temperature Tc= 283 K; all other surfaces are adiabatic.
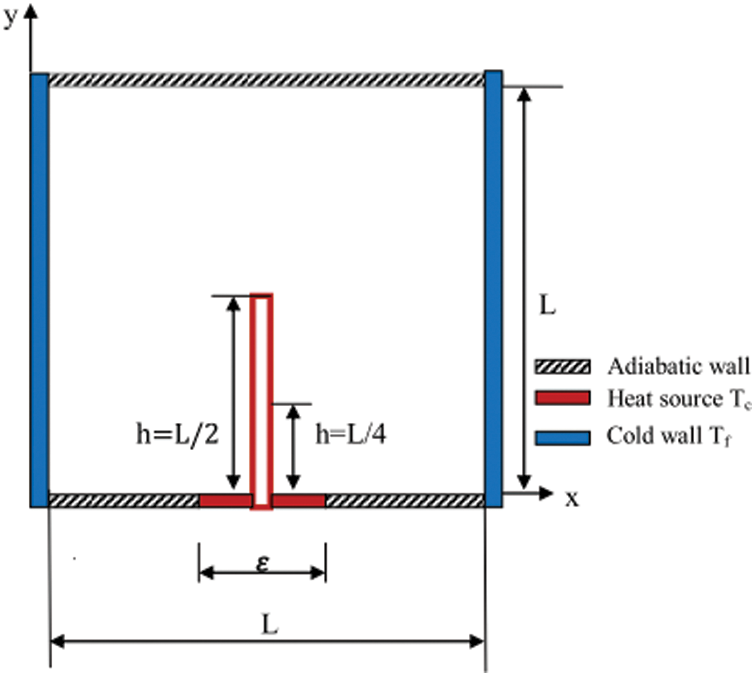
Figure 1: Physical domain
The viscous incompressible flow inside the enclosure and a temperature distribution are described by the Navier-Stokes and the energy equations. The governing equations for this case are for laminar and two-dimensional flow. In the model development, the following assumptions are adopted:
-The process is in steady state.
-The power dissipated is negligible.
-The Boussinesq approximation applies, which implies that, except for the density in the gravitational term, all other properties in the governing equations are kept constant.
-There is no source or sink in the system.
Once above assumptions are employed into the conservation equation of mass, momentum and energy and the following dimensionless variable are introduced:
The dimensionless governing equations in Cartesian coordinates for the present study then take the following forms:
The geometry of the tested cavity is shown in Fig. 1.
The study is completed with the definition of the following boundary conditions:
(Left and right wall)
(Upper wall)
(Unheated part from the bottom wall)
(Hot part of the bottom wall)
The overall heat transfer characteristics are described by the average Nusselt number which is defined over the hot wall as follows:
With: 0.2 ≤ ε ≤ 0.8 and λ = 0.0262 W/mK.
The stream function can be defined as
and the dimensionless stream function which is determined from:
A 2D uniform grid is used with a control volume formulation for the discretization (Fig. 2). The central difference scheme is employed for the convective diffusive transport variables. Pressure correction and velocity correction are implemented in accordance with the SIMPLE algorithm to achieve a converged solution. The adiabatic boundary structure condition is treated by the additional source term method. A grid independency test was carried out, and the results are indicated in Table 1. Four sets of grids 100 × 100, 110 × 110, 120 × 120 and 130 × 130 were employed (Fig. 3).

Figure 2: Grid of the geometry(h = H/4 and ε = 0.4)
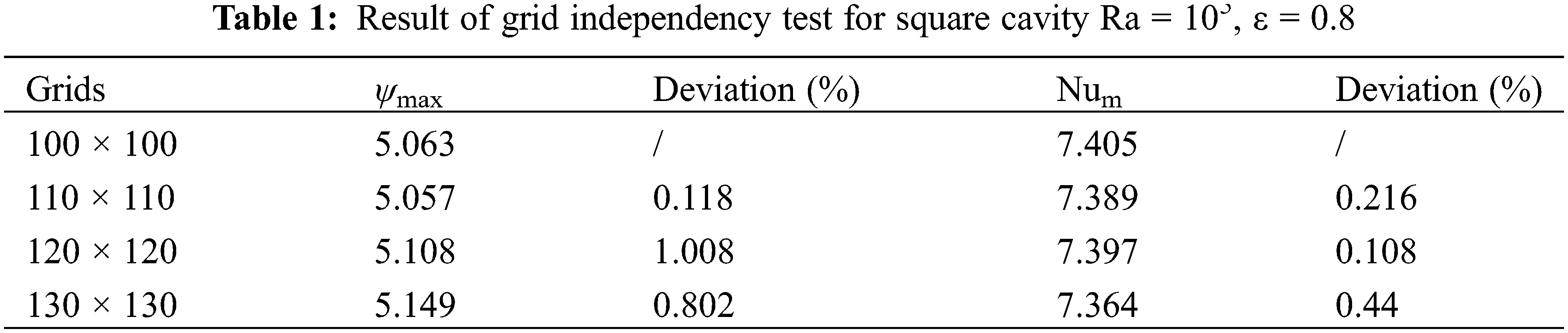
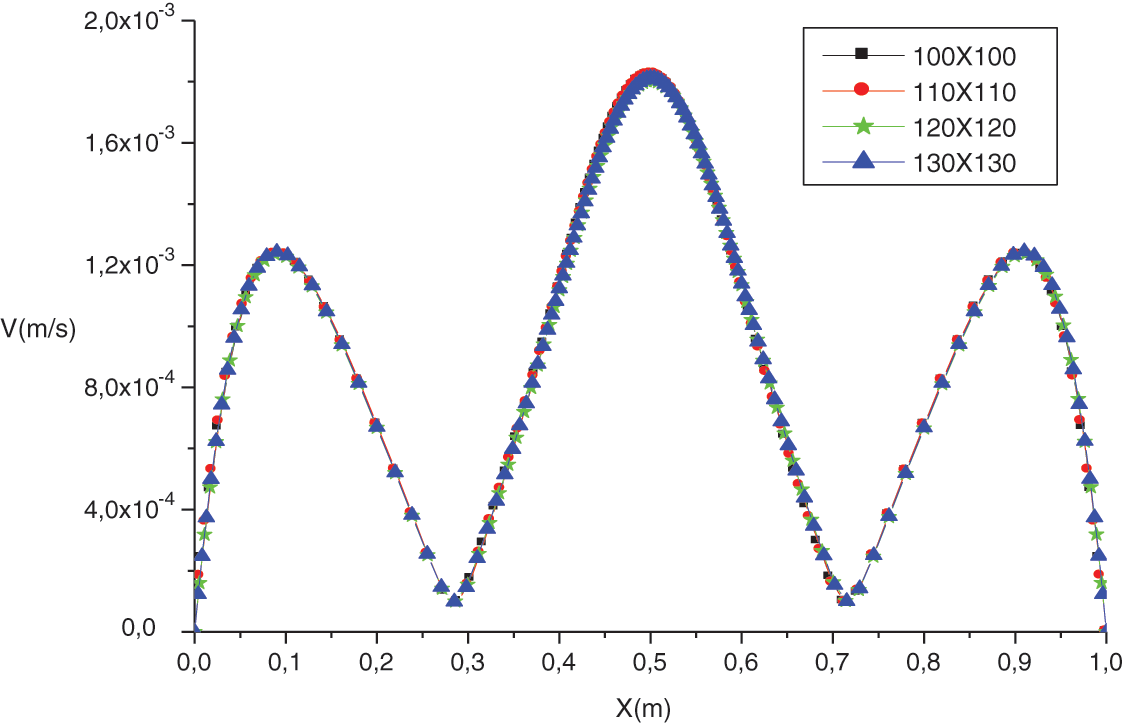
Figure 3: Velocity profile at Y = 0.5 for ε = 0.2 and Ra = 105
The independency on the grid is considered on the basis of less deviation in non-dimensional stream function and Nusselt number which calculated by relative error analysis. Table 1 explicates the less deviation at the grid 110 × 110 and 120 × 120 comparing to others. Hence, 120 × 120 grids was recommended to the present work for taking both the accuracy and convergence rate into account.
In order to verify the accuracy of the numerical results obtained in the present work, a validation of the present numerical simulation is compared with the experimental studies of Calcagni et al. [6] (Figs. 4 and 5).
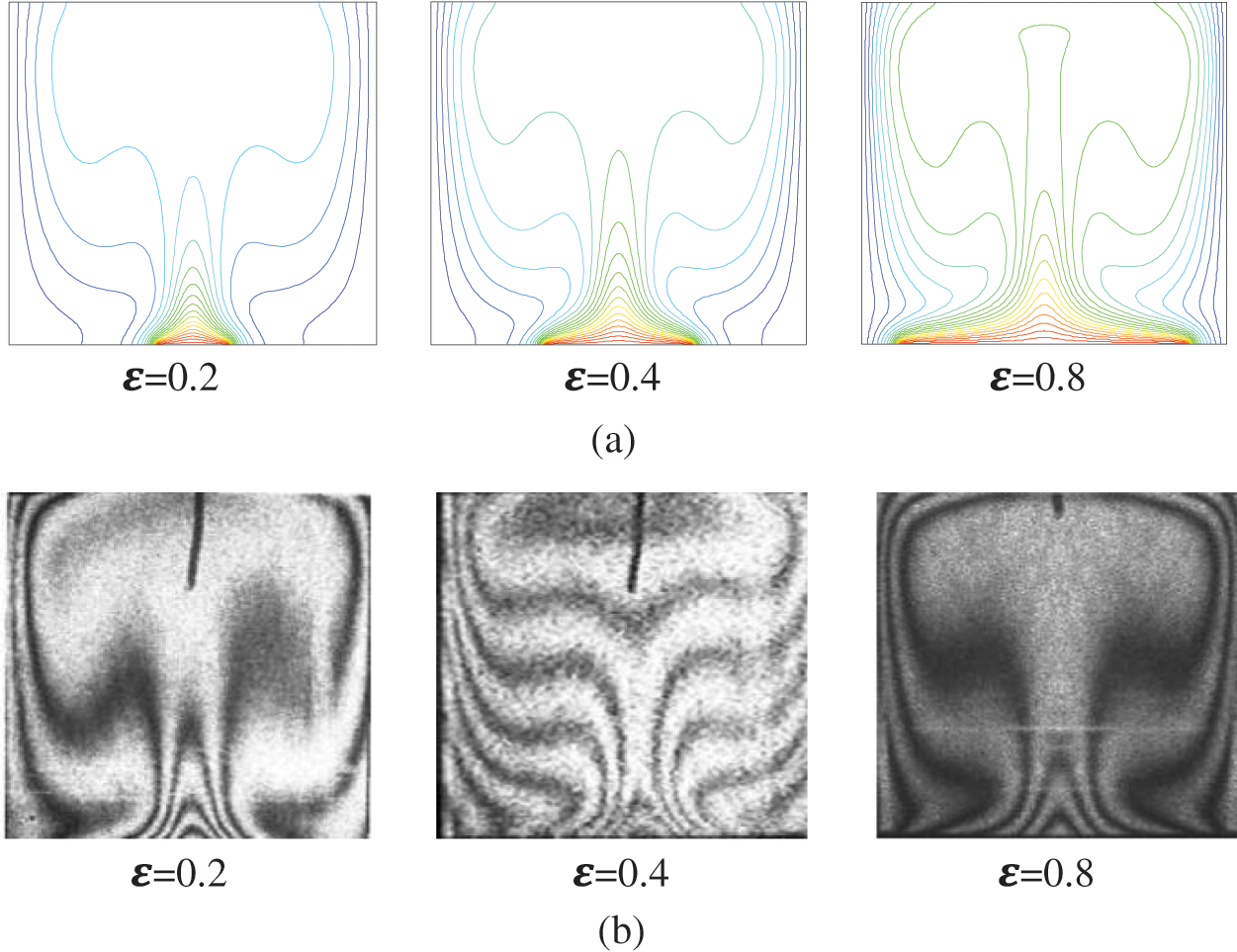
Figure 4: Comparison of isotherms, (a) Present work (b) Experimental results of Calcagni et al. [6]. Ra = 1.836 × 105
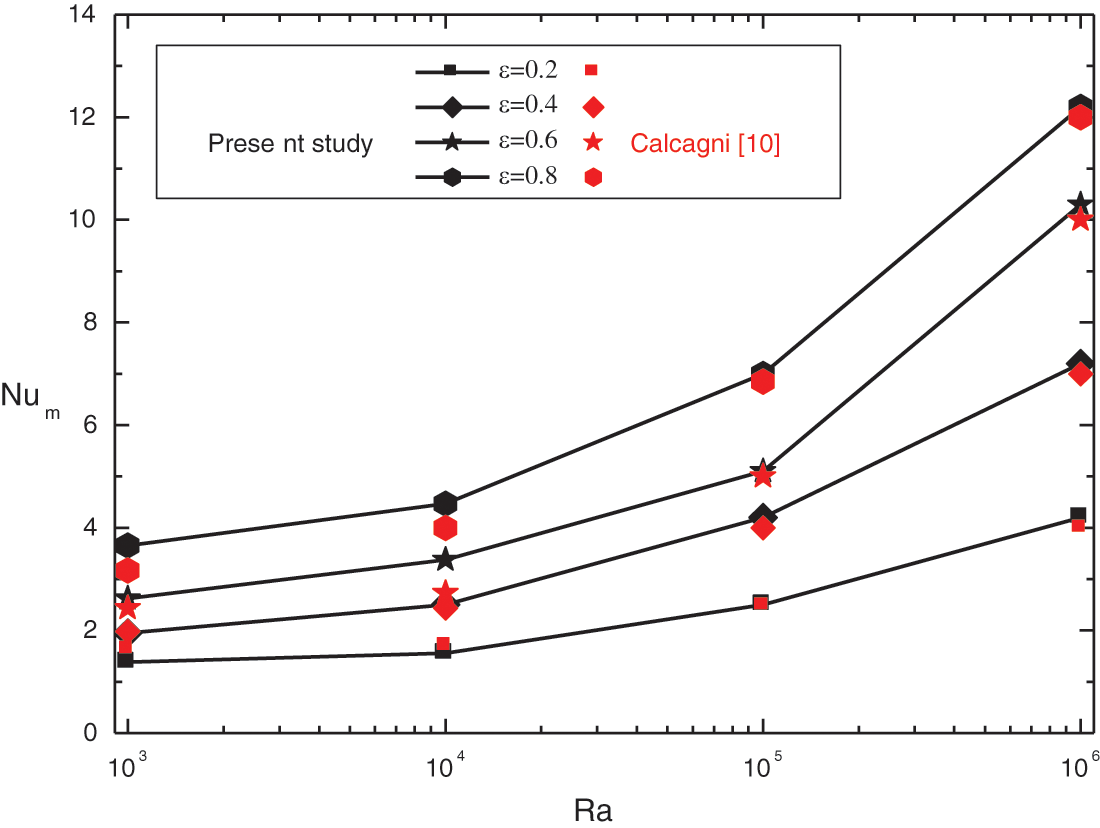
Figure 5: Evaluation of the average nusselt number of the heated wall with the published work of Calcagni et al. [6]
The comparison of isotherms (Fig. 4) with experimental results of Calcagni et al. [6], and the variation of the mean Nusselt as a function of Ra (Fig. 5) showed an excellent agreement.
The isotherms are represented in Fig. 6 for h = 0.5, and Fig. 8 for h = 0.25 with different Rayleigh numbers (103–106) and the ratio ε from 0.2 to 0.8. The streamlines are represented in Fig. 7 for h = 0.5 and Fig. 9 for h = 0.25.
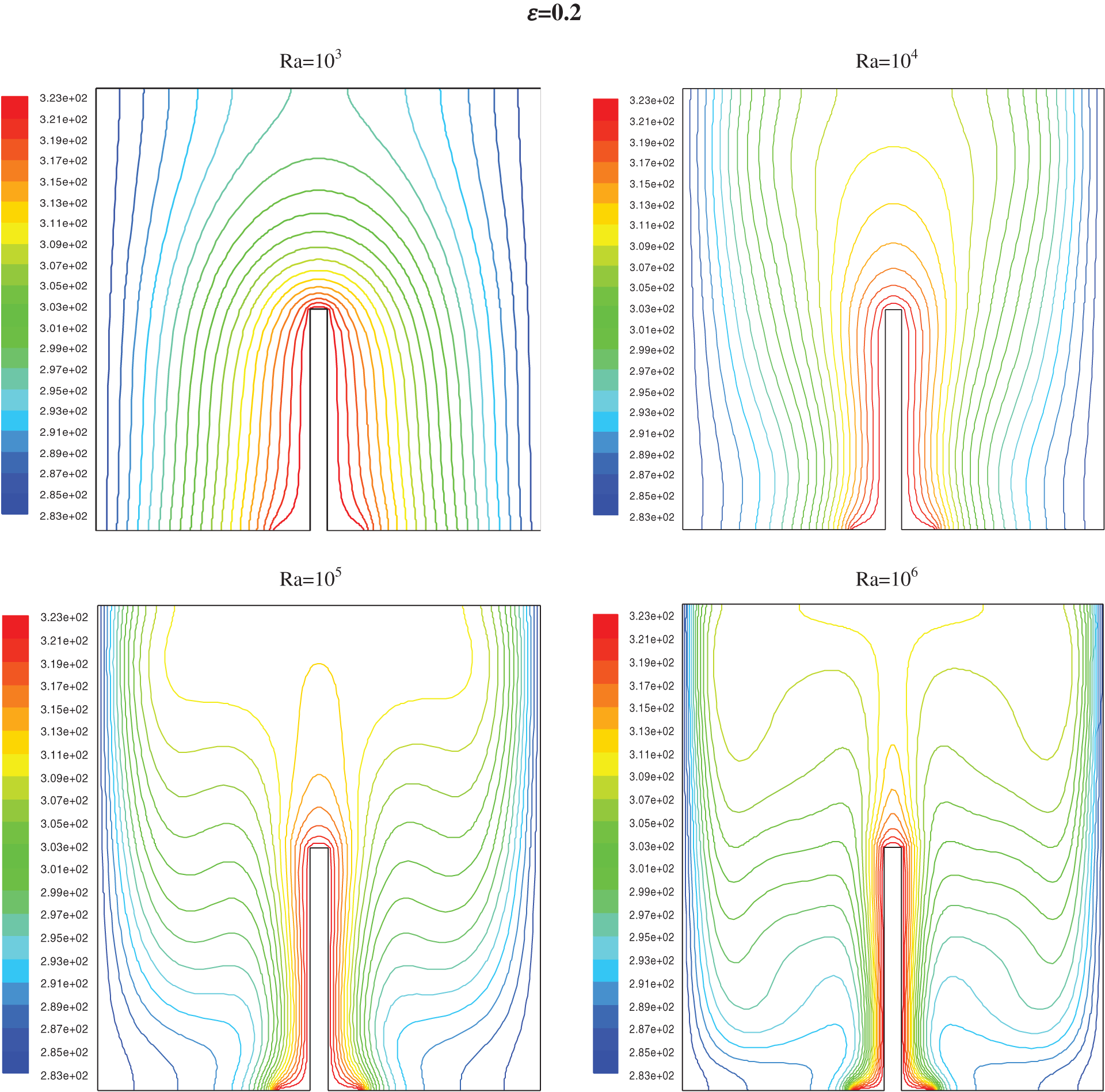

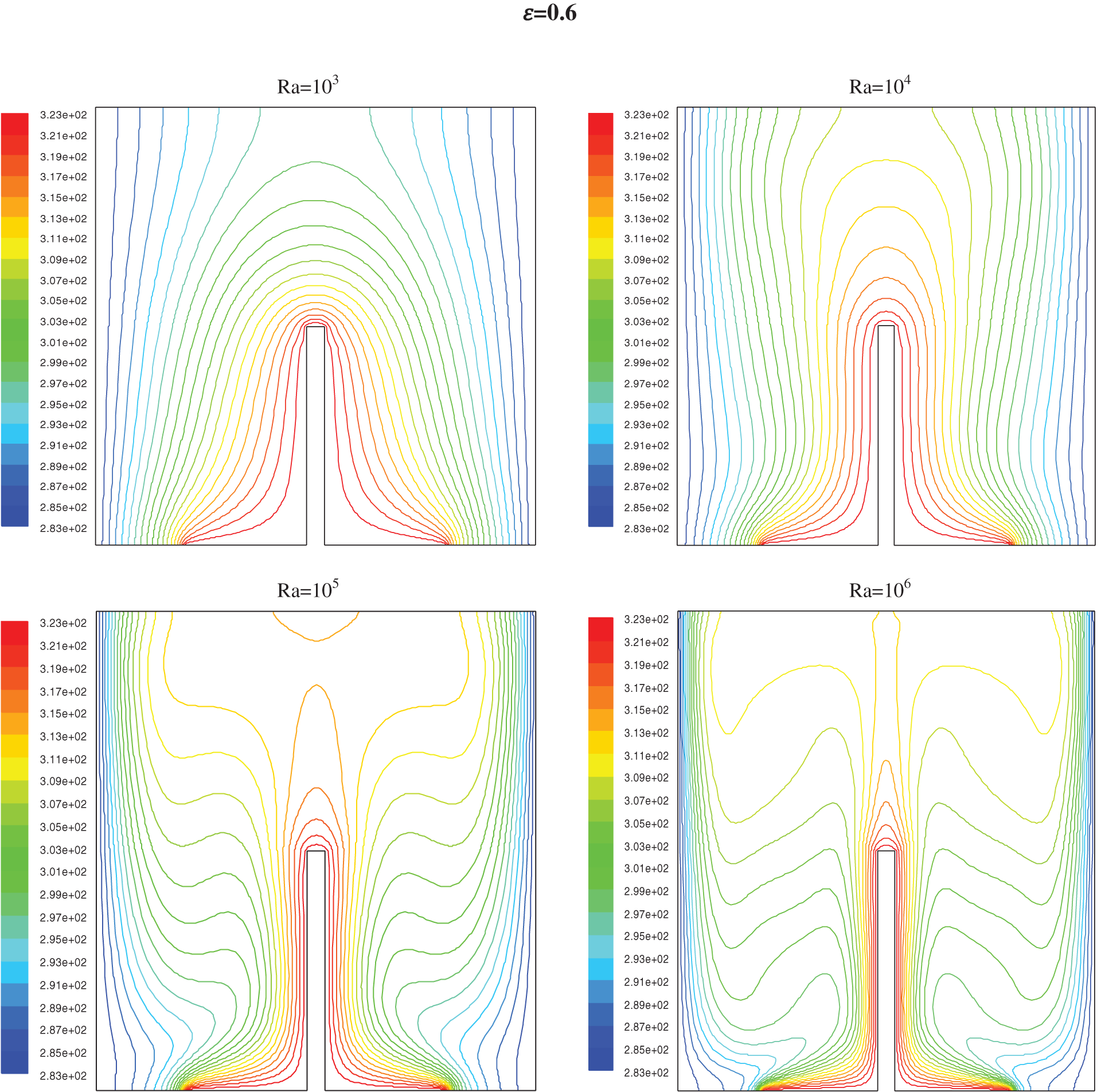
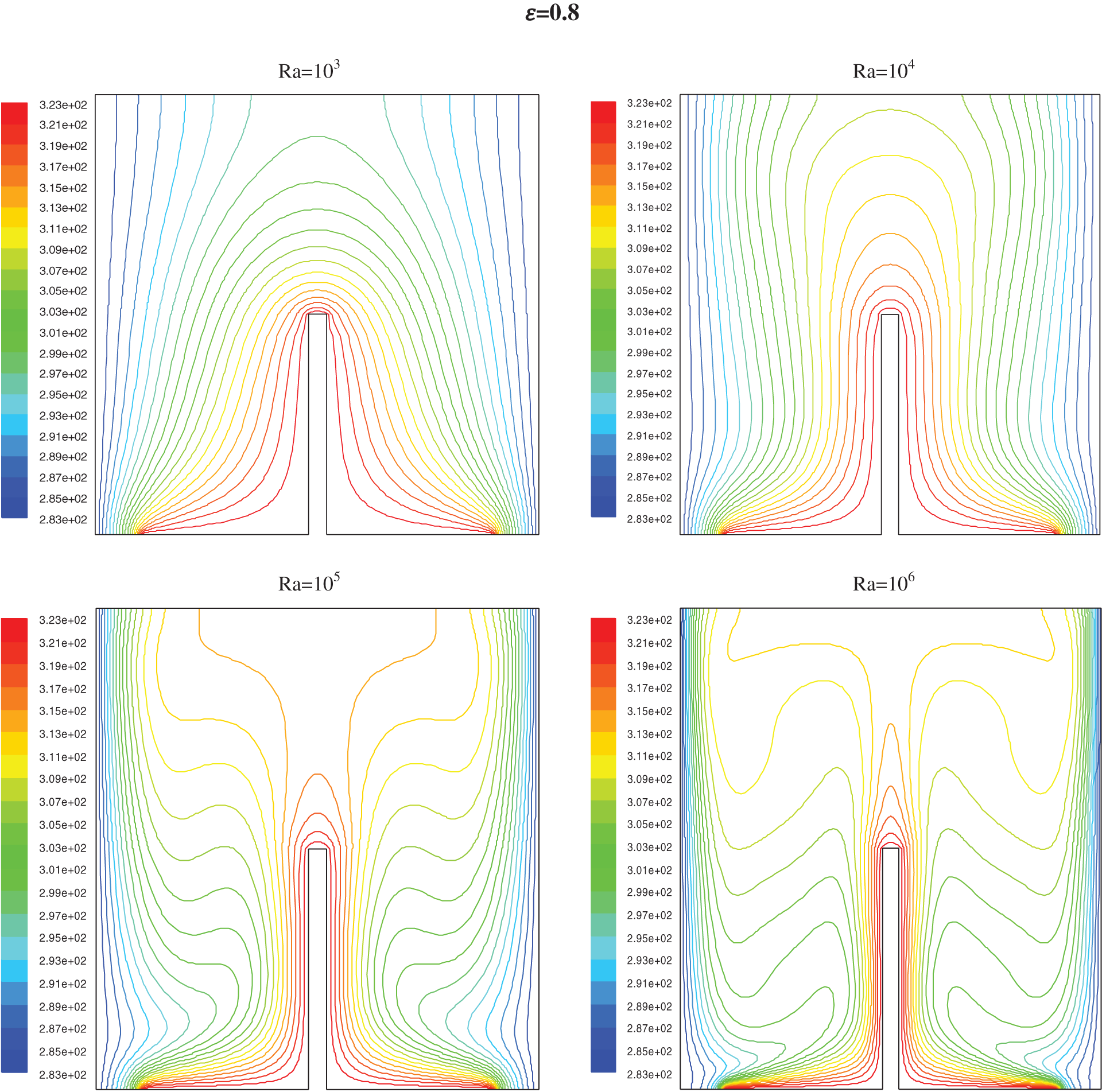
Figure 6: Isotherms for h = 0.5 for different values of ε and Ra
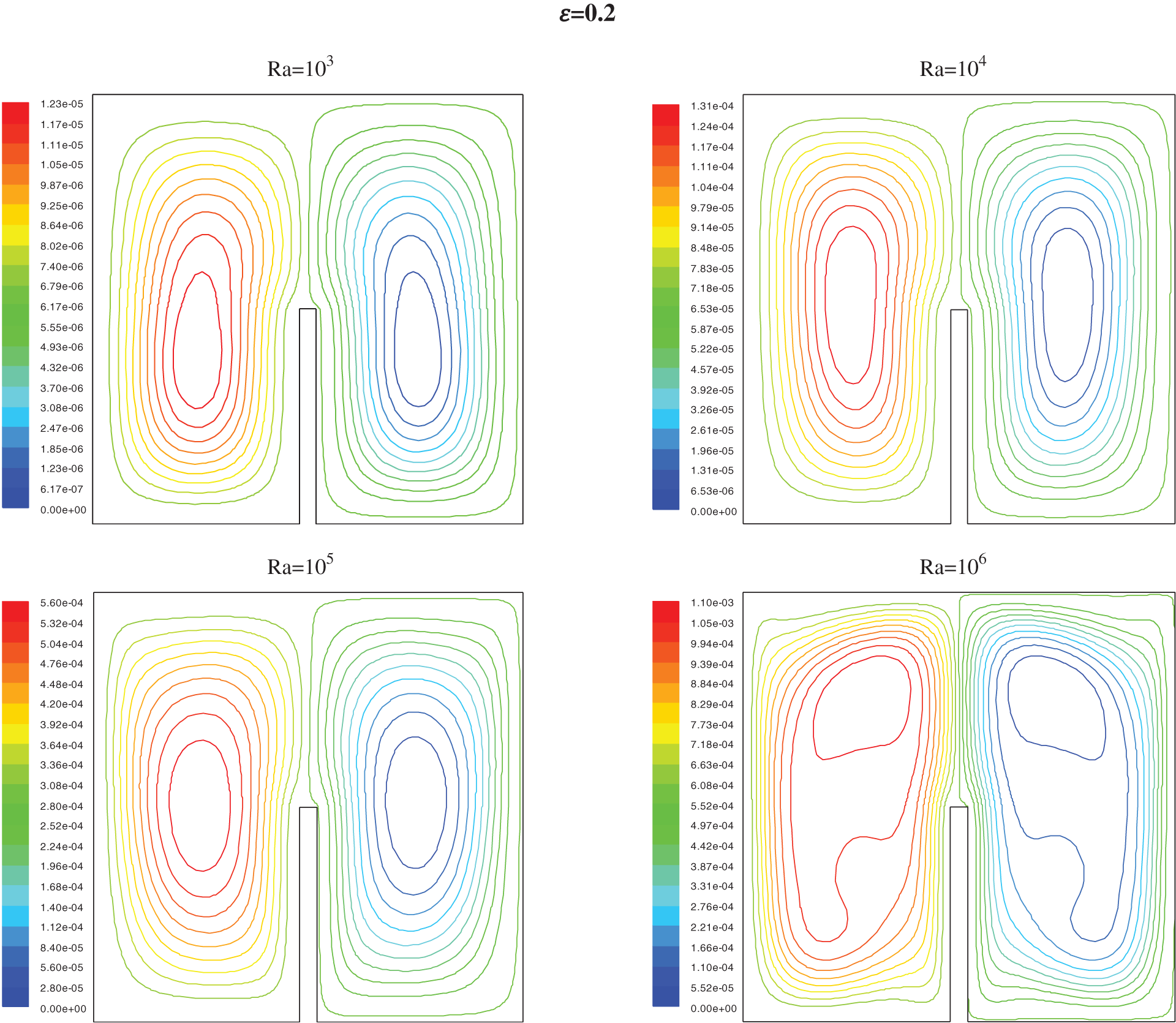
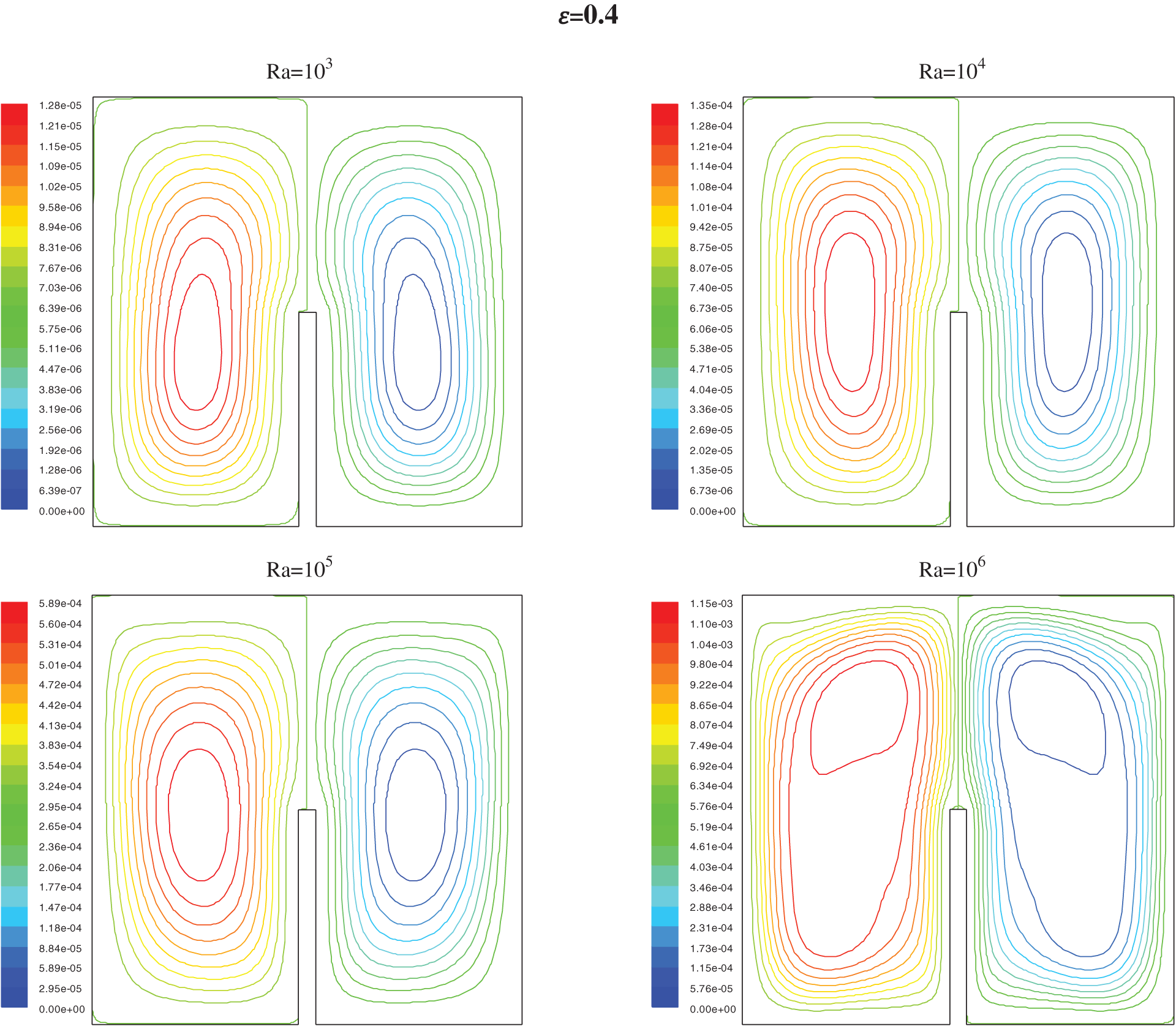
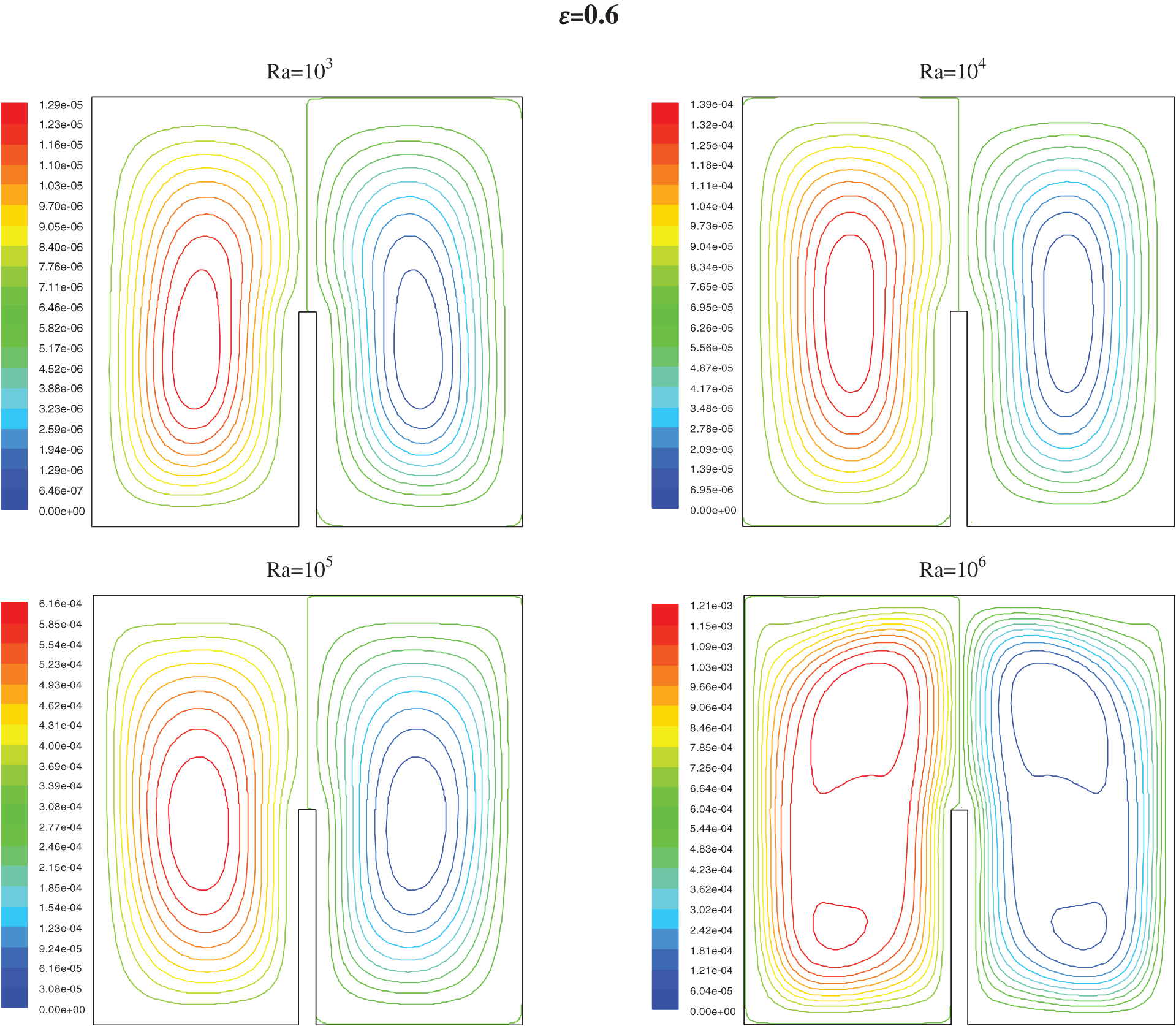
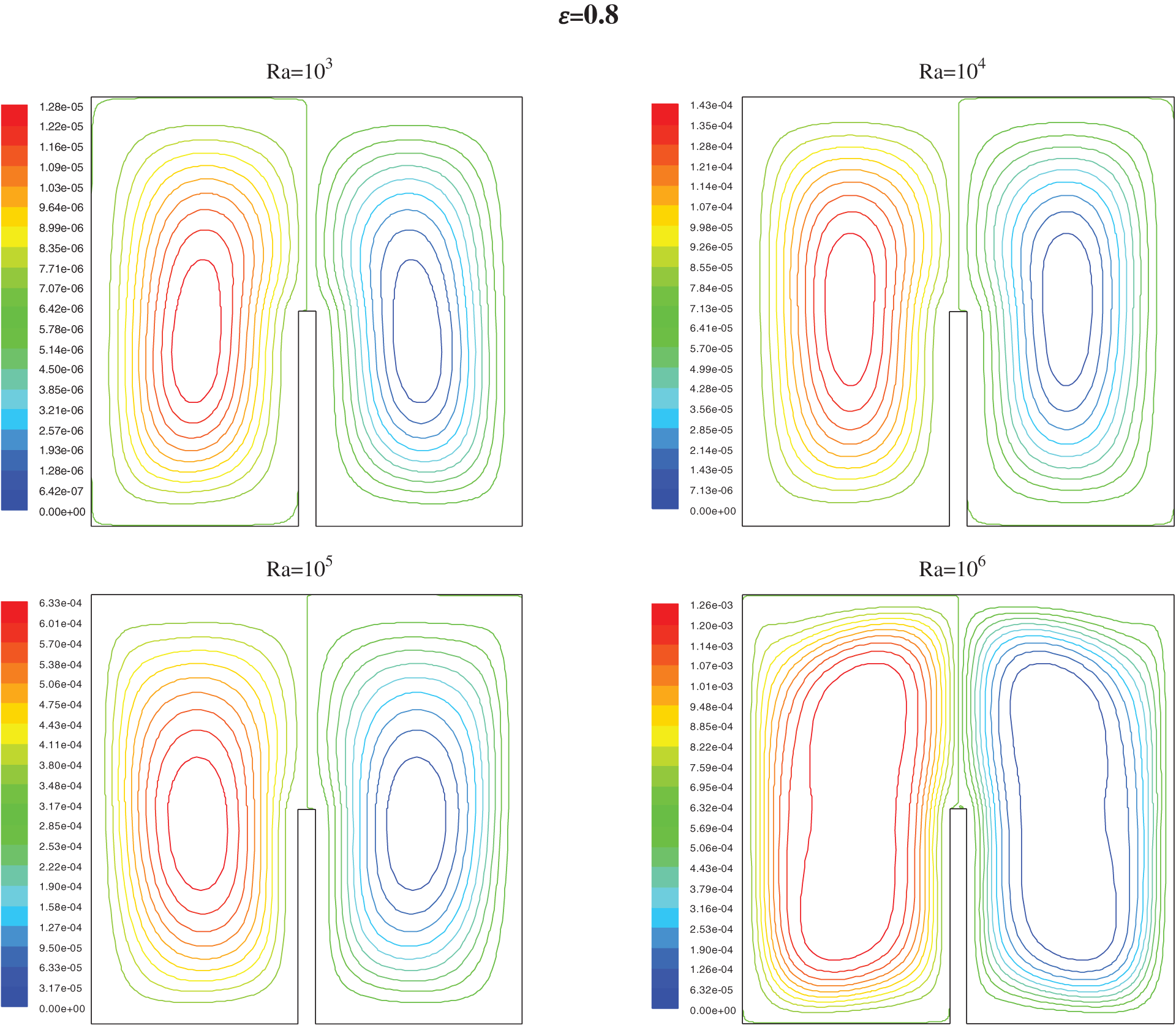
Figure 7: Streamlines for h = 0.5 for different values of ε and Ra
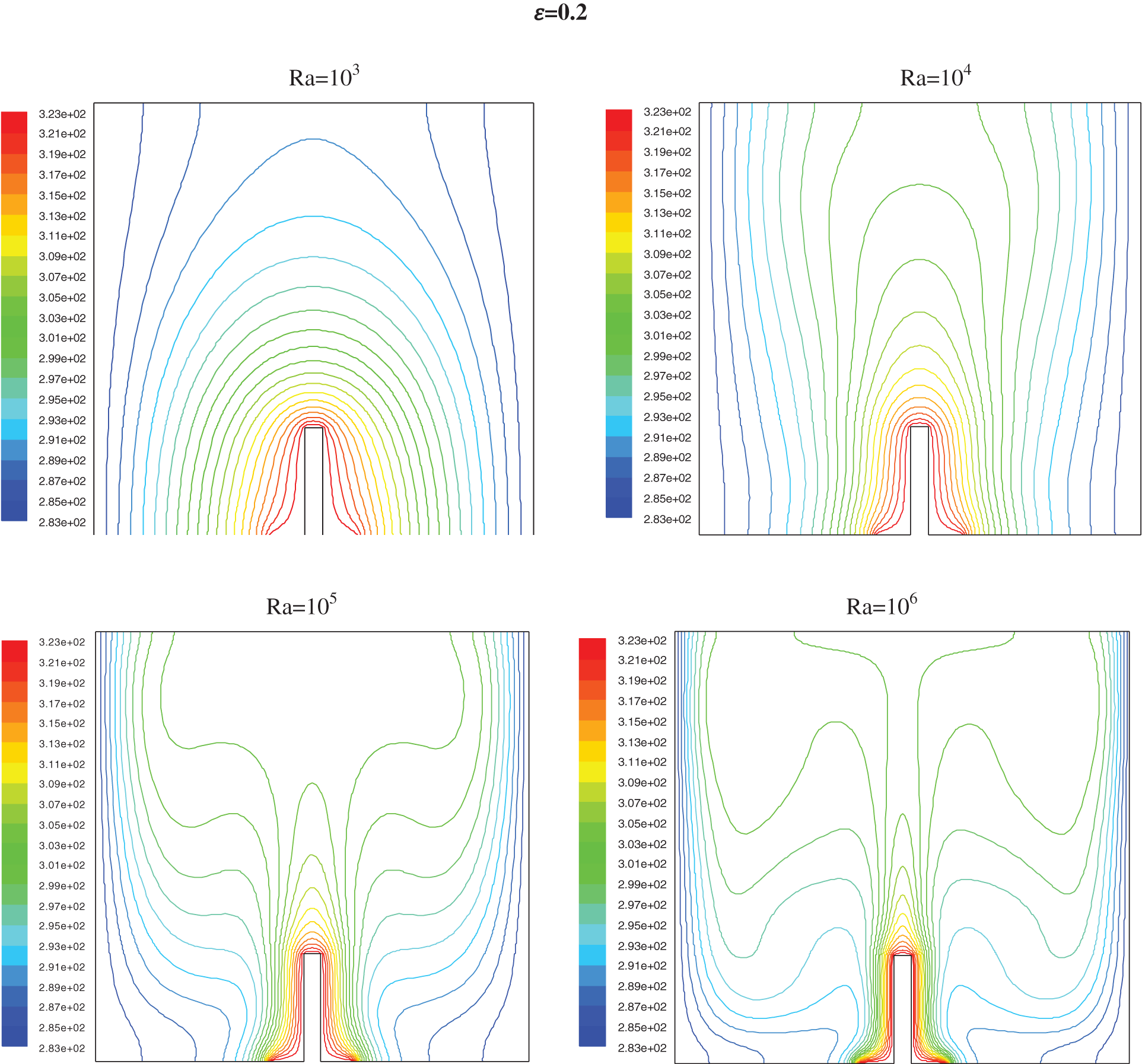

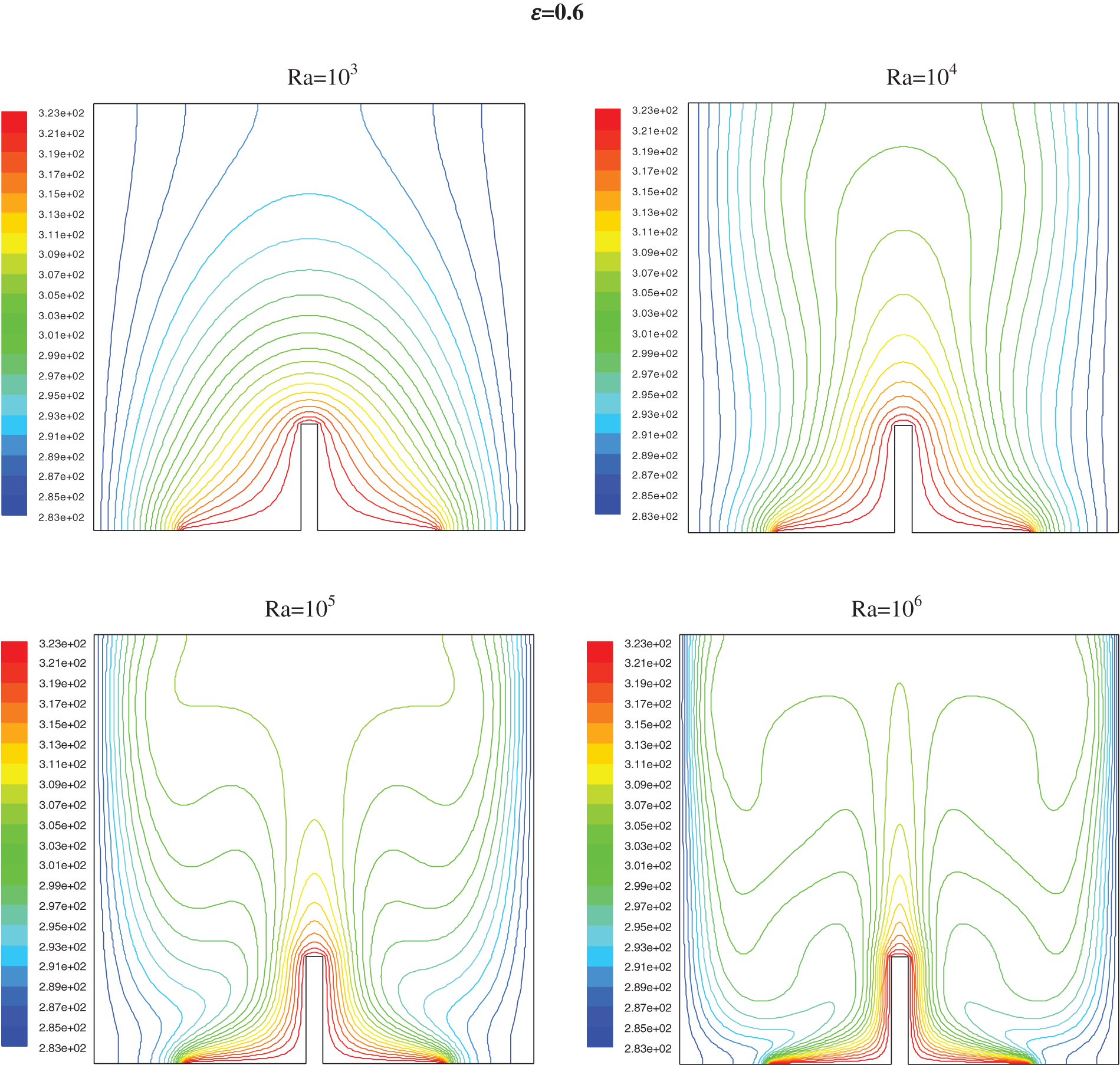
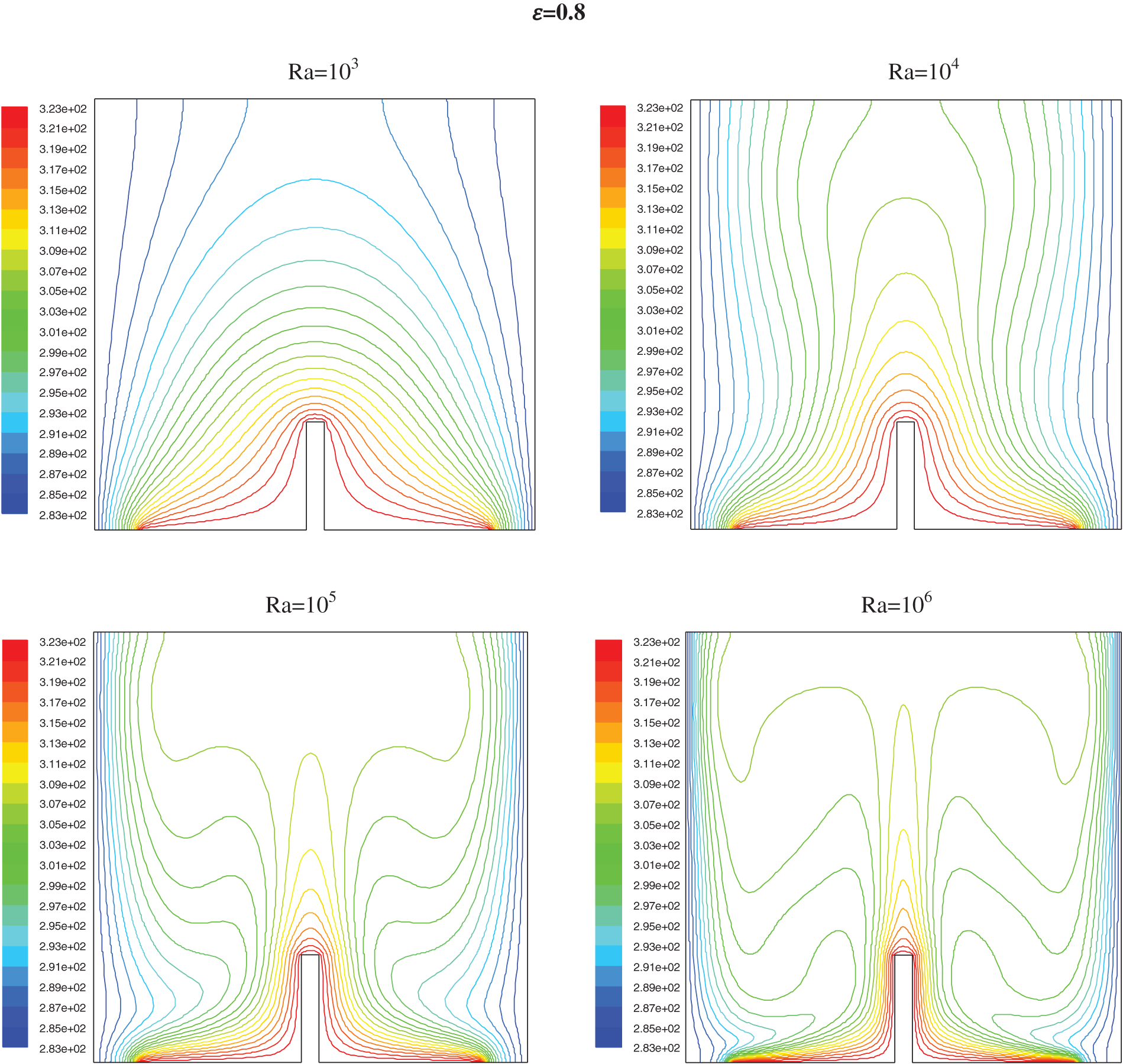
Figure 8: Isotherms for h = 0.25 and different values of ε and Ra
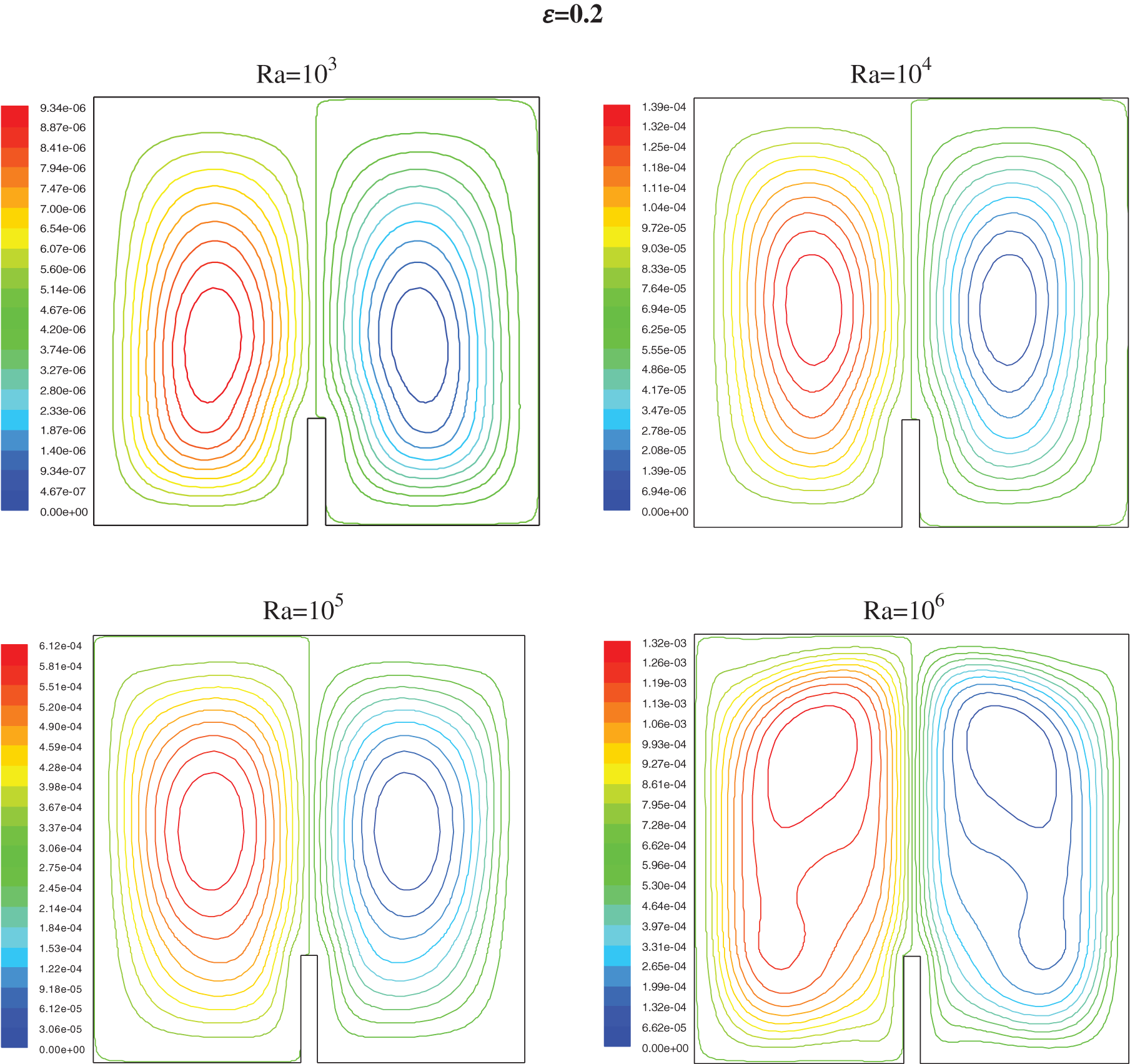

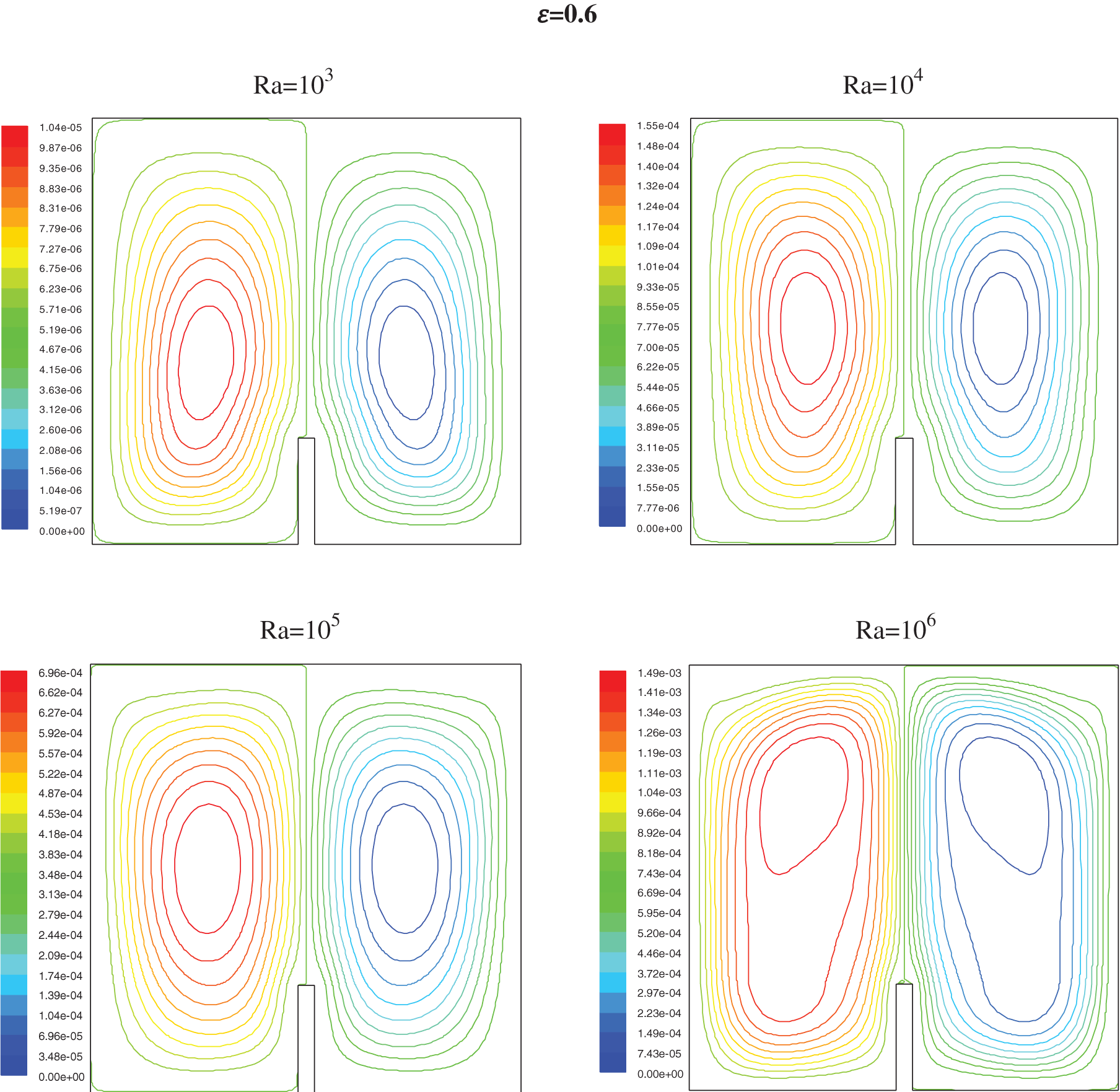
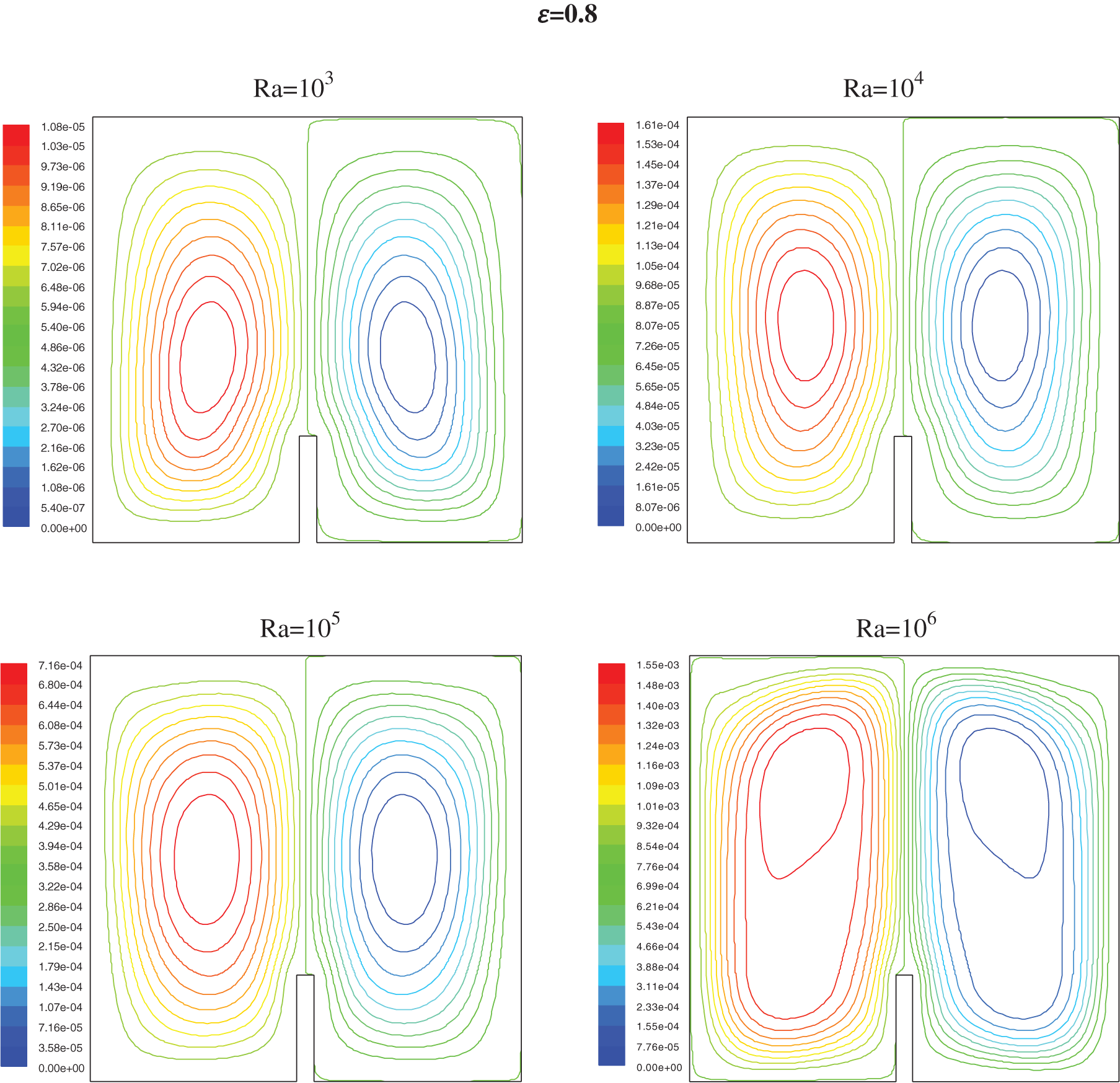
Figure 9: Streamlines for h = 0.25 for different values of ε and Ra
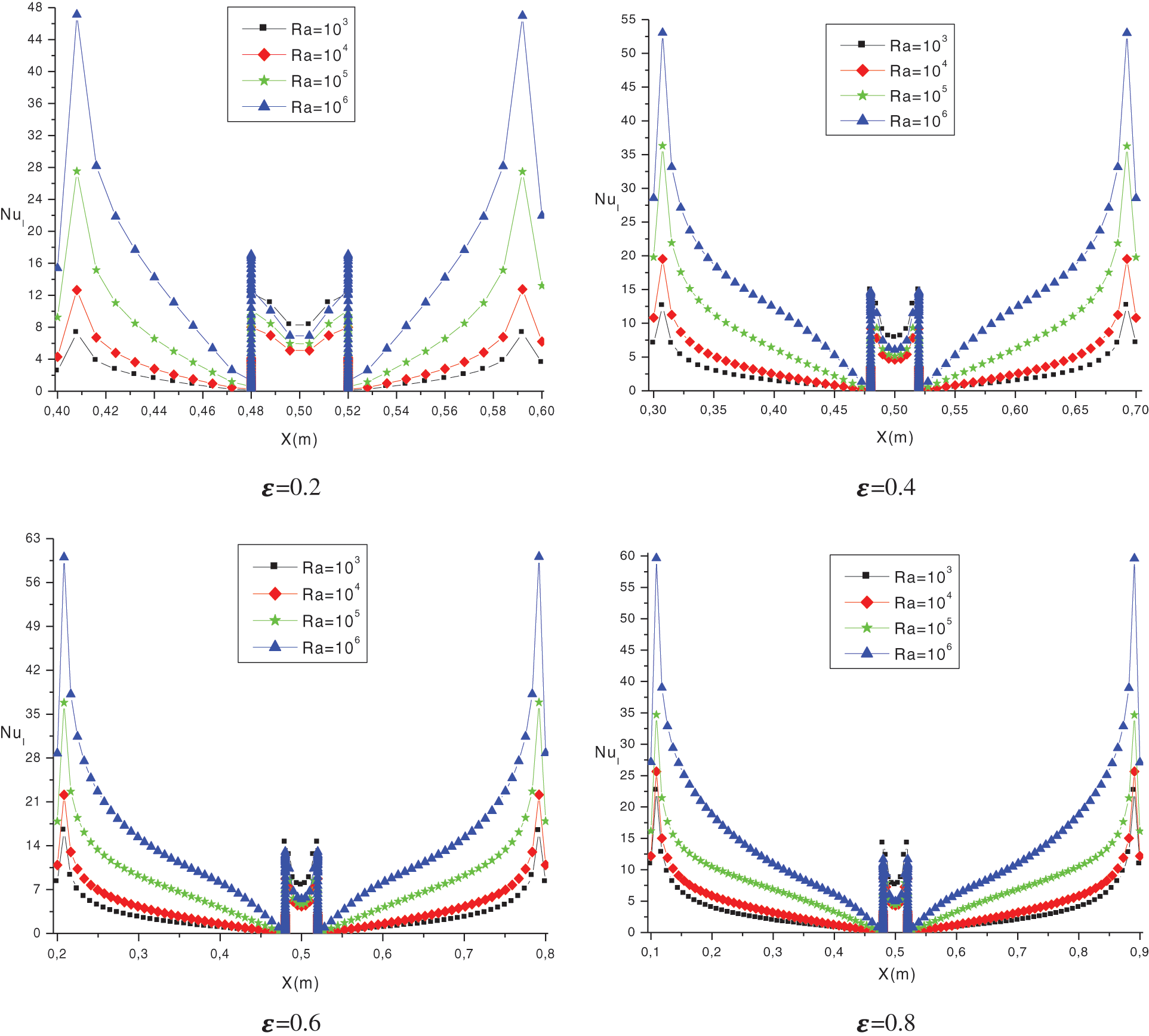
Figure 10: Variation of the local Nusselt number along the heated part for h = 0.5 and different values from ε
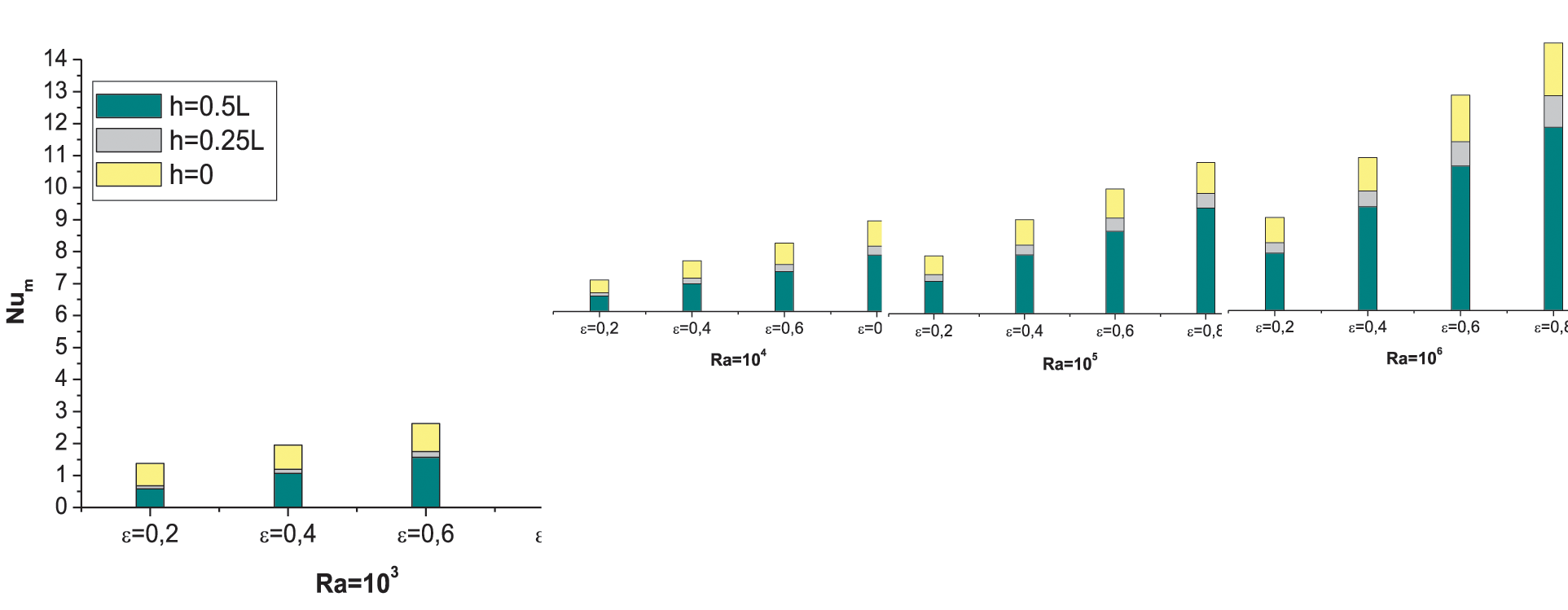
Figure 11: Effect of heat source length ε and partition length on mean Num at the hot wall for different Ra numbers
For Ra lower than 104 the conductive heat transfer dominates; it is only when the Ra tops 104 (Figs. 6 and 8) a deformation of the isotherms shows the start of a low convection. For Ra near 105, the cooled fluid has a down motion with an increase of the circular flow and convection became the prime procedure for heat transfer; this phenomena is seen by a second curvature of isotherms which handle a mushroom profile
It has been noted that near the partition, the thickness of the thermal boundary layer increases and decreases just before the partitions, this shows the induction of the partition high on the isothermal distributions. It has been clearly seen that an increase in partition height seems to increase in the thickness of the thermal boundary layer.
The streamlines (Figs. 7 and 9) show that the two vertical ellipses show the formation of a pair of counter-rotating cylinder. The fluid, heated by the localized source, raise centrally to the upper adiabatic wall through which it divides in two fluxes that move horizontally towards the cold walls; due to the impact of cooling, the fluid descends along the vertical surfaces closing the convective circle.
For further justification regarding the temperature distribution in the enclosure, Fig. 12 shows the temperature profiles along the Y = 0.5 for h = 0.25 and h = 0.5 for different Ra, and Fig. 13 shows the velocity profiles along the Y = 0.5 for h = 0.25 and h = 0.5 for different Ra.

Figure 12: Temperature profiles at Y = 0.5 for ε = 0.6 (a) h = 0.5 (b) h = 0.25

Figure 13: Velocity profiles at Y = 0.5 for different Ra and ε = 0.6 (a) h = 0.5 (b) h = 0.25
The evolution of the average Nusselt number as a function of the Rayleigh number for h = 0, 0.25 and h = 0.5, for different values of ε is shown in Fig. 11. It is observed that the Nusselt number increases when ε increases and h decreases. For a given value of ε and h, the average Nusselt number increases when Ra increases and, a larger heat source increases the heating effect and the enhancement of the heat transfer is greater at high Ra. It has been clearly seen that there is an influence of the partition length on the average Nusselt number; the tendency of the curve decreases clearly with increasing partition length. The temperature gradient improves the heat transfer.
Although, comparing the average Nusselt number for ε = 0.8, the average Nusselt number of h = 0.5, is 14.68% lower than h = 0.25 and is 31.51% lower than cavity without partition at Ra = 106. However, for ε = 0.2 and Ra = 104, the average Nusselt number of h = 0.5, is 17.39% lower than h = 0.25 and is 51.28% lower than cavity without partition.
The variation of the local Nusselt number along the heated part is represented in the Fig. 10 for h = 0.5, and different values from ε. It has been observed that, in the cavity with partition, the heat transfer decreases compared to the cavity without partition. As a result, it can be stated that the augmentation in Ra, along bottom wall, is more effective to augment heat transfer for most of the cases. The local Nu numbers around the partition, furthermore, are very low due to insufficient flow actions at these points which consequently reduce the rate of heat transfer.
A numerical study of laminar natural convection in a square enclosure filled with air with a partially heated bottom wall was carried out. The hot source is considered to be located at the lower wall with different heated widths varied from 20% to 80% (ε = 0.2−0.8) of the total width of the lower wall with different height of the partition (h = H/4 and H/2). This numerical work is investigated to define the effect of partition height. The influence of the Rayleigh number (Ra = 103 to 106), the hot wall length on the isotherms and streamlines and on the heat transfer has been established. It was observed that the average Nusselt number increases when ε increases and when h decreases. For a given value of ε and h, the average Nusselt number increases as Ra increases. It is concluded that the partition height decreases the average Nusselt number.
It is shown that the average Nusselt number of h = 0.5, is 14.68% lower than h = 0.25 and, it is 31.51% lower than cavity without partition at Ra = 106. However, for ε = 0.2 and Ra = 104, the average Nusselt number of h = 0.5, is 17.39% lower than h = 0.25 and is 51.28% lower than cavity without partition.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Ostrach, S. (1972). Natural convection in enclosures. Advances in Heat Transfer, 8, 161–227. DOI 10.1016/S0065-2717(08)70039-X. [Google Scholar] [CrossRef]
2. Anderson, R., Lauriat, G. (1986). The horizontal natural convection boundary layer regime in a closed cavity. International Heat Transfer Conference, vol. 4, pp. 1453–1458. San Francisco, CA. [Google Scholar]
3. Yao, L. S. (1983). Natural convection along a vertical wavy surface. Journal of Heat Transfer, 105, 465–468. DOI 10.1115/1.3245608. [Google Scholar] [CrossRef]
4. Chu, T. Y., Hichox, C. E.(1990). Thermal convection with large viscosity variation in an enclosure with localized heating. Journal of Heat Transfer, 112, 388–395. DOI 10.1115/1.2910389. [Google Scholar] [CrossRef]
5. Sharif, M. A. R., Mohammad, T. R. (2005). Natural convection in cavities with constant flux heating at the bottom wall and isothermal cooling from the sidewalls. International Journal of Thermal Sciences, 44(9), 865–878. DOI 10.1016/j.ijthermalsci.2005.02.006. [Google Scholar] [CrossRef]
6. Calcagni, B., Marsili, F., Paroncini, M.( (2005). Natural convective heat transfer in square enclosures heated from below. Applied Thermal Engineering, 25(16), 2522–2531. DOI 10.1016/j.applthermaleng.2004.11.032. [Google Scholar] [CrossRef]
7. Caronna, G., Corcione, M., Habib, E., (2009). Natural convection heat and momentum transfer in rectangular enclosures heated at the lower portion of the sidewalls and the bottom wall and cooled at the remaining upper portion of the sidewalls and the top wall. Heat Transfer Engineering, 30(14), 1166–1176. DOI 10.1080/01457630902972777. [Google Scholar] [CrossRef]
8. Zemani, F., Sabeur-Bendehina, A., Boussoufi, M. (2014). Numerical investigation of natural convection in air filled cubical enclosure with Hot wavy surface and partial partitions. Procedia Computer Science, 32, 622–630. DOI 10.1016/j.procs.2014.05.469. [Google Scholar] [CrossRef]
9. Belkadi, M., Aounallah,M., Imine, O., Adjlout, L. (2006). Free convection in an inclined square cavity with partial partitions on a wavy hot wall. Progress in Computational Fluid Dynamics, an International Journal, 6(7), 428–434. DOI 10.1504/PCFD.2006.010968. [Google Scholar] [CrossRef]
10. Yigit, S., Battu, M., Turan, O., Chakraborty, N. (2019). Free convection of power-law fluids in enclosures with partially heating from bottom and symmetrical cooling from sides. International Journal of Heat and Mass Transfer, 145, 118782. DOI 10.1016/j.ijheatmasstransfer.2019.118782. [Google Scholar] [CrossRef]
11. Torabi, M., Keyhani, A., Peterson, G. P. (2017). A comprehensive investigation of natural convection inside a partially differentially heated cavity with a thin fin using two-set lattice boltzmann distribution functions. International Journal of Heat and Mass Transfer, 115, 264–277. DOI 10.1016/j.ijheatmasstransfer.2017.07.042. [Google Scholar] [CrossRef]
12. Mebarek-Oudina, F. (2017). Numerical modeling of the hydrodynamic stability in vertical annulus with heat source of different lengths. Engineering Science and Technology, an International Journal, 20(4), 1324–1333. DOI 10.1016/j.jestch.2017.08.003. [Google Scholar] [CrossRef]
13. Zaim, A., Aissa, A., Mebarek-Oudina, F., Mahanthesh, B., Lorenzini, G. et al. (2020). Galerkin finite element analysis of magnetohydrodynamic natural convection of Cu-water nanoliquid in a baffled U-shaped enclosure. Propulsion and Power Research, 9(4), 383–393. DOI 10.1016/j.jppr.2020.10.002. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools