 Open Access
Open Access
ARTICLE
Numerical Investigation of the Temperature and Flow Fields in a Solar Chimney Power Plant
1 Laboratory of Environment, Larbi Tebessi University, Tebessa, Algeria
2 Department of Fluid Dynamics, University of Kassel, Kassel, Germany
* Corresponding Author: Roudouane Laouar. Email:
(This article belongs to the Special Issue: Materials and Energy an Updated Image for 2021)
Fluid Dynamics & Materials Processing 2023, 19(4), 1055-1066. https://doi.org/10.32604/fdmp.2022.022677
Received 20 March 2022; Accepted 26 May 2022; Issue published 02 November 2022
Abstract
In this work, a parametric two-dimensional computational fluid dynamics (CFD) analysis of a solar chimney power plant (a prototype located in Manzanares, Spain) is presented to illustrate the effects of the solar radiation mode in the collector on the plant performances. The simulations rely on a mathematical model that includes solar radiation within the collector; energy storage; air flow and heat transfer, and a turbine. It is based on the Navier-Stokes equation for turbulent flow formulated according to the standard k-ε model. Moreover, the Boussinesq approach is used to account for the fluid density variations. Different solar radiation modes in the collector are compared and discussed. The obtained results are also compared with available experimental results. It is shown that the radiation model is essential to avoid overestimation of the energy absorbed by the plant and that results based on a two-dimensional model can resemble closely those produced by three-dimensional models.Keywords
Nomenclature
| | specific heat capacity ( |
| E | energy ( |
| h | convective heat transfer coefficient ( |
| I | solar radiation ( |
| P | power ( |
| Pgage | gage pressure (Pa) |
| Q | volumetric heat source ( |
| Qv | volume flow rate ( |
| q | heat flux ( |
| Ra | Rayleigh number (−) |
| SCPP | solar chimney power plant |
| | absorptivity (−) |
| | emissivity |
| | transmittance (−) |
| | reflectivity (−) |
| | dynamic fluid viscosity (N s m−2) |
Environmental pollution and declining oil reserves make renewable energies a viable option to provide clean and cost-competitive energy in the future. In fact, solar power plants have become one of the most promising candidates for supplying most of the world’s clean energy needs [1].
The solar chimney power plant (SCPP) is one of the world’s most ambitious projects meant to produce alternative energy. It is a clean and safe renewable energy plant that could provide significant electrical power. It is capable of operating continuously through the use of the sun during the day and of stored thermal energy in the storage layer at night. The solar chimney power plant combines three well-known principles: the greenhouse effect, the chimney, and wind turbines in an innovative way to convert solar radiation (direct and diffuse) into electricity. The sun generates hot air in the collector. This is drawn upwards by a chimney in the middle of the collector. The air flow drives a turbine installed at the chimney’s base that generates electricity. A schematic of the SCPP is illustrated in Fig. 1.

Figure 1: Geometry and dimensions of the SCPP [25]
The solar chimney concept was originally proposed by Professor Schlaich of Stuttgart in the late of 1970s [2]. Fundamental investigations for the Spanish system were reported by Haaf et al. [3] including a brief discussion of the energy balance, design criteria, and cost analysis [3]. The initial experimental results of the Spanish prototype were published by Haaf in another study [4]. Since then, several research namely experimental, theoretical, and computational have been published. Some experimental prototypes have been reported in [5–10]. The typical analytical approach is based mostly on a one-dimensional thermal equilibrium study within the collector. Pasumarthi et al. [7,11], for example, proposed an approximation model to study the influence of different factors on air temperature and velocity distribution. Many studies have focused on various models of theoretical and mathematical investigation to estimate the SCPP’s effectiveness, output air speed, and energy production [12–16]. Analytical methods are simple and deliver a rapid result, but often include assumptions that limit their ability to offer descriptions of physical processes across the whole plant. Furthermore, last few years have seen a significant increase in the use of commercial CFD packages to study fluid flow and heat transfer in SCPP systems. As an example, Pastohr et al. [17] used the commercial software Fluent to perform a two-dimensional steady numerical investigation of the SCPP in Manzanares. Xu et al. [18] employed a similar numerical technique, with the only difference being the configurations for the energy storage layer and turbine model. After then, many researchers have conducted several numerical studies of the SCPP using the software Fluent.
The complete simulation of the solar chimney power plant consists of 4 sub-models: the solar radiation, the energy storage, the air flow and heat transfer, and the turbine models [19]. The flow and heat exchange in the SCPP can be considered as incompressible convective heat transfer induced by buoyancy force. The energy storage was in previous studies, modeled as solid, porous and phase changed medium. Due to the small temperature difference in the SCPP, the Boussinesq approximation is generally adopted to take in account the temperature dependency of the air density [19–22]. To simulate the turbine, most papers currently use a fan model in Fluent. When compared to the analytical technique, numerical simulations require fewer assumptions, but more detailed interpretations of the temperature and flow field may be performed. Many numerical studies using Fluent have been published. The main difference between them lies in the radiation model.
In the literature, various approaches that account for solar radiation were used. For example, Guo et al. [22] and Gholamlizadeh et al. [23] proposed a three-dimensional numerical approach incorporating the radiation, solar load, and turbine models to investigate the effects of solar radiation, turbine pressure drop, and ambient temperature on system performance. For that, the discrete ordinate (DO) radiation model was adopted to solve the radiative transfer equation. As solar ray-tracing model provided by FLUENT was used to calculate the radiation effects of the sun’s rays entering the computational domain. However, solar load radiation is available for 3-D simulation only. Huang et al. [19] proposed an enhanced two-dimensional radiation method for the SCPP simulation that considers the spectral property of the collector. This approach was adopted to model the Manzanares plant, and excellent convergence between the experimental and expected results was observed. The two-dimensional model has an accuracy comparable to the three-dimensional method with the solar ray tracing model and the discrete ordinate radiation model, but with significantly lower computational power.
Algeria is a key player in global energy markets as the largest producer and exporter of natural gas and liquefied natural gas. Algeria’s energy mix depends almost exclusively on fossil fuels, especially natural gas and oil. However, the country has immense potential for renewable energy, especially solar power. Recently, the government has tried to harness this by creating an ambitious renewable energy and energy efficiency program [24].
This program aims to produce 22,000 MW of power from renewable sources from 2011 to 2030. Of the 22,000 MW, 12,000 MW will be destined for domestic consumption and the remainder for export [24]. It aims to develop and expand the use of renewable resources, including solar, wind, biomass, geothermal, and hydropower, in order to promote the sustainable development of the country.
To predict the mode of action of SCPP at sites in Algeria, numerical simulations of the plant heat transfer process are helpful. On the one hand, the prevailing thermal boundary conditions have to be taken into account, but also the reflection properties leading to a reduction of the efficiency. In this numerical case study, different model assumptions are discussed in order to establish realistic predictions for the operation of such plants.
The Spanish SCPP of Manzanares was selected as the physical model for the CFD calculation. Fig. 1 illustrates the geometry and dimensions of the SCPP.
Because the geometry has rotational symmetry, it is sufficient to consider the process in only one intersection. The computational finite volume grids used in this study with and without a heat storage layer are shown in Fig. 2. Preliminary investigations have confirmed that the resolution shown with 50.000 finite volumes represents sufficient accuracy with moderate computation times.

Figure 2: Computational grid for Mode 1 (right) and Modes 2 and 3 (left)
To simulate the fluid flow and heat transfer through the system, the steady-state conservation equations of mass, momentum, and energy were solved using the commercial CFD package ANSYS Fluent 19.2.
In an SCPP, the Rayleigh number is used to determine the strength of the buoyancy-induced flow. The Rayleigh number in a SCPP as the Spanish prototype is higher than 1010. Thus, convective heat transport clearly predominates. Due to the low viscosity of the air, the Reynolds number is also high, so that the flow inside the system is turbulent. We use the standard k-ε model in the numerical simulation.
To account for the temperature dependence of air density, the Boussinesq approach is used. This model treats density as a constant value in all solved equations, except for the buoyancy term in the momentum equation. In our model, the reverse fan interior boundary condition was given to account for the pressure drop across the turbine at the chimney base. The thickness of the ground in the computational domain was set to 5 m, and the bottom temperature was set as the ambient temperature. Table 1 displays the boundary condition settings.
To take into account solar radiation in the simulation, three distinct modes are studied:
The first mode based on the classical models, does not consider the canopy absorption and transmission of solar radiation. It consists of two methods: the first one sets a heat flux as the boundary conditions for the surface of the ground. It does not include an energy storage model. The second method includes an energy storage model. By this mode, the total solar radiation is absorbed from the ground surface and participates in the heating of the airflow.
The second mode takes into consideration the collector cover absorption and transmission of solar short-wave radiation (known as τ-α model, Fig. 2b). It uses solar radiation as the boundary condition, for example, a heat source embedded in a thin ground layer, a specified wall temperature, or heat flux on the soil surface. This mode includes an energy storage model [19].
The first and second modes do not take into account the greenhouse effect of the collector.
The third mode is based on the idea of Huang et al. [19]. It includes the solar short-wave radiation (considered as radiation with wave length equal to and <2.5 μm) and the soil surface long-wave radiation (considered as radiation with wave length within 3–120 μm).
As shown in Fig. 3c, it is possible to describe the net solar heat flux received by the collector as an infinite geometric series, which yields to [26,27]:

Figure 3: (a) Mode 1; (b) Mode 2 and (c) Mode 3 of solar irradiation in the collector
where t and b denote the top and the bottom walls inside the cover, consecutively. The notation s indicates the solar radiation. Table 2 shows the results for

To verify the CFD model, the fluid temperature increase through the collector and the upward flow velocity in the case of an unloaded turbine are first compared with experimental results of the prototype in Manzanares, Spain, and with numerical results of Rabehi et al. [25] using Mode 1. The experimental results showed that for solar insolation of 1000 W/m2, the air velocity at the chimney inlet is 15 m/s, and the temperature difference in the collector with unloaded turbine attains 20°C as illustrated in Table 3.

In comparison, the CFD results show an average air velocity of 16 m/s and a temperature increase of 24.5°C. Nevertheless, the results of the numerical simulation can be seen as reasonable.
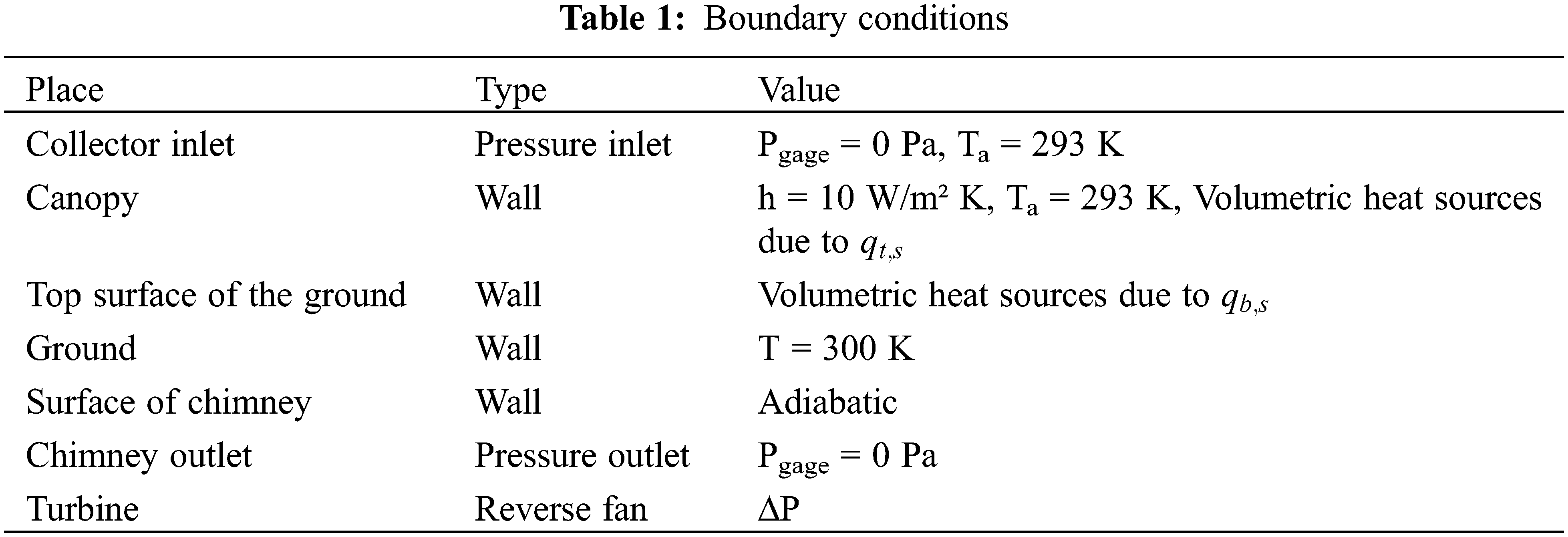
Now we compare the operation without and with turbine. The temperature profile across the collector in the case of unloaded and during turbine operation is illustrated in Fig. 4. It can be seen that in both cases the temperature rises inside the collector as expected, However, the presence of a turbine produces an even higher elevation in temperature. Because of the increased pressure jump through the turbine, the flow velocity of the air is reduced and thus the air has more time to absorb heat. With a given turbine pressure jump of 100 Pa, the temperature at the chimney inlet rises by about 5 K. This effect will increase by higher pressure drops.
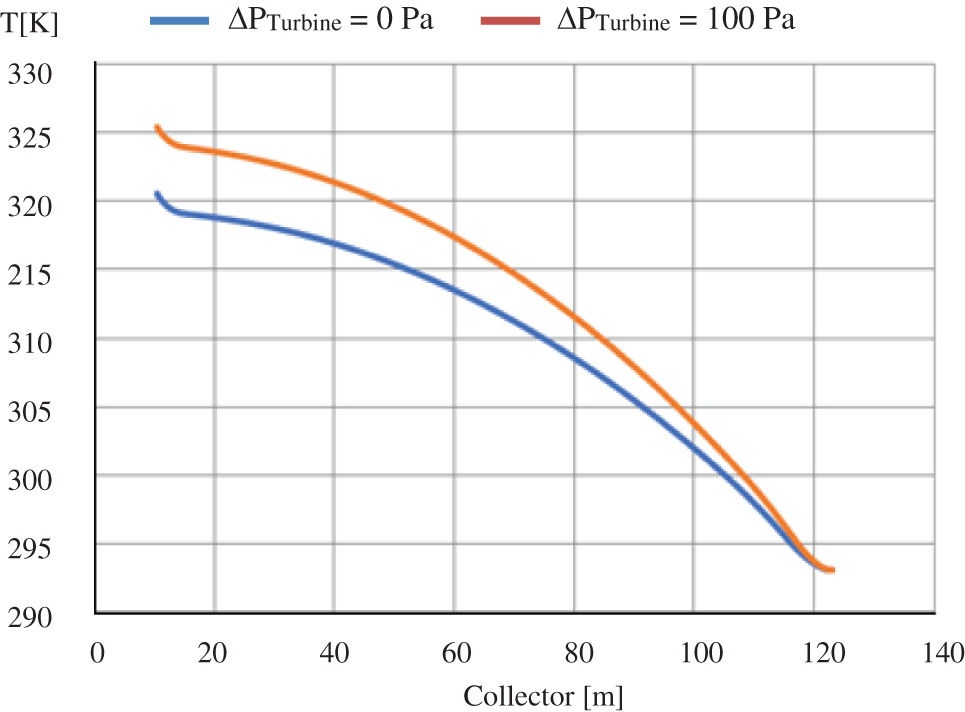
Figure 4: Temperature profile inside the collector
Fig. 5 shows a comparison of the collector temperature by different ground boundary conditions under no-load conditions. In all three modes, there is a similar pattern of temperature change, although Mode 1 temperatures are greater than Mode 3. Mode 1 considers that the soil surface absorbs the total incident solar energy, causing the air temperature in the collector to be overestimated. Based on experimental data from Manzanares, the temperature difference between the collector inlet and outlet is ∆T = 20°C. So, the results of Mode 3 are close to the experiment data, so that modeling with both shortwave and longwave radiation reflects reality much better.
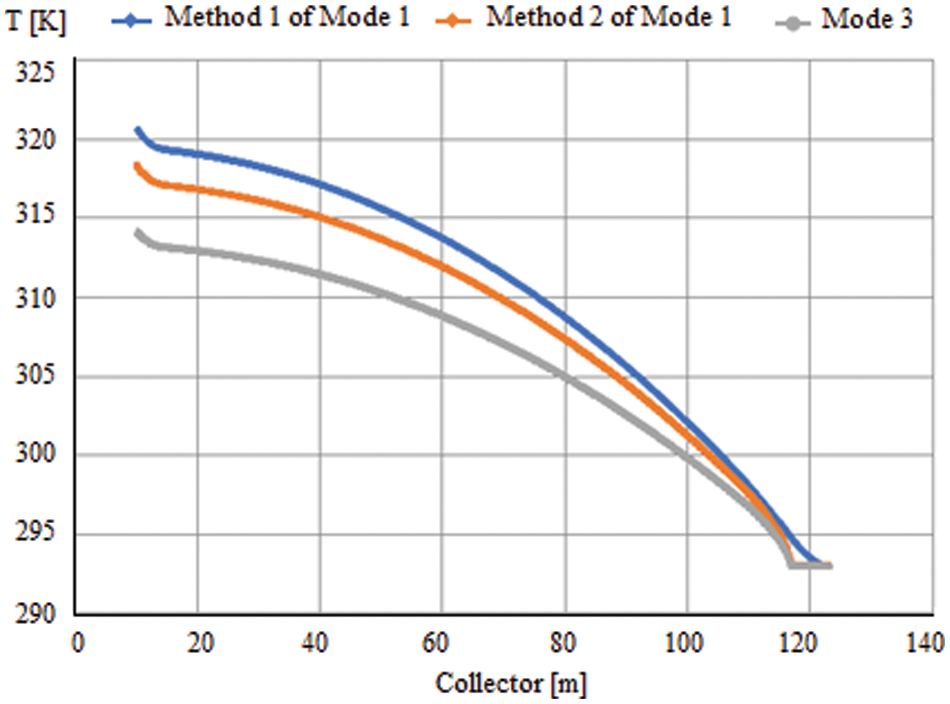
Figure 5: Temperature profile inside the collector by different methods
Fig. 6 indicates the influences of turbine pressure drop on the turbine output power of the SCPP system by different method. There, the turbine’s efficiency is adjusted to 80%. As shown in the figure, the effect of turbine pressure drop on system output power is quite complex. Under small pressure drop, the system output power increases with the turbine pressure drop. The SCPP power output formula is as follows:
Figure 6: The influence of the turbine pressure jump on turbine power output in different modes
where
Effect of solar radiation mode
The collector efficiency
where
Table 4 displays the collector effectiveness of the SCPP in Modes 1, 2, and 3. Adopting Mode 1 results in the maximum collector efficiency since the soil surface absorbs the most amount of heat (see Table 2). But this mode considers that the total incident solar energy is absorbed by the soil surface, causing the received solar radiation of SCPP to be overestimated. However, when the real spectral radiation properties of canopy and soil are included in Modes 2 and 3, the solar irradiance absorbed by the collector base is considerably reduced. Note that the variance in the integral efficiency between Modes 2 and 3 is quite small. The difference to Mode 1 is caused by the collector’s greenhouse effect, which is here neglected.

A closer look at the temperature distribution across the ground surface affirms the incorrect assessment of efficiency in Mode 1. As illustrated in Fig. 7, all four temperature curves show a similar form of change; however, Mode 1 has the highest values. And higher surface temperatures will result in a higher mass flowrate and an increase in air temperature. Thus, ignoring the greenhouse effect in the collector in Mode 1 (methods 1 and 2) will affect the accuracy of the soil surface temperature evaluation and the collector performance of the power plant.
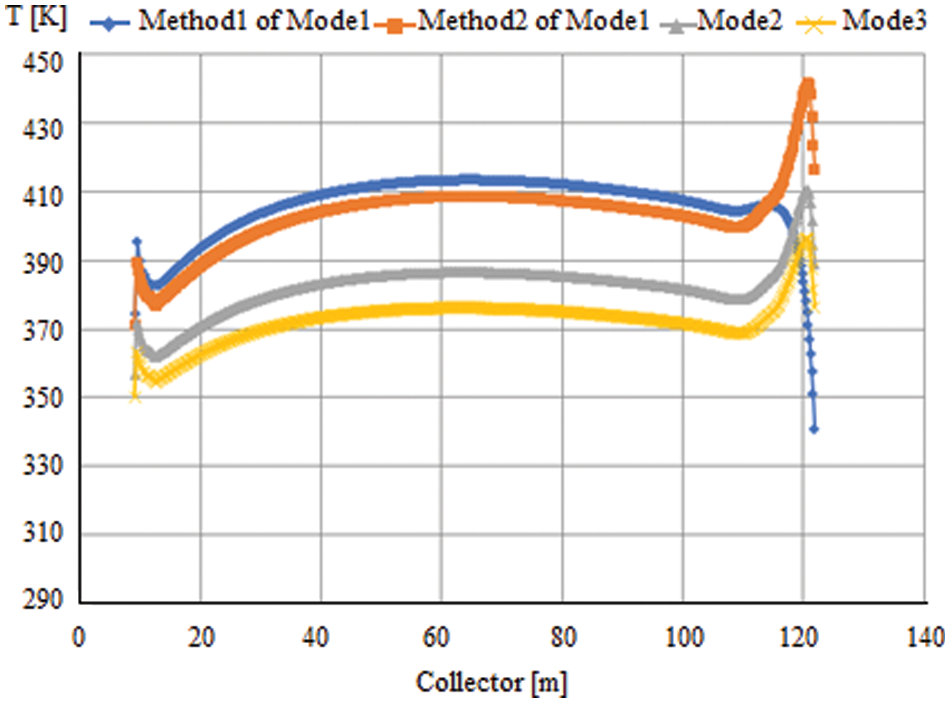
Figure 7: Temperature profile of the ground surface
Fig. 8 shows a comparison of ground surface temperature profiles obtained using different approaches. Data from the Manzanares SCPP reveals that when the solar insolation is around 800 W/m², the maximum soil surface temperature in the midst of the collector reaches 348 K [4]. Pastohr et al. [17] and Ming et al. [20] results without the greenhouse effect are much higher than the experimental value. They used Mode 1 for the solar radiation mode. The value of Pasumarthi et al. [11] is less than the last two but remains well above the experimental result. The temperature obtained in this study by including the greenhouse effect shows a deviation of 13% above the experimental results. Gholamalizadeh et al. [23] employed the three-dimensional solar ray tracing model and discrete ordinates radiation model and obtained a good result. The maximum temperature reported by this approach is 352 K, while the value estimated by the proposed Mode 3 is 376 K. The major overvaluation of the soil surface temperature while ignoring the greenhouse effect will cause an increase in the temperature of air flow through the collector, thus leading to an overestimated system flow rate. According to Eq. (3), as a result of the exaggerated system flow rate, the power output will be overestimated.

Figure 8: Comparison of ground surface temperature distribution
Additionally, as shown in Eq. (3), numerical results may be compared to test data only for air flow rate (or updraft velocity in the chimney) using measured turbine pressure difference as input data, but not for SCPP power production, where the turbine effectiveness is chosen arbitrarily [19].
The significant variation in the temperature profile of the ground surface indicates that previous approaches were unable to accurately describe the system’s heat transfer. The major causes behind this are as follows: 1) because solar radiation is regarded as a heat source in previous models, it differs from the real energy transfer mechanism. 2) the greenhouse effect in solar collectors has not been taken into account.
A 2D steady-state numerical analysis for the SCPP, which consists of the collector, chimney, turbine and energy storage layer, was performed. Three different modes taking solar radiation into consideration are used and their results are compared. The turbine is regarded as pressure-based and the energy storage layer is considered as solid media, aiming at analyzing the pressure, velocity, and temperature distributions of the system. Meanwhile, the influence of the turbine pressure drop on the flow and heat transfer characteristics and the output power of the SCPP.
The numerical results were initially verified using experimental data from Manzanares SCPP and other research. The numerical results were then compared under no-load and turbine operating conditions to determine the effect of turbine operation on SCPP parameters. In addition, the effect of solar irradiation on flow and heat transfer parameters was examined.
The analysis of the performed numerical results can be concluded as follows:
• The pressure differences during the turbine operation must be considered in modelling of SCPP, because the temperature inside the collector increases.
• Furthermore, variations in solar radiation have a noticeable influence on upwind speed, temperature increase, and chimney outlet parameters under no-load and loaded turbine conditions. These dependencies must be taken into account when designing SCPP plants.
• The main result is that disregarding the greenhouse effect in the collector will affect the accuracy of the soil surface temperature estimation, collector efficiency, and power output of the SCPP. Even with simple approaches to this effect (Mode 2), realistic results can be produced.
As a future work, the effect of other factors as the incidence angle of the solar radiation on the flow and temperature fields and the chimney efficiency will be studied. The independence on the temperature of the thermal source term in Mode 3 will be considered. The results obtained from this study will also be applied to a case study in Algeria.
Acknowledgement: The authors would like to acknowledge the support provided by the German Academic Exchange Service DAAD and the support provided by Professor Olaf Wünsch (University of Kassel, Germany) to realize this work.
Funding Statement: DAAD Funding Program/ID: Research Stays for University Academics and Scientists, 2019 (57440915).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Bonnet, S., Alaphilippe, M., Stouffs, P. (2006). Thermodynamic solar energy conversion: Reflections on the optimal solar concentration ratio. International Journal of Energy, Environment and Economics, 12, 141–152. [Google Scholar]
2. Schlaich, J., Schiel, W., Friedrich, K., Schwarz, G., Wehowsky, P. et al. (1990). Übertragbarkeit der ergebnisse von manzanares auf größere anlagen, Abschlussbericht Aufwindkraftwerk. BMFT-Förderkennzeichen 0324249D Stuttgart. [Google Scholar]
3. Haaf, W., Friedrich, K., Mayr, G., Schlaich, J. (1983). Solar chimneys Part I: Principle and construction of the pilot plant in Manzanares. International Journal of Solar Energy, 2(1), 3–20. DOI 10.1080/01425918308909911. [Google Scholar] [CrossRef]
4. Haaf, W. (1984). Solar chimneys Part II: Preliminary test results from the Manzanares pilot plant. International Journal of Solar Energy, 2(2), 141–161. DOI 10.1080/01425918408909921. [Google Scholar] [CrossRef]
5. Krisst, R. J. K. (1983). Energy transfer system. Alternative Source Energy, 63, 8–11. [Google Scholar]
6. Kulunk, H. (1985). A prototype solar convection chimney operated under Izmit conditions. Proceedings of the 7th Miami International Conference on Alternative Energy Sources, pp. 162Miami Beach, Florida, USA. [Google Scholar]
7. Pasumarthi, N., Sherif, S. A. (1998). Experimental and theoretical performance of a demonstration solar chimney model–Part II: Experimental and theoretical results. International Journal of Energy Research, 22, 443–461. DOI 10.1002/(ISSN)1099-114X. [Google Scholar] [CrossRef]
8. Zhou, X., Yang, J., Xiao, B., Hou, G. (2007). Experimental study of temperature field in a solar chimney power setup. Applied Thermal Engineering, 27(11–12), 2044–2050. DOI 10.1016/j.applthermaleng.2006.12.007. [Google Scholar] [CrossRef]
9. Kasaeian, A. B., Heidari, E., Vatan, N. S. (2011). Experimental investigation of climatic effects on the efficiency of a solar chimney pilot power plant. Renewable and Sustainable Energy Reviews, 15(9), 5202–5206. DOI 10.1016/j.rser.2011.04.019. [Google Scholar] [CrossRef]
10. Zuo, L., Yuan, Y., Zheng, Z., Li, Y. (2012). Experimental research on solar chimneys integrated with seawater desalination under practical weather condition. Desalination, 298, 22–33. DOI 10.1016/j.desal.2012.05.001. [Google Scholar] [CrossRef]
11. Pasumarthi, N., Sherif, S. A. (1998). Experimental and theoretical performance of a demonstration solar chimney model–Part I: Mathematical model development. International Journal of Energy Research, 22, 277–288. DOI 10.1002/(ISSN)1099-114X. [Google Scholar] [CrossRef]
12. Bernardes, M. A., Dos, S., Voss, A., Weinrebe, G. (2003). Thermal and technical analyzes of solar chimneys. Solar Energy, 75(6), 511–524. DOI 10.1016/j.solener.2003.09.012. [Google Scholar] [CrossRef]
13. von Backström, T. W., Fluri, T. P. (2006). Maximum fluid power condition in solar chimney power plants–An analytical approach. Solar Energy, 80(11), 1417–1423. DOI 10.1016/j.solener.2006.04.001. [Google Scholar] [CrossRef]
14. Zhou, X., Yang, J., Xiao, B., Hou, G. (2007). Simulation of a pilot solar chimney thermal power generating equipment. Renewable Energy, 32(10), 1637–1644. DOI 10.1016/j.renene.2006.07.008. [Google Scholar] [CrossRef]
15. Li, J. Y., Guo, P. H., Wang, Y. (2012). Effects of collector radius and chimney height on power output of a solar chimney power plant with turbines. Renewable Energy, 47(1), 21–28. DOI 10.1016/j.renene.2012.03.018. [Google Scholar] [CrossRef]
16. Gholamalizadeh, E., Mansouri, S. H. (2013). A comprehensive approach to design and improve a solar chimney power plant: A special case–Kerman project. Applied Energy, 102(1), 975–982. DOI 10.1016/j.apenergy.2012.06.012. [Google Scholar] [CrossRef]
17. Pastohr, H., Kornadt, O., Gürlebeck, K. (2004). Numerical and analytical calculations of the temperature and flow field in the upwind power plant. International Journal of Energy Research, 28, 495–510. DOI 10.1002/(ISSN)1099-114X. [Google Scholar] [CrossRef]
18. Xu, G. L., Ming, T. Z., Pan, Y., Meng, F. L., Zhou, C. (2011). Numerical analysis on the performance of solar chimney power plant system. Energy Conversion and Management, 52(2), 876–883. DOI 10.1016/j.enconman.2010.08.014. [Google Scholar] [CrossRef]
19. Huang, M. H., Lei, C., He, Y. L., Cao, J. J., Tao, W. Q. (2017). A two-dimensional simulation method of the solar chimney power plant with a new radiation model for the collector. International Communications in Heat and Mass Transfer, 85(10), 100–106. DOI 10.1016/j.icheatmasstransfer.2017.04.014. [Google Scholar] [CrossRef]
20. Ming, T., Liu, W., Pan, Y., Xu, G. (2008). Numerical analysis of flow and heat transfer characteristics in solar chimney power plants with energy storage layer. Energy Conversion and Management, 49(10), 2872–2879. DOI 10.1016/j.enconman.2008.03.004. [Google Scholar] [CrossRef]
21. Amori, K. E., Mohammed, S. W. (2012). Experimental and numerical studies of solar chimney for natural ventilation in Iraq. Energy and Building, 47, 450–457. DOI 10.1016/j.enbuild.2011.12.014. [Google Scholar] [CrossRef]
22. Guo, P. H., Li, J. Y., Wang, Y. (2014). Numerical simulations of solar chimney power plant with radiation model. Renewable Energy, 62, 24–30. DOI 10.1016/j.renene.2013.06.039. [Google Scholar] [CrossRef]
23. Gholamalizadeh, E., Kim, M. H. (2014). 3D CFD analysis for simulating the greenhouse effect in solar chimney power plants using a two-band radiation model. Renewable Energy, 63(1), 498–506. DOI 10.1016/j.renene.2013.10.011. [Google Scholar] [CrossRef]
24. Rabehi, R., Chaker, A., Aouachria, Z., Tingzhen, M. (2017). CFD analysis on the performance of a solar chimney power plant system case study in Algeria. International Journal of Green Energy, 14(12), 971–982. DOI 10.1080/15435075.2017.1339043. [Google Scholar] [CrossRef]
25. Rabhi, R., Chaker, A., Ming, T., Gong, T. (2018). Numerical simulation of solar chimney power plant adopting the fan model. Renewable Energy, 126(12), 1093–1101. DOI 10.1016/j.renene.2018.04.016. [Google Scholar] [CrossRef]
26. Cengel, Y. A., Ghajar, A. J. (2011). Heat and mass transfer: Fundamentals and applications. 4th edition. New York: McGraw-Hill. [Google Scholar]
27. Yang, S. M., Tao, W. Q. (2006). Heat transfer. 4th edition. Beijing, China: Higher Education Press. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools