 Open Access
Open Access
ARTICLE
Performance Prediction of an Optimized Centrifugal Pump with High Efficiency
1 School of Mechanical Engineering, Chaohu University, Chaohu, 238024, China
2 College of Engineering, Technological University of the Philippines, Manila, 1106, Philippines
3 School of Mechanical Engineering, Anhui Polytechnic University, Wuhu, 241000, China
* Corresponding Author: Yuqin Wang. Email:
Fluid Dynamics & Materials Processing 2023, 19(9), 2215-2228. https://doi.org/10.32604/fdmp.2023.027188
Received 18 October 2022; Accepted 19 January 2023; Issue published 16 May 2023
Abstract
The main structural parameters of the IR100-80-100A type chemical centrifugal pump have been optimized by means of an orthogonal test approach. The centrifugal pump has been modeled using the CFturbo software, and 16 sets of orthogonal-test schemes have been defined on the basis of 4 parameters, namely, the blade number, blade outlet angle, impeller outlet diameter, and impeller outlet width. Such analysis has been used to determine the influence of each index parameter on the pump working efficiency and identify a set of optimal combinations of such parameters. The internal flow field in the centrifugal pump has been simulated by using the PumLinx software. These numerical results have shown that, compared with the prototype pump, the outlet pressure and shaft power of the optimized pump can be significantly reduced, and the pump working efficiency can be improved by 5.59%. In the present study, some arguments are also provided to demonstrate that, with respect to other optimization methods, the orthogonal test approach is more convenient, and requires less test times.Graphic Abstract
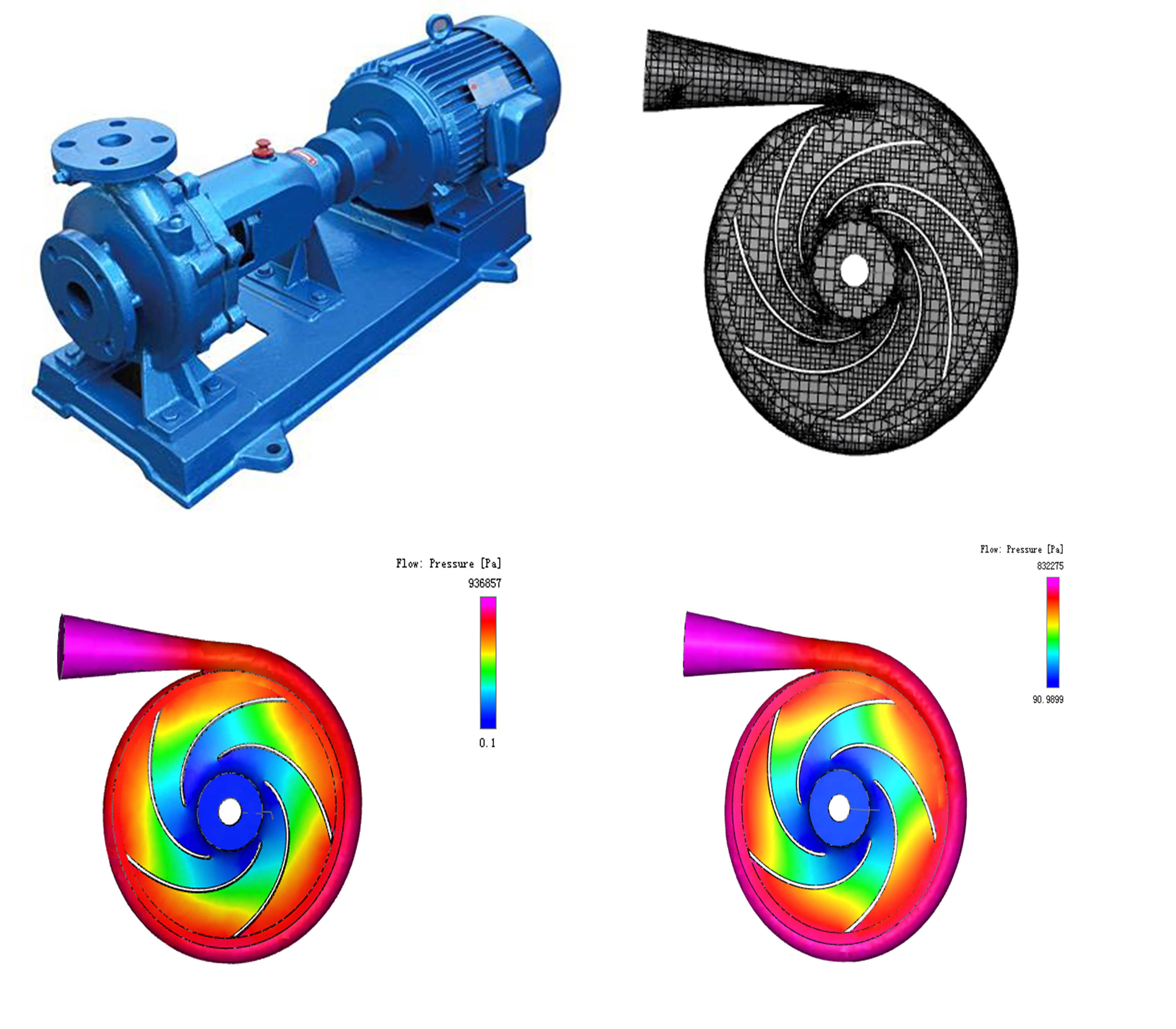
Keywords
The first to propose the concept of the centrifugal pump was the French engineer Papin, he made the world’s first centrifugal pump for lifting liquids in 1705. Due to its simple structure, low production cost and wear resistance, the centrifugal pump, which is used for energy conversion, is widely used in various fields [1–5]. However, in the energy conversion process of the centrifugal pump, various energy losses are inevitably generated, resulting in the low working efficiency of the pump. How to improve the pump working efficiency has become a key research direction for the majority of researchers and manufacturers. At present, many experts and scholars are committed to studying how to reduce energy loss and improve pump efficiency in the working process, and have achieved certain results. Li et al. [6] used the crowd search algorithm to optimize the blade structure parameters, and obtained the optimal parameter combination, which improved the working efficiency of the centrifugal pump. He et al. [7] used the response surface method to fit the impeller structural parameters, head and efficiency, and obtained the best combination of multiple factors, which significantly improved the efficiency of the centrifugal pump. Xing et al. [8] obtained better impeller structure parameters based on the Box-Behnken simulation test platform with no-load wind speed as the indicator. Sun [9] used the Pro/Mechanica to design a lightweight impeller model, reducing the impeller mass and saving costs. Hoseinib et al. [10] used the multi-objective genetic algorithm to optimize the design of impeller parameters, reducing the power consumption of centrifugal pumps. Adiaconitei et al. [11] used additive manufacturing technology to design an impeller, which improved the surface accuracy of the impeller.
To improve the working efficiency of a centrifugal pump and reduce power consumption, the orthogonal test method will be used to optimize the main parameters of the pump to obtain better impeller combination parameters. In this paper, the relevant structural parameters of the centrifugal pump will be calculated, the CFturbo software will be used to model the centrifugal pump, and the internal flow field will be simulated based on PumLinx software. Finally, through orthogonal test and range analysis, the optimal combination of impeller structural parameters will be obtained, so as to improve the centrifugal pump’s working efficiency in use and reduce the use cost.
2 Design of the Main Structural Parameters of Centrifugal Pump
The IR100-80-100A type chemical centrifugal pump is selected as the prototype pump, as shown in Fig. 1. The basic parameters of the prototype pump are: Q = 59 m3/h; head H = 100 m; and rotational speed n = 2900 r/min.

Figure 1: IR100-80-100A type chemical centrifugal pump
To improve the calculation accuracy, the variation range of the main structural parameters of the centrifugal pump impeller is restricted. The restriction conditions for each performance parameter are given in Eq. (1) [12].
In Eq. (1),
The main structural parameters of the centrifugal pump impeller are calculated by the velocity coefficient method [6], as presented in Table 1.

The system performance will be restricted by many factors, and to clarify the influence sequence of various factors on the system, relevant tests are needed. The traditional permutation and combination method needs to test all combinations of the various factors, but the number of tests is numerous and the workload of tests is large. To reduce the number of trials and workload, mathematicians have developed a new test method–the orthogonal test. The method of the orthogonal test is to establish an orthogonal test table by selecting some representative factors, and carrying out statistical analysis, overall design, and comprehensive comparison to obtain the horizontal combination which is closest to the best scheme [7–9]. The orthogonal test only selects some factors to carry out the test and does not consider the arrangement and combination of all factors, thus improving the test efficiency. It is a fast and convenient method of optimization.
Considering the influence of various factors on the centrifugal pump efficiency, 4 parameters including the blade number
According to the
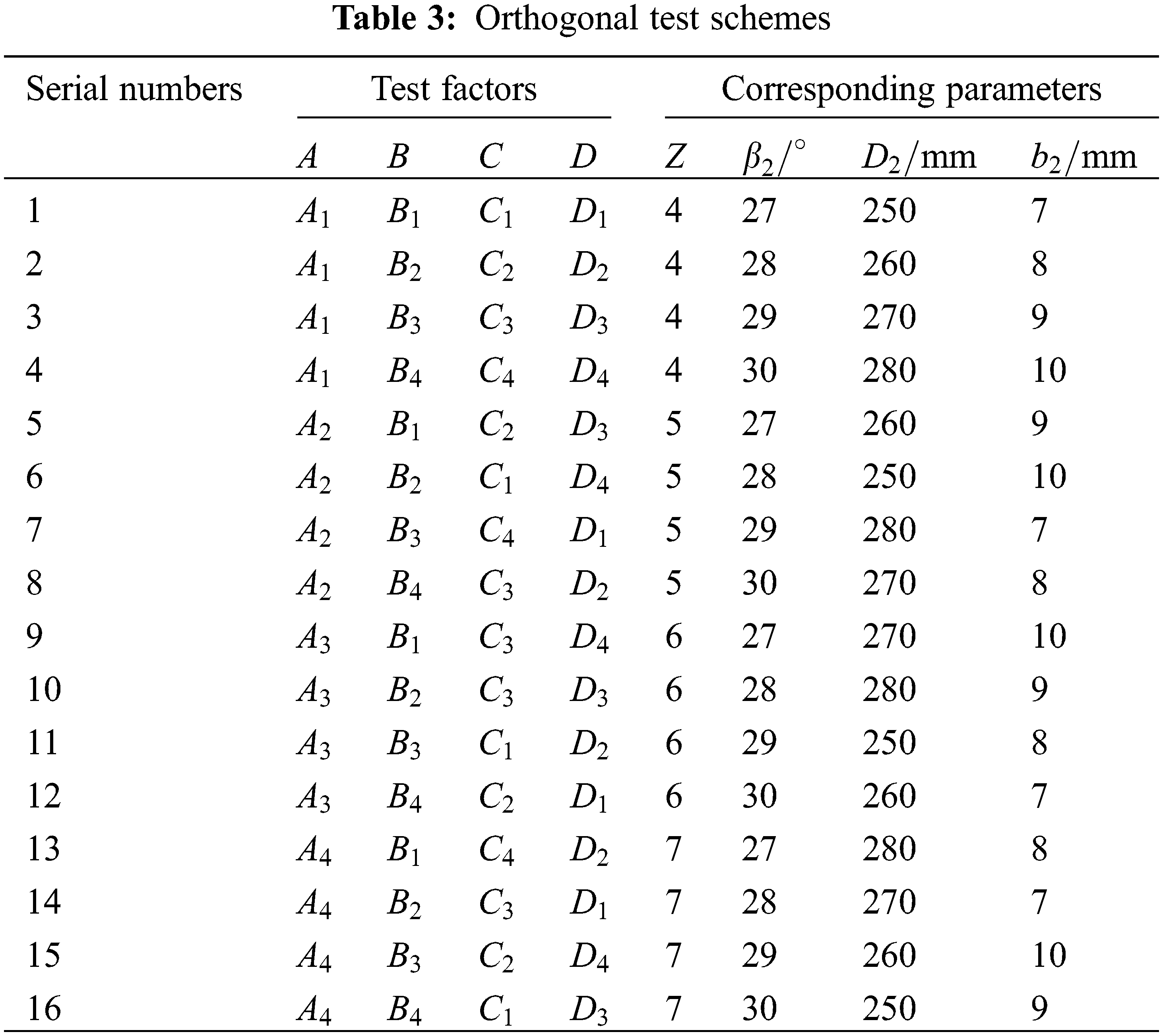
4 Simulation and Analysis of Internal Flow Field
PumpLinx is a hydraulic simulation software specifically designed for fluid mechanical analysis, which can accurately simulate fluid flow and cavitation, etc. [10–12]. The built three-dimensional model of the centrifugal pump is imported into PumLinx software and the Cartesian grid is divided, as shown in Fig. 2.
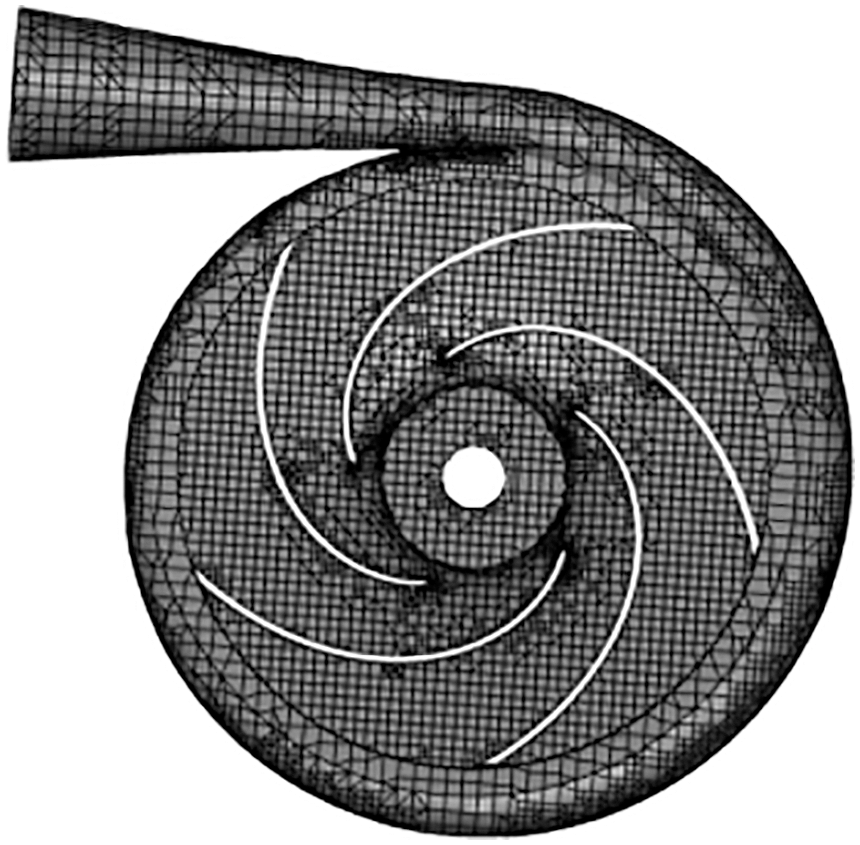
Figure 2: Centrifugal pump grid division
Because the grid number of centrifugal pump has a great influence on the experimental results, grid independence analysis is required. Taking the outlet pressure and head of the volute as the index, the influence of different grid numbers on the index is considered. The grid independence analysis results are shown in Table 4.

As can be seen from Table 4, when the number of grids is 2,356,897, each index has reached a stable state, and the working performance of the system is stable. After comprehensive consideration, the number of grids is determined to be 2,356,897.
4.2 Boundary Condition Setting
The boundary conditions mainly include the import boundary condition, export boundary condition, wall boundary condition, and interface boundary condition. The selection criteria of the turbulence model mainly include whether the fluid is compressible, establishing special feasible problems, accuracy requirements, computer capabilities, and time constraints. Turbulence model calculation methods mainly include Reynolds time average simulation, scale analytical simulation, and direct numerical simulation. Among them, the
The Reynolds time average
In Eq. (2),
The Reynolds time averaged
In Eq. (3),
Using the quality exit boundary condition, there is no slippage on each solid wall surface. The interface between the inlet and impeller and between the impeller and volute shall be the interface between the dynamic and static coupling platform [16].
The finite volume method is used to discretize the control equation [17]. The second order fully implicit scheme is used to discretize the time term [18]. The diffusion term and pressure term are discretized by the central difference scheme [19]. Second-order upwind scheme is adopted for convection term [20]. And the pressure and velocity equations are solved by full coupling technique [21].
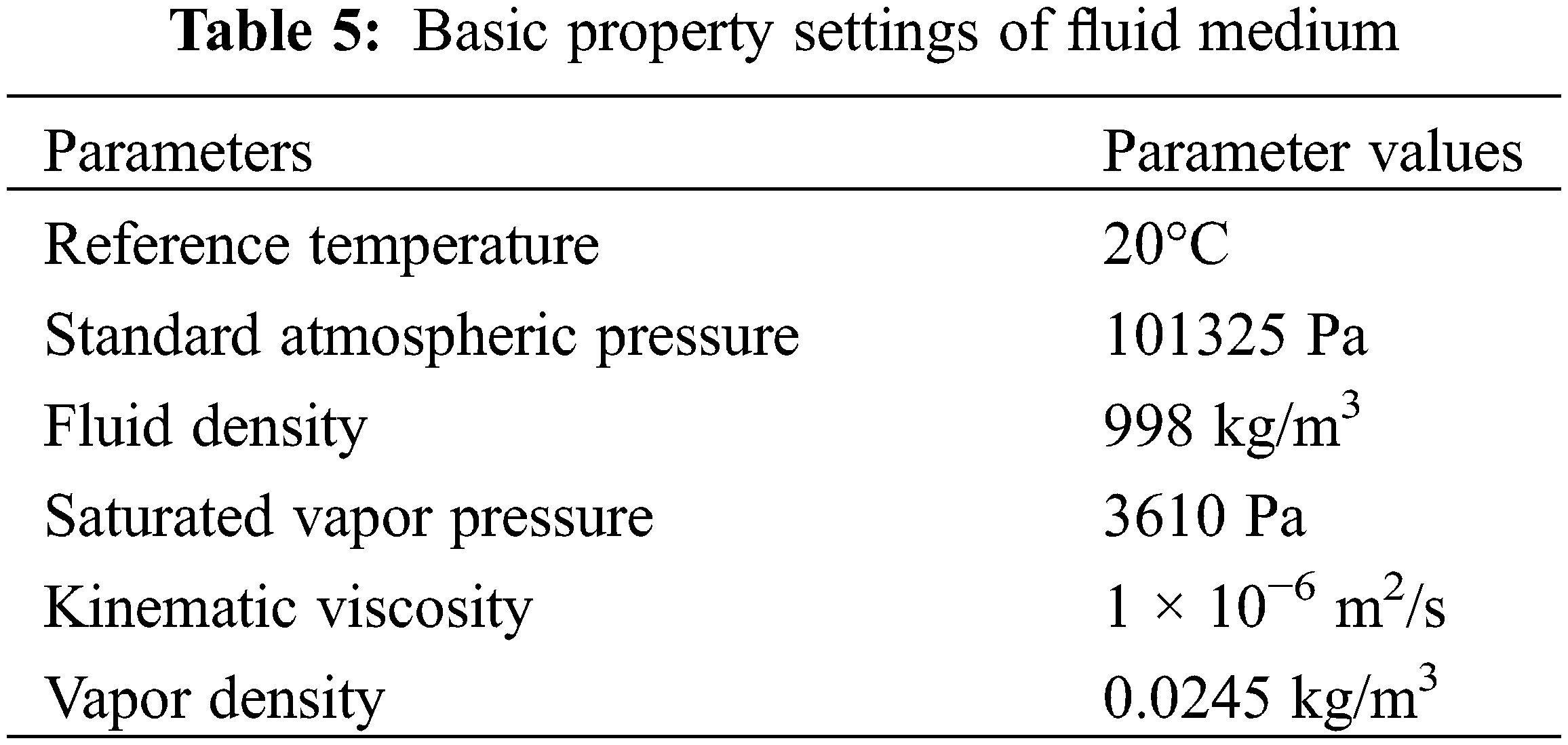
Assuming that the fluid medium inside the centrifugal pump is an incompressible Newtonian fluid, and the fluid medium is water, its basic properties are given in Table 5 [22].
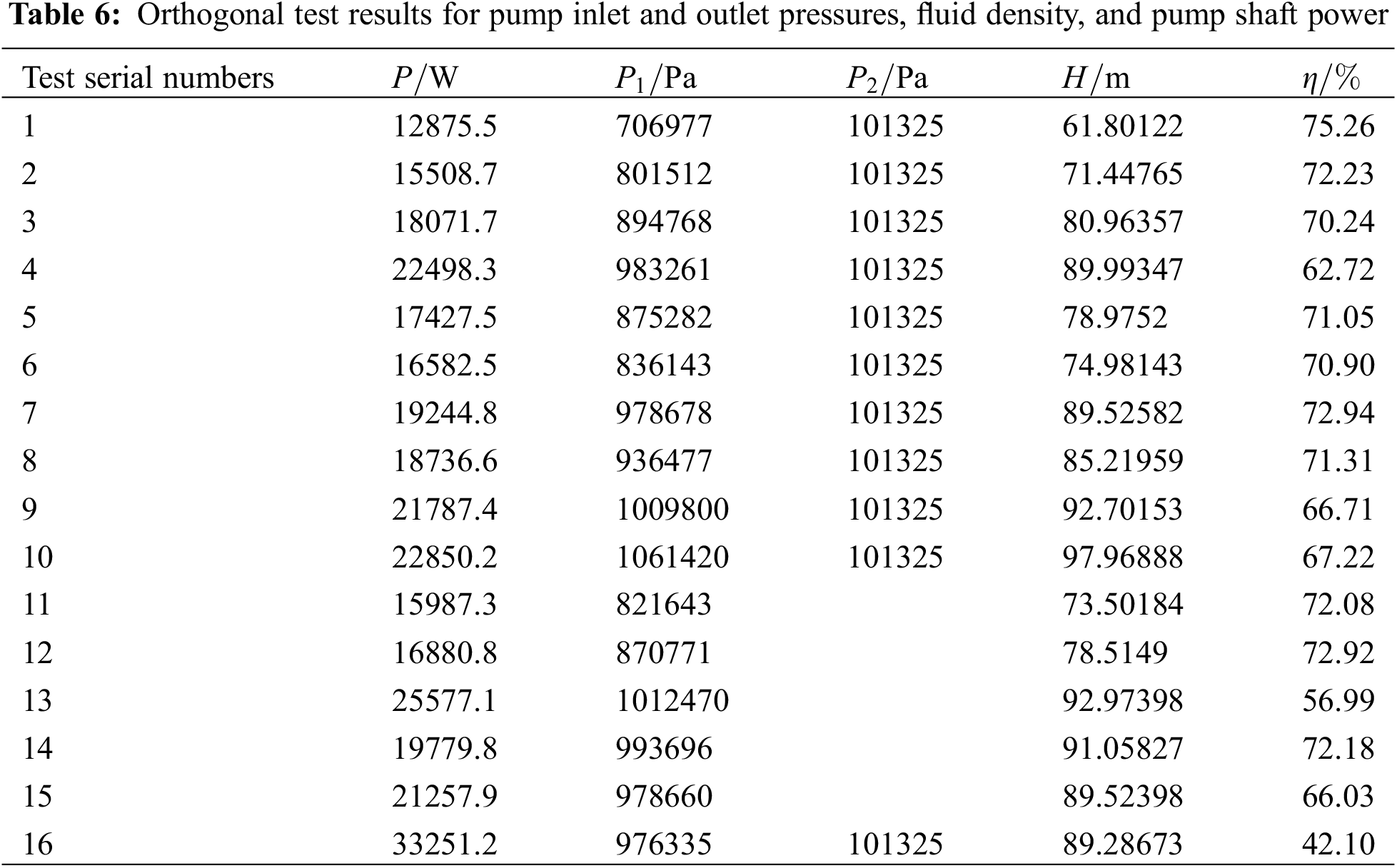
According to the orthogonal test schemes in Table 3, 16 different centrifugal pump models were established [23]. The internal flow field simulation was performed by using PumpLinx software to obtain the corresponding shaft power, outlet pressure and inlet pressure of the pump. The head and efficiency of the centrifugal pump were calculated by Eq. (4), and the obtained results are presented in Table 6.
In Eq. (4),
The range analysis method, also known as the intuitive analysis method, is the most commonly used method of analysis of orthogonal test results, and it has the advantages of simple calculation, intuitive image, is simple and easy to understand, etc., Eq. (5) is a range method analysis and calculation formula. The results of the orthogonal test are analyzed by Eq. (5), and the order of influence of each parameter on the centrifugal pump efficiency is obtained [24].
In Eq. (5),
The range calculation was performed on the orthogonal test results of the centrifugal pump by Eq. (5), and the calculation results are presented in Table 7.
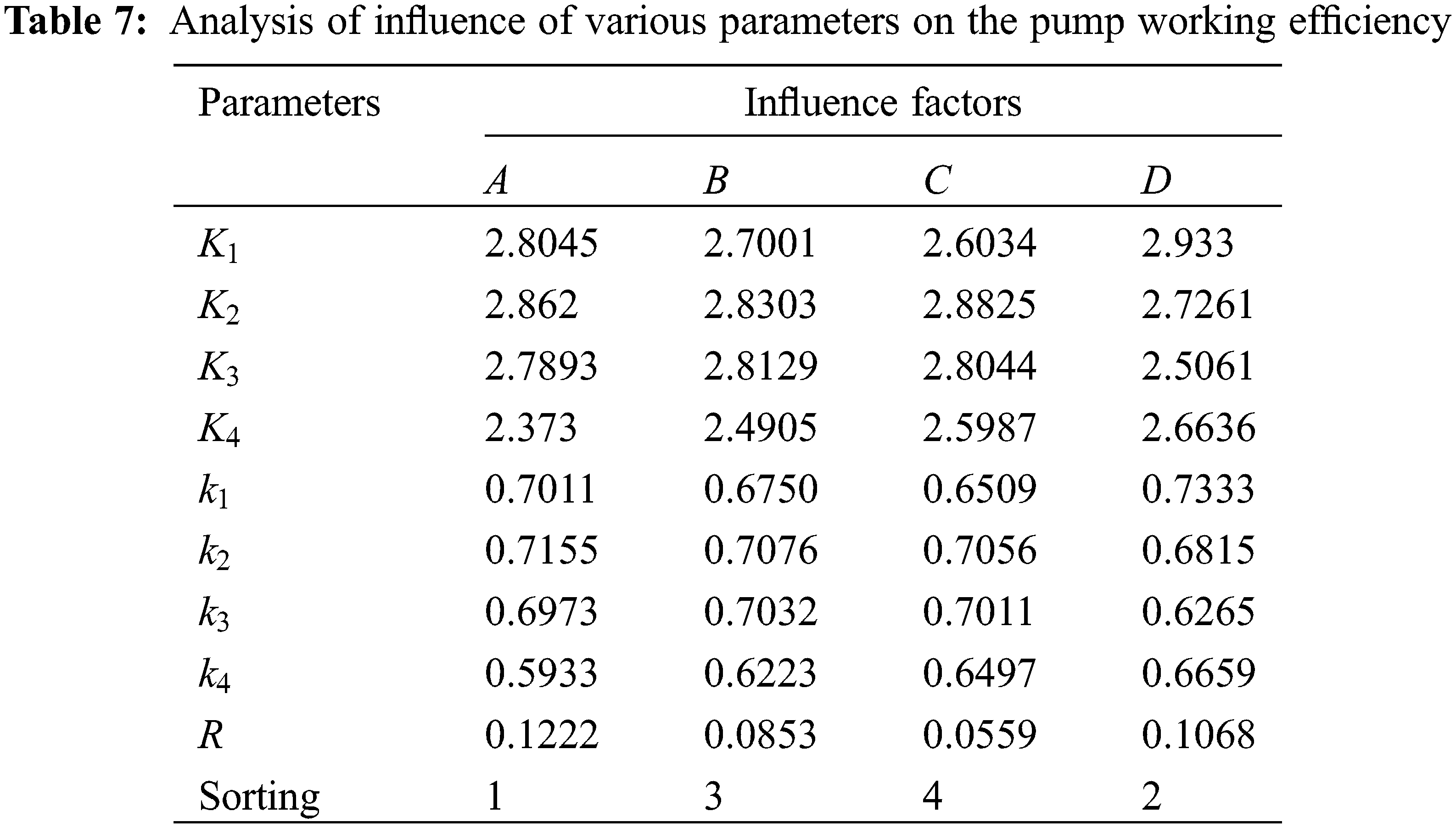
As can be seen from Table 7, the order of the degree influence of the selected parameters on the centrifugal pump working efficiency is
4.5 Simulation of Internal Flow Feld in Centrifugal Pump
To verify the feasibility of the orthogonal test optimization scheme, the internal flow field simulations are carried out on the prototype pump and the optimized pump at a rated speed (

Figure 3: Simulation results of the prototype pump internal flow field
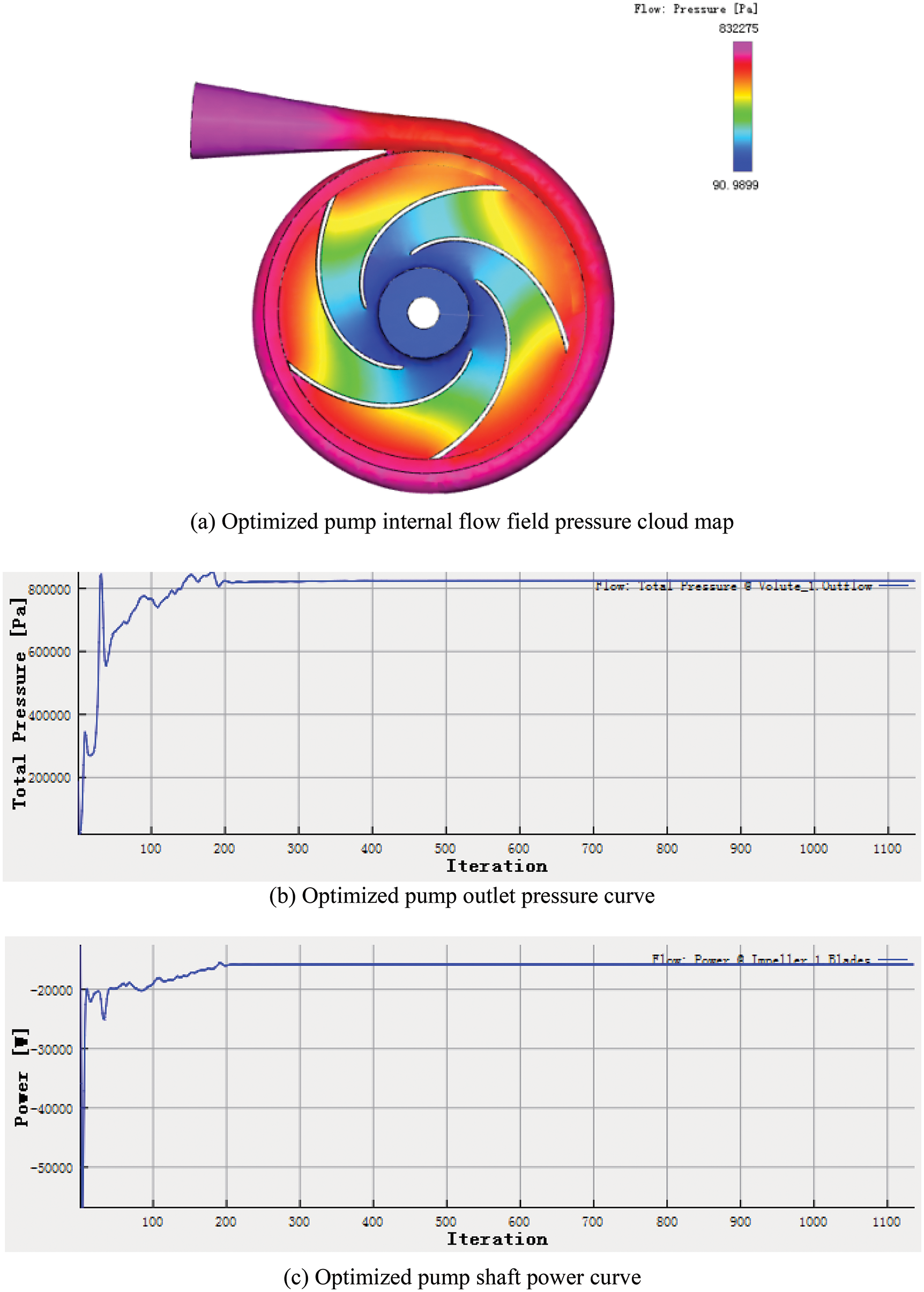
Figure 4: Simulation results of the optimized pump internal flow field
As can be seen from Figs. 3 and 4, the centrifugal pump outlet pressure before optimization is 936857 Pa, and the pump shaft power is 18668.7 W. The optimized centrifugal pump outlet pressure is 832275 Pa and the pump shaft power is 15493.1 W. Combined with Eq. (2), the centrifugal pump working efficiency before and after optimization can be calculated to be 73.3% and 77.4%, respectively, which means that the working efficiency is increased by 5.59%.
5 Verification and Analysis of External Characteristic Test
To verify the correctness of the optimization scheme, the IR100-80-100A type chemical centrifugal pump is selected to build the external characteristic test platform. The impeller is made based on the optimal combination parameters. The impeller material is polylactic acid (PLA), as shown in Fig. 5.

Figure 5: Optimized pump impeller
The external characteristics of the prototype pump and the optimized pump are tested by CFD technology. The flow rate of the working conditions are

Figure 6: Comparison of external characteristics of the prototype pump and optimized pump
As can be seen from Fig. 6, with the increase of flow rate, the centrifugal pump working efficiency gradually increases, reaching the maximum value near the rated flow rate. The change trend of the working efficiency curve of the optimized pump and the prototype pump is basically the same, and the change law can be clearly expressed.
The pump working efficiency under different operating conditions is extracted from Fig. 6, and presented in Table 8.

From Table 8, the optimized value of the pump working efficiency under different working conditions is greater than the prototype pump value, and the performance is improved significantly, achieving the expected optimization goal. The main reason for this is that the three structural parameters of optimized pump blade outlet angle, impeller outlet diameter, and impeller outlet width are all reduced, which reduces wear on the surfaces of the impeller and guide vanes, reduces hydraulic losses, improves the efficiency of fluid flow, and thus improves the centrifugal pump’s working efficiency. The accuracy of the optimization method of centrifugal pump efficiency based on orthogonal test is further verified through the external characteristic test of centrifugal pump working efficiency.
(1) The IR 100-80-100A type chemical centrifugal pump was selected as the prototype pump, and the mathematical model with the optimal pump working efficiency as its objective function was established. The main structural parameters of the impeller were optimized by orthogonal test. The order of degree of influence of the main structural parameters of the centrifugal pump on the pump working efficiency was obtained through range analysis and calculation, and a set of optimal combination parameters was obtained.
(2) The internal flow field simulation of the prototype pump and the optimized pump was carried out by using PumpLinx software. The simulation results showed that the outlet pressure and shaft power of the optimized pump had both decreased significantly, and the pump working efficiency had increased by 5.59%, which verified the feasibility of the orthogonal test optimization scheme.
(3) The external characteristic test platform of the centrifugal pump was built and the optimized pump impeller was made. The external characteristic test results showed that the optimized pump working efficiency under different working conditions was greater than the prototype pump value, and the system performance was improved obviously, which further verified the accuracy of the orthogonal test scheme.
(4) Taking the centrifugal pump as the research object, the orthogonal design and range analysis were used to optimize the main structural parameters of the pump, which improved the pump working efficiency. Based on the external characteristic test bench, the accuracy of the optimization method was verified. In the next step, the multi-objective optimization design method of centrifugal pump will be focused on to comprehensively improve the centrifugal pump’s hydraulic performance.
Funding Statement: This project is supported by the Anhui Province University Discipline (Professional) Top Talent Academic Funding Project (No. gxbjZD2021076). This project is supported by the Key Project of Natural Science Research in Colleges and Universities of Anhui Province (No. KJ2021A1026). This project is supported by the Key Project of Natural Science Foundation of Chaohu University (No. XLZ-201902).
Author Contributions: Y. W.: Structure Design, Algorithm Design; M. H.: Drawing Graphics; L. S.: Experiment. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Wang, W. J., Yuan, S. Q., Pei, J., Zhang, J. F., Yuan, J. P. et al. (2015). Two-point hydraulic optimization of pump impeller based on kriging model and neighborhood cultivation genetic algorithm. Journal of Mechanical Engineering, 51(15), 33–38. https://doi.org/10.3901/JME.2015.15.033 [Google Scholar] [CrossRef]
2. Tan, L., Cao, S., Wang, Y., Zhu, B. (2012). Direct and inverse iterative design method for centrifugal pump impellers. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 226(6), 764–775. https://doi.org/10.1177/0957650912451411 [Google Scholar] [CrossRef]
3. Kim, S., Choi, Y. S., Lee, K. Y., Yoon, J. Y. (2009). Design optimization of centrifugal pump impellers in a fixed meridional geometry using DOE. International Journal of Fluid Machinery & Systems, 2(2), 172–178. https://doi.org/10.5293/IJFMS.2009.2.2.172 [Google Scholar] [CrossRef]
4. Sakthivel, N. R., Sugumaran, V., Nair, B. B. (2012). Automatic rule learning using roughset for fuzzy classifier in fault categorization of mono-block centrifugal pump. Applied Soft Computing, 12(1), 196–203. https://doi.org/10.1016/j.asoc.2011.08.053 [Google Scholar] [CrossRef]
5. Derakhshan, S., Pourmahdavi, M., Abdolahnejad, E., Reihani, A., Ojaghi, A. (2013). Numerical shape optimization of a centrifugal pump impeller using artificial bee colony algorithm. Computers & Fluids, 81(9), 145–151. https://doi.org/10.1016/j.compfluid.2013.04.018 [Google Scholar] [CrossRef]
6. Li, Y. L., Sun, X. W., Yang, H. R., Wang, H. Y., Liu, Y. et al. (2022). Optimization of impeller structure parameters of cementing mud flowmeter based on response surface and crowd search algorithm. Journal of Electronic Measurement and Instrumentation, 36(5), 12–20. [Google Scholar]
7. He, K. J., Heng, Y. G., Zhang, W. B., Jiang, Q. F. (2021). Research on optimization of disc pump impeller based on response surface method. Journal of Engineering for Thermal Energy and Power, 36(8), 8–15. [Google Scholar]
8. Xing, H. N., Ma, S. C., Mo, J. L., Zeng, B. S., Liang, W. P. et al. (2021). Optimization and experiment of parameters for the impeller structure of extractor in a sugarcane chopper harvester. Transactions of the Chinese Society of Agricultural Engineering, 37(12), 12–19. [Google Scholar]
9. Sun, W. (2020). Design optimization of impeller structure of liquid ring vacuum pump: A simulation study. Chinese Journal of Vacuum Science and Technology, 40(5), 395–399. [Google Scholar]
10. Hoseini, S. S., Najafi, G., Ghobadian, B., Akbarzadeh, A. H. (2021). Impeller shape-optimization of stirred-tank reactor: CFD and fluid structure interaction analyses. Chemical Engineering Journal, 413(1), 2–18. https://doi.org/10.1016/j.cej.2020.127497 [Google Scholar] [CrossRef]
11. Adiaconitei, A., Vintila, I. S., Mihalache, R., Paraschiv, A., Frigioescu, T. F. et al. (2021). Manufacturing of closed impeller for mechanically pump fluid loop systems using selective laser melting additive manufacturing technology. Materials, 14(20), 1–17. [Google Scholar]
12. Wang, Y. Q., Huo, X. W., Ji, H. L. (2018). Multiobjective optimization design and experimental study of desulfurization dust removal centrifugal pump based on immune particle swarm algorithm. Advances in Materials Science & Engineering, 2018(1), 1–10. https://doi.org/10.1155/2018/6294824 [Google Scholar] [CrossRef]
13. Noor, I., Qamar, I. (2021). Simulation of internal flow field of pitot-tube jet pump. Intermational Jourmnal of Aerospace and Mechanical Engineering, 15(2), 102–106. [Google Scholar]
14. Shigemitsu, T., Nakaishi, E., Maeda, M., Araki, Y. (2021). Influence of blade number on performance and internal flow condition of centrifugal pump for low viscous fluid food. International Journal of Fluid Machinery and Systems, 14(1), 132–141. https://doi.org/10.5293/IJFMS.2021.14.1.132 [Google Scholar] [CrossRef]
15. Tanaka, T., Toyomoto, T., Nasu, K., Tabaru, M. (2021). Transient characteristics of a centrifugal pump at rapid startup. Journal of Physics: Conference Series, 1909(1), 012032. https://doi.org/10.1088/1742-6596/1909/1/012032 [Google Scholar] [CrossRef]
16. Khoeini, D., Tavakoli, M. R. (2018). The optimum position of impeller splitter blades of a centrifugal pump equipped with vaned diffuser. FME Transactions, 46(2), 205–210. https://doi.org/10.5937/fmet1802205K [Google Scholar] [CrossRef]
17. Mousmoulis, G., Kassanos, I., Aggidis, G., Anagnostopoulos, I. (2021). Numerical simulation of the performance of a centrifugal pump with a semi-open impeller under normal and cavitating conditions. Applied Mathematical Modelling, 83(3), 1814–1834. [Google Scholar]
18. Sugiyama, D., Ichinose, A., Takeda, T., Miyagawa, K., Negishi, H. et al. (2021). Investigation of internal flow in centrifugal pump diffuser using laser doppler velocimetry (LDV) and computational fluid dynamics. Journal of Physics: Conference Series, 1909(1), 1–10. https://doi.org/10.1088/1742-6596/1909/1/012075 [Google Scholar] [CrossRef]
19. Kim, S. J., Suh, J. W., Yang, H. M., Park, J., Kim, J. H. (2022). Internal flow phenomena of a pump-turbine model in turbine mode with different thoma numbers. Renewable Energy, 184(3), 510–525. https://doi.org/10.1016/j.renene.2021.11.101 [Google Scholar] [CrossRef]
20. Hosotani, T., Shigemitsu, T., Kawaguchi, Y., Inamoto, T., Ishiguro, T. et al. (2021). Influence of meridional plane shape on performance and internal flow of high head contra-rotating small hydroturbine. Journal of Physics: Conference Series, 1909(1), 1–8. https://doi.org/10.1088/1742-6596/1909/1/012044 [Google Scholar] [CrossRef]
21. Matsumoto, R., Kainuma, S., Toda, K., Yoshioka, D., Sawa, Y. (2021). Cool seal unit obstruction as an unusual cause of pump exchange of centrifugal pump EVAHEART. Artificial Organs, 45(7), 786–788. https://doi.org/10.1111/aor.13902 [Google Scholar] [PubMed] [CrossRef]
22. Wang, Y. Q., Ding, Z. W., Huo, X. W., Ji, H. L. (2018). Optimization design of centrifugal pump cavitation performance based on orthogonal test. Journal of Shaoyang University (Natural Science Edition), 15(3), 26–33. [Google Scholar]
23. Liu, H. L., Tan, M. G. (2013). Modern design methods for centrifugal pumps. Beijing, China: China Machine Press. [Google Scholar]
24. Si, Q. R., Lin, G., Yuan, S. Q., Cao, R. (2016). Multi-objective optimization on hydraulic design of non-overload centrifugal pumps with high efficiency and low noise. Transactions of the Chinese Society of Agricultural Engineering, 32(4), 69–77. [Google Scholar]
25. Wei, X. L., Xue, B. J., Zhao, Q. (2010). Optimization design of the stability for the plunger assembly of oil pumps based on multi-target orthogonal test design. Journal of Hebei University of Engineering (Natural Science Edition), 27(3), 95–99. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools