 Open Access
Open Access
ARTICLE
Averaged Dynamics of Fluids near the Oscillating Interface in a Hele-Shaw Cell
Laboratory of Vibrational Hydromechanics, Perm State Humanitarian Pedagogical University, Perm, 614990, Russia
* Corresponding Author: Denis Polezhaev. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(4), 847-857. https://doi.org/10.32604/fdmp.2024.048271
Received 02 December 2023; Accepted 12 January 2024; Issue published 28 March 2024
Abstract
The steady flow in a Hele-Shaw cell filled with fluids with a high viscosity contrast in the presence of fluid oscillations is experimentally studied. The control of oscillatory dynamics of multiphase systems with interfaces is a challenging technological problem. We consider miscible (water and glycerol) and immiscible (water and high-viscosity silicone oil PMS-1000) fluids under subsonic oscillations perpendicular to the interface. Observations show that the interface shape depends on the amplitude and frequency of oscillations. The interface is undisturbed only in the absence of oscillations. Under small amplitudes, the interface between water and glycerol widens due to mixing. When the critical amplitude is reached, the interface becomes unstable to the fingering instability: Aqueous fingers penetrate the high-viscosity glycerol and induce intensive mixing of miscible fluids and associated decay of the instability. After the disappearance of the fingers, the interface takes a U-shape in the central part of the cell. A similar effect is observed for immiscible fluids: The oscillating interface tends to bend to the side of a high-viscosity fluid. Again, when the critical amplitude is reached, the fingering instability arises at the convex interface. This paper focuses on the causes of bending of the initially undisturbed interface between miscible or immiscible fluids. For this purpose, we measure the steady flow velocity near the interface and in the bulk of a high-viscosity fluid using Particle Image Velocimetry (PIV).Keywords
Nomenclature
| b | Amplitude of oscillations, cm |
| d | Gap width of the Hele-Shaw cell, cm |
| f | Frequency of oscillations, Hz |
| h | Height of the Hele-Shaw cell, cm |
| L | Length of the tongue-like pattern, cm |
| l | Width of the Hele-Shaw cell, cm |
| t | Time, min |
| V | Velocity of the time-averaged fluid flow, cm/min |
Mass transfer in porous media is essential for many natural and technological processes, such as pollution spreading in soil [1], petroleum engineering [2,3], chemical reactions [4,5], and food processing [6,7]. It is modeled in laboratory studies by conducting experiments in radial or rectangular Hele-Shaw cells. An example is the Saffman–Taylor or viscous fingering instability that occurs when a low-viscosity fluid displaces a high-viscosity one [8–10]. Depending on the situation, viscous fingering instability can be an obstacle or a benefit. For example, in oil recovery, it is mostly undesirable. On the other hand, the intense fingering destabilization does favor fluid mixing in confined systems, such as in microfluidic devices.
Typically, a low-viscosity fluid is continuously injected from one side of a rectangular cell and displaces a high-viscosity fluid towards the other one (in a radial cell, a low-viscosity fluid is injected at the center of a cell). Therefore, the interface between two fluids also shifts from one side of a cell to the other one. In the present study, we use a different technique: The interface between miscible or immiscible fluids oscillates around the equilibrium position. This technique allows us to study the long-term dynamics of the interface between fluids.
When studying the Saffman–Taylor instability in a Hele-Shaw cell, many investigators have concluded that the dynamics of the interface between fluids is strongly dependent on the injection policy [11,12], and fluid oscillations have the potential to control the interface shape [13,14]. For example, Li et al. [11] reported that the Saffman – Taylor instability at the interface between immiscible fluids can be suppressed by injecting the displacing fluid at the rate Q ~ t−1/3 in a radial Hele-Shaw cell. Later, numerical studies of the interface dynamics between miscible fluids in a radial Hele-Shaw cell confirmed the stabilizing role of this protocol [12]. Lins et al. [13] investigated monotonic and time-dependent injection schemes for immiscible flows and demonstrated that modifying the amplitude and frequency can be used as a tool to reduce the extent of instabilities. Also, Yuan et al. [14] studied the effect of inertia in time-dependent injections and reported that instabilities may vary non-monotonically with respect to the frequency and amplitude of the injection rate.
Recently, Kozlov et al. studied the oscillatory dynamics of the interface between immiscible fluids in a rectangular Hele-Shaw cell [15,16]. According to their observations, the interface becomes unstable to viscous fingering when reaching the critical amplitude of oscillations. Also, they found that when the oscillation amplitude is not sufficient to cause viscous fingering, the initially straight interface bends towards the high-viscosity fluid. Almost immediately, a similar effect was found in the experiments with miscible fluids [17]. In the experiments with a radial Hele-Shaw cell, the oscillating interface between immiscible fluids is found to be unstable to viscous fingering but stable to bending in the subcritical region [18,19]. This effect was found within the project N 20-41-596011 (supported by RFBR and the Government of Perm Region) and needs further investigation.
This paper focuses on the causes of bending of the initially undisturbed interface between miscible or immiscible fluids. When discussing the oscillatory dynamics of the interface between immiscible fluids in a rectangular Hele–Shaw cell, the authors assume that the effect of bending is associated with dynamic contact angle hysteresis [15]. In other words, the dynamic contact angle depends on whether the interface moves towards a low-viscosity fluid or a high-viscosity one. We consider another possible explanation of the interface bending, namely the origin of the steady (time-averaged) fluid flow pulling the interface towards the high-viscosity fluid. For this purpose, we measure the steady flow velocity near the interface and in the bulk of a high-viscosity fluid using PIV.
The stability of the interface between two miscible fluids is studied in the rectangular Hele-Shaw cell of height h = 25.0 cm, width l = 14.7 cm, and gap thickness d = 0.25 cm. Also, this cell and another cell with dimensions of 34.0 cm × 9.0 cm × 0.11 cm are used in the experiments with immiscible fluids.
The cell of gap thickness d = 2.5 mm is formed by connecting two mirror-symmetric parts of an experimental setup (Fig. 1). The interface dynamics is examined through the thick glass wall 1. The gap thickness of the cell is equal to the thickness of long textolite strips 2 that are glued to one of the two glass walls.
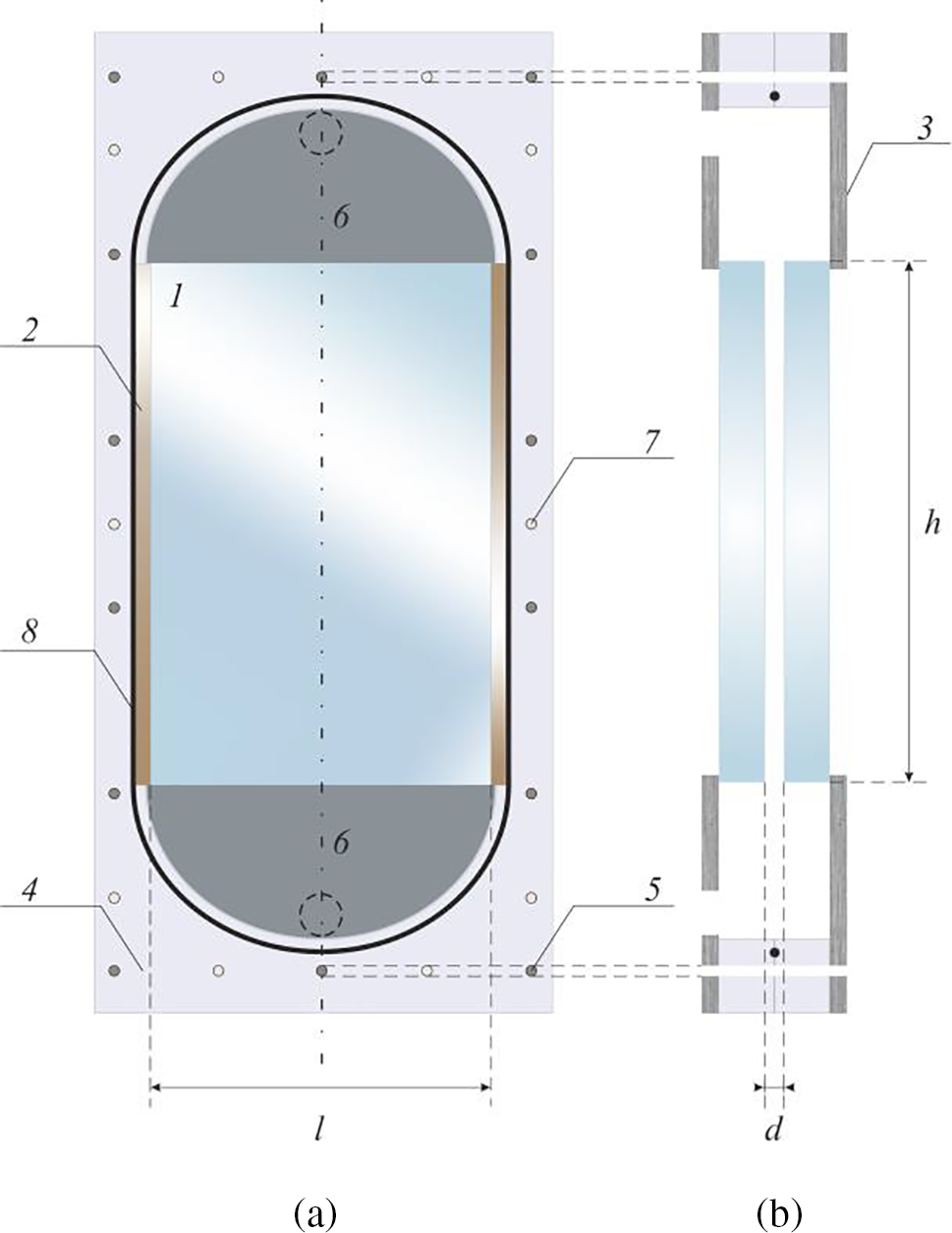
Figure 1: Sketch of Hele-Shaw cell: (a) front view and (b) cross-section of the cell
The skeleton of both parts of the cell is made of aluminum substrate 3 of thickness 6 mm. A plexiglass plate 4 with a hole cut out for the glass plates is attached to the aluminum substrate using bolts 5. The wide and deep pockets 6 are designed to distribute fluid pressure evenly across the top and bottom of the cell. Also, these pockets link the Hele-Shaw cell with the hydraulic circuit and the pump. The two parts of the cell are joined to each other by bolts 7. To ensure the tightness of the cell, a rubber seal 8 is laid around the perimeter of the cell. The design of a thin cell differs slightly from that given above; its description can be found in [15].
Fluid oscillations of the desired frequency and amplitude are provided by a hydraulic pump. The pump is connected to the Hele-Shaw cell by polypropylene pipes and two elastic membranes that separate the water in the pipes from the working fluids in the Hele-Shaw cell. The pump produces oscillatory water flow in the pipes between the membranes. When the upper membrane bends toward the upper working fluid and pushes it toward the lower fluid, the other membrane bends toward the water in the pipe, and the lower fluid flows into the vacant space, and vice versa. So, the interface between the working fluids oscillates around the equilibrium position rather than moves toward the cell edge, and the long-term dynamics of the interface can be studied. A detailed description of the technique for producing fluid oscillations using a hydraulic pump can be found in [18].
In the experiments with miscible fluids, we use glycerol with a viscosity of 940 mPa∙s and density of 1.26 g/cm3 and water colored with food coloring “Idacol” (ROHA Dyechem L.L.C., St. Petersburg, Russia) with a viscosity of 1 mPa∙s and a density of 1.0 g/cm3 at room temperature. Colored water and silicone oil with a viscosity of 103 mPa⋅s and a density of 0.96 g/cm3 are used as immiscible liquids. The surface tension between colored water and silicone oil is found to be 38 mN/m. The food coloring “Idacol” is a fine blue powder that is highly soluble in water. In all experiments, the mass concentration of the dye is less than 0.1 g/l, so that the dye does not affect the density and viscosity of water.
When the cell is filled with two fluids, the horizontal interface is formed. If the fluids are immiscible, the thickness of the interfacial layer is nearly zero. When glycerol and water come into contact, the mutual diffusion starts, so that the initial thickness of the interfacial layer is equal to several millimeters.
The Hele-Shaw cell is filled with working fluids in approximately equal volumes; therefore, the interface is located in the center of the cell at the beginning of the experiment. Observation of the interface is carried out using a digital camera which is placed opposite the cell and the backlight LED. In the series of experiments with miscible fluids, the oscillation amplitude varies from 0 to 1.3 cm while the frequency f ranges from 0 to 2 Hz. In the experiments with water and silicone oil, the amplitude varies over a range from 0 to 1.5 cm while the frequency ranges from 0 to 10 Hz.
Experiments with miscible fluids are carried out in a vertical Hele-Shaw cell thus and so glycerol is located in the lower half of the cell and water is in the upper half of it (Fig. 2a). When the pump starts working, both fluids begin to oscillate with a constant frequency f and amplitude b (here and further in the text b is half of the peak-to-peak displacement of the interface in the center of the cell). When the interface shifts in the direction of the high-viscosity glycerol, the low-viscosity water penetrates it, and the fluids mutually mix. The intensity of the mixing can be assessed by the color variations of the interfacial layer.

Figure 2: Temporal dynamics of the interface: (a) interface immediately after filling the Hele-Shaw cell with water and glycerol, (b) fingering instability at the interface of two fluids in the phase of the first maximum downward displacement; (c) mixing zone after approximately 10 cycles of oscillations
When oscillating with relatively small amplitudes, the initially thin interfacial layer transforms into a mixing zone of finite thickness. Long-term observations indicate that the interface between the water-glycerol mixture (turquoise area in Fig. 2a) and pure glycerol (white area) remains straight and undisturbed while the interfacial layer slowly thickens.
When the oscillation amplitude is large enough, the fingering instability occurs in the initial phase of the experiment (Fig. 2b). Observations show that low-viscosity “fingers” exist only for a few seconds (a few oscillation cycles) and then disappear completely. Immediately after the disappearance of the “fingers”, the interface between the water-glycerol mixture and pure glycerol takes a U-shape (Fig. 2c). A few seconds later, a tongue-like pattern appears in the central part of the interface (Fig. 3). The amplitude of fluid oscillations varies along the interface: The amplitude is maximum in the center of the cell and is minimum near the sidewalls.
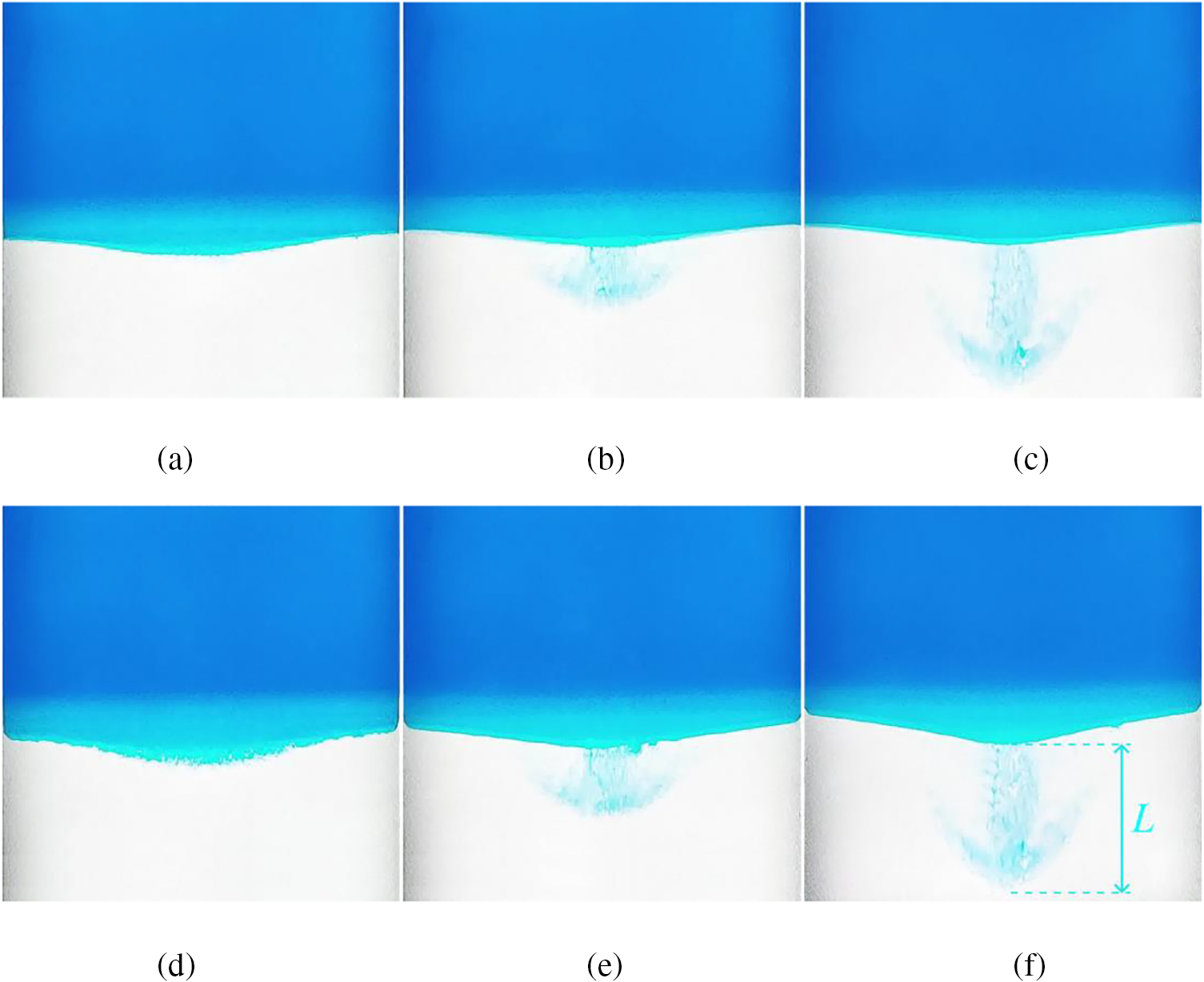
Figure 3: Temporal evolution of the U-shaped area: Photos are obtained in the phases of the maximum upward (a–c) and downward (d–f) displacement; time t = 1, 4, and 8 min is counted from the moment the “fingers” disappear; L indicates the length of the tongue-like pattern. The oscillation frequency is equal to 1.9 Hz, the amplitude of oscillations is equal to 1.2 cm
Long-term observations show that the length L of the tongue-like pattern monotonically increases over time. The downward motion of the tongue-like pattern continues until it reaches the bottom of the Hele-Shaw cell. Measurements show that the velocity of the steady flow depends on the amplitude of fluid oscillations and is of the order of one centimeter per minute (Fig. 4). The emergence of a U-shape interface and the associated tongue-like pattern will be discussed in more detail in the section “Discussion of the steady flow”.
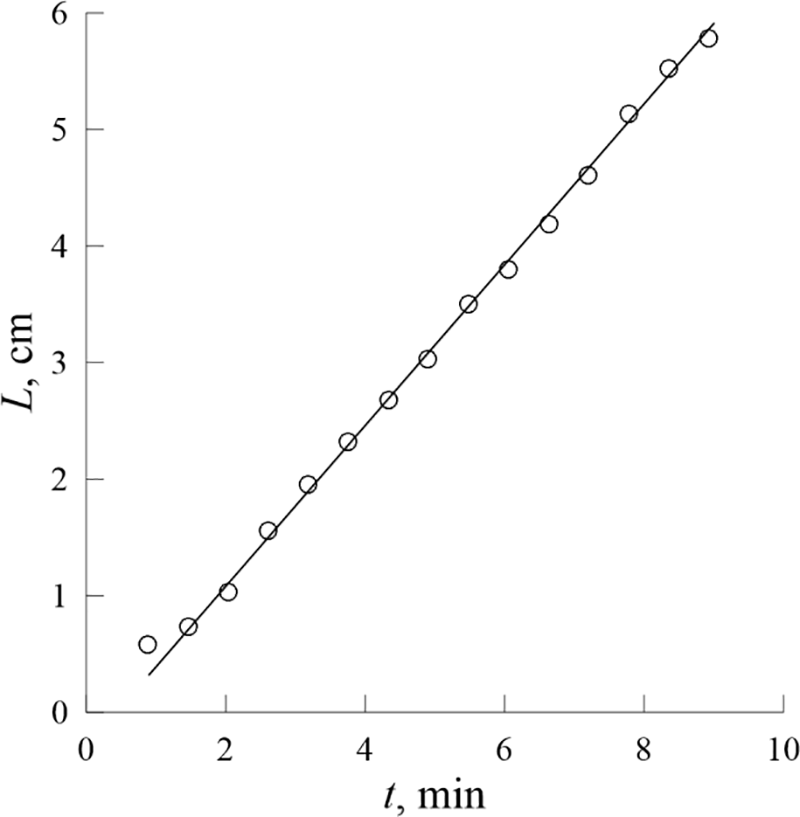
Figure 4: Dependence of the “tongue” length on time. Time is counted from the moment the aqueous fingers disappear. The frequency of oscillations is equal to 1.9 Hz and the amplitude of oscillations is equal to 1.2 cm
Experiments with immiscible fluids are performed in a horizontal cell. In the absence of oscillations, the interface between immiscible fluids is perpendicular to the cell axis and is slightly curved (Fig. 5a). When oscillating with relatively small amplitudes, the interface undergoes longitudinal oscillations and takes a U-shape bending towards the high-viscosity fluid (Fig. 5b). This effect is similar to that observed in the experiments with miscible fluids. Also, one can find that the low-viscosity fluid penetrates the high-viscosity fluid. The width of the penetration layer or in other words the length of the “tongue” is the same along the interface (thin turquoise area in Fig. 5b).
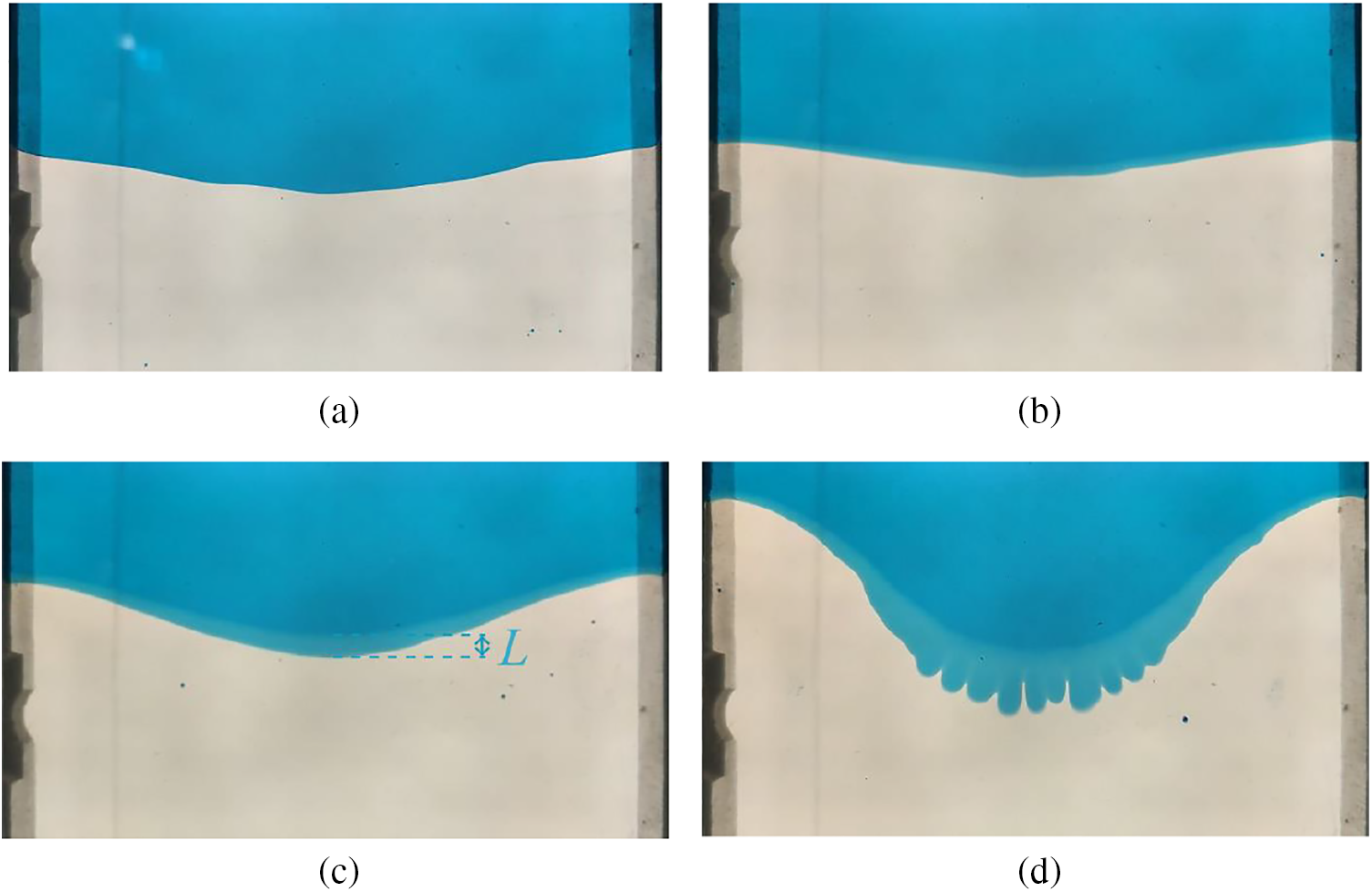
Figure 5: Photo of the interface between colored water and silicone oil (a) in the absence of oscillations; (b–d) in the phase of the maximum interface displacement towards the high-viscosity fluid at b = 0.21, 0.36, and 0.46 cm (f = 10 Hz). L indicates the length of the “tongue”
The increase in the oscillation amplitude causes the inhomogeneity of the interface oscillations: The amplitude in the center of the cell is much higher than near the sidewalls. Measurements show that the displacement of the top of the U-shaped interface increases with increasing amplitude (compare Figs. 5b and 5c). According to the observations, the light-scattering particles no longer oscillate along the axis of symmetry but move perpendicular to the bent interface.
When the oscillation amplitude is large enough, the interface becomes unstable to the fingering instability (Fig. 5d). This effect has been studied in detail in [15] and is outside the focus of this study.
4 Discussion of the Steady Flow
We conducted additional experiments to examine the steady flow field near the U-shaped interface and the tongue-like pattern using Particle Image Velocimetry. The high-viscosity fluid is seeded with neutrally buoyant high-reflective 50 μm diameter polystyrene particles. The volume fraction of tracer particles is sufficiently small (10−6) so that they do not affect the fluid flow.
A laser light sheet illuminates the fluid flow in the target area, and images are acquired using a high-speed camera (the time interval between successive images is chosen to be equal to the period of the oscillations 1/f). The velocity vectors are extracted from dozens of images analyzed by PIVlab [20].
In the experiments with miscible fluids, the cell is almost filled with high-viscosity glycerol so that the interface between glycerol and water is composed near the top of the cell. Fig. 6a demonstrates the steady flow field in glycerol in the experiments with miscible fluids. One can find that the steady vortical flows near the interface are directed from the sidewalls of the Hele-Shaw cell to its center. In the center of the cell, two vortices induce a downward flow co-directed with the “tongue” motion. At the bottom of the cell, the downward flow divides into two streams directed to the sidewalls.
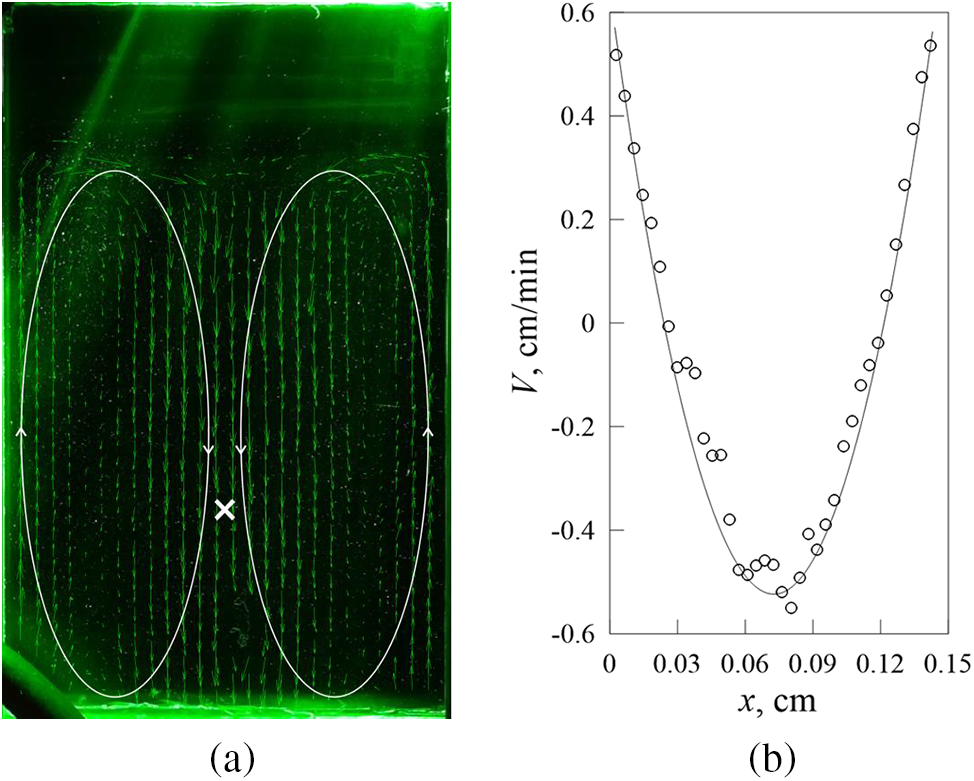
Figure 6: (a) PIV measurements of the steady flow velocity in glycerol: The cross indicates the location where the steady flow velocity is measured; (b) vertical component of the steady flow velocity measured at a distance of 13 cm from the initial position of the interface between water and glycerol (the distance x is measured from the left side of the Hele-Shaw cell). The oscillation frequency is equal to 2.0 Hz, the amplitude of oscillations is equal to 1.2 cm
Fig. 6b shows the results of measuring the vertical velocity of the steady fluid flow in the cross-section of the cell at a distance of 13 cm from the initial position of the interface between water and glycerol. It is clear that the flow is symmetric relative to the vertical axis of the cell. The fluid velocity is directed in opposite directions in the center and near the sidewalls of the cell but is the same in magnitude. A comparison of measurement results of the velocity of the “tongue” growth (Fig. 4) and the velocity of the downward flow in the center of the cell (Fig. 6b) indicates that these two phenomena are linked.
Experiments with immiscible fluids show that the steady flow field of a high-viscosity fluid depends on the oscillation amplitude. When the amplitude is small, we observe a vortical pair with vorticity opposite to that of the vortical flow generated in the experiments with miscible fluids (Fig. 7a). As the amplitude increases, the initial vortices decrease in size and move away from the interface. Instead, a new pair of vortices appear near the interface. The rotation sense of that pair of secondary vortices is opposite to the rotation sense of the pair of primary vortices (Fig. 7b). At large amplitudes, secondary vortices expel primary vortices from the cell, and the flow field becomes similar to that observed in the experiments with miscible fluids (compare Figs. 6a and 7c).

Figure 7: Steady flow velocity field of silicone oil PMS-1000 (a) in a horizontal Hele-Shaw cell and (b, c) in a vertical one at increasing amplitude (oscillation frequency f = 2.5 Hz)
Fig. 8 shows the steady flow velocity at two different points at the axis of symmetry located opposite the primary and secondary vortices in dependence on the oscillation amplitude. At small amplitudes, we observe only primary slowly rotating vortices (circles at b < 0.5 cm). On the contrary, there are only rapidly rotating secondary vortices at large amplitudes (squares at b > 1 cm).
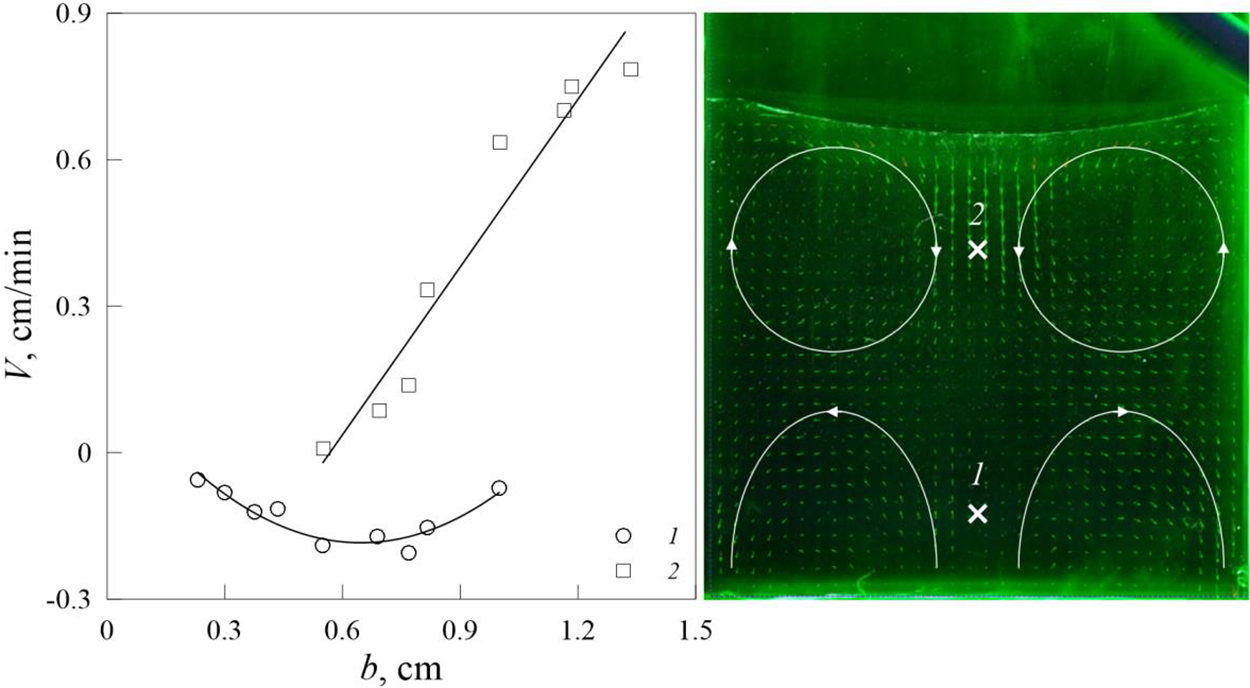
Figure 8: Dependence of the steady flow velocity of silicone oil on the oscillation amplitude at points 1 and 2 at the axis of symmetry of the cell (f = 2.5 Hz). The calculation points are located opposite the centers of the vortices
Thus, the bending of the interface and the emergence of the vortical flow are related to each other. It is noteworthy that the interface between immiscible fluids retains U-shape only under the condition of oscillations: The interface becomes straight when oscillations are turned off. This is not true in the case of miscible fluids: The U-shaped interface remains stable after the oscillations have disappeared.
When discussing experiments with immiscible fluids, Vlasova et al. assumed that the interface bending related to the hysteresis of the dynamic angle in the course of the oscillation cycle [15]. However, the researchers did not measure the instantaneous value of the contact angle and could not verify the hypothesis by observations. The hypothesis was motivated by previous findings. Namely, Zhang et al. theoretically analyzed the fluid film deposited by an oscillating fluid meniscus in a capillary tube and revealed an inharmonic variation of both the meniscus curvature and the contact angle [21].
Here, we consider another possible explanation of the interface bending, namely the origin of the time-averaged flow pulling the interface towards the high-viscosity fluid. However, it turns out that the origin of the time-averaged fluid flow remains unclear and requires further investigation. We believe that the steady fluid flow is generated due to amplitude heterogeneity of the interface oscillations [22]: The amplitude of the interface oscillations in the center of the cell usually is greater than the amplitude of the interface oscillations near the sidewalls. If this is so, the steady flow is a consequence of the interface bending but not the reason for it.
The averaged dynamics of two fluids with a high viscosity contrast in a Hele-Shaw cell filled in the presence of fluid oscillations is experimentally studied. Miscible and immiscible pairs of fluids are considered. It is found that the oscillating interface tends to bend to the side of a high-viscosity fluid. The interface bending is accompanied by the emergence of the vortical flow of a high-viscosity fluid. We observe one pair of vortices under the oscillating interface between miscible fluids in the studied range of amplitude and frequency of oscillations. The sign of the vorticity is such that it induces a downward steady flow along the cell axis of symmetry. In the experiments with immiscible fluids, the number of vortices and the sense of rotation depend on the oscillation amplitude. When the curvature of the interface is large, the direction of the steady flow coincides with the direction of the high-viscosity fluid flow in the experiments with miscible fluids.
We suggest that the steady fluid flow is generated due to the amplitude heterogeneity of the interface oscillations. The steady downward flow induces the growth of a tongue-like pattern in the center of the cell filled with miscible fluids.
In conclusion, we believe that the origin of time-averaged flow is not the cause but the consequence of the interface bending. A side effect of the emergence of the steady vortical flow is the growth of a tongue-like pattern at the interface between miscible fluids. There is another hypothesis about the origin of the interface bending that relates to the hysteresis of the dynamic angle in the course of the oscillation cycle [15]. Our further efforts will be made to study the effect of dynamic contact angle on the steady flow field and the shape of the interface between oscillating fluids.
Acknowledgement: The authors are grateful to Professor Victor Kozlov for fruitful discussions.
Funding Statement: This research was financially supported by the Ministry of Education of the Russian Federation (Project KPZU–2023–0002).
Author Contributions: Study conception and design: Olga Vlasova and Denis Polezhaev; Data collection: Olga Vlasova, Anastasia Bushueva, and Denis Polezhaev; Analysis and interpretation of results: Olga Vlasova and Denis Polezhaev; Draft manuscript preparation: Olga Vlasova and Denis Polezhaev. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Ragui, K., Boutra, A., Benkahla, Y. (2016). On the validity of a numerical model predicting heat and mass transfer in porous square cavities with a bottom thermal and solute source: Case of pollutants spreading and fuel leaks. Mechanics and Industry, 17(3), 311. [Google Scholar]
2. Afzali, S., Rezaei, N., Zendehboudi, S. (2018). A comprehensive review on enhanced oil recovery by water alternating gas (WAG) injection. Fuel, 227, 218–246. [Google Scholar]
3. Lake, L. W. (1989). Enhanced oil recovery, pp. 550. New Jersey, USA: Prentice-Hall. [Google Scholar]
4. Neffah, Z., Kahalerras, H., Fersadou, B. (2018). Heat and mass transfer of a non-newtonian fluid flow in an anisotropic porous channel with chemical surface reaction. Fluid Dynamics & Materials Processing, 14(1), 39–56. https://doi.org/10.3970/fdmp.2018.014.039 [Google Scholar] [CrossRef]
5. De Wit, A. (2020). Chemo-hydrodynamic patterns and instabilities. Annual Review of Fluid Mechanics, 52, 531–555. [Google Scholar]
6. Donsì, F., Ferrari, G., Pataro, G. (2010). Applications of pulsed electric field treatments for the enhancement of mass transfer from vegetable tissue. Food Engineering Reviews, 2, 109–130. [Google Scholar]
7. Bhargava, N., Mor, R., Kumar, K., Sharanagat, V. (2021). Advances in application of ultrasound in food processing: A review. Ultrasonics Sonochemistry, 70, 105293. [Google Scholar] [PubMed]
8. Homsy, G. M. (1987). Viscous fingering in porous media. Annual Review of Fluid Mechanics, 19(1), 271–311. [Google Scholar]
9. Suzuki, R., Nagatsu, Y., Mishra, M., Ban, T. (2020). Phase separation effects on a partially miscible viscous fingering dynamics. Journal of Fluid Mechanics, 898, A11. [Google Scholar]
10. Sorbie, K., Al Ghafri1, A., Skauge, A., Mackay, E. (2020). On the modelling of immiscible viscous fingering in two-phase flow in porous media. Transport in Porous Media, 135(2), 331–359. [Google Scholar]
11. Li, S., Lowengrub, J., Fontana, J., Palffy-Muhoray, P. (2009). Control of viscous fingering patterns in a radial Hele-Shaw cell. Physical Review Letters, 102(17), 174501. [Google Scholar] [PubMed]
12. Chen, C. Y., Huang, C. W., Wang, L. C., Miranda, J. (2010). Controlling radial fingering patterns in miscible confined flows. Physical Review E, 82(5), 056308. [Google Scholar]
13. Lins, T. F., Azaiez, J. (2016). Flow instabilities of time-dependent injection schemes in immiscible displacements. The Canadian Journal of Chemical Engineering, 94(11), 2061–2071. [Google Scholar]
14. Yuan, Q., Azaiez, J. (2015). Inertial effects in cyclic time-dependent displacement flows in homogeneous porous media. The Canadian Journal of Chemical Engineering, 93(8), 1490–1499. [Google Scholar]
15. Kozlov, V., Vlasova, O. (2022). Oscillatory dynamics of immiscible liquids with high viscosity contrast in a rectangular Hele-Shaw channel. Physics of Fluids, 34(3), 032121. [Google Scholar]
16. Vlasova, O., Kozlov, V. (2021). Oscillatory dynamics of two liquids interface in straight narrow gap. Journal of Physics: Conference Series, 1809(1), 012028. [Google Scholar]
17. Bushueva, A., Melekhina, U., Polezhaev, D. (2022). Experimental study of the stability of an oscillating interface between miscible fluids in a vertical Hele-Shaw cell. Proceedings of Perm Hydrodynamics Scientific Readings, pp. 100–102 (In Russian). Perm, Russia. [Google Scholar]
18. Kozlov, V., Karpunin, I., Kozlov, N. (2020). Finger instability of oscillating liquid-liquid interface in radial Hele-Shaw cell. Physics of Fluids, 32(10), 102102. [Google Scholar]
19. Karpunin, I., Kozlov, V. (2023). Oscillatory dynamics of a fluid interface in a radial Hele-Shaw cell. Journal of Applied Mechanics and Technical Physics, 64(3), 413–422. [Google Scholar]
20. Thielicke, W., Sonntag, R. (2021). Particle image velocimetry for MATLAB: Accuracy and enhanced algorithms in PIVLab. Journal of Open Research Software, 9(1), 12. [Google Scholar]
21. Zhang, X., Nikolayev, V. (2021). Liquid film dynamics with immobile contact line during meniscus oscillation. Journal of Fluid Mechanics, 923, A4. [Google Scholar]
22. Batchelor, G. K. (1967). An introduction to fluid dynamics. Cambridge, UK: Cambridge University Press. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools