Steady-State Solution of MHD Flow with Induced Magnetic Field

1  Introduction

MHD has been recognized as a significant area of research due to its multiple applications in astrophysical and geophysical problems over the past several decades. Flows perturbed by external magnetic forces over plates play a central role in various industrial operations, mechanical engineering, civil engineering, and biomechanical processes. The buoyancy effect of thermal and mass diffusion facilitates simultaneous transport processes in both industry and nature. Free convection fluid flows over vertical walls, considering magnetic forces on the transport process, has significant applications in nuclear engineering, particularly in the cooling of reactors. There are myriad uses of transfer phenomena in polymer production and food processing industries. The generation of an IMF catalyzes the process of removing contaminants from crude oil.

In recent decades, numerous studies have focused on solving MHD equations to obtain exact solutions using various advanced techniques. These approaches include group analysis, symmetry methods, invariant solutions, and Laplace integral transformations, which researchers have extensively employed to tackle the complexities of MHD equations [1–3]. Parida et al. [4] analyzed the behavior of nonlinear heat transfer flow with a similarity solution technique numerically. The results from quasilinear shooting methods reveal an increase in temperature and velocity with the rise of the temperature ratio parameter. Sehra et al. [5] studied the MHD flow of time-varying random shear stresses, along with the impacts of molecular diffusivity by employing the Laplace transformation (LT) technique. They observed an increase in temperature when they ignored the heat source parameter. An investigation of MHD flow over a moving plate was presented by Ellahi et al. [6] to analyze the behavior of entropy generation under slip conditions. The exact closed-form solution of thermally radiative MHD flow with constant fluxes for heat energy was described by Kumar Pandit et al. [7]. They reported that mass diffusion reduces fluid velocity, whereas thermal radiation has the opposite effect throughout the BL region. Hussain et al. [8] studied closed-form solutions for MHD oscillatory fluid flow by employing periodically changing pressure gradients. This study on Burger’s fluid noted that the response of the magnetic field on Oldroyd-B fluid is less prominent than that on Burger’s fluid.

Chen [9] scrutinized the dissipative criteria for MHD conductive fluid flow adjacent to a vertical boundary using an efficient solving technique known as FDM of implicit type. They reported that the skin friction, Nusselt number, and Sherwood number decreased when applying a magnetic field. Incorporating the iterative shooting procedure of the Nachtsheim-Swigert type, Alam et al. [10] computed the Soret impact regarding heat generation on the MHD flow under the employment of a porous medium. Pal et al. [11] modeled and solved a flow problem using the Runge-Kutta-Fehlberg method on a stretching sheet while considering first order chemical reaction. They reported that the Dufour effect significantly influences the temperature profiles. Javaherdeh et al. [12] studied how natural convection fluid flows near a boundary surface, using a power law to describe the changes in temperature and concentration. This study noted that the higher the Grashof number, the greater the flow velocity. Aslam et al. [13] investigated hybrid numerical methods based on machine learning to study water-based nanofluids. They concluded that the artificial neural network-based numerical approach is more effective than traditional slow analytic and numerical methods. Reddy et al. [14] conducted a study on the thermal diffusion of MHD radiative fluid flow under the assumption of a vertical surface. Several investigations [15–18] have extensively utilized explicit FDM techniques to solve complex flow problems. These studies have demonstrated the effectiveness and reliability of FDM, establishing it as a scientifically sound and robust method for addressing a wide range of fluid dynamics challenges.

Researchers have studied IMF phenomena for decades, utilizing them to advance technologies such as plasma physics, astrophysics, and electromagnetic propulsion. Haque et al. [19] analyzed the Soret impact on MHD flow along with magnetic field induction under the arrangement of a vertical porous plate. Ahmed et al. [20] delineated chemically reacting flow on the cooling case with IMF. Their results described both the average and local profiles, demonstrating a decrease in local and average shear stresses with the rise of the porous medium and magnetic parameters. Kumar et al. [21] substantially inquired about magnetic field induction, observing a decrease in velocity with the magnetic field parameter. A stable and converging solutions-based approach to MHD flow on suction motion control has been scrutinized by Poddar et al. [22]. This model reported a decrease in flow velocity as the suction impact amplified. The examination by Shankar Goud et al. [23] reported numerical results of microchannel flow, noting a significant decrease in the flow volume rate as the strength of the Hartmann number intensified. Kumar [24] demonstrated an analytical report of MHD flow between insulated walls, reporting an increase in velocity as radiation occurs during BL enhancement. Khan et al. [25] explored the IMF response to water-based GO (graphene oxide) flow at a stationary point, noting a 4.18% increase in shear stress with higher nanoparticle concentration. Mahato et al. [26] employed the shooting method to investigate the flow problem of Casson rheology on a stretching wall with an active chemical reaction. Recently, a numerical simulation was conducted by Bilal et al. [27] to assess the impact of IMF on the thermally radiative channel flow of Sisko nanofluid, noting that an increase in heat radiation may reduce temperature distribution, thereby enhancing cooling effects.

Many physics and engineering operations have vital applications for radiation effects. Thermal radiation has meaningful applications in numerous industrial processes. Patel [28] established the conditions for BL with symmetry and asymmetry to inspect the microrotation of the vertically subjected micropolar fluid flow, mentioning heat energy production in the BL zone with the rise of thermal radiation. Kho et al. [29] considered constant wall temperature to analyze the radiative response on Casson rheological flow, reporting that the nanofluidic temperature inside the BL increased under the influence of higher values of the Casson parameter. Ali et al. [30] utilized copper particles in a water-based nanofluid to analyze the flow’s thermophysical properties, noting that as the magnetic field intensified, the velocity decreased. Zigta [31] used the perturbation method to analyze channel Couette flow under the assumption of oscillation and suction on the channel wall, noting that the radiation impact tends to boost the BL energy. Later, Zigta [32] conducted a theoretical investigation of blood flow under the influence of a time-varying magnetic field, considering time-dependent blood concentration and showing diminishing behavior with rising settings of the chemical reaction. Many other researchers have studied different flow structures with thermal radiation, as noted in [33–37].

As reviewed above, MHD flow models with the IMF have been incorporated to explore their effects on the flow of various scaled systems. Based on these contextual discussions, the authors propose a numerical inquiry into unsteady viscous incompressible MHD radiative and dissipative fluid flow over a semi-infinite vertical plate with magnetic field induction, the Dufour effect, and the Soret effect. The numerical inquiry has been conducted using explicit FDM under the control of relevant stability restrictions and boundary conditions. Along with substantial flow analysis, this study aims to address the following vital research questions:

•   How does the flow behave to attain a steady state?

•   How does the IMF influence the flow over the plate within the BL?

•   What are the reasons behind the trends of profiles with all the pertinent parameters?

2  Mathematical Formulation

The transient two-dimensional flow of radiative and dissipative nature over a semi-infinite vertical plate has been considered with a relatively high concentration level of foreign mass. The schematic structure of the flow problem is physically demonstrated in Fig. 1. The variation of density in the buoyancy terms is taken into account, while the other characteristics of the fluid remain constant. With a familiar introduction to coordinates (x′,y′,z′), where the x′-axis is modeled in the upward direction along the boundary and perpendicular to the x′-axis, y′-axis is modeled. At the wall, the heat flux (−κ∂T′∂y′)=q, and species mass flux (−Dm∂C′∂y′)=Γ are set to be constant. A uniform magnetic field H0′ is imposed perpendicular to the plate. The constant magnetic field causes the generation of magnetic field induction H′=(Hx′′,Hy′′,0), while Maxwell’s divergence equation ∇.H′=0 gives Hy′′=H0′ (constant). The divergence equation of electric charge density ∇.J=0 generates Jy′′=0, where J′=(Jx′′,Jy′′,Jz′′). No chemical reaction has been deemed for the fluid with foreign mass. T′ and T∞′ are the temperatures inside and outside the BL, while C′ and C∞′ are the concentrations inside and outside the BL.

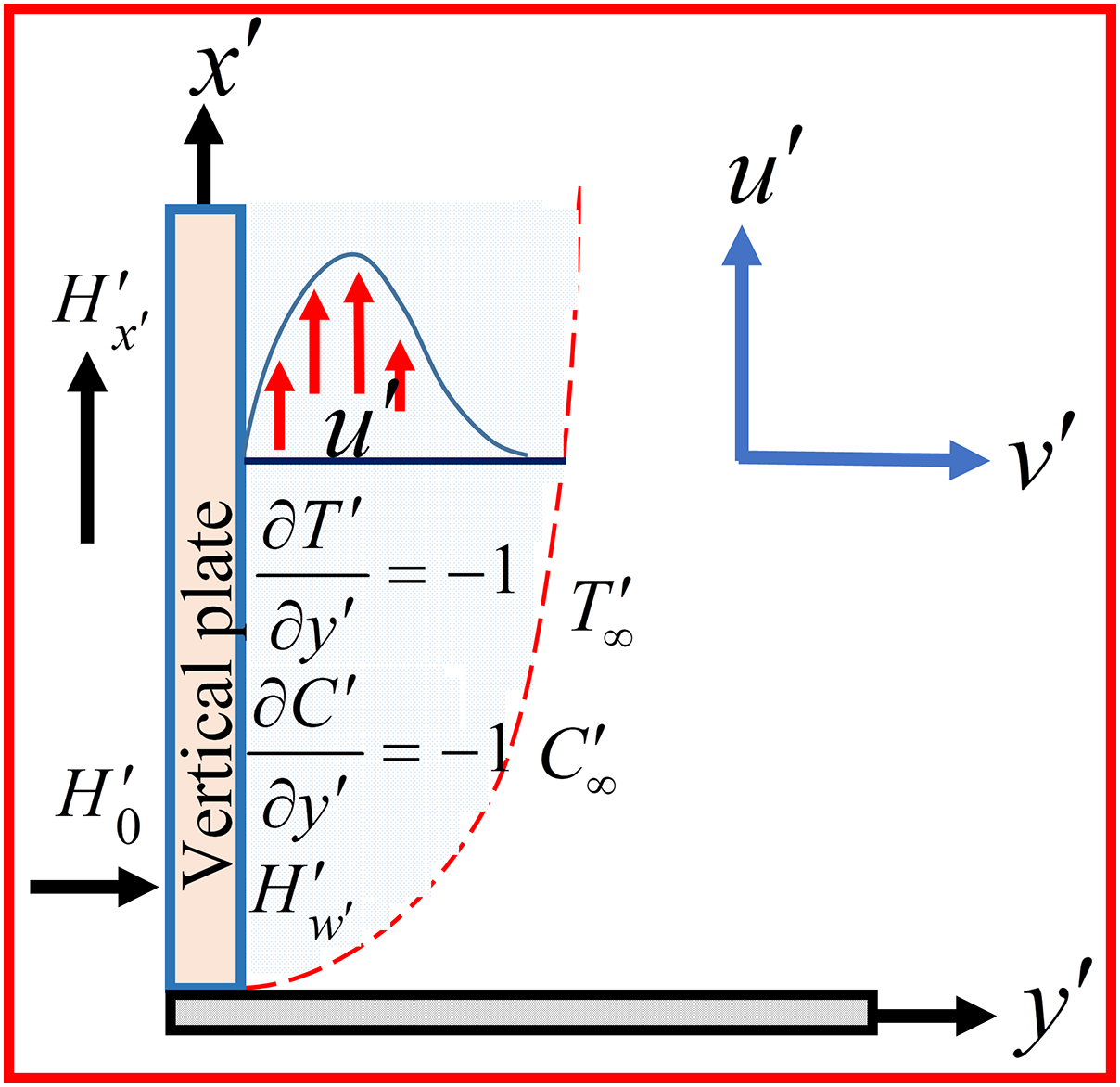
Figure 1: Physical scheme and coordinate system

Using the typical BL approximations, the prevailing system of coupled nonlinear PDEs for MHD flow, IMF, temperature, and concentration can be expressed as follows, using conventional notation along with the work of Ahmed et al. [20] and Poddar et al. [22].

The continuity equation:

∂u′∂x′+∂v′∂y′=0.(1)

The momentum equation:

∂u′∂t′+u′∂u′∂x′+v′∂u′∂y′=υ∂2u′∂y′2+gβ(T′−T∞′)+gβ∗(C′−C∞′)+μeρH0′∂Hx′′∂y′.(2)

The magnetic induction equation:

∂Hx′′∂t′+u′∂Hx′′∂x′+v′∂Hx′′∂y′=Hx′′∂u′∂x′+H0′∂u′∂y′+1σμe∂2Hx′′∂y′2.(3)

The energy equation:

∂T′∂t′+u′∂T′∂x′+v′∂T′∂y′=κρcp∂2T′∂y′2+1ρcpσ(∂Hx′′∂y′)2+υcp(∂u′∂y′)2+DmkT′cscp∂2C′∂y′2+16σ∗T∞′33k∗ρcp∂2T′∂y′2.(4)

The concentration equation:

∂C′∂t′+u′∂C′∂x′+v′∂C′∂y′=Dm∂2C′∂y′2+DmkT′Tm′∂2T′∂y′2.(5)

The Rosseland approximation approximates the radiative heat flux as qa=−4σ∗3k∗∂T′4∂y′ (Kumar [24]) and then the familiar Taylor series expansion for T′4 gives qa=−16σ∗T∞′33k∗∂T∂y.

The settings for initial and boundary conditions are:

t′≤0;u′=0,v′=0,Hx′′=0,T′→T∞′,C′→C∞′ everywhere}.(6)

t′>0;u′=0,v′=0,Hx′′=0,T′→T∞′,C′→C∞′ at x′=0u′=0,v′=0,Hx′′=Hw′,∂T′∂y′=−qκ,∂C′∂y′=−ΓDm at y′=0u′=0,v′=0,Hx′′=0,T′→T∞′,C′→C∞′ at y′→∞}.(7)

The dimensional agreement among the governing equations is compulsory since the equations have been solved simultaneously. The preferable normalization quantities for making the nonlinear PDEs dimensionless have been introduced as follows:

t=υt′L2,x=x′L,y=y′L,u=u′Lυ,v=v′Lυ,T=T′−T∞′qLκ,C=C′−C∞′ΓLDm,Hx=μeρHx′′Lυ.(8)

After normalization, the prevailing system of PDEs with dimensional agreement is:

∂u∂x+∂v∂y=0,(9)

∂u∂t+u∂u∂x+v∂u∂y=T+C+∂2u∂y2+M∂Hx∂y,(10)

∂Hx∂t+u∂Hx∂x+v∂Hx∂y=Hx∂u∂x+M∂u∂y+Pm∂2Hx∂y2,(11)

∂T∂t+u∂T∂x+v∂T∂y=(1+R∗Pr)∂2T∂y2+EcPm(∂Hx∂y)2+Ec(∂u∂y)2+Du∂2C∂y2,(12)

∂C∂t+u∂C∂x+v∂C∂y=1Sc∂2C∂y2+So∂2T∂y2.(13)

The non-dimensional procedure introduced the characteristic length scale as:

L=(υ2gβ(qκ))14=(υ2gβ∗(ΓDm))14,

The dimensionless initial and boundary conditions are:

t≤0;u=0,v=0,Hx=0,T→0,C→0 everywhere},(14)

t>0;u=0,v=0,Hx=0,T→0,C→0 at x=0u=0,v=0,Hx=b=1,∂T∂y=−1,∂C∂y=−1 aty=0u=0,v=0,Hx=0,T→0,C→0 at y→∞},(15)

where b=Hw′Lυμeρ, (say).

The dimensionless parameters are:

M=H0′Lυμeρ (magnetic parameter), Pr=υcpρκ (Prandtl number), Pm=1υσμe (magnetic Prandtl number), R∗=16σ∗T′3∞3κk∗ (radiation parameter), Ec=υ2cp(qLκ)L2 (Eckert number), Du=DmkT′(ΓLDm)υcscp(qLκ) (Dufour number), Sc=υD∗ (Schmidt number), So=DmkT′(qLκ)υTm′(ΓLDm) (Soret number).

3  Quantities of Significance

Shear stress, along with current density, are key terms of significant physical interest in various engineering operations. The shear stress coefficient indicates the characteristics of the fluid layer on the boundary (plate). The dimensionless form of the local shear stress, τL=(∂u∂y)y=0 and the dimensionless form of the local current density, JL=−(∂Hx∂y)y=0.

4  Numerical Calculation Technique

The set of Eqs. (9)–(13) has been solved using the FDM of explicit type. The inward BL zone is discretized with the backward difference technique for the derivative of unit order, while the larger order derivative has been calculated using the central difference technique [15,16]. In the FDM schemes, the following discretized equations have been used [17–20].

∂u∂t=ui,j∗−ui,jΔt,∂u∂x=ui,j−ui−1,jΔx,∂u∂y=ui,j−ui,j−1Δy,∂2u∂y2=ui,j+1−2ui,j+ui,j−1(Δy)2,

∂T∂t=Ti,j∗−Ti,jΔt,∂T∂x=Ti,j−Ti−1,jΔx,∂T∂y=Ti,j−Ti,j−1Δy,∂2T∂y2=Ti,j+1−2Ti,j+Ti,j−1(Δy)2,

∂C∂t=Ci,j∗−Ci,jΔt,∂C∂x=Ci,j−Ci−1,jΔx,∂C∂y=Ci,j−Ci,j−1Δy,∂2C∂y2=Ci,j+1−2Ci,j+Ci,j−1(Δy)2,

∂Hx∂t=Hxi,j∗−Hxi,jΔt,∂Hx∂x=Hxi,j−Hxi−1,jΔx,∂Hx∂y=Hxi,j−Hxi,j−1Δy,

∂2Hx∂y2=Hxi,j+1−2Hxi,j+Hxi,j−1(Δy)2,∂v∂y=vi,j−vi,j−1Δy.

The time-domain values are computed such that the previous values are used to enumerate the new time-step values. The length of the vertical surface (plate) is taken as x(=100)max, and the width of the flow zone within the BL is regarded as y(=15)max. This is a random choice based on the assumption that the height of the plate is larger. A 200×200 meshes in the flow zone have been created in the directions of x and y, respectively, to perform the numerical computations. This mesh layout is illustrated in Fig. 2. With a minimal time difference Δt=0.001, The uniform cell shapes are counted for the flow region as

Δx=0.50(0≤x≤100),

Δy=0.075(0≤y≤15).

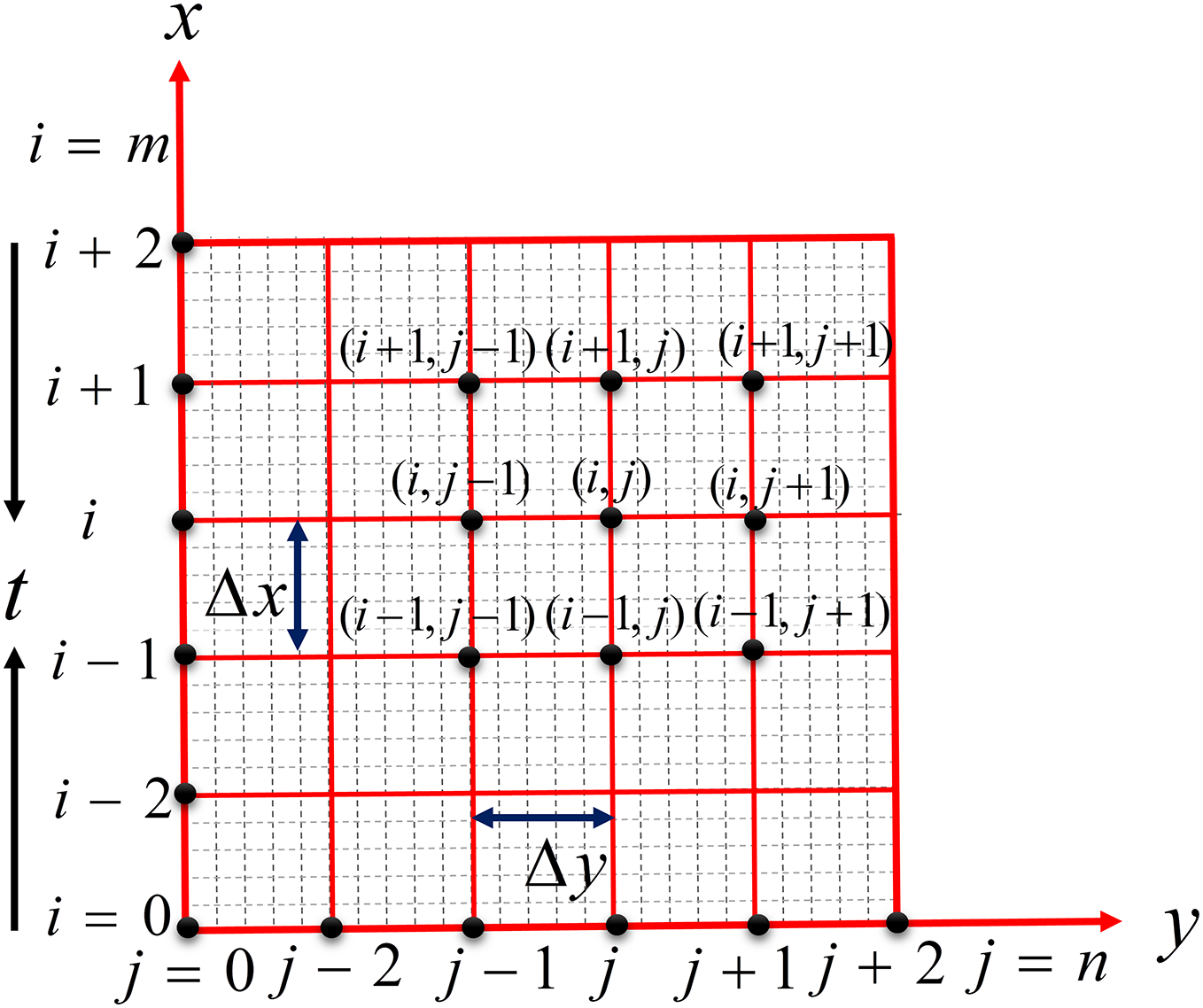
Figure 2: Layout of meshes [36]

Although FDM is a well-established technique to solve a set of nonlinear PDEs, it can still introduce some numerical errors. This article reports a sensitivity test on meshes to minimize this possibility in Section 6.1. Further, the analysis of stable and converging solutions in Section 5 provides a secondary source for the accuracy of the solutions. Round-off errors might occur since numerical calculations are performed with finite precision.

5  Stability and Convergence

The investigation of FDM would remain inefficient without testing the stability and convergence criteria. The analysis does not involve Eq. (9) because Δt is not a part of it. Fourier’s expansions for u,Hx,T, and C at t=0 in Eqs. (10)–(13) led us to determine the stability and convergence criteria for the numerical schemes by following the detailed process given by Mondal et al. [17]. It is essential to ensure that the steady-state solutions are converging and stable. The converging and stability conditions for the present solution schemes are:

uΔtΔx−|v|ΔtΔy+2Δt(Δy)2≤1,(16)

uΔtΔx−|v|ΔtΔy+Pm2Δt(Δy)2≤1,(17)

uΔtΔx−|v|ΔtΔy+(1+R∗Pr)2Δt(Δy)2≤1,(18)

uΔtΔx−|v|ΔtΔy+1Sc2Δt(Δy)2≤1.(19)

On setting, Δt=0.001, Δy=0.075 along with the initial conditions, generate the elementary constraints as Pm≤2.82,0.00≤R∗≤20,0.35≤Pr≤7.46, and Sc≥0.35 with Ec=0.01.

6  Results and Discussion

This work numerically scrutinizes the steady-state solution of MHD dissipative and radiative flow with magnetic field induction over a semi-infinite vertical plate. Additionally, the high concentration level of foreign mass has also been considered. Under the necessary BL approximations, the governing equations are simplified. The execution of all numerical calculations aims to determine the dimensionless velocity u, IMF Hx, temperature T, and concentration C along with high physically interesting quantities, local shear stress τL, and local current density JL. A competent mesh resolution has been established for calculating the flow profiles and constructing the elementary steady state. Furthermore, the numerical codes of MATLAB R2015a have been verified through the simulation software studio developer FORTRAN 6.6a. The numerical results have been recorded for the magnetic parameter (M), magnetic Prandtl number (Pm), Dufour number (Du), radiation parameter (R∗), Prandtl number (Pr), Schmidt number (Sc), Eckert number (Ec)and Soret number (So). Numerical values of τL and JL for different parameters are reported in Table 1. A compliance check of the current results with published investigations has been demonstrated in Table 2 with the magnetic parameter (M).

6.1 Searching Mesh Agreement

Although FDM is an effective technique to solve complex sets of PDEs, it may introduce truncation errors or unstable solutions. The stability of the model equations has been analyzed in Section 5 to address these issues. Some values of meshes have been trialed to find the best fit for numerical estimations, such as m=180,n=180; m=200,n=200, and m=220,n=220. This experimentation has been illustrated graphically for velocity and IMF in Fig. 3a,b, by taking the values M=0.10,Pm=1.50,R∗=0.20, Ec=0.01,Du=0.30,So=0.40 and Sc=0.60 at time t=22 (steady-state). It can be summarized by observing the resulting graphs (Fig. 3a,b) that the profiles are characteristically converging and smooth. Further computations will thus be based on the 200×200 meshes.

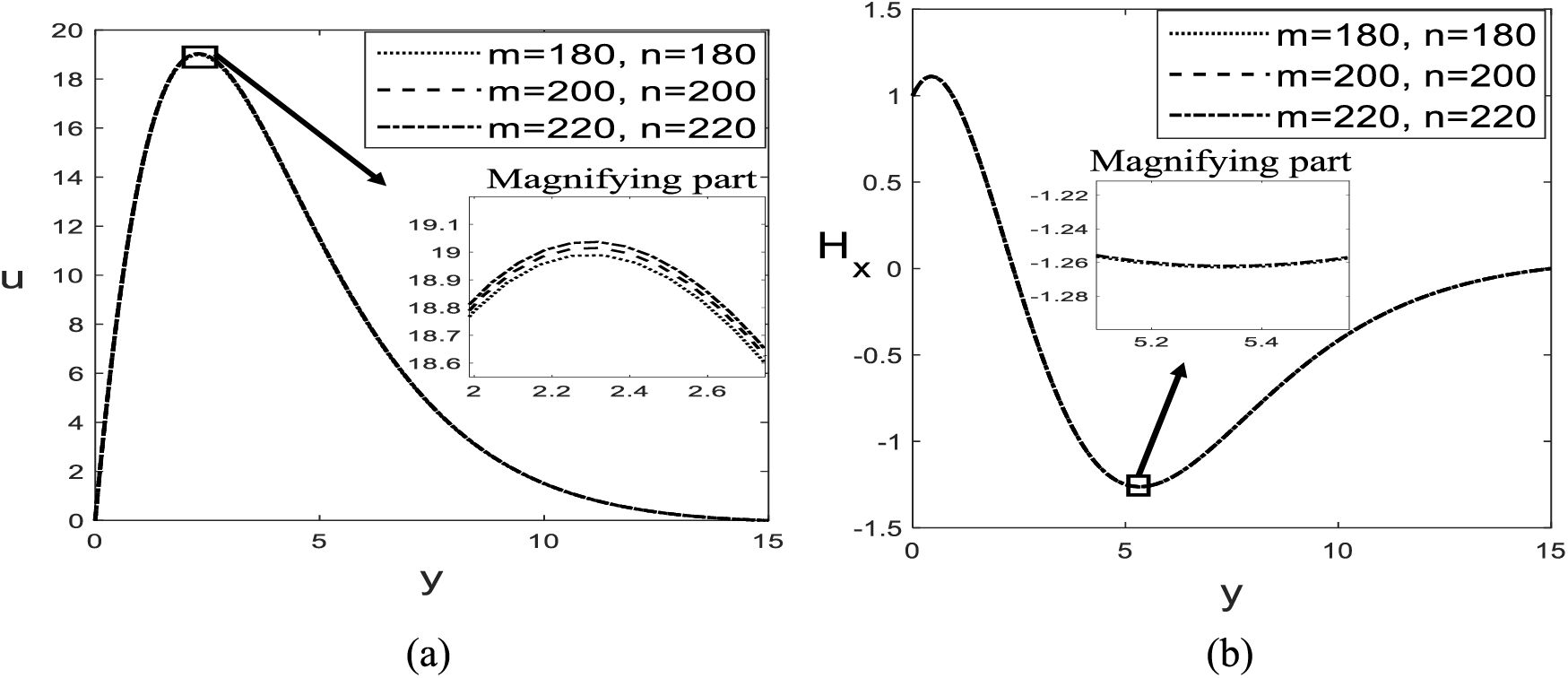
Figure 3: Mesh agreement for (a) velocity and (b) induced magnetic field

6.2 Searching Steady State

The search for a steady state leads us to experiment on all the profiles. This is done by taking specific quantities as t=2,4,6,8,10,12,14,16,18,20,22 and 24. The final results have been demonstrated through Fig. 4a–d, with M=0.10,Pr=0.71,Pm=1.50, R∗=0.20, Ec=0.01,Du=0.30,So=0.40 and Sc=0.60. A judgment is made by paying attention to the resulting graphs (Fig. 4a–d) that the computations for the IMF express a tiny change after t=18, whereas velocity and temperature reveal insignificant changes after t=12. The concentration profile demonstrates negligible variation after t=10. The negligible variation for velocity and temperature has been marked at t=14, whereas this state is acquired for the IMF after t=22. Thus, the steady-state solutions for all the variables at t=22 are essentially taken for calculations. It is worth noting that the profile of the IMF is comparatively slower to reach a steady state than other profiles.

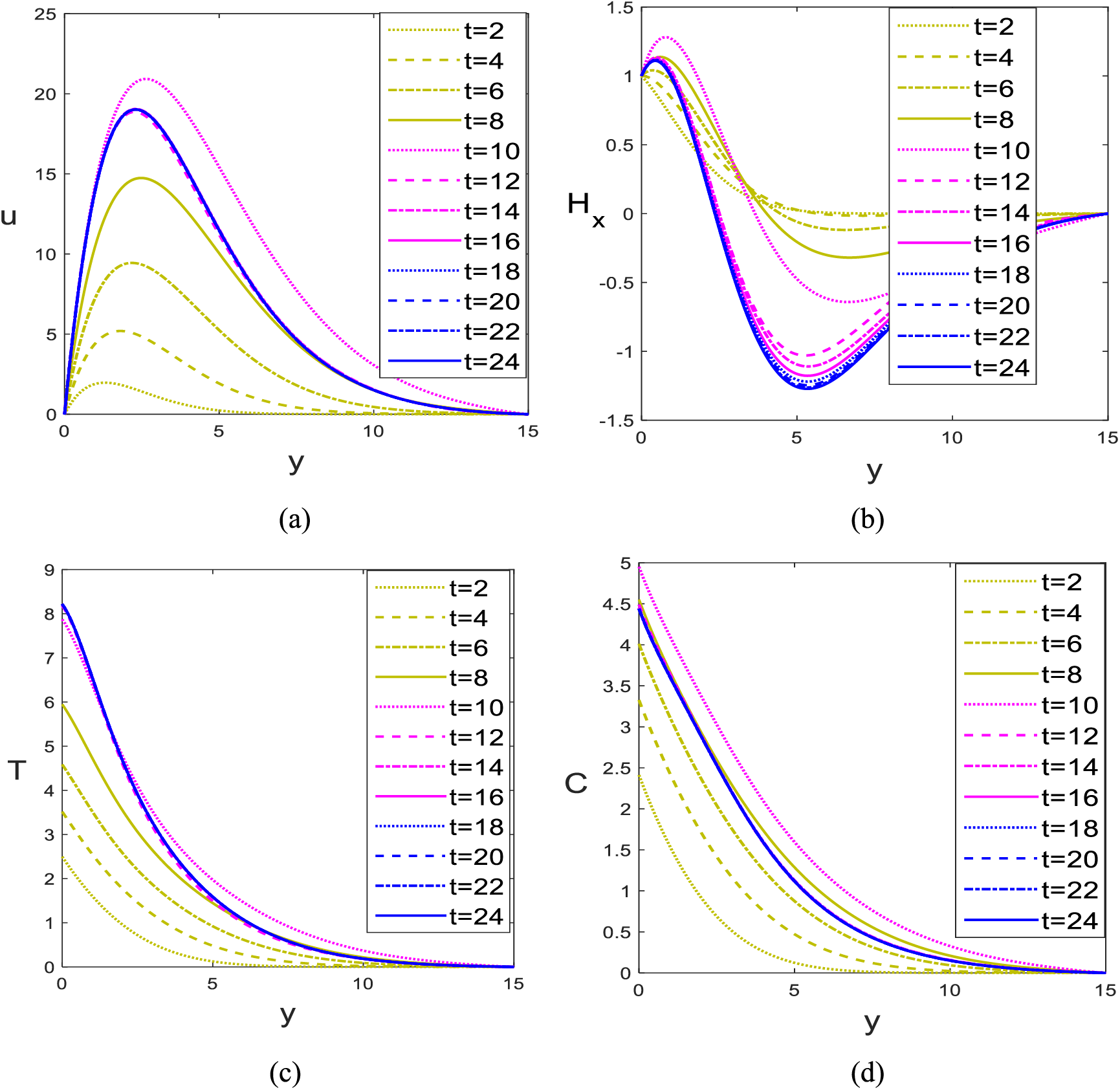
Figure 4: Steady-state for (a) velocity, (b) induced magnetic field, (c) temperature, and (d) concentration

6.3 Code Verification

To claim the precision of the numerical results for the commercial software MATLAB R 2015a, a validation of the codes has been verified through studio developer FORTRAN 6.6a. Excellent compliance has been found between the results from the two different codes. The results are shown in Fig. 5a,b for the velocity profile with the magnetic parameter M.

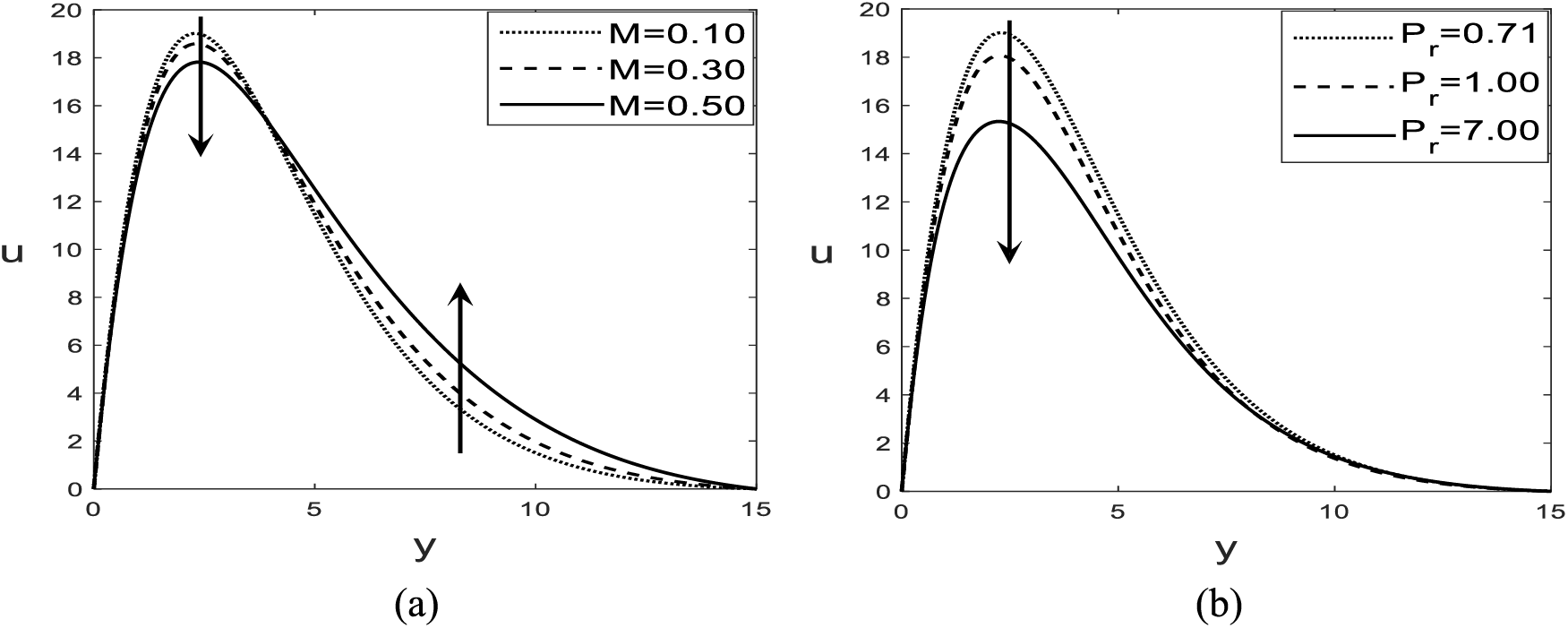
Figure 5: Code verification for velocity with the magnetic parameter M by (a) MATLAB, (b) FORTRAN

6.4 Major Parameter Effects

With the general assumptions of M=0.10,Pr=0.71,Pm=1.50,R∗=0.20,Ec=0.01,Du=0.30, So=0.40, and Sc=0.60 at time t=22 (steady state), the response of various parameters on velocity u, magnetic induction profile Hx, temperature T, and concentration C are portrayed in Figs. 6–9. Table 1 shows the responses to effect of the significant parameters on local shear stress τL and local current density JL. This study was conducted for some regular fluids with Pr=0.71 (air at 20∘C), Pr=1.00 (electrolytic solution at 20∘C), and Pr=7.00 (water at 20∘C). Certain realistic diffusing species are elected through Schmidt number Sc, for example Sc=0.60 (water vapor), Sc=0.78 (ammonia), Sc=0.94 (carbon-di-oxide), and Sc=2.62 (propyl-benzene). The stability conditions lead us to choose other parameters to show the variations of different profiles.

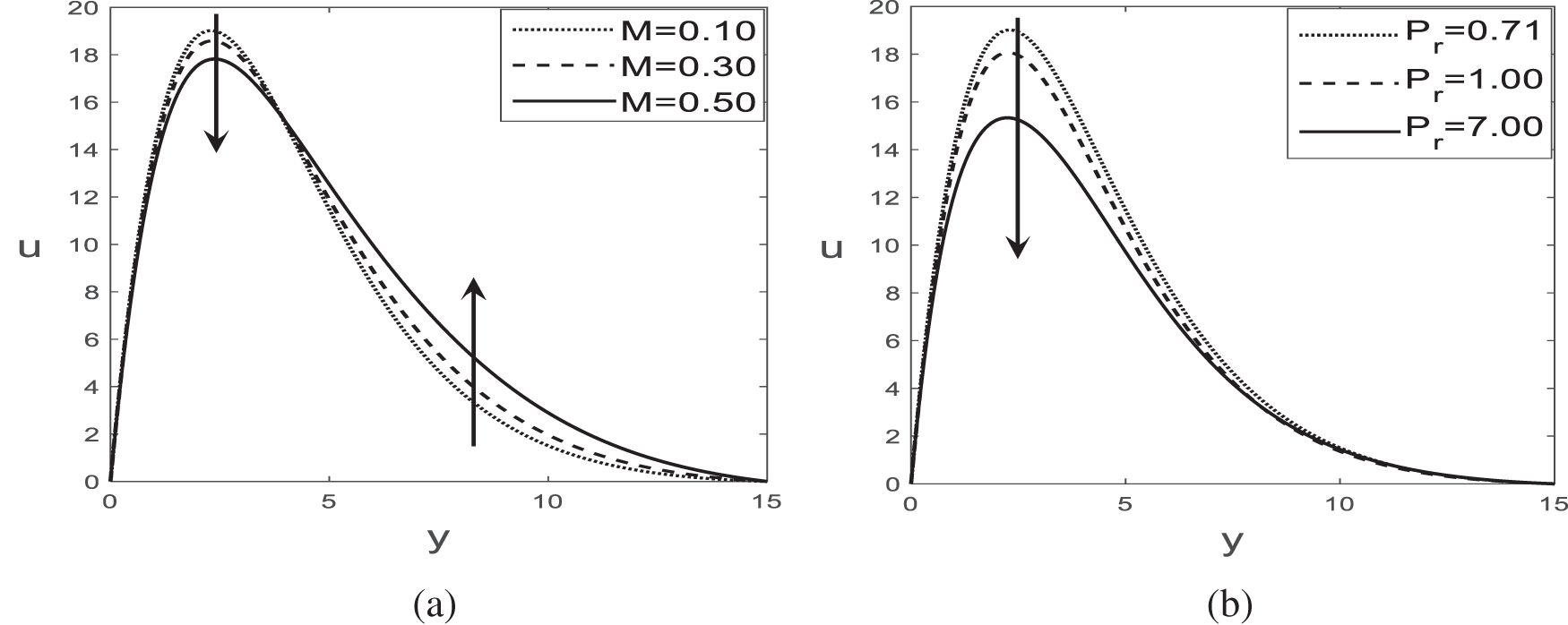
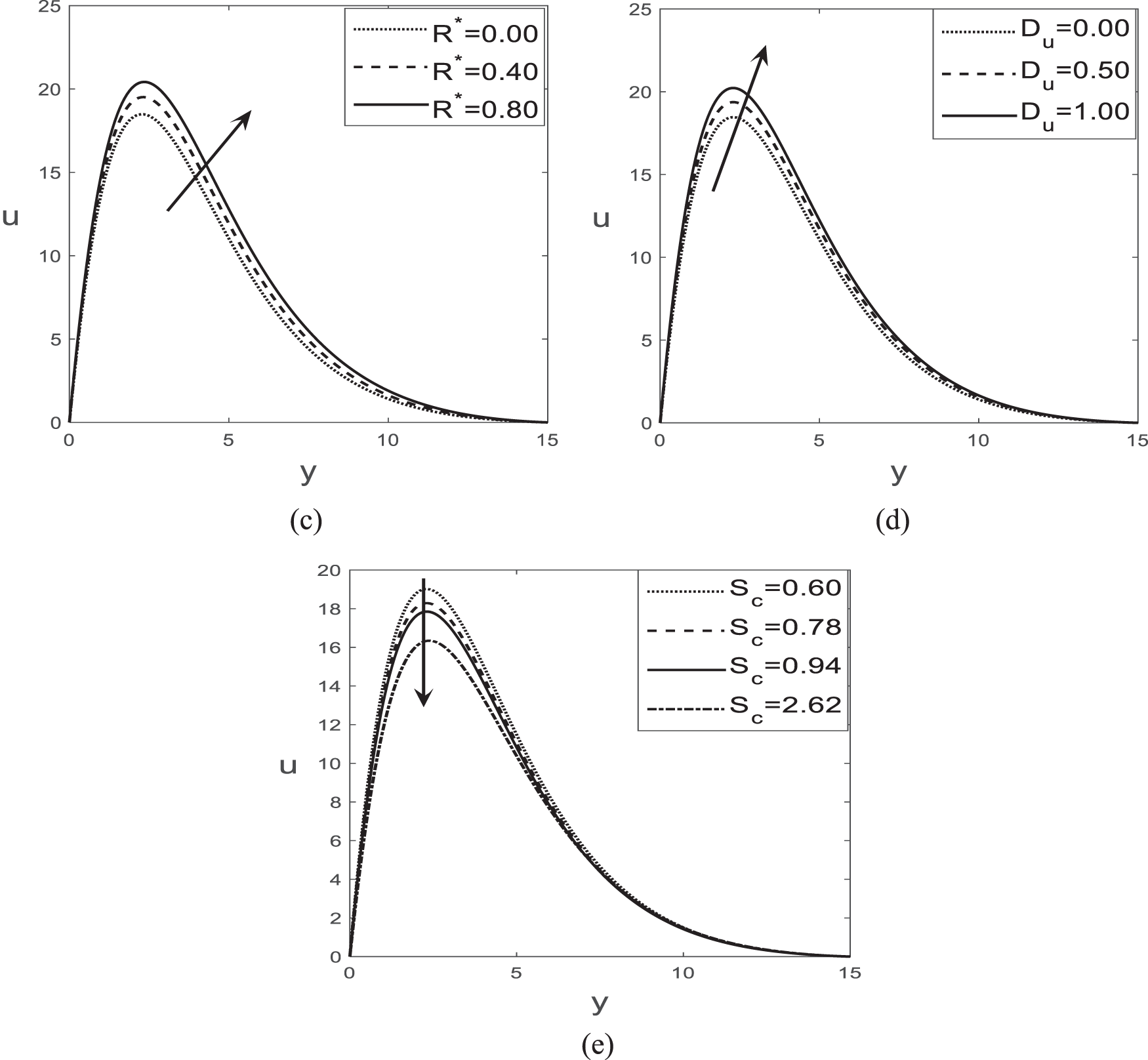
Figure 6: Variations of velocity for (a) (M); (b) (Pr); (c) (R∗); (d) (Du) and (e) (Sc) at time t=22 (steady state)

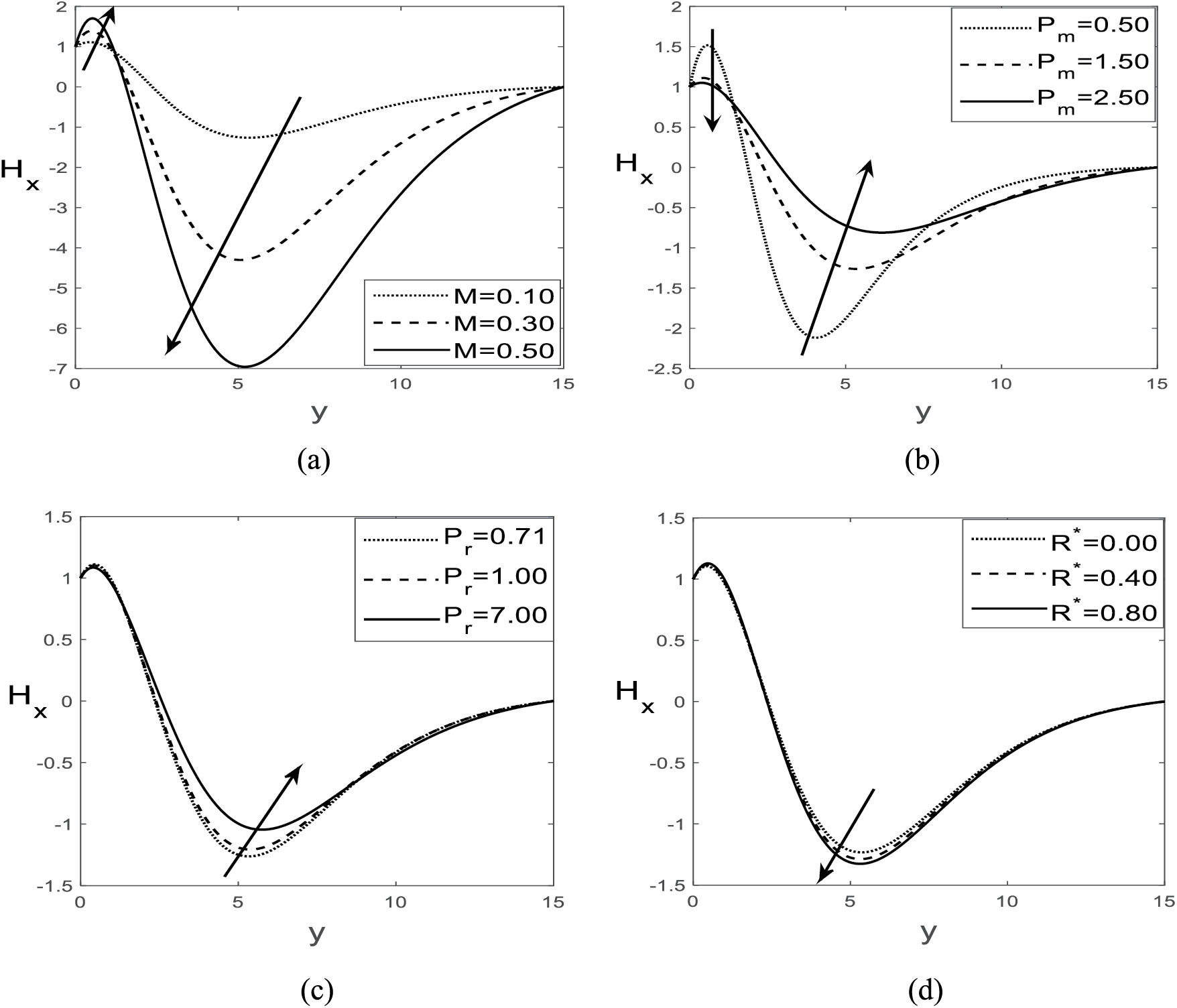
Figure 7: Variations of induced magnetic field for (a) (M); (b) (Pm); (c) (Pr) and (d) (R∗) at time t=22 (steady state)

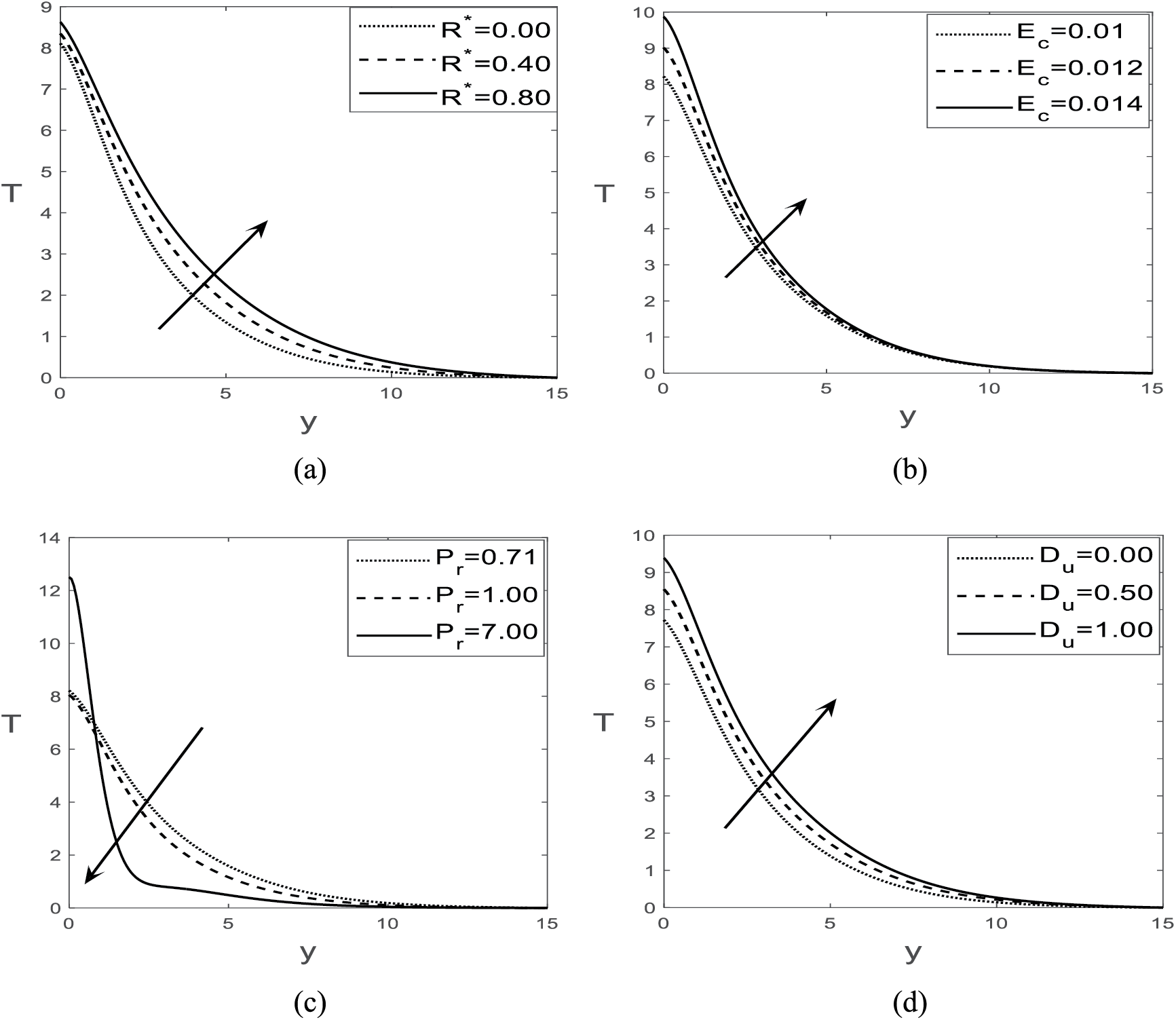
Figure 8: Variations of temperature for (a) (R∗); (b) (Ec); (c) (Pr) and (d) (Du) at time t=22 (steady state)

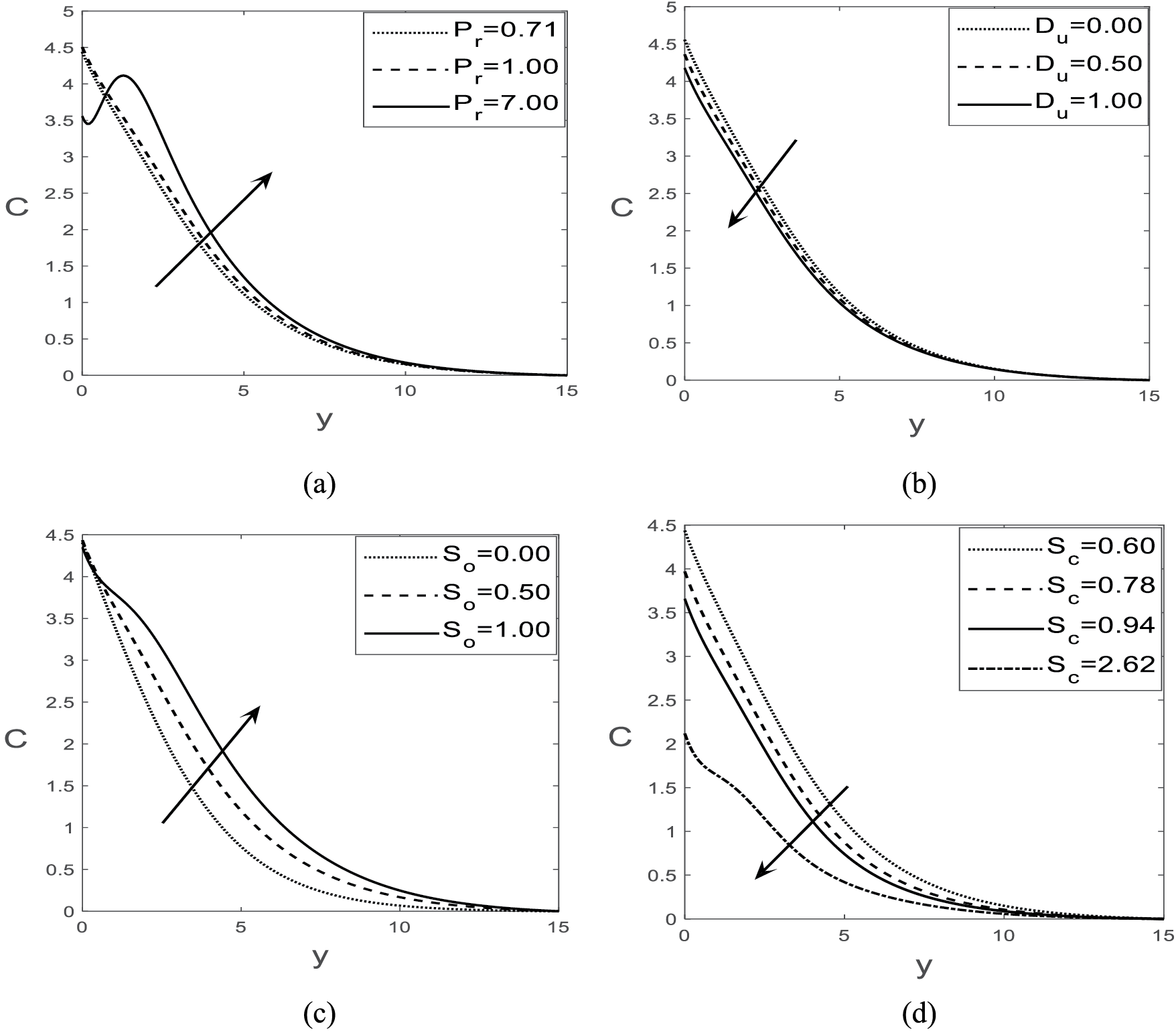
Figure 9: Variations of concentration for (a) (Pr); (b) (Du); (c) (So) and (d) (Sc) at time t=22 (steady state)

Fig. 6a–e illustrates the response of the velocity under the influence of different parameter variations. All combinations of parameters do not cause any backflow in the flow territory. Fig. 6a indicates that the magnetic parameter M decelerates velocity contiguous to the plate, i.e., for relatively smaller estimations of y whereas it accelerates for larger estimations of y. With increasing values of the Prandtl number Pr, the velocity decreases (see Fig. 6b). This occurs due to the thinning of the momentum BL when enhancing the Prandtl number Pr. This phenomenon arises from the development of kinematic viscosity criteria alongside the increasing Prandtl number, leading to a reduction in heat diffusivity. Fig. 6c shows that the radiation parameter R∗ helps increase the flow velocity. The underlying cause is the augmentation of the energy of the fluid particles due to molecular collisions among them by the heat flux of the radiation. It is marked in Fig. 6d that the acceleration of flow occurs with increasing settings of the Dufour number Du. In contrast, as shown in Fig. 6e, rising estimations of the Schmidt number Sc(0.60,0.78,0.94,2.62) pull down the velocity, indicating that the thinning of the momentum BL occurs. This means the fluid can be driven with a faster velocity for water, while propyl-benzene slows it down.

The influence of several major parameters on magnetic field induction is displayed in Fig. 7a–d. All individual figures for magnetic field induction reach a cusp in the negative direction. After that, it declines to the null value corresponding to the region of the outward BL. For very small settings of y, i.e., in the vicinity of the plate, an enhancement in the IMF is observed with the magnetic parameter M; after that, it falls off far from the plate (see Fig. 7a). Near the plate, the interaction between the fluid and the magnetic field is strongest, resulting in a higher IMF due to the active effect of the Lorentz force. As the distance from the plate increases (for larger y), the influence of the magnetic field weakens. This occurs because the flow far from the plate experiences less direct impact from the applied magnetic field, causing the IMF to diminish. Fig. 7b shows an exact opposite variation in magnetic field induction with the magnetic Prandtl number Pm. It is observed from the sketch that for values of y ranging from 0 to approximately 1.8, the IMF profile shows a downward trend with increasing magnetic Prandtl number Pm. However, for 1.8≤y≤7 (approximately), the IMF profile shows an upward trend. The profile becomes irregular for the remainder of the BL with more frequent variations along the BL. The Prandtl number enhances the BL of magnetic induction. Consequently, the IMF rises with the amplification of the Prandtl number Pr from 0.71 (air) to 7.00 (water) (see Fig. 7c). The rising values of the radiation parameter R∗ causes a slow and continuous decrease in magnetic field induction (see Fig. 7d).

Fig. 8a–d illustrates the variations of temperature estimations with some relevant parameters. Since the radiative heat flux generates internal heat (energy) through the friction of the internal molecules, the increment of the radiation parameter R∗ may intensify the temperature, thereby enlarging the temperature BL. As per the physical interpretation, the temperature increases with the rise of the radiation parameter R∗ (see Fig. 8a), as a higher radiation parameter indicates more significant thermal radiation in the system. This study deals with positive estimations of the Eckert number Ec. The positive Eckert number Ec stands for the plate cooling, and the temperature penetrates the fluid due to this cooling process. This is the reason behind the temperature increase for a positive Eckert number Ec. Fig. 8c reveals a diminution in temperature with the rise of the Prandtl number Pr. This happens due to the contraction of the thermal BL with larger settings of the Prandtl number Pr. The diffusion-thermo effect, i.e., the rise in the Dufour number Du, augments the temperature, as illustrated in Fig. 8d. The Dufour number Du inherently contributes to speeding up the convective heat transfer process, ultimately amplifying the temperature inside the BL.

The response of concentration to several pertinent parameters is delineated in Fig. 9a–d. The rise in the Prandtl number Pr enhances the concentration level for the diffusing species (see Fig. 9a). Conversely, the diffusion-thermo (Dufour) effect exhibits an opposite action on concentration (see Fig. 9b). As energy is transferred, it modifies the temperature field, affecting the diffusion rates of different species and leading to a lower concentration. A rising concentration estimation from Fig. 9c has been identified with a higher counting of thermal diffusion, i.e., Soret number So. Thus, the bigger values of thermal diffusion prolong the concentration BL. The Schmidt number Sc quantifies the diffusion of mass transport and momentum in their effectiveness. The higher the Schmidt number Sc, the lower the mass diffusion attributes of the fluids. The Schmidt number Sc effectively modifies the concentration level inside the flow region. Therefore, from a physical viewpoint, it reveals that the larger estimations of the Schmidt number, Sc, oppose the concentration level, as shown in Fig. 9d. A higher Sc means that the fluid’s viscosity dominates over its mass diffusion, contributing to slower mass diffusion relative to momentum. Consequently, the species concentration diffuses more slowly. Since the calculations are done for Sc(0.60,0.78,0.94,2.62), the diffusing species propyl-benzene has lower molecular diffusivity, which causes contraction in the concentration BL compared to water.

Table 1 denotes the numerical computation of local shear stress and local current density for the cross-section x. The local primary shear stress increases with the enhancement of Pm,R∗,Ec,Du, and So while it is opposed by the increasing estimations of M,Pr, and Sc. The local current density increases with the promotion of Pm,Pr, and Sc on the contrary, it declines with M,R∗,Ec,Du, and So.

6.5 Comparison

A comparative view of the current study with several published articles has been observed in Table 2. The papers of Haque et al. [19], Ahmed et al. [20], and Kumar et al. [21] with magnetic field induction have been considered to compare the current work.

7  Conclusions

Steady-state and explicit FDM-based solutions of unsteady MHD flow with an IMF have been investigated. Based on the graphical representation of the results, some crucial findings are summarized below:

1.    Materially, the steady state is assured at t=22.

2.    The magnetic field induction is slower to acquire the steady state than other profiles.

3.    200×200 meshes have been essentially taken for calculations.

4.    The velocity increases with the rise of R∗ and Du, while it diminishes with the increase of Pr and Sc. The increment in M causes a decrement in velocity near the plate and then increases.

5.    The IMF responds increasingly near the plate and then falls with the augmentation of M. For 0≤y≤1.8 (approximately), the IMF profile shows a downward trend with increasing magnetic Prandtl number Pm. However, for 1.8≤y≤7 (approximately), the trend is upward. The profile becomes somewhat uneven for the rest of the BL.

6.    The rising behavior of the temperature profile is identified with the augmentation of R∗,Ec, and Du, while it behaves oppositely with the increase of Pr. A positive Eckert number Ec signifies that the plate is cooling, transferring the temperature into the fluid due to this cooling effect.

7.    The concentration profile shows an increment with the rising estimations of Pr and So while it starts falling with the increase of Du and Sc.

8.    The local shear stress increases with the augmentation of R∗, Ec, Du, and So, while it begins to decrease with the increase of M, Pr, and Sc.

9.    The local current density develops with Pm, Pr, and Sc, while it falls with M, R∗, Ec, Du, and So.

The findings from this investigation could play a vital role in understanding the movement of oil, gas, and water within the reservoirs of oil and gas fields. They may also provide insights into the migration of groundwater and oil, as well as processes related to filtration and water purification.

Future Research Directions: Although steady-state 2D models offer insightful insights, we wish to focus on expanding our study into 3D simulations in the future to better capture the complex behaviors of MHD flow found in practical, real-world scenarios.

Acknowledgement: None.

Funding Statement: The research work is supported by the NST Fellowship under the Ministry of Science and Technology, Government of the People’s Republic of Bangladesh (Session: 2019–2020, merit number: 334, serial number: 714, physical science).

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Saykat Poddar, Muhammad Minarul Islam, Md. Mahmud Alam; analysis and interpretation of results: Saykat Poddar, Jui Saha, Badhan Neogi, Mohammad Sanjeed Hasan; draft manuscript preparation: Saykat Poddar, Mohammad Sanjeed Hasan, Giulio Lorenzini; supervision: Muhammad Minarul Islam, Md. Mahmud Alam. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

Greek Symbols

Subscripts

References

1. Gridnev NP. Study of the group properties of magnetohydrodynamics equations and their invariant solutions. J Appl Mech Tech Phys. 1968;9(6):103–7. [Google Scholar]

2. Golovin SV, Sesma LT. Exact solutions of stationary equations of ideal magnetohydrodynamics in the natural coordinate system. J Appl Mech Tech Phys. 2019;60(2):234–47. doi:10.1134/s0021894419020056. [Google Scholar] [CrossRef]

3. Kaptsov EI, Meleshko SV. One class of MHD equations: conservation laws and exact solutions. Stud Appl Math. 2023;151(3):957–74. doi:10.1111/sapm.12616. [Google Scholar] [CrossRef]

4. Parida SK, Panda S, Rout BR. MHD boundary layer slip flow and radiative nonlinear heat transfer over a flat plate with variable fluid properties and thermophoresis. Alex Eng J. 2015;54(4):941–53. doi:10.1016/j.aej.2015.08.007. [Google Scholar] [CrossRef]

5. Sehra, Haq SU, Shah SIA, Nisar KS, Jan SU, Khan I. Convection heat mass transfer and MHD flow over a vertical plate with chemical reaction, arbitrary shear stress and exponential heating. Sci Rep. 2021;11:4265. doi:10.1038/s41598-021-81615-8. [Google Scholar] [PubMed] [CrossRef]

6. Ellahi R, Alamri SZ, Basit A, Majeed A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J Taibah Univ Sci. 2018;12(4):476–82. doi:10.1080/16583655.2018.1483795. [Google Scholar] [CrossRef]

7. Kumar Pandit K, Singh SI, Sarma D. Heat and mass transfer analysis of an unsteady MHD flow past an impulsively started vertical plate in presence of thermal radiation. Int J Fluid Mech Therm Sci. 2018;4(2):18. doi:10.11648/j.ijfmts.20180402.11. [Google Scholar] [CrossRef]

8. Hussain M, Qayyum M, Afzal S. Modeling and analysis of MHD oscillatory flows of generalized Burgers’ fluid in a porous medium using Fourier transform. J Math. 2022;2022:295. doi:10.1155/2022/2373084. [Google Scholar] [CrossRef]

9. Chen C-H. Combined heat and mass transfer in MHD free convection from a vertical surface with Ohmic heating and viscous dissipation. Int J Eng Sci. 2004;42(7):699–713. doi:10.1016/j.ijengsci.2003.09.002. [Google Scholar] [CrossRef]

10. Alam MS, Rahman MM, Samad MA. Numerical study of the combined free-forced convection and mass transfer flow past a vertical porous plate in a porous medium with heat generation and thermal diffusion. Nonlinear Anal Model Control. 2006;11(4):331–43. doi:10.15388/NA.2006.11.4.14737. [Google Scholar] [CrossRef]

11. Pal D, Mondal H. Influence of chemical reaction and thermal radiation on mixed convection heat and mass transfer over a stretching sheet in Darcian porous medium with Soret and Dufour effects. Energy Convers Manage. 2012;62:102–8. doi:10.1016/j.enconman.2012.03.017. [Google Scholar] [CrossRef]

12. Javaherdeh K, Mirzaei Nejad M, Moslemi M. Natural convection heat and mass transfer in MHD fluid flow past a moving vertical plate with variable surface temperature and concentration in a porous medium. Eng Sci Technol Int J. 2015;18(3):423–31. doi:10.1016/j.jestch.2015.03.001. [Google Scholar] [CrossRef]

13. Aslam MN, Shaukat N, Riaz A, Nigar N, Shaukat S, Naveed M. A machine learning investigation of the ZnO-water nanofluid flow with magnetic field through convergent and divergent channels: a numerical study. Int J Ambient Energy. 2024;45(1):2316793. doi:10.1080/01430750.2024.2316793. [Google Scholar] [CrossRef]

14. Reddy DS, Sarma GS, Govardhan K. Numerical study of MHD, thermal radiation free convection heat and mass transfer from vertical surfaces in porous media considering Soret and Dufour effects. Heat Technol. 2014;32(1–2):179–84. doi:10.18280/ijht.320125. [Google Scholar] [CrossRef]

15. Mollah MT, Poddar S, Islam MM, Alam MM. Non-isothermal Bingham fluid flow between two horizontal parallel plates with Ion-slip and Hall currents. SN Appl Sci. 2021;3:115. doi:10.1007/s42452-020-04012-2. [Google Scholar] [CrossRef]

16. Mollah MT, Rasmussen HK, Poddar S, Islam MM, Parvine M, Alam MM, et al. Ion-slip effects on Bingham fluid flowing through an oscillatory porous plate with suction. Math Model Eng Probl. 2021;8(5):673–81. doi:10.18280/mmep.080501. [Google Scholar] [CrossRef]

17. Mondal M, Biswas R, Shanchia K, Hasan M, Ahmmed S. Numerical investigation with stability convergence analysis of chemically hydromagnetic Casson nanofluid flow in the effects of thermophoresis and Brownian motion. Heat Technol. 2019;37(1):59–70. doi:10.18280/ijht.370107. [Google Scholar] [CrossRef]

18. Lutera JN, Shekar MNR, Goud BS. Numerical solution of an unsteady nanofluid flow with magnetic, endothermic reaction, viscous dissipation, and solid volume fraction effects on the exponentially moving vertical plate. Partial Differ Equ Appl Math. 2024;11:100772. doi:10.1016/j.padiff.2024.100772. [Google Scholar] [CrossRef]

19. Haque MM, Ferdows M, Alam MM. Explicit finite difference and steady state solutions of heat and mass transfer flow from a vertical porous plate with thermal diffusion and induced magnetic field. Acta Tech CSAV. 2017;62(1):13–26. [Google Scholar]

20. Ahmed T, Alam MM, Ferdows M, Tzirtzilakis EE. Chemically reacting ionized radiative fluid flow through an impulsively started vertical plate with induced magnetic field. Int J Appl Mech Eng. 2019;24(1):5–36. doi:10.2478/ijame-2019-0001. [Google Scholar] [CrossRef]

21. Kumar A, Singh AK. Unsteady MHD free convective flow past a semi-infinite vertical wall with induced magnetic field. Appl Math Comput. 2013;222:462–71. doi:10.1016/j.amc.2013.07.044. [Google Scholar] [CrossRef]

22. Poddar S, Islam MM, Ferdouse J, Alam MM. Characteristical analysis of MHD heat and mass transfer dissipative and radiating fluid flow with magnetic field induction and suction. SN Appl Sci. 2021;3:470. doi:10.1007/s42452-021-04452-4. [Google Scholar] [CrossRef]

23. Shankar Goud B, Pramod Kumar P, Malga BS. Induced magnetic field effect on MHD free convection flow in nonconducting and conducting vertical microchannel walls. Heat Trans. 2022;51(2):2201–18. doi:10.1002/htj.22396. [Google Scholar] [CrossRef]

24. Kumar D. Radiation effect on magnetohydrodynamic flow with induced magnetic field and Newtonian heating/cooling: an analytic approach. Propuls Power Res. 2021;10(3):303–13. doi:10.1016/j.jppr.2021.07.001. [Google Scholar] [CrossRef]

25. Khan U, Zaib A, Ishak A, Waini I, Pop I, Elattar S et al. Stagnation point flow of a water-based graphene-oxide over a stretching/shrinking sheet under an induced magnetic field with homogeneous-heterogeneous chemical reaction. J Magn Magn Mater. 2023;565:170287. doi:10.1016/j.jmmm.2022.170287. [Google Scholar] [CrossRef]

26. Mahato R, Das M, Sen SSS, Nandkeolyar R. Hydromagnetic mixed convection unsteady radiative Casson fluid flow towards a stagnation-point with chemical reaction, induced magnetic field, Soret effect, and convective boundary conditions. Heat Trans. 2023;52(2):1142–60. doi:10.1002/htj.22733. [Google Scholar] [CrossRef]

27. Bilal S, Akram S, Saeed K, Athar M, Riaz A, Razia A. A computational simulation for peristaltic flow of thermally radiative sisko nanofluid with viscous dissipation, double diffusion convection and induced magnetic field. Numer Heat Transf A. 2024;37:1–22. doi:10.1080/10407782.2024.2335557. [Google Scholar] [CrossRef]

28. Patel HR. Thermal radiation effects on MHD flow with heat and mass transfer of micropolar fluid between two vertical walls. Int J Ambient Energy. 2021;42(11):1281–96. doi:10.1080/01430750.2019.1594371. [Google Scholar] [CrossRef]

29. Kho YB, Hussanan A, Sarif NM, Ismail Z, Salleh MZ. Thermal radiation effects on MHD with flow heat and mass transfer in Casson nanofluid over A stretching sheet. MATEC Web Conf. 2018;150:06036. doi:10.1051/matecconf/201815006036. [Google Scholar] [CrossRef]

30. Ali A, Khan HS, Saleem S, Hussan M. EMHD nanofluid flow with radiation and variable heat flux effects along a slandering stretching sheet. Nanomater. 2022;12(21):3872. doi:10.3390/nano12213872. [Google Scholar] [PubMed] [CrossRef]

31. Zigta B. Mixed convection on MHD flow with thermal radiation, chemical reaction and viscous dissipation embedded in a porous medium. Int J Appl Mech Eng. 2020;25(1):219–35. doi:10.2478/ijame-2020-0014. [Google Scholar] [CrossRef]

32. Zigta B. Effect of thermal radiation and chemical reaction on MHD flow of blood in stretching permeable vessel. Int J Appl Mech Eng. 2020;25(3):198–211. doi:10.2478/ijame-2020-0043. [Google Scholar] [CrossRef]

33. Mollah MT. EMHD laminar flow of Bingham fluid between two parallel Riga plates. Heat Technol. 2019;37(2):641–8. doi:10.18280/ijht.370236. [Google Scholar] [CrossRef]

34. Hussain A, Saddiqa A, Riaz MB, Martinovic J. A comparative study of peristaltic flow of electro-osmosis and MHD with solar radiative effects and activation energy. Int Commun Heat Mass Transf. 2024;156:107666. doi:10.1016/j.icheatmasstransfer.2024.107666. [Google Scholar] [CrossRef]

35. Ahmed N, Sarma K, Deka H. Soret and radiation effects on a transient MHD mass transfer flow past an infinite vertical porous plate in a rotating system with hall current. Heat Technol. 2013;31(1):109–16. doi:10.18280/ijht.310114. [Google Scholar] [CrossRef]

36. Poddar S, Islam MM, Ferdouse J, Alam MM. Steady-state solution of MHD heat and mass transfer fluid flow over a semi-infinite vertical plate in a rotating system dipped in a porous medium with Hall current, thermal radiation, heat generation/absorption and joule heating. Heat Technol. 2022;40(2):457–67. doi:10.18280/ijht.400213. [Google Scholar] [CrossRef]

37. Alfwzan WF, Allehiany FM, Riaz A, Sikandar S, Alhamzi G. Mathematical model of ciliary flow and entropy for carreau nanofluid with electroosmosis and radiations in porous medium: a numerical work. Case Stud Therm Eng. 2023;49:103230. doi:10.1016/j.csite.2023.103230. [Google Scholar] [CrossRef]