Numerical Study on 3D MHD Darcy-Forchheimer Flow Caused by Gyrotactic Microorganisms of the Bio-Convective Casson Nanofluid across a Stretched Sheet

Nomenclature

1  Introduction

Due to their involvement in several mechanisms, such as power engineering, petroleum production, chemical processes, and broad-spectrum, researchers’ and academics’ interest in the rheology of non-Newtonian fluid has been sparked by a variety of industrial uses. Over the past several years, there has been a notable rise in the number of academic papers discussing the issue of non-Newtonian fluid flow. Since no one equation can adequately explain the properties of all non-Newtonian fluids, they are separated into a variety of fluid models (such as tangent hyperbolic, power-law, Sisko, Oldroyd-B, Williamson, Casson, and others). Of the several fluid models, the Casson fluid model is the subject of the current study. Casson fluid is a non-Newtonian fluid having pseudoplastic features. According to Alwawi et al. [1], a sodium alginate sphere was passed through a Casson nanofluid exhibiting MHD and natural convection. The Casson liquid created by a stretched sheet that was subjected to blowing and suction was explored by Mukhopadhyay [2] about how heat radiation affected it. Mabood et al. [3] looked at how a stretched surface and the Casson fluid flow affected the magnetic field. They examined the impact of thermal radiation by assuming that the surface is porous. Analysis of the natural convective unsteady MHD Casson fluid flow by Anwar et al. [4] took into account the varying wall temperature. Furthermore, Sandeep et al.’s [5] in-depth investigation involved closely examining the reactive chemical Casson fluid flow over a curved heated surface. The Casson fluid flows through a tube was investigated by Saleem et al. [6] and the tube wall was believed to be wavy and stretchy. Hafez et al. [7] demonstrated the impact of rotation on an inclined surface’s MHD Casson fluid flow. Makkar et al. [8] investigated the behavior of the MHD Casson nanofluid under convective and gyrotactic microorganism environments.

An important application of bio-convection is in biotechnology, environmental systems, and biofuels. Microorganisms that are swimming increase the initial density of a fluid and create a density gradient, which causes bio-convection. Microfluidics, nanomaterials, microcontrollers, and bioinformatics are just a few of the many fields that use bio-convection in various ways. Another essential component of bio-convection is the coupling of nanotechnology and motile microorganisms which enhances the heat and mass transfer, and the stability of nanomaterials. It has also been utilized in biomedicine to treat cancer. To demonstrate the flow of Prandtl nano-liquid, Mekheimer et al. [9] used an illustration of gyrotactic microorganisms on a stretching/shrinking plane. Khan’s [10] analysis of the bio-convection brought on by gyrotactic microorganisms and nanoparticles revealed that conductivity increased along with a rise in the convective form’s buoyancy factor, whereas nanoparticle concentration rose along with a rise in the Brownian motion constriction. On the foundation of the mechanism determining the directional motion of various kinds of microorganisms, many bio-convection systems have been researched by several scholars, including [11–13].

Stretchable sheets with fluid motion are essential for both industrial and biomedical research. The dynamics of various slip barriers and their effects on the flow of a stretched sheet on MHD Casson-Williamson nanofluid with double-diffusive were examined by Humane et al. [14]. Numerical simulations by Rana et al. [15] show how energy is transferred over a nonlinearly extending sheet via nano-liquid flow. The flow of Casson nanofluid along an extended surface with various consequences was observed by Ali et al. [16]. Another research are also found [17,18].

The phenomena of flow transfer in porous space have received recent attention in engineering and geophysical processes. Grain storage, groundwater systems, high power density machines, gas-cooled reactor vessels, gas-cleaning filtration, porous pipes, porous bearings, casting solidification, fossil fuel beds, blood circulation in the lungs or the arteries, etc., are just a few examples of the applications for these processes. Scientists and engineers from a variety of disciplines may be interested in these applications. Rashid et al. [19] included Darcy-Forchheimer’s model in the momentum conservation equation to study 3D convective nanoliquid flows along a stretched rotating surface enclosed in a non-linear porous medium in the existence of chemical reaction and activation energy. Seddeek [20] investigated the mixture of convective thermophoretic movement saturation in porous space using the Darcy-Forchheimer hypothesis. Numerous researchers in related domains have demonstrated the value of the porosity of a medium in a variety of contexts [21–28].

In light of the afore-stated surveys, no study has been reported on 3D MHD Darcy–Forchheimer flow of Casson nanofluid-induced bio-convection past a stretched sheet.

The importance of the heat and mass transportation of 3D MHD Casson nanofluid along a stretch surface susceptible to convective circumstances, gyrotactic microorganisms, and Darcy-Forchheimer law received little attention in the aforementioned literature. Hence, this extensive research’s main goal was to use the Casson nanofluid model to optimize heat and mass transportation. The elaborated fluid model was chosen as a result of the aforementioned uses of this fluid in the literature. The Runge-Kutta-Fehlberg approach [29–32] was used to solve ODEs after the geometrical problems in three dimensions were reduced to ODEs dimensions by employing a similarity transformation. There are many significant applications for a Casson type incompressible viscous nanofluid that passes through the specified porous medium using the Darcy-Forchheimer relation, including numerous engineering, industrial, and environmental setups like chemical action reactors, heat exchangers, geological setups, geothermic systems, and many others [33–39]. The results were then tested and coded using MATLAB software. By contrasting the numerical results with previously accessible data, the results were confirmed. Additionally, these data are shown in graphical, bar charts, and tabular form. This study discusses the different uses that have produced paints, crude oil purification systems, liquid materials, heat exchangers, spinning of plastic, polymer extrusion, etc. The non-Newtonian Casson nanofluid model, along with the managing parameters, has more effective thermal conductivity, stability, chemical inertness, cost-effectiveness, and environmental friendliness, making it useful in a variety of engineering and industrial applications where thermal improvement is crucial. The findings of this investigation can be used to guide future work in which the thermal performance of a thermal system can be determined by the dispersion of various kinds of NPs into other non-Newtonian fluids like Casson Fluid.

2  Mathematical Formulation

Consider a three-dimensional stretched sheet with a Darcy-Forchheimer-subjected Casson nanofluid flowing steadily and incompressibly over it and transmits electricity when gold particles of minuscule size (GNPs) move in sp. Nanoparticles can improve fluid thermal stability, provide better lubricity, hole cleaning and wellbore stability, and mitigate hydrates formation within the fluid circulation system. Furthermore, the majority of cancer patients face a hazardous and fatal condition. Due to their large atomic numbers, which produce heat and help treat cancerous tumours, gold nanoparticles (GNPs) are able to treat and eradicate it. GNPs possesses numerous qualities that are crucial in the treatment of cancer. They can pierce deep into the body while being quite little. It is believed that the sheet is stretched in the “xy” plane while the fluid is positioned along the z-axis. Investigations were done into bio-convection’s impacts. The inclusion of the nanoparticles was also made possible by their peculiar properties, such as remarkable thermal conductivity, which are important in heat exchangers and cutting-edge nanotechnology. The geometry of this research model is shown in Fig. 1. Additionally considered are thermophoresis, Brownian motion effects, and heat and mass transfer. The nanoparticle suspension was believed to be a stable substance, which is crucial for the presence of motile microorganisms and the agglomeration of microscopic particles was disregarded. Additionally, we speculate that probably surface concentration and temperature as well as the ambient concentration and temperature are Cw, Tw and C∞,T∞, respectively. Thermophoresis, Brownian motion effects, and heat and mass transfer are also taken into account.

Figure 1: Sketch and problem-solving scheme

Following is an example of the rheological equation of an isotropic and steady flow of a Casson fluid [32]:

Sij={ 2(μB+Pz2π)eij,π > πc(μB+Pz2π)eij,π < πc(1)

According to the equation above π=eijeij, where eij stands for the (i,j) component of the deformation rate, πc be the crucial value of this product based on the non-Newtonian model, μB be the plastic dynamic viscosity of the Casson fluid, and Pz be the fluid yield stress.

The following are the equations for continuity, momentum, heat, and mass transfer:

∂u∂x+∂v∂y+∂w∂z=0,(2)

(u∂u∂x+v∂u∂y+w∂u∂z)=ν(1+1γ)∂2u∂z2−σB02uρf−νuk−Fu2,(3)

(u∂v∂x+v∂v∂y+w∂v∂z)=ν(1+1γ)∂2v∂z2−σB02vρf−νvk−Fv2,(4)

(u∂T∂x+v∂T∂y+w∂T∂z)=KT(ρcp)f∂2T∂z2+τ(DB∂T∂z∂C∂z+DTT∞(∂T∂z)2),(5)

(u∂C∂x+v∂C∂y+w∂C∂z)=DB∂2C∂z2+DTT∞∂2T∂z2,(6)

(u∂N∂x+v∂N∂y+w∂N∂z)=DN∂2T∂z2−bWc(Cw−C∞)∂∂z(N∂C∂z).(7)

We use the convective boundary conditions. There are many Important applications of such flows and conditions include the MHD pump, radiation therapy, MHD generator, melt spinning process, soil mechanics thermal insulation as well as many others. Practical applications of convective BC are often encountered in laser damage or laser processing. BCs take the following form:

{u=Uw=Ax,v=Vw=By,w=0,hf(Tw−T)+Kf(∂T∂z)=0,hc(Cw−C)+DB(∂C∂z)=0,hn(Nw−N)+DN(∂N∂z)=0,atz=0,u=0,v=0,T=T∞,C=C∞,N=N∞,atz→∞.(8)

Assumptions for the similarity transformations include the following:

η=Aυz,u=Axf1′(η),v=Byf2′(η),w=−Aυ[f1(η)+cf2(η)],

θ(η)=T−T∞Tw−T∞,ϕ(η)=C−C∞Cw−C∞,ξ(η)=N−N∞Nw−N∞.(9)

The skin friction coefficients Cfx and Cfy, local Nusselt number Nux, and Sherwood number Shx are stated as follows:

{Cfx=2τwxρUx2,Cfy=2τwyρVx2,Nux=xqwK(Tw−T∞),Shx=xjwDB(Cw−C∞),Nnx=xMwDN(Tw−T∞),(10)

where τwx, τwy, qw, and Mw are defined by:

τwx=μ(1+1β3)(∂u∂z)∣z=0,τwy=μ(1+1β3)(∂v∂z)∣z=0,qw=−K(∂T∂z)∣z=0jw=−DB(∂C∂z)∣z=0,Mw=−DN(∂C∂z)∣z=0.(11)

3  Solution of the Problem

The continuity equation Eq. (2) is immediately satisfied by Eq. (9), and the ensuing Eqs. (3)–(7) are as follows:

(1+1γ)f1‴+(f1+cf2)f1″−(1+Fr)f1′2−(M+β)f1′=0,(12)

(1+1γ)f2‴+(f1+cf2)f2″−(1+Fr)cf2′2−(M+β)f2′=0,(13)

θ″+Pr(f1+cf2)θ′+Nbθ′ϕ′+Ntθ′2=0,(14)

ϕ″+LePr(f1+cf2)ϕ′+NtNbθ″=0,(15)

ξ″+LbPr(f1+cf2)ξ′−Pe[(ξ+ϵ)ϕ″+ξ′ϕ′]=0.(16)

Following that, the changed boundary conditions are provided by:

f1(0)=0,f2(0)=0,f1′(0)=1,f2′(0)=1,θ(0)=−Bi1(1−θ(0)),ϕ(0)=−Bi2(1−ϕ(0)),ξ(0)=−Bi3(1−ξ(0)),f1′(∞)=0,f2′(∞)=0,θ(∞)=0,ϕ(∞)=0,ξ(∞)=0.(17)

The following are the receptively dimensionless relationships between skin-friction coefficients, local Nusselt, Sherwood, and density numbers:

{CfxRe1/2=(1+1β3)f1″(0),CfyRe1/2=(1+1β3)f2″(0),NuxRe−12=−θ′(0),ShxRe−12=−ϕ′(0),NuxRe−1/2=−ξ′(0).(18)

where it is possible to use the corresponding expressions for dimensionless parameters

γ=(PyμB2πc)−1,β=νkA,Fr=Cbk0.5,M=σB02ρf,α=KT(ρcp),Pr=ν(ρcp)KT,Lb=αDN,Le=αDB,Pe=bWcDN,Nt=τDt(Tw−T∞)ν,Nb=τDB(Cw−C∞)ν,ϵ=bN∞Nw−N∞,Bi1=hfAυKf,Bi2=hsAυDB,Bi1=hnAυDN.(19)

4  Numerical Procedure

An effective 4th order “Runge-Kutta” method and the Shooting method were applied to scrutinize the flow model from the above mentioned coupled ODEs (12)–(16) for several values of controlling factors like Nt, Nb, Le, Pr, and β. The ODEs are first broken up into a set of 1st ODEs. The coupled ODEs (12)–(16) are 3rd order in f1, 3rd order in f2, 2nd order in θ, 2nd order in ϕ, and 2nd order in ξ which were decreased to twelve simultaneous equations for 12 unknowns. To numerically resolve the equation system via the “Runge-Kutta” technique, the solution needs 7 initial conditions, however, 4 initial conditions are recognized in f1,f2 along with 3 initial condition all of θ, ϕ,ξ, respectively. Nevertheless, the values of φ, θ, ξ and f1,f2 are given at η → ∞. These constraints are used by the shooting technique to create unknown initial conditions η = 0. The key step in this approach is to take proper finite values η∞. Therefore, to calculate the η∞ value with the aid of a certain initial value and resolve the BVP containing Eqs. (12)–(16) to get f1‴ (0), θ′′(0), φ′′ (0) and f2‴(0).

The solution procedure is continued with an additional bigger value η∞ till 2 consecutive values of f1‴ (0), θ′′(0), φ′′ (0) and f2‴(0) differ merely after the required substantial digit. The final η∞ value is regarded as the limit for finite value η∞ for the specific collection of physical variables for measuring concentration, temperature along velocity are f1‴ (0), θ′′(0), φ′′(0) and f2‴(0) in the boundary layer. After, starting conditions we resolve this simultaneous equation system employing the 4th order “Runge-Kutta Integration” method. The η∞ is chosen between range 5–20 based on physical variables controlling the fluid flow to avoid numerical oscillation.

This research first converts the BVP into an IVP: “Initial Value Problem”. This is addressed by properly estimating the missing initial value applying the shooting technique for multiple parameter combinations. The size of step h = 0.1 is utilized for computation applications. The findings are expressed via graphs and tables, and the major characteristics of the issues are addressed and evaluated.

The Runge-Kutta-Fehlberg (RKF) method is used to solve the non-linear coupled and non-dimensional transformed ODEs Eqs. (12)–(16) and the boundary conditions Eq. (17) numerically using MATLAB R2016a’s built-in function “bvp-4c” solver. The boundary value problem is transformed into the initial issue by converting the nonlinear ODEs system into a linear first-order differential equation. The following are the freshly defined variables:

f1(η)=ω1,f1′(η)=ω2,f1″(η)=ω3,f2(η)=ω4,f2′(η)=ω5,f2″(η)=ω6,θ(η)=ω7,θ′(η)=ω8,ϕ(η)=ω9,ϕ′(η)=ω10,ξ(η)=ω11,ξ′(η)=ω12.(20)

We get:

ω3′=(γ1+γ)[r−(ω1+cω4)ω3+(1+Fr)ω22+(M+β)ω2],(21)

ω6′=(γ1+γ)[−(ω1+cω4)ω6+(1+Fr)ω52+c(M+β)ω5],(22)

ω8′=−Pr[(ω1+cω4)ω8+Nbω8ω10+Ntω82],(23)

ω10′=−Le Pr(ω1+cω4)ω10−NtNbω8,(24)

ω12′=−Lb Pr(ω1+cω4)ω12+Pe[(ω11+ϵ)ω10+ω10ω12].(25)

Taking into account both:

f1‴(η)=ω3′,f2‴(η)=ω6′,θ″(η)=ω8′,ϕ′(η)=ω10′,ξ′(η)=ω12′.(26)

Bvp-4c approach with matching boundary conditions as:

{ωa(1),ωa(2)−1,ωa(4),ωa(5)−1ωa(8)+Bi1(1−ω(7)),ωa(10)+Bi2(1−ω(9))ωa(12)+Bi3(1−ω(11)),ωb(2),ωb(5),ωb(7),ωb(9),ωb(11).(27)

5  Results and Discussion

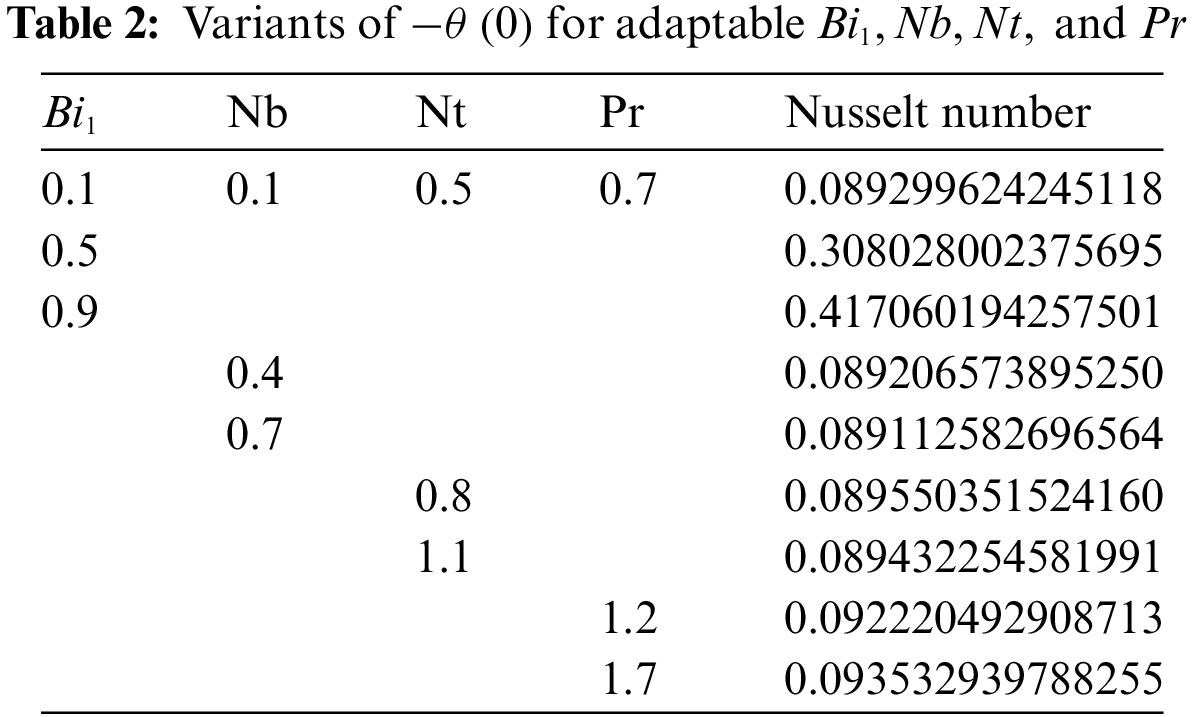
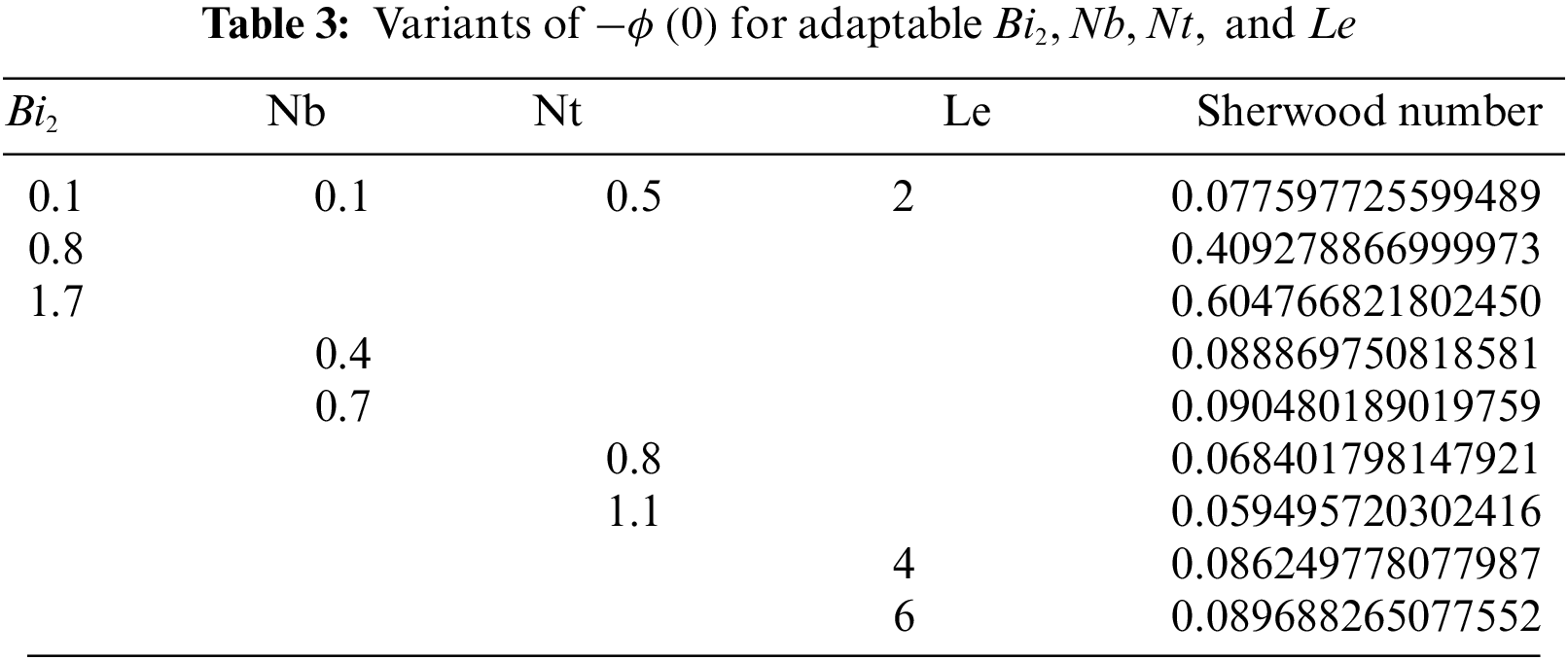
An important factor in the boundary layer flow of a “Casson nanofluid” across a stretched plate is the heat transmission characteristics. Understanding the characteristics of heat transport over a stretched plate is important to achieving the requisite quality. This is because the value of the finished product depends mainly on the rates of stretching and heat transmission. In this section, to understand the problem physically, a parametric analysis is carried out on a non-Newtonian Casson nanofluid to demonstrate the effects of different regulating parameters. The Runge-Kutta-Fehlberg approach is used to numerically solve the nonlinear ODEs (10) through (14) using Eqs. (15) and (16) and the shooting method. The findings are obtained by observing how various functions, such as velocities, temperature, concentration, and density of motile microorganisms in Casson nanofluid, behave. We contrasted our numerical results with those described by Makkar et al. [8] with some special assumptions to show the legitimacy and accuracy of our numerical approach (see Table 1). Table 1 shows that the current statistics are consistent with Makkar et al. ’s findings [8]. Tables 2–4 assess and display physical quantities, including the Nusselt number, Sherwood number, and density number of microorganisms.

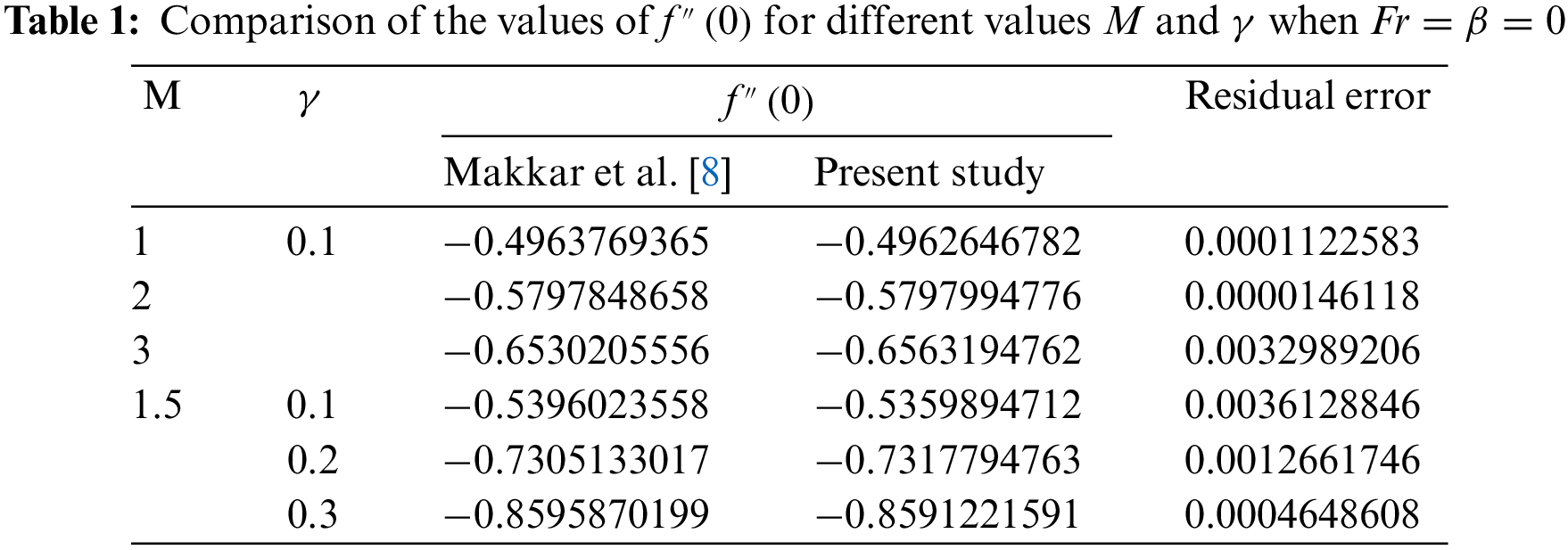
The impacts of the magnetic parameter (M) and Forchheimer number (Fr) on the non-dimensional velocities are shown in Fig. 2. In Figs. 2a and 2b, it is clear that the dimensionless velocities (f1′(η), f2′(η)) “horizontal and vertical” decrease as the magnetic parameter increases. The magnetic field opposes the movement’s flow. As the magnetic field grows, the dimensionless velocities usually decrease significantly. This is due to the Lorentz force, a retarding body force, being introduced by the magnetic field. This is brought about by the interaction of the magnetic and electric fields with the movements of an electrically conducting fluid, i.e. Physically, the presence of a magnetic field causes a resistive force to arise in the flow of the nanofluid. The nanofluid’s velocity can be slowed down by this force. The nanofluid consequently receives some heat energy from the same force as a result. The variation of velocities (f1′(η), f2′(η) as a consequence of the change in the Fr parameter is depicted in Figs. 2c and 2d. When one can elevate, the amount of fluid flow decreases, which slows the motion.The fluid’s connection with the porous substance, which raises its viscosity and generates resistance, is what reduces its speed, i.e. It should also be noticed that when the same parameter Fr grows larger, an obstructing force acts against the velocity and the boundary layer thickness.

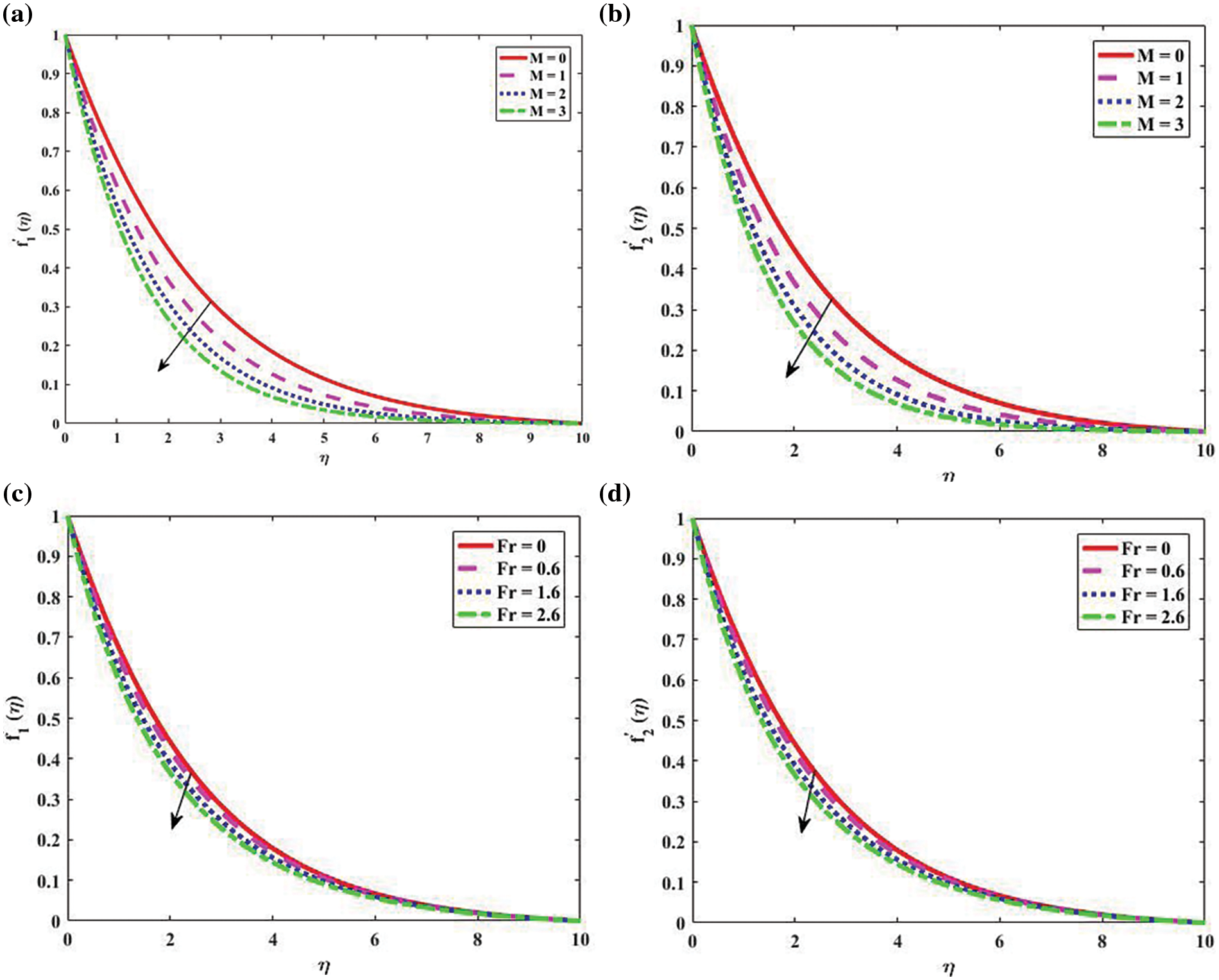
Figure 2: Velocity profile “(f1′(η) and (f2′(η)” variations. (a & b) vs. M. (c & d) vs. Fr

Under the effect of the Casson parameter (γ), and porous parameter (β). Fig. 3 considers velocity distribution. Casson fluid is treated as fluid with variable plastic dynamic viscosity with a strong effect of yield stress, the velocity increases near the wall and negligibly decreases far from the vertical heated wall for an increase in the values of Casson fluid parameter (γ). As seen in both graphs, Figs. 3a and 3b indicate that higher fluid flow non-Newtonian behavior causes a decrease in velocity distribution. Additionally, in Figs. 3c and 3d, the porous parameter, displays a comparable impact compared to its greater strength.

Figure 3: Velocity profile “f1′(η) and f2′(η)” variations. (a & b) vs. γ. (c & d) vs. β

In contrast to the thermophoresis parameter (Nt) and the parameters of Brownian motion and (Nb), Fig. 4 portrays the implications of temperature distribution θ(η) and concentration distribution ϕ(η). It is envisaged that the temperature function at η∞ will resemble that of a typical fluid. According to the thickening of the thermal boundary layer fluid thickness, temperature rises as Nt and Nb rise. As Nt rises, it is seen that nanoparticles in Figs. 4a and 4b migrate from the warmer to the colder region, improving the temperature distribution. Additionally, Nt enhancement increases the abundance of nanoparticles so the concentration also increases. As Nb rises, nanoparticles move quickly, causing their kinetic energy to rise and their temperature to rise, as shown in Fig. 4a. However, contrary conduct is seen for concentration, as shown in Fig. 4b.

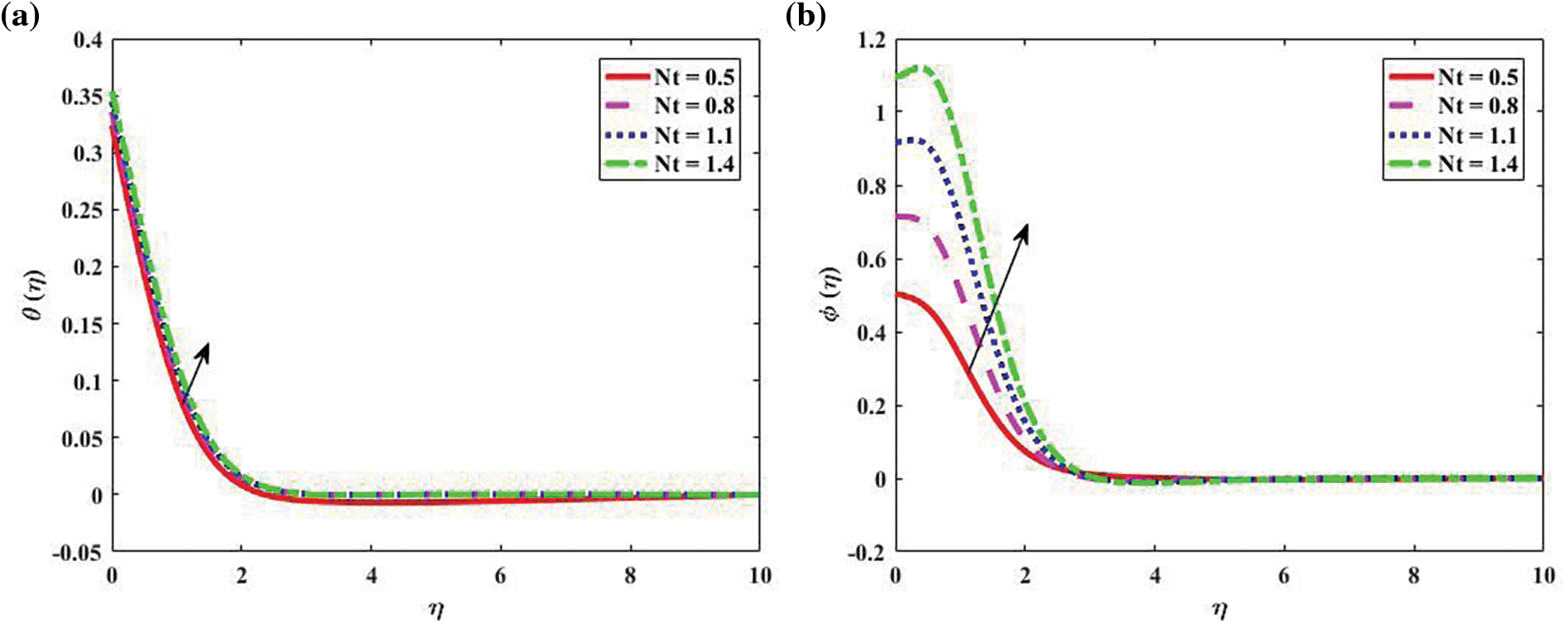
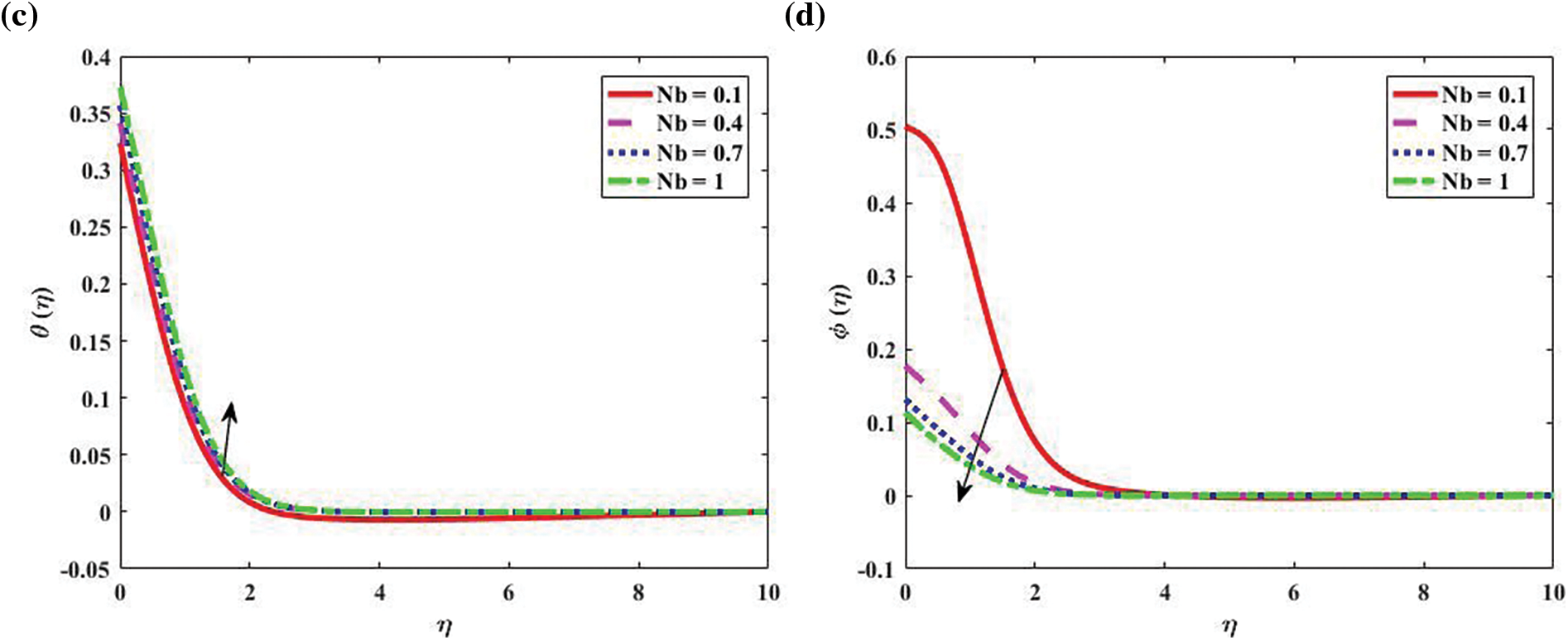
Figure 4: Temperature and concentration profiles “θ(η) and ϕ(η)” variations (a & b) vs. Nt (c & d) vs. Nb

Fig. 5 depicts how (Pr) affects temperature θ(η), concentration ϕ(η), and motile density distribution ξ(η) for the Prandtl number Pr. The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. Because higher Pr reduces the thermal diffusion rate, it has been found that raising Pr lowers the temperature profile. The distribution of concentration and motile density also declines for higher Pr because increasing Pr indicates that the heat conduction is more significant compared to convection, so thermal diffusivity is dominant.

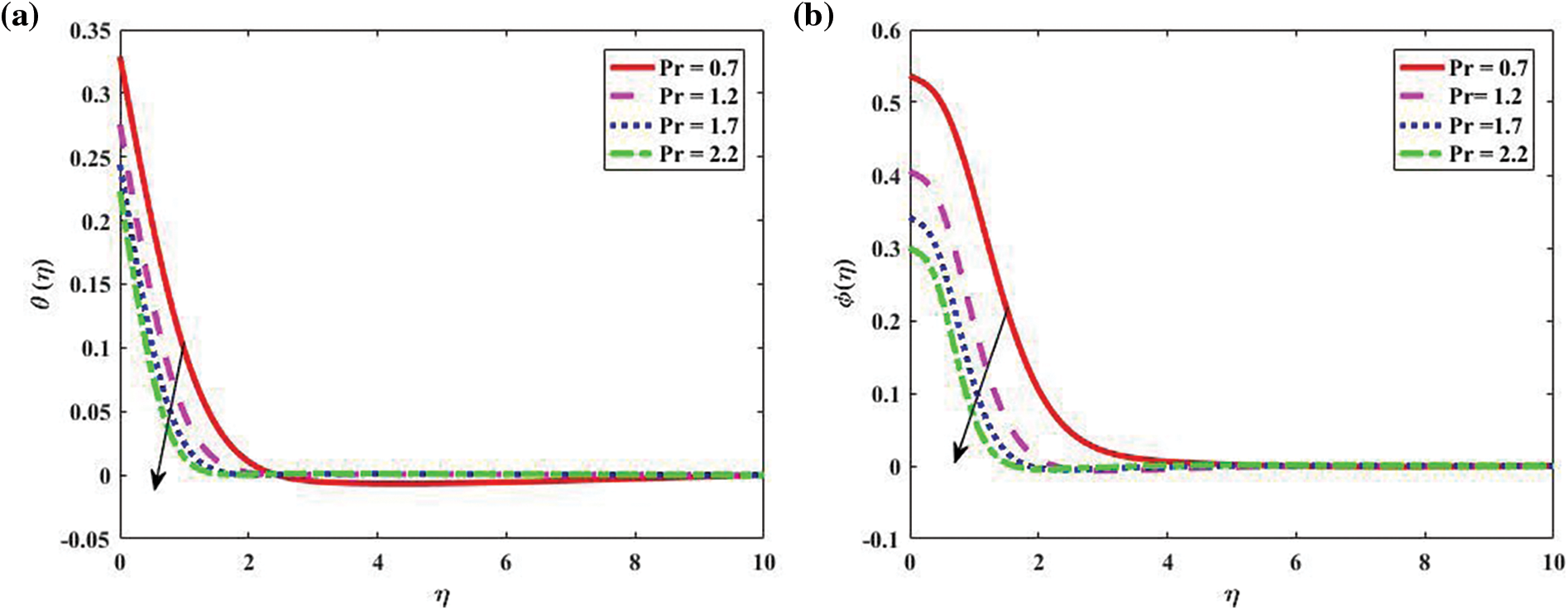
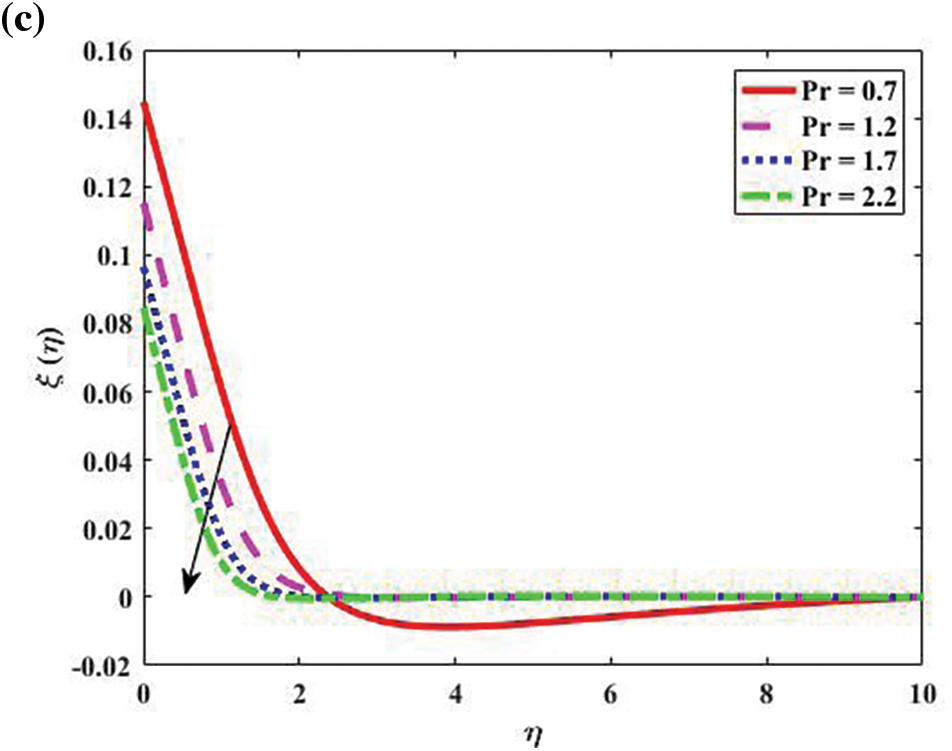
Figure 5: Temperature, concentration, and Motile density distribution for bio-convective profiles “θ(η),ϕ(η), and ξ(η)” variations (a & b & c) vs. Pr

In Fig. 6, we describe the effects on the microorganism density ξ(η) by changing the Peclet number (pe), bio-convection Lewis number (Lb), and bio-convective constant (ϵ). Since is a crucial component of liquid motility, higher inputs of can reduce the proportion of bacteria that move in liquids. Microorganisms’ behaviours, such as how swiftly they swim and how responsively they respond to environmental signals, can also affect the motile density distribution. The distribution of motile density may be impacted by variations in temperature. Bioconvection is significantly influenced by temperature gradient. The distribution of motile density can be affected by the fluid’s viscosity by changing the bioconvection patterns. Fig. 6a debates how Peclet quantity affects microorganism density. The graph illustrates that for a higher Pe in the range [1.2–4.9], motile microorganism density drops which complies with the convergence requirement of eta as η→∞. Fig. 6b displays the bio-convection Lewis number’s effect (Lb) on microorganism proliferation functions. These curves yield asymptotic patterns that preserve boundary conditions, and it is investigated how they demonstrate that as Lb increased, the density function of microorganisms dropped. Variation in ξ(η) about the bioconvective constant ϵ is presented in Fig. 6c. Additionally, this figure shows a decrease in motile microorganism density for heavier ϵ in the range [0.87–6.7].

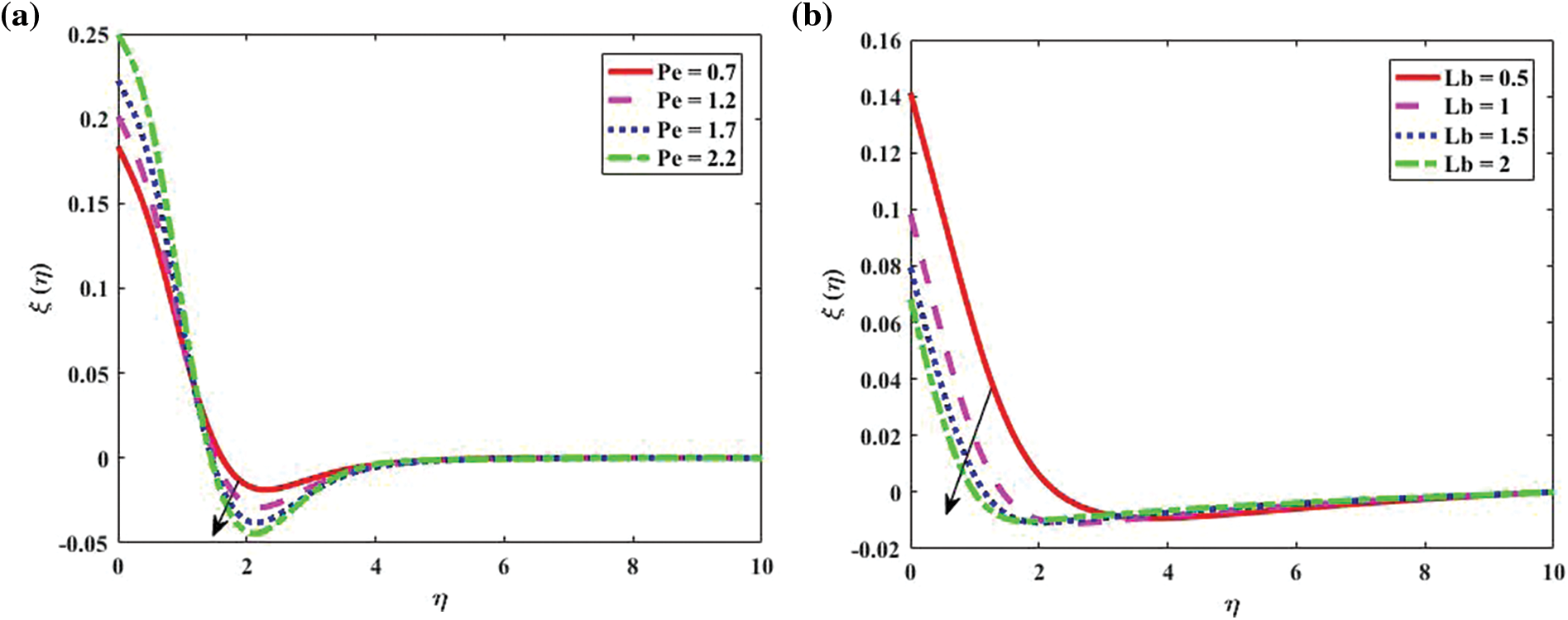
Figure 6: Motile density distribution for bio-convective profile “ξ(η)” variations (a) vs. Pe. (b) vs. Lb, (c) vs. ϵ

Fig. 7 presents the data collected regarding the Nusselt, Sherwood, and local density numbers in a bar chart format against various values of Bi1,Bi2, and Bi3, respectively.

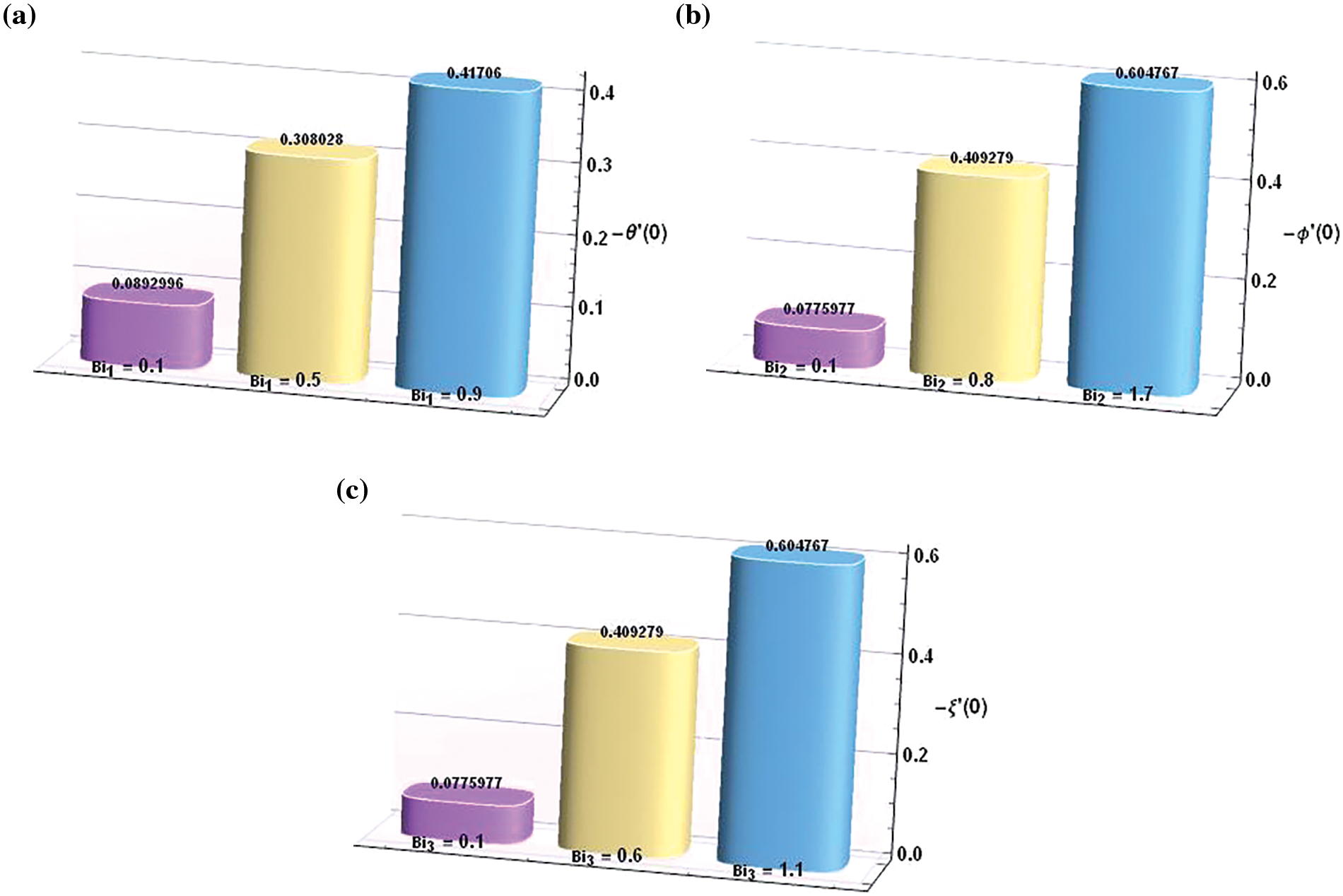
Figure 7: Bar Chart depiction of “Nusselt, Sherwood and local density numbers” (a) vs. Bi1. (b) vs. Bi2. (c) vs. Bi3

6  Conclusion

Particularly when it comes to heat transfer and energy transmission, melting thermal transport can have a considerable impact on bioconvection in fluids. Due to physical or chemical gradients, such as light, temperature, or chemical concentrations, microorganisms or biological particles may assemble in a fluid. We call this process “bioconvection.” Mobile microorganisms can be used in bioprocessing to produce useful products including biofuels, medications, and food additives. Their motility allows them to move around freely in the fluid, which enhances the mixing and distribution of other substrates like nutrition. In the current research, it has been examined how gyrotactic microorganisms affect MHD bio-convective Casson nanofluid Darcy-Forchheimer flow caused by a 3D stretching surface. We use an effective conventional Runge–Kutta method together with shooting methodology to solve them for various values of some key parameters. Moreover, the current results are validated against earlier literature. The following are the research’s main ramifications:

•   With both the bio-convection Lewis and Peclet numbers, motile microorganisms’ rescaled density drops.

•   Brownian motion parameter and bio-convection Lewis number have the propensity to accelerate mass transfer.

•   Biot numbers tend to regulate the rapidity of mass and heat transfer.

•   As the number of the bio-convective constant (ϵ) and Peclet number (pe) rise, the reduced density number of the motile microorganisms diminishes.

•   The results were largely consistent with the most current, state-of-the-art studies that had been published in the literature. The present results were said to have potential for advancing fluid mechanics, biomedical sciences, as well as engineering.

•   The information in this study may be helpful to scientists, engineers, and those working on the advancement of nanofluid mechanics.

Future Perceptions: Finite Difference method, the Chebyshev spectral method, and Keller-box scheme may be employed for the numerical treatment of numerous prospective applications appearing in bioinformatics, fluid mechanics problems, financial mathematics of vital implication.

Acknowledgement: The researchers would like to acknowledge Deanship of Scientific Research, Taif University for funding this work.

Funding Statement: The author received no specific funding for this study.

Author Contributions: This study is solely done by S. H. Elhag.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Alwawi, F. A., Alkasasbeh, H. T., Rashad, A. M., Idris, R., (2020). MHD natural convection of sodium alginate casson nanofluid over a solid sphere. Results in Physics, 16, 102818. https://doi.org/10.1016/j.rinp.2019.102818 [Google Scholar] [CrossRef]

2. Mukhopadhyay, S. (2013). Effects of thermal radiation on casson fluid flow and heat transfer over an unsteady stretching surface subjected to suction/blowing. Chinese Physics B, 22(11), 114702. [Google Scholar]

3. Mabood, F., Das, K. (2019). Outlining the impact of melting on MHD casson fluid flow past a stretching sheet in a porous medium with radiation. Heliyon, 5(2), e01216. [Google Scholar] [PubMed]

4. Anwar, T., Kumam, P., Watthayu, W. (2021). Unsteady MHD natural convection flow of casson fluid incorporating thermal radiative flux and heat injection/suction mechanism under variable wall conditions. Scientific Reports, 11(1), 4275. [Google Scholar] [PubMed]

5. Sandeep, N., Sulochana, C., Ashwinkumar, G. P. (2022). Understanding the dynamics of chemically reactive casson liquid flow above a convectively heated curved expanse. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 236(24), 11420–11430. [Google Scholar]

6. Saleem, S., Akhtar, S., Nadeem, S., Saleem, A., Ghalambaz, M. et al. (2021). Mathematical study of electroosmotically driven peristaltic flow of casson fluid inside a tube having systematically contracting and relaxing sinusoidal heated walls. Chinese Journal of Physics, 71, 300–311. [Google Scholar]

7. Hafez, N. M., Abd-Alla, A. M., Metwaly, T. M. N. (2023). Influences of rotation and mass and heat transfer on MHD peristaltic transport of casson fluid through inclined plane. Alexandria Engineering Journal, 68, 665–692. [Google Scholar]

8. Makkar, V., Poply, V., Sharma, N. (2023). Three-dimensional magnetohydrodynamic non-newtonian bioconvective nanofluid flow influenced by gyrotactic microorganisms over stretching sheet. Heat Transfer, 52(1), 548–562. [Google Scholar]

9. Mekheimer, S. K. H., Shaimaa Ramadan, F., (2020). New insight into gyrotactic microorganisms for bio-thermal convection of Prandtl nanofluid past a stretching/shrinking permeable sheet. SN Applied Sciences, 2, 450. [Google Scholar]

10. Khan, N. S. (2018). Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Brazilian Journal of Physics, 48(3), 227–241. [Google Scholar]

11. Kuznetsov, A. V. (2011). Bio-thermal convection induced by two different species of microorganisms. International Communications in Heat and Mass Transfer, 38(5), 548–553. [Google Scholar]

12. Ahmed, M. F., Zaib, A., Ali, F., Bafakeeh, O. T., Tag-ElDin, E. M. et al. (2022). Numerical computation for gyrotactic microorganisms in MHD radiative eyring-powell nanomaterial flow by a static/moving wedge with darcy-forchheimer relation. Micromachines, 13(10), 1768. [Google Scholar] [PubMed]

13. Ayano, M. S., Magagula, V. M., Mathunjwa, J. S. (2021). Spectral local linearisation method for MHD casson fluid on stratified bioconvective porous medium flow due to gyrotactic microorganisms. Heat Transfer, 50(2), 1371–1391. [Google Scholar]

14. Humane, P. P., Patil, V. S., Patil, A. B., Shamshuddin, M., Rajput, G. R. (2022). Dynamics of multiple slip boundaries effect on MHD casson-williamson double-diffusive nanofluid flow past an inclined magnetic stretching sheet. Proceedings of the Institution of Mechanical Engineers Part E: Journal of Process Mechanical Engineering, 236(5), 1906–1926, 9544089221078153. [Google Scholar]

15. Rana, P., Bhargava, R. (2012). Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study. Communications in Nonlinear Science and Numerical Simulation, 17(1), 212–226. [Google Scholar]

16. Ali, L., Liu, X. M., Ali, B., Mujeed, S., Abdal, S. (2019). Finite element analysis of thermo-diffusion and multi-slip effects on MHD unsteady flow of casson nano-fluid over a shrinking/stretching sheet with radiation and heat source. Applied Sciences, 9(23), 5217. [Google Scholar]

17. Hussain, M., Khan, W., Farooq, U., Razzaq, R. (2023). Impact of non-similar modeling for thermal transport analysis of mixed convective flows of nanofluids over vertically permeable surface. Journal of Nanofluids., 12(4), 1074–1081. [Google Scholar]

18. Cui, J., Jan, A., Farooq, U., Hussain, M., Khan, W. A. (2022). Thermal analysis of radiative darcy-forchheimer nanofluid flow across an inclined stretching surface. Nanomaterials, 12(23), 4291. https://doi.org/10.3390/nano12234291 [Google Scholar] [PubMed] [CrossRef]

19. Rashid, S., Hayat, T., Qayyum, S., Ayub, M., Alsaedi, A. (2019). Three-dimensional rotating Darcy-Forchheimer flow with activation energy. International Journal of Numerical Methods for Heat & Fluid Flow, 29, 935–948. [Google Scholar]

20. Seddeek, M. A. (2006). Influence of viscous dissipation and thermophoresis on darcy-forchheimer mixed convection in a fluid saturated porous media. Journal of Colloid and Interface Science, 293(1), 137–142. [Google Scholar] [PubMed]

21. Ragupathi, P., Muhammad, T., Islam, S., Wakif, A. (2021). Application of arrhenius kinetics on MHD radiative von karman casson nanofluid flow occurring in a darcy-forchheimer porous medium in the presence of an adjustable heat source. Physica Scripta, 96(12), 125228. [Google Scholar]

22. Alam, M. M., Arshad, M., Alharbi, F. M., Hassan, A., Haider, Q. et al. (2023). Comparative dynamics of mixed convection heat transfer under thermal radiation effect with porous medium flow over dual stretched surface. Scientific Reports, 13(1), 12827. [Google Scholar] [PubMed]

23. Arshad, M., Alharbi, M., Hassan, F. M., Haider, A., Alhushaybari, Q. et al. (2023). Effect of inclined magnetic field on radiative heat and mass transfer in chemically reactive hybrid nanofluid flow due to dual stretching. Scientific Reports, 13(1), 7828. [Google Scholar] [PubMed]

24. Abd-Alla, A. M., Abo-Dahab, S. M., Thabet, E. N., Abdelhafez, M. A. (2022). Peristaltic pump with heat and mass transfer of a fractional second grade fluid through porous medium inside a tube. Scientific Reports, 12(1), 10608. [Google Scholar] [PubMed]

25. Arshad, M., Alharbi, F. M., Alhushaybari, A., Eldin, S. M., Ahmad, Z. et al. (2023). Exploration of heat and mass transfer subjected to first order chemical reaction and thermal radiation: Comparative dynamics of nano, hybrid and tri-hybrid particles over dual stretching surface. International Communications in Heat and Mass Transfer, 146, 106916. [Google Scholar]

26. Abd-Alla, A. M., Thabet, E. N., Bayones, F. S., Alsharif, A. M. (2023). Heat transfer in a non-uniform channel on MHD peristaltic flow of a fractional Jeffrey model via porous medium. Indian Journal of Physics, 97, 1799–1809. [Google Scholar]

27. Arshad, M., Karamti, H., Awrejcewicz, J., Grzelczyk, D., Galal, A. M. (2022). Thermal transmission comparison of nanofluids over stretching surface under the influence of magnetic field. Micromachines, 13(8), 1296. [Google Scholar] [PubMed]

28. Akinshilo, A. T., Mabood, F., Ilegbusi, A. O. (2021). Heat generation and nonlinear radiation effects on MHD casson nanofluids over a thin needle embedded in porous medium. International Communications in Heat and Mass Transfer, 127, 105547. [Google Scholar]

29. Abd-Alla, A. M., Thabet, E. N., Bayones, F. S. (2022). Numerical solution for MHD peristaltic transport in an inclined nanofluid symmetric channel with porous medium. Scientific Reports, 12(1), 3348. [Google Scholar] [PubMed]

30. Alotaibi, H., Althubiti, S., Eid, M. R., Mahny, K. L. (2020). Numerical treatment of MHD flow of casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Computers, Materials & Continua, 66(1), 229–245. https://doi.org/10.32604/cmc.2020.012234 [Google Scholar] [CrossRef]

31. Abd-Alla, A. M., Abo-Dahab, S. M., Thabet, E. N., Bayones, F. S., Abdelhafez, M. A. (2022). Heat and mass transfer for MHD peristaltic flow in a micropolar nanofluid: Mathematical model with thermophysical features. Scientific Reports, 12(1), 21540. [Google Scholar] [PubMed]

32. Sulochana, C., Ashwinkumar, G. P., Sandeep, N. (2016). Similarity solution of 3D Casson nanofluid flow over a stretching sheet with convective boundary conditions. Journal of the Nigerian Mathematical Society, 35, 128–141. [Google Scholar]

33. Shoaib, M., Kausar, M., Nisar, K. S., Zahoor Raja, M. A., Morsy, A. (2022). Impact of thermal energy on MHD Casson fluid through a Forchheimer porous medium with inclined non-linear surface: A soft computing approach. Alexandria Engineering Journal, 61(12), 12211–12228. [Google Scholar]

34. Arshad, M., Hussain, A., Elfasakhany, A., Gouadria, S., Awrejcewicz, J. et al. (2022). Magneto-hydrodynamic flow above exponentially stretchable surface with chemical reaction. Symmetry, 14(8), 1688. [Google Scholar]

35. Roja, A., Gireesha, B. J., Nagaraja, B. (2021). Irreversibility investigation of Casson fluid flow in an inclined channel subject to a Darcy-Forchheimer porous medium: A numerical study. Applied Mathematics and Mechanics, 42, 95–108. https://doi.org/10.1007/s10483-021-2681-9 [Google Scholar] [CrossRef]

36. Arshad, M., Hussain, A., Hassan, A., Karamti, H., Wroblewski, P. et al. (2022). Scrutinization of slip due to lateral velocity on the dynamics of engine oil conveying cupric and alumina nanoparticles subject to Coriolis force. Mathematical Problems in Engineering, 2022, 1–13. [Google Scholar]

37. Rehman, S. U., Fatima, N., Ali, B., Imran, M., Ali, L. et al. (2022). The casson dusty nanofluid: Significance of darcy-forchheimer law, magnetic field, and non-fourier heat flux model subject to stretch surface. Mathematics, 10(16), 2877. https://doi.org/10.3390/math10162877 [Google Scholar] [CrossRef]

38. Haider, Q., Hassan, A., Hajjej, F., Alharbi, F. M., Saeed, A. M. et al. (2023). Effect of thermal radiation on electrically conducting nanofluid with slip conditions and heat source using artificial neural networks. BioNanoScience, 13(4), 2483–2506. [Google Scholar]

39. Bejawada, S. G., Reddy, Y. D., Jamshed, W., Nisar, K. S., Alharbi, A. N. et al. (2022). Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alexandria Engineering Journal, 61(10), 8207–8220. [Google Scholar]