Bioconvective Hybrid Flow with Microorganisms Migration and Buongiorno’s Model under Convective Condition

Nomenclature

1  Introduction

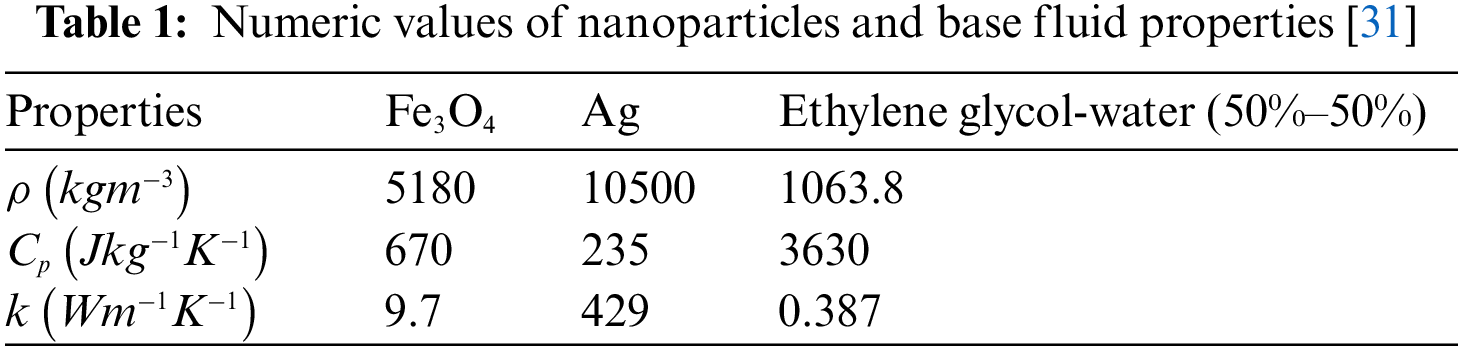
Recently, the new idea of “hybrid nanofluids” has surfaced in which more than one nano-meter nanoparticle is dispersed into the working fluid, and the formed solution is termed a hybrid nanofluid. The importance of improving heat transfer is emphasized by the industry’s production sectors, where it finds notable uses. Mainstream fluids, such as water, ethylene glycol (EG), oils, biological fluids, etc., may transmit heat and are employed in many engineering projects, such as heating systems and electronic devices. These base liquids do not transmit heat well. A substance known as nanofluid, a combination of base liquid and nanoparticles, was created to get a boost of thermal conductivity. By incorporating nano-scale solid particles into convection fluids, Choi et al. [1] first described the concept of nanofluids. Buongiorno [2] discussed the convective heat transfer in the nanofluids using thermophoretic particle diffusion and Brownian motion. With the use of the slip factor, Turkyilmazoglu [3] showed the comparative analysis of single and several phasing streams of nanofluids in radial annuli. Sarada et al. [4] studied the behaviour of a non-Newtonian fluid movement under an extended sheet under global thermal non-equilibrium conditions.

Babu et al. [5] explored non-Newtonian fluid flow across a thin stretched sheet under the influence of cross-diffusion phenomena. Sharma et al. [6] investigated the impact of heat radiation on a two-dimensional non-Newtonian fluid flow over a stretched surface. Ibrahim et al. [7] studied the impact of chemical reactions and radiation on the creation of heat and non-Newtonian fluid flow along a stretched sheet with an uneven depth. The flow of mixed convection in a non-Newtonian fluid flow with entropy and energy activation production was predicted by Ijaz Khan et al. [8]. The effects of activation energy and chemical reactions in viscoelastic liquids traveling over a stretched surface were examined by Ramesh [9]. In order to understand how activation energy affects the nanofluid’s radiative stream under a convective boundary situation, Ijaz Khan et al. [10] looked into the issue. Saleem et al. [11] conducted theoretical research on the thermodynamic properties of hybrid nanofluids propelled by cilia. Beg et al. [12] discussed the Von Karman hydro-magnetic flow with heat transfer, joule heating, and viscous dissipation effect. Dinarvand et al. [13] studied the dual solution of the hybrid nanofluids over a thin moving needle. Mansourian et al. [14] examined hybrid nanofluids over non-linearly stretched porous surfaces. Naz et al. [15] investigated the cross fluid with entropy generation and motile microorganisms. Balla et al. [16] elaborated on the bioconvection in microorganisms in a square cavity with a thermal radiation effect. Hussain et al. [17] examined the magnetic hybrid nanofluid flow of carbon nanotube with thermal radiation. Arshad et al. [18] explored hybrid nanofluids between permeable rotating systems numerically. Rao et al. [19] used graphene nanoparticles to optimize linseed biodiesel using response surface methodology.

Bioconvection is the term used to describe the process by which microorganisms randomly travel in single-cell or colony-like shapes. To show the bioconvection phenomenon, Vincent et al. [20] used a floated algae solution. Li et al. [21] discussed bioconvection heat transfer in third-grade fluid using activation energy. Hussain et al. [22] explored the bioconvection effect on hybrid nanofluid with microorganisms Cattaneo-Christov heat flux. Elsebaee et al. [23] studied microorganism flow with tri-hybrid particles using a magnetic field over a slandering sheet. Khashi’ie et al. [24] studied the dual solutions of hybrid nanofluids using microorganisms towards a vertical plate. Sreedevi et al. [25] investigated the Williamson hybrid nanofluid with microorganisms and Cattaneo-Christov heat flux. Xu et al. [26] examined Maxwell fluid with microorganisms within parallel plates.

The heated surface has the potential to improve the heat transfer further over the infinite stretch surfaces. This provides researchers with options, along with higher thermal conductivity of the hybrid nanofluids. We can also employ the convective boundary to boost the heat transfer process in many engineering applications such as MEMS and solar through collectors. In the Newtonian and non-Newtonian flow examination over the stretched surface with different body force effects, many researchers have considered the heated surface while modeling the boundary conditions of the problems. Jusoh et al. [27] discussed heat transfer with viscous dissipation and convective boundary conditions using hybrid nanofluids. Rashid et al. [28] examined hyperbolic tangent fluid over a stretching surface with convective conditions. Waini et al. [29] explored heat transfer over stretching/shrinking surfaces with convective boundaries. Aly et al. [30] magneto-hydrodynamic flow with hybrid nanofluid over stretching/shrinking using heated boundary conditions. Hassan et al. [31] investigated the hybrid ferrofluid over a stretching surface using the thermal slip condition with a nanoparticle shape effect. Srinivasulu et al. [32] studied inclined magnetization with convective boundary conditions for the non-Newtonian fluid over a stretched surface. Yamda et al. [33] discussed the effective thermal conductivity whereas, Xue [34] examined the thermal conductivity of the carbon nanotube base materials.

In the above literature review on the hybrid nanofluids, it was discovered that there is a lack of information on the dynamics of a mixture base as working fluid over a stretched surface. It is worth mentioning here the convective boundary condition plays a significant role in heat transfer. Additionally, the modified Buongiorno nanofluid model has not been employed with the Prandtl fluid model and microorganism profiles at the same time. Moreover, the magnetite and silver nanoparticles with a mixture base working fluid were not examined with the assumptions mentioned above. Therefore, in this article, we focus on investigating the Bioconvective hybrid nanofluid using a mixture base working fluid over the heated stretched surface, considering the modified Buongiorno nanofluid model with swimming microorganisms. We utilize a suitable similarity transformation to convert the partial differential equations into ordinary differential equations. In order to obtain the necessary numerical solution of modified partial differential equations, Matlab software is used with the bvp4c package. It will be possible to comprehend how emerging parameters affect fluid flows. Dimensionless parameters will be utilized to examine the behaviour of several physical and heat transfer characteristics of the hybrid nanofluid flow. This study focuses on the following research questions:

•   How does mixed convection affect the flow of hybrid Prandtl nanofluid through a stretched heated sheet?

•   How do the Prandtl number, thermophoresis, and Brownian motion affect the mixture-base hybrid nanofluid in the presence of microorganisms?

•   Interpret the manner in which bio-convection affects the motile microbe dispersion.

•   How do thermophoretic diffusion, Brownian motion, mixed convection, thermal Biot number, and Prandtl number affect the skin friction and Nusselt number?

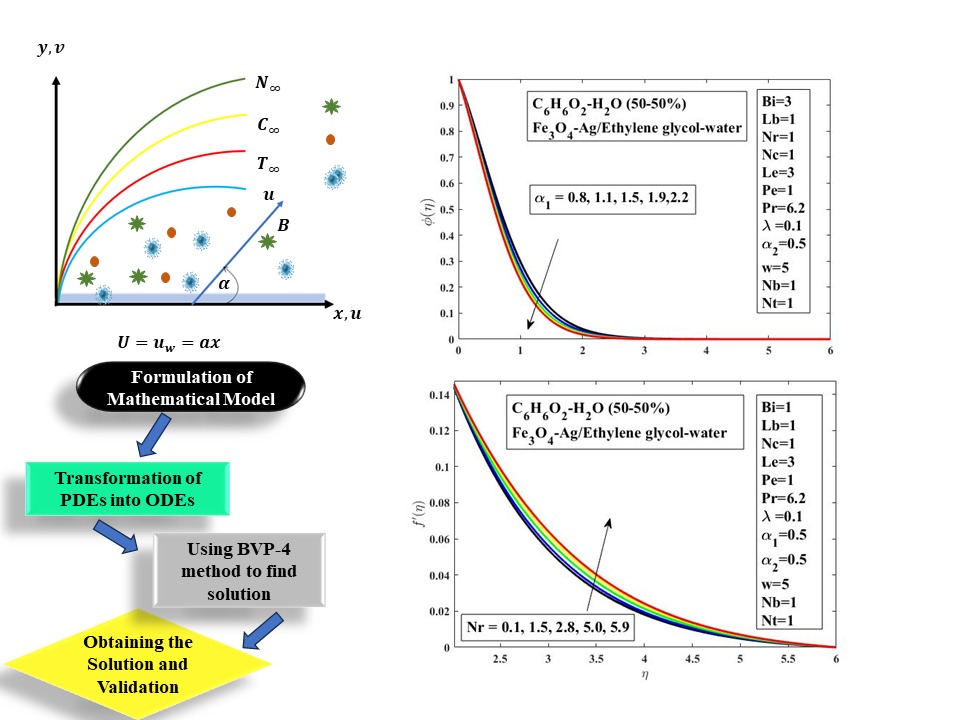
2  Mathematical Modeling of the Problem

In this section, the flow governing mathematical model has been developed using the following assumptions:

The surface is stretched horizontally with some stretching velocity.

The convective boundary condition is applied at the surface.

Modified Buongiorno nanofluid has been taken into consideration.

Magnetite Fe2O4 and silver Ag are used as nanoparticles. Mixture base fluid comprising (50%–50%) ethylene glycol C6H6O2 and water H2O are used to constitute the desired hybrid nanofluid Fe2O4−Ag/C6H6O2−H2O.

2.1 Statement of Problem

Let us consider two dimensions: a steady, incompressible flow of hybrid nanofluid over the stretched surface, stretched with some stretching velocity in the x-direction. The flow is restricted to the upper half of the plane, i.e., y>0. Cartesian coordinated system has been taken into account. The surface is heated with applied heating. The surface contains microorganisms. Fig. 1 shows the configuration of the problem.

Figure 1: Geometry of problem

Buongiorno [2] presented a nanofluid model using thermophoretic particle diffusion and Brownian motion. We employed its modified form, as discussed by Hussain et al. [22]. Following are the flow governing equations conservation of mass (continuity) (1), conservation of momentum (2), energy Eq. (3), concentration (4), and motile microorganisms Eq. (5), respectively, developed using the above-mentioned flow assumptions.

∂u∂x+∂v∂y=0.(1)

u∂u∂x+v∂u∂y =VhnfAC(∂2u∂y2)+VhnfA2C3(∂2u∂2y)(∂u∂y)2+1ρhnf[g(T−T∞)ρfβ(1−C∞)+g(C∞−C)(ρp−ρf)−(ρm−ρp)(N∞−N)gγ ′].(2)

u∂T∂x+v∂T∂y=αhnf(∂2T∂y2)+τ((∂2T∂y2)DTT∞+∂T∂yDB∂C∂y).(3)

u∂C∂x+v∂C∂y+=DB∂2C∂y2+(∂2T∂y2)DTT∞.(4)

u∂N∂x+v∂N∂y=Dm∂2N∂y2+bwc(C∞−Cw)∂∂y(N∂C∂y).(5)

All of the variables used in these equations are specified using nomenclature. The next are the appropriate boundary conditions for the present literature [22]:

Wheny→0,Nw=N,Cw=C,v=0,u=uw=ax,∂T∂y=−(Tw–T)hkhnf.(6)

Wheny→∞,u→0,T→T∞,C→C∞,N→N∞.(7)

The flowing suitable similarity transform is used to transform dimensional equations into dimensionless flow governing equations [22]:

η=avfy,Ψ(η)=f(η)avfx,

u=∂Ψ∂y,v=−∂Ψ∂x,θ(η)=T−T∞Tw−T∞,

φ(η)=C−C∞Cw−C∞,X(η)=N−N∞Nw−N∞.(8)

In accordance with the above-mentioned similarity relations, Eq. (1) is demonstrated as being identical, and Eqs. (2) to (5) are reconstructed as:

f′′ ′(α1+α2f′′2)+D1(ff′′−f′2)+D2(θ−Nrφ−NcX)λ=0.(9)

1PrD3D4θ ″+fθ ′+NTθ ′2+Nbθ ′φ ′=0.(10)

φ ″+Lefφ ′+NTNbθ ″=0.(11)

X ″−(X ′φ ′+(ω+X)φ ″)Pe+fLbX ′=0.(12)

Then the Eqs. (6) and (7) are reconstructed as:

Whenη→0,f ′=1,f=0,X=1,θ ′=kfkhnfBi(θ−1),φ=1.(13)

Whenη→∞,φ→0,θ→0,f ′→0,X→0.(14)

where θ, φ,X and f are functions of η. Furthermore, prime denotes the differentiation w.r.t η, Pr=vf(ρCp)fkf is Prandtl number, Lb=vfDm is Bioconvection Lewis number, Le=vfDB indicates Lewis number, λ=(1−C∞)βg(Tw−T∞)ax2andNt=τDT(Tw−T∞)νfT∞ denotes mixed convection and thermophoresis particle diffusion, respectively, Bi=hkfvfα is thermal Biot number, Peclet number is Pe=bwcDm, the bioconvection constant is denoted as ω=N∞Nw−N∞, the Rayleigh number bioconvection is Nc=γ ′(ρm−ρf)(N∞−Nw)(C∞−1)ρfβ(Tw−T∞), Nb=τDB(Cw−C∞)νf indicate the Brownian motion parameter, Nr=(ρp−ρf)(Cw−C∞)(1−C∞)ρfβ(Tw−T∞) denotes the buoyancy ratio parameter, the parameter of Prandtl fluid is shown as α1=AC, the elastic parameter is defined as α2=a3x2A2vfC3.

Now, the useful thermo-physical properties are the same as those explored by Hassan et al. [17,31]:

D1=(1−φ1)+φ1ρs1ρs(1−φ2)+φ2ρs2ρs(1−φ2)2.5(1−φ1)2.5,(15)

D2=(1−φ2)2.5(1−φ1)2.5,(16)

D3=((1−φ1)+φ1(ρCP)S1(ρCP)f)(1−φ2)+(ρCP)S1(ρCP)fφ1,(17)

D4=(kbf–ks2)φ2+ks2+(m−1)kbf(m−1)kf+ks2−(m−1)(kf−ks2)φ2.

(kf−ks1)φ1+ks1+(m−1)kf(m−1)kf+ks1−(m−1)(kf−ks1)φ1.(18)

Physical quantities are defined by Hussain et al. [22]:

Cfx=τwρfuw2, And Nux=xq∗wkf(Tw−T∞).(19)

The heat flux q∗w=−khnf(∂T∂y)y=0. The shear stress at the surface is τw=μhnf(AC∂u∂y+A2C3(∂u∂y)3).

Expressions (19) are transformed using the established similarity relations.

Cfx=1B2Rex−0.5(α1+α2f ″(0)2)f ″(0),(20)

Nux=−khnfkfRex0.5θ ′(0).(21)

So, the relevant Reynolds number is Rex=uwxvf.

3  Numerical Solution

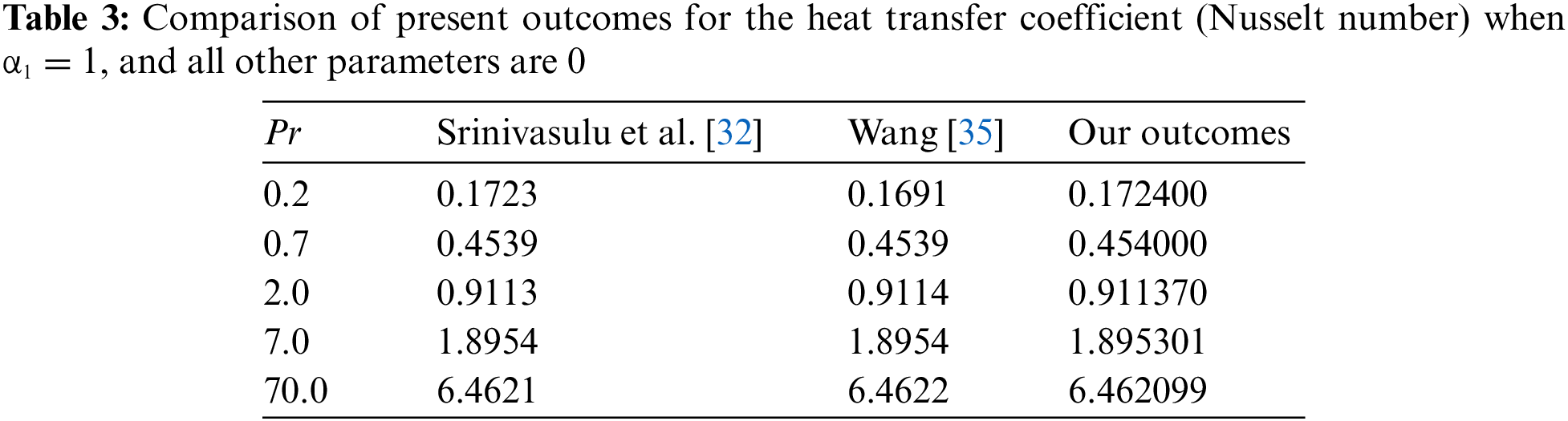
The non-dimensional Eqs. (9)–(12), which also have limits (13) and (14), have a nonlinear nature, making it challenging to compute them analytically. Due to the nonlinear nature of these differential equations, analytical solutions are not achievable. In the problem that is explained here, ordinary differential equations involving the boundary conditions are established to be capable of being resolved numerically. These solvable mathematical equations in the non-dimensional form have been numerically resolved as a result of adopting the bvp4c package, together with boundary conditions (13), (14). First-order PDEs are created by converting the associated nonlinear ordinary differential Eqs. (9)–(12) in Matlab using the bvp4c solver. The Matlab software is used to perform the above-mentioned mathematical programming in order to find a solution for the hybrid nanofluid over an extended sheet. The computing outcomes of the proposed method are compared with those acquired by other researchers, Wang [35] and Srinivasulu et al. [32], under restrictive conditions. Table 3 demonstrate that the present outcomes are consistent.

f′=s2,f=s1,f′′=s3,f′′ ′=ss1,

θ=s4,θ ′=s5,θ‘‘=ss2,

φ=s6,φ‘=s7,φ‘‘=ss3,

χ=s8,χ‘=s9,χ‘‘=ss4.(22)

ss1=1(α1+α2s3)(−D1(s1s3−s22)−D2λ(s4−Nrs5− Ncs8)),(23)

ss2=−PrD3D4[(s1s5)+Nbs5s7+NTs52],(24)

ss3=−Les1s7−NTNbss5,(25)

ss4=(s8s9+(w+s8)ss3)Pe−Lbs1s9.(26)

The boundary conditions are also:

When η→0,s2=1,s1=0,s8=1,s5=kfkhnfBi(θ−1),s6=1.(27)

Whenη→∞,s6→0,s4→0,s2→0,s8→0.(28)

3.1 Code Validation

In this part, the results of the current study are verified using previously released findings by Srinivasulu et al. [32], using modified parametric values. By altering the Prandtl number between 0.7<Pr≤70.2 and while maintaining the elasticity ratio fixed at unity and setting all other parametric values to zero, we were able to compare the Nusselt number. The comparative findings are shown in Tables 3 and 4.

4  Results and Discussion

In this section the influence of different study parameters has been presented in a graphical manner on the distinct study profiles such as velocity, temperature, concentration, and microorganism profiles have been discussed. The effective range of the parametric values are as follows: elastic parameter (1≤α2≤9), Prandtl fluid parameter (0.8≤α1≤2.2), mixed convection (0.1≤λ≤3), Prandtl number (1≤Pr≤1.8), Lewis number (3≤Le≤3.8), Bioconvection Lewis number (0.5≤Lb≤0.9), and (1≤Pe≤1.16). The influences of the elastic parameter (1≤α2≤9) and the Prandtl fluid parameter (0.8≤α1≤2.2) on the velocity profile are demonstrated in Figs. 2 and 3, respectively. With the increment in the elasticity and Prandtl fluid values, the velocity profile also enhances. Physically, when Prandtl fluid levels are increased the fluid viscosity decreases eventually raising the motion profile.

Figure 2: Prandtl fluid α1 effect on velocity f ′

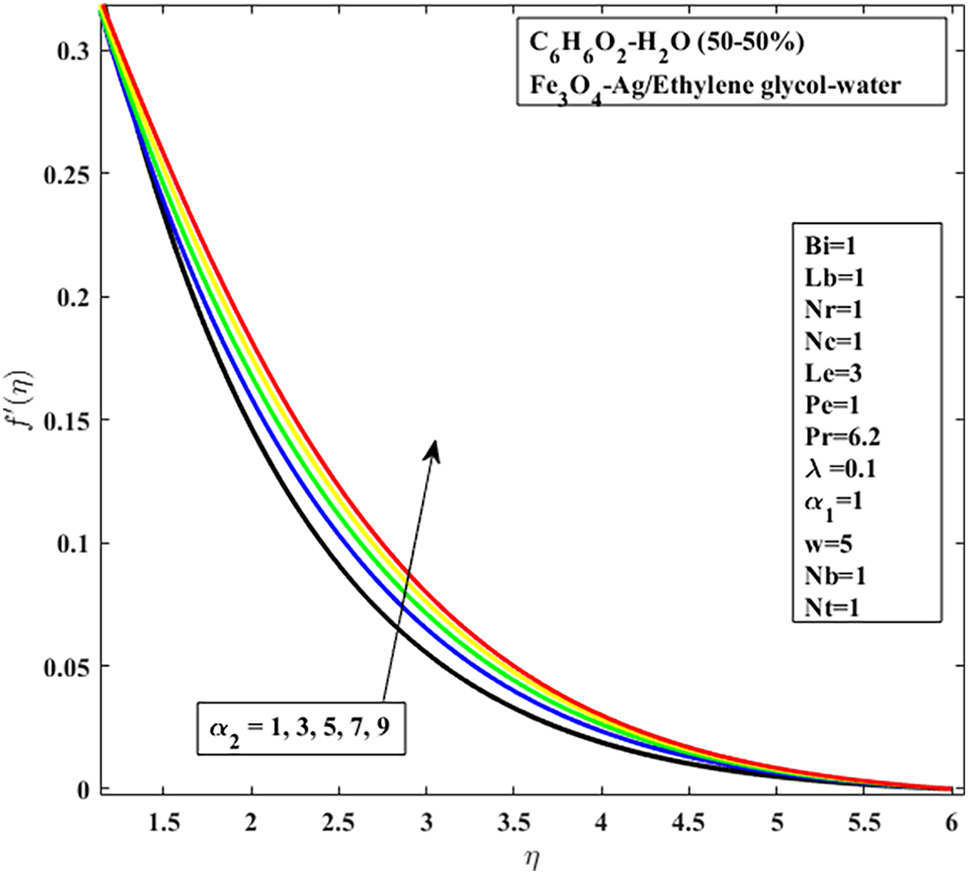
Figure 3: Elasticity α2 impact on velocity profile f ′

The overall outcome of mixed convection (0.1≤λ≤3) on the distribution of velocity in the hybrid nanofluid is demonstrated in Fig. 4. This tendency is brought on by the beneficial mixed convection, which acts as a helpful pressure gradient and accelerates the fluid in the boundary layer. The velocity profile for hybrid nanofluid flow grows as these mixed convection levels rise. Figs. 5 and 6 show the outcomes of the Rayleigh bioconvection number and buoyancy ratio, respectively, on the motion profile of hybrid nanofluid. The hybrid nanofluid flow velocity profile is grown by increasing the standard values of the Nr parameter. Nr has a sustaining force-like behaviour that accelerates the fluid nanoparticles close to the sheet. Similarly, the velocity profile for hybrid nanofluid flow rises as Nc parameter values increase.

Figure 4: Mixed convection λ effect on f ′

Figure 5: Rayleigh bio-number Nc vs. f ′

Figure 6: Buoyancy ratio Nr impact on f ′

The effects of Nb and Pr on temperature are shown in Figs. 7, 8. It has been demonstrated that as the Prandtl number (1≤Pr≤1.8) values increase, the temperature curves of hybrid nanofluids go down, as shown in Fig. 7. The opposite behaviour is shown by the Nb parameter in Fig. 8. Brownian motion parameter temperature curves grow as parameter values rise. The effects of Bi and Nt on temperature are shown in Figs. 9, 10, respectively. Figs. 9, 10 show that the temperature profile of hybrid nanofluids is enhanced when the thermal Biot number and levels of thermophoresis particle diffusion are increased. By extending the energy gradient, moving forward towards the surface results in a drop in the temperature boundary layer thickness, as seen by the thermal Biot number.

Figure 7: Brownian motion Nb effect on θ

Figure 8: Prandtl number Pr impact on θ

Figure 9: Thermal Biot number Bi vs. θ

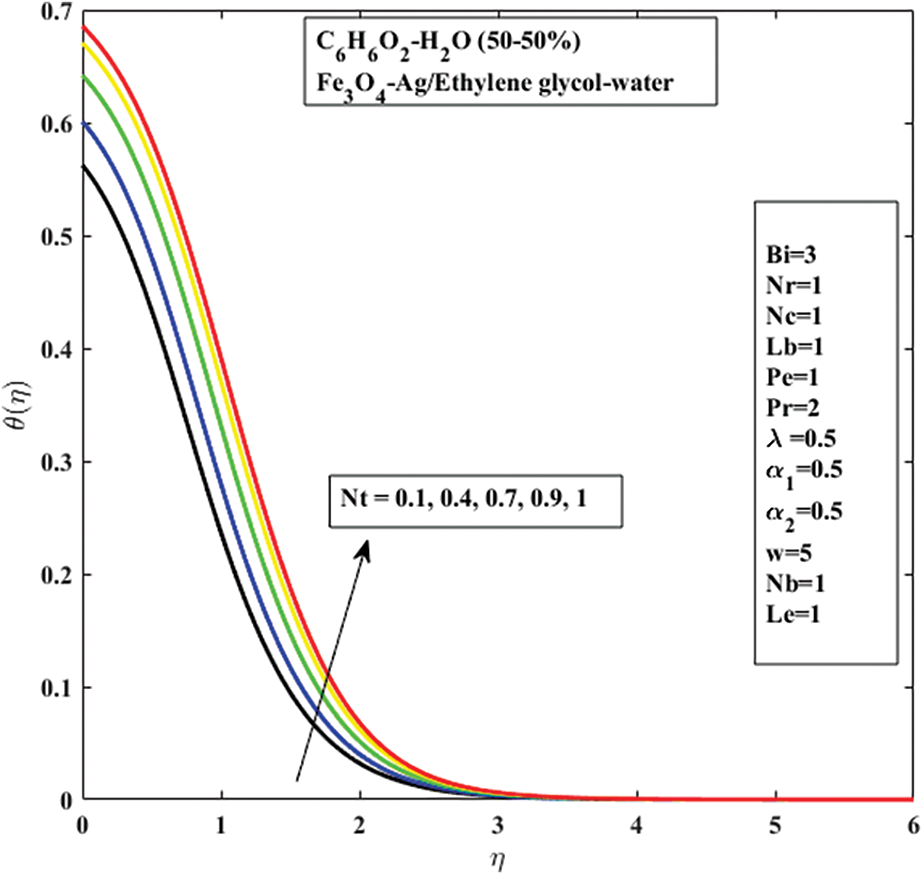
Figure 10: Thermophoretic Nt effect on θ

Fig. 11 demonstrates the effect of the Lewis number (3≤Le≤3.8) on hybrid nanofluid profile over the heated surface. Fig. 11 demonstrates that fluid concentration dropped as Le values were augmented. The boost in kinetic energy brought through the fluid particles and accelerated velocity causes the boundary layer to enlarge. Theoretically, the particle migrating from peak locations to bottom areas accelerates quickly as (Le) parameter values grow. Figs. 12, 13 demonstrate the pattern of the hybrid nanofluid concentration curve for rising values of Nb and Nt on the concentration curves. Thermophoresis and Brownian motion have opposite effects on the concentration profile. The increase in Brownian motion declines the concentration profile abruptly, while the increment in thermophoresis motion enhances the concentration profile. Further, it has been observed that with an increase in thermophoresis particle diffusion, the concentration layer thickness has increased.

Figure 11: Lewis number Le impact on φ

Figure 12: Brownian motion Nb effect on φ

Figure 13: Thermophoretic Nt effect over φ

Figs. 14, 15 demonstrate the hybrid nanofluid behaviour of motile microbes (X(η)) under the impact of bio-convective and Peclet numbers, respectively. Fig. 14 demonstrates the effect of the Bioconvection Lewis number (0.5≤Lb≤0.9). Based on outcomes, when Lb levels rise, microbe profiles also decline. Additionally, it is worth mentioning here that with an increase in the bio-convection number, the thickness of the microbe’s boundary layer has expanded rapidly. Microorganism trends are shown in Fig. 15 under the influence of the Peclet number (1≤Pe≤1.16). It has been observed that with an increase in Peclet number, the microbes profile significantly enhances. In Figs. 16–18, skin friction and Nusselt number have been demonstrated in a graphical manner under the variation of buoyancy and Brownian motion effect.

Figure 14: Bioconvective Lewis number Lb effect vs. X

Figure 15: Peclet number Pe effect on X

Figure 16: Skin friction under Buoyanct ratio effect

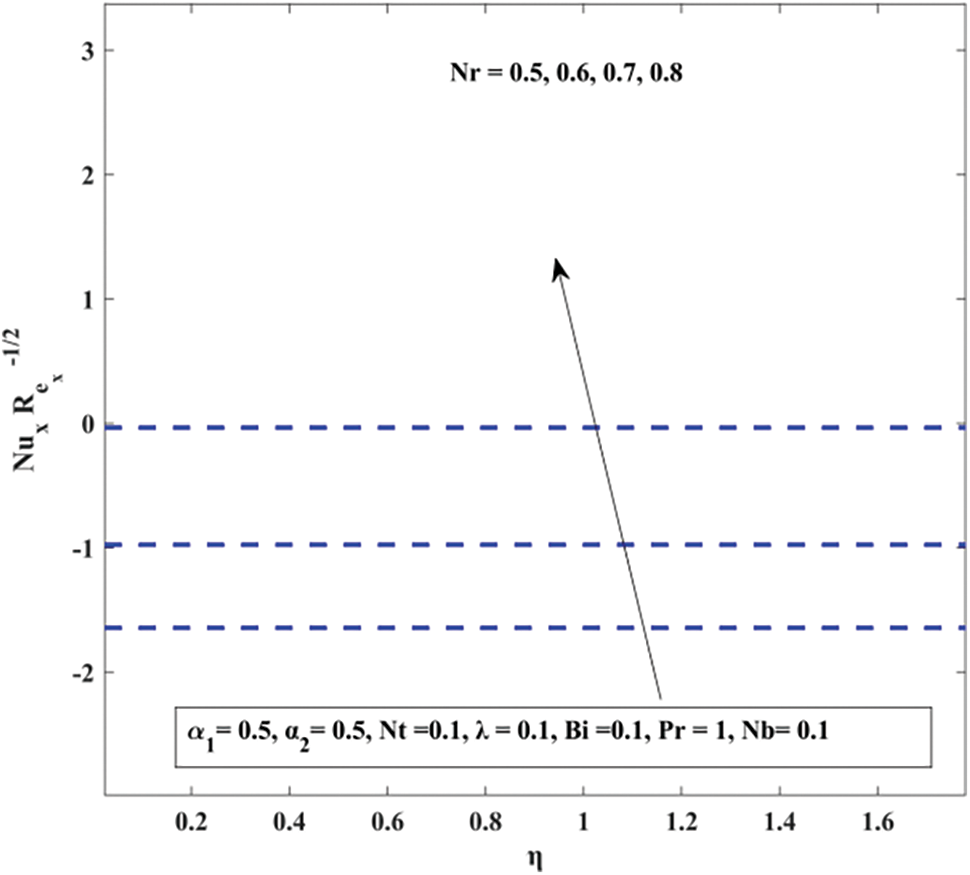
Figure 17: Nusselt number with buoyancy ratio

Figure 18: Nusselt number with Brownian motion

Table 1 gives the values of the thermophysical properties of the nanoparticles and working base fluid. Table 2 provides thermophysical relations used in this study for different fluid hybrid nanofluid properties. Table 3 demonstrates the comparison between current results and already published results. Table 4 shows the numerical outcome of the skin friction coefficient and Nusselt number under the influence of different study parameters such as Prandtl fluid parameter α1, Elastic parameter α2, Brownian motion Nb, thermophoresis diffusion Nt, mixed convection parameter λ, thermal Biot number Bi, Prandtl number Pr and buoyancy ratio Nr.

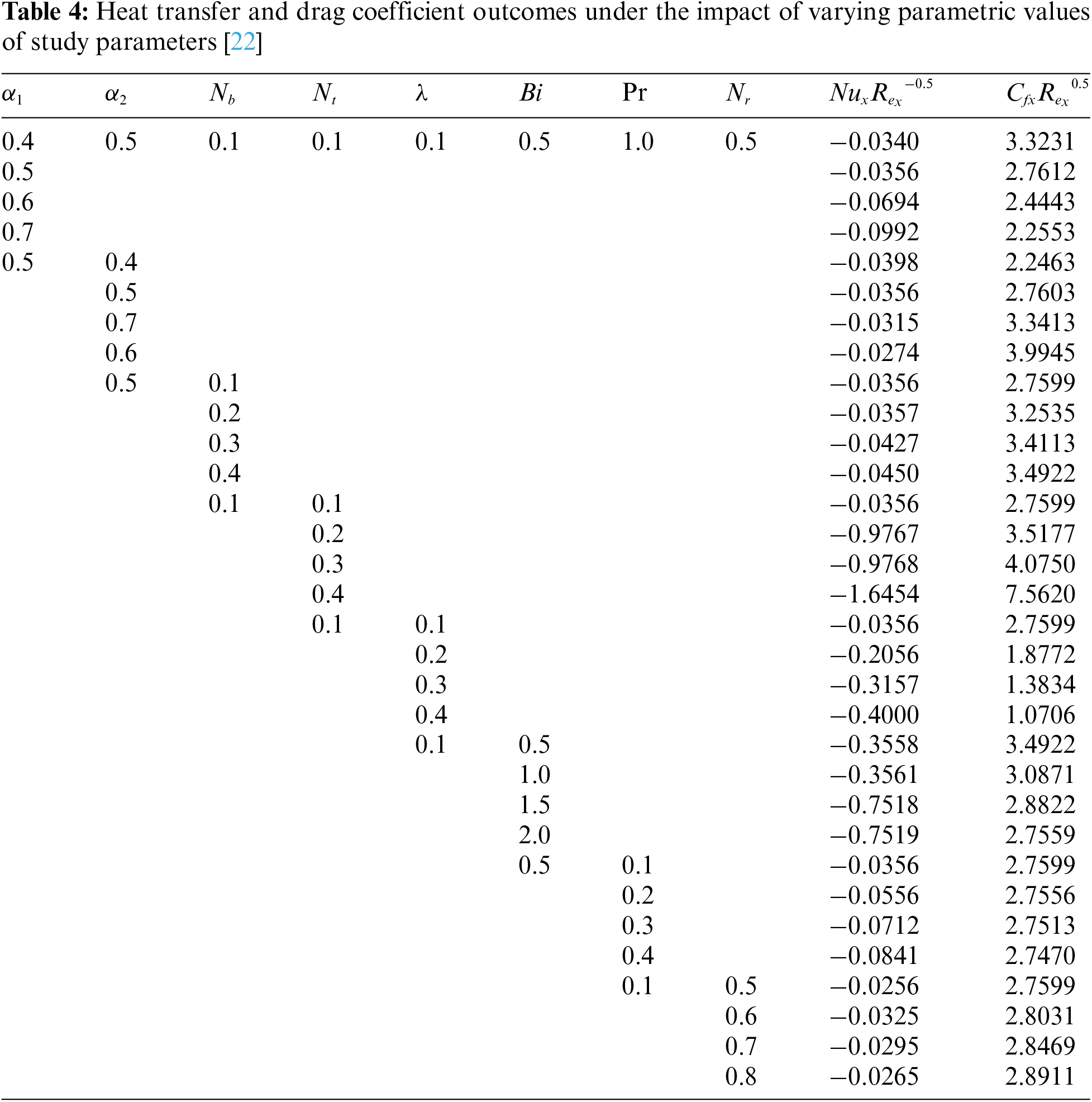
It has been observed that skin friction and Nusselt number both decrease when the Prandtl fluid parameter and elastic parameter values are in the range of 0.4<α1≤0.7 and 0.5<α2≤0.7, respectively. When the Brownian motion values are in the range of 0.1<Nb≤0.4, the Nusselt number is enhanced whereas the skin friction also increases Thermophoretic particle diffusion 0.1<Nt≤0.4 significantly decrease the Nusselt number but increase the surface drag. It can be verified from Table 3 that mixed convection 0.1<λ≤0.4 parameters decrease both Nusselt number and skin friction.

Raising the values of thermal Biot number 0.5<Bi≤2.0 decrease the Nusselt number and skin friction. A significant decline has been observed in the Nusselt number by raising the values of Prandtl number 1<Pr≤4. Whereas buoyancy ratio 0.5<Nr≤0.8 decrease the surface drag but it improves the Nusselt number.

4.1 Models of Thermal Conductivity and Viscosity

It can be easily observed through the above conducted literature review that theoretical viscosity and thermal conductivity models are commonly used by researchers (Srinivasulu et al. [32], Hassan et al. [31] and Saleem et al. [11]). These models have their own pros and cons. In this study, we have utilized thermophysical relations proposed in Yamada Ota (Yamada et al. [33]) model hybrid nanofluid. This model has been used by numerous researchers such as Hussain et al. [22], Saleem et al. [11], and Srinivasulu et al. [32]. The advantage of these theoretical models is that they are easy to use, time-saving, and easily available, whereas it is difficult to find experimental data and experiments are costly. It is generally more easy to use an already established theory rather than looking for the experimental outcomes. Additionally, with theoretical thermophysical relation optimal outcomes can never be possibly achieved as demonstrated by Xue [34]. Therefore, researchers prefer to use already established results or thermophysical relations.

5  Conclusion

In this work, the bio-convection enhanced heat transfer using the hybrid nanofluids with modified Buongiorno’s model over a stretched surface has been investigated. The Prandtl fluid model has been utilized and convective boundary condition is also taken into consideration. The flow governing the nonlinear partial differential model is converted into ordinary dimensionless differential equations. The dimensionless flow equations are solved numerically using the bvp4c package in MATLAB. The following are the key findings of the present study:

•   The velocity curve of the Fe3O4-Ag/EG-water-base hybrid nanofluid increases by raising the levels of the buoyancy ratio and mixed convection.

•   Elastic, thermophoresis parameter and thermal Biot number values enhance temperature profile. The Brownian motion and the Prandtl number, however, exhibit the reverse trend.

•   On the concentration profile, the hybrid nanofluid exhibits a decrease in the Lewis number but increases in the elasticity, thermophoresis, and buoyancy ratio.

•   Peclet parameters, elastic parameters, and bio-convection numbers all demonstrate an enhancement in the microorganisms’ profile in hybrid nanofluids. The Bioconvection Lewis number, however, displays the reverse trend.

•   The skin friction coefficient of hybrid nanofluid demonstrates a tendency to decrease for greater inputs of Pr, α1, and Bi, but an increasing tendency is shown for Nb, Nt, α2, and Nr.

•   The Nusselt number falls for Pr, Nb, and Nt, whereas it increases for α2, Bi, and Nr.

Acknowledgement: The authors would like to acknowledge the constructive remarks by worthy reviewers that led to this revised article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Azad Hussain and Ali Hassan; data collection: Saira Raiz; analysis and interpretation of results: Saira Raiz and Ali Hassan; original draft manuscript preparation: Saira Raiz; writing review and editing: Ali Hassan; investigation and validation: Mohamed R. Ali and Abdulkafi Mohammed Saeed. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data can be made available from the corresponding author following a special request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of Fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne, IL, USA: Argonne National Lab. (ANL). [Google Scholar]

2. Buongiorno, J. (2006). Convective transport in nanofluids, ASME Journal of Heat and Mass Transfer, 128(3), 240–250. https://doi.org/10.1115/1.2150834 [Google Scholar] [CrossRef]

3. Turkyilmazoglu, M. (2019). Fully developed slip flow in a concentric annuli via single and dual phase nanofluids models. Computer Methods and Programs in Biomedicine, 179, 104997. https://doi.org/10.1016/j.cmpb.2019.104997 [Google Scholar] [PubMed] [CrossRef]

4. Sarada, K., Gowda, R. J. P., Sarris, I. E., Kumar, R. N., Prasannakumara, B. C. (2021). Effect of magnetohydrodynamics on heat transfer behaviour of a non-Newtonian fluid flow over a stretching sheet under local thermal non-equilibrium condition. Fluids, 6(8), 264. [Google Scholar]

5. Babu, M. J., Sandeep, N. (2016). MHD non-Newtonian fluid flow over a slendering stretching sheet in the presence of cross-diffusion effects. Alexandria Engineering Journal, 55(3), 2193–2201. [Google Scholar]

6. Sharma, R. P., Avinash, K., Sandeep, N., Makinde, O. D. (2017). Thermal radiation effect on non-Newtonian fluid flow over a stretched sheet of non-uniform thickness. In: Defect and diffusion forum, vol. 377, pp. 242–259. Switzerland: Trans Tech Publications Ltd. https://doi.org/10.4028/www.scientific.net/DDF.377.242 [Google Scholar] [CrossRef]

7. Ibrahim, S. M., Kumar, P. V., Makinde, O. D. (2018). Chemical reaction and radiation effects on non-Newtonian fluid flow over a stretching sheet with non-uniform thickness and heat source. In: Defect and diffusion forum, vol. 387, pp. 319–331. Switzerland: Trans Tech Publications Ltd. https://doi.org/10.4028/www.scientific.net/DDF.387.319 [Google Scholar] [CrossRef]

8. Ijaz Khan, M., Alzahrani, F. (2021). Numerical simulation for the mixed convective flow of non-Newtonian fluid with activation energy and entropy generation. Mathematical Methods in the Applied Sciences, 44(9), 7766–7777. [Google Scholar]

9. Ramesh, G. K. (2020). Analysis of active and passive control of nanoparticles in viscoelastic nanomaterial inspired by activation energy and chemical reaction. Physica A: Statistical Mechanics and its Applications, 550, 123964. [Google Scholar]

10. Ijaz Khan, M., Alzahrani, F. (2020). Activation energy and binary chemical reaction effect in nonlinear thermal radiative stagnation point flow of Walter-B nanofluid: Numerical computations. International Journal of Modern Physics B, 34(13), 2050132. [Google Scholar]

11. Saleem, N., Munawar, S., Tripathi, D. (2021). Entropy analysis in ciliary transport of radiated hybrid nanofluid in presence of electromagnetohydrodynamics and activation energy. Case Studies in Thermal Engineering, 28, 101665. [Google Scholar]

12. Beg, A., Balaji, R., Prakash, J., Tripathi, D. (2023). Heat transfer and hydromagnetic electroosmotic Von Kármán swirling flow from a rotating porous disc to a permeable medium with viscous heating and Joule dissipation. Heat Transfer, 52(5), 3489–3515. https://doi.org/10.1002/htj.22837 [Google Scholar] [CrossRef]

13. Dinarvand, S., Mousavi, S. M., Yousefi, M., Nademi Rostami, M. (2022). MHD flow of MgO-Ag/water hybrid nanofluid past a moving slim needle considering dual solutions: An applicable model for hot-wire anemometer analysis. International Journal of Numerical Methods for Heat & Fluid Flow, 32(2), 488–510. [Google Scholar]

14. Mansourian, M., Dinarvand, S., Pop, I. (2022). Aqua cobalt ferrite/Mn-Zn ferrite hybrid nanofluid flow over a nonlinearly stretching permeable sheet in a porous medium. Journal of Nanofluids, 11(3), 383–391. [Google Scholar]

15. Naz, R., Noor, M., Hayat, T., Javed, M., Alsaedi, A. (2020). Dynamism of magneto-hydrodynamic cross nanofluid with particulars of entropy generation and gyrotactic motile microorganisms. International Communications in Heat and Mass Transfer, 110, 104431. [Google Scholar]

16. Balla, C. S., Ramesh, A., Kishan, N., Rashad, A. M., Abdelrahman, Z. M. A. (2020). Bioconvection in oxytactic microorganism-saturated porous square enclosure with thermal radiation impact. Journal of Thermal Analysis and Calorimetry, 140, 2387–2395. [Google Scholar]

17. Hussain, A., Hassan, A., Al Mdallal, Q., Ahmad, H., Rehman, A. et al. (2021). Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Studies in Thermal Engineering, 27, 101244. [Google Scholar]

18. Arshad, M., Hassan, A. (2022). A numerical study on the hybrid nanofluid flow between a permeable rotating system. The European Physical Journal Plus, 137(10), 1126. [Google Scholar]

19. Rao, P. M., Dhoria, S. H., Patro, S. G. K., Gopidesi, R. K., Alkahtani, M. Q. et al. (2023). Artificial intelligence based modelling and hybrid optimization of linseed oil biodiesel with graphene nanoparticles to stringent biomedical safety and environmental standards. Case Studies in Thermal Engineering, 51, 103554. https://doi.org/10.1016/j.csite.2023.103554 [Google Scholar] [CrossRef]

20. Vincent, R. V., Hill, N. A. (1996). Bioconvection in a suspension of phototactic algae. Journal of Fluid Mechanics, 327, 343–371. [Google Scholar]

21. Li, X., Abbasi, A., Al-Khaled, K., Ameen, H. F. M., Khan, S. U. et al. (2023). Thermal performance of iron oxide and copper (Fe3O4, Cu) in hybrid nanofluid flow of Casson material with Hall current via complex wavy channel. Materials Science and Engineering: B, 289, 116250. [Google Scholar]

22. Hussain, A., Raiz, S., Hassan, A., Karamti, H., Saeed, A. M. et al. (2023). Significance of cattaneo-christov heat flux on heat transfer with bioconvection and swimming micro organisms in magnetized flow of magnetite and silver nanoparticles dispersed in prandtl fluid. BioNanoScience, 13, 2276–2292. https://doi.org/10.1007/s12668-023-01161-7 [Google Scholar] [CrossRef]

23. Elsebaee, F. A. A., Bilal, M., Mahmoud, S. R., Balubaid, M., Shuaib, M. et al. (2023). Motile microorganism based trihybrid nanofluid flow with an application of magnetic effect across a slender stretching sheet: Numerical approach. AIP Advances, 13(3), 035237. https://doi.org/10.1063/5.0144191 [Google Scholar] [CrossRef]

24. Khashi’ie, N. S., Arifin, N. M., Pop, I., Nazar, R. (2021). Dual solutions of bioconvection hybrid nanofluid flow due to gyrotactic microorganisms towards a vertical plate. Chinese Journal of Physics, 72, 461–474. [Google Scholar]

25. Sreedevi, P., Reddy, P. S. (2021). Williamson hybrid nanofluid flow over swirling cylinder with Cattaneo–Christov heat flux and gyrotactic microorganism. Waves in Random and Complex Media, 1–28. https://doi.org/10.1080/17455030.2021.1968537 [Google Scholar] [CrossRef]

26. Xu, Y. J., Bilal, M., Al-Mdallal, Q., Khan, M. A., Muhammad, T. (2021). Gyrotactic microorganism flow of Maxwell nanofluid between two parallel plates. Scientific Reports, 11(1), 15142. [Google Scholar] [PubMed]

27. Jusoh, R., Naganthran, K., Jamaludin, A., Ariff, M. H., Basir, M. F. M. et al. (2020). Mathematical analysis of the flow and heat transfer of Ag-Cu hybrid nanofluid over a stretching/shrinking surface with convective boundary condition and viscous dissipation. Data Analytics and Applied Mathematics (DAAM), 1(1), 11–22. [Google Scholar]

28. Rashid, A., Ayaz, M., Islam, S., Saeed, A., Kumam, P. et al. (2022). Theoretical analysis of the MHD flow of a tangent hyperbolic hybrid nanofluid over a stretching sheet with convective conditions: A nonlinear thermal radiation case. South African Journal of Chemical Engineering, 42, 255–269. [Google Scholar]

29. Waini, I., Ishak, A., Pop, I. (2019). Hybrid nanofluid flow and heat transfer past a permeable stretching/shrinking surface with a convective boundary condition. Journal of Physics: Conference Series, 1366(1), 12022. [Google Scholar]

30. Aly, E. H., Pop, I. (2019). MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. International Journal of Numerical Methods for Heat & Fluid Flow, 29(9), 3012–3038. [Google Scholar]

31. Hassan, A., Alsubaie, N., Alharbi, F. M., Alhushaybari, A., Galal, A. M. (2023). Scrutinization of Stefan suction/blowing on thermal slip flow of ethylene glycol/water based hybrid ferro-fluid with nano-particles shape effect and partial slip. Journal of Magnetism and Magnetic Materials, 565, 170276. [Google Scholar]

32. Srinivasulu, T., Goud, B. S. (2021). Effect of inclined magnetic field on flow, heat and mass transfer of Williamson nanofluid over a stretching sheet. Case Studies in Thermal Engineering, 23, 100819. [Google Scholar]

33. Yamada, E., Ota, T. (1980). Effective thermal conductivity of dispersed materials. Wärme-und Stoffübertragung, 13(1–2), 27–37. [Google Scholar]

34. Xue, Q. Z. (2005). Model for thermal conductivity of carbon nanotube-based composites. Physica B: Condensed Matter, 368(1–4), 302–307. [Google Scholar]

35. Wang, C. Y. (1989). Free convection on a vertical stretching surface. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 69(11), 418–420. [Google Scholar]