 Open Access
Open Access
ARTICLE
Enhancing Hygrothermal Performance in Multi-Zone Constructions through Phase Change Material Integration
1 Laboratory of Biomaterials and Transport Phenomena, University of Medea, Medea, 26000, Algeria
2 Unité de Recherche Appliquée en Energies Renouvelables (URAER) Centre de Développement des Energies Renouvelables (CDER), Ghardaïa, 47133, Algeria
3 Laboratoire de Génie des Procédés Chimiques, Department of Process Engineering, University of Ferhat Abbas, Setif, 19000, Algeria
4 Université de Rennes, Ecole Nationale Supérieure de Chimie de Rennes, CNRS, ISCR—UMR6226, Rennes, 35000, France
5 College of Engineering, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, 11432, Saudi Arabia
6 School of Engineering, Merz Court, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
* Corresponding Author: Jie Zhang. Email:
Frontiers in Heat and Mass Transfer 2024, 22(3), 769-789. https://doi.org/10.32604/fhmt.2024.050330
Received 03 February 2024; Accepted 29 May 2024; Issue published 11 July 2024
Abstract
As buildings evolve to meet the challenges of energy efficiency and indoor comfort, phase change materials (PCM) emerge as a promising solution due to their ability to store and release latent heat. This paper explores the transformative impact of incorporating PCM on the hygrothermal dynamics of multi-zone constructions. The study focuses on analyzing heat transfer, particularly through thermal conduction, in a wall containing PCM. A novel approach was proposed, wherein the studied system (sensitive balance) interacts directly with a latent balance to realistically define the behavior of specific humidity and mass flow rates. In addition, a numerical model implemented in MATLAB software has been developed to investigate the effect of integrating PCM on the hygrothermal balances inside the building. The obtained results indicate a consistent response in internal temperatures, specific humidity, and mass flow rates, with temperature differences ranging from 5°C to 13°C and a maximum phase shift of 13 h. In addition, the findings provided valuable insights into optimizing the design and performance of multi-zone constructions, offering a sustainable pathway for enhancing building resilience and occupant well-being.Keywords
Nomenclature
| Symbols | |
| Cas | Heat capacity of the air mass (J kg–1 K–1) |
| CIs, CIe | Internal sensitive and latent powers (devices, household appliances, occupants, lighting, etc.) (W) |
| Cp | Specific heat (J kg–1 K–1) |
| Cv | Heat capacity at constant volume (J kg–1 K–1) |
| e | Thickness (m) |
| F | Form factor between the exchange surfaces |
| G | Incident solar illuminance (W m–2) |
| hconv | Convective heat transfer coefficient (W m–2 K–1) |
| He(i) | Enthalpy of the mass of humid air entering zone i (J) |
| Hr | Relative humidity (%) |
| Hs(i) | Enthalpy of the mass of humid air leaving zone i (J) |
| Hs, rs(i) | Specific humidity: mass of water vapor per unit mass of dry air (kgvap/kgas or %) |
| j | Numbers of the interior surface (wall, door and window) in zone i |
| Lv | Latent heat of the vaporization of water (J kg–1) |
| n | Node numbers |
| NW(i) | Total number of interior surfaces (wall, door and window) in zone i |
| Ps, Pe | Sensible and latent powers provided by the air conditioning installation (W) |
| Psat | Steam saturation pressure (Pa) |
| Qemas(n,i) | Mass flow passing from zone n to zone k (kg/s) |
| Qsmas(n,i) | Mass flow of dry air passing from zone i to zone n (kg/s) |
| S | Area (m2) |
| Ta(n) | Air temperature of zone n = temperature of air entering zone i (K) |
| Tsij, TA | Temperature of surface j in zone i (K) |
| V(i) | Volume of zone i (m3) |
| Vs(i) | Specific volume of humid air in zone i (m3) |
| Vwind | Wind speed (m s–1) |
| Greek Letters | |
| α | Absorption coefficient |
| ε | Thermal emissivity |
| λ | thermal conductivity (W K–1 m–1) |
| ρ | density (kg m–3) |
| σ | Stephane-Boltzmann constant (W m–2 K–4) |
The built environment plays a crucial role in global energy consumption, with buildings accounting for a large share of energy use worldwide. Therefore, addressing energy efficiency in this sector is essential for reducing overall energy demand and mitigating environmental impacts. In Algeria, the building sector is the largest energy consumer, accounting for more than 41% of the overall energy consumption, surpassing the agriculture (33%), energy (19%), and industry and transport (7%) sectors. The Algerian National Agency for the Promotion and Rationalization of Energy Use (APRUE) aims to reduce energy consumption in residential and tertiary sectors by 10% to 15% by 2030. This goal presents several challenges, encompassing political, economic, social, cultural, and geographical issues [1,2].
Addressing this crisis requires aligning the architectural and energy strategies of housing. Recent data shows that natural gas and electricity dominate energy consumption, accounting for 53.61% and 33.7%, respectively, while liquefied petroleum gas and biomass represent just 12.46% and 0.01% of global consumption [3]. However, statistics indicate that useful energy is primarily consumed for heating, air conditioning, and domestic hot water production, and it is also essential for food cold storage (refrigerators and freezers), cooking, and lighting [4]. To tackle these challenges, the strategy must focus on finding more suitable solutions, exploring energy alternatives, and harnessing various potentials for energy use to develop applications beneficial to this energy-intensive sector. The overarching goal of this effort is to achieve more efficient and rational energy management. Actions and procedures will concentrate on enhancing thermal comfort and improving energy efficiency [5,6].
As the demand for heating and cooling in buildings rises during colder and warmer seasons, their energy consumption has increased significantly. Consequently, phase change materials (PCM) have become the preferred choice for latent thermal storage applications in the building industry. This approach is gaining popularity in Algeria, where incorporating PCM has proven to be ideal and effective for significantly reducing energy costs in buildings, refrigeration systems, and water heaters. The importance of these contributions is directly related to quantifying the energy needs for heating and cooling. Implementing these measures can lead to more environmentally friendly solutions [7]. First, latent heat can be stored with limited storage volumes and it is possible to store six to eight times more thermal energy than sensible heat in the same volume In addition, the phenomena generated using PCM (energy storage or release) lead to a stabilization of operating temperatures [8–10]. Furthermore, incorporating phase change materials (PCM) into buildings can decrease energy dependency by utilizing latent heat storage to boost thermal inertia without significantly adding to the building’s weight [11–13]. Finally, integrating PCM into the building’s structure can enhance the thermal inertia of its envelope, which can slow down heat transfer during peak times and minimize large indoor temperature variations. This results in improved thermal comfort and reduced energy consumption [14–17].
Among the standards necessary for the thermal design of buildings, two basic standards must be considered, user comfort and efficient energy management, which can lead to contradictory recommendations. In the analysis of these two aspects, the humidity content of the air can have significant impacts. However, the majority of building energy simulation codes neglect air humidity or represent it in a very simplified manner. Often humidity is simply transported by the air, whereas in the majority of real cases, its interactions with hygroscopic materials cannot be neglected. In the design of an efficient building (in the energy efficiency sense), in addition to the need to offer more efficient and less energy-consuming equipment, it is essential to control thermal exchanges through the envelope.
The energy balance results from a balance between thermal gains and losses, between the envelope and its environments (interior and exterior). The design of envelopes, capable of exploiting free energy gains while limiting losses, must contribute to reducing energy needs without harming interior comfort. The envelope then becomes a real heat exchanger that can be managed and adapted to indoor and outdoor environments [18].
Bioclimatic design has developed significantly since the 1970s and has given rise to numerous research which has made it possible to produce bioclimatic design tools, for architects, design offices, and engineers. Through this work, we want to achieve a reliable and comprehensive tool. The desired completeness is achieved by considering all the physical phenomena necessary for a complete representation of reality. We are also interested in the study of certain parameters that can be decisive for indoor comfort, in particular relative humidity, temperatures, and incoming mass flow rates. In current buildings, it is preferred to reduce the thickness of the walls to reduce costs while respecting standards to limit thermal losses. However, such structures do not provide sufficient thermal inertia capable of dampening fluctuations in the external temperature. One of the ways to reduce the energy needs of a building is therefore the design of an energy-efficient envelope, limiting losses and recovering passive contributions as much as possible. To achieve these objectives, a certain number of basic principles need to be considered and the most important ones are insulation and thermal inertia as well as the use of solar gain.
This paper addresses the pressing issue of energy consumption in the building sector in Algeria, which accounts for a significant portion of the nation’s energy usage. Despite the dominance of natural gas and electricity in energy consumption, the focus remains on heating, air conditioning, domestic hot water production, and other essential services. To tackle these challenges, a comprehensive strategy is necessary, one that integrates energy-efficient solutions and harnesses available resources effectively. The utilization of PCM allows for the storage of latent heat, leading to stabilized operating temperatures and improved energy efficiency. Moreover, the paper highlights the significance of considering air humidity in building energy simulations, as it plays a crucial role in indoor comfort and energy management.
The present study emphasizes the importance of bioclimatic design principles and the development of reliable tools to optimize building performance. By considering all relevant physical phenomena and parameters such as relative humidity and temperature, the research aims to provide a comprehensive understanding of indoor comfort factors. Additionally, the paper underscores the importance of energy-efficient envelopes in reducing thermal losses and passive contributions. The research methodology involves simulating the thermo-aeraulic behavior of a multi-zone home in Ghardaïa, Algeria, using a coupled mathematical model. Furthermore, a wall model incorporating PCM is implemented, considering the region’s climatic conditions. The melting temperature of the PCM material used is specified at 22.6°C [19–21].
The majority of building energy simulation codes neglect air humidity or represent it in a very simplified manner. In this study, the proposed model focuses on the description of thermo-aeraulic transfers in this construction.
Let zone i be in contact with N + 1 other zones (zone No. 0 is exterior), the enthalpy variation per unit of time for zone i can be written as follows:
where:
In building thermal, the variations in mass,
From this equation, the sum of the mass flow rates of dry air entering zone i is equal to the sum of the flow rates leaving zone i. This equation makes it possible to simplify the enthalpy balances [22].
2.3 Sensitive and Latent Balances
The enthalpy balance equation can be written as:
The term
In this case, the following approaches can be assumed:
This simplification makes it possible to write the following enthalpy balance equation [23]:
In the field of residential thermal energy, mass variations over time represent very small quantities. Consequently, the variation in enthalpy can therefore be assimilated by the variation in temperatures [23]:
Therefore, a system of N equations with N unknowns is obtained which represent the air temperature of each zone. The surface temperatures Tsij can be obtained by establishing the thermal balance of the walls. The empirical formula of Nadeau et al. [24] can be also used directly.
The specific humidity can be given as a function of relative humidity by the following relationships:
2.4 Exchange by Conduction and Coupling with Superficial Exchanges
The translation of a thermal problem of conduction into an electrical problem is called thermoelectric analogy. By making this analogy, the nodal method leads to the establishment of an electrical network as shown in Fig. 1. The nodes that lie in the equipotential electrical directions symbolize isothermal lines. These are connected by the analogy resistance of the physical layer of the wall which separates them. Consequently, each of these nodes makes it possible to obtain an electric capacitor reflecting the thermal storage of the corresponding part of the wall and allowing the translation of thermal inertia effects.

Figure 1: Spatial discretization of a wall and conduction model
The multilayer system is represented by a model proposed by Rumianowski et al. [25]. The developed model is based on the following assumptions:
– Heat transfers through the walls are assumed to be unidirectional and perpendicular to these walls.
– Natural convection is assumed.
– The permanent regime is established.
– The temperature distribution on the walls is uniform.
– The characteristics of the materials are constant and independent of weather conditions.
– The celestial vault is likened to a black body for long-wavelength radiation.
For the system shown in Fig. 1, the following can be established:
Thermal capacities are determined as follows:
The building’s energy balance for surface areas is represented by the following equations:
The energy balance of a habitat zone represented by a node is an air balance model of the zone, which represents the heat capacity of the air volume of the zone. The energy balance of the construction of a zone is represented by the equation below which constitutes the variation of the air energy of the zone in the time interval
The thermal energy transfer rates of ventilation air infiltration and flow are respectively calculated by the following equations:
The thermal energy due to the exchange between the air and the interior surfaces of the walls is calculated by the following equation [26]:
The detailed modeling and calculation methodology have been presented and validated in previous works [27–30].
2.5 Direct Incorporation of Plaster-PCM into Partitions
The effectiveness of PCMs strongly depends on the characteristics (mainly the melting temperature) of the material for a given application. The choice of the melting temperature is particularly important and depends on the type of integration and the application that is desired. To take advantage of latent heat, the melting temperature of the material must be close to the average temperature of the environment in which it will be installed. This melting temperature is one of the essential characteristics of the material and it represents the limit at which the storage or release of latent heat is triggered. PCMs are therefore interesting in low inertia buildings because they make it possible to limit temperature fluctuations in summer and/or power in winter. They can be placed for example inside plaster panels which is a material compatible with many PCMs. The latter must be close to the comfort temperature between 20°C and 30°C. The basic model used in our approach is that developed by Kuznik et al. [31] and the equations formulated to best reproduce the heat capacity curve are given:
3 Nodal Structure and Habitat Description
The proposed construction is made up of several glass rooms, walls, doors, and windows. The division of the habitat into thermal zones induces the creation of temperature nodes by zone. A certain number of information fields are connected to a node, reflecting for example the assignment of a node in an area or the topology of the overall electrical network associated with the house. In addition, a type was assigned to each node. Indeed, compared to the equations, the nodes are concerned with different phenomena.
For example, a node that represents a wall will concern heat conduction terms. This same node, depending on its situation, can also involve convection processes. On the external face of the envelope wall, the surface node is affected by external radiation and convective exchanges. We should note that the size of this structure can quickly become large as this building is divided into multiple areas and each area has multiple glass walls and windows. The size of this structure is linked to the dimensions of the systems to be solved and the notion of calculation time must not be neglected.
The present study was carried out on a habitat in the Ghardaïa region (Southern Algeria) where the exterior envelope promotes the development of a comfortable indoor environment by controlling the exchange of energy between the interior space and the environment. The house has a living area of 71.3 m2 and the height of the walls is 2.8 m, while the other dimensions are shown in detail in Fig. 2. Windows and doors contribute significantly to the energy balance. Their contributions depend on several parameters such as climate, orientation, setting, and local relative surface (window-ground). The apartment has an area of 95.74 m2 with a living space of 71.3 m2.

Figure 2: Plan of the house, types of nodes, and zonal structure with dimensions in meters
A certain amount of information is connected to a typical node, reflecting for example the assignment of this node in an area or the topology of the associated global electrical network. Indeed, compared to the equations, the nodes are concerned with different phenomena. Then, it appears necessary to assign a type to each node. For a given building, when the node structure is established, it is easy to fill in each element of the mathematical model. Indeed, all that has to be done is to scan the node structure and assign the relevant terms.
For this house, the exterior wall envelope is made up of a heavy stone structure (40 cm thick) surrounded by two layers with a thickness of 1.5 cm of mortar cement. The internal face is covered with a layer of plaster 1 cm thick. The internal walls (or dividing walls) are considered heavy stone structures 15 cm wide, surrounded by two layers of cement mortar 1.5 cm thick and two layers of plaster 1 cm thick. The windows are single glazing, clear with a thermal transmission coefficient equal to
Fig. 3 shows the instantaneous evolution of the solar illumination incident on the facades. The curves plotted in Figs. 4 and 5 describe the behavior of outdoor ambient air temperatures and wind speed, respectively. All results were calculated using data from 25–30 August, 2013.

Figure 3: Incident solar lighting on the roof and the facades

Figure 4: Ambient temperatures at Ghardaïa from 25–30 August, 2013
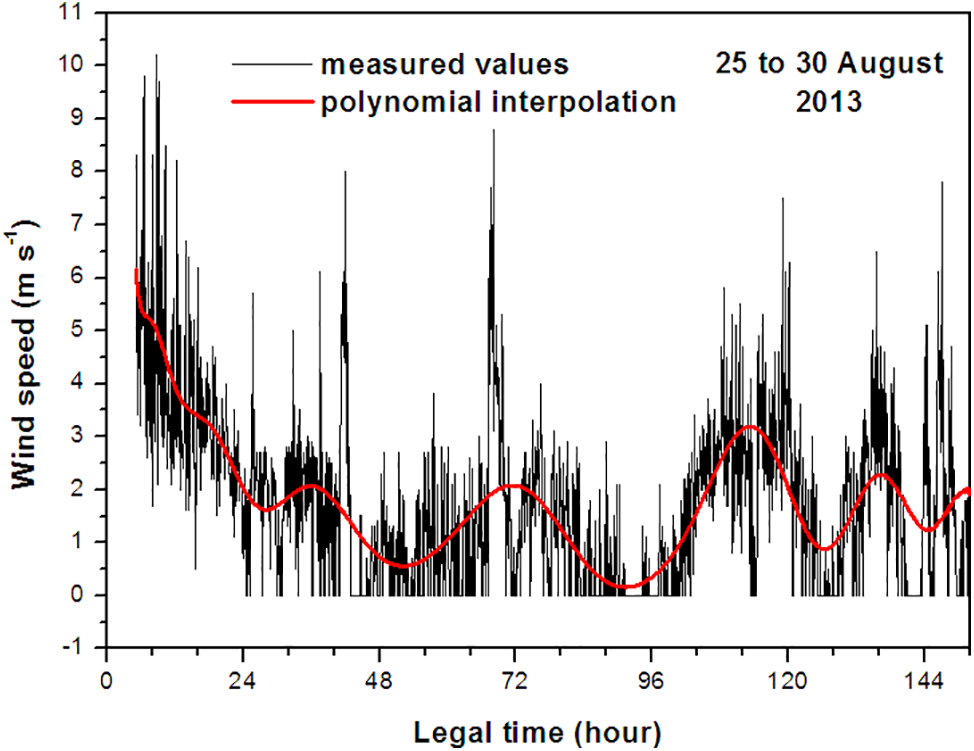
Figure 5: Wind speed at Ghardaïa during 25–30 August, 2013
Figs. 6 and 7 show the variations in temperatures and specific humidity of rooms in the home. It can be seen that the two parameters vary with the same scenario. Upon closer examination, it becomes evident that the fluctuations in temperatures follow a consistent pattern across different scenarios. Specifically, the variation between the minimum and maximum temperatures for the same profile falls within the range of 1.2°C to 1.7°C. This narrow range of temperature fluctuations can be attributed to the thermal characteristics of the building envelope, primarily composed of stone. Stone possesses significant energy storage capacity, which enables it to absorb and release heat gradually, thereby regulating indoor temperatures and minimizing temperature variations.

Figure 6: Temperature variations of each room studied as a function of the weather during 25–30 August 2013
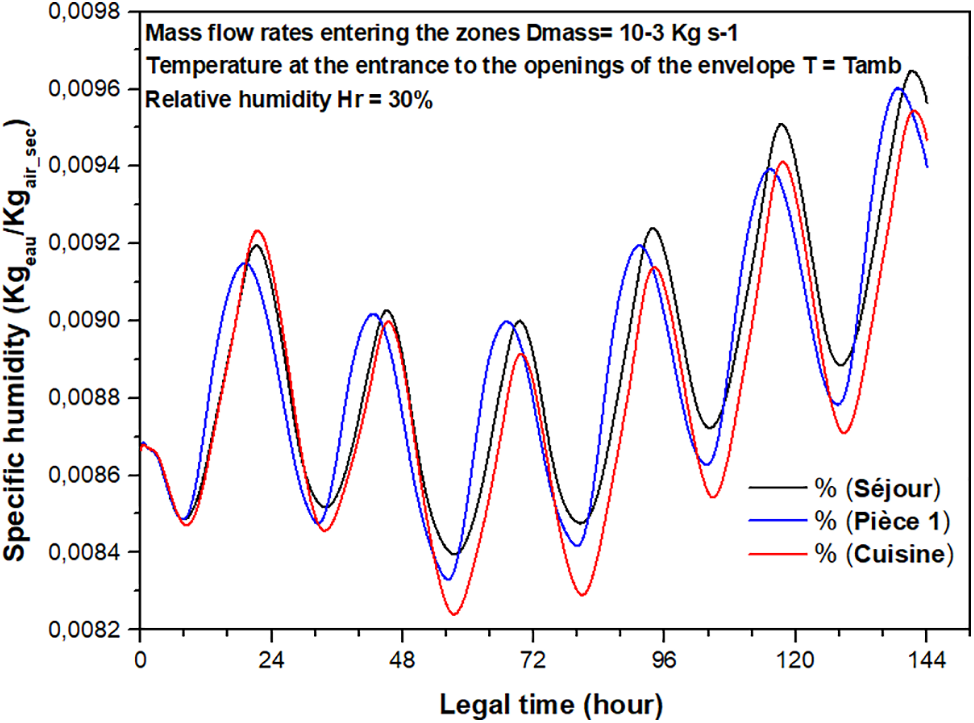
Figure 7: Variations in specific humidity in each room were studied as a function of time from 25–30 August 2013
Furthermore, the variations in specific humidity exhibit a proportional relationship with temperatures. As temperatures rise or fall, specific humidity levels also adjust accordingly. This correlation between temperature and specific humidity underscores the dynamic interplay between thermal conditions and moisture content within the indoor environment.
The mass flow of the incoming air also influences the interior temperatures and humidity of the rooms of the home, which is reflected respectively in Figs. 8 and 9. The increase in the incoming mass flow reduces the thermal inertia of the envelope. By definition, a material with high thermal inertia causes a significant phase shift and stabilization of temperatures. The variation in specific humidity is proportional to indoor temperatures and follows the same scenario.
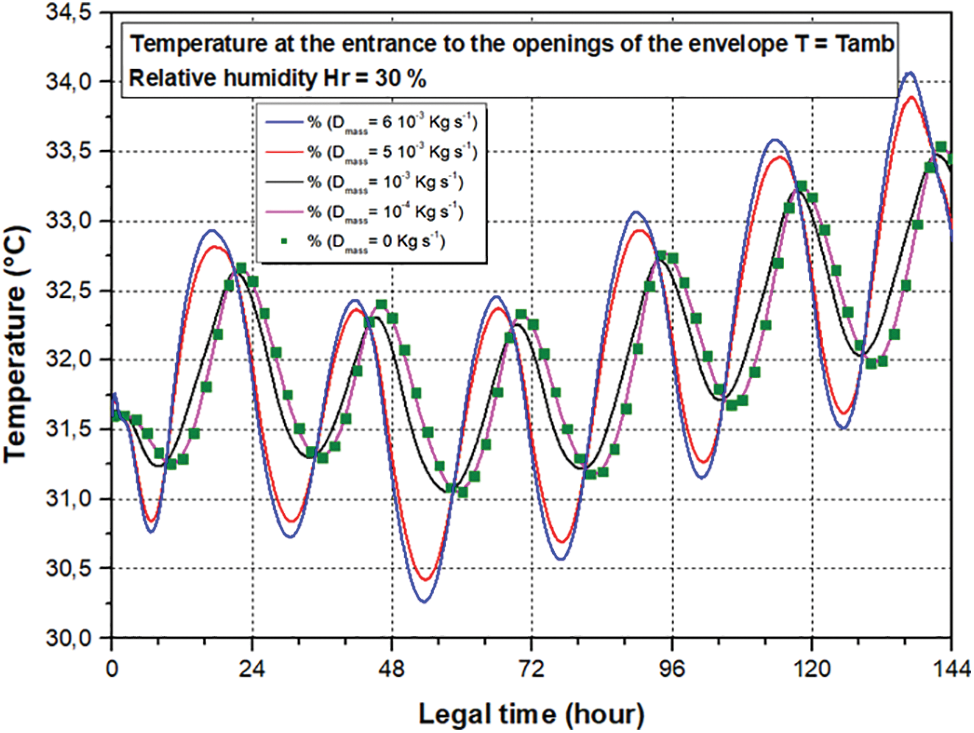
Figure 8: The influence of mass flow rates on internal temperatures during 25–30 August, 2013

Figure 9: The influence of mass flow rates on internal humidity during 25–30 August, 2013
The influence of relative humidity is not considerable given that the phenomenon of propagation of specific humidity is long. However, the influence is significant on specific humidity as shown in Fig. 10. Figs. 11 and 12 show the model simulation results for different incoming air temperatures. The change in the temperature of the incoming air has a direct effect on the values obtained from the simulation. Moreover, this change does not affect the degree of thermal inertia of the home.

Figure 10: The influence of relative humidity on the specific humidity of housing during 25–30 August, 2013

Figure 11: The influence of ambient temperature on internal temperatures

Figure 12: The influence of ambient temperature on specific humidity
Figs. 13 to 16 highlight the benefit of incorporating PCMs within the partition walls of rooms 1 and 2, specifically positioned between two layers of plasterboard. In this setup, the PCMs are situated at the center of the partition wall, with a thickness of 4 cm, while the plasterboards on either side have a thickness of 1.5 cm each. These walls are strategically chosen for rooms oriented towards the south-facing windows, allowing for optimal utilization of solar radiation. The simulations were conducted under conditions of clear sky and utilized climatic data from Ghardaïa during 21–22 December, 2013. It is worth noting that the model parameters and equations remained consistent throughout the simulations, except for the partition wall’s conduction properties. In this case, the thermophysical parameters of the partition wall varied based on the temperature level of the PCM material.

Figure 13: Experimental and analytical models of the heat capacity of the PCM used

Figure 14: Ambient temperature

Figure 15: Relative humidity

Figure 16: Wind speed
The results depicted demonstrate the significant impact of PCM integration on thermal performance. Specifically, the PCM’s ability to absorb and release latent heat during phase transitions contributes to maintaining stable indoor temperatures, even under fluctuating external conditions. By leveraging solar radiation absorbed through the south-facing windows, the PCM-enhanced partition walls effectively regulate indoor temperatures, reducing the need for active heating or cooling systems.
Moreover, the thickness and positioning of the PCM within the partition wall play a crucial role in optimizing thermal performance. The strategic placement of the PCM at the center of the wall maximizes its heat absorption capacity while minimizing thermal bridging effects. This configuration ensures efficient utilization of the PCM’s thermal storage capabilities, resulting in improved comfort levels and energy savings.
Thanks to increasingly detailed simulations, we were able to predict the behavior of this complex system using the nodal method [22] and the Runge-Kutta numerical method of order 4. Figs. 17 and 18 represent the simulated temperatures and specific humidities of the interior air of room 1 for two cases: one assuming that the closed habitat satisfies the characteristics given in Table 1, and the other considering that the habitat satisfies the same characteristics but with the interior walls facing the open south windows (with solar gain) of rooms 1 and 2 replaced by a plaster-PCM type partition wall. These results justify that the use of PCM improves indoor comfort given that the temperatures traced can increase by 1°C in our case. In this situation, the opening represents 20% of the facade, so it can be enlarged to take greater advantage of these direct contributions.

Figure 17: Temperature of room 1
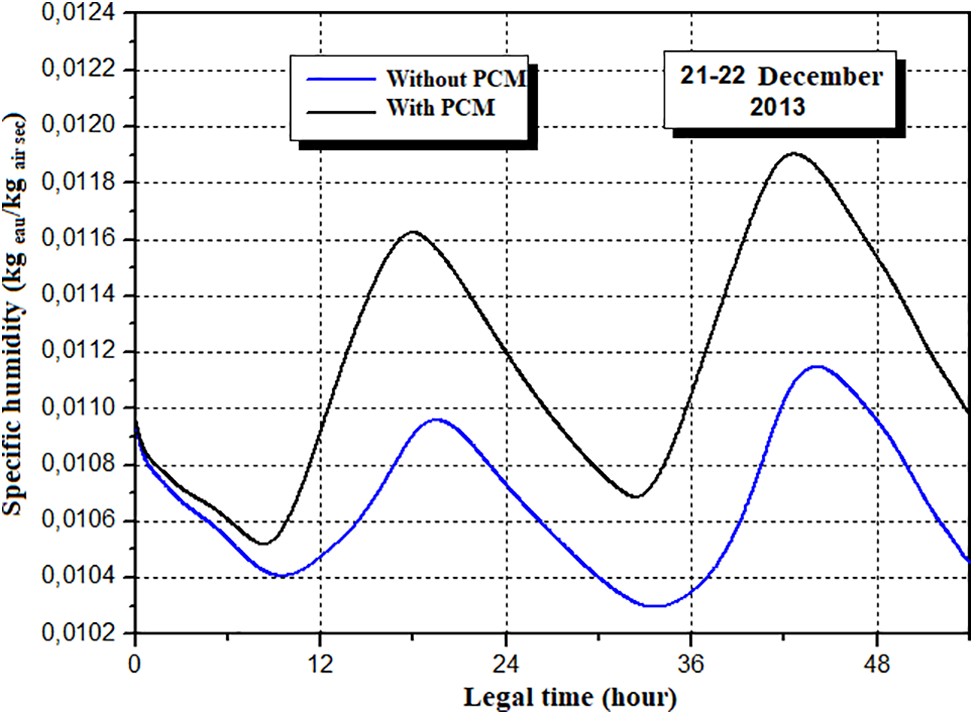
Figure 18: Specific humidity of room 1
Fig. 19 shows the temperature profiles of the interior wall composed of the layers set out in Table 2, but increasing the thickness of the stone to 25 cm. The curves obtained in Fig. 20 represent the temperatures of the inner, middle, and outer surfaces of the wall panel containing a layer of 1 cm of plaster plus 4 cm of PCM plus another similar layer of plaster.

Figure 19: Temperature of the stone partition
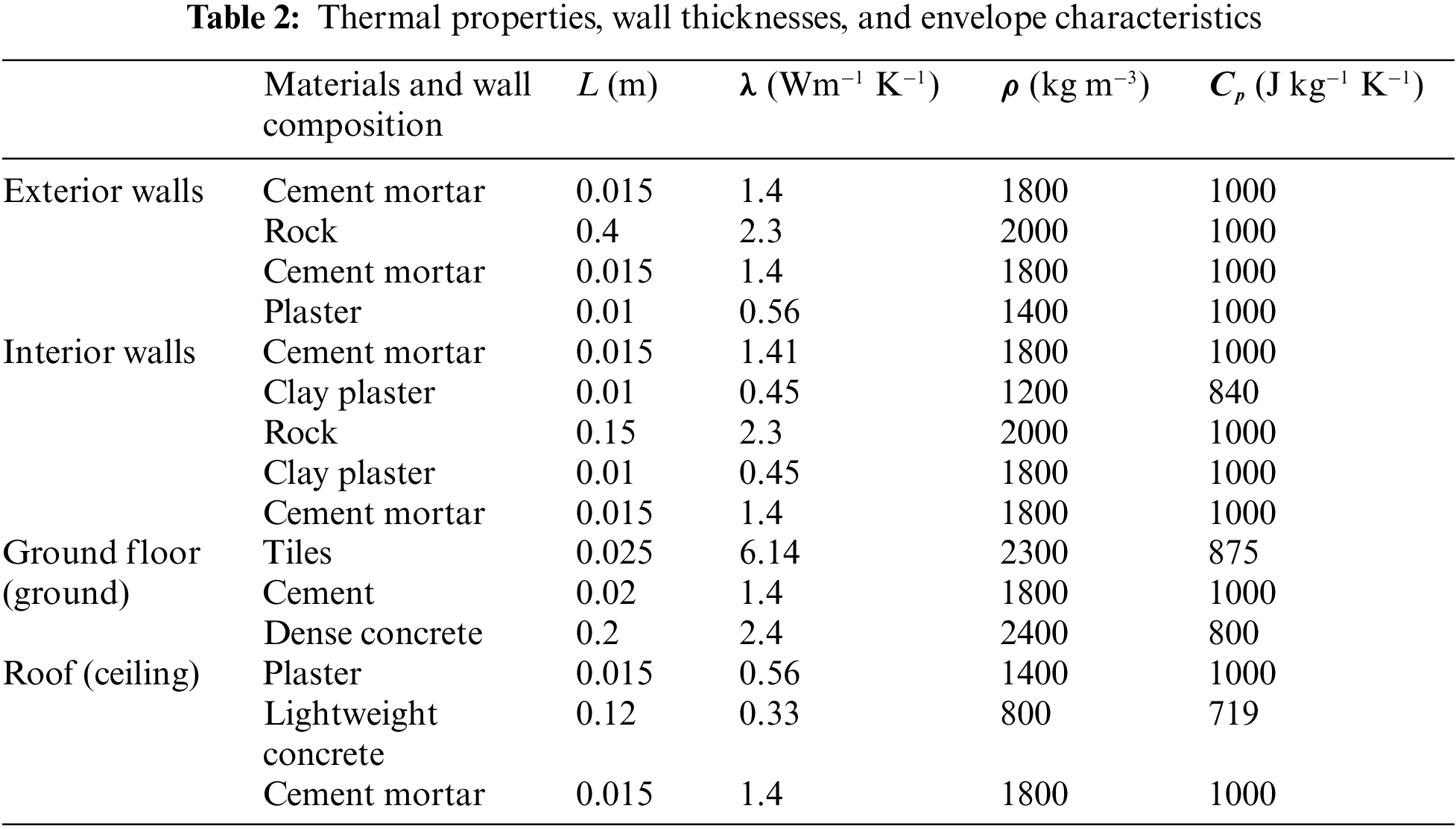

Figure 20: Partition temperature with PCM
To discuss the obtained results, emphasis is placed on the level of thermal inertia, i.e., the temperature fluctuations and the phase shift which represents the time difference between the peaks of ambient temperatures and in the middle of the wall. These aspects are more significant for a PCM partition. The PCM wall panel in this case ensures better thermal inertia.
The present research aimed to contribute to a comprehensive understanding of energy management strategies in the building sector, with a focus on improving thermal comfort and energy efficiency. Specifically, we seek to investigate the thermo-aeraulic behavior of a multi-zone home located in Ghardaïa, Algeria, utilizing a coupled mathematical model. Furthermore, it aimed to develop and implement a wall model incorporating PCM technology, tailored to the climatic conditions of the region. The obtained results have shown coherent responses in temperatures, specific humidity levels, and mass flow rates, indicating the effectiveness of PCM-integrated building envelopes in mitigating energy consumption and stabilizing indoor environments. The observed temperature differentials and phase shifts underscore the dynamic nature of PCM technology and its ability to adapt to varying environmental conditions. In addition, the simulation results revealed that to improve the thermal inertia of a built structure, it is possible to introduce PCM into solid wall materials which, thanks to their latent heat, make it possible to store or release a large quantity of energy. The incorporation of a layer of PCM makes it possible to increase the performance of a wall or partition by damping temperature fluctuations during the summer and winter seasons. The judicious integration of smart materials is an effective way to reduce energy consumption and carbon emissions linked to housing. The results obtained in this regard show the impact of PCMs on the thermal comfort of a Saharan house.
Moreover, Introducing PCMs into a wall, thanks to their latent heat, makes it possible to store/release a large quantity of energy and improve the main comfort parameters by delaying heat transfer and dampening temperature fluctuations depending on the energy content and water from the air. The situation was more affordable in November because the comfort is almost perfect. The operating regime is quasi-stationary for a relatively long time during this transition period. The results of the work also showed that significant financial savings can be made by improving the insulation of buildings. Proper use of PCMs must be done by combining them with a thermally insulating material. Among the solutions for increasing the inertia and thermal capacity of the internal walls, PCMs are a great choice. The advantage of this type of material is the weight saving and easy implementation adapted to existing products. PCMs can improve comfort and become a good alternative to heavy walls.
Finally, while the study aims to improve hygrothermal performance through PCM integration, it may overlook other important aspects of building performance, such as structural integrity, acoustic insulation, or indoor air quality. This narrow focus could limit the overall understanding of the potential benefits and drawbacks of PCM integration in multi-zone constructions.
Acknowledgement: This work was supported in entire part by the Biomaterials and Transport Phenomena Laboratory Agreement No. 303 03-12-2003, at the University of Medea. The authors acknowledge and gratefully thank the financial support provided by DG-RSDT of Algeria.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Conceptualization, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Methodology, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Software, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane and Jie Zhang; Validation, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Formal analysis, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Investigation, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Resources, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane and Jie Zhang; Data curation, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Abdeltif Amrane and Jie Zhang; Writing–original draft, Abir Abboud, Zakaria Triki and Rachid Djeffal, Sidi Mohammed El Amine Bekkouche; Writing–review & editing, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Visualization, Abir Abboud, Zakaria Triki, Rachid Djeffal, Sidi Mohammed El Amine Bekkouche, Hichem Tahraoui, Abdeltif Amrane, Aymen Amin Assadi, Lotfi Khozami and Jie Zhang; Supervision, Zakaria Triki, Abdeltif Amrane and Jie Zhang; Project administration, Zakaria Triki, Hichem Tahraoui, Abdeltif Amrane and Jie Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Badeche, M., Bouchahm, Y. (2020). Design optimization criteria for windows providing low energy demand in office buildings in Algeria. Environmental and Sustainability Indicators, 6, 100024. [Google Scholar]
2. Report, A. (2016). Final energy consumption of Algeria, key figure-year 2015. Ministry of Mines and Energy, 16, 1–34. [Google Scholar]
3. Ghedamsi, R. (2018). Development of a design methodology for passive energy buildings in Algeria (Ph.D. Thesis). University of Ouargla, Algeria. [Google Scholar]
4. Allibe, B. (2012). Modeling of long-term energy consumption in the French residential sector—improvement of behavioral realism and proactive scenarios (Ph.D. Thesis). Ecole des Hautes Etudes en Sciences Sociales, France. [Google Scholar]
5. Lv, Y. (2023). Transitioning to sustainable energy: Opportunities, challenges, and the potential of blockchain technology. Frontiers in Energy Research, 11, 1–20. [Google Scholar]
6. Schaefer, L., Atreya, A. (2024). Exploring the potentials and challenges of renewable energy sources. Journal of Computing and Natural Science, 4(2), 85–95. [Google Scholar]
7. Wohrer, M. (2009). Industrial challenges, sophia antipolis énergy dévelopment: A new type of thermodynamic solar power plants. Industrial Realities, 2009(4), 74–80 (In French). [Google Scholar]
8. Aadmi, M., Karkri, M., El Hammouti, M. (2015). Heat transfer characteristics of thermal energy storage for PCM (phase change material) melting in horizontal tube: Numerical and experimental investigations. Energy, 85(2), 339–352. https://doi.org/10.1016/j.energy.2015.03.085 [Google Scholar] [CrossRef]
9. Jouhara, H., Żabnieńska-Góra, A., Khordehgah, N., Ahmad, D., Lipinski, T. (2020). Latent thermal energy storage technologies and applications: A review. International Journal of Thermofluids, 5–6(1), 100039. https://doi.org/10.1016/j.ijft.2020.100039 [Google Scholar] [CrossRef]
10. Djeffal, R., Cherier, M. K., Younsi, Z., Hamdani, M., Al-Saadi, S. (2022). Concept development and experimentation of a phase change material (PCM) enhanced domestic hot water. Journal of Energy Storage, 51, 104400. https://doi.org/10.1016/j.est.2022.104400 [Google Scholar] [CrossRef]
11. Rebelo, F., Figueiredo, A., Vicente, R., Ferreira, V. M. (2022). Study of a thermally enhanced mortar incorporating phase change materials for overheating reduction in buildings. Journal of Energy Storage, 46, 103876. https://doi.org/10.1016/j.est.2021.103876 [Google Scholar] [CrossRef]
12. Abdel-Mawla, M. A., Hassan, M. A., Khalil, A. (2022). Impact of placement and design of phase change materials in thermally activated buildings. Journal of Energy Storage, 56, 105886. https://doi.org/10.1016/j.est.2022.105886 [Google Scholar] [CrossRef]
13. Elhamy, A. A., Mokhtar, M. (2024). Phase change materials integrated into the building envelope to improve energy efficiency and thermal comfort. Future Cities and Environment, 10(1), 9. [Google Scholar]
14. Aggoune, A., Hamdani, M., Yassine, M., Cherier, M. K., Rachid, D. (2020). Improvement of the thermal comfort of building roofs equipped with a phase change materials (PCM) layer under desert weather conditions. Proceeding of the 6th International Symposium on New and Renewable Energy (SIENR), Ghadaia, Algeria. [Google Scholar]
15. Al-Yasiri, Q., Szabó, M. (2021). Incorporation of phase change materials into building envelope for thermal comfort and energy saving: A comprehensive analysis. Journal of Building Engineering, 36, 102122. [Google Scholar]
16. Lajimi, N., Boukadida, N. (2023). Effect of the position of the PCM on the thermal behavior of a multilayer wall of a building in summer period. Frontiers in Environmental Science, 11, 1–10. [Google Scholar]
17. Djeffal, R., Lalmi, D., Bechouat, T., Younsi, Z. (2023). New method for solving the inverse thermal conduction problem (Θ-scheme combined with CG method under strong wolfe line search). Buildings, 13(1), 243. [Google Scholar]
18. Maha, A. (2004). New active components for energy management of lightweight building envelopes: Coupling phase change materials, super-insulation, and solar gains (Ph.D. Thesis). University of Joseph Fourier, Grenoble, Freance. [Google Scholar]
19. Sarbu, I., Sebarchievici, C. (2018). A comprehensive review of thermal energy storage. Sustainability, 10(1), 191. [Google Scholar]
20. Pielichowska, K., Pielichowski, K. (2014). Phase change materials for thermal energy storage. Progress in Materials Science, 65, 67–123. https://doi.org/10.1016/j.pmatsci.2014.03.005 [Google Scholar] [CrossRef]
21. DIN 1946-4 (2018). Ventilation and air conditioning—Part 4: Ventilation in buildings and rooms of health care. Germany: DIN. [Google Scholar]
22. Pujol, O. (2000). Energy in physics. Proceedings of the 57th Congress of the Union of Physics and Chemistry Teachers, Toulouse, France. [Google Scholar]
23. Roux, J. J. (2000). Thermal behavior of buildings (In French). INSA de Lyon: Institut National des Sciences Appliquées, Département de génie Civil. [Google Scholar]
24. Nadeau, J. P., Puiggali, J. R. (1995). Drying-physical processes to industrial processes. Paris: Tec & Doc-Lavoisier. [Google Scholar]
25. Rumianowski, P., Brau, J., Roux, J. J. (1989). An adapted model for simulation of the interaction between a wall and the building heating system. Proceedings of the Thermal Performance of the Exterior Envelopes of Buildings IV Conference, pp. 224–233. Orlando, FL, USA. [Google Scholar]
26. Bekkouche, S. M. A., Benouaz, T., Cherier, M. K., Hamdani, M., Benamrane, N. et al. (2014). Thermal resistances of local building materials and their effect upon the interior temperatures case of a building located in Ghardaïa region. Construction and Building Materials, 52(6), 59–70. https://doi.org/10.1016/j.conbuildmat.2013.10.052 [Google Scholar] [CrossRef]
27. Bekkouche, S. M. A., Benouaz, T., Cherier, M. K., Hamdani, M., Yaiche, M. R. et al. (2013). Influence of building orientation on internal temperature in saharan climates, building located in Ghardaïa region (Algeria). Thermal Science, 17(2), 349–364. https://doi.org/10.2298/TSCI110121112B [Google Scholar] [CrossRef]
28. Hamdani, M., Benouaz, T., Belarbi, R., Cherier, M. K. (2017). The study natural ventilation by using buildings windows: Case study in a hot dry climate, Ghardaïa. Algeria Energy Procedia, 139(2), 475–480. https://doi.org/10.1016/j.egypro.2017.11.240 [Google Scholar] [CrossRef]
29. Bekkouche, S. M. A., Benouaz, T., Hamdani, M., Cherier, M. K., Yaiche, M. R. et al. (2015). Judicious choice of the building compactness to improve thermo-aeraulic comfort in hot climate. Journal of Building Engineering, 1, 42–52. https://doi.org/10.1016/j.jobe.2015.03.002 [Google Scholar] [CrossRef]
30. Haddam, M. A. C., Benouaz, T., Hamdani, M., Cherier, M. K., Benamran, N. (2015). Integration of eaves and shading devices for improving the thermal comfort in a multi-zone building. Thermal Science, 19(suppl. 2), 615–624. https://doi.org/10.2298/TSCI140422117H [Google Scholar] [CrossRef]
31. Kuznik, F., Virgone, J., Roux, J. J. (2008). Energetic efficiency of room wall containing PCM wallboard: A full-scale experimental investigation. Energy and Buildings, 40(2), 148–156. https://doi.org/10.1016/j.enbuild.2007.01.022 [Google Scholar] [CrossRef]
32. Jannot, Y. (2012). Heat transfer (In French). Nancy: Ecole des Mines. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools