 Open Access
Open Access
ARTICLE
Performance of Thermal Insulation of Different Composite Walls and Roofs Materials Used for Energy Efficient Building Construction in Iraq
Engineering Technical College of Mosul, Cultural Group, Northern Technical University, Mosul, 41002, Iraq
* Corresponding Author: Omar Rafae Alomar. Email:
Frontiers in Heat and Mass Transfer 2024, 22(4), 1231-1244. https://doi.org/10.32604/fhmt.2024.053770
Received 10 May 2024; Accepted 01 July 2024; Issue published 30 August 2024
Abstract
This study numerically involves the performance of thermal insulation of different types of composite walls and roofs to demonstrate the best model that can be used for energy-efficient building construction in Iraq. The mathematical model is solved by building its code using the Transmission Matrix Method in MATLAB software. The weather data of 21st July 2022 in Baghdad City/Iraq is selected as a test day. The wall types are selected: the first type consists of cement mortar, brick, and gypsum, the second type consists of cement mortar, brick, gypsum, and plaster and the third type consists of cement mortar, brick, gypsum, air cavity, and sheathing timber. The roof types are chosen: the first type consists of reinforced concrete, gypsum, and plaster, and the second type consists of the precast concrete flag, river sand, tar, reinforced concrete, gypsum, and plaster. The obtained solutions are compared with previous studies for the same city but with different types of walls and roofs. The findings display that the second and third types of walls reduce the entry heat flux by 4% and 10% as compared to the first type of wall. Also, the results indicate that the second type of roof reduces the entry heat flux by 21% as compared to the first type of roof. The results confirm that the best models of walls and roofs in Iraq are the third and second types, respectively, as compared to other models and hence, the performance of insulation material strongly depends on the materials used while building them.Keywords
Nomenclature
| A, B, C, D | Complex matrix element |
| a | Thermal diffusivity (m2/sec) |
| cp | Specific heat (J/kg.°C) |
| F | Coefficient of elements A, B, C (1/m) |
| H | Surface heat transfer coefficient (W/m2.°C) |
| J | Complex operator |
| K | Thermal conductivity (W/m.°C) |
| Greek Symbol | |
| Density (kg/m3) | |
| Harmonic frequency (1/sec) | |
| Phase lag | |
| Average temperature differential across layers (°C) | |
Recently, about 40% of energy in the world goes to residential structures, which are responsible for increasing the percentage of carbon dioxide emissions to 30% [1]. It is estimated that home air conditioning accounts for about 40% of all energy used in the residential sector [2]. In Iraq, however, due to weather and inadequately insulated materials used in the buildings, this number has increased to 66% [3]. In summer, the temperature in Iraq can reach over 48°C, whereas it can plummet to −10°C in the winter within brief periods [3,4]. The combination of rising global temperatures and the continued use of old reinforced concrete slabs, which are poorly insulated, has led to a steady increase in this consumption (approximately 5% per year [3]) in Iraq. Ipseng et al. [5] provided an overview of the methods of determining conductive heat transfer, known as the conduction transfer function (CTF) and the periodic response factor (PRF). In their study, they evaluated and contrasted several distinct types of equations that are utilized in the process of calculating cooling loads. Özbalta et al. [6] investigated the heat gain through Trombe walls using solar energy for winter heating applications in the cold region part of Turkey. The results demonstrated how to calculate the heat gain through the Trombe wall.
Luo et al. [7,8] used a new stable finite volume method for modelling wall heat transfer. They have indicated that the measured surface temperatures may be used to monitor a building’s thermal performance. Using these data, the authors also developed an in-house thermal modelling software package to examine the house’s thermal performance. Maimagani1 et al. [9] assessed the cooling loads linked with a system of building. The estimation is carried out by utilizing the steady-state methodology. The findings displayed the possibility of deciding the capacity and sizing of the air conditioning equipment. Also, several elements are required to estimate the heating load, e.g., the modalities of heat transport, solar radiation geometry, evaporation, and ventilation effects. Abdullah et al. [10] analyzed the thermal performance of a building that is around 600 m3 in size. Their study investigated the impact of insulation material on reducing energy consumption in buildings. The structure is constructed in one of three distinct layouts. Brick is used in the construction of the walls in the original model. A polystyrene foam with a thickness of four centimeters is used inside the walls and roof as an additional layer of insulation material for the second model. In the third model, the walls are built from two different portions separated by an air gap with 8 cm width. Additionally, a secondary roof is added to this model.
Pekdogan et al. [11] organized a category for CO2 emissions and anticipated energy consumption. The value of the overall heat transfer coefficient of the external wall is equal to 0.25 W/m2·°C according to the Silver Standard, whereas it is equal to 0.15 W/m2 K according to the Gold Standard. These values are used while calculating the amount of heat loss and heat gain, where the findings are compared. Wei et al. [12] numerically simulated the heat and moisture transfer of walls with insulation by including the temperature and humidity dependency of the material’s effective thermal conductivity and vapour permeability. Heat and moisture transfer through the wall could be recreated using cellulose batt insulation. It was found that the temperature, relative humidity, and the thickness of insulation layers affect the relationship between the heat flux passed through the wall and the air inside the building. Jannat et al. [13] presented a comparative study on the thermal performance of envelope wall materials of buildings in the tropics to determine which varieties are the best and worst. Their study explained the fundamental conditions for the parametric simulation used. As a result, the primary objective of this study is to serve as a guide for the architects as they conduct a preliminary analysis of the building designs and wall materials to determine which option offers the highest level of thermal efficiency. Hagentoft et al. [14] concentrated on approximating the calculation of the surface heat flux of a composite wall in which a defined step change in surface temperature takes place. The approximations are provided using lumped analyses and solutions from the Laplace network. The results are validated with analytical and numerical solutions. Qian et al. [15] presented a study on predicting the temperature field of space equipment under periodic external heat flow to perform the heat transfer analysis for reducing the variations in exterior and interior surface temperatures. The transfer function approach is used to analyze the thermal control of spacecraft equipment.
Mohammed et al. [16] investigated the effects of adding insulation material on the thermal performance of composite walls of buildings. The findings indicated that the insulation materials may be highly evaluated in the construction sector and future works. Hasan et al. [17] presented a comparative study on four various materials combinations employed for roof insulation. The findings indicated that the heat transfer rate is highly decreased using material combinations compared to concrete without Insulation. Abdulsada et al. [18] experimentally investigated the impacts of using insulation material on the thermal performance of walls and roofs under the weather of Kirkuk City, Iraq, using the passive house criteria method. Two different buildings are used, and one of them is well-insulated. The data are collected in the summer. The results show that the indoor temperature of the efficient building is reduced by 8°C compared to standard buildings. Liu et al. [19] numerically presented the effect of using different thicknesses of insulation material on the thermal performance of a hypothetical building during the hot summer season in China. The outcomes indicated that the optimal thickness for the best condition is 70 mm. While Sharma et al. [20] studied the heat gained by buildings in hot regions using three different methods to calculate the heat gain (CLTD/GLF, CLF/SCL/CLTD, and RLF), Oktay et al. [21] investigated the effect of the thermophysical properties of materials that used in the building on the amount of heat gain. Thomas et al. [22] studied the impact of exterior environment conditions on the heat gain and losses for several building walls. Ghanim et al. [23] experimentally investigated the effects of different materials made from double-skin roofs, which were widely used in the construction of Iraqi buildings. It has been pointed out that the increase in the thickness of insulation material leads to overheating resulting from increasing the cooling load of the air conditioning system in some cases, where the insulation surface can restrain the dissipation of the internal gain to the exterior ambient [24,25].
In recent years, however, some researchers have used experiments to test real PCM in warm environments, even though computer models are faster at getting results. Austin et al. [26] examined how much the temperature dropped in a building with PCM-embedded bricks with one and two layers. Qudama et al. [27] looked at how the building responded to heat in a natural tropical climate by putting up two concrete cubes, but only one had PCM. Global concerns have been raised over the energy inefficiency of older structures. The energy-conservation system seems promising for enhancing the construction industry’s environmental safeguard capacity. Al-Tamimi [28] examined the impact of various kinds and quantities of thermal insulation on the energy consumption of an ordinary household in three localities in Saudi Arabia. Yamoul et al. [29] implemented a passive solutions-focused approach by modelling the energy needs of prototype residential buildings in two different climate zones.
A complete literature review shows that most previous investigations of heat transfer through either compound walls or roofs are experimentally and numerically performed. Moreover, the literature reveals no numerical investigation about evaluating the amount of heat flux through compound walls or roofs using the transmission matrix method. One of the significant targets of building construction is to obtain and keep the specific thermal conditions inside the building as energy-efficient as possible. The evolution of machine computation has allowed scientists to discover new methods to solve the same problem more accurately and in a shorter time. A z-transform of the heat transmission matrix is necessary to reach a final solution involving the current and previous temperatures and the heat fluxes through walls and roofs. Thus, in this study, the amount of heat flux through three different types of walls and two different types of roofs are numerically evaluated to determine the influences of their layer arrangements and which kind of insulation material is the best for reducing the amount of heat flux. The transmission matrix method and a computer program are used to solve the governing equations. The feature of this method is reducing the computational time of simulations. The test is made on 21st July 2022 in Baghdad/Iraq for 24 h. As a result, the optimum summer construction strategy is used to reduce the building’s peak cooling demand or shift it to a time when the building is not required to use it.
2 Problem Formulation-Multilayer Composite Material
The computer model code for simulating the conduction heat flow through walls and roofs is developed using the transmission matrix method. The transmission matrix method is related to the periodic temperature and heat flux on one side of a homogenous layer to the regular temperature and heat flux on the other side, employing a transmission matrix. Hence, it can be written as [30,31]:
where it is the inside temperature of the layer (°C), to is the outside surface temperature of the layer (°C), qi is the inside heat flux (W/m2), and qo is the outside heat flux (W/m2). The complex matrix elements A, B, C, and D can be written according to thermal properties of layer as [31]:
where L is the slab thickness (m), a is the thermal diffusivity (m2/s), w is the harmonic frequency (1/s), ρ is the density (kg/m3), cp is the specific heat (J/kg.°C), k is the thermal conductivity (W/m.oC), and j is the complex operator. The overall transmission matrix is obtained by chain multiplying the individual matrices in the order the matrices appear in the composite wall section from outside to inside as follows:
In general, the temperature is presented in the complex form of a Fourier series expression as follows [32]:
where
where Mn and Nn are the Fourier coefficients, where their values are calculated. The steady-state portion of heat flux is calculated as follows:
where ∆t is the average temperature differential across layer (°C) and R is the thermal resistance of layer (m2.°C/W). The value of R is calculated as follows [33,34]:
The total entry heat flux for n harmonics is obtained by summation or superimposing the steady-state and transient portions as:
The physical meaning of Eq. (14) is a Fourier decomposition of the incoming heat flux, which is then used to calculate the target response to harmonic heat fluxes. It can be noted here that Eq. (13) can be used for calculating either the inside or outside heat flux. In the developed simulation code, the transient inside and outside air temperatures are expressed in the complex form of Fourier series expression. The inside and outside (t)s and (q)s then refer to the conditions inside the building and the outside ambient conditions. The surface air film resistances are treated as extra layers of the composite layer, where the transmission matrix elements values for a resistance air film are obtained as follows:
where h is the surface heat transfer coefficient (W/m2.°C), when determining the heat flow through several materials (multilayer), the overall transmission matrix is the product of the transmission matrix for each material in the order it appears in the composite layer. Assuming the transmission matrix, given in Eq. (1), is the overall transmission matrix for a composite wall section, where the inside and outside air temperatures are known, one can solve for qi. The transient heat flux on the interior of the building is obtained as follows:
For the particular case, when the inside–air temperature remains constant concerning time (ti = 0) in Eq. (14), the transient heat flux on the interior of the building is obtained as follows:
The transmission matrix method calculates a system’s state transition matrix without identifying the roots to ascertain the thermal response factors of a multilayer wall and roof. This approach is straightforward, precise, and suitable for thermal engineering. Table 1 shows the specifications of materials used in walls and roofs [35–37], Tables 2 and 3 show the types of walls and roofs used in this study. The types of wall roofs used in the current study are presented in Tables 2 and 3 under standard materials used in Iraq buildings [38,39]. Fig. 1 displays the configuration of walls, and Fig. 2 represents the configuration of roofs. Table 4 illustrates the corresponding outdoor temperature in Baghdad City on 21st July 2022.
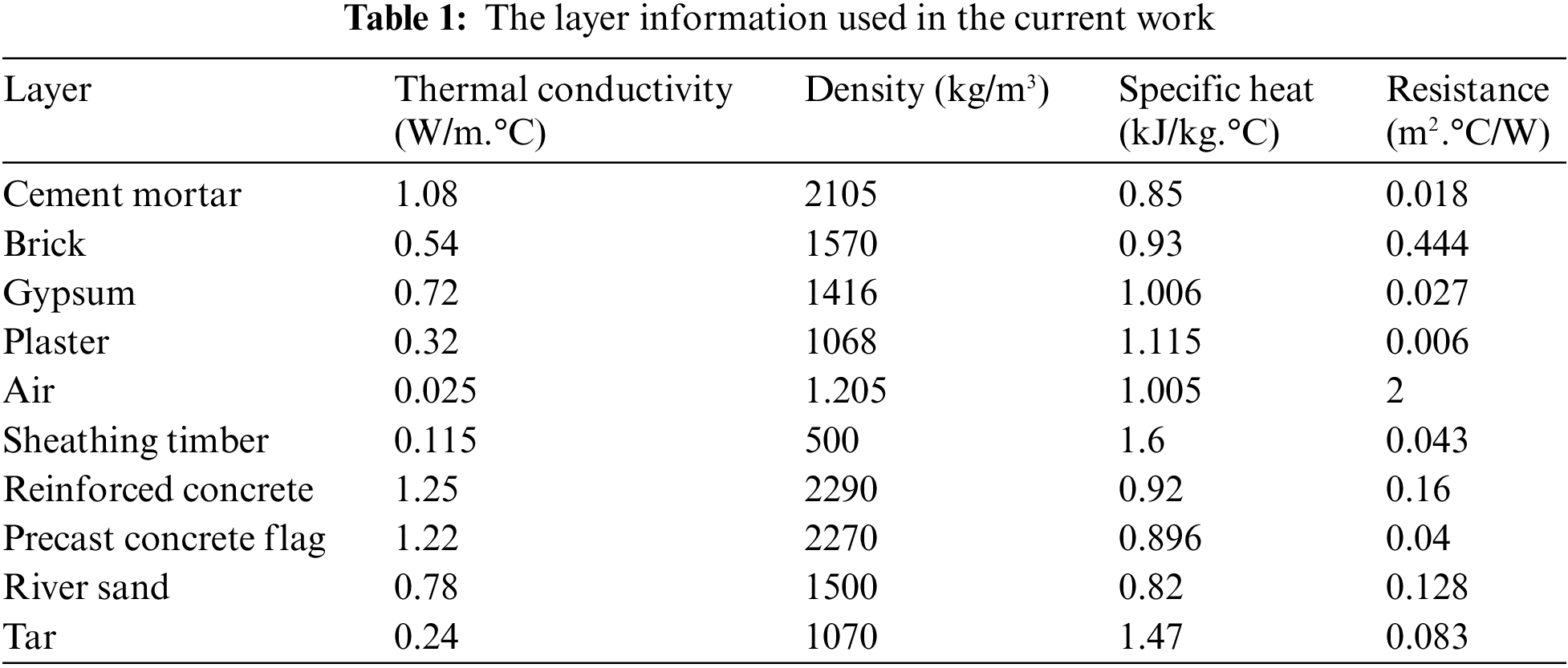
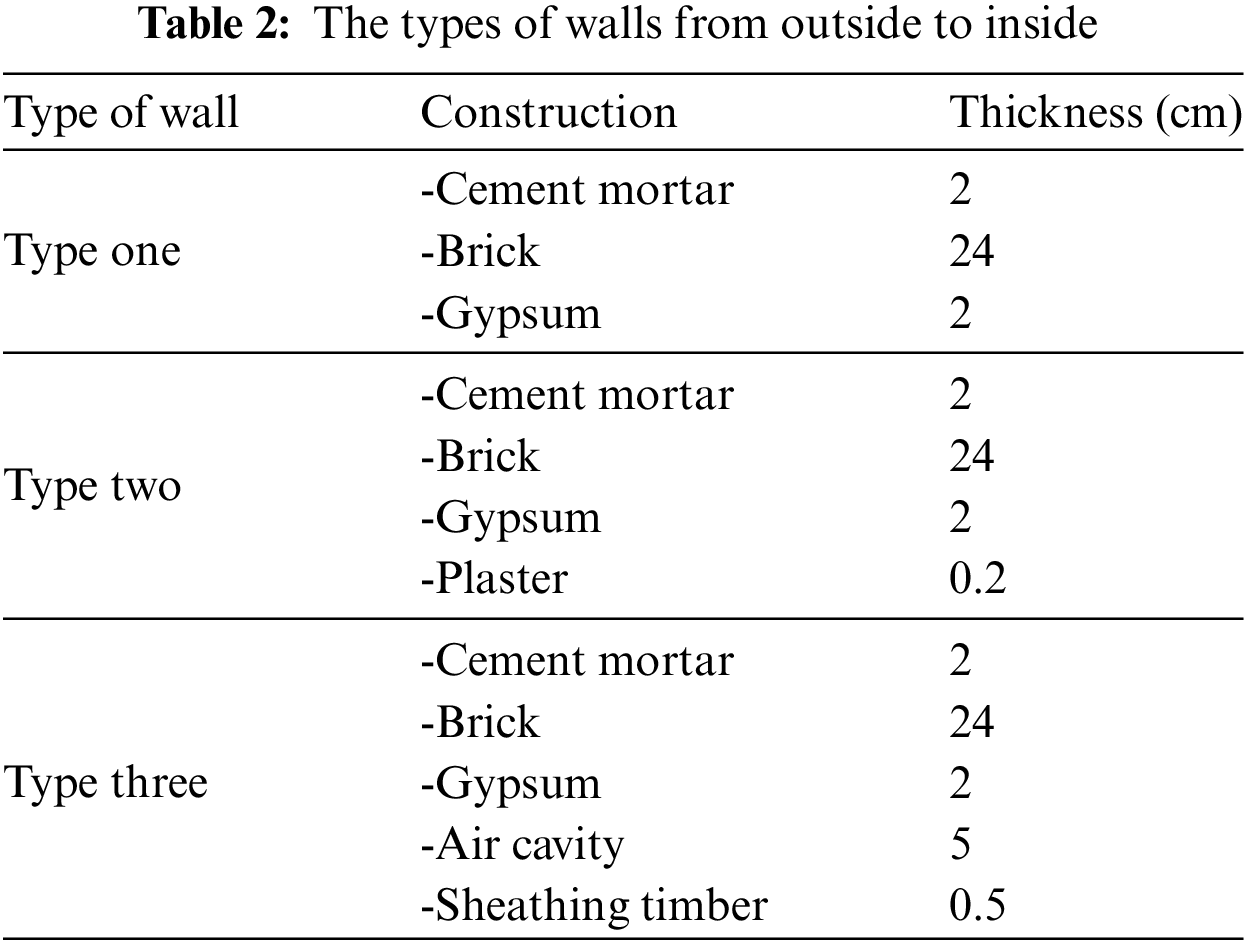
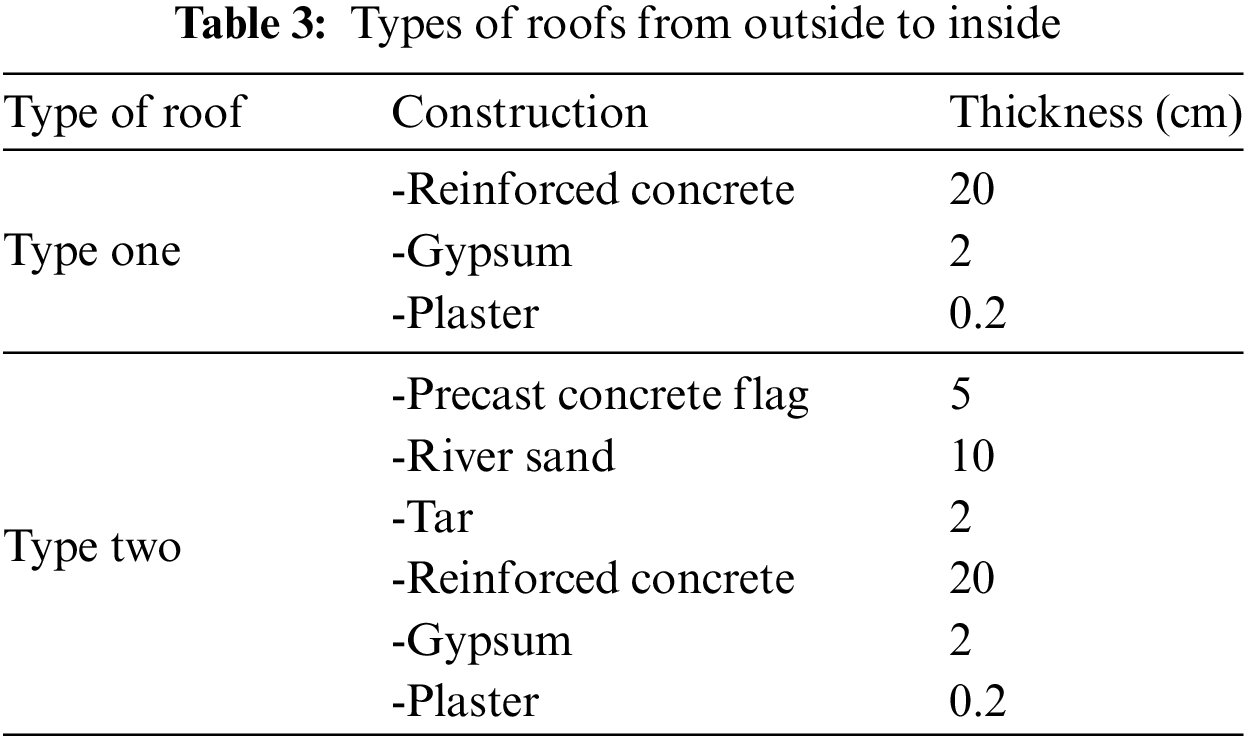
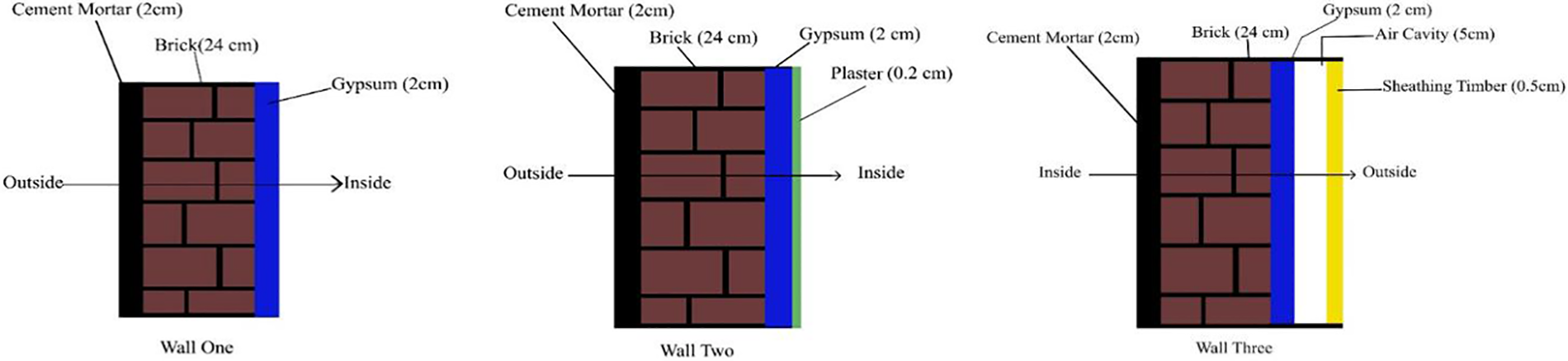
Figure 1: External walling configurations
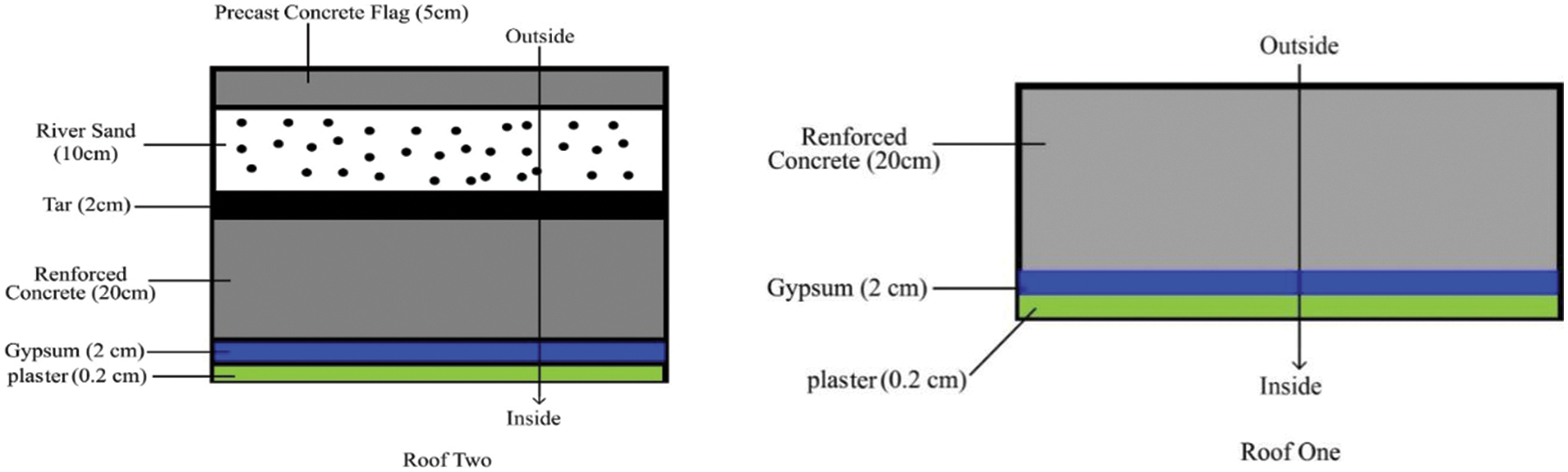
Figure 2: External roofing configurations

For thermal resistances in series: the general case of thermal resistances arranged in series is shown in Figs. 1 and 2.
The Matlab software is used to solve the governing equations, where the solutions are computed with a minimum period of 10–15 min. This time can be problematic for detailed control studies, where the time step of 1 min is used. The algorithm is explained as follows:
1. Finding the complex matrix elements, A, B, C, and D, using Eqs. (2)–(5) that give the thickness Lj and the thermal properties kj, ρj, cpj of the layer j.
2. Calculating the complex form of a Fourier series expression using Eq. (9).
3. Calculating the exponential coefficient T and phase lag Ф for each harmonic n using Eqs. (10) and (11).
4. Calculating the steady-state portion of heat flux by Eq. (12).
5. Calculating the total inside heat flux for n harmonics by summating or superimposing the steady-state and transient portions by Eq. (14).
6. Calculating the transient heat flux on the interior of the building by Eq. (15).
7. Since the inside air temperature remains constant over time, the transient heat flux on the interior of the building is evaluated using Eq. (16).
4.1 Solutions of Different Wall Types
Fig. 3 shows the inside heat flux transfer behaviour through the walls used in this study. We note that the maximum heat flux transfer occurs through the first type of wall (Cement Mortar, Brick, and Gypsum). The inlet heat flux begins to decrease through the walls and then starts to increase with time. The findings show that the inlet heat flux of the second type of wall is lower than the first type of wall due to the addition of the layer of plaster, which works to increase the thickness of the wall and also works to improve the thermal conductivity coefficient leading to enhance the heat capacity of the wall. When using the third type of wall, the internal heat flux transfer is as small as possible because the thickness of the wall increases by adding layers (Air Cavity and Sheathing Timber), which in turn works to increase the thermal resistance of the wall and thus increases the heat capacity of the wall.
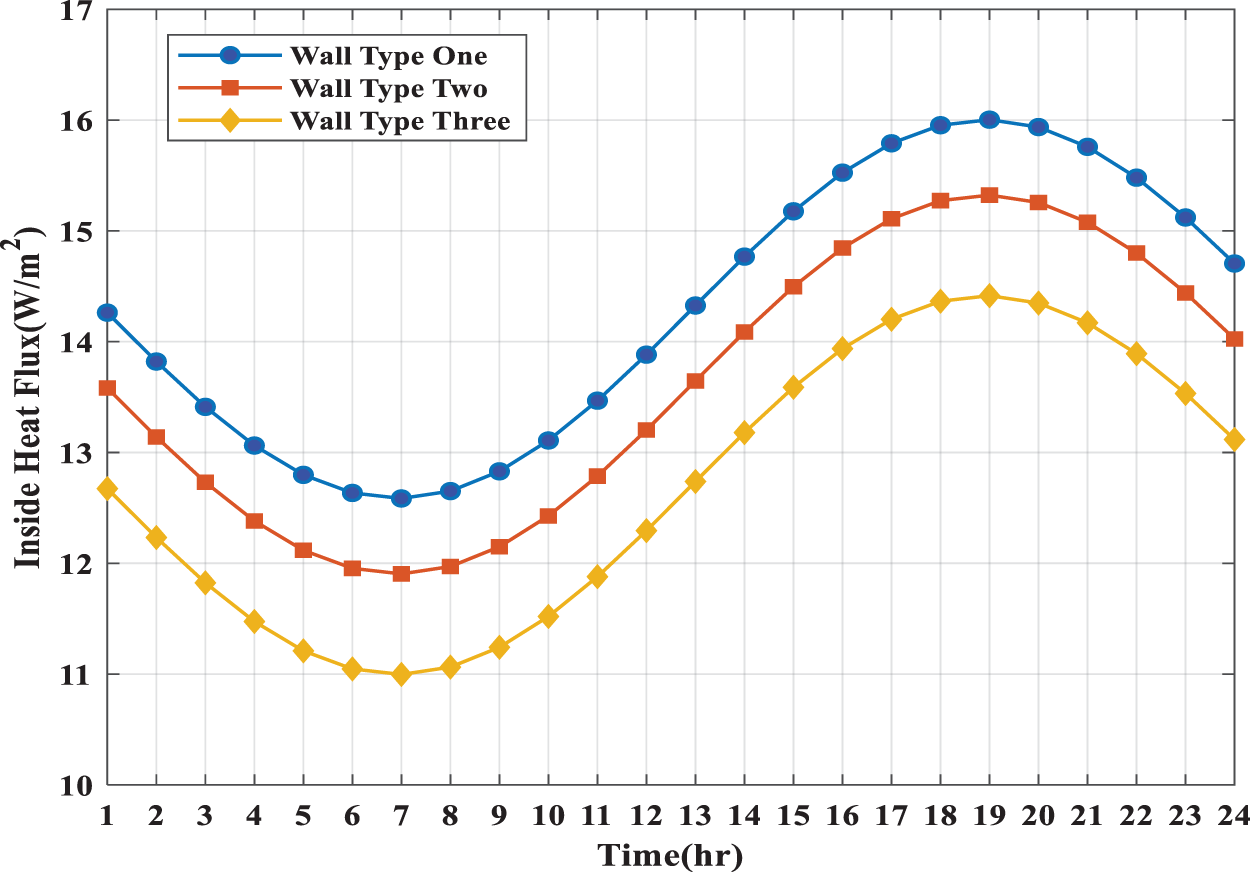
Figure 3: Variations of entry heat flux for various types of walls
It can be noted from the results of Fig. 3 that when adding the (plaster layer) in the second wall type, as well as when adding the (Air Cavity and Sheathing Timber) layers in the third wall type, there is a reduction in the amount of heat flux acquired in the presence of these layers, due to the effect of the specific heat capacity possessed by these materials, which leads to a reduction in the amount of flux [40].
4.2 Solutions of Different Roof Types
Fig. 4 shows the inside heat flux through the various types of roofs in terms of time. It can be noted here that the amount of inside heat flux through the first type of roof (reinforced concrete, gypsum, and plaster) is higher than the inside heat flux through the second type. The reduction in the amount of inside heat flux through the second type of roof is due to the addition of materials (precast concrete flag, river sand, and tar), which in turn works to increase the thickness of the roof as well as the coefficient of thermal conductivity and improving the thermal resistance of the roof leading to reduce the diffusion of inside heat flux by rising the heat capacity of the roof. From the results of Fig. 4, we note that the heat flux gained from the second type roof is less than the first type roof under the same weather conditions. This is due to the thermal properties possessed by the second roof materials, especially the effect of the specific heat of the (Tar) added to the second roof, which works to reduce the amount of heat flux gained [41].
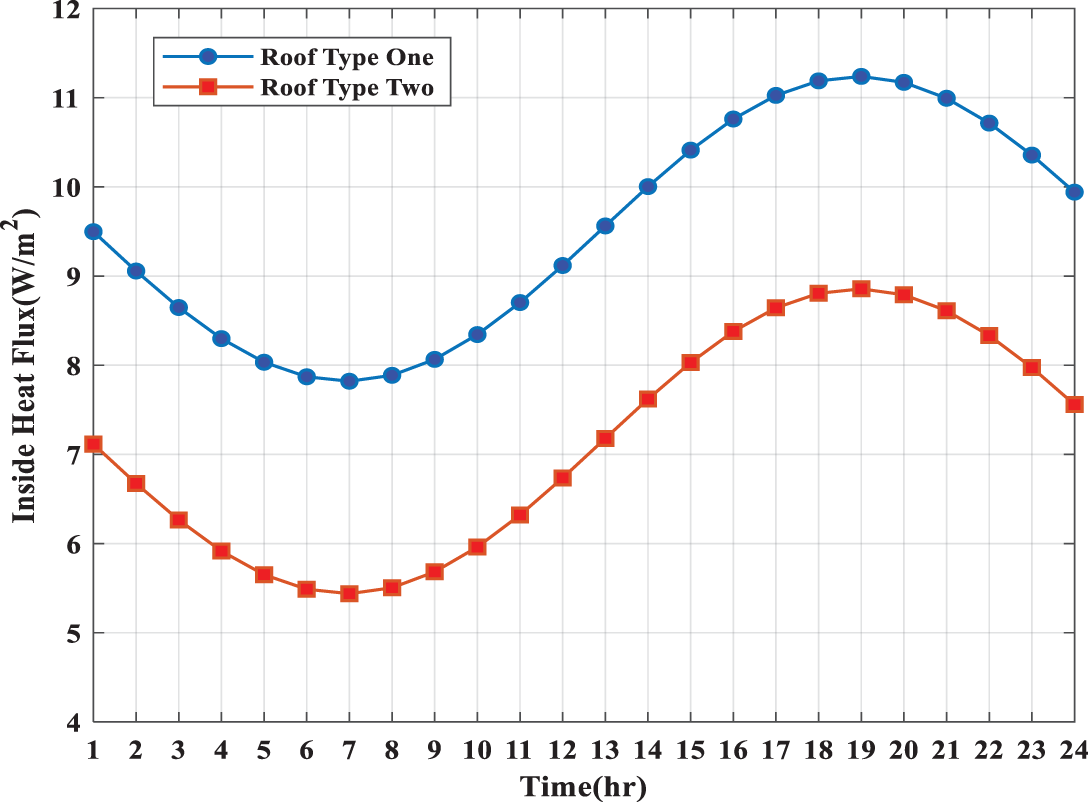
Figure 4: Variations of entry heat flux for various types of roofs
4.3 Comparison with Previous Study
The current solutions are compared with the work of Joudi et al. [39] and Qatta [42] for the same City in Iraq, which uses different types of material for the walls and roofs. Fig. 5 compares the results of this research for the various types of roofs with the results obtained by Joudi et al. [39]. Fig. 6 compares the results obtained from the current work for three wall types with the results obtained by Qatta [42]. It can be noted here that the roof material used by Joudi et al. [39] is (cement shtyger, sand, felt, Membrane, sty-rubber, and high-density concrete). In contrast, the materials used by Qatta [42] for the wall are (Cement, Brick, Palm Fiber, and Gypsum). The comparison shows that the type of wall used by Qatta [42] is better than the current wall types due to a reduction in the amount of internal heat flux, the hot climate in Iraq, and the type of wall used in their study compared to the current work. The comparison shows that the material of roof type used by Joudi et al. [39] is better than the first type of current roof by reducing the amount of heat flux entering compared to the first type of roof used in this study. However, the findings show that the current second type of roof is better than that used by Joudi et al. [39]. The results for comparison indicated that the amount of heat flux entering strongly depends on the material used for the walls and roofs. Comparing the results of this study with previous research gives us validation for the results of our analysis by noting that the behaviour of the heat flux acquired through the walls and roofs of previous studies is the same as in our research for the same city (Baghdad) at the same climatic conditions, despite the difference in the method of calculating the heat flux of previous studies from the technique used in our research.
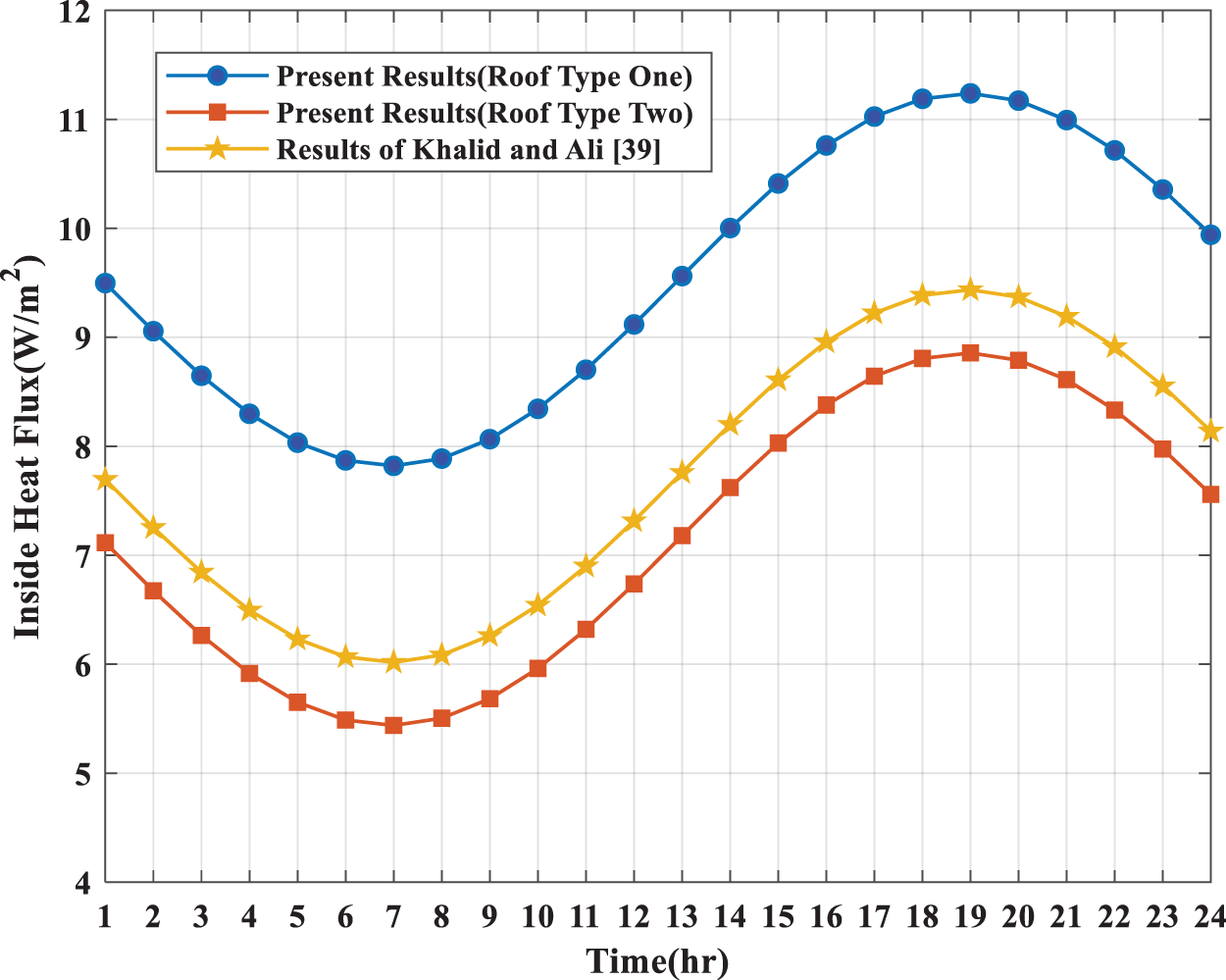
Figure 5: Comparison between the current solutions and solutions obtained by Joudi et al. [39] for various types of roofs
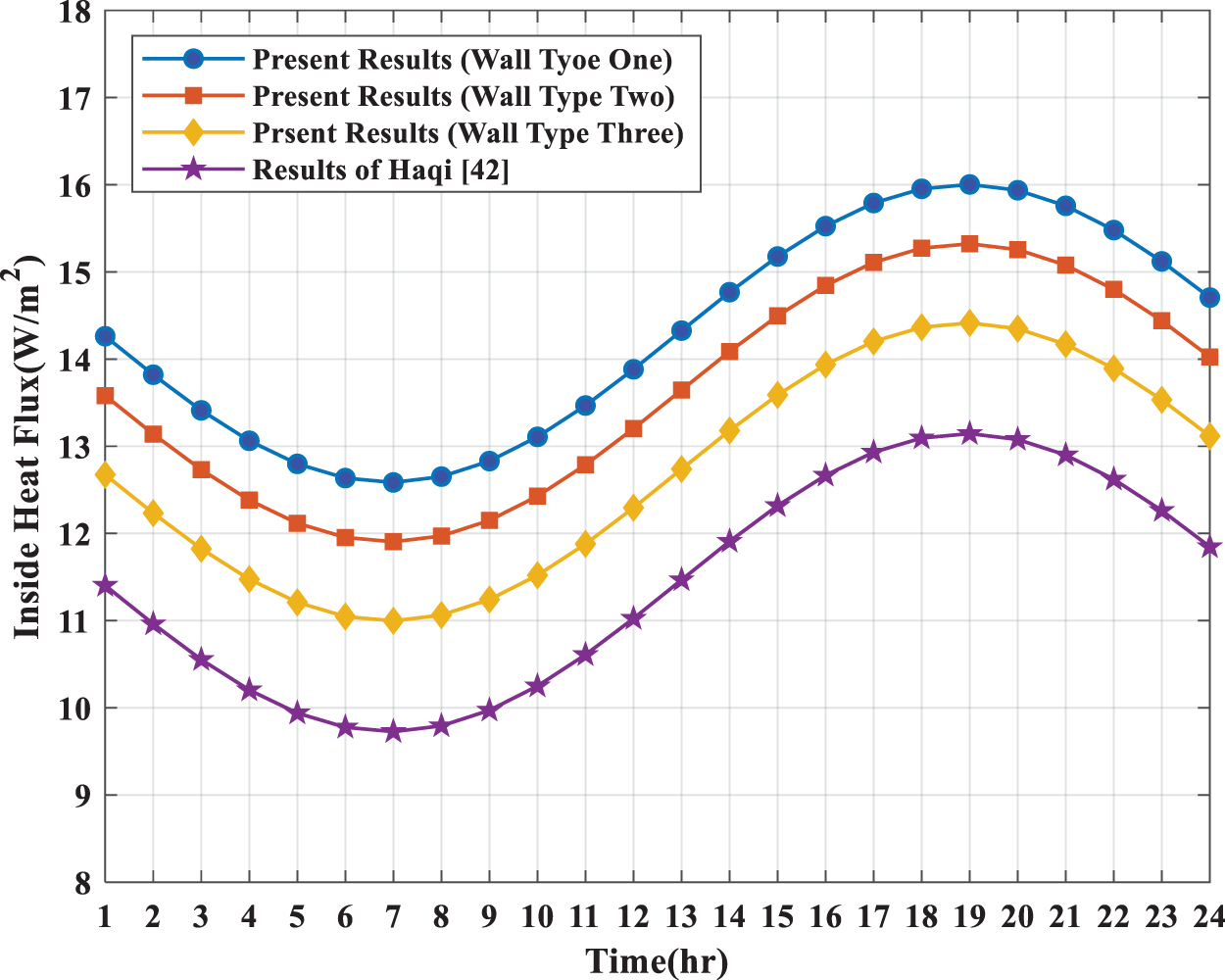
Figure 6: Comparison between the current solutions and solutions obtained by Qatta [42] for various types of walls
In the current work, the effectiveness of thermal insulation of various types of composite walls and roofs is numerically investigated to display the best model that can be employed for energy building construction in Iraq. The governing equations are solved using the transmission matrix method in MATLAB software. The weather data for 21st July 2022 in Baghdad City/Iraq, was selected as a test day. From the results of this study, the following conclusions are set:
1. The results indicated that the transmission matrix method has limited input elements. The linear relationship between the temperature and the heat transfer rate at the system’s heat source and environment sides is characterized by a matrix that does not surpass the 2
2. The findings display that the thermal capacity of the building rises with an increase in the number of insulation layers. Hence, this issue leads to an increase in the thermal resistance of the construction.
3. The results confirm that the cooling load of a building depends on the types of materials used while building it.
4. The findings show that the entry heat flux is reduced by 4% (for the second type of wall) and 10% (for the third type of wall) compared to the first type of wall.
5. The outcomes show that the entry heat flux is reduced by 21% using the second type of roof compared to the first type.
6. Finally, the results confirm that the third type of wall and the second type of roof represent the best models that can be used in the weather conditions in Iraq compared to the other models.
The current work can be extended for future projects using Phase Change Material (PCM) on walls and roofs. Phase Change Materials (PCM) can efficiently absorb a significant amount of solar energy that falls on the walls or roofs of residential structures. PCM’s high thermal mass allows them to mitigate the impact of considerable temperature variations on the indoor climate of buildings [44].
Acknowledgement: We humbly thank Northern Technical University for their laboratory support for this study.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ahmed Mustaffa Saleem, Abdullah A. Badr; data collection: Bahjat Hassan Alyas; analysis and interpretation of results: Omar Rafae Alomar; draft manuscript preparation: Omar Rafae Alomar. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data is available on request.
Conflicts of Interest: The authors declare that there are no conflicts of interest to report regarding the present study.
References
1. Al-Doury MA, Mohammed RK. Thermal conductivity of building materials in Iraq. Tikrit J Eng Sci. 2021;28(4):37–49. doi:10.25130/tjes.28.4.4. [Google Scholar] [CrossRef]
2. Aldawi F, Alam F, Khan I, Alghamdi M. Effect of climates and building materials on house wall thermal performance, in procedia engineering. Fifth BSME Int Conf Therm Eng. 2013;56:661–6. doi:10.1016/j.proeng.2013.03.175. [Google Scholar] [CrossRef]
3. Waheb JH. Contribution of thermal insulation in reducing the cooling load for Iraqi building. Int J Innov Sci, Eng Technol. 2015;2(9):32–40. [Google Scholar]
4. Waheba JH, Yaseenb TA. Enhance the thermal performance of Iraqi house using new passive systems. Int J Sci: Basic Appl Res. 2016;30(4):335–3342. doi:10.13140/RG.2.1.1319.2560. [Google Scholar] [CrossRef]
5. Ipseng IU, Fisher DE. Application of conduction transfer functions and periodic response factors in cooling load calculation procedures. ASHRAE Trans. 2004;109(2):829–41. [Google Scholar]
6. Özbalta TG, Kartal S. Heat gain through Trombe wall using solar energy in a cold region of Turkey. Sci Res Essays. 2010;5(18):2768–78. [Google Scholar]
7. Luo C, Moghtaderi B, Page A. Modelling of wall heat transfer using modified conduction transfer function, finite volume, and complex fourier analysis methods. Energy Build. 2010;42:605–17. doi:10.1016/j.enbuild.2009.10.031. [Google Scholar] [CrossRef]
8. Luo C, Moghtaderi B, Sugo H, Page A. A new stable finite volume method for predicting thermal performance of a whole building. Build Environ. 2008;43:37–43. doi:10.1016/j.buildenv.2006.11.037. [Google Scholar] [CrossRef]
9. Maimagani1 SS, Majid RA, Chung LP. Thermal performance of classroom block: a comparison of hobo datalogger and design builder. J Inform Syst Technol Manage. 2022;7(25):224–37. doi:10.35631/JISTM.725019. [Google Scholar] [CrossRef]
10. Abdullah HK, Aboud SM. Reduction of heat transfer through walls in buildings by using insulation. Int J Comput Appl. 2016;141(4):1–6. [Google Scholar]
11. Pekdogan T, Basaran T. Thermal performance of different exterior wall structures based on wall orientation. Appl Therm Eng. 2017;112:15–24. doi:10.1016/j.applthermaleng.2016.10.068. [Google Scholar] [CrossRef]
12. Wei M, Wang B, Liu S. Numerical simulation of heat and moisture transfer of wall with insulation. IOP Conf Series: J Phys: Conf Series. 2019;1300:1–7. doi:10.1088/1742-6596/1300/1/012029. [Google Scholar] [CrossRef]
13. Jannat N, Hussien A, Abdullah B, Cotgrave A. A comparative simulation study of the thermal performances of the building envelope wall materials in the tropics. Sustainability. 2020;12:1–26. doi:10.3390/su12124892. [Google Scholar] [CrossRef]
14. Hagentoft C-E, Pallin S. Thermal step response of N-layer composite walls—accurate approximative formulas. J Heat Transf. 2020;142:1–6. doi:10.1115/1.4045642. [Google Scholar] [CrossRef]
15. Qian J, Sun L. Application of transfer function in predicting the temperature field of space equipment under periodic external heat flow. Front Energy Res. 2022;10:1–11. doi:10.3389/fenrg.2022.833071. [Google Scholar] [CrossRef]
16. Mohammed AR, Naimi S. The effectiveness of thermal insulation of the exterior composite walls of buildings in Iraq based on different materials and climate regions using engineering applications. Int J Intell Syst Appl Eng. 2023;11(4s):594–601. [Google Scholar]
17. Hasan ASh, Ali OM, Hussein AA. Comparative study of the different materials combinations used for roof insulation in Iraq. Mat Today: Proc. 2021;42(5):2285–9. doi:10.1016/j.matpr.2020.12.317. [Google Scholar] [CrossRef]
18. Abdulsada GK, Salih TWM. The impact of efficient insulation on the thermal performance of building elements in a hot arid region. Renew Energy Environ Sustain. 2022;7(2):1–6. doi:10.1007/978-3-030-76221-6. [Google Scholar] [CrossRef]
19. Liu X, Chen X, Shahrestani M. Optimization of insulation thickness of external walls of residential buildings in hot summer and cold winter zone of China. Sustainability. 2020;12(4):1–21. doi:10.3390/su12041574. [Google Scholar] [CrossRef]
20. Sharma An, Sengar N. Heat gain study of a residential building in hot-dry climatic zone on basis of three cooling load method. Eur J Eng Res Sci. 2019;4:186–94. doi:10.24018/ejers.2019.4.9.1508. [Google Scholar] [CrossRef]
21. Oktay H, Yumrutaş R, Zerrakki Işık M. Comparison of heat gain values through multilayer walls utilizing or non-utilizing the relationships between thermophysical properties. In: International Engineering and Natural Sciences Conference; 2019 Nov 6–8; Dicle University, Diyarbakır, Turkey. p. 252–61. [Google Scholar]
22. Thomas LP, Marino BM, Muñoz N. Steady-state and time-dependent heat fluxes through building envelope walls: a quantitative analysis to determine their relative significance all year round. J Build Eng. 2020;29: 1–33. doi:10.1016/j.jobe.2019.101122. [Google Scholar] [CrossRef]
23. Ghanim MR, Ahmed ST. Reducing roof solar heat gain by using double-skin ventilated roofs. Eng Technol J. 2020;38:402–11. doi:10.30684/etj.v38i3A.462. [Google Scholar] [CrossRef]
24. Melo AP, Lamberts R, Versage RD, Zhang Y. Is thermal insulation always beneficial in hot climate?. In: Proceedings of BS2015: 14th Conference of International Building Performance Simulation Association; 2015; India. p. 1353–60. doi:10.26868/25222708.2015.2188. [Google Scholar] [CrossRef]
25. Divsalar R. Building problems in hot climates (MSc Thesis). Eastern Mediterranean University: North Cyprus; 2010. [Google Scholar]
26. Austin MC, Araúz J, Mora D. Numerical assessment of different phase change materials as a passive strategy to reduce energy consumption in buildings under tropical climates. Buildings. 2022;12, 906(7):1–25. doi:10.3390/buildings12070906. [Google Scholar] [CrossRef]
27. Qudama A-Y, Mohammed A, Marta S, Müslüm A. Building envelope-enhanced phase change material and night ventilation: effect of window orientation and window-to-wall ratio on indoor temperature. Renew Energy.2023;218:119263. doi:10.1016/j.renene.2023.119263. [Google Scholar] [CrossRef]
28. Al-Tamimi N. Passive design strategies for energy efficient buildings in the arabian desert. Front Built Environ. 2022;7:1–11. doi:10.3389/fbuil.2021.805603. [Google Scholar] [CrossRef]
29. Yamoul N, Dlimi L, El Harrouni K, Chakir BA. Improving the passive building energy efficiency: a case study of a moroccan modern house. Civil Eng Archit. 2023;11(5):2435–46. doi:10.13189/cea.2023.110514. [Google Scholar] [CrossRef]
30. Stanca S. Improving energy efficiency in a building using passive energy-saving measures. J Appl Eng Sci. 2023;13(26):269–74. [Google Scholar]
31. Shaik S, Gorantla KK, Setty ABTP. Investigation of building walls exposed to periodic heat transfer conditions for green and energy efficient building construction. Procedia Technol. 2016;23:496–503. doi:10.1016/j.poly.2016.03.055. [Google Scholar] [CrossRef]
32. Kunze O, Fariborz H. A procedure for calculating thermal response factors of multilayer wallsstate space method. Build Environ. 1991;26(2):173–7. doi:10.1016/0360-1323(91)90024-6. [Google Scholar] [CrossRef]
33. Debnath L. A short biography of Joseph Fourier and historical development of Fourier series and Fourier transforms. Int J Math Educ Sci Technol. 2012;43(5):589–612. doi:10.1080/0020739X.2011.633712. [Google Scholar] [CrossRef]
34. Fokaides A, Kalogirou SA. Application of infrared thermography for the determination of the overall heat transfer coefficient (U-Value) in building envelopes. Appl Energy. 2011;88:4358–65. doi:10.1016/j.apenergy.2011.05.014. [Google Scholar] [CrossRef]
35. Najima KB, Fadhil OT. Assessing and improving the thermal performance of reinforced concrete-based roofing systems in Iraq. Energy Build. 2015;89:213–21. doi:10.1016/j.enbuild.2014.12.049. [Google Scholar] [CrossRef]
36. Najim KB. External load-bearing walls configuration of residential buildings in Iraq and their thermal performance and dynamic thermal behaviour. Energy Build. 2014;84:169–81. doi:10.1016/j.enbuild.2014.07.064. [Google Scholar] [CrossRef]
37. Antwan NF. Effect of Iraqi insulation position in walls and roofs on cooling load in Iraqi buildings using TFM. J Techniques. 2008;21:198–210. [Google Scholar]
38. Al-Yasiri Q, Al-Furaiji MA, Alshara AK. Comparative study of building envelope cooling loads in Al-Amarah City, Iraq. J Eng Technol Sci. 2019;51(5):632–48. doi:10.5614/j.eng.technol.sci.2019.51.5.3. [Google Scholar] [CrossRef]
39. Joudi KA, Hussien AN. Cooling load calculations for typical Iraqi roof and wall constructions using Ashrae’s RTS method. J Eng. 2015;21:98–114. doi:10.31026/j.eng.2015.05.08. [Google Scholar] [CrossRef]
40. Zeki A, Hasan O, Recep Y. Comparison of heat gain values obtained for building structures with real and constant properties. BEU J Sci. 2019;8(4):1518–32. [Google Scholar]
41. Abubakar A, Mohan Kumar A. Temperature distribution in a concrete slab with sand, gravel and radiant barrier. Mat Today: Proc. 2022;55(2):399–403. doi:10.1016/j.matpr.2021.11.651. [Google Scholar] [CrossRef]
42. Qatta HI. Reduction of heat transfer through walls in building by using local natural insulation in IRAQ. Iraqi J Mech Mat Eng. 2013;13(3):439–57. [Google Scholar]
43. Bácsi Á. The number of independent elements in heat transmission matrices. Int J Therm Sci. 2019;138: 496–503. doi:10.1016/j.ijthermalsci.2019.01.005. [Google Scholar] [CrossRef]
44. Santiago-Acosta RD, Otero JA, Hernández-Cooper EM. Thermal performance improvement of PCM layers. Energy Rep. 2023;9(12):81–6. doi:10.1016/j.egyr.2023.09.152. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools