 Open Access
Open Access
ARTICLE
Melting Flow Analyzation of Radiative Riga Plate Two-Phase Nano-Fluid Across Non-Flatness Plane with Chemical Reaction
1 Department of Mathematics, P. B. Siddhartha College of Arts and Science, Vijayawada, 520010, India
2 Department of Physics, Faculty of Sciences, University of 20 Août 1955-Skikda, Skikda, 21000, Algeria
3 Department of Mathematics, Narasaraopeta Engineering College, Yellamanda, Narasaraopet, 522601, India
4 Department of Mathematics, Sri Aravinda Satajayanthi Government Degree College, Narayanapuram, Ungutur Mandalam, 534406, India
5 Department of Mathematics, Vijayanagara Sri Krishnadevaraya University, Ballari, Karnataka, 583104, India
* Corresponding Authors: F. Mebarek-Oudina. Email: ,
(This article belongs to the Special Issue: Advances in Computational Thermo-Fluids and Nanofluids)
Frontiers in Heat and Mass Transfer 2024, 22(5), 1515-1532. https://doi.org/10.32604/fhmt.2024.057854
Received 29 August 2024; Accepted 12 October 2024; Issue published 30 October 2024
Abstract
There is a strong relationship between analytical and numerical heat transfers due to thermodynamically anticipated findings, making thermo-dynamical modeling an effective tool for estimating the ideal melting point of heat transfer. Under certain assumptions, the present study builds a mathematical model of melting heat transport nanofluid flow of chemical reactions and joule heating. Nanofluid flow is described by higher-order partial non-linear differential equations. Incorporating suitable similarity transformations and dimensionless parameters converts these controlling partial differential equations into the non-linear ordinary differential equations and resulting system of nonlinear equations is established. Plotted graphic visualizations in MATLAB allow for an in-depth analysis of the effects of distinguishing factors on fluid flow. Innovative applications of the findings include electronic cooling, heat transfer, reaction processes, nuclear reactors, micro heat pipes, and other related fields. If the exponential index increases, however, the thermal profile becomes worse. By comparing the current findings to those already published in the literature for this particular example, we find that they are highly congruent, therefore validating the present work. Every one of the numerical findings exhibits asymptotic behavior by meeting the specified boundary conditions.Keywords
Nomenclature
| a | Width of magnets between electrodes |
| U0 | Physical parameter related to a stretching sheet |
| b | Physical parameter related to a stretching sheet |
| C | Concentration of the nano fluid |
| Tm | Melting temperature |
| A* | Stretching parameter |
| ρ | Fluid density |
| Cf | Skin-friction co-efficient |
| Cp | Specific heat at constant pressure (J·kg−1·K−1) |
| C∞ | Concentration far away from the sheet |
| DB | Brownian diffusion co-efficient (kg·m−1·s·K) |
| DT | Thermophoresis diffusion co-efficient (kg·m−1·s·K) |
| Ec | Eckert number |
| F | Dimensionless velocity (m·s−1) |
| f | Dimensionless velocity (m·s−1) |
| J0 | Applied current density in the electrodes (A·m−2) |
| K | The thermal conductivity of the fluid (W·m−1·K−1) |
| Chemical reaction rate | |
| Kr | Chemical reaction parameter |
| m | Velocity index parameter |
| M0 | Magnetization parameter (Tesla) |
| Nb | Brownian motion parameter |
| Nt | Thermophoresis parameter |
| Pr | Prandtl number |
| Q | Modified Hartmann number |
| Q0 | Heat generation/absorption parameter (W·m−3·K−1) |
| T | Temperature (K) |
| Sc | Schmidt number |
| T∞ | Temperature far away from the sheet (K) |
| u, v | Velocity components in x and y directions (m·s−1) |
| U∞ | Ambient velocity (m·s−1) |
| Ue | Free stream velocity (m·s−1) |
| Uw | Stretching velocity |
| x, y | Cartesian co-ordinates |
| α | Divider thickness parameter (m) |
| β1 | Dimensionless parameter |
| η, ξ | Similarity variables |
| μ | Dynamic viscosity (N·s·m−2) |
| υ | Kinetic viscosity (m2·s−1) |
| ϕ | Dimensionless concentration |
| τ | Sheer stress tensor |
| θ | Dimensionless temperature (K) |
Although there are many different kinds of fluids found in nature, nanofluids stand out for all the many uses they may fulfill. Metal-oxides, oxide-ceramics, and stabled-chemical metals are the most prevalent components of nanofluids. It is common practice to employ lubricants, oils, polymerics, glycols, bio-fluids, and biofuels as the base fluids. Fluids with a base size of up to 100 nm are considered like nanofluids, they are two-phase mixes created by dispersing particles that are nanometers in size. One important aspect of heat transfer study is the use of nanoparticles. The practical uses of liquid film flow, however, are expanding daily. A wide variety of operations make use of these flows, the most prevalent of which being heat exchange, coating, industrial, and distillation procedures. Liquid film flow has exciting practical applications that bring together technological advances, structural mechanics, and fluid mechanics. The fluidization of the reactor, representation of plastic sheets, processing of foodstuffs, and extrusion of polymers and metals are among the practical applications.
Nanofluids have been the subject of two separate models for examination. Two-phase model, initially put forward by Tiwari et al. [1], is rooted in the homogeneity principle. In his second model, Buongiorno [2] postulated a dispersion model that takes into account the slip mechanism that exists between conducting fluids and nanoparticles. The second model incorporates several slide processes, including Brownian and thermophoresis, and addresses their ramifications. Many researches have used these models to investigate different aspects of nanofluid flows.
Dharmaiah et al. [3] studied magnetic dipole implications towards radiative magnetic ferro liquid streaming across stretchable plane with Brownian motion and thermophoresis present. Ramesh et al. [4] illustrated real-world applications of a number of concepts, including radiation, nanofluids, magnetohydrodynamics, heat and mass transport. The progressive heat transfer processes during nanofluids across stretchy plane boundary have been studied by Sohail et al. [5]. The entire model includes Brownian motion, radiation, thermophoresis, Cattaneo-Christov implication. According to Fayz-Al-Asad et al. [6], the purpose of their study was to investigate the magneto convective heat transfer via lid-driven upright wavy confinement by a bottom fin. Mebarek-Oudina et al. [7], among others, reported a quadratic Rosseland approximation effect and an exponential Cattaneo-Christov heat flow in space. A solution containing nanoparticles and microorganisms could significantly increase the thermal efficiency of heat transfer, as demonstrated by Dharmaiah et al. [8]. The entropy formation in hybrid nanofluid magneto-convective flow was studied by Mebarek-Oudina et al. [9].
Many modern technical and industrial processes rely on the phenomena of liquefaction heat transfer, which has piqued, researcher’s interest. Experts in the field have shown a strong desire to find better, more long-term solutions for energy storage. (i) Thermal chemical energy storage; (ii) energy storage by sensible heat; and (iii) energy storage by latent heat are the three most efficient ways to store thermal energy. The use of latent heat for energy storage is more efficient and long-term viable in these approaches. Some examples of melting phenomena include the following: the solidification of magma, permafrost melting, semiconductor material preparation, frozen thawing grounds, welding and casting, and soil freezing. Initially, Robert [10] addressed the features of melted ice slab heat transmission, put in hot air. In his study on magnetohydrodynamic flow caused by a moving object, Das [11] looked at the effects of melting and heat radiation. Researchers Ch et al. [12] examined the transport of melting heat in nanofluids moving toward a stretched sheet at their stagnation points. Williamson nanofluid saturated with porous media was reported by Krishnamurthy et al. [13] in their boundary layer flow study. Research conducted by Hayat et al. [14] examines the dynamics of water-carbon nanofluid flow over a nonlinear stretching sheet with varying thickness. Characteristics of the generated magnetic field in nanofluid flows over surfaces undergoing melting, Gireesha et al. [15] conducted research in this area.
A plate with a circular arrangement of magnetic material and interchangeable resistors may be prepared to serve as an electrostatic operator, also known as a Riga plate. As a pair, the letters N and S′ denote the north and south poles of the magnet, respectively, and when read separately they mean these things. As previously stated by Pantokratoras et al. [16], Riga plate generates Lorentz forces at wall-parallel. So many technical and industrial applications rely on the flow properties of Riga plates. Incorporating these methods into the design of liquid metal cooling-magneto generators, nuclear reactors, flow blood meters, pumps, etc., is a common practice. Moreover, thermal reactors use it to control the diffusion rate of neutrons. Fluid flows properties generated by the Riga surface have not been thoroughly studied by researchers yet. Thermogravimetric and homogenous heat transfer in viscous fluid flow, Riga surface with varying thicknesses was addressed by Farooq et al. [17]. Regarding heat transmission across nonlinearly thicker Riga plane with stratified thermal viscous liquid, Anjum et al. [18] addressed the matter. According to Ragupathi et al. [19], several fluids passing through a Riga plate were studied for heat transmission with Fe3O4 and Al2O3 nanoparticles. Hosseinzadeh et al. [20] explored the heat transfer caused by nanofluid flow across two elongated spinning discs with magnetohydrodynamic and solar radiation. Zinb et al. [21] detailed the radiation-induced changes in titanium alloy mixed convective micropolar nanofluid flow across the Riga plate. To study the heat transfer between two spinning discs, Shoaib et al. [22] built neural network for a magneto nano liquid flow.
It has been neglected in these studies that the surface’s thickness might change with motion if the sheet experiences non-uniform stretching velocities in various places. Additionally, surfaces with varying thicknesses and flows through needles with varying diameters are frequent in engineering and practical applications. Stretching sheet non-flatness drastically changes boundary layer structure, Fang et al. [23] discussed thickness on flow over a stretchy sheet. Abdel-Wahed et al. [24] expanded this research to include nanofluid flows by factoring in heat production and absorption. Regarding the MHD flow on a surface of varying thickness, Hayat et al. [25] investigated homogeneous-heterogeneous reaction implications and melting transfer. The authors Babu et al. [26] detailed the three-dimensional maximum hydrodynamic drag (MHD) flow of a nanofluid across a thin stretchy sheet that is contained in the slip flow regime. Hayat et al. have carried out stagnation point flow across a stretched sheet of varying thickness taking into account single and multiwall carbon nanotubes [27].
Many researchers consider chemical reactions important for a variety of purposes, including studying pollution, creating polymers and fibrous insulation, designing, dispersing fog, distributing moisture and temperature over agricultural fields, preventing crop damage from freezing, and many more. The molecular dispersion of species owing to chemical reactions is undeniable in this case since it is such a frequent sight. Homogeneous and heterogeneous processes are involved in several systems, including biological systems, combustion, and catalysis. Different rates of reactant species consumption and generation characterize these reactions.
Air and water emissions, fiber insulation, flow of air, several other chemical engineering issues may be greatly improved by understanding the influence of chemical reactions on boundary layer flows. Across a moving plate, Hussain et al. [28] examined the relevance of a chemical reaction with ramping surface concentration. In their study, Sarojamma et al. [29] investigated, under different circumstances, hydrodynamic Casson liquid flow across a stretched regime accompanied by a chemical reaction. The point of stagnation flow of a Jeffrey fluid across a stretched surface with viscous dissipation was discussed by Azhar et al. [30]. A chemical reaction convection flow in a channel were recently shown by Yusuf et al. [31]. The point of stagnation flow of Buongiorno’s nanofluid across a rotating disk that is stretched outwards was studied by Khan et al. [32].
Decades of research into heat transfer and boundary layer flow across a stretched regime paid off attention because of the many technical and commercial uses for the concepts. Nanofluids and convective heat transfer studies have recently advanced several industrial processes. Many researchers have examined nanofluid thermal conductivity, both theoretically and experimentally. Because of their versatility, nanofluids have become more prominent in recent years, especially when it comes to solving the boundary layer flow issue. Utilizing nanofluids may enhance the governing fluid’s thermo-physical properties, including convection, conductivity, and thermal diffusivity. While researchers have paid minimal attention to studying fluid dynamics across a uniform or variable-thickness Riga plate, they have not yet explored this area in relation to melting heat transfer. Filling this void is, hence, our primary goal. It is via joule dissipation that chemical reactions may be studied. An expanded understanding of the flow and heat transfer properties of various nanofluids as a function of many engineering-related physical parameters is now available in a paper based on the aforementioned experiments.
Joule dissipation’s impacts on MHD flow and heat transfer are worth examining due to their extensive applications. A wide range of heating devices, including those involved in crystal growth, the cooling of electronic chips and metallic sheets, paper manufacture, glass fiber drawing, and other operations that rely on the rate of heating or cooling, rely on it.
Recent work in chemical reaction research has focused on developing a mathematical model to forecast reactor performance. Investigations into the impact of varying thicknesses on stretched sheets reveal a chemical reaction involving foreign masses and fluids that may be controlled using homogeneous or heterogeneous approaches. The fields of mechanical engineering, civil engineering, marine engineering, aeronautical engineering, and design all make use of this kind of thinking. Earthenware, food, polymer, and other product manufacture is affected by chemical reaction procedures. Research into the movement of mass and heat during chemical reactions is of paramount importance to the chemical and hydrometallurgical sectors.
Authors are aware, still, no one has investigated joule heating and chemical reactions impacts on nanofluid flow via a Riga plate of varying thickness. As a result, the effects of joule heating and chemical reactions over a Riga plate of varying thickness are the primary foci of the current work. Filling such a gap is the goal of this academic study. Thermophoresis and Brownian motion impacts are taken. The novelty of the work is to examine an impacts of Joule heating and chemical reaction across the Riga-stretching plate. Particularly, the following features make the current endeavor unique. Our first consideration is the Riga plate, which may have a surface thickness that varies. The second step is to consider the Riga plate in melting temperature conditions while formulating the test. The third objective is to concentrate the nanoparticles at the Riga plate bulk. The analysis’s important factors are shown and explained.
Future directions: Researchers should hopefully think about this for many fluid models, Newtonian and non-Newtonian heating, activation energy, etc., in the future using various computational methods, flexible blade [33], thermo-hydraulic nano fluids [34] with radition [35].
An incompressible, stable, two-dimensional electrically conducting nanofluid may be considered flowing in a boundary layer toward a stretchy Riga plate that has a modest relative thickness d and is long. An additional component of Riga plate is a flat surface that is connected to an alternating array of permanent magnets and electrodes (see Fig. 1). This thickness is known to be little as compared to the length of the extendable Riga plate. At its surface, Riga plate has electrodes and a magnet. We have examined heat delivery in the context of an energy equation that includes unique effects such as joule heating and surface temperature, which includes the melting phenomena, and in the Buongiorno nanofluid model, which includes important aspects such as Brownian and thermophoretic diffusion.
i) Both the Joule heating effect and chemical reactions are taken into account.
ii) No fluctuation temperature at wall Tm, T∞ and C∞ are ambient θ(η) and C(η).
iii) The free stream velocity is
iv) Sheet elasticity speed is
v) The assumption is made that the viscous fluid across the Riga plate generates internal heat.
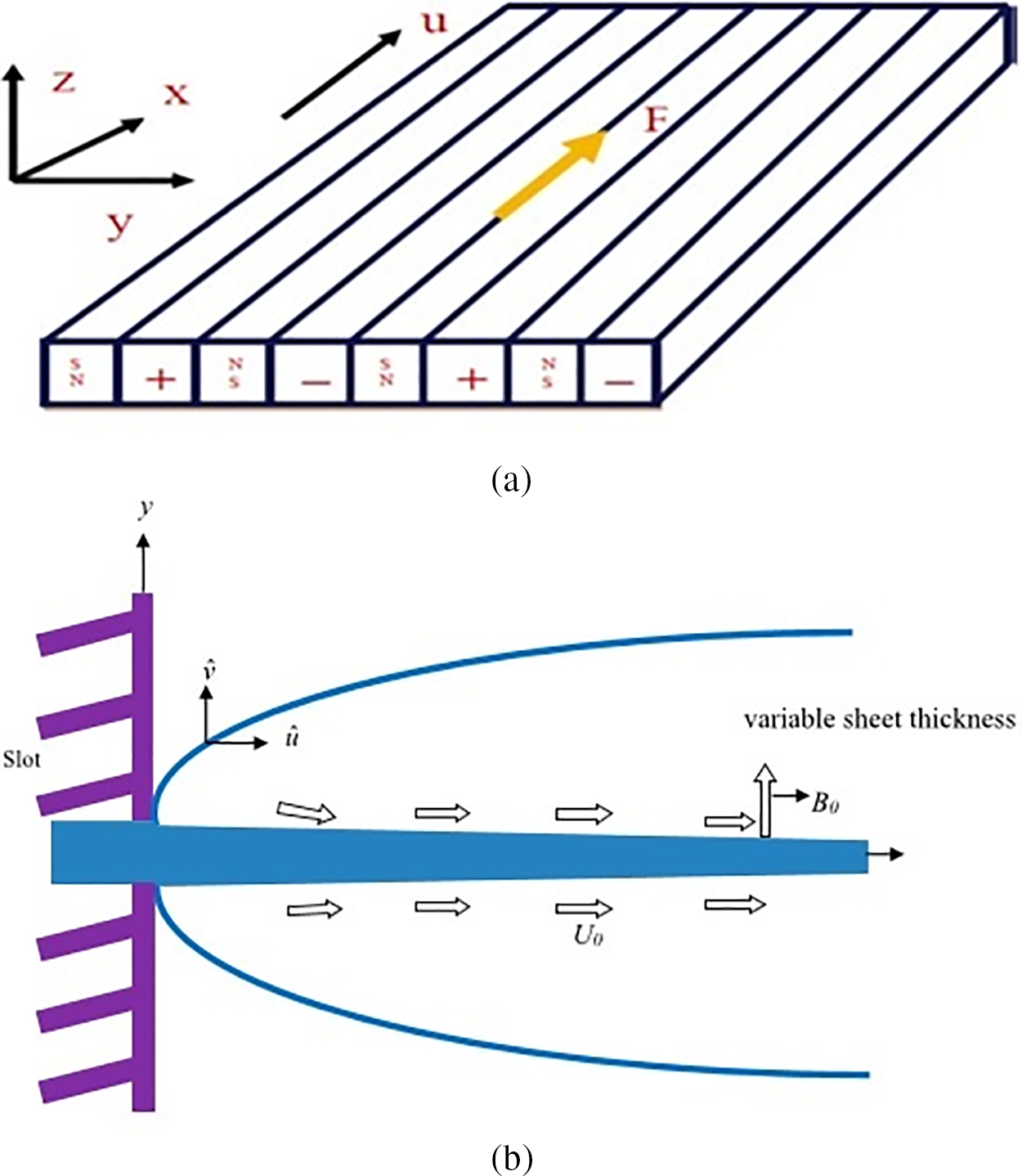
Figure 1: (a, b) Geometrical representations of flow
Equations that regulate the model are given by [14,17,18]:
Suitable boundary conditions [14,17,18]:
The similarity transformations being considered are:
By using Eq. (7), Eqs. (1)–(6) undergo a transformation:
The boundary conditions that are in relation to each other:
Here
Let
After reducing Eqs. (8) to (10) and Eqs. (11) to (12), the Eqs. (1) through (6) are transformed using (7) as:
Obtained boundary conditions:
The dimensional Cf, Nu and Sh are [35]:
The non-dimensional Cf, Nu and Sh are:
Eqs. (13)–(17) of the nonlinear coupled boundary-layer system are numerically solved with the help of bvp4c. A methodology is presented as Pictorial representation in Fig. 2.
(i) To begin, we get first-order simultaneous nonlinear differential equations by converting higher-order nonlinear differential Eqs. (13) to (15).
(ii) The method of bvp4c is utilized, to convert the equations into initial value problems.
(iii) The resulting initial value issue may be handled using the bvp4c method.
(iv) The numerical solution is obtained using ∆η = 0.001 as the condition for convergence.
(v) The skin-friction, Nusselt, and relative proportions of −f″(0), −θ′(0), and ϕ′(0) are also determined.

Figure 2: Pictorial representation
An extensive analyzation of dimensionless physical elements impact the numbers f′, θ, ϕ, Cf, Nu, and Sh is presented in this division. Graphs representing physical quantities take up the bulk of the work’s figures. Velocity profiles of the magnetic parameter in Fig. 3. At greater levels of magnetic parameter, the flow velocity drops dramatically over the whole fluid domain. With an applied magnetic field, an electrically conducting fluid experiences a drag-like force known as the Lorentz force. In the boundary layer, this force reduces fluid velocity because the magnetic field counteracts the transport phenomenon.

Figure 3: Magnetic parameter impact on velocity
The Lorentz force interaction is the physical explanation for the retarding nature of velocity. Alternatively, as seen in Fig. 4, the temperature distribution becomes hotter as the magnetic values go higher. Lorentz force acting on velocity profiles caused a form of flow friction, which increased the amount of heat energy created and, in the end, the temperature distribution within the flow (refer to Fig. 4). In terms of physical mechanism, the Lorentz force created by the transverse magnetic field relaxes the distribution of fluid temperature. As the magnetic parameter increases, the temperature boundary layer thickness increases as well. Fig. 5 shows the dimensionless temperature curves for various Eckert numbers. Sheet temperature rises as a function of Eckert number because to thermal impact resistivity. The Eckert number is derived from the link between the variations in kinetic energy and heat enthalpy. Physically, When Ec rises, fluid friction increases, and fluid particles strike more frequently to one another, which leads to the medium generating heat energy. On increasing dissipation parameter, temperature boundary layer thickness increases. The impact of chemical reactions on concentration profiles without dimensions has been shown in Fig. 6. Increases to the chemical reaction parameter swiftly reduce the concentration profile, as shown in Fig. 6. Increases in chemical reaction parameters result in a decrease in nanofluid concentration. Due to an enhanced chemical reaction parameter, the nanofluid concentration drops. Physically, a drop in the concentration field occurs when the number of solute molecules involved in the chemical reaction grows in relation to the size of the reaction. And so, the thickness of the solutal boundary layer is drastically reduced. With the help of the chemical reaction and magnetic parameter, CfX, NuX, and ShX can be shown in Figs. 7–9. The skin-friction and Nusselt numbers both rise with an increase in the magnetic parameter. The reason for this is because the momentum barrier layer becomes thicker as the magnetic parameter becomes larger sizes. For this reason, when the magnetic parameter rises, the skin friction coefficient and heat transfer rate also rise. Increasing the chemical reaction parameter reduces the mass transfer rate and lowers the Sherwood number. The values of the heat transfer rate for the increasing-manner parameters Pr, λ, and Ec, as well as the decreasing-manner parameter δ, are shown in Figs. 10–13. Figs. 14–17 show the directions of the streams.

Figure 4: Magnetic parameter impact on temperature

Figure 5: Eckert number impact on temperature

Figure 6: Chemical reaction parameter impact on concentration

Figure 7: Skin-friction for M

Figure 8: Nusselt number for M

Figure 9: Sherwood number for Kr

Figure 10: Nux relation verses

Figure 11: Nux relation verses

Figure 12: Nux relation verses

Figure 13: Nux relation verses

Figure 14: Stream lines with β1 = 0

Figure 15: Stream lines with β1 = 0.2

Figure 16: Stream lines with Q = 0

Figure 17: Stream lines with Q = 0.5
Under certain assumptions, the present study builds a mathematical model of melting heat transport across Riga surface variable thick in the context of a nanofluid flow of chemical reactions and joule heating. Incorporating suitable similarity transformations and dimensionless parameters converts these controlling partial differential equations into the non-linear ordinary differential equations.
• With rising values of the magnetic parameter, the flow velocity drops dramatically over the fluid domain.
• As magnetic values rise, so does the temperature distribution.
• Sheet temperature rises as a function of Eckert number because to thermal impact resistivity.
• As Kr is increased, the concentration profile is quickly reduced.
• The skin-friction and Nusselt numbers both rise with an improve in the magnetic parameter.
• Increasing Kr reduces the mass transfer and lowers the Sherwood number.
• Velocity of heat transfer for the increasing-manner Pr, λ, and Ec parameters, and the decreasing-manner δ.
Acknowledgement: None.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, data collection, analysis and interpretation of results, draft manuscript preparation: Jupudi Lakshmi Rama Prasad, F. Mebarek-Oudina, G. Dharmaiah, Putta Babu Rao, H. Vaidya. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data are available on request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.
References
1. Tiwari RK, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf. 2007;50(9–10):2002–18. doi:10.1016/j.ijheatmasstransfer.2006.09.034. [Google Scholar] [CrossRef]
2. Buongiorno J. Convective transport in nanofluids. J Heat Transf. 2006;128:240–50. doi:10.1115/1.2150834. [Google Scholar] [CrossRef]
3. Dharmaiah G, Mebarek-Oudina F, Balamurugan KS, Vedavathi N. Numerical analysis of the magnetic dipole effect on a radiative ferromagnetic liquid flowing over a porous stretched sheet. Fluid Dyn Mater Proc. 2024;20(2):293–310. doi:10.32604/fdmp.2023.030325. [Google Scholar] [CrossRef]
4. Ramesh K, Mebarek-Oudina F, Souayeh B. Mathematical modelling of fluid dynamics and nanofluids. 1st ed. Boca Raton, FL, USA: CRC Press (Taylor & Francis); 2023. doi:10.1201/9781003299608 [Google Scholar] [CrossRef]
5. Sohail M, Rafique E, Singh A, Tulu A. Engagement of modified heat and mass fluxes on thermally radiated boundary layer flow past over a stretched sheet via OHAM analysis. Discover Appl Sci. 2024;6(5):240. doi:10.1007/s42452-024-05833-1. [Google Scholar] [CrossRef]
6. Fayz-Al-Asad M, Mebarek-Oudina F, Vaidya H, Hasan MS, Sarker MMA, Ismail AI. Finite element analysis for magneto-convection heat transfer performance in vertical wavy surface enclosure: fin size impact. Front Heat Mass Transf. 2024;22(3):817–37. doi:10.32604/fhmt.2024.050814. [Google Scholar] [CrossRef]
7. Mebarek-Oudina F, Dharmaiah G, Balamurugan KS, Ismail AI, Saxena H. The role of quadratic-linearly radiating heat source with carreau nanofluid and exponential space-dependent past a cone and a wedge: a medical engineering application and renewable energy. J Comput Biophy Chem. 2023;22(8):997–1011. doi:10.1142/S2737416523420073. [Google Scholar] [CrossRef]
8. Dharmaiah G, Mebarek-Oudina F, Rama Prasad JL, Baby Rani C. Exploration of bio-convection for slippery two-phase Maxwell nanofluid past a vertical induced magnetic stretching regime associated for biotechnology and engineering. J Mol Liq. 2023;391(B):123408. doi:10.1016/j.molliq.2023.123408. [Google Scholar] [CrossRef]
9. Mebarek-Oudina F, Chabani I, Vaidya H, Ismail AI. Hybrid nanofluid magneto-convective flow and porous media contribution to entropy generation. Int J Num Methods Heat Fluid Flow. 2024;34(2):809–36. doi:10.1108/HFF-06-2023-0326. [Google Scholar] [CrossRef]
10. Roberts L. On the melting of a semi infinite body of ice placed in a hot stream of air. J Fluid Mech. 1958;4:505–28. [Google Scholar]
11. Das K. Radiation and melting effects on MHD boundary layer flow over a moving surface. Ain Shams Eng J. 2014;5:1207–14. [Google Scholar]
12. Ch KK, Bandari S. Melting heat transfer in boundary layer stagnation-point flow of a nanofluid towards a stretching-shrinking sheet. Can J Phys. 2014;92(12):1703–8. doi:10.1139/cjp-2013-0508. [Google Scholar] [CrossRef]
13. Krishnamurthy MR, Prasannakumara BC, Gireesha BJ, Gorla RSR. Effect of chemical reaction on MHD boundary layer flow and melting heat transfer of Williamson nanofluid in porous medium. Eng Sci Tech Int J. 2016;19(1):53–61. doi:10.1016/j.jestch.2015.06.010. [Google Scholar] [CrossRef]
14. Hayat T, Muhammad K, Farooq M, Alsaedi A. Melting heat transfer in stagnation point flow of carbon nanotubes towards variable thickness surface. AIP Adv. 2016;6(1):015214. doi:10.1063/1.4940932. [Google Scholar] [CrossRef]
15. Gireesha BJ, Mahanthesh B, Shivakumara IS, Eshwarapp KM. Melting heat transfer in boundary layer stagnation-point flow of nanofluid toward a stretching sheet with induced magnetic field. Eng Sci Tech Int J. 2016;19:313–21. [Google Scholar]
16. Pantokratoras A, Magyari E. EMHD free-convection boundary-layer flow from a riga-plate. J Eng Math. 2009;64(3):303–15. doi:10.1007/s10665-008-9259-6. [Google Scholar] [CrossRef]
17. Farooq M, Anjum A, Hayat T, Alsaedi A. Melting heat transfer in the flow over a variable thicked riga plate with homogeneous-heterogeneous reactions. J Mol Liquids. 2016;224:1341–7. [Google Scholar]
18. Anjum A, Mir N, Farooq M, Khan MI, Hayat T. Influence of thermal stratification and slip conditions on stagnation point flow towards variable thicked riga plate. Results Phys. 2018;9:1021–30. [Google Scholar]
19. Ragupathi P, Hakeem AA, Al-Mdallal QM, Ganga B, Saranya S. Non-uniform heat source/sink effects on the three-dimensional flow of Fe3O4/Al2O3 nanoparticles with different base fluids past a riga plate. Case Stud Therm Eng. 2019;15:100521. [Google Scholar]
20. Hosseinzadeh K, Asadi A, Mogharrebi A, Khalesi J, Mousavisani S, Ganji D. Entropy generation analysis of (CH2OH)2 containing CNTs nanofluid flow under effect of MHD and thermal radiation, Case Stud. Therm Eng. 2019;14:100482. [Google Scholar]
21. Zaib A, Khan U, Khan I, Seikh AH, Sherif E-SM. Entropy generation and dual solutions in mixed convection stagnation point flow of micropolar Ti6Al4V nanoparticle along a riga surface. Processes. 2019;8(1):14. [Google Scholar]
22. Shoaib M, Raja MAZ, Khan MAR, Farhat I, Awan SE. Neuro-computing networks for entropy generation under the influence of MHD and thermal radiation. Surf Interfaces. 2021;25(1):101243. doi:10.1016/j.surfin.2021.101243. [Google Scholar] [CrossRef]
23. Fang T, Zhang J, Zhong Y. Boundary layer flow over a stretching sheet with variable thickness. Appl Math Comput. 2012;218(13):7241–52. doi:10.1016/j.amc.2011.12.094. [Google Scholar] [CrossRef]
24. Abdel-Wahed MS, Elbashbeshy EMA, Emam TG. Flow and heat transfer over a moving surface with non-linear velocity and variable thickness in a nanofluids in the presence of Brownian motion. Appl Math Comput. 2015;254(3):49–62. doi:10.1016/j.amc.2014.12.087. [Google Scholar] [CrossRef]
25. Hayat T, Khan MJ, Alsaedi A, Khan MI. Homogeneous-heterogeneous reactions and melting heat transfer effects in the MHD flow by a stretching surface with variable thickness. J Mol Liq. 2016;223:960–8. doi:10.1016/j.molliq.2016.09.019. [Google Scholar] [CrossRef]
26. Babu MJ, Sandeep N. 3D MHD flow of a nanofluid over a slendering stretching sheet with thermophoresis and Brownian motion effects. J Mol Liq. 2016;222(1):1003–9. doi:10.1016/j.molliq.2016.08.005. [Google Scholar] [CrossRef]
27. Hayat T, Hussain Z, Alsaedi A, Asghar S. Carbon nanotubes effects in the stagnation point flow towards a nonlinear stretching sheet with variable thickness. Adv Powder Technol. 2016;27(4):1677–88. doi:10.1016/j.apt.2016.06.001. [Google Scholar] [CrossRef]
28. Hussain SM, Jain J, Seth GS, Rashidi MM. Free convective heat transfer with hall effects, heat absorption and chemical reaction over an accelerated moving plate in a rotating system. J Magn Magn Mater. 2017;422(6):112–23. doi:10.1016/j.jmmm.2016.08.081. [Google Scholar] [CrossRef]
29. Sarojamma G, Sreelakshmi K, Animasaun IL. Numerical study of non-linear thermal radiative heat transfer in a non Darcy chemically reactive Casson fluid flow. SN Appl Sci. 2019;1:1136. [Google Scholar]
30. Azhar E, Iqbal Z, Maraj EN. Viscous dissipation performance on stagnation point flow of Jefrey fluid inspired by internal heat generation and chemical reaction. Thermal Sci Eng Progress. 2019;13(1–6):100377. doi:10.1016/j.tsep.2019.100377. [Google Scholar] [CrossRef]
31. Yusuf TA, Mabood F, Gbadeyan JA, Adesanya SO. Nonlinear convective flow for MHD Oldroyd 8-constant fluid in a channel with chemical reaction and convective boundary condition. J Thermal Sci Eng Appl. 2020;12(5):1–13. doi:10.1115/1.4046908. [Google Scholar] [CrossRef]
32. Khan M, El Shafey AM, Salahuddin T, Khan F. Chemically Homann stagnation point flow of Carreau fluid. Phys A. 2020;551:124066. doi:10.1016/j.physa.2019.124066. [Google Scholar] [CrossRef]
33. Mahariq I, Kavyanpoor M, Ghalandari M, Alhuyi MN, Bui DT. Identification of nonlinear model for rotary high aspect ratio flexible blade using free vibration response. Alex Eng J. 2020;59(4):2131–9. doi:10.1016/j.aej.2020.01.029. [Google Scholar] [CrossRef]
34. Ayed H, Arsalanloo A, Khorasani S, Youshanlouei MM, Jafarmadar S, Abbasalizadeh M, et al. Experimental investigation on the thermo-hydraulic performance of air-water two-phase flow inside a horizontal circumferentially corrugated tube. Alex Eng J. 2022;61(9):6769–83. doi:10.1016/j.aej.2021.12.024. [Google Scholar] [CrossRef]
35. Ramesh K, Mebarek-Oudina F, Ismail AI, Jaiswal BR, Warke AS, Lodhi RK, et al. Computational analysis on radiative non-Newtonian Carreau nanofluid flow in a microchannel under the magnetic properties. Sciencia Iranica. 2023;30(2):376–90. doi:10.24200/sci.2022.58629.5822. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools