Numerical Simulation via Homotopy Perturbation Approach of a Dissipative Squeezed Carreau Fluid Flow Due to a Sensor Surface

1  Introduction

Squeezed flows occur when fluid is pushed through a tight passage, boosting its speed and lowering pressure sideways. This happens because the total mass flow stays steady in an incompressible fluid. As the fluid moves through the narrow area, its volume shrinks, leading to acceleration. These flows are crucial in engineering, particularly in microfluidics, for precise control in devices like lab-on-a-chip systems and medical diagnostics. This area has numerous practical uses, spanning chemical engineering, biophysical engineering, food engineering, polymer processing, biaxial expansion of bubble boundaries, liquid-metal lubrication, and the creation of dampers using motor bearings and electro-rheological fluids. Rashidi et al. [1] studied the flow of a viscous, incompressible fluid squeezed between two parallel plates. The unsteady two-dimensional flow of a viscous MHD fluid between two parallel infinite plates was examined by Siddiqui et al. [2]. The squeezing flow was thought to be caused by the two infinite plates approaching each other symmetrically. Mustafa et al. [3] researched the characteristics of heat and mass transport in a viscous fluid squeezed between parallel plates. The problem’s series solution was built using the homotopy analysis method (HAM). Khan et al. [4] researched how a viscous fluid flows when it is squeezed. Axisymmetric and two-dimensional flows, respectively, were the two types of flows that were studied.

Recent studies have extensively examined Casson fluid dynamics in various configurations: Khan et al. [5] analyzed heat transfer in Casson fluid compressed between parallel circular plates, while Ahmed et al. [6] studied its squeezing flow in electrically conductive media using the variation of parameters method (VPM). Al-Saif and Abeer [7] investigated MHD effects on Casson fluid compression flows, and Mat Noor et al. [8] explored MHD Casson nanofluid behavior in porous media with velocity slip, viscous dissipation, and chemical reactions. Sivasankaran et al. [9,10] experimentally examined unsteady MHD copper-water nanofluid flow between plates with chemical reactions, whereas Abbas et al. [11] analyzed heat transfer in squeezed particle fluids with thermal radiation effects.

Several recent studies have contributed significantly to the understanding of squeezed Casson fluid flows and associated heat transfer phenomena. Obalalu et al. [12] explored the unsteady squeezing flow and thermal behavior of a dissipative Casson fluid influenced by solar radiation, employing the optimal homotopy analysis method to capture transient effects. Jyothi et al. [13] extended the investigation to hybrid nanofluids, analyzing Casson hybrid nanofluid flow between parallel plates, accounting for thermophoretic effects and internal heat generation or absorption. Khan et al. [14] presented a detailed study on the influence of quadratic thermal stratification and slip boundary conditions in squeezed Casson fluid flow over a convectively heated surface, highlighting stratification’s role in thermal regulation. Qureshi et al. [15] provided both analytical and numerical insights into the fundamental mechanics of squeezing flow between two parallel plates, offering a benchmark for validating theoretical models in thermal engineering applications. Using an analytical method, Abdul-Ameer et al. [16] developed a model of heat and mass transfer in an unsteady squeezing flow between parallel plates.

Numerous scholars and researchers have worked to understand the characteristics of fluids throughout the years, especially non-Newtonian fluids, which have gained enormous popularity in a variety of the manufacturing sector, biofluid, food production, and medical sectors. One of the non-Newtonian fluid models that is vital in multiple fields is the Carreau fluid model. This constitutive model offers distinct advantages for characterizing shear-thinning fluids, particularly due to its ability to accurately capture the gradual transition between Newtonian and power-law regimes across varying shear rates. Such rheological precision is especially valuable for simulating both biological and synthetic fluids in microfluidic environments, making it particularly appropriate for our research objectives. The significance rheological properties of Carreau fluids have prompted extensive investigation into their behavior in geometrically complex flow configurations.

Several studies have explored magnetohydrodynamic (MHD) peristaltic flows of non-Newtonian fluids in complex geometries. Akbar et al. [17] analyzed the peristaltic motion of a Carreau nanofluid through an asymmetric channel under magnetic effects. Abbasi et al. [18] extended this research by studying Carreau-Yasuda fluid dynamics in curved configurations with applied magnetic fields. Kothandapani et al. [19] further investigated how wall permeability and magnetic interactions influence Carreau fluid flow in tapered asymmetric channels. Complementary work by Hashim and Khan [20], and Khan and Azam [21] examined coupled heat and mass transfer mechanisms, incorporating nanoparticle behaviors through Brownian motion and thermophoresis effects. Yousef et al. [22] analyzed how chemical kinetics, magnetohydrodynamics, and porous structures influence the flow of a dissipative Casson–Williamson fluid over a stretching surface with slip. Similarly, Alali and Megahed [23] addressed the unsteady flow of a Casson nanofluid film under magnetic and radiative effects, incorporating slip conditions and highlighting transient thermal dynamics.

Many investigations have advanced our understanding of non-Newtonian fluid dynamics in porous media under various conditions. Attia et al. [24] studied porous media flow of incompressible Bingham plastic fluids containing dust particles through circular pipes. Nasr et al. [25] numerically investigated MHD boundary layer behavior for Reiner-Philippoff fluids, focusing on thermal and mass transport phenomena. In a comprehensive study, Megahed and Abbas [26] systematically examined chemical reaction effects on laminar cross fluid flow coupled with heat and mass transfer processes.

Due to the significance of sensor surfaces in various processes, researchers have recently focused a lot of attention on them. One such example is the microcantilever, which can be used to precisely feel several biowarfare or dangerous substances as well as be able to identify various diseases. The temperature-dependent viscosity-affected magnetohydrodynamics (MHD) squeezed flow of nanofluid across a sensor shell was investigated by Akbar and Khan [27]. Nayak et al. [28], investigated the magneto-hydrodynamic flow of sodium chloride-carbon nano-powder nano-fluid across a sensor surface in a time-dependent manner. Hussain et al. [29] examined how an electrically conductive pseudoplastic fluid moved across a sensor surface in an unstable squashing hydromagnetic manner. The combined effects of radiation and heat generation on the electrokinetically produced hydromagnetic squeezed flow of a pseudoplastic fluid were investigated by Hussain et al. [30]. Located in the superficial free stream, a microcantilever sensor surface was being traversed by the fluid.

Drawing upon the insights gleaned from the comprehensive examination of existing literature, our current research focuses on exploring the magnetohydrodynamic dissipative characteristics of fluid flow within a narrow channel or conduit, specifically in conjunction with the flow of squeezed Carreau fluid, building upon existing literature and innovation in the field. Findings from this study have the potential to enhance process management, optimize flow dynamics, and improve efficiency across diverse operations. This understanding can guide the development and implementation of fluid-handling systems such as pumps, pipelines, and heat exchangers.

2  Theoretical Framework

This section develops the mathematical framework for analyzing the squeezed flow of a non-Newtonian Carreau fluid influenced by a magnetic field and viscous dissipation. Squeezed flow occurs when a fluid is compressed within a confined space, such as a narrow channel. Specifically, we examine the flow of a Carreau fluid between two parallel plates separated by a time-dependent distance, h(t). The velocity components along the x and y directions are denoted as u(x,y) and v(x,y), respectively, as illustrated in Fig. 1.

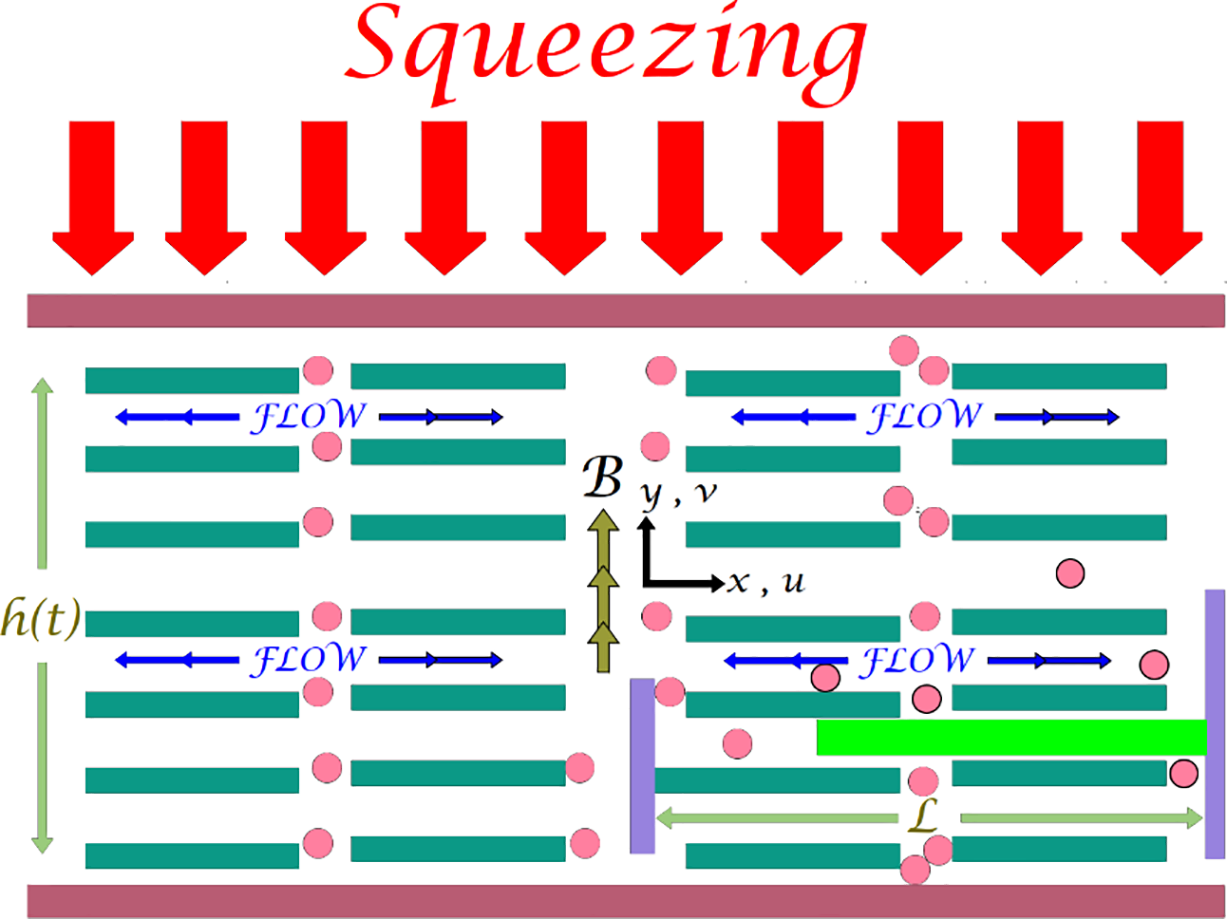
Figure 1: Physical model of sensor surface

Additionally, the analysis considers that the free-stream flow is subjected to squeezing.

The system configuration involves fluid motion from the tip region toward the surface, with a fixed lower plate and a movable upper plate generating the squeezing action. A micro cantilever sensor of length L is aligned with the stationary lower plate of the microchannel. In such squeezing flow configurations, the fluid dynamics near the sensor surface becomes particularly significant as the pressure distribution is directly affected by the plate movement. As the upper plate approaches the lower one, fluid compression creates elevated pressure zones that induce measurable surface deformation on the sensor. This deformation subsequently modifies the sensor’s output signal, which serves as the basis for determining key flow parameters including velocity and viscosity. The flow is driven by an external free stream velocity U, while a transverse magnetic field of intensity B0 is imposed in the y-direction, normal to the channel orientation.

The micro cantilever sensor was selected for its exceptional responsiveness to both pressure variations and thermal fluctuations in constrained flow environments. Within microfluidic and MEMS systems, the sensor’s bending deformation under squeeze flow conditions enables precise characterization of key fluid parameters, including flow velocity and dynamic viscosity. This operational principle validates the experimental configuration while demonstrating its utility for practical micro-scale flow diagnostics.

Applying the boundary layer approximation, the governing equations for mass conservation, momentum balance, thermal energy transport, and species concentration can be formulated as follows [1,2]:

∂u∂x+∂v∂y=0(1)

∂u∂t+u∂u∂x+v∂u∂y=−1ρ(∂p∂x)+μρ∂∂y(∂u∂y(1+Γ2(∂u∂y)2)n−12)−σB02ρu(2)

∂U∂t+U∂U∂x=−1ρ∞(∂p∂x)−σB02ρU(3)

∂T∂t+u∂T∂x+v∂T∂y=κρcp(∂2T∂y2)+μρcp(∂u∂y)2(1+Γ2(∂u∂y)2)n−12−1ρcp∂qr∂y(4)

In the previous model, it is important to emphasize that viscous dissipation in the energy equation represents the transformation of kinetic energy into thermal energy through fluid friction, an effect particularly pronounced in high-shear-rate flows or microscale systems. Similarly, the inclusion of magnetic effects in the momentum equation is critical for manipulating electrically conductive fluids, with direct applications in thermal management systems, microfluidic pumping, and magnetohydrodynamic (MHD) flow regulation.

The fluid properties are characterized by density ρ, dynamic viscosity μ, and specific heat capacity cp. The velocity field is described by components (u,v) in Cartesian coordinates (x,y) evolving with time (t). Key physical parameters include radiative heat flux (qr), power-law index (n), applied magnetic field intensity (B0), pressure (P), relaxation time constant (Γ), and thermal conductivity (κ). The governing boundary conditions reflecting the system geometry are specified as follows [1]:

u(x,y,t)=0,v(x,y,t)=v0(t),T(x,y,t)=Tw=T∞+q1xμaρ,aty=0(5)

u(x,y,t)=ax,T(x,y,t)=T∞,asy→∞(6)

The implemented boundary conditions model conventional squeezing flow dynamics, featuring a fixed lower plate and an opposing upper plate in motion towards it, generating pressure buildup, commonly observed in lubrication systems, polymer processing, and MEMS devices.

The governing equations employ the following notation: q1 denotes wall heat flux, while μ characterizes fluid viscosity. The permeable velocity v0(t) is typically modeled as a constant value vi. In computational fluid dynamics, similarity transformations serve as a powerful analytical tool for reducing partial differential equation systems to more tractable forms. This technique introduces dimensionless variables through appropriate scaling relationships, commonly expressed as:

η=yaρμ,ψ=xaμρ,u=axf′(η),a=1S+bt(7)

υ=−aμρf(η),θ(η)=T−T∞Tw−T∞,U=ax(8)

The analysis employs dimensionless variables to streamline the mathematical formulation of the physical problem. The key transformed parameters include: η (similarity variable), S (dimensionless constant), b (squeezing flow index), θ (normalized temperature), and f (dimensionless stream function). In fluid dynamics, the stream function ψ serves as an analytical tool for characterizing flow patterns, defined by its orthogonal gradient relative to the flow direction and its inherent satisfaction of the two-dimensional continuity Eq. (1) for incompressible flows. This mathematical approach frequently enables the reduction of complex physical systems into more manageable ordinary differential equations. Through implementation of Eqs. (7) and (8) while maintaining continuity via Eq. (1), the governing equations simplify to the following form:

(1+We2f′′2)n−32(1+nWe2f′′2)f′′′+(b2η+f)f′′+(b−M−f′)f′+(M−b+1)=0(9)

1Pr(1+R)θ′′+(fθ′−f′θ)+Ecf′′2(1+We2f′′2)n−12−b2(θ−ηθ′)=0(10)

here, we must mention the importance of the surface motion topics especially on nonlinear flow behavior has also been explored in some of recent works, including stretched or moving boundaries [31]. Furthermore, the corresponding boundary conditions can be expressed as follows:

f=−ℱ𝒪,f′=0,θ=1,atη=0(11)

f′=1,θ=0,asη→∞(12)

Additionally, the system’s behavior is primarily controlled by the following key parameters:

We=(a3x2Γ2ν)12,M=σB02aρ,Pr=μCpκ,Ec=U2Cp(Tw−T∞),R=16σ∗T∞33k∗κ,ℱ𝒪=υiav(13)

The key dimensionless parameters governing the system include the Weissenberg number, magnetic parameter, Prandtl number, Eckert number, radiation parameter, and surface permeability. Furthermore, critical physical metrics such as the local skin-friction coefficient Cfx and Nusselt number Nux quantitatively characterize the flow dynamics, heat transfer, and mass transfer phenomena. They are defined as follows:

Rex12Cfx=−[1+We2(f′′(0))2]n−12f′′(0)(14)

Rex−12Nux=−θ′(0)(15)

where Rex=ax2v is the local Reynolds number.

3  Solution Procedure

The homotopy perturbation method (HPM) is an analytical technique employed for nonlinear problems. Unlike traditional perturbation methods, HPM does not necessitate a small parameter in equations. It integrates homotopy theory, where a homotopy embedding parameter p within the range of [0, 1] serves as a small perturbation factor. Thus, the method, named HPM, combines homotopy techniques with conventional perturbation methods for comprehensive problem-solving. HPM is applicable to a range of nonlinear fractional models and offers simplicity and effectiveness. In addition to addressing both weakly and highly nonlinear problems, HPM eliminates the need for physical parameter assumptions, thereby overcoming limitations associated with traditional perturbation techniques. Furthermore, it outperforms standard numerical methods by obviating the need for discretization or linearization. Now, we can rewrite Eqs. (9) and (10) as:

u′′′+f(u)=0(16)

v′′+g(v)=0(17)

in which:

u′′′=f′′′(18)

f(u)=nWe2f′′2f′′′+(b2η+f)f′′+(b−M−f′)f′+(M−b+1)(1+We2f′′2)n−32(19)

v′′=θ′′(20)

g(v)=Rθ′′+Pr[(fθ′−f′θ)+Ecf′′2(1+We2f′′2)n−12−b2(θ−ηθ′)](21)

Applying procedure for homotopy perturbation method in unbounded domain [28–31], we can construct a homotopy equation for Eqs. (16) and (17) as:

u′′′−h2u′+q(f(u)+h2u′)=0(22)

v′′−h2⁡v+q⁢(g⁡(v)+h2⁡v)=0(23)

with boundary conditions,

u=−ℱ𝒪,u′=0,v=1,at η=0(24)

u′=1,v=0,as η→∞(25)

here, q denotes an artificial parameter where belongs to closed interval [0,1]. The equation system becomes a simpler form with an easily known analytical solution when q = 0. The system of equations changes to the necessary form as q is raised until a value of 1, and it is expected that the answer will become closer to the desired value. When q = 1, the parameter h will be further determined [32,33]. We suppose that the solution to Eqs. (22) and (23) may be expressed as a power series in q according to the homotopy perturbation method as following:

u=u0+qu1+q2u2+q3u3+…(26)

v=v0+qv1+q2v2+q3v3+…(27)

by equating the like powers of q, we construct the following system of equations by substituting for u and v from Eqs. (26) and (27) into (22) and (23):

Zero order system (q0):

u0′′′−h2u0′=0(28)

v0′′−h2v0=0(29)

with boundary conditions:

u0(0)=−ℱ𝒪,u0′(0)=0,u0′(∞)=1,v0(0)=1,v0(∞)=0(30)

The solution of Eqs. (28) and (29) with boundary conditions (30) can be easily obtained as following:

u0(η)=η−ℱ𝒪 h+1h+e−hηh(31)

v0(η)=e−hη(32)

First order system (q1):

u1′′′−h2u1′+nWe2u0′′2u0′′′+(b2η+u0)u0′′+(b−M−u0′)u0′+(M−b+1)(1+We2u0′′2)n−32+h2u0′=0(33)

v1′′−h2v1+Rv0′′+Pr[(u0v0′−u0′v0)+Ecu0′′2(1+We2u0′′2)n−12−b2(v0−ηv0′)]+h2v0=0(34)

with boundary conditions:

u1(0)=0,u1′(0)=0,u1′(∞)=0,v1(0)=0,v1(∞)=0(35)

Solving the above system using MATLAB yields the following:

u1(η)=2h2e4h∫04σ2dx+2h2e−4h∫04σ3dxh3σ4−e−hη(σ1−∫0ησ3dx)h−ehη(σ1+∫0ησ2dx)h−∫0η(e−hx−e−hxσ5h2−Me−hxσ5h2+ae−hxσ5h+be−hxσ5h2−xe−hxσ5h+We2h2ne−3hx−bxe−hxσ52h)dx(36)

v1(η)=e−hη(σ7+∫0ησ8dx)h−ehη(σ7+∫0ησ9dx)h(37)

where:

σ1=h2e4h∫04σ2dx+h2e−4h∫04σ3dxh2σ4

σ2=σ6σ52−h2σ62+Mσ6σ52−bσ6σ52−ahσ6σ52+hxσ6σ52+hxσ6σ52h−We2h4ne−4hx2h

σ3=h2+ℱ𝒪σ52−xσ52−σ52h−bxσ54−Mσ52h+bσ52h+We2h3nσ62

σ4=e−4h−e4h

σ5=(We2h2σ6+1)32−n2

σ6=e−2hx

σ7=e4h∫04σ9dx−e−4h∫04σ8dxe−4h−e4h

σ8=Rh22−Prb4+h22+Prℱ𝒪h2−Prhx2−Prbhx4+EcPrh2e−hxσ10n2−122

σ9=h2σ112+Rh2σ112−Prbσ114+Prℱ𝒪hσ112−Prhxσ112−Prbhxσ114+EcPrh2σ11σ10n/22e2hx+We2h2

σ10=We2h2σ11+1

σ11=e−2hx

There are numerous options for selecting the auxiliary parameter h [34,35]. The solution should be selected so that no secular terms are used. We consequently look for solutions devoid of secular terms. We can accomplish this if we set.

h=ℱ𝒪2+4M−2b+82−ℱ𝒪2(38)

An approximation solution can be obtained by taking the limit of Eqs. (26) and (27) and letting q approach to unity as follows:

f=limq→1u=u0+qu1+…(39)

θ=limq→1v=v0+qv1+…(40)

hence,

f=η−ℱ𝒪h+1h+e−hηh+2h2e4h∫04σ2dx+2h2e−4h∫04σ3dxh3σ4−e−hη(σ1−∫0ησ3dx)h−ehη(σ1+∫0ησ2dx)h−∫0η(e−hx−e−hxσ5h2−Me−hxσ5h2+ae−hxσ5h+be−hxσ5h2−xe−hxσ5h+We2h2ne−3hx−bxe−hxσ52h)dx(41)

θ=e−hη+e−hη(σ7+∫0ησ8dx)h−ehη(σ7+∫0ησ9dx)h(42)

Finally, we must mention here that this study distinguishes itself from prior research by utilizing the homotopy perturbation method to analyze the intricate behavior of Carreau fluid in a microchannel. This method is applied to a coupled nonlinear system that describes the fluid’s flow under the combined influences of squeezing, magnetic, and radiative effects, proving its effectiveness in accurately representing these complex conditions.

4  Code Validation

Initially, it’s imperative to verify the outcomes derived from applying the homotopy perturbation method. This validation is achieved by juxtaposing our current findings with those of Khaled and Vafai’s [33] previous studies, particularly in specific scenarios. When comparing various values of the squeezed flow index parameter, denoted as b, the comparison was carried out with the condition θ′(0)=−1 instead of the initial condition being θ(0)=1. Yet, the credibility of the present numerical solutions via homotopy perturbation method is affirmed by the subsequent Table 1, validating their precision and dependability.

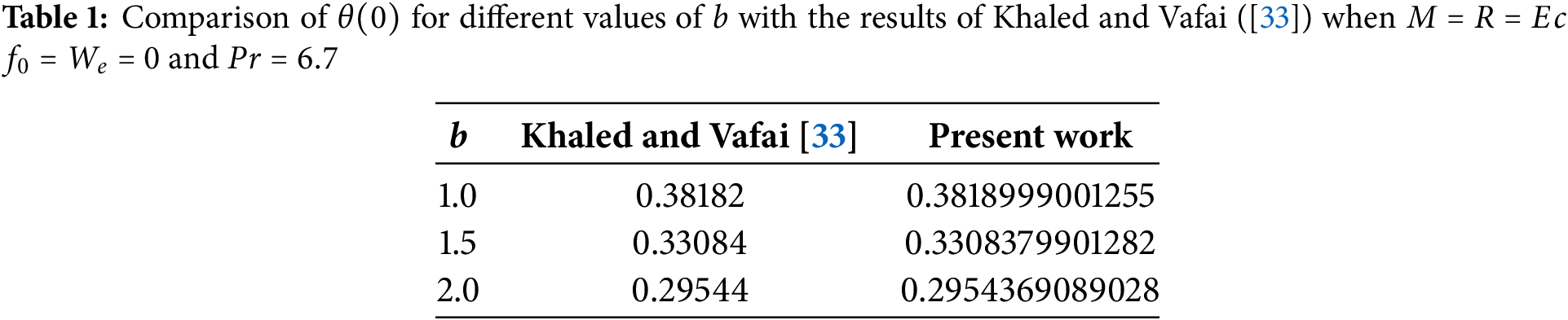
Further, the solution accuracy was verified through systematic examination of the homotopy perturbation series’ convergence properties. The iterative series expansion demonstrates excellent convergence characteristics, with each successive term diminishing rapidly in magnitude. Computational implementation involves truncating the series once successive term differences fall below an established threshold (10−6). All calculations were confined to parameter ranges guaranteeing method validity and numerical stability. These convergence properties are further corroborated by strong alignment with established benchmark solutions (Table 1), confirming the solution’s reliability.

5  Graphical and Tabular Findings with Discussion

This section of the paper makes use of various variables that relate to the flow under study to illustrate how velocity and temperature profiles are physically described. The Homotopy Perturbation Method is used with the aid of MATLAB software to obtain the following results. Subsequently, the graphical representations of the semi-analytical solutions provided in Eqs. (41) and (42) are presented through a series of diagrams. These diagrams allow us to manage the effects of the problem parameters on the different distributions. Fig. 2 depicts the temperature and velocity profiles in relation to the dimensionless vertical coordinate η for varying Weissenberg number values. The figure clearly demonstrates that as the Weissenberg number rises, the velocity profiles also increase, while a marginal reversed trend is noticeable in the temperature distribution. Physically, when a squeezed fluid flows, an increase in the Weissenberg number leads to faster fluid velocity. This is because a higher Weissenberg number indicates a stronger elastic response from the fluid, which affects how it deforms and moves under compression. Therefore, the Weissenberg number is crucial for understanding and predicting the viscoelastic behavior of non-Newtonian fluids in various deformation scenarios.

Figure 2: (a) f′(η) for various values of We; (b) θ(η) for various values of We

Fig. 3 is provided to analyze alterations in dimensionless velocity and dimensionless temperature patterns induced by variations in the power-law index. In a physical sense, an increase in the power-law index leads to heightened viscosity. Due to the fluid’s shear-thinning nature, this viscosity increase amplifies both fluid movement and dimensionless temperature. However, the impact on temperature distribution is minimal, as the power-law index indirectly influences temperature. Further, we must mention that the importance of the power-law index lies in determining the fluid’s shear-thinning or shear-thickening behavior, which directly affects velocity profiles and heat transfer rates in non-Newtonian flow systems [36].

Figure 3: (a) f′(η) for various values of n; (b) θ(η) for various values of n

Fig. 4 analyzes how the suction velocity parameter influences fluid dynamics and thermal distribution. The results demonstrate that increasing the suction magnitude boosts velocity profiles while simultaneously reducing temperature values. Physically, stronger suction effects cause greater accumulation of Carreau fluid near the sensor boundary, explaining these opposing trends in momentum and thermal transport. This accumulation intensifies the fluid’s momentum in the vicinity of the surface, resulting in a noticeable rise in velocity. As a consequence, the increased kinetic activity contributes to higher energy transfer within the fluid layer, thereby elevating the dimensionless temperature profile for the corresponding parameter setting.

Figure 4: (a) f′(η) for various values of fo; (b) θ(η) for various values of fo

Fig. 5 illustrates how variations in the squeezed flow index affect the velocity and temperature profiles. The dimensionless velocity initially decreases as the index increases up to η = 1.8, after which it begins to rise. Additionally, a higher squeezed flow index leads to a drop in temperature. This thermal decline is physically attributed to the inverse relationship between the squeezing index b and the squeezing rate a. As b increases, the squeezing intensity weakens, reducing compressive forces between fluid layers and decreasing kinetic energy input. This leads to lower viscous dissipation and diminished frictional heating, causing a measurable drop in dimensionless temperature. The effect stems from shifted energy conversion dynamics, where reduced mechanical work input translates directly into weaker thermal generation, particularly evident in viscoelastic fluids under constrained flow conditions.

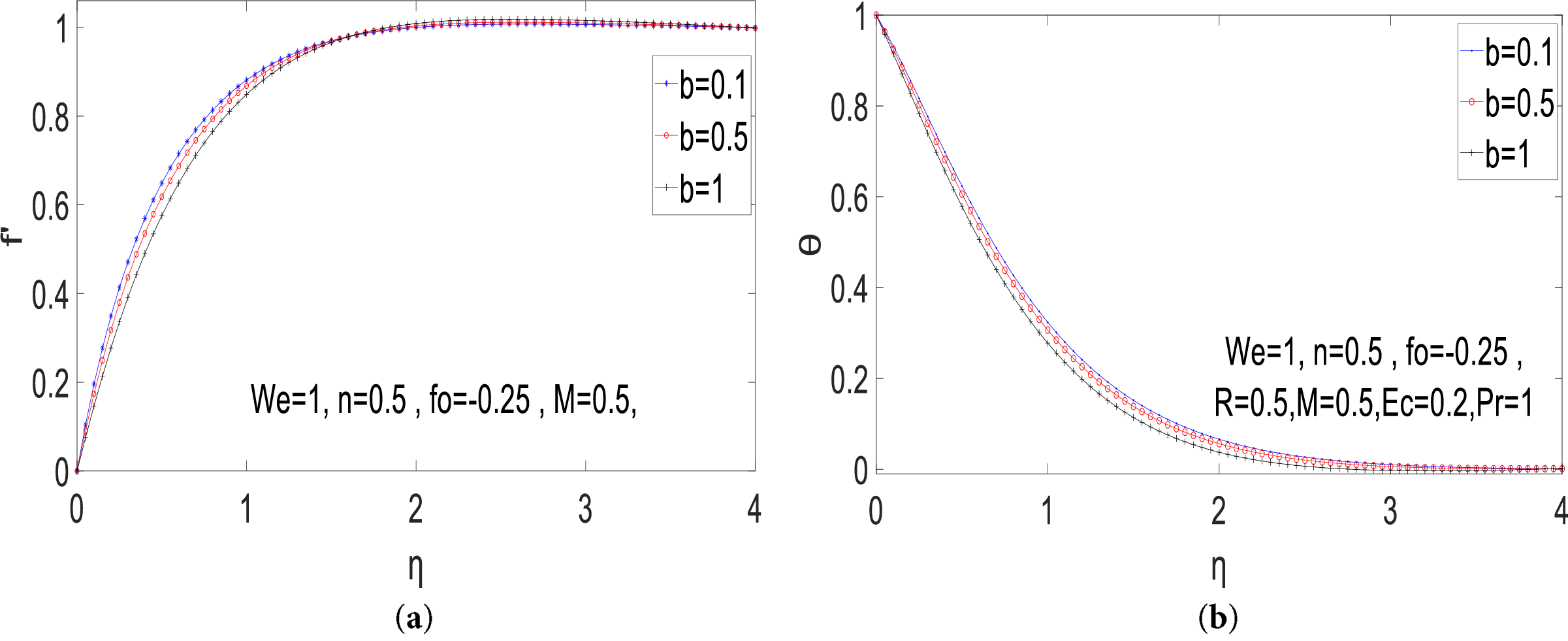
Figure 5: (a) f′(η) for various values of b; (b) θ(η) for various values of b

Fig. 6 outlines the characteristics of fluid movement and energy resulting from the influence of the magnetic number.

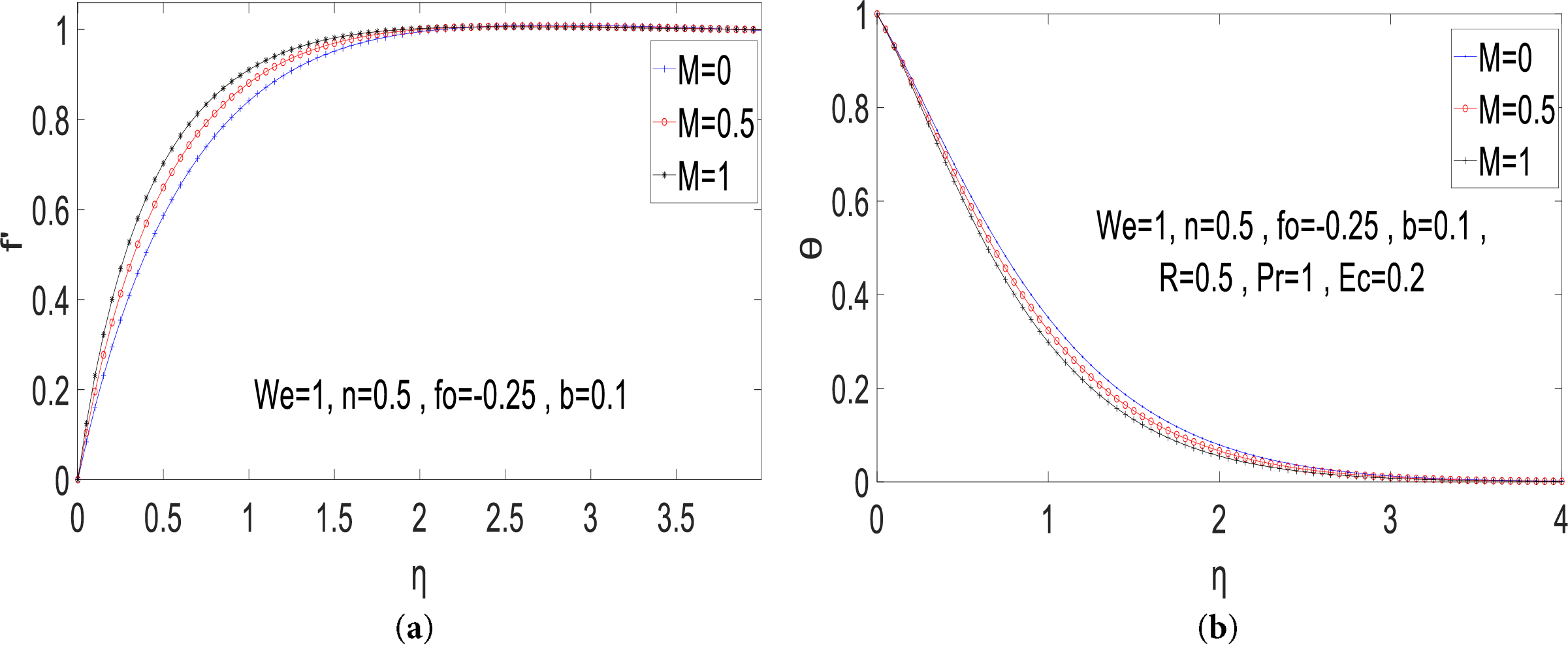
Figure 6: (a) f′(η) for various values of M; (b) θ(η) for various values of M

A moderate rise in the magnetic parameter results in greater velocity of the non-Newtonian fluid. Physically, while stronger magnetic effects typically introduce more resistance, the dominant squeezing action from the upper surface counteracts this, causing the fluid to accelerate. The influence of this parameter on temperature distribution is also illustrated in the corresponding figure. It’s evident that there is a reduction in temperature with an increase in the magnetic parameter. Physically, the heightened magnetic parameter strengthens the interplay between the magnetic field and the fluid, resulting in escalated energy dissipation. This, in turn, leads to a decrease in the fluid’s temperature within squeezed fluid flow scenarios.

Fig. 7a demonstrates how the thermal radiation parameter affects dimensionless temperature distribution. As this parameter increases, both the fluid temperature and thermal boundary layer thickness rise, reflecting enhanced radiative heat transfer and greater energy absorption. Conversely, Fig. 7b reveals the inverse relationship between the Prandtl number and temperature, higher Prandtl values reduce both temperature and thermal boundary layer thickness. From a physical standpoint, the thermal conductivity decreases as the Prandtl number is heightened. This change in thermal conductivity contributes to the decline in the thermal profile.

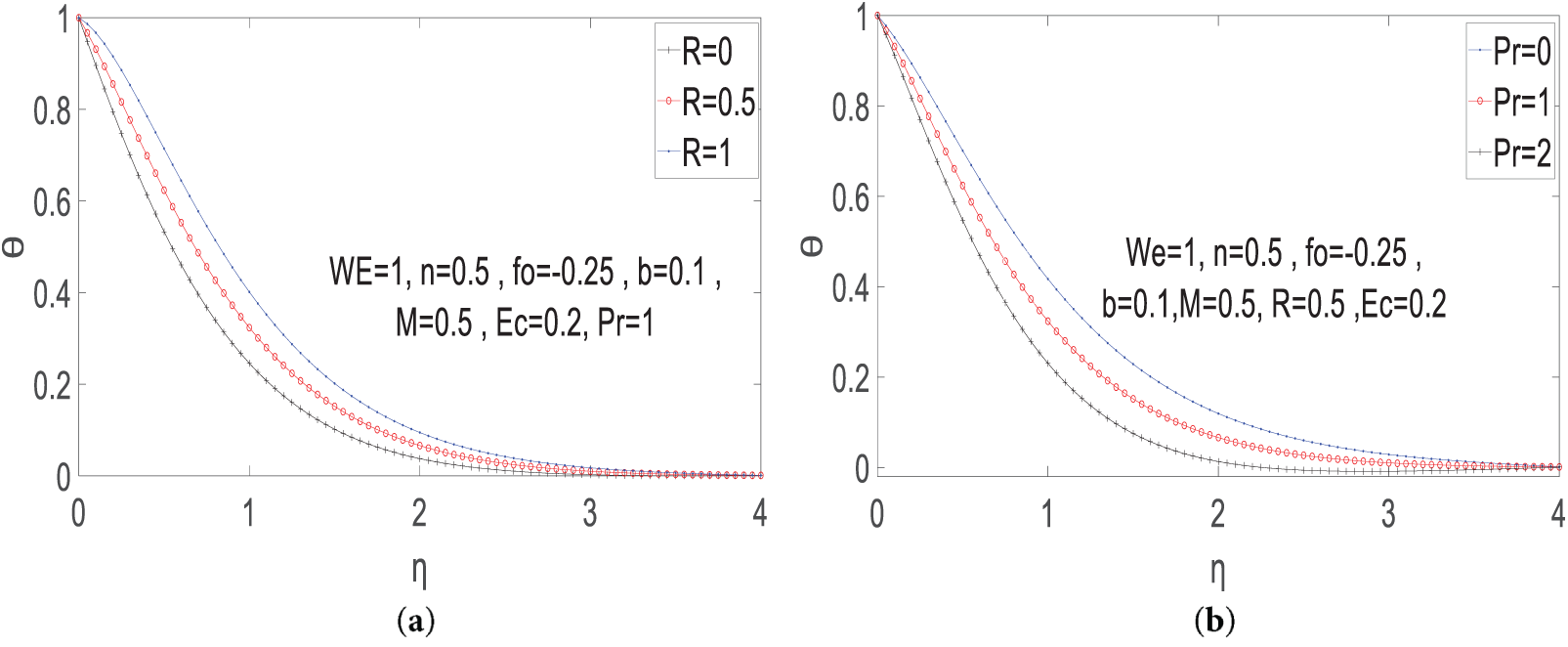
Figure 7: (a) θ(η) for various values of R; (b) θ(η) for various values of Pr; (c) θ(η) for various values of Ec

Fig. 7c demonstrates the impact of the parameter related to viscous dissipation on the dimensionless temperature distribution. Here, the Eckert number, associated with the phenomenon of viscous dissipation, is a dimensionless parameter utilized in heat transfer. It measures the ratio between convective heat transfer and the kinetic energy of fluid motion within a system. The figure makes it evident that the Eckert number has a subtle impact on the temperature field, leading to a minor thickening of the thermal boundary layer. Subsequently, it is necessary to investigate how the controlling parameters affect both the skin friction coefficient Rex1/2Cfx and the local Nusselt number Rex−1/2Nux, as these parameters are indicative of significant and essential engineering quantities. Evidently shown in the Table 2, the Weissenberg number leads to a reduction in the local skin friction coefficient and an increase in the local Nusselt number. Conversely, the power-law index exhibits the entirely opposite trend. Furthermore, the magnetic parameter or the absolute value of the suction velocity parameter tends to increase both the local skin friction coefficient and the local Nusselt number. Moreover, the local Nusselt number is negatively affected by both the radiation parameter and the Eckert number, while the Prandtl number exhibits an opposite trend with an increasing impact. Further, a brief sensitivity analysis was conducted to assess the influence of the Weissenberg number We on the flow and heat transfer behavior. The analysis reveals that progressive enhancement of fluid elasticity induces two key phenomena. The first is the reduction behavior in skin friction coefficient magnitude, demonstrating shear stress attenuation near boundaries due to viscoelastic effects, while the second is a corresponding Nusselt number enhancement, indicating superior convective heat transfer efficiency.

6  Conclusions

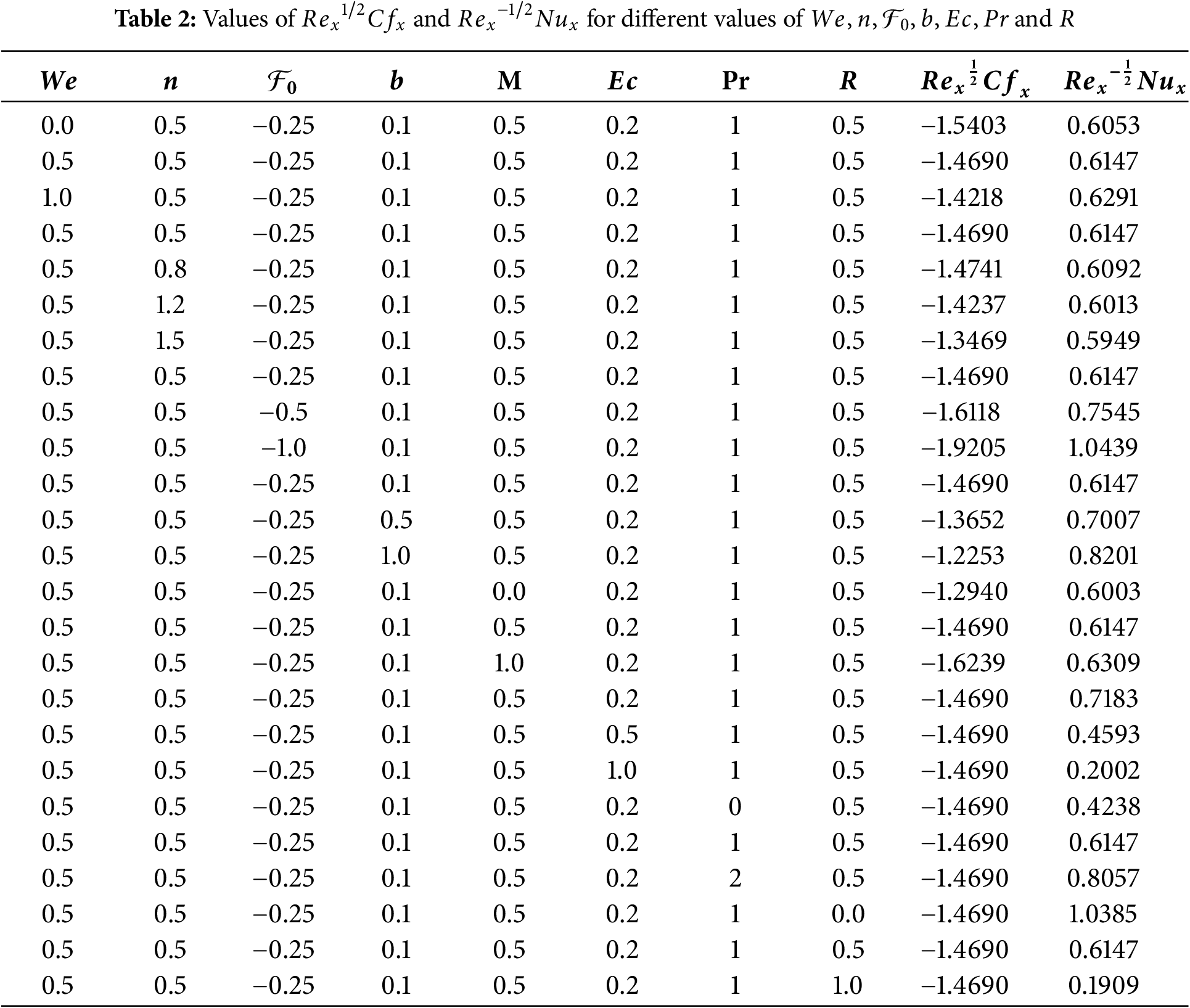
This study examines the flow of a Carreau fluid through a narrow duct past a sensor surface, accounting for viscous dissipation and magnetic field effects. The governing equations are simplified via dimensionless transformations, reducing them to a system of nonlinear ODEs. Using the Homotopy Perturbation Method (HPM), key flow characteristics, including velocity, temperature, skin friction, and Nusselt number—are analyzed. The major findings are summarized as follows:

•   Increasing velocity profiles and declining temperature distribution are correlated with rising Weissenberg number.

•   Higher viscosity results from an increase in the power-law index. This viscosity rise magnifies fluid motion and dimensionless temperature since the fluid is shear-thinning in nature.

•   The velocity distribution increases as the suction parameter’s absolute values rise, whereas the temperature field exhibits the reverse pattern.

•   As the squeezed flow index parameter is increased from the squeezing sheet to η=1.8, the dimensionless velocity starts to decrease before starting to increase. Additionally, there is a decrease in the temperature distribution as the squeezed flow index parameter is increased.

•   The application of a magnetic field demonstrates dual effects on the fluid dynamics, while even modest increases in magnetic field strength produce measurable velocity enhancement, they simultaneously lead to temperature reduction within the fluid system.

•   Temperature and thermal thickness both increase in response to an increase in the thermal radiation parameter.

•   When the Prandtl number rises, the temperature and corresponding thermal thickness also decline.

•   The precise regulation of both suction intensity and magnetic field strength can optimize microcantilever sensor performance for simultaneous viscosity and thermal measurements, especially in integrated microfluidic lab-on-chip systems.

Acknowledgement: Sara I. Abdelsalam expresses her deep gratitude to Fundación Mujeres por África for supporting this work through the fellowship awarded to her.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Sara I. Abdelsalam and Ahmed M. Megahed; Methodology, Sara I. Abdelsalam; Software, Sara I. Abdelsalam; Validation, Sara I. Abdelsalam, W. Abbas, and Hassan M. H. Sadek; Formal analysis, Sara I. Abdelsalam; Investigation, Sara I. Abdelsalam; Resources, Ahmed M. Megahed and M. S. Emam; Data curation, Sara I. Abdelsalam; Writing—original draft preparation, Ahmed M. Megahed and W. Abbas; Writing—review and editing, Sara I. Abdelsalam; Visualization, Sara I. Abdelsalam; Supervision, Ahmed M. Megahed and W. Abbas. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Rashidi MM, Shahmohamadi H, Dinarvand S. Analytic approximate solutions for unsteady two-dimensional and axisymmetric squeezing flows between parallel plates. Math Probl Eng. 2008;2008(1):935095. doi:10.1155/2008/935095. [Google Scholar] [CrossRef]

2. Siddiqui AM, Irum S, Ansari AR. Unsteady squeezing flow of a viscous MHD fluid between parallel plates, a solution using the homotopy perturbation method. Math Model Anal. 2008;13(4):565–76. doi:10.3846/1392-6292.2008.13.565-576. [Google Scholar] [CrossRef]

3. Mustafa M, Hayat T, Obaidat S. On heat and mass transfer in the unsteady squeezing flow between parallel plates. Meccanica. 2012;47(7):1581–9. doi:10.1007/s11012-012-9536-3. [Google Scholar] [CrossRef]

4. Khan U, Ahmed N, Khan SI, Ali Zaidi Z, Yang XJ, Mohyud-Din ST. On unsteady two-dimensional and axisymmetric squeezing flow between parallel plates. Alex Eng J. 2014;53(2):463–8. doi:10.1016/j.aej.2014.02.002. [Google Scholar] [CrossRef]

5. Khan U, Khan SI, Ahmed N, Bano S, Mohyud-Din ST. Heat transfer analysis for squeezing flow of a Casson fluid between parallel plates. Ain Shams Eng J. 2016;7(1):497–504. doi:10.1016/j.asej.2015.02.009. [Google Scholar] [CrossRef]

6. Ahmed N, Khan U, Khan SI, Bano S, Mohyud-Din ST. Effects on magnetic field in squeezing flow of a Casson fluid between parallel plates. J King Saud Univ Sci. 2017;29(1):119–25. doi:10.1016/j.jksus.2015.03.006. [Google Scholar] [CrossRef]

7. Al-Saif AJA, Jasim AM. A novel algorithm for studying the effects of squeezing flow of a casson fluid between parallel plates on magnetic field. J Appl Math. 2019;2019(1):3679373. doi:10.1155/2019/3679373. [Google Scholar] [CrossRef]

8. Mat Noor NA, Shafie S, Admon MA. Effects of viscous dissipation and chemical reaction on MHD squeezing flow of Casson nanofluid between parallel plates in a porous medium with slip boundary condition. Eur Phys J Plus. 2020;135(10):855. doi:10.1140/epjp/s13360-020-00868-w. [Google Scholar] [CrossRef]

9. Sivasankaran S, Bhuvaneswari M, Chandrapushpam T, Karthikeyan S. Influence of thermal radiation on squeezing flow of copper-water nanofluid between parallel plates. Mater Today Proc. 2021;42(1–3):457–64. doi:10.1016/j.matpr.2020.10.184. [Google Scholar] [CrossRef]

10. Sivasankaran S, Chandrapushpam T, Bhuvaneswari M, Karthikeyan S, Alzahrani AK. Effect of chemical reaction on double diffusive MHD squeezing copper water nanofluid flow between parallel plates. J Mol Liq. 2022;368(1–3):120768. doi:10.1016/j.molliq.2022.120768. [Google Scholar] [CrossRef]

11. Abbas W, Mekheimer KS, Ghazy MM, Moawad AMA. Thermal radiation effects on oscillatory squeeze flow with a particle-fluid suspension. Heat Transf. 2021;50(3):2129–49. doi:10.1002/htj.21971. [Google Scholar] [CrossRef]

12. Obalalu AM, Ajala AO, Akindele AO, Oladapo OA, Adepoju O, Jimoh MO. Unsteady squeezed flow and heat transfer of dissipative casson fluid using optimal homotopy analysis method: an application of solar radiation. Partial Differ Equ Appl Math. 2021;4(9):100146. doi:10.1016/j.padiff.2021.100146. [Google Scholar] [CrossRef]

13. Jyothi AM, Varun Kumar RS, Madhukesh JK, Prasannakumara BC, Ramesh GK. Squeezing flow of Casson hybrid nanofluid between parallel plates with a heat source or sink and thermophoretic particle deposition. Heat Transf. 2021;50(7):7139–56. doi:10.1002/htj.22221. [Google Scholar] [CrossRef]

14. Khan Q, Farooq M, Ahmad S, Ben Moussa S. Investigation of quadratically stratified squeezed Casson fluid flow with slip features over a convectively heated surface. Mater Sci Eng B. 2023;294(3):116518. doi:10.1016/j.mseb.2023.116518. [Google Scholar] [CrossRef]

15. Qureshi MA, Rafiq M, Bashir Y, Ahmad A. Analytical and numerical approach for the analysis of heat transfer of squeezing flow between two parallel plates. Case Stud Therm Eng. 2024;54(4):103979. doi:10.1016/j.csite.2024.103979. [Google Scholar] [CrossRef]

16. Abdul-Ameer YA, Ali Al-Saif ASJ. Fourier-homotopy perturbation method for heat and mass transfer with 2D unsteady squeezing viscous flow problem. J Comput Appl Mech. 2023;54(2):219–35. [Google Scholar]

17. Akbar NS, Nadeem S, Khan ZH. Numerical simulation of peristaltic flow of a Carreau nanofluid in an asymmetric channel. Alex Eng J. 2014;53(1):191–7. doi:10.1016/j.aej.2013.10.003. [Google Scholar] [CrossRef]

18. Abbasi FM, Hayat T, Alsaedi A. Numerical analysis for MHD peristaltic transport of Carreau-Yasuda fluid in a curved channel with hall effects. J Magn Magn Mater. 2015;382(8):104–10. doi:10.1016/j.jmmm.2015.01.040. [Google Scholar] [CrossRef]

19. Kothandapani M, Prakash J, Srinivas S. Peristaltic transport of a MHD Carreau fluid in a tapered asymmetric channel with permeable walls. Int J Biomath. 2015;8(4):1550054. doi:10.1142/s1793524515500540. [Google Scholar] [CrossRef]

20. Hashim, Khan M. A revised model to analyze the heat and mass transfer mechanisms in the flow of Carreau nanofluids. Int J Heat Mass Transf. 2016;103(10):291–7. doi:10.1016/j.ijheatmasstransfer.2016.07.049. [Google Scholar] [CrossRef]

21. Khan M, Azam M. Unsteady heat and mass transfer mechanisms in MHD Carreau nanofluid flow. J Mol Liq. 2017;225(4):554–62. doi:10.1016/j.molliq.2016.11.107. [Google Scholar] [CrossRef]

22. Yousef NS, Megahed AM, Ghoneim NI, Elsafi M, Fares E. Chemical reaction impact on MHD dissipative Casson-Williamson nanofluid flow over a slippery stretching sheet through porous medium. Alex Eng J. 2022;61(12):10161–70. doi:10.1016/j.aej.2022.03.032. [Google Scholar] [CrossRef]

23. Alali E, Megahed AM. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnol Rev. 2022;11(1):463–72. doi:10.1515/ntrev-2022-0031. [Google Scholar] [CrossRef]

24. Attia HA, Abbas W, Aboul-Hassan AL, Abdeen MAM, Ibrahim MA. Unsteady flow of a dusty Bingham fluid through a porous medium in a circular pipe. J Appl Mech Tech Phys. 2016;57(4):596–602. doi:10.1134/S0021894416040039. [Google Scholar] [CrossRef]

25. Nasr ME, Gnaneswara Reddy M, Abbas W, Megahed AM, Awwad E, Khalil KM. Analysis of non-linear radiation and activation energy analysis on hydromagnetic Reiner-Philippoff fluid flow with Cattaneo-Christov double diffusions. Mathematics. 2022;10(9):1534. doi:10.3390/math10091534. [Google Scholar] [CrossRef]

26. Megahed AM, Abbas W. Non-Newtonian Cross fluid flow through a porous medium with regard to the effect of chemical reaction and thermal stratification phenomenon. Case Stud Therm Eng. 2022;29(2):101715. doi:10.1016/j.csite.2021.101715. [Google Scholar] [CrossRef]

27. Akbar NS, Khan ZH. Variable fluid properties analysis with water based CNT nanofluid over a sensor sheet: numerical solution. J Mol Liq. 2017;232(1):471–7. doi:10.1016/j.molliq.2017.02.107. [Google Scholar] [CrossRef]

28. Nayak MK, Bhatti MM, Makinde OD, Akbar NS. Transient magneto-squeezing flow of NaCl-CNP nanofluid over a sensor surface inspired by temperature dependent viscosity. Defect Diffus Forum. 2018;387:600–14. doi:10.4028/www.scientific.net/ddf.387.600. [Google Scholar] [CrossRef]

29. Hussain A, Zetoon R, Ali S, Nadeem S. Magnetically driven flow of pseudoplastic fluid across a sensor surface. J Braz Soc Mech Sci Eng. 2019;41(4):185. doi:10.1007/s40430-019-1691-1. [Google Scholar] [CrossRef]

30. Hussain A, Zetoon R, Ali S, Nadeem S. Magneto-hydro dynamic squeezed flow of Williamson fluid transiting a sensor surface. Heliyon. 2020;6(9):e04875. doi:10.1016/j.heliyon.2020.e04875. [Google Scholar] [PubMed] [CrossRef]

31. Ariel PD, Hayat T, Asghar S. Homotopy perturbation method and axisymmetric flow over a stretching sheet. Int J Nonlinear Sci Numer Simul. 2006;7(4):399–406. doi:10.1515/ijnsns.2006.7.4.399. [Google Scholar] [CrossRef]

32. He JH. Comparison of homotopy perturbation method and homotopy analysis method. Appl Math Comput. 2004;156(2):527–39. doi:10.1016/j.amc.2003.08.008. [Google Scholar] [CrossRef]

33. Khaled ARA, Vafai K. Hydromagnetic squeezed flow and heat transfer over a sensor surface. Int J Eng Sci. 2004;42(5–6):509–19. doi:10.1016/j.ijengsci.2003.08.005. [Google Scholar] [CrossRef]

34. Xu L. He’s homotopy perturbation method for a boundary layer equation in unbounded domain. Comput Math Appl. 2007;54(7–8):1067–70. doi:10.1016/j.camwa.2006.12.052. [Google Scholar] [CrossRef]

35. Ariel PD. The three-dimensional flow past a stretching sheet and the homotopy perturbation method. Comput Math Appl. 2007;54(7–8):920–5. doi:10.1016/j.camwa.2006.12.066. [Google Scholar] [CrossRef]

36. Puneeth V, Sarpabhushana M, Anwar MS, Aly EH, Gireesha BJ. Impact of bioconvection on the free stream flow of a pseudoplastic nanofluid past a rotating cone. Heat Transf. 2022;51(5):4544–61. doi:10.1002/htj.22512. [Google Scholar] [CrossRef]