Methods of Selecting Adaptive Artificial Viscosity in Completely Conservative Difference Schemes for Gas Dynamics Equations in Euler Variables

1  Introduction

The gas dynamics equations are the expressions of the basic conservation laws (mass, momentum, and energy) in a continuous medium. Therefore, it is natural to construct a discrete model of the medium under study in such a way that the discrete analogues for these laws are also fulfilled in it. Practice shows that the application of such difference schemes is especially effective for solving the problems in which solution profiles change sharply in time and space. Further developing the integral consistency principles for the mass, momentum, and various types of energies led to the completely conservative difference schemes (CCDS) [1], which discretely conserve also the internal and kinetic energies of the system and are used in Lagrangian and Eulerian methods of describing the continuous medium [2–4]. Introducing the adaptive artificial viscosity (AAV) [5] into the CCDS allows to suppress the oscillations arising in the numerical solution locally. It is made by controlling the spatial approximation of the discrete model without changing its properties of conservative consistencies by the various types of energy, mass transfer and momentum components. In this case, a qualitative physical solution of the problem is obtained. The solution of the nonlinear algebraic equations system corresponding to the implicit CCDS is realized by some iterative process. Note also that the different iterative processes used in this work affect the choice of the AAV type in the difference scheme and thus determine the dynamically generated local approximation of this difference scheme.

In the last years, the introduction of the AAV is a widely used method for suppressing the computational instabilities arising in discrete modelling of transport processes in the mathematical physics problems [6–18]. In work [6], a method of the global AAV by space for the conservative laws was developed, but it was required to refine the AAV coefficient on a coarse grid, then perform the calculation on a fine grid. In work [7], a new method for constructing the adaptive artificial viscosity in the context of one-dimensional, staggered-grid Lagrangian hydrodynamics, was proposed to accurately model the non-viscous flow with the shock wave. In work [8], a wave number based on the AAV addition method for quintic spline reconstruction scheme was studied for flows with discontinuities and a broad range of scales, e.g., shock-turbulence interactions. In work [9], the AAV model depending on the smoothness indicator was considered. In work [10], the difference schemes with Lax-Wendroff corrections and the AAV were proposed. In work [11], the corrective mechanism with an entropy-based adaptive artificial viscosity was investigated. In work [12], an entropy-stable artificial viscosity with the production of coefficients for the first-order Graph Viscosity and high-order Graph Viscosity (entropy viscosity) methods was also used for the Euler equations system. In work [13], a provably entropy stable shock capturing approach for the high order entropy stable discontinuous Galerkin spectral element method based on a hybrid blending with a subcell low order variant was studied. The AAV was also used for solving the shallow water flows problem [14], reducing grid orientation effect in numerical modelling for steam thermal recovery [15], modelling the two-phase flow in porous media [16] and modelling the atmosphere dynamics process [17]. This work presents the methods for selecting the local AAV that is automatically tuned in the iterative processes.

The present study is a continuation of the work [19]. In work [19], a calculation of artificial viscosity coefficients was an internal iterative process at each iteration of the sweep algorithm. In the present work, some realisations of the CCDS with the AAV using the different iterative processes are proposed. We present the method of the explicit iterations, the method of the sweep algorithm with a one-time change of the artificial viscosity coefficients at one iteration and the improved method of the explicit iterations, which are used to solve the problem of arbitrary discontinuity decay (Sod’s problem [20]) and the problem of two symmetric rarefaction waves propagation in the opposite directions (Einfeldt’s problem [21]). A simple implementation of the developed methods is shown. To solve the Sod’s problem and the Einfeldt’s problem, the methods are implemented using the same algorithms with the same parameters of the AAV selection algorithms. This study also presents the method to incorporating the AAV to effectively suppress the oscillations in the velocity and pressure profiles. A comparative analysis of the developed iterative methods and approaches to the AAV selection is carried out, and their efficiency compared to the works of other authors [6–9,22–24] is shown. This work also proposes the grid embedding method to solve the problem on spatially irregular grids.

Due to the impossibility of applying the sweep method in the spatially multidimensional case on the irregular grids, the improved method of explicit iterations developed in this work can be effectively used to solve such problems.

The Section 2 presents the initial formulation of the gas dynamics problem in Euler variables, a two-layer time-dependent fully conservative difference scheme for its solution and approximation operators for the system of equations in Euler variables. The Section 3 describes the methods and approaches developed and used in this work, which are the method of explicit iterations, the method of joint iterations, the improved method of explicit iterations, the velocity viscosity approach and the grid embedding method. Section 4 demonstrates the computational results obtained by the different methods and gives their comparative analyses.

2  Formulation of the Gas Dynamics Problem in Eulerian Variables

Consider a spatially one-dimensional flow of a compressible gas in Euler variables in the Cartesian coordinate system:

DDt(dM)=−dV∂μ∂x,(1)

DDt(udM)=−dV∂P∂x−dV∂∂x(μu)+df,(2)

DDt(εdM)=−PdV∂u∂x−dV∂∂x(με)+dQ,(3)

DDt(u22dM)=−udV∂P∂x−dV∂∂x(μu22)+udf.(4)

Here DDt represents material derivative with respect to t, ∂∂x is the partial derivative with respect to x, u is the velocity of flow, ρ is the density of medium, μ=ρ⋅u is the mass flux density, P is the pressure, df is the external force, ε is the specific internal energy, dQ is the external heat. It is considered that mass dM is enclosed in the volume dV, through the boundaries of which flows the mass flux μ carrying the momentum μ⋅u and internal energy με.

Fig. 1 corresponds to the difference scheme Eqs. (5)–(8). Here ω are the nodes of the difference grid, Ω are the cells. Thermodynamic quantities ρ,ε,P and internal energy E=ρε refer to the nodes ω. We will also refer the velocity u, volume v and node mass m=ρv to the nodes ω, and the volume V—to the grid cells. Here k is an arbitrary index numbering the nodes and i is an index numbering the cells. The sign function at the boundary of node’s domain ω is 1 on the right cell of the node ω and −1 on the left cell of the node ω. Σω(Ω) involves summing over the nodes ω which form the cell Ω. Also ΣΩ(ω) is sum over the cells Ω adjacent to the node ω.

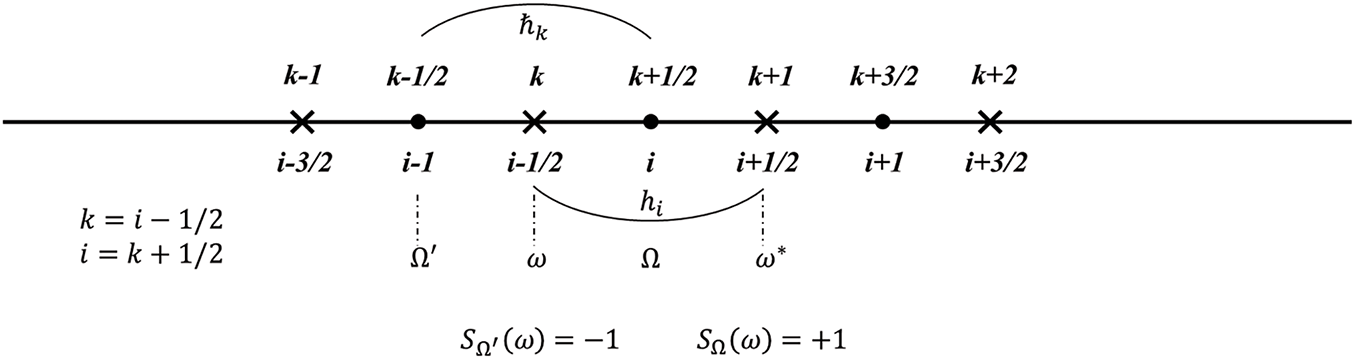
Figure 1: Difference grid. Scheme of grid’s nodes (ω) and grid’s cells (Ω) in space

Obviously:

vω=ℏk=hk+1/2+hk−1/22=hi+hi−12,VΩ=hi,ρω=ρk=mωvω,

where h and ℏ refer to the sizes of cells Ω and node domains ω, respectively.

For the system of Eqs. (1)–(4) we write out the two-layer time completely conservative difference scheme in Euler variables:

mt=−vDINDμD∼,(5)

(mu)t=−vGRADσπ∼−vDITD(μD∼⋅uD∼),(6)

(mε)t=−12∑Ω(ω)(π∼VDIVσu∼)Ω−vDINDμED∼,(7)

(mu22)t=−v(u∼,GRADσπ∼)−vDIND(μD∼uD2∼2),(8)

where

μ=ρu, μE=εμ=Eu, E=ρε, ρ∼=ρ(ψρ), ψρ=const,MD∼=12∑ω(Ω)(ρωuω)(0.5), μD∼=MD∼−νρ∼GRANDρ∼,πΩ∼=PΩ(0.5)−νu∼DIVσ(ρ∼u(ψu)), PΩ=12∑ω(Ω)Pω, ψu=const,MED∼=12∑ω(Ω)(Eωuω)(0.5), μED∼=MED∼−νE∼GRAND(ρ∼ε(ψε)), ψε=const.

Quantities from a set of artificial viscosities ν={νρ∼,νu∼,νE∼} are defined in the cells by the formulas νρ∼=βρh2τ, νu∼=βuh2τ νE∼=βEh2τ [25], where β={βρ,βu,βE} is the viscous filling, depending on Courant–Friedrichs–Lewy (CFL) number kr. According to the sufficient conditions obtained in [25] for satisfying the maximum principle in modeling the mass transfer process with the continuity equation in the presence of the AAV, the lower bound of the coefficient β is related to the CFL number kr, which thus becomes a scaling physical factor influencing the suppression of the local instabilities in the problem. In this regard, in this work, to suppress local instabilities, a gradual increase in the coefficient of reduced artificial viscosity by fractions of the CFL number in the form of ρ⋅kr is used, where constρ is a constant that can be adjusted in practice. The mathematical justifications for the stability of the momentum and energy equations exhibit an analogous character. In addition, by MD∼ and MED∼ we understand some approximations of the mass flux and internal energy flux in the cell Ω, respectively. Also in cell formed by the nodes ω and ω′ we can define the following quantities:

uD∼=12(uω(δω)+uω′(δω′)),uD2∼=(uω(δω),uω′(δω′)).

On the explicit and implicit time layers t and t^=t+τ (τ>0 is the time step), the difference time derivatives and spatial-point time interpolations are introduced as at=a^−aτ, a(δ)=δa^+(1−δ)a. Here interpolation weight δ can be related to the nodes ω of the spatial grid, e.g., by the law: δ=m^/(m^+m). ψ={ψρ,ψu,ψε} are the constant time interpolation weights. By arbitrary time interpolation of the grid functions a and a^ between the layers t and t^ we mean some interpolation values a∼, e.g., for velocity we assume u∼=u(δ).

The difference analogues of the vector analysis operations used in Eqs. (5)–(8) and the range and codomain of the corresponding operation analogue are defined as follows:

DINDμD=1v∑Ω(ω)SΩ(ω)μD(Ω),DIND:(Ω)→(ω),(9)

DITD(μD⋅uD)=1v∑Ω(ω)SΩ(ω)μD(Ω)uD(Ω),DITD:(Ω)→(ω),(10)

GRAND P=1vΔΩP,GRAND:(ω)→(Ω),(11)

GRADσπ=1vΔσπ,GRADσ:(Ω)→(ω),(12)

DIVσu=−1V∑ω(Ω)SΩ(ω)uω,DIVσ:(ω)→(Ω),(13)

where ΔΩP=−Σω(Ω)SΩ(ω)Pω, Δσπ=+ΣΩ(ω)SΩ(ω)πΩ+S∂ωπ∂ω. Finally, in the expression for Δσπ at the boundary node ω=∂ω, a term π∂ω is added at the boundary of the domain with the sign function S∂ω=±1 depending on the direction of the boundary normal.

3  Methods for Computing Completely Conservative Difference Schemes

In this work, the improved method of explicit iterations (Section 3.3) based on the method of explicit iterations (Section 3.1) and the method of joint iterations (Section 3.2) are used to realise the nonlinear implicit CCDS. In addition, the velocity viscosity method is used to approximate the velocity (Section 3.4), and the grid embedding method is developed for the problem on a non-uniform grid (Section 3.5).

Hereinafter, all quantities are defined at the nodes except the CFL number and the viscosities (viscous filling β and artificial viscosity ν). In addition, variables with a hat sign “ ^ ” denote the quantities at the implicit time layer, e.g., ρ^, u^, E^, and those without a hat sign denote the quantities at the explicit time layer, e.g., ρ, u, E. External iterations are used to compute quantities from the explicit layer to the implicit layer in time and are denoted by the index s, while internal iterations are also used in an iterative process or procedure within a single external iteration.

3.1 Method of Explicit Iterations

This work presents the explicit iteration method (hereafter Method 1), which also uses additional optimization criteria for the AAV selection in rarefaction wave, shock wave and contact rupture structures, which were tested on solving the Sod’s problem [20]. In the following Sections 3.2 and 3.3, such optimization is not required. Using this method, the satisfactory results are obtained, but the processor time spent on the iterative processes is significant.

In Method 1, an explicit iterative process is performed to calculate the quantities in the next time step. The formulas of this iterative process for the Eqs. (5)–(7) are as follows:

ρks+1=fρ(ρ,ρs,u,us,βρ)=ρk−τℏk(μi∼−μi−1∼),(14)

uks+1=fu(ρ,ρs+1,u,us,E,Es,βu)=1ρks+1(ρkuk−τℏk(πi∼−πi−1∼)−τℏk(μi∼ui∼−μi−1∼ui−1∼)),(15)

Eks+1=fε(ρ,ρs+1,u,us+1,E,Es,βE)==Ek−τ2ℏk(πi∼(uk+1∼−uk∼)+πi−1∼(uk∼−uk−1∼))−τℏk(μE,i∼−μE,i−1∼).(16)

When determining the viscosity in the flux μ∼ in the Eq. (14), the time interpolation ρ∼=ψρρs+(1−ψρ)ρ is used. Also for the Eq. (15) u∼=ψuus+(1−ψu)u and Eq. (16) E∼=ψεEs+(1−ψε)E. In the s-th iteration, the quantities are denoted by the upper index s, e.g., ρs,us,Es. In the external iteration, the viscosity is selected in computing ρs+1 as follows: at the beginning of a given external iteration, β=0 is assumed and the computation is performed. If oscillations occur, β is increased and the internal iteration is repeated in a loop until the value of β reaches its limiter [25]. Analogous actions are performed in the momentum Eq. (15) and energy Eq. (16) groups when computing us+1 and Es+1. The convergence of the external iterative process is defined as follows. If |yks+1−yks|<εrel⋅ymax+εabs, y={ρ,u,E}, k=1,n¯ (where εrel is the relative error, εabs is the absolute error, ymax is the maximum value of the desired quantity in space), then the result of the external process converges and the quantities at the next layer in time are obtained.

The algorithm of Method 1 is shown in Algorithm 1.

3.2 Method of Joint Iterations

In the current work, in order to optimize the computational process of the CCDS implementation and the AAV selection, we propose the method of joint iterations (hereinafter referred to as Method 2), which simultaneously refines the iterative difference solution and corrects the AAV. Along with Method 1, Method 2 uses the sweep algorithm for the difference balances Eqs. (5)–(7), in which the increments are calculated from the s-th iteration to the (s+1)-th iteration.

This method is implemented as follows. If oscillations occurred during the computation of ρs+1, their suppression unrestricted by limiter is performed only once at a given iteration following the (s+1)-th iteration. This process proceeds as follows. The reduced viscosity β is the product of the coefficient q by the CFL number β=q⋅kr. For monotonizing, a constant corresponding to a particular variable (e.g., it is constρ for ρ) is added to the coefficient q once at each iteration. The density increment δρs+2 is then calculated and added to ρs+1, i.e., ρs+2=δρs+2+ρs+1. Then, this algorithm is repeated in the same way to calculate velocity and energy. If the values obtained at this iteration satisfy the convergence condition |yks+1−yks|<εrel⋅ymax+εabs, y={ρ,u,E}, k=1,n¯, and no further monotonization is performed (oscillations are not present or the corresponding β reaches its limiter), then the iterative process ends and the next time step with the values calculated at the last iteration starts. Otherwise, the iterative process continues. According to work [25], in order to limit the increase of the viscous filling β, a limiter βlimiter is introduced, which should be less than one and greater than the CFL number according to the maximum principle. Also, for correct application of the sweep algorithm for the difference analog of the momentum conservation Eq. (6), the condition of diagonal dominance of the sweep algorithm coefficients is checked.

At the beginning of each time step before the iterations begin, all viscosities are assumed to be 0, the values at the first iteration are equal to those at the explicit layer {ρk1,uk1,Ek1}={ρk,uk,Ek}, k=1,n¯, and a local CFL number is chosen for each cell. Hereinafter, the CFL number is defined locally using the following formula:

kri=0.5|uk+uk+12+Ci|τhi,(17)

where Ci=γ(Pk+Pk+1)ρk+ρk+1 is local speed of sound.

The algorithm of Method 2 is shown in Algorithm 2.

3.3 Improved Method of Explicit Iterations

The efficiency of Method 2, which gives good accuracy in test problems and low processor time, led to a modification of Method 1, increasing its implicit margin (Method 1 is realized by a explicit scheme and explicit iterations). Such an algorithm (hereinafter Method 3) is represented as follows below in the form Algorithm 3, where in the following values are held: (δyk)old,(δyk)new are the increments of each value at the previous and current iterations to check convergence at node k, ypredictor, ks+1 is the predictor-correcting value at the implicit (s+1)-th iteration obtained by Eqs. (18)–(20), at node k.

At the s-th iteration, the computations are first performed by the explicit scheme, and predictor values are obtained at the implicit (s+1)-th iteration. Then, using these predictor values, a predictor-correcting procedure is executed, converging to the (s+1)-th implicit value of the external iteration. This procedure may be repeated 1 or more times, bringing the (s+1)-th iterative value closer to its convergence. The predictor-correcting procedure is performed with a fixed viscosity. If the viscosity needs to be corrected (in the presence of oscillations), the iterative process will continue, as well as when its convergence conditions are violated. Correspondingly Eqs. (14)–(16) in Method 3 for iterations will have the following form:

ρks+1=fρ(ρ,ρpredictors+1,u,us,βρ)=ρk−τℏk(μi∼−μi−1∼),(18)

uks+1=fu(ρ,ρs+1,u,upredictors+1,E,Es,βu)==1ρks+1(ρkuk−τℏk(πi∼−πi−1∼)−τℏk(μi∼ui∼−μi−1∼ui−1∼)),(19)

Eks+1=fε(ρ,ρs+1,u,us+1,E,Epredictors+1,βE)==Ek−τ2ℏk(πi∼(uk+1∼−uk∼)+πi−1∼(uk∼−uk−1∼))−τℏk(μE,i∼−μE,i−1∼).(20)

When determining the viscosities in the flux μ∼ in the Eq. (18), the time interpolation ρ∼=ψρρpredictors+1+(1−ψρ)ρ is used. Also for Eq. (19) we have u∼=ψuupredictors+1+(1−ψu)u and Eq. (20) E∼=ψεEpredictors+1+(1−ψε)E.

This process of realizing the solution by explicit iterations introduces an internal iterative process with fixed viscosity. Then, in the presence of oscillations, viscosities are increased and the external iterative process ends when oscillations are corrected and convergence to the solution is available. Algorithm of realization of Method 3 is presented in the form of Algorithm 4.

Thus, Method 3 differs from Method 1 by the procedure of calculating at the (s+1)-th iteration the values of {ρs+1,us+1,Es+1} by an internal predictor-correcting iterative process. The viscosity selection procedures in Method 1 and Method 3 are similar. The local CFL numbers for each cell are chosen by the Eq. (17). At the beginning of each next (s+1)-th iteration, the viscosity β is assumed to be zero. Also, at the beginning of each time step before the iterations, all viscosities are assumed to be 0. The values at the first iteration are equal to the values at the explicit layer {ρk1,uk1,Ek1}={ρk,uk,Ek}, k=1,n¯ and local CFL number is chosen for each cell by Eq. (17).

Due to the predictor-correcting procedure, which does not require matrix inversion for a system of algebraic equations in grid space, the implicit scheme is realized by explicit iterations (Method 3). Method 3 in this work is implemented only in the one-dimensional case, but it is possible in two-dimensional and three-dimensional cases, which will be investigated in the future. In Section 4.1.2, it will be shown that Method 3 has higher accuracy than Method 1. In addition, compared to Method 1 calculations, the implicit scheme reduces the convergence time to the solution, although an additional predictor-correcting procedure is performed at each iteration in Method 3.

3.4 Transition from Momentum Viscosity to Velocity Viscosity

When numerically solving by described methods, oscillations in the density and velocity profiles may occur, while oscillations in the momentum profiles are absent. This phenomenon is caused by the momentum viscosity included in πΩ∼=PΩ(0.5)−vu∼DIVσ(ρ∼u(ψu)). In this formula, the viscosity was chosen according to the condition of monotonicity of the momentum. At the same time, since the velocity is determined by dividing the momentum by the density, there is a risk of oscillations in the velocity profiles. Therefore, in the momentum conservation equation, the AAV is selected taking into account the possibility of velocity non-monotonicity and is added to the pressure as follows:

πΩ∼=PΩ(0.5)−vu∼ρ∼DIVσ(u(ψu)).(21)

A comparison of the velocity profiles for Method 3 calculations using velocity and momentum viscosity is presented in Fig. 2. The effectiveness of the velocity viscosity in smoothing the oscillations behind the rarefaction wave zone, also in the contact rupture zone, is shown.

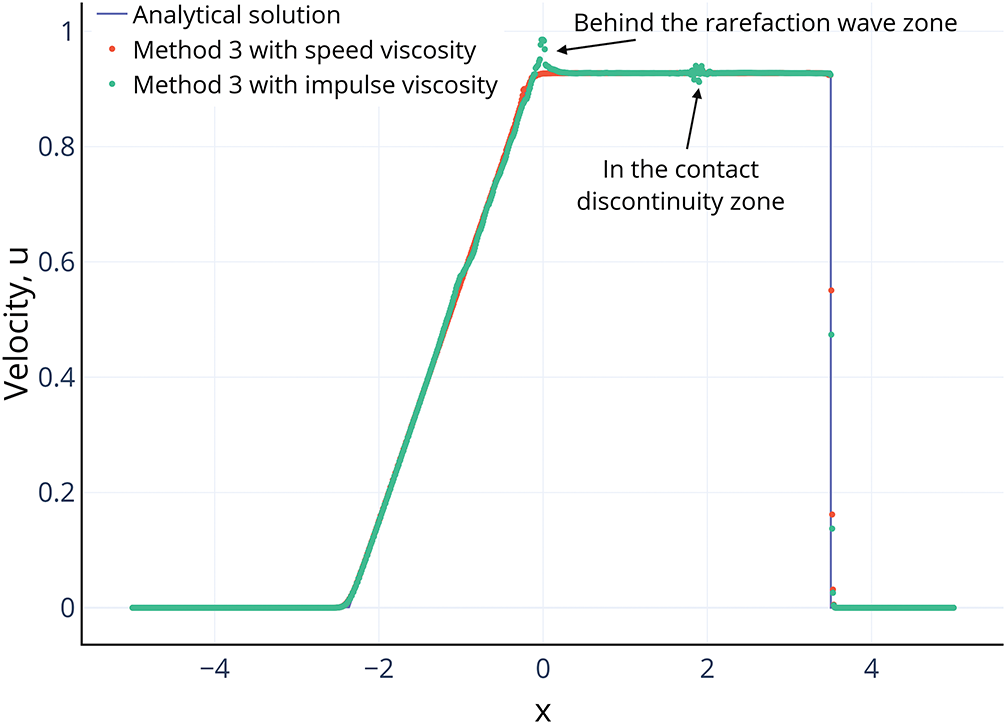
Figure 2: The distribution of over space when solving the Sod’s problem using Method 3 with impulse viscosity (red dots) and with velocity viscosity (green dots) for time T=2.0 s, as well as the analytical solution (blue line)

3.5 Grid Embedding Method

When calculating on spatially non-uniform grid with a significant change in grid sizes, the loss of accuracy of the solution may occur near the point of transition from one grid size to another. In this case, it is proposed to define the values of gas-dynamic quantities not in the initial nodes of the grid, but in the centers of gravity of their nodal domains. To improve the accuracy of calculation on a non-uniform grid, the method of grid embeddings given below is used.

In the zone of break of uniformity of the grid (a node around which two neighboring cells of different lengths), a new node is defined as the center of gravity of two neighboring half-cells. In this way, a new grid (in the case of a uniform grid, completely identical to the original grid), called a centroid with first-order embedding, is generated. For example, for a one-dimensional grid with a change of cell length from 2 to 1 (the irregularity coefficient is 2), after one such embedding the irregularity coefficient of the centroid grid becomes 87 (see Fig. 3). This process can be repeated until the non-uniformity coefficient becomes acceptable and the number of such grid embedding is small. After finding the centroid grid, the system of difference Eqs. (5)–(7) is solved on the new grid.

Figure 3: Example of grid embeddings

4  Numerical Experiments and Analysis of Results

To test the constructed scheme and the developed methods, the Sod’s problem [20] on the decay of an arbitrary discontinuity and the Einfeldt’s problem [21] on the propagation of two symmetric rarefaction waves in opposite directions have been solved.

4.1 Sod’s Problem

Table 1 shows the initial conditions of the Sod’s problem [20]. The position on the distribution to the left of the center point is the left domain, to the right—the right domain (the center point is included in the right domain). The SI system is taken as the system of units in calculations. Adiabatic index is γ=1.4. The calculation domain is a spatial segment [−5, 5]. The moment of time of calculation termination is T=2.0 s, time step is τ=0.001 s.

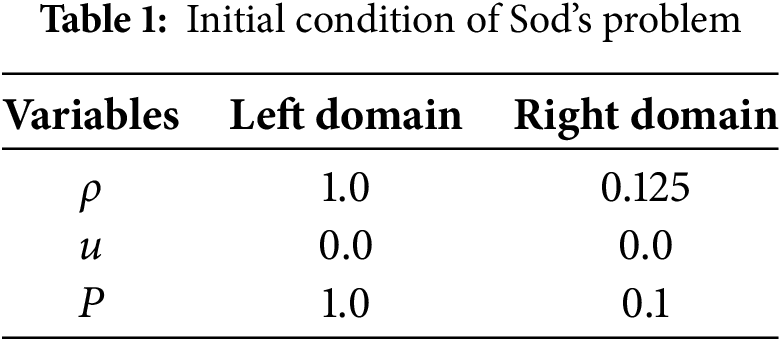
The obtained results coincide completely with the results of [5]. In all further calculations, νE=νρ is assumed. Time weights are chosen by ψρ=0.5, ψu=0.5, ψε=0.5. In the calculations using Methods 1 and 3, the condition νu⩾ν is satisfied, since νu=ν, βu=βρ is assumed before viscous correction for momentum balance. But this is not the case in Method 2 because the initial viscous corrections are assumed to be zero. In Method 1, the limiter of viscous filling βlimiter=0.2 and AAV increment constants are chosen as constρ=0.1, constu=0.1. The calculations are performed on uniform and non-uniform grids. The step length over the space of the uniform grid is h=0.01. The non-uniform grid is divided into 4 zones, in two of which the step length over space h=0.02, and in the other two zones the spatial step length h=0.01:

h(x)={0.02,−5⩽x⩽−2,0.01,−2<x⩽0,0.02,0<x⩽3,0.01,3<x⩽5.

4.1.1 Calculation Using the Method of Joint Iterations on a Uniform Grid

The density, velocity, pressure, and internal energy distributions are shown in Fig. 4. It can be seen from Fig. 4 that Method 2 improves the results of calculations in the zones of rarefaction wave and contact discontinuity. At the same time, the plots of calculations performed by Method 2 are more close to the analytical solution than the plots of calculations performed by Method 1 in the rarefaction wave zones in all profiles. Also due to the choice of velocity viscosity in the contact discontinuity zone, the oscillations are completely absent in Method 2, while in Method 1 their small amplitude is observed. Method 2 significantly reduces the processor time spent on calculations and more accurately approaches the analytical solution than Method 1. This is due to the implicit nature of finding the increments by the sweep algorithm in the iterative process. Also, in all Method 2 calculations, the viscous limiter βlimiter is achieved by selected AAVs due to the implicit nature of the sweep algorithm. It is assumed that βlimiter=0.8. In the calculations, constρ=0.2, constu=1.0 are assumed.

Figure 4: The distributions of (a) density, (b) velocity, (c) pressure, and (d) internal energy over space obtained by solving the Sod’s problem by Method 1 (red line) and Method 2 (green line) for time T=2.0 s, as well as the analytical solution (blue line)

4.1.2 Calculation Using the Improved Method of Explicit Iterations on a Uniform Grid

The improved method of explicit iterations (Method 3) does reduce the processor time and number of iterations for convergence compared to Method 1. Fig. 5 shows the distributions of density, velocity, pressure, and internal energy. From Fig. 5, we can see that the accuracy of the solutions in Method 3 is significantly higher (in the sense of convergence to the analytical solution) than in Method 1. Also, no peak in velocity and pressure profiles is observed in the contact discontinuity zone in Method 3. The processor time in Method 3 is an order of magnitude less than in Method 1 and about the same as in Method 2. In Method 3, the limiter βlimiter=0.2 and the AAV increment constants constρ=1.0, constu=0.5.

Figure 5: The distributions of (a) density, (b) velocity, (c) pressure, and (d) internal energy over space obtained by solving the Sod’s problem by Method 1 (red line) and Method 3 (green line) for time T=2.0 s, as well as the analytical solution (blue line)

4.1.3 Calculation Using the Improved Method of Explicit Iterations on Non-Uniform Grid

Fig. 6 shows the distributions of density, velocity, pressure and internal energy obtained by solving the Sod’s problem using Method 3 on non-uniform and uniform grids. Satisfactory results are observed both without and with the grid embedding method. Although in the two zones the space steps on the non-uniform grid are larger by a factor of 2 than the space steps on the uniform grid space, the results actually coincide.

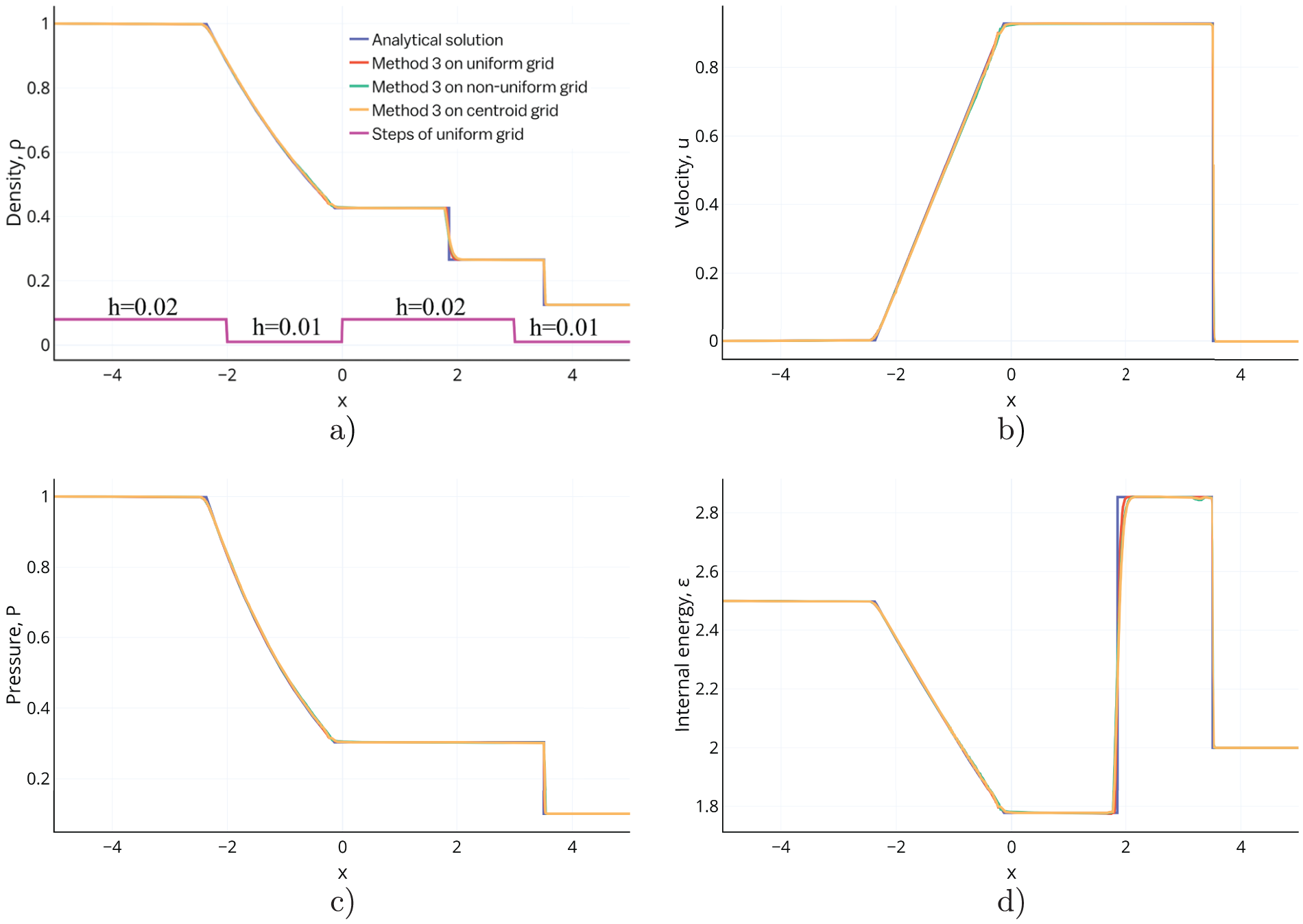
Figure 6: The distributions of (a) density, (b) velocity, (c) pressure, and (d) internal energy over space obtained by solving the Sod’s problem by Method 3 on uniform (red line), non-uniform (green line) and centroid (yellow line) grids for time T=2.0 s, as well as analytical solution (blue line) and space step length (pink line)

Fig. 7 shows a highly zoomed-in scale of the density profile after passing the transition (discontinuity) from coarse to fine grid in the direction of shock wave motion. On this scale, we can see the decrease of the density peak on the centroid grid.

Figure 7: The distribution of density over space on zoomed-in scale Fig. 6

4.1.4 Comparison of Results

The Sod’s problem is the most common problem in testing computational gas dynamics program packages because it contains zones of rarefaction wave, contact discontinuity, and shock wave. Comparing our calculations with [9], we note that both works have quite good results (without oscillations in the usual scale), although the calculations in [9] are performed on a finer grid (the space step length of which is equal to 1/200). Comparing the calculations of this work with those of [22], we observe that the results of our calculations of the Sod’s problem with the same step length in space are significantly better. The obtained results have an accuracy not lower than the results obtained when solving the Sod’s problem using the entropy-stable AAV in [12]. Comparing this work with the Interface Sharpening Technique (IST) method [24], we see that the accuracy of our calculations is significantly better (see Table 2). Also, the front structure, which is larger than the 2 nodes of the grid in our work, is smeared by 3–4 nodes when using the IST method. In [24], based on Godunov’s scheme of cell-centered control volume method, the IST is proposed as a postprocessor to preserve the fineness of the shock wave structure.

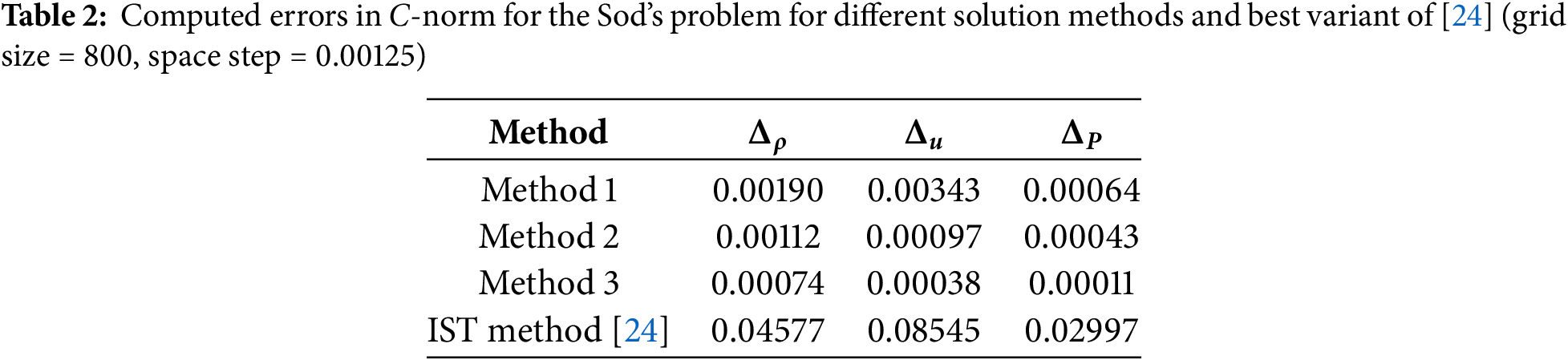
Table 2 shows that Method 2 and Method 3 have a fairly high calculation accuracy along with Method 1 and the IST method, with a smaller error by a factor of 2 or more. In addition, in our calculations there are fewer points in the shock wave zone than those of [24].

4.2 Einfeldt’s Problem

Table 3 shows the initial conditions of the Einfeldt’s problem [21]. The SI system is taken as the system of units in the calculations. The adiabatic index γ=1.4. The computational domain is the spatial segment [–1, 1]. The position on the distribution to the left of the center point is the left domain, to the right—the right domain (the center point is included in the right domain). A spatially one-dimensional symmetric gas spread with a singular discontinuity of velocity at the origin and a homogeneous thermodynamic (P,ρ) spatial distribution is presented. The reason of the singularity is the absence of an analytical solution at the initial time instant T0=0.0 s.

Since the efficiency of the methods developed in Section 3 has already been demonstrated in the Sod’s problem, the results of calculations using Methods 2 and 3 on uniform grid will be shown for the Einfeldt’s problem because of their higher efficiency compared to Method 1. All parameters βlimiter, constρ and constu for Method 2 and Method 3 are set in the same way as in the Sod’s problem.

When calculating from the initial moment of time T0=0.0 s, satisfactory plots of density and pressure profiles are obtained. However, there are obvious inconsistencies and oscillations in the center in the profiles of velocity and internal energy due to the singularity of the solution at time T0=0.0 s. In the following, our calculations start from some later moment of time, due to which the influence of the initial singularity is reduced.

4.2.1 Calculations of Einfeldt’s Problem

Using the analytical solution obtained by stitching the Riemann invariant with the constant flow zones [21], the right-hand position of the boundary of the stable “horizontal” zone is calculated by the formula

x∗=(c0−γ−12uR)T0,(22)

where c0=γPρ is speed of sound at the initial moment of time, uR=2.0 is the initial velocity on the right domain. Similarly, the left position of such a boundary is symmetric about the center point. In this case, to reduce the influence of singularity, the initial value of x∗ is larger than the length of one spatial step h. When h=0.002, according to Eq. (22) T0≳0.006 s. Next, the calculations will be performed from moments T0=0.01 s (one node is located to the right of the center point in the “horizontal” zone) and T0=0.05 s (eight nodes are located to the right of the center point in the “horizontal” zone).

Fig. 8 presents the distributions of density, velocity, pressure, and internal energy from the initial moment T0=0.01 s and shows that Method 2 and Method 3 give almost the same results with high accuracy. The approach of singularity reduction does improve the accuracy of the calculation, although small oscillations remain in the center of the profiles of velocity and internal energy. These fluctuations arise due to the singularity of the initial data in the Einfeldt’s problem, which is specified at an initial moment of time approaching zero. They naturally disappear with a consistent change in the start time of the calculation and a consistent reduction in the grid spatial step.

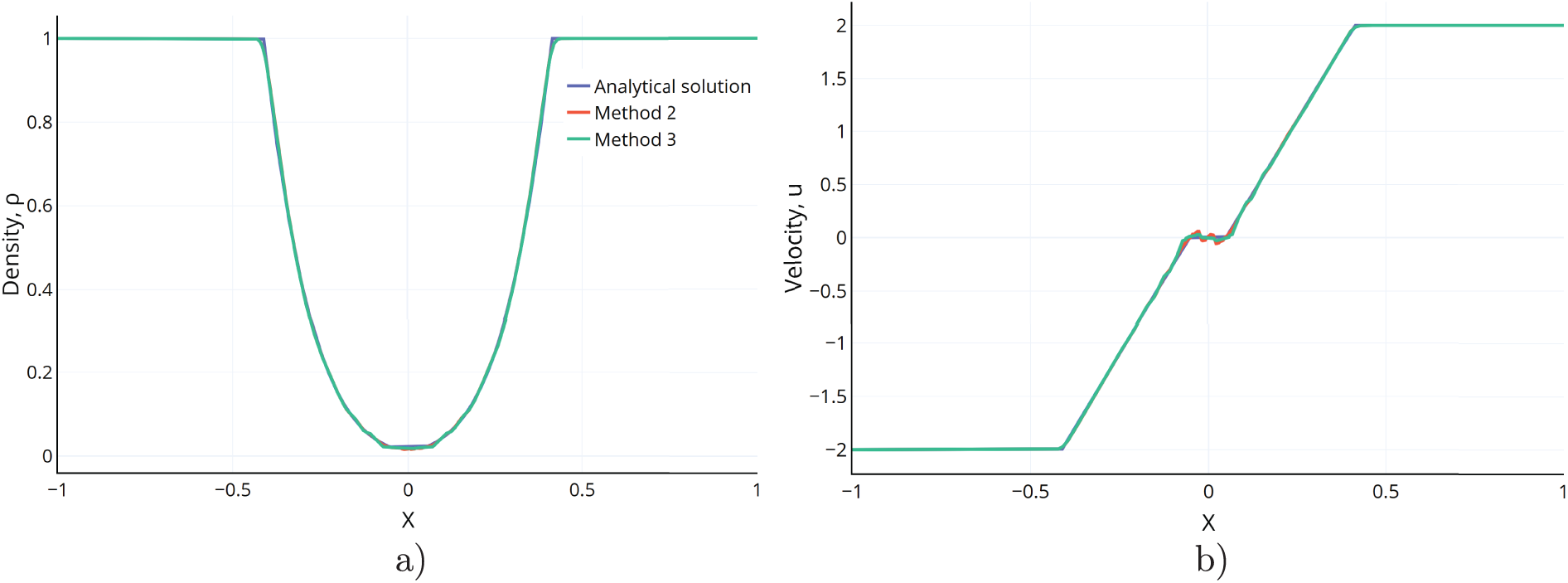
Figure 8: The distributions of (a) density, (b) velocity, (c) pressure and (d) internal energy over space obtained by solving the Einfeldt’s problem by Method 2 (red line) and Method 3 (green line) for time T=0.15 s at initial time T0=0.01 s, as well as the analytical solution (blue line)

Fig. 9 presents the distributions of density, velocity, pressure and internal energy from the initial moment T0=0.05 s, which show that singularity affects the accuracy of the calculation results. At the initial moment T0=0.05 s the plots of Method 2 and Method 3 calculations almost coincide with the plots of the analytical solution.

Figure 9: The distributions of (a) density, (b) velocity, (c) pressure and (d) internal energy over space obtained by solving the Einfeldt’s problem by Method 2 (red line) and Method 3 (green line) for time T=0.15 s at initial time T0=0.05 s, as well as the analytical solution (blue line)

In [19], the Einfeldt’s problem is also solved from the initial moment T0=0.01 s. The distributions of density, velocity, pressure, and temperature obtained from the calculations in [19] coincide with the results obtained by Method 3 with good accuracy.

5  Conclusion

The completely conservative difference schemes with adaptive artificial viscosity were considered, and the problem of modeling the gas dynamic processes described by equations in Euler variables was studied. The artificial viscosity method was shown as an effective way for improving the stability and suppressing the numerical oscillations. This work presented the effective methods for selecting adaptive artificial viscosity for completely conservative difference schemes. In particular, the improved method of explicit iterations with a predictor-correcting procedure was demonstrated. The developed methods were characterized by simplicity of realization. The calculations of classical Sod’s and Einfeldt’s problems were carried out to test the developed methods of artificial viscosity selection. Their results showed the efficiency and accuracy of the proposed methods. Comparing the results of this work with the analytical solutions and the calculation results of other authors was given. In addition, the method of velocity viscosity as an additive to pressure was proposed. The calculation results also showed the effectiveness of the velocity viscosity method for reducing the amplitude of the velocity and pressure profiles oscillations in the contact discontinuity zone. The grid embedding method was also developed, which improved the accuracy on a spatially non-uniform grid. The proposed mathematical method could be used to solve gas dynamics problems, including those with discontinuous data. The developed methods were not applicable to calculations with multi-temperature (two-temperature) approximations, as well as with non-isotropic force tensors acting in a continuous medium. In future works, it was planned to use the presented algorithms and methods in applied problems, as well as their generalization to the spatially multidimensional case.

Acknowledgement: The work of Marina Ladonkina, Viktoriia Podryga, Yury Poveshchenko was supported by KIAM RAS. The work of Haochen Zhang was supported by MIPT NRU.

Funding Statement: The work was carried out within the framework of the state assignment of KIAM RAS (No. 125020701776-0).

Author Contributions: The authors confirm contribution to the paper as follows: formal analysis and supervision: Marina Ladonkina; project administration and writing—review and editing: Viktoriia Podryga; conceptualization and methodology: Yury Poveshchenko; investigation, software, validation and writing—original draft preparation: Haochen Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the Corresponding Author, Viktoriia Podryga, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Popov YuP, Samarskii AA. Completely conservative difference schemes for the equations of gas dynamics in Euler’s variables. USSR Comput Math Math Phys. 1970;10(3):265–73. doi:10.1016/0041-5553(70)90133-3. [Google Scholar] [CrossRef]

2. Popov YuP, Samarskii AA. Completely conservative difference schemes. USSR Comput Math Math Phys. 1969;9(4):296–305. doi:10.1016/0041-5553(69)90049-4. [Google Scholar] [CrossRef]

3. Kuzmin AV, Makarov VL. An algorithm for constructing completely conservative difference schemes. USSR Comput Math Math Phys. 1982;22(1):128–38. doi:10.1016/0041-5553(82)90170-7. [Google Scholar] [CrossRef]

4. Kuzmin AV, Makarov VL. On one completely conservative difference scheme for the equation of gas dynamics in Euler variables. Comput Math Math Phys. 1980;20(1):171–81. doi:10.1016/0041-5553(80)90072-5. [Google Scholar] [CrossRef]

5. Popov IP, Fryazinov IV. Adaptive artificial viscosity method numerical solution of equations of gas dynamics. Moscow, Russia: Krasand; 2014. (In Russian). [Google Scholar]

6. Kurganov A, Liu Y. New adaptive artificial viscosity method for hyperbolic systems of conservation laws. J Comput Phys. 2012;231(24):8114–32. doi:10.1016/j.jcp.2012.07.040. [Google Scholar] [CrossRef]

7. Albright J, Shashkov M. Locally adaptive artificial viscosity strategies for Lagrangian hydrodynamics. Comput Fluids. 2020;205(3):104580. doi:10.1016/j.compfluid.2020.104580. [Google Scholar] [CrossRef]

8. Huang W, Ren Y, Tu G, Yuan X, Chen J. An adaptive artificial viscosity method for quintic spline reconstruction scheme. Comput Fluids. 2022;240(1):105435. doi:10.1016/j.compfluid.2022.105435. [Google Scholar] [CrossRef]

9. Wu Z, Ren Y. A shock capturing artificial viscosity scheme in consistent with the compact high-order finite volume methods. J Comput Phys. 2024;516(8):113291. doi:10.1016/j.jcp.2024.113291. [Google Scholar] [CrossRef]

10. Popov IV, Gasilov VA, Krukovskiy AYu, Boldarev AS. Difference scheme with adaptive artificial viscosity for gas-dynamic computations on nonuniform meshes. Math Models Comput Simul. 2024;16(Suppl 2):S263–71. doi:10.1134/S2070048224700960. [Google Scholar] [CrossRef]

11. Ogban PU, Naterer GF. Entropy-based artificial dissipation as a corrective mechanism for numerical stability in convective heat transfer. Numer Heat Transf B-Fundam. 2023;84(1):1–23. doi:10.1080/10407790.2023.2174625. [Google Scholar] [CrossRef]

12. Guermond JL, Nazarov M, Popov B, Tomas I. Second-order invariant domain preserving approximation of the Euler equations using convex limiting. SIAM J Sci Comput. 2018;40(5):A3211–39. doi:10.1137/17M1149961. [Google Scholar] [CrossRef]

13. Hennemann S, Rueda-Ramírez AM, Hindenlang FJ, Gassner GJ. A provably entropy stable subcell shock capturing approach for high order split form DG for the compressible Euler equations. J Comput Phys. 2021;426:109935. doi:10.1016/j.jcp.2020.109935. [Google Scholar] [CrossRef]

14. Zhang T, Zhan C, Cai B, Lin C, Guo X. An improved meshless artificial viscosity technology combined with local radial point interpolation method for 2D shallow water equations. Eng Anal Bound Elem. 2021;133(6):303–18. doi:10.1016/j.enganabound.2021.09.002. [Google Scholar] [CrossRef]

15. Yue M, Wang X, Liu Z, Cao W-D, Wang Y, Hu J, et al. Application of adaptive artificial viscosity method to reduce grid orientation effect in numerical simulations for steam thermal recovery. Arab J Sci Eng. 2025;50(13):10359–84. doi:10.1007/s13369-024-09865-y. [Google Scholar] [CrossRef]

16. Wang X, Yue M, Liu Z, Cao W, Wang Y, Hu J, et al. Numerical strategy on the grid orientation effect in the simulation for two-phase flow in porous media by using the adaptive artificial viscosity method. Int J Numer Anal Methods Geomech. 2025;49(2):541–54. doi:10.1002/nag.3886. [Google Scholar] [CrossRef]

17. Clinco N, Girfoglio M, Quaini A, Rozza G. Filter stabilization for the mildly compressible Euler equations with application to atmosphere dynamics simulations. Comput Fluids. 2023;266(2):106057. doi:10.1016/j.compfluid.2023.106057. [Google Scholar] [CrossRef]

18. Margolin LG, Lloyd-Ronning NM. Artificial viscosity-then and now. Meccanica. 2023;58(6):1039–52. doi:10.1007/s11012-022-01541-5. [Google Scholar] [CrossRef]

19. Rahimly OR, Poveshchenko YuA, Popov SB. Two-layer 1D completely conservative difference schemes of gas dynamics with adaptive regularization. Math Models Comput Simul. 2022;14(5):771–82. doi:10.1134/S2070048222050118. [Google Scholar] [CrossRef]

20. Sod GA. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J Comput Phys. 1978;27(1):1–31. doi:10.1016/0021-9991(78)90023-2. [Google Scholar] [CrossRef]

21. Einfeldt B, Munz CD, Roe PL, Sjögreen B. On Godunov-type methods near low densities. J Comput Phys. 1991;92(2):273–95. doi:10.1016/0021-9991(91)90211-3. [Google Scholar] [CrossRef]

22. Bourgeois R, Tremblin P, Kokh S, Padioleau T. Recasting an operator splitting solver into a standard finite volume flux-based algorithm. The case of a Lagrange-projection-type method for gas dynamics. J Comput Phys. 2024;496(2):112594. doi:10.1016/j.jcp.2023.112594. [Google Scholar] [CrossRef]

23. Laibe G, Price DJ. Dusty gas with smoothed particle hydrodynamics-I. Algorithm and test suite. Mon Not R Astron Soc. 2012;420(3):2345–64. doi:10.1111/j.1365-2966.2011.20202.x. [Google Scholar] [CrossRef]

24. Nguyen V, Phan T, Park W. Numerical modeling of multiphase compressible flows with the presence of shock waves using an interface-sharpening five-equation model. Int J Multiphase Flow. 2021;135:103542. doi:10.1016/j.ijmultiphaseflow.2020.103542. [Google Scholar] [CrossRef]

25. Ladonkina ME, Poveschenko YuA, Rahimly OR, Zhang H. Theoretical study of stability of nodal completely conservative difference schemes with viscous filling for gas dynamics equations in Euler variables. Zhurnal SVMO. 2022;24(3):317–30. doi:10.15507/2079-6900.24.202203.317-330. [Google Scholar] [CrossRef]