Semi Analytical Solution of MHD and Heat Transfer of Couple Stress Fluid over a Stretching Sheet with Radiation in Porous Medium

Nomenclature

1  Introduction

Non-Newtonian fluids are a broad category that encompasses a large range of materials with wildly different material structures. Their primary similarity is that the standard linearly viscous Newtonian model is unable to adequately describe their behavior. A few examples of materials that fall under the category of non-Newtonian fluids are polymeric liquids, biological fluids, slurries, suspensions, and liquid crystals. Certain materials only flow under shear stress if a critical value is achieved. To simulate the behavior of non-Newtonian fluids, numerous fluids of the rate type have been proposed. Koh et al. [1] investigated the impact of inlet velocity and temperature on a nonnewtonian fluid’s flow. The development of a propeller mixer to stir non-Newtonian fluid flow is described in detail. The process is transparent throughout the entire design process because it is founded on analytical principles submitted by Reviol et al. [2]. It has been studied the effects of mass transfer and heat on non-Newtonian a paraboloid’s highest catalytic surface is exposed to Walter’s B fluid flow studied by Nazir et al. [3]. Muduganti et al. [4] expanded the effect of a transverse magnetic field on the continuous flow of an incompressible conducting couple stress fluid in a rectangular channel with a uniform cross-section, with suction or injection at the lateral walls. Conducting non-Newtonian lubricant is used as a couple of stress fluids to fill the space between the plates presented by Devani et al. [5].

The importance of flow and heat transfer characteristics over stretched surfaces in numerous industrial, scientific, and technological applications, including Fiber production, condensation processes, and textile machines and plastic sheets, piqued researchers’ interest. Nadeem and Hussain [6] Examined the Williamson fluid flow’s heat transmission through a porous stretched sheet. Megahed [7] investigated the heat transfer for Powell-Eyring fluid flow across an exponentially extended continuous porous surface with a changing thermal conductivity and an increasing temperature distribution of heat flux. Humane et al. [8] studied the effects of heat radiation, chemical reactions, and an external magnetic field on Casson-Williamson fluid flow through a stretched porous sheet. The Williamson nanofluid flows across an exponentially stretched sheet with affected of heat radiation, viscosity dissipation, and chemical interactions was investigated by Pallavi et al. [9]. Madan Kumar et al. [10] analyzed the properties of Williamson nanofluid flow via a nonlinear stretching sheet submerged in a permeable medium. Recent articles related to studying the steady flow of fluids past stretching surfaces, exploring various physical conditions include references [11–13]. This focus arises from the crucial role such flows play in numerous industrial and engineering applications.

Furthermore, Numerous researchers are interested in magnetohydrodynamic (MHD) flow because of its significance in numerous engineering applications, including MHD generators, nuclear reactor cooling, MHD pumps, plasma physics, and the petroleum industry. Raju et al. [14] examined the impact of heat source/sink, temperature-dependent viscosity on the natural convective heat transfer of a MHD non-Newtonian nanofluid over a cone. The Hartmann magnetohydrodynamic flow of two immiscible fluids between two horizontal plates containing two porous media with oscillating lateral wall mass flux was studied by Bég et al. [15]. The impact of Cattaneo Christov heat and mass fluxing, active energy and convective heat and mass flux boundary conditions on electromagnetic Maxwell nanofluid flow in Buongiorno model was studied by Wang et al. [16]. Alomari et al. [17] investigated numerically of variables including magnetohydrodynamic influences on the forced/free convection and entropy generation in a curvelinear lid-driven cavity with carbon nanotubes and an adiabatic cylinder. The Reiner Philippoff nanofluids across an etched sheet in a porous medium, taking into account thermal radiation, chemical processes, viscous dissipation, and magnetic field was examined by Adel et al. [18]. Asokakumar Sreekala and Sengupta [19] investigated the influence of varying magnetic field strengths on vortex shedding around a cylinder.

HPM, is a method that created by He [20,21], has become a key semi-analytical approach for tackling a wide variety of nonlinear issues, particularly in fluid dynamics, heat transfer, and porous media. The central concept behind HPM is to use a homotopy to smoothly deform a tough problem into an easier one, so the solution can be found in a fast-converging series. This technique combines the rigor of analytical techniques with the iterative structure of numerical schemes. A major advantage of HPM is its effectiveness in solving highly nonlinear problems without needing to discretize or linearize them, or to use small parameters. This makes it both fast and computationally affordable. Many studies have shown that HPM is very successful at solving magnetohydrodynamic (MHD) flow problems, especially in porous media where magnetic fields, viscous forces, and thermal effects all interact in complex ways [22–24]. Therefore, HPM was the method used in this research because it is a reliable, straightforward tool that can accurately model the crucial physical dynamics of MHD flows in non-Newtonian fluids flowing through porous structures.

The goal of this research is to improve heat transfer in engineering systems that involve MHD flows, couple stress fluids, and porous media. To make it more relevant to real-world applications like cooling systems and material manufacturing, the study incorporates the effects of heat generation, thermal radiation, and magnetic fields. The research uses the HPM to gain a better understanding of the flow’s behavior. Its practical importance is highlighted through applications in enhanced oil recovery, geothermal energy systems, and thermal management in porous medium.

2  Analysis of the Problem

In this research, we assume the flow of the proposed fluid is steady, two-dimensional and incompressible. The proposed model is the non-Newtonian couple stress fluid and moving through a magnetized Darcy porous medium due to a continuously impermeable vertical stretching sheet, indicated as in Fig. 1. The fluid is assumed to have a constant density ρ, constant conductivity κ, constant specific heat Cp and constant convection coefficient hf. The model is considered to be impacted by both heat generation and thermal radiation. The analysis is conducted within a Cartesian coordinate system x,y, where the stretching sheet is positioned along the plane y=0. In this research, it is considered that the stretching sheet can stretched with a velocity denoted as uw=bx, where b describe the rate of stretching, which means that the sheet is stretched linearly. Perpendicular to the stretching surface, we assumed a magnetic field with strength B0 impact the flow. In this physical model, the sheet is considered to have a constant temperature Tw, which is higher than the the ambient temperature T∞. This physically means that the direction of temperature translation is from the heated sheet to the fluid. Further, the earlier assumptions for the problem are summarized below:

i.   All fluid physical properties such as density, thermal conductivity, and specific heat are taken to be constant.

ii.   The model analysis accounts for the impact of heat generation, magnetic field, mixed convection phenomenon and thermal radiation.

iii.   A non-Newtonian couple stress fluid flows over a vertical stretching sheet embedded in a Darcy porous medium.

iv.   The flow is modeled as a steady, two-dimensional, and incompressible system.

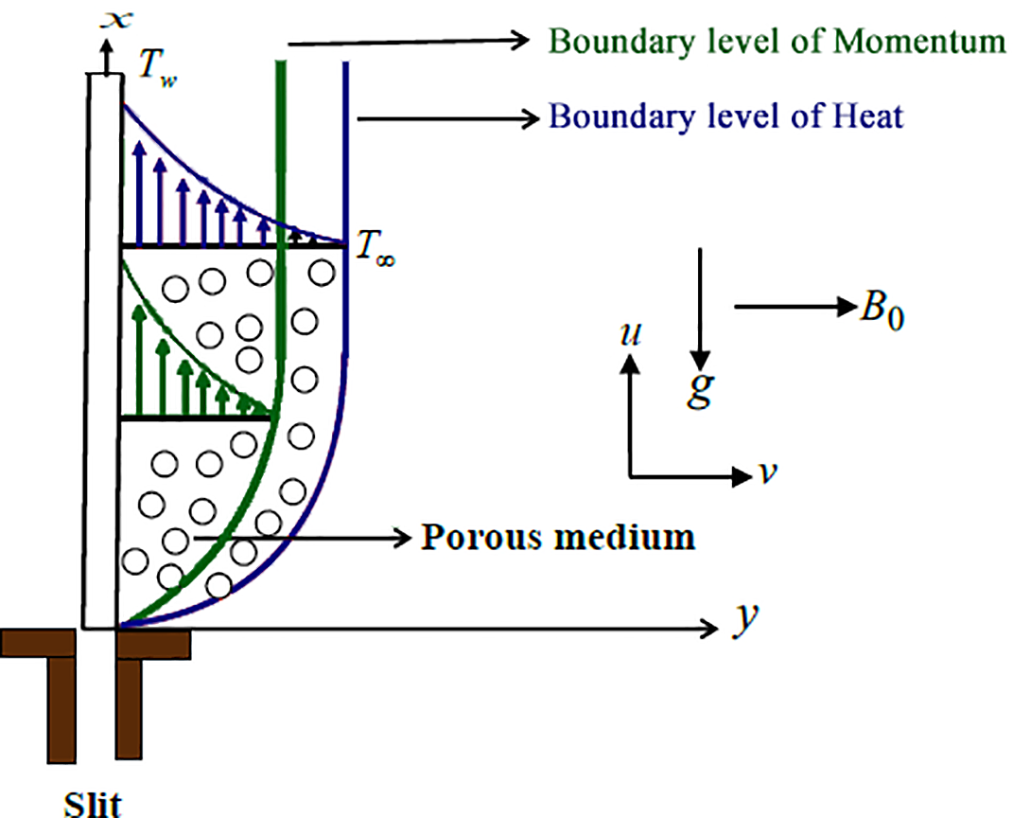
Figure 1: Schematic configuration of flow

Now, according to these previous assumptions and using the boundary layer approximation (Boussinesq’s approximation), we reached to the following simplified forms of the continuity, momentum, and energy equations as follows [25]:

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y=ν∂2u∂y2+gβt(T−T∞)−(η0ρ)∂4u∂y4−σB02ρu−νϕku,(2)

u∂T∂x+v∂T∂y=κρCp∂2T∂y2+QρCp(T−T∞)−1ρCp∂qr∂y,(3)

clearly that the previous system of equation include u,v, which represent the velocity components in x− and y− directions, respectively. g is the acceleration, η0 is the coefficient of couple stress fluid, Q is the coefficient of heat generation, βt is the coefficient of thermal expansion, σ is the electrical conductivity, k is the porous medium permeability and T is the dimension temperature. Further, qr is the radiative heat flux, which can be expressed as follows:

qr=−4σ∗3k∗∂T4∂y,(4)

where k∗ is the coefficient of mean absorption and σ∗ is the Stephan Boltzmann constant. Likewise, the fluid flow is governed by the following boundary conditions which describe the interaction between the elastic sheet and the surrounding fluid. These conditions defines as:

u=uw=bx,v=0,∂2u∂y2=0,−κ(∂T∂y)=hf(Tf−Tw)aty=0,(5)

u→0,∂u∂y→0,T→T∞asy→∞.(6)

Here, as appropriate dimensionless variables for our study, we can suggest the following:

ψ=bνxf(η),η=bνy,θ(η)=T−T∞Tf−T∞(7)

Again, by referring to the definition of radiative flux qr after defining the previous similarity transformations, we assume the following:

T4=(θ(Δ−1)+1)4T∞4,(8)

where Δ=TwT∞ is the parameter of wall temperature ratio. Considering the dimensionless similarity transformations introduced earlier, the new form of the governing equations are reformulated as follows:

Γfv+(M+β)f′−f′′′−ff′′+f′2−Grθ=0,(9)

{R[1+(Δ−1)θ]3+1}θ′′+3R(Δ−1){1+(Δ−1)θ}θ′2+Pr⁡δθ+Pr⁡fθ′=0,(10)

f(0)=0,f′(0)=1,f′′′(0)=0,θ′(0)=−λ(1−θ(0)),(11)

f′→0,f′′→0,θ→0,asη→∞,(12)

where M=σB02ρb is the magnetic field parameter, β=νϕkb is the porous parameter, Γ=bη0ρν2 is the couple stress parameter, Gr=gβt(Tf−T∞)uw3b3ν2 is the Grashof number, Pr=μcpκ is the Prandtl number, R=16σ∗T∞33k∗κ is the radiation parameter, δ=QρbCp is the heat generation parameter and λ=hfκμbρ is the mixed convection parameter. Additionally, analyzing the features of both the fluid temperature and fluid velocity fields, particularly after obtaining the numerical solution for the proposed model, we may have enabled to determine the values of the local skin-friction coefficient Cfx and the local Nusselt number Nux as outlined below:

CfxRe12=−f′′(0)+Γf′′′′(0),NuxRe−12=−(1+RΔ3)θ′(0),(13)

where Re=uwxν∞ is the local Reynolds number.

3  Procedure Solution

In this part, the governing non-linear ordinary differential Eqs. (9) and (10) with related boundary conditions (11) and (12) are solved using a semi-analytical method known as the HPM. Because HPM provides an approximate analytical solution that converges quickly with little computational effort, it offers a substantial advantage over conventional numerical approaches. In contrast to strictly numerical methods, HPM enables insight into the influence of various parameters on the flow and thermal profiles without the need for extensive computational resources. Further it has capability to solve strongly nonlinear problems without requiring discretization. The procedure and the main definition of this method have been previously introduced in many publications [26,27]. Therefore, HPM is applied to the governing non-linear ordinary differential Eqs. (9) and (10) and based on He’s method [3], the definition of linear operators for each equation is set to be:

Lf(f)=Γfν,LΘ(Θ)=((R(1+(△−1)Θ))3+1)Θ′′.

The governing non-linear ordinary differential Eqs. (9) and (10) can be built as follows in accordance with the Homotopy Perturbation structure:

H(f;p)=p[ΓLfν(f)]+(1−p)[(M+β)Lf′(f)−Lf′′′(f)−Lf(f)Lf′′(f)+(Lf′(f))2−GrLΘ(Θ)]=0(14)

H(Θ;p)=p[{(R(1+(△−1)LΘ(Θ)))3+1}LΘ′′(Θ)]+(1−p)[3R(△−1){1+(△−1)LΘ(Θ)}(LΘ′(Θ))2+PrδLΘ(Θ)+PrLf(f)LΘ′(Θ)]=0(15)

After making certain simplifications and rearranging based on the powers of p-terms in conjunction with the boundary conditions, we obtain the following after substituting into Eqs. (14) and (15):

f(η)=f0+f1η+f2η2+f3η3+…(16)

Θ(η)=Θ0+Θ1η+Θ2η2+Θ3η3+…(17)

where,

f1=(6Gr+6M+6β−24Grλ−24Mλ−24βλ)6(γλ4−4γλ3+6γλ2−4γλ+γ)+36Grλ2−24Grλ3+6Grλ4+36Mλ2−24Mλ3+6Mλ46(γλ4−4γλ3+6γλ2−4γλ+γ)+36βλ2−24βλ3+6βλ46(γλ4−4γλ3+6γλ2−4γλ+γ),

f2=(6(Gr+M+β−4Grλ−4Mλ−4βλ)γλ4−4γλ3+6γλ2−4γλ+γ+6Grλ2−4Grλ3+Grλ4+6Mλ2−4Mλ3+Mλ4γλ4−4γλ3+6γλ2−4γλ+γ+6βλ2−4βλ3+βλ4−AGrγλ4−4γλ3+6γλ2−4γλ+γ,

f3=AGrλ2(γλ4−4γλ3+6γλ2−4γλ+γ)

Θ1=exp⁡(−2y)(Pr2+3R2−3Rδ2−3AR2+3ARδ−3ARδ22)2R(3Aδ3−3A2(−2+δ)(−1+δ)2+A3(−1+δ)3−15Aδ2)+ 2Prexp⁡(−y)(σ−1),

Θ2 = −Pr−5R+7Rδ−2Prσ−2Rδ2+3AR−6ARδ+3ARδ2R(3(−5+Aδ)Aδ2+A2(6+A(−1+δ)−3δ)(−1+δ)2),

Θ3=−APrσ.

Further, a comprehensive flowchart (Fig. 2) providing a step-by-step illustration of the numerical method is presented below for better clarity and understanding.

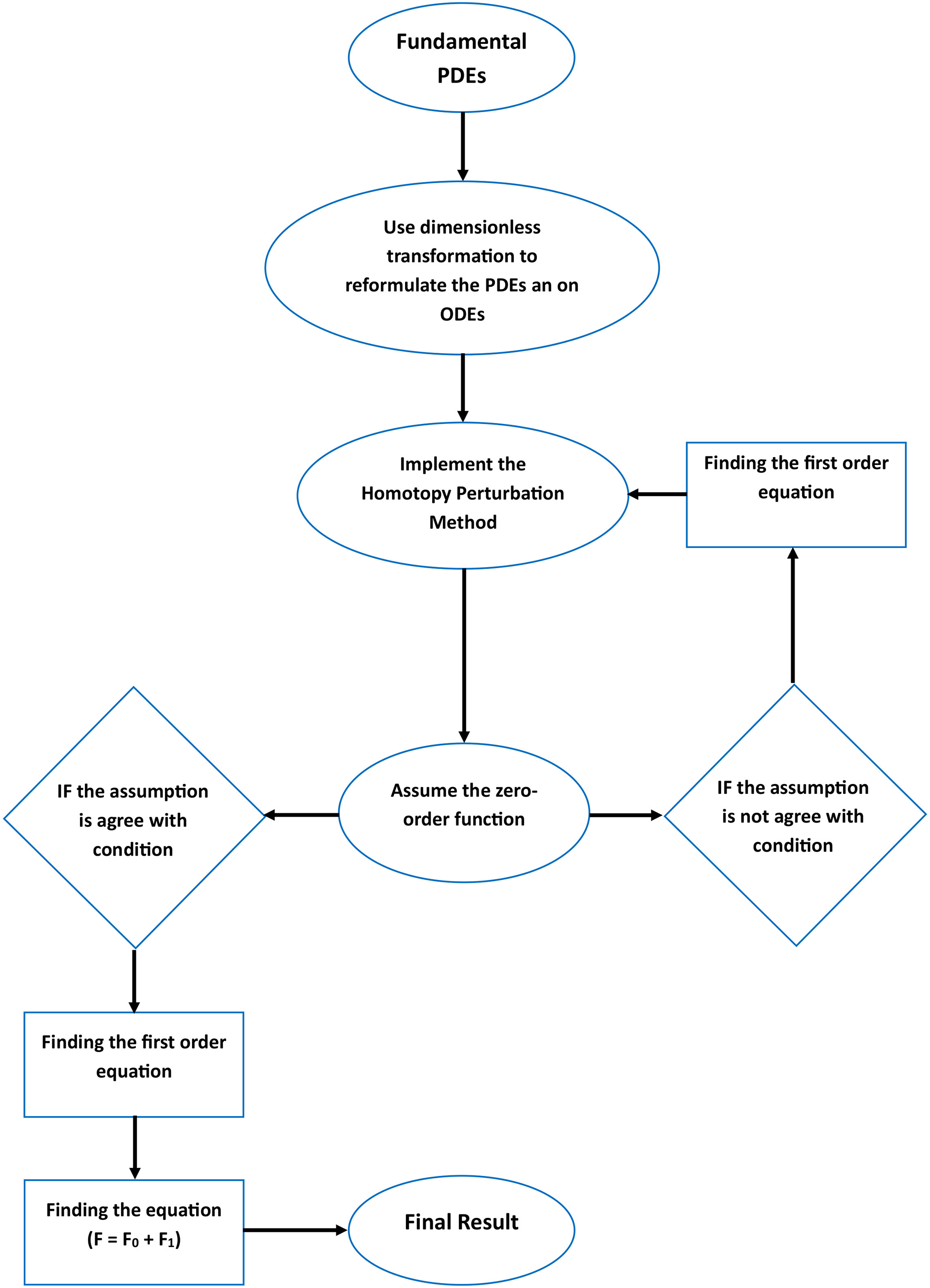
Figure 2: Chart representing the numerical technique

4  Validation of the HPM

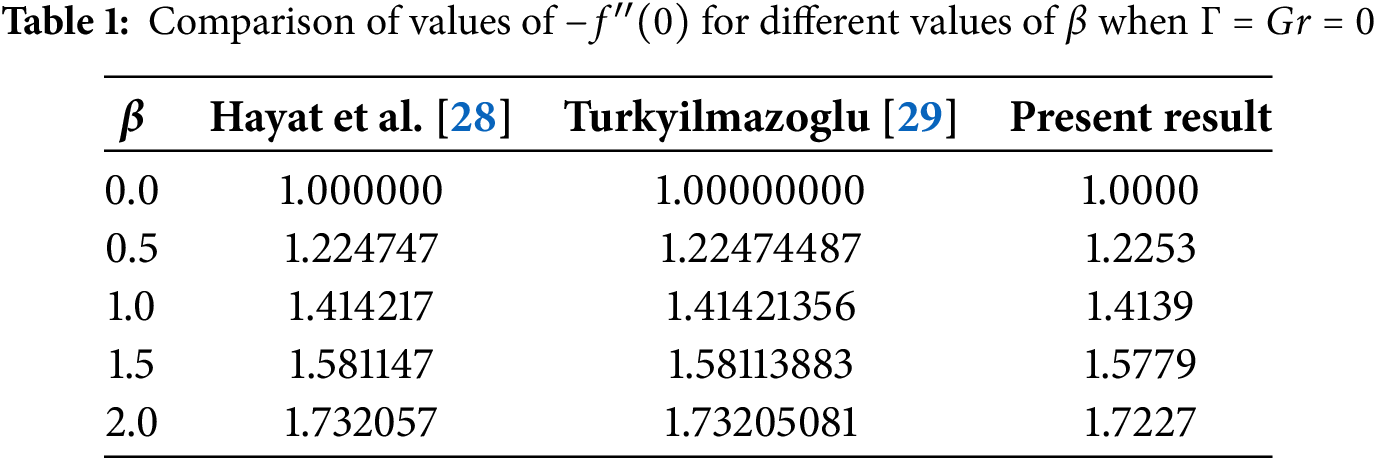
In this section, a comparison was made between the proposed results that obtained by the HPM and the previously published results in reliable scientific research such as Hayat et al. [28] and Turkyilmazoglu [29]. As we observed from the Table 1, the outcome of the comparison introduced an excellent agreement between the all results. This strong consistency confirms the reliability and the accuracy of the HPM in solving this type of these physical problems. These findings corroborate the models employed, suggesting broader applicability of HPM across different scientific fields.

5  Results and Discussion

This section provides a comprehensive analysis of the computational findings to clarify how key parameters affect velocity and temperature profiles in the magnetohydrodynamic (MHD) flow of a couple stress fluid past a porous, vertically stretching sheet. Through appropriate similarity transformations, the governing nonlinear partial differential equations were converted into ordinary differential equations, which were subsequently solved using the HPM. This semi-analytical technique combines simplicity with precision, effectively modeling the intricate interactions among magnetic fields, thermal radiation, heat generation, and couple stress effects. The analysis emphasizes the role of parameter variations in modifying flow behavior and heat transfer characteristics, offering deeper insights into the underlying physical phenomena. Before we begin our discussion, it’s important to note that while we vary the governing parameters, the other parameters are held constant at Γ=1.2,β=0.5,λ=0.3,M=0.5,Gr=0.2,δ=0.5,Δ=1.2 and R=0.5. Fig. 3a demonstrates that augmenting the couple stress parameter Γ significantly boosts fluid velocity near the stretching surface. The velocity enhancement observed with increased couple stress parameter stems from microstructural effects, mitigating internal fluid resistance and promoting streamlined flow. This characteristic is especially crucial in applications utilizing lubricants or non-Newtonian fluids, where improved flow behavior is essential for optimizing heat and mass transfer. Also, as depicted in the Fig. 3b, an elevated temperature ratio parameter Δ results in an increase in the fluid’s temperature distribution. Here, the enhancement in temperature observed with a higher temperature ratio parameter can be attributed to increased thermal interaction between the fluid and its environment. Physically, the velocity enhancement observed with increasing couple stress parameter stems from microstructural impacts which built in the non-Newtonian fluid that decrease viscous resistance, promoting improved near-surface fluid flow, a valuable trait for engineering applications involving non-Newtonian fluids. Concurrently, elevated temperature ratio parameters intensify thermal exchange at the boundary layer, resulting in greater heat absorption due to strengthened fluid-environment thermal coupling.

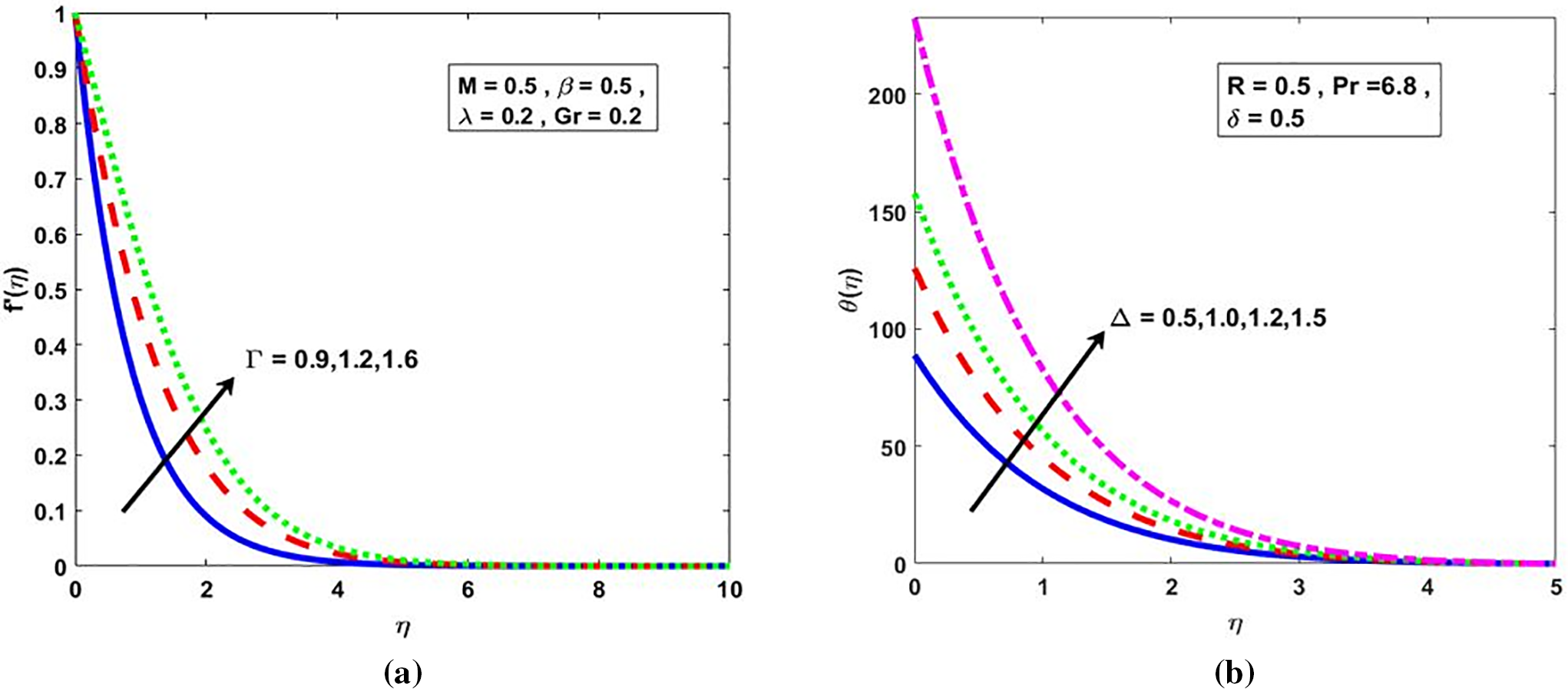
Figure 3: (a) f′(η) for assorted Γ (b) θ(η) for assorted Δ

As depicted in Fig. 4a, an elevation in the porous medium parameter β leads to a discernible decrease in the fluid velocity profile. This observation suggests that the presence of greater porosity within the medium exerts a significant resistance to fluid flow, consequently diminishing its velocity. Furthermore, as porosity decreases, the medium’s permeability diminishes. This reduction in permeability translates to an increased drag force acting on the fluid, thereby slowing its movement. This effect is of considerable importance in filtration systems and geological applications, where the ability to regulate flow rates through porous media is crucial. Further, as depicted in Fig. 4b, an elevated heat generation parameter δ is associated with an increase in the fluid’s temperature distribution. Here, this increase in temperature with a higher heat generation parameter is a consequence of the intensified thermal energy generation arising from the internal heat source within the fluid. Physically, increasing the heat generation parameter d intensifies the internal thermal energy source, leading to a rise in fluid temperature, as clearly observed in Fig. 4b.

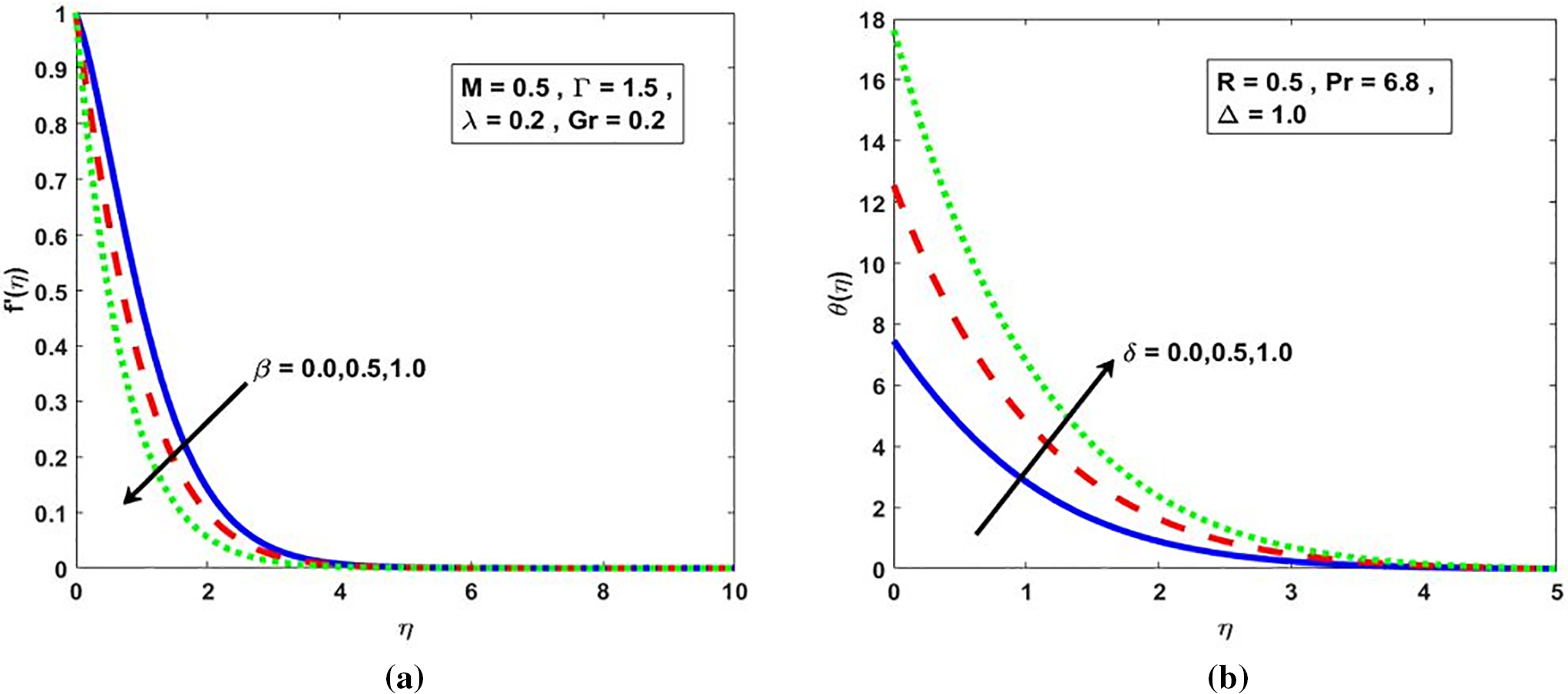
Figure 4: (a) f′(η) for assorted β (b) θ(η) for assorted δ

As illustrated in Fig. 5a, the mixed convection parameter λ exerts a significant influence on the fluid’s velocity profile, leading to a notable enhancement with increasing values. This parameter characterizes the relative importance of buoyancy forces compared to forced convection forces within the flow. An increase in the mixed convection parameter signifies a greater dominance of buoyancy forces, which act to accelerate the fluid and enhance its velocity. Additionally, Fig. 5b demonstrates that as the radiation parameter rises, the fluid’s temperature distribution also increases. Physically, higher radiation intensifies heat transfer within the fluid due to increased thermal radiation effects. This results in greater heat retention and elevated temperatures, which is particularly important in high-temperature applications like energy systems and material processing.

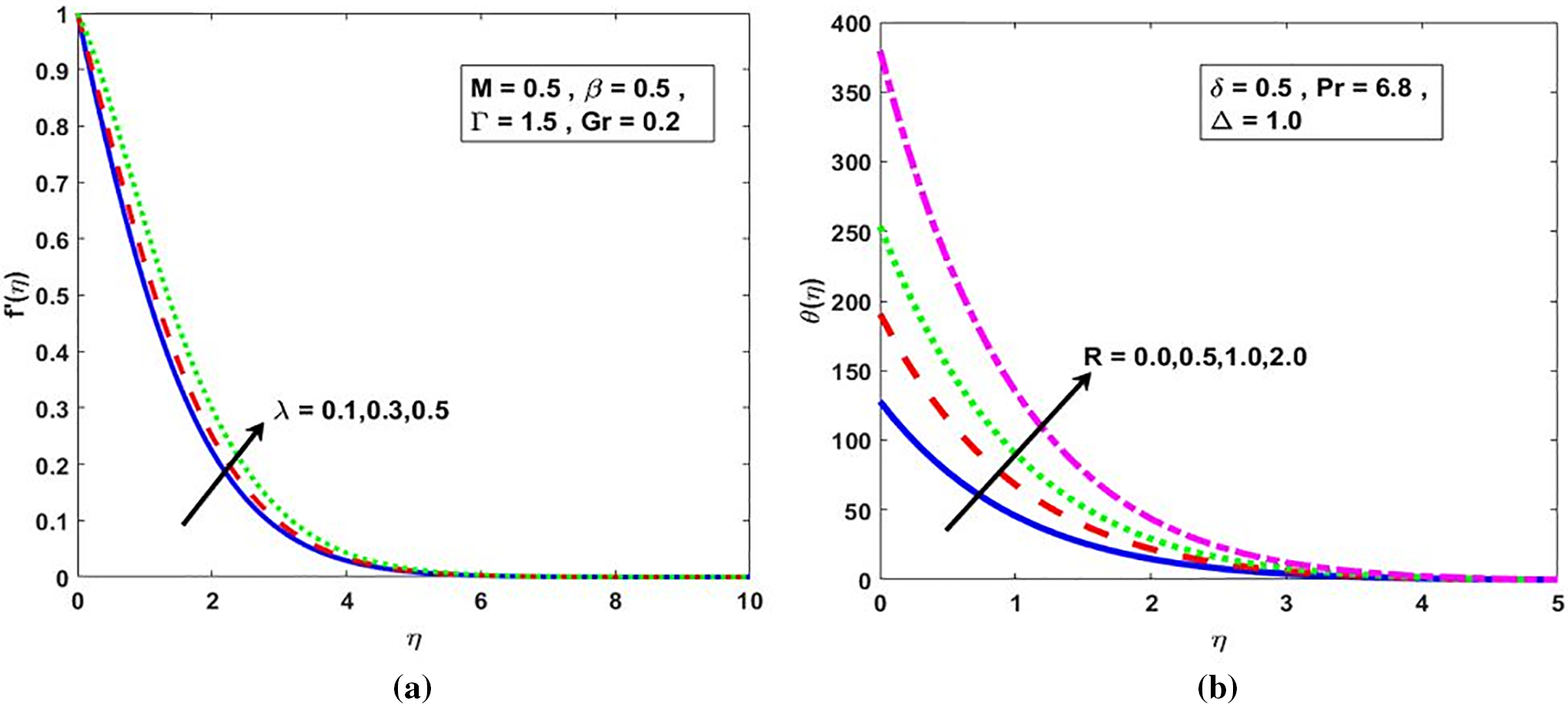
Figure 5: (a) f′(η) for assorted λ (b) θ(η) for assorted R

Fig. 6a illustrates a negative correlation between the magnetic number and the fluid’s velocity profile. Physically, a higher magnetic field strength produces a Lorentz force that exerts a drag on the fluid, thereby reducing its velocity. This effect is of significant importance in MHD applications, such as plasma flows and electromagnetic casting, where controlling fluid velocity through magnetic fields is essential for process improvement. Further, Fig. 6b demonstrates a positive correlation between the Grashof number Gr and the fluid’s velocity profile. The Grashof number’s physical significance lies in its direct relationship with buoyancy effects caused by thermal expansion in fluids. Higher values amplify natural convection currents by strengthening the upward thrust generated from temperature variations. This enhanced buoyant force becomes particularly influential in systems where free convection dominates, as steeper thermal gradients produce more vigorous fluid circulation and faster flow development. Further, the studies by Reddy and Kumar [30] and Suhasini et al. [31] support the idea that magnetic fields are essential for influencing fluid flow. Their research highlights the significant role magnetic fields play in controlling fluid motion and improving heat transfer.

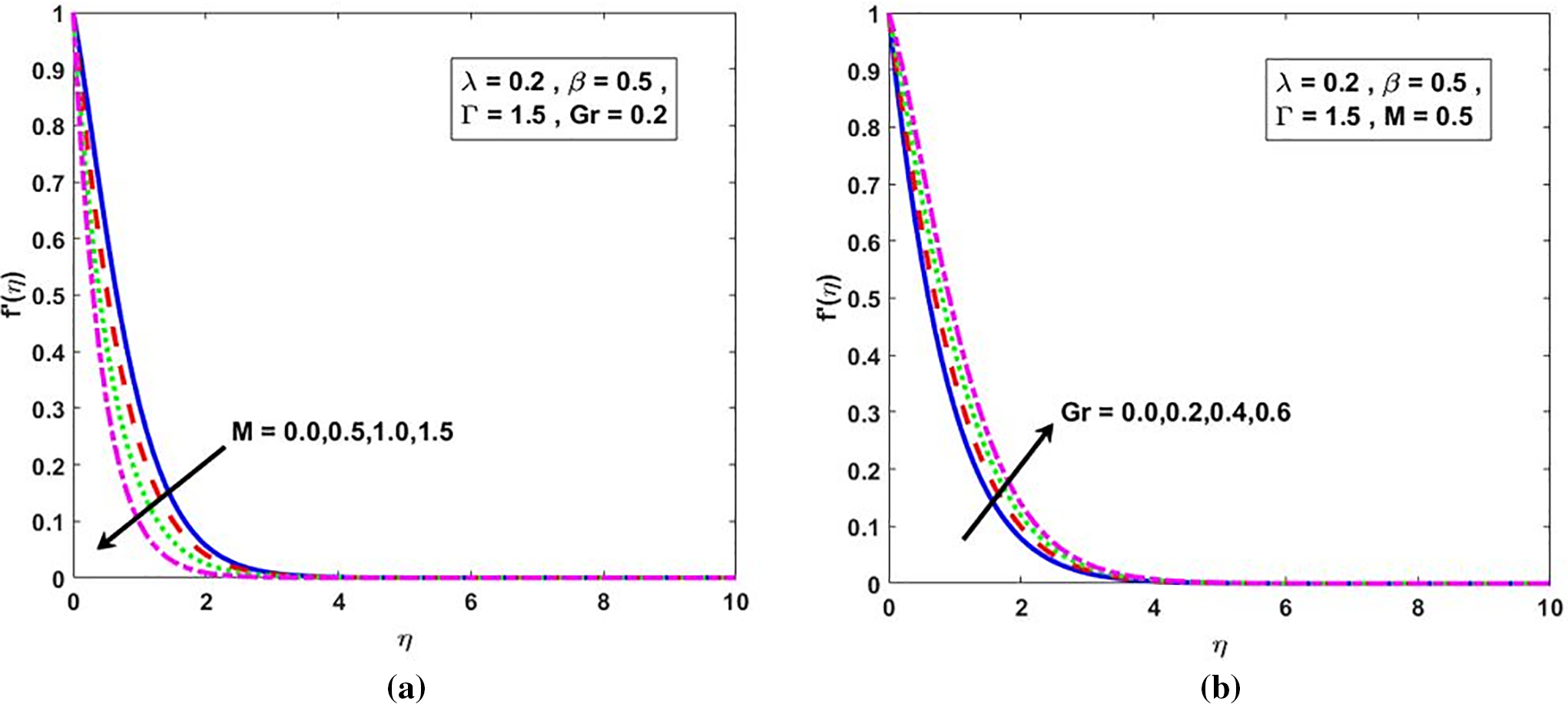
Figure 6: (a) f′(η) for assorted M (b) f′(η) for assorted Gr

It is crucial to complement this physical and applied study with an analysis of both the skin friction coefficient Cfx(Rex)12 and the heat transfer rate Nux(Rex)−12, as well as their response to the governing parameters. Therefore, the following Table 2 has been created for a comprehensive evaluation. Analysis of the data reveals a positive correlation between the magnetic field, couple stress, porous parameters, and both the rate of heat transfer and the coefficient of surface friction. Conversely, the mixed convection parameter appears to have a contrasting effect, increasing heat transfer while simultaneously decreasing the surface friction coefficient. Finally, the numerical results indicate a clear positive correlation between the thermal radiation parameter, Grashof number, heat generation parameter, and the heat transfer coefficient. Increases in each of these parameters correspond to increases in the heat transfer coefficient.

6  Main Remarks

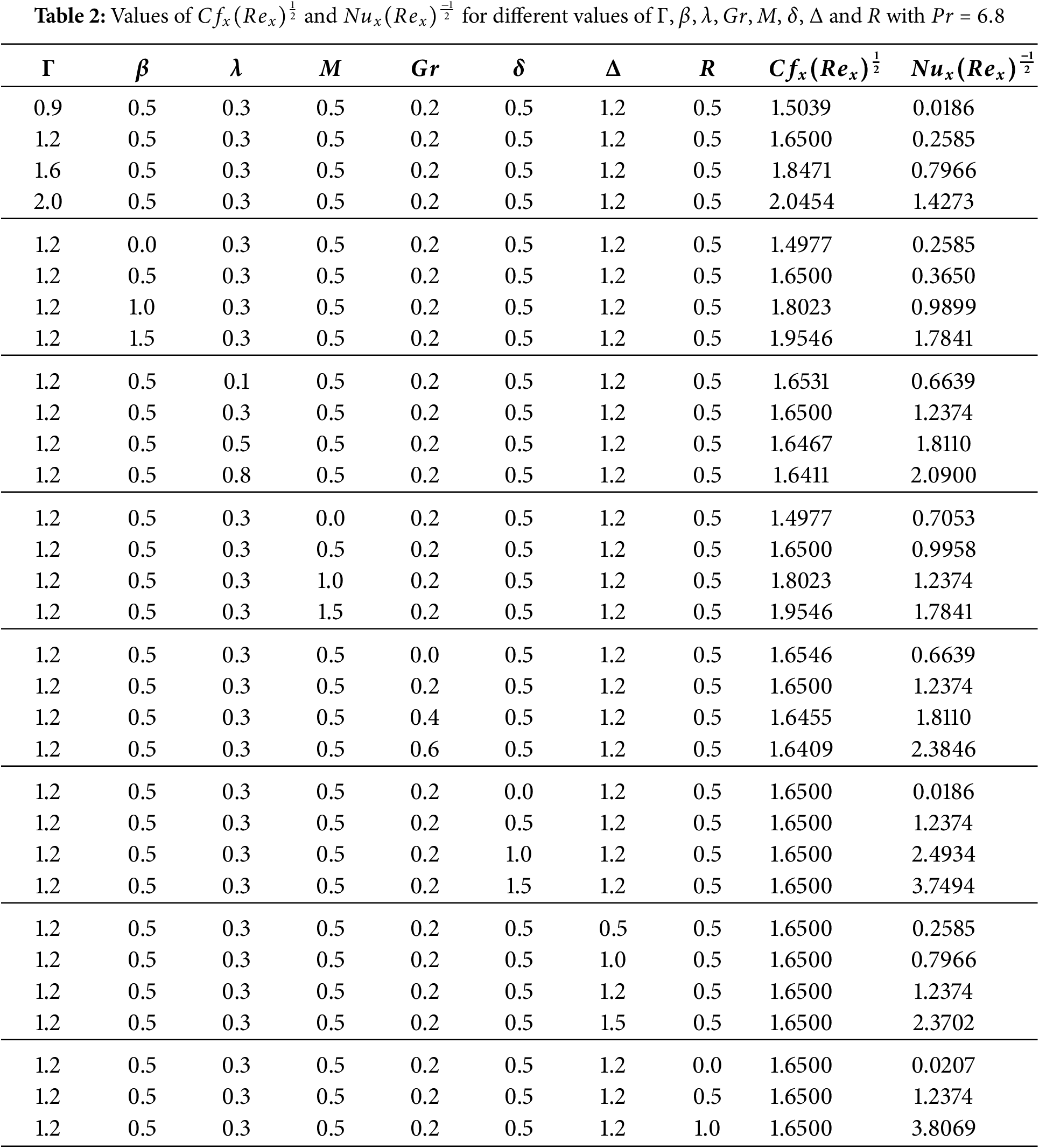
This research investigates the flow and heat transfer features for a non-Newtonian couple stress fluid past a vertical stretched impermeable sheet within a Darcy porous medium, considering magnetic field, heat generation and thermal radiation. Using dimensionless transformations and the HPM, the governing equations of the model are converted to a highly nonlinear ordinary differential equations, then the approximate analytical solution for this system obtained, respectively. In summary, the findings indicate the following:

Results show the mixed convection parameter increases velocity, while the magnetic field parameter decreases it. The effects of porosity, couple stress, and thermal radiation on velocity and temperature are also analyzed, offering practical industrial insights.

1.   Increasing both the couple stress parameter and the mixed convection factor results in a higher fluid flow velocity and a thicker boundary layer.

2.   Enhancing temperature ratio parameter or radiation factor or heat source parameter leads to heating the fluid and thickening the thermal boundary layer.

3.   A stronger magnetic field strength or greater porous medium factor results in decreasing both the fluid flow velocity and the boundary layer thickness.

4.   Increased values in the magnetic field, couple stress, and porous parameters are associated with higher heat transfer rates and surface friction coefficients.

5.   The heat transfer coefficient is positively impacted by the thermal radiation, Grashof, and heat generation parameters.

6.   The future scope of this study could be applied to more complex scenarios, such as unsteady flows, nanofluid dynamics, and models that account for variable properties.

Acknowledgement: Sara I. Abdelsalam expresses her deep gratitude to Fundación Mujeres Por África for supporting this work through the fellowship awarded to her.

Funding Statement: Not applicable.

Author Contributions: Conceptualization, Ahmed M. Megahed and W. Abbas; Methodology, M. S. Emam and M. Khairy; Formal analysis, M. Khairy and Sara I. Abdelsalam; Investigation, M. S. Emam; Data curation, Sara I. Abdelsalam; Writing—original draft preparation, M. Khairy and Ahmed M. Megahed; Writing—review and editing, Sara I. Abdelsalam and W. Abbas; Visualization, Sara I. Abdelsalam; Supervision, Ahmed M. Megahed and W. Abbas; Validation, M. S. Emam. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No data.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Koh YH, Ong NS, Chen XY, Lam YC, Chai JC. Effect of temperature and inlet velocity on the flow of a nonnewtonian fluid. Int Commun Heat Mass Transf. 2024;31(7):1005–13. doi:10.1016/j.icheatmasstransfer.2004.05.010. [Google Scholar] [CrossRef]

2. Reviol T, Kluck S, Böhle M. A new design method for propeller mixers agitating nonNewtonian fluid flow. Chem Eng Sci. 2018;190(1):320–32. doi:10.1016/j.ces.2018.06.033. [Google Scholar] [CrossRef]

3. Nazir S, Kashif M, Zeeshan A, Alsulami H, Ghamkhar M. A study of heat and mass transfer of non-Newtonian fluid with surface chemical reaction. J Indian Chem Soc. 2022;99(5):100434. doi:10.1016/j.jics.2022.100434. [Google Scholar] [CrossRef]

4. Muduganti PKR, Podila A, Nalimela P, Garvandha M, Josyula VRM. Steady flow of couple stress fluid through a rectangular channel under transverse magnetic field with suction. Part Differ Equat Appl Mathem. 2024;12(5):100956. doi:10.1016/j.padiff.2024.100956. [Google Scholar] [CrossRef]

5. Devani U, Patil J, Bilal S, Hanumagowda BN, Trimbak VB, Tawade J, et al. Study of MHD on porous flat and curved circular plate lubricated with couple stress fluid—a slip velocity model. Res Eng. 2024;24(8):102914. doi:10.1016/j.rineng.2024.102914. [Google Scholar] [CrossRef]

6. Nadeem S, Hussain ST. Heat transfer analysis of Williamson fluid over exponentially stretching surface. Appl Math Mech. 2014;35(4):489–502. doi:10.1007/s10483-014-1807-6. [Google Scholar] [CrossRef]

7. Megahed AM. Flow and heat transfer of Powell-Eyring fluid due to an exponential stretching sheet with heat flux and variable thermal conductivity. Zeitschrift Für Naturforschung A. 2015;70(3):163–9. doi:10.1515/zna-2014-0310. [Google Scholar] [CrossRef]

8. Humane PP, Patil VS, Patil AB. Chemical reaction and thermal radiation effects on magnetohydrodynamics flow of Casson-Williamson nanofluid over a porous stretching surface. Proc Institut Mech Eng Part E J Process Mech Eng. 2021;235(6):2008–18. doi:10.1177/09544089211025376. [Google Scholar] [CrossRef]

9. Pallavi SP, Veena MB, Tawade JV, Kulkarni N, Khan SU, Waqas M, et al. Effects of exponentially stretching sheet for MHD Williamson nanofluid with chemical reaction and thermal radiative. Part Differen Equat Appl Mathem. 2024;12(4):100975. doi:10.1016/j.padiff.2024.100975. [Google Scholar] [CrossRef]

10. Madan Kumar R, Srinivasa Raju R, Mebarek-Oudina F, Anil Kumar M, Narla VK. Cross-diffusion effects on an MHD Williamson nanofluid flow past a nonlinear stretching sheet immersed in a permeable medium. Front Heat Mass Transfer. 2024;22(1):15–34. doi:10.32604/fhmt.2024.048045. [Google Scholar] [CrossRef]

11. Thenmozhi D, Eswara Rao M, Nagalakshmi C, Devi RR, Selvi P. Lie similarity analysis of MHD Casson fluid flow with heat source and variable viscosity over a porous stretching sheet. Int J Thermoflu. 2024;23(6):100804. doi:10.1016/j.ijft.2024.100804. [Google Scholar] [CrossRef]

12. Khan ZH, Swain K, Ibrahim SM, Khan WA, Huang Z. Transient flow and heat transfer characteristics of single-phase nanofluid past a stretching sheet under the influence of thermal radiation and heat source. Alex Eng J. 2024;108(3):122–34. doi:10.1016/j.aej.2024.07.071. [Google Scholar] [CrossRef]

13. Sohail M, Ali MH, Abodayeh K, Abbas ST. Bio-convective boundary layer flow of Maxwell nanofluid via optimal homotopic procedure with radiation and Darcy-Forchheimer impacts over a stretched sheet. Int J Ambient Energy. 2025;46(1):2462583. doi:10.1080/01430750.2025.2462583. [Google Scholar] [CrossRef]

14. Raju CSK, Sandeep N, Malvandi A. Free convective heat transfer of MHD Cu-kerosene nanofluid over a cone with temperature dependent viscosity. Acta Astronaut. 2016;129(2):419–28. doi:10.1016/j.actaastro.2016.10.011. [Google Scholar] [CrossRef]

15. Bég OA, Zaman A, Ali N, Gaffar SA, Bég ET. Numerical computation of nonlinear oscillatory two-immiscible magnetohydrodynamic flow in dual porous media system: FTCS and FEM study. Heat Transf Asian Res. 2019;48(4):1245–63. doi:10.1002/htj.21429. [Google Scholar] [CrossRef]

16. Wang F, Jamshed W, Usman, Ibrahim RW, Abdalla NSE, Abd-Elmonem A, et al. Solar radiative and chemical reactive influences on electromagnetic Maxwell nanofluid flow in Buongiorno model. J Magn Magn Mater. 2023;576(4):170748. doi:10.1016/j.jmmm.2023.170748. [Google Scholar] [CrossRef]

17. Alomari MA, Al-Salami QH, Alyousuf FQ, Alqurashi F, Flayyih MA. Numerical analysis of magnetohydrodynamic mixed convection and entropy generation in a curvelinear lid-driven cavity with carbon nanotubes and an adiabatic cylinder. Int J Thermof. 2024;24(11):100852. doi:10.1016/j.ijft.2024.100852. [Google Scholar] [CrossRef]

18. Adel M, Khader MM, Abbas W. Nanofluid dissipative Reiner-Philippoff model with thermal radiation: numerical investigation using the modified Adomian decomposition method associated with Mohand transforms. Phys Scr. 2024;99(12):125287. doi:10.1088/1402-4896/ad92af. [Google Scholar] [CrossRef]

19. Asokakumar Sreekala V, Sengupta B. Characterizing nonlinear flow dynamics in hydrodynamic and magnetohydrodynamic regimes through modal decomposition. European J Mech-B/Fluids. 2025;109(7–9):37–54. doi:10.1016/j.euromechflu.2024.08.008. [Google Scholar] [CrossRef]

20. He JH. Homotopy perturbation technique. Comput Meth Appl Mech Eng. 1999;178:257–62. [Google Scholar]

21. He JH, Wu XH. Variational iteration method: new development and applications. Comput Mathem Applicat. 2007;54(7–8):881–94. doi:10.1016/j.camwa.2006.12.083. [Google Scholar] [CrossRef]

22. Ghotbi AR. Homotopy analysis method for solving the MHD flow over a non-linear stretching sheet. Commun Nonlinear Sci Numer Simul. 2009;14(6):2653–63. doi:10.1016/j.cnsns.2008.08.006. [Google Scholar] [CrossRef]

23. Raftari B, Yildirim A. The application of homotopy perturbation method for MHD flows of UCM fluids above porous stretching sheets. Comput Math Appl. 2010;59(10):3328–37. doi:10.1016/j.camwa.2010.03.018. [Google Scholar] [CrossRef]

24. Jhankal AK. Homotopy perturbation method for MHD boundary layer flow with low pressure gradient over a flat plate. J Appl Fluid Mech. 2014;7(01):177–85. doi:10.36884/jafm.7.01.19577. [Google Scholar] [CrossRef]

25. Ali N, Khan SU, Sajid M, Abbas Z. MHD flow and heat transfer of couple stress fluid over an oscillatory stretching sheet with heat source/sink in porous medium. Alex Eng J. 2016;55(2):915–24. doi:10.1016/j.aej.2016.02.018. [Google Scholar] [CrossRef]

26. Abbas W, Magdy MM. Heat and mass transfer analysis of nanofluid flow based on, and over a moving rotating plate and impact of various nanoparticle shapes. Math Probl Eng. 2020;2020:9606382. doi:10.1155/2020/9606382. [Google Scholar] [CrossRef]

27. Mostapha DR, El-dabe Nabil TM, Abbas W. Entropy generation and impacts of activation energy with electroosmosis of couple stresses on the peristaltic transport of bingham blood nanofluid. J Nonlinear Math Phys. 2023;31(1):1–24. doi:10.1007/s44198-024-00251-8. [Google Scholar] [CrossRef]

28. Hayat T, Mustafa M, Pop I. Heat and mass transfer for Soret and Dufour’s effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Commun Nonlinear Sci Numer Simul. 2010;15(5):1183–96. doi:10.1016/j.cnsns.2009.05.062. [Google Scholar] [CrossRef]

29. Turkyilmazoglu M. The analytical solution of mixed convection heat transfer and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface. Int J Mech Sci. 2013;77:263–8. doi:10.1016/j.ijmecsci.2013.10.011. [Google Scholar] [CrossRef]

30. Reddy MS, Kumar MA. Influence of magnetic field chemical reaction and Soret-Dufour parameters on Maxwell nanofluid flow over a porous vertical stretching surface—a numerical study. Case Stud Chem Environ Eng. 2024;10(2024):100958. doi:10.1016/j.cscee.2024.100958. [Google Scholar] [CrossRef]

31. Suhasini R, Srinivasa Raju R, Anil Kumar M, Jithender Reddy G, Rajakumar KVB. A numerical study on magneto-micropolar nanofluid flow across a stretching/shrinking surface: impacts of heat source, viscous dissipation, and chemical reaction. Radiat Eff Def Sol. 2025;565(4):1–23. doi:10.1080/10420150.2025.2526389. [Google Scholar] [CrossRef]