 Open Access
Open Access
ARTICLE
New Ranking of Generalized Quadrilateral Shape Fuzzy Number Using Centroid Technique
Department of Mathematics, Sathyabama Institute of Science and Technology, Chennai, 600119, Tamilnadu, India
* Corresponding Author: A. Thiruppathi. Email:
Intelligent Automation & Soft Computing 2023, 36(2), 2253-2266. https://doi.org/10.32604/iasc.2023.033870
Received 30 June 2022; Accepted 22 September 2022; Issue published 05 January 2023
Abstract
The output of the fuzzy set is reduced by one for the defuzzification procedure. It is employed to provide a comprehensible outcome from a fuzzy inference process. This page provides further information about the defuzzification approach for quadrilateral fuzzy numbers, which may be used to convert them into discrete values. Defuzzification demonstrates how useful fuzzy ranking systems can be. Our major purpose is to develop a new ranking method for generalized quadrilateral fuzzy numbers. The primary objective of the research is to provide a novel approach to the accurate evaluation of various kinds of fuzzy integers. Fuzzy ranking properties are examined. Using the counterexamples of Lee and Chen demonstrates the fallacy of the ranking technique. So, a new approach has been developed for dealing with fuzzy risk analysis, risk management, industrial engineering and optimization, medicine, and artificial intelligence problems: the generalized quadrilateral form fuzzy number utilizing centroid methodology. As you can see, the aforementioned scenarios are all amenable to the solution provided by the generalized quadrilateral shape fuzzy number utilizing centroid methodology. It’s laid out in a straightforward manner that’s easy to grasp for everyone. The rating method is explained in detail, along with numerical examples to illustrate it. Last but not least, stability evaluations clarify why the Generalized quadrilateral shape fuzzy number obtained by the centroid methodology outperforms other ranking methods.Keywords
One definition of a fuzzy number (FN) is a real number whose fuzzy set (FS) is both normal and convex. The FN approach is fantastic since it allows for the combination of subjective and objective information. Ranking fuzzy numbers (RFNs) is necessary for many fuzzy application systems, including those dealing with linguistic decision-making, risk management, Industrial engineering, optimization, medicine, artificial intelligence etc. We shall investigate the ordering of quadrilateral fuzzy number generalizations (GQFNs). For a problem with four points and two levels of representational depth, GQFNs can be used. The ranking of FNs is arguably the most essential part, and there are many different ways to do it using techniques from data analysis, optimization, and other disciplines. In the future, it may be used for problems in decision-making, data analysis, optimization, engineering, and technology. Decisions can be aided by RFN measurements (DMP). Since 1976, many systems for categorizing ranking events have been created. Zadeh [1] is credited with coming up with the concept of an FS. An original FRA method for handling risk uncertainty is described by Lee et al. [2]. Fuzzy integers of varying sizes and variances form the basis of the process. Fuzzy numbers are crucial to conveying uncertain values. In this research, we propose many mathematical operations on generalized quadrilateral fuzzy numbers (GQFNs) using the defuzzification technique. Additionally, several features of the defuzzification method are presented, along with relevant numerical examples to back up the features. In the beginning, Jain [3] predicted the positions of FNs for the DMP. Dubois et al. [4]. This article employs a fuzzification approach to allow conventional algebraic operations to be applied to fuzzy numbers. The work of Mizumoto et al. [5,6]. When it comes to the difficulty of making decisions, several approaches have been developed, such as the Pythagorean fuzzy Dombi aggregation operators, the Extended TOPSIS technique, and the Intuitionistic Fuzzy Rough Frank Aggregation Operator-Based EDAS Method.
By comparing the rankings obtained by using the FRA problem with the positive, negative, and centroid of the generalized numbers, Ming Chen et al. [7] suggested a hypothesis. Using the counter example of Lee and Chen, Singh [8] advocated a new way of RFN based on the expectation of centroid predictions of varying heights and demonstrated that the sorting method is erroneous. In [9], Pathinathan et al. organized a pentagonal QFN using mathematical computation. Using the mathematical function CEFM, Stephen Dinagar et al. [10] presented a GQF transportation problem. In their essay “defuzzification of QFN and arithmetic operation of CEFM,” authors Dinagar et al. examined the characteristics of CEFM. There is a GQF optimum solution to Assignment issues, and it was proposed by Stephen Dinagar et al. [11]. The GQF economic inventory model, which takes into account backorders, was created by Stephen Dinagar et al. [12,13]. Fuzzy Assignment Tricky makes use of a technique proposed by Thiruppathi et al. [14,15] called Ranking of Hexagonal Fuzzy Using Centroids. Using the center of gravity, Barazandeh et al. [16] calculated the score of a generalized fuzzy trapezoidal number (GFTN) with a range of left and right heights. A better system of rankings was created by Jiang et al. [17]. The strengths and disadvantages of current fuzzy ranking systems are investigated, and the elements of FN regions, including the upsides and downsides, and the spreads, are discussed. Hajjari [18] offered a fresh magnitude method for sorting trapezoidal fuzzy numbers (TFNs) using lowest and maximum points and the value of FNs, and he compared and approved the benefits of the supplied strategy comparison. In this study, Rezvani [19] presented a method for using Euclidean distance and central centroids. Results from the proposed method are checked against those of other popular approaches to ensure they are reliable. Yu Vincent et al. [20] proposes a novel method of rating FNs that displays their updated left, right and total integral values. After that, we utilize the median value ranking approach to identify FNs that have area compensation. This article by Ming wang et al. [21] discusses an optional ranking method for FNs based on positive and negative ideal foci, and calls it “area ranking.” Predicting the efficacy and modesty of non-preemptive priority fuzzy queues necessitates the use of performance measurements, and Vinnarasi et al. presented the Bell-shaped fuzzy number using the centroid of centroids method [22]. To rate items, only a select few authors have turned to generalized quadrilateral fuzzy numbers. The suggested technique, however, is unique among existing methods and provides a straightforward identification ranking strategy for fuzzy numbers in a quadrilateral form.
The work is coordinated as follows Section 3 provides a fundamental depiction of a GQFN. The method proposed for ordering the integers that can be found in any generalized quadrilateral is discussed in Section 4. (RGQNs). Equivalent Properties in the Classical Period It has been proven that fuzzy arithmetic operations do exist. The sixth section provides an overview of one of the problems with Lee and Chen’s RA has been highlighted. In Section 7, we see the implementation of mathematical operations on GQFNs. The Algorithm for Comparing Two Fuzzy Quantities is discussed in Section 8. Existing approaches are compared to the new GQSFN-CT methods in Section 9. This is the tenth section. This section offers guidance on how to use RA to the FRA problem. The final section summarises the entire paper.
Note: Throughout the paper the following abbreviations are used

Let
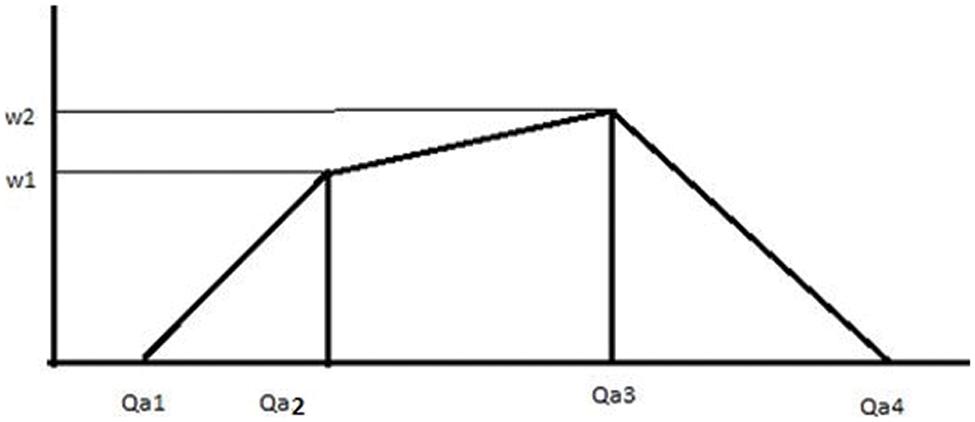
Figure 1: Generalizations of quadrilateral fuzzy number
A FN that is GQFNs is defined as
When
A technique suggested for ranking generalized fuzzy number (RGFN) of quadrilateral form. (
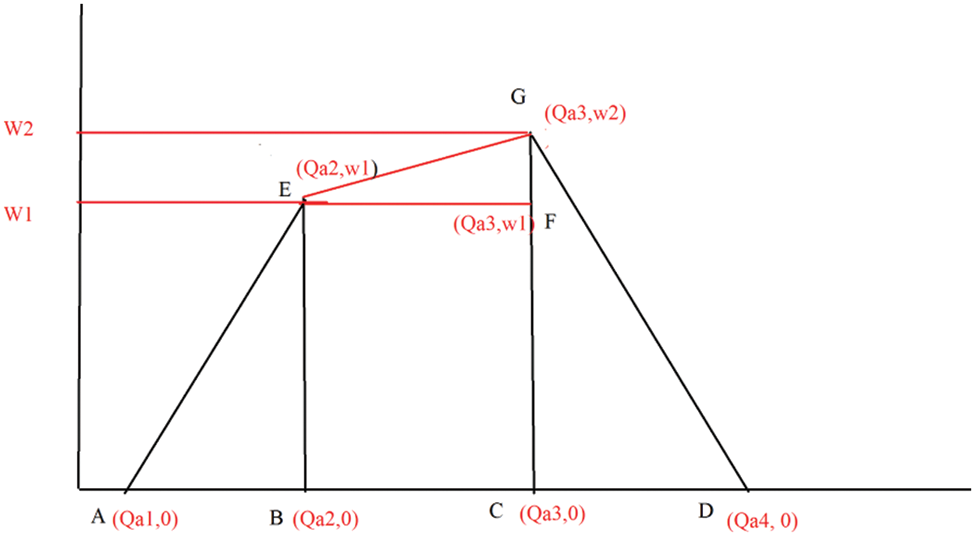
Figure 2: Diagram for Ranking GQFN
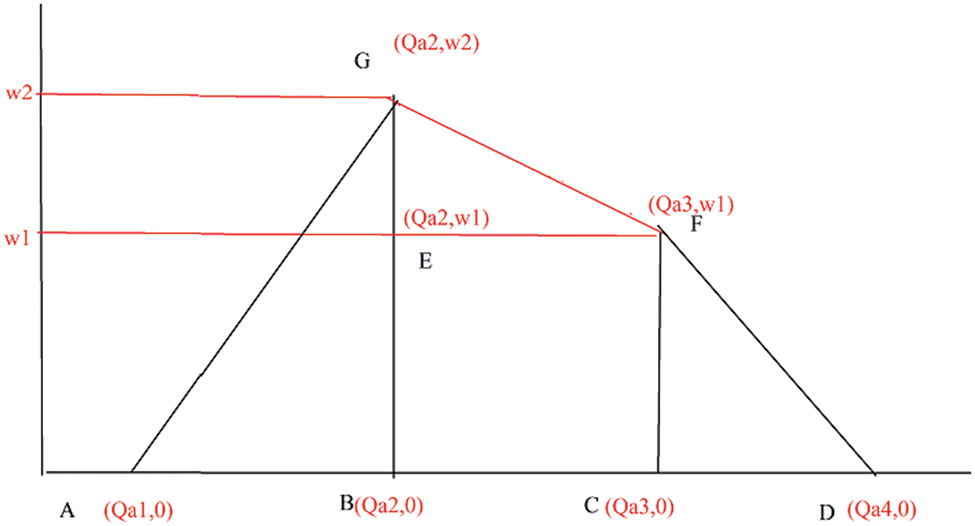
Figure 3: Diagram for Ranking GQFN
The centroid point triangle ABE, Triangle CDG and triangle EFG respectively,
Subsequently, connect the points
The GQFN ranking function
GQFN
Ranking approach method
A technique suggested for RGFN of quadrilateral form.
Three fig were created by vertically dividing the GQFN. Draw the horizontal line parallel to
The centroid point triangle ABE, Triangle CDG and triangle EFG respectively
Subsequently, connect the points
The GQFN ranking function
GQFN
5 Properties of Classical Equivalent Fuzzy Arithmetic Operation; [10–12]
Property: 5.1
Let
Property: 5.2
Let
Proof:
Property: 5.3
Let
Similar to the above proof
6 A Shortcoming of Lee and Chen’s Ra
Wang and Keere proposed the following acceptable conditions for ranking function validation.
where
Example 1. [12] Let
Example 2. [12] Let
Our new RA has been implemented. Mathematical operations on GQFNS have been proposed as follows [9–11].
Example-1
Based on Classical equivalent Fuzzy mean mathematical operations on GQFNS.
Addition
Example-2
Based on Classical equivalent Fuzzy mean mathematical operations on GQFNS.
Addition
Example-3
Based on Classical equivalent Fuzzy mean mathematical operations on GQFNS.
Subtraction
Example-4
Using arithmetic operation on GQFNS based on CEFM
Subtraction
Example-5
Based on Classical equivalent Fuzzy mean mathematical operations on GQFNS.
Multiplication if
Example-6
Based on Classical equivalent Fuzzy mean mathematical operations on GQFNS.
Multiplication if
8 Algorithm for Comparing Two Fuzzy Quantities
Step 1: when heights
Step 2: when heights
Step 3: when heights
Step 4: when heights
Compare
If,
If,
If,
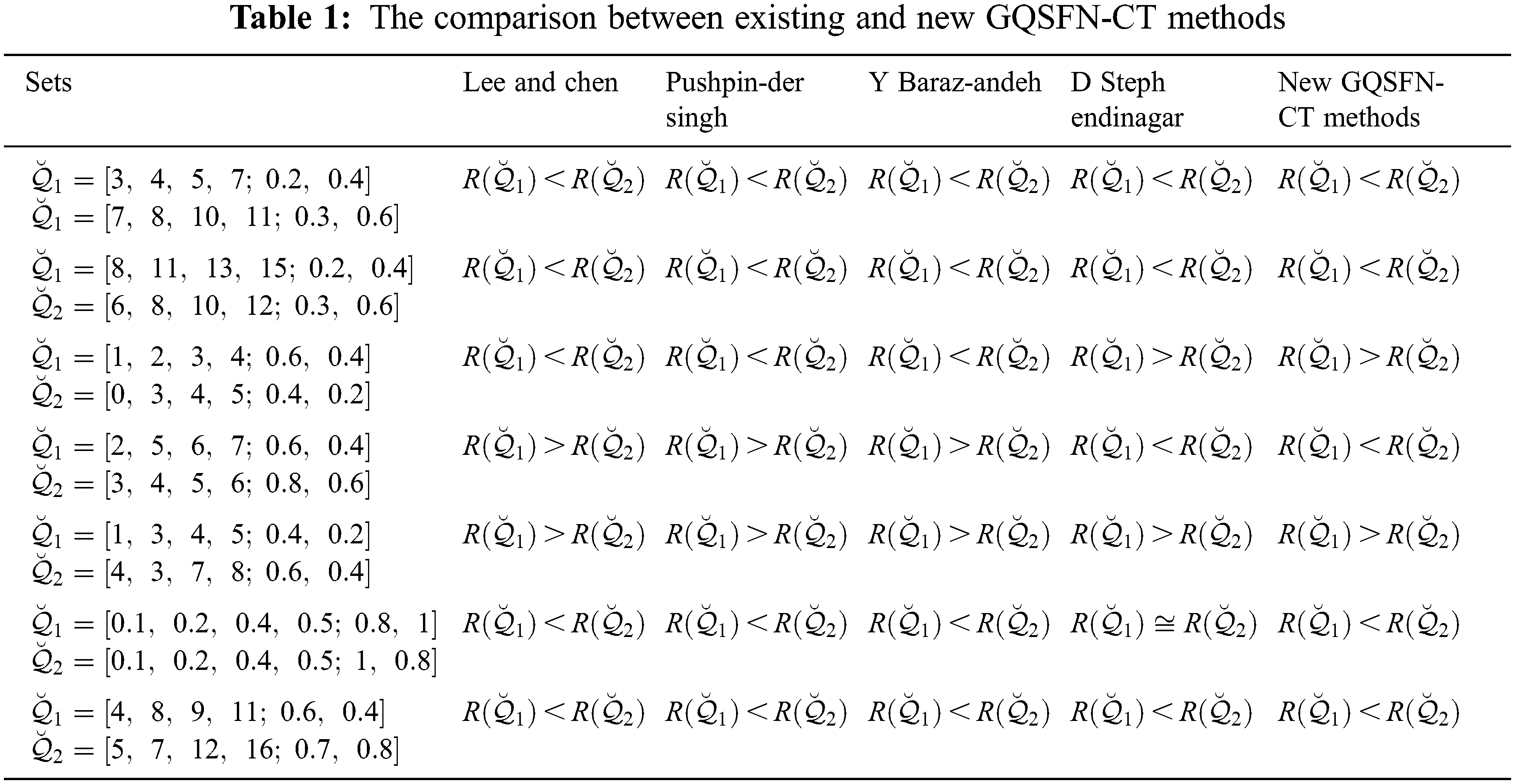
Table 1 specifies, the comparison between the proposed methods and existing benchmark methods tested by various researchers in different times.
In this section, we will appertain the suggested ranking technique to FRA. Let’s assume that there are three manufactories
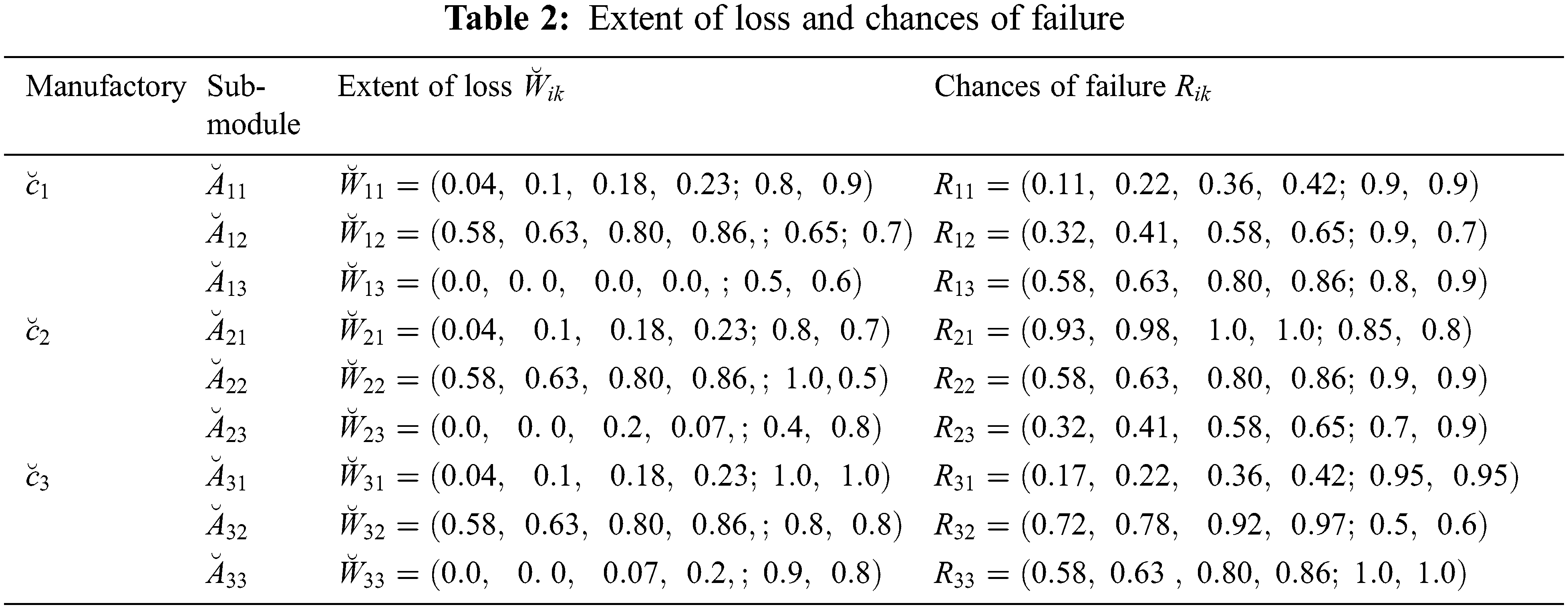
In the final stage, we concentrate our efforts on solving that case using our new ranking GQSFN-CT methods. Now, the probability of failure of each Sub-module
Using Y. Barazandeh and B. Ghazanfari
Rank (
Using Shyi-Ming Chen,
Rank (
D. Stephen Dinagar
Rank (
Our new methods
Rank (
Therefore
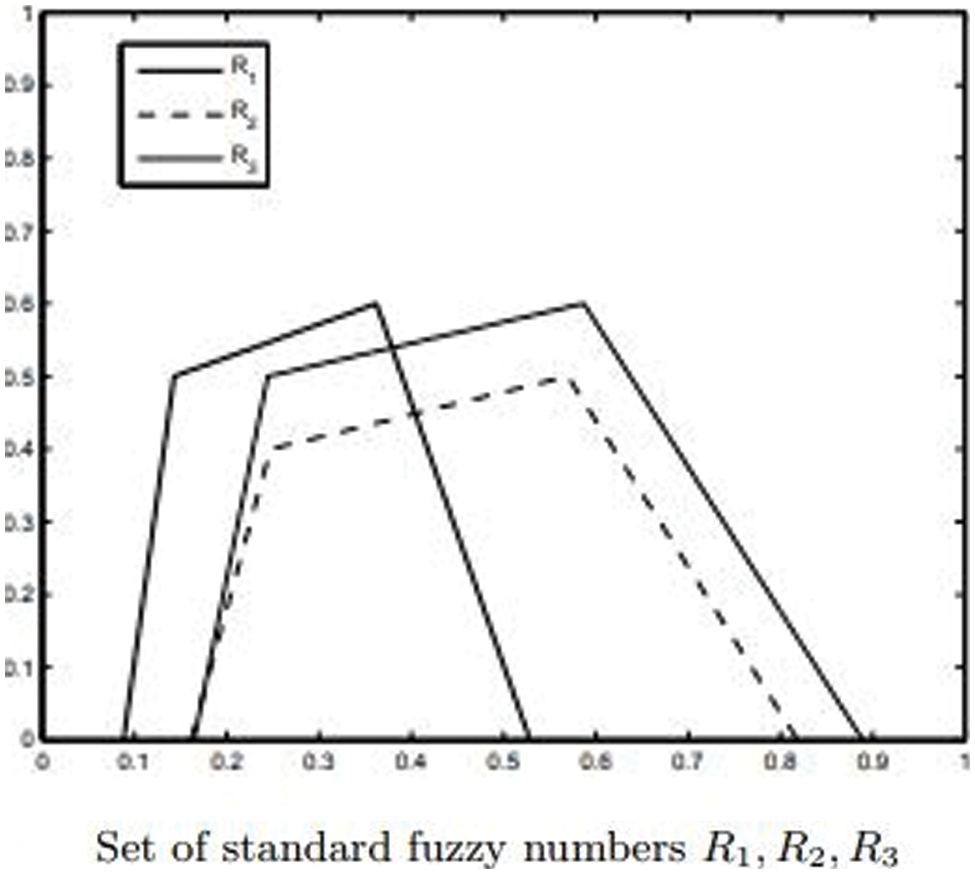
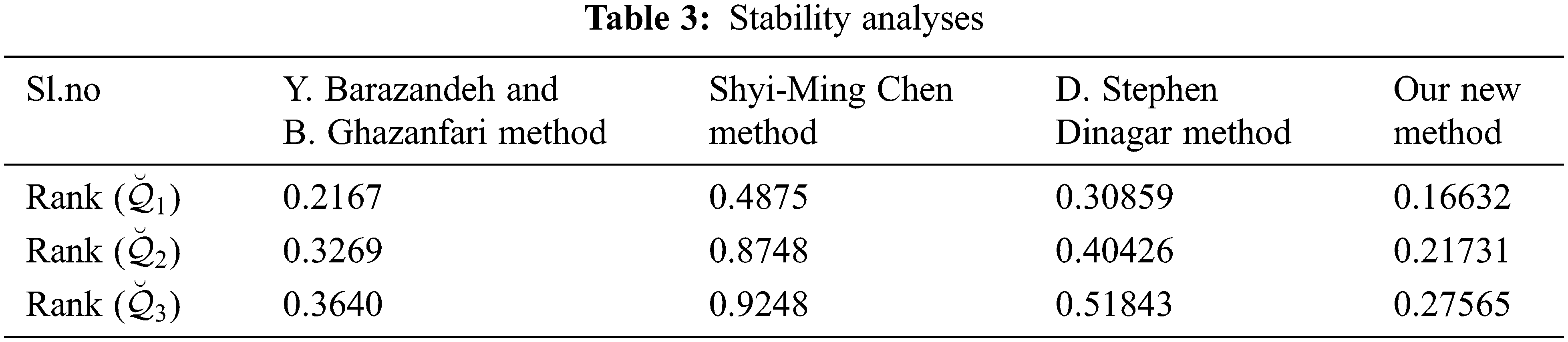
From the above Table 3 shows the effective ranking technique using our new ranking methods compared to others previous existing methods this method reduce the failure time more with other methods.
We’ve provided a simple technique for ranking generalized quadrilateral shape fuzzy numbers (QFN) by directly transforming them into a suggested crisp quantity. Finally, we compared the performance of our technique to that of other methods designed to achieve similar ends and offered numerical examples to back up our claims. Our innovative GQSFN-CT technique has the lowest coefficient of variance compared to other approaches. Our primary fields of focus were industrial engineering, optimization, medicine, and AI, all of which made extensive use of positive fuzzy numbers. The outcomes of the recommended procedure are verified by comparing them to those of other prevalent approaches. The GQSFN-CT methods we propose here have the potential to forecast correct numbers and might prove valuable to researchers in the future across a wide range of disciplines. This strategy makes use of a modality index that evaluates how important the central value is in comparison to the two extremes and the optimistic decision maker. In addition to producing excellent outcomes for issues with clear parameters, this technique also gives a superior answer for problem ranking. We hope that our GQSFN-CT approach will provide a more realistic way to evaluate GQSFN-CT and its potential future uses in the near future. This technique may also be applied to fuzzy numbers in the spherical shape, such as sine trigonometric spherical form fuzzy numbers.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 2, pp. 338–353, 1965. [Google Scholar]
2. W. E. Lee and S. M. Chen, “Fuzzy risk analysis based on fuzzy number with different shapes and different deviation,” Expert System with Application, vol. 34, no. 2, pp. 2763–2771, 2008. [Google Scholar]
3. R. Jain, “Decision making in the presence of fuzzy variables,” IEEE Transactions on Systems, vol. 6, no. 10, pp. 698–703, 1976. [Google Scholar]
4. D. Dubois and H. Prade, “Operations on fuzzy numbers,” International Journal of Systems Science, vol. 9, no. 6, pp. 613–626, 1978. [Google Scholar]
5. M. Mizumoto and K. Tanaka, “The four operations of arithmetic on fuzzy numbers,” Systems Computer and Controls, vol. 7, no. 5, pp. 73–81, 1977. [Google Scholar]
6. M. Mizumoto and K. Tanaka, “Some properties of fuzzy numbers,” Advances in Fuzzy Set Theory and Applications, vol. 2, no. 3, pp. 156–164, 1979. [Google Scholar]
7. S. Ming Chen, A. Munif, G. Chen, H. Chuan Liu and B. Chen Kuo, “Fuzzy risk analysis based on ranking generalized fuzzy numbers with different left heights and right heights,” Expert Systems with Applications, vol. 39, no. 7, pp. 6320–6334, 2012. [Google Scholar]
8. P. Singh, “A new approach for the ranking of fuzzy sets with different heights,” Journal of Applied Research and Technology, vol. 10, no. 2, pp. 1665–6423, 2012. [Google Scholar]
9. T. Pathinathan and S. Santhoshkumar, “Quadrilateral fuzzy number,” International Journal of Engineering and Technology, vol. 7, no. 10, pp. 1018–1021, 2018. [Google Scholar]
10. D. Stephen Dinagar and B. Christopar Raj, “A method for solving fully fuzzy transportation problem with GQFNs,” Malaya Journal of Matematik, vol. 12, no. 1, pp. 24–27, 2019. [Google Scholar]
11. D. Stephen Dinagar and B. Christopar Raj, “A distinct method for solving fuzzy assignment problem with GQFNs,” International Conference on Mathematical Analysis and Computing, vol. 8, no. 2, pp. 221–229, 2021. [Google Scholar]
12. D. Stephen Dinagar and M. Manvizhi, “Fully fuzzy economic inventory model with backorders using GQFNs,” Advances and Applications in Mathematical Sciences, vol. 19, no. 11, pp. 1143–1158, 2020. [Google Scholar]
13. D. Stephen Dinagar and M. Manvizhi, “A study on GQFNs,” Malaya Journal of Matematik, vol. 1, no. 5, pp. 295–298, 2020. [Google Scholar]
14. A. Thiruppathi and C. K. Kirubhashankar, “Novel fuzzy assignment problem using hexagonal fuzzy numbers,” Journal of Physics, vol. 4, no. 5, pp. 23–34, 2021. [Google Scholar]
15. A. Thiruppathi and C. K. Kirubhashankar, “New ranking of generalized hexagonal fuzzy number using centroids of centroided method,” Advances in Mathematics: Scientific Journal, vol. 9, no. 8, pp. 6229–6240, 2020. [Google Scholar]
16. Y. Barazandeh and B. Ghazanfari, “A novel method for ranking generalized fuzzy numbers with two different heights and its application in fuzzy risk analysis,” Iranian Journal of Fuzzy Systems, vol. 18, no. 2, pp. 81–91, 2021. [Google Scholar]
17. W. Jiang, Y. Luo, X. Yun Qin and J. Zhan, “An improved method to rank generalized fuzzy numbers with different left heights and right heights,” Journal of Intelligent & Fuzzy Systems, vol. 28, no. 5, pp. 2343–2355, 2015. [Google Scholar]
18. T. Hajjari, “Fuzzy risk analysis based on ranking of fuzzy numbers via new magnitude method,” Iranian Journal of Fuzzy Systems, vol. 12, no. 3, pp. 17–29, 2015. [Google Scholar]
19. S. Rezvani, “Ranking generalized fuzzy numbers with Euclidian distance by the incentre of centroid,” Mathematica Aeterna, vol. 3, no. 2, pp. 103–114, 2013. [Google Scholar]
20. F. Yu Vincent and L. Quoc, “An improved ranking method for fuzzy numbers with integral values,” Applied. Soft Computing, vol. 14, no. 2, pp. 603–608, 2014. [Google Scholar]
21. Y. Ming Wang and Y. Luo, “Area ranking of fuzzy numbers based on positive and negative ideal points,” Computers & Mathematics with Applications, vol. 58, no. 9, pp. 1769–1779, 2009. [Google Scholar]
22. S. J. Vinnarasi and W. Ritha, “Bell shaped fuzzy number with centroid of centroids method,” Journal of Information and Computational Science, vol. 9, no. 9, pp. 279–289, 2019. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools