Sequence-Based Predicting Bacterial Essential ncRNAs Algorithm by Machine Learning

1  Introduction

Bacterial non-coding RNA (ncRNA) is a newly discovered gene expression regulator in bacterial genome in recent years [1]. The molecular size of ncRNA is 40–500 nucleotides. It plays an important role in RNA transcription regulation, chromosome replication, RNA processing and modification, mRNA translation and stability, protein degradation and transport, bacterial infection and other biological processes [2]. With the rapid increase in the number of bacterial ncRNAs discovered and their important role in organisms, bacterial ncRNAs have become one of the hot spots in microbial research. Since ncRNAs play important roles in organisms, the identification of new ncRNAs is of great scientific significance and commercial value [3].

Some ncRNAs are indispensable for the survival of organisms. Thus, they are called “essential non-coding RNA” (essential ncRNA) [4]. Although essential ncRNAs cannot encode proteins, they are as important as essential coding genes in biology. For example, bacterial essential ncRNAs play vital role ranging from structural regulation to catalysis, affecting a variety of processes, such as bacterial toxicity, development control, mRNA stability and protein degradation. Therefore, these groups of ncRNA could be used as a potential target for drug development [5]. Furthermore, significant number of theoretical researches revealed that essential ncRNAs are helpful to understand and determine the composition and lifestyle of minimum genome. For example, Gil and Christen et al. explored that a complete minimum genome should include regulatory and structural elements in addition to encoding proteins, such as 5′-UTRs and ncRNA [6,7]. Similarly, Maria et al., reported a minimal cell containing essential ncRNA [8]. In our previous work, we also constructed a minimum bacterial gene set, which also contain the minimum non-coding RNA set besides the minimum coding gene sets [9].

With the development of high-throughput sequencing and genome-scale inactivation technologies, it has been possible to identify the essential ncRNAs contained in the genome. At present, the determination of essential ncRNAs mainly relies on experimental methods. However, these traditional methods are time-consuming, laborious and costly. In addition, traditional experimental methods are limited by the organisms, as less than 1% of bacteria can be cultured in the laboratory. In this context, it is urgent to establish effective new algorithms for theoretical analysis, and to mine the information and knowledge of essential ncRNA [10]. Pattern recognition and informatics theory play an extremely important role in biological data analysis, especially in sequence recognition research. With the development of machine learning and artificial intelligence [11,12], more and more research groups are applying machine learning to the prediction of essential genes and essential ncRNAs [13]. Zhang integrated features derived from sequence data and protein-protein interaction network and developed a machine learn method called DeepHE to predict human essential genes [14]. In terms of recognition of essential genes of bacteria, we have developed general recognition software Geptop for genome-wide recognition of essential genes, with recognition accuracy is the best so far [15]. The intrinsic features of sequences are the easiest to access for constructing a predicting essential model [16]. Using the intrinsic features of sequences, the accuracy of the identification of essential genes could be significantly increased. Machine learning is an effective predictive method [17], which has been used in classification of medical field and image processing [11,17–23]. At present, there are few researches on the theoretical recognition of “essential ncRNA”. Therefore, it is important and necessary to develop theories and methods for the recognition of essential non-coding RNA.

At present, the number of species required for the determination of essential ncRNAs in the whole genome scale is still very few. The essential ncRNAs have important scientific significance and application in biomedical research. Facing the urgent need to obtain essential ncRNAs, we have conducted in-depth research on the theoretical identification of bacterial essential ncRNAs. The purpose of this study was to design a universal model, which is less dependent on training sets, and to develop a computer based automatic method for identification of essential ncRNA of bacteria with high accuracy and universality. The findings of the study can be utilized to extend the existing drug target library, greatly accelerate the process of new drug research and shorten the research cycle, reduce costs, promote the development of new rapid detection of pathogenic bacteria system. The findings can also assist development of new pathogenic bacteria prevention and treatment methods, and the minimal genome chassis in synthetic biology research.

2  Materials and Methods

2.1 Training and Dataset Constructed

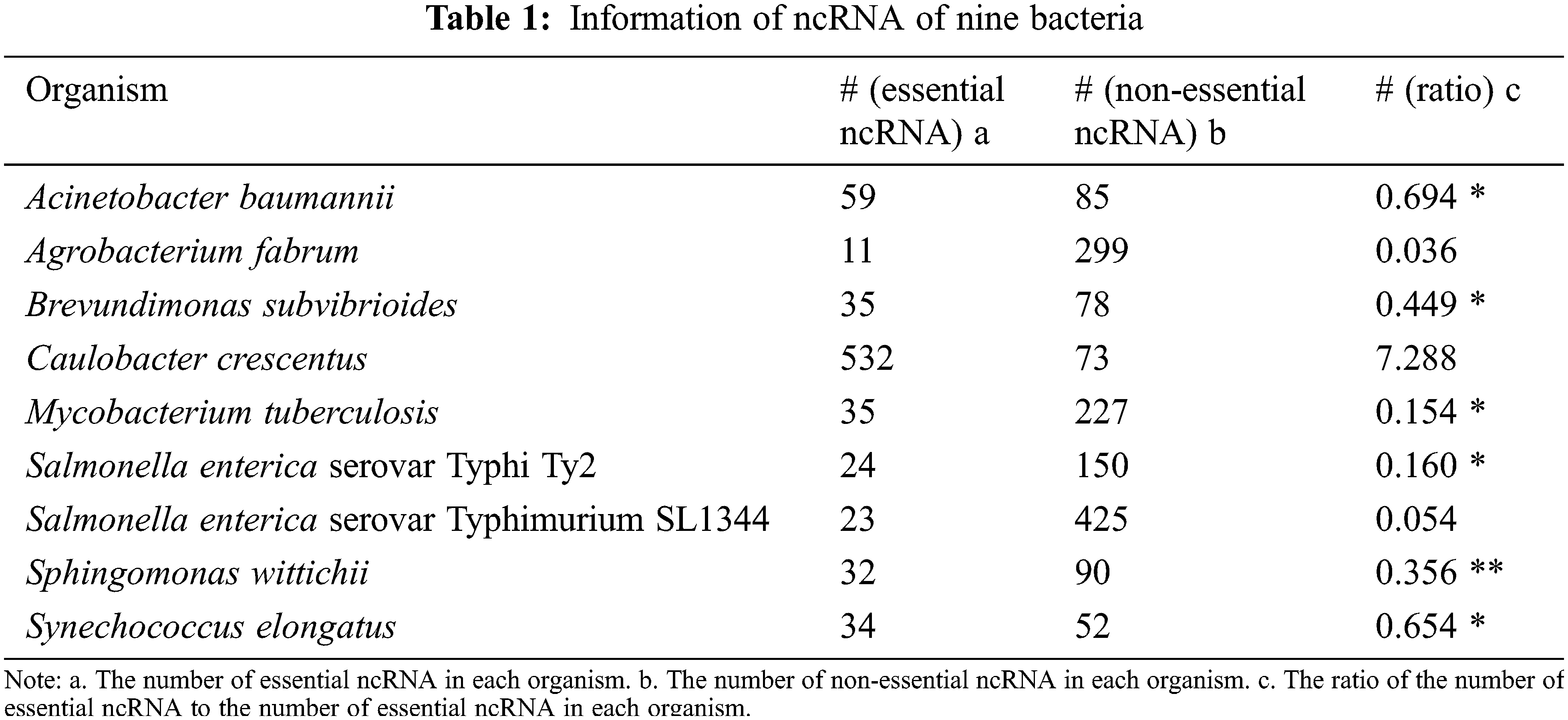
The quality of training dataset has a great influence on the predicted performance in machine learning field. The cross-organism validation result of Geptop shows that not all species achieve a high area under the curve (AUC). The essential gene dataset of species with low AUC may be unreliable due to differences in wet-lab experimental conditions. To build a reliable training dataset for developing a predicted essential ncRNA model in bacteria, we analyze the bacterial essential genes in database of essential gene (DEG) by Geptop and CEG_Match [24,25]. There are nine bacteria with their essential ncRNAs determined through wet-lab experiment. Their essential ncRNAs are obtained from DEG, and the non-essential ncRNAs were downloaded from RNAcentral (https://rnacentral.org), as shown in Table 1 [26]. The ratio of the number of essential ncRNA to the number of non-essential ncRNA in each bacterium is calculated in order to construct a reliable training dataset for proposing a bacterial essential ncRNA recognition algorithm. Six datasets with ratio in the range from 0.1 to 0.7 are extracted for further analyses. Data of Sphingomonas wittichii is used as test dataset for assessing the accuracy of model of essential ncRNA recognition. Data of the remaining bacteria is used as the training dataset.

2.2 Training and Data Marking

In this paper, we use the support vector machine learning approach, a supervised machine-learning method, to predict the essential ncRNA. Thus, every piece of data in the training dataset must be marked. In the training dataset, the essential ncRNA is marked as 1 and non-essential ncRNA is marked as 0.

2.3 Features Extraction

2.3.1 Homology Feature

For a DNA sequence, the sequence homology is often used in prediction of protein function [10]. Because negative selection acts more strongly on essential ncRNA, essential ncRNAs are more conserved than non-essential ncRNAs. Thus, this is an important feature that distinguishes between essential and non-essential ncRNA. For a predicted gene or ncRNA, we compared it with both essential and non-essential ncRNA in the reference library by BLASTN with e < 10−10 [27]. After sequence alignment, we use the average value of 10 sequences with the highest BLASTN score as the indicator for homology feature. For those alignments less than 10 hits, we use the average value of all hit sequences as the as the indicator for homology feature.

2.3.2 Sequence Related Feature

The first sequence feature is the length of sequence, which is defined as L. The GC content is a main factor shaping the amino acid usage during bacterial evolution process [28]. Thus, the GC content is used as a feature for perdition of essential ncRNAs. The GC content (GC%) is calculated using the following formula:

GC%=count(G)+count(C)L (1)

where count (G) is the number of guanine in a DNA sequence, and count (C) is the number of cytosine in a DNA sequence. The L indicates the length of a DNA sequence, including guanine, cytosine, thymine and adenine.

2.3.3 Nucleotide Concatemer Feature

We obtain the contents of single-nucleotide, dimeric-nucleotide, triplet-nucleotide, quadruplexes-nucleotide, pentamers-nucleotide and hexon-nucleotide as the features in the prediction models [29]. The above-mentioned features were calculated considering phase-independent. We calculate the content of triplet-nucleotide as an example in following paragraph.

We set window length of three and step size of one when intercepting and calculating the counts of triplet-nucleotide in a sequence. For triplet-nucleotide, sixty-four (43) combinations were computed, such as ATG, ACG, GTC and so on. For each combination, we calculate its frequency in following formula:

fi=Ci∑i=164Ci,i=1,2,...64 (2)

where i is the ith triplet-nucleotide. Ci indicates the number of the ith triplet-nucleotide in a sequence. The frequencies of other nucleotide concatermers are calculated using similar approached used to calculate the triplet-nucleotide using Eq. (3).

fik=Ci∑i=14kCi,i=1,2,…4k (3)

2.3.4 Markov Remotely Related Base Feature

The Markov chain model in stochastic process theory assumes that the state of the next character is determined by successive characters adjacent to it [30]. Thus, we used this theory to obtain the remote correlation information of nucleotide in gene or ncRNA sequences. It means that a nucleotide in a gene or ncRNA is determined by successive nucleotides adjacent to it. DNA is not linear in organisms. Gene and ncRNA have a specific structure due to the curling of DNA and the principle of nucleotide complementarity among nucleotides at different locations.

By the same analogy, we extend Markov chain model that nucleotides spaced some distance apart (lambda nucleotides) are also correlated. This correlation is not the actual correlation of a Markov chain but the correlation between sequence and tertiary structure. Experimental evidence for this correlation is three-dimensional genomics studies. The formula used for calculating the correction is presented in Eq. (4).

{xkx=(pk(XA)+pk(XG))−(pk(XC)+pk(XT))ykx=(pk(XA)+Pk(XC))−(pk(XG)+pk(XT)),X=A,C,G,T, k=1:λ+1,2:λ+2,3:λ+3zkx=(pk(XA)+pk(XI))−(pk(XG)+pk(XC)) λ=1,2,3…L (4)

where A, C, G and T indicate the four nucleotides in DNA sequence, respectively. The x, y and z mean the effects among the four nucleotides (guanine, cytosine, thymine and adenine) depending on the bond properties among them, respectively [31]. k represents the position of two relevant nucleotides. The first nucleotide of k respectively falls into first, second and third phases. λ denotes the spacing of positions between two nucleotides in sequences level. And L represents the maximum spacing in a sequence. Thus, a DNA sequence could be transformed into 3 × 4 × λ variables.

2.3.5 Mutual Information Feature

The mutual information is used for measuring the correlation of two random variables [32,33]. Based on the mutual information, the information of a random variable could be provided by another random variable. In predicting essential gene and ncRNA model, the mutual information is used to measure the information between successive nucleotides X and Y of a DNA sequence, which is defined as:

I(X,Y)=∑x∈Ω∑y∈ΩP(x,y)log2P(x,y)P(x)P(y) (5)

where Ω is the set of,{A, T, C, G} and P(x,y) is the joint probability of X and Y. P(x) and P(y) correspond to the probability of X nucleotide and Y nucleotide, respectively. The mutual information of a DNA sequence is calculated with the Eq. (5). For each dimeric-nucleotide (x,y), its mutual information is defined by the below formula as a feature:

P(x,y)log2P(x,y)P(x)P(y) (6)

For a DNA sequence, there are 42 = 16 dimeric-nucleotides and hence generating 16 features. Thus, considering the mutual information of a DNA sequence, we obutain 17 mutual informations features in total.

2.3.6 Conditional Mutual Information Feature

Conditional mutual information refers to the mutual information between the random variables X and Y in the case of a third random variable Z [34]. It is defined as:

I(X;Y|Z)=∑z∈ΩP(z)∑x∈Ω∑y∈ΩP(x,y|z)log2P(x,y|z)P(x|z)P(y|z)=∑z∈Ω∑x∈Ω∑y∈ΩP(x,y,z)log2P(z)P(z,y,z)P(x,z)P(y,z) (7)

where P(x,y,z), P(x,z) and P(y,z) are the joint probability of the random variables in brackets. The three positions of triplet-nucleotide are considered to the random variables of X, Y and Z, in sequence. According to the formula (7), the mutual information between the first base and the third base in the condition of the second base is calculated, and is used as a feature. In a DNA sequence, we could obtain 43 = 64 triplet-nucleotide. The conditional mutual information of each triplet-nucleotide is calculated by the formula given in Eq. (8):

∑z∈Ω∑x∈Ω∑y∈ΩP(x,y,z)log2P(z)P(x,y,z)P(x,z)P(y,z) (8)

In total, there are 65 conditional mutual information features.

2.3.7 Kullback-Leibler Divergence Feature

Kullback-Leibler divergence is used for mensuration of the similarity between probability distribution P(x) and model distribution Q(x), which is calculated by the formula in [35] :

KLD=∑iP(x)log2P(x)Q(x) (9)

The frequencies of nucleotide, dinucleotides and trinucleotides in a given sequence to be predicted are compared with the corresponding frequencies of the genomes used to train the model. For a given dataset, one feature is extracted by Kullback-Leibler Divergence method. In total, we get three features in this step.

2.4 Feature Normalization

After obtaining a large number of features generated by the sequences and information theory of essential ncRNA and non-essential ncRNA, all features need to be normalized to the same scale. Accordingly,, we used the Min-Max Normalization approach [36]. The formula is used for normalizing each feature.

X∗=X−minmax−min (10)

2.5 Positive and Negative Samples Balanced

Table 1 shows that the number of essential ncRNA and non-essential ncRNA are differ greatly. It is possible to misevaluate the performance of a machine learning model. For example, Bacillus subtilis 168 has 271 essential genes and 4175 non-essential genes. If all genes are predicted as non-essential genes in a model, then the accuracy rate of the model is still as high as 94% (4175/(4175+271) = 0.939). However, this model is worthless.

To avoid this situation, balancing the number of positive and negative samples is crucial process. The conventional method to solve the imbalance of positive and negative samples is the subset sampling method, which randomly select the same amount of negative sample as the positive sample [37]. However, only part of the known information from the negative sample is used with subset sampling method [38]. Thus, a large amount of potentially helpful information can be lost, which in turn affects the accuracy of the model. In this paper, we attempt to introduce principal component regression to solve this problem. As a new multivariate statistical method, principal component regression is mainly used in multivariate correlation analysis. Principal component regression has hardly been applied to the classification of biomolecules. Principal component regression uses regression technique to make classification prediction, which is not affected by sample size. The principal component regression includes steps of principal component analysis and correlation analysis at the same time, which can be used to eliminate the redundancy of variables and screen significant variables at a time.

In general, the number of negative samples (non-essential coding gene and ncRNAs) is tens of times that of positive samples (essential coding gene and ncRNAs). For example, the number of non-essential gene is 14 times more than essential gene in Bacteroides thetaiotaomicron VPI 5482, (Table 1). And the number of non-essential ncRNA is 6 times more than essential ncRNA in Mycobacterium tuberculosis, (Table 2). In order to use information as much as possible of negative samples, we implemented a K-means clustering center substitution method. In K-means clustering method, if there are K sequences of positive samples, then the negative samples will be divided into K categories. In K-mean clusters, the center of each category of negative samples will be taken as the characteristic of negative samples. The information regarding each non-essential ncRNA is reservation, and the number of negative samples obtained should be consistent with that of positive samples. For instance, B. subtilis 168 has 271 essential genes and 4175 non-essential genes. The 4175 non-essential genes would be divided in to 271 categories with K-means clustering method and this gives balanced sample for building the predicting model.

2.6 Data Dimension Reduction

The features collected through interval correlation and phase heterogeneous adjacency correlation of sequence composition created a characteristic variable data matrix with huge dimensions. Thus, this requires a computational tool to reduce the dimensions of the matrix.

The least absolute shrinkage and selection operator (Lasso regression) can be used for feature extraction, which has been successfully applied in the classification of cancer [39,40]. Thus, we have applied the Lasso regression method to reduce the dimensions. In the end, we obtained 231 variables to construct the essential ncRAN prediction model by SVM.

2.7 Machine Learning Algorithm

In this work, we use sequence features to characterize essential and non-essential ncRNAs. The essential and non-essential ncRNAs were computationally identified and analyzed as the characteristic variables of machine learning.

The first step was analysis of sequence homology and corresponding features are extracted. And then, the support vector machine (SVM) is used to build essential ncRNA models.

2.7.1 SVM Model Training

The 70% of the data were selected as training data. The remaining 30% was used as a test data. The prediction model was created by executing the SVMLIB training program---Svm-train.exe with the default parameters.

2.7.2 Prediction Model

We marked two different labels (1 and 0) to essential ncRNAs and non-essential ncRNAs sequences respectively and combined the 231 parameters into a training data. After optimizing the SVM parameters, C and Gamma by running grid.py program while the training, an accuracy of 89% was obtained under 5-fold cross-validation, which further indicated that the model could significantly separate the positive and negative sets. Finally, we obtained the classification model with the optimized parameters by executing the command: svm-train -b l -C xx - g xx training set file.

3  Results and Discussions

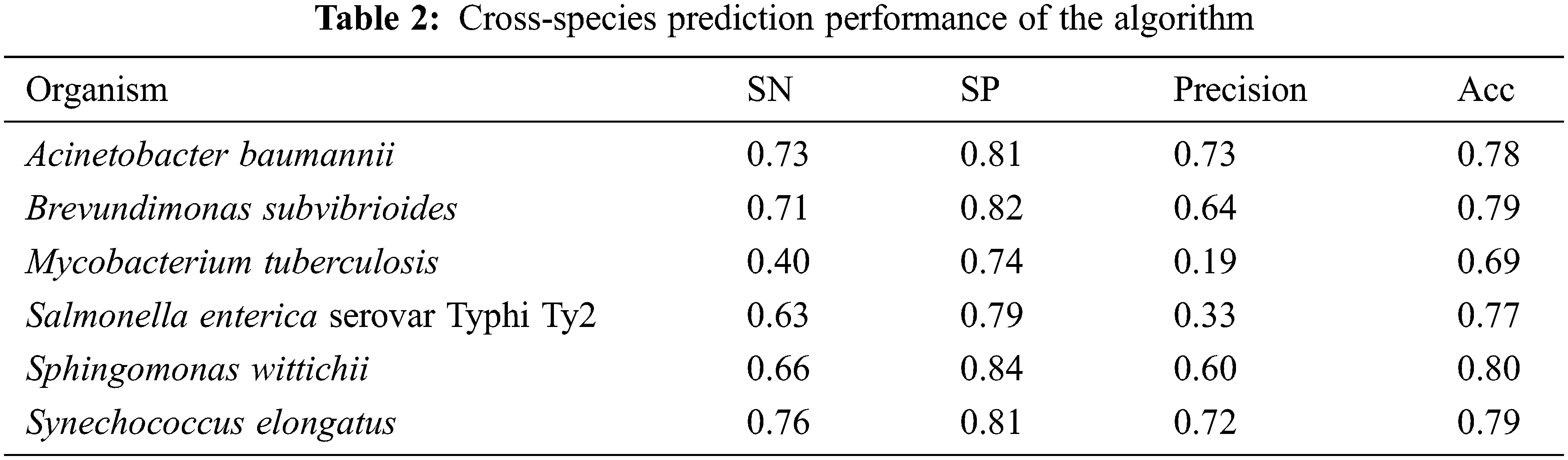
To verify the performance of the algorithm, we used the across-species validation to test the accuracy of the algorithm.

Accordingly, we used sensitivity (SN), specificity (SP), precision (precision) and accuracy (Acc) to measure the predictive performance of algorithm, respectively. These indicators are calculated as follows:

SN=TPTP+FN (11)

SP=TNTN+FP (12)

precision=TPTP+FP (13)

Acc=TP+TNTP+FP+TN+FN (14)

where TP indicates the number of the essential genes predicted as essential genes, FP indicates the number of the non-essential genes predicted as essential genes, TN indicates the number of the non-essential genes predicted as non-essential genes, FN indicates the number of the essential genes predicted as non-essential genes. The results of predictive performance are shown in Table 2.

Only the six datasets with ratio in the range from 0.1 to 0.7 are used for construction of essential ncRNA prediction model. The accuracy was found to be between 0.69 and 0.81 through cross-species cross-validation. It shows that the features we selected have good performance for prediction of essential ncRNA. And there is a potential application for discovering essential ncRNAs in bacteria for further analysis, such as antimicrobial target discovery, minimal genome construction and evolution analysis. However, the prediction accuracy fluctuated greatly for different bacteria. In order to further analyze the reasons for the different accuracy, we analyzed the relationship between the above four indicators (SN, SP, Precision and Acc) and the ratio of the number of essential ncRNA to the number of essential ncRNA in each organism (ratio), which is shown in Fig. 1.

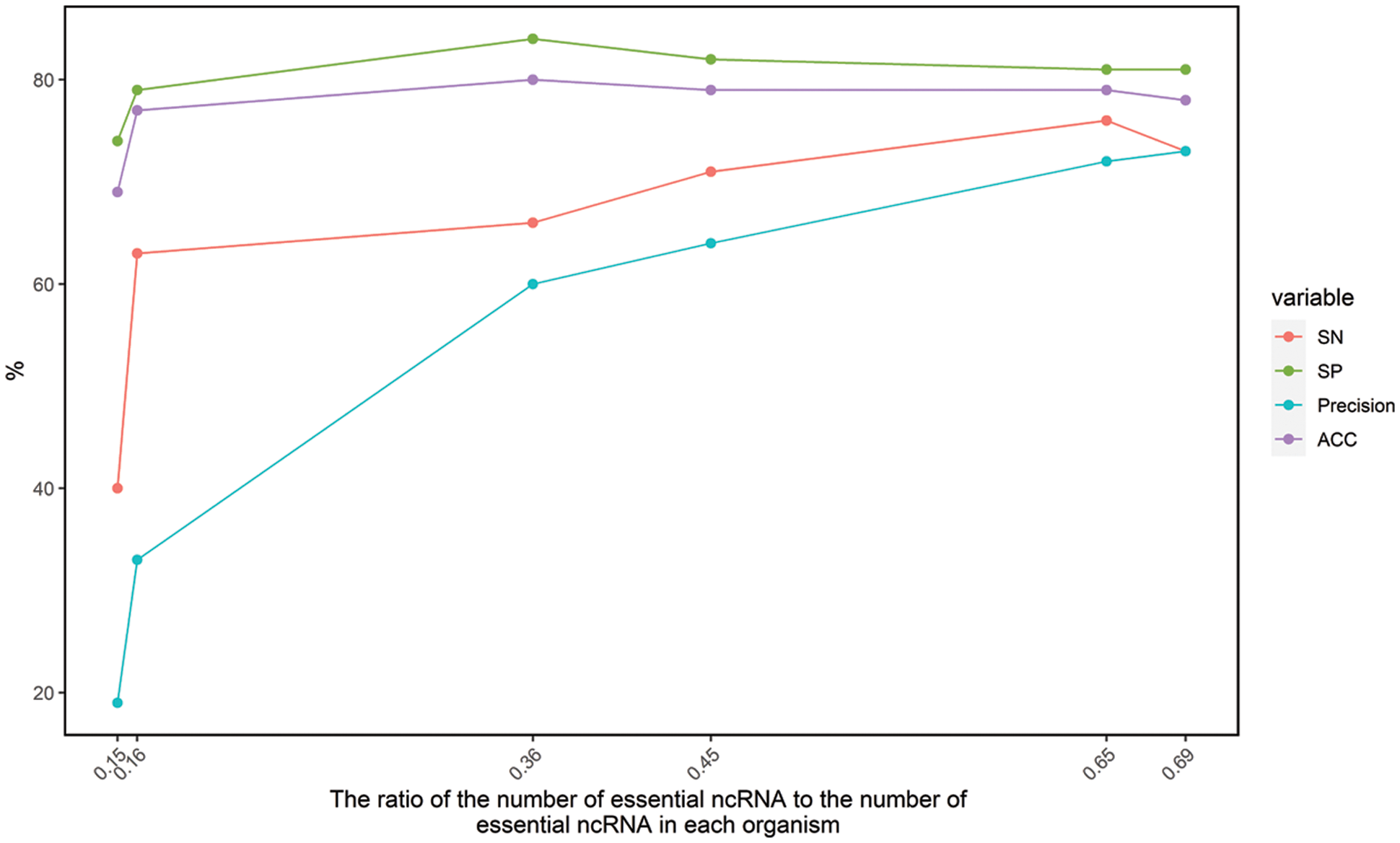
Figure 1: The relationship between SN, SP, Precision, Acc and ratio

Fig. 1 shows that the accuracy of the algorithm is related to the ratio. It had been mentioned that accuracy of an algorithm would be unreliable due to differences in wet-lab experimental conditions. It was further found that when the ratio was about 0.35, the prediction effect was the best.

Acknowledgement: The authors are grateful to anonymous reviewers for their valuable suggestions and comments, which have led to the improvement of this paper.

Funding Statement: This study was jointly funded by the National Natural Science Foundation of China (61803112, 32160151), the Science and Technology Foundation of Guizhou Province (2019-2811).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. Cui, Y. Zhang, K. U. Kakar, X. Kong, R. Li et al., “Involvement of non-coding RNAs during infection of rice by Acidovorax oryzae,” Environmental Microbiology Reports, vol. 13, no. 4, pp. 540–554, 2021. [Google Scholar] [PubMed]

2. Q. Xu, Y. Song, Z. Lin, G. Banuelos, Y. Zhu et al., “The small RNA chaperone hfq is a critical regulator for bacterial biosynthesis of selenium nanoparticles and motility in Rahnella aquatilis,” Applied Microbiology and Biotechnology, vol. 104, no. 4, pp. 1721–1735, 2020. [Google Scholar] [PubMed]

3. D. Ramirez, V. Kohar and M. Y. Lu, “Toward modeling context-specific EMT regulatory networks using temporal single cell RNA-seq data,” Frontiers in Molecular Biosciences, vol. 7, pp. 54, 2020. [Google Scholar] [PubMed]

4. P. Zeng, J. Chen, Y. Meng, Y. Zhou, J. Yang et al., “Defining essentiality score of protein-coding genes and long noncoding RNAs,” Frontiers in Genetics, vol. 9, pp. 380, 2018. [Google Scholar] [PubMed]

5. A. P. Quendera, A. F. Seixas, R. F. dos Santos, I. Santos, J. P. N. Silva et al., “RNA-binding proteins driving the regulatory activity of small non-coding RNAs in bacteria,” Frontiers in Molecular Biosciences, vol. 7, pp. 78, 2020. [Google Scholar] [PubMed]

6. R. Gil, F. J. Silva, J. Pereto and A. Moya, “Determination of the core of a minimal bacterial gene set, table of contents,” Microbiology and Molecular Biology Reviews, vol. 68, no. 3, pp. 518–537, 2004. [Google Scholar] [PubMed]

7. B. Christen, E. Abeliuk, J. M. Collier, V. S. Kalogeraki, B. Passarelli et al., “The essential genome of a bacterium,” Molecular Systems Biology, vol. 7, no. 1, pp. 528, 2011. [Google Scholar] [PubMed]

8. M. Lluch-Senar, J. Delgado, W. H. Chen, V. Lloréns-Rico, F. J. O’Reilly et al., “Defining a minimal cell: Essentiality of small ORFs and ncRNAs in a genome-reduced bacterium,” Molecular Systems Biology, vol. 11, no. 1, pp. 780, 2015. [Google Scholar] [PubMed]

9. Y. N. Ye, B. G. Ma, C. Dong, H. Zhang, L. L. Chen et al., “A novel proposal of a simplified bacterial gene set and the neo-construction of a general minimized metabolic network,” Scientific Reports, vol. 6, no. 1, pp. 35082, 2016. [Google Scholar] [PubMed]

10. J. C. Whisstock and A. M. Lesk, “Prediction of protein function from protein sequence and structure,” Quarterly Reviews of Biophysics, vol. 36, no. 3, pp. 307–340, 2003. [Google Scholar] [PubMed]

11. J. Liu, W. T. Wang, J. Chen, G. Z. Sun and A. L. Yang, “Classification and research of skin lesions based on machine learning,” CMC-Computers, Materials & Continua, vol. 62, no. 3, pp. 1187–1200, 2020. [Google Scholar]

12. X. Zhang, W. Zhang, W. Sun, X. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

13. C. Li, X. Yu, J. Lu, L. Zheng and K. Li, “Contributions of gene modules regulated by essential noncoding RNA in colon adenocarcinoma progression,” Biomed Research International, vol. 2020, no. 3, pp. 1–12, 2020. [Google Scholar]

14. X. Zhang, W. X. Xiao and W. J. Xiao, “DeepHE: Accurately predicting human essential genes based on deep learning,” Plos Computational Biology, vol. 16, no., pp. 9, 2020. [Google Scholar]

15. W. Wei, L. W. Ning, Y. N. Ye and F. B. Guo, “Geptop: A gene essentiality prediction tool for sequenced bacterial genomes based on orthology and phylogeny,” PLoS One, vol. 8, no. 8, pp. e72343, 2013. [Google Scholar] [PubMed]

16. O. Aromolaran, T. Beder, M. Oswald, J. Oyelade and R. Koenig, “Essential gene prediction in Drosophila melanogaster using machine learning approaches based on sequence and functional features,” Computational and Structural Biotechnology Journal, vol. 10, no. 18, pp. 612–621, 2020. [Google Scholar]

17. W. Fang, F. H. Zhang, Y. W. Ding and J. Sheng, “A new sequential image prediction method based on LSTM and DCGAN,” CMC-Computers, Materials & Continua, vol. 64, no. 1, pp. 217–231, 2020. [Google Scholar]

18. W. Fang, L. Pang and W. Yi, “Survey on the application of deep reinforcement learning in image processing,” Journal on Artificial Intelligence, vol. 2, no. 1, pp. 39–58, 2020. [Google Scholar]

19. D. Nigatu, P. Sobetzko, M. Yousef and W. Henkel, “Sequence-based information-theoretic features for gene essentiality prediction,” BMC Bioinformatics, vol. 18, no. 1, pp. 473, 2017. [Google Scholar] [PubMed]

20. P. Plawiak, M. Abdar, J. Plawiak, V. Makarenkov and U. R. Acharya, “DGHNL: A new deep genetic hierarchical network of learners for prediction of credit scoring,” Information Sciences, vol. 516, no. Supplement C, pp. 401–418, 2020. [Google Scholar]

21. Y. T. Chang, M. C. Hsueh, S. P. Hung, J. M. Lu, J. H. Peng et al., “Prediction of specialty coffee flavors based on near-infrared spectra using machine and deep learning methods,” Journal of the Science of Food and Agriculture, vol. 101, no. 11, pp. 4705–4714, 2021. [Google Scholar] [PubMed]

22. L. Li, Y. Wei, L. Zhang and X. Wang, “Efficient virtual resource allocation in mobile edge networks based on machine learning,” Journal of Cybersecurity, vol. 2, no. 3, pp. 141, 2020. [Google Scholar]

23. N. E. M. Khalifa, M. H. N. Taha, G. Manogaran and M. Loey, “A deep learning model and machine learning methods for the classification of potential coronavirus treatments on a single human cell,” Journal of Nanoparticle Research, vol. 22, no. 11, pp. 313, 2020. [Google Scholar] [PubMed]

24. S. Liu, S. X. Wang, W. Liu, C. Wang, F. Z. Zhang et al., “CEG 2.0: An updated database of clusters of essential genes including eukaryotic organisms,” Database (Oxford), vol. 2020, pp. baaa112, 2020. [Google Scholar] [PubMed]

25. Y. N. Ye, Z. G. Hua, J. Huang, N. Rao and F. B. Guo, “CEG: A database of essential gene clusters,” BMC Genomics, vol. 14, no. 1, pp. 769, 2013. [Google Scholar] [PubMed]

26. The RNAcentral Consortium, “RNAcentral: An international database of ncRNA sequences,” Nucleic Acids Research, vol. 43, no. D1, pp. D123–D129, 2015. [Google Scholar]

27. T. A. Tatusova and T. L. Madden, “BLAST 2 sequences, a new tool for comparing protein and nucleotide sequences,” FEMS Microbiology Letters, vol. 174, no. 2, pp. 247–250, 1999. [Google Scholar] [PubMed]

28. M. Z. Du, C. J. Zhang, H. Wang, S. Liu, W. Wei et al., “The GC content as a main factor shaping the amino acid usage during bacterial evolution process,” Frontiers in Microbiology, vol. 9, pp. 2948, 2018. [Google Scholar] [PubMed]

29. C. Dong, Y. Z. Yuan, F. Z. Zhang, H. L. Hua, Y. N. Ye et al., “Combining pseudo dinucleotide composition with the Z curve method to improve the accuracy of predicting DNA elements: a case study in recombination spots,” Molecular BioSystems, vol. 12, no. 9, pp. 2893–2900, 2016. [Google Scholar] [PubMed]

30. X. Huang, W. Wang and T. Emura, “A copula-based Markov chain model for serially dependent event times with a dependent terminal event,” Japanese Journal of Statistics and Data Science, vol. 4, no. 2, pp. 917–951, 2021. [Google Scholar]

31. F. B. Guo, C. Dong, H. L. Hua, S. Liu, H. Luo et al., “Accurate prediction of human essential genes using only nucleotide composition and association information,” Bioinformatics, vol. 32, no. 12, pp. 1758–1764, 2017. [Google Scholar]

32. Q. Dong and W. K. Cheung, “Enhancing variational autoencoders with mutual information neural estimation for text generation,” in Proc. of the 2019 Conf. on Empirical Methods in Natural Language Processing and the 9th Int. Joint Conf. on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, pp. 4047–4057, 2019. [Google Scholar]

33. G. Zhu, W. Liu, S. Zhang, X. Chen and C. Yin, “The method for extracting new login sentiment words from Chinese micro-blog basedf on improved mutual information,” Computer Systems Science and Engineering, vol. 35, no. 3, pp. 223–232, 2020. [Google Scholar]

34. S. Mukherjee, H. Asnani and S. Kannan, “CCMI: Classifier based conditional mutual information estimation,” in Uncertainty in Artificial Intelligence, Toronto, Canada: PMLR, pp. 1083–1093, 2020. [Google Scholar]

35. Y. Huang, Y. Zhang and J. A. Chambers, “A novel Kullback-Leilber Divergence minimization-based adaptive student’s t-filter,” IEEE Transactions on Signal Processing, vol. PP, no. 99, pp. 1, 2019. [Google Scholar]

36. L. Munkhdalai, T. Munkhdalai, K. H. Park, H. G. Lee, M. J. Li et al., “Mixture of activation functions with extended min-max normalization for forex market prediction,” IEEE Access, vol. 7, pp. 183680–183691, 2019. [Google Scholar]

37. M. A.Tahirab, J. Kittlera and F. Yan, “Inverse random under sampling for class imbalance problem and its application to multi-label classification,” Pattern Recognition, vol. 45, no. 10, pp. 3738–3750, 2012. [Google Scholar]

38. X. Zhang, X. Sun, X. Sun, W. Sun and S. -K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

39. R. Zhang, F. Zhang, W. Chen, H. Yao, J. Ge et al., “A new strategy of least absolute shrinkage and selection operator coupled with sampling error profile analysis for wavelength selection,” Chemometrics and Intelligent Laboratory Systems, vol. 175, pp. 47–54, 2018. [Google Scholar]

40. S. M. Kim, Y. Kim, K. Jeong, H. Jeong and J. Kim, “Logistic LASSO regression for the diagnosis of breast cancer using clinical demographic data and the BI-RADS lexicon for ultrasonography,” Ultrasonography, vol. 37, no. 1, pp. 36–42, 2018. [Google Scholar] [PubMed]