Data-Driven Probabilistic System for Batsman Performance Prediction in a Cricket Match

1  Introduction

Cricket is a bat-and-ball game played on a cricket field between two teams of eleven players each. Each side tries to score as many runs as possible. The opponent team tries to dismiss the batsmen and thus limits the target score. If the game is tied at the end of regulation, ten-minute overtime is played. The team that scores the most runs in the overtime period is the winner. The batsman plays a significant role in making runs. The batsman’s primary role is to score runs. They do this by hitting the ball with their bat and running between the wickets. The batsman can also score runs by hitting the ball over the boundary for a six or a four. A batsman’s ability to score huge is determined by the player’s ability to hit the ball with precision. Many factors can affect a batsman’s performance, such as the quality of the opposition, the pitch conditions, the weather, etc. Batsmen are the backbone of any cricket team. They are the ones who score the runs and provide the team with the momentum it needs to win. A good batsman can single-handedly win a match for his team. That is why the selection of batsmen is very crucial. The selection purpose of the batter is to score the maximum runs. The batsman performance prediction is a supervised learning problem, where we are given the past performance data of batsmen, and we need to predict their future performance. So, it is important to consider all these factors when training the model. The target variable will be the runs scored by the batsman in the next ball.

Cricket batsman score prediction is a difficult task, as many factors can affect a batsman’s score. Although umpire biased decisions may completely change the results [1]. However, machine learning can be used to create a model that can predict a batsman’s score based on past data. This model can then be used to predict the score of a batsman in future matches. This prediction can be used to make strategic decisions, such as selecting a batsman for a particular match.

Researchers have majorly [2–7] focused on a match’s overall outcome. They have used different machine learning classifiers such as the Support vector machine [8,9], k-nearest neighbors’ algorithm (k-NN) [10], Decision tree [11], and Random Forest [12] and predicted the overall match performance in different ways. A Data Envelopment Analysis (DEA) model [13] was developed having batting-bowling parameters for estimating the cricket player’s efficiency. A genetic algorithm-based framework [14] was suggested for thirty players from the Bangladesh crew to choose the best squad. This research utilizes numerical investigation along with a genetic algorithm for selecting talented performers. Statistical techniques are applied for the evaluation and rating of the players. Bailey et al. [15] examined the current game and did not use the previous output of the past matches. They forecasted the first batting team’s score, and the prediction accuracy was 71%. They predicted the output of One Day International (ODI) cricket during the match using statistical models. Sparks et al. [16] used Machine learning to predict the winning prize for cricketers. He predicted the best man of the match by using the previous record. He used random forest, decision trees, KNN, and logistic regression to build the model. Muthuswamy et al. [17] examined the performance of the Indian team in various matches. He also examined the capability of bowlers against seven international teams. It also predicted the performance of bowlers and how many wickets they would take. Wickramasinghe [18] used a hierarchical linear model, to predict the performance of the batter. Barr et al. [19] used graphical representation along with the new measure of probability. This procedure is used for the selection of eligible batters in matches. Lyer et al. [20] divided the performance of batter into three orders, performer, moderate, and failure. Besides conventional contextual factors such as home ground and winning toss, strong motivation and financial aspects also play vital roles in individual performance [21]. Lemmer [22] in his study, analyzed the bowler’s performance by combining the bowling rate method. Three bowling factors; bowling average, strike rate, and economy were combined to get the desired result. Bhattacharjee et al. [23] used the collective bowling percentage of players to predict the player’s performance in the Indian Premier League (IPL). Using this research, other factors are checked which could affect the bowler’s performance, and to find those factors they used a multiple regression model which was responsible for the performance of the bowler. Bukiet et al. [24] used a mathematical method for batting orders in One Day International matches. Haghighat et al. [25] explained the mining system which is used in sports for prediction and also added the pros and cons of those systems. Mukharjee [26] used social network analysis to give rank to the batter and bowler. He used players’ performance and introduced weighted work. Shah [27] presented new measures to examine the performance of players and proved that the quality of players could affect the bowler’s performance. Parkash et al. [28] presented a batting rank index and a bowling rank index for player ranking. Using this information, the study predicted the results of IPL matches. Sankaranarayanan et al. [29] used six factors and their accuracy prediction was 68.1% to 70.3%. Lemmer [30] used one-day data for the T20 series and developed a ranking to find the performance of the player. Nimmagadda et al. [31] introduced a model by using statistical techniques for reliable outcomes. He applied these techniques to predict the T-20 matches. He applied multiple regression models. These techniques are used in matches to gain the correct outcome.

As most of the literature work is related to the prediction of which team will win, our research is exclusive and unique in predicting the batter’s performance. We predicted the batter’s ability to score runs based on his previous records. For this purpose, we have used Markov Model to analyze the data and predict the best possible selection of players for each game. The major goal of using this Markov model is to predict players’ performance based on their previous records. This suggested model aims to estimate how many runs a batter will score in the upcoming match. This paper is structured as follows. Section 2 describes the overall system design. This section explains briefly the methodology of our proposed system. This section also justifies the system mathematically. Section 3 shows the results of our proposed methodology and discusses outcomes. Finally, Section 4 is our conclusion.

2  System Design

Our system comprises of two modules. The data extraction module will extract the data. To extract our required data, we get access to the Cricinfo website and search for the required data. The score of each player is only available in commentary form as shown in Fig. 1. Selenium is a very good tool and is used at a large scale for data extraction from any website. It supports finding elements based on different strategies such as the element id, XPath expressions, or CSS selectors. This required data can be accessed through the scrappy library.

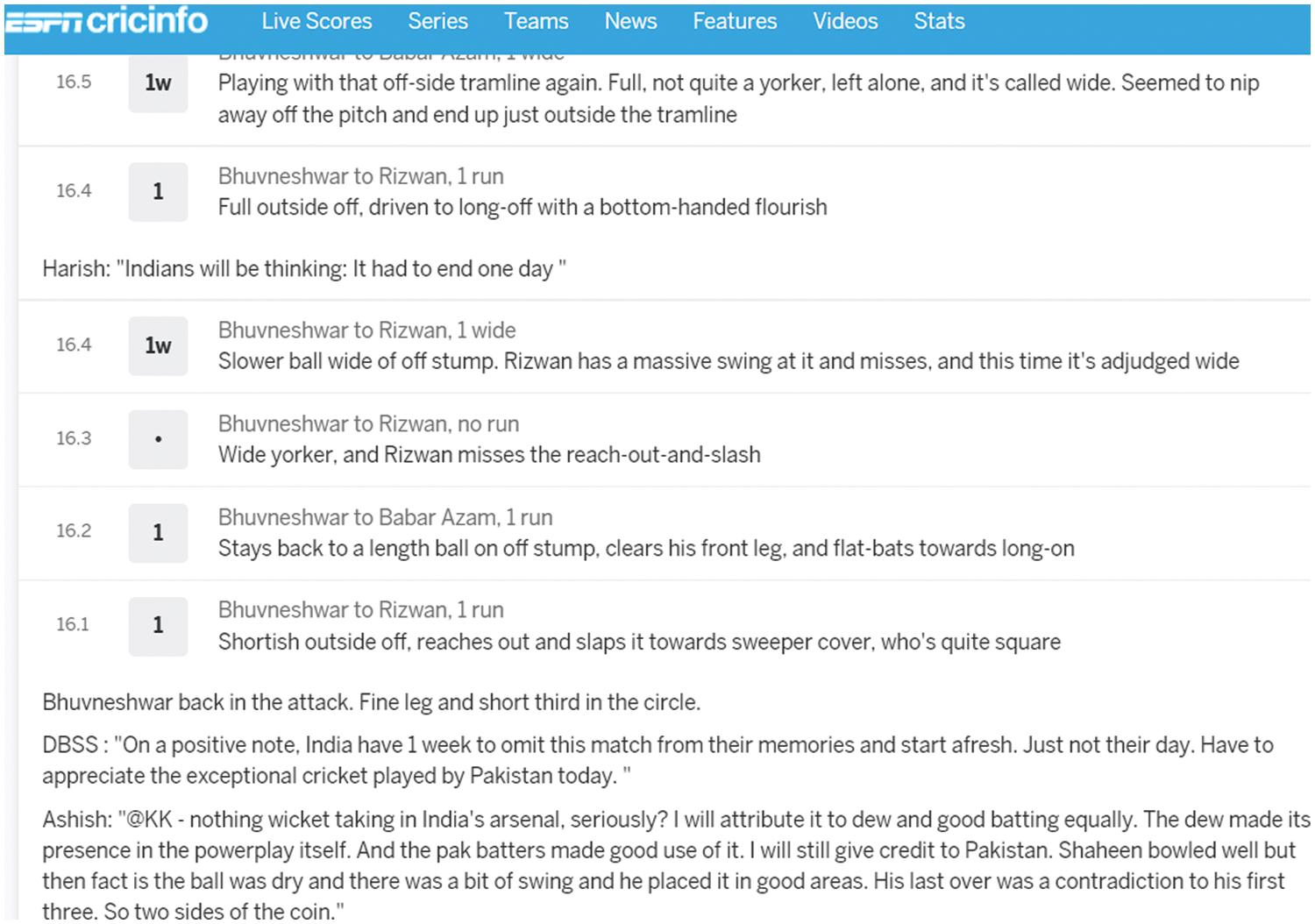
Figure 1: Cricinfo player’s ball-by-ball data

From the full commentary page, we select the name and score attributes regarding every batter and send the request for full commentary link to the web browser and the browser gives an HTML response. We extract every batter’s data and store the run sequence.

To calculate the probability of observable events, the Markov chain model is much more suitable to use. In the real world, many of the events have hidden meanings that we cannot see directly. In natural language sentences, for instance, we look for the words and letters in a sentence instead of going through the syntax and semantics of the sentence. The occurrence of each event is statistically dependent on the leading one, which is called the Markov chain first order. Predicting the probability of a future state for the states Q = q1 … qn requires only the current observation; all past observations are irrelevant. This first-order Markov chain supposition is expressed in probabilistic terms Eq. (1).

p(qn|q1, …, qn−1)=p(qn|qn−1)  (1)

To predict the probability of forthcoming observations, require previous observations. For this purpose, we use mth order Markov chain presupposition as shown in Eq. (2).

p(qn|qn−1, …, q1)=p(qn|qn−1, …, qn−m)  (2)

To construct the combined probability distributions of a set of nth arbitrary random observations, we use Eq. (3) chain rule

p(Q)=p(q1, q2, …, qn)=p(q1)p(q2|q1)p(q3|q2, q1)… p(qn|qn−1, …, q1) =∏i=1n⁡p(qn|qn−1, …, q1)  (3)

The calculation of combined probability is simplified if the random observation in Q is consecutive in character and follows the generic mth order Markov chain model as shown in Eq. (4).

p(Q)=∏i=1n⁡p(qn|qn−1, …, qn−m) (4)

Based on the previous ball score, we projected the current ball score using the first-order Markov model as shown in Fig. 2. By using the second-order Markov model, we predicted the current ball score based on the last two ball scores.

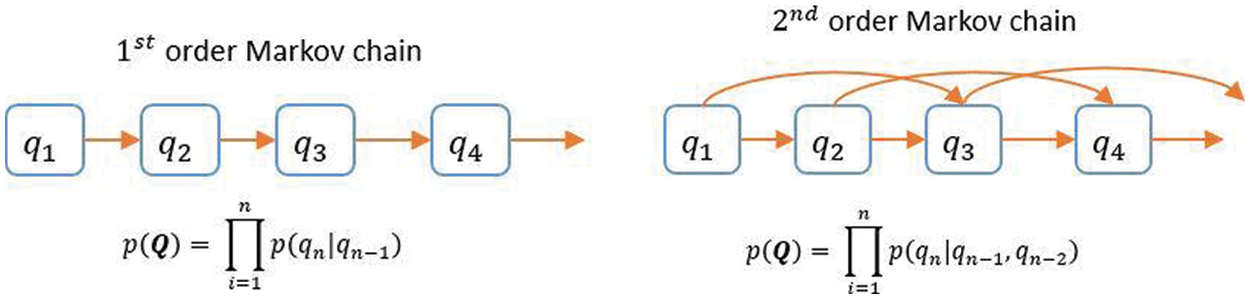
Figure 2: Summarizes the Markov assumptions for first and second-order Markov models

We apply the 1st and 2nd order Markov models on the score sequence to get the probability matrix. We generate two types of matrices first order and second order from the score sequence. Let the values are 0, 2, 0, 4, 1. In Fig. 3, the current ball score works horizontally and the last ball score work vertically which is given in the sequence like [(0, 2), (2, 0), (0, 4), (4, 1)]. Here (4, 1) 4 refers to the last ball score and 1 shows the current ball score Every index will be divided by total balls to get the probability matrix. The last index shows the dismissal of the wicket.

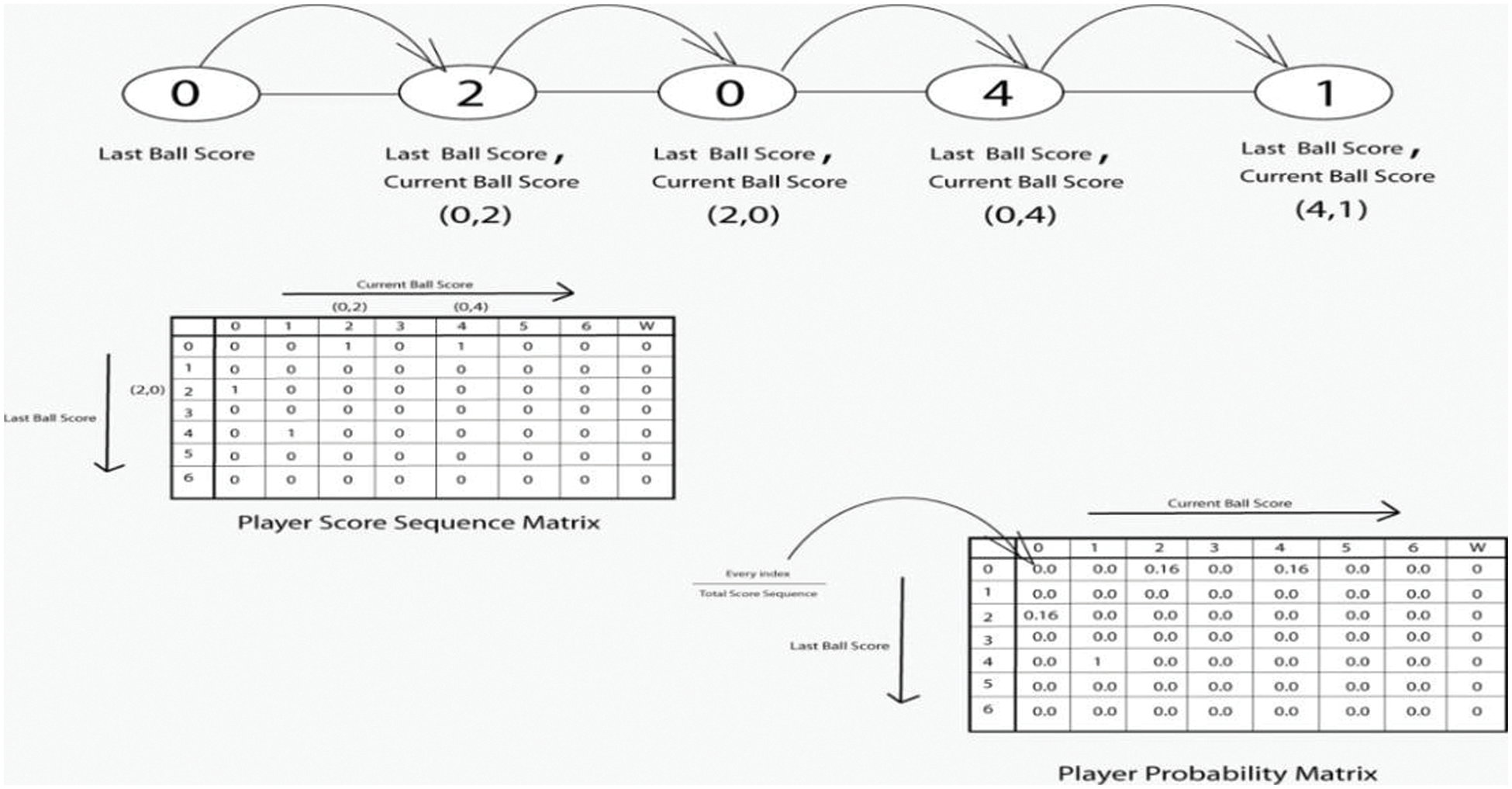
Figure 3: Markov 1st order sequence and probabilistic matrix

The second-order matrix is generated with the last two balls’ scores as shown in Fig. 4. Let the values be 0, 0, 1, 2, 0, 1, 3, 6, 0, 4, 1 and then in the player sequence matrix, every index is divided by the total number of player sequences and generates the probability matrix. 2nd order matrix predictions are generated based on the probability matrix. We check the player’s sequences one by one with a probability matrix. If the probability will be high and accurate according to sequence then it will be considered accurate. In such predictions, we add randomness. Based on the probabilities, we create a random number and through this model, we acquire the predictions and replace them with a random number. To fill this gap, we use randomness probability. Because of the by-chance nature of the cricket game as no one knows what will happen in the next moment that’s why randomness method is used to remove loopholes.

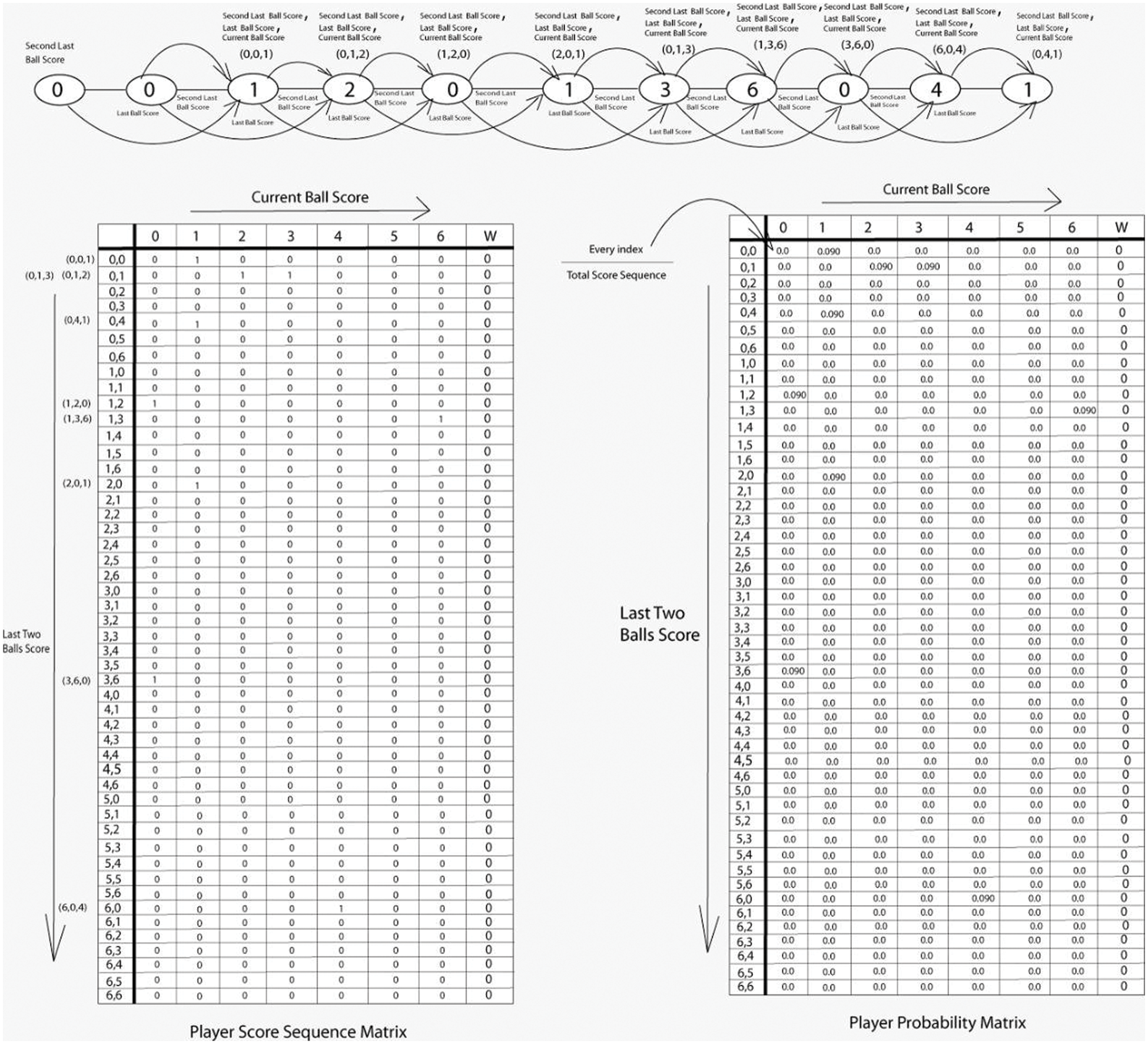
Figure 4: Markov 2nd order sequence and probabilistic matrix

Fig. 5 shows the overall system diagram.

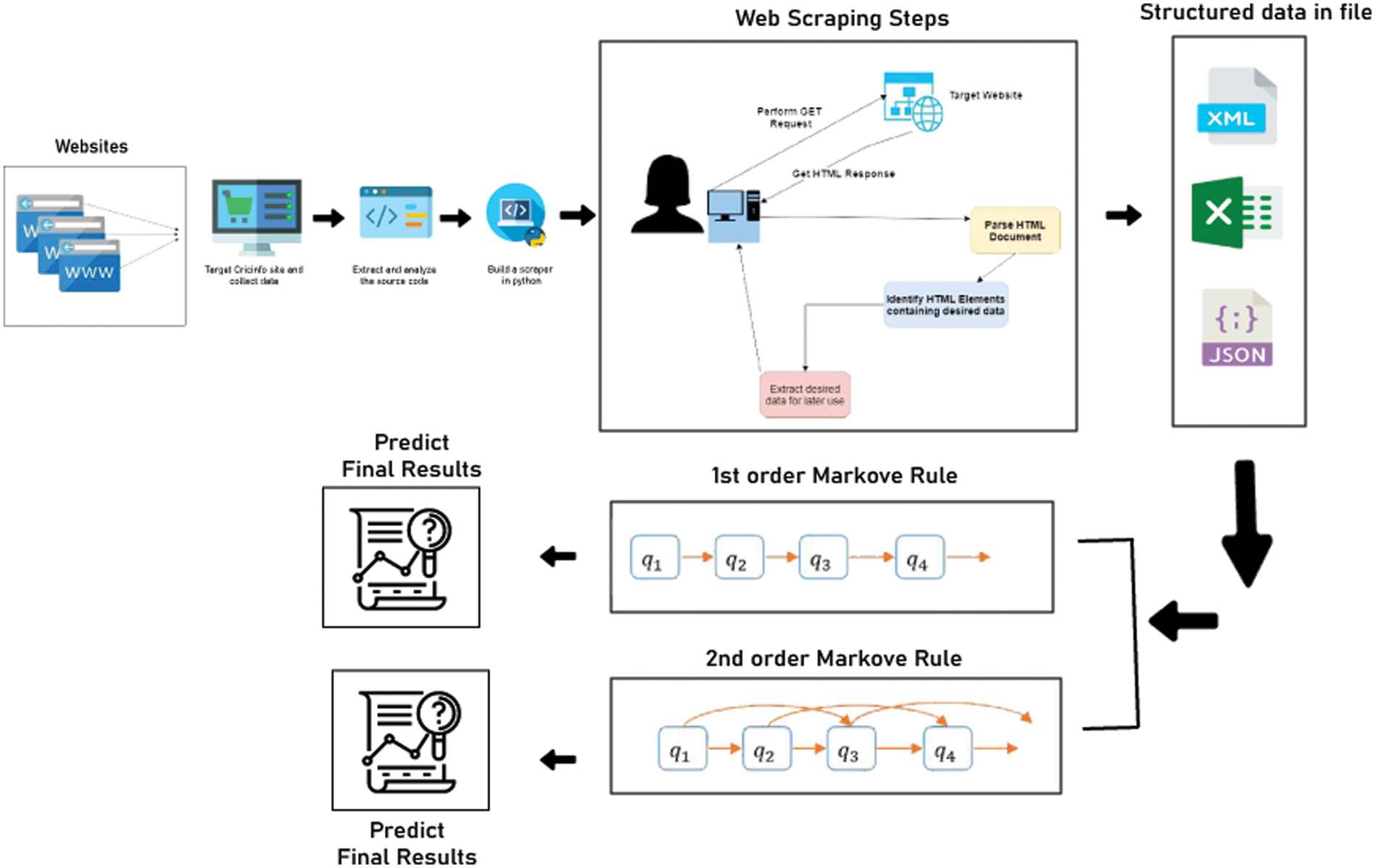
Figure 5: System design

3  Results and Discussion

We give the web address in the prediction file of a specific match and get the commentary of one match. According to the match commentary, we check the probability matrix of the batter and then get the accurate and wrong predictions. While predicting we read the first-order and second-order probability matrix files.

We will discuss Muhammad Rizwan and Babar Azam’s score prediction. We get the score sequences from the Cricinfo website. We developed the sequence matrix over the last three years. A sequence matrix is just like a counter that counts the scores of the previous ball score. For instance, if the last ball’s score is (2) which shows the row and the current ball is ‘1’ and ‘1’ shows the column. On the basis of the previous ball, we update it in the current index. We will repeat this step again and again until the score sequence does not end. On the basis of the sequence matrix, we generated a probability matrix and predict the accuracy through the probability matrix. Now we divide the total number of score sequences with every index of the sequence matrix to get the probability matrix which is given below in Tables 1 and 2.

For 2nd order matrices, we predicted the current ball score on the basis of the previous two balls’ scores. Then we generated three year’s records of Muhammad Rizwan and Babar Azam. For this purpose, we first developed the sequence matrix of the last three years. On the basis of the sequence matrix, we generated a probability matrix and predicted the accuracy through probability matrices which is given below in Tables 3 and 4.

The First-order and second-order prediction matrix is generated on the basis of a probability matrix, we check each player’s sequence one by one with the probability matrix, and analyze where the probability is high and accurate according to the sequence. It will be considered an accurate prediction if it is high and accurate. Otherwise, it will be considered an incorrect prediction. In the given Table 5 prediction of one match is done on the basis of the probability matrix. Here the accurate prediction is that we compare the batter’s score sequence with the probability matrix which is taken from the player’s score sequence. We check the score sequence of one number and compare it with a specific player’s probability matrix. According to the score sequence if the probability matrix is high the prediction will be considered accurate. According to the score sequence, if the probability matrix is low as compared to other indexes in a specific row, then the prediction will be considered wrong. Now to check the accurate prediction % and wrong prediction %, we find out the ratio between accurate prediction values and wrong prediction values and calculate the percentage between accurate and wrong results.

4  Conclusion

Our research will expand the knowledge within the existing literature with the addition of new variables and results. Unique factors have been studied to produce outcomes that would help people play cricket at various levels. The results will allow teams to form strategies that give them a competitive advantage over their rivals. This research work can be used by policymakers before the start of the game to determine which batters are more accurate and skilled than the opposing player. The player’s performance for each match is essential for the success of the team. An exact prediction that how many runs will be scored by a batter in an upcoming ball is the main aim of team management. This research shows a way of the best selection of players on the basis of their performance and also the best selection procedure. Due to the shortage of data, some other factors which can affect players’ performance, for instance, weather and nature of the wicket, the performance of the opposing team, the crowd in the stadium, and the venue of the game, were not included in this study. This method will minimize biases in the player’s selection process while also assisting our cricket team to choose the best player from the squad.

Funding Statement: The authors are pleased to announce that this research is sponsored by The Superior University, Lahore, Pakistan.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. O. B. Chedzoy, “The effect of umpiring errors in cricket,” Journal of the Royal Statistical Society: Series D (The Statistician), vol. 46, no. 4, pp. 529–540, 1997. [Google Scholar]

2. M. M. Rahman, M. O. Faruque Shamim and S. Ismail, “An analysis of Bangladesh one day international cricket data: A machine learning approach,” in 2018 Int. Conf. on Innovations in Science, Engineering and Technology (ICISET), Chittagong, Bangladesh, pp. 190–194, 2018. [Google Scholar]

3. W. Ahmed, “A multivariate data mining approach to predict match outcome in one-day international cricket,” M.S. Dissertation, Karachi Institute of Economics and Technology, Pakistan, 2015. [Google Scholar]

4. P. Shah and M. Shah, “Predicting ODI cricket result,” Journal of Tourism, Hospitality and Sports, vol. 5, pp. 19–20, 2015. [Google Scholar]

5. M. G. Jhawar, S. Viswanadha, K. Sivalenka, and V. Pudi, “Dynamic winner prediction in Twenty20 cricket: Based on relative team strengths,” Machine Learning for Sports Analytics at ECML-PKDD, vol. 10, pp. 41–50, 2017. [Google Scholar]

6. M. Yasir, L. I. Chen, S. A. Shah, K. Akbar, and M. U. Sarwar, “Ongoing match prediction in T20 international,” International Journal of Computer Science and Network Security, vol. 17, no. 11, pp. 176–181, 2017. [Google Scholar]

7. N. Pathak and H. Wadhwa, “Applications of modern classification techniques to predict the outcome of ODI cricket,” Procedia Computer Science, vol. 87, pp. 55–60, 2016. [Google Scholar]

8. A. I. Anik, S. Yeaser, A. G. M. I. Hossain and A. Chakrabarty, “Player’s performance prediction in ODI cricket using machine learning algorithms,” in 2018 4th Int. Conf. on Electrical Engineering and Information & Communication Technology (iCEEiCT), Dhaka, Bangladesh, pp. 500–505, 2018. [Google Scholar]

9. P. Somaskandhan, G. Wijesinghe, L. B. Wijegunawardana, A. Bandaranayake and S. Deegalla, “Identifying the optimal set of attributes that impose high impact on the end results of a cricket match using machine learning,” in 2017 IEEE Int. Conf. on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, pp. 1–6, 2017. [Google Scholar]

10. M. G. Jhanwar and V. Pudi, “Predicting the outcome of ODI cricket matches: A team composition based approach,” Machine Learning and Data Mining for Sports Analytics, ECML-PKDD’16, vol. 1842, 2016. [Google Scholar]

11. F. Munir, M. Hasan, and S. Ahmed, “Predicting a T20 cricket match result while the match is in progress,” Ph.D. Dissertation, Brac University, Bangladesh, 2015. [Google Scholar]

12. V. Punjabi, R. Chaudhari, D. Pal, K. Nhavi, N. Shimpi et al., “A survey on team selection in game of cricket using machine learning,” International Research Journal of Engineering and Technology (IRJET), vol. 9, no. 3, pp. 3406–3409, 2020. [Google Scholar]

13. R. Chaudhary, S. Bhardwaj and S. Lakra, “A DEA model for selection of Indian cricket team players,” in 2019 Amity Int. Conf. on Artificial Intelligence (AICAI), Dubai, United Arab Emirates, pp. 224–227, 2019. [Google Scholar]

14. M. J. Hossain, M. A. Kashem, M. S. Islam and M. E-Jannat, “Bangladesh cricket squad prediction using statistical data and genetic algorithm,” in 2018 4th Int. Conf. on Electrical Engineering and Information & Communication Technology (iCEEiCT), Dhaka, Bangladesh, pp. 178–181, 2018. [Google Scholar]

15. M. Bailey and S. R. Clarke, “Predicting the match outcome in one day international cricket matches, while the game is in progress,” Journal of Sports Science & Medicine, vol. 5, no. 4, pp. 480–487, 2006. [Google Scholar]

16. R. L. Sparks and D. L. Abrahamson, “A mathematical model to predict award winners,” Math Horizons, vol. 12, no. 4, pp. 5–13, 2005. [Google Scholar]

17. S. Muthuswamy and S. S. Lam, “Bowler performance prediction for one-day international cricket using neural networks,” in IIE Annual Con. Proc. Institute of Industrial and Systems Engineers (IISE), Norcross, GA, USA, pp. 1391–1395, 2008. [Google Scholar]

18. I. P. Wickramasinghe, “Predicting the performance of batsmen in test cricket,” Journal of Human Sport and Exercise, vol. 9, no. 4, pp. 744–751, 2015. [Google Scholar]

19. G. D. I. Barr and B. S. Kantor, “A criterion for comparing and selecting batsmen in limited overs cricket,” Journal of the Operational Research Society, vol. 55, no. 12, pp. 1266–1274, 2004. [Google Scholar]

20. S. R. Iyer and R. Sharda, “Prediction of athletes performance using neural networks: An application in cricket team selection,” Expert Systems with Applications, vol. 36, no. 3, pp. 5510–5522, 2009. [Google Scholar]

21. P. Puram, S. Roy, D. Srivastav and A. Gurumurthy, “Understanding the effect of contextual factors and decision making on team performance in Twenty20 cricket: An interpretable machine learning approach,” Annals of Operations Research, pp. 1–28, 2022. [Google Scholar]

22. H. H. Lemmer, “The combined bowling rate as a measure of bowling performance in cricket,” South African Journal for Research in Sport, Physical Education and Recreation, vol. 24, no. 2, pp. 37–44, 2002. [Google Scholar]

23. D. Bhattacharjee and D. G. Pahinkar, “Analysis of performance of bowlers using combined bowling rate,” International Journal of Sports Science and Engineering, vol. 6, no. 3, pp. 1750–9823, 2012. [Google Scholar]

24. B. Bukiet and M. Ovens, “A mathematical modelling approach to one-day cricket batting orders,” Journal of Sports Science & Medicine, vol. 5, no. 4, pp. 495, 2006. [Google Scholar]

25. M. Haghighat, H. Rastegari, N. Nourafza, N. Branch, and I. Esfahan, “A review of data mining techniques for result prediction in sports,” Advances in Computer Science: An International Journal, vol. 2, no. 5, pp. 7–12, 2013. [Google Scholar]

26. S. Mukherjee, “Quantifying individual performance in cricket—A network analysis of batsmen and bowlers,” Physica A: Statistical Mechanics and its Applications, vol. 393, pp. 624–637, 2014. [Google Scholar]

27. P. Shah, “New performance measure in cricket,” IOSR Journal of Sports and Physical Education, vol. 4, no. 3, pp. 28–30, 2017. [Google Scholar]

28. C. D. Prakash, C. Patvardhan, and C. V. Lakshmi, “Data analytics based deep mayo predictor for IPL-9,” International Journal of Computer Applications, vol. 152, no. 6, pp. 6–10, 2016. [Google Scholar]

29. V. V. Sankaranarayanan, J. Sattar, and L. V. S. Lakshmanan, “Auto-play: A data mining approach to ODI cricket simulation and prediction,” in Proc. of the 2014 SIAM Int. Conf. on Data Mining, Philadelphia, Pennsylvania, USA, pp. 1064–1072, 2014. [Google Scholar]

30. H. H. Lemmer, “An analysis of players’ performances in the first cricket Twenty20 world cup series,” South African Journal for Research in Sport, Physical Education and Recreation, vol. 30, no. 2, pp. 71–77, 2008. [Google Scholar]

31. A. Nimmagadda, N. V. Kalyan, M. Venkatesh, N. N. S. Teja, and C. G. Raju, “Cricket score and winning prediction using data mining,” International Journal for Advance Research and Development, vol. 3, no. 3, pp. 299–302, 2018. [Google Scholar]