 Open Access
Open Access
ARTICLE
MNIST Handwritten Digit Classification Based on Convolutional Neural Network with Hyperparameter Optimization
1 Department of Electrical and Computer Engineering, University of Nevada Las Vegas, Las Vegas, 89154, NV, USA
2 Ed W. Clark High School, Las Vegas, 89102, NV, USA
3 School of Computer, Jiangsu University of Science and Technology, Zhenjiang, 212003, China
* Corresponding Author: Shengjie Zhai. Email:
Intelligent Automation & Soft Computing 2023, 36(3), 3595-3606. https://doi.org/10.32604/iasc.2023.036323
Received 26 September 2022; Accepted 14 November 2022; Issue published 15 March 2023
Abstract
Accurate handwriting recognition has been a challenging computer vision problem, because static feature analysis of the text pictures is often inadequate to account for high variance in handwriting styles across people and poor image quality of the handwritten text. Recently, by introducing machine learning, especially convolutional neural networks (CNNs), the recognition accuracy of various handwriting patterns is steadily improved. In this paper, a deep CNN model is developed to further improve the recognition rate of the MNIST handwritten digit dataset with a fast-converging rate in training. The proposed model comes with a multi-layer deep arrange structure, including 3 convolution and activation layers for feature extraction and 2 fully connected layers (i.e., dense layers) for classification. The model’s hyperparameters, such as the batch sizes, kernel sizes, batch normalization, activation function, and learning rate are optimized to enhance the recognition performance. The average classification accuracy of the proposed methodology is found to reach 99.82% on the training dataset and 99.40% on the testing dataset, making it a nearly error-free system for MNIST recognition.Keywords
The Modified National Institute of Standards and Technology (MNIST) handwritten digit database, one of the most important areas of research in pattern recognition, has excellent research and practical value. Generally speaking, handwriting classification techniques can be divided into either statistical feature-related methods or structural feature-related approaches [1–7]. The former is usually caused by features other than the beginning and end points, intersections, contours, and unevenness; whereas the latter is mostly due to the density and feature area of handwritten pointers, and it is easier to mitigate the impact of irregular writing. However, traditional image processing algorithms focusing on static feature analysis at pixel level meet tremendous difficulties in MNIST handwriting recognition due to the two primary causes: 1) the glyph information for Arabic numerals is scarce and may share common features over different numbers; 2) the handwriting varies dramatically from person to person, and some features may only occur under very specific but rare scenarios. These challenges mandate the use of dynamic information, such as the coordinates of the stroke trajectory point [8–13]. In recent years, there is a growing interest in using prevailing machine learning (ML) techniques in handwriting classification with outstanding performance and generalization capabilities. By combining aforementioned typewritten features with traditional classification methods, such as k-Nearest Neighbor (k-NN) and histogram of dimensional gradient (HOG) features [5,11], statistical classification model [14–18], support vector machine (SVM) [19–21] and clustering [22,23], the classification and recognition accuracy has been tremendously promoted.
In comparison to these approaches that rely on manual feature extraction, convolutional neural network (CNN)-based deep learning (DL) architectures, which is also known as deep neural networks (DNNs), can automatically extract the implicit correlation within and amongst data to find useful patterns [5,24–26]. DNNs can process both shallow and deep features of the data in a thorough manner to produce more abstract and higher-level features with stronger semantic information [27–32]. Additionally, they are easier to design, modularize, and modify for different applications. By replacing the fully linked layer section of CNNs by Gated Recurrent Units (GRU), Vantruong Nguyen merged CNNs and GRU and achieve a recognition accuracy of up to 99.21% [20]. Typically, in order to achieve a higher recognition rate, more complex algorithm is required, which demands more computational time and higher space usage. However, the increasing number of hidden layers in the DNN may degrade the network’s capacity for generalization. As a result, using CNNs to accomplish error-free MNIST recognition remains difficult, and there really is no methodology which can reach a 100% classification performance for distinct character traits.
This paper is organized as follows. The key CNN design method is introduced in Section 2, focusing on the design of feature extraction, classification method, hyper-parameter optimization, over-fitting prevention strategy, and model verification strategy. The model structure design and optimization analysis, particularly the experimental results of model performance validation, are discussed in Section 3. Finally, the fourth part summarizes the paper.
2 The Proposed Approach for MNIST Handwritten Digit Classification
The core steps of CNN-based recognition model primarily include extraction, classification yield, and backpropagation to alter parameters in the network. The overall algorithm design process is presented in Fig. 1, where training, validation and testing share the similar process, except for using different datasets and the trained parameters are fixed during the validation and testing process. The validation samples are utilized for cross-validation at the end of each training epoch/iteration. In order to maximize CNN classification accuracy and highlight extraction for MINST recognition, a multi-layer deep arrange structure is constructed upon Keras and/or Tensorflow, which includes three convolution and activation layers for feature extraction and two fully connected layers (i.e., dense layers) for classification (Fig. 2). The optimization strategy of hyperparameters (e.g., batch sizes, kernel sizes, batch normalization, activation function, dropout rate, etc.) is illustrated afterwards to get the best performance from the model.
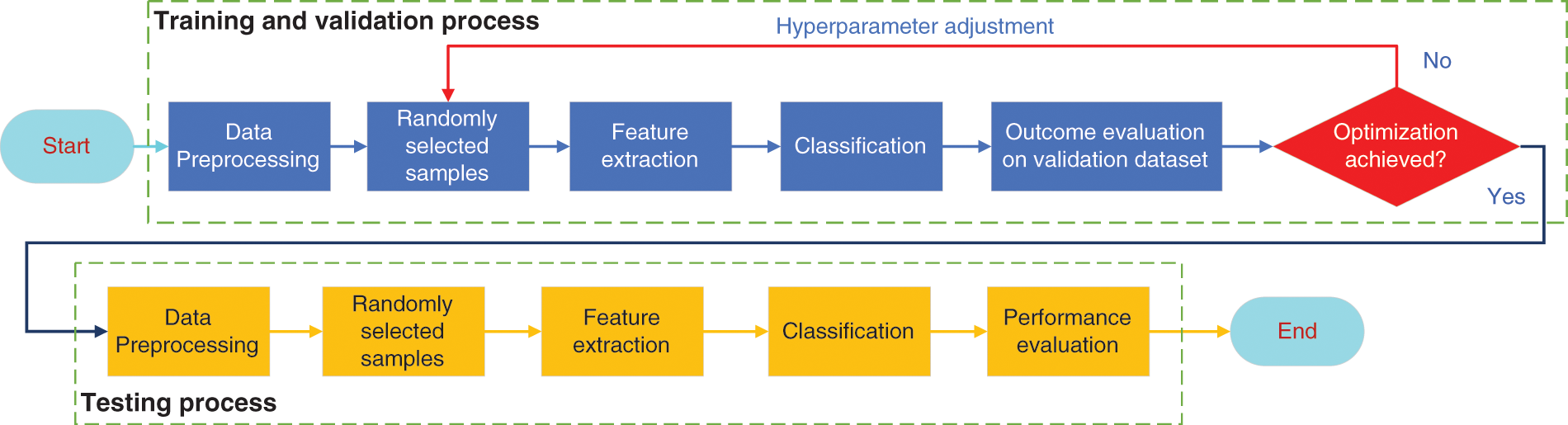
Figure 1: The proposed DL-based data processing diagram
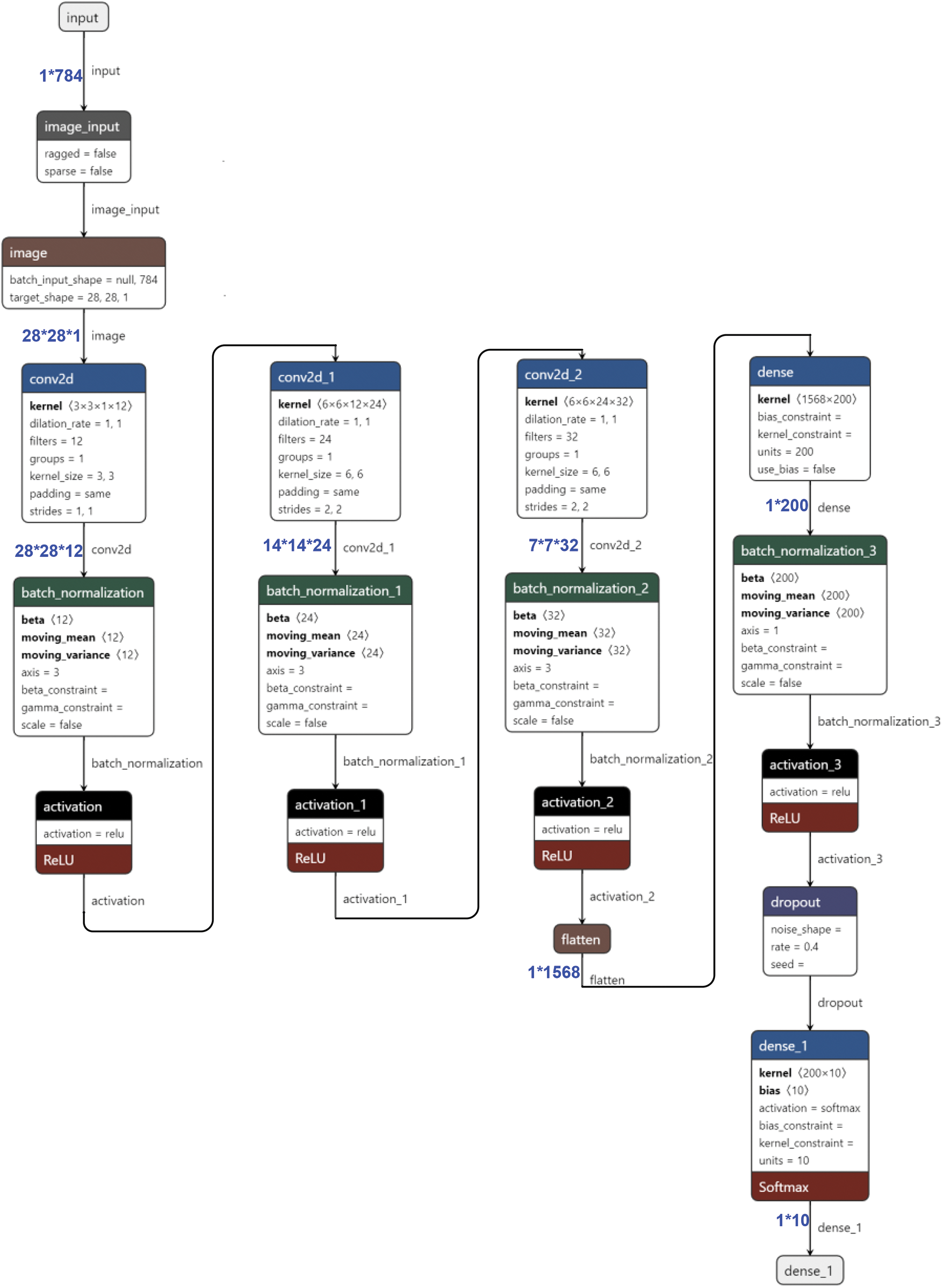
Figure 2: The architecture of the designed CNN model
2.1 Deep Neural Network Design
CNNs rely on multiple convolutional layers and non-linear layers (e.g., activation layer) for feature extraction, and key features can be retained through feature reduction techniques (e.g., max pooling, etc.). Detail steps can be specified as follows: 1) convolution layers can be employed multiple times throughout the DNN; each convolution layer can be individually implemented by the Keras/Tensorflow built-in two-dimensional (2D) convolution function, with appropriate kernel size, stride steps, input and output channels; “Padding” is set to ‘SAME’ so that the output of the convolution function remains the same size as the input; 2) initialize each neuron/kernel in each CNN layer with a weight matrix and a bias scalar; to avoid the vanishing gradient problem and break the symmetry of neurons, a truncated normal distribution with a standard deviation of 0.1 is employed to initialize the weight matrix; in addition, for sake of avoiding the “death” of the neuron node (i.e., the output is always 0), a small positive number (e.g., 0.1) needs to be used to initialize the bias term; 3) batch normalization may be exploited to regulate the convoluted results within a certain range, to facilitate the following Rectified Linear Unit (ReLU) as the activation function to extract the features; 4) max pooling and/or other data reduction techniques are optionally applied to reduce the data dimension and computational cost, as well as to retain the key features.
The output of the last convolutional layer includes the extracted features, which are flattened into a one-dimensional tensor and then forwarded to two fully connected (i.e., dense) layers. A Softmax layer is connected after the last fully connected layer to predict the likelihood of each category for each sample. The class with the highest probability is chosen as the sample’s predicted category.
In this study, three convolution layers are exploited for feature extraction (Fig. 2). The first layer is equipped with a kernel of 3 × 3 and a stride of (1, 1), while the other two use a kernel of 6 × 6 and a stride of (2, 2) for two main purposes: 1) speeding up the converging rate with larger kernel size in deeper layers, and 2) use larger stride as an alternative to the max pooling layer for data dimension reduction. After three convolution layers, each of which is accompanied with a batch normalization and an activation layer, a total number of 1568 features are extracted and fed to two dense layers for classification. Finally, the output layer has 10 nodes for the 10 different number digit categories.
2.2 Model Hyperparameter Optimization Strategy
Once a CNN backbone architecture is established, detailed hyperparameters (e.g., batch size, learning rate, etc.) need to be tweaked to determine the best shape of this CNN model to fit the training and validation dataset, with a hope of achieving the best performance (e.g., accuracy, loss, etc.) upon other general data of the same kind.
2.2.1 Batch Size Analysis and Selection Method
The training batch size frequently has a significant impact on the training outcomes. Too small batch size results in long training time and even may generate severe gradient oscillations, which will make the models converge slowly or even impossible. In contrast, too large value may lure the model to converge to a local rather than a global optimal value. Consequently, it is challenging to get the ultimate ideal solution through training. Thus, by appropriately adjusting the batch size, it is possible to effectively increase memory utilization, increase the parallel efficiency of high-dimensional matrix multiplication, reduce training time and the likelihood of gradient oscillation, pushing the model convergence to the optimal results. Empirically, the global batch size can be set as Batch_size = 128*Number of Accelerators (e.g., parallel network replicas); tf.data will automatically split the global batch size among all replicas.
2.2.2 Learning Rate Decay Technique
When an alternative mini-batch gradient descent method is available for training because of the intriguing project’s noise, employing a fixed learning rate leads the error to decline and evolves toward the local minimum, but may eventually oscillate around rather than truly converges at the global optimal point. Thus, the learning rate should be gradually decreased throughout the training process to minimize this problem. The research uses the attenuation of learning rate to strike a compromise between rapid convergence and stability. A relatively large initial training step size can be utilized to speed up the training convergence at early stage, and then it is gradually decreased to approach the global optimum, or swing back and forth in the vicinity of the optimum, as the strategic alignment and hidden layers are intensified to improve the training accuracy at convergence. This prevents gradient descent from falling into local minimum values or even gradient divergence.
2.2.3 Techniques to Prevent Overfitting
Generally speaking, deep learning networks are susceptible to overfitting problems: the model’s performance on both the training and validation datasets improves over the training iterations, but drops on the validation dataset after a certain number of iterations while it continues to rise on the training dataset. This indicates that the model fits the training sample too closely, limiting its generalizability. In addition, encoding sample labels (e.g., one-hot encoding) may unnecessarily increase the difference between the full probability and zero probability categories, causing the prediction model to rely excessively on the predicted category, thereby increasing the likelihood of overfitting.
Common approaches to ameliorate this issue includes 1) reasonable data fitting and 2) using one or more “Dropout” layers to nullify a random portion of the trained parameters in the CNN after each training epoch. This work analyzes the incorrect predictions on the dataset to avoid overfitting and achieve the highest classification accuracy. Whenever the model’s performance on the validation set begins to deteriorate during the training process, the model’s training is interrupted and the trained parameters are preserved to avoid the overfitting induced by excessive training. By doing so, a model with the minimum validation loss and potentially better test outcomes can be achieved. In this study, if the validation loss stops dropping and starts to converge or increase in two consecutive training epochs, the training process should be stopped, and the epoch when the local validation loss is the lowest, or validation accuracy is the highest, must be noted to ease the process of reloading model parameters for model deployment.
2.2.4 Model Validation and Evaluation
In order to evaluate the built model, the cross-entropy, Eq. (1), is employed as the COST function to quantify the loss of the model outcomes. The index is minimized over the training process to improve the recognition ability of the model.
where y and
3.1 MNIST Handwritten Digit Dataset
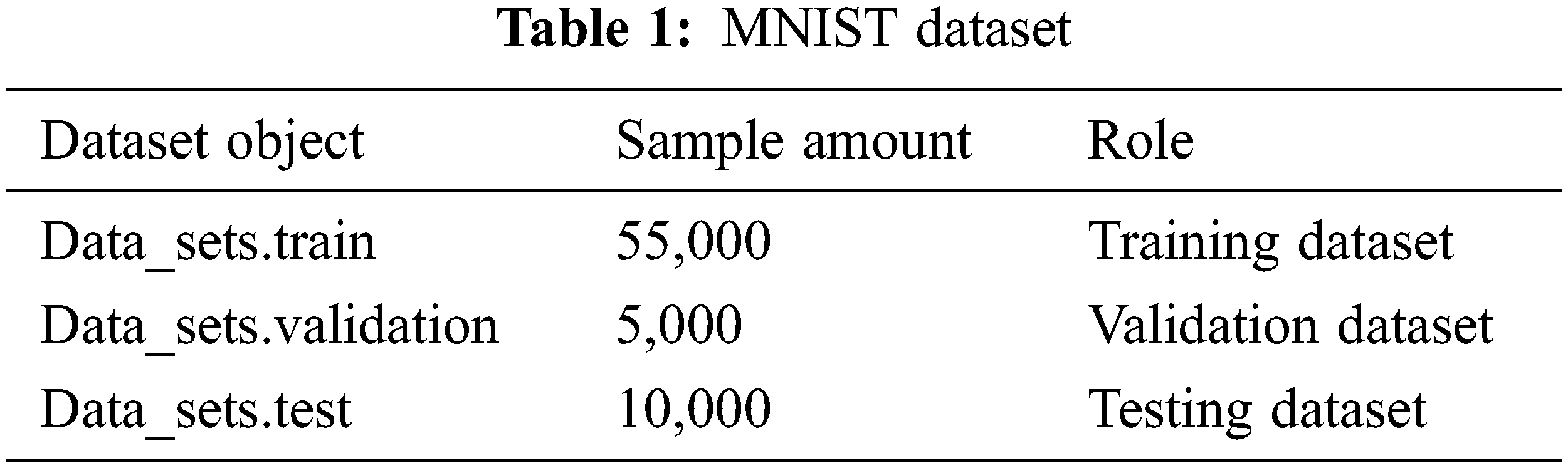
MNIST database is one of the foremost classical imaging datasets within the field of machine learning, and is broadly utilized for benchmarking in image classification. The MNIST database contains 60,000 training samples and 10,000 testing samples (Table 1), each consisting of a 28*28 pixel grayscale image of a handwritten Arabic digit. The number sample in each image is normalized/standardized and centered. The 60,000 training samples are further divided into 55,000 training dataset and 5,000 validation dataset.
3.2 Model Hyperparameter Optimization
i) Placeholder and parameter setting.
A placeholder is created for each input image and its label: X represents the one-dimensional (1*784) vector associated with a 28*28 image, and Y represents the corresponding label (i.e., the ground truth of classification). Subsequently, the one-dimensional image vector is transformed into a two-dimensional matrix, i.e., the image data vector of 1*784 is converted into the original structure of 28*28. Since the MNIST is a grayscale image dataset, the color channel for each image is 1 (3 for RGB images). For training and testing with different numbers of images, the conversion number is set to −1, indicating an indefinite number, for automatic matching of the number of images.
ii) The design of convolutional layer and activation layer.
In the first layer, the size of the convolution kernel is set to be 3 × 3, and the weight and bias terms are initialized. The output channel is 12 to extract 12 different features. Then, the inner product of the convolution kernel and the input is computed, and the bias term is added to the convolution result. A batch normalization layer is employed to regulate the convolution results, followed by an ReLU activation function/layer for non-linear processing and feature extraction. The second layer is also a combination of convolution, batch normalization and activation functions, but with a kernel size of 6*6 and a stride of (2, 2) in the convolution layer, which reduces the image tensor size to a half, i.e., 14*14. In addition, the number of features is increased to 24. The third layer is similar to the second in kernel size and stride, but is extended to 32 features in total. In the end, the output of the third layer is flattened to a 1* (7*7*32) = 1*1568 tensor, fed to the following fully connected layers for classifications.
iii) Fully connected layers and dropout layer for classification and overfitting reduction.
The first fully connected layer has 200 hidden nodes, and an ReLU activation function is applied afterwards to make the input with bias terms have nonlinear characteristics. The Dropout is employed during training to randomly discard 40% of the trained neurons (i.e., weights and biases) to reduce overfitting. The output of the second dense layer is connected to the Softmax classifier to obtain the probability of each category of classification, and the class with the highest probability is selected as the predicted class of the corresponding sample. When the neural network model is validated, all nodes are retained to obtain the best predictive classification performance.
3.3 Learning Rate Attenuation and Classification Analysis
As aforementioned that a variable learning rate should be considered to achieve the optimum training outcomes, in this paper, exponential decay is used as the learning rate decay method. The initial learning rate is set at 0.001 and the learning rate decay factor is set at 0.99. As a result, the recognition accuracy of the model has been significantly improved by 2.9% on the test set, while the loss has been drastically reduced. The improvements in accuracy of various numbers/classes are also observed. This shows that the learning rate decay can effectively improve the recognition accuracy of the MNIST handwritten dataset.
3.4 Model Optimization and Performance Evaluation
By defining the cross-entropy loss function and a small value of the initial learning rate (i.e., 1*10−3), the Adam optimizer is used to automatically to minimize the loss function during the training process. In this process, the loss will be backpropagated to adjust the network parameters to better fit the training sample data. Here, the batch size is set to 1000, which means 1000 training samples are sent to the model for training with random gradient descent. The proper batch size can reduce computational overhead while generalize the overall characteristics of the dataset. The dropout rate is set to 0.4. One can see that the training loss and accuracy converge within 10 iterations (Table 2) and each iteration uses 5000 validation samples for cross-validation (Table 1 and Fig. 3). Some of the predicted digit with recognition rate are shown in Fig. 4. Over the training process, the model’s classification accuracy improves, the loss decreases, yet the best validation performance is achieved at Epoch 8 (Fig. 3). Visualization of the training and validation dataset is provided in Fig. 5, and some of the validation digits with incorrect predictions are provided in Fig. 6.
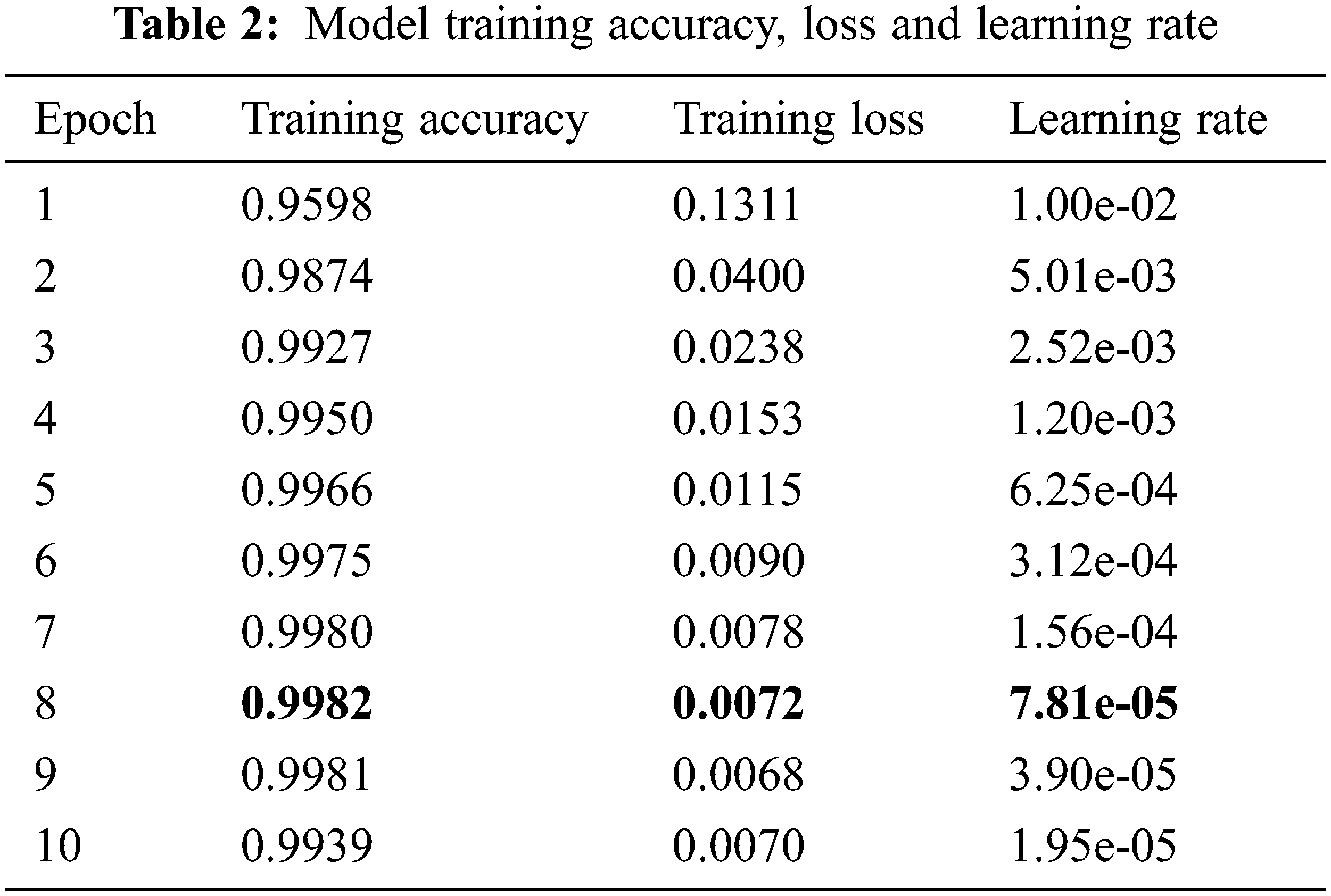
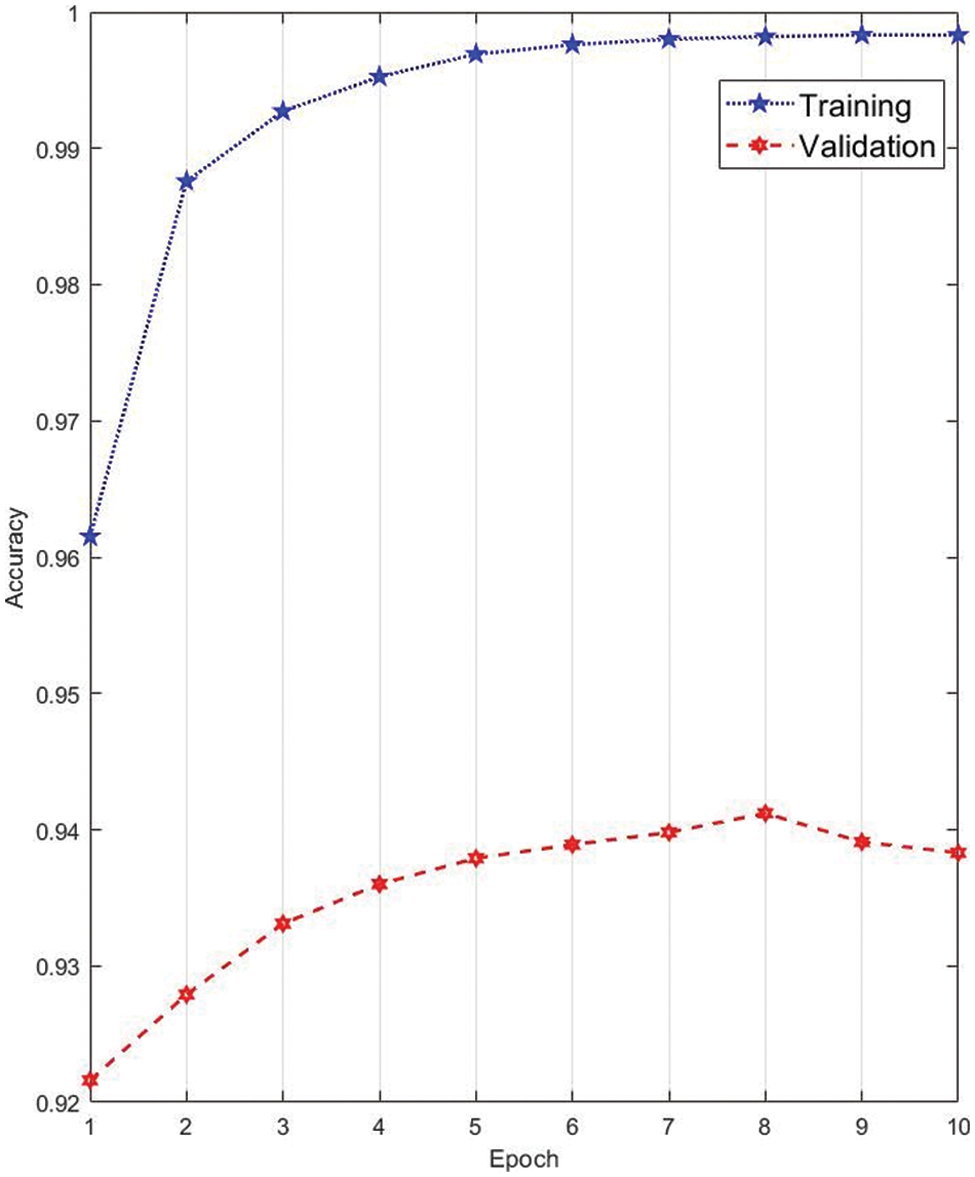
Figure 3: Training and validation accuracies
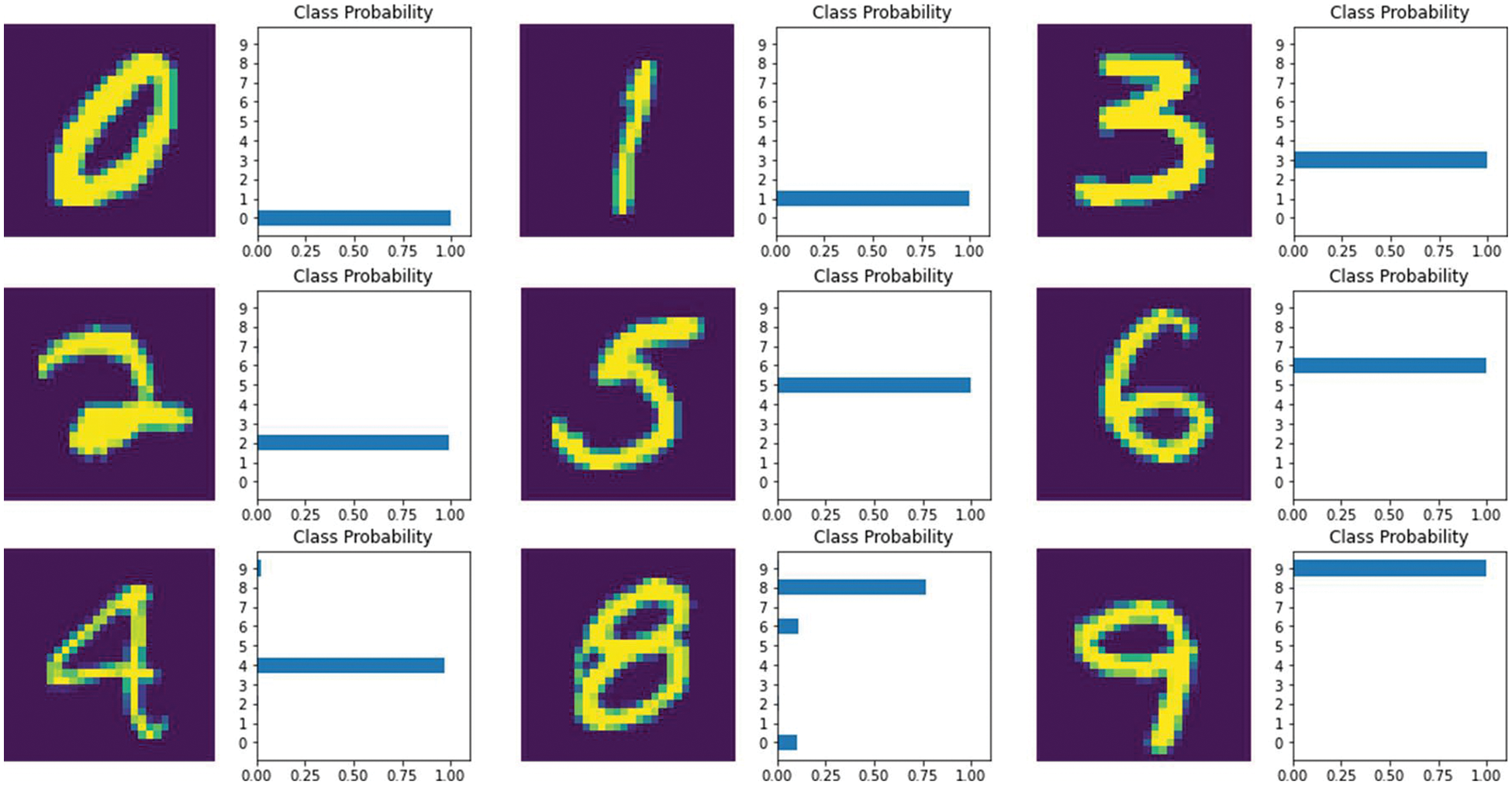
Figure 4: Some of the predicted digit with recognition rate

Figure 5: Visualization of the training and validation dataset
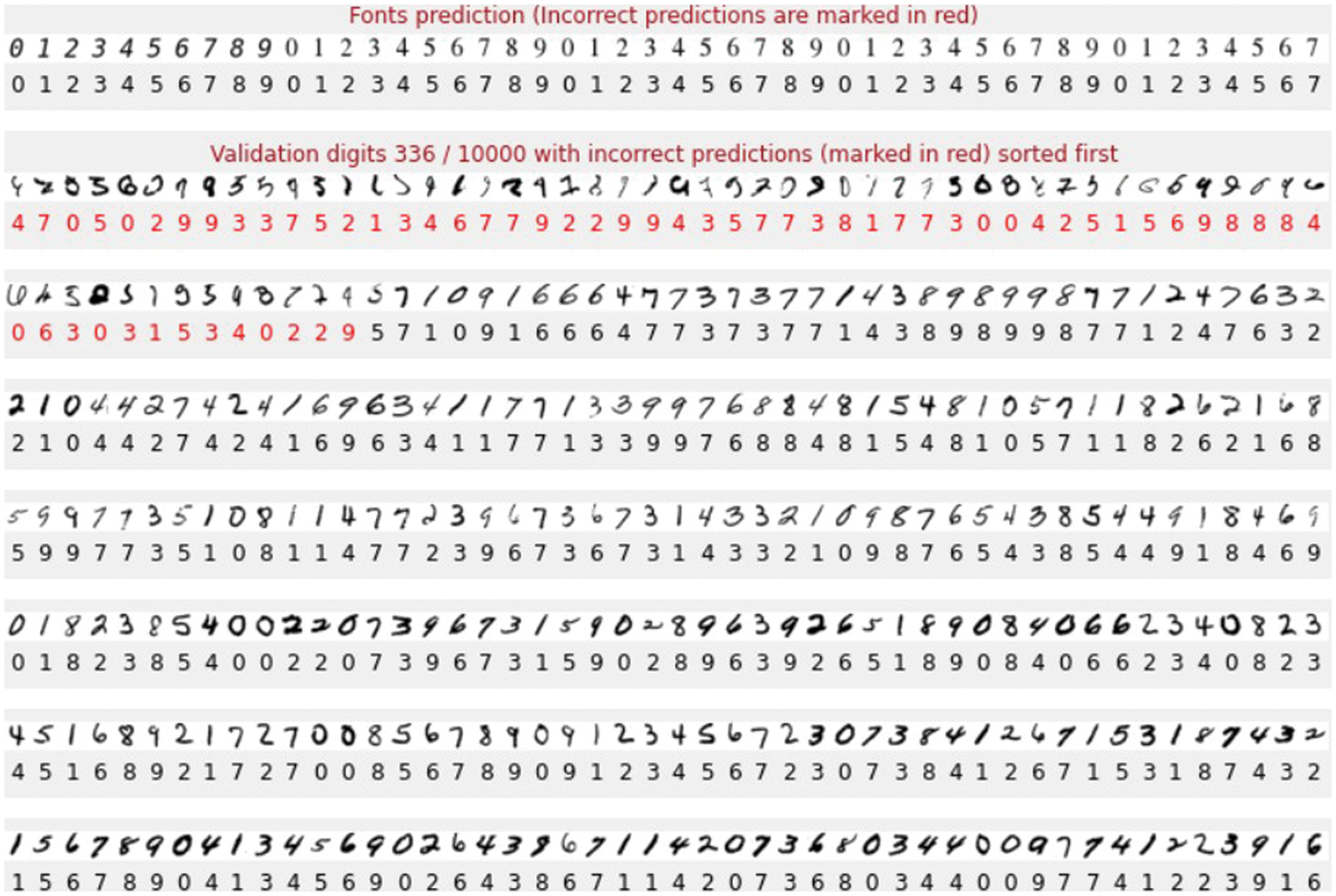
Figure 6: Some of the validation digits with incorrect predictions
The testing dataset is finally examined to verify the entire training and validation process, and achieve an accuracy of 99.40% and loss of 0.0171. The performance of the model on the test set resembles the training results. On the other hand, the accuracy rates vary on different digits. For example, 97% of number “6” are correctly classified while “1” reaches 100%. Fig. 7 displays figures that are challenging to recognize correctly. Additionally, the convolution kernels provide the feature set of the input pictures, and they can be used to visualize the characteristics of the input images. However, there is currently no efficient analysis method for thoroughly evaluating and modelling the significance of each neuron in convolutional layers because it contains lots of high-dimensional elements which are difficult to comprehend intuitively. Nevertheless, assessing the features extracted by each convolution kernel by analyzing the model with a larger sample and displaying the output of each layer is still beneficial. The classification accuracy of the proposed structure is compared with other state-of-the-art models (Table 3), and has demonstrated significant improvement in classification accuracy.
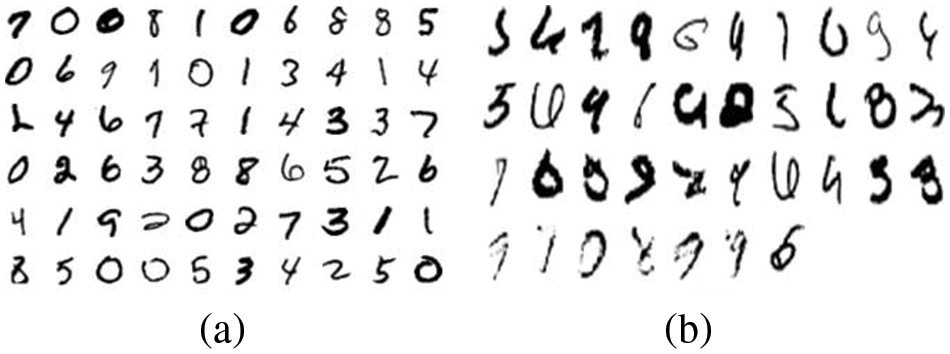
Figure 7: (a) Numbers with high recognition rates; (b) Numbers with low recognition rates
This study elaborates the details of developing a light-weight DNN for handwriting digital recognition/classification using the MNIST dataset. The CNN-based backbone architecture and the methodology of numerous hyperparameter optimizations, including batch size, learning rate, etc., are explored in detail to enhance the training and testing outcomes. The developed neural network model is evaluated upon Keras/Tensorflow framework, and the overall accuracy of the developed model can reach 99.4% on the MNIST dataset, compatible with the results from other state-of-the-art models.
Acknowledgement: We would like to thank the editors and anonymous reviewers for their thoughtful comments and efforts towards improving our manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Z. Gao, Y. Li and S. Wan, “Exploring deep learning for view-based 3D model retrieval,” ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM), vol. 16, no. 1, pp. 1–21. 2020. [Google Scholar]
2. Z. Gao, H. Z. Xuan, H. Zhang, S. Wan and K. K. R. Choo, “Adaptive fusion and category-level dictionary learning model for multiview human action recognition,” IEEE Internet of Things Journal, vol. 6, no. 6, pp. 9280–9293, 2019. [Google Scholar]
3. R. Herrera-Pereda, A. T. Crispi, D. Babin, W. Philips and M. H. Costa, “A review on digital image processing techniques for in-vivo confocal images of the cornea,” Medical Image Analysis, vol. 73, pp. 102188, 2021. https://doi.org/10.1016/j.media.2021.102188 [Google Scholar] [PubMed] [CrossRef]
4. R. Janeliukstis and X. Chen, “Review of digital image correlation application to large-scale composite structure testing,” Composite Structures, vol. 271, pp. 114143. 2021. [Google Scholar]
5. S. R. Lowe, “Pattern recognition in handwriting,” in Advances in Pattern Recognition and Artificial Intelligence, World Scientific, pp. 77–95, 2021. https://doi.org/10.1142/9789811239014_0005 [Google Scholar] [CrossRef]
6. Y. Zhao, H. Li, S. Wan, A. Sekuboyina, X. Hu et al., “Knowledge-aided convolutional neural network for small organ segmentation,” IEEE Journal of Biomedical and Health Informatics, vol. 23, no. 4, pp. 1363–1373, 2019. [Google Scholar] [PubMed]
7. S. Bera, V. K. Shrivastava and S. C. Satapathy, “Advances in hyperspectral image classification based on convolutional neural networks: A review,” CMES-Computer Modeling in Engineering & Sciences, vol. 133, no. 2, pp. 219–250, 2022. [Google Scholar]
8. K. Cheng, R. Tahir, L. K. Eric and M. Li, “An analysis of generative adversarial networks and variants for image synthesis on MNIST dataset,” Multimedia Tools and Applications, vol. 79, no. 19, pp. 13725–13752, 2020. [Google Scholar]
9. A. Jain and B. K. Sharma, “Analysis of activation functions for convolutional neural network based mnist handwritten character recognition,” International Journal of Advanced Studies of Scientific Research, vol. 3, no. 9, pp. 1–7, 2019. [Google Scholar]
10. S. Tabik, R. F. Alvear-Sandoval, M. M. Ruiz, J. L. Sancho-Gómez, A. R. Figueiras-Vidal et al., “MNIST-NET10: A heterogeneous deep networks fusion based on the degree of certainty to reach 0.1% error rate. Ensembles overview and proposal,” Information Fusion, vol. 62, pp. 73–80, 2020. https://doi.org/10.1016/j.inffus.2020.04.002 [Google Scholar] [CrossRef]
11. S. Wan, S. Ding and C. Chen, “Edge computing enabled video segmentation for real-time traffic monitoring in internet of vehicles,” Pattern Recognition, vol. 121, pp. 108146, 2022. https://doi.org/10.1016/j.patcog.2021.108146 [Google Scholar] [CrossRef]
12. Y. Wang, N. Afzal, S. Fu, L. Wang, F. Shen et al., “MedSTS: A resource for clinical semantic textual similarity,” Lang Resources & Evaluation, vol. 54, no. 1, pp. 57–72, 2020. [Google Scholar]
13. Y. Wang, F. Li, H. Sun, W. Li, C. Zhong et al., “Improvement of MNIST image recognition based on CNN,” in IOP Conf. Series: Earth and Environmental Science. 7th Annual Int. Conf. on Geo-Spatial Knowledge and Intelligence, Guangzhou, China, vol. 428, no. 1, 2020. https://doi.org/10.1088/1755-1315/428/1/012097 [Google Scholar] [CrossRef]
14. D. Chen, Y. Tian and X. Liu, “Structural nonparallel support vector machine for pattern recognition,” Pattern Recognition, vol. 60, pp. 296–305, 2016. [Google Scholar]
15. S. S. Kadam, A. C. Adamuthe and A. B. Patil, “CNN model for image classification on MNIST and fashion-MNIST dataset,” Journal of Scientific Research, vol. 64, no. 2, pp. 374–384, 2020. [Google Scholar]
16. W. Liang, Y. Wu, M. Li and Y. Cao, “Adaptive multiple kernel fusion model using spatial-statistical information for high resolution SAR image classification,” Neurocomputing, vol. 492, pp. 382–395, 2022. https://doi.org/10.1016/j.neucom.2022.03.062 [Google Scholar] [CrossRef]
17. A. Palvanov and Y. Cho, “Comparisons of deep learning algorithms for MNIST in real-time environment,” International Journal of Fuzzy Logic and Intelligent Systems, vol. 18, no. 2, pp. 126–134, 2018. [Google Scholar]
18. Z. Xue, M. Zhang, Y. Liu and P. Du, “Attention-based second-order pooling network for hyperspectral image classification,” IEEE Transactions on Geoscience and Remote Sensing, vol. 59, no. 11, pp. 9600–9615, 2021. [Google Scholar]
19. S. R. Kulkarni and B. Rajendran, “Spiking neural networks for handwritten digit recognition—Supervised learning and network optimization,” Neural Networks, vol. 103, pp. 118–127, 2018. https://doi.org/10.1016/j.neunet.2018.03.019 [Google Scholar] [PubMed] [CrossRef]
20. V. Nguyen, J. Cai and J. Chu, “Hybrid CNN-GRU model for high efficient handwritten digit recognition,” in Proc. of the 2nd Int. Conf. on Artificial Intelligence and Pattern Recognition, New York, NY, USA, pp. 66–71, 2019. https://doi.org/10.1145/3357254.3357276 [Google Scholar] [CrossRef]
21. J. Yang, D. Parikh and D. Batra, “Joint unsupervised learning of deep representations and image clusters,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 5147–5156, 2016. [Google Scholar]
22. Z. Jan and B. Verma, “Multiple strong and balanced cluster-based ensemble of deep learners,” Pattern Recognition, vol. 107, pp. 107420. 2020. https://doi.org/10.1016/j.patcog.2020.107420 [Google Scholar] [CrossRef]
23. W. Xia, X. Zhang, Q. Gao and X. Gao, “Adversarial self-supervised clustering with cluster-specificity distribution,” Neurocomputing, vol. 449, pp. 38–47, 2021. https://doi.org/10.1016/j.neucom.2021.03.108 [Google Scholar] [CrossRef]
24. R. Plamondon, G. Pirlo, É. Anquetil, C. Rémi, H. Teulings et al., “Personal digital bodyguards for e-security, e-learning and e-health: A prospective survey,” Pattern Recognition, vol. 81, pp. 633–659, 2018. https://doi.org/10.1016/j.patcog.2018.04.012 [Google Scholar] [CrossRef]
25. P. Radoglou-Grammatikis, K. Rompolos, P. Sarigiannidis, V. Argyriou, T. Lagkas et al., “Modeling, detecting, and mitigating threats against industrial healthcare systems: A combined software defined networking and reinforcement learning approach,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 2041–2052, 2021. [Google Scholar]
26. S. Wan, Y. Xia, L. Qi, Y. Yang and M. Atiquzzaman, “Automated colorization of a grayscale image with seed points propagation,” IEEE Transactions on Multimedia, vol. 22, no. 7, pp. 1756–1768, 2020. [Google Scholar]
27. A. Garg, D. Gupta, S. Saxena and P. P. Sahadev, “Validation of random dataset using an efficient CNN model trained on MNIST handwritten dataset,” in IEEE in 2019 6th Int. Conf. on Signal Processing and Integrated Networks (SPIN), Noida, India, pp. 602–606, March 2019. https://doi.org/10.1109/SPIN.2019.8711703 [Google Scholar] [CrossRef]
28. Y. Jiang, J. Kang and X. Wang, “RRAM-Based parallel computing architecture using k-nearest neighbor classification for pattern recognition,” Scientific Reports, vol. 7, no. 1, pp. 1–8, 2017. [Google Scholar]
29. Z. Kayumov, D. Tumakov and S. Mosin, “Hierarchical convolutional neural network for handwritten digits recognition,” Procedia Computer Science, vol. 171, pp. 1927–1934, 2020. https://doi.org/10.1016/j.procs.2020.04.206 [Google Scholar] [CrossRef]
30. Y. Li, J. Ma and Y. J. Zhang, “Image retrieval from remote sensing big data: A survey,” Information Fusion, vol. 67, pp. 94–115, 2021. https://doi.org/10.1016/j.inffus.2020.10.0082021 [Google Scholar] [CrossRef]
31. P. Thangamariappan and J. C. Pamila, “Handwritten recognition by using machine learning approach,” International Journal of Engineering Applied Sciences and Technology, vol. 4, no. 11, pp. 564–567, 2020. [Google Scholar]
32. X. Zenggang, T. Zhiwen, C. Xiaowen, Z. Xue-min, Z. Kaibin et al., “Research on image retrieval algorithm based on combination of color and shape features,” Journal of Signal Processing Systems, vol. 93, no. 2, pp. 139–146, 2021. [Google Scholar]
33. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed et al., “Going Deeper with Convolutions,” Ithaca. NY, USA: Cornell University Press, 2014. [Online]. Available: https://arxiv.org/abs/1409.4842v1. [Google Scholar]
34. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens and Z. Wojna, “Rethinking the Inception Architecture for Computer Vision,” Ithaca. NY, USA: Cornell University Press, 2015. [Online]. Available: https://arxiv.org/abs/1512.00567v3. [Google Scholar]
35. F. Chollet, “Xception, Deep Learning with Depthwise Separable Convolutions,” Ithaca. NY, USA: Cornell University Press, 2017. [Online]. Available: https://arxiv.org/abs/1610.02357. [Google Scholar]
36. K. Simonyan and A. Zisserman, “Very Deep Convolutional Networks for Large-Scale Image Recognition,” Ithaca. NY, USA: Cornell University Press, 2014. [Online]. Available: https://arxiv.org/abs/1409.1556. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF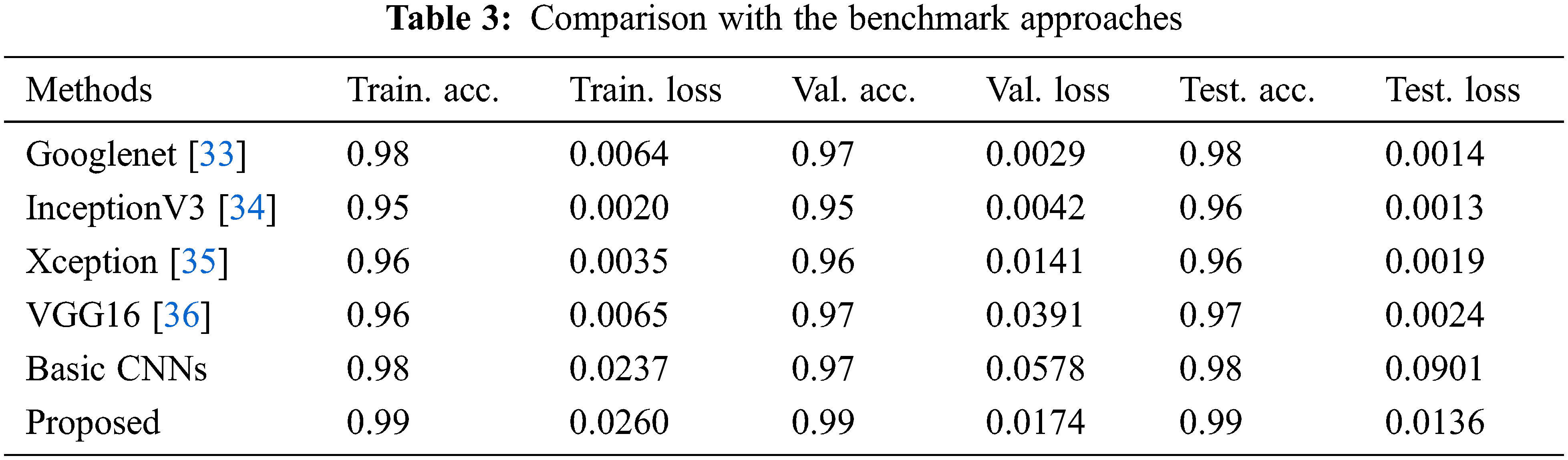
 Downloads
Downloads
 Citation Tools
Citation Tools