Adaptive Multi-Updating Strategy Based Particle Swarm Optimization

1  Introduction

Particle swarm optimization (PSO) is a swarm intelligent optimization algorithm that is based on the metaphors of social interaction and communication (e.g., bird flocking and fish schooling) [1]. Due to the merits of swarm intelligence, intrinsic parallelism, easy implementation, inexpensive computation and few parameters to be adjusted, PSO has drawn a great attention of numerous researchers in the field of evolutionary computation [2–8] and has been successfully applied in a wide range of optimization problems in many different areas in the past two decades [9–21]. However, like other nature-inspired evolutionary algorithms (EA), PSO still suffers from loss of diversity and slow convergence caused by the contradiction between exploration and exploitation, especially when dealing with complex multimodal problems. This will inevitably impair the performance of particle swarm optimization to a large extent. To this end, a large number of PSOs have been developed from different perspectives to circumvent these issues in literature [2,4–12]. It is known that the performance of PSO is heavily dependent on the parameters associated with the update scheme. Concerning the inertia weight, it is believed that the overall performance of PSO is strongly affected by the inertia weight through balancing the exploration and exploitation during the search process. As a consequence, much research effort has been devoted to the development of various types of inertia weight, including fixed-value [22], linear [23], nonlinear [2], random [3], fuzzy rules [9], chaos [4], and others [5]. Regarding the acceleration coefficients, it is reported that the appropriate acceleration coefficients can enhance the global search in the early stage of the optimization and to encourage the particle to converge towards the global optima at the end of the search process. From the literature, it can be seen that a variety of acceleration coefficients, ranging from fixed-value [1], linear [6], nonlinear [10] and random [11] to adaptive paradigm [7], have been introduced into the update scheme of PSO to get a better trade-off between the global and local search abilities. Hence, this work will further investigate the effects of the acceleration coefficients and employ different values of them to enhance the performance of PSO according to the different statuses of particle. Besides, the two random numbers in PSO system also have a significant influence on the convergence behavior of the swarm [8,12], especially the chaotic sequence, instead of the random number, is used in the velocity update equation [12]. To strike a better balance between exploration and exploitation, this paper proposes an adaptive multi-updating strategy based particle swarm optimization (AMS-PSO). On the one hand, the chaos-based sequence is used to generate high-quality initial particles to accelerate the convergence rate of AMS-PSO. On the other hand, according to current iteration, different update schemes are leveraged to regulate the particle search process at different evolution stages. Specifically, two different sets of velocity update strategies are utilized to enhance the exploration ability in the early stage while the other set of update strategy as well as the Gaussian mutation is applied to improve the exploitation capability in the later stage. Followed by the unequal weightage of acceleration coefficients is harnessed to guide the search for the global worst position (gworst) of particle so as to strengthen the swarm diversity. Besides, an auxiliary update strategy is exclusively applied to the global best position (gbest) of particle in order to ensure the convergence of the proposal. In actual fact, the key idea behind AMS-PSO is somewhat similar to multi-swarm based PSOs, viz., different update scheme is used for different subgroup of particles so as to enhance the communications within and between subgroups. At length, conducted experiments validate the superiority of AMS-PSO over several existing competitive PSO variants in the literature.

The rest of this paper is organized as follows. Section 2 discusses the related work, involving the update strategies based on acceleration coefficients, gworst particle, and gbest particle, respectively. In Section 3, the standard particle swarm optimization is briefly introduced. Section 4 elaborates on the proposed AMS-PSO from three aspects of swarm initialization, update scheme for the gbest particle and update scheme for the gworst and other particles, respectively. In Section 5, extensive experiments on two sets of well-known benchmark functions are reported and analyzed. Finally, the concluding remarks and future work are discussed in Section 6.

2  Related Work

Ever since the introduction of particle swarm optimization in 1995, researchers have been working hard to explore more and more efficient PSOs from different aspects to enhance their performance. Loosely speaking, most of the current existing PSO variants can be roughly classified into the following five categories:

(i)   Swarm initialization. As a crucial step in any evolutionary computation, swarm initialization has a great effect on the convergence rate and the quality of the final solution. The most common method is random initialization which is used to generate initial particles without any prior information about the solution to the problems [24]. To produce high-quality initial particles, several advanced swarm initialization methods, including chaos-based sequence [25], opposition-based learning method [12], chaotic opposition-based learning method [26], and other initial strategies [27], have been developed and widely applied in the field of swarm intelligence optimization with substantial performance improvement.

(ii)   Parameter selection. Proper parameters can significantly affect the performance of particle swarm optimization. In general, an appropriate inertia weight can achieve an effective balance between exploration and exploitation. A larger inertia weight is beneficial for global exploration whereas a smaller one is conducive to local exploitation for fine-tuning the current search region [23], such as fitness-based dynamic inertia weight [12], sigmoid-based inertia weight [2] and chaotic-based inertia weight [28], to name a few. By changing inertia weight dynamically, the search capability of PSO can be also dynamically adjusted. Besides, both acceleration coefficients [7] and random numbers [12] have a significant effect on the convergence behavior of swarm. All of them have been deeply studied in the literature and widely applied in many real-world optimization problems.

(iii)   Topology structure. The neighborhood topology aims to enrich the swarm diversity and undoubtedly influence the flow rate of the best information among particles. The early notable topologies include circle, wheel, star, and random topology [29]. Instead of using the fixed neighborhood topology, the dynamic multi-swarm PSO variants are developed in literature [13], whose basic idea is that a larger swarm is divided into many small-sized sub-swarms that can be regrouped after a predefined regrouping period. Besides, a ring topology in exemplar generation is adopted to enhance the swarm diversity and exploration ability of the genetic learning PSO [30]. Compared with basic PSO, it is not difficult to see that the topology structure-based PSOs have a more powerful ability in keeping the swarm diversity and preventing premature convergence.

(iv)   Learning strategy. PSO adopts different learning strategies to regulate global exploration and local exploitation that has attracted considerable attention. It’s known that a particle usually learns from its history personal best and the global best of the entire swarm, but such a learning strategy tends to cause particle to oscillate between the two exemplars when they are located on the opposite sides of the candidate particle [14]. Hence, a variety of learning strategy-based PSO variants have been proposed in this regard, such as heterogeneous CLPSO [31], hybrid learning strategies-based PSO [32], PSO with elite and dimensional learning strategies [33], PSO with enhanced learning strategy [34], to keep swarm diversity and to avoid premature convergence.

(v)   Hybrid mechanism. Since each algorithm has its own merits and demerits, two methods are usually complementary to each other and the combination makes them benefit from each other. Based on this recognition, the goal of hybrid PSO with other meta-heuristics or auxiliary search techniques is to well balance the global search and local search without being trapped into local optima. Classical work includes hybrid PSO with genetic algorithm [15], hybrid PSO with artificial bee colony [35], integrating PSO with firefly [36], hybrid PSO with gravitational search algorithm [16], hybrid PSO with chaos searching technique [17] and so forth. Besides, the most often used genetic operators (crossover [34] and mutation [26]) are integrated into PSO to enhance the diversity of swarm.

As reviewed above, most of the PSOs can achieve state-of-the-art performance and motivate us to explore more efficient particle swarm optimization algorithms with the help of their excellent experiences and knowledge. Different from previous studies of the related work, here, we exclusively focus on the existing PSO update schemes in the literature from the aspects of acceleration coefficients, gworst particle, and gbest particle, respectively. More details can be found in the following sections.

2.1 Review of Acceleration Coefficients-Based Updating Strategy

From the literature, it can be clearly observed that acceleration coefficients can be divided into two categories: fixed-value [1] and time-varying [7]. For the limited space, here we only provide a brief survey on the constant acceleration coefficients. Since the introduction of the acceleration factors into the update scheme of PSO, they come into effect on the movement of particle, particularly they are greatly importance to the success of PSO in both the social-only model and the cognitive-only model. A large value of the acceleration factor c1 makes a particle fly towards its own ever-known best position (pbest) faster and a large value of the acceleration factor c2 makes a particle move towards the best particle (gbest) of the entire swarm faster. In general, c1 and c2 are set equal (c1 = c2 = 2) [1] to give equal weightage to both the cognitive component and the social component simultaneously. In [37], the acceleration coefficients are also set equal (c1 = c2 = 2.05) to control magnitudes of particle’s velocity and to ensure convergence of particle swarm optimization. As for the values of c1 and c2, it is reported that acceleration coefficient with big values tends to cause particle to separate and move away from other, while taking small values causes limitation of the movements of particle, and not being able to scan the search space adequately [38].

Alternatively, it is to be noted that particles are allowed to move around the search space rather than move toward the gbest with a large cognitive component and a small social component in the early stage. On the contrary, a small cognitive component and a large social component allow particle to converge to the global optima in the latter stage of the search process. Based on this argument, much research effort is devoted to the development of unequal acceleration coefficients for PSO [12,18,39,40]. In the early work [39], the cognitive and social values of c1 = 2.8 and c2 = 1.3 yield good results for their chosen set of problems. In literature [40], the acceleration coefficients c1 and c2 are first initialized to 2 and adaptively controlled according to four evolutionary states: increasing c1 and decreasing c2 in an exploration state, increasing c1 slightly and decreasing c2 slightly in an exploitation state, increasing c1 slightly and increasing c2 slightly in a convergence state, and decreasing c1 and increasing c2 in a jumping-out state. To accelerate the convergence, a larger value is assigned to the social component (c1 = 0.5, c2 = 2.5) [18], which enables the convergence rate of PSO to be markedly improved than that with an equal setting of c1 = 1.5 and c2 = 1.5. Besides, the unbalanced setting of c1 and c2 (c1 = 3, c2 = 1) is exclusively used for gworst particle whereas the balanced setting of c1 and c2 (c1 = c2 = 2) is used for all the other particles [12]. It draws direction of the newly updated particle towards its pbest. That is, the unequal weightage is only applied in the case of stagnation of the particle that helps the newly generated particle to avoid drifting towards the gbest and explore a new region in the search space. Thus it can avoid stagnation of swarm at a suboptimal solution. In sum, proper adaptation and proper value setting of c1 and c2 can be promising in enhancing the performance of PSO. This is the main motivation to develop AMS-PSO in this work by varying the value of acceleration coefficients to control the influence of cognitive information and social information, respectively.

2.2 Review of the gworst Particle-Based Updating Strategy

In PSO system, the personal best position (pbest) and global best position (gbest) play an important role in regulating particle search around a region. In contrast, there is almost no research and analysis about the global worst position (termed as gworst) in literature. However, just as the cask effect says that how much water a wooden bucket can hold does not depend on the longest board but the shortest board, which can increase the water storage of the wooden bucket by replenishing the length of the shortest board and eliminating the restricting factors formed by this short board. Similarly, gworst particle does not mean that the particle does not contain any valuable information for the search process. All particles may carry useful information, and the performance of the entire swarm may be enhanced to some extent by strengthening the worst particle. Inspired by this argument, the personal worst position (pworst) and the gworst of particles are introduced into the velocity update equation as a means to dictate the motion of particle [41]. Afterward, only the pworst is integrated into the basic update scheme to help particles to remember their previously visited worst position [19]. This modification is beneficial for exploring the search space very effectively to identify the promising solution region. Likewise, only gworst particle is embedded in the velocity update equation that is called impelled or penalized learning according to the corresponding weight coefficient to balance the exploration and exploitation abilities by changing the flying direction of particles [42]. Subsequent work [43] incorporates both pworst and gworst into the update scheme to ensure that the extra velocity given from the worst position is always in the direction of the best position as well as the extra velocity given to a particle is maximized when the particle is at its worst position and decreases as the particle moves away.

To increase swarm diversity and to avoid local optima, a fourth part is added to the standard velocity update scheme that enables particles to move away from the gworst can disturb particle distribution and make swarm more diversified [20]. In literature [12], the gworst particle is updated based on an unequal acceleration factors c1 = 3 and c2 = 1 while the other particles are updated with the equal setting of c1 = 2 and c2 = 2. Unlike the traditional update scheme, the worst replacement strategy is used to update swarm, whereby the gworst in swarm is replaced by a better newly generated position in [44]. In more recent work [45], a worst-best example learning strategy is devised, in which the worst particle learns from the gbest particle to strengthen itself. In essence, it also belongs to social learning as in PSO, but it is used only on the gworst particle, not on all the particles, which will significantly improve not only the worst particle but also the quality of the whole swarm. To sum up, gworst particle can enhance the performance of PSO by fighting against premature convergence and avoiding local optima, which is well worth exploring in the field of swarm intelligence optimization.

2.3 Review of the gbest Particle-Based Updating Strategy

In standard particle swarm optimization, it is known that the movement of a particle is usually directed by the velocity and position update formula, in which the personal best position (pbest) and global best position (gbest) play a critical role in regulating particle search around a region. From the literature, it is observed that the majority of the existing PSO variants adopt pbest and gbest to guide the search process. Classical work includes the SRPSO [46], in which the self-regulating inertia weight is utilized by the gbest particle for a better exploration and the self-perception of the global search direction is used by the rest of particles for intelligent exploitation of the solution space. In literature [47], IDE-PSO adopts three velocity update schemes for different kinds of particles: good particles, weak particles, and normal particles. Note that except for the normal particle, both the cognitive component associated with pbest and the social component associated with gbest have been removed from the velocity update formula for the other two cases. After that, the PSOTL [25] is proposed, in which an auxiliary velocity-position update scheme is exclusively used for gbest particle to guarantee the convergence of PSO while the other set of the ordinary update scheme is exploited for the updating of other particles.

Despite a great deal of research work dedicated to gbest particle for better optimization performance, however, it seems that PSO is somewhat arbitrary to make all the particles get acquainted with the same information from the gbest. In this case, no matter how far particle is from the gbest, each particle learns information from the global best position. As a result, all of them are quickly attracted to the optimal position and the swarm diversity starts to drastically decrease. Moreover, the search information of gbest in standard PSO is merely used to guide the search direction, which will also inevitably impair the diversity of swarm. As a result, it increases the possibility of PSO falling into local optima. Because of this, some PSO variants adopt the concept of an exemplar instead of gbest to direct the flying of particles, such as the orthogonal learning PSO [48], in which the exemplar comes from pbest or gbest resulting from the construction of the experimental orthogonal design. In [49], the leader particle selected from the archive that provides the best aggregation value (Lbest) is utilized to replace gbest to update the velocity. In literature [50], the non-parametric PSO is developed by discarding the parameters of inertia weight and acceleration coefficients. In particular, each particle uses the best position found by its neighbors (plbest) to update its velocity, and the effect of gbest is integrated into the position update scheme. Recent work [28] makes use of the Spbest and Mpbest to replace the personal best position and global best position in standard PSO update scheme, respectively. Specifically, stochastic learning gives particles ability to learn from other excellent individuals in the swarm and moves particles more diverse (Spbest). On the other hand, the overemphasis on gbest will lead to the quick loss of swarm diversity, thus the mean of the personal best positions (Mpbest) of all particles is devised to solve this potential problem by enhancing communication between particles in the dimensional aspect. Similarly, to pull the entire swarm toward the true Pareto-optimal front quickly, MaPSO is developed in [51], in which the leader particle is selected from several historical solutions by using the scalar projections, and a sign function is used to adaptively adjust the search direction for each particle. In more recent work [52], the distance from the particle to its pbest and gbest are respectively used to replace the cognitive and social components associated with the pbest and gbest in the velocity update scheme. In a nutshell, it is of utmost importance that the careful incorporation of gbest into particle swarm optimization is instrumental in achieving good performance.

3  Standard PSO

Particle swarm optimization is a powerful nature-inspired meta-heuristic optimization technique that emulates the social behavior of bird flocking and fish schooling [1]. In standard PSO (SPSO), each particle denotes a candidate solution in the search space and the method searches for the global optimal solution by updating generations. Given that in an n-dimensional hyperspace, two vectors are related to the ith particle (i = 1, 2,…,N), one is the velocity vector Vi = [vi1, vi2,…, vin], and the other is the position vector Xi = [xi1, xi2,…, xin], where N denotes the swarm size. During the search process, each particle dynamically updates its position based on its previous position and new information regarding velocity. Moreover, the ith particle (i = 1, 2,…,N) will remember its current personal best location found in the search space so far, usually denoted as pbesti = [pbesti1, pbesti2,…, pbestin], and the best previous location found by the whole swarm described as gbest = [gbest1, gbest2,…, gbestn]. After these two best values are identified, the velocity and position update as follows:

Vi=w×Vi+c1×rand1×(pbesti−Xi)+c2×rand2×(gbest−Xi)(1)

Xi=Xi+Vi(2)

where w is the inertia weight used for the balance between the global and local search capabilities of the particle. A large inertia weight, w, at the beginning of the search increases the global exploration ability of swarm. In contrast, a small value of w near the end of the search enhances the local exploitation ability. c1 and c2, termed as acceleration coefficients, are positive constants reflecting the weighting of stochastic acceleration terms that pull each particle toward pbest and gbest positions respectively in the flight process. rand1 and rand2 are two random numbers uniformly distributed in the interval [0, 1]. Besides, the velocity is confined within a range of [Vmin, Vmax] to prevent particles from flying out of the search space. Note that if the sum of the accelerations causes the velocity of that dimension to exceed a predefined limit, the velocity of that dimension is clamped to a defined range.

So far, the complete procedure of standard PSO can be described below:

Step 1: Initialization

      Initialize the parameters and swarm with random positions and velocities.

Step 2: Evaluation

      Evaluate the fitness value (the desired objective function) for each particle.

Step 3: Find pbest

      If the fitness value of particle i is better than its best fitness value (pbest) in history, then

      set the current fitness value as the new pbest of particle i.

Step 4: Find gbest

      If any updated pbest is better than the current gbest, then set gbest as the current value of

      the whole swarm.

Step 5: Update

      Update the velocity and move to the next position according to Eqs. (1)–(2).

Step 6: Termination

      If the termination condition is reached, then stop; otherwise turn to Step 2.

4  Proposed AMS-PSO

4.1 Swarm Initialization

For any swarm intelligence computation, swarm initialization is a crucial step since it affects the convergence rate and the quality of final solutions. From the literature, it can be seen that the most common method is random initialization [24], which is often exploited to generate initial particles without any information about the solution to the problems. However, it is reported that PSO with random initialization cannot be guaranteed to provide stable performance and fast convergence [2]. Based on this recognition, large amounts of research have been devoted to the development of high-quality initial particles for PSO to improve its performance, including chaos based sequence [7], opposition-based learning [12], chaotic opposition-based method [26], and other paradigms based swarm initialization [27]. As one of the most often used chaotic systems, logistic map [2,7,8,25] has been attracting significant research attention in the evolutionary computation area in the most recent years owing to its properties of randomness, ergodicity, regularity, and non-repeatability, especially in the community of particle swarm optimization. As a result, it is observed that many PSO studies make full use of chaotic systems to enhance their search capabilities without being trapped in local optima from different aspects of chaos-based sequence for swarm initialization [25], chaos-based sequence for parameter setting [8], chaos-based sequence for mutation [26] and so forth. Given this, the classical logistic map is exploited in this work, which can be described as follows:

xi+1=μ×xi×(1−xi),i=0,1,2,…(3)

where xi represents the ith chaotic variable in the interval 0 and 1 under the conditions that x0 is generated randomly for each independent run without being equal to some periodic fixed points 0, 0.25, 0.5, 0.75, and 1. μ is a predefined constant termed as bifurcation coefficient. Note that the value of μ determines the bifurcation of the logistic map. In the case of μ < 3, xi converges to a single point. When μ = 3, xi oscillates between two points, and this characteristic change in behavior is called bifurcation. For μ > 3, xi encounters further bifurcation, eventually resulting in chaotic behavior. Due to the limited space, here we only give a brief introduction to logistic map and for more details please refer to literatures [2,7,8,12,25]. Algorithm 1 illustrates the pseudocode of the chaos-based swarm initialization, which mainly consists of two stages: generating a chaotic variable and mapping the chaotic variable to the search space of the problem to be solved. Note also that xmin and xmax denote the lower and upper bounds of the optimization variable.

4.2 Update for gbest Particle

As discussed in Section 2, the movement of particles heavily depends on pbest and gbest, and the acceleration coefficients stand for the weighting of pbest and gbest. Hence, the proper control of these two components is very important in finding the optimal solution accurately and efficiently. Moreover, they are capable of achieving an effective balance between exploration and exploitation during the evolution process under the conditions of proper pertinent parameters, especially the cognitive weighting factor c1 and the social weighting factor c2. Because of this, the velocity update equation of particles is devised by varying the value of acceleration factors to control the influence of cognitive information and social information, respectively. On one side, instead of introducing complex learning strategies adopted by most existing PSOs, the ultimate goal of this work is to explore how to obtain much better PSO performance through the use of learning strategies as simple as possible. On the other side, since all of the particles may carry useful information and the performance of swarm may be enhanced by updating all particles, including pbest, pworst, and normal particles. Hence, different updating strategies are adopted for different particles in different evolution stages. Specifically, to guarantee the convergence of AMS-PSO, an auxiliary update strategy is exclusively used to keep the gbest particle moving until it has reached a local minimum under the assumption of minimization [53], which can be expressed as below:

vξd(t+1)=−xξd(t)+pgd(t)+wvξd(t)+ρ(t)(1−2r2d(t))(4)

xξd(t+1)=xξd(t)+vξd(t+1)=pgd(t)+wvξd(t)+ρ(t)(1−2r2d(t))(5)

where ζ denotes the index of the gbest particle, −xζd(t) resets the particle’s position to the gbest pgd(t), wvζd(t) indicates the current search direction, ρ(t)(l−2r2d(t)) generates a random sample from a sample space with side lengths 2ρ(t). Note that ρ is a scaling factor defined below. The addition of the ρ term enables PSO to perform a random search in an area surrounding the gbest. It determines the diameter of the search area to proceed with exploring.

ρ(t+1)={2ρ(t),if # successes >sc0.5ρ(t),if # failures >fcρ(t),otherwise(6)

where #successes and #failures denote the numbers of consecutive successes and failures, respectively. Here, a failure is defined as f(pg(t)) = f(pg(t − 1)) whereas success is just the opposite. sc and fc are preset thresholds, the optimal choice of their values depends on the objective function. In common cases a default initial value ρ(0) = 1.0 has been found empirically to produce encouraging results.

4.3 Update for gworst and Other Particles

Note that compared to the studies of the gbest particle, almost none of the researchers pay attention to the gworst particle, thus unable to discover the potential information concealed around it. However, the gworst particle does not mean it does not contain any useful information at all. On the contrary, just as the cask effect says that the weak part often determines the level of the whole organization. So the effect of the gworst particle will be fully considered in this work. At the same time, it must be emphasized that both exploration and exploitation are equally important and should be explored cleverly during the evolution process. Based on this scenario, it is expected to realize the twin goals of balancing the global and local search abilities as well as decreasing the risk of falling into local optima by adjusting parameters c1 and c2 for PSO. Without loss of generality, a large cognitive weighting factor c1 and a small social weighting factor c2 are applied to guide the search for gworst particle to avoid possible stagnation [12]. In addition, for other normal particles in swarm, three sets of different acceleration coefficients are utilized to direct the search process. To be specific, the equal weightage is applied to c1 and c2 in the early evolution stage to enhance the exploration ability when the fitness of particle is less than or equal to the average fitness of the whole swarm, otherwise, a small c1 and a large c2 is adopted to speed up the convergence rate. Accordingly, a large c1 and a small c2 are exploited in the velocity update formula to improve the exploitation capability when the fitness of particle is greater than the average fitness of the entire swarm, otherwise, Gaussian mutation [26] is timely applied to mutate pbest of particles to sustain the swarm diversity in the later evolution stage for fine-tuning the search process.

pbestij′=pbestij+gaussianj()(7)

where gaussianj() is a random number generated by Gaussian distribution.

In contrast to most existing PSO variants that formulate the velocity and position updates based on large amounts of complex mechanisms, such as various devised parameters [2], topology structure [30], hybrid learning strategy [32], elite and dimensional learning strategies [33], enhanced learning strategy [34] and so on. Different from the existing update strategies, however, AMS-PSO takes advantage of distinct update schemes for different particles based on the simple yet very effective constant acceleration factors to enhance the performance of PSO. In essence, the idea behind AMS-PSO is somewhat identical to the multi-swarm particle swarm optimization [13]. That is to say, the larger swarm is first divided into several small-sized sub-swarms that can be regrouped after a predefined period during the evolution process, whose main aim is to explore different sub-regions of the solution space with different search strategies and to take advantage of the experience gathered by others through sharing information until the end of the search process.

Besides that, the classical linear decreasing inertia weight is leveraged in AMS-PSO method as follows [23]:

w(t)=(wmax−wmin)×(itermax−iter)itermax+wmin(8)

where wmax and wmin are the initial and final values of inertia weight, iter, and itermax denote the current iteration and the maximal allowed the number of iterations, respectively.

Up to this point, the succinct procedure of AMS-PSO can be described as follows:

5  Experimental Results and Analysis

5.1 Basic Test Functions

To demonstrate the effectiveness of AMS-PSO proposed in this paper, six well-known benchmark functions are adopted for simulation, they are expressed as follows:

(1)  Sphere function

minf1(x)=∑i=1d⁡xi2

where the global optimum x* = 0 and f(x*) = 0 for −10 ≤ xi ≤ 10.

(2)  Schwefel function

minf2(x)=∑i=1d⁡|xi|+∏i=1d⁡|xi|

where the global optimum x* = 0 and f(x*) = 0 for −100 ≤xi ≤ 100.

(3)  Rosenbrock function

minf3(x)=∑i=1d−1⁡[100(xi2−xi+1)2+(xi−1)2]

where the global optimum x* = (1, 1,…, 1) and f(x*) = 0 for −30 ≤xi ≤ 30.

(4)  Rastrigin function

minf4(x)=∑i=1d⁡[xi2−10cos⁡(2πxi)+10]

where the global optimum x* = 0 and f(x*) = 0 for −5.12 ≤xi ≤ 5.12.

(5)  Griewank function

minf5(x)=14000∑i=1d⁡(xi)2−∏i=1d⁡cos⁡(xii)+1

where the global optimum x* = 0 and f(x*) = 0 for −600 ≤xi ≤ 600.

(6)  Ackley function

minf6(x)=−20exp⁡(−0.21d∑i=1d⁡xi2)−exp⁡(1d∑i=1d⁡cos⁡(2πxi))+20+e

where the global optimum x* = 0 and f(x*) = 0 for −32 ≤xi ≤ 32.

Fig. 1 depicts the 2-dimensional graphical shows of the six test functions.

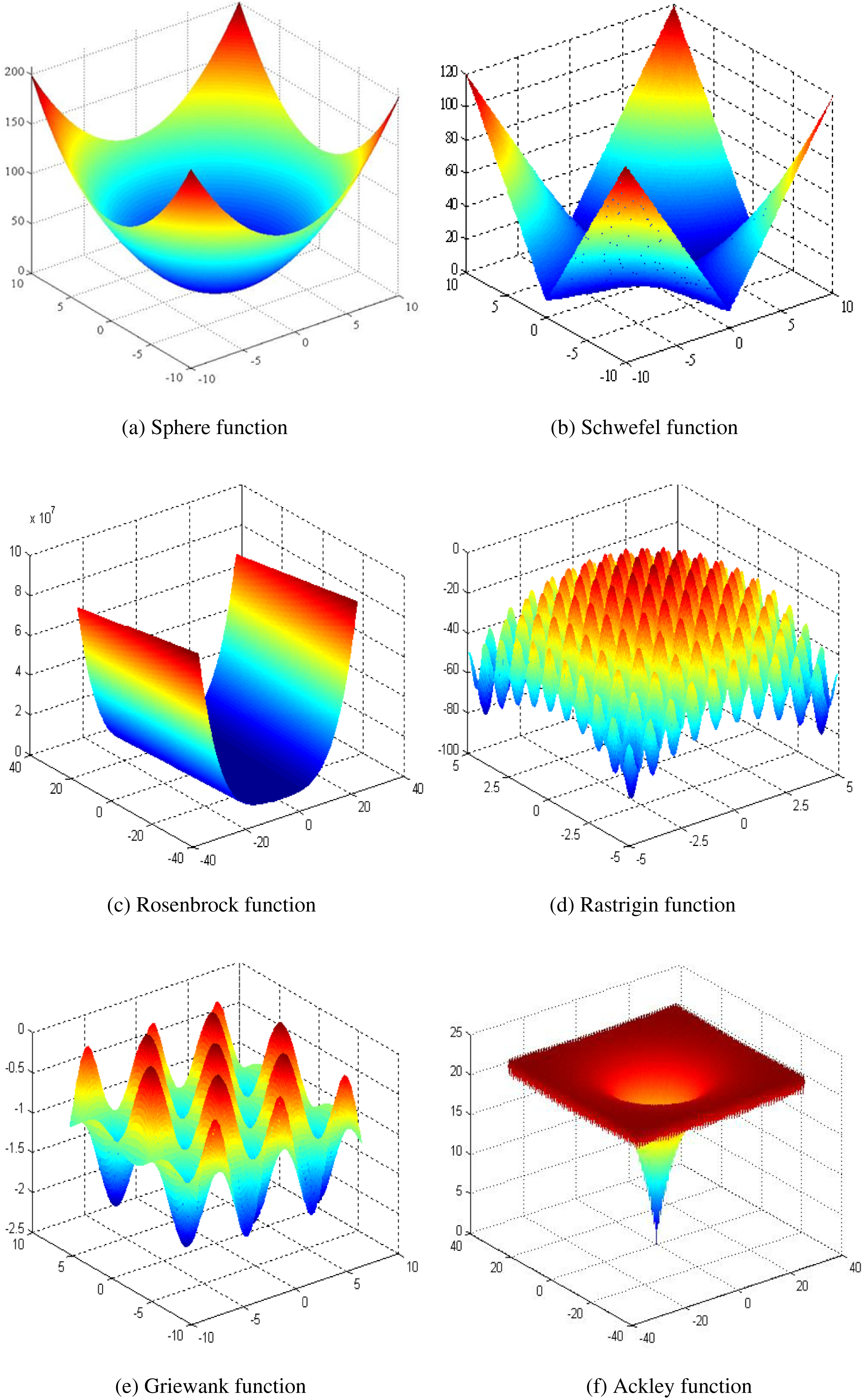
Figure 1: Graphical shows of the test functions

Table 1 shows the search range, optimal x*, global optimum and property of test functions. Note that all of the test functions are to be minimized. The first three functions are unimodal whereas the last three are multimodal. Specifically, f1 is a continuous and convex function that has several local minima except for the global one. f2 is complex, with many local minima. It is deceptive in that the global minimum is geometrically distant, over the parameter space, from the next best local minima. Hence the search method is potentially prone to convergence in the wrong direction. Note that f3 is also referred to as the valley or banana function, which is a popular test problem for the gradient-based optimization algorithms and the global minimum lies in a narrow, parabolic valley. However, even if this valley is easy to find, convergence to the minimum is difficult. f4 has several local minima, but locations of the minima are regularly distributed. Similarly, f5 has many widespread local minima that are regularly distributed in the allowable search space. As for function f6, it is widely used for testing optimization algorithms. In its two-dimensional form as shown in the plot above, it is characterized by a nearly flat outer region and a large hole at the center, this function poses a risk for the optimization algorithm, particularly hill climbing, to be trapped in one of its many local minima.

5.2 Parameter Settings

The parameter settings can be described as follows: the bifurcation coefficient μ is set to be 4, swarm size N = 40, time-varying inertia weight starts at 0.9 and ends at 0.4 according to Eq. (8), viz. wmax = 0.9 and wmin = 0.4, the control factor β is set as 0.5 by trial and error by taking into account the tradeoff between convergence rate and computational accuracy. In particular, the equal acceleration coefficients are set to be 2 (c1 = c2 = 2) whereas the unequal setting of c1 = 3 and c2 = 1 is exclusively used for gworst particle. At the same time, the first group of the unbalanced setting of c1 = 1.5 and c2 = 2.5 is leveraged in the case of the fitness of particle is greater than the average of swarm in the early evolution process while the second group of the unequal setting of c1 = 2.5 and c2 = 1.5 is applied under the conditions of the fitness of particle is greater than the average of the entire swarm in the later search process. In such a case, a well-balanced exploration and exploitation can be achieved. For each test function, 30 independent runs are performed by AMS-PSO, and each run is with 1000 iterations. Without loss of generality, the most often used metrics, including best solution, average solution, and standard deviation, are leveraged to demonstrate the performance of AMS-PSO proposed in this paper.

5.3 Results and Analysis

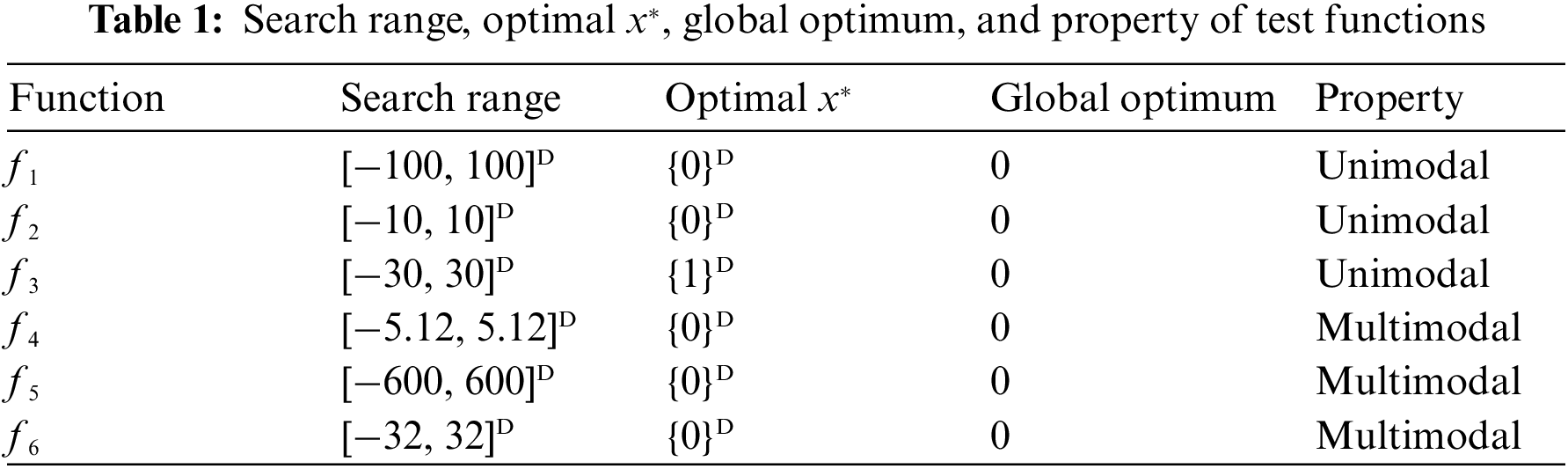
Note that since the superiority of chaos-based swarm initialization has already been validated in our previous studies [2,7,25], so we will not detail it anymore here. Instead, to illustrate the effect of different update schemes for PSO, AMS-PSO is first compared with its three variants in this section, involving AMS-PSO-gb, which denotes the acronym of AMS-PSO without the auxiliary update strategy that is exclusively applied to gbest particle. Likewise, AMS-PSO-gw is the acronym of AMS-PSO without an update strategy based on the unequal acceleration factors that are applied to gworst particle. Besides, AMS-PSO-no is the acronym of AMS-PSO without an update strategy based on unequal acceleration factors that are applied to normal particles. In other words, except for the different update schemes based on different acceleration factors, all the experiments are carried out under the same conditions described in Subsection 5.2.

From Table 2, it is observed that AMS-PSO markedly outperforms its three variants on all the test functions except on f3 and f4 with the same optimization results. For the first two unimodal functions, AMS-PSO achieves an advantage of 6, 8, and 13 along with 29, 14, and 36 orders of magnitude over the other corresponding variants in terms of best solution, respectively. As for the third unimodal function, since the global minimum of f3 lies in a narrow and parabolic valley, it is rather difficult to converge to the minimum even if the valley is easy to be found. Hence, the optimized result on function f3 is relatively poor compared to the best solutions of other functions achieved by our proposal. What is more, all the AMS-PSOs converge to the same global minimum with dimension 10. In comparison, f4 is multimodal, which is the widely used test function in the research of evolutionary computation. Likewise, it is prone to be trapped in a local minimum on its way to the global minimum. However, by achieving an effective balance between the exploration and exploitation search ability, AMS-PSO gets the global optima on each dimension on f4. This is largely attributed to the different update schemes applied to regulate the particle search process at different evolution stages. Meanwhile, the stability of PSO is improved obviously due to the high-quality initial particles generated by the chaotic map. Concerning the rest two multimodal functions f5 and f6, AMS-PSO can also get promising results in terms of best solution, average solution, and standard deviation in comparison with its three variants, which further validates the respective merit of the auxiliary update strategy for the global best particle, the unequal weightage for the global worst particle as well as equal weightage and Gaussian mutation for other particles, and all of these strategies should be used together for good performance based on their complementary information.

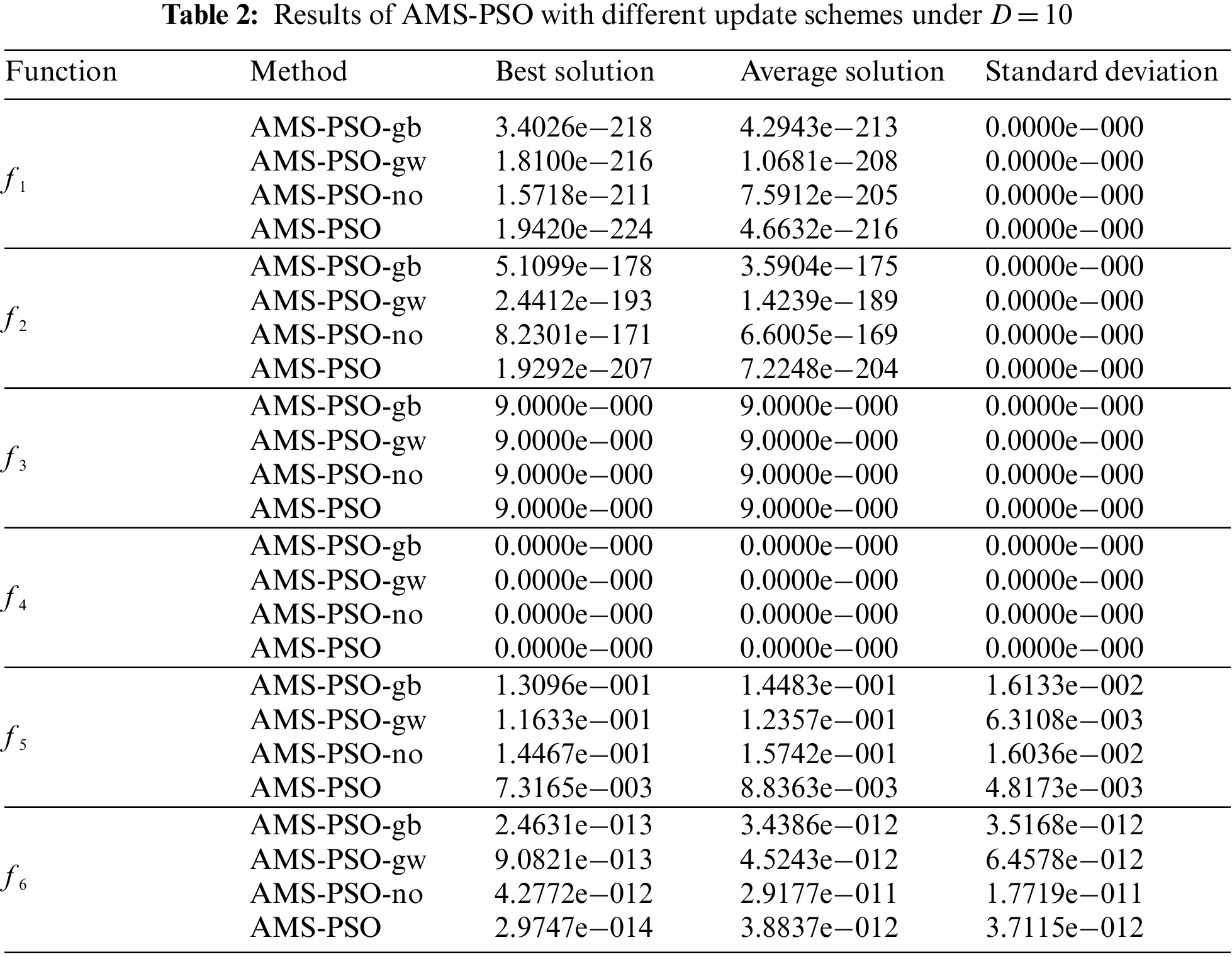
To illustrate the convergence process of different AMS-PSOs, Fig. 2 depicts the evolution curves of PSOs with different update schemes for all the test functions. Taking Fig. 2a for example, the evolution curves of the four AMS-PSOs decline at almost the same rate during the whole search process, and they are very close to each other. It is worth noting that the evolution trends for function f2 are somewhat similar to Fig. 2a except for obvious differences. Note that an interesting observation comes from Fig. 2c, all of the convergence curves decrease sharply in the first 50 iterations. After that, they converge very slowly and flatly until the end of the search. That is to say, all of them get stuck in local optimal at this point. This shows that the multiple update strategies formulated in this work have a marginal effect on the optimization performance for function f3. Similarly, one can see that all the PSOs evolve very fast on f5 and f6 at the early 100 iterations, and subsequently evolve very slowly and flatly without obvious improvement except for AMS-PSO tested by function f6. Besides, it can be seen that AMS-PSO quickly converges to the optimal solution before 200 iterations on f4. In contrast, AMS-PSO-no evolves with a slow convergence rate even though it converges to the optimal solution at the end. Note that the convergence curves of AMS-PSO-gb and AMS-PSO-gw lie between the above two cases, and AMS-PSO-gw evolves much faster than AMS-PSO-gb. That is, the global best particle plays an important role in guaranteeing the convergence of PSO.

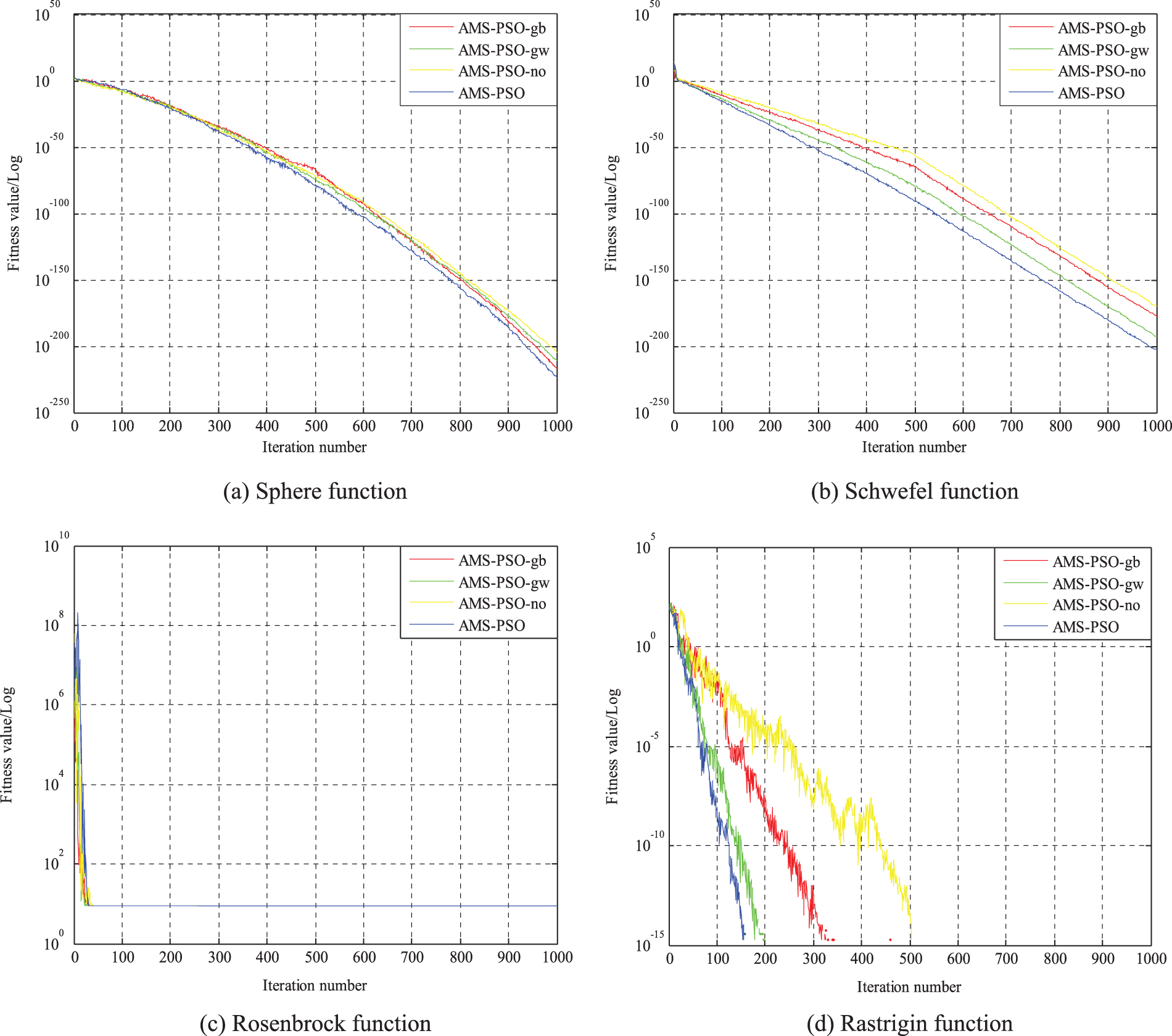
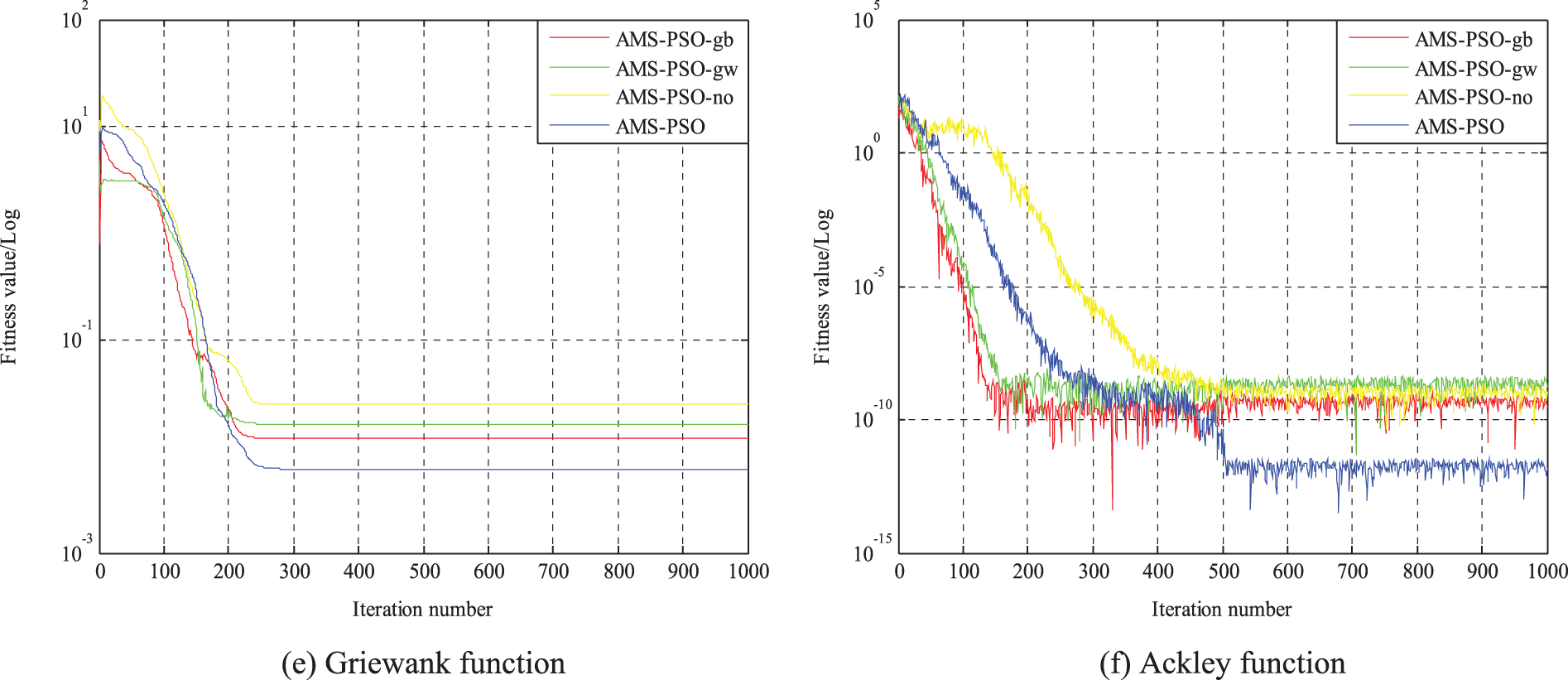
Figure 2: Evolution curves of different AMS-PSO variants

5.4 CEC’17 Test Suite

To further illustrate the effect of the proposed AMS-PSO algorithm, experiments are also conducted on the well-known CEC 2017 test suite [54] that has been widely used by researchers [55–58]. It includes 30 functions, which can be roughly classified into four groups. Specifically, the first group involves three unimodal functions (f1–f3), in which function f2 has been excluded here because it shows unstable behavior especially for higher dimensions. Functions f4–f10 belongs to the second group, and all of them are multimodal functions. The third group comprises ten hybrid functions (f11–f20), and the last group includes ten composition functions (f21–f30). Thus the total number of test functions is twenty-nine. Note that Table 3 lists the name, search range, global optimum, and property of CEC’17 test functions.

To fully demonstrate the advantages of our proposal, AMS-PSO is conducted with dimension 30 and is compared with seven state-of-the-art PSO variants, including MPSO [28], IH-PSO [59], LIPS [60], CDWPSO [61], EPSO [62], HCLPSO [31] and CLPSO [63]. Among the compared PSOs, LIPS, EPSO, HCLPSO and CLPSO1 as well as MPSO2 have been reproduced and the experimental results are used to evaluate their performance. As for IH-PSO and CDWPSO, for the sake of fair comparison, their experimental results are directly taken from [59,61,64] to be compared because it is almost impossible to reproduce these two PSO variants exactly as they were in their original literature, even including the running environment of program. Without loss of generality, the mean best solution (Mean) and standard deviation (Std.) are utilized to verify the performance, and the best result in a comparison is emphasized as bold font. Table 4 lists the parameter settings employed in the experiment. Likewise, the swarm size is 50, each PSO variant is run 30 times on every test function with 2000 iterations for each run, and the stopping criterion is set as reaching the total number of iterations.

From the results reported in Table 5, it can be clearly observed that AMS-PSO achieves better performance than other PSO variants on most of the functions. To be specific, AMS-PSO obtains the best result on functions f3, f5, f7, f8, f11, f22, f24, f25 and f28 respectively in terms of the mean value. At the same time, it is worth noting that our proposal obtains the same mean as EPSO, HCLPSO and CLPSO on functions f6 and f25, EPSO and CLPSO on function f17, MPSO and IH-PSO on function f20, HCLPSO on function f23 and CDWPSO on function f27, respectively. Particularly, it achieves the global optimum on f6. Another interesting observation is that even if AMS-PSO performs slightly worse than EPSO on f9 and f21, CLPSO on f16 and HCLPSO on f29 and f30 according to the mean, it achieves much better standard deviation on these functions, especially on functions f9, f29 and f30, it outperforms EPSO and HCLPSO with 1, 1 and 2 orders of magnitude difference. This can be largely attributed to the high-quality initial particles generated by the logistic map. In addition, note that AMS-PSO ranks first 14 times, second 9 times, third twice, fourth twice and fifth twice among the twenty-nine test functions. In contrast, MPSO, IH-PSO, LIPS, CDWPSO, EPSO, HCLPSO and CLPSO achieve 3, 1, 3, 1, 8, 6 and 5 first-place ranks, respectively. The average rank of AMS-PSO is 1.93, much lower than that of other PSO variants listed in Table 5. As a result, its overall rank is the first. In sum, all the experimental results demonstrate that AMS-PSO possesses promising optimization performance, at least for the functions of CEC’17 test suite employed here.

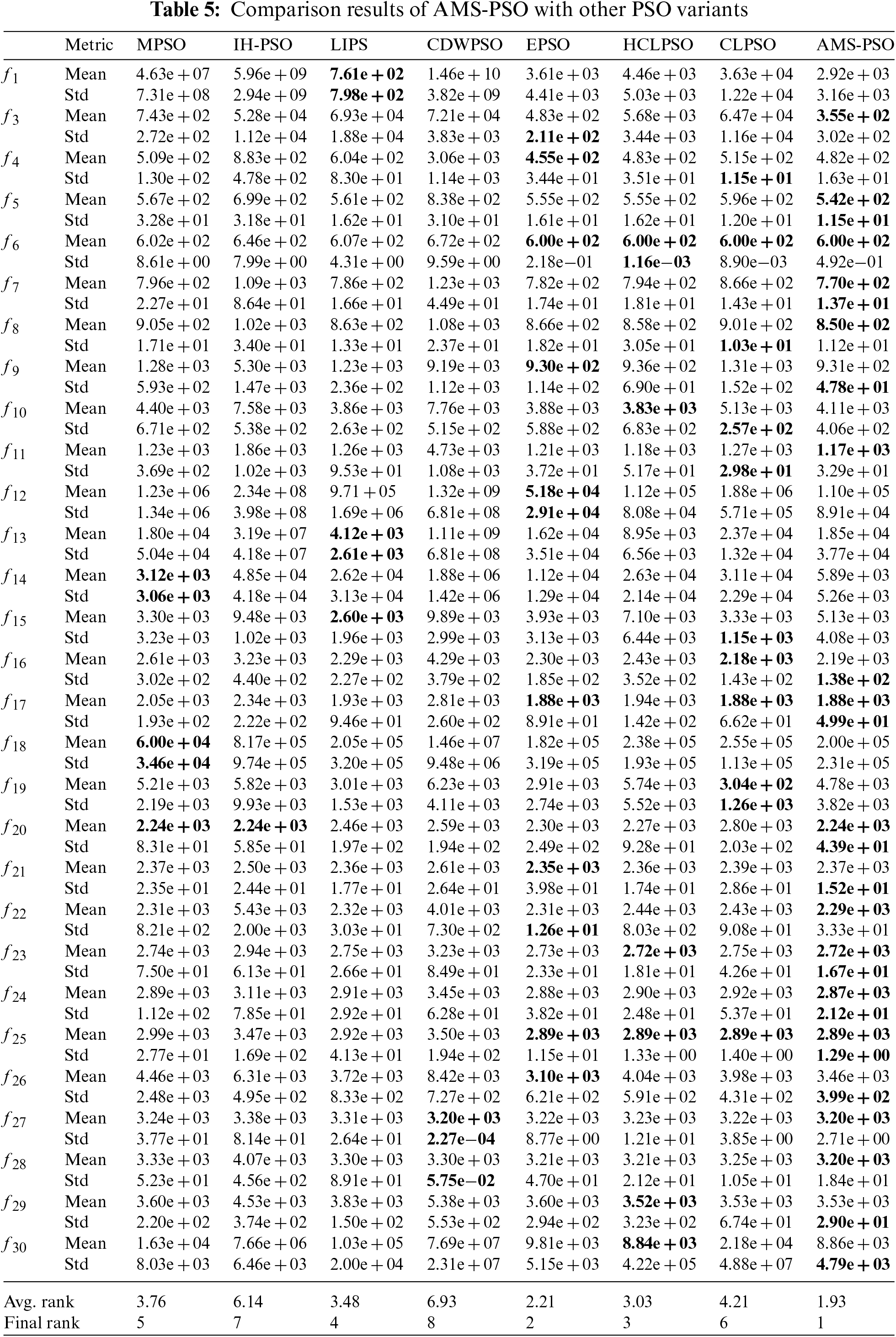
Fig. 3 illustrates the histogram of mean ranks for AMS-PSO and the compared PSOs mentioned in this section, which is mainly used to indicate the number of times each PSO has acquired the ranks in the range of 1 to 8. Our proposal achieves the top ranks compared to other PSO variants, which further bears out the effect of AMS-PSO for numerical function optimization.

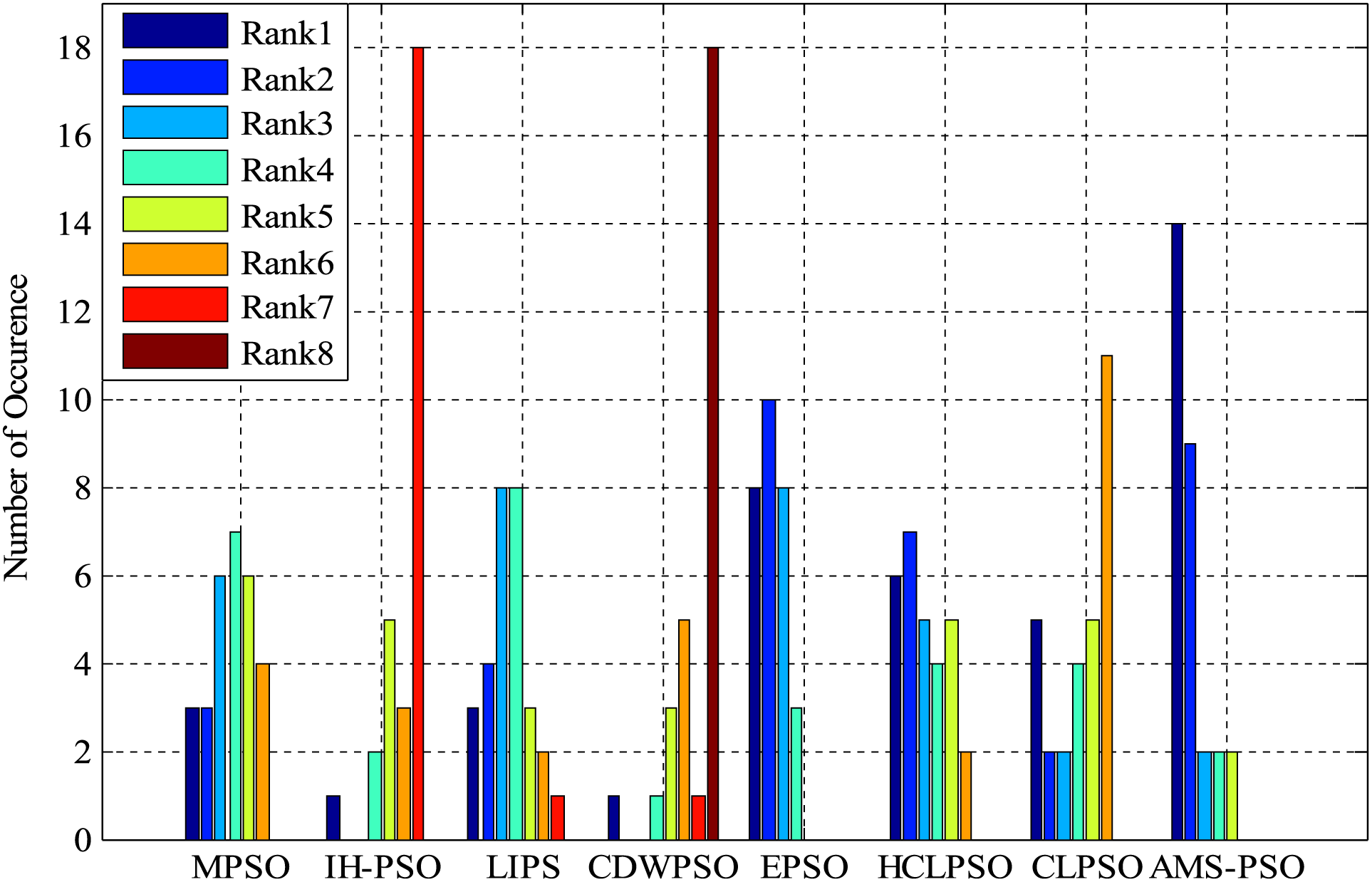
Figure 3: Histogram of the mean rank

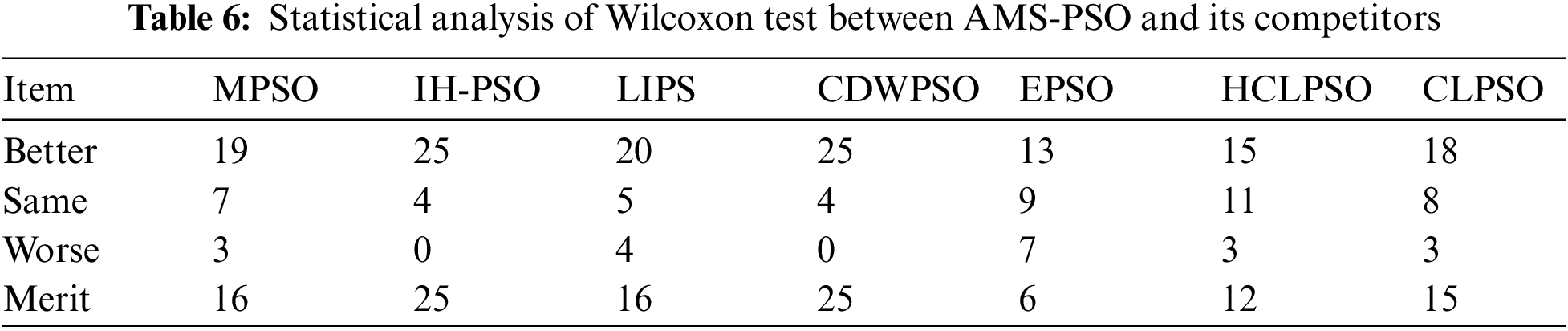
In addition, to thoroughly and fairly compare AMS-PSO with other methods, we have validated it from the perspective of statistical analysis [65,66] by trial and error. To be specific, a pairwise statistical test named Wilcoxon signed-rank test is conducted between the results of the proposed AMS-PSO and the results of other PSO variants with the significance level of 5%, which is a non-parametric test that can be used to check for the statistical significance difference between two algorithms. As shown in Table 6, the number of test functions showing that AMS-PSO is significantly better than the compared PSO (Better), almost the same as the compared PSO (Same), and significantly worse than the compared PSO (Worse), respectively. Note that the “Merit” score is calculated by subtracting the “worse” score from the “better” score. From Table 6, it can be seen that AMS-PSO has achieved excellent performance and performed significantly better than the other seven PSOs on the majority of the test functions.

6  Conclusions and Future Work

This paper presents an adaptive multi-updating strategy based particle swarm optimization, which takes advantage of the chaotic sequence to generate high-quality initial particles to increase the stability and accelerate the convergence rate of the PSO, the different update schemes to regulate the particle search process at different evolution stages, the unequal weightage of acceleration coefficients to guide the search for the global worst particle, and an auxiliary update strategy for the global best particle to ensure convergence of the PSO. Conducted experiments demonstrate that the proposed PSO outperforms several state-of-the-art PSOs in terms of solution accuracy and effectiveness.

As for future work, AMS-PSO will be compared with more competitive PSOs on more complex functions and in some real-world applications such as image processing, feature selection, optimization scheduling, and robot path planning, etc. More importantly, we intend to delve deeper into the use of different update schemes in different scenarios, especially for adequate acceleration coefficients tuning in a wide range of applications. Last but not the least, we will probe into the relationship between different acceleration coefficients and convergence of PSO as well as the relationship between stability and well-distributed initial particles generated by the logistic map from a computational efficiency perspective.

Acknowledgement: The authors would like to sincerely thank the editor and anonymous reviewers for their valuable comments and insightful suggestions that have helped us to improve the paper.

Funding Statement: This work is sponsored by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (No. 2022D01A16) and the Program of the Applied Technology Research and Development of Kashi Prefecture (No. KS2021026).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1https://github.com/P-N-Suganthan/CODES

2https://github.com/lhustl/MPSO

References

1. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in IEEE Conf. on Neural Networks (ICNN), Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]

2. D. P. Tian and Z. Z. Shi, “MPSO: Modified particle swarm optimization and its applications,” Swarm and Evolutionary Computation, vol. 41, pp. 49–68, 2018. [Google Scholar]

3. R. Eberhart and Y. H. Shi, “Tracking and optimizing dynamic systems with particle swarms,” in IEEE Congress on Evolutionary Computation (CEC), Seoul, Korea (Southpp. 94–100, 2001. [Google Scholar]

4. K. Chen, F. Y. Zhou, Y. G. Wang and L. Yin, “An ameliorated particle swarm optimizer for solving numerical optimization problems,” Applied Soft Computing, vol. 73, no. 6, pp. 482–496, 2018. [Google Scholar]

5. A. Nickabadi, M. M. Ebadzadeh and R. Safabakhsh, “A novel particle swarm optimization algorithm with adaptive inertia weight,” Applied Soft Computing, vol. 11, no. 4, pp. 3658–3670, 2011. [Google Scholar]

6. A. Ratnaweera, S. K. Halgamuge and H. C. Watson, “Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients,” IEEE Transactions on Evolutionary Computation, vol. 8, no. 3, pp. 240–255, 2004. [Google Scholar]

7. D. P. Tian, X. F. Zhao and Z. Z. Shi, “Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization,” Swarm and Evolutionary Computation, vol. 51, pp. 100573, 2019. [Google Scholar]

8. M. Pluhacek, R. Senkerik and D. Davendra, “Chaos particle swarm optimization with ensemble of chaotic systems,” Swarm and Evolutionary Computation, vol. 25, pp. 29–35, 2015. [Google Scholar]

9. S. A. Khan and A. Engelbrecht, “A fuzzy particle swarm optimization algorithm for computer communication network topology design,” Applied Intelligence, vol. 36, no. 1, pp. 161–177, 2012. [Google Scholar]

10. H. A. Illias, X. R. Chai and A. H. A. Bakar, “Hybrid modified evolutionary particle swarm optimization-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis,” Measurement, vol. 90, pp. 94–102, 2016. [Google Scholar]

11. S. U. Khan, S. Y. Yang, L. Y. Wang and L. Liu, “A modified particle swarm optimization algorithm for global optimizations of inverse problems,” IEEE Transactions on Magnetics, vol. 52, no. 3, pp. 1–4, 2016. [Google Scholar]

12. K. K. Bharti and P. K. Singh, “Opposition chaotic fitness mutation based adaptive inertia weight BPSO for feature selection in text clustering,” Applied Soft Computing, vol. 43, pp. 20–34, 2016. [Google Scholar]

13. X. W. Xia, L. Gui and Z. H. Zhan, “A multi-swarm particle swarm optimization algorithm based on dynamical topology and purposeful detecting,” Applied Soft Computing, vol. 67, pp. 126–140, 2018. [Google Scholar]

14. P. K. Das, H. S. Behera and B. K. Panigrahi, “A hybridization of an improved particle swarm optimization and gravitational search algorithm for multi-robot path planning,” Swarm and Evolutionary Computation, vol. 28, pp. 14–28, 2016. [Google Scholar]

15. Y. Wang, X. L. Ma, M. Z. Xu, Y. Liu and Y. H. Wang, “Two-echelon logistics distribution region partitioning problem based on a hybrid particle swarm optimization-genetic algorithm,” Expert Systems with Applications, vol. 42, no. 12, pp. 5019–5031, 2015. [Google Scholar]

16. M. A. Mosa, “A novel hybrid particle swarm optimization and gravitational search algorithm for multi-objective optimization of text mining,” Applied Soft Computing, vol. 90, pp. 106189, 2020. [Google Scholar]

17. Z. P. Wan, G. M. Wang and B. Sun, “A hybrid intelligent algorithm by combining particle swarm optimization with chaos searching technique for solving nonlinear bilevel programming problems,” Swarm and Evolutionary Computation, vol. 8, pp. 26–32, 2013. [Google Scholar]

18. C. Y. Tsai and I. W. Kao, “Particle swarm optimization with selective particle regeneration for data clustering,” Expert Systems with Applications, vol. 38, no. 6, pp. 6565–6576, 2011. [Google Scholar]

19. A. Selvakumar and K. Thanushkodi, “A new particle swarm optimization solution to nonconvex economic dispatch problems,” IEEE Transactions on Power Systems, vol. 22, no. 1, pp. 42–51, 2007. [Google Scholar]

20. X. H. Yan, F. Z. He and Y. L. Chen, “A novel hardware/software partitioning method based on position disturbed particle swarm optimization with invasive weed optimization,” Journal of Computer Science and Technology, vol. 32, no. 2, pp. 340–355, 2017. [Google Scholar]

21. S. Y. Ho, H. S. Lin, W. H. Liauh and S. J. Ho, “OPSO: Orthogonal particle swarm optimization and its application to task assignment problems,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 38, no. 2, pp. 288–298, 2008. [Google Scholar]

22. Y. H. Shi and R. Eberhart, “A modified particle swarm optimizer,” in IEEE Cong. on Evolutionary Computation (CEC), Anchorage, AK, USA, pp. 69–73, 1998. [Google Scholar]

23. Y. H. Shi and R. Eberhart, “Empirical study of particle swarm optimization,” in IEEE Cong. on Evolutionary Computation (CEC), Washington, DC, USA, pp. 101–106, 1999. [Google Scholar]

24. S. L. Wang, G. Y. Liu, M. Gao, S. L. Cao, A. Z. Guo et al., “Heterogeneous comprehensive learning and dynamic multi-swarm particle swarm optimizer with two mutation operators,” Information Sciences, vol. 540, pp. 175–201, 2020. [Google Scholar]

25. D. P. Tian, “Particle swarm optimization with chaos-based initialization for numerical optimization,” Intelligent Automation and Soft Computing, vol. 24, no. 2, pp. 331–342, 2018. [Google Scholar]

26. D. P. Tian, X. F. Zhao and Z. Z. Shi, “DMPSO: Diversity-guided multi-mutation particle swarm optimizer,” IEEE Access, vol. 7, no. 1, pp. 124008–124025, 2019. [Google Scholar]

27. M. Kohler, M. Vellasco and R. Tanscheit, “PSO+: A new particle swarm optimization algorithm for constrained problems,” Applied Soft Computing, vol. 85, pp. 105865, 2019. [Google Scholar]

28. H. Liu, X. W. Zhang and L. P. Tu, “A modified particle swarm optimization using adaptive strategy,” Expert Systems with Applications, vol. 152, pp. 113353, 2020. [Google Scholar]

29. J. Peng, Y. B. Li, H. W. Kang, Y. Shen, X. P. Sun et al., “Impact of population topology on particle swarm optimization and its variants: An information propagation perspective,” Swarm and Evolutionary Computation, vol. 69, pp. 100990, 2022. [Google Scholar]

30. A. P. Lin, W. Sun, H. S. Yu, G. Wu and H. W. Tang, “Global genetic learning particle swarm optimization with diversity enhancement by ring topology,” Swarm and Evolutionary Computation, vol. 44, pp. 571–583, 2019. [Google Scholar]

31. N. Lynn and P. N. Suganthan, “Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation,” Swarm and Evolutionary Computation, vol. 24, pp. 11–24, 2015. [Google Scholar]

32. X. M. Tao, X. K. Li, W. Chen, T. Liang, Y. T. Li et al., “Self-adaptive two roles hybrid learning strategies-based particle swarm optimization,” Information Sciences, vol. 578, pp. 457–481, 2021. [Google Scholar]

33. R. Wang, K. R. Hao, L. Chen, T. Wang and C. L. Jiang, “A novel hybrid particle swarm optimization using adaptive strategy,” Information Sciences, vol. 579, pp. 231–250, 2021. [Google Scholar]

34. S. Molaei, H. Moazen, S. Najjar-Ghabel and L. Farzinvash, “Particle swarm optimization with an enhanced learning strategy and crossover operator,” Knowledge-Based Systems, vol. 215, pp. 106768, 2021. [Google Scholar]

35. L. Vitorino, S. Ribeiro and C. Bastos-Filho, “A mechanism based on artificial bee colony to generate diversity in particle swarm optimization,” Neurocomputing, vol. 148, pp. 39–45, 2015. [Google Scholar]

36. I. B. Aydilek, “A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems,” Applied Soft Computing, vol. 66, pp. 232–249, 2018. [Google Scholar]

37. M. Clerc and J. Kennedy, “The particle swarm-explosion, stability, and convergence in a multidimensional complex space,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 1, pp. 58–73, 2002. [Google Scholar]

38. Y. Ortakci, “Comparison of particle swarm optimization methods in applications,” Graduate School of Natural and Applied Sciences, Graduate Dissertation, Karabuk University, 2011. [Google Scholar]

39. A. Carlisle and G. Dozier, “An off-the-shelf PSO,” in Proc. of the Workshop on Particle Swarm Optimization, Indianapolis, IN, pp. 1–6, 2001. [Google Scholar]

40. Z. H. Zhan and J. Zhang, “Adaptive particle swarm optimization,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 39, no. 6, pp. 1362–1381, 2009. [Google Scholar]

41. C. M. Yang and D. Simon, “A new particle swarm optimization technique,” in IEEE Conf. on Systems Engineering (ICSEng), Las Vegas, NV, USA, pp. 164–169, 2005. [Google Scholar]

42. H. Liu, G. Xu, G. Y. Ding and Y. B. Sun, “Human behavior-based particle swarm optimization,” The Scientific World Journal, vol. 2014, pp. 1–14, 194706, 2014. [Google Scholar]

43. K. Mason and E. Howley, “Exploring avoidance strategies and neighbourhood topologies in particle swarm optimization,” International Journal of Swarm Intelligence, vol. 2, no. 2–4, pp. 188–207, 2016. [Google Scholar]

44. L. L. Cao, L. H. Xu and E. D. Goodman, “A neighbor-based learning particle swarm optimizer with short-term and long-term memory for dynamic optimization problems,” Information Sciences, vol. 453, pp. 463–485, 2018. [Google Scholar]

45. X. M. Zhang and Q. Lin, “Three-learning strategy particle swarm algorithm for global optimization problems,” Information Sciences, vol. 593, pp. 289–313, 2022. [Google Scholar]

46. M. R. Tanweer, S. Suresh and N. Sundararajan, “Self regulating particle swarm optimization algorithm,” Information Sciences, vol. 294, pp. 182–202, 2015. [Google Scholar]

47. J. Gou, Y. X. Lei, W. P. Guo, C. Wang, Y. Q. Cai et al., “A novel improved particle swarm optimization algorithm based on individual difference evolution,” Applied Soft Computing, vol. 57, pp. 468–481, 2017. [Google Scholar]

48. Z. H. Zhan, J. Zhang, Y. Li and Y. H. Shi, “Orthogonal learning particle swarm optimization,” IEEE Transactions on Evolutionary Computation, vol. 15, pp. 832–846, 2011. [Google Scholar]

49. N. Moubayed, A. Petrovski and J. McCall, “D2MOPSO: MOPSO based on decomposition and dominance with archiving using crowding distance in objective and solution spaces,” Evolutionary Computation, vol. 22, no. 1, pp. 47–77, 2014 [Google Scholar] [PubMed]

50. Z. Beheshti and S. M. Shamsuddin, “Non-parametric particle swarm optimization for global optimization,” Applied Soft Computing, vol. 28, pp. 345–359, 2015. [Google Scholar]

51. Y. Xiang, Y. R. Zhou, Z. F. Chen and J. Zhang, “A many-objective particle swarm optimizer with leaders selected from historical solutions by using scalar projections,” IEEE Transactions on Cybernetics, vol. 50, no. 5, pp. 2209–2222, 2020 [Google Scholar] [PubMed]

52. W. B. Liu, Z. D. Wang, Y. Yuan, N. Y. Zeng, K. Hone et al., “A novel sigmoid-function-based adaptive weighted particle swarm optimizer,” IEEE Transactions on Cybernetics, vol. 51, no. 2, pp. 1085–1093, 2021 [Google Scholar] [PubMed]

53. F. Bergh and A. P. Engelbrecht, “A new locally convergent particle swarm optimizer,” in IEEE Conf. on Systems, Man and Cybernetics, Yasmine Hammamet, Tunisia, pp. 94–99, 2002. [Google Scholar]

54. N. H. Awad, M. Z. Ali, J. J. Liang, B. Qu and P. N. Suganthan, “Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization,” Nanyang Technological University, Jordan University of Science and Technology, 2016. [Google Scholar]

55. A. W. Mohamed, A. A. Hadi and A. K. Mohamed, “Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm,” International Journal of Machine Learning and Cybernetics, vol. 11, pp. 1501–1529, 2020. [Google Scholar]

56. J. Brest, M. S. Maučec and B. Bošković, “Single objective real-parameter optimization: Algorithm jSO,” in IEEE Cong. on Evolutionary Computation (CEC), Donostia, Spain, pp. 1311–1318, 2017. [Google Scholar]

57. A. Mohamed, A. A. Hadi, A. M. Fattouh and K. M. Jambi, “LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems,” in IEEE Cong. on Evolutionary Computation (CEC), Donostia, Spain, pp. 145–152, 2017. [Google Scholar]

58. A. Kumar, R. Misra and D. Singh, “Improving the local search capability of effective butterfly optimizer using covariance matrix adapted retreat phase,” in IEEE Cong. on Evolutionary Computation (CEC), Donostia, Spain, pp. 1835–1842, 2017. [Google Scholar]

59. X. F. Yuan, Z. A. Liu, Z. M. Miao, Z. L. Zhao, F. Y. Zhou et al., “Fault diagnosis of analog circuits based on IH-PSO optimized support vector machine,” IEEE Access, vol. 7, pp. 137945–137958, 2019. [Google Scholar]

60. B. Qu, P. N. Suganthan and S. Das, “A Distance-based locally informed particle swarm model for multimodal optimization,” IEEE Transactions on Evolutionary Computation, vol. 17, no. 3, pp. 387–402, 2013. [Google Scholar]

61. K. Chen, F. Y. Zhou and A. L. Liu, “Chaotic dynamic weight particle swarm optimization for numerical function optimization,” Knowledge Based Systems, vol. 139, pp. 23–40, 2018. [Google Scholar]

62. N. Lynn and P. N. Suganthan, “Ensemble particle swarm optimizer,” Applied Soft Computing, vol. 55, pp. 533–548, 2017. [Google Scholar]

63. J. J. Liang, A. K. Qin, P. N. Suganthan and S. Baskar, “Comprehensive learning particle swarm optimizer for global optimization of multimodal functions,” IEEE Transactions on Evolutionary Computation, vol. 10, no. 3, pp. 281–295, 2006. [Google Scholar]

64. K. T. Zheng, X. Yuan, Q. Xu, L. Dong, B. S. Yan et al., “Hybrid particle swarm optimizer with fitness-distance balance and individual self-exploitation strategies for numerical optimization problems,” Information Sciences, vol. 608, pp. 424–452, 2022. [Google Scholar]

65. J. Derrac, S. García, D. Molina and F. Herrera, “A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms,” Swarm and Evolutionary Computation, vol. 1, no. 1, pp. 3–18, 2011. [Google Scholar]

66. A. W. Mohamed, A. A. Hadi and K. M. Jambi, “Novel mutation strategy for enhancing SHADE and LSHADE algorithms for global numerical optimization,” Swarm and Evolutionary Computation, vol. 50, pp. 100455, 2019. [Google Scholar]