An Advantage Actor-Critic Approach for Energy-Conscious Scheduling in Flexible Job Shops

1  Introduction

Scheduling plays a fundamental role in manufacturing and production systems, directly influencing operational efficiency, productivity, and overall performance. Effective scheduling ensures optimal resource allocation, adherence to production timelines, and operational cost minimization, which collectively enhance resource management, boost production capacity, and improve product quality. In today’s manufacturing landscape, which is characterized by increasing customization and small-batch production, mechanisms that adapt swiftly to new orders or disruptions, and maintain stable performance under uncertainty are essential to meet diverse customer demands while maintaining operational efficiency [1].

At the core of manufacturing efficiency improvements lies the Flexible Job Shop Scheduling Problem (FJSP), an optimization problem. The FJSP involves assigning a set of jobs to a set of machines, where each job consists of a sequence of operations that can be processed on multiple machines with varying processing times. This inherent flexibility allows for better resource utilization and adaptability to changes in the production environment, thereby enhancing both energy and charge efficiency [2,3]. Furthermore, FJSP models could be extended to incorporate various real-world constraints, such as periodic maintenance and machine outages, ensuring that production schedules remain optimal and resilient [4,5]. In many scenarios, deterministic setup times and transportation times are also integrated into the models, providing additional precision in scheduling and further optimizing operational performance [6].

Energy efficiency has become a critical aspect of industrial operations, driven by both economic and environmental imperatives [7]. Energy consumption not only constitutes a significant portion of operational charges but also has profound implications for environmental sustainability. Efficient energy management can lead to substantial cost savings and reduced greenhouse gas emissions, contributing to broader sustainability goals [8–10]. Integrating energy-efficient practices into scheduling frameworks, such as the FJSP, enables the creation of production schedules that balance energy consumption with operational demands, enhancing both economic and environmental performance [11].

Moreover, the evolving industrial landscape, characterized by the Fourth Industrial Revolution and the advent of Industry 4.0 technologies, has amplified the importance of energy-efficient scheduling. The incorporation of cyber-physical systems and real-time data analytics into manufacturing processes offers new avenues for optimizing energy usage and enhancing overall operational efficiency [12]. These advancements highlight the need for sophisticated scheduling models that can dynamically adapt to changing production environments while maintaining stringent energy efficiency standards [13].

Consequently, the FJSP is critical for optimizing manufacturing efficiency. By effectively managing multiple objectives and constraints, adapting to dynamic production environments, and integrating energy-efficient practices, it significantly improves resource utilization, reduces production costs, and boosts overall productivity [14]. Our motivation stems from the growing emphasis on energy conservation driven by both economic and environmental concerns, highlighting the necessity of advanced scheduling models for sustainable large-scale industrial operations.

The remainder of this paper is organized as follows: the Literature Review surveys current developments; the Methodology section outlines our proposed approach to address the energy-conscious FJSP; the Results section presents a comprehensive evaluation of the model’s performance; and the Conclusion summarizes the research contributions, managerial insights, future research perspectives, and limitations.

2  Literature Review

The Flexible Job Shop Scheduling Problem (FJSP) poses significant challenges in manufacturing due to its NP-hard complexity, dynamic real-world constraints, and the growing emphasis on sustainability. Over the years, various methodologies have been developed, from traditional optimization techniques and heuristic methods to modern reinforcement learning approaches, with each contributing insights toward more efficient scheduling solutions.

2.1 Traditional, Heuristic, and Energy-Aware Approaches

Traditional approaches to FJSP employed exact algorithms like Mixed Integer Linear Programming (MILP) to systematically search for optimal solutions. These studies highlight the potential of MILP in generating precise solutions. Subsequent research has developed refined MILP models that incorporate complexities such as sequence-dependent setup and transportation times, aiming to balance optimality with enhanced energy efficiency [15,16]. However, due to the inherent nature of exact methods, computation times and resource demands tend to increase significantly as the problem size grows.

Heuristic methods have been widely adopted to address scalability issues, including Genetic Algorithms (GA), Iterated Greedy Algorithms (IGA), and various metaheuristics. These methods have effectively optimized complex scheduling challenges while maintaining practical computation times [17–19]. Additionally, integrated approaches that combine MILP with heuristic strategies, such as tabu search, have demonstrated enhanced robustness in dynamic scheduling environments [20]. For example, a matheuristic approach that embeds a simplified MILP model within a GA has improved lot-sizing plans and enhanced production efficiency [21]. Similarly, another study introduced a cooperative co-evolutionary matheuristic algorithm that employs MILP-based evolution methods to optimize machine and auxiliary module assignments in flexible assembly job shops [22]. A recent study formulates a sustainable distributed permutation flow-shop scheduling model with real-time rescheduling, introduces four problem-specific heuristics, employs Lagrangian relaxation and Benders decomposition reformulations, and applies customized tabu search and simulated annealing algorithms for large-scale instances [23].

Parallel to these developments, energy-aware scheduling models have emerged. These models leverage techniques ranging from linear programming and genetic algorithms to iterative greedy approaches and MILP, all aimed at minimizing energy consumption and operational costs while balancing traditional performance metrics [24–27].

Although these energy-aware models effectively capture energy-saving objectives, their reliance on static optimization frameworks can limit computing adaptability as modern job shop complexity increases.

2.2 Reinforcement Learning Approaches for Flexible Job Shop Scheduling

Researchers have increasingly turned to reinforcement learning (RL) as a dynamic, data-driven alternative to overcome this limitation.

In recent years, RL has emerged as a promising alternative for tackling the complexities of FJSP. Deep RL techniques such as Proximal Policy Optimization (PPO), Deep Q-Networks (DQN), and Double DQN have been applied to capture the dynamic relationships between production activities and scheduling objectives, enabling real-time decision-making [28–30].

Further advances in RL have seen the incorporation of Graph Neural Networks (GNNs) to model intricate operational relationships, along with Multi-Agent RL (MARL) approaches that handle dual flexibility and variable transportation times in decentralized systems [31–34]. Moreover, attention mechanisms and dual attention networks have contributed to more effective extraction of deep features from complex scheduling environments [35–37].

An up-and-coming development is found in actor-critic algorithms. These methods treat scheduling as a sequential decision-making process where an actor network proposes actions and a critic network evaluates them, refining the overall scheduling strategy over time [38–40]. Recent enhancements based on integrating value-based and policy-based methods, attention-based encoders, and hierarchical graph structures have further boosted the performance of actor-critic frameworks on both static and dynamic scheduling benchmarks [41–44].

2.3 Drawing Industry 4.0 Parallels

In Industry 4.0 manufacturing, machines, conveyors, and transporters play roles analogous to virtualized network functions and links in cloud/fog systems. Just as Network Function Virtualization (NFV) instantiates network functions on demand and Software-Defined Networking (SDN) centrally routes flow to balance load and minimize idle power, an Energy-Conscious FJSP can assign operations to machines and sequence them to reduce standby energy while meeting deadlines. By treating machines as “nodes,” jobs as “flows,” and energy costs as routing metrics, it becomes possible to draw conceptual parallels between cloud/fog orchestration and shop-floor scheduling. Recent advances in IoT and Software-Defined IoT (SD-IoT) further highlight the potential of real-time, adaptive scheduling informed by sensor data, digital twin models, and AI-driven coordination [45,46]. These developments offer additional context for understanding the broader landscape of innovative scheduling approaches in flexible manufacturing.

To explore this analogy further, we consider NFV and SDN research contributions in the context of energy-efficient resource orchestration. NFV and SDN techniques have demonstrated dynamic, energy-aware resource allocation through integrated optimization models that provision virtual network functions (VNFs) on demand and route flows using multi-objective formulations, significantly reducing energy consumption while maintaining quality of service (QoS) [47]. The deployment of parallelized service function chains via integer linear programming (ILP) and heuristic algorithms, which strategically co-locate VNFs to minimize energy use and resource contention under delay constraints, exemplifies this potential [48]. Digital twin–assisted VNF migration frameworks leveraging multi-agent deep reinforcement learning have been shown to predict resource demands and optimize migrations, reducing network energy consumption and synchronization delays in IoT environments [49]. Similarly, reinforcement learning–based VNF scheduling algorithms employing hierarchical reward mechanisms have addressed energy-delay trade-offs, reducing idle energy loss and makespan [50]. These innovations present noteworthy parallels to energy-conscious flexible job shop scheduling aspects, including dynamic resource allocation, global operation sequencing, and scenario-based learning models.

Expanding on SDN’s role in cloud and fog environments, SDN-enabled scheduling and load-balancing algorithms have been studied for their ability to reduce energy consumption by optimizing task placement and data paths. Techniques such as an adaptive load-balancing approach combining optimal edge server placement (LB-OESP) with a dynamic greedy heuristic (SDN-GH) have shown improved performance in latency-sensitive applications like healthcare systems [51]. Other schedulers based on deep reinforcement learning, such as the Deep-Q-Learning Network for Multi-Objective Task Scheduling (DRLMOTS), have achieved significant energy reductions by distributing tasks between fog nodes and cloud servers [52]. Fuzzy logic–based task offloading mechanisms, such as the Binary Linear Weight JAYA (BLWJAYA) algorithm, have further contributed to energy reduction while maintaining service quality under bandwidth and latency constraints [53]. Hybrid models incorporating load prediction (e.g., via Markov chains) with arithmetic optimization strategies have also been proposed to improve energy and delay performance in cloud-fog task scheduling [54]. Additionally, QoS-aware SD-IoT task scheduling studies offer insights into how latency-sensitive operations, such as those in multimedia streaming, can be prioritized using resource-aware techniques to reduce delay and energy use [55,56].

Distributed and decentralized orchestration models further contribute to this discussion. In Fog IoT environments, decentralized SDN control using gravitational search algorithms has been explored to reduce task offloading latency and increase assignment rates [57]. Blockchain-integrated SDN architectures have been proposed to manage services across geographically dispersed fog nodes via smart contracts, enhancing availability and reducing coordination delay [58]. Healthcare-specific IoT networks have also benefited from deep learning–based fog node selection under SDN control, achieving low latency and controlled energy use [59]. Other approaches, such as the Mountain Gazelle Optimization algorithm, use metaheuristics to balance virtual machine load, response time, and energy consumption in decentralized scheduling environments [60]. While these models originate from networked and computational systems, they provide a broader context for understanding how distributed control and local optimization strategies might be framed within energy-conscious manufacturing scheduling.

These parallels offer a suggestive conceptual backdrop that inspires, rather than dictates, the direction of our proposed approach, detailed in the following conclusion.

2.4 Conclusion and Proposed Approach

Despite the progress made with traditional and RL-based methods, several challenges remain, particularly in generating energy-efficient schedules that are computed rapidly and optimize resource utilization under deterministic conditions. Balancing energy constraints with conventional scheduling metrics is complex, necessitating an approach that combines the robustness of deep reinforcement learning with effective decision-making.

Motivated by these challenges, our work proposes an Advantage Actor-Critic algorithm that leverages the actor-critic framework for effective resource management and energy control. Building on current research in deep reinforcement learning, this method develops scheduling solutions that are robust, scalable, and energy-conscious across varying job shop scenarios and instances for modern manufacturing environments, aiming to ensure they remain computationally fast and feasible.

3  Methodology

This section presents a comprehensive methodology to address the Energy-Conscious Flexible Job Shop Scheduling Problem with Deterministic Setup and Transportation Times.

3.1 System Description

Flexible Job Shop Scheduling Problem with Deterministic Setup and Transportation Times: FJSP involves scheduling a set of jobs comprising a sequence of operations on a set of machines. Unlike the classical Job Shop Scheduling Problem (JSP), FJSP allows each operation to be processed on any machine from a predefined subset, providing flexibility in machine assignment.

Machine Slots (Positions): Each machine is equipped with multiple slots, each representing a unique position or resource unit. These slots enable the machine to handle multiple operations concurrently, increasing its processing capacity and flexibility. Assigning different operations to separate slots on the same machine allows for parallel processing, optimizing the overall scheduling efficiency.

Setup Times (ST): The setup time required before initiating an operation is influenced by the specific machine on which the operation will be processed. The preparation time for a machine varies based on the operation being processed, introducing complexity to the scheduling process. Consequently, optimizing the assignment of operations to machines and scheduling the setup times is crucial to minimize overall setup durations and enhance operational efficiency.

Transportation Times (T): Transportation time accounts for the time taken to move a job from one machine to another. This is particularly relevant when jobs require processing on multiple machines located in different areas, necessitating physical movement between them.

Energy-Conscious Scheduling: Incorporating energy considerations involves accounting for various parameters, such as energy consumed during processing, setup, transportation, idle machine time(s), and turning machines on or off. All energy metrics are measured in British Thermal Units (Btu), while all time-related parameters are measured in minutes. The goal is to schedule all jobs effectively while being mindful of the associated energy consumption and ensuring efficient use of resources.

3.2 Advantage Actor-Critic for Energy-Conscious Scheduling

This study employs the Advantage Actor-Critic (A2C) algorithm from the stable-baselines3 library for energy-conscious job shop scheduling [61]. A2C is selected based on its documented effectiveness in comparable environments: (1) In edge-cloud systems, A2C demonstrated superior load balancing and reduced task rejection rates compared to heuristic methods [62]; (2) For 5G networks, it improved latency and Quality of Service (QoS) satisfaction over other Deep Reinforcement Learning (DRL) approaches [63]; and (3) In energy management systems, A2C shows particular robustness in isolated or uncertain scenarios, outperforming other methods in demand coverage during connectivity disruptions [64].

Comparative studies further support this choice: A2C matches Deep Q-Learning’s (DQL) performance in Network Function Virtualization (NFV) cloud networks with faster execution [65], achieves better privacy-service tradeoffs than DQN in edge computing [66], and shows versatility in hybrid implementations like aircraft recovery systems [67]. While techniques combining A2C with graph networks have demonstrated enhanced scalability for complex scheduling problems [68], the base A2C algorithm remains particularly suitable for our energy-conscious Energy-Conscious Flexible Job Shop Problem context due to its proven balance of adaptability and computational efficiency across diverse operational conditions [69].

3.2.1 Advantage Actor-Critic Architecture

The A2C algorithm [70,71] integrates two neural networks: the actor and the critic. The actor πθ(a|s), parameterized by θ, proposes actions based on the current state, while the critic Vϕ(s), parameterized by ϕ, evaluates the value of the current state (architecture overview shown in Fig. 1).

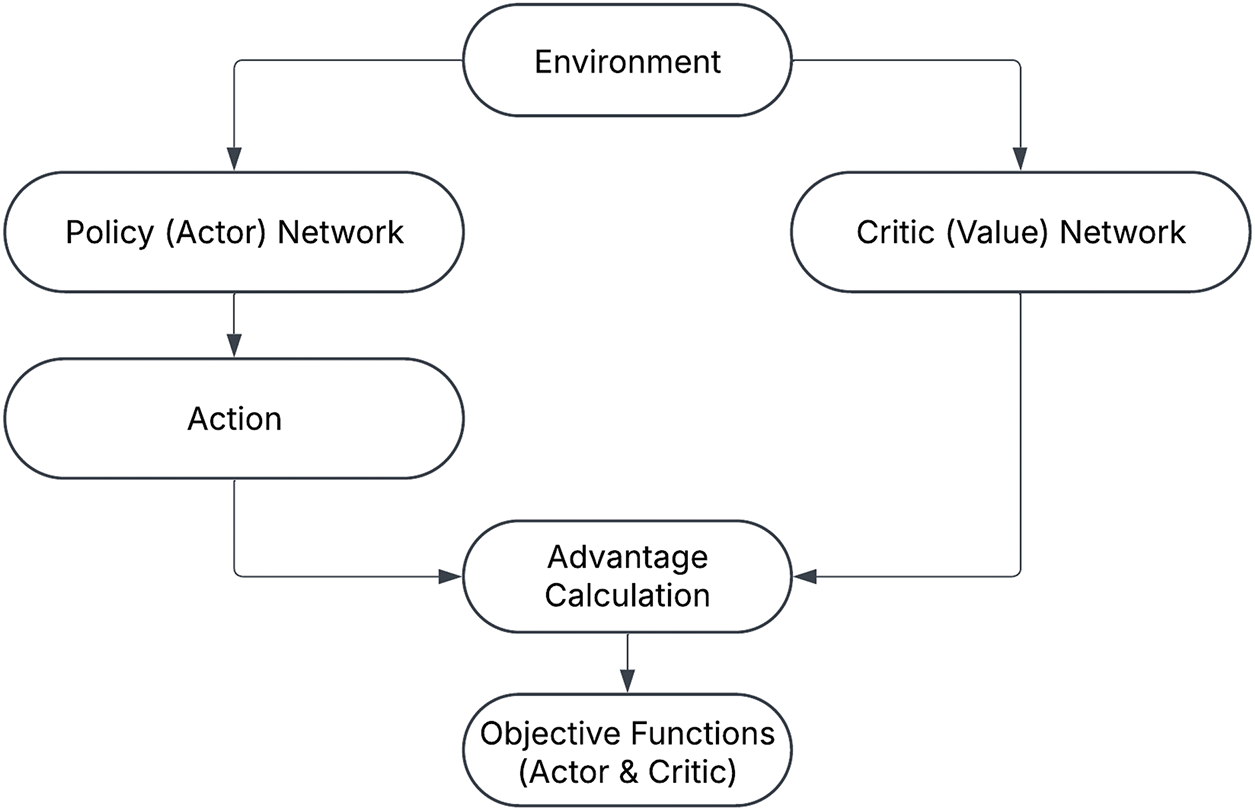
Figure 1: Advantage actor critic

Policy (Actor) Network

The actor network defines a stochastic policy πθ(a|s), which outputs a probability distribution over actions for a given state:

πθ(a|s)=exp⁡(fθ(s,a))∑a′exp⁡(fθ(s,a′))(1)

where fθ(s,a) is a function parameterized by θ that scores the compatibility of action a with state s.

Value (Critic) Network

The critic network estimates the state-value function Vϕ(s):

Vϕ(s)=Eπθ[∑t=0∞γtℛt∣s0=s](2)

where ℛt is the reward received at time step t.

Advantage Function

The advantage function A(s,a) measures the relative value of taking action a in state s compared to the average value of state s:

A(s,a)=Q(s,a)−V(s)(3)

where Q(s,a) is the action-value function:

Q(s,a)=Eπθ[∑t=0∞γtℛt∣s0=s,a0=a](4)

Objective Functions

The A2C algorithm optimizes two objective functions corresponding to the actor and the critic: Actor Objective: The objective for the actor is to maximize the expected advantage:

ℒactor(θ)=Es∼ρπθ,a∼πθ[Aϕ(s,a)log⁡πθ(a|s)](5)

where ρπθ denotes the state distribution under the policy πθ.

Critic Objective: The critic minimizes the mean squared error between the predicted value and the actual return:

ℒcritic(ϕ)=Es∼ρπθ[(ℛ+γVϕ(s′)−Vϕ(s))2](6)

where ℛ represents the immediate reward and s′ is the subsequent state.

3.2.2 Energy-Conscious Scheduling in a Flexible Job Shop Environment

The scheduling operation is modeled as a Markov Decision Process (MDP) defined by the tuple:

(𝒮,𝒜,𝒫,ℛ,γ)

where:

•   𝒮 is the state space, representing the current status of jobs, machines, and energy metrics.

•   𝒜 is the action space, consisting of scheduling decisions such as assigning jobs to machines.

•   𝒫:𝒮×𝒜×𝒮→[0,1] denotes the state transition probabilities.

•   ℛ:𝒮×𝒜→R is the reward function, designed to incentivize energy-conscious scheduling.

•   γ∈[0,1) is the discount factor, balancing immediate and future rewards.

The objective of energy-conscious scheduling is to effectively assign jobs to machines in a manner that conserves energy. This is achieved by embedding energy considerations and operational constraints within the reinforcement learning framework. The key components are described below.

The Environment

The environment simulates a job shop scenario in which multiple jobs are processed on a limited number of machines under various constraints. At each decision point (timestep), the agent selects an action that either assigns operations to machine slots or leaves them idle. The environment then advances in simulated time, updates the status of operations and machines, accumulates energy and idle charges, and provides the next state representation along with a reward signal.

Key elements include:

•   Constraints and Charge Factors: The environment incorporates several operational constraints and charge factors:

–   Operational Constraints:

*   Job operations must be executed in their predefined sequence.

*   Each job operation must be assigned to exactly one machine and slot.

*   Each machine slot can accommodate only one setup or processing operation at a time.

*   When switching machines, the sequence must follow: transportation first, then setup, and finally processing.

*   If a machine remains continuously idle beyond a predefined break-even duration, it must be turned off.

*   There is a strict, fixed limit on the number of turn-off events allowed per machine.

*   Machines transitioning from an off state to an on state undergo a heat-up phase, while those transitioning from on to off experience a cool-down phase.

*   An operation can commence only after the previous operation’s setup and processing have been completed, and, if switching machines, after any required transportation time has elapsed.

–   Energy Consumption Factors:

*   Processing Energy Charge: Energy consumed per unit of time while a machine processes an operation. Conscious scheduling can help minimize prolonged processing on less efficient machines.

*   Setup Energy Charge: Energy consumed per unit time during reconfiguration activities (e.g., tool changes, fixture adjustments) is required before an operation can begin. Scheduling strategies that reduce the frequency of retooling or batch similar operations can lower setup energy consumption across the job shop.

*   Transportation Energy Charge: Energy consumed per unit of time when transferring operations between machines. Scheduling decisions (e.g., sequencing) can reduce the frequency of transfers and create as many machine–job overlaps as possible, thus reducing transportation needs and the associated energy consumption.

*   Idle Energy Charge: The energy consumed when a machine is switched on but is not actively processing or setting up an operation. Careful scheduling, for instance, can minimize machine idle time by coordinating the start and finish times of consecutive jobs.

*   Turn-On Energy Charge: A one-time cost is incurred each time a machine is switched on. A scheduler can decide when (and how often) to power machines off and on, balancing idle-time savings against restart charges. Repeated turn-ons can also affect machine lifespan, so carefully planning these actions supports energy efficiency and extended machine life.

*   Common Energy Charge: A baseline energy overhead consumed per unit of total makespan, representing the cost of keeping the job shop operational. Because this overhead scales with the schedule length, efficient sequencing and resource allocation help reduce the associated fee.

•   Assumptions:

–   Infinite, identical transkporters are available from time 0, each carrying one job at a time without interruption.

–   Operations are non-preemptive: once started, an operation runs to completion on its assigned machine and slot.

–   All jobs, machines, and transporters are ready and available at t=0.

–   The environment is fully observable and deterministic: no unexpected job arrivals, machine breakdowns, or stochastic time variations occur.

–   The problem instance (jobs, machines, parameters, penalty levels) is static and loaded at t=0, with no dynamic changes during scheduling.

Action Space

The enhanced action space, 𝒜′, is defined as the Cartesian product of discrete sets encompassing both operation assignments and machine state decisions. The agent can assign any available operations for each machine slot or opt for a no-operation (idle) action. Additionally, the agent can decide to change the state of each machine (e.g., turn it on or off). Formally, the action space is represented as:

𝒜′=∏i=1Total Slots{0,1,2,…,|𝒪|}×∏j=1M{0,1,2},(7)

where:

•   |𝒪| is the total number of operations.

•   Total Slots is the sum of all machine slots.

•   M is the total number of machines.

For each machine j, exactly one state action is selected at each scheduling timestep:

∑k∈{0,1,2}δ(astate,j=k)=1∀j∈{1,2,…,M},(8)

where δ(⋅) is the Kronecker delta function, ensuring that only one state action (No Change, Turn On, Turn Off) is chosen per machine.

For illustration, let |𝒪|=3, Total Slots=2 across M=2. Thus, an example slot vector (2,0) means slot one runs operation 2, slot two idles. An example machine vector (1,0) means machine 1 turns on, machine 2 remains unchanged. The full action 𝒜′ is then the pair ((2,0),(1,0)).

State and Observation Space

Each state s∈𝒮 encapsulates the current status of all jobs and machines, including:

•   Pending jobs and their respective operations.

•   Machine statuses (e.g., active, idle, heating, cooling, on, off).

•   Energy metrics such as current energy consumption and historical usage.

The observation space is defined as a subset of RD, where

D=Jobs×Operations per Job+Total Slots+Machines,(9)

and is formally given by:

𝒮={s∈RD | 0≤sj≤500∀j=1,2,…,D}.(10)

Specifically:

•   Operation Durations: The first Jobs×Operations per Job elements of s represent the remaining processing time for each operation across all jobs (a zero value indicates a completed operation).

•   Machine Remaining Times: The next Total Slots elements represent the remaining processing time for each machine slot.

•   Machine Turn-On Counts: The final Machines elements indicate the number of times each machine has been turned on.

•   Machine States: Encoded implicitly within the machine remaining times and turn-on counts, reflecting whether a machine is active, idle, heating, or cooling.

Reward Function

In reinforcement learning, the reward function provides immediate (per-decision step) and terminal (end-of-scheduling-episode) feedback, rewarding or penalizing actions to steer the learning process. The reward function ℛ(s,a) is constructed to encourage both energy efficiency and robust operational performance:

ℛ(s,a)=−(Etotal+λTmakespan+κ⋅Incomplete_Penalty),(11)

where:

•   Etotal quantifies the total energy expenditure associated with taking action a in state s.

•   Tmakespan measures the total time required to complete all scheduled jobs.

•   λ=0.1 is the coefficient applied to the makespan term, chosen to impose a relatively moderate penalty for delays compared to the energy cost. Our empirical findings indicate that the model maintains robustness for λ values within the range [0.01,1.0], emphasizing the predominant role of energy consumption.

•   κ=1000 scales the penalty for incomplete operations, thereby strongly encouraging the completion of all jobs. Values of κ below 500 do not provide sufficient penalization, while overly high values (i.e., κ≫2000) can destabilize the system.

The ratio κ/λ=104 establishes a clear hierarchy of priorities, with complete job execution being paramount, followed by minimizing energy usage and, finally, reducing makespan.

Optimization Objective

The ultimate goal is to learn a policy πθ that maximizes the expected cumulative reward, minimizing energy consumption and makespan while ensuring the complete processing of all jobs. This is formally stated as:

maxθEπθ[∑t=0∞γtℛ(st,at)].(12)

Adapted Scheduling Algorithm

Building upon the A2C framework, we adapt the algorithm to cater to the specific requirements of energy-conscious scheduling in job shops. The scheduling procedure is detailed in Algorithm 1.

3.2.3 Training Procedure

The Advantage Actor-Critic (A2C) agent is trained within a custom reinforcement learning environment using the Stable Baselines3 (SB3) library. The training process enables the agent to learn scheduling policies that balance energy consumption and job completion time through iterative interactions with the environment.

Training Setup

The training procedure involves the agent interacting with the environment to collect experiences, which are then used to update the policy (actor) and value (critic) networks. The key components of the training setup are as follows:

•   Policy Network (πθ): Determines the probability distribution over actions given the current state.

•   Value Network (Vϕ): Estimates the expected return from a given state.

•   Hyperparameters: Configured to facilitate stable and efficient learning.

Learning Hyperparameters

The selection of hyperparameters is crucial for the agent’s performance. The following values are employed to accommodate the complexity of the job shop scheduling environment:

•   Learning Rate (α): Set to 0.001 to balance convergence speed and stability. This value ensures that gradients remain within a stable regime and prevents divergence during training [72,73]. In our A2C model, which targets minimizing total energy consumption, a high learning rate destabilizes gradients, impairing scheduling performance and increasing energy usage. In contrast, a lower learning rate slows convergence and results in inefficient energy utilization [74].

•   Discount Factor (γ): Chosen as 0.99 to emphasize long-term rewards, this setting guarantees that future energy costs and scheduling efficiency are adequately considered over the entire horizon. A discount below 0.99 favors immediate rewards and increases overall energy consumption.

•   Number of Steps (n_steps): Set to 1024 to accumulate sufficient experience per update, thereby reducing variance in the advantage estimates in our high-dimensional state space [75]. This parameter supports consistent scheduling performance and lower total energy consumption, in contrast to lower values yield higher variance.

•   Entropy Coefficient (ent_coef): Set to 0.005 to balance initial exploration with subsequent exploitation. This value facilitates the convergence of the policy toward schedules with reduced energy consumption by avoiding excessive randomness and premature convergence on suboptimal strategies [76,77].

•   Value Function Coefficient (vf_coef): Set to 0.5 to allocate appropriate emphasis on accurate value estimation. This balance is essential for reliably predicting long-term energy costs and underpins the generation of schedules that minimize total energy consumption [78–80].

•   Maximum Gradient Norm (max_grad_norm): Limited to 0.7 to constrain parameter updates and maintain training stability. This restriction ensures smooth policy updates and contributes to scheduling solutions with lower energy consumption [81].

Training Modality

To thoroughly evaluate the agent’s capability in handling complex scheduling scenarios, the A2C agent is trained under a single, high-penalty scenario, referred to as the Stress Test Level scenario. This scenario represents the most challenging job shop scheduling problem by maximizing the number of jobs, machines, and operations, thereby assessing the agent’s ability to generalize and perform effectively under strenuous conditions. The agent undergoes training for a total of 500,000 timesteps, ensuring extensive interaction with the environment to develop robust scheduling policies. Adopting a worst-case-aware policy optimization approach [82], our strategy leverages the idea that mastering this extreme scenario cultivates robust scheduling strategies and enables improved performance under less extreme testing conditions such as the Control Level, Moderate Treatment Level, and Extreme Condition (documented in Section 3.3).

Mathematical Framework

The training process can be formalized as follows:

1.    Trajectory Collection:

The agent interacts with the environment to generate a trajectory of experiences:

τ={(s0,a0,r0,s1),(s1,a1,r1,s2),…,(sT−1,aT−1,rT−1,sT)}(13)

where st∈𝒮 is the state at time t, at∈𝒜 is the action taken, and rt is the reward received.

2.    Advantage Estimation:

For each time step t, the advantage function is estimated as:

A(st,at)=ℛt+γVϕ(st+1)−Vϕ(st)(14)

This measure indicates how much better taking action at in state st is compared to the policy’s average performance.

3.    Policy and Value Updates:

The actor and critic networks are updated using the following gradients, where T represents the number of time steps in the collected trajectory:

∇θℒactor(θ)=1T∑t=0T−1A(st,at)∇θlog⁡πθ(at|st)(15)

∇ϕℒcritic(ϕ)=1T∑t=0T−1(ℛt+γVϕ(st+1)−Vϕ(st))∇ϕVϕ(st)(16)

These gradients are then clipped to a maximum norm to ensure stable updates:

Clip(∇)=min(1,max_grad_norm‖∇‖)∇(17)

The parameters are subsequently updated as:

θ←θ+α⋅∇θℒactor(θ)(18)

ϕ←ϕ−α⋅∇ϕℒcritic(ϕ)(19)

3.3 Benchmark Instances Extended to Energy-Based Scenarios

To evaluate the performance of our A2C model, we utilized a set of benchmark instances and extended them to incorporate energy-based scenarios with varying penalty levels. This extension allows for a comprehensive analysis of the model’s efficiency under different operational constraints and energy considerations.

3.3.1 Parsing and Extending Benchmark Instances

We developed a parsing mechanism to integrate energy considerations into the benchmark scheduling instances that extracts the essential scheduling information and augments it with energy-related parameters. The parsing process involves the following steps:

1.    Benchmark Instance Data: Raw data from benchmark instances is parsed to identify jobs, operations, machines, and their respective processing times. The benchmark instances include MK01 to MK10 [83] and MFJS01 to MFJS10 [84], for 20 instances.

2.    Energy Parameter Assignment: Each benchmark instance is extended with energy-related parameters based on predefined scenarios. These parameters include setup times, machine slots, transportation times, processing energy consumption, machine idle energy consumption, setup energy consumption, machine turn-on energy consumption, machine break-even times, heat-up and cool-down times, transporter energy consumption, common energy consumption, and turn-off limits.

3.3.2 Energy-Based Scenarios with Varying Penalty Levels

To assess the model’s robustness and adaptability, we defined three distinct energy-based scenarios with different penalty levels: Control Level, Moderate Treatment Level, and Extreme Condition. Each scenario adjusts specific energy-related parameters to simulate varying operational conditions and constraints. The configurations for these scenarios are detailed in Table 1.

•   Control Level: This scenario serves as the baseline, maintaining penalties for tardiness and inefficiencies at a standard level. It establishes a performance benchmark, allowing comparisons with scenarios that impose more stringent penalties.

•   Moderate Treatment Level: Representing an intermediate condition, this scenario increases penalties from the Control Level without reaching extreme levels. It helps in observing the model’s performance under moderately stringent operational constraints.

•   Extreme Condition: This scenario applies significant penalties to simulate challenging operational conditions that test the model’s ability to maintain efficiency under extreme constraints.

Note: The energy-related attributes, including processing energy consumption, machine idle energy consumption, setup energy consumption, machine turn-on energy consumption, machine break-even time(s), heat-up times, cool-down times, transporter energy consumption, common energy consumption, and turn-off limit(s), are sourced from [15]. To comprehensively evaluate the model under the full range of operational conditions and to preclude potential bias toward lower-end parameter values that may arise from random selection, these parameters were deliberately partitioned into three groups corresponding to the Control Level, Moderate Treatment Level, and Extreme Condition scenarios.

Stress Test Level Scenario

The Stress Test Level scenario introduces the highest level of penalties and operational constraints, pushing the model to its limits. It includes the longest setup and transportation times, the highest machine idle and turn-on energy consumption, and reduces machine slots to a minimum. The configuration for is detailed in Table 2.

4  Results

4.1 Performance across Benchmark Instances

The Energy-Conscious A2C exhibits progressively stronger performance relative to [15]’s MILP (as shown in Table 3), as problem complexity increases, with a decisive transition at medium-scale job shop instances (MFJS04/MK01). While MILP retains energy efficiency benefits (0%–7%) for small-scale job shop instances (MFJS01–03), A2C consistently outperforms beyond this threshold, demonstrating 30%–80% lower energy consumption in larger job shop instances while maintaining perfect feasibility (100% success rate vs. MILP’s 75%) and sub-second solve times (vs. MILP’s 3600s timeouts). Under extreme conditions, A2C’s robust performance contrasts with MILP’s frequent failures and unsustainable consumption spikes as job shop instance size grows.

4.2 Sensitivity Analysis of Energy Consumption

Fig. 2 illustrates a sensitivity analysis of energy consumption under three treatment levels—Control level, Moderate treatment level, and Extreme condition—comparing the total job shop energy consumption against the sum of the processing, setup, and transportation energy components. The results demonstrate that the A2C agent actively minimizes controllable energy usage (the sum of processing, setup, and transportation energy consumption). The policy avoids unnecessary machine switches and excessive movement, which would otherwise increase setup and transportation energy consumption, suggesting a preference for lean routing and efficient operation sequencing.

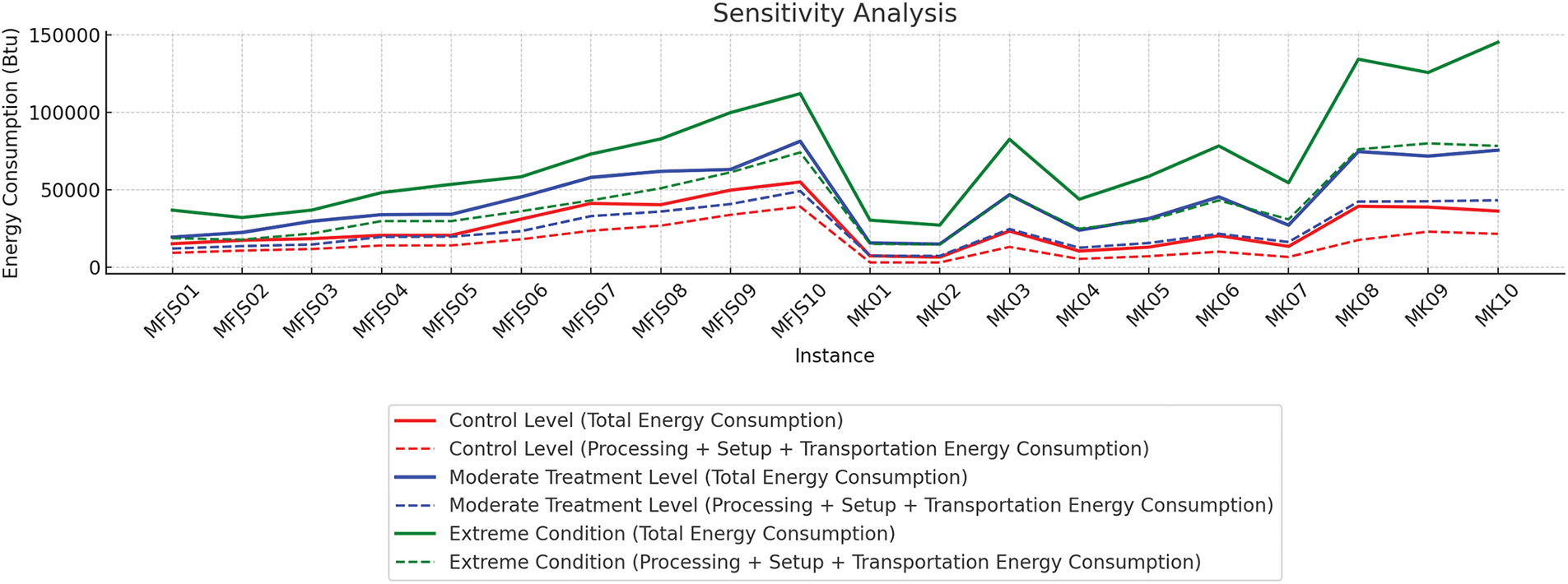
Figure 2: Scheduling sensitivity analysis

Notably, the controllable energy trends remain relatively stable even as the overall job shop energy consumption increases across treatment levels. This indicates that the agent maintains its energy-efficiency focus under more constrained operational conditions.

Moreover, as the number of jobs and machines scales across instances, the controllable energy components do not exhibit abrupt spikes. This implies that the A2C policy generalizes well, consistently optimizing energy per job across a spectrum of instance sizes. The policy demonstrates robust energy-conscious scheduling behavior and effective generalization under increasing complexity and stress.

4.3 Schedule Gantt Charts

To visualize the scheduling performance of the Advantage Actor-Critic (A2C) model across different scenarios, we present Gantt charts for two benchmark instances: MK01 under all three energy-based scenarios and MFJS10.

4.3.1 MK01 Scheduling under Different Scenarios

Observations on MK01 Scheduling

The MK01 scheduling results (Fig. 3a–c) show a clear trend across the Control Level, Moderate Treatment Level, and Extreme Condition scenarios in both energy consumption and operational efficiency. As energy constraints tighten from the Control Level to the Extreme Condition, total energy consumption increases significantly due to higher setup and transportation energy requirements. Due to increased setup and transportation times, these added demands contribute to the makespan (representing the total time to complete all jobs) doubling from the Control Level to the Extreme Condition. Despite these challenges, the model still executes relatively efficiently, demonstrating its capability to manage more complex, energy-aware scheduling without excessive computational overhead. This trade-off between energy efficiency and operational speed is further reflected in the allocation of resources: notably, Machine 4 is used in the Control Level and Moderate Treatment Level scenarios but remains unused in the Extreme Condition scenario, indicating how machine usage adapts as resource constraints become more stringent.

Figure 3: Schedule Gantt Charts for MK01 under Different Energy-based Scenarios. (a) Control Level (b) Moderate Treatment Level (c) Extreme Condition. Note: The labels in the Gantt chart follow a format where the initial digits represent the job number, and the final digit(s) indicate the operation number. For instance, “XY” refers to Job X, Operation Y, while “XYZ” refers to Job XY, Operation Z. Labels with an asterisk (*) indicate repeated work, as we would see in practical scenarios, where multiple operations are scheduled consecutively or in shifts from the same job(s)

4.3.2 MFJS10 Scheduling

Observations on MFJS10 Scheduling

The scheduling performance for the MFJS10 benchmark instance under the Extreme Condition scenario (as shown in Fig. 4) demonstrates the model’s capability to handle large-scale and complex job shop environments effectively. The total energy consumption for the scenario amounted to 111,984 Btu, which includes 62,841 Btu for processing, 9396 Btu for setup, 1800 Btu for transportation, 720 Btu for machine turn-on, 12,927 Btu for idle energy, and 24,300 Btu as common energy consumption. This breakdown highlights the model’s ability to allocate energy resources efficiently across various operational activities.

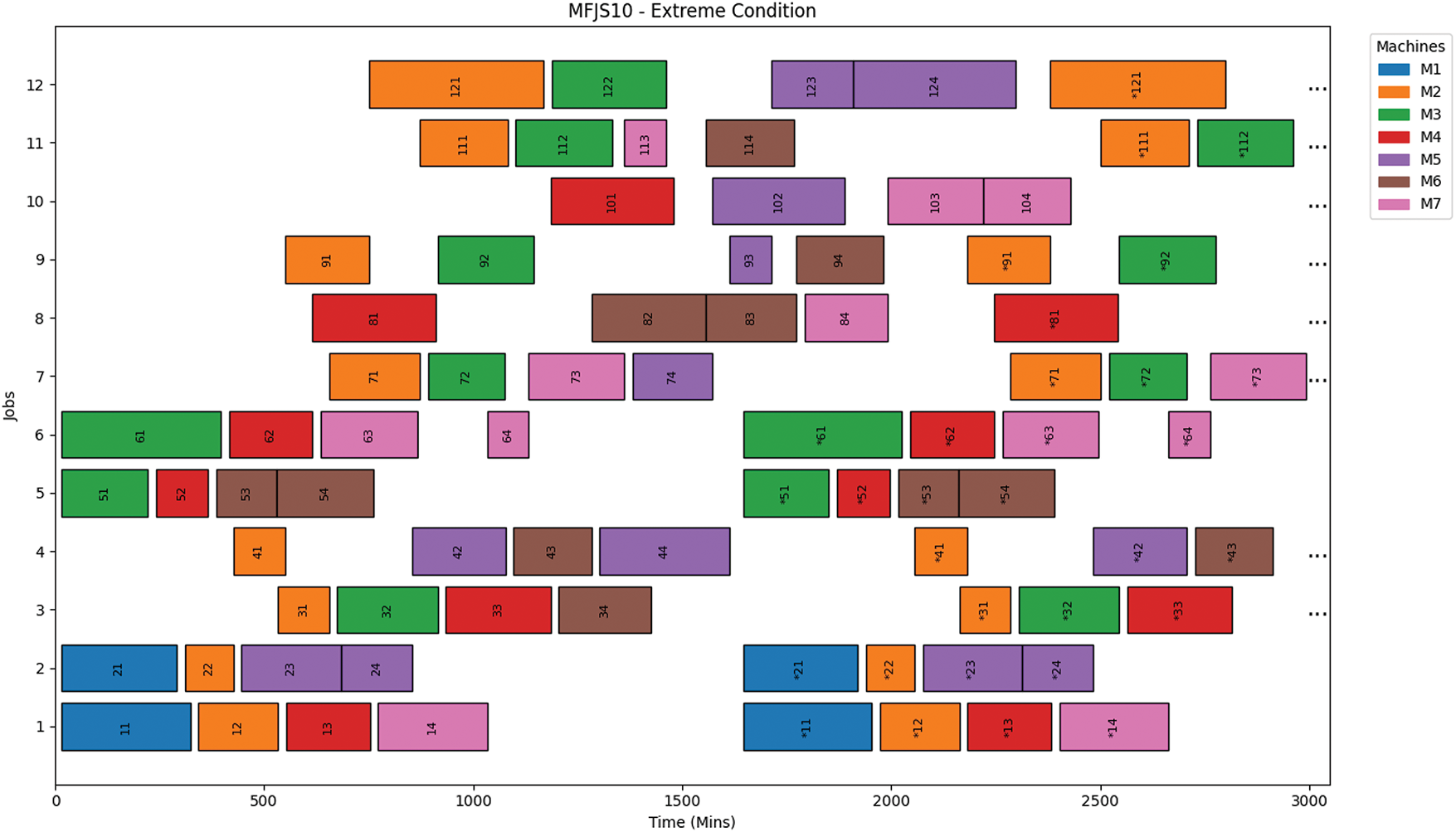
Figure 4: Schedule Gantt Chart for MFJS10 - Extreme Condition. Note: The labels in the Gantt chart follow a format where the initial digits represent the job number, and the final digit(s) indicate the operation number. For instance, “XY” refers to Job X, Operation Y, while “XYZ” refers to Job XY, Operation Z. Labels with an asterisk (*) indicate repeated work, as we would see in practical scenarios, where multiple operations are scheduled consecutively or in shifts from the same job(s)

The scheduling resulted in a makespan of 2430 min (40.5 h), reflecting the challenges associated with scheduling a substantial number of jobs and operations while adhering to stringent energy constraints. Despite the complexity and high energy demands, the model maintained a highly efficient computation time of 0.2535 s, showcasing its robustness and computational efficiency.

4.4 Processing Platform Specifications

The computational resources used for the scheduling model were pivotal for efficiently training and testing the complex model in high-dimensional state and action spaces. The processing platform is based on the x86_64 architecture and powered by an Intel(R) Xeon(R) Gold 6240 CPU operating at a base frequency of 2.60 GHz, with a maximum frequency of 3.9 GHz. The system includes 72 total CPU cores, distributed across 2 sockets, each with 18 cores per socket and 2 threads per core. The cache memory architecture features L1d: 1.1 MiB and L1i: 1.1 MiB (36 instances each), L2: 36 MiB (36 instances), and L3: 49.5 MiB (2 instances). Additionally, the system is configured with 2 NUMA nodes, ensuring optimized memory access for parallel processing tasks. These specifications enabled efficient handling of the demanding computational requirements of the scheduling model.

5  Conclusion

The A2C framework for Energy-Conscious Flexible Job Shop Scheduling effectively addresses the core research question posed in this manuscript. It demonstrates strong energy-conscious scheduling capabilities, computational efficiency, and scalability. Specifically, the proposed A2C model consciously minimizes energy consumption while maintaining 100% feasibility and sub-second response times across all tested benchmark instances. It sustains robust, sub-second scheduling for every instance size across all scenarios, from the Control Level to the Extreme Condition. Moreover, this performance directly realizes the proposed goal of developing scheduling solutions that are robust, scalable, and energy-conscious across varying job shop scenarios. Prior research demonstrates that such energy-conscious approaches can advance Industry 4.0 goals:

•   Scheduling optimization capable of reducing energy costs by 6.9% [85]

•   Scheduling mechanisms that significantly lower CO2 emissions [86]

The proposed A2C implementation extends these principles through distinct state representation and reward shaping for energy-conscious, flexible job shop environments.

5.1 Industrial Relevance and Potential Impact

•   What-if Simulation: Fast schedule generation enables rapid scenario analysis to compare multiple predetermined production strategies before execution [87].

•   Digital Twin Orchestration: High-speed scheduling supports virtual replicas of production systems, allowing continuous optimization of energy-management policies before deployment [88].

•   Surrogate Modeling: Deep learning–based surrogate predictors accelerate the evaluation of candidate schedules, supporting fast decision-making in complex, heterogeneous environments [89–91].

5.2 Managerial Insights for Decision Makers

•   Enhanced Efficiency and Sustainable Resource Management: The A2C model empowers decision makers by enabling proactive energy management and reliable scheduling, which minimizes downtime and drives productivity while reducing operational costs.

•   Scalability and Competitive Edge: Its robust adaptability across diverse industrial scenarios ensures effective performance even under stringent conditions, providing a sustainable competitive advantage in growing markets.

5.3 Research Perspectives

Future work can be expanded on further refinements of the A2C model:

•   A2C in Dynamic Environments: Enhance the A2C framework by integrating dynamic programming approaches to manage scheduling under highly volatile and uncertain production conditions, thereby boosting adaptability. Possible extensions can include:

–   New Job Arrivals: New jobs might arrive on the shop floor while existing jobs are being processed.

–   Machine Breakdowns: Machines might fail or require maintenance, making them temporarily unavailable.

–   Processing Time Changes: Actual processing times may vary from initial estimates due to factors like worker proficiency or equipment issues.

–   Urgent Orders: New high-priority jobs may be introduced, requiring immediate scheduling.

–   Other Dynamic Events: Changes in due dates, order cancellations, material shortages, etc., can also occur.

•   A2C with Local Search Enhancements: Explore the synergy between the Actor-Critic (A2C) model and local search methodologies, such as Large Neighborhood Search (LNS) or Tabu Swap, to enhance solution quality in complex scheduling problems. A promising research direction could involve a two-stage pipeline in which the A2C agent generates an initial schedule, followed by LNS, which then refines the schedule to address higher energy-consuming jobs, operations, and machines.

5.4 Research Limitations

•   Simplified energy model: The current formulation uses fixed, linear per-event energy consumption and does not capture dynamic behaviors such as variable power draws during processing peaks and nonlinear machine heat-up/cool-down energy consumption, which may lead to optimistic estimates of actual energy savings.

•   High computational and tuning demands: Achieving stable A2C convergence requires hundreds of thousands of interaction steps and extensive hyperparameter exploration, creating a barrier for deployment in environments with limited computing resources or expertise.

•   Static, offline policy: Once trained, the policy cannot respond to unanticipated changes, such as new job types, machine breakdowns, or shifting production priorities, without integrating continual-learning methods, potentially affecting validity in some operational scenarios.

Acknowledgement: The authors would like to thank Wichita State University for providing access to the High Performance Computing (HPC) cluster, which was instrumental in conducting the computational experiments for this research.

Funding Statement: This work was funded in part by the U.S. Department of Energy (DOE) Office of Energy Efficiency and Renewable Energy’s Advanced Manufacturing Office (AMO) through the Industrial Training and Assessment Center (ITAC) program.

Author Contributions: Saurabh Sanjay Singh contributed to conceptualization, methodology, formal analysis, investigation, data curation, visualization, writing—original draft, and writing—review and editing. Rahul Joshi contributed to conceptualization, investigation, data curation, and validation. Deepak Gupta contributed to supervision, validation, project administration, resources, and writing—review and editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and code supporting the findings of this study are available from the corresponding author, Saurabh Sanjay Singh, upon reasonable request. Requests can be made via email.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Sang Y, Tan J. Many-objective flexible job shop scheduling problem with green consideration. Energies. 2022;15(5):1884. doi:10.3390/en15051884. [Google Scholar] [CrossRef]

2. Du Y, Li J, Li C, Duan P. A reinforcement learning approach for flexible job shop scheduling problem with crane transportation and setup times. IEEE Trans Neural Netw Learn Syst. 2024;35(4):5695–709. doi:10.1109/TNNLS.2022.3208942. [Google Scholar] [PubMed] [CrossRef]

3. Chang J, Yu D, Hu Y, He W, Yu H. Deep reinforcement learning for dynamic flexible job shop scheduling with random job arrival. Processes. 2022;10(4):760. doi:10.3390/pr10040760. [Google Scholar] [CrossRef]

4. Su J, Huang H, Li G, Li X, Hao Z. Self-organizing neural scheduler for the flexible job shop problem with periodic maintenance and mandatory outsourcing constraints. IEEE Trans Cybern. 2022;53(9):5533–44. doi:10.1109/TCYB.2022.3158334. [Google Scholar] [PubMed] [CrossRef]

5. An Y, Chen X, Gao K, Li Y, Zhang L. Multiobjective flexible job-shop rescheduling with new job insertion and machine preventive maintenance. IEEE Trans Cybern. 2022;53(5):3101–13. doi:10.1109/TCYB.2022.3151855. [Google Scholar] [PubMed] [CrossRef]

6. Joshi R, Singh S. Energy-aware optimization of distributed flexible job shop scheduling problems with deterministic setup and processing time. In: 9th North American Conference on Industrial Engineering and Operations Management; 2024 Jun 4–6; Washington, DC, USA. 2024. p. 570–81. doi:10.46254/NA09.20240141. [Google Scholar] [CrossRef]

7. Matsunaga F, Zytkowski V, Valle P, Deschamps F. Optimization of energy efficiency in smart manufacturing through the application of cyber-physical systems and Industry 4.0 technologies. J Energy Resour Technol. 2022;144(10):102104. doi:10.1115/1.4053868. [Google Scholar] [CrossRef]

8. Miao Z, Guo A, Chen X, Zhu P. Network technology, whole-process performance, and variable-specific decomposition analysis: solutions for energy-economy-environment nexus. IEEE Trans Eng Manag. 2024;71:2184–201. doi:10.1109/TEM.2022.3165146. [Google Scholar] [CrossRef]

9. Santos E, Albuquerque A, Lisboa I, Murray P, Ermis H. Economic assessment of energy consumption in wastewater treatment plants: applicability of alternative nature-based technologies in Portugal. Water. 2022;14(13):2042. doi:10.3390/w14132042. [Google Scholar] [CrossRef]

10. Yang L, Liu Q, Xia T, Ye C, Li J. Preventive maintenance strategy optimization in manufacturing system considering energy efficiency and quality charge. Energies. 2022;15(21):8237. doi:10.3390/en15218237. [Google Scholar] [CrossRef]

11. Li R, Gong W, Lu C, Wang L. A learning-based memetic algorithm for energy-efficient flexible job-shop scheduling with type-2 fuzzy processing time. IEEE Trans Evol Comput. 2023;27(3):610–20. doi:10.1109/TEVC.2022.3175832. [Google Scholar] [CrossRef]

12. Miao S, Tuo Y, Zhang X, Hou X. Green fiscal policy and ESG performance: evidence from the energy-saving and emission-reduction policy in China. Energies. 2023;16(9):3667. doi:10.3390/en16093667. [Google Scholar] [CrossRef]

13. Parichehreh M, Gholizadeh H, Fathollahi-Fard AM, Wong KY. An energy-efficient unrelated parallel machine scheduling problem with learning effect of operators and deterioration of jobs. Int J Environ Sci Technol. 2024;21(15):9651–76. doi:10.1007/s13762-024-05595-8. [Google Scholar] [CrossRef]

14. Fernandes JMRC, Homayouni SM, Fontes DBMM. Energy-efficient scheduling in job shop manufacturing systems: a literature review. Sustainability. 2022;14(10):6264. doi:10.3390/su14106264. [Google Scholar] [CrossRef]

15. Meng L, Zhang B, Gao K, Duan P. An MILP model for energy-conscious flexible job shop problem with transportation and sequence-dependent setup times. Sustainability. 2023;15(1):776. doi:10.3390/su15010776. [Google Scholar] [CrossRef]

16. Yang S, Meng L, Ullah S, Zhang B, Sang H, Duan P. MILP modeling and optimization of multi-objective three-stage flexible job shop scheduling problem with assembly and AGV transportation. IEEE Access. 2025;13:25369–86. doi:10.1109/ACCESS.2025.3535825. [Google Scholar] [CrossRef]

17. Li J, Du Y, Gao K, Duan P, Gong D, Pan Q, et al. A hybrid iterated greedy algorithm for a crane transportation flexible job shop problem. IEEE Trans Autom Sci Eng. 2022;19(3):2153–70. doi:10.1109/TASE.2021.3062979. [Google Scholar] [CrossRef]

18. Kong X, Yao Y, Yang W, Yang Z, Su J. Solving the Flexible job shop scheduling problem using a discrete improved grey wolf optimization algorithm. Machines. 2022;10(11):1100. doi:10.3390/machines10111100. [Google Scholar] [CrossRef]

19. Pan Z, Lei D, Wang L. A bi-population evolutionary algorithm with feedback for energy-efficient fuzzy flexible job shop scheduling. IEEE Trans Syst Man Cybern: Syst. 2022;52(8):5295–307. doi:10.1109/TSMC.2021.3120702. [Google Scholar] [CrossRef]

20. Hajibabaei M, Behnamian J. Flexible job-shop scheduling problem with unrelated parallel machines and resources-dependent processing times: a tabu search algorithm. Int J Manag Sci Eng Manag. 2021;16(4):242–53. doi:10.1080/17509653.2021.1941368. [Google Scholar] [CrossRef]

21. Fan J, Zhang C, Tian S, Shen W, Gao L. Flexible job-shop scheduling problem with variable lot-sizing: an early release policy-based matheuristic. Comput Ind Eng. 2024;193(2):110290. doi:10.1016/j.cie.2024.110290. [Google Scholar] [CrossRef]

22. Hu Y, Zhang L, Zhang Z, Li Z, Tang Q. Flexible assembly job shop scheduling problem considering reconfigurable machine: a cooperative co-evolutionary matheuristic algorithm. Appl Soft Comput. 2024;166:112148. doi:10.1016/j.asoc.2024.112148. [Google Scholar] [CrossRef]

23. Fathollahi-Fard AM, Woodward L, Akhrif O. A distributed permutation flow-shop considering sustainability criteria and real-time scheduling. J Ind Inf Integr. 2024;39(11):100598. doi:10.1016/j.jii.2024.100598. [Google Scholar] [CrossRef]

24. Homayouni S, Fontes D. Optimizing job shop scheduling with speed-adjustable machines and peak power constraints: a mathematical model and heuristic solutions. Int Trans Oper Res. 2025;32(1):194–220. doi:10.1111/itor.13414. [Google Scholar] [CrossRef]

25. Wei H, Li S, Quan H, Liu D, Rao S, Li C, et al. Unified multi-objective genetic algorithm for energy efficient job shop scheduling. IEEE Access. 2021;9:54542–57. doi:10.1109/ACCESS.2021.3070981. [Google Scholar] [CrossRef]

26. Qin H, Han Y, Chen Q, Wang L, Wang Y, Li J, et al. Energy-efficient iterative greedy algorithm for the distributed hybrid flow shop scheduling with blocking constraints. IEEE Trans Emerg Top Comput Intell. 2023;7(5):1442–57. doi:10.1109/TETCI.2023.3271331. [Google Scholar] [CrossRef]

27. Ham A, Park M, Kim K. Energy-aware flexible job shop scheduling using mixed integer programming and constraint programming. Math Probl Eng. 2021. doi:10.1155/2021/8035806. [Google Scholar] [CrossRef]

28. Liu R, Piplani R, Toro C. Deep reinforcement learning for dynamic scheduling of a flexible job shop. Int J Prod Res. 2022;60(13):4049–69. doi:10.1080/00207543.2022.2058432. [Google Scholar] [CrossRef]

29. Ruiz J, Mula J, Escoto R. Job shop smart manufacturing scheduling by deep reinforcement learning. J Ind Inf Integr. 2024;38(72):100582. doi:10.1016/j.jii.2024.100582. [Google Scholar] [CrossRef]

30. Pu Y, Li F, Rahimifard S. Multi-agent reinforcement learning for job shop scheduling in dynamic environments. Sustainability. 2024;16(8):3234. doi:10.3390/su16083234. [Google Scholar] [CrossRef]

31. Song W, Chen X, Li Q, Cao Z. Flexible job-shop scheduling via graph neural network and deep reinforcement learning. IEEE Trans Ind Inform. 2023;19(2):1600–10. doi:10.1109/TII.2022.3189725. [Google Scholar] [CrossRef]

32. Peng S, Xiong G, Yang J, Shen Z, Tamir T, Tao Z, et al. Multi-agent reinforcement learning for extended flexible job shop scheduling. Machines. 2023;12(1):8. doi:10.3390/machines12010008. [Google Scholar] [CrossRef]

33. Zeng Z, Li X, Bai C. A deep reinforcement learning approach to flexible job shop scheduling. In: 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC); 2022 Oct 9–12; Prague, Czech Republic. 2022. p. 884–90. doi:10.1109/SMC53654.2022.9945107. [Google Scholar] [CrossRef]

34. Zhu X, Xu J, Ge J, Wang Y, Xie Z. Multi-operation multi-agent reinforcement learning for real-time scheduling of a dual-resource flexible job shop with robots. Processes. 2023;11(1):267. doi:10.3390/pr11010267. [Google Scholar] [CrossRef]

35. Wang R, Wang G, Sun J, Deng F, Chen J. Flexible job shop scheduling via dual attention network based reinforcement learning. IEEE Trans Neural Netw Learn Syst. 2024;35(3):3091–102. doi:10.1109/TNNLS.2023.3306421. [Google Scholar] [PubMed] [CrossRef]

36. Zhao Y, Chen Y, Wu J, Guo C. Dual dynamic attention network for flexible job scheduling with reinforcement learning. In: 2024 International Joint Conference on Neural Networks (IJCNN); 2024 Jun 30–Jul 5; Yokohama, Japan. 2024. p. 1–8. doi:10.1109/IJCNN60899.2024.10649988. [Google Scholar] [CrossRef]

37. Huang D, Zhao H, Zhang L, Chen K. Learning to dispatch for flexible job shop scheduling based on deep reinforcement learning via graph gated channel transformation. IEEE Access. 2024;12:50935–48. doi:10.1109/ACCESS.2024.3384923. [Google Scholar] [CrossRef]

38. Elsayed A, Elsayed E, Eldahshan K. Deep reinforcement learning based actor-critic framework for decision-making actions in production scheduling. In: 2021 Tenth International Conference on Intelligent Computing and Information Systems (ICICIS); 2021 Dec 5–7; Cairo, Egypt. 2021. p. 32–40. doi:10.1109/ICICIS52592.2021.9694207. [Google Scholar] [CrossRef]

39. Liu C, Chang C, Tseng C. Actor-critic deep reinforcement learning for solving job shop scheduling problems. IEEE Access. 2020;8:71752–62. doi:10.1109/ACCESS.2020.2987820. [Google Scholar] [CrossRef]

40. Monaci M, Agasucci V, Grani G. An actor-critic algorithm with policy gradients to solve the job shop scheduling problem using deep double recurrent agents. Eur J Oper Res. 2021;312(3):910–26. doi:10.1016/j.ejor.2023.07.037. [Google Scholar] [CrossRef]

41. Gebreyesus G, Fellek G, Farid A, Fujimura S, Yoshie O. Gated-attention model with reinforcement learning for solving dynamic job shop scheduling problem. IEEJ Trans Electr Electron Eng. 2023;18(6):932–44. doi:10.1002/tee.23788. [Google Scholar] [CrossRef]

42. Zhang L, Li D. Reinforcement learning with hierarchical graph structure for flexible job shop scheduling. In: 2023 International Annual Conference on Complex Systems and Intelligent Science (CSIS-IAC); 2023 Oct 20–22; Shenzhen, China. 2023. p. 942–7. doi:10.1109/CSIS-IAC60628.2023.10364146. [Google Scholar] [CrossRef]

43. Wang S, Guo S, Hao J, Ren Y, Qi F. DPU-enhanced multi-agent actor-critic algorithm for cross-domain resource scheduling in computing power network. IEEE Trans Netw Serv Manag. 2024;21(6):6008–25. doi:10.1109/TNSM.2024.3434997. [Google Scholar] [CrossRef]

44. Zhang W, Zhao F, Yang C, Du C, Feng X, Zhang Y, et al. A novel Soft Actor-Critic framework with disjunctive graph embedding and autoencoder mechanism for Job Shop Scheduling Problems. J Manuf Syst. 2024;76(14):614–26. doi:10.1016/j.jmsy.2024.08.015. [Google Scholar] [CrossRef]

45. Tariq A, Khan S, But W, Javaid A, Shehryar T. An IoT-enabled real-time dynamic scheduler for flexible job shop scheduling (FJSS) in an Industry 4.0-based manufacturing execution system (MES 4.0). IEEE Access. 2024;12:49653–66. doi:10.1109/ACCESS.2024.3384252. [Google Scholar] [CrossRef]

46. Gu W, Duan L, Liu S, Guo Z. A real-time adaptive dynamic scheduling method for manufacturing workshops based on digital twin. Flexible Serv Manuf J. 2024;27(2):557. doi:10.1007/s10696-024-09585-3. [Google Scholar] [CrossRef]

47. Baban N. Refine energy efficiency in LTE networks: a proposal for reducing energy consumption through NFV and SDN optimization. J Eng Res Rev. 2025;2(1):22–47. doi:10.5455/jerr.20241120121616. [Google Scholar] [CrossRef]

48. Chintapalli VR, Partani R, Tamma BR, Chebiyyam SRM. Energy efficient and delay aware deployment of parallelized service function chains in NFV-based networks. Comput Netw. 2024;243(1):110289. doi:10.1016/j.comnet.2024.110289. [Google Scholar] [CrossRef]

49. Tang L, Li Z, Li J, Fang D, Li L, Chen Q. DT-assisted VNF migration in SDN/NFV-enabled IoT networks via multiagent deep reinforcement learning. IEEE Internet Things J. 2024;11(14):25294–315. doi:10.1109/JIOT.2024.3392574. [Google Scholar] [CrossRef]

50. Yang X, Wu X, Shao Y, Tang G. Energy-delay-aware VNF scheduling: a reinforcement learning approach with hierarchical reward enhancement. Cluster Comput. 2024;27(6):7657–71. doi:10.1007/s10586-024-04335-4. [Google Scholar] [CrossRef]

51. Jasim A, Al-Raweshidy H. An adaptive SDN-based load balancing method for edge/fog-based real-time healthcare systems. IEEE Syst J. 2024;18(2):1139–50. doi:10.1109/JSYST.2024.3402156. [Google Scholar] [CrossRef]

52. Choppara P, Mangalampalli S. An efficient deep reinforcement learning based task scheduler in cloud-fog environment. Cluster Comput. 2024;28(1):67. doi:10.1007/s10586-024-04712-z. [Google Scholar] [CrossRef]

53. Mahapatra A, Majhi S, Mishra K, Pradhan R, Rao D, Panda S. An energy-aware task offloading and load balancing for latency-sensitive IoT applications in the fog-cloud continuum. IEEE Access. 2024;12:14334–49. doi:10.1109/ACCESS.2024.3357122. [Google Scholar] [CrossRef]

54. Khaledian N, Razzaghzadeh S, Haghbayan Z, Voelp M. Hybrid Markov chain-based dynamic scheduling to improve load balancing performance in fog-cloud environment. Sustain Comput: Inform Syst. 2024;45(1):101077. doi:10.1016/j.suscom.2024.101077. [Google Scholar] [CrossRef]

55. Hussain M, Nabi S, Hussain M. RAPTS: resource aware prioritized task scheduling technique in heterogeneous fog computing environment. Cluster Comput. 2024;27(9):13353–77. doi:10.1007/s10586-024-04612-2. [Google Scholar] [CrossRef]

56. Zhang S, Tang Y, Wang D, Karia N, Wang C. Secured SDN based task scheduling in edge computing for smart city health monitoring operation management system. J Grid Comput. 2023;21(1):1–14. doi:10.1007/s10723-023-09707-5. [Google Scholar] [CrossRef]

57. Chaudhary S, Kapadia F, Singh A, Kumari N, Jana P. Prioritization-based delay sensitive task offloading in SDN-integrated mobile IoT network. Pervasive Mob Comput. 2024;103(1):101960. doi:10.1016/j.pmcj.2024.101960. [Google Scholar] [CrossRef]

58. Núñez-Gómez C, Carrión C, Caminero M, Martínez F. S-HIDRA: a blockchain and SDN domain-based architecture to orchestrate fog computing environments. arXiv:2401.16341. 2024. [Google Scholar]

59. Babar M, Tariq M, Qureshi B, Ullah Z, Arif F, Khan Z. An efficient and hybrid deep learning-driven model to enhance security and performance of healthcare Internet of Things. IEEE Access. 2025;13(2):22931–45. doi:10.1109/ACCESS.2025.3536638. [Google Scholar] [CrossRef]

60. Maashi M, Alabdulkreem E, Maray M, Alzahrani A, Yaseen I, Shankar K. Elevating survivability in next-gen IoT-Fog-Cloud networks: scheduling optimization with the metaheuristic mountain gazelle algorithm. IEEE Trans Consum Electron. 2024;70(1):3802–9. doi:10.1109/TCE.2024.3371774. [Google Scholar] [CrossRef]

61. Raffin A, Hill A, Gleave A, Kanervisto A, Ernestus M, Dormann N. Stable-Baselines3: reliable reinforcement learning implementations. J Mach Learn Res. 2021;22(268):1–8. [Google Scholar]

62. Lu J, Yang J, Li S, Li Y, Jiang W, Dai J, et al. A2C-DRL: dynamic scheduling for stochastic edge-cloud environments using A2C and deep reinforcement learning. IEEE Internet Things J. 2024;11(9):16915–27. doi:10.1109/JIOT.2024.3366252. [Google Scholar] [CrossRef]

63. Zhang W, Vucetic B, Hardjawana W. 5G real-time QoS-driven packet scheduler for O-RAN. In: 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring); 2024; Jun 24–27; Singapore. 2024. p. 1–6. doi:10.1109/VTC2024-Spring62846.2024.10683043. [Google Scholar] [CrossRef]

64. Jones G, Li X, Sun Y. Robust energy management policies for solar microgrids via reinforcement learning. Energies. 2024;17(12):2821. doi:10.3390/en17122821. [Google Scholar] [CrossRef]

65. Tran T, Jaumard B, Duong Q, Nguyen K. 5G service function chain provisioning: a deep reinforcement learning-based framework. IEEE Trans Netw Serv Manag. 2024;21(6):6614–29. doi:10.1109/TNSM.2024.3438438. [Google Scholar] [CrossRef]

66. Jang H, Li T. Adaptive privacy-preserving task scheduling with user device collaboration in high-density edge computing environments. In: 2024 IEEE Conference on Communications and Network Security (CNS); 2024; Sep 30–Oct 3; Taipei, Taiwan. 2024. p. 1–6. doi:10.1109/CNS62487.2024.10735512. [Google Scholar] [CrossRef]

67. Żurek D, Pietroń M, Piórkowski S, Karwatowski M, Faber K. RLEM: deep reinforcement learning ensemble method for aircraft recovery problem. In: 2024 IEEE International Conference on Big Data (BigData); 2024 Dec 15–18; Washington, DC, USA. 2024. p. 2932–38. doi:10.1109/BigData62323.2024.10826050. [Google Scholar] [CrossRef]

68. Weng C, Wan Y, Xie H. DeepWS: dynamic workflow scheduling in heterogeneous cloud clusters with edge-aware reinforcement learning and graph convolution networks. In: 4th International Conference on Neural Networks, Information and Communication (NNICE); 2024 Jan 19–21; Guangzhou, China. 2024. p. 410–4. doi:10.1109/NNICE61279.2024.10498440. [Google Scholar] [CrossRef]

69. Choppara P, Mangalampalli S. Reliability and trust aware task scheduler for cloud-fog computing using advantage actor critic (A2C) algorithm. IEEE Access. 2024;12(2):102126–45. doi:10.1109/ACCESS.2024.3432642. [Google Scholar] [CrossRef]

70. Mnih V, Puigdomènech Badia A, Mirza M, Graves A, Lillicrap TP, Harley T, et al. Asynchronous methods for deep reinforcement learning. arXiv:1602.01783. 2016. [Google Scholar]

71. Huang S, Kanervisto A, Raffin A, Wang W, Ontañón S, Dossa RFJ. A2C is a special case of PPO. arXiv:2205.09123. 2022. [Google Scholar]

72. Oymak S. Provable super-convergence with a large cyclical learning rate. IEEE Signal Process Lett. 2021;28:1645–9. doi:10.1109/LSP.2021.3101131. [Google Scholar] [CrossRef]

73. Lee D. Effective Gaussian mixture learning for video background subtraction. IEEE Trans Pattern Anal Mach Intell. 2005;27(5):827–32. doi:10.1109/TPAMI.2005.102. [Google Scholar] [PubMed] [CrossRef]

74. Qian G, Ning X, Wang S. Recursive constrained maximum correntropy criterion algorithm for adaptive filtering. IEEE Trans Circuits Syst II: Express Briefs. 2020;67(10):2229–33. doi:10.1109/TCSII.2019.2944271. [Google Scholar] [CrossRef]

75. Kaul A, Jandhyala V, Fotopoulos S. An efficient two step algorithm for high dimensional change point regression models without grid search. J Mach Learn Res. 2019;20(111):1–40. [Google Scholar]

76. Yan R, Gan Y, Wu Y, Liang L, Xing J, Cai Y, et al. The exploration-exploitation dilemma revisited: an entropy perspective. arXiv:2408.09974. 2024. doi:10.48550/arXiv.2408.09974. [Google Scholar] [CrossRef]

77. Jianfei M. Entropy augmented reinforcement learning. arXiv:2208.09322. 2022. [Google Scholar]

78. Gao H, Pan Y, Tang J, Zeng Y, Chai P, Cao L. Value function dynamic estimation in reinforcement learning based on data adequacy. In: Proceedings of the 2020 4th High Performance Computing and Cluster Technologies Conference.& 2020 3rd International Conference on Big Data and Artificial Intelligence; 2020 Jul 3–6; Qingdao, China. 2020. p. 204–8. doi:10.1145/3409501.3409517. [Google Scholar] [CrossRef]

79. Yu X, Bai C, Guo H, Wang C, Wang Z. Diverse randomized value functions: a provably pessimistic approach for offline reinforcement learnings. arXiv:2404.06188. 2024. [Google Scholar]

80. Liu Q, Li Y, Liu Y, Lin K, Gao J, Lou Y. Data efficient deep reinforcement learning with action-ranked temporal difference learning. IEEE Trans Emerg Top Comput Intell. 2024;8(4):2949–61. doi:10.1109/TETCI.2024.3369641. [Google Scholar] [CrossRef]

81. Campbell R, Yoon J. Automatic curriculum learning with gradient reward signals. arXiv:2312.13565. 2023. [Google Scholar]

82. Liang Y, Sun Y, Zheng R, Huang F. Efficient adversarial training without attacking: worst-case-aware robust reinforcement learning. arXiv:2210.05927. 2022. [Google Scholar]

83. Brandimarte P. Routing and scheduling in a flexible job shop by tabu search. Ann Oper Res. 1993;41(3):157–83. doi:10.1007/BF02023073. [Google Scholar] [CrossRef]

84. Fattahi P, Saidi-Mehrabad M, Jolai F. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. J Intell Manuf. 2007;18(3):331–42. doi:10.1007/s10845-007-0026-8. [Google Scholar] [CrossRef]

85. Park M-J, Ham A. Energy-aware flexible job shop scheduling under time-of-use pricing. Int J Prod Econ. 2022;248(16):108507. doi:10.1016/j.ijpe.2022.108507. [Google Scholar] [CrossRef]

86. Shrouf F, Ordieres Meré JB, García-Sánchez Á, Ortega-Mier M. Optimizing the production scheduling of a single machine to minimize total energy consumption costs. J Clean Prod. 2014;67:197–207. doi:10.1016/j.jclepro.2013.12.024. [Google Scholar] [CrossRef]

87. Zhao J, Zhang F. Agent-based simulation system for optimising resource allocation in production process. IET Collab Intell Manuf. 2025;7(1):e70020. doi:10.1049/cim2.70020. [Google Scholar] [CrossRef]

88. Khaleel M. The application of hybrid spider monkey optimization and fuzzy self-defense algorithms for multi-objective scientific workflow scheduling in cloud computing. Internet Things. 2025;30(12):101517. doi:10.1016/j.iot.2025.101517. [Google Scholar] [CrossRef]

89. Lin C, Cao Z, Zhou M. Autoencoder-embedded iterated local search for energy-minimized task schedules of human-cyber–physical systems. IEEE Trans Autom Sci Eng. 2025;22:512–22. doi:10.1109/TASE.2023.3267714. [Google Scholar] [CrossRef]

90. Liu H, Tian L, Guo M. ESDN: edge computing task scheduling strategy based on dilated convolutional neural network and quasi-Newton algorithm. Cluster Comput. 2025;28(3):151. doi:10.1007/s10586-024-04789-6. [Google Scholar] [CrossRef]

91. Nambi S, Thanapal P. EMO-TS: an enhanced multi-objective optimization algorithm for energy-efficient task scheduling in cloud data centers. IEEE Access. 2025;13(2):8187–200. doi:10.1109/ACCESS.2025.3527031. [Google Scholar] [CrossRef]