Optimized Energy Storage Dispatch Strategy Considering Reliability and Economy

1  Introduction

With the rapid growth of variable renewable energy (VRE) such as wind and solar PV, modern power systems face new operational challenges. Heightened variability and uncertainty in renewable output strain both the safety and the economics of grid operations [1,2]. Energy storage systems (ESS) can mitigate these effects by smoothing VRE fluctuations and supplying reserve capacity [3]. However, designing a rigorous ESS dispatch strategy that achieves a sound balance between economic efficiency and system reliability remains a central challenge in both research and practice.

Existing work has primarily focused on storage sizing and siting. For example, Reference [4] formulates a robust optimization model to minimize investment cost; Reference [5] optimizes locations along with power and energy ratings; Reference [6] develops a bi-level model that couples capacity planning with system operation; Reference [7] proposes an optimal capacity configuration method for energy storage based on electrochemical energy storage operation modes; and Reference [8] presents an optimization model for storage configuration in distribution networks to improve overall economic efficiency. While these studies on storage planning advance the field from multiple angles, most do not explicitly embed reliability into the configuration process, which can result in deployments that fail to meet reliability targets after installation.

Research that explicitly incorporates reliability includes several strands. Reference [9] proposes a feeder-level storage configuration method that accounts for both economic performance and reliability. Reference [10] quantifies reliability improvements from storage and formulates an optimization model with reliability constraints. Reference [11] develops a bi-level planning model that optimizes both economic and reliability objectives simultaneously. Reference [12] designs a user-side storage optimization model based on a high-reliability power-trading mechanism between utilities and customers. Reference [13] establishes an energy storage planning model with the optimization objectives of minimizing investment costs, operational costs, and the Expected Energy Not Supplied (EENS) of the system. Reference [14] presents an economic sizing model for islanded microgrids that considers reliability constraints. While such research incorporates reliability into planning, sizing alone is not sufficient. In real-world operations, storage charging/discharging strategies are pivotal for mitigating load fluctuations and improving renewable-energy utilization—underscoring the need for further work on optimal dispatch.

On storage dispatch optimization, Reference [15] proposes an optimal dispatch model for active distribution networks, with the objective function of minimizing electricity purchase costs, grid loss costs, and voltage deviation penalties. Reference [16] integrates battery energy storage systems (BESS) into microgrid dispatch to enhance flexibility and economic performance. Reference [17] develops a two-stage dispatch model for energy storage systems, considering both power and capacity aspects. Reference [18] leverages large-scale BESS to construct a day-ahead optimal dispatch model. Reference [19] proposes a wind–storage coordinated dispatch approach to track wind power forecasts. Reference [20] proposes a global optimization model for distributed renewable-energy storage. Although these studies provide rich insights into the economic operation of storage, they rarely embed reliability indicators systematically throughout the optimization process.

In summary, existing studies on energy storage dispatch seldom consider reliability and economic performance in a unified manner. To address this gap, this paper proposes an optimal dispatch method that jointly accounts for system reliability and operational economy. The model incorporates supply-reliability constraints and minimizes total cost, including storage dispatch, renewable curtailment, and load loss. Additionally, it establishes a multidimensional evaluation framework—encompassing reliability, economic performance, renewable energy utilization, and technical indicators—to facilitate a more comprehensive assessment of dispatch strategies.

2  Energy Storage Dispatch Model Considering Reliability and Economy

To enable efficient operation under high renewable penetration, this paper formulates an energy storage dispatch optimization model that jointly considers reliability and economic performance. By embedding supply-reliability constraints and penalizing loss of load, the model internalizes the reliability objective within the optimization, achieving a unified treatment of safety and economy.

2.1 Objective Function

The objective is to minimize the system’s total operating cost, comprising energy-storage dispatch cost, curtailed wind/photovoltaic (PV) cost, and loss-of-load cost.

minJ=Cess+Ccurt+Closs(1)

where J is the total system operating cost, Cess denotes the energy storage dispatch cost, Ccurt represents the wind/PV curtailment cost, and Closs is the loss-of-load cost.

(1) Cost of Energy Storage Dispatch

The dispatch cost of the storage system comprises the operating costs incurred during charging and discharging across all time periods [21]:

Cess=cess∑t=1T(Pch(t)+Pdis(t))⋅Δt(2)

where cess is the unit operating cost of energy storage, T is the total number of planning horizon over the one-year simulation horizon, and Pch(t) and Pdis(t) represent the charging and discharging power of the energy storage system at time t, respectively, and Δt is the dispatch interval (1 h).

It should be noted that the energy storage dispatch cost coefficient Cess in Eqs. (1) and (2) only accounts for the electricity cost and general operation and maintenance expenses, and does not explicitly include the economic impact of battery cycle aging and capacity degradation. This simplified treatment is adopted to facilitate a comparative analysis of system-level economic and reliability characteristics under various operating scenarios.

(2) Cost of Wind and PV Curtailment

The cost of curtailed wind and PV arises when renewable generation cannot be fully utilized due to power-balance constraints [22]:

Ccurt=ccurt∑t=1T(Pwind,curt(t)+Ppv,curt(t))⋅Δt(3)

where ccurt is the unit cost of curtailed renewable power, and Pwind,curt(t) and Ppv,curt(t) denote the curtailed wind and PV power at time t, respectively.

(3) Cost of Load Loss

The loss-of-load cost penalizes unmet demand caused by insufficient conventional or renewable generation [23]:

Closs=closs∑t=1TPload,unmet(t)⋅Δt(4)

where closs is the unit cost of unserved load, and Pload,unmet(t) represents the power of unmet demand at time t.

2.2 Constraints

(1) Power Balance Constraint

At each time step, supply–demand balance must hold, accounting for wind, PV, storage, curtailment, and any unserved load:

Pload(t)−Pload,unmet(t)=Pwind(t)−Pwind,cur(t)+Ppv(t)−Ppv,cur(t)+Pdis(t)−Pch(t)(5)

where Pload(t) denotes the load demand at time t; Pwind(t) and Ppv(t) represent the wind power, and photovoltaic power at time t, respectively.

(2) Energy Storage Power Limits

The charging and discharging power of the energy storage system are limited by their rated capacities:

0≤Pch(t)≤δch(t)Pess,max(6)

0≤Pdis(t)≤δdis(t)Pess,max(7)

δch(t)+δdis(t)≤1(8)

where Pess,max is the maximum charging/discharging power, and δch(t) and δdis(t) are binary variables that indicate the charging and discharging states of the energy storage system at time t.

(3) Energy Storage Capacity Limits

The stored energy of the system must remain within its operational capacity range:

Ssoc,minEess≤Eess(t)≤Ssoc,maxEess(9)

where Eess(t) is the stored energy in the system at time t; Eess is the rated capacity of the energy storage system; and Ssoc,min and Ssoc,max represent lower and upper bounds of the state of charge (SOC), respectively.

(4) SOC Continuity Constraint

The state of charge (SOC) follows the dynamic energy-balance equation:

Eess(t)=Eess(t−1)+(ηchPch(t)−1ηdisPdis(t))Δt(10)

where ηch and ηdis are the charging and discharging efficiencies of the energy storage system, respectively.

(5) Wind and PV Curtailment Limits

The curtailed renewable power must not exceed the available generation at any time:

0≤Pwind,cur(t)≤Pwind(t)(11)

0≤Ppv,cur(t)≤Ppv(t)(12)

(6) Load Loss Limit

The unserved load power cannot exceed the current demand:

0≤Pload,unmet(t)≤Pload(t)(13)

(7) System Reliability Constraint [11]

To ensure supply reliability, the expected energy not supplied (EENS) must not exceed a prescribed limit:

∑t=1TPload,unmet(t)⋅Δt≤EEENS,max(14)

where EEENS,max denotes the maximum allowable limit for EENS.

3  Evaluation Indicators of Energy Storage Dispatch

To comprehensively assess how the proposed dispatch strategy meets demand, controls cost, and utilizes renewable energy, we construct a multi-indicator evaluation system spanning four dimensions: (i) power-supply reliability, (ii) economic efficiency, (iii) renewable-energy utilization, and (iv) technical performance of the energy storage system.

(i) Reliability Indicators

a) Loss of Load Probability (LOLP)

LOLP is the probability that the system fails to meet demand during the scheduling horizon. It is defined as the ratio of time intervals with unmet load to the total number of intervals:

LOLP=∑t=1Tα(t)T×100%(15)

where LOLP represents the loss-of-load probability; α(t)=1 indicates a loss of load at time t; and α(t)=0 indicates that no loss of load at time t.

b) Expected Energy Not Supplied (EENS)

EENS measures the total unmet energy over the entire scheduling horizon:

EENS=∑t=1TPload,unmet(t)⋅Δt(16)

where EENS represents the expected energy not supplied during the scheduling period. This indicator reflects the severity of power supply shortages, with units of megawatt-hours (MWh).

c) Reliability Indicator (RI)

RI denotes the fraction of load that is successfully served:

RI=1−EENS∑t=1TPload(t)⋅Δt(17)

where RI represents the reliability indicator over the scheduling horizon. Higher values indicate greater reliability and a stronger supply-assurance capability.

(ii) Economic Indicators

The economic indicators correspond to the cost terms in Section 2:

•   Cess: energy storage dispatch cost,

•   Ccurt: wind/PV curtailment cost,

•   Closs: loss-of-load cost.

(iii) Renewable Energy Utilization Indicator

To quantify the effect of energy storage dispatch on renewable energy consumption, the Abandonment Rate (AR) is defined as:

AR=∑t=1TPwind,cur(t)+Ppv,cur(t)Pwind(t)+Ppv(t)(18)

where AR represents the abandonment rate of wind and PV power during the scheduling horizon. A lower AR value indicates better renewable energy absorption.

(iv) Technical Indicators of Energy Storage System

To comprehensively assess the operational efficiency and technical characteristics of the storage system, three representative indicators are defined.

a) Annual Equivalent Full-Load Hours (FEH)

FEH reflects the total equivalent full-load discharge hours of the energy storage system during the year:

FEH=∑t=1TEdis(t)Pess,max(19)

where FEH represents the annual equivalent full-load hours of the energy storage system during the scheduling period, and Edis(t) denotes the discharge energy of the storage system at time t. A higher FEH indicates more efficient utilization of the energy storage system.

b) Annual Equivalent Cycle Number (ECN)

ECN represents the equivalent number of complete charge–discharge cycles performed by the energy storage system within one year:

ECN=∑t=1TEdis(t)Eess(20)

where ECN represents the annual equivalent number of discharge cycles of the energy storage system during the scheduling period. A larger ECN value corresponds to higher utilization intensity and faster degradation.

c) Annual Charge–Discharge Energy Ratio (CDER)

CDER measures the ratio of total annual charging energy to discharging energy, reflecting the energy balance and loss characteristics of the system:

CDER=∑t=1TEch(t)∑t=1TEdis(t)(21)

where CDER represents the annual charge–discharge energy ratio of the energy storage system during the scheduling period, and Ech(t) denotes the charging energy of the storage system at time t. A CDER value close to 1 indicates balanced operation and high round-trip efficiency.

4  Experimental Results and Analysis

To verify the effectiveness of the proposed energy storage dispatch model, which considers both reliability and economy, a case study is conducted using historical wind and photovoltaic (PV) generation data from a region in China. The study sets the energy storage capacity to 5000 MWh. The unit dispatch cost of energy storage is 80 RMB/MWh [24], the unit curtailment cost of wind/PV power is 150 RMB/MWh [25], and the unit load loss cost is 20 RMB/MWh [26]. All simulations are implemented in MATLAB R2021b using the GUROBI solver.

4.1 System Dispatch Results Analysis

To analyze the impact of reliability considerations on dispatch outcomes, three different scenarios are compared:

Scenario 1: Dispatch considering only the reliability.

Scenario 2: Dispatch considering only the economy.

Scenario 3: Dispatch considering both reliability and economy.

Table 1 summarizes the optimization results for the three scenarios.

Table 1 compares the optimization results under three dispatch strategies.

•   Scenario 1 achieves zero loss of load (LOLP = 0, EENS = 0) with 100% reliability. However, this comes at the cost of high storage utilization (FEH = 662.7 h, ECN = 133), and the dispatch cost exceeds half of the total. Moreover, the renewable curtailment rate (AR = 40.21%) remains high, indicating weak economic performance and low utilization of renewable energy.

•   Scenario 2 significantly reduces total cost (−27%), with nearly halved storage operation cost and improved renewable absorption (AR = 20.98%). Nevertheless, reliability declines noticeably (LOLP = 0.0911%, RI = 99.95%), as the model allows load loss to minimize system cost.

•   Scenario 3 strikes a better balance between reliability and economy. Although the total cost increases by only 0.014% compared with Scenario 2, the LOLP decreases by 37.42%, the EENS is reduced by half, and RI improves to 99.98%. This indicates that, under the current coefficients and system conditions, the economically oriented dispatch in Scenario 2 is already close to the reliability constraint boundary. As a result, tightening the reliability constraint in Scenario 3 mainly reshapes the charging/discharging pattern of the energy storage system, leading to significant reliability improvements with an almost negligible increase in total cost.

•   Under the above modelling assumption adopted in Eqs. (1) and (2), the ECN values in Table 1 are mainly used as a relative indicator of the storage cycling intensity among different scenarios, rather than a precise estimate of the actual battery lifetime. Future research will consider introducing more detailed degradation models to improve further the comprehensive assessment of the long-term lifetime and economic performance of the energy storage system.

4.2 Comparative Analysis of Costs in Scenarios 2 and 3

To further investigate why the optimal cost difference between Scenario 2 and Scenario 3 is slight, this section considers three approaches: increasing the load level to 105%, reducing the wind/PV output to 95%, and decreasing the ESS capacity. Table 2 reports the corresponding economic and reliability results of the system under these approaches.

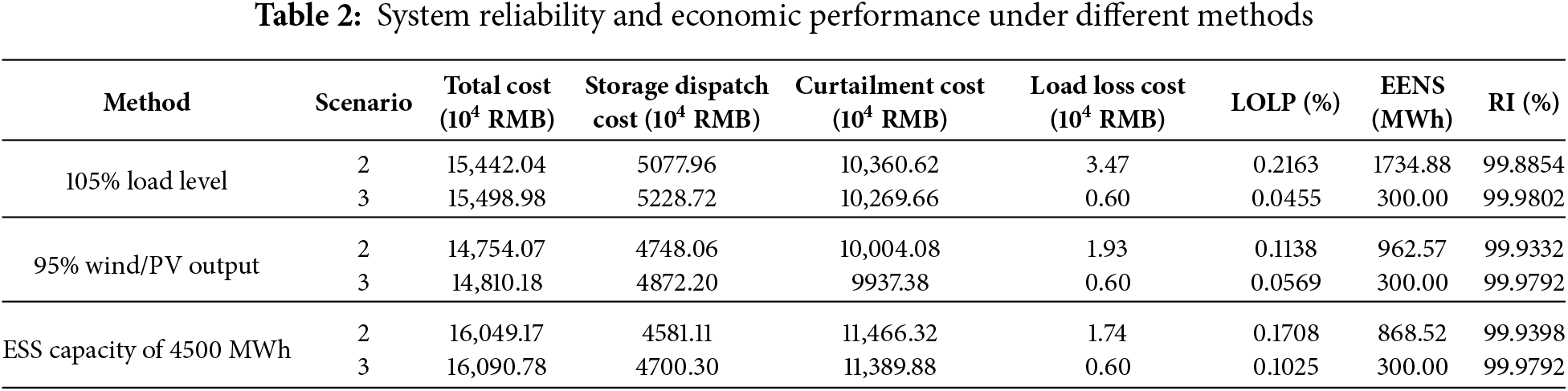
From Table 2, under more stringent conditions such as increased load level, reduced wind/PV output, or decreased ESS capacity, the total-cost difference between Scenario 2 and Scenario 3 expands from the negligible gap observed in Table 1 to approximately 0.26%–0.38%. This is because, as the system margin decreases, the reliability constraint exerts a much stronger influence on the temporal charging/discharging schedule of the ESS. Compared with Scenario 2, Scenario 3 increases the intensity of ESS dispatch to constrain the EENS to 300 MWh, thereby markedly reducing the loss-of-load probability and the outage-loss cost. Meanwhile, since the ESS contributes more effectively to system balancing during critical periods, the wind/PV curtailment loss is also reduced. However, the increase in ESS dispatch cost required to satisfy the reliability requirement is usually larger than the combined reductions in curtailment loss and outage-loss cost, resulting in a slight increase in total cost but a substantial improvement in reliability. Overall, Table 2 further indicates that when the system margin decreases, the impact of the reliability constraint on the dispatch strategy becomes stronger, making the differences between the two scenarios more pronounced.

4.3 Power Balance Analysis under Different Scenarios

To further illustrate the impact of dispatch strategies on system operation, Figs. 1–3 display the power balance curves of the system for a typical 24-h day under the three scenarios.

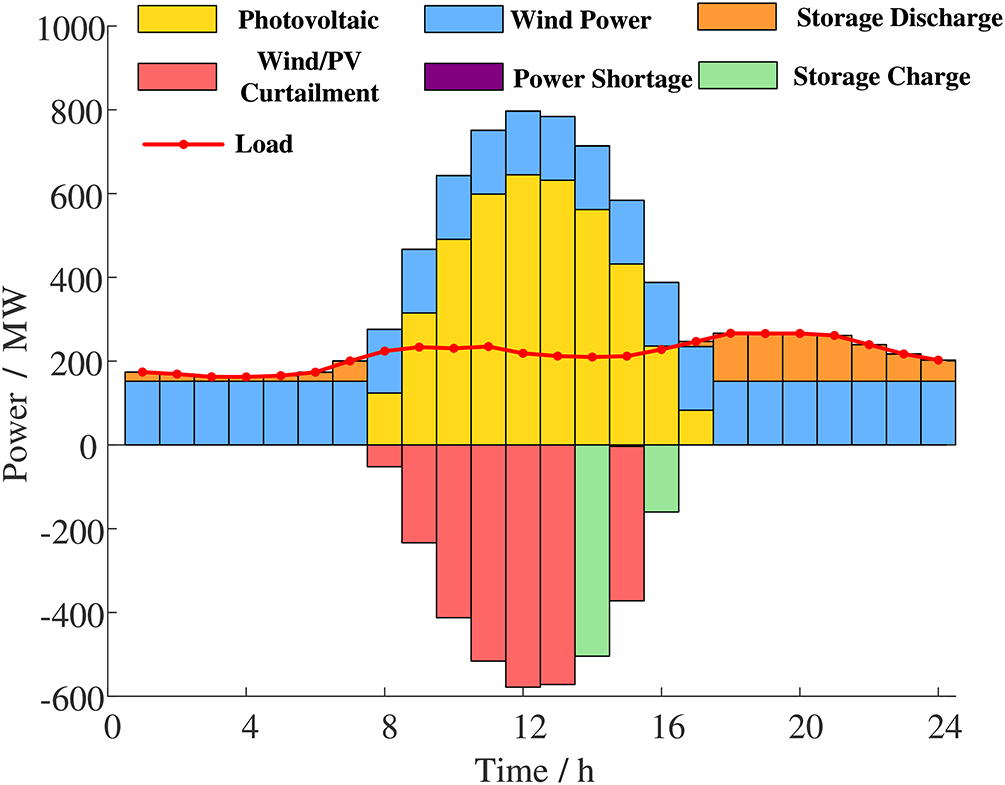
Figure 1: System power balance considering only the reliability

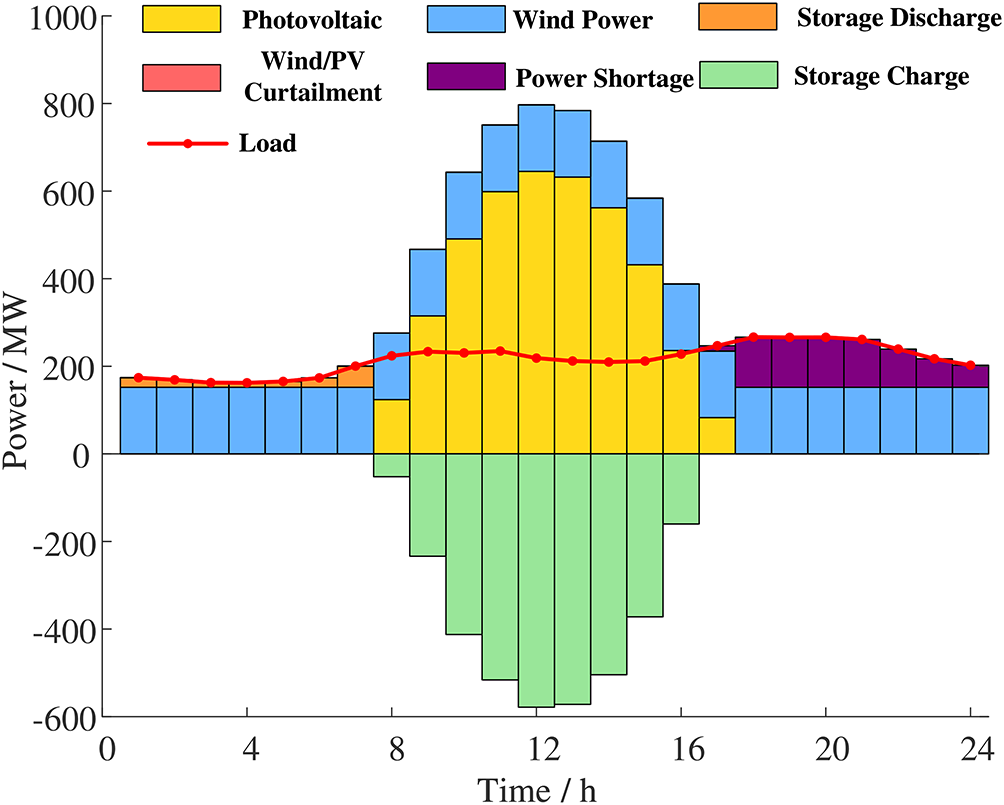
Figure 2: System power balance considering only the economy

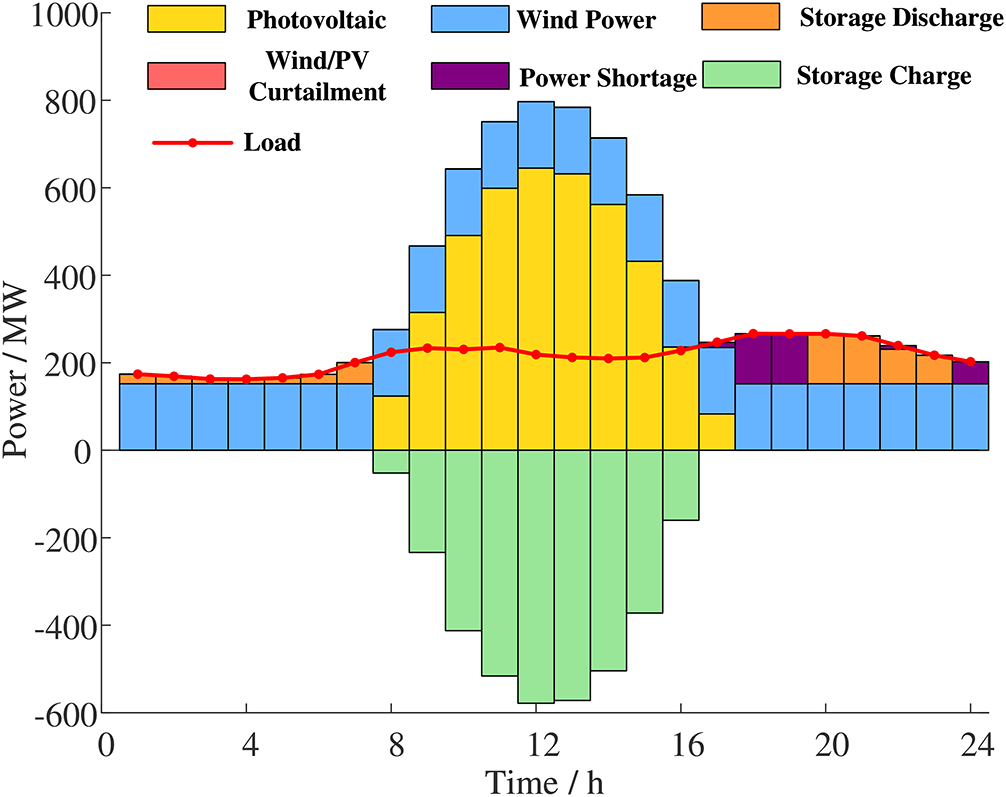
Figure 3: System power balance considering both reliability and economy

In Fig. 1, during low-load hours (0–7 h), wind generation and storage discharge meet demand without shortages. Between 8 and 13 h, when wind/PV output peaks, substantial curtailment occurs because storage does not charge promptly, resulting in wasted surplus renewable energy. Although reliability is maintained, economic performance is poor. Between 17 and 23 h, storage discharges to cover peak demand, sustaining supply but revealing a delayed response and suboptimal resource utilization.

In Fig. 2, during the renewable peak (8–13 h), the system proactively charges storage, reducing curtailment and improving economic performance. However, from 17–23 h, the model permits partial load shedding rather than discharging storage because the discharge cost exceeds the penalty for unserved energy. Allowing partial load shedding lowers total cost but degrades reliability.

In Fig. 3, under the proposed strategy, storage discharges moderately during peak demand (17–23 h), cutting shortages while keeping costs low. Compared with Scenario 2, reliability improves markedly with only a negligible increase in cost, confirming the benefit of jointly considering reliability and economy.

4.4 Effect of EENS Constraint on Dispatch Results

To assess the impact of the EENS constraint, Table 3 presents system performance under different EEENS,max values.

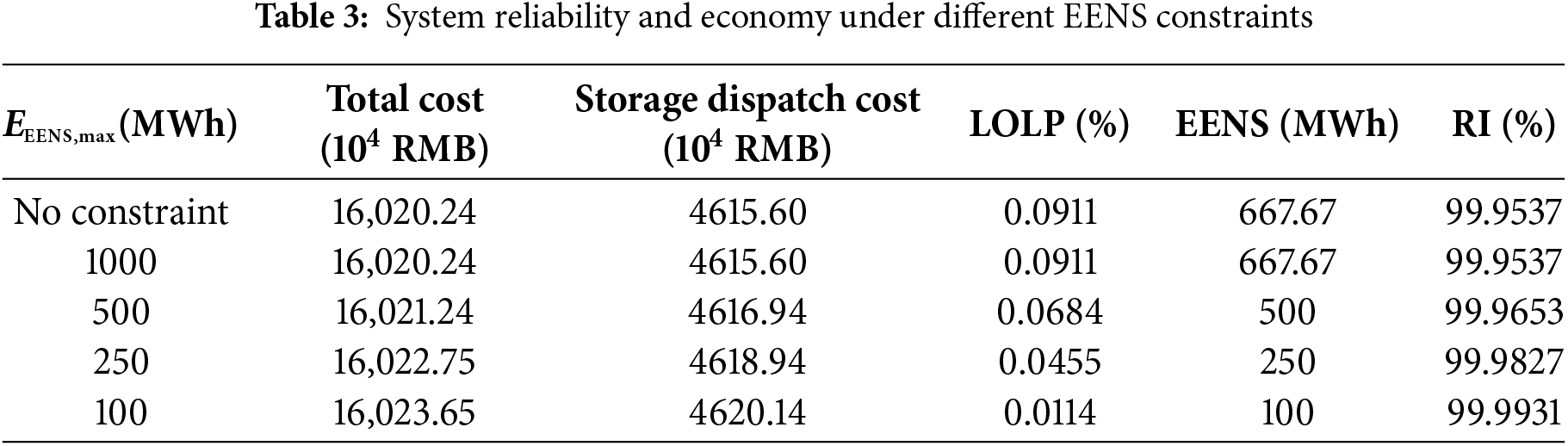
As shown in Table 3, when the constraint is loose (≥1000 MWh), outcomes are nearly identical, indicating high inherent reliability. As EEENS,max tightens, dispatch cost rises slightly while LOLP falls and RI improves. In other words, stricter reliability limits trigger more proactive storage operations, enhancing supply assurance at a modest economic cost.

4.5 Effect of Unit Load Loss Cost on Dispatch Results

To further investigate the role of the unit loss-of-load cost (closs) in the model, Table 4 summarizes the results under different closs values.

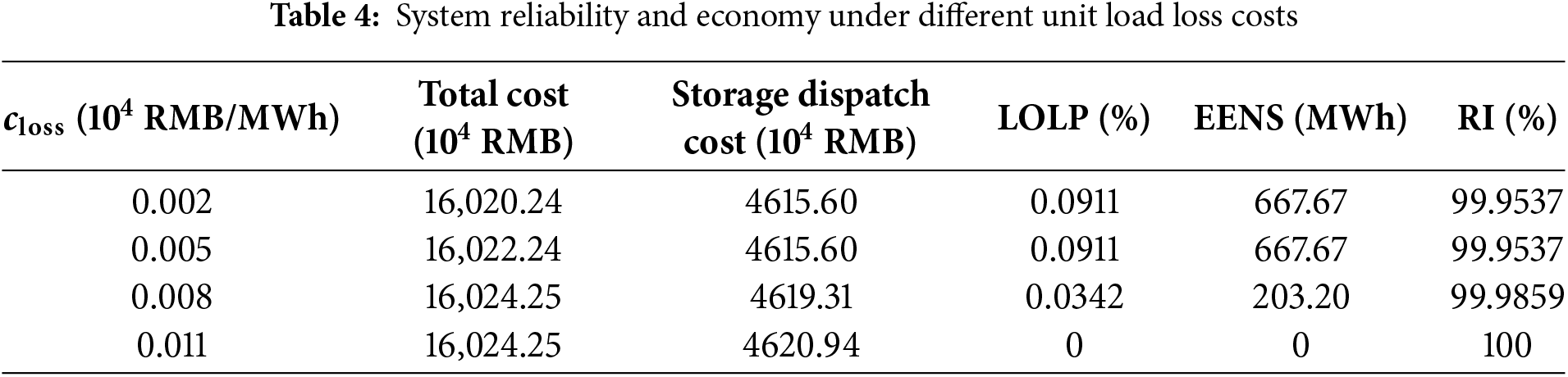
According to Table 4, when closs ≤ 0.005 × 104 RMB/MWh, the system tolerates small load losses to minimize cost, resulting in lower reliability. When closs ≥ 0.008 × 104 RMB/MWh, storage discharge becomes more intensive, LOLP and EENS drop significantly, and RI rises above 99.98%. At closs = 0.011 × 104 RMB/MWh, no load loss occurs (RI = 100%), and total cost increases only marginally. Thus, increasing closs effectively enhances reliability with minimal impact on economic performance.

5  Conclusion

This paper proposes an energy storage dispatch optimization model that simultaneously considers system reliability and economic performance. Based on real data from a regional power system, a series of case studies was conducted to verify the model’s effectiveness. The main conclusions are as follows:

1.    Integrated reliability–economy framework. By incorporating reliability constraints and a loss-of-load penalty into the objective function, the model internalizes reliability within economic dispatch, enabling high supply reliability while minimizing total operating costs.

2.    Significant performance gains. With only a 0.014% increase in total cost, the loss-of-load probability (LOLP) falls by 37.42%, the expected energy not supplied (EENS) decreases by 50%, and the reliability indicator (RI) reaches 99.98%.

3.    More substantial impact under tighter operating conditions. When the system margin decreases, the reliability constraint becomes more influential, widening the cost difference to 0.26%–0.38% while delivering substantial improvements in reliability.

4.    Regulatory role of reliability parameters. Tightening the EENS limit or increasing the unit loss-of-load cost drives more proactive storage response during peak demand or low renewable output, thereby enhancing reliability.

5.    Improved renewable utilization. The proposed method reduces curtailment, increases renewable absorption, and raises overall system efficiency.

Overall, the results show that the proposed reliability–economy coordinated dispatch strategy achieves a balanced trade-off between economic efficiency and supply security, offering practical guidance for the operation and planning of future power systems with large-scale renewable–storage integration. It is worth noting that the case study presented in this paper is based on deterministic wind/PV generation, as well as load profiles. In practical operation, forecasting errors and stochastic fluctuations may affect the dispatch performance. In future work, uncertainty will be explicitly modelled through scenario-based simulation or stochastic/robust optimisation to further evaluate the applicability of the proposed strategy under prediction errors.

From the perspective of intelligent operation, the proposed optimization framework can serve as a foundational environment for intelligent dispatch: load, wind/PV generation, and ESS SOC can be treated as system states; ESS charging/discharging as the decision variables; and cost–reliability indicators as the evaluation signal, which is suitable for reinforcement learning training. Meanwhile, the optimization results can be used to generate labeled state–decision–indicator samples, providing training data for data-driven dispatch models. Future work will leverage the labelled data generated from the optimization solutions to train approximate policy models, thereby accelerating online decision-making and enhancing real-time dispatch capabilities.

Acknowledgement: Not applicable.

Funding Statement: This work was supported by Graduate Research and Innovation Program Project of Nanjing Institute of Technology (No. TB202517025).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization: Fan Chen; methodology: Jiale Hu; software: Jiale Hu and Yue Yang; validation: Jiale Hu and Man Wang; formal analysis: Yue Yang; investigation: Yue Yang and Man Wang; writing—original draft preparation: Jiale Hu; writing—review and editing: Jiale Hu and Man Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Glossary

References

1. Ali JS, Qiblawey Y, Alassi A, Massoud AM, Muyeen SM, Abu-Rub H. Power system stability with high penetration of renewable energy sources: challenges, assessment, and mitigation strategies. IEEE Access. 2025;13:39912–34. doi:10.1109/ACCESS.2025.3546491. [Google Scholar] [CrossRef]

2. Cavus M. Advancing power systems with renewable energy and intelligent technologies: a comprehensive review on grid transformation and integration. Electronics. 2025;14(6):1159. doi:10.3390/electronics14061159. [Google Scholar] [CrossRef]

3. Muzammal Islam M, Yu T, Giannoccaro G, Mi Y, la Scala M, Rajabi Nasab M, et al. Improving reliability and stability of the power systems: a comprehensive review on the role of energy storage systems to enhance flexibility. IEEE Access. 2024;12:152738–65. doi:10.1109/ACCESS.2024.3476959. [Google Scholar] [CrossRef]

4. Lv X, Li X, Xu C. A robust optimization model for capacity configuration of PV/battery/hydrogen system considering multiple uncertainties. Int J Hydrogen Energy. 2023;48(21):7533–48. doi:10.1016/j.ijhydene.2022.11.220. [Google Scholar] [CrossRef]

5. Peng S, Zhu L, Dou Z, Liu D, Yang R, Pecht M. Method of site selection and capacity setting for battery energy storage system in distribution networks with renewable energy sources. Energies. 2023;16(9):3899. doi:10.3390/en16093899. [Google Scholar] [CrossRef]

6. Huang Q, Huang D, Cai L, Xu Q. Analysis of optimal configuration of energy storage in wind-solar micro-grid based on improved gray wolf optimization. Sci Tech Energ Transition. 2024;79:81. doi:10.2516/stet/2024070. [Google Scholar] [CrossRef]

7. Hu G, Zhao X, Cheng S, Zhang Q, Zhang Q, Bai J, et al. The optimal configuration of energy storage capacity based on the NSGA-II algorithm and electrochemical energy storage operational modes. Processes. 2025;13(5):1432. doi:10.3390/pr13051432. [Google Scholar] [CrossRef]

8. Wang K, Wang Y, Gao J, Liang Y, Ma Z, Liu H, et al. Multi-objective optimization of energy storage station configuration in power grids considering the flexibility of thermal load control. Energies. 2025;18(10):2527. doi:10.3390/en18102527. [Google Scholar] [CrossRef]

9. Gholami M, Mousavi SA, Muyeen SM. Enhanced microgrid reliability through optimal battery energy storage system type and sizing. IEEE Access. 2023;11:62733–43. doi:10.1109/ACCESS.2023.3288427. [Google Scholar] [CrossRef]

10. Fang T, Sun W, Wang Z, Wang B, Pan H, Shen J. Research on optimization of energy storage configuration with reliability constraints. In: 2024 5th International Conference on Power Engineering (ICPE); 2024 Dec 13–15; Shanghai, China. p. 627–33. doi:10.1109/ICPE64565.2024.10929174. [Google Scholar] [CrossRef]

11. Atawi IE, Abuelrub A, Al-Shetwi AQ, Albalawi OH. Design of a wind-PV system integrated with a hybrid energy storage system considering economic and reliability assessment. J Energy Storage. 2024;81:110405. doi:10.1016/j.est.2023.110405. [Google Scholar] [CrossRef]

12. Ouyang S, Peng Z, Fang Z, Kang L, Wang F. Dual-layer optimization configuration of user-side energy storage system considering high reliability power supply transaction model between the power grid company and the user. J Energy Storage. 2025;113:115637. doi:10.1016/j.est.2025.115637. [Google Scholar] [CrossRef]

13. Hamidan MA, Borousan F. Optimal planning of distributed generation and battery energy storage systems simultaneously in distribution networks for loss reduction and reliability improvement. J Energy Storage. 2022;46:103844. doi:10.1016/j.est.2021.103844. [Google Scholar] [CrossRef]

14. Deng D, Tang X. Research on optimal configuration of energy storage in microgrid considering the reliability of power supply for critical loads. In: 2023 3rd New Energy and Energy Storage System Control Summit Forum (NEESSC); 2023 Sep 26–28; Mianyang, China. p. 63–6. doi:10.1109/NEESSC59976.2023.10349309. [Google Scholar] [CrossRef]

15. Li Y, Xiao XB, He XM, Huang BY, Fang Y, He XY. Robust optimization dispatch method for distribution network considering four-quadrant power output of energy storage devices. J Electr Eng Technol. 2024;19(2):919–30. doi:10.1007/s42835-024-01813-y. [Google Scholar] [CrossRef]

16. Kumar N, Dahiya S, Singh Parmar KP. Multi-objective economic emission dispatch optimization strategy considering battery energy storage system in islanded microgrid. J Oper Autom Power Eng. 2024;12(4):296–311. doi:10.22098/joape.2023.11399.1852. [Google Scholar] [CrossRef]

17. Ding Y, Xu Q, Hao L, Xia Y, Li D, Chen J. Day-ahead robust dispatch of interconnected multi-microgrids considering two-stage model of hybrid energy storage. J Energy Storage. 2024;92:112120. doi:10.1016/j.est.2024.112120. [Google Scholar] [CrossRef]

18. Zhang M, Li W, Yu SS, Wen K, Muyeen SM. Day-ahead optimization dispatch strategy for large-scale battery energy storage considering multiple regulation and prediction failures. Energy. 2023;270:126945. doi:10.1016/j.energy.2023.126945. [Google Scholar] [CrossRef]

19. Li Z, Xiang Y, Liu J. Forecasting error-aware optimal dispatch of wind-storage integrated power systems: a soft-actor-critic deep reinforcement learning approach. Energy. 2025;318:134798. doi:10.1016/j.energy.2025.134798. [Google Scholar] [CrossRef]

20. Zhou Z, Bian J, Yu Z. Incremental cost analysis model of distribution network based on economic dispatch of distributed new-energy storage system. Clean Energy. 2024;8(2):89–103. doi:10.1093/ce/zkae007. [Google Scholar] [CrossRef]

21. Shen Y, Cheng Q, Chen Y, Lu Z, Mo X, Wu L. Optimized dispatch control of V2G charging piles and smart terrace energy storage accounting for carbon emissions. Distrib Util. 2025;42(06):59–66. (In Chinese). doi:10.19421/j.cnki.1006-6357.2025.06.007. [Google Scholar] [CrossRef]

22. Peng G, Kou QL, Fang T, Geng X, Kong XW, Xu YY. An optimal strategy for energy storage allocation in active distribution networks considering new energy consumption rates. Zhejiang Electr Power. 2025;44(1):84–94. (In Chinese). doi:10.19585/j.zjdl.202501009. [Google Scholar] [CrossRef]

23. Hao FZ, Liu H, Hu YR, He X, Wei XZ, Sun Y, et al. Day-ahead risk scheduling strategy of independent microgrid considering source-load correlation. Power Demand Side Manag. 2024;26(3):34–40. (In Chinese). doi:10.3969/j.issn.1009-1831.2024.03.006. [Google Scholar] [CrossRef]

24. Teng MJ, Chen C, Zhao YH, Zhong J, Geng J, Lü JH, et al. Distribution robust optimal day-ahead dispatch method for power systems with uncertain wind power access considering deep peak regulation of coal-fired units and energy storage. Power Syst Technol. 2024;48(8):3122–32. (In Chinese). doi:10.13335/j.1000-3673.pst.2023.1619. [Google Scholar] [CrossRef]

25. Wang ZH, Ma S, Li GQ, Bian J. Day-ahead and intra-day two-stage rolling optimal dispatch of power grid considering access of composite energy storage power stations. Acta Energiae Solaris Sin. 2022;43(10):400–8. (In Chinese). doi:10.19912/j.0254-0096.tynxb.2021-0444. [Google Scholar] [CrossRef]

26. Chen ZX, Wang P, Xiao WF, Jia DQ, Geng XY, Yang L. Integrated optimal configuration of flexible multi-state switch and distributed generation in distribution network considering reliability gain. Electr Power Constr. 2022;43(6):93–100. (In Chinese). doi:10.12204/j.issn.1000-7229.2022.06.010. [Google Scholar] [CrossRef]