 Open Access
Open Access
ARTICLE
A Novel Math-Inspired Metaheuristic Algorithm for Retinal Vessel Segmentation: Quadratic Interpolation Optimization (QIO) Algorithm
1 Department of Mechatronics Engineering, Faculty of Engineering, Erciyes University, Kayseri, Türkiye
2 Department of Electronics and Automation, Vocational School of Hendek, Sakarya University of Applied Sciences, Sakarya, Türkiye
3 Mechatronics Engineering, Graduate School of Natural and Applied Sciences, Erciyes University, Kayseri, Türkiye
* Corresponding Author: Mehmet Bahadır Çetinkaya. Email:
Journal on Artificial Intelligence 2026, 8, 89-106. https://doi.org/10.32604/jai.2026.074459
Received 11 October 2025; Accepted 06 January 2026; Issue published 13 February 2026
Abstract
Math-inspired metaheuristic algorithms stand out with their simple algorithm structures and the inclusion of fewer control parameters. In this study, the recently proposed math-inspired Quadratic Interpolation Optimization (QIO) algorithm was improved as a clustering-based algorithm and then applied to retinal vessel segmentation. Afterwards, its performance was compared with the math-inspired Sine Cosine Algorithm (SCA) and Arithmetic Optimization Algorithm (AOA), which have been frequently applied to engineering problems. First, the performance of the QIO algorithm was analyzed in terms of sensitivity (Se), specificity (Sp), accuracy (Acc), and precision (Prec). An average success rate of approximately 70% or higher indicates that the QIO algorithm is able to provide sufficient performance in clustering. Subsequently, detailed convergence analyses were performed in terms of mean squared error (MSE), CPU time, and convergence speed. The results demonstrate that the QIO algorithm reaches low MSE values at early cycles and shorter CPU times. Finally, to compare the statistical performance of the algorithms, analyses were also conducted based on standard deviation and the Wilcoxon Rank-Sum test. The results demonstrated the stability and robustness of the QIO algorithm. Consequently, it can be concluded that the QIO algorithm can be successfully applied to image processing.Keywords
Vasomotion in retinal vessels provides important information about symptoms related to vascular pathology. In particular, accurate segmentation of diseased vessels affected by diabetic retinopathy (DR) is crucial. As a result of DR, structural deformations such as vasoconstriction, vasodilation, rupture, or clot formation may occur in the retinal vessels. To enable the most appropriate diagnosis and treatment, pixel-based analysis of retinal images should be performed with high accuracy. Although segmentation of retinal vessels can be successfully carried out using gradient-based algorithms, artificial intelligence (AI)-based approaches frequently offer higher performance compared to traditional methods. In the literature, while deep learning (DL)-based approaches are widely used in retinal vessel segmentation, metaheuristic algorithms have a limited number of applications. In this study, the Quadratic Interpolation Optimization (QIO) algorithm [1], a recently proposed math-inspired metaheuristic algorithm, was applied to retinal vessel segmentation. Subsequently, the performance of the QIO algorithm was compared to that of the SCA [2] and AOA [3], which are among the most commonly used math-inspired metaheuristic algorithms in the literature.
In the literature, studies on retinal vessel segmentation can be classified into three main groups: i.) gradient-based algorithmic approaches, ii.) metaheuristic-based algorithmic approaches, and iii.) DL-based approaches. Among these, metaheuristic and DL-based approaches stand out with their robust structures. For retinal vessel segmentation, the most commonly used databases are Digital Retinal Images for Vessel Extraction (DRIVE), Structured Analysis of the Retina (STARE), and Child Heart and Health Study in England (CHASE DB1). An improved U-Net-based DL architecture consisting of three novel preprocessing algorithms was proposed for retinal vessel segmentation [4]. In another study, an efficient DL network structure called the plenary attention mechanism-UNet (PAM-UNet) was proposed, and its excellent feature extraction performance was demonstrated using both DRIVE and CHASE DB1 databases [5]. In another similar study, an effective approach called the rough channel attention residual U-Net (RCAR-UNet), which integrates deep neural networks with a rough channel attention mechanism, was proposed, and its performance was evaluated on the DRIVE, STARE, and CHASE DB1 databases [6]. An integrated multi-scale feature fusion segmentation network known as IMFF-Net was proposed and applied to the segmentation of retinal images taken from the DRIVE, STARE, and CHASE DB1 databases [7]. In another study, a novel deep ensemble learning-based framework was improved to achieve accurate retinal vessel segmentation [8]. A hybrid network structure called CoVi-Net, which combines convolutional neural networks and the vision transformer, was proposed, and then its performance was evaluated on the DRIVE, STARE, and CHASE DB1 databases [9]. In another study, a DL structure consisting of a new U-form architecture was proposed to provide higher segmentation performance while reducing computational complexity [10]. On the other hand, there are only a few studies in the literature related to the application of metaheuristic algorithms to retinal vessel segmentation. An optimized U-shaped network model was developed using a binary teaching learning-based algorithm for retinal vessel segmentation [11]. In [12], a collaborative transformer attention U-Net (CTA-UNet) framework incorporating a swin transformer module and a collaborative feature fusion mechanism was proposed for retinal vessel segmentation, and its performance was evaluated on the DRIVE, STARE, and CHASE DB1 databases. A micro-vessel extraction mechanism based on an encoder–decoder neural network architecture was improved and then applied to the segmentation of retinal images taken from the DRIVE, STARE, and CHASE DB1 databases [13]. In [14], a spatial reconstruction feature interaction transformer retinal vessel segmentation algorithm (SFIT-Net), which achieves high performance in extracting local vessel features and capturing global relationships, was proposed, and its performance was evaluated on the DRIVE, STARE, and CHASE DB1 databases. In another study, the most recently proposed evolutionary, swarm intelligence, and physics-based metaheuristic algorithms were applied to retinal vessel segmentation [15]. Similarly, the performance of well-known heuristic approaches in the segmentation of retinal images was also analyzed [16]. A multiscale line detection method, enhanced using the particle swarm optimization algorithm, was proposed for retinal vessel segmentation, and its performance was evaluated on the DRIVE, STARE, and HRF databases [17]. Finally, the most recently proposed math-inspired metaheuristic algorithms were improved as clustering-based, and their performance was compared in terms of retinal vessel segmentation [18].
Although DL-based approaches have achieved high performance in terms of evaluation metrics, these approaches generally require large-scale datasets, long training times, and high computational resources, which limit their applicability in low-resource clinical environments. In addition, generalization across different image acquisition conditions remains a challenging issue for many DL-based approaches. In contrast, metaheuristic algorithms provide a training-free and computationally efficient alternative that can operate effectively with limited data and lower hardware requirements.
To provide a more detailed comparison, the state-of-the-art studies in the literature are categorized in Table 1. Conventional approaches frequently get stuck at local minima on multi-modal error surfaces and exhibit high dependence on control parameter values. On the other hand, DL-based approaches require complex network architectures and longer computational times. However, metaheuristic approaches provide competitive performance compared to conventional and DL-based approaches due to their effective exploration and exploitation abilities and higher convergence rates. In this study, the segmentation performance of the math-inspired QIO algorithm was analyzed in detail, and it was demonstrated that it produces results similar to other approaches in the literature.
The main contributions of this study to the literature can be summarized as follows:
• The math-inspired QIO algorithm was improved as clustering-based and then applied to retinal vessel segmentation for the first time in the literature.
• The segmentation results and statistical analyses show that the math-inspired QIO algorithm is able to produce effective results despite its simple algorithm structure.
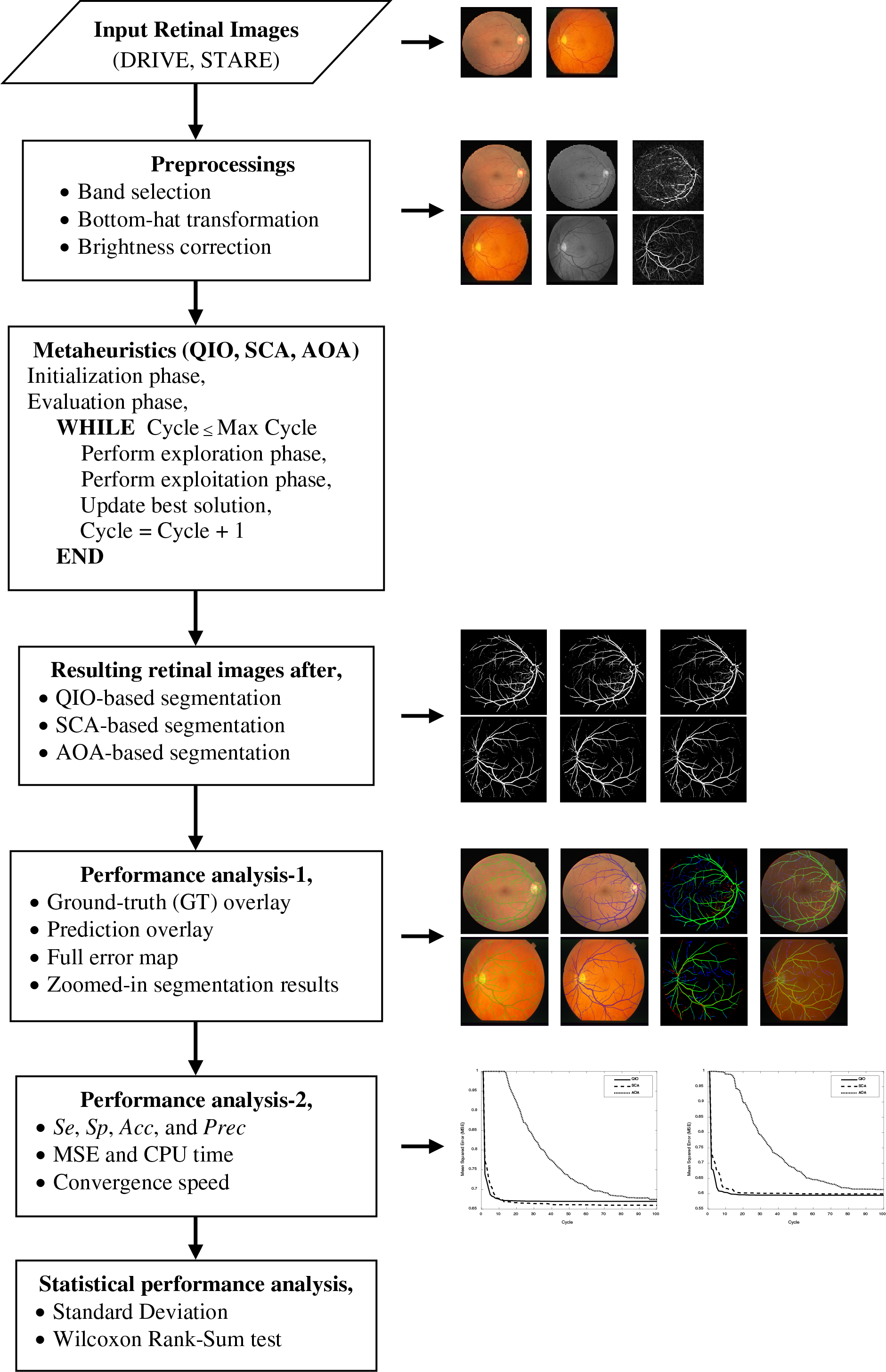
Retinal images consist of red (R), green (G), and blue (B) layers. To achieve segmentation with high accuracy, the retinal images should be enhanced by applying preprocessing steps such as band selection, bottom-hat transformation, and brightness correction. In the band selection, all layers were analyzed separately and it was observed that the highest clustering performance was obtained for the G layer. In other words, the segmentation process was carried out on the G layer due to its higher illuminance, contrast, and brightness levels. Afterwards, the bottom-hat transformation given in Eq. (1) was applied to increase the contrast difference between the vessel pixels and the background pixels.
where,
The retinal images in the DRIVE database were obtained by Canon CR5 3CCD camera under a 45° angle with an image resolution of (565 × 584) pixels. The DRIVE database contains a total of 40 retinal images, consisting of 33 healthy images and 7 images with pathological findings. The STARE database was constructed using a TopCon TRV-50 fundus camera under a 35° angle with an image resolution of (700 × 605) pixels. This database contains 10 healthy retinal images and 10 diseased retinal images. For both databases, half of the retinal images were used for training, and the remaining half which correspond to the mask images were used for performance evaluation.
Figs. 1a,d and 2a,d show the retinal images taken from the DRIVE [24] and STARE [25] databases, respectively. The green layers obtained after band selection preprocessing are shown in Figs. 1b,e and 2b,e. Finally, the resulting images after applying the bottom-hat filtering and brightness correction are shown in Figs. 1c,f and 2c,f.
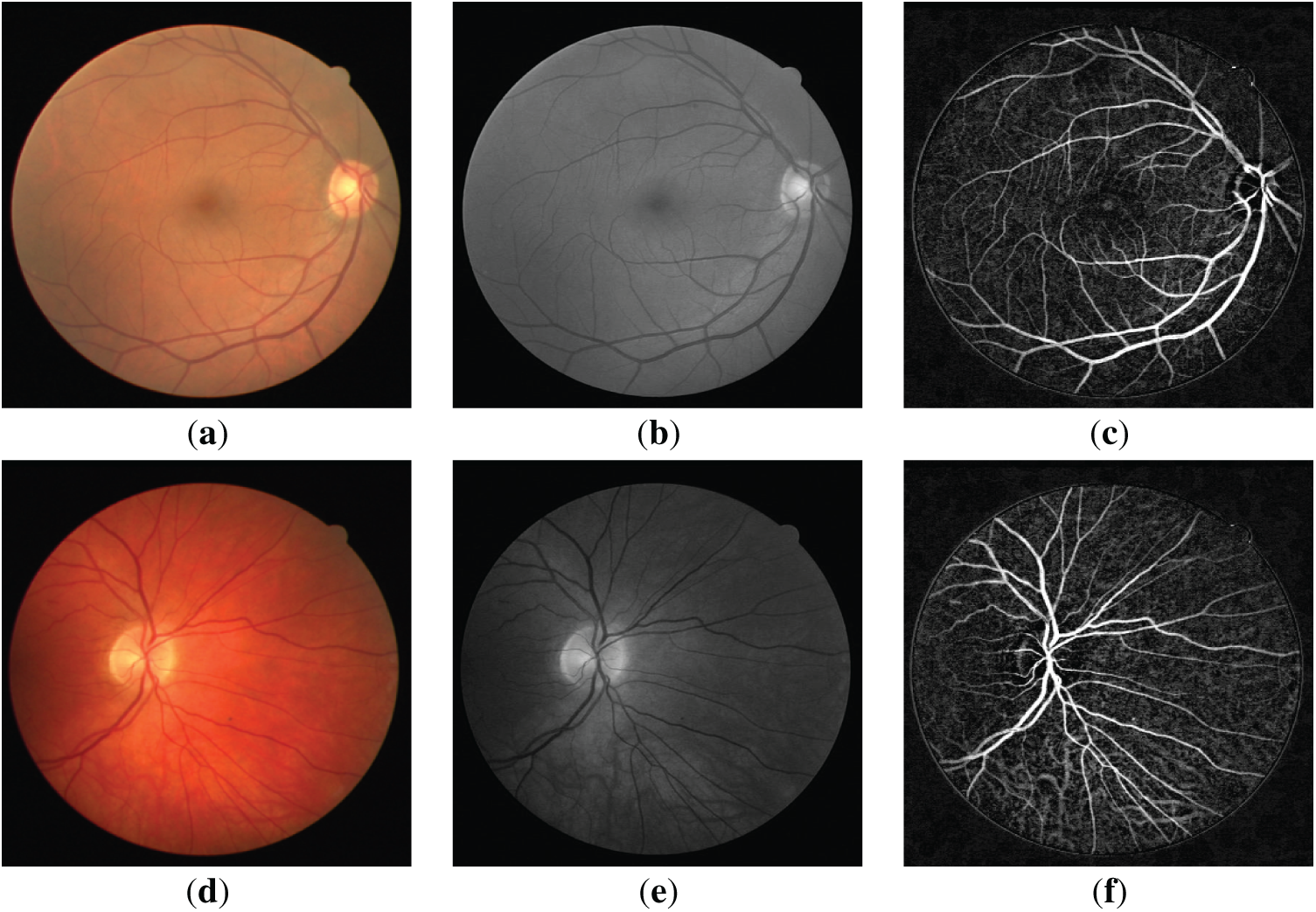
Figure 1: (a,d) are the three-dimensional retinal images taken from the DRIVE database; (b,e) are the green layer images obtained as a result of band selection; (c,f) are the enhanced retinal images obtained after the bottom-hat filtering and the brightness correction.
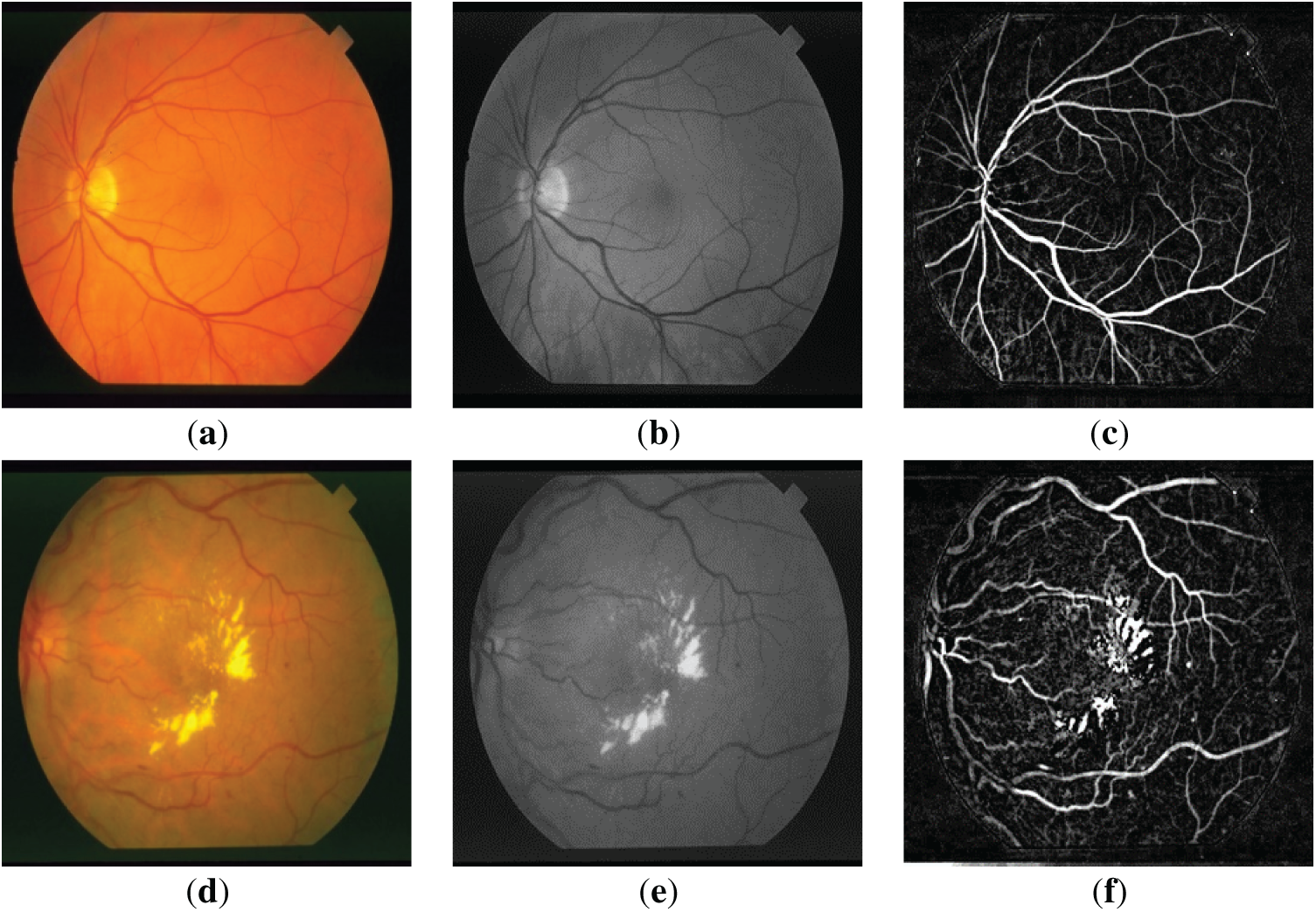
Figure 2: (a,d) are the three-dimensional retinal images taken from the STARE database; (b,e) are the green layer images obtained as a result of band selection; (c,f) are the enhanced retinal images obtained after the bottom-hat filtering and the brightness correction.
2.1 Quadratic Interpolation Optimization (QIO) Algorithm
QIO is a novel math-inspired metaheuristic algorithm that uses exploration and exploitation strategies to provide an effective optimization [1]. In the exploration phase, the global search ability of the QIO algorithm is enhanced through a generalized quadratic interpolation (GQI) approach [1]. In this phase, a global search is carried out using the minimizer of the GQI function and two randomly selected solutions. In the exploitation phase, the local search ability of the QIO algorithm is enhanced using the minimizer of the GQI function and the best solution found so far.
The detailed pseudo-code of the QIO algorithm can be given as follows (Algorithm 1).

In the QIO algorithm,
The GQI-1 function can be calculated using Eq. (2).
Subsequently, the exploration phase for each solution can be applied using Eq. (3).
where,
Subsequently, the exploitation phase for each solution can be applied using Eq. (5).
where,
Finally, in the exploitation phase, each solution can be updated using Eq. (6),
In order to present a detailed performance analysis, the performance of the QIO, SCA, and AOA algorithms was first evaluated in terms of Se, Sp, Acc, and Prec metrics. Se analyzes the success of the algorithm in terms of true positive rate by evaluating the ratio of correctly classified positive pixels to the total positive pixels. Sp focuses on the success of the algorithm in terms of true negative rate, namely, it identifies the ratio of correctly classified negative pixels to the total negative pixels. Acc demonstrates the success of the algorithm in terms of correctly classified pixels and can be defined as the ratio of correctly classified pixels to the total pixels. Finally, Prec measures the success of the algorithm in terms of positive pixels by evaluating the ratio of correctly classified positive pixels to the total positive pixels.
The performance metrics of Se, Sp, Acc, and Prec can be defined as follows:
where, TP represents the number of correctly classified vessel pixels, FN represents the number of vessel pixels incorrectly classified as background pixels, TN represents the number of correctly classified background pixels, and FP represents the number of background pixels incorrectly classified as vessel pixels.
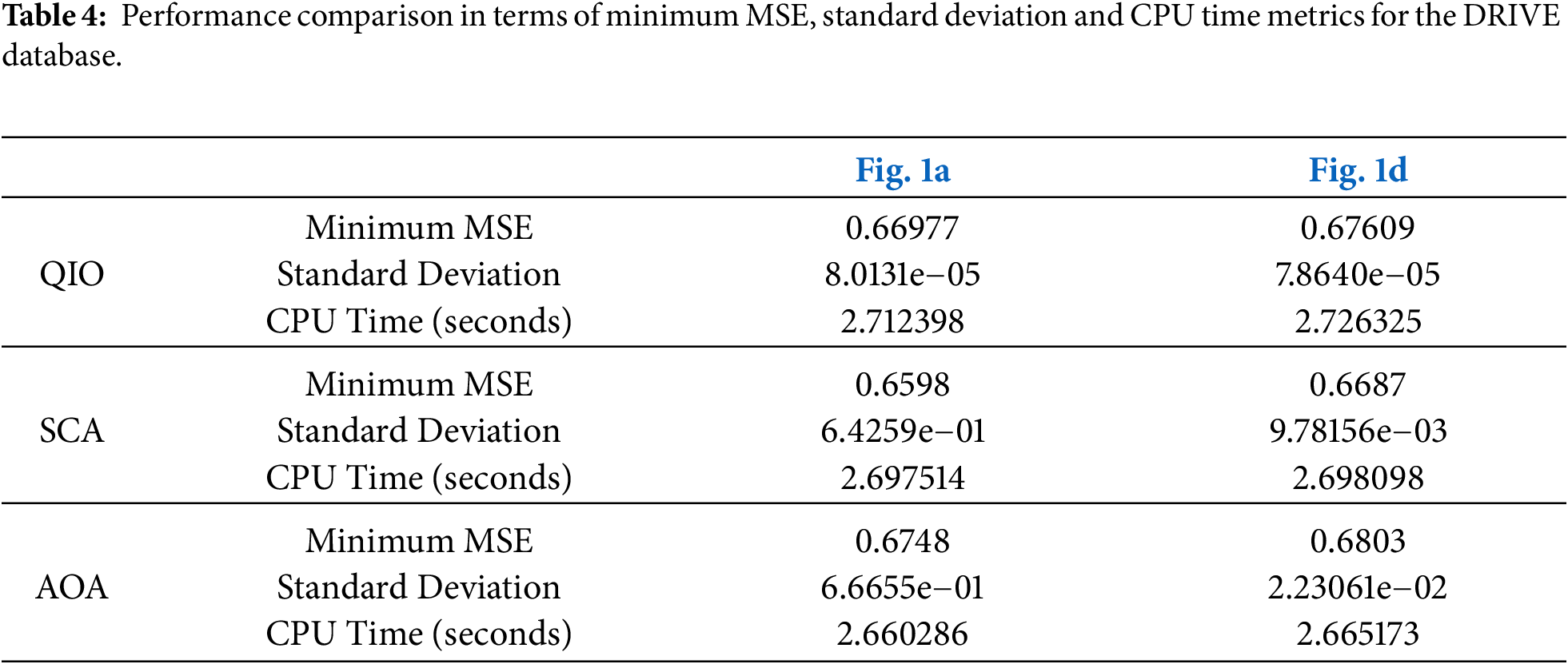
Afterwards, the MSE performance of the QIO, SCA, and AOA algorithms was presented via the minimum MSE values reached, CPU times, and the convergence speeds. MSE establishes a relation between the ideal cluster centers and the cluster centers detected by the algorithm. The expression of the MSE function can be given as follows:
where,
CPU time is a metric representing the duration of each run in seconds. The convergence speed demonstrates the cycle-based evolution of the MSE function. It can be stated that an algorithm able to reach low MSE values in earlier cycles will produce high performance in terms of convergence speed. In this study, the convergence speeds were obtained as the average of 20 random runs.
The statistical performance of the QIO, SCA, and AOA algorithms was analyzed in terms of standard deviation and Wilcoxon Rank-Sum test. An algorithm that converges to similar MSE values at each run is statistically stable, namely, it produces low standard deviation values. In this study, the standard deviation values were calculated over 20 random runs carried out for each retinal image. To verify the validity of the numerical results and to establish a statistical relation among the algorithms, the Wilcoxon Rank-Sum test was applied. In the statistical analyses carried out, the desired accuracy rate was defined as 95%, which also corresponds to a confidence interval of (p < 0.05).
To present the methodology proposed in detail, a flowchart illustrating the entire process is presented below.
Retinal images obtained as a result of QIO-, SCA-, and AOA-based segmentation were shown in Figs. 3 and 4 for the DRIVE database. Similarly, Figs. 5 and 6 demonstrate the segmentation results for the STARE database. As shown in the figures, the vessel structure of each retinal image was successfully obtained. In other words, only a limited number of vessel pixels that have almost the same pixel value as the background pixels were classified incorrectly, and all other pixels were classified with high accuracy.
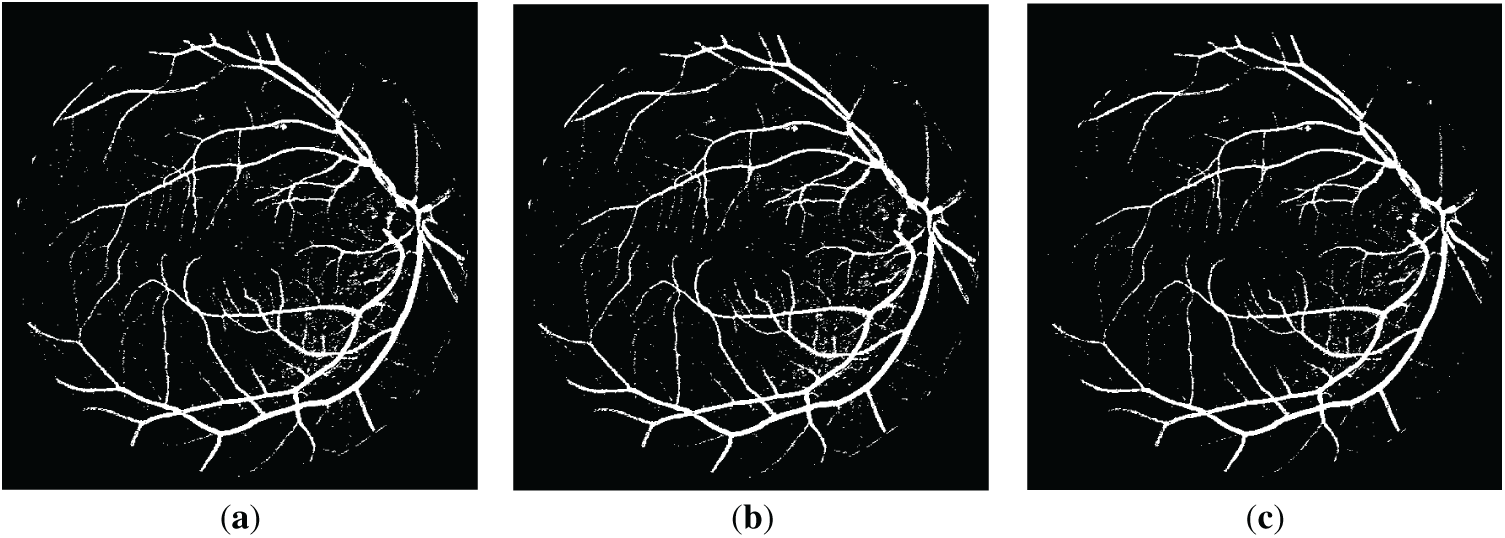
Figure 3: The resulting retinal images after applying QIO-, SCA- and AOA-based segmentation to the image of Fig. 1a: (a) QIO-based segmentation; (b) SCA-based segmentation; (c) AOA-based segmentation.
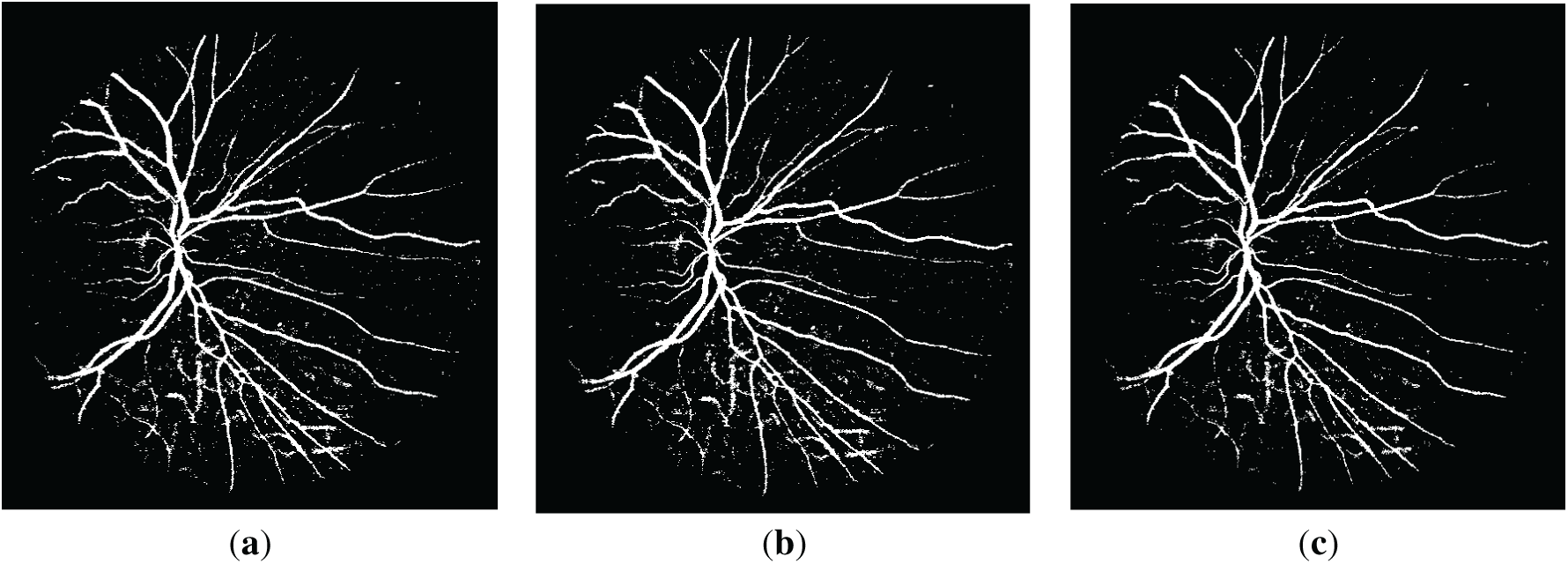
Figure 4: The resulting retinal images after applying QIO-, SCA- and AOA-based segmentation to the image of Fig. 1d: (a) QIO-based segmentation; (b) SCA-based segmentation; (c) AOA-based segmentation.
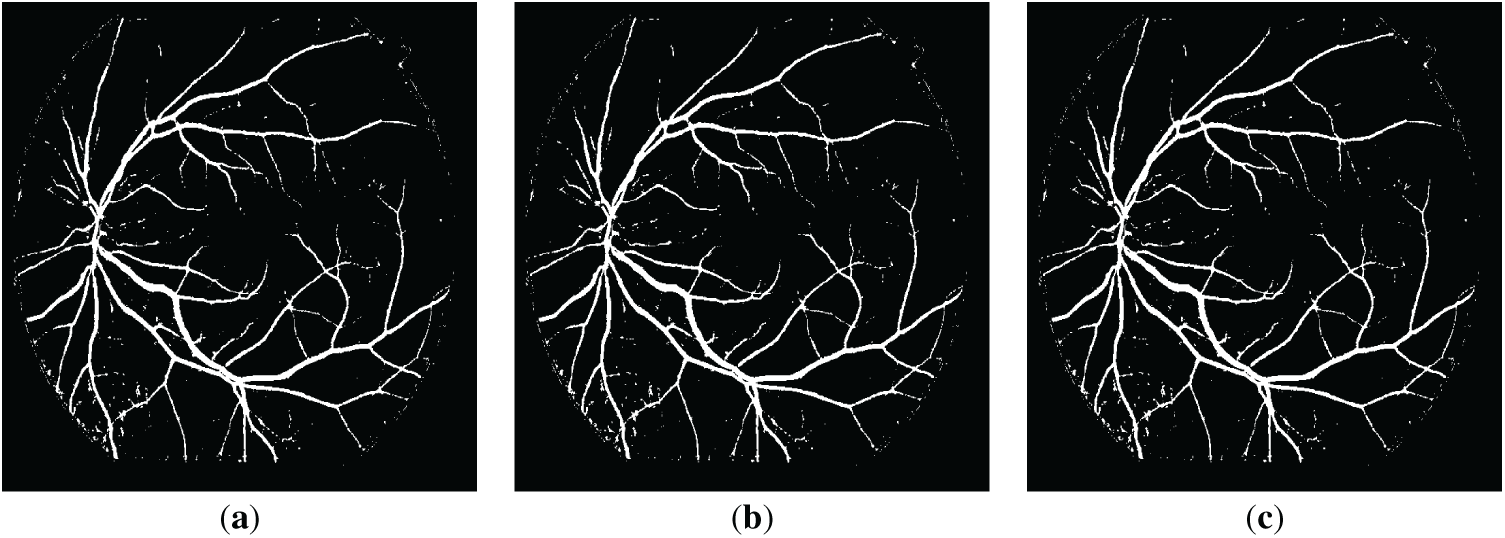
Figure 5: The resulting retinal images after applying QIO-, SCA- and AOA-based segmentation to the image of Fig. 2a: (a) QIO-based segmentation; (b) SCA-based segmentation; (c) AOA-based segmentation.
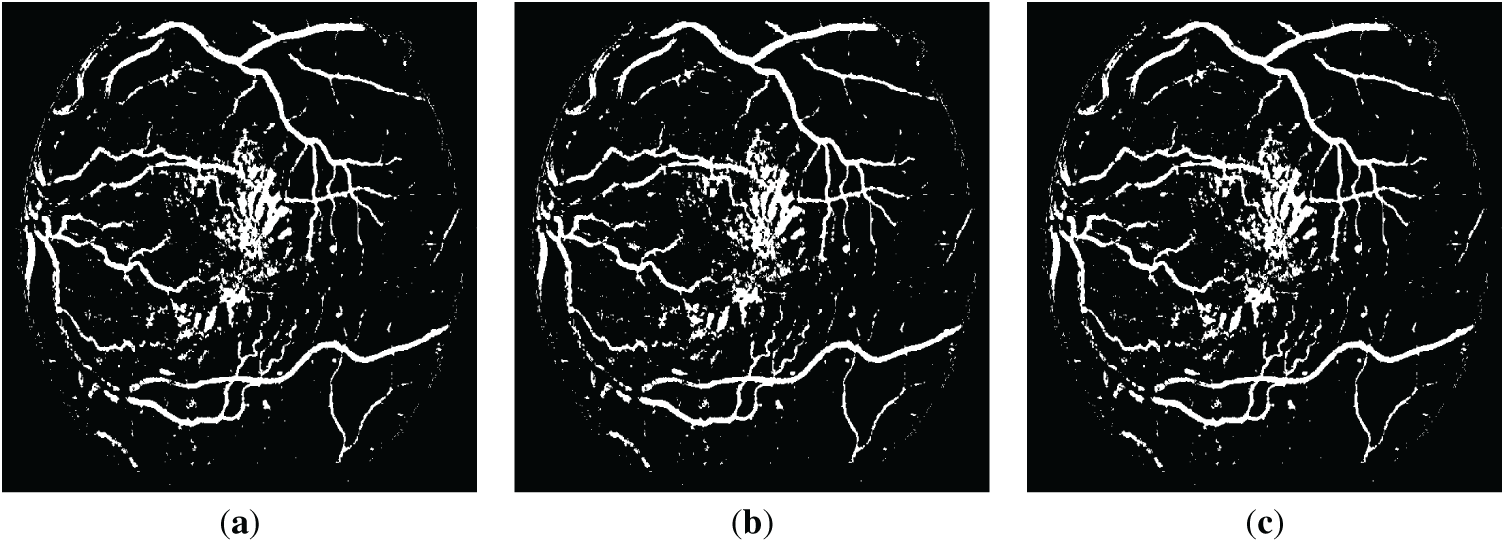
Figure 6: The resulting retinal images after applying QIO-, SCA- and AOA-based segmentation to the image of Fig. 2d: (a) QIO-based segmentation; (b) SCA-based segmentation; (c) AOA-based segmentation.
To enhance the visualization of the segmentation results, in addition to the binary masks, the ground-truth (GT) overlay, prediction overlay, and full error map results are also presented in Fig. 7 for the DRIVE database. Similarly, Fig. 8 shows the relevant results for the STARE database. In the GT overlay images, the entire vessel structure is represented using semi-transparent green overlays to enable intuitive inspection of the true vessel structure. The predicted segmentation masks are overlaid on the original retinal image using a semi-transparent blue overlay, enabling direct comparison with the GT overlay. Finally, in the full error map images, a pixel-wise visualization of TP, FP, FN, and TN pixels is provided to highlight segmentation mismatches and to facilitate intuitive assessment of FP and FN behavior.
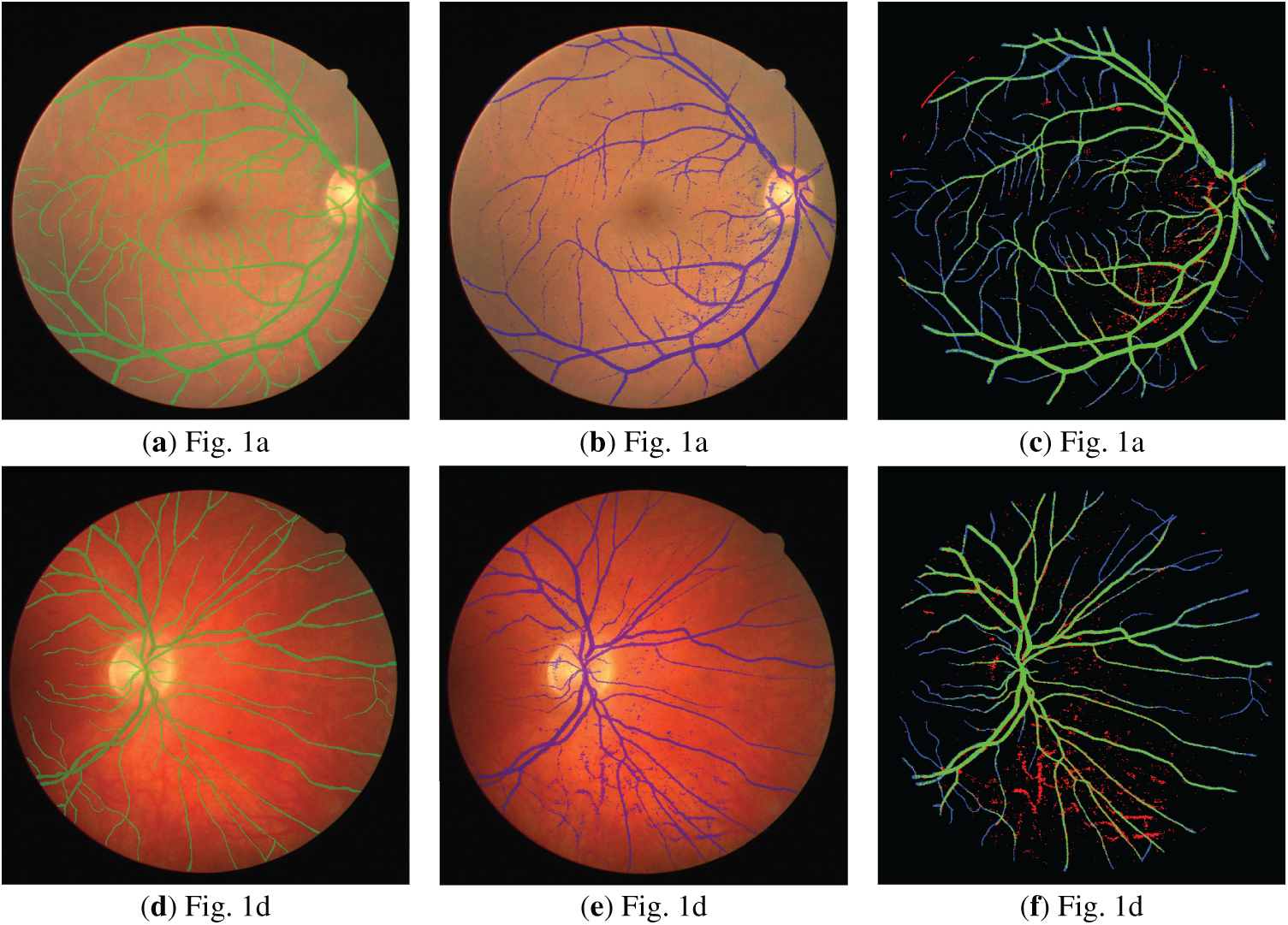
Figure 7: Visualized segmentation results for the DRIVE database: (a,d) Ground-truth (GT) overlay; (b,e) Prediction overlay; (c,f) Full error map (TP: Green, FP: Red, FN: Blue, TN: Black).
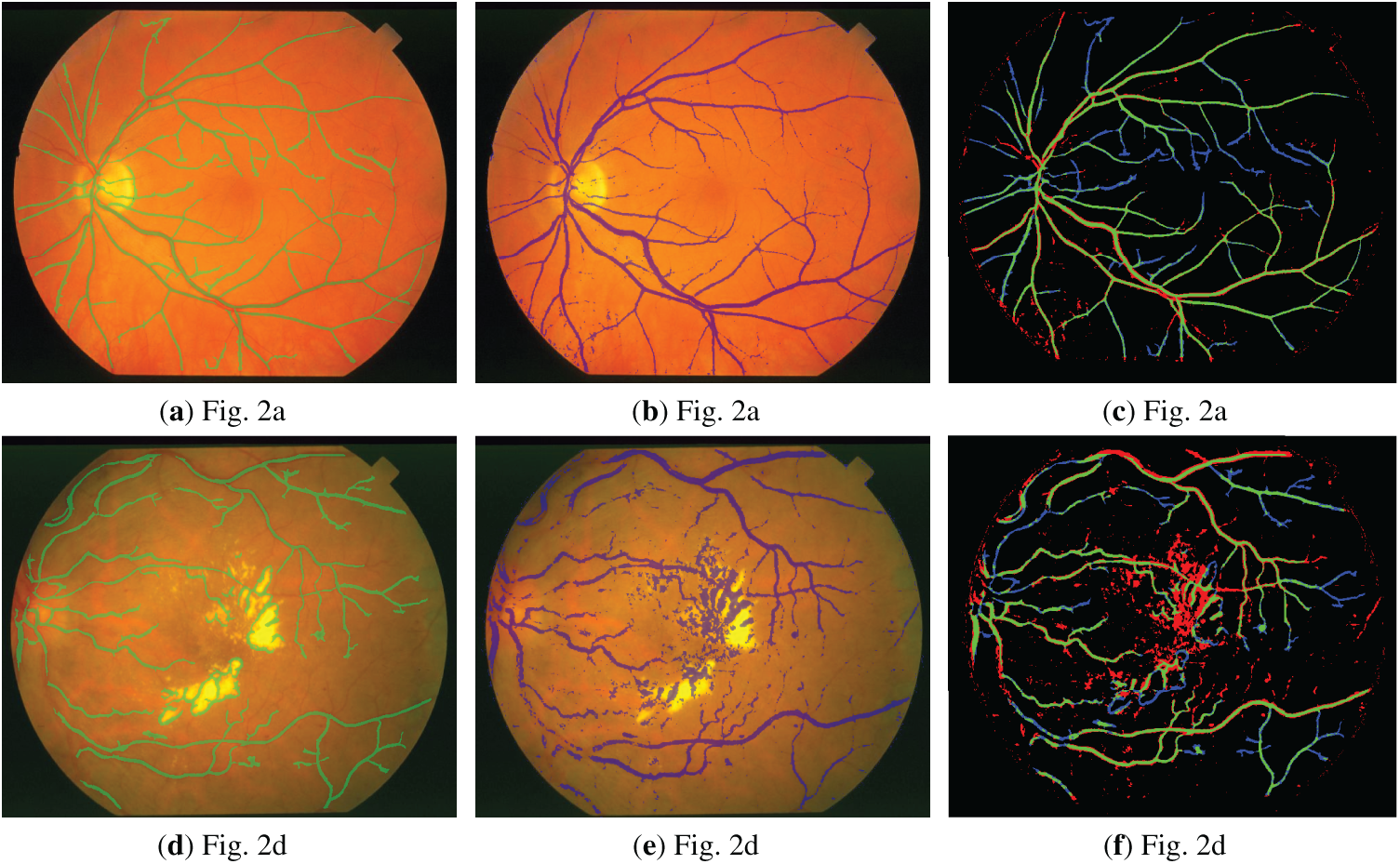
Figure 8: Visualized segmentation results for the STARE database: (a,d) Ground-truth (GT) overlay; (b,e) Prediction overlay; (c,f) Full error map (TP: Green, FP: Red, FN: Blue, TN: Black).
Additionally, to enable detailed inspection of boundaries and fine-scale discrepancies, local regions are magnified and presented as zoomed-in regions as shown in Fig. 9 for the DRIVE database. Similarly, Fig. 10 demonstrates the zoomed-in regions obtained for the STARE database.
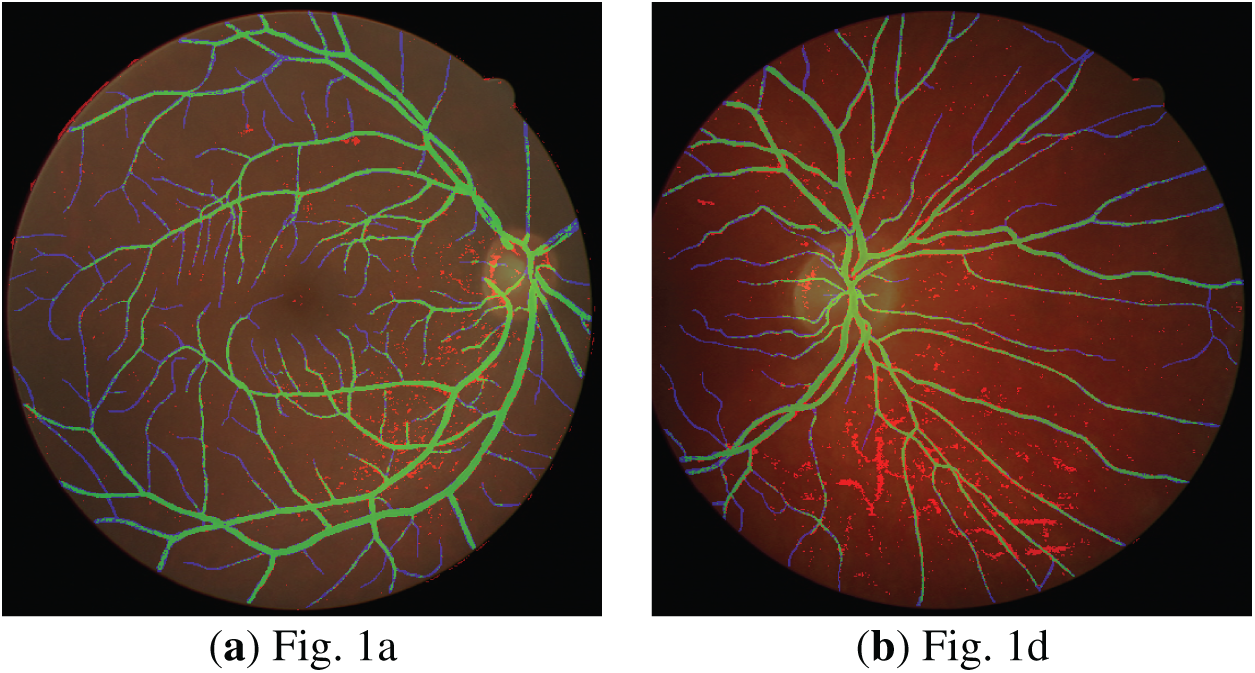
Figure 9: Zoomed-in segmentation results obtained for error overlay (DRIVE database).
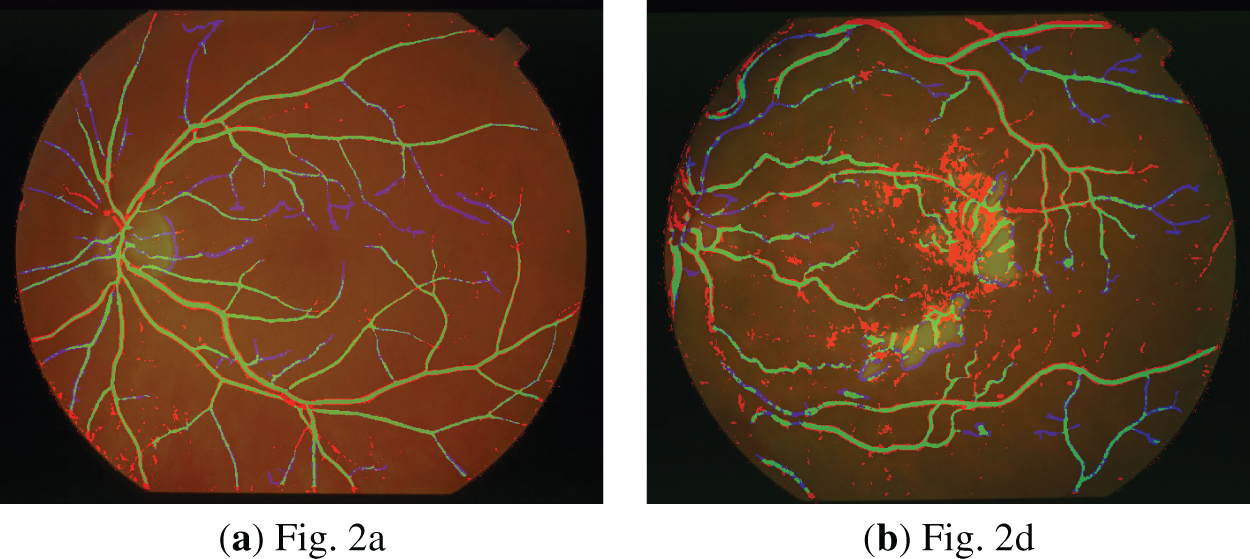
Figure 10: Zoomed-in segmentation results obtained for error overlay (STARE database).
The Se, Sp, Acc, and Prec values obtained as a result of QIO-, SCA-, and AOA-based segmentation were presented in Table 2 for the 20 retinal images taken from the DRIVE database. When the Se values are analyzed, it can be observed that the QIO algorithm achieves approximately 75% average success in terms of the true positive pixel rate. The 97% average success for Sp and the 95% average success for Acc demonstrates the superior performance of the QIO algorithm in terms of the true negative pixel rate and the total number of correctly classified pixels, respectively. Finally, the average success rate of 72% obtained for Prec demonstrates that the QIO algorithm achieves high performance in terms of the total number of correctly classified positive pixels. Consequently, the QIO algorithm is able to produce similar results with the SCA and AOA algorithms despite its simpler structure.
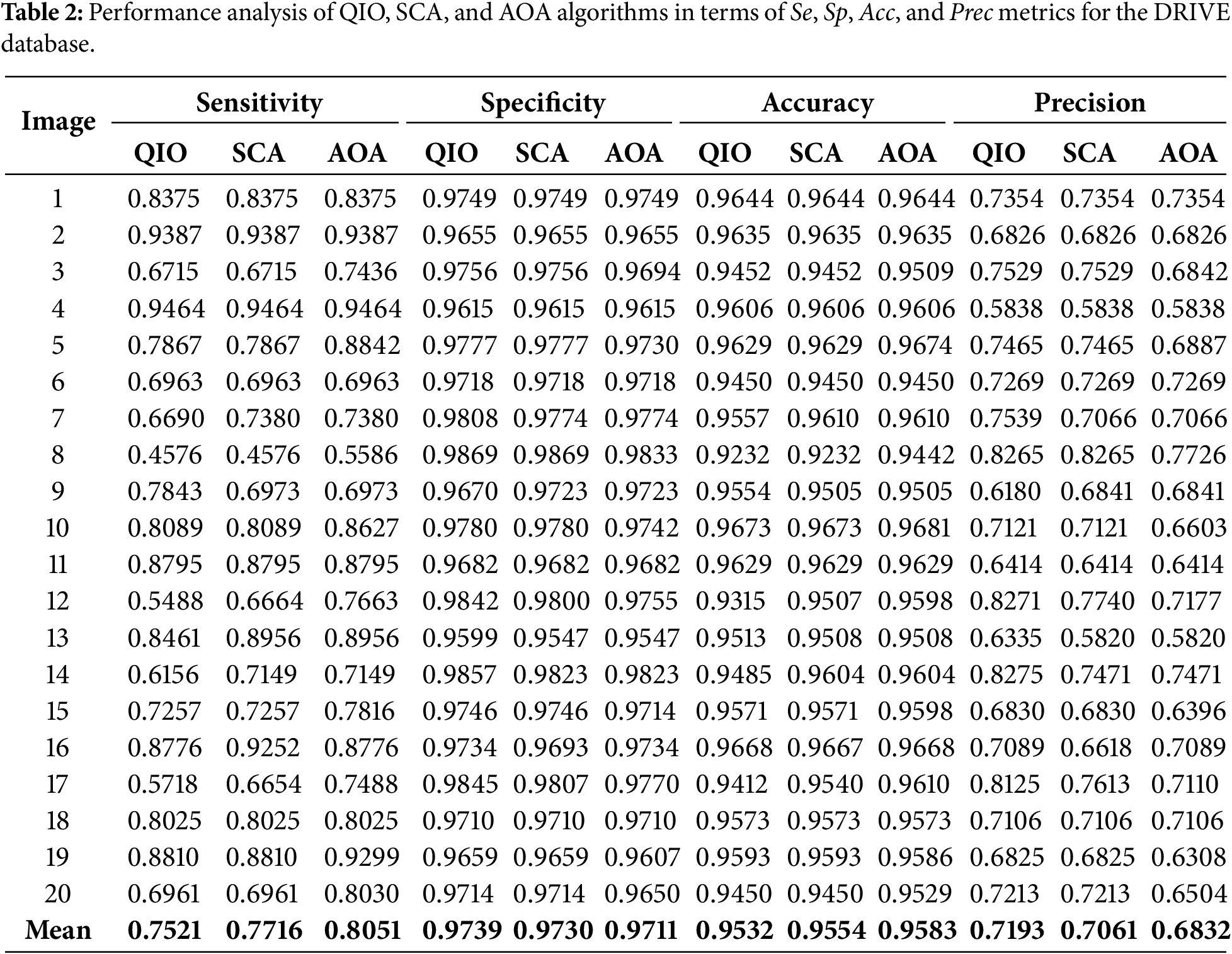
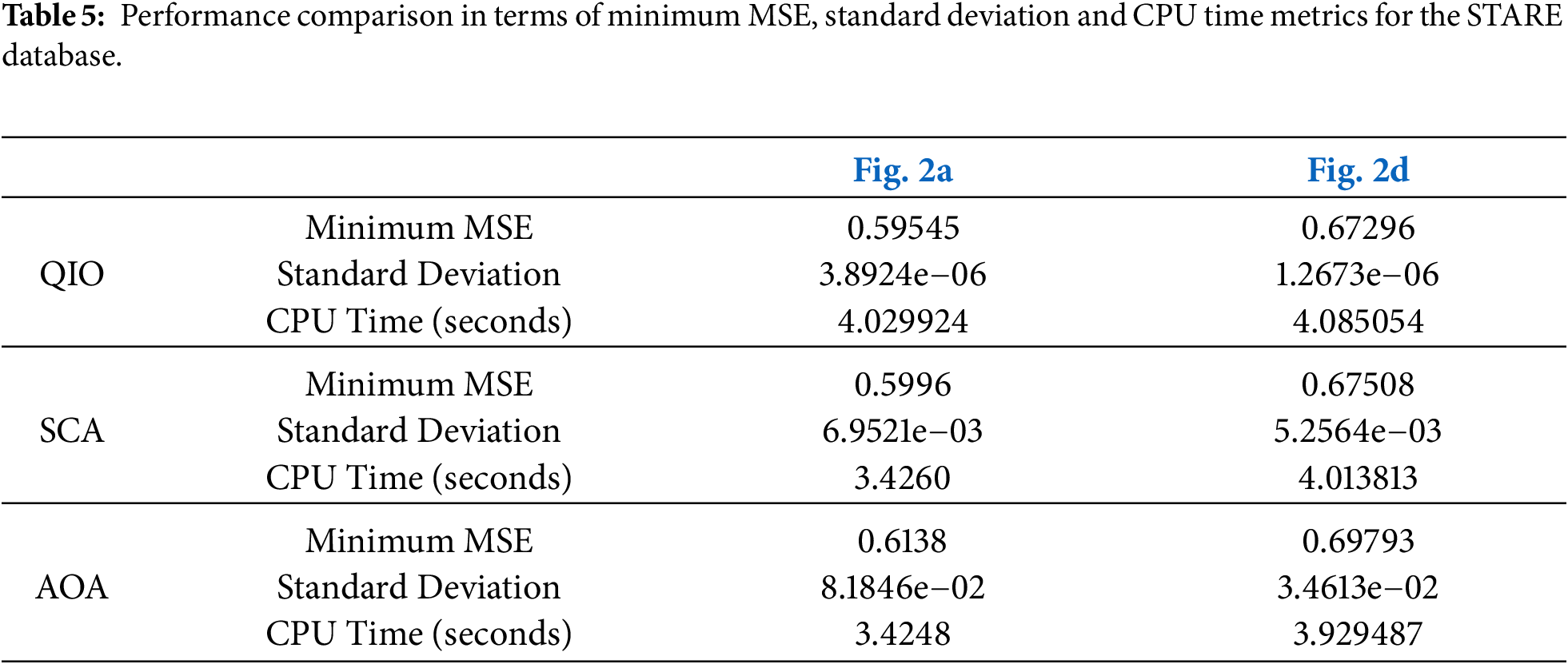
Table 3 presents the Se, Sp, Acc, and Prec values obtained for the 20 retinal images taken from the STARE database. As seen in the table, the average success rates are produced as 62%, 97%, 93%, and 65% for the Se, Sp, Acc, and Prec metrics, respectively. These results prove that, similar to the DRIVE database, the QIO algorithm can also achieve high segmentation performance in the STARE database.
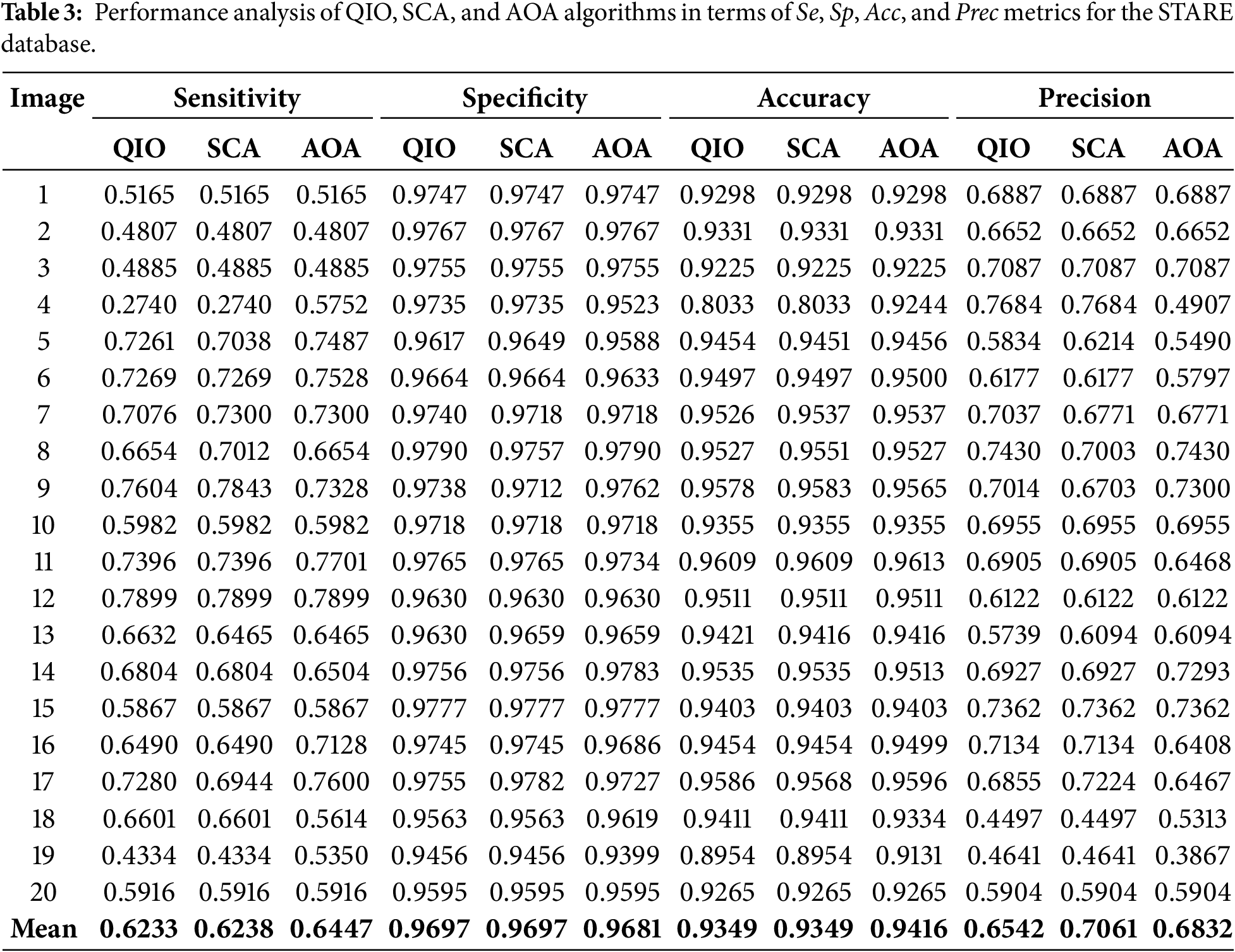
To present a more detailed analysis, the minimum MSE values reached, the corresponding CPU times, and the standard deviation values are presented in Tables 4 and 5 for the DRIVE and STARE databases, respectively. The analyses were conducted using a computer having a 3.4 GHz Intel i7-6700 CPU, 16 GB of RAM and 64 bit Windows 10 Pro. The minimum MSE values reached demonstrate that the QIO algorithm can identify the vessel pixels with high accuracy. Moreover, the resulting CPU time values show that the QIO algorithm performs optimization at high speed. Finally, the lower standard deviation values demonstrate the stability and robustness of the QIO algorithm.
Tables 6 and 7 present the statistically significant differences (p < 0.05) observed between the algorithms for the DRIVE and STARE databases, respectively. The results indicate that the QIO algorithm produces statistically better performance than the SCA and AOA algorithms. However, for the DRIVE database, the results show that the SCA and AOA algorithms for Fig. 1a and the SCA algorithm for Fig. 1d do not yield statistically significant differences compared to the other algorithms. Similarly, for the STARE database, the results indicate that the AOA algorithm for Fig. 2a,d does not yield statistically significant differences compared to the other algorithms.
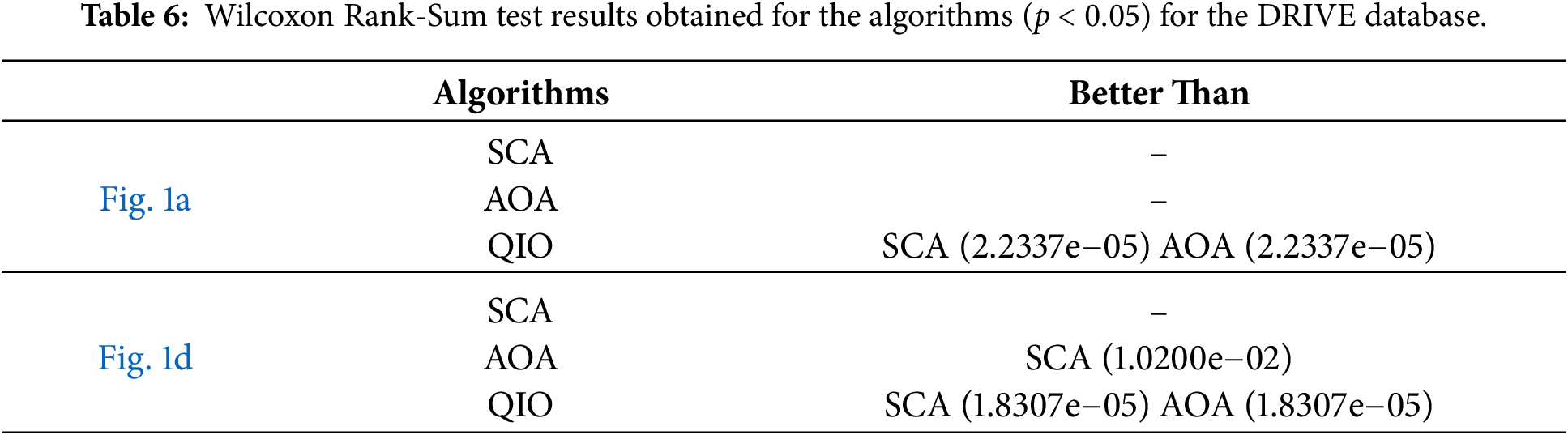
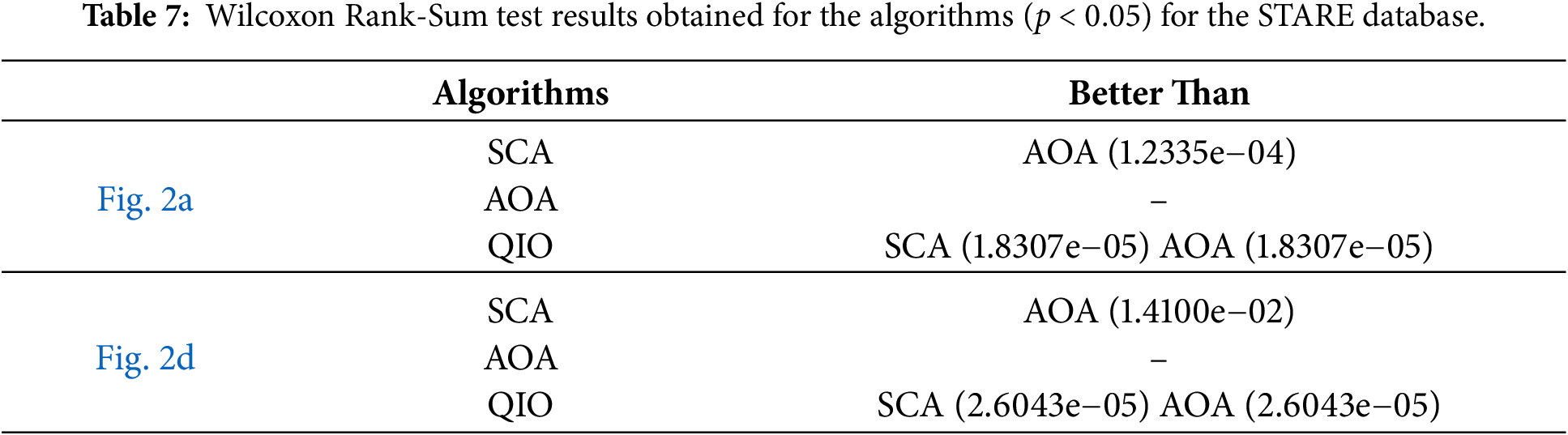
Fig. 11 demonstrates the convergence speeds of the algorithms for DRIVE database. As seen in Fig. 11a, for the retinal image shown in Fig. 1a, the QIO and SCA algorithms converge to the minimum MSE value after about ten cycles, whereas the AOA algorithm requires around one hundred cycles. On the other hand, for the retinal image shown in Fig. 1d, the QIO algorithm converges to the optimal MSE value more quickly than the other algorithms. The results indicate that the QIO algorithm exhibits high convergence rates, and the minimum MSE values reached also confirm its superior segmentation performance.
Figure 11: Convergence speeds obtained for the retinal images: (a) Fig. 1a; (b) Fig. 1d.
Finally, as seen in Fig. 12, the QIO algorithm produces similar but slightly better performance than the SCA algorithm in terms of convergence speed for the STARE database. Furthermore, it can be stated that the AOA algorithm converges to relatively higher MSE values and requires more cycles to reach the optimal solutions.
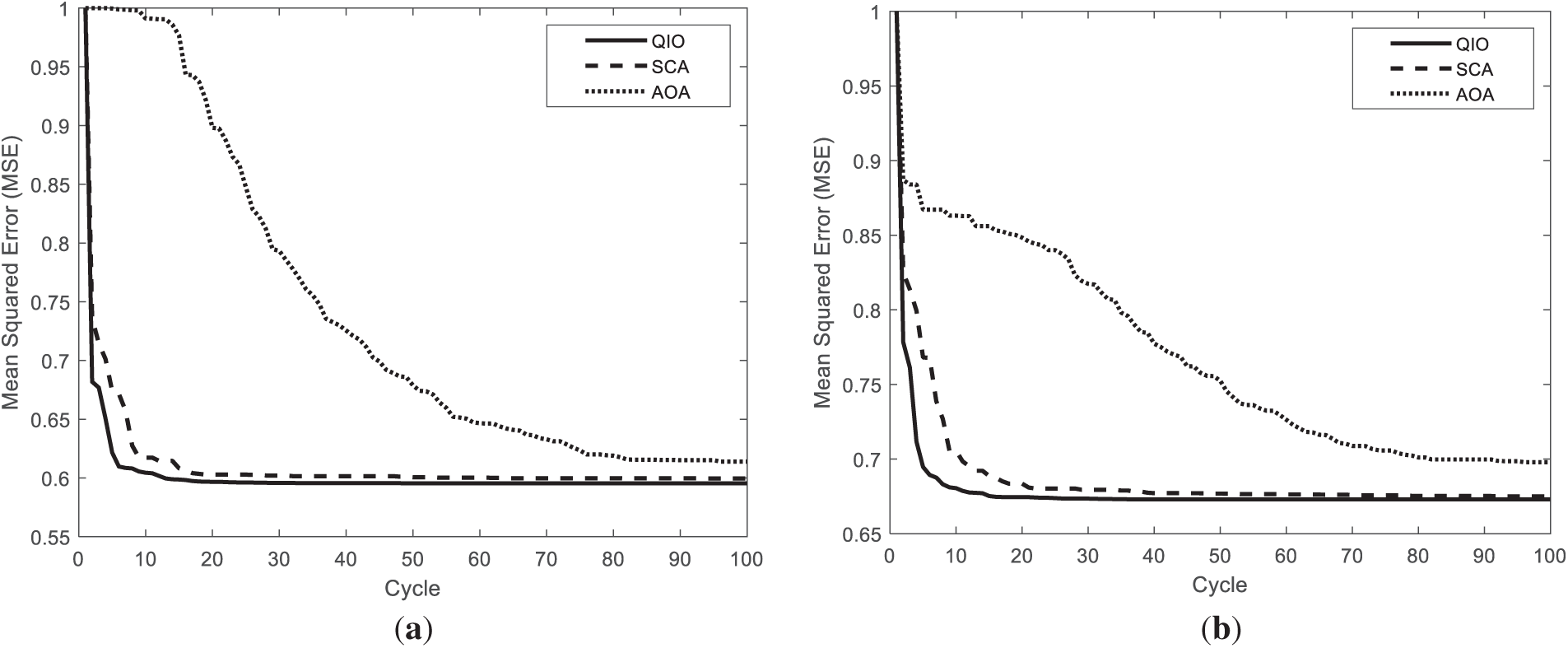
Figure 12: Convergence speeds obtained for the retinal images: (a) Fig. 2a; (b) Fig. 2d.
As seen from the results, the QIO algorithm relies on a simple algorithm structure with a limited number of control parameters and does not require large-scale datasets and computationally inefficient training process. This structural simplicity leads to lower sensitivity values, particularly for low-contrast vessels, which can be considered as a limitation of the proposed approach. However, this limitation is compensated by several advantages, including low computational complexity, better CPU time values, stable convergence behavior, and robustness across multiple runs. Moreover, the results demonstrate that the QIO algorithm achieves performance comparable to other well-established math-inspired metaheuristic algorithms such as SCA and AOA, while exhibiting competitive convergence speed and lower standard deviation. Therefore, the proposed method represents a practical and efficient alternative for retinal vessel segmentation, especially in low-resource or real-time clinical environments where computational efficiency and algorithmic simplicity are critical.
In this study, the recently proposed math-inspired QIO algorithm was improved for retinal vessel segmentation, and its performance was analyzed on two retinal images taken from the DRIVE and STARE databases. In both databases, the results for Se, Sp, Acc, and Prec demonstrate that the QIO algorithm performs clustering with high accuracy. In the DRIVE database, the average success rates of the QIO algorithm for Se, Sp, Acc, and Prec were obtained as 75%, 97%, 95%, and 72%, respectively. Similarly, in the STARE database, the QIO algorithm achieved average success rates of 62%, 97%, 93%, and 65% for the Se, Sp, Acc, and Prec metrics, demonstrating its high segmentation performance. The results for both DRIVE and STARE databases also show that the QIO and SCA algorithms converge to the global solutions at similar cycles, and the minimum MSE values reached by the QIO, SCA, and AOA algorithms are close to each other. In addition, the CPU times of approximately 2.7 and 4.0 s demonstrate that the QIO, SCA, and AOA algorithms perform optimization at high speed. However, despite its insufficient convergence rate, the AOA algorithm achieves better CPU times than the QIO and SCA algorithms for both databases. The standard deviation values obtained over 20 random runs and emerged around
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Mehmet Bahadır Çetinkaya; methodology, Mehmet Bahadır Çetinkaya and Sevim Adige; software, Mehmet Bahadır Çetinkaya; validation, Mehmet Bahadır Çetinkaya; formal analysis, Mehmet Bahadır Çetinkaya and Sevim Adige; investigation, Mehmet Bahadır Çetinkaya and Sevim Adige; resources, Mehmet Bahadır Çetinkaya; data curation, Sevim Adige; writing—original draft preparation, Mehmet Bahadır Çetinkaya; writing—review and editing, Mehmet Bahadır Çetinkaya and Sevim Adige; visualization, Sevim Adige; supervision, Sevim Adige; project administration, Mehmet Bahadır Çetinkaya; funding acquisition, Sevim Adige. All authors reviewed and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The author declares no conflicts of interest.
References
1. Zhao W, Wang L, Zhang Z, Mirjalili S, Khodadadi N, Ge Q. Quadratic interpolation optimization (QIOa new optimization algorithm based on generalized quadratic interpolation and its applications to real-world engineering problems. Comput Meth Appl Mech Eng. 2023;417(4):116446. doi:10.1016/j.cma.2023.116446. [Google Scholar] [CrossRef]
2. Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]
3. Abualigah L, Abusaleem A, Ikotun AM, Zitar RA, Alsoud AR, Khodadadi N, et al. Arithmetic optimization algorithm: a review and analysis. In: Metaheuristic optimization algorithms. Cambridge, MA, USA: Morgan Kaufmann; 2024. p. 73–87. doi: 10.1016/b978-0-443-13925-3.00012-1. [Google Scholar] [CrossRef]
4. Sanjeewani Yadav AK, Akbar M, Kumar M, Yadav D. Retinal blood vessel segmentation using a deep learning method based on modified U-NET model. Multimed Tools Appl. 2024;83(35):82659–78. doi:10.1007/s11042-024-18696-w. [Google Scholar] [CrossRef]
5. Wang Y, Wu S, Jia J. PAM-UNet: enhanced retinal vessel segmentation using a novel plenary attention mechanism. Appl Sci. 2024;14(13):5382. doi:10.3390/app14135382. [Google Scholar] [CrossRef]
6. Ding W, Sun Y, Huang J, Ju H, Zhang C, Yang G, et al. RCAR-UNet: retinal vessel segmentation network algorithm via novel rough attention mechanism. Inf Sci. 2024;657(3):120007. doi:10.1016/j.ins.2023.120007. [Google Scholar] [CrossRef]
7. Liu M, Wang Y, Wang L, Hu S, Wang X, Ge Q. IMFF-Net: an integrated multi-scale feature fusion network for accurate retinal vessel segmentation from fundus images. Biomed Signal Process Control. 2024;91(1):105980. doi:10.1016/j.bspc.2024.105980. [Google Scholar] [CrossRef]
8. Du L, Liu H, Zhang L, Lu Y, Li M, Hu Y, et al. Deep ensemble learning for accurate retinal vessel segmentation. Comput Biol Med. 2023;158(27):106829. doi:10.1016/j.compbiomed.2023.106829. [Google Scholar] [PubMed] [CrossRef]
9. Jiang M, Zhu Y, Zhang X. CoVi-Net: a hybrid convolutional and vision transformer neural network for retinal vessel segmentation. Comput Biol Med. 2024;170(7):108047. doi:10.1016/j.compbiomed.2024.108047. [Google Scholar] [PubMed] [CrossRef]
10. Boudegga H, Elloumi Y, Akil M, Hedi Bedoui M, Kachouri R, Ben Abdallah A. Fast and efficient retinal blood vessel segmentation method based on deep learning network. Comput Med Imaging Graph. 2021;90:101902. doi:10.1016/j.compmedimag.2021.101902. [Google Scholar] [PubMed] [CrossRef]
11. Rajesh C, Sadam R, Kumar S. An evolutionary U-shaped network for retinal vessel segmentation using binary teaching-learning-based optimization. Biomed Signal Process Control. 2023;83(1):104669. doi:10.1016/j.bspc.2023.104669. [Google Scholar] [CrossRef]
12. Punn NS, Kumar S. CTAUNet: improved retinal blood vessel segmentation with collaborative transformer attention U-Net. Neural Comput Appl. 2025;37(20):15705–18. doi:10.1007/s00521-025-11332-0. [Google Scholar] [CrossRef]
13. Getahun MN, Rogov OY, Dylov DV, Somov A, Bouridane A, Hamoudi R. FS-Net: full scale network and adaptive threshold for improving extraction of micro-retinal vessel structures. Pattern Recognit Lett. 2025;189(5):188–94. doi:10.1016/j.patrec.2025.01.019. [Google Scholar] [CrossRef]
14. Liang L, Lu B, Wu J, Li Y, Sheng X. SFIT-net: spatial reconstruction feature interaction transformer retinal vessel segmentation algorithm. Biomed Signal Process Control. 2025;106(5):107688. doi:10.1016/j.bspc.2025.107688. [Google Scholar] [CrossRef]
15. Çetinkaya MB, Duran H. Performance comparison of most recently proposed evolutionary, swarm intelligence, and physics-based metaheuristic algorithms for retinal vessel segmentation. Math Probl Eng. 2022;2022(1):4639208. doi:10.1155/2022/4639208. [Google Scholar] [CrossRef]
16. Çetinkaya MB, Duran H. A detailed and comparative work for retinal vessel segmentation based on the most effective heuristic approaches. Biomed Tech. 2020;66(2):181–200. doi:10.1515/bmt-2020-0089. [Google Scholar] [PubMed] [CrossRef]
17. Khomri B, Christodoulidis A, Djerou L, Babahenini MC, Cheriet F. Particle swarm optimization method for small retinal vessels detection on multiresolution fundus images. J Biomed Opt. 2018;23(5):1–13. doi:10.1117/1.JBO.23.5.056004. [Google Scholar] [PubMed] [CrossRef]
18. Çetinkaya MB, Adige S. Retinal vessel segmentation using math-inspired metaheuristic algorithms. Appl Sci. 2025;15(10):5693. doi:10.3390/app15105693. [Google Scholar] [CrossRef]
19. Yang J, Lou C, Fu J, Feng C. Vessel segmentation using multiscale vessel enhancement and a region based level set model. Comput Med Imag Graph. 2020;85(1):101783. doi:10.1016/j.compmedimag.2020.101783. [Google Scholar] [PubMed] [CrossRef]
20. Ghislain F, Beaudelaire ST, Daniel T. An improved semi-supervised segmentation of the retinal vasculature using curvelet-based contrast adjustment and generalized linear model. Heliyon. 2024;10(18):e38027. doi:10.1016/j.heliyon.2024.e38027. [Google Scholar] [PubMed] [CrossRef]
21. Chakour EM, Mrad Y, Mansouri A, Elloumi Y, Benatiya Andaloussi I, Hedi Bedoui M, et al. Enhanced retinal vessel segmentation using dynamic contrast stretching and mathematical morphology on fundus images. Appl Comput Intell Soft Comput. 2025;2025(1):8831503. doi:10.1155/acis/8831503. [Google Scholar] [CrossRef]
22. Liu Y, Shen J, Zhai C, Yang L, Bian G. A retinal vessel segmentation network with dual-stage network and vessel pixel emendation. IEEE Trans Instrum Meas. 2025;74:2501117. doi:10.1109/TIM.2024.3500060. [Google Scholar] [CrossRef]
23. Ling Z, Yu J, Zuo Q, Lei B. Multi-stage cascaded refinement with wavelet downsampling for retinal vessel segmentation. Biomed Signal Process Control. 2026;112(2):108824. doi:10.1016/j.bspc.2025.108824. [Google Scholar] [CrossRef]
24. Alonso-Montes C, Vilariño DL, Dudek P, Penedo MG. Fast retinal vessel tree extraction: a pixel parallel approach. Int J Circuit Theory Appl. 2008;36(5–6):641–51. doi:10.1002/cta.512. [Google Scholar] [CrossRef]
25. Hoover AD, Kouznetsova V, Goldbaum M. Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE Trans Med Imaging. 2000;19(3):203–10. doi:10.1109/42.845178. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2026 The Author(s). Published by Tech Science Press.
Copyright © 2026 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF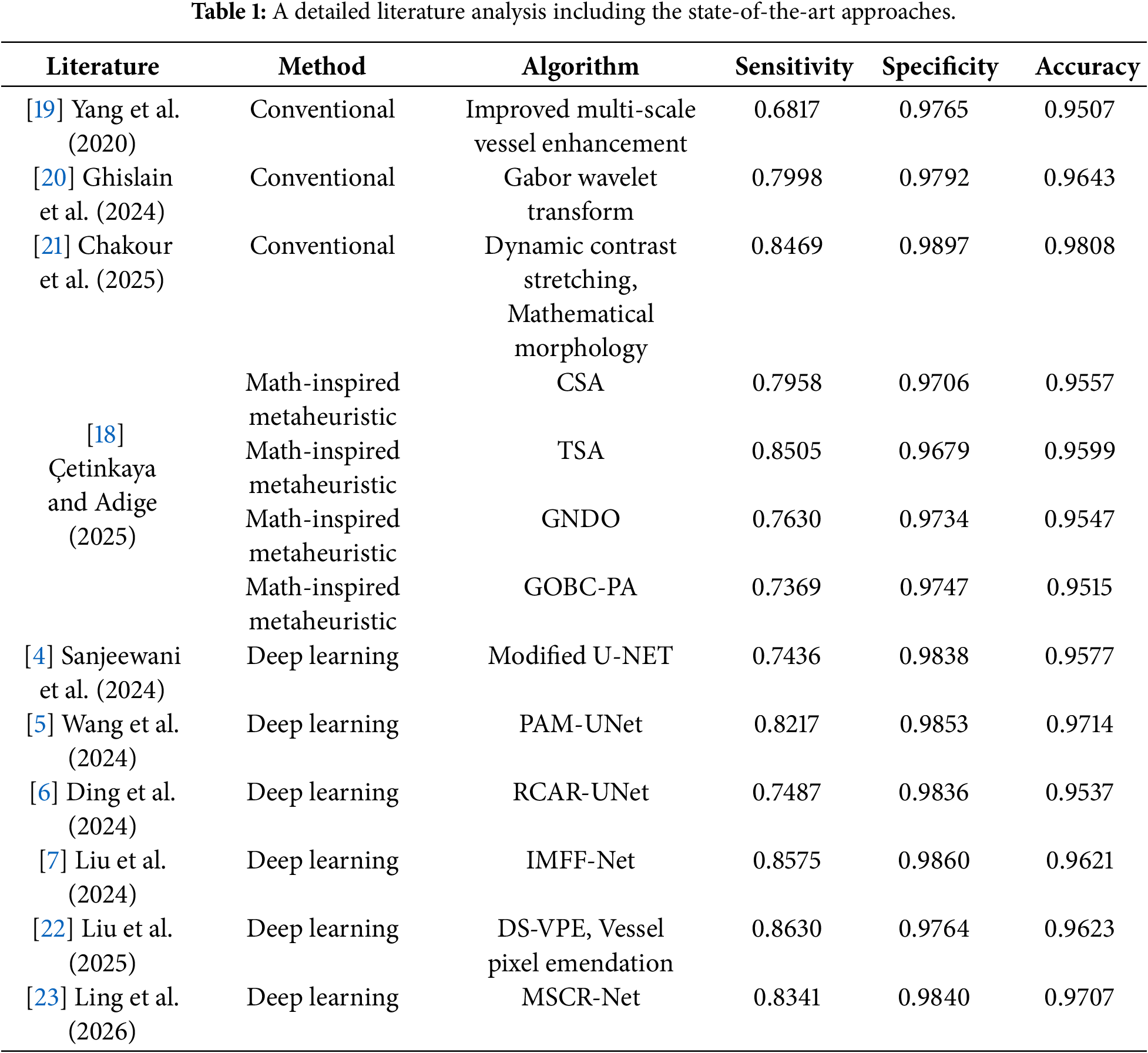
 Downloads
Downloads
 Citation Tools
Citation Tools