The Failure Analysis of Carbon Fiber-Reinforced Epoxy Composites against Impact Loading with Numerical and Experimental Investigations

1  Introduction

High-performance composite materials are desired in automobiles, aerospace, buildings, bridges, and other lightweight applications. The design and analysis methods for fiber-reinforced composites at multiple stages have always been points of interest. Optimization of CFRC’s performance considering cost, manufacturing, and liability of the product poses a challenge for engineers [1]. Polymers embedded with reinforcing fibers in one or more orientations in the matrix have a vital role to play in the construction of aerospace vehicles and components [2,3]. Epoxy is widely used as a matrix over many other alternatives, such as phenolics, polyurethanes, and polyimides. Carbon fiber provides excellent performance in harsh environments compared to glass and Kevlar fibers, as they are prone to humidity. Carbon fibers not only have high strength and high elastic moduli but also possess the characteristics of lightweight and high durability. Carbon fibers have mainly been used in the aerospace and auto industries due to their high strength and lightweight. Recently, they have been used to reinforce concrete structures, piers, tunnels, and buildings. They are capable of resisting corrosion and withstanding high temperatures. A clear epoxy consisting of resin and hardener is a low-odor and solvent-free mixture that can be used to create a variety of items or even to repair damage. Anisotropic properties of CFRCs can be exploited as a benefit to obtain the required directional properties by laying up the fibers at different orientations and placing laminates in different configurations. A root-cause failure analysis can lead to the development of a mechanism to prevent the corresponding failure. Mechanical performances of composites can be investigated with a finite element analysis (FEA) [4], constitutive modeling with a cohesive damage model, a continuum damage model, stress-strain mapping, energy equivalence methods [5–8], multi-continuum mechanics [9–11], mechanism-based failure [12], fractography [13,14], and experimental observations [15–18]. Energy absorption, fracture toughness, and Von-Mises stresses can be used as measures of failures in an experimental characterization, numerical analysis, and finite element simulation. FEA is capable of investigating a crack initiation, propagation, and energy absorption with the viscoelastic and plastic behavior. In addition, it attenuates the barriers of experimental studies with a variety of loading conditions, such as quasi-static loading, vibration, shock, blast, including the combinations of mechanical, electrical, and thermal loads [5]. The number of failed elements can be compared with the total elements to report the percentage of failures in FEA. However, the robustness of the predictions depends on modeling techniques. The development of microdefects and their effects on the macroscale are modeled by a continuum damage model. Thermodynamics free energy functions concerning damage model parameters, including thermal and hygroscopic effects, can be formulated to determine the stiffness tensor. An incremental crack growth is considered as a displacement jump to model the crack propagation and delamination for the cohesive damage model. The mesh size plays a crucial role in the predicted values of damage initiation and propagation. Tension and three-point bending can be observed with a cohesive zone model. A space transformation tensor and its properties of distinct phases have been used in constitutive modeling techniques. A homogenization technique is applied to formulate a representative volume element (RVE) for multiphase materials in multiscale modeling. A Voronoi cell finite element model can be used to analyze the micromechanical response of composites and porous materials, considering elastic and elastic-plastic materials. Eulerian descriptions are used for solid and flexible materials to develop a nonlinear model. The multi-continuum approach based on constituent stress and strain decomposition is used to observe distinct stresses for fiber and laminates and design hybrid composites. A mechanism-based failure analysis sets distinctive measures for fiber, matrix, and interface failure [12]. Fractured surfaces are examined with a microscopy to decode information about a defect formation, crack initiation, propagation, and failure mechanisms. Fractography has been a useful tool for polymer composites [13,14].

Multiple experimental studies have been reported on investigating fiber tensile, compressive, shear, and delamination failures [15–18]. Numerous factors trigger the initiation of a crack and its propagation, such as manufacturing defects, impact damage, geometric discontinuities, e.g., free edges, notches, and joints that may generate interlaminar stresses [19]. The width-tapered double cantilever beam (WTDCB) and end-notched flexure (ENF) specimens have been tested to investigate interlaminar fracture of carbon/epoxy composites with tensile and flexural loading, respectively [20]. A weak interlayer bonding and interlayer porosity come into play, determining the properties of such composites [21]. The impact resistance of a composite constituent of individual fibers, interlaminar, and interfacial strength between fibers and a matrix can be determined by an Izod impact tester that measures the energy required to break a specimen by impacting it with a pendulum [22,23]. Carbon-fiber epoxy composites have been reported for energy absorptions under different loading conditions, as well as acoustic band gaps [24–27].

Epoxy nanocomposites reinforced by functionalized carbon nanotubes and graphene nanoplatelets were studied [28]. Poor dispersibility and the low interfacial strength of nanofillers negatively impact their applications, whereas the higher aspect ratio of a hexagonal nanoplatelet has a positive enhancement in its pull-out energy [28]. To achieve a better dispersion of multi-walled carbon nanotubes (MWCNTs) in the epoxy resin, acetone solvent is used as a volatile medium in the mixing process [29]. The effect of agglomeration of carbon nanotubes (CNT) on fracture toughness was studied by Zeinedini et al. [30]. Alexopoulos et al. found that the crack bridging at the interphases increases the fracture toughness in graphene-reinforced epoxy nanocomposites [31]. Fard et al. studied the strain rate effect of epoxy resin under tension and compression [32]. The effects of the size of globules, microporosity, and the appearance of local plastic deformation of samples processed by different curing techniques are observed through scanning electron microscopy [33]. A Digital Image Correlation (DIC) technique is useful to study the fracture behavior of composites [34]. This is a noncontact optical method that captures high-speed images, either with a single or multiple cameras, for two-dimensional or three-dimensional photos, respectively, during the deformation. Then, image processing techniques are applied to the collected images to track the crack propagation, deformations, and thus to predict the stress intensity factors in different modes. In addition to experimental study and finite element analysis, fracture energy for carbon nanotube-epoxy composites can be obtained from molecular dynamics simulations [35].

However, a detailed study on the orientation-dependent impact resistance of CRFCs with a numerical approach, finite element analysis, fracture experiments, and a scanning electron microscope has not yet been reported, which is studied in this report. In this study, (a) a mathematical model is applied to predict the fracture toughness of orientation-dependent carbon fiber reinforced composites at different weight percentages, (b) finite element analysis is conducted to observe the stress distribution, (c) energy absorption is characterized using an Izod impact testing machine, and (d) the fractured surfaces are observed through an SEM. Results obtained from these studies agree with each other and suggest that crack propagation can be arrested by placing the fibers at angular orientations; however, a higher weight percentage of the fibers may be required to interact with each other to place a barrier against a crack propagation.

2  Numerical Modeling

Multiple factors play an important role in a mathematical modeling of CFRCs against impact loading. The higher the load, the severe the damage is, or the weaker the CFRC, the severe the damage is going to be. To strengthen the CFRC, we can increase the reinforcing fraction, stiffness of lamina/laminate, load transfer capability, interfacial strength, or inter-laminar strength to reduce the damage. On the other hand, a higher magnitude of force, a longer duration of impact, a heavier weight of the impactor, or a higher impact velocity will correspond to higher damage. The response of the CFRCs to an applied impact will begin with oscillations at a certain frequency. Then, as the severity of impact increases relative to the materials’ capabilities, the initial oscillations escalate to a maximum displacement, causing strain to be higher than the ultimate strain of the matrix. Therefore, the matrix initiates to failure, then the crack propagates through the matrix corresponding to a fiber failure, resulting in a fiber pullout, and finally, the interlaminar failure occurs. Fig. 1a shows the schematic of an impactor on the CFRC applying an impact force, F,^ and Fig. 1b shows the deformation mode of a matrix and fibers. To analyze the first step of the impact effect on the maximum displacement, the change in momentum was calculated as the impulse force:

F^=F∗Δt=mv(τ+ε)−mv(τ−ε)=mimpactor∗vimpactor(1)

whereas, F is the applied force, ∆t is the time duration of impact, τ is the instant time of impact, ε is the time step before and after impact, m is the mass of the impactor, and v is the velocity of the impactor.

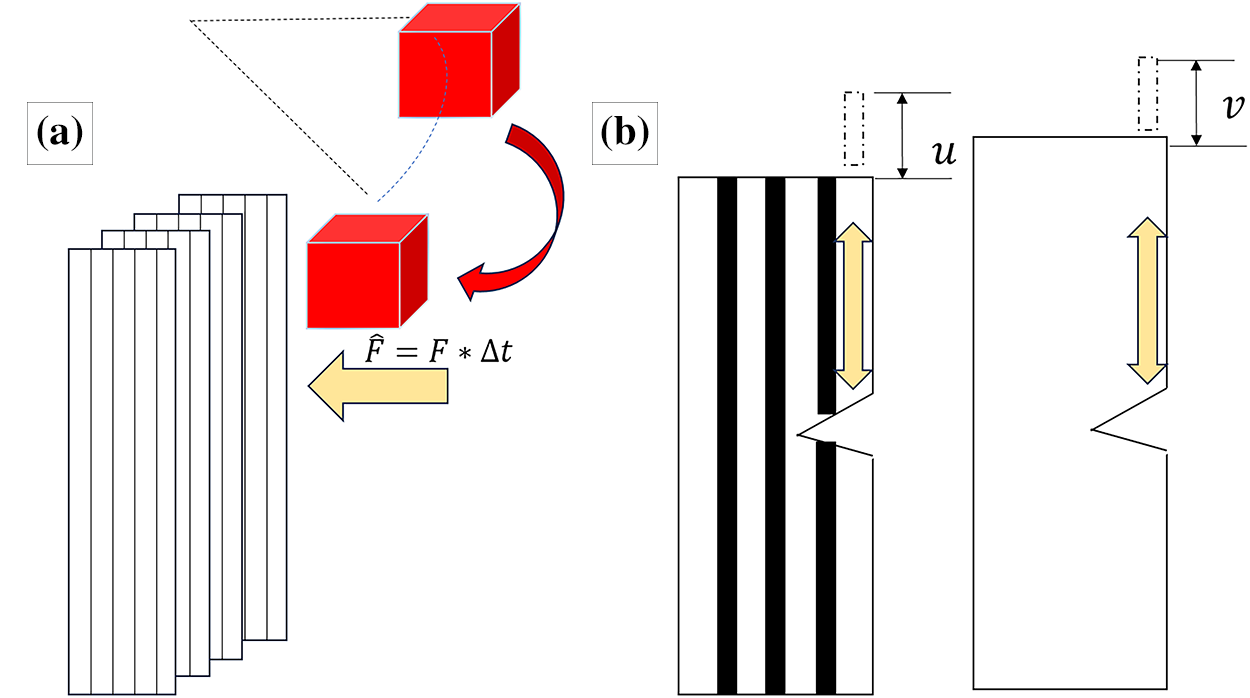
Figure 1: Numerical modeling of impact loading on fiber reinforced composites: (a) demonstration of impact loading and (b) the deformation of composites transformed into fiber and matrix displacement field

Assuming an underdamped system, the displacement response of the CFRC was predicted using the following equation:

x(t)=F^mc∗ωd∗e−ζ∗ωn∗t∗sin⁡(ωd∗t+φ)(2)

where, mc is the mass of the CFRC, ζ is the damping ratio, ωd is the damped natural frequency of CFRC, ωn is the critical natural frequency of CFRC, t is the time, and φ is the phase lag. The damping ratio for an epoxy itself is not too large to exhibit a viscoelastic response; however, for the carbon-reinforced epoxy composites, it should be included for predicting viscoelastic responses. As a linear elastic fracture mechanics approach is applied to this study, the damping effect is not considered. In addition, the damping effect will slow down the displacement due to the viscoelastic effect, but the maximum displacement remains unaffected. Having ζ=0, the maximum displacement of the CFRC can be calculated as:

Xmax=mimpactor∗vimpactormc∗ωc(3)

However, before using this maximum displacement for orientation-dependent constitutive modeling at different weight fractions, the natural frequency of the CFRC has to be modeled accordingly using the following equation and applying composite laminate theory:

ωn=kcmc=3∗Ec∗b∗h312∗mc∗l3(4)

where, Ec is the effective Young’s modulus of the composite sample, b is the width, h is the height, l is the length, and mc is the mass of the composite. The effective properties of the composites will vary for different weight fractions of the sample. Therefore, the macro-mechanics of a laminate theory was sought to find these properties of the laminated composites using compliance and stiffness matrices, i.e., Q and S matrices, respectively [36].

Aij=∑k=1n[Qij¯]k(hk−hk−1),i=1,2,6;j=1,2,6(5)

Bij=12∑k=1n[Qij¯]k(hk2−hk−12),i=1,2,6;j=1,2,6(6)

Dij=13∑k=1n[Qij¯]k(hk3−hk−13),i=1,2,6;j=1,2,6(7)

where, hk is the distance of the top surface of the ply from the mid-plane of the laminate; Aij, Bij, and Dij are the extensional, coupling, and bending stiffness matrices, respectively. Qij¯ is the transformed reduced-stiffness matrix to consider the orientations of the plies. This matrix will consider the effect of orientations of the fiber from their material properties to the effective properties of the laminate. As the composites are under a bending load due to this impact of this study, the bending effective properties were calculated as follows:

Exc=12Mxκxh3=12h3D11∗(8)

Eyc=12h3D22∗(9)

Gxyc=12h3D66∗(10)

ϑxyc=−D12∗D11∗(11)

ϑyxc=−D12∗D22∗(12)

where, κx, κy, and κxy are mid-plane curvatures; [A∗], [B∗], and [D∗] matrices are the extensional compliance matrix, coupling compliance matrix, and bending compliance matrix, respectively. These compliance matrices are obtained by inverting the stiffness matrices [A], [B], and [D]. Fig. 2a–e shows the plot of effective material properties of the composite samples under bending, i.e., Young’s modulus in the x−direction (Exc), Young’s modulus in the y−direction (Eyc), shear modulus in the xy−plane (Gxyc), Poisson’s ratio in the xy direction (ϑxyc), and Poisson’s ratio in the yx direction (ϑyxc).

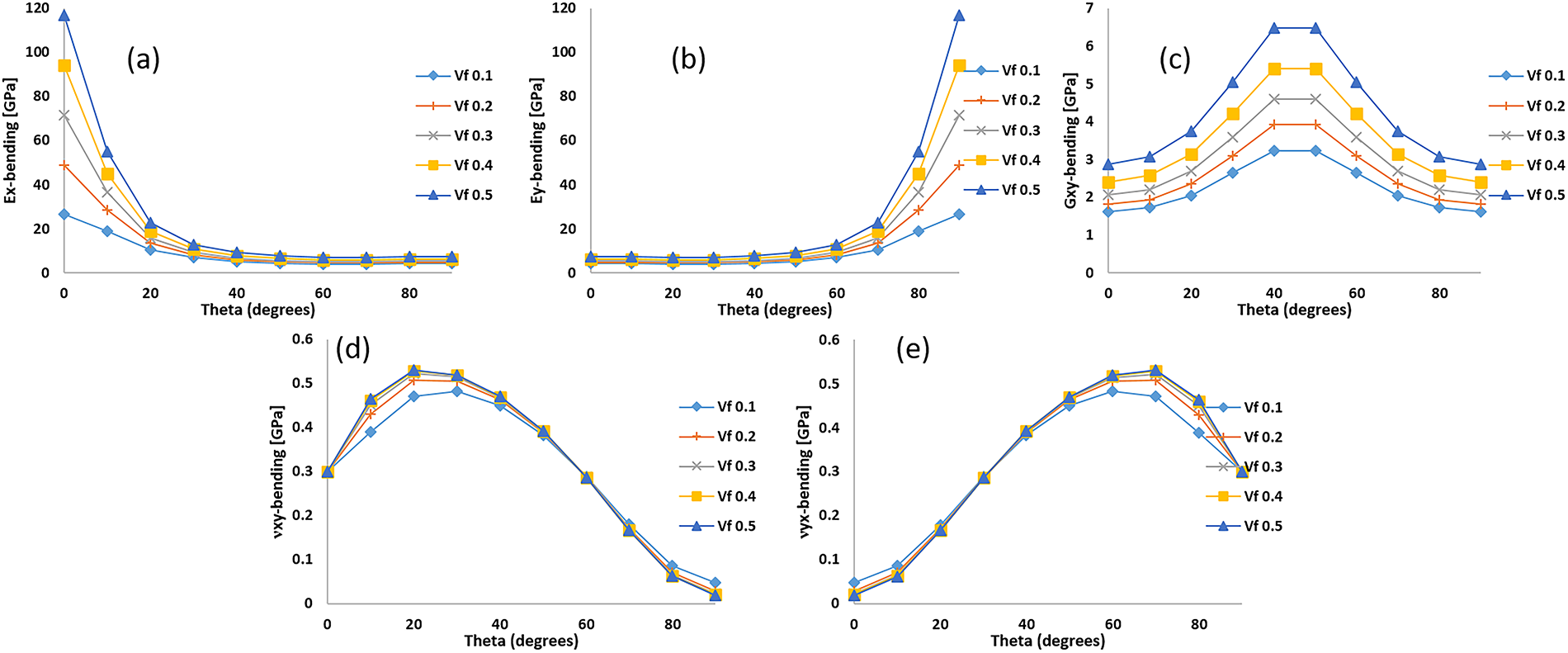
Figure 2: Prediction of elastic properties of carbon fiber-reinforced composites

Assuming the fiber failure strain is less than that of the matrix, the composite’s ultimate failure strain under shear loading was calculated as follows:

εfult=σfultEf(13)

σcult=σfult∗Vf+εfult∗Em∗(1−Vf)(14)

τcult=0.577∗σcult(15)

Maximum displacements, as found using Eq. (3) from these effective properties, cause ultimate stresses that are way above the ultimate strength of the composites for all orientations and weight fractions. This ensures that the composites are failing at this impact loading. Therefore, micro-mechanics is adopted to investigate the fracture properties at the fiber-level after the failure occurs, having the following assumptions [37]:

a) The fibers are extended from one end to the other.

b) Flexural stiffness of a single fiber is negligible.

c) The load is applied to the free edges/surfaces.

d) Linear, elastic, isotropic material properties are used for the constituents.

e) Fibers are uniformly distributed throughout the matrix and rigidly bonded to it.

f) The stress transfer between fibers and matrix depends on their displacements.

Fig. 3a demonstrates how the impactor is transmitting load to the fiber after breaking the first fiber using a shear mechanism. Fig. 3b was adopted to observe the stress transmission across the length of the fiber [37]. Fiber-matrix interactions primarily occur through shear stresses. The effect of a coupling agent, interfacial compatibility, and surface energies from an experimental perspective is broadly modeled as the shear stresses transmitted to the fiber. The corresponding work done from the numerical perspective is described as follows using Eqs. (16)–(33):

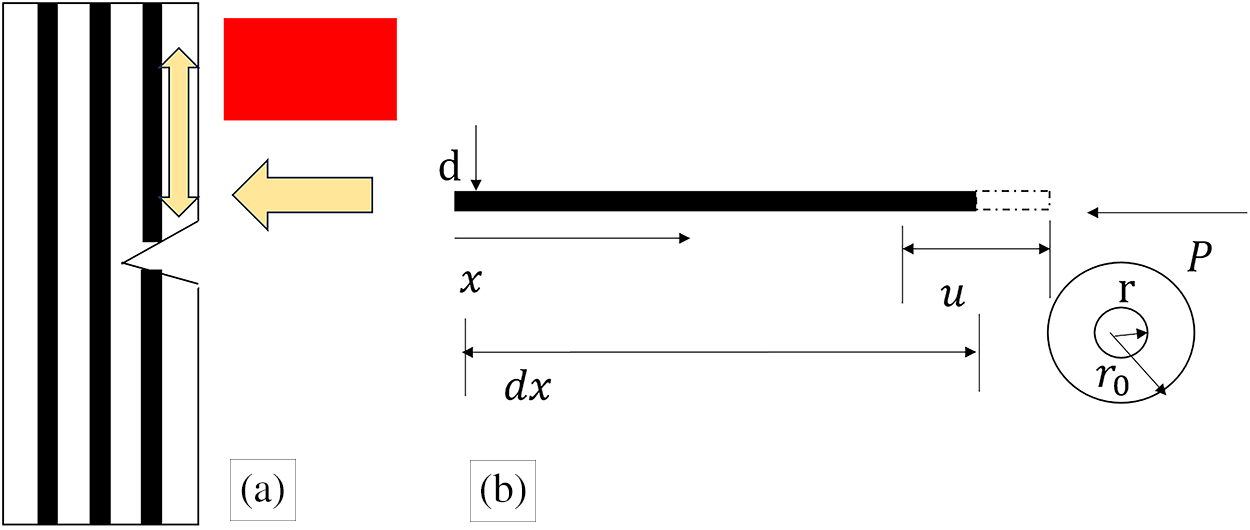
Figure 3: (a) transferring external load to the fibers and (b) longitudinal and shear stresses acting on the fiber

If τ is the shear stress transmitted to the fiber, the force transmitted is πdτu, where d is the diameter of the fiber, and u is the deformation in the longitudinal direction. Therefore, the work done (U1) due to this shear stress up to any distance (x0) along the length from one end is formulated as:

U1=∫0x0πdτudx(16)

In addition, if a longitudinal force (P) is applied at one end, the work done (U2) for a certain strain created on the fiber (εf) is expressed:

U2=12∫0x0Pεfdx(17)

Axial force transfer (dP) acting on a smaller element of length dx due to the shear stress (dτ) can be equated as:

dPdx=−πdτ(18)

Eq. (18) can be written as follows:

dεfdx=−4τdEf(19)

To find the distance where the fiber will fail, the boundary conditions are used as at x=0,εf=σultEf=−πdτ, which leads to the expression of x0 as follows:

x0=dσult4τ(20)

Therefore, the failure strain of the fiber can be calculated as:

εf=4τdEf(x0−x)(21)

The deformation of the fiber at failure is found as:

u=∫x0xεfdx(22)

Total Work done (U) can be calculated by summing both work done from Eqs. (16) and (17):

U=U1+U2=πd3σult348τEf(23)

However, the shear stress transferred (τ) has to be found yet. Eq. (18) could be used to derive the shear stress; however, the axial load transfer (P) is unknown due to the impact loading. To derive an expression for P, it is assumed that the axial load carried by the fiber per unit length on a smaller element (dPdx) is proportional to the difference between the deformation of the composites (u) and the deformation of the pure matrix (v), i.e., without the presence of the fiber. Assuming the proportionality constant as H, dPdx is written as:

dPdx=H(u−v)(24)

In addition, using Hook’s law, P can be written as:

P=EA(dudx)(25)

dudx=PEA(26)

Assuming the matrix as a linear material, the strain developed in the matrix is:

dvdx=ε=const(27)

Differentiating Eq. (24) and plugging values of (26) and (27), we obtain:

d2Pdx2=H(PEA−ε)(28)

Assumed solution of P of this Eq. (28) is:

P=EAε+asinh(βx)+bcosh(βx)(29)

where, a,b are constants to be found from boundary conditions and β=HEA. Using at x=0,andx=l,P=0, meaning no axial force at the free ends:

H=2πGxylog⁡(rr0)(30)

whereas, rr0=1V0 as depicted in Fig. 3b. Therefore, the solution of Eq. (28) with the constants being found is expressed as:

P=EAε[1−cosh⁡β(l2−x)cosh⁡βl2](31)

Therefore, if we return to the formulation of stress transfer dPdx=−πdτ, the shear stress transferred can be expressed by plugging the solution of P as follows:

τ=βr2Efε(Sinhβxcosh⁡βl2)(32)

Maximus shear stress occurs at the middle of the fiber, i.e., at, x=l2, maximum shear stress is written as:

τmax=βr2Efεtanh⁡βl2(33)

At this point, we have derived all the necessary expressions to find out the total work done in Eq. (23). Using Linear Elastic Fracture Mechanics, the fracture toughness can be expressed by the work done as follows:

Kc=2Ec(1−ϑc2)[(1−p)γm+(πd3σult348τEf)](34)

where, p is the volume fraction of the fiber. Fig. 4 shows the fracture toughness predicted for the composites for different orientations and volume fractions. The predicted results agree well with those obtained from experiments, as published in different reports. For instance, stress intensity factor varies at different times during the crack propagations corresponding to different crack lengths [34]. Li et al. reported the stress intensity factor for mode I fracture of graphite/epoxy composites using the digital image correlation method that varies from 0.5 MPa−m1/2 to reach a maximum of 2.5 MPa−m1/2, and then drops below 1.0 MPa−m1/2 at different times for different velocities [34]. These reported values are for longitudinal directions only, whereas the properties will be less at different angles. In addition, the weight percentages are unknown in this report. Whereas, the prediction of stress intensity factors in this study, for carbon fiber-reinforced epoxy composites, varies from 0.26 to 0.56 MPa−m1/2 for different orientations and weight percentages. Cha et al. functionally modified epoxy composites and reported the fracture toughness of carbon nanotubes (CNT)-epoxy composites as 1.5 MPa−m1/2, graphene nanoplatelets (GNP)-epoxy composites as 1.5 MPa−m1/2, melamine functionalized CNT (M-CNT)-epoxy composites as 2.0 MPa−m1/2, and melamine functionalized GNP (M-GNP)-epoxy composites as 2.25 MPa−m1/2 [28]. Fracture toughness of epoxy composites toughened by multi-wall carbon nanotubes varies from 0.5 to 2.0 MPa−m1/2 as reported by Rajsekhar and Gattu [29]. However, these results vary based on orientations, agglomerations, and alignments. Fracture toughness for CNT-reinforced epoxy composites reported by Zenedini et al. varies from 0.82 to 1.79 MPa−m1/2 for different factors such as orientation and agglomeration factors [30]. Critical stress intensity factors for GNP-epoxy composites begins at 0.4 MPa−m1/2, reaches a maximum of around 1.4 MPa−m1/2, then drops down to around 0.2–0.5 MPa−m1/2 for different weight percentages of GNPs [31].

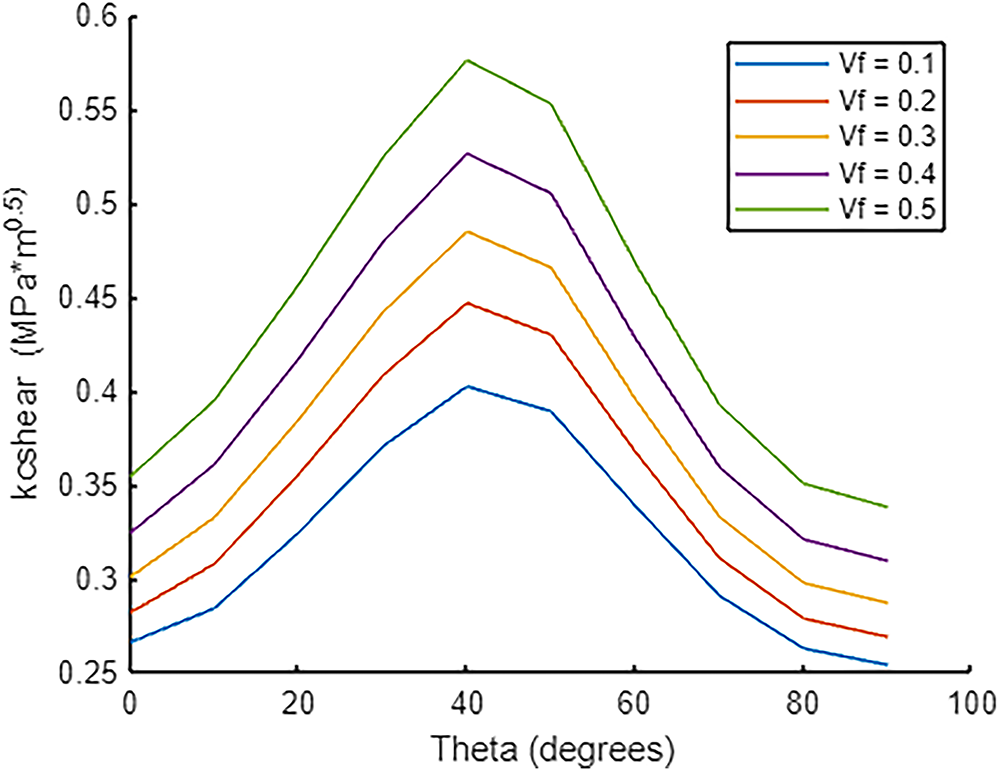
Figure 4: Prediction of fracture toughness of carbon fiber-reinforced composites

3  Finite Element Simulations

To investigate the stress distributions of fiber-reinforced composites at the micro-level, a small-scale model with 5 micron(μ) of diameter of the fiber was created on ANSYS Workbench to conduct finite element analysis (FEA). The fibers were modeled at an actual diameter on the microscale, and thus, it restricted building the composites at experimental dimensions. Therefore, reduced dimensions were used for finite element simulations. The samples had to be reduced in size, because at the normal size, it would be difficult to create many layers, resulting in compensation with the actual fiber diameter. If the FEA models with microscale fibers were built to the experimental size of the samples, a huge number of elements of microscale dimensions would make the computations difficult to converge and solve. High-performance computing (HPC) with customized numerical code may be sought to address this problem. Even with the reduced sizes of the models, a smaller mesh would be difficult to solve; however, the solutions reported in this study reached convergence with generated meshed elements capturing curvature, along with edge sizing. Hence, with this reduced size of the models, up to two fibers were incorporated in longitudinal, i.e., 0∘ orientation; up to four fibers in transverse and angular orientations, i.e., 90∘ and 45∘, respectively. The matrix size was used as 15µ×30µ×90µ. The ratio of these dimensions was comparable to the experimental sample dimensions, which were adopted following the ASTM standard [38]. The composite samples were fixed with two rigid blocks similar to the Izod impact testing, and impacted by another rigid block at the top of the sample. The epoxy resin was modeled as a solid body with an automatic shared topology method. The reinforcing fibers were modeled as line bodies with a circular cross-section assigned using a centroid offset type and edge joints shared topology method. The matrix was considered flexible for stiffness behavior with Lagrangian frame and line bodies for reinforcing agents were considered as beams. The two rigid blocks and the impactor were considered rigid. Structural steel was assigned for the materials properties of the fixture, and an aluminum alloy for the impactor from the workbench default materials library. Young’s moduli for the carbon fibers and epoxy matrix were used as 135 and 35 GPa for the material properties. The contact between reinforcing agents and the matrix body was considered as bonded for reinforcement with a maximum offset of 0.1 μm. No breakable condition was used in this study. The contact between the composites and the rigid blocks was used as bonded with an automatic scoping method and program-controlled for behavior and trim contact with a trim tolerance of 0.38 μm, and a maximum offset of 0.1 μm. Friction was not considered for any contact in these simulations. 2 μm of edge sizing was used for the composite samples, with a default growth rate of 1.5, maximum size of 3.84 μm, curvature control as yes, with a default minimum size of 1.92 μm, and curvature normal of angle (72°). Mesh defeaturing size was selected as default (0.38 μm). No biases were used. Skewness was found to be within a minimum of 0.1 to a maximum of 0.3 with an average of 3.3×10−2 and standard deviation of 9.9×10−2, which demonstrated the mesh quality to be considered as acceptable. Topology checking was used with a default pinch tolerance of 1.73 μm. There were 5692 nodes, 4119 elements that included 4095 Hex8 elements and 24 beam elements in the 0°-model with one fiber. For the convergence study, the edge sizing was set to different values, and the maximum von Mises stresses were recorded until the results converged for the mesh sensitivity. The velocity of the impactor block was defined as a vector. The pendulum/impactor moved at 3.476 m/s velocity directed toward the sample. The striking velocity was calculated based on the initial position and mass of the pendulum of the experimental setup. Explicit time integration was used for the load step type. Characteristic dimensions were used as diagonals. A bending type was used for a beam solution. An artificial viscosity for the shells under a damping control and a geometric strain limit under erosion controls were used. An analysis setting type was selected as program-controlled.

Fig. 5 shows the energy summary plot of a simulation of 0∘-orientation for a one-fiber model. An hourglass energy remained at a constant near-zero value, which indicated the meshing was acceptable. However, the results presented from these simulations may not match any experimental study due to the energy differences, as a very high velocity from the experiment is applied at a micrometer scale. A multiscale modeling approach may be necessary to address this scale discrepancy. The simulation results are useful for investigating the effect of orientation and wt% on the stress transfer mechanism and their relative changes.

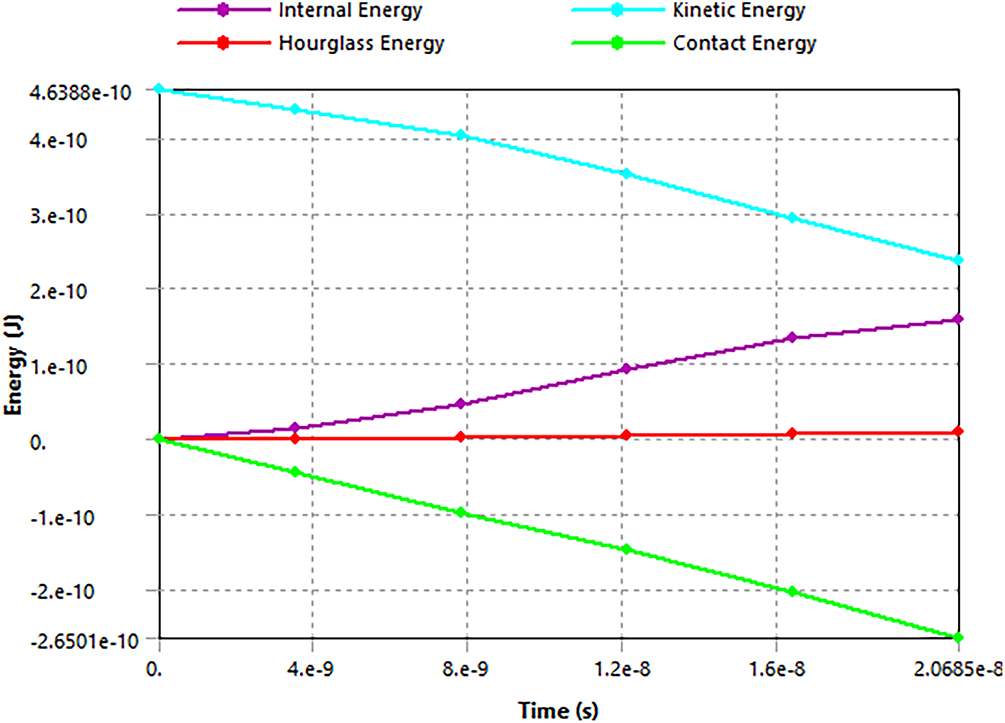
Figure 5: Energy summary of a simulation

Fig. 6a–f shows the Von-Mises stress plots for models with longitudinal one and two fibers, transverse two and four fibers, and angularly oriented two and four fibers, respectively. Stress distributions in the FEA models with longitudinal fibers show that the stress starts developing at the impacting face and propagates through the sample; however, it is interfered with by the presence of the carbon fiber. Cutout view of Fig. 6a shows the parabolic stress peak, where the peak stops at the location of the carbon fiber. However, the depth of the peak is shallower in the two-longitudinal fibers model, as shown in Fig. 6b. Because the stress transmission is interfered with at the first fiber with a shorter travel distance, whereas the second fiber experiences a much lower stress compared to the first one. Different phases of stress contours are obvious, while stress propagates in Fig. 6b. A different scenario happens while the fibers are placed in the transverse direction, as depicted in Figs. 6c,d. As the fibers do not confront stress in the perpendicular directions and stress flows parallel to the fibers, stress starts distributing conically along the length of the sample. Maximum stress occurs near the fibers on the front-impacting face, and then the conical stress distribution is observed as it travels across the depth. In this scenario, the matrix is more likely to fail even without optimizing the full reinforcement from the fibers. Fig. 6d,e shows that the stress travels at an angle for the models with fibers placed in angular directions. The hot spot for maximum stress occurs in the vicinity of the fiber in an interior location. Multiple bands of stress propagation are observed; however, single or multiple hot spots may exist depending on the amount of fibers present. Hot spots in the vicinity of the impacting zones will be intense, and they will diminish for other fibers gradually as stress propagates. Maximum Von Mises stress for a model with a longitudinal one fiber (6.58 wt%) was found to be 1.28×107 Pa, whereas a two longitudinal fibers-composite (13.17 wt%) showed 1.51×107 Pa, which gave a rise to 17.97\% . Two transverse fibers in the composite (4.38 wt%) exhibited a maximum Von Mises stress of 1.18×107 Pa, whereas four fibers in the transverse direction (8.78 wt%) showed 1.05×107 Pa, which was 11\%  less. In the other words, a higher weight percentage of fibers aligned in the transverse direction will not improve the impact resistance when the load is parallel to the fiber direction. Two fibers placed in a 45∘ angular orientation (6.21 wt%) exhibited a maximum Von Mises stress of 1.21×107 Pa, whereas the model with four fibers (12.41 wt%) showed 1.34×107 Pa, which was 10.74\%  higher.

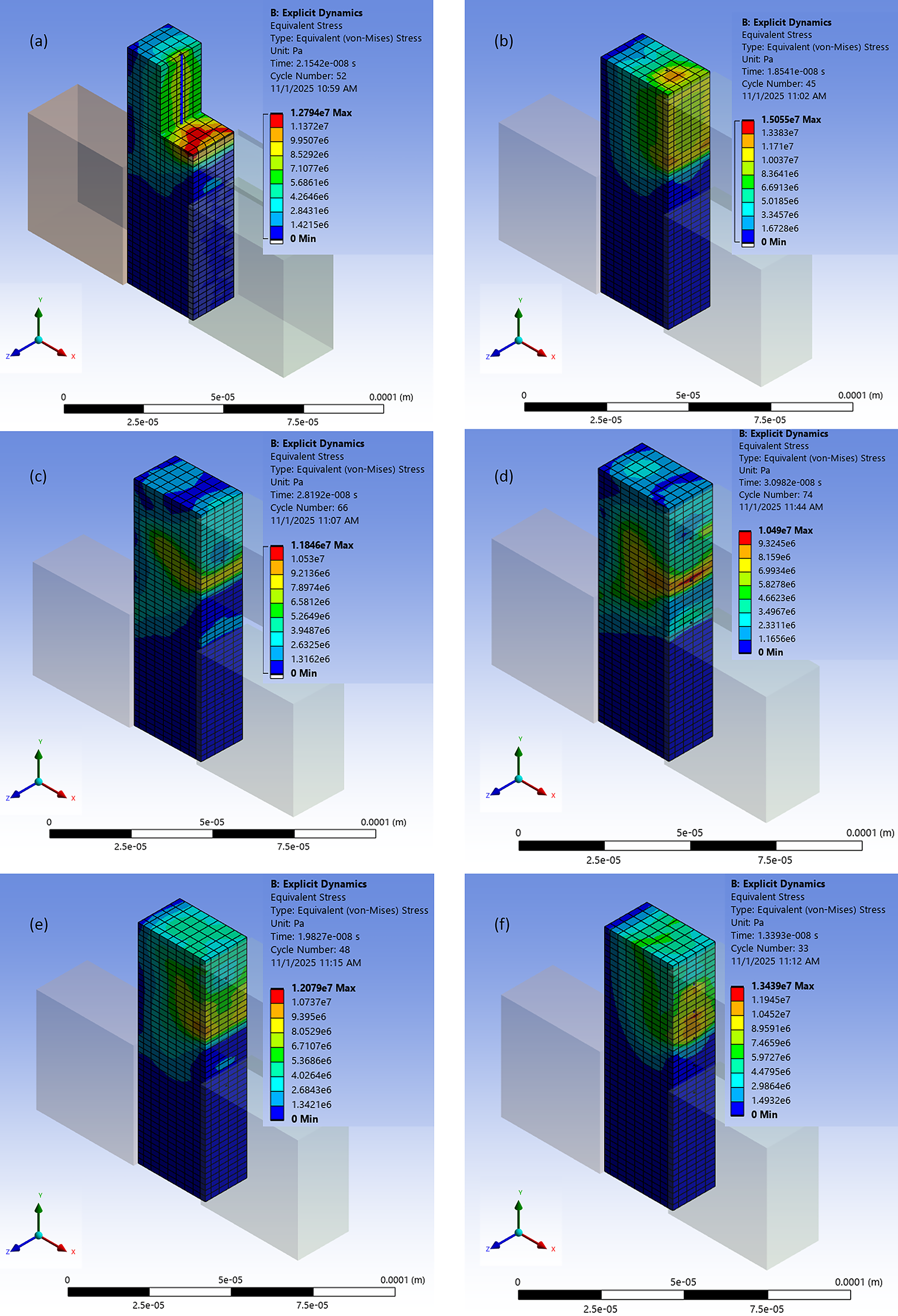
Figure 6: Von-Mises stress profiles of carbon fiber-reinforced epoxy composites against impact loading for (a) one longitudinal fiber, (b) two longitudinal fibers, (c) two transverse fibers, (d) four transverse fibers, (e) two angularly oriented fibers, and (f) four angularly oriented fibers

4  Experimental Characterizations

4.1 Composites Sample Preparation

Unidirectional carbon fibers were purchased from ACP Composites [39]. The fibers were placed in a clear epoxy at three different angular orientations, i.e., 0∘,45∘, and 90∘ to the longitudinal direction of the samples by cutting the fibers at different orientations as shown in Fig. 7a. Unidirectional carbon fibers were cut to the desired dimensions of the samples to be placed in the epoxy matrix. Each of these three orientations was fabricated for five different weight percentages ranging from 10% to 50% of carbon fiber in the epoxy matrix. The weight of a single layer was measured to calculate how many layers of carbon fibers were required to manufacture the samples corresponding to a certain weight percentage. Table 1 shows the number of layers corresponding to the weight percentages. A 3-D printed sample with a prebuilt 45° V-notch at the center as a stress concentration, to facilitate the fracture, was fabricated following the dimensional guidelines of ASTM D256 for Izod Impact testing of plastics [38]. The 3-D printed sample was used to create a mold in an aluminum sheet with a hot glue gun. Different numbers of layers were placed uniformly with a clear epoxy in the mold to prepare samples for varying weight percentages. The inside of an aluminum mold was covered with a grease to prevent the epoxy from sticking to the foil and facilitating easy removal. The epoxy resin and hardener were mixed at a 1:1 ratio, and the specimens reinforced with fibers were allowed 72 h to fully cure at room temperature. After the specimens were fully cured, the aluminum foil was removed. The final dimensions of the specimen were 65 mm long × 11 mm wide × 4 mm thick.

Figure 7: (a) Carbon fiber-reinforced epoxy composites sample preparations and (b) the position of the pendulum just before hitting a sample captured from a recorded video

4.2 Energy Absorption by Izod Testing

A tabletop Izod testing analog apparatus was used to determine the energy absorption of the composite specimens as depicted in Fig. 7b. A pendulum with a striking hammer reached the highest potential energy at an initial position of 150° to the vertical direction. A pendulum, an arm, and a vice were placed in a clear plastic guard for safety purposes while testing, and a hand clutch from outside was used to release the pendulum from an initial position to fracture the sample. After the fracture, the angular positions of the pendulum were read on the dial. The length of the pendulum arm was 0.33 m, and it held a mass of 1.425 kg. Specimens were fitted vertically and received an impact at a height to the middle of the specimen (22 mm in this case) for Izod testing. The specimen’s notch had to face towards the incoming direction of the impacting hammer, while the lower side of the notch was leveled with the vice. The energy absorption was calculated by subtracting the final energy after breaking the samples from the initial energy possessed, using the following equations:

Eabsorbed=Einitial−Efinal=mgL(cosβ−cosα)(35)

where, Einitial is the initial energy, Efinal is the final energy, m is the mass of the pendulum, g is the gravitational acceleration (9.81 m/s2), L is the length of the pendulum arm, α and β are angles with the vertical axes at the initial and final position, respectively. Two free swings were performed to calibrate the equipment and calculate the friction loss of the apparatus. The pendulum was allowed to swing freely with no interference, and the needle was allowed to rotate as the pendulum reaches its destination. Without resetting the needle of the dial, the second free swing was allowed, which rotated the dial to a further final position, even though no samples were fractured. The differences between these two free swings were used to calculate the loss (Wloss) due to friction and hence to calibrate the equipment using a similar concept of Eq. (35), where the angle from the first swing is α1 and the angle from the second is α2. Therefore, the final absorbed energy found using Eq. (35) was corrected for the friction loss as follows:

Eabsorbed_final=Eabsorbed−Wloss(36)

Energy loss due to friction was calculated as 0.157 J. Fig. 8 shows the comparison of the absorbed energy for different weight percentages and at different orientations. At lower weight percentages, the samples of the 0∘ orientation, where layers were deposited along the length of the samples, displayed a superior strength and an impact resistance over all the other orientations; samples at 90∘ showed the lowest, and 45∘ laid-up samples fell in between these two limits. However, 45∘ laid-up samples superseded the strength of 0∘ laid-up samples at higher weight percentages. Because when the crack tried to propagate, the fibers oriented at an angle prohibited its propagation. However, this phenomenon was not shown at a lower loading fraction as the amount of fiber was not sufficient to have a close inter-fiber distance to arrest the crack, and it propagated in alternative directions instead of breaking the adjacent fibers. The trend also showed that more energy was required to break specimens with higher weight percentages of carbon fiber than lower weight percentages for any orientations. The rate of increment of absorbed energy to the weight percentages was the highest for 45∘ orientations. However, the rate declined at a higher weight percentage, e.g., at 30%, where the data were close to those of 0∘ orientation, but still higher. The SEM images provided evidence for such a conclusion, which is discussed in the following section.

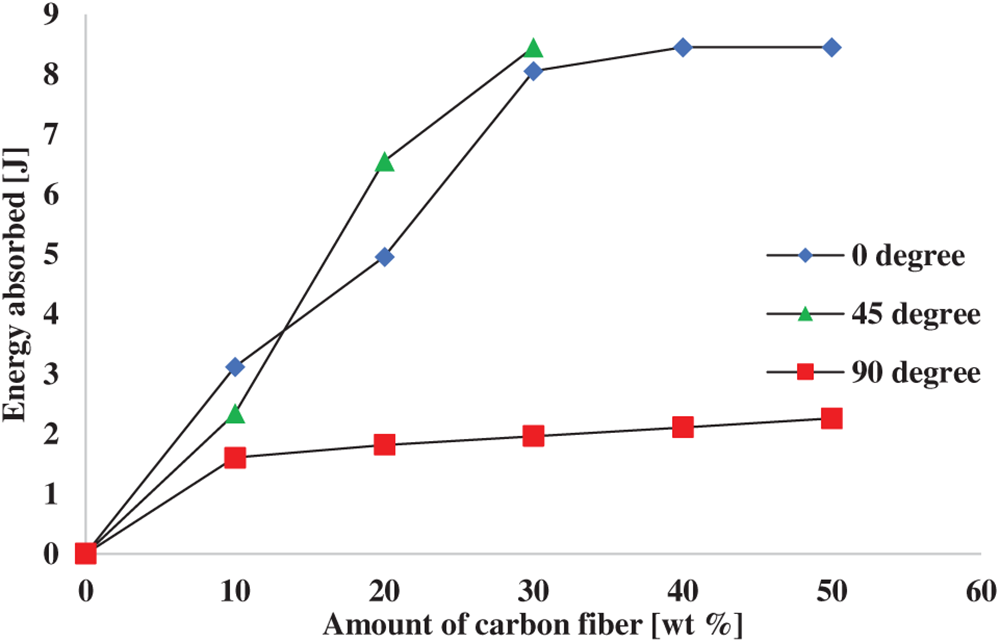
Figure 8: Comparison of energy absorption at different weight percentages of carbon fibers in different orientations

Table 2 displays the energy absorption data. It shows that the energy absorption for the samples with 0∘-orientation increased from 3.12 to 8.45 J for different weight percentages of carbon fibers varying from 10% to 50%. The samples with 45∘-orientations absorbed 2.34 J for 10 wt%, which increased up to 8.49 J for 30 wt% of carbon fiber, surpassing the value for 50 wt% with 0∘ orientation. Energy absorptions for the samples having fibers in the 90∘-orientation exhibited the lowest values, starting from 1.61 J for 10 weight percentages increased up to 2.26 J for 50 weight percentages of carbon fibers.

4.3 Fractography

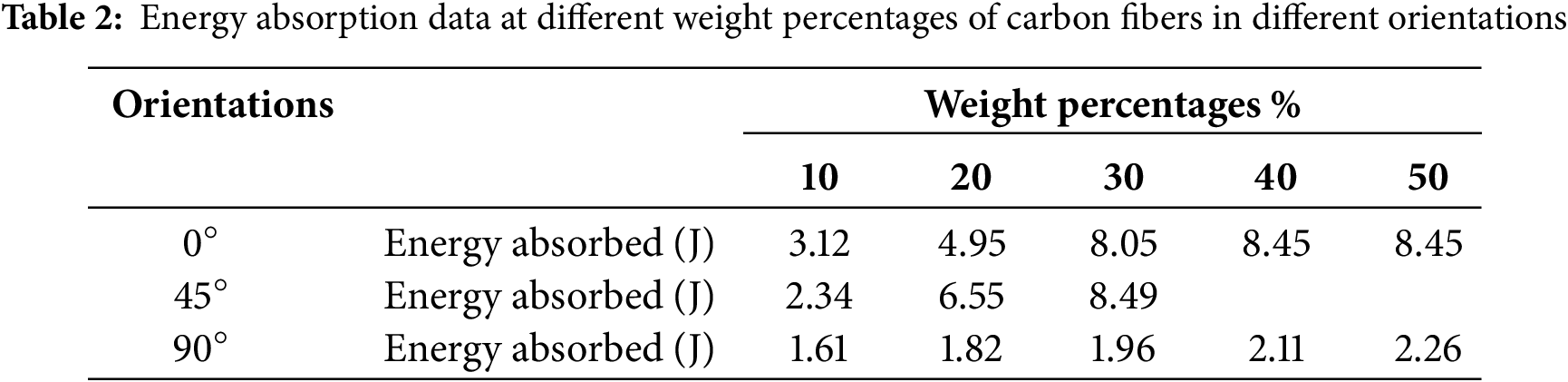
The fractured samples were collected for fractography analysis to investigate the effect of carbon fiber orientations and weight percentages on fracture behavior. Fig. 9 depicts the fractured samples which were gathered to be examined with a scanning electron microscope (SEM). All SEM images were obtained using high voltage (30 kV) at 100× resolution.

Figure 9: Fractured samples at different weight percentages of carbon fiber in different orientations

Fig. 10a–e shows the scanning electron microscope images of the fractured surfaces for 0° orientations at different weight percentages, i.e., 10%–50%, respectively. The fractured fibers were irregular at 10 wt% for a 0° orientation as the relative amount of the fibers was smaller to carry the load. The matrix mainly carried the load and transferred it to the distant fibers, exhibiting a more ductile manner of failure. However, as the weight percentages increased to higher values, the fractured surfaces became more uniform, as shown in Fig. 10b, which exhibited phenomena similar to brittle failures. Even though the samples at 0° orientations showed irregular fiber fracture, this was not capable of inhibiting the crack propagation because of their lower amount, thus there was no interference between propagations. Delamination between larger groups of fibers occurs at higher loading fractions with 0° orientation, as shown in Fig. 10e. Fiber pull-out length for a 0∘ oriented 10 wt% sample was measured as 0.52 mm, as shown in Fig. 10a, whereas no pull-out was observed in the following samples with higher content of carbon fibers. One matrix crack site was observed in a 3.21 mm2 area, which is 0.16 mm deep, meaning 0.05 mm of crack per unit area in 10 wt%. Four crack sites of the same length were observed in a 20 wt\%  sample of the same orientations as shown in Fig. 10b, whereas six crack sites (0.25 mm each) were shown for 30 wt% as shown in Fig. 10c. No delamination had been observed yet, which began at 40 wt%. The delamination was 0.25 mm deep in the 40 wt% sample, whereas it was 0.41 mm in the 50 wt% sample. This identifies the failure modes as primarily fiber pull-out for a lower fraction of fiber, then matrix crack increased with higher content, and finally delamination occurred.

Figure 10: SEM images at 0° orientations for (a) 10 wt%, (b) 20 wt%, (c) 30 w%, (d) 40 wt%, and (e) 50 wt%

Fig. 11 depicts the fractured surfaces at 45° orientations for 10 to 30 wt%. Samples with higher weight percentages for this orientation could not be fractured due to the limitations of the machine’s capabilities. A lower amount, such as 10 wt%, did not possess enough barriers to inhibit the crack, and a group of fibers slid over another group to fail the sample easily. However, as the amount increased, a group of fractured fibers oriented in a different direction compared to other fractured groups, as depicted in Fig. 11b,c. Thus, the crack was hindered from propagating and absorbing more energy before fracture. These observations strongly agree with the experimental results of energy absorptions for angular orientations at higher weight percentages. Crack deflection angles are measured as 18∘,37∘, and 41∘ in the 45∘-oriented samples for 10%,20%, and 30%, respectively.

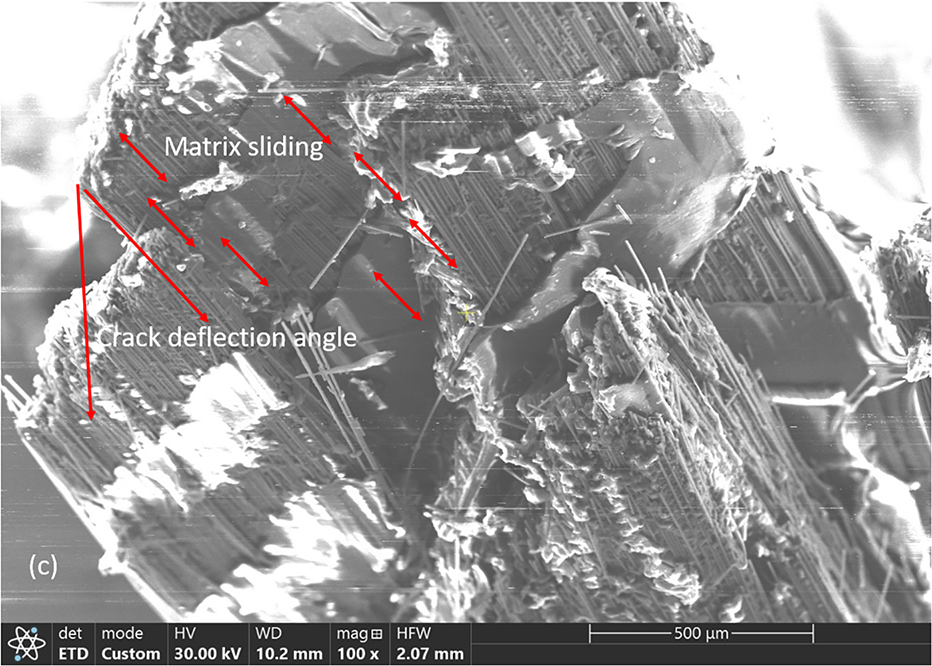
Figure 11: SEM images at 45° orientation for (a) 10 wt%, (b) 20 wt%, and (c) 30 w%

Fig. 12 demonstrates the fractured surfaces at the 90° orientation for 10 to 50 wt%. Fibers were oriented in the parallel direction of the striker to hit, and fibers slid over each other very easily, as shown in Fig. 12, demonstrating lower resistance to fracture at all different loading fractions. This configuration showed the lowest value of absorbed energy, as discussed earlier in this study, compared to other orientations. In addition, the rate of increment for different wt% for this orientation was the lowest, becoming almost flat after 10% and insignificant compared to the two other orientations.

Figure 12: SEM images at 90° orientation for (a) 10 wt%, (b) 20 wt%, (c) 30 w%, (d) 40 wt%, and (e) 50 wt%

5  Discussion

Investigations of fracture and crack propagation with a built-in V-notch carbon fiber-reinforced epoxy composite samples have been conducted in this study to guide a better design of composites against impact failure. This work would be useful in many applications, including but not limited to aerospace components, building materials, automotive parts, composite pipelines, and sports goods. Energy absorption to fracture by an impactor determines its ability to withstand impact and crack propagation. Multiple configurations with varying weight percentages have been investigated to predict their behaviors. Experimental sample preparations, fracturing with an Izod impact tester, observations under a scanning electron microscope, numerical analysis, and finite element simulations suggest consistent findings. Higher loading fractions of the fibers make the composites stronger; however, as CFRCs are anisotropic, stronger composites can be designed by tuning their orientations with lower loading fractions. A threshold loading fraction may exist to activate this phenomenon through the interactions between fibers and matrix. When the fiber’s longitudinal directions are placed perpendicular to the direction of the impact, maximum resistances are observed. When they are placed in a parallel direction, they exhibit the lowest resistance. Any angular orientations should fall between these two limits; however, angular orientations at higher concentrations may supersede the impact resistance compared to others. The fibers at the fracture surface are irregular at lower concentrations when their longitudinal directions are placed perpendicular to the impact directions; however, they fail in a brittle manner at higher concentrations. Fibers cross each other or form layers of fractured fibers for angular orientations, which provides another barrier against crack propagation. When fiber’s longitudinal directions are parallel to the impact directions, they provide less resistance, and no significant differences are found between lower and higher loading fractions. Von-Mises stresses from impact tests in finite element simulations, considering the actual dimensions of the fiber and fracture toughness from numerical analysis, agree well with the experimental observations. Temperature-dependent fracture for fiber-reinforced composites against impact loading can be explored in the future [40]. Cured epoxy resin, as well as carbon fiber, may not show significant viscoelastic/plastic response, as they are brittle in behavior. However, as those areas are wide and demand detailed investigations, those effects will be studied in the future with numerical/experimental methods as well as with molecular dynamics. This paper primarily focuses on numerical and experimental investigations of the fracture behavior of composites. Detailed study on functional modification of the reinforcing fibers, synthesis of the composites with different techniques, and structural characterizations are left for future study. The impact on composites may have different modes and require different types of investigations, depending on the mass of the impactor, the time of impact, the thickness of the laminates, and the orientations of the reinforcing agents. For example, if impact energy is below the delamination threshold, a load deflection or indentation analysis might be helpful [41]. To design based on inter-laminar failure when it is evident from the loading condition, one might need a double-cantilever beam (DCB) or end-loaded split (ELS) test [42]. Out-of-plane impact may be necessary for thinner panels; however, in-plane impact analysis helps investigate crack propagation through composite components. However, separate investigations are required for short and long fibers, which are left for future studies. As we used a tabletop impact testing machine with a lesser capacity, the stronger samples, such as 40 and 50 wt% for 45°-oriented samples, were not broken due to insufficient impact energy. Therefore, the maximum capacity of the testing equipment should be selected based on the samples prepared. However, the predictions are consistent with the numerical estimation, as shown in Fig. 4 and the Finite element simulation as depicted in Fig. 6. Numerical predictions in this study are lower compared to the similar experimental data, as the experiments did not consider the fiber orientation effect. For the fiber-reinforced composites, the angled fibers inhibit crack propagation and enhance toughness, whereas they could still be lower than the functional modification of nanofiller composites. Modified nanofillers will have a stronger bonding with the matrix itself compared to unmodified reinforcements. Fibers are assumed to be uniformly distributed and rigidly bonded in the numerical model to apply linear elastic fracture mechanics for the estimation of fracture toughness. Whereas SEM images show debonding, matrix cracking, delamination, and sliding during fracture, an internal cohesion model or interface friction model may be incorporated in both numerical and finite element analysis to observe the crack propagation behavior in the future.

6  Conclusions

Carbon fiber-reinforced epoxy composites are prepared using a hand layup method. An Izod impact tester has been used to fracture the samples. Energy absorptions for breaking are calculated and plotted for various loading fractions and orientations to compare and analyze. Fractured surfaces are observed with a scanning electron microscope. Finite element simulations are also conducted, considering the actual diameter of the fiber. All of these studies conclude that orientation and loading fractions of carbon fibers open design space to optimize composite properties for light-weight applications, with the following key points:

•   Resistance against impact failure increases as the carbon percentage increases.

•   The rate of increment of fracture resistance to weight percentages is the highest in an angular orientation and lowest in the transverse direction, i.e., 90° orientation.

•   Fracture resistance may not increase after a certain weight percentage of reinforcing elements. Stress is transferred from the matrix to the reinforcing agent through interfacial bonding. There is a threshold for the reinforcement, beyond which a lesser amount of matrix material offers inadequate bonding. In this situation, reinforcing agents become a burden instead of carrying the load for the composites.

•   Non-uniform rupture occurs with 0° samples, i.e., fibers placed in longitudinal directions and with the impact directions perpendicular to them.

•   Uniform rupture with 90° samples showing lower resistance and no significant changes, even with higher loading fractions.

•   Samples with angular orientations produce a crisscrossed layered pattern of the fractured fiber under impact loading that exhibits the mechanism of creation of an additional barrier against crack propagation. The absorbed energy for 45∘ angular orientation at 30 wt% is 8.49 J, which already exceeds the value of 0∘ angular orientation at 30 wt%, which is 8.05 J.

Acknowledgement: The author would like to thank Esteban Garcia1, Rodolfo Garcia, and Alejandro Sosa for preparing composite samples by hand-layup method and conducting the Izod testing, and appreciates Tazrian Ismail for running a MATLAB code for a few of the composite effective properties. The author appreciates Dr. Mesut Yurukcu’s help with the scanning electron microscope and Jim McPherson’s help in slicing the fractured surface for SEM imaging. The author would like to acknowledge the Texas Water and Energy Institute (TWEI) for the use of a scanning electron microscope (SEM).

Funding Statement: This study has been partially supported by the University of Texas (UT) system STARs grant, Semester Undergraduate Research Experience (SURE) program at the College of Engineering at the University of Texas Permian Basin (UTPB), and EM-STEP (Engineering Minority Student Engagement Project) at UTPB College of Engineering, funded by Department of Education.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.

References

1. Egbo MK. A fundamental review on composite materials and some of their applications in biomedical engineering. J King Saud Univ-Eng Sci. 2021;33(8):557–68. doi:10.1016/j.jksues.2020.07.007. [Google Scholar] [CrossRef]

2. Sabet M. Revolutionizing structures: the rise of high-performance composite and nanocomposite polymers. Polym Bull. 2025;82(10):4257–306. doi:10.1007/s00289-025-05720-8. [Google Scholar] [CrossRef]

3. Chung DD. Composite materials: science and applications. Berlin/Heidelberg, Germany: Springer; 2010. doi:10.1007/978-1-84882-831-5. [Google Scholar] [CrossRef]

4. Emayavaramban E, Raj ELP. Finite element analysis of different composite materials using multi continuum method. IOSR J Mech Civ Eng. 2014;11(5):94–9. doi:10.9790/1684-11559499. [Google Scholar] [CrossRef]

5. Guo Q, Yao W, Li W, Gupta N. Constitutive models for the structural analysis of composite materials for the finite element analysis: a review of recent practices. Compos Struct. 2021;260:113267. doi:10.1016/j.compstruct.2020.113267. [Google Scholar] [CrossRef]

6. Latorre M, Montáns FJ. Stress and strain mapping tensors and general work-conjugacy in large strain continuum mechanics. Appl Math Model. 2016;40(5–6):3938–50. doi:10.1016/j.apm.2015.10.045. [Google Scholar] [CrossRef]

7. Zhang L, Jasa J, Gazonas G, Jérusalem A, Negahban M. Extracting continuum-like deformation and stress from molecular dynamics simulations. Comput Meth Appl Mech Eng. 2015;283:1010–31. doi:10.1016/j.cma.2014.10.018. [Google Scholar] [CrossRef]

8. Egner H, Ryś M. Total energy equivalence in constitutive modeling of multidissipative materials. Int J Damage Mech. 2017;26(3):417–46. doi:10.1177/1056789516679496. [Google Scholar] [CrossRef]

9. Nelson E, Gies J, Hansen A, Fertig R. The virtues of multicontinuum mechanics for composites analysis. In: 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference; 2009 May 4–7; Palm Springs, CA, USA. doi:10.2514/6.2009-2477. [Google Scholar] [CrossRef]

10. Key CT, Schumacher SC, Hansen AC. Progressive failure modeling of woven fabric composite materials using multicontinuum theory. Compos Part B Eng. 2007;38(2):247–57. doi:10.1016/j.compositesb.2006.03.006. [Google Scholar] [CrossRef]

11. Mayes JS, Hansen A. Multicontinuum failure analysis of composite structural laminates. Mech Adv Mat Struct. 2001;8(4):249–62. doi:10.1080/107594101753172502. [Google Scholar] [CrossRef]

12. Dutra TA, Ferreira RTL, Resende HB, Blinzler BJ, Asp LE. Mechanism based failure of 3D-printed continuous carbon fiber reinforced thermoplastic composites. Compos Sci Technol. 2021;213:108962. doi:10.1016/j.compscitech.2021.108962. [Google Scholar] [CrossRef]

13. Ojha S, Bisaria H, Mohanty S, Kanny K. Fractographic analysis of fiber-reinforced polymer laminate composites for marine applications: a comprehensive review. Polym Compos. 2024;45(8):6771–87. doi:10.1002/pc.28271. [Google Scholar] [CrossRef]

14. Hernandez DA, Soufen CA, Orlandi MO. Carbon fiber reinforced polymer and epoxy adhesive tensile test failure analysis using scanning electron microscopy. Mat Res. 2017;20(4):951–61. doi:10.1590/1980-5373-mr-2017-0229. [Google Scholar] [CrossRef]

15. Sun Q, Guo H, Zhou G, Meng Z, Chen Z, Kang H, et al. Experimental and computational analysis of failure mechanisms in unidirectional carbon fiber reinforced polymer laminates under longitudinal compression loading. Compos Struct. 2018;203:335–48. doi:10.1016/j.compstruct.2018.06.028. [Google Scholar] [CrossRef]

16. Ren M, Weng F, Sun J, Zhang Z, Ma Z, Li T. Numerical and experimental failure analysis of carbon fiber-reinforced polymer-based pyrotechnic separation device. Int J Aerosp Eng. 2020;2020:2180927. doi:10.1155/2020/2180927. [Google Scholar] [CrossRef]

17. Mortazavian S, Fatemi A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos Part B Eng. 2015;72:116–29. doi:10.1016/j.compositesb.2014.11.041. [Google Scholar] [CrossRef]

18. Monteiro SN, Lopes FPD, Nascimento DCO, da Silva Ferreira A, Satyanarayana KG. Processing and properties of continuous and aligned curaua fibers incorporated polyester composites. J Mater Res Technol. 2013;2(1):2–9. doi:10.1016/j.jmrt.2013.03.006. [Google Scholar] [CrossRef]

19. Cahill LMA, Natarajan S, Bordas SPA, O’Higgins RM, McCarthy CT. An experimental/numerical investigation into the main driving force for crack propagation in uni-directional fibre-reinforced composite laminae. Compos Struct. 2014;107:119–30. doi:10.1016/j.compstruct.2013.05.039. [Google Scholar] [CrossRef]

20. Hwang JH, Lee CS, Hwang W. Effect of crack propagation directions on the interlaminar fracture toughness of carbon/epoxy composite materials. Appl Compos Mater. 2001;8(6):411–33. doi:10.1023/A:1012663722334. [Google Scholar] [CrossRef]

21. Es-Said OS, Foyos J, Noorani R, Mendelson M, Marloth R, Pregger BA. Effect of layer orientation on mechanical properties of rapid prototyped samples. Mater Manuf Process. 2000;15(1):107–22. doi:10.1080/10426910008912976. [Google Scholar] [CrossRef]

22. Roberson DA, Torrado Perez AR, Shemelya CM, Rivera A, MacDonald E, Wicker RB. Comparison of stress concentrator fabrication for 3D printed polymeric izod impact test specimens. Addit Manuf. 2015;7:1–11. doi:10.1016/j.addma.2015.05.002. [Google Scholar] [CrossRef]

23. Carvelli V, Betti A, Fujii T. Fatigue and Izod impact performance of carbon plain weave textile reinforced epoxy modified with cellulose microfibrils and rubber nanoparticles. Compos Part A Appl Sci Manuf. 2016;84:26–35. doi:10.1016/j.compositesa.2016.01.005. [Google Scholar] [CrossRef]

24. Ataabadi PB, Karagiozova D, Alves M. Crushing and energy absorption mechanisms of carbon fiber-epoxy tubes under axial impact. Int J Impact Eng. 2019;131:174–89. doi:10.1016/j.ijimpeng.2019.03.006. [Google Scholar] [CrossRef]

25. Feraboli P, Cleveland T, Ciccu M, Stickler P, DeOto L. Defect and damage analysis of advanced discontinuous carbon/epoxy composite materials. Compos Part A Appl Sci Manuf. 2010;41(7):888–901. doi:10.1016/j.compositesa.2010.03.002. [Google Scholar] [CrossRef]

26. Ryzińska G, David M, Prusty G, Tarasiuk J, Wroński S. Effect of fibre architecture on the specific energy absorption in carbon epoxy composite tubes under progressive crushing. Compos Struct. 2019;227:111292. doi:10.1016/j.compstruct.2019.111292. [Google Scholar] [CrossRef]

27. Li CL, Jiang DZ, Zeng JC, Ju S. The use of cutting carbon fiber fabric/epoxy composites as band-pass frequency selective surfaces. J Compos Mater. 2014;48(18):2281–8. doi:10.1177/0021998313497495. [Google Scholar] [CrossRef]

28. Cha J, Kim J, Ryu S, Hong SH. Comparison to mechanical properties of epoxy nanocomposites reinforced by functionalized carbon nanotubes and graphene nanoplatelets. Compos Part B Eng. 2019;162:283–8. doi:10.1016/j.compositesb.2018.11.011. [Google Scholar] [CrossRef]

29. Rajsekhar V, Gattu M. Fracture and energetic strength scaling of epoxy-resins toughened with multi-walled carbon nanotubes. Eng Fract Mech. 2022;268:108495. doi:10.1016/j.engfracmech.2022.108495. [Google Scholar] [CrossRef]

30. Zeinedini A, Shokrieh MM, Ebrahimi A. The effect of agglomeration on the fracture toughness of CNTs-reinforced nanocomposites. Theor Appl Fract Mech. 2018;94:84–94. doi:10.1016/j.tafmec.2018.01.009. [Google Scholar] [CrossRef]

31. Alexopoulos ND, Paragkamian Z, Poulin P, Kourkoulis SK. Fracture related mechanical properties of low and high graphene reinforcement of epoxy nanocomposites. Compos Sci Technol. 2017;150:194–204. doi:10.1016/j.compscitech.2017.07.030. [Google Scholar] [CrossRef]

32. Fard MY, Liu Y, Chattopadhyay A. Characterization of epoxy resin including strain rate effects using digital image correlation system. J Aerosp Eng. 2012;25(2):308–19. doi:10.1061/(asce)as.1943-5525.0000127. [Google Scholar] [CrossRef]

33. Matveev EV, Mamontov AV, Gajdar AI, Lapshinov BA, Vinogradov AN. Measurement of the strength and microstructural characteristics of epoxy polymers cured by thermal and microwave methods. Meas Tech. 2021;63(12):986–92. doi:10.1007/s11018-021-01882-9. [Google Scholar] [CrossRef]

34. Lee D, Tippur H, Kirugulige M, Bogert P. Experimental study of dynamic crack growth in unidirectional graphite/epoxy composites using digital image correlation method and high-speed photography. J Compos Mater. 2009;43(19):2081–108. doi:10.1177/0021998309342139. [Google Scholar] [CrossRef]

35. Kim JH, Lee J, Wang H, Shin H. Theoretical understanding of fracture toughness improvement in carbon nanotube-coated fiber/epoxy composites: a multiscale study. Eng Fract Mech. 2025;325:111276. doi:10.1016/j.engfracmech.2025.111276. [Google Scholar] [CrossRef]

36. Kaw AK. Mechanics of composite materials. Boca Raton, FL, USA: CRC Press; 1979. [Google Scholar]

37. Cox HL. The elasticity and strength of paper and other fibrous materials. Br J Appl Phys. 1952;3(3):72–9. doi:10.1088/0508-3443/3/3/302. [Google Scholar] [CrossRef]

38. ASTM D. ASTM D 256-10 standard test methods for determining the Izod pendulum impact resistance of plastics. West Conshohocken, PA, USA: American Society for Testing and Materials; 2010. doi:10.1520/D0256-24. [Google Scholar] [CrossRef]

39. ACP Composites, Inc. [cited 2025 Nov 1]. Available from: https://acpcomposites.com/. [Google Scholar]

40. Hastie JC, Guz IA, Kashtalyan M. Response of carbon/PEEK automotive driveshafts with/without an inner isotropic layer at high temperature considering temperature-dependent material properties. Proc Inst Mech Eng Part L J Mater Des Appl. 2023;237(6):1406–15. doi:10.1177/14644207221143342. [Google Scholar] [CrossRef]

41. Davies GAO, Olsson R. Impact on composite structures. Aeronaut J. 2004;108(1089):541–63. doi:10.1017/s0001924000000385. [Google Scholar] [CrossRef]

42. Cintra GG, Vieira JD, Cardoso DCT, Keller T. Mode I and Mode II fracture behavior in pultruded glass fiber-polymer—experimental and numerical investigation. Compos Part B Eng. 2023;266:110988. doi:10.1016/j.compositesb.2023.110988. [Google Scholar] [CrossRef]